Abstract
The natural ventilation of buildings can be achieved effectively with solar chimneys, which are classified into wall, roof, and combined wall–roof configurations. Among the combined systems investigated in the literature, vertical wall–horizontal roof solar chimneys have not been evaluated thoroughly. This study investigates the performance of a combined vertical wall–horizontal roof solar chimney numerically. A two-dimensional Computational Fluid Dynamics (CFD) model is employed to examine the flow and thermal characteristics under various influencing factors relating to the chimney’s geometry, the flow resistance caused by the bend connecting the vertical and horizontal portions, the reverse flow at the outlet, and the location of the heat source. Compared to a vertical wall chimney at the same cavity height, the combined system always had a lower flow rate but had a higher thermal efficiency at some length-to-total-height ratios. Heating the upper walls induced higher flow rates but lower thermal efficiency. Particularly, the effect of the bend on the flow rate was more important than that of the reverse flow at the outlet. These results imply that a combined chimney is preferred over a vertical one for heating applications, wherein the combined chimney should have transparent upper walls.
1. Introduction
Solar chimneys offer numerous options for energy-saving solutions for green buildings. Particularly, they have been proven to be effective in natural ventilation and increasing the energy performance of the building envelope. The flow induced due to the stack effects in a 3.0 m high solar chimney can provide a sufficient ventilation rate for a house of 970 m3 [1]. The air warmed in a chimney cavity used for room heating could save up to 20% of the heating load for an office building in Japan [2]. According to Al Touma and Ouahrani [3], a solar chimney embedded in a window can provide an 11.3% reduction in daily heat gain. Therefore, solar chimneys could help to improve the scores of building ventilation in green building standards, such as LEED or BEAM [4]
The performance of a solar chimney depends significantly on its specific configuration [5]. The typical solar chimney configurations in the literature can be classified into three groups of wall, roof, and combined systems. For the solo wall or roof solar chimneys, the induced flow rate increases with the gap, height, and heat flux [6,7,8,9]. The opening size also significantly influences their performance. In general, the flow rate increases with the opening size until it becomes constant when the opening height is larger than 3.0–6.0 times the air gap of a wall solar chimney [10]. For roof solar chimneys, Al-Kayiem et al. [11] claimed that the highest flow rate was achieved with a horizontal inlet flow direction. Particularly, the optimal inclination angle of a roof solar chimney for maximizing the flow rate is [12] for a constant heat flux, from to at a latitude of 28.4 [13], and at a latitude of [14]
For a combined system, the wall and roof solar chimneys can be separate [15] or connected serially [16,17,18]. In either case, the performance of the combined system is enhanced significantly. Liu et al. [16] investigated a combined wall–inclined roof solar chimney and reported that the flow rate of the combined system was significantly higher than that of isolated wall and roof chimneys. In addition, the combined system also helped to eliminate the problem of overheating in winter, which happened with the solo wall chimney. With similar configurations, AboulNaga and Abdrabboh [17] claimed that a combined wall–inclined roof solar chimney enhanced the flow rate to three times that of a roof chimney. Wei et al. [18] reported that increasing the height of the wall chimney was more effective to boost the flow rate of the entire system. The roof chimney even helped to increase the flow rate in the wall one when they were isolated [15].
In the above combined systems, the wall solar chimney was vertical while the roof one was either vertical [15] or inclined [16,17,18]. The integration of such a system into a horizontal roof faces both aesthetic and structural issues as the vertical or inclined roof is separated from the horizontal roof or requires additional structures for support. Meanwhile, a combined vertical wall–horizontal roof solar chimney is easier to implement into a building with a horizontal roof as the horizontal part of the chimney can be attached to the roof.
A few previous studies have investigated the combined wall–inclined roof solar chimney. The inclination angles of the solo roof solar chimneys in Bassiouny and Kourah [15] and Harris and Helwig [14]’s research were and , respectively. The roof solar chimneys in the combined systems studied by Serageldin et al. [19] and Wei et al. [18] were, respectively and . Particularly, in Nguyen and Wells [6], the air channel of the solar chimney was horizontal, and it had two vertical inlet and outlet ducts to induce the stack effects. However, as the heat source was applied on only the horizontal channel, the effects of the heat source in the vertical inlet section were not considered. Nguyen et al. [20] reported the ventilation performance of two vertical wall solar chimneys connected to a horizontal outlet. Although the heat source was also distributed in the horizontal section, their analysis was only on the vertical parts.
In this study, the performance of a combined vertical wall–horizontal roof solar chimney was investigated, particularly considering the effects of the reverse flow at the outlet, flow resistance at the bend connecting the vertical and horizontal sections, and the location of the heat source, as previous studies have demonstrated the crucial roles of these factors. A reverse flow at the outlet of a vertical solar chimney has been found to lessen the induced flow rate significantly [12,21,22,23,24], but its effects were not reported in Nguyen et al. [20]. Zamora and Kaiser [25] and Nguyen and Wells [6] claimed that the bend resistance was even enhanced when its downstream recirculation zone merged with the reverse flow. Particularly, Nguyen and Wells [7] showed that for a vertical wall solar chimney, the performance was different when the heat source was either on the wall or opposite to the wall.
The remaining part of this paper is structured in three sections. First, the numerical method is described. Second, the results are presented and discussed. Finally, the main findings are summarized.
2. Numerical Method
2.1. Governing Equations
Two-dimensional steady flow and heat transfer in a solar chimney has been modeled successfully in the literature using RANS (Reynolds-Averaged Navier–Stokes) equations based on the conservations of mass, momentum, and energy, as presented in Equations (1)–(3) [8,25,26].
The following techniques were employed for solving Equations (1)–(3):
- Turbulence terms of and were computed with the RNG model, which has been utilized intensively in the literature [8,20,26].
- Boussinesq approximation was adapted for the variation of the air properties with temperature.
- The flow and thermal characteristics of the solar chimney were determined according to the heat transfer from the inner surface to the air inside the cavity. Accordingly, the solar heat gain was modeled with a heat source distributed on one side of the air cavity.
- The governing equations were discretized with the Finite Volume Method facilitated with the commercial CFD software Ansys Fluent (Academic version).
- Radiative heat transfer among the inner surfaces of the cavity was computed with the S2S model available in Ansys Fluent.
Other numerical setups in Ansys Fluent Solver included the following:
- The SIMPLEC method for pressure–velocity coupling.
- The PRESTO! Scheme for the discretization of the pressure term.
- Second-order discretization for all equations.
- A standard wall function for the near-wall treatment. However, as seen in Section 2.2, the employed mesh had several cells inside the laminar viscous sublayer, meaning a wall function was not required [25].
- Details of the above settings can be found in our previous works [6,7,20]
2.2. Computational Domain, Mesh, and Boundary Conditions
Figure 1 depicts the main dimensions of the solar chimney, the computational domain, and the mesh structure. The combined chimney had a vertical section (wall chimney) connected to a horizontal portion (roof chimney). The cavity gap is denoted as and was uniform along the whole chimney. The lengths of the right wall of the wall chimney and of the lower wall of the roof chimney are denoted as and , respectively, and were named the “lower walls”, while the opposite walls, i.e., the left wall of the vertical section and the upper wall of the horizontal portion, were named the “upper walls”. Accordingly, the wall and roof portions of the solar chimney are presented by the cavities of and , respectively. According to Gan [26], the domain must be sufficiently extended beyond the openings of the cavity to obtain a good prediction of the flow field, particularly when there is a reverse flow at the outlet of the air cavity, as seen in Figure 1b. The extensions of the domain from the inlet and outlet are denoted as and , accordingly. The mesh cells were rectangular and became finer near the walls. The finest mesh cells were near the inner surfaces of the cavity.
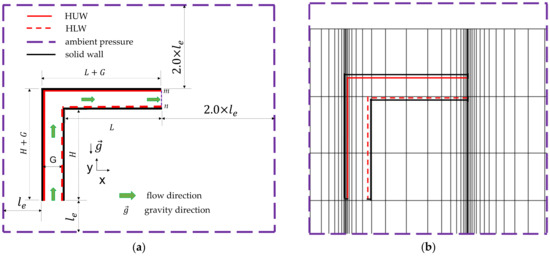
Figure 1.
Sketches of the extended computational domain (a) and the mesh pattern (b).
Boundary conditions were applied to facilitate the natural convective flow in the cavity, as follows:
- Atmospheric pressure and temperature were applied on the domain boundary to allow ambient air to freely enter and leave the domain.
- All solid surfaces were non-slip surfaces.
- A uniform heat flux, I, of was applied on either side of the air cavity in two cases, namely in heating the upper and lower walls, as displayed in Figure 1a to represent two cases of the absorbing surface of the chimney. A chimney with opaque upper walls absorbs solar radiation on the upper walls. Accordingly, the upper walls are heated by solar radiation. The absorbed heat is then transferred to the air in the cavity from the inner surfaces of the upper walls. Therefore, this case is named “heating the upper walls (HUW)”. On the other hand, with transparent upper walls such as glass-plate walls, solar radiation is transmitted through the upper walls, heats the lower surfaces, and then is transferred to the air in the cavity. Consequently, this case is named “heating the lower walls (HLW)”. With the dimensions denoted in Figure 1a, the heating length of the upper and lower surfaces are and , respectively.
- Other solid walls were adiabatic.
From the CFD solutions, the flow rate, Q, induced through the cavity and the temperature rise, , through the cavity were calculated using Equations (4) and (5), respectively, where Q, , and the mean air temperature at the outlet, , were evaluated at the outlet of the cavity. Q represents the ventilation performance, while and relate to the thermal performance of the chimney.
In Equations (4) and (5), is the horizontal (x) velocity component of the cell whose length is and temperature is . Equations (4) and (5) were calculated along the line mn along the gap and at the outlet, as seen in Figure 1a.
The mesh density and the extension were also carefully evaluated. First, an extension = was applied. The mesh density was then increased gradually by increasing the number of cells as well as changing the growth rate of the cell sizes from the solid surfaces. Accordingly, the value also decreased gradually. Figure 2 shows the variations in the flow rate and temperature rise versus for the case of L = H = 0.5 m and G = 0.05 m. Q and were compared to those of the coarse-mesh case, which had a value of 1.375. As seen in Figure 2, Q and converged as decreased. Particularly, the variation in Q and was within 0.5% when became less than 0.35, which had 40 cells in G and 50 cells in L or H. This result agrees with those reported in previous reports [6,25].
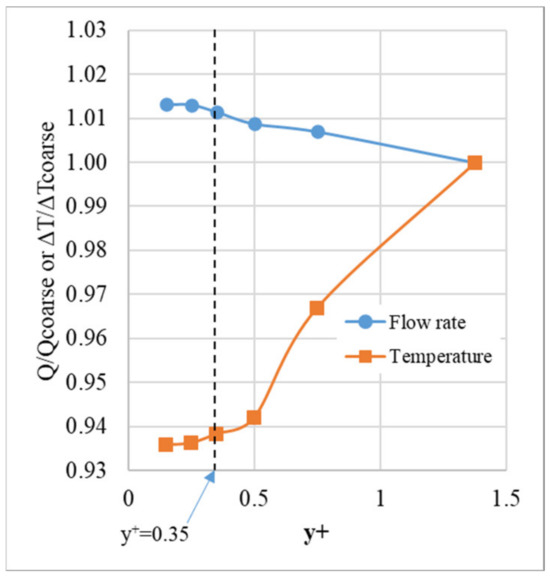
Figure 2.
Variations in the flow rate and temperature rise versus (HLW).
Next, the mesh resulting was kept and different extension lengths of 0.0 G, 5.0 G, and 10.0 G were evaluated. Table 1 presents the flow rate and temperature rise obtained with these three extension lengths and scaled by those of for the two combined chimneys. It is seen that increasing from 0.0 G to 5.0 G changed Q and up to 0.8% (G = 0.05 m) and 1.7% (G = 0.1 m), respectively. However, increasing from 5.0 G to 10.G modified Q and less than 0.2% in both chimneys.

Table 1.
Comparison of the flow rates and air temperatures obtained with different domains. and indicate the results obtained for .
In addition, the length of the reverse flow, , which is the horizontal distance from the outlet to the last streamline of the reverse flow, was also examined. changed from 0.158 m in Figure 3a (no extension) to 0.142 m in Figure 3b (5.0 G extension). However, increasing from 5.0 G to 10.0 G (Figure 3c) resulted in a similar of 0.14 m. Therefore, was selected and employed hereafter.
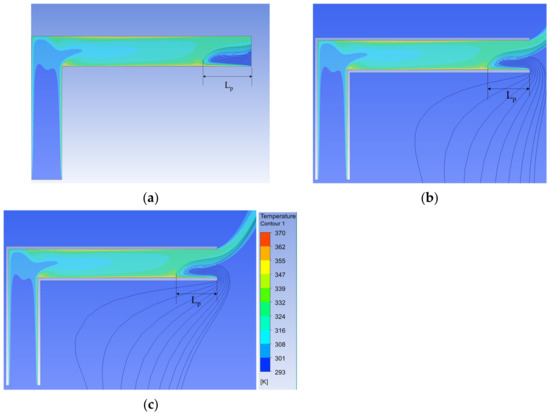
Figure 3.
Temperature fields and streamlines of the reverse flow at the outlet obtained with different domains of (a) no extension, (b) 5 G extension, and (c) 10 G extension.
2.3. Validation
The numerical model was validated against the experiment by Burek and Habeb [27] for the induced flow rate of a vertical solar chimney with H = 1.025 m and G = 0.04 m–0.08 m. A heat source of 400–1000 was applied on one side of the wall surface. Figure 4 plots the flow rates predicted with the present CFD model and measured by Burek and Habeb [27]. As seen, the predicted flow rates match well with the measured ones. The maximum difference between the results is within 8.0%, showing the accuracy of the CFD model.
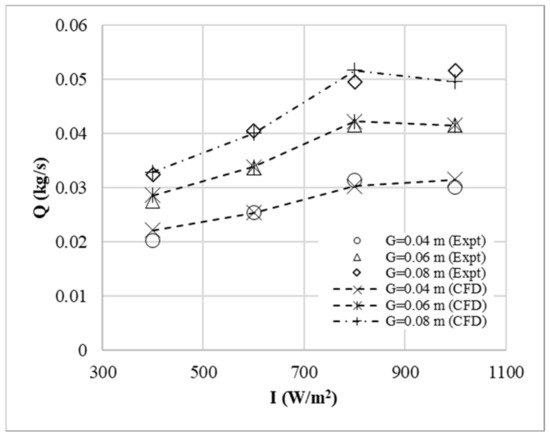
Figure 4.
Comparison of the induced flow rates computed (CFD) with the present CFD model and measured (Expt) by Burek and Habeb [27].
3. Results and Discussion
The flow and heat transfer characteristics of the combined vertical wall–horizontal roof solar chimney were examined under different combinations of L, H, and G, as presented in Table 2. The according Rayleigh number was from to , where the flow was turbulent [12]. The examined parameters consisted of the flow rate, the length of the reverse flow, and thermal efficiency. The performance of the combined solar chimney was also compared to that of a vertical one named the base case in Table 2.

Table 2.
Dimensions of the combined solar chimney.
3.1. Flow and Temperature Fields
The flow and temperature fields obtained with the CFD model are displayed in Figure 5, Figure 6 and Figure 7 to demonstrate the effects of L, H (Figure 5), G (Figure 6), and the heat source’s location (Figure 6 and Figure 7).
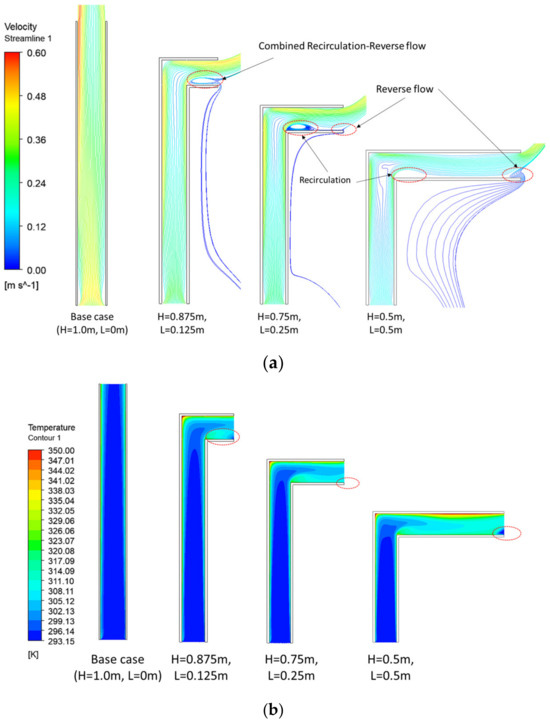
Figure 5.
Streamlines (a) and temperature fields (b) as L and H change ( = 1.0 m, G = 0.1 m, HUW).
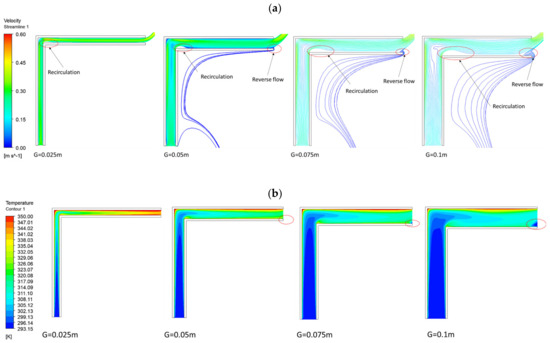
Figure 6.
Streamlines (a) and temperature fields (b) as G changes ( = 1.0 m, L = H = 0.5 m, HUW).
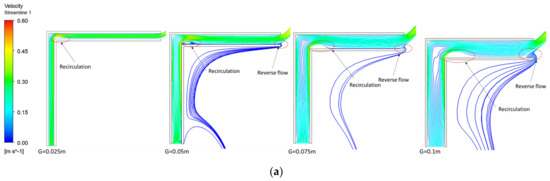
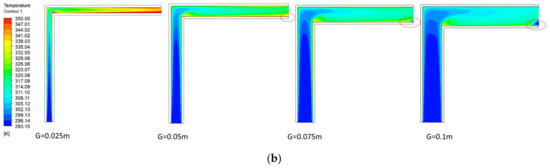
Figure 7.
Streamlines (a) and temperature fields (b) as G changes ( = 1.0 m, L = H = 0.5 m, HLW).
Figure 5 demonstrates different cases of L ( and G = 0.1 m). The velocity and thermal boundary layers are observed on both walls of the channel. Figure 5a shows a decrease in the flow velocity as L increases and H decreases accordingly due to the fixed . In contrast, the temperature on the L portion of the combined chimney is much higher and increases with L. There occurs a recirculation zone downstream of the bend in the combined chimney, which has also been reported in vertical solar chimneys with a horizontal inlet [24,25]. Particularly, a reverse flow appears at all L values in Figure 5a and brings air at an ambient temperature into the air channel near the outlet (Figure 5b, L = 0.5 m). In Figure 5a, the reverse flow is detached from the recirculation at L = 0.25 m and 0.5 m, but they combine at L = 0.125 m. Such a combination was also demonstrated by Zamora and Kaiser [25] at = 0.175.
Figure 6 displays the flow and temperature fields as the gap changes for the case of and L = H = 0.5 m (HUW). Increasing the gap changes the temperature and flow fields as follows:
- The flow velocity and temperature decrease, particularly in the L portion.
- A recirculation occurs at all gaps, but its size enlarges as G increases.
Because of the nature of the HUW scenario, higher air temperatures are seen near the upper walls. In contrast, in Figure 7, in HLW, higher air temperatures are seen near the lower walls. Nevertheless, the flow and temperature fields are visually similar in Figure 6 and Figure 7. Indeed, Figure 8a and Figure 9a reveal that they exhibit similar lengths of flow reversal, but HUW has a slightly higher flow rate.
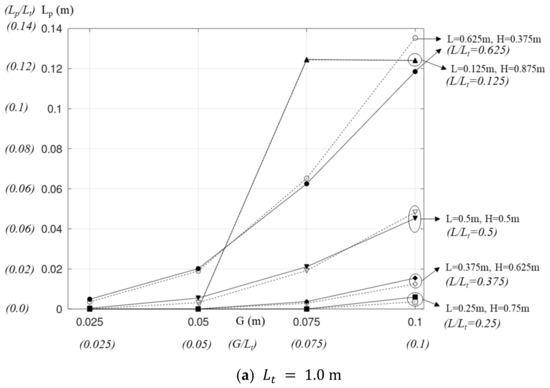
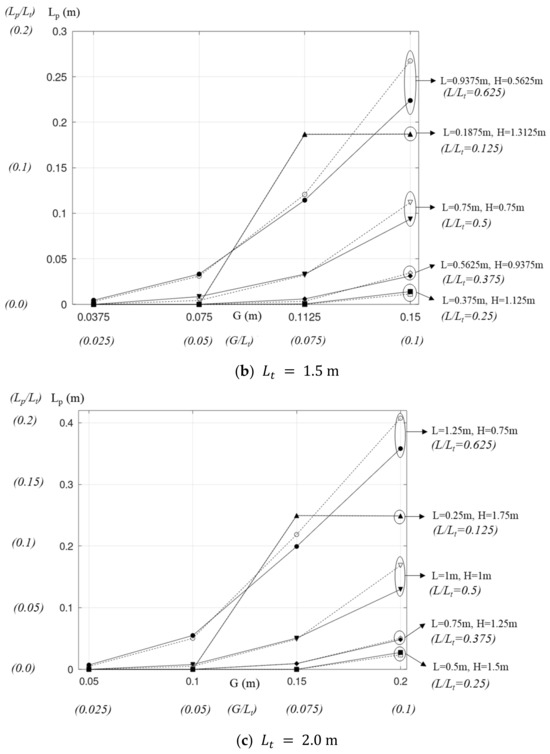
Figure 8.
Lengths of the reverse flow obtained with different chimney lengths, chimney heights, and sizes of the chimney gap (dashed lines: HUW, solid lines: HLW).
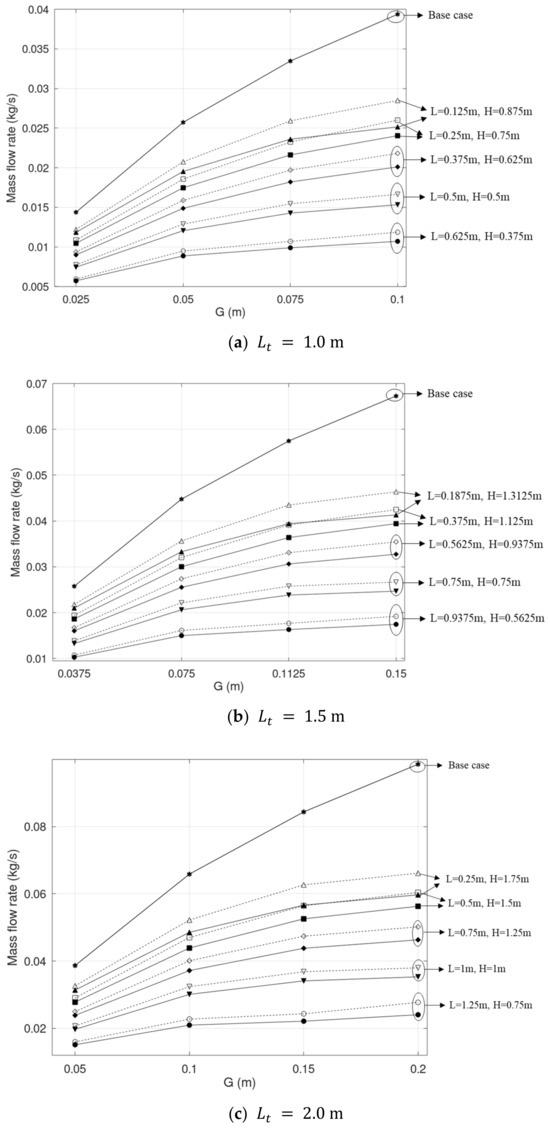
Figure 9.
Induced flow rates obtained with different chimney lengths, chimney heights, and sizes of the chimney gap (dashed lines: HUW, solid lines: HLW).
3.2. Length of the Reverse Flow
Figure 8 displays the lengths of the reverse flow obtained with the combined chimney. The length was also normalized by the total chimney length, i.e., , and is plotted as a function of other non-dimensional parameters and .
A reverse flow was not observed in the base chimney with all heights. This is not surprising, as Bouchair [28] and Chen et al. [12] claimed that a reverse flow appeared when and 0.3, respectively. The highest in the base chimney was only 0.1 and thus was lower than that threshold gap.
The lengths of the reverse flow in the combined chimney are presented in Figure 8. As seen for all values of , is 0 or ignorable at the lowest gap of . Further increases in both G and L show the following trends, which apply to all cases of .
First, the threshold for the occurrence of a reverse flow decreases with L but is similar for all values of , as seen in Table 3. Increasing from 0.25 to 0.5 results in a decrease in the threshold from 0.075 to 0.025. Particularly, for = 0.625, a reverse flow is observed at = 0.025. Accordingly, its threshold gap is expected to be less than 0.025. The threshold gap in Table 3 is much lower than that for a vertical solar chimney, which was higher than 0.25 observed in the experiments by Bouchair [28] and Chet et al. [12]. This difference can be explained by observing the flow fields in Figure 5, Figure 6 and Figure 7. The upward air flow at the outlet of the combined chimney facilitates the reverse flow at the lower portion of the outlet.

Table 3.
Threshold at different values of L and .
Second, increases with G and L while increases with . Such dependence of on G was also reported by Khanal and Lei [22] and Nguyen [29] and was explained as the increased the gap enlarging the volume of less-heated air at the outlet, hence facilitating a reverse flow. For the combined chimney, increasing L is associated with a decrease in H and, accordingly, a reduction in the flow rate due to the lower stack height. Therefore, increasing L enhances the reverse flow. The fact that increases with was also shown by Khanal and Lei [22] and Nguyen [29] for vertical solar chimneys. Khanal and Lei [22] changed the Rayleigh number, which is proportional to (Table 2), from to and obtained an increase in from 0.46 to 0.73. In Figure 8 (HUW, , ), increasing from 1.0 m to 2.0 m is associated with an increase in from 0.135 to 0.204.
3.3. Mass Flow Rate
Figure 9 shows the flow rates obtained with both the base and combined solar chimneys. The flow rate is plotted as a function of G, L, and the heating location.
Figure 9 shows consistent trends of the increase in the flow rate with the gap and height for both the base and combined solar chimneys. In all cases of , the base case always offers the highest flow rate, which increases with both G and . For example, when G increases from 0.025 m to 0.1 m (), the flow rate increases 2.7 times, from 0.0144 to 0.0394 kg/s. Increasing from 1.0 m to 1.5 m (G = 0.075 m) results in an increase in the flow rate by 1.3 times, from 0.0335 to 0.0448 kg/s. In the experiment by Burek and Habeb [27] on a stand-alone vertical solar chimney, the flow rate also increased 3.4 times as the gap increased from 0.02 m to 0.1 m. For a wall-embedded solar chimney, Nguyen and Nguyen [10] reported an increase of 1.35 times as the height increased from 1.0 m to 1.5 m. Increasing the gap and the height results in increases in the effective flow area and the stack height, respectively, hence enhancing the flow rate [5].
Figure 9 reveals that the flow rate of the combined chimney also increases with the gap, similar to the base case. However, the combined case induces a notably lower flow rate. The reduction in the flow rate increases with L. The rate of the increase in the flow rate versus in the combined case is also less than that in the base case. For comparison, Figure 9 is replotted in Figure 10, where the flow rate of the combined case is scaled with that of the base case. The following is seen when applied to both cases of heating:
Figure 10.
Normalized flow rates of the combined chimney: (a) HLW; (b) HUW.
- decreases as increases, showing that the increasing rate of the flow rate versus the gap in the combined case is less than that in the base case.
- depends on but is almost independent of . The differences among the scaled flow rates of the three values of at a value of increases with , but the maximum discrepancy is only 5.0%.
Figure 9 and Figure 10 show that HUW offers higher flow rates, due to the larger heating area of , as discussed in Section 2.2. Table 4 displays a comparison of the flow rates obtained in both cases of heating. With , the heating area of the upper walls is from 5% to 20% times that of the lower one. is from 3.0% to 15% higher than , and this enhancement increases with . Moreover, is similar for all values of at each . The influence of also seems insignificant.

Table 4.
Comparison of the flow rates for both cases of heating, .
For the combined chimney, increasing L results in lower values for both the flow rate and the rate of its increase, as shown in Figure 9 and Figure 10. According to the literature, the three main factors causing this reduction consist of (i) the reduction in the stack height as L increases [18], (ii) the pressure loss associated with the bend, particularly the recirculation downstream of the bend, and (iii) the reverse flow at the outlet, as seen in Figure 5, Figure 6 and Figure 7 [6,21,25]. To estimate the effect of the bend, the data in Figure 8 were replotted as a function of and . Furthermore, they were also fitted with quadratic polynomials, which have good values of , as seen in Figure 11. As , the effects of the stack height reduction and those of the reverse flow vanish; thus, there remains the sole effect of the bend. Applying to the regression equations in Figure 11 offers the corresponding , as seen in Table 5.
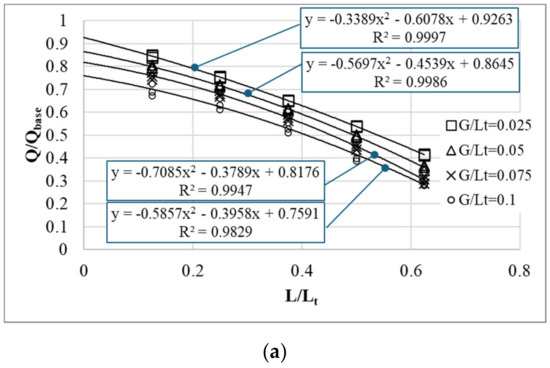
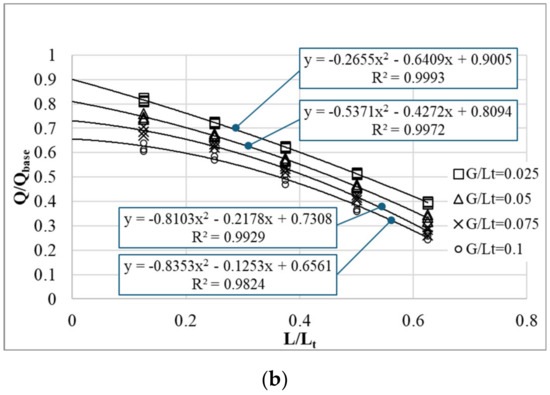
Figure 11.
plotted as a function of and for HUW (a) and HLW (b). In the regression equations, y and x denote and , respectively.

Table 5.
obtained with in the regression equations in Figure 11.
Table 5 shows that as the gap increases, decreases; hence, the bend effect becomes more significant. Its influence is also stronger for HLW. The reduction in the flow rate as increases from 0.025 to 0.1 is from 7.4% to 24%, and from 10% to 35%, for HUW and HLW. Therefore, the bend effect is crucial in a combined solar chimney.
Concerning the two other factors, taking the case of , Figure 8 shows that a reverse flow does not occur or is ignorable. Accordingly, the effect of the reverse flow vanishes, and the further decrease in as increases in Figure 11 is solely due to the stack height reduction. For other cases of , as the trends of the regression curves are similar to that of the case, and these curves are almost shifted down from the curve of the scenario by the according values in Table 3, it is deduced that the effect of the reverse flow is minor compared to the effects of the bend and the stack height reduction. This finding is in contrast with the results of a vertical solar chimney study by Jing et al. [21], who tried to model the effects of the reverse flow in an analytical model for a vertical solar chimney. They showed that taking the reverse flow into account significantly improved the accuracy of their mathematical model and achieved results close to the experimental ones. Zamora and Kaiser [25] and Nguyen and Wells [6] also reported that a combination of the reverse flow and the recirculation downstream of the bend caused an abrupt reduction in the flow rate, which did not happen in this study for the case of , as seen in Figure 5a and Figure 10. A possible explanation for this difference is that in a vertical solar chimney, as reported by Khanal and Lei [22] and Ren et al. [23], the reverse flow almost occupies the whole outlet area except for the thermal layer and yields a higher flow resistance than those seen in Figure 5, Figure 6 and Figure 7.
The fact that the effect of the bend is more significant than that of the reverse-flow resistance in the combined solar chimney is useful for practical applications. In previous studies, to enhance the performance of vertical solar chimneys, the focus has been mainly placed on suppressing the reverse flow. Khanal and Lei [22] employed an inclined wall in the air channel. Nguyen [29], Nguyen et al. [30], and Ren et al. [23] distributed heat sources on both sides of the air channel. These methods effectively eliminated the reverse flow and enhanced the flow rate. For the combined solar chimney in this study, the focus should be on the bend design to reduce the resistance and particularly to eliminate the recirculation zone.
3.4. Thermal Efficiency
The thermal efficiency of a solar chimney is defined using Equation (6), where Q and are obtained from Equations (4) and (5).
Figure 11, Figure 12, Figure 13 and Figure 14 present the thermal efficiency of the combined solar chimney. The data show that the general trends are as follows:
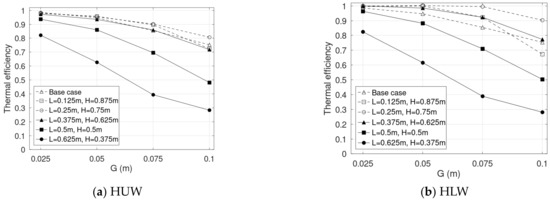
Figure 12.
Thermal efficiency rates of the combined solar chimneys with .
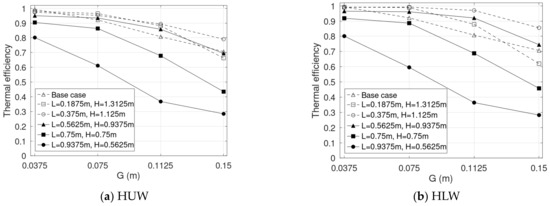
Figure 13.
Thermal efficiency rates of the combined solar chimneys with .
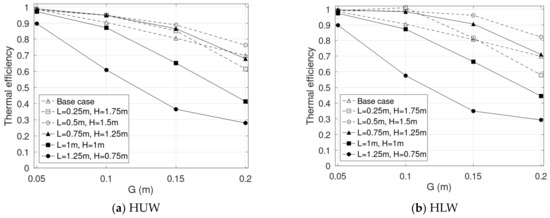
Figure 14.
Thermal efficiency rates of the combined solar chimneys with .
- decreases as the gap increases. This observation applies to both the base and the combined solar chimneys and aligns with the results reported in the literature.
- Increasing results in a decrease in . However, for , the highest is obtained with .
- of the base case is close to that of the case where .
- slightly decreases as increases, as seen for both the base and the combined chimneys.
- HLW shows a higher thermal efficiency than HUW.
Previous studies have shown that thermal efficiency decreases as the gap increases [6,7]. As seen in Equation (6), is proportional to both the flow rate and the temperature rise in the channel, which is again determined by the temperature at the outlet using Equation (5). Although increasing the gap offers higher flow rates (Figure 9), it also results in a higher volume of unheated air, and accordingly lower and values (Figure 5b, Figure 6b and Figure 7b). With the occurrence of a reverse flow, is lessened even further.
Though the general trend is that decreases as L increases, the value of is still lower than that of for . This may be due to the combination of the reverse flow and the recirculation (Figure 5a), resulting in lower air temperatures at the outlet (Figure 5b). Nguyen and Wells [6] also observed a sharp reduction in the thermal efficiency when there appeared to be a combination of a reverse-flow zone and a recirculation zone at the vertical outlet of a horizontal absorber surface solar chimney.
It is interesting to note that of the base case is not the highest and is even lower than that of . This may be due to better air mixing in the combined chimney. Figure 5 shows that the reverse flow of is minor (Figure 5a) and the air temperature at the outlet of the combined chimney (307.9 K) is much higher that of the base case (300.8 K). Though the flow rate of this case of the combined chimney is lower than that of the base case, i.e., 0.026 vs. 0.0384 kg/s, the thermal efficiency calculated with Equation (6) for the combined case is higher, i.e., 0.8 vs. 0.75. This finding may be useful for heating applications employing the combined chimney where the outlet air temperature is more desired. With the same values, between the two design options of either a vertical or a combined chimney, the latter is expected to offer better performance.
The reduction in η as increases has been shown in Ong [31] for a vertical solar chimney of G = 0.145 m. His mathematical model predicted that decreased from 0.27 to 0.22 as H increased from 1.0 m to 4.0 m. In Figure 12, Figure 13 and Figure 14, the maximum reduction in the base and the combined cases is about 7% and 15%, respectively. The higher reduction rate for of the combined case is also possibly due to the larger reverse-flow length as increases (Figure 8).
When comparing HUW and HLW, although HUW induces higher flow rates (Table 2), its thermal efficiency is slightly lower. For example, when taking , G = 0.1 m, and , , while . The main source of this higher may be due to a lower (Figure 8a) and correspondingly higher , i.e., compared to . Accordingly, in practical applications, a combined chimney in an HUW scenario, i.e., opaque upper walls, would be preferred for ventilation applications where a higher flow rate is expected. On the other hand, for heating applications, a combined chimney with the HLW scenario, i.e., transparent upper walls, should be selected due to its higher thermal efficiency.
4. Conclusions
The performance of a combined vertical wall–horizontal roof solar chimney has been numerically examined and compared to that of a base solar chimney, being a vertical one, considering the effects of L, G, , and the heating location, i.e., HUW and HLW. The main findings are summarized as follows.
First, a reverse flow does not occur in the base case but takes place at the outlet of the combined cases when is beyond a threshold gap, which decreases with L but is independent of . The threshold decreases from 0.075 to below 0.025 for = 0.25–0.625. Above the threshold, increases with G and L, while increases with . The difference between HUW and HLW is significant only at and , where HUW has a higher . Particularly, in the case = 0.125, the reverse flow is combined with recirculation, resulting in a higher and a lower thermal efficiency, which does not follow the general trends seen in the other cases.
Second, the flow rates of both the base and combined cases increase with G and . The flow rate of the base case is higher than that of the combined case, which decreases as L increases and also has a lower increasing rate with G. Noticeably, is almost unchanged with . Due to it having a higher heating area of 5–20%, HUW has higher flow rates of 3%–15% compared to HLW. Particularly, the bend effect is crucial as it may contribute to the reduction in the flow rate in the combined chimney of 7.4% to 24%, and of 10% to 35%, for HUW and HLW, respectively. The effects of the reverse flow on the flow rate are found to be minor.
Third, the thermal efficiency decreases as G, L, and increase. The highest is obtained at = 0.25, while of the base case is similar to that of = 0.375. Between the heating cases, HLW shows a higher thermal efficiency. The reverse flow plays a crucial role in the reduction in thermal efficiency.
As the results indicate that the bend significantly affects the induced flow rate of the combined chimney, potential future works may examine this factor in more detail using both numerical simulations and experiments. In addition, cost analyses may be considered alongside technical investigations.
Author Contributions
Conceptualization, Y.Q.N.; methodology, Y.Q.N. and T.N.H.; software, Y.Q.N. and T.N.H.; validation, Y.Q.N. and T.N.H.; data curation, Y.Q.N. and T.N.H.; writing—original draft preparation, Y.Q.N. and T.N.H.; writing—review and editing, Y.Q.N.; visualization, Y.Q.N. and T.N.H. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financially supported by Van Lang University, Vietnam.
Data Availability Statement
All data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| non-dimensional maximal distance of the first cells on the walls,, where is the friction velocity (m/s) and is the distance of the first mesh cell from the wall; | |
| thermal diffusivity of air (); | |
| thermal expansion coefficient of air (1/K); | |
| thermal efficiency; | |
| thermal conductivity (W/m·K); | |
| kinematic viscosity of air (); | |
| density of air (); | |
| turbulent kinetic energy dissipation rate (); | |
| A | heating length (m); |
| CFD | Computational Fluid Dynamics; |
| Expt. | experiment; |
| G | chimney gap (m); |
| g | gravitational acceleration (); |
| H | height of the wall section (m); |
| I | heat flux (); |
| L | length of the roof section or total length or length of the reverse-flow zone (m); |
| p | pressure (Pa); |
| Pr | Prandtl number; |
| Q | mass flow rate (kg/s); |
| Ra | Rayleigh number; |
| T | time-averaged temperature (K); |
| u | velocity (m/s); |
| turbulence kinetic energy (). | |
| Subscripts: | |
| a | ambient; |
| base | base case; |
| e | extension; |
| HLW | heating the lower walls; |
| HUW | heating the upper walls; |
| p | reverse flow; |
| o | outlet; |
| sc | case of no domain extension; |
| t | total. |
| Superscripts: | |
| fluctuating component; | |
| time-averaged. | |
References
- Shi, L.; Ziem, A.; Zhang, G.; Li, J.; Setunge, S. Solar chimney for a real building considering both energy-saving and fire safety—A case study. Energy Build. 2020, 221, 110016. [Google Scholar] [CrossRef]
- Miyazaki, T.; Akisawa, A.; Kashiwagi, T. The effects of solar chimneys on thermal load mitigation of office buildings under the Japanese climate. Renew. Energy 2006, 31, 987–1010. [Google Scholar] [CrossRef]
- Al Touma, A.; Ouahrani, D. Performance assessment of evaporatively-cooled window driven by solar chimney in hot and humid climates. Sol. Energy 2018, 169, 187–195. [Google Scholar] [CrossRef]
- Zhou, Y.; Ni, M. Feasibility study on applications of solar chimney and earth tube systems for BEAM/LEED assessment: Ventilation and energy efficiency. Int. J. Energy Res. 2016, 40, 1207–1220. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, G.; Yang, W.; Huang, D.; Cheng, X.; Setunge, S. Determining the influencing factors on the performance of solar chimney in buildings. Renew. Sustain. Energy Rev. 2018, 88, 223–238. [Google Scholar] [CrossRef]
- Nguyen, Y.Q.; Wells, J.C. A numerical study on induced flowrate and thermal efficiency of a solar chimney with horizontal absorber surface for ventilation of buildings. J. Build. Eng. 2020, 28, 101050. [Google Scholar] [CrossRef]
- Nguyen, Y.Q.; Wells, J.C. Effects of wall proximity on the airflow in a vertical solar chimney for natural ventilation of dwellings. J. Build. Phys. 2020, 44, 174425912090951. [Google Scholar] [CrossRef]
- Zavala-Guillén, I.; Xamán, J.; Hernández-Pérez, I.; Hernández-Lopéz, I.; Gijón-Rivera, M.; Chávez, Y. Numerical study of the optimum width of 2a diurnal double air-channel solar chimney. Energy 2018, 147, 403–417. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, H. Flow and heat transfer characteristics of natural convection in vertical air channels of double-skin solar façades. Appl. Energy 2019, 242, 107–120. [Google Scholar] [CrossRef]
- Nguyen, Y.Q.; Nguyen, V.T. Characterizing the induced flow through the cavity of a wall solar chimney under the effects of the opening heights. J. Build. Phys. 2023, 46, 630–653. [Google Scholar] [CrossRef]
- Al-Kayiem, H.H.; Sreejaya, K.V.; Chikere, A.O. Experimental and numerical analysis of the influence of inlet configuration on the performance of a roof top solar chimney. Energy Build. 2018, 159, 89–98. [Google Scholar] [CrossRef]
- Chen, Z.D.; Bandopadhayay, P.; Halldorsson, J.; Byrjalsen, C.; Heiselberg, P.; Li, Y. An experimental investigation of a solar chimney model with uniform wall heat flux. Build. Environ. 2003, 38, 893–906. [Google Scholar] [CrossRef]
- Bassiouny, R.; Korah, N.S.A. Effect of solar chimney inclination angle on space flow pattern and ventilation rate. Energy Build. 2009, 41, 190–196. [Google Scholar] [CrossRef]
- Harris, D.J.; Helwig, N. Solar chimney and building ventilation. Appl. Energy 2007, 84, 135–146. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, G.; Wu, Q.; Li, W.; Shi, L. A combined wall and roof solar chimney in one building. Energy 2022, 240, 122480. [Google Scholar] [CrossRef]
- Liu, H.; Li, P.; Yu, B.; Zhang, M.; Tan, Q.; Wang, Y.; Zhang, Y. Contrastive Analysis on the Ventilation Performance of a Combined Solar Chimney. Appl. Sci. 2021, 12, 156. [Google Scholar] [CrossRef]
- AboulNaga, M.M.; Abdrabboh, S.N. Improving night ventilation into low-rise buildings in hot-arid climates exploring a combined wall–roof solar chimney. Renew. Energy 2000, 19, 47–54. [Google Scholar] [CrossRef]
- Wei, D. A study of the ventilation performance of a series of connected solar chimneys integrated with building. Renew. Energy 2011, 36, 265–271. [Google Scholar] [CrossRef]
- Serageldin, A.A.; Abdelrahman, A.K.; Ookawara, S. Parametric study and optimization of a solar chimney passive ventilation system coupled with an earth-to-air heat exchanger. Sustain. Energy Technol. Assess. 2018, 30, 263–278. [Google Scholar] [CrossRef]
- Nguyen, Y.Q.; Nguyen, V.T.; Tran, L.T.; Wells, J.C. CFD Analysis of Different Ventilation Strategies for a Room with a Heated Wall. Buildings 2022, 12, 1300. [Google Scholar] [CrossRef]
- Jing, H.; Chen, Z.; Li, A. Experimental study of the prediction of the ventilation flow rate through solar chimney with large gap-to-height ratios. Build. Environ. 2015, 89, 150–159. [Google Scholar] [CrossRef]
- Khanal, R.; Lei, C. Flow reversal effects on buoyancy induced air flow in a solar chimney. Sol. Energy 2012, 86, 9. [Google Scholar] [CrossRef]
- Ren, X.-H.; Liu, R.-Z.; Wang, Y.-H.; Wang, L.; Zhao, F.-Y. Thermal driven natural convective flows inside the solar chimney flush-mounted with discrete heating sources: Reversal and cooperative flow dynamics. Renew. Energy 2019, 138, 354–367. [Google Scholar] [CrossRef]
- Kim, K.M.; Nguyen, D.H.; Shim, G.H.; Jerng, D.-W.; Ahn, H.S. Experimental study of turbulent air natural convection in open-ended vertical parallel plates under asymmetric heating conditions. Int. J. Heat Mass Transf. 2020, 159, 120135. [Google Scholar] [CrossRef]
- Zamora, B.; Kaiser, A.S. Optimum wall-to-wall spacing in solar chimney shaped channels in natural convection by numerical investigation. Appl. Therm. Eng. 2009, 29, 762–769. [Google Scholar] [CrossRef]
- Gan, G. Impact of computational domain on the prediction of buoyancy-driven ventilation cooling. Build. Environ. 2010, 45, 1173–1183. [Google Scholar] [CrossRef]
- Burek, S.A.M.; Habeb, A. Air flow and thermal efficiency characteristics in solar chimneys and Trombe Walls. Energy Build. 2007, 39, 128–135. [Google Scholar] [CrossRef]
- Bouchair, A. Solar chimney for promoting cooling ventilation in southern Algeria. Build. Serv. Eng. Res. Technol. 1994, 15, 81–93. [Google Scholar] [CrossRef]
- Nguyen, Y.Q. Studying convective flow in a vertical solar chimney at low Rayleigh number by Lattice Boltzmann Method: A simple method to suppress the reverse flow at outlet. In Proceedings of the International Conference on Advances in Computational Mechanics 2017, ACOME 2017, Phu Quoc Island, Vietnam, 2–4 August 2017; Nguyen-Xuan, H., Phung-Van, P., Rabczuk, T., Eds.; Lecture Notes in Mechanical Engineering. Springer: Singapore, 2018. [Google Scholar]
- Nguyen, Y.Q.; Nguyen-Tan, S.T.; Pham, H.-T.; Manh-Thuy, A.; Huynh-Nhat, T. Performance of a Solar Chimney for Cooling Building Façades under Different Heat Source Distributions in the Air Channel. Int. J. Adv. Sci. Eng. Inf. Technol. 2021, 11, 158–164. [Google Scholar] [CrossRef]
- Ong, K.S. A mathematical model of a solar chimney. Renew. Energy 2003, 28, 1047–1060. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).