Recent Advances of Self-Healing Materials for Civil Engineering: Models and Simulations
Abstract
1. Introduction
2. Materials and Methods
2.1. Self-Healing Concrete Materials
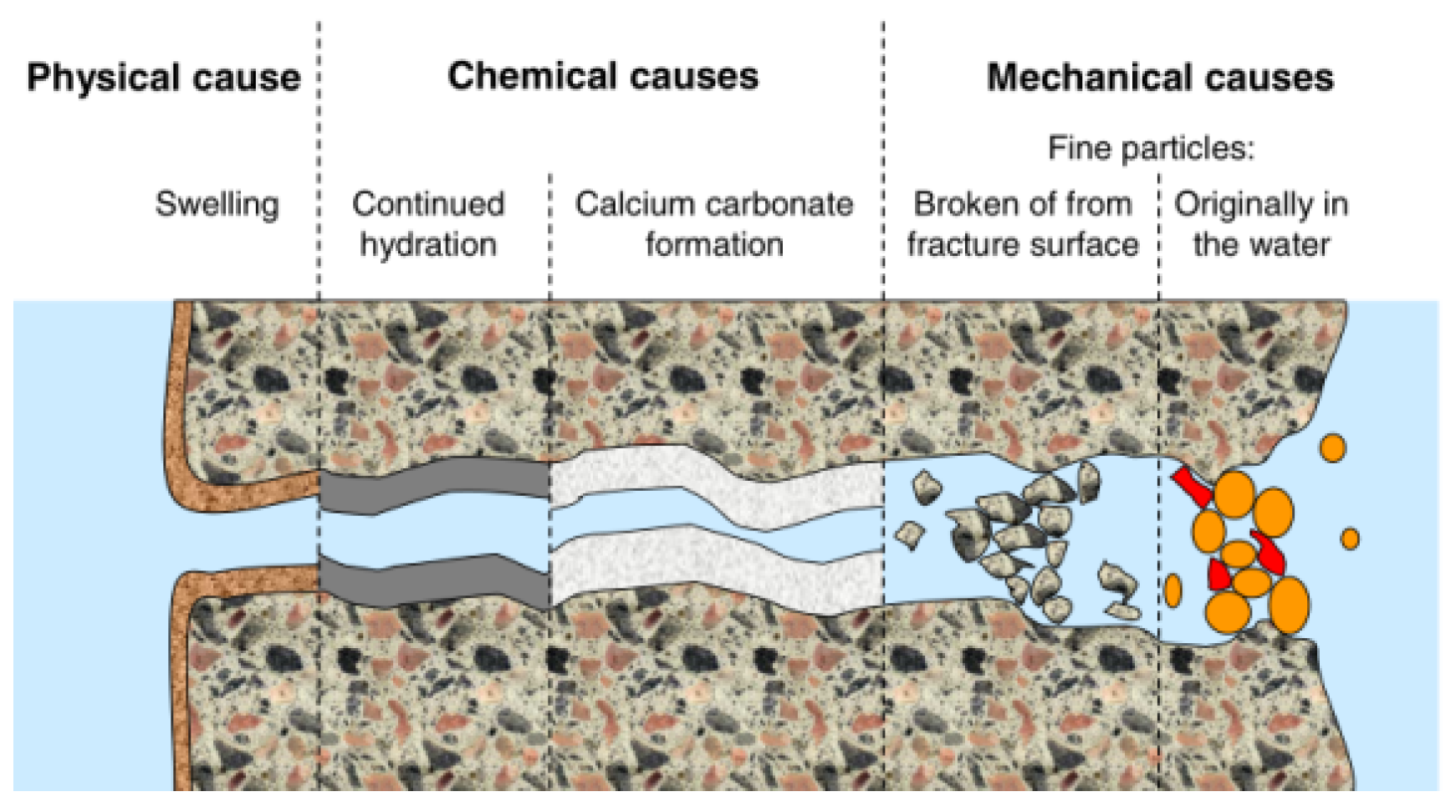
2.1.1. Autogenous Healing
2.1.2. Autonomic Self-Healing
2.2. Self-Healing Polymers
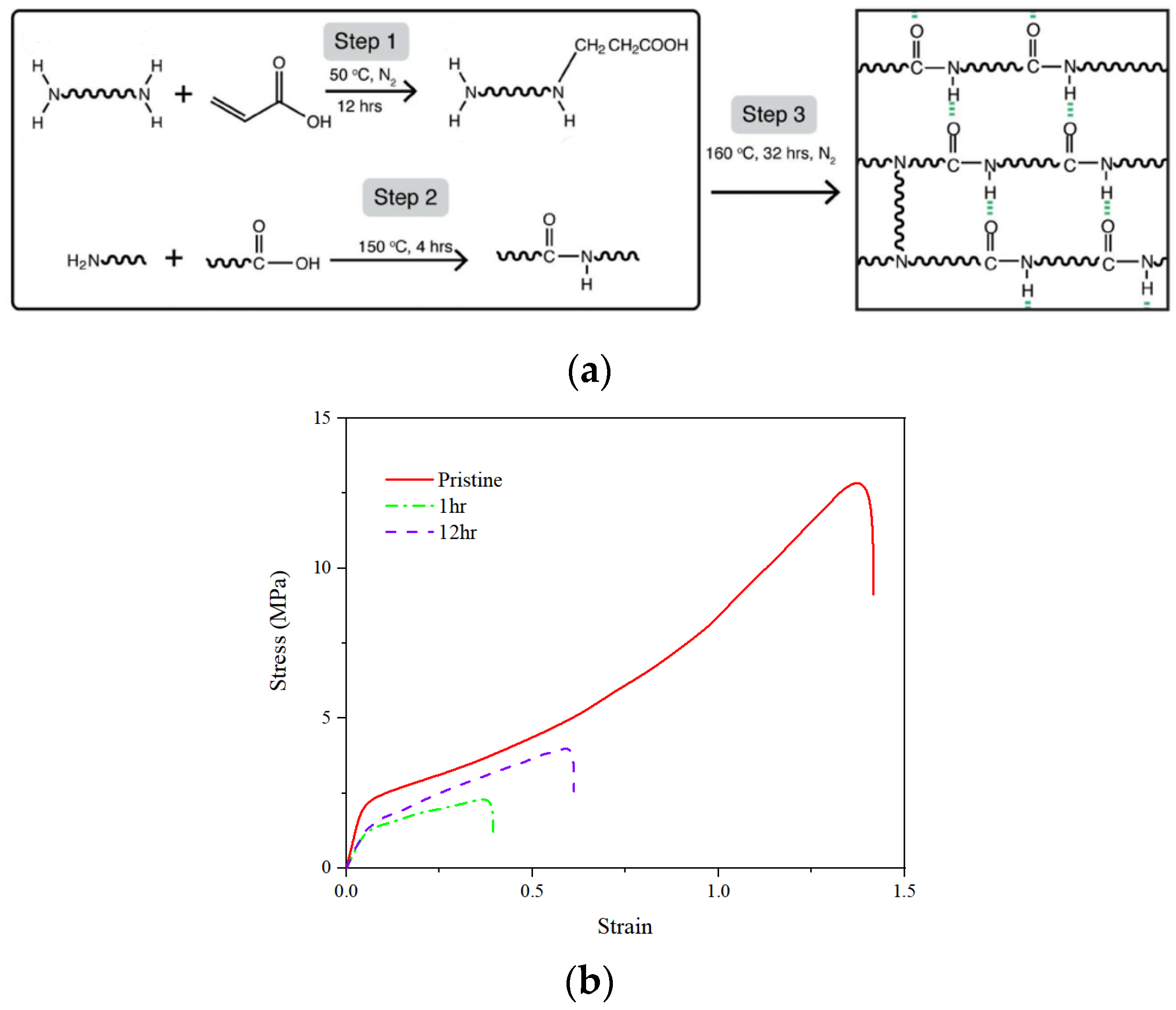
2.2.1. Intrinsic Self-Healing
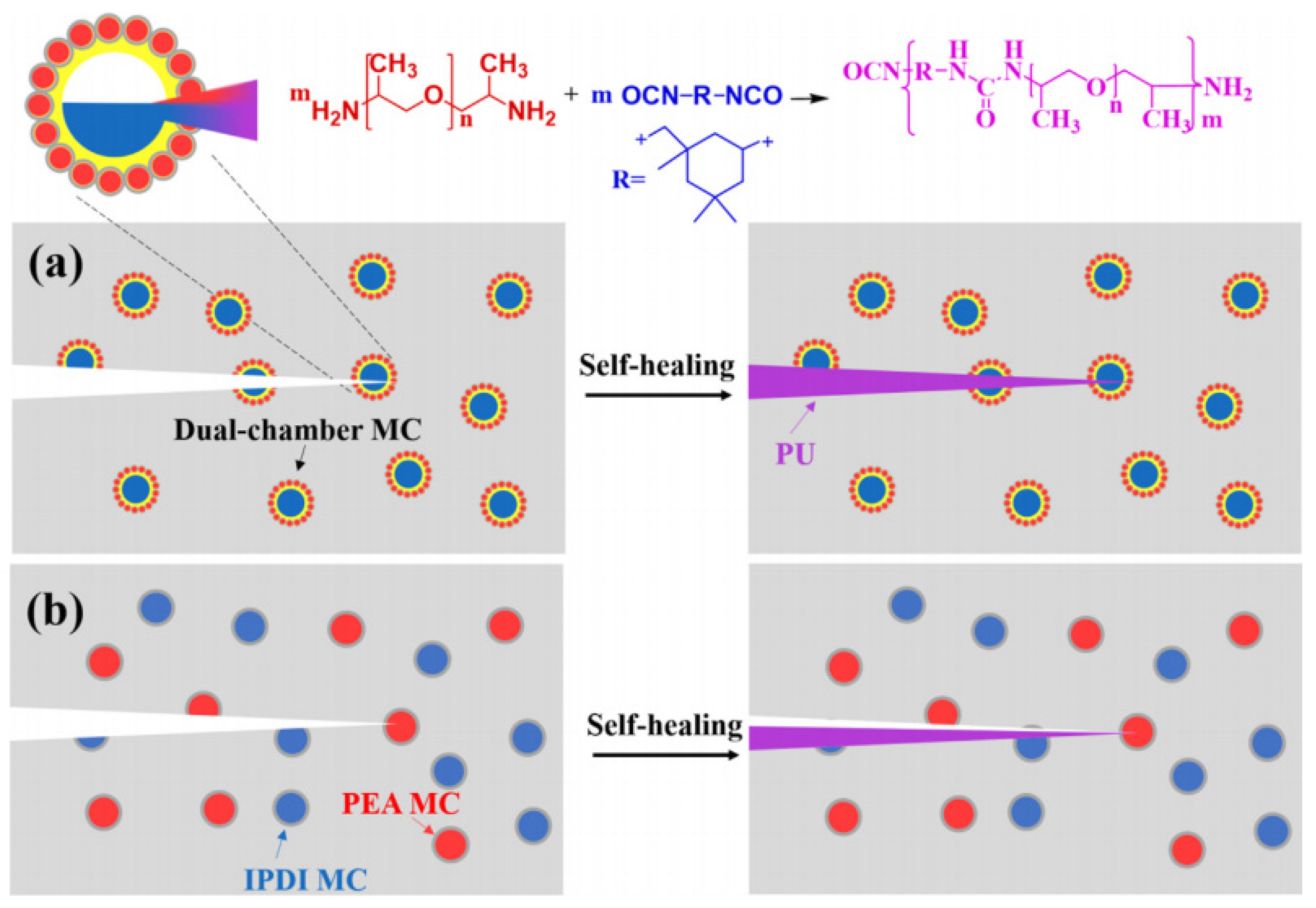
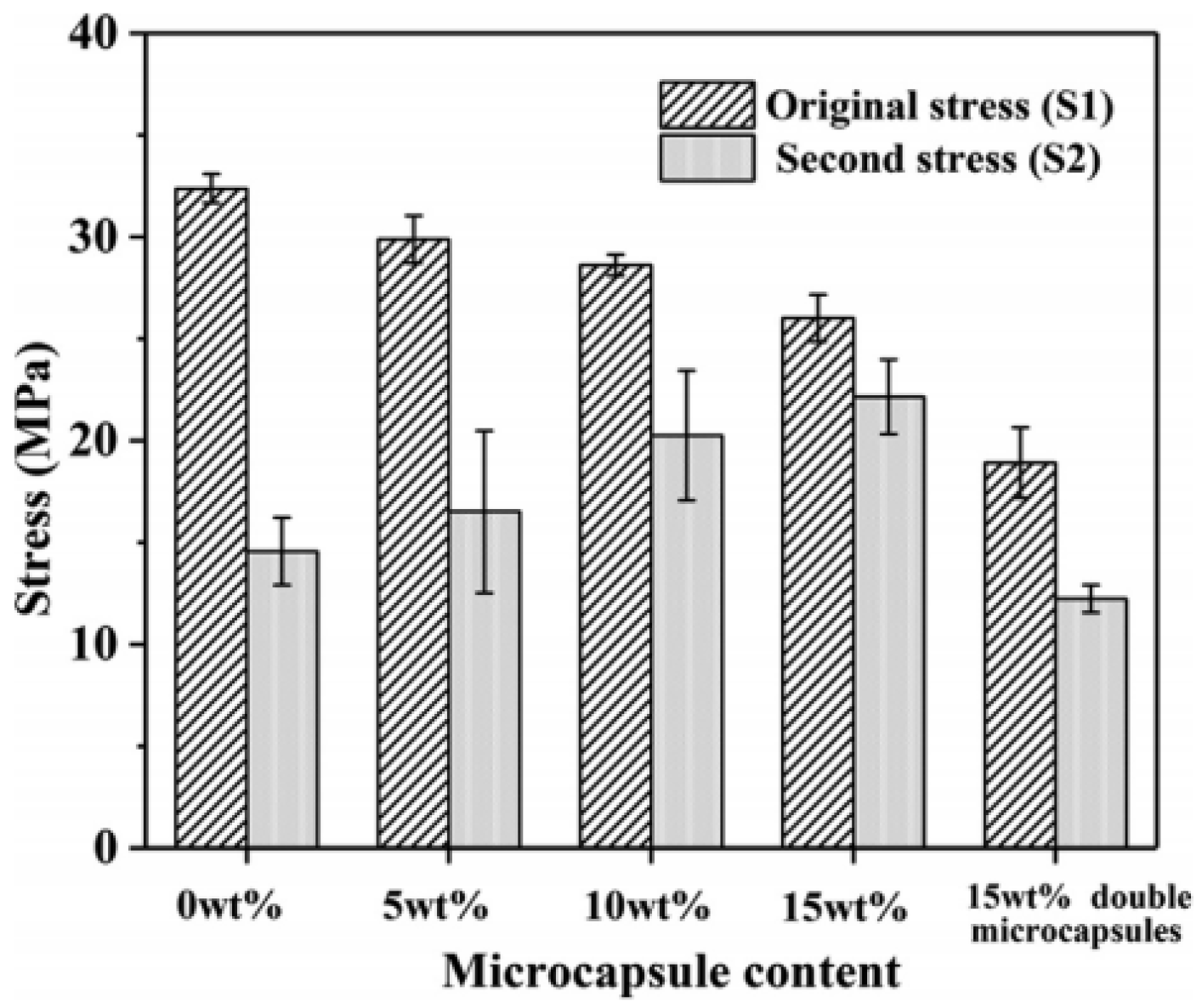
2.2.2. External Self-Healing
2.3. Self-Healing Asphalt
2.3.1. Intrinsic Healing of Asphalt Materials
2.3.2. Induction Heating
2.4. Self-Healing Models
2.4.1. Continuum Damage-Healing Mechanics
2.4.2. The Cohesive Zone Model
2.4.3. Machine Learning
2.5. Computational Simulation
3. Results and Discussion
4. Conclusions
- (1)
- The CDHM, grounded in continuum thermodynamics, encapsulates the transition from damage to healing through internal variables. This model is currently the most extensively applied in the field.
- (2)
- Within certain limits, healing capacity is positively correlated with time and temperature. Although there are specialized models for studying external mechanical loads, experimental research in this area is relatively limited.
- (3)
- Using machine learning to build a predictive model of self-healing performance based on simulations of existing experimental data will be helpful for future research efforts.
- (4)
- Multiscale characterization can help deepen our understanding of repair mechanisms and predict and evaluate the performance of self-healing materials, especially via molecular dynamics simulations.
Funding
Conflicts of Interest
References
- Haines-Gadd, M.; Charnley, F.; Encinas-Oropesa, A. Self-healing materials: A pathway to immortal products or a risk to circular economy systems? J. Clean. Prod. 2021, 315, 128193. [Google Scholar] [CrossRef]
- Hossain, M.R.; Sultana, R.; Patwary, M.M.; Khunga, N.; Sharma, P.; Shaker, S.J. Self-healing concrete for sustainable buildings. A review. Environ. Chem. Lett. 2022, 20, 1265–1273. [Google Scholar] [CrossRef]
- Ayar, P.; Moreno-Navarro, F.; Rubio-Gámez, M.C. The healing capability of asphalt pavements: A state of the art review. J. Clean. Prod. 2016, 113, 28–40. [Google Scholar] [CrossRef]
- Paolillo, S.; Bose, R.K.; Santana, M.H.; Grande, A.M. Intrinsic self-healing epoxies in polymer matrix composites (PMCs) for aerospace applications. Polymers 2021, 13, 201. [Google Scholar] [CrossRef] [PubMed]
- White, S.R.; Sottos, N.R.; Geubelle, P.H.; Moore, J.S.; Kessler, M.R.; Sriram, S.R.; Brown, E.N.; Viswanathan, S. Autonomic healing of polymer composites. Nature 2001, 409, 794–797. [Google Scholar] [CrossRef] [PubMed]
- Qureshi, T.; Al-Tabbaa, A. Self-healing concrete and cementitious materials. Adv. Funct. Mater. 2020, 32, 137–144. [Google Scholar]
- Anupam, B.R.; Sahoo, U.C.; Chandrappa, A.K. A methodological review on self-healing asphalt pavements. Constr. Build. Mater. 2022, 321, 126395. [Google Scholar] [CrossRef]
- Kadam, S.; Chavan, S.; Kanu, N.J. An insight into advance self-healing composites. Mater. Res. Express 2021, 8, 052001. [Google Scholar] [CrossRef]
- Tavangarian, F.; Hui, D.; Li, G. Crack-healing in ceramics. Compos. Part B Eng. 2018, 144, 56–87. [Google Scholar] [CrossRef]
- Sun, D.; Sun, G.; Zhu, X.; Guarin, A.; Li, B.; Dai, Z.; Ling, J. A comprehensive review on self-healing of asphalt materials: Mechanism, model, characterization and enhancement. Adv. Colloid Interface Sci. 2018, 256, 65–93. [Google Scholar] [CrossRef]
- Barbero, E.J.; Greco, F.; Lonetti, P. Continuum damage-healing mechanics with application to self-healing composites. Int. J. Damage Mech. 2005, 14, 51–81. [Google Scholar] [CrossRef]
- Oucif, C.; Voyiadjis, G.Z.; Kattan, P.I.; Rabczuk, T. Investigation of the super healing theory in continuum damage and healing mechanics. Int. J. Damage Mech. 2019, 28, 896–917. [Google Scholar] [CrossRef]
- Smojver, I.; Ivančević, D.; Brezetić, D. Modelling of micro-damage and intrinsic self-healing in unidirectional CFRP composite structures. Compos. Struct. 2022, 286, 115266. [Google Scholar] [CrossRef]
- Pittala, R.K.; Dhanaraju, G.; Ben, B.S.; Ben, B.A. Self-healing of matrix cracking and delamination damage assessment in microcapsules reinforced carbon fibre epoxy composite under flexural loading. Compos. Struct. 2022, 291, 115691. [Google Scholar] [CrossRef]
- Muhammad, N.Z.; Shafaghat, A.; Keyvanfar, A.; Majid, M.Z.A.; Ghoshal, S.K.; Yasouj, S.E.M.; Ganiyu, A.A.; Kouchaksaraei, M.S.; Kamyab, H.; Taheri, M.M. Tests and methods of evaluating the self-healing efficiency of concrete: A review. Constr. Build. Mater. 2016, 112, 1123–1132. [Google Scholar] [CrossRef]
- Demo, P.; Přeučil, F.; Prošek, Z.; Tichá, P.; Domonkos, M. Self-Healing of Cementitious Materials via Bacteria: A Theoretical Study. Crystals 2022, 12, 920. [Google Scholar] [CrossRef]
- Indhumathi, S.; Dinesh, A.; Pichumani, M. Diverse perspectives on self healing ability of Engineered Cement Composite-All-inclusive insight. Constr. Build. Mater. 2022, 323, 126473. [Google Scholar]
- Brasileiro, P.P.F.; Brandão, Y.B.; Sarubbo, L.A.; Benachour, M. Self-healing concrete: Background, development, and market prospects. Biointerface Res. Appl. Chem. 2021, 11, 14709–14725. [Google Scholar]
- Amran, M.; Onaizi, A.M.; Fediuk, R.; Vatin, N.I.; Muhammad Rashid, R.S.; Abdelgader, H.; Ozbakkaloglu, T. Self-healing concrete as a prospective construction material: A review. Materials 2022, 15, 3214. [Google Scholar] [CrossRef]
- Kanellopoulos, A. Self-Healing Cement-Based Materials: Mechanisms and Assessment. In Self-Healing Construction Materials: Fundamentals, Monitoring and Large Scale Applications; Springer: Berlin/Heidelberg, Germany, 2022; pp. 13–41. [Google Scholar]
- Rose, J.; Grasley, Z.; Tang, M.; Wang, F. Accelerated autogenous healing of concrete pipe sections with crack and decalcification damage. J. Mater. Civ. Eng. 2018, 30, 04018308. [Google Scholar] [CrossRef]
- Reinhardt, H.W.; Jonkers, H.; Van Tittelboom, K.; Snoeck, D.; De Belie, K.; De Muynck, W.; Verstraete, W.; Wang, J.; Mechtcherine, V. Recovery against environmental action. In Self-Healing Phenomena in Cement-Based Materials: State-of-the-Art Report of RILEM Technical Committee 221-SHC: Self-Healing Phenomena in Cement-Based Materials; Springer: Berlin/Heidelberg, Germany, 2013; pp. 65–117. [Google Scholar]
- De Belie, N.; Gruyaert, E.; Al-Tabbaa, A.; Antonaci, P.; Baera, C.; Bajare, D.; Darquennes, A.; Davies, R.; Ferrara, L.; Jefferson, T. A review of self-healing concrete for damage management of structures. Adv. Mater. Interfaces 2018, 5, 1800074. [Google Scholar] [CrossRef]
- Giannaros, P.; Kanellopoulos, A.; Al-Tabbaa, A. Sealing of cracks in cement using microencapsulated sodium silicate. Smart Mater. Struct. 2016, 25, 084005. [Google Scholar] [CrossRef]
- Yang, S.; Aldakheel, F.; Caggiano, A.; Wriggers, P.; Koenders, E. A review on cementitious self-healing and the potential of phase-field methods for modeling crack-closing and fracture recovery. Materials 2020, 13, 5265. [Google Scholar] [CrossRef] [PubMed]
- Saillio, M.; Baroghel-Bouny, V.; Pradelle, S.; Bertin, M.; Vincent, J.; de Lacaillerie, J.B.D.E. Effect of supplementary cementitious materials on carbonation of cement pastes. Cem. Concr. Res. 2021, 142, 106358. [Google Scholar] [CrossRef]
- Sherir, M.A.A.; Hossain, K.M.A.; Lachemi, M. The influence of MgO-type expansive agent incorporated in self-healing system of Engineered cementitious Composites. Constr. Build. Mater. 2017, 149, 164–185. [Google Scholar] [CrossRef]
- De Nardi, C.; Cecchi, A.; Ferrara, L.; De Nardi, C.; Benedetti, A. Effect of age and level of damage on the autogenous healing of lime mortars. Compos. Part B Eng. 2017, 124, 144–157. [Google Scholar] [CrossRef]
- Qureshi, T.; Kanellopoulos, A.; Al-Tabbaa, A. Autogenous self-healing of cement with expansive minerals-I: Impact in early age crack healing. Constr. Build. Mater. 2018, 192, 768–784. [Google Scholar] [CrossRef]
- Qureshi, T.; Kanellopoulos, A.; Al-Tabbaa, A. Autogenous self-healing of cement with expansive minerals-II: Impact of age and the role of optimised expansive minerals in healing performance. Constr. Build. Mater. 2019, 194, 266–275. [Google Scholar] [CrossRef]
- Tomczak, K.; Jakubowski, J. The effects of age, cement content, and healing time on the self-healing ability of high-strength concrete. Constr. Build. Mater. 2018, 187, 149–159. [Google Scholar] [CrossRef]
- Huang, H.; Ye, G.; Damidot, D. Effect of blast furnace slag on self-healing of microcracks in cementitious materials. Cem. Concr. Res. 2014, 60, 68–82. [Google Scholar] [CrossRef]
- Yuan, L.; Chen, S.; Wang, S.; Huang, Y.; Yang, Q.; Liu, S.; Wang, J.; Du, P.; Cheng, X.; Zhou, Z. Research on the improvement of concrete autogenous self-healing based on the regulation of cement particle size distribution (PSD). Materials 2019, 12, 2818. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.; Jing, K.; Bai, J.; Ding, Z.; Yang, D.; Huang, H.; Gong, Y. Effects of curing conditions and supplementary cementitious materials on autogenous self-healing of early age cracks in cement mortar. Crystals 2021, 11, 752. [Google Scholar] [CrossRef]
- Suleiman, A.R.; Nehdi, M.L. Effect of autogenous crack self-healing on mechanical strength recovery of cement mortar under various environmental exposure. Sci. Rep. 2021, 11, 7245. [Google Scholar] [CrossRef] [PubMed]
- Ferrara, L.; Krelani, V.; Carsana, M. A “fracture testing” based approach to assess crack healing of concrete with and without crystalline admixtures. Constr. Build. Mater. 2014, 68, 535–551. [Google Scholar] [CrossRef]
- Wang, H.; Habibi, M.; Marzouki, R.; Majdi, A.; Shariati, M.; Denic, N.; Zakić, A.; Khorami, M.; Khadimallah, M.A.; Ebid, A.A.K. Improving the self-healing of cementitious materials with a hydrogel system. Gels 2022, 8, 278. [Google Scholar] [CrossRef] [PubMed]
- Huseien, G.F.; Sam AR, M.; Faridmehr, I.; Baghban, M.H. Performance of epoxy resin polymer as self-healing cementitious materials agent in mortar. Materials 2021, 14, 1255. [Google Scholar] [CrossRef] [PubMed]
- Soltaninejad, S.; Marandi, S.M.; Bp, N. Performance Evaluation of Clay Plastic Concrete of Cement and Epoxy Resin Composite as a Sustainable Construction Material in the Durability Process. Sustainability 2023, 15, 8987. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, X.; Sheng, M.; Qin, D.; Ren, J.; Zhou, X.; Zhu, J.; Xing, F. Dynamic behavior of microcapsule-based self-healing concrete subjected to impact loading. Constr. Build. Mater. 2021, 301, 124322. [Google Scholar] [CrossRef]
- Wang, X.; Liang, J.; Ren, J.; Wang, W.; Liu, J.; Xing, F. Constitutive relations, mechanical behavior, and failure criterion of microcapsule-based self-healing concrete under uniaxial and triaxial compression. J. Build. Eng. 2023, 65, 105773. [Google Scholar] [CrossRef]
- Kanellopoulos, A.; Giannaros, P.; Al-Tabbaa, A. The effect of varying volume fraction of microcapsules on fresh, mechanical and self-healing properties of mortars. Constr. Build. Mater. 2016, 122, 577–593. [Google Scholar] [CrossRef]
- Sun, J.; Shang, W.; Chen, A. Mechanical and Thermal Properties of Phase Change Aerated Concrete with Paraffin Microcapsule. J. Aerosp. Eng. 2023, 36, 04022132. [Google Scholar] [CrossRef]
- Ying, Y.; Hu, M.; Han, J.; Liu, W.; Qi, B.; Guo, J. Self-healing in cementitious system using interface enhanced capsules prepared at room temperature. J. Clean. Prod. 2023, 395, 136465. [Google Scholar] [CrossRef]
- Lin, Z.; Kanwal, H.; Hao, W. Effects of Crack Width and Healing Time on Healing Performance of Microcapsule-Based Self-Healing Concrete. J. Test. Eval. 2022, 50, 2043–2053. [Google Scholar] [CrossRef]
- Wu, M.; Johannesson, B.; Geiker, M. A review: Self-healing in cementitious materials and engineered cementitious composite as a self-healing material. Constr. Build. Mater. 2012, 28, 571–583. [Google Scholar] [CrossRef]
- Van Tittelboom, K.; De Belie, N.; De Muynck, W.; Verstraete, W. Use of bacteria to repair cracks in concrete. Cem. Concr. Res. 2010, 40, 157–166. [Google Scholar] [CrossRef]
- Choi, S.G.; Wang, K.; Wen, Z.; Chu, J. Mortar crack repair using microbial induced calcite precipitation method. Cem. Concr. Compos. 2017, 83, 209–221. [Google Scholar] [CrossRef]
- Tang, Y.; Xu, J. Application of microbial precipitation in self-healing concrete: A review on the protection strategies for bacteria. Constr. Build. Mater. 2021, 306, 124950. [Google Scholar] [CrossRef]
- Gollapudi, U.K.; Knutson, C.L.; Bang, S.S.; Islam, M.R. A new method for controlling leaching through permeable channels. Chemosphere 1995, 30, 695–705. [Google Scholar] [CrossRef]
- Ramachandran, S.K.; Ramakrishnan, V.; Bang, S.S. Remediation of concrete using micro-organisms. ACI Mater. J.-Am. Concr. Inst. 2001, 98, 3–9. [Google Scholar]
- Algaifi, H.A.; Bakar, S.A.; Sam, A.R.M.; Ismail, M.; Abidin, A.R.Z.; Shahir, S.; Altowayti, W.A.H. Insight into the role of microbial calcium carbonate and the factors involved in self-healing concrete. Constr. Build. Mater. 2020, 254, 119258. [Google Scholar] [CrossRef]
- Garg, R.; Garg, R.; Eddy, N.O. Microbial induced calcite precipitation for self-healing of concrete: A review. J. Sustain. Cem.-Based Mater. 2023, 12, 317–330. [Google Scholar] [CrossRef]
- Skevi, L.; Reeksting, B.J.; Hoffmann, T.D.; Gebhard, S.; Paine, K. Incorporation of bacteria in concrete: The case against MICP as a means for strength improvement. Cem. Concr. Compos. 2021, 120, 104056. [Google Scholar] [CrossRef]
- Zhang, L.V.; Nehdi, M.L.; Suleiman, A.R.; Allaf, M.M.; Gan, M.; Marani, A.; Tuyan, M. Crack self-healing in bio-green concrete. Compos. Part B Eng. 2021, 227, 109397. [Google Scholar] [CrossRef]
- Khushnood, R.A.; Qureshi, Z.A.; Shaheen, N.; Ali, S. Bio-mineralized self-healing recycled aggregate concrete for sustainable infrastructure. Sci. Total Environ. 2020, 703, 135007. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Xu, G.; Duan, Y.; Dong, S. Self-healing cement composites based on bleaching earth immobilized bacteria. J. Clean. Prod. 2022, 358, 132045. [Google Scholar] [CrossRef]
- Gao, M.; Guo, J.; Cao, H.; Wang, H.; Xiong, X.; Krastev, R.; Nie, K.; Xu, H.; Liu, L. Immobilized bacteria with pH-response hydrogel for self-healing of concrete. J. Environ. Manag. 2020, 261, 110225. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Qian, C.; Rui, Y.; Feng, J. Exploring the coupled mechanism of fibers and bacteria on self-healing concrete from bacterial extracellular polymeric substances (EPS). Cem. Concr. Compos. 2021, 116, 103896. [Google Scholar] [CrossRef]
- Luo, J.; Chen, X.; Crump, J.; Zhou, H.; Davies, D.G.; Zhou, G.; Zhang, N.; Jin, C. Interactions of fungi with concrete: Significant importance for bio-based self-healing concrete. Constr. Build. Mater. 2018, 164, 275–285. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, X.; Li, M.; Samia, A.; Yu, X.B. Study on the behaviors of fungi-concrete surface interactions and theoretical assessment of its potentials for durable concrete with fungal-mediated self-healing. J. Clean. Prod. 2021, 292, 125870. [Google Scholar] [CrossRef]
- Yuan, W.Q.; Liu, G.L.; Huang, C.; Li, Y.D.; Zeng, J.B. Highly stretchable, recyclable, and fast room temperature self-healable biobased elastomers using polycondensation. Macromolecules 2020, 53, 9847–9858. [Google Scholar] [CrossRef]
- Hua, J.; Liu, C.; Fei, B.; Liu, Z. Self-Healable and Super-Tough Double-Network Hydrogel Fibers from Dynamic Acylhydrazone Bonding and Supramolecular Interactions. Gels 2022, 8, 101. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, D.; Lansade, D.; Lewandowski, S.; Perraud, S.; Llevot, A.; Carlotti, S. Combination of permanent hydrosilylation and reversible Diels–Alder reactions for self-healing poly (dimethylsiloxane) materials with enhanced ageing properties. Mater. Today Chem. 2022, 24, 100860. [Google Scholar] [CrossRef]
- Zhang, L.; Liang, J.; Jiang, C.; Liu, Z.; Sun, L.; Chen, S.; Xuan, H.; Lei, D.; Guan, Q.; Ye, X. Peptidoglycan-inspired autonomous ultrafast self-healing bio-friendly elastomers for bio-integrated electronics. Natl. Sci. Rev. 2021, 8, nwaa154. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Zhang, Q.; Feringa, B.L.; Tian, H.; Qu, D.H. Toughening a self-healable supramolecular polymer by ionic cluster-enhanced iron-carboxylate complexes. Angew. Chem. 2020, 132, 5316–5321. [Google Scholar] [CrossRef]
- Han, T.Y.; Lin, C.H.; Lin, Y.S.; Yeh, C.M.; Chen, Y.A.; Li, H.Y.; Xiao, Y.T.; Chang, J.W.; Su, A.C.; Jeng, U.S. Autonomously self-healing and ultrafast highly-stretching recoverable polymer through trans-octahedral metal-ligand coordination for skin-inspired tactile sensing. Chem. Eng. J. 2022, 438, 135592. [Google Scholar] [CrossRef]
- Um, J.G.; Habibpour, S.; Jun, Y.S.; Elkamel, A.; Yu, A. Development of π–π interaction-induced functionalized graphene oxide on mechanical and anticorrosive properties of reinforced polyurethane composites. Ind. Eng. Chem. Res. 2020, 59, 3617–3628. [Google Scholar] [CrossRef]
- Zhang, L.; Guan, Q.; Shen, A.; Neisiany, R.E.; You, Z.; Zhu, M. Supertough spontaneously self-healing polymer based on septuple dynamic bonds integrated in one chemical group. Sci. China Chem. 2022, 65, 363–372. [Google Scholar] [CrossRef]
- Wu, J.; Cai, L.H.; Weitz, D.A. Tough self-healing elastomers by molecular enforced integration of covalent and reversible networks. Adv. Mater. 2017, 29, 1702616. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Yang, Y.; Wu, Q.; Wang, S.; Huang, G.; Wu, J. Strong and tough self-healing elastomers enabled by dual reversible networks formed by ionic interactions and dynamic covalent bonds. Polymer 2018, 157, 172–179. [Google Scholar] [CrossRef]
- Mirmohseni, A.; Akbari, M.; Najjar, R.; Hosseini, M. Self-healing waterborne polyurethane coating by pH-dependent triggered-release mechanism. J. Appl. Polym. Sci. 2019, 136, 47082. [Google Scholar] [CrossRef]
- Parsaee, S.; Mirabedini, S.M.; Farnood, R.; Alizadegan, F. Development of self-healing coatings based on urea-formaldehyde/polyurethane microcapsules containing epoxy resin. J. Appl. Polym. Sci. 2020, 137, 49663. [Google Scholar] [CrossRef]
- Hu, Z.X.; Hu, X.M.; Cheng, W.M.; Zhao, Y.Y.; Wu, M.Y. Performance optimization of one-component polyurethane healing agent for self-healing concrete. Constr. Build. Mater. 2018, 179, 151–159. [Google Scholar] [CrossRef]
- Trask, R.S.; Williams, G.J.; Bond, I.P. Bioinspired self-healing of advanced composite structures using hollow glass fibers. J. R. Soc. Interface 2007, 4, 363–371. [Google Scholar] [CrossRef] [PubMed]
- Aghamirzadeh, G.R.; Khalili SM, R.; Eslami-Farsani, R.; Saeedi, A. Experimental investigation on the smart self-healing composites based on the short hollow glass fibers and shape memory alloy strips. Polym. Compos. 2019, 40, 1883–1889. [Google Scholar] [CrossRef]
- Kosarli, M.; Bekas, D.G.; Tsirka, K.; Baltzis, D.; Vaimakis-Tsogkas, D.Τ.; Orfanidis, S.; Papavassiliouc, G.; Paipetis, A.S. Microcapsule-based self-healing materials: Healing efficiency and toughness reduction vs. capsule size. Compos. Part B Eng. 2019, 171, 78–86. [Google Scholar] [CrossRef]
- Mercy, J.L.; Prakash, S.; Krishnamoorthy, A.; Ramesh, S.; Anand, D.A. Multi response optimisation of mechanical properties in self-healing glass fiber reinforced plastic using grey relational analysis. Measurement 2017, 110, 344–355. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Y.; Luo, J.; Liu, R.; Sun, G.; Liu, X. Preparation of dual-chamber microcapsule by Pickering emulsion for self-healing application with ultra-high healing efficiency. J. Colloid Interface Sci. 2021, 600, 660–669. [Google Scholar] [CrossRef]
- Wool, R.P.; O’connor, K.M. A theory crack healing in polymers. J. Appl. Phys. 1981, 52, 5953–5963. [Google Scholar] [CrossRef]
- Salih, S.; Gómez-Meijide, B.; Aboufoul, M.; Garcia, A. Effect of porosity on infrared healing of fatigue damage in asphalt. Constr. Build. Mater. 2018, 167, 716–725. [Google Scholar] [CrossRef]
- Huang, M.; Huang, W. Laboratory investigation on fatigue performance of modified asphalt concretes considering healing. Constr. Build. Mater. 2016, 113, 68–76. [Google Scholar] [CrossRef]
- Sun, D.; Lin, T.; Zhu, X.; Tian, Y.; Liu, F. Indices for self-healing performance assessments based on molecular dynamics simulation of asphalt binders. Comput. Mater. Sci. 2016, 114, 86–93. [Google Scholar] [CrossRef]
- Shirzad, S.; Hassan, M.M.; Aguirre, M.A.; Mohammad, L.N.; Cooper, S.; Negulescu, I.I. Microencapsulated sunflower oil for rejuvenation and healing of asphalt mixtures. J. Mater. Civ. Eng. 2017, 29, 04017147. [Google Scholar] [CrossRef]
- García, Á. Self-healing of open cracks in asphalt mastic. Fuel 2012, 93, 264–272. [Google Scholar] [CrossRef]
- Liu, Q.; Schlangen, E.; van de Ven, M. Induction healing of porous asphalt concrete beams on an elastic foundation. J. Mater. Civ. Eng. 2013, 25, 880–885. [Google Scholar] [CrossRef]
- Tang, J.; Liu, Q.; Wu, S.; Ye, Q.; Sun, Y.; Schlangen, E. Investigation of the optimal self-healing temperatures and healing time of asphalt binders. Constr. Build. Mater. 2016, 113, 1029–1033. [Google Scholar] [CrossRef]
- García, Á.; Schlangen, E.; De Ven, M.V.; Liu, Q. Electrical conductivity of asphalt mortar containing conductive fibers and fillers. Constr. Build. Mater. 2009, 23, 3175–3181. [Google Scholar] [CrossRef]
- Liu, Z.; Luo, S.; Wang, Y.; Chen, H. Induction heating and fatigue-damage induction healing of steel fiber–reinforced asphalt mixture. J. Mater. Civ. Eng. 2019, 31, 04019180. [Google Scholar] [CrossRef]
- Yang, C.; Wu, S.; Xie, J.; Amirkhanian, S.; Liu, Q.; Zhang, J.; Xiao, Y.; Zhao, Z.; Xu, H.; Li, N.; et al. Enhanced induction heating and self-healing performance of recycled asphalt mixtures by incorporating steel slag. J. Clean. Prod. 2022, 366, 132999. [Google Scholar] [CrossRef]
- Apostolidis, P.; Liu, X.; Scarpas, A.; Kasbergen, C.; Van De Ven, M.F.C. Advanced evaluation of asphalt mortar for induction healing purposes. Constr. Build. Mater. 2016, 126, 9–25. [Google Scholar] [CrossRef]
- Zhao, H.; Zhong, S.; Zhu, X.; Chen, H. High-efficiency heating characteristics of ferrite-filled asphalt-based composites under microwave irradiation. J. Mater. Civ. Eng. 2017, 29, 04017007. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Y.; Liu, Z.; Dong, Q.; Zhao, X. Temperature analyses of porous asphalt mixture using steel slag aggregates heated by microwave through laboratory tests and numerical simulations. J. Clean. Prod. 2022, 338, 130614. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, T.; Guo, H.; Wang, Z.; Wang, X. Evaluation of self-healing properties of asphalt mixture containing steel slag under microwave heating: Mechanical, thermal transfer and voids microstructural characteristics. J. Clean. Prod. 2022, 342, 130932. [Google Scholar] [CrossRef]
- Lou, B.; Sha, A.; Li, Y.; Wang, W.; Liu, Z.; Jiang, W.; Cui, X. Effect of metallic-waste aggregates on microwave self-healing performances of asphalt mixtures. Constr. Build. Mater. 2020, 246, 118510. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Guo, H.; Yan, F. Thermal transfer characteristics of asphalt mixtures containing hot poured steel slag through microwave heating. J. Clean. Prod. 2021, 308, 127225. [Google Scholar] [CrossRef]
- Yalcin, E. Effects of microwave and induction heating on the mechanical and self-healing characteristics of the asphalt mixtures containing waste metal. Constr. Build. Mater. 2021, 286, 122965. [Google Scholar] [CrossRef]
- Xu, S.; Liu, X.; Tabaković, A.; Schlangen, E. The prospect of microwave heating: Towards a faster and deeper crack healing in asphalt pavement. Processes 2021, 9, 507. [Google Scholar] [CrossRef]
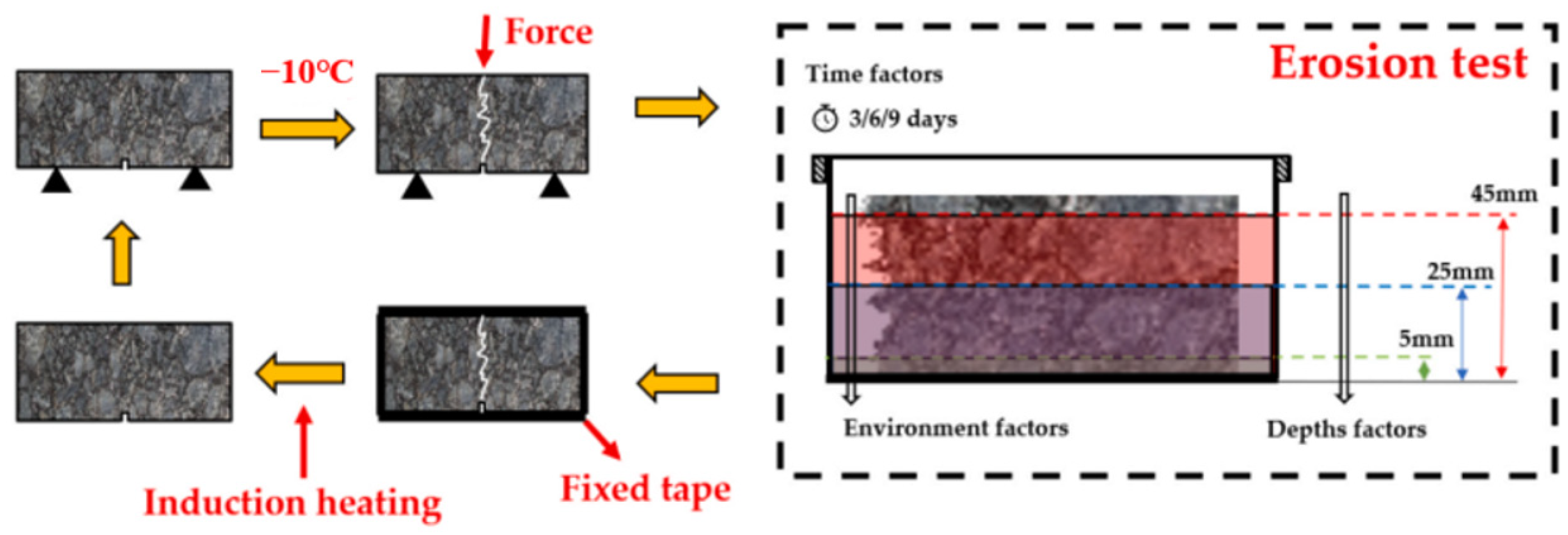
- Xu, H.; Wu, S.; Chen, A.; Zou, Y. Influence of erosion factors (time, depths and environment) on induction heating asphalt concrete and its mechanism. J. Clean. Prod. 2022, 363, 132521. [Google Scholar] [CrossRef]
- Ju, J.W. Isotropic and anisotropic damage variables in continuum damage mechanics. J. Eng. Mech. 1990, 116, 2764–2770. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. Damage mechanics with fabric tensors. Mech. Adv. Mater. Struct. 2006, 13, 285–301. [Google Scholar] [CrossRef]
- Sun, L.Z.; Liu, H.T.; Ju, J.W. Effect of particle cracking on elastoplastic behavior of metal matrix composites. Int. J. Numer. Methods Eng. 2003, 56, 2183–2198. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. Introduction to the mechanics and design of undamageable materials. Int. J. Damage Mech. 2013, 22, 323–335. [Google Scholar] [CrossRef]
- Oucif, C.; Voyiadjis, G.Z.; Rabczuk, T. Modeling of damage-healing and nonlinear self-healing concrete behavior: Application to coupled and uncoupled self-healing mechanisms. Theor. Appl. Fract. Mech. 2018, 96, 216–230. [Google Scholar] [CrossRef]
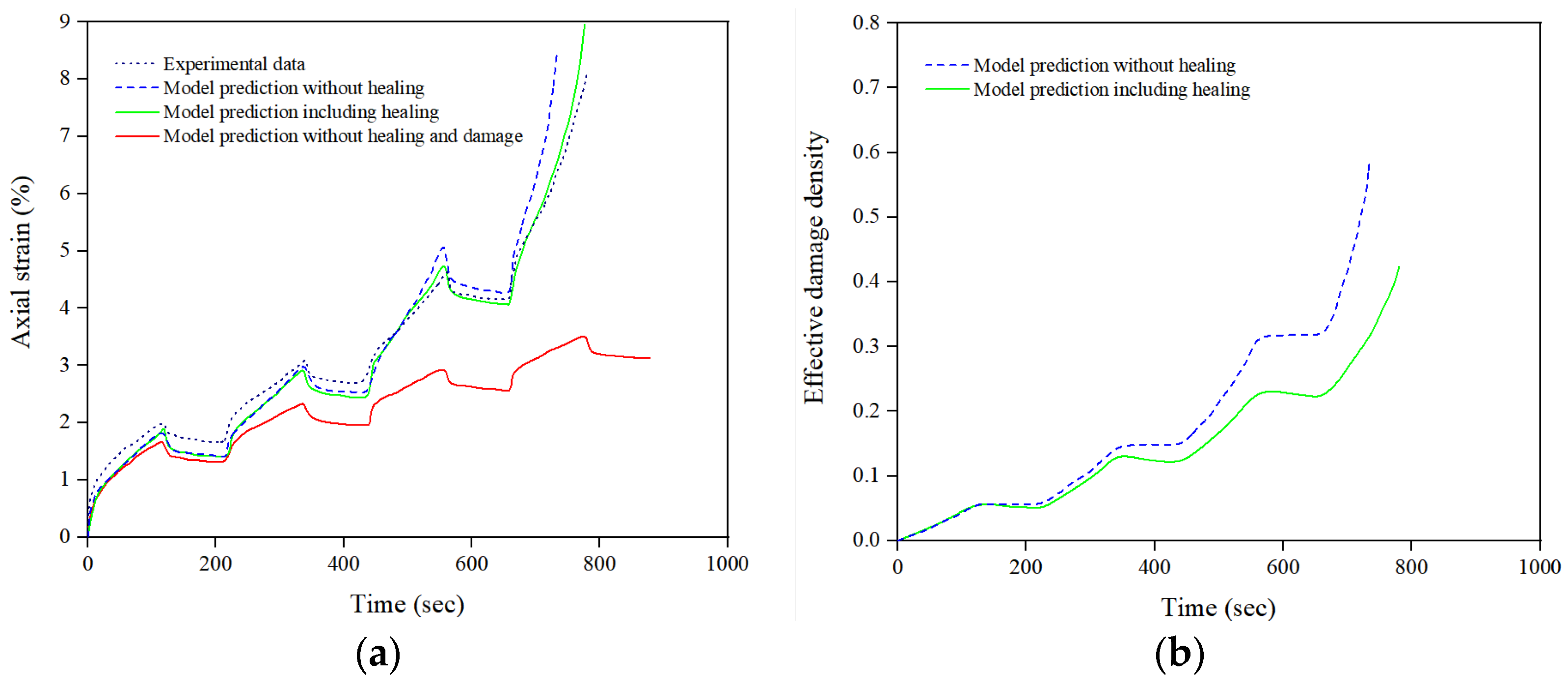
- Al-Rub, R.K.A.; Darabi, M.K.; Little, D.N.; Masad, E.A. A micro-damage healing model that improves prediction of fatigue life in asphalt mixes. Int. J. Eng. Sci. 2010, 48, 966–990. [Google Scholar] [CrossRef]
- Darabi, M.K.; Al-Rub RK, A.; Little, D.N. A continuum damage mechanics framework for modeling micro-damage healing. Int. J. Solids Struct. 2012, 49, 492–513. [Google Scholar] [CrossRef]
- Shahsavari, H.; Baghani, M.; Naghdabadi, R.; Sohrabpour, S. A thermodynamically consistent viscoelastic-viscoplastic constitutive model for self-healing materials. J. Intell. Mater. Syst. Struct. 2018, 29, 1065–1080. [Google Scholar] [CrossRef]
- Pan, Y.; Tian, F.; Zhong, Z. A continuum damage-healing model of healing agents based self-healing materials. Int. J. Damage Mech. 2018, 27, 754–778. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Shojaei, A.; Li, G. A thermodynamic consistent damage and healing model for self healing materials. Int. J. Plast. 2011, 27, 1025–1044. [Google Scholar] [CrossRef]
- Esgandani, G.A.; El-Zein, A. Thermodynamic based model for coupled elastoplastic damage-healing behavior of unsaturated geomaterials. Mech. Mater. 2020, 145, 103395. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, X.; Zhu, H.; Ju, J.W.; Yongjian, X.; Jiang, Z.; Yan, Z. Continuum damage-healing framework for the hydration induced self-healing of the cementitious composite. Int. J. Damage Mech. 2021, 30, 681–699. [Google Scholar] [CrossRef]
- Shahsavari, H.; Baghani, M.; Sohrabpour, S.; Naghdabadi, R. Continuum damage-healing constitutive modeling for concrete materials through stress spectral decomposition. Int. J. Damage Mech. 2016, 25, 900–918. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. Healing and super healing in continuum damage mechanics. Int. J. Damage Mech. 2014, 23, 245–260. [Google Scholar] [CrossRef]
- Joseph, C.; Jefferson, A.D.; Isaacs, B.; Lark, R.; Gardner, D. Experimental investigation of adhesive-based self-healing of cementitious materials. Mag. Concr. Res. 2010, 62, 831–843. [Google Scholar] [CrossRef]
- Oucif, C.; Voyiadjis, G.Z.; Kattan, P.I.; Rabczuk, T. Nonlinear superhealing and contribution to the design of a new strengthening theory. J. Eng. Mech. 2018, 144, 04018055. [Google Scholar] [CrossRef]
- Maiti, S.; Shankar, C.; Geubelle, P.H.; Kieffer, J. Continuum and molecular-level modeling of fatigue crack retardation in self-healing polymers. J. Eng. Mater. Technol. 2006, 128, 595–602. [Google Scholar] [CrossRef]
- Abu Al-Rub, R.K.; Alsheghri, A. Cohesive zone damage-healing model for self-healing materials. Appl. Mech. Mater. 2015, 784, 111–118. [Google Scholar] [CrossRef]
- Alsheghri, A.A.; Al-Rub, R.K.A. Thermodynamic-based cohesive zone healing model for self-healing materials. Mech. Res. Commun. 2015, 70, 102–113. [Google Scholar] [CrossRef]
- Alsheghri, A.A.; Al-Rub, R.K.A. Finite element implementation and application of a cohesive zone damage-healing model for self-healing materials. Eng. Fract. Mech. 2016, 163, 1–22. [Google Scholar] [CrossRef]
- Jud, K.; Kausch, H.H. Load transfer through chain molecules after interpenetration at interfaces. Polym. Bull. 1979, 1, 697–707. [Google Scholar] [CrossRef]
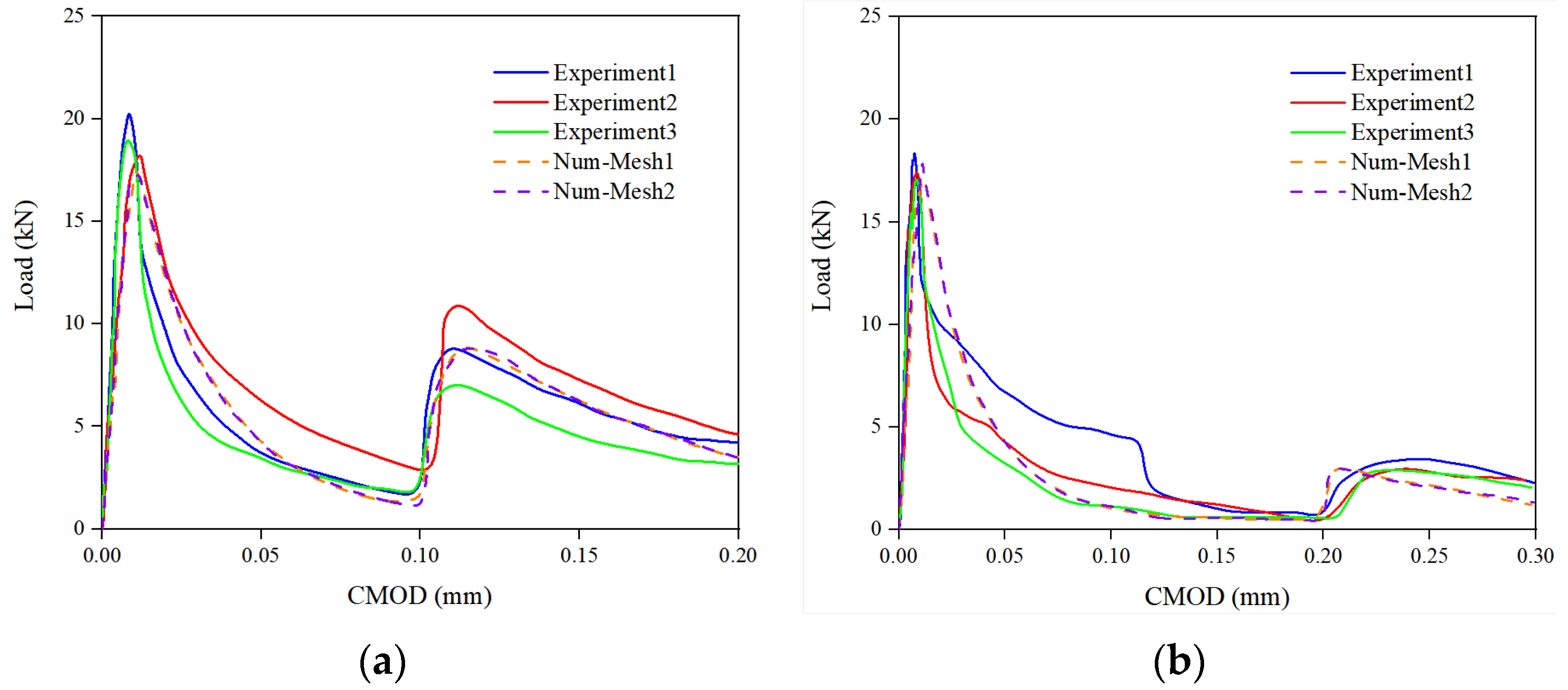
- Jefferson, A.D.; Freeman, B.L. A crack-opening-dependent numerical model for self-healing cementitious materials. Int. J. Solids Struct. 2022, 244, 111601. [Google Scholar] [CrossRef]
- Freeman, B.L.; Bonilla-Villalba, P.; Mihai, I.C.; Alnaas, W.F.; Jefferson, A.D. A specialised finite element for simulating self-healing quasi-brittle materials. Adv. Model. Simul. Eng. Sci. 2020, 7, 32. [Google Scholar] [CrossRef]
- Xin, A.; Du, H.; Yu, K.; Wang, Q. Mechanics of bacteria-assisted extrinsic healing. J. Mech. Phys. Solids 2020, 139, 103938. [Google Scholar] [CrossRef]
- Ponnusami, S.A.; Krishnasamy, J.; Turteltaub, S.; van der Zwaag, S. A cohesive-zone crack healing model for self-healing materials. Int. J. Solids Struct. 2018, 134, 249–263. [Google Scholar] [CrossRef]
- Wang, W.; Moreau, N.G.; Yuan, Y.; Race, P.R.; Pang, W. Towards machine learning approaches for predicting the self-healing efficiency of materials. Comput. Mater. Sci. 2019, 168, 180–187. [Google Scholar] [CrossRef]
- Paruelo, J.M.; Tomasel, F. Prediction of functional characteristics of ecosystems: A comparison of artificial neural networks and regression models. Ecol. Model. 1997, 98, 173–186. [Google Scholar] [CrossRef]
- Theja, A.R.; Reddy, M.S.; Jindal, B.B.; Sashidhar, C. Predicting the Strength Properties of Self Healing Concrete Using Artificial Neural Network. J. Soft Comput. Civ. Eng. 2023, 7, 56–71. [Google Scholar]
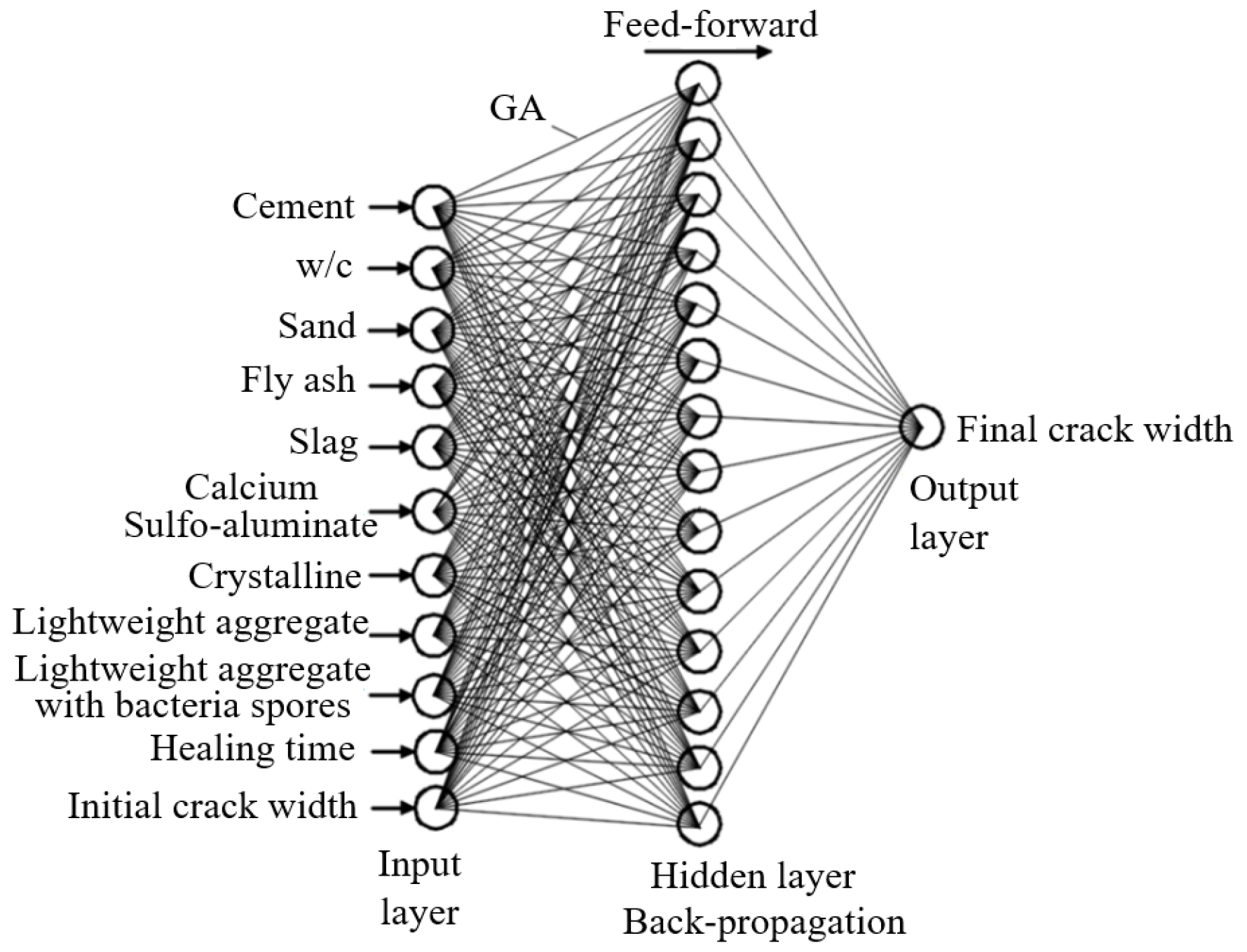
- Ramadan Suleiman, A.; Nehdi, M.L. Modeling self-healing of concrete using hybrid genetic algorithm–artificial neural network. Materials 2017, 10, 135. [Google Scholar] [CrossRef] [PubMed]
- Anwar Ali, H.P.; Zhao, Z.; Tan, Y.J.; Yao, W.; Li, Q.; Tee, B.C. Dynamic Modeling of Intrinsic Self-Healing Polymers Using Deep Learning. ACS Appl. Mater. Interfaces 2022, 14, 52486–52498. [Google Scholar] [CrossRef]
- Chen, G.; Tang, W.; Chen, S.; Wang, S.; Cui, H. Prediction of self-healing of engineered cementitious composite using machine learning approaches. Appl. Sci. 2022, 12, 3605. [Google Scholar] [CrossRef]
- Gilabert, F.A.; Garoz, D.; Van Paepegem, W. Macro-and micro-modeling of crack propagation in encapsulation-based self-healing materials: Application of XFEM and cohesive surface techniques. Mater. Des. 2017, 130, 459–478. [Google Scholar] [CrossRef]
- Hanna, J. Computational modelling for the effects of capsular clustering on fracture of encapsulation-based self-healing concrete using XFEM and cohesive surface technique. Appl. Sci. 2022, 12, 5112. [Google Scholar] [CrossRef]
- Gao, C.; Ruan, H.; Yang, C.; Wang, F. Investigation on microcapsule self-healing mechanism of polymer matrix composites based on numerical simulation. Polym. Compos. 2021, 42, 3619–3631. [Google Scholar] [CrossRef]
- Pan, X.; Gencturk, B.; Alnaggar, M.; Sohail, M.G.; Kahraman, R.; Al Nuaimi, N.; Rodrigues, D.F.; Yildirim, Y. Numerical simulation of the fracture and compression response of self-healing concrete containing engineered aggregates. Cem. Concr. Compos. 2023, 136, 104858. [Google Scholar] [CrossRef]
- Cusatis, G.; Pelessone, D.; Mencarelli, A. Lattice discrete particle model (LDPM) for failure behavior of concrete. I: Theory. Cem. Concr. Compos. 2011, 33, 881–890. [Google Scholar] [CrossRef]
- Bhasin, A.; Bommavaram, R.; Greenfield, M.L.; Little, D.N. Use of molecular dynamics to investigate self-healing mechanisms in asphalt binders. J. Mater. Civ. Eng. 2011, 23, 485–492. [Google Scholar] [CrossRef]
- Sun, D.; Sun, G.; Zhu, X.; Ye, F.; Xu, J. Intrinsic temperature sensitive self-healing character of asphalt binders based on molecular dynamics simulations. Fuel 2018, 211, 609–620. [Google Scholar] [CrossRef]
- He, L.; Li, G.; Lv, S.; Gao, J.; Kowalski, K.J.; Valentin, J.; Alexiadis, A. Self-healing behavior of asphalt system based on molecular dynamics simulation. Constr. Build. Mater. 2020, 254, 119225. [Google Scholar] [CrossRef]
- Fu, Y.; Wu, M.; Hei, T.; Dong, Z.; Hu, J.; Zhang, W. Research on the Adhesion and Self-healing Properties of Bio-asphalt Based on Molecular Simulation. Adv. Res. Civ. Eng. 2022, 4, 24–43. [Google Scholar]
- Li, J.; Ji, X.; Fang, X.; Hu, Y.; Hua, W.; Zhang, Z.; Shao, D. Self-healing performance and prediction model of microcapsule asphalt. Constr. Build. Mater. 2022, 330, 127085. [Google Scholar] [CrossRef]




| Type | Mechanism | Conditions | Test | Performance | Ref |
|---|---|---|---|---|---|
| Autogenous | MgO expansion agent | Accelerated autoclaved condition | Compressive test | Improved repair effect | [27] |
| Lime mortar | 14 days of water immersion | SEM/EDS | Compressive strength restored by 40% | [28] | |
| Expanded minerals | Normal temperature environment | XRD, TGA and SEM-EDX, compressive test | Strength restored by 60% | [29] | |
| Blast furnace slag | Solidification in saturated Ca(OH)2 solution | ESEM | Crack filling rate reaches 60% | [32] | |
| SCMs | Wet and dry cycle | XRD and SEM | Crack healing rate exceeds 70% | [34] | |
| Hydrogel | Standing at room temperature | Autogenous shrinkage test | Decrease in autogenous shrinkage | [37] | |
| Epoxy resin | Standard curing | Compressive test | Healing efficiency is 71.8% | [38] | |
| Autonomic | Microcapsules | Standard curing | X-ray diffraction analysis | Adsorption power reduced by 45% | [25] |
| Microcapsules | Standard curing | SEM, compressive test | Best effect by 2.5% microcapsule | [43] | |
| Epoxy resin microcapsules | Preloading | Compressive test | 86.8% | [44] | |
| MICP | Distilled water soak | SEM | Completely healed | [48] | |
| MICP | Keep in tap water for 5–7 days at room temperature | SEM, bending test, compressive test | Healing efficiency increased by 13.79% | [52] |
| Type | Mechanism | Conditions | Test | Performance | Ref |
|---|---|---|---|---|---|
| Intrinsic | Re-formable chemical bond | Acidic environments/heating | Tensile test | 96% | [63] |
| Re-formable chemical bond | Exposure at room temperature | Tensile test | 93.3% | [67] | |
| Re-formable chemical bond | Standing at room temperature | Tensile test | 96.1% ± 14.7% | [69] | |
| External | Hollow glass fibers | High temperature for 2 h | Four-point bending test | 91% | [75] |
| Microcapsules | Room temperature and high pressure | Three-point bending test | 71.3% | [14] | |
| Dual-chamber microcapsules | Standing at room temperature | SEM | 85% | [79] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, C.-Y.; Zhang, L.; Hu, S.-Y.; Xia, S.-J.; Li, D.M. Recent Advances of Self-Healing Materials for Civil Engineering: Models and Simulations. Buildings 2024, 14, 961. https://doi.org/10.3390/buildings14040961
Liao C-Y, Zhang L, Hu S-Y, Xia S-J, Li DM. Recent Advances of Self-Healing Materials for Civil Engineering: Models and Simulations. Buildings. 2024; 14(4):961. https://doi.org/10.3390/buildings14040961
Chicago/Turabian StyleLiao, Cen-Ying, Lin Zhang, Si-Yu Hu, Shuai-Jie Xia, and D. M. Li. 2024. "Recent Advances of Self-Healing Materials for Civil Engineering: Models and Simulations" Buildings 14, no. 4: 961. https://doi.org/10.3390/buildings14040961
APA StyleLiao, C.-Y., Zhang, L., Hu, S.-Y., Xia, S.-J., & Li, D. M. (2024). Recent Advances of Self-Healing Materials for Civil Engineering: Models and Simulations. Buildings, 14(4), 961. https://doi.org/10.3390/buildings14040961







