Behavior of Stiffened Rafts Resting on Expansive Soil and Subjected to Column Loads of Lightweight-Reinforced Concrete Structures
Abstract
1. Introduction
2. Analysis Method
2.1. Limitations in Existing Design Methods
2.2. Computer Program SLAB97
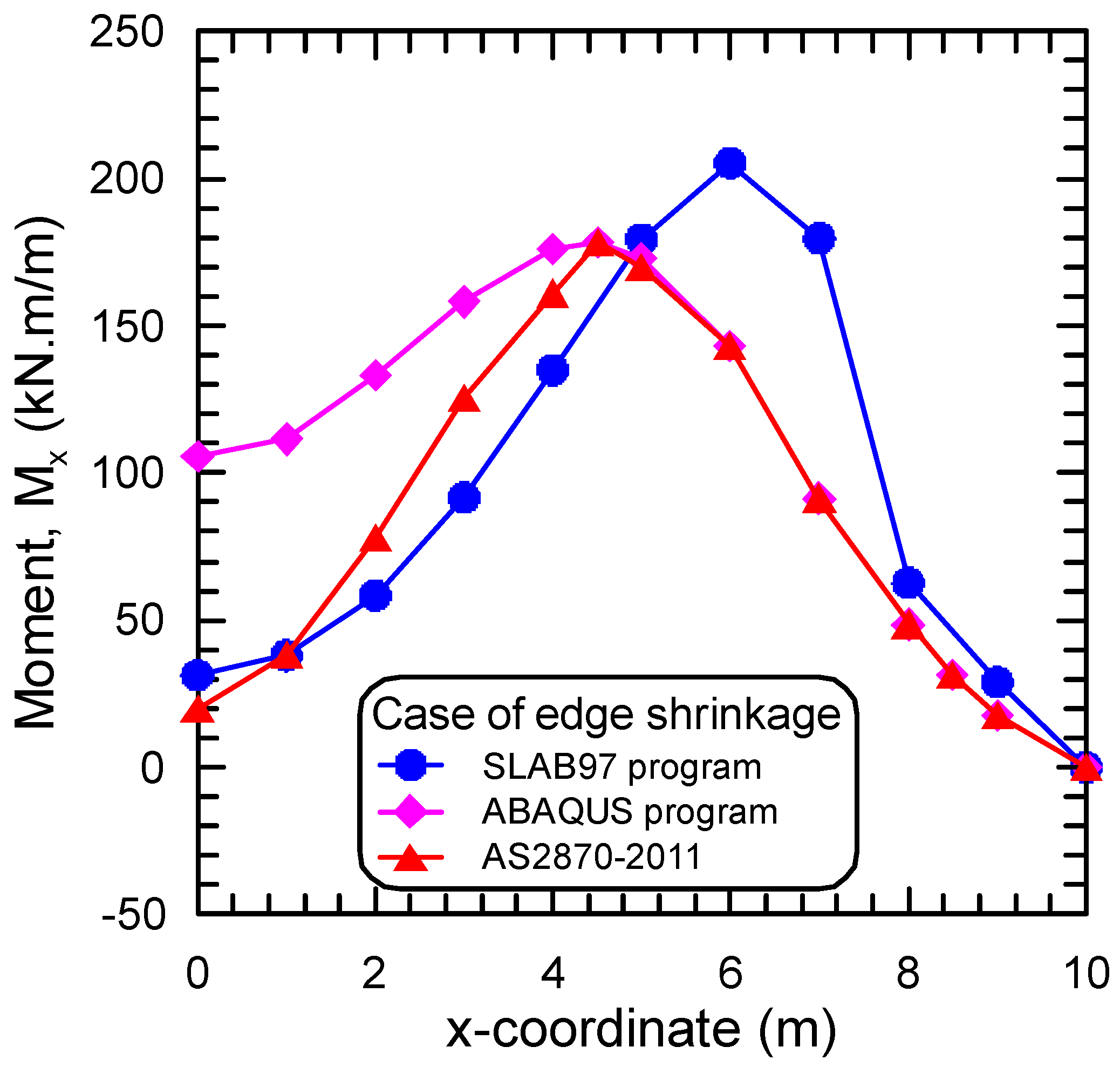
Validation of the Program SLAB97
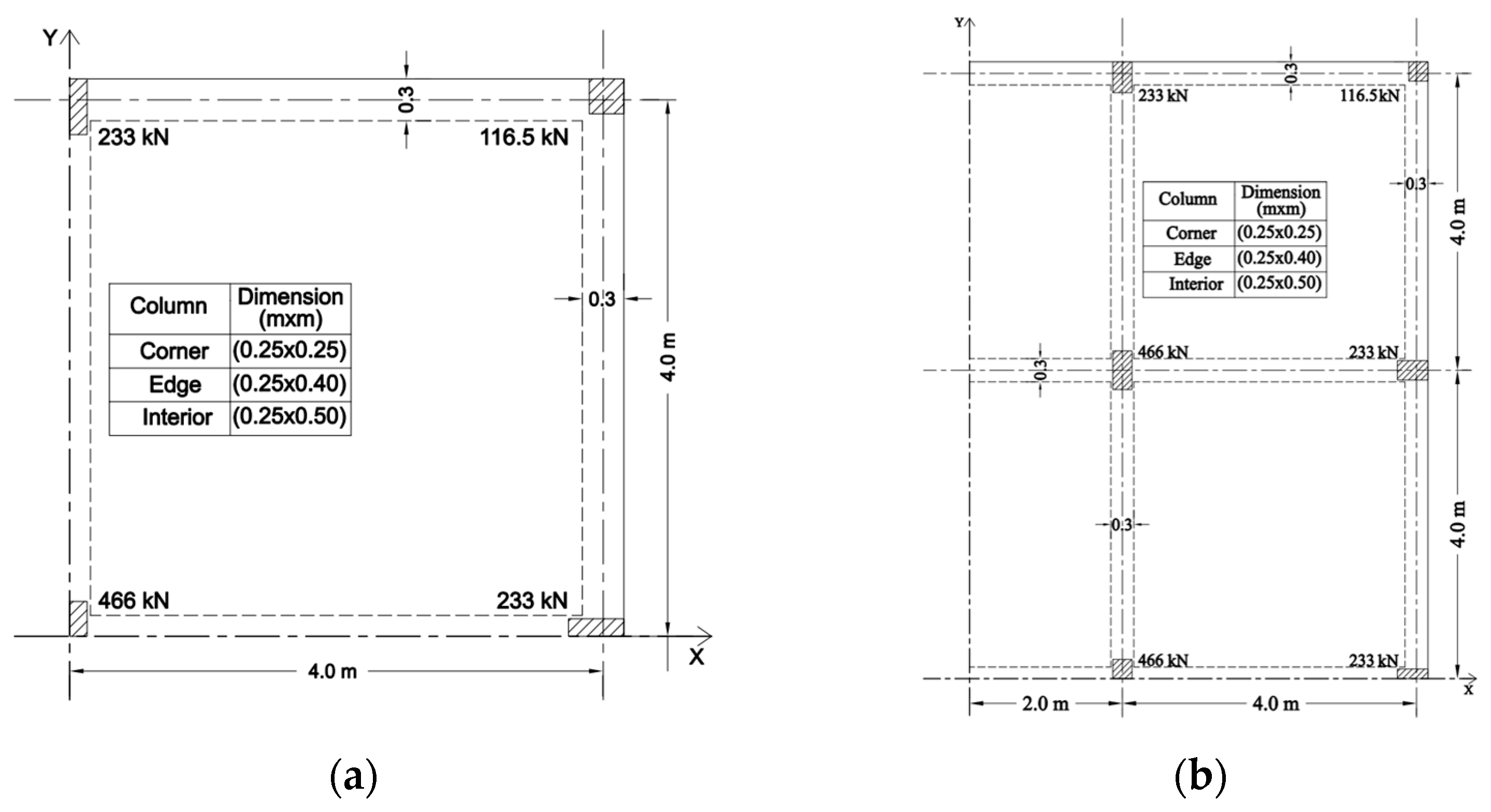
3. Parametric Study
4. Analysis of Results
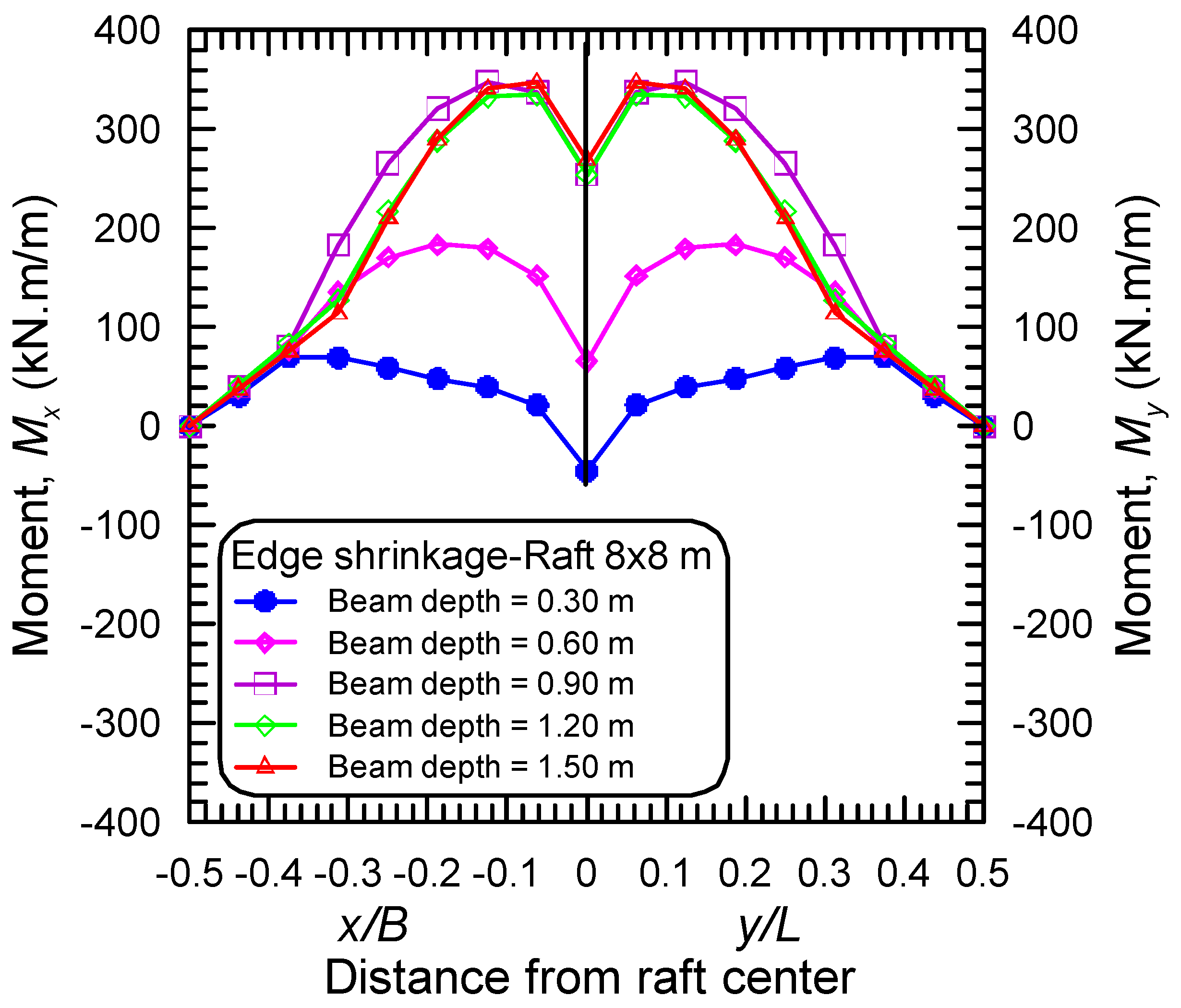
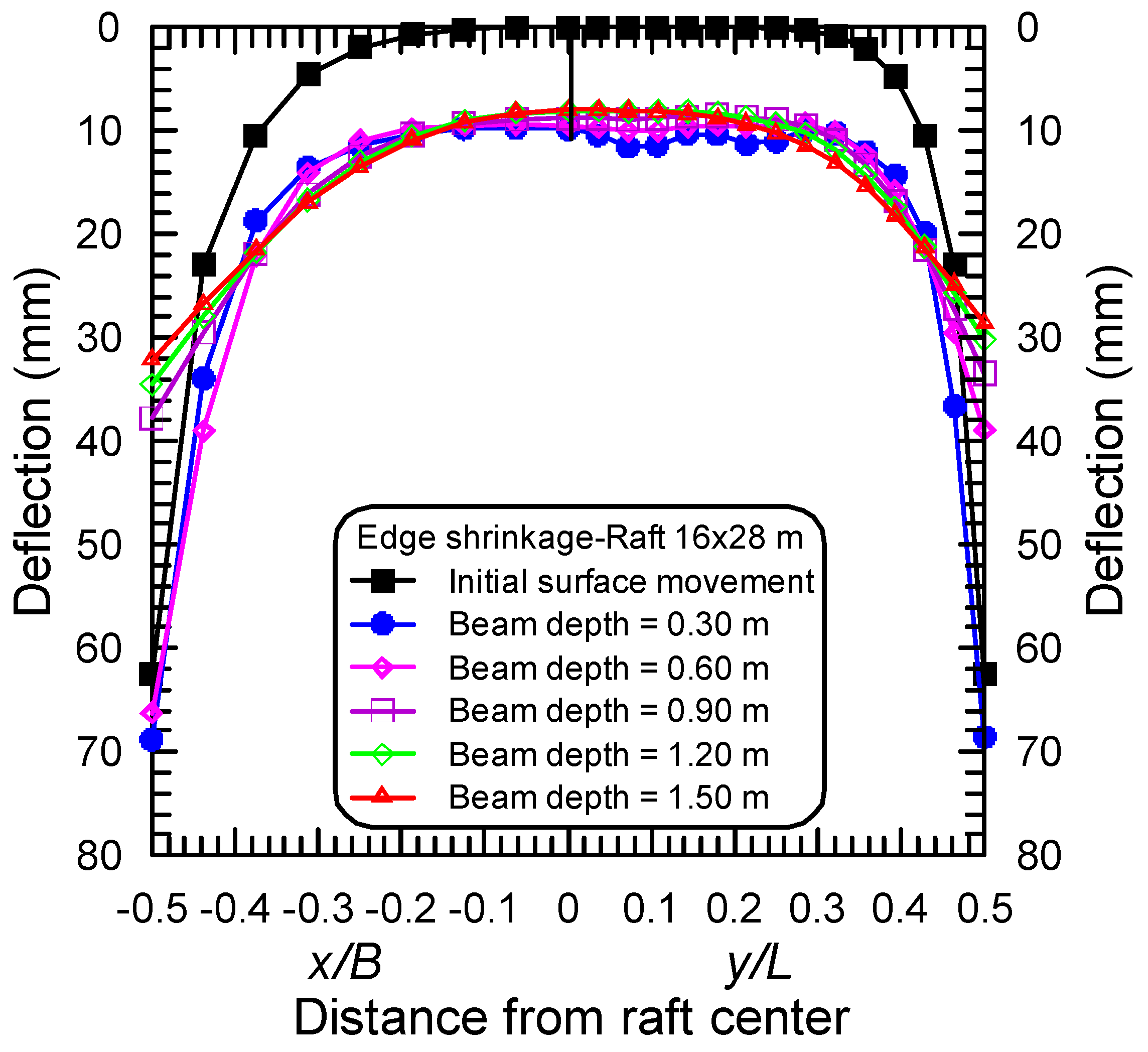
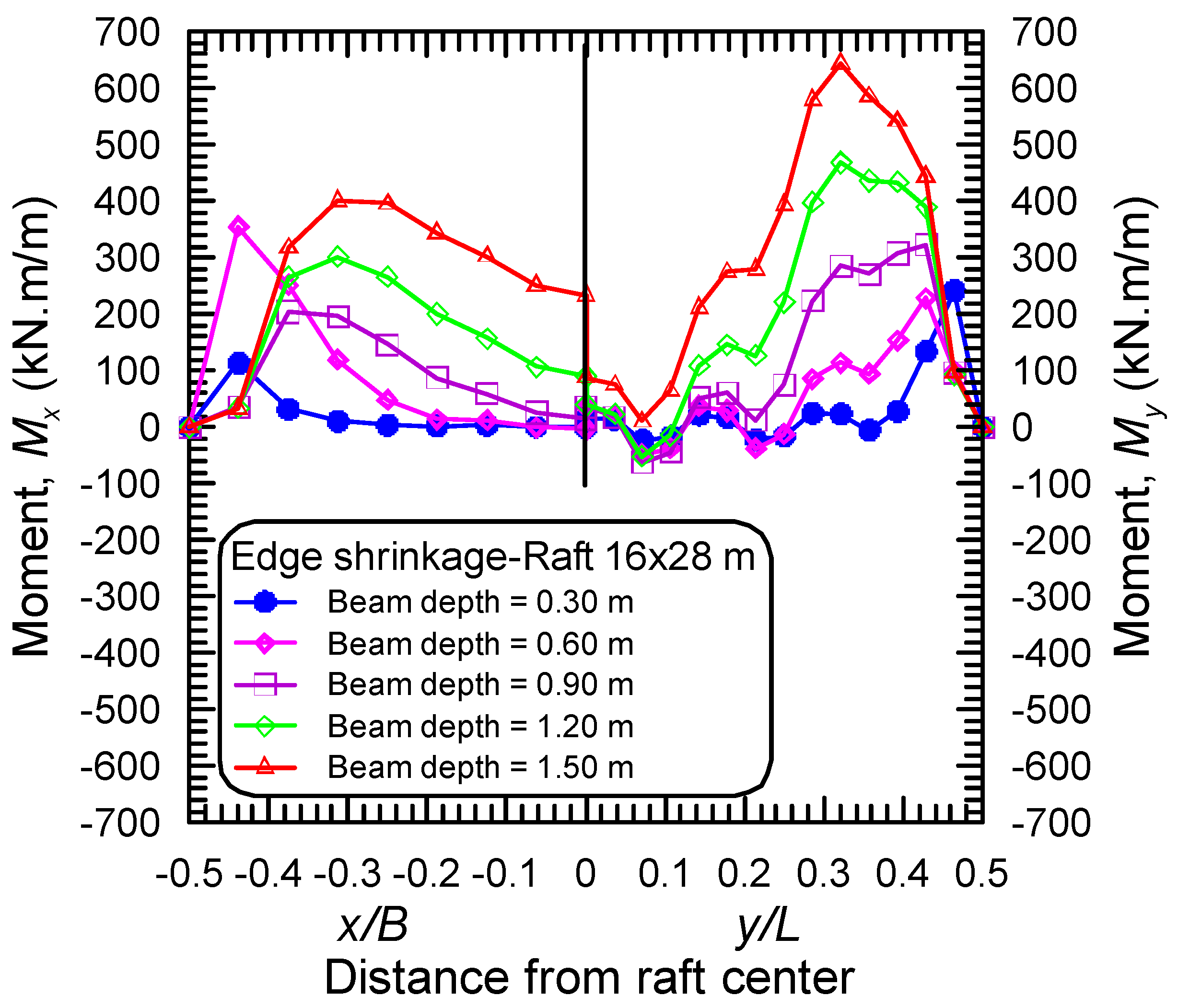
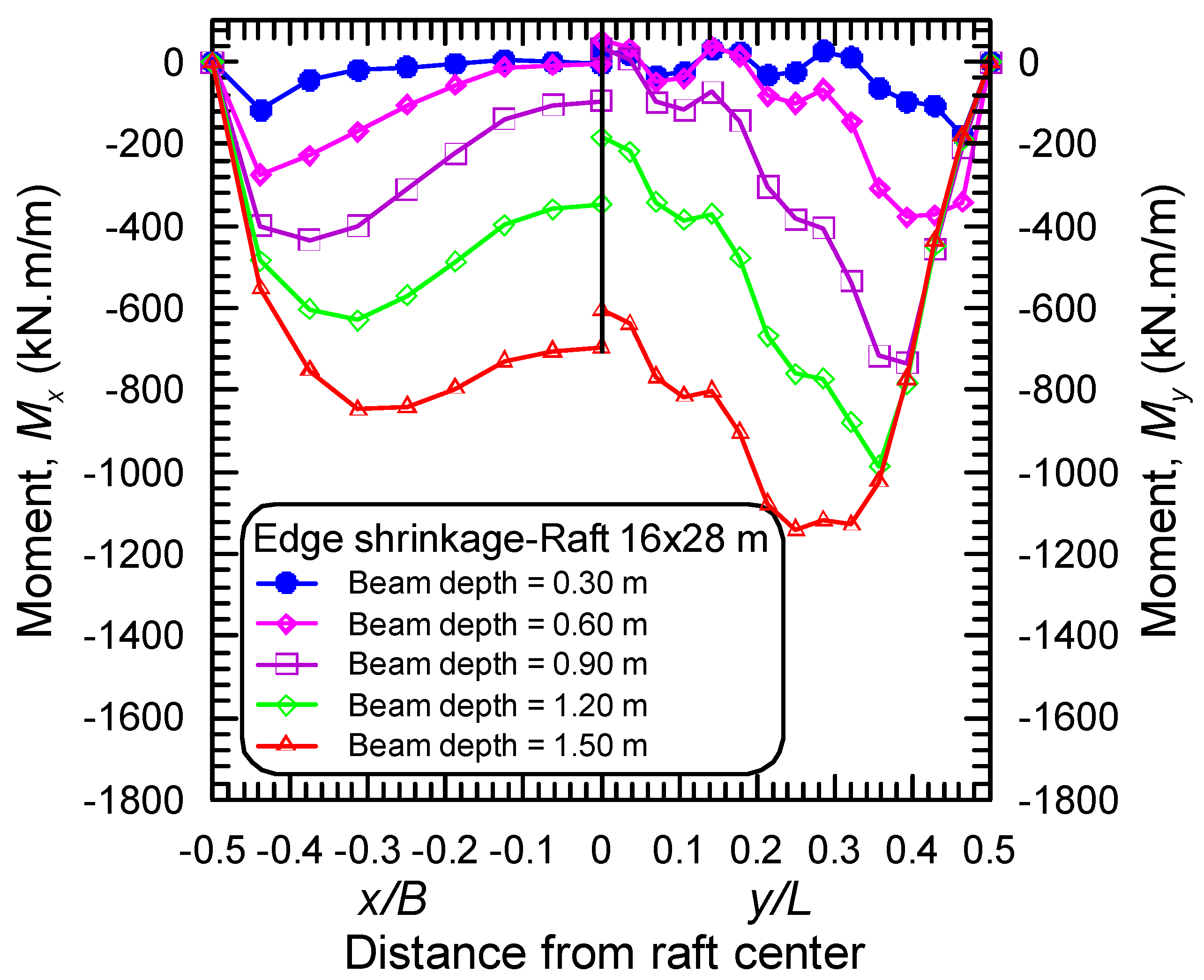
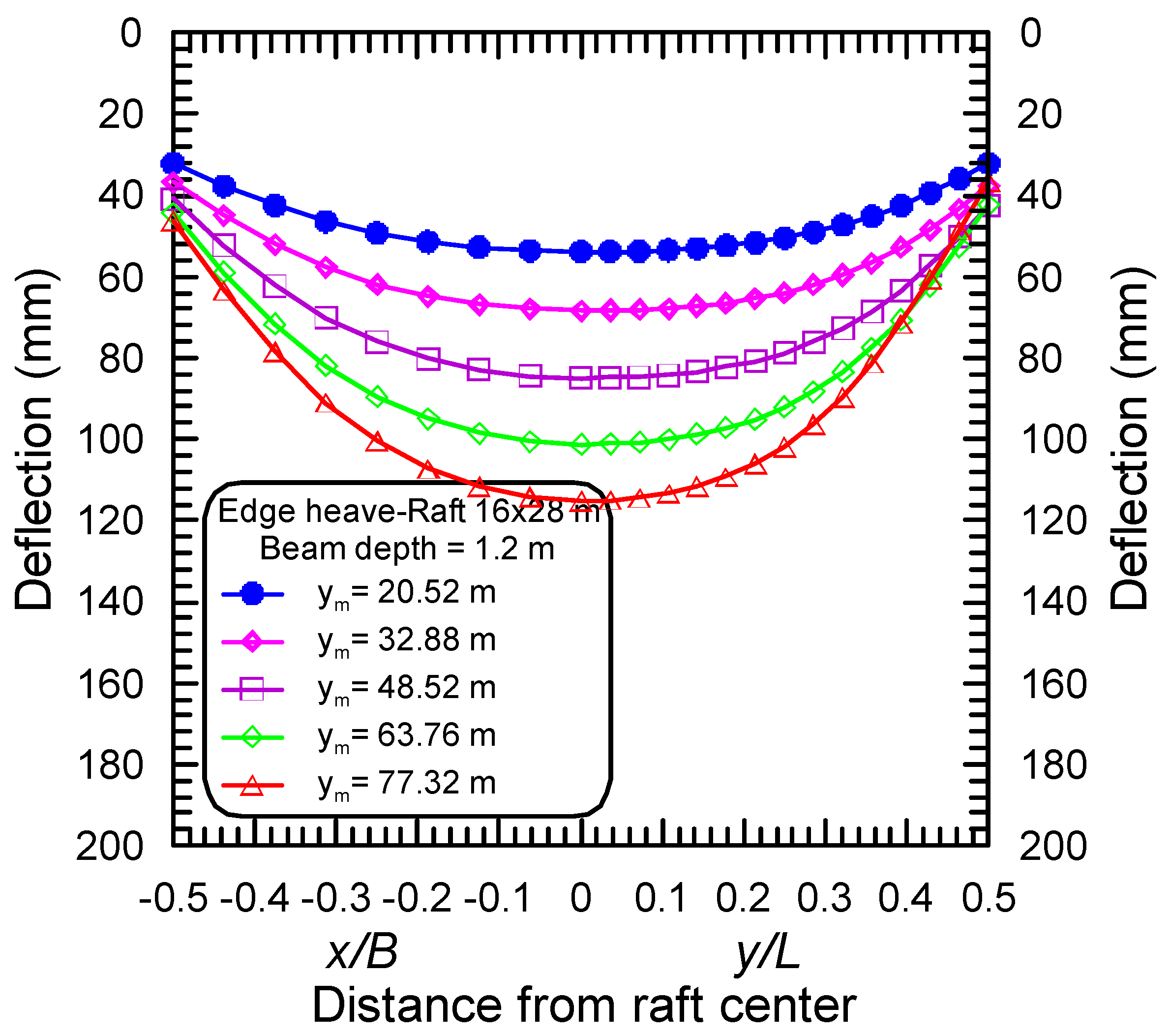
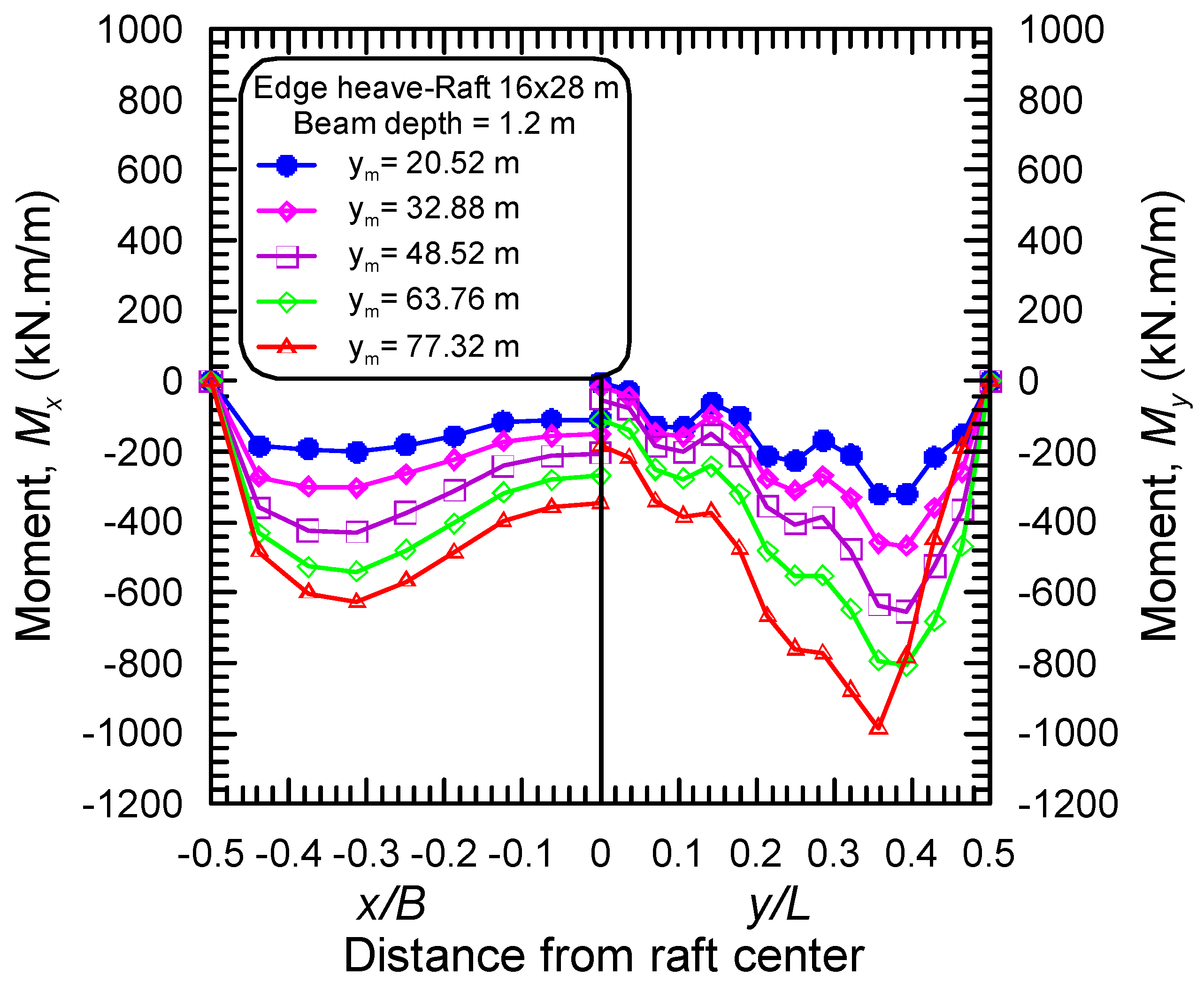
4.1. Effect of the Stiffening Beam Depth
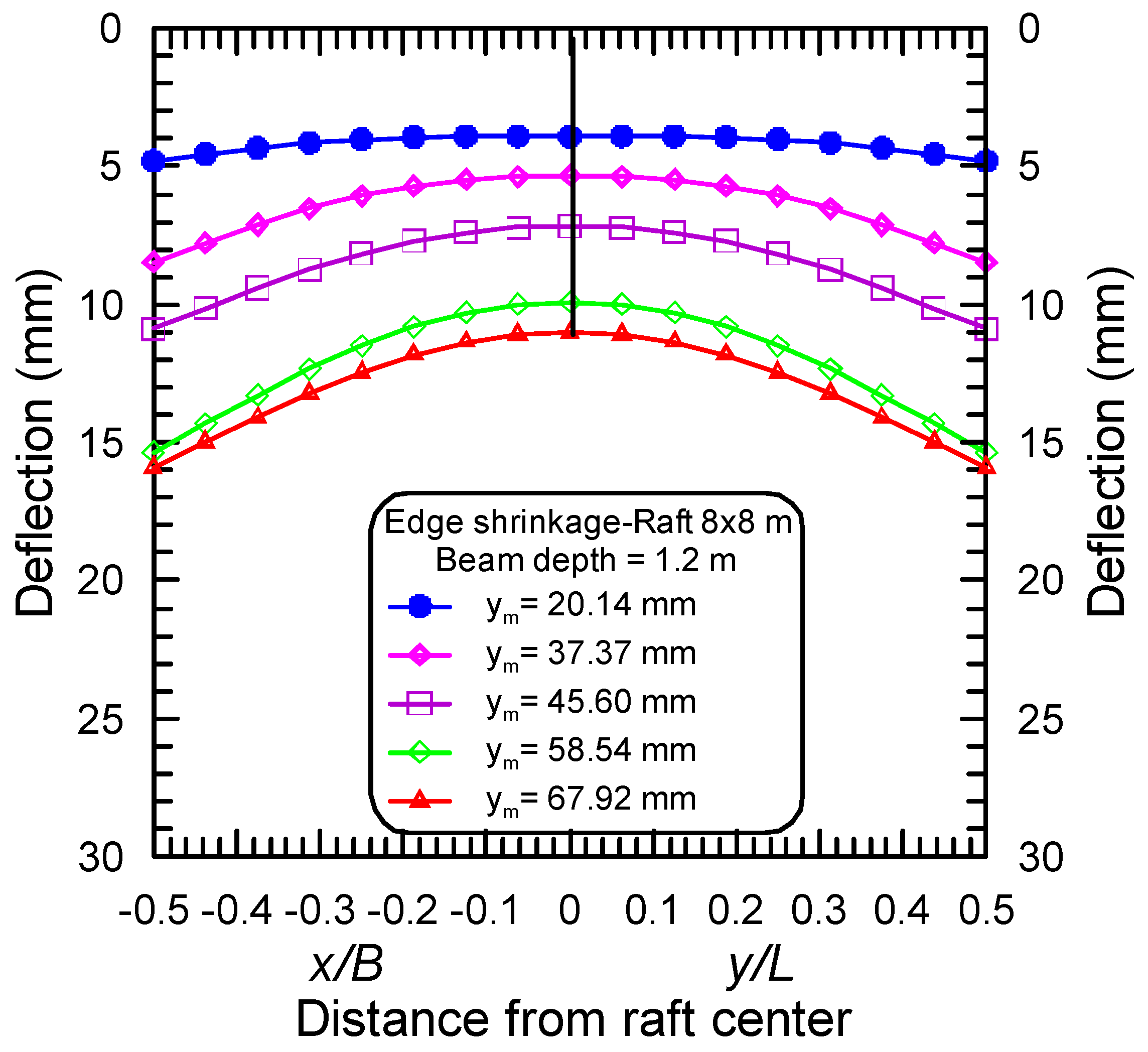
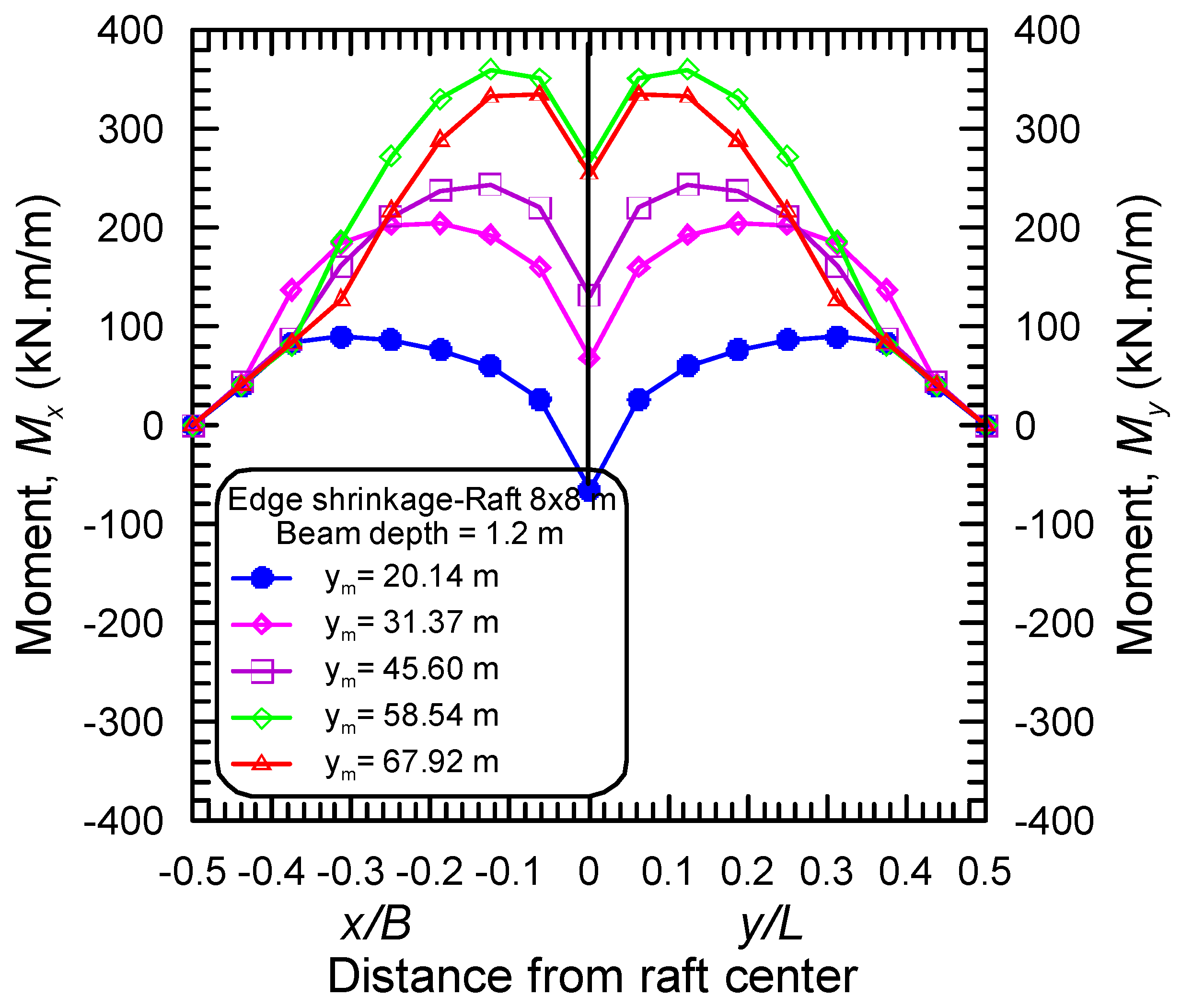
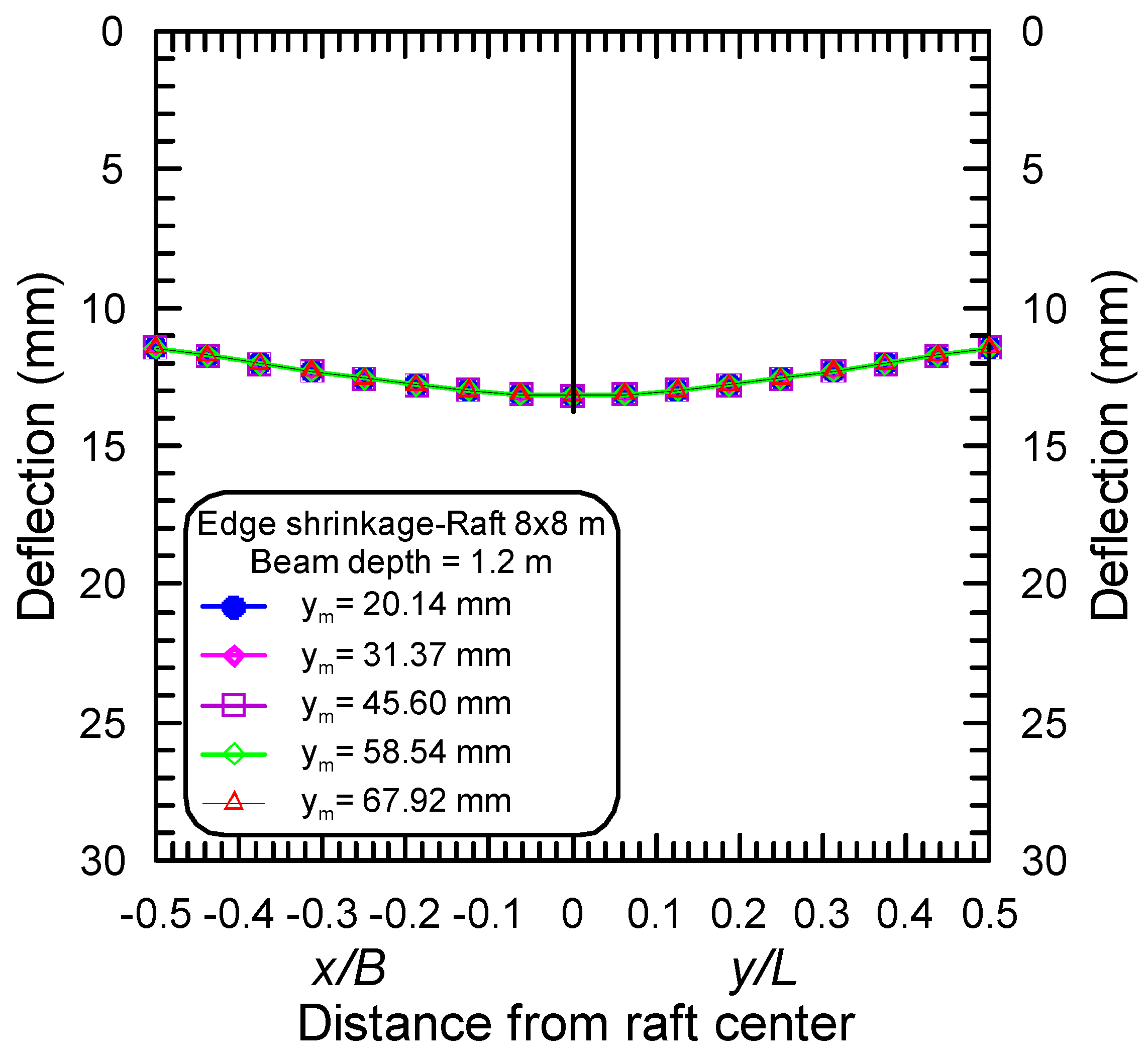
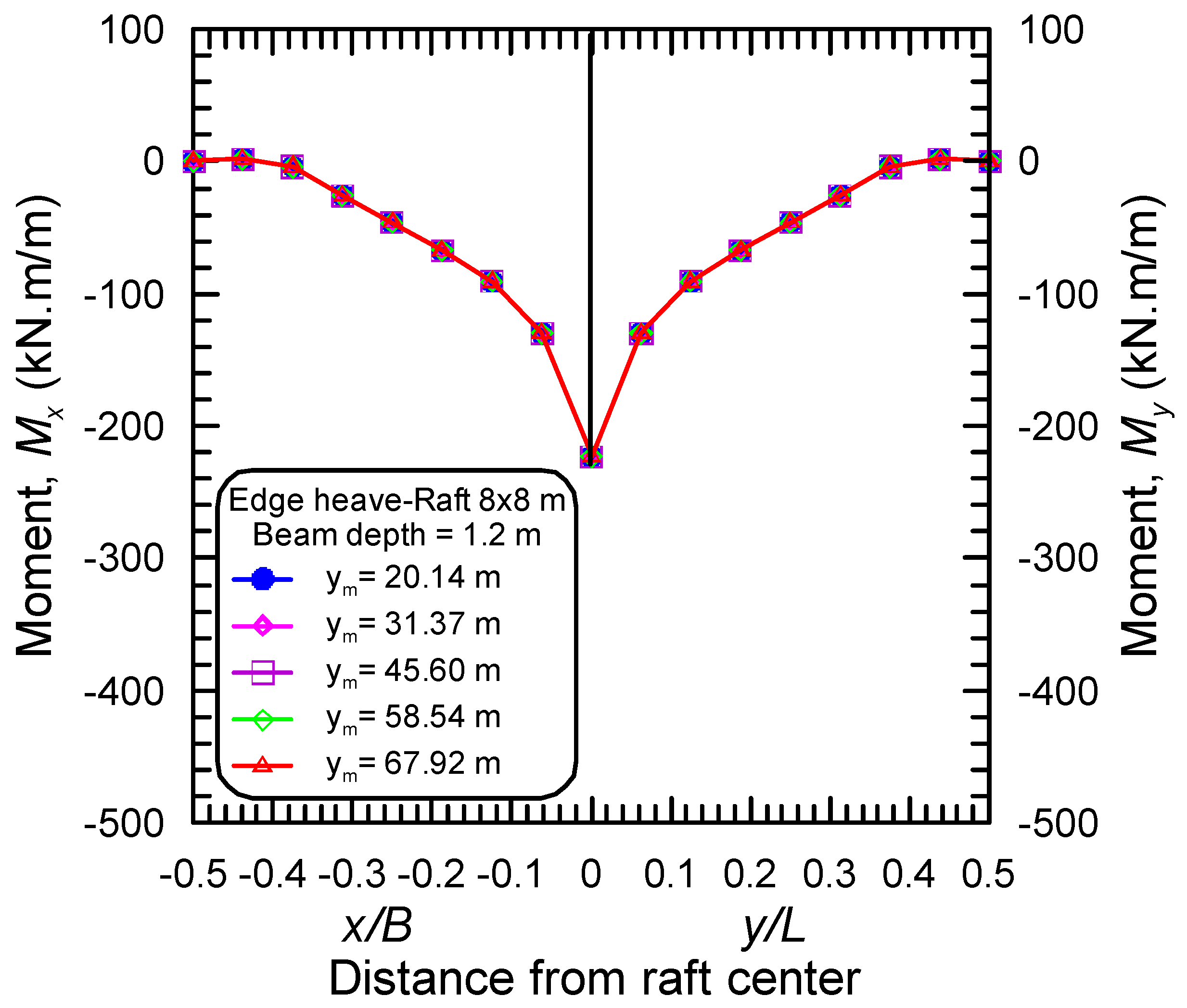
4.2. Effect of the Differential Movement of Mound Shape
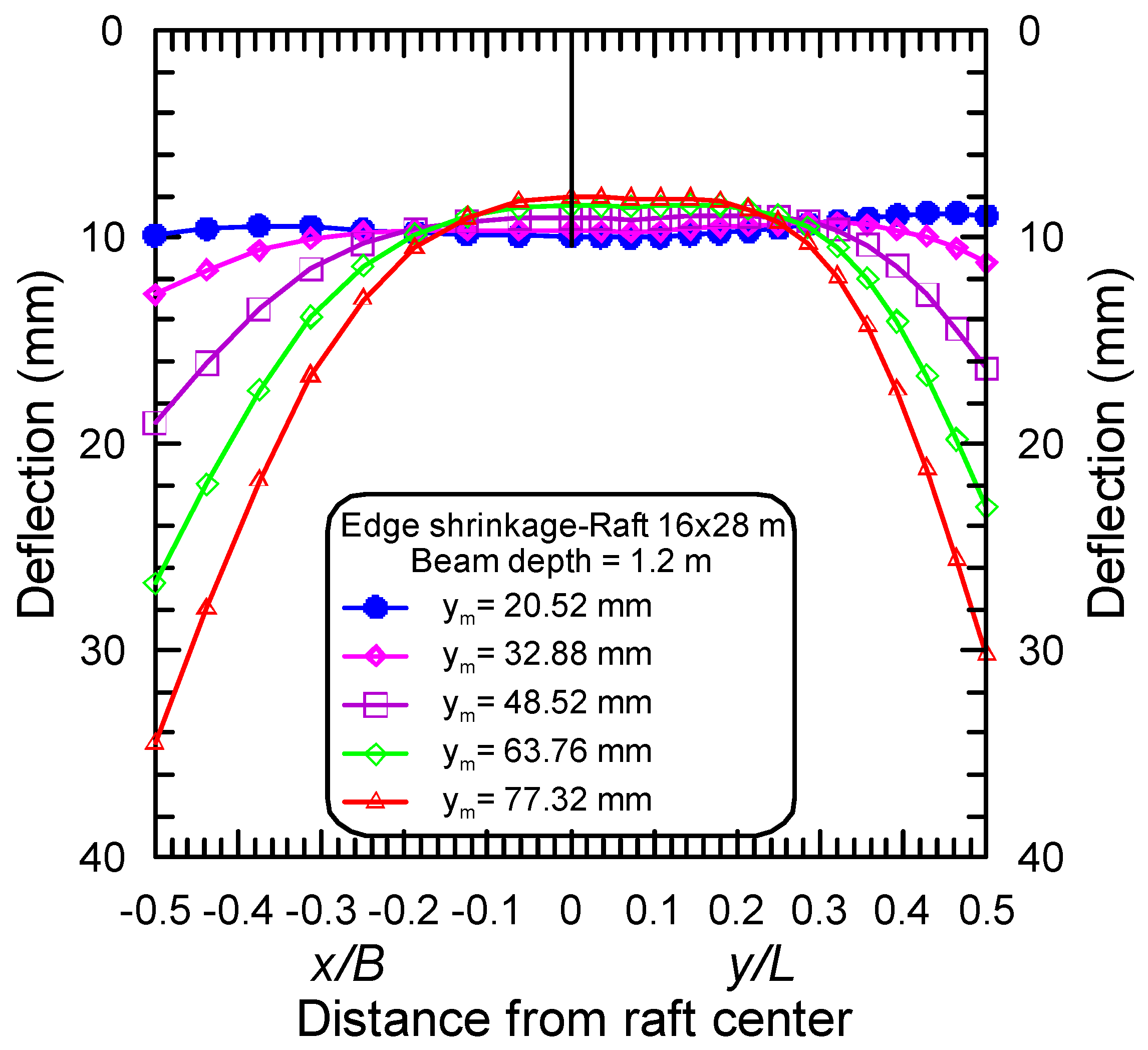
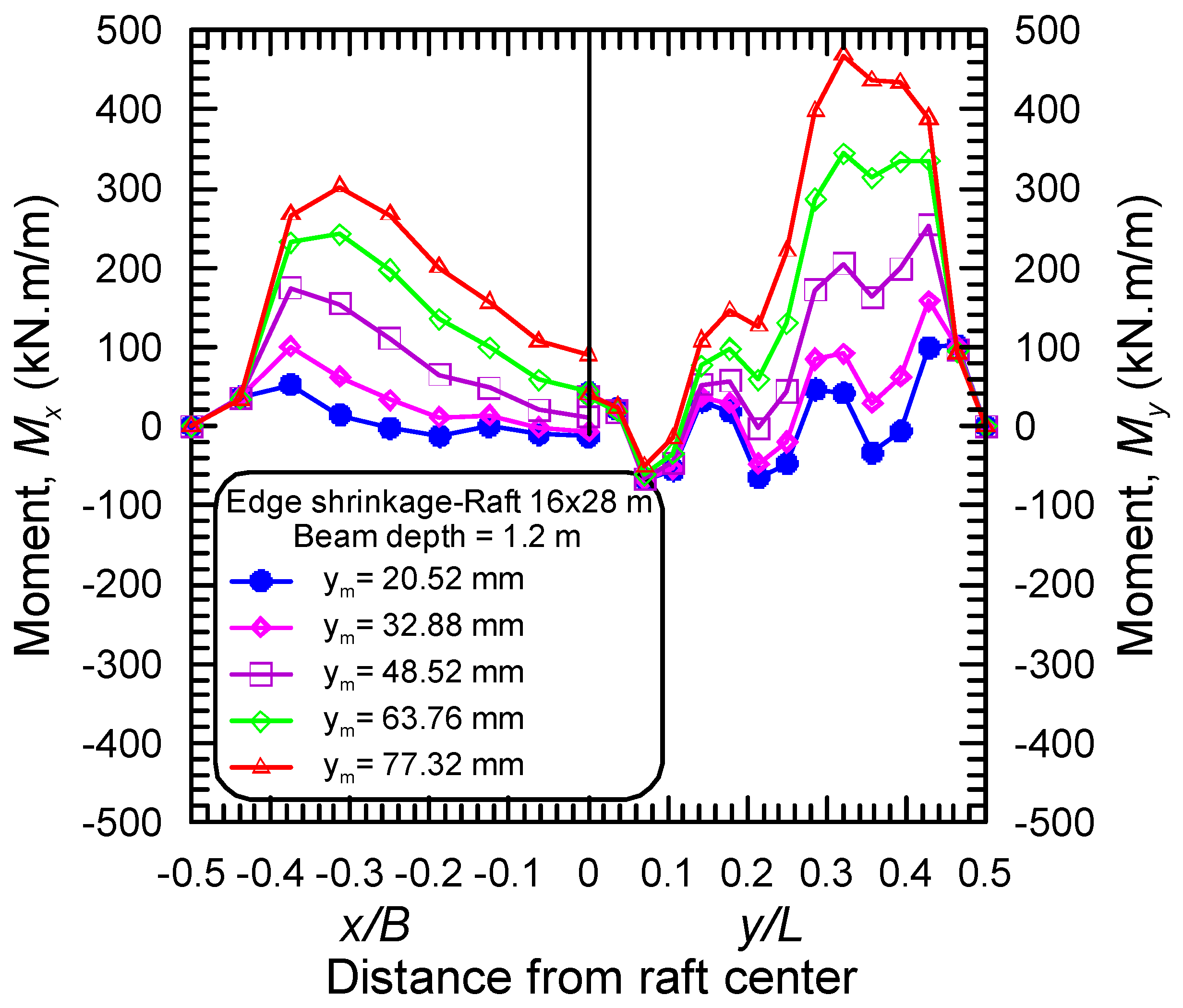
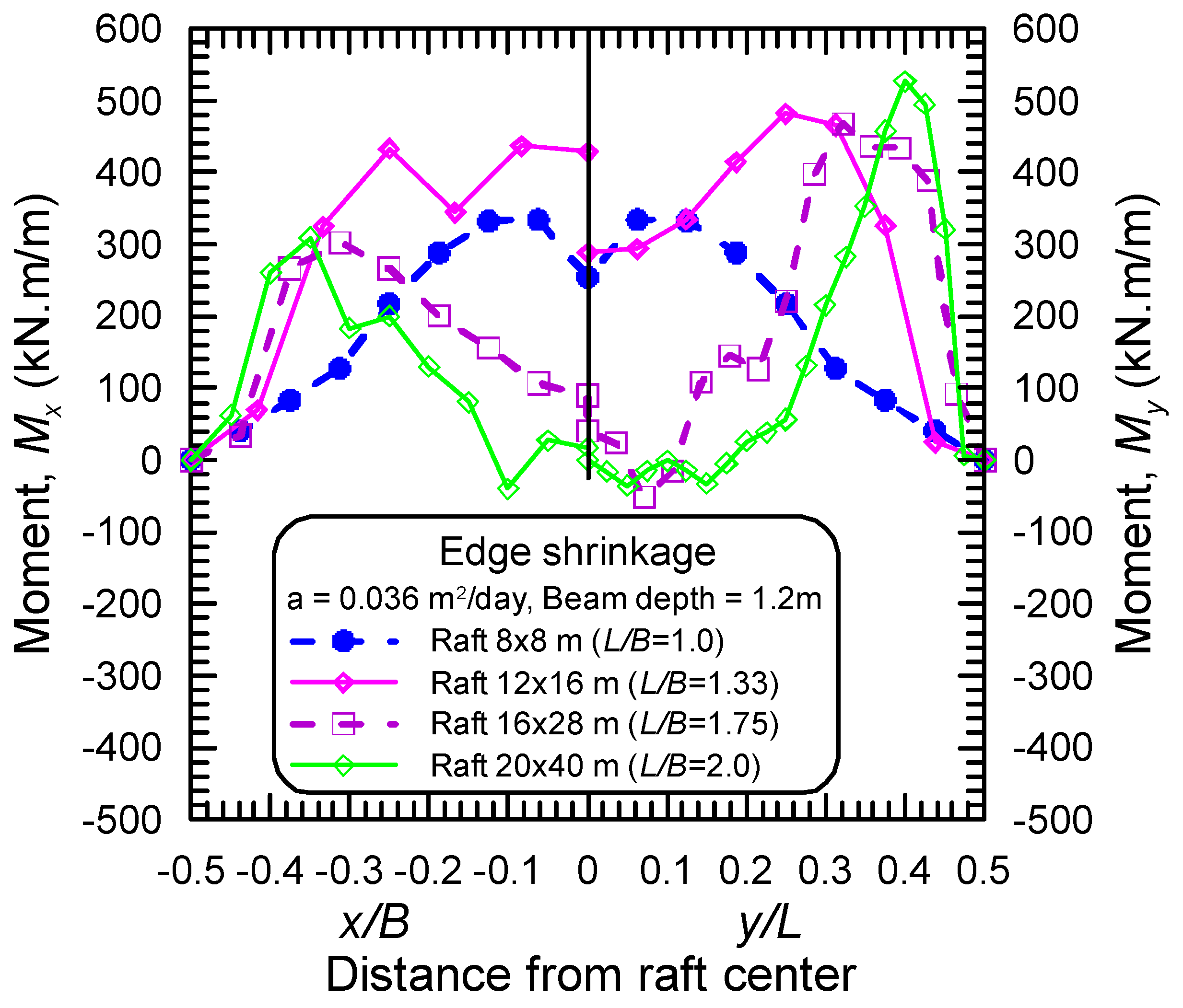
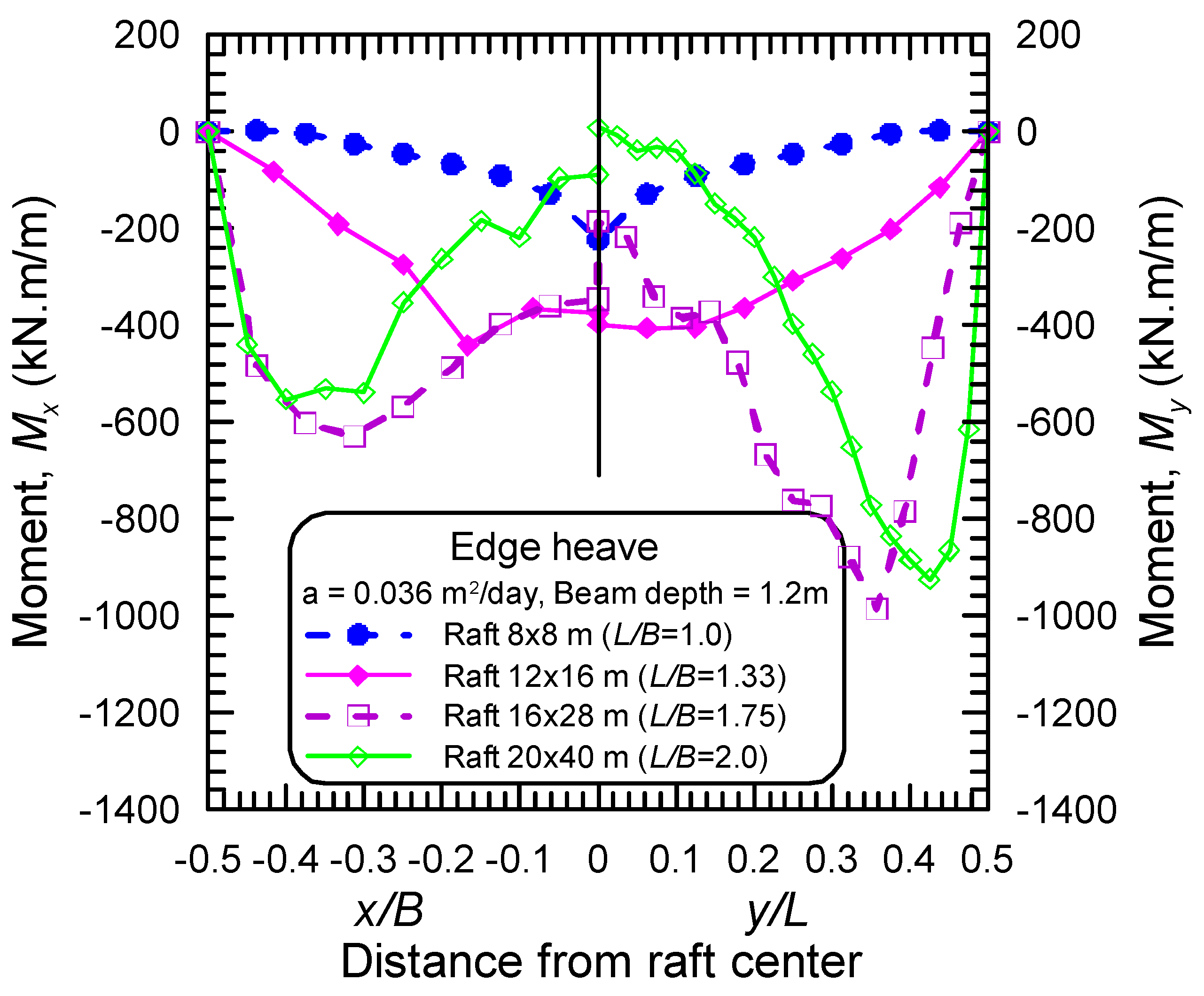
4.3. Effect of Raft Dimensions
5. Conclusions
- The stiffened rafts subjected to concentrated columns’ loads exhibit a similar shape of raft deformation and distribution of bending moments to those of the stiffened rafts subjected to uniform and perimeter line loads in both cases of distortion modes; however, the values of the design parameters (i.e., maximum deflection, maximum differential deflection, and maximum bending moments) are completely different.
- For the case of EH distortion mode, two conditions of soil support were observed; these are simply-support condition and multiple-supports condition (i.e., support at the raft perimeter and support at the raft core area), depending on the stiffness of the raft.
- The maximum bending moments in long and short directions, in both distortion modes, occur near the raft edge, and the distance from the raft edge to the locations of maximum moments depends on the stiffening beam depth, the maximum differential movement, and the aspect ratio of the raft.
- The greatest amount of differential deflection was found to occur at the corner of the raft, and its value is dependent on the stiffening beam depth, the maximum differential movement, and the raft dimensions.
- The stiffened raft components should be designed to withstand both negative moments and positive moments arising from both two distortion modes of ES and EH, respectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Cameron, D.A.; Ren, G. Case Study and Back Analysis of a Residential Building Damaged by Expansive Soils. Comput. Geotech. 2014, 56, 89–99. [Google Scholar] [CrossRef]
- Nelson, J.D.; Chao, K.C.; Overton, D.D.; Nelson, E.J. Foundation Engineering for Expansive Soils; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Wray, W.K. So Your Home Is Built on Expansive Soils: A Discussion of How Expansive Soils Affect Buildings; American Society of Civil Engineers: Reston, VA, USA, 1995. [Google Scholar]
- Krohn, J.P.; Slosson, J.E. Assessment of expansive soils in the United States. In Proceedings of the 4th International Conference on Expansive Soils, ASCE, Denver, CO, USA, 16–18 June 1980; pp. 596–608. [Google Scholar]
- Robert, L.; Andrew, B.; Mary, L.C. Soils Shrink, Trees Drink, and Houses Crack; ECOS Magazine; The Science Communication Unit of CSIRO’s Bureau of Scientific Services: Adelaide, Australia, 1980; pp. 13–15. [Google Scholar]
- Dafalla, M.A.; Al-Shamrani, M.A.; Al-Mahbashi, A. Expansive soils foundation practice in a semiarid region. J. Perform. Constr. Facil. 2017, 31, 04017084. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Fredlund, D.G. The Implementation of Unsaturated Soil Mechanics into Geotechnical Engineering. Can. Geotech. J. 2000, 37, 963–986. [Google Scholar] [CrossRef]
- Erol, O.A.; Dhowian, A.W. Swell and shrinkage behavior of Madinish active clays. J. Eng. Sci. 1982, 1–8. [Google Scholar]
- Dhowian, A.W.; Ruwaih, I.A.; Erol, A.O. The distribution and evaluation of the expansive soils in Saudi Arabia. In Proceedings of the Second Saudi Engineers Conference, Dhahran, Saudi Arabia, 17–19 November 1985; Volume 1, pp. 308–326. [Google Scholar]
- Ruwaih, I.A. Experiences with Expansive Soils in Saudi Arabia. In Proceedings of the 6th International Conference on Expansive Soils, New Delhi, India, 1–4 December 1987; pp. 317–322. [Google Scholar]
- Abduljauwad, S.N.; Al-Sulaimani, G.J.; Al-Buraim, I.; Basunbul, I.A. Laboratory and field studies of response of structures to heave of expansive clay. Géotechnique 1998, 48, 103–121. [Google Scholar] [CrossRef]
- Slater, D.E. Potential Expansive Soils in Arabian Peninsula. American Society for Civil Engineering. Geotherm. Eng. 1983, 109, 744–746. [Google Scholar]
- Abduljauwad, S.N.; Ahmed, R. Expansive Soil in Al-Qatif Area. Arab. J. Sci. Eng. 1990, 15, 133–144. [Google Scholar]
- Dhowian, A.W.; Erol, A.O.; Youssef, A. Evaluation of Expansive Soils and Foundation Methodology in the Kingdom of Saudi Arabia; General Directorate Research Grants Programs, King Abdulaziz City for Science and Technology: Riyadh, Saudi Arabia, 1990.
- Abduljauwad, S.N. Swelling Behavior of Calcareous Clays from the Eastern Province of Saudi Arabia. J. Eng. Geol. 1994, 27, 333–351. [Google Scholar]
- Al-Refeai, T.; Al-Ghamdy, D. Geological and geotechnical aspects of Saudi Arabia. Geotech. Geol. Eng. 1994, 12, 253–276. [Google Scholar] [CrossRef]
- Dafalla, M.; Al-Shamrani, M. Geocharacteristics of Tabuk Expansive Shale and Its Links to Structural Damage; Geo-Congress 2014 Technical Papers; American Society of Civil Engineers: Reston, VA, USA, 2014; pp. 882–889. [Google Scholar]
- Sabtan, A.A. Geotechnical Properties of Expansive Clay Shale in Tabuk, Saudi Arabia. J. Asian Earth Sci. 2005, 25, 747–757. [Google Scholar] [CrossRef]
- Dafalla, M.A.; Al-Shamrani, M.A. “Performance-Based Solutions for Foundations on expansive Soils-Al Ghatt Region”, Saudi Arabia. In Proceedings of the International Conference on Geotechnical Engineering, Chiangmai, Thailand, 10–12 December 2008. [Google Scholar]
- Dafalla, M.A.; Al-Shamrani, M.A. Expansive Soil Properties in a Semi-Arid Region. Res. J. Environ. Earth Sci. 2012, 4, 930–938. [Google Scholar]
- Dafalla, M.A.; Al-Shamrani, M.A.; Puppala, A.; Ali, H.E. Use of Rigid Foundation System on Expansive Soils; GSP (Geotechnical Special Publication); American Society for Civil Engineers (ASCE): Reston, VA, USA, 2010; p. 199. [Google Scholar]
- Shams, M.A.; Shahin, M.A.; Ismail, M.A. Design of stiffened slab foundations on reactive soils using 3D numerical modeling. Int. J. Geomech. 2020, 20, 04020097. [Google Scholar] [CrossRef]
- Wray, W.K.; El-Garhy, B.M.; Youssef, A.A. Three-Dimensional Model for Moisture and Volume Changes Prediction in Expansive Soils. American Society of Civil Engineering, ASCE. J. Geotech. Geoenviron. Eng. 2005, 131, 311–324. [Google Scholar] [CrossRef]
- Briaud, J.L.; Abdelmalak, R.; Zhang, X.; Magbo, C. Stiffened slab-on-grade on shrink-swell soil: New design method. J. Geotech. Geoenviron. Eng. 2016, 142, 04016017. [Google Scholar] [CrossRef]
- Building Research Advisory Board (BRAB). Criteria for Selection and Design of Residential Slabs-on-Ground; National Research Council, Academy of Sciences, Publication 1571; Building Research Advisory Board (BRAB): Washington, DC, USA, 1968. [Google Scholar]
- Lytton, H. Observation Studies of Parent-Child Interaction, A Methodological Review. Child Dev. 1971, 42, 651–684. [Google Scholar] [CrossRef]
- Walsh, D.S. Papers in Pidgin and Creole Linguistics No. 1. (Pacific Linguistics A-54); Australian National University Press: Canberra, Australia, 1978; pp. 185–197. [Google Scholar]
- Holland, J.E.; Pitt, W.G.; Lawrance, C.E.; Cimino, D.J. The Behavior and Design of Housing Slabs on Expansive Soils. In Proceedings of the Fourth International Conference on Expansive Soils, Denver, CO, USA, 16–18 June 1980; Volume 1, pp. 448–468. [Google Scholar]
- Mitchell, P. A Simple method of design of shallow footings on expansive soil. In Proceedings of the 5th International Conference on Expansive Soils, Adelaide, SA, USA, 21–23 May 1984. [Google Scholar]
- Post-Tensioning Institute (PTI). Design and Construction of Post-Tensioned Slabs-on-Ground, 2nd ed.; Post-Tensioning Institute: Phoenix, AZ, USA, 1996. [Google Scholar]
- Wray, W.K. Development of a Design Procedure for Residential and Light Commercial Slabs-on-Ground Constructed over Expansive Soils. Ph.D. Dissertation, Texas A&M University, College Station, TX, USA, 1978. [Google Scholar]
- Mitchell, P.W. The Design of Footings on Expansive Soils. Engineering Problems of Regional Soils. In Proceedings of the International Conference, Beijing, China, 8–12 August 1988; pp. 127–135. [Google Scholar]
- Teodosio, B.; Baduge, K.S.K.; Pmendis, P. A review and comparison of design methods for raft substructures on expansive soils. J. Build. Eng. 2021, 41, 102737. [Google Scholar] [CrossRef]
- Pidgeon, J.D. A Comparison of the suitability of two soils for direct drilling of spring barley. Eur. J. Soil Sci. 1980, 31, 581–594. [Google Scholar] [CrossRef]
- El-Garhy, B.M.; Wray, W.K.; Youssef, A.A. Using Soil Diffusion to Design Raft Foundation on Expansive Soils. In Proceedings of the Sessions of Geo-Denver, Denver, CO, USA, 3–8 August 2000; Geotechnical Special Publication No. 99. ASCE: Reston, VA, USA, 2000; pp. 586–602. [Google Scholar]
- El-Garhy, B.M.; Youssef, A.A.; Wray, W.K. Predicted and Measured Suction and Volume Changes in Expansive Soil. In Proceedings of the International Symposium on Suction, Swelling, Permeability and Structure of Clays, Shizuoka, Japan, 11–13 January 2001. [Google Scholar]
- El-Garhy, B.M.; Wray, W.K. Method for Calculating the Edge Moisture Variation Distance. J. Geotech. Geoenviron. Eng. 2004, 130, 945–955. [Google Scholar] [CrossRef]
- Mitchell, P.W. The Structural Analysis of Footings on Expansive Soil; Research Report No. I; Kenneth W. G. Smith and Associates: Adelaide, Australia, 1979. [Google Scholar]
- Wray, W.K. Using Soil Suction to Estimate Differential Soil Shrink or Heave; Unsaturated Soil Engineering Practice, Geotechnical Special Publication No. 68; American Society of Civil Engineers: Reston, VA, USA, 1997; pp. 66–87. [Google Scholar]
- E1-Garhy, B.M. Soil Suction and Analysis of Raft Foundation Resting on Expansive Soils. Ph.D. Dissertation, Civil Engineering Department, Menoufia University, Shebin EI-Koon, Egypt, 1999. [Google Scholar]
- Abu-Ali, M.H.; El-Garhy, B.; Boraey, A.; Al-Rashed, W.S.; Abdel-Daiem, H. Estimating the Climate-Controlled Soil Parameters and the Distorted Mound Shape for Analysis of Stiffened Rafts on Expansive Soils. Adv. Civ. Eng. 2024, 2024, 5599356. [Google Scholar] [CrossRef]
- Shams, M.A.; Shahin, M.A.; Ismail, M.A. Analysis and Modelling of Stiffened Slab Foundation on Expansive Soils. In Numerical Analysis of Nonlinear Coupled Problems, GeoMEast 2017, Sustainable Civil Infrastructures; Shehata, H., Rashed, Y., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- AS2870-2011; Residential Slabs and Footings. Australian Standards: Sydney, NSW, Australia, 2011.
- Hibbeler, R.C. Structural Analysis, 7th ed.; Prentice Hall: Saddle River, NJ, USA, 2011. [Google Scholar]












|
(m) |
(kPa) |
(kPa) |
|
|
| ||
|---|---|---|---|---|---|---|---|
| 5.0 | 4.0 (1000) | 2.0 (10) | 0.02 | 0.00144 0.00432 0.0104 0.0200 0.0360 | 8 × 8 12 × 16 16 × 28 20 × 40 | 1.00 1.33 1.75 2.00 | 0.30 0.60 0.90 1.20 1.50 |
| Site Classes According to AS2870-2011 [44] | ||||||
|---|---|---|---|---|---|---|
| Class | Site classification | ) | ) | |||
| S | Slightly reactive | 20.14 | 20.52 | 20.52 | 20.52 | |
| M | Moderately reactive | 31.37 | 32.88 | 32.88 | 32.88 | |
| H1 | Highly reactive | 45.60 | 48.52 | 48.52 | 48.51 | |
| H2 | Highly reactive | 58.54 | 63.68 | 63.76 | 63.75 | |
| E | Extremely reactive | 67.92 | 76.77 | 77.32 | 77.37 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abu-Ali, M.H.; El-Garhy, B.; Boraey, A.; Alrashed, W.S.; El-Shami, M.; Abdel-Daiem, H.; Alrefahi, B. Behavior of Stiffened Rafts Resting on Expansive Soil and Subjected to Column Loads of Lightweight-Reinforced Concrete Structures. Buildings 2024, 14, 588. https://doi.org/10.3390/buildings14030588
Abu-Ali MH, El-Garhy B, Boraey A, Alrashed WS, El-Shami M, Abdel-Daiem H, Alrefahi B. Behavior of Stiffened Rafts Resting on Expansive Soil and Subjected to Column Loads of Lightweight-Reinforced Concrete Structures. Buildings. 2024; 14(3):588. https://doi.org/10.3390/buildings14030588
Chicago/Turabian StyleAbu-Ali, Mohamed H., Basuony El-Garhy, Ahmed Boraey, Wael S. Alrashed, Mostafa El-Shami, Hassan Abdel-Daiem, and Badrelden Alrefahi. 2024. "Behavior of Stiffened Rafts Resting on Expansive Soil and Subjected to Column Loads of Lightweight-Reinforced Concrete Structures" Buildings 14, no. 3: 588. https://doi.org/10.3390/buildings14030588
APA StyleAbu-Ali, M. H., El-Garhy, B., Boraey, A., Alrashed, W. S., El-Shami, M., Abdel-Daiem, H., & Alrefahi, B. (2024). Behavior of Stiffened Rafts Resting on Expansive Soil and Subjected to Column Loads of Lightweight-Reinforced Concrete Structures. Buildings, 14(3), 588. https://doi.org/10.3390/buildings14030588







