Axial Compression Behavior of Elliptical Concrete-Filled Steel Tube Composite Short Columns with Encased Steel Considering Spherical-Cap Gap
Abstract
1. Introduction
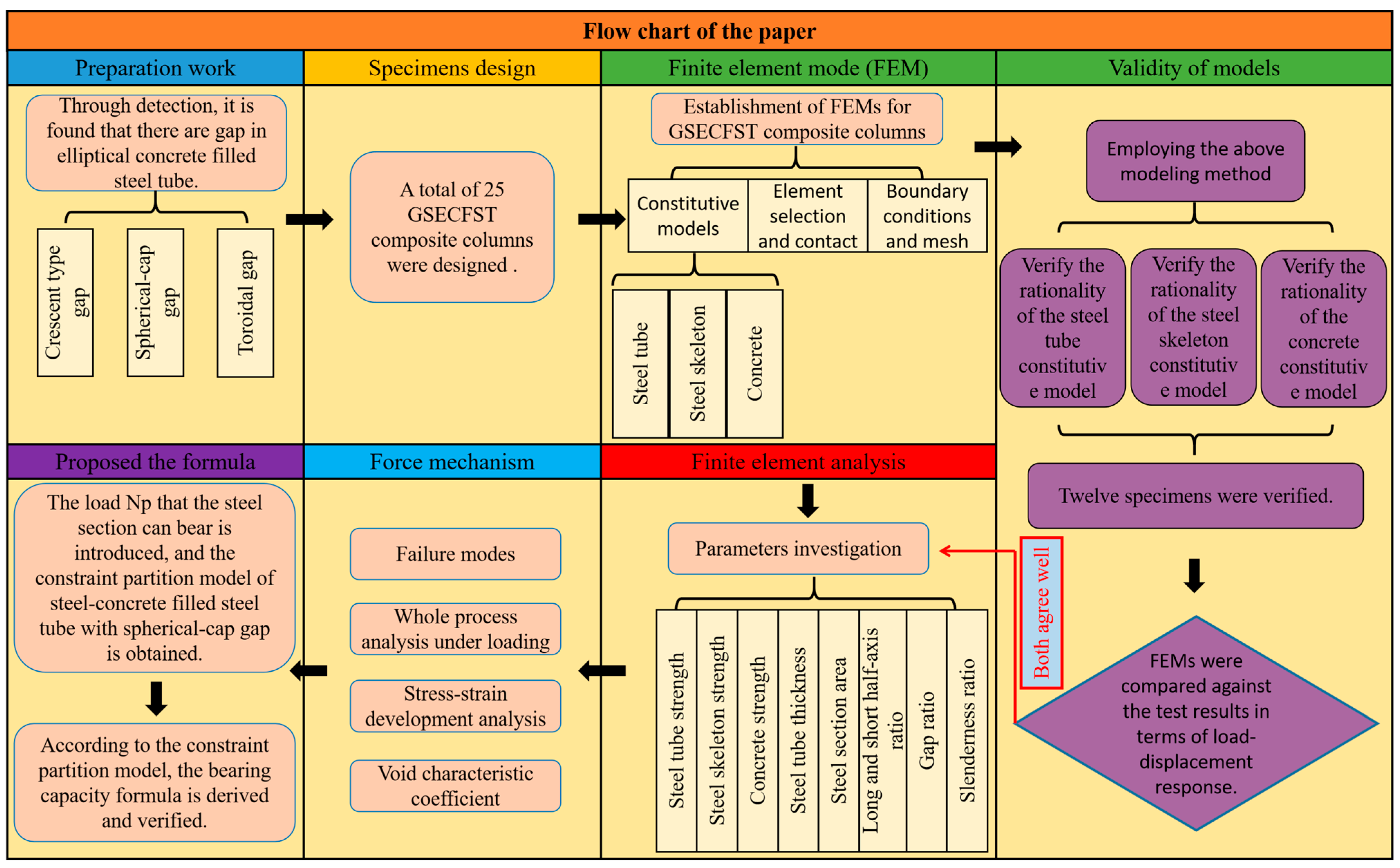
2. Analysis of the Paper
3. Specimen Design
4. Finite Element Model (FEM)
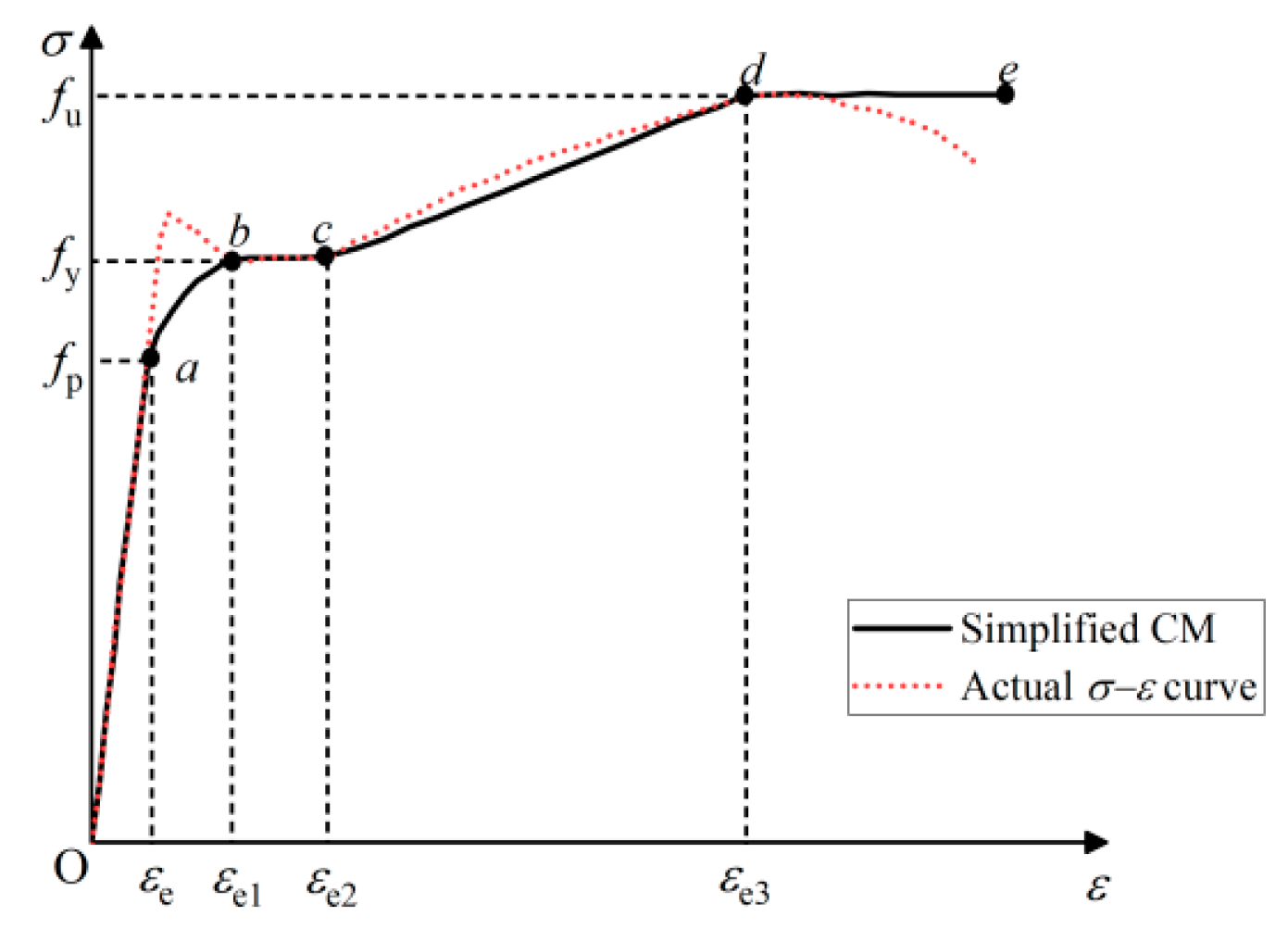
4.1. Constitutive Model for the Materials
4.1.1. Constitutive Models of Steel Tube
4.1.2. Constitutive Models of Cross-Shaped Steel Skeleton
4.1.3. Concrete Constitutive Models
4.2. Element Selection and Contact
4.3. Boundary Conditions
5. Experimental Verification of Finite Element Model
5.1. Existing Test
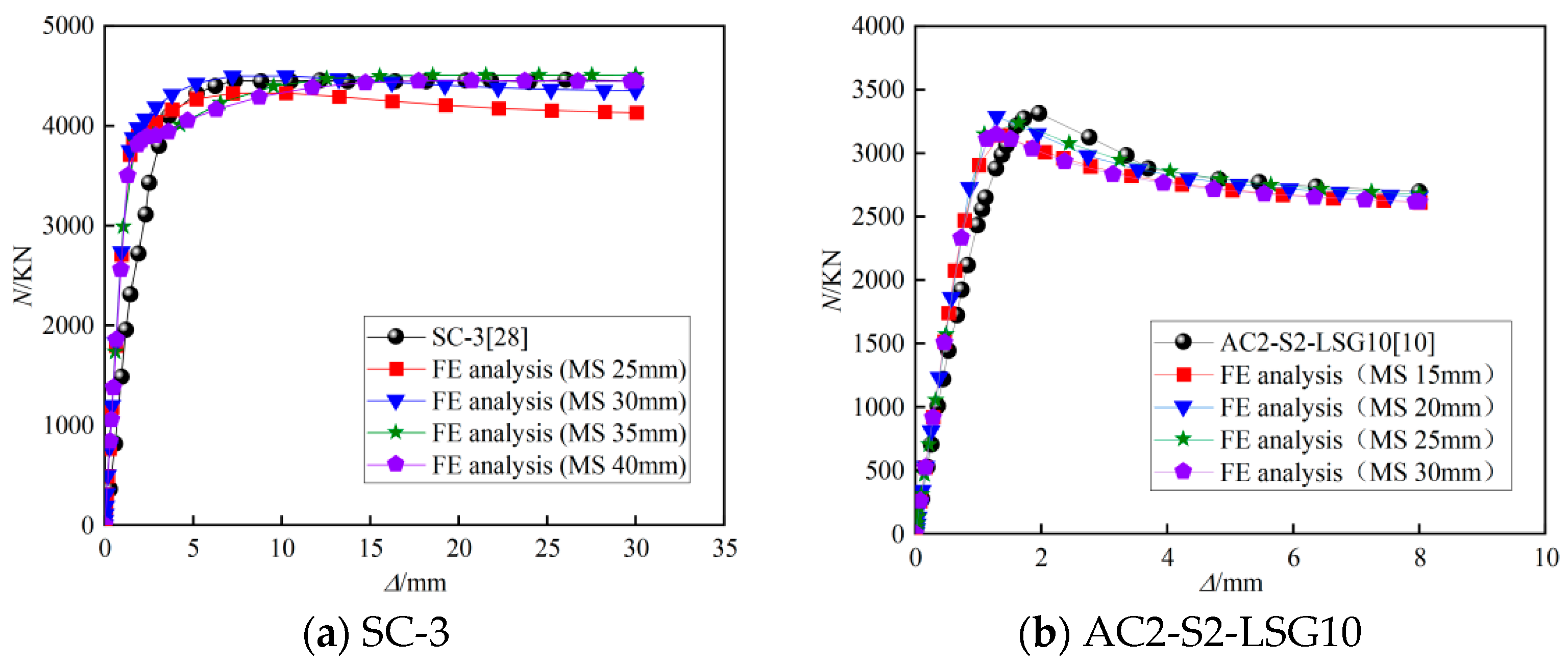
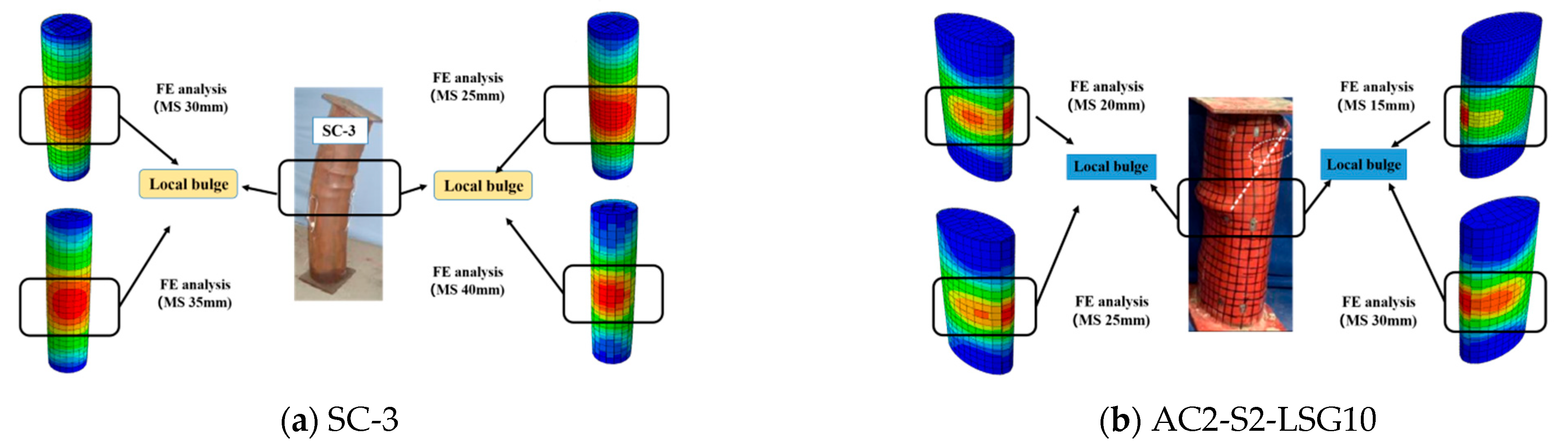
5.2. Grid Independence Analysis
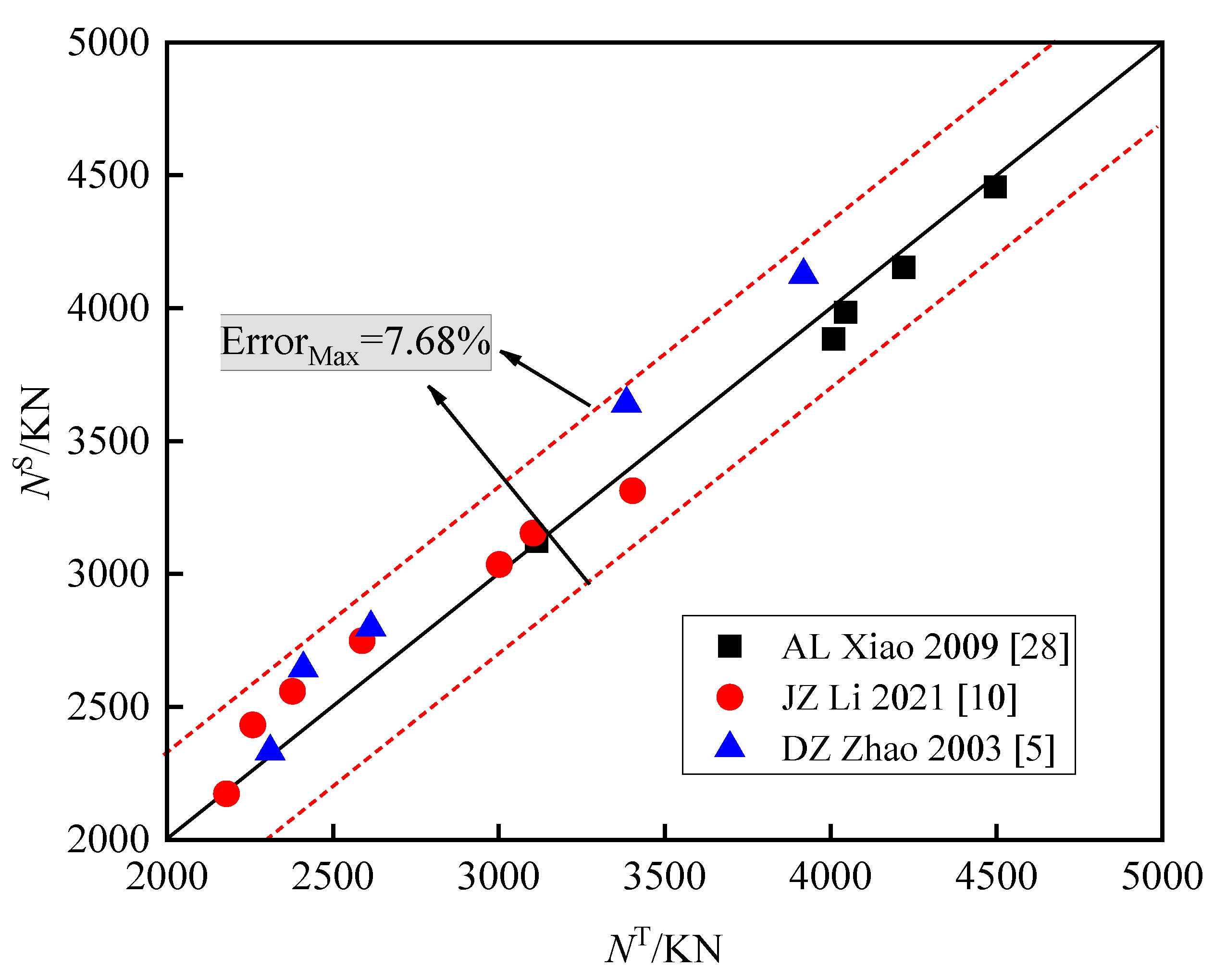
5.3. Verification Result
6. Parametrical Investigations
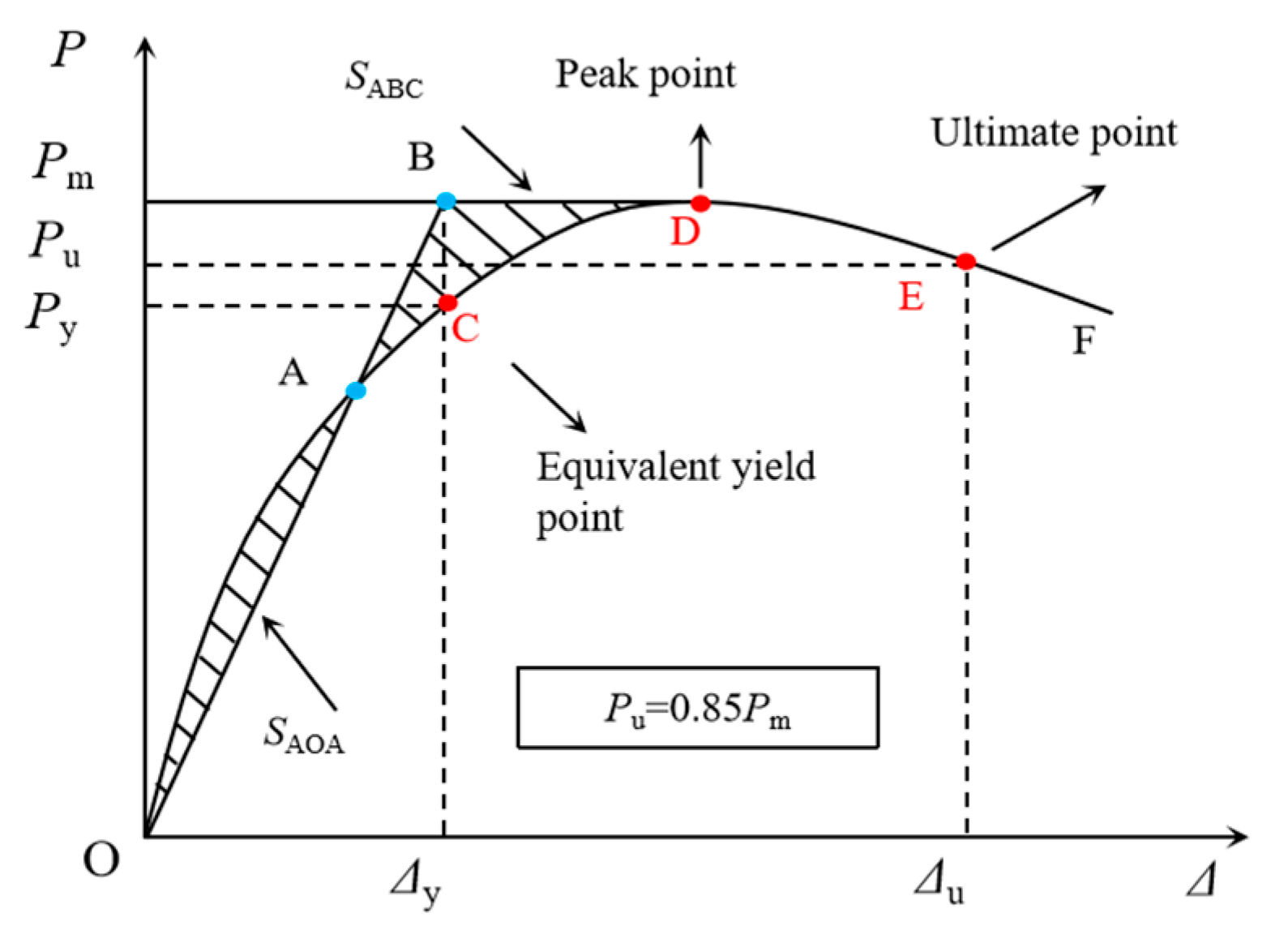
6.1. Ductility
6.2. Steel Tube Yield Strength (fty)
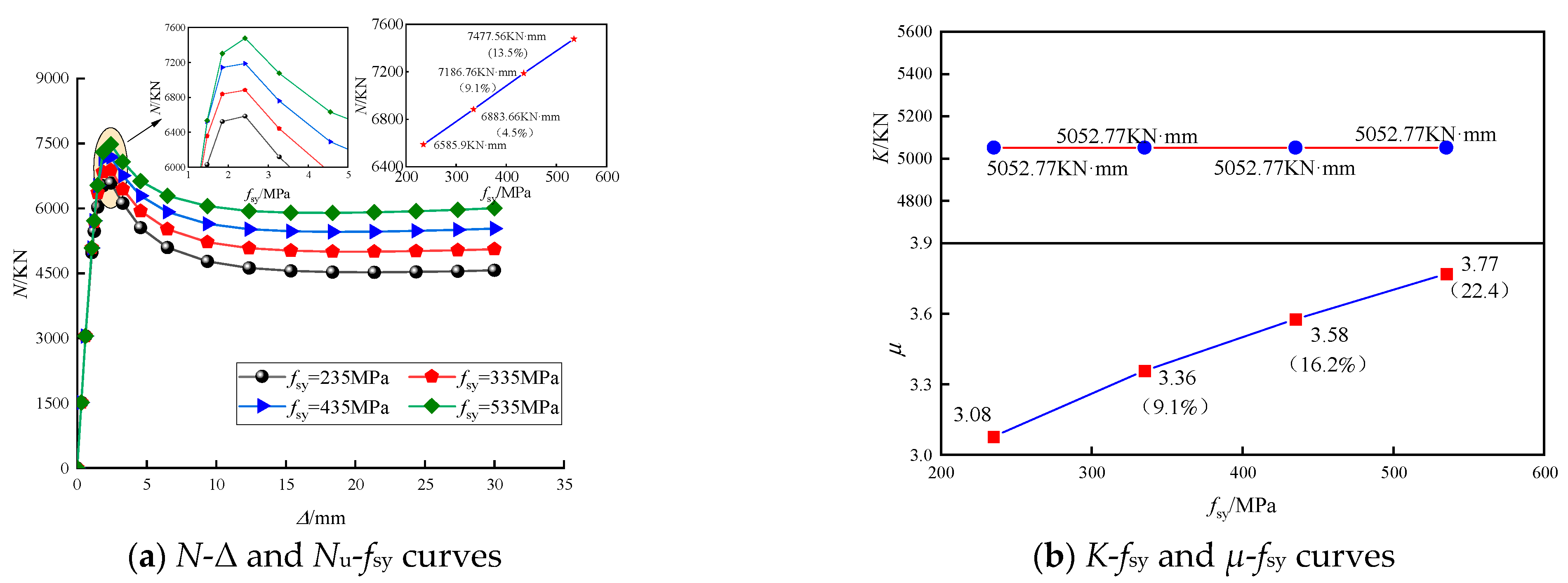
6.3. Steel Skeleton Yield Strength (fsy)
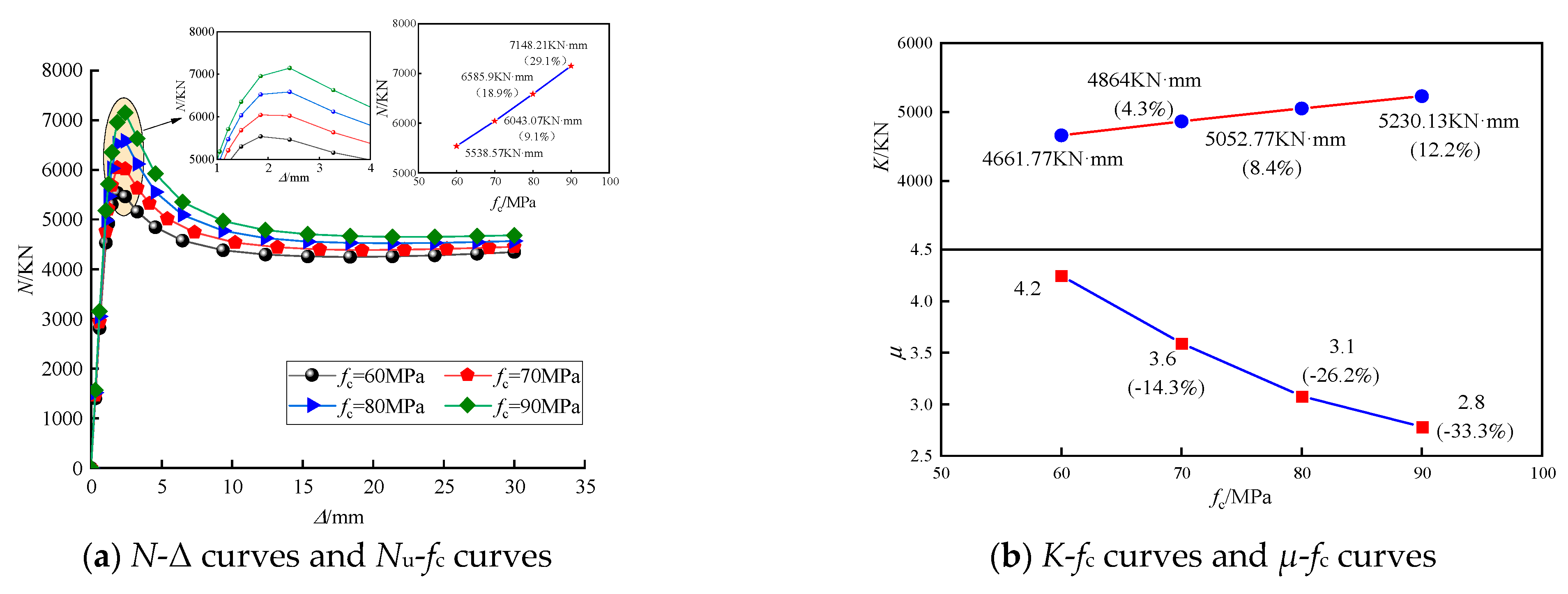
6.4. Concrete Axial Compressive Strength (fc)
6.5. Steel Tube Thickness (t)
6.6. Steel Cross-Sectional Area (Asy)
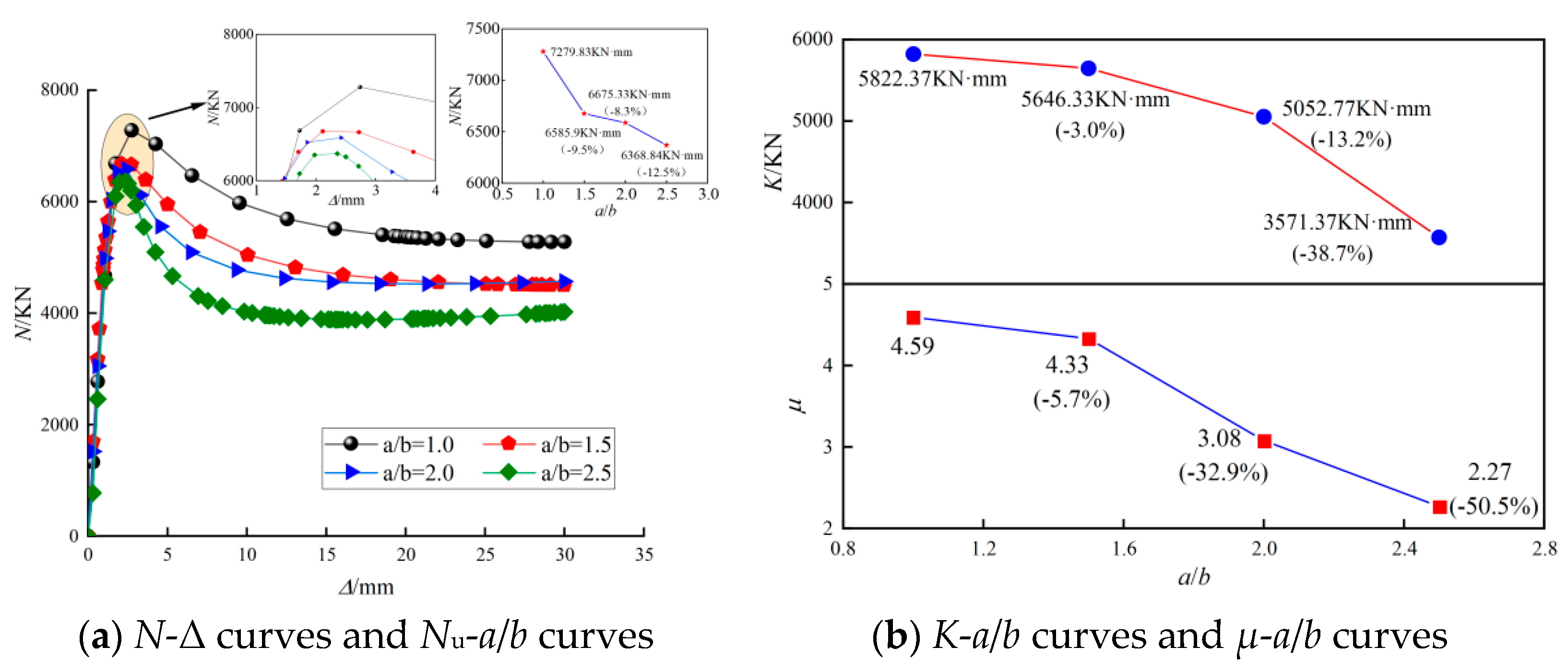
6.7. Long and Short Half Axis Ratio (a/b)
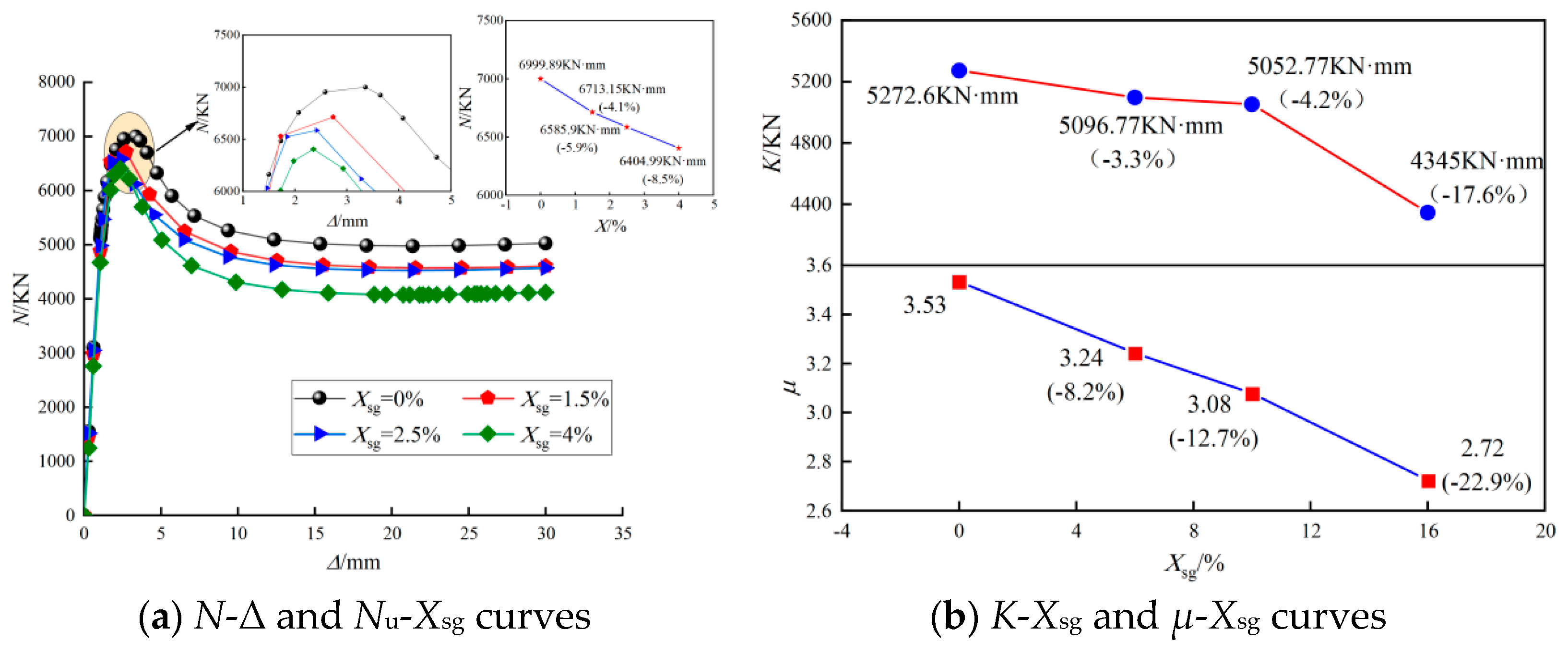
6.8. The Gap Ratio (Xsg)
6.9. The Slenderness Ratio (λ)
7. Force Mechanism
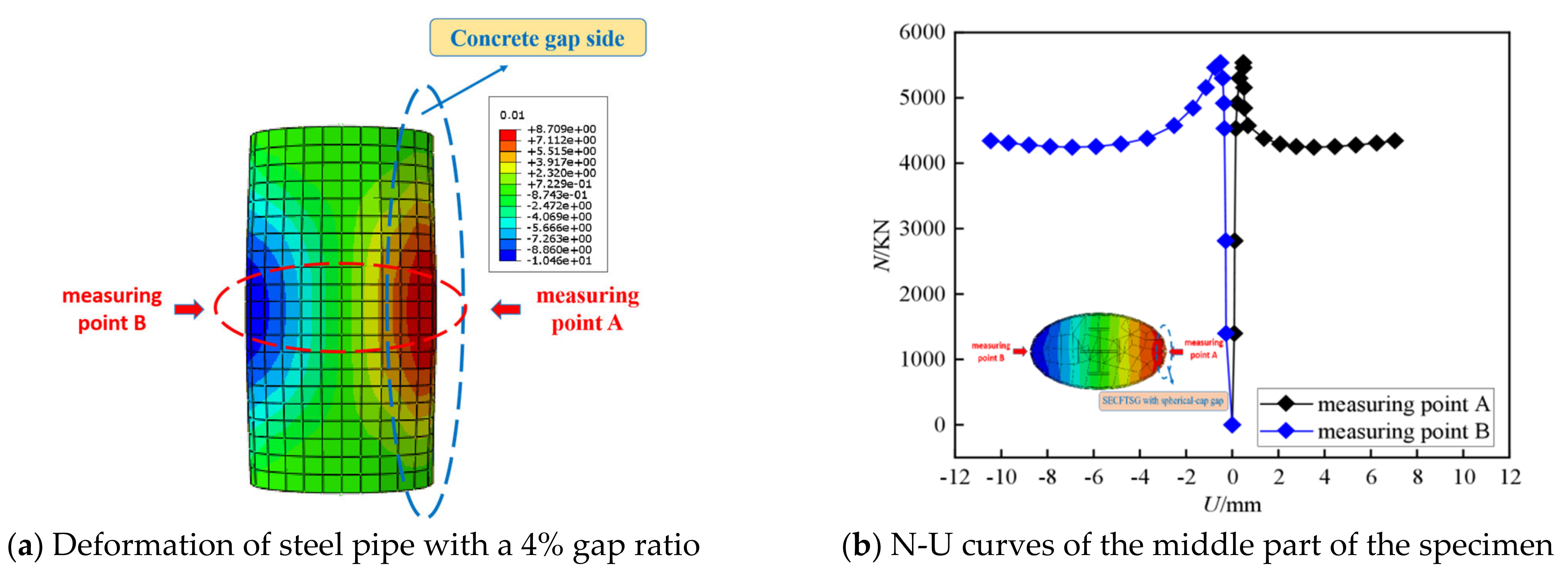
7.1. Failure Mode
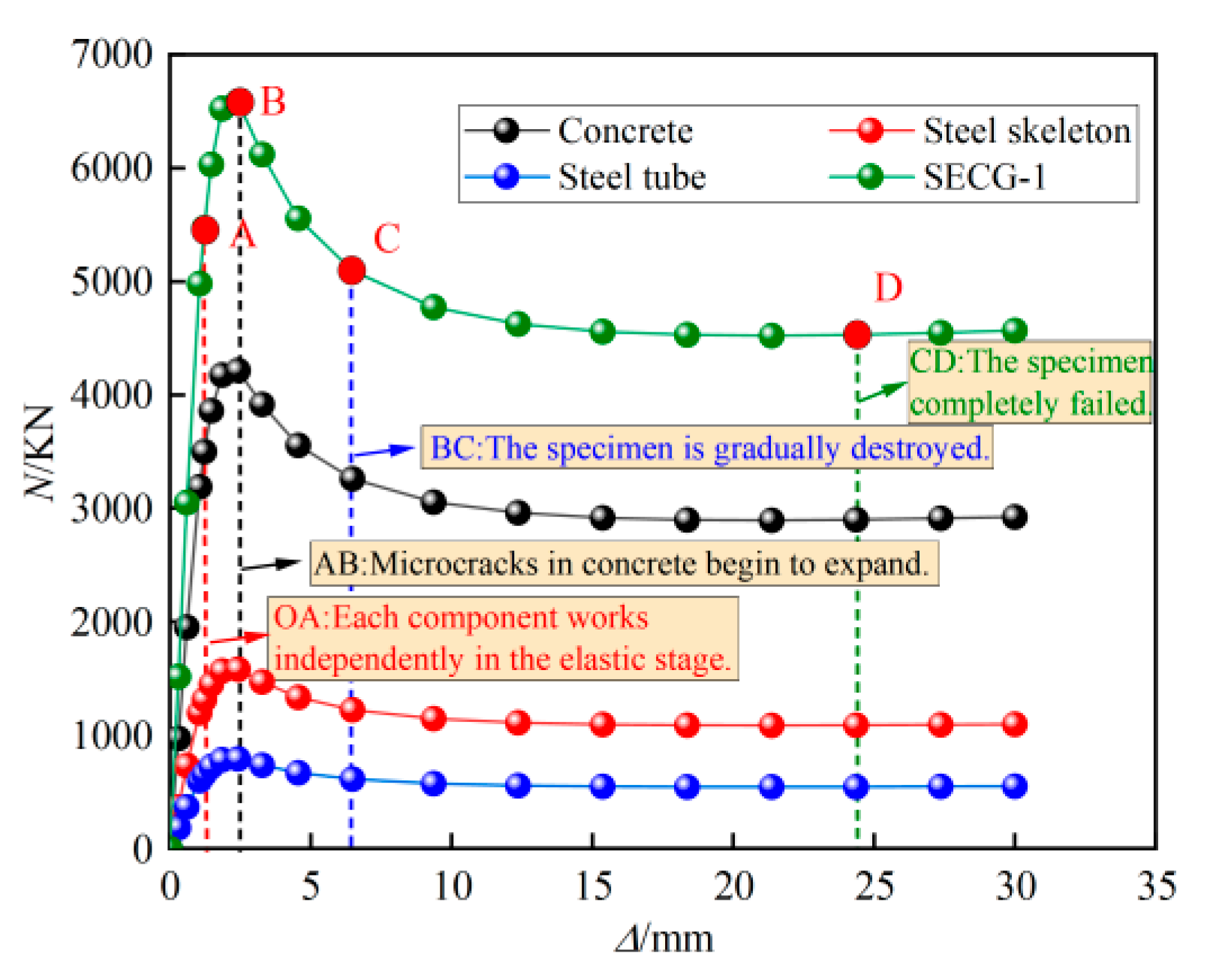
7.2. Whole N-Δ Process Analysis
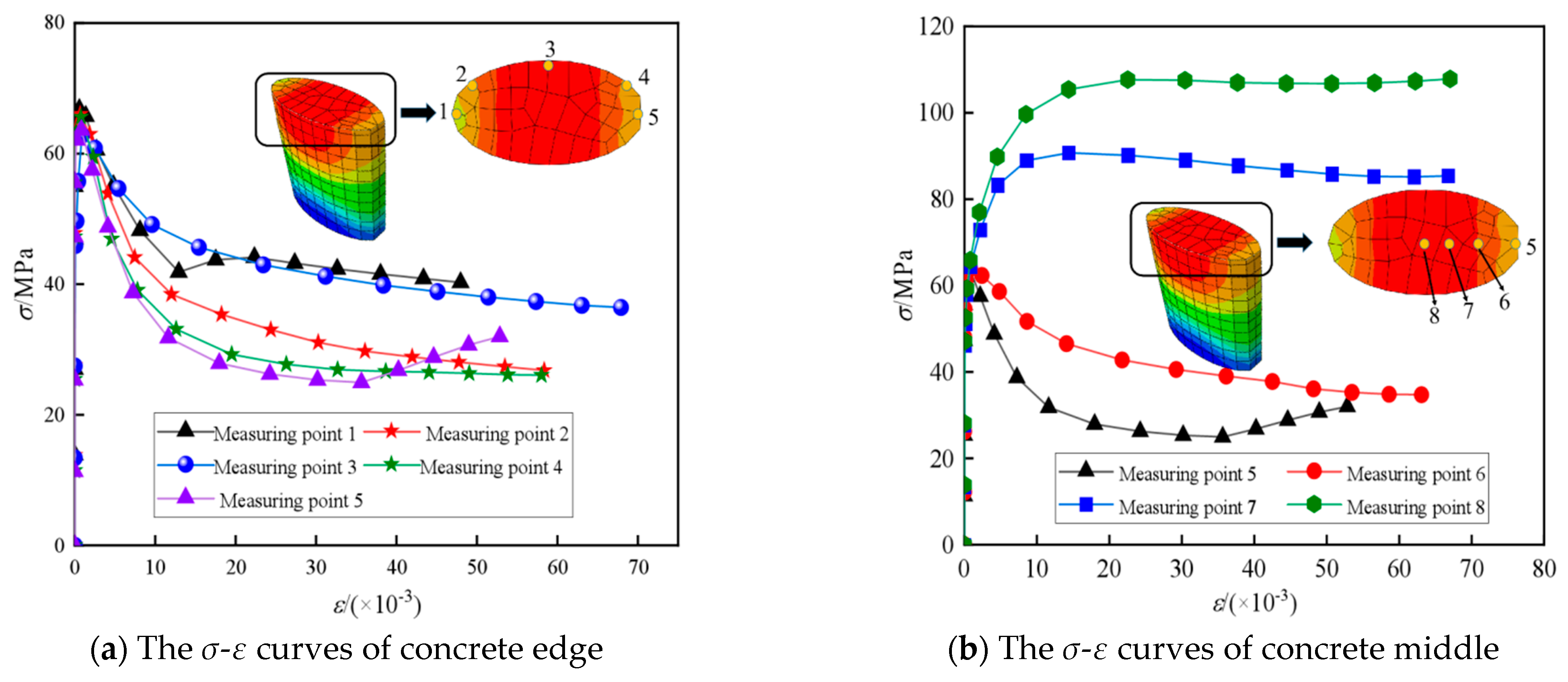
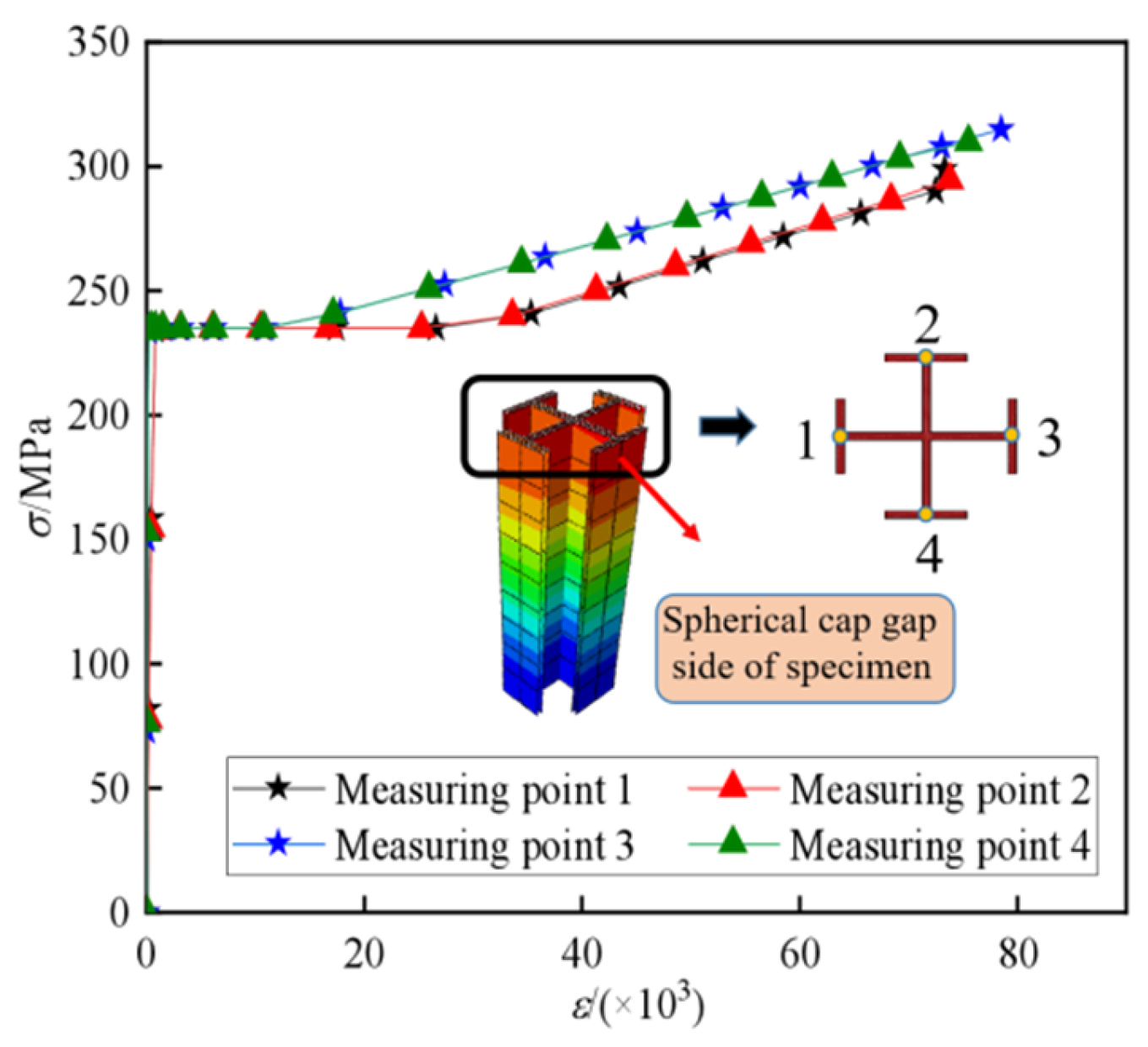
7.3. Stress-Strain Development Analysis
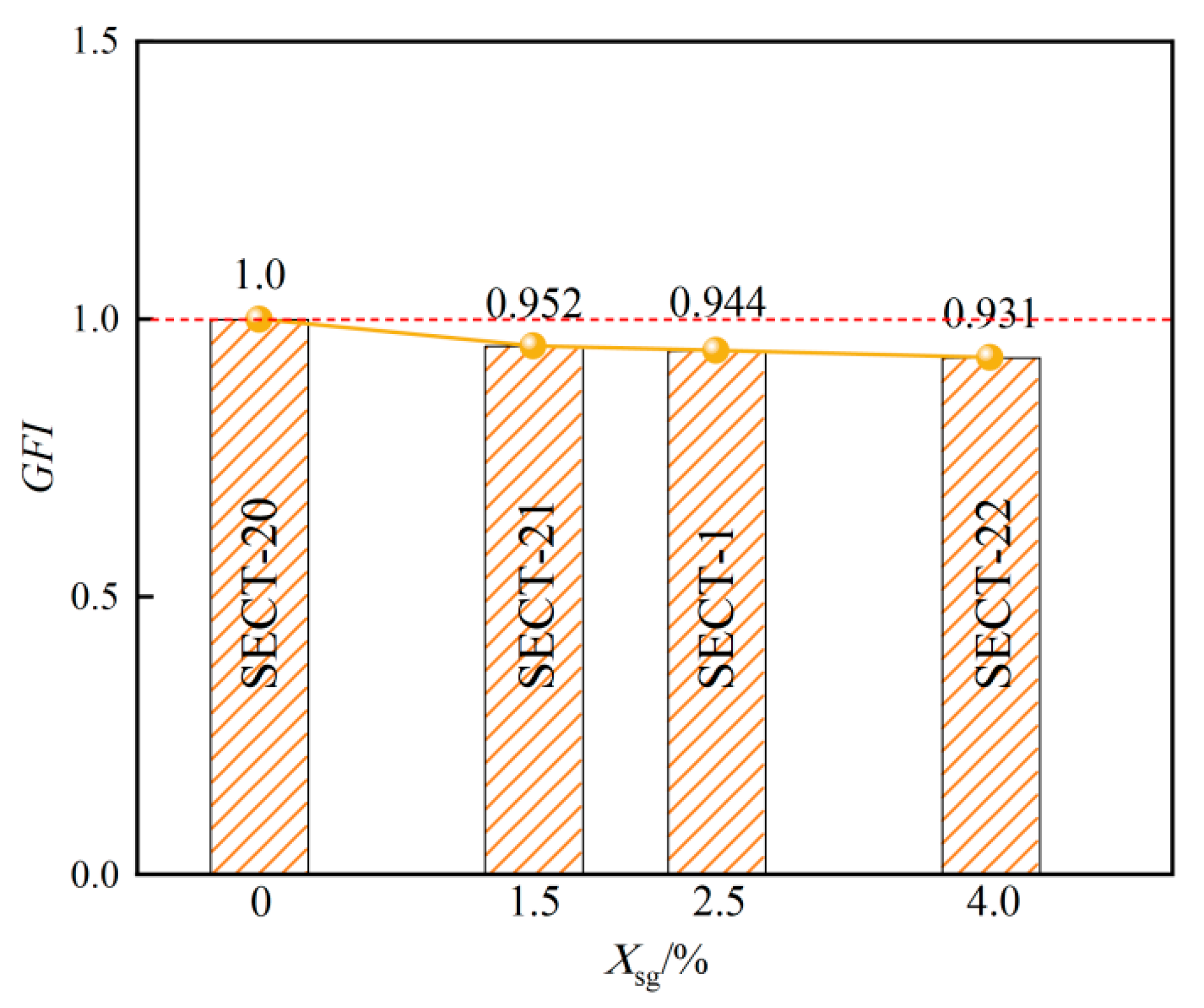
7.4. Gap Feature Index (GFI)
8. Axial Compressive Bearing Capacity of Composite Short Columns
9. Conclusions
- (1)
- Based on the simplified bilinear constitutive model of steel, the secondary back-flow constitutive model and the nonlinear constitutive model of concrete (considering the defect), the numerical simulation of 25 composite short-column test specimens was carried out by ABAQUS software, and the vertical load-displacement relationship curve of the short column was obtained. Comparing the axial compression bearing capacity of the extracted specimen with the existing test data, the maximum error was 7.68%, which verifies the rationality of the material nonlinear constitutive model and the finite element modeling method.
- (2)
- The ultimate bearing capacity of GSECFST composite short columns increased with the steel tube strength (fty), steel skeleton strength (fsy), concrete strength (fcu), steel tube thickness (t), and steel section area (As). The steel tube strength, concrete strength, and steel tube thickness significantly improved the bearing capacity of the specimens. However, by increasing the ratio of the long and short half axis (a/b), the gap ratio (Xsg), and the slenderness ratio (λ), the ultimate bearing capacity of the steel-elliptical concrete-filled steel tube short column with a spherical-cap gap decreased gradually. The spherical-cap gap would reduce the axial compression bearing capacity, stiffness, and ductility of steel skeleton elliptical concrete-filled steel tubular short columns. When the gap ratio at the long axis end increased from 0 to 4.0%, the axial compression bearing capacity of the specimen decreased by 8.5%, the initial stiffness decreased by 17.6%, and the ductility coefficient decreased by 22.9%. Therefore, the spherical-cap gap of the specimen weakened the axial compression behavior of the steel-elliptical steel tube concrete short column and intensified with the increase in the gap ratio.
- (3)
- The N-∆ curves of GSECFST composite short columns were divided into elastic, elastic-plastic, plastic, and failure stages. The characteristic form was driven by the gap ratio. With the increase in the gap ratio, the restraint effect of steel tubes on core concrete decreased. All the failure modes of the specimens under axial load were manifested as the outward expansion of steel tube, steel bone, core concrete, and the local outward bulging of the specimens. The stress–strain analysis shows that the existence of gap defects in the long axis direction of the specimen deviated from the neutral axis of the specimen section, and the initial eccentricity promotes the longitudinal compressive strain of the concrete on the gap side to develop faster than that on the non-gap side. Finally, the concrete in the gap area is broken, and the steel pipe is yielded first.
- (4)
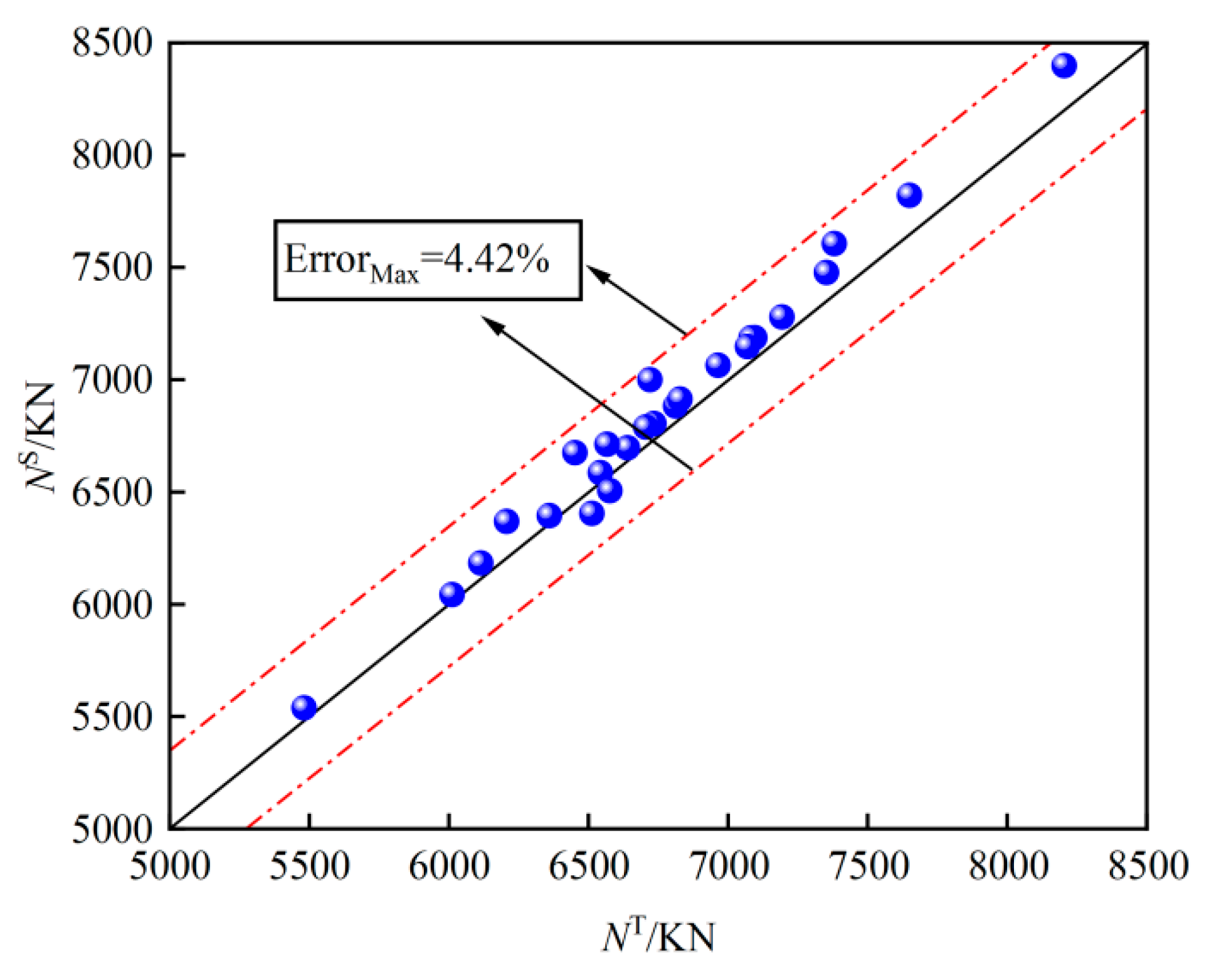
- Based on the existing bearing capacity formula of GSECFST composite short columns, the load Np that the steel section can bear was introduced, and the axial compression bearing capacity formula that considered the influence of elliptical section characteristics and gap defects was proposed. The maximum error was 4.42%, meeting the engineering requirements.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J. Research on Mechanical Properties of Anti-Bending for Concrete Filled Steel Tube Circular Arch and Its Application. Ph.D. Thesis, China University of Mining and Technology, Beijing, China, 2014. [Google Scholar]
- Wang, J.F.; Liu, W.; Shen, Q.H.; Li, J.Z. Study on axial compression performance of elliptical concrete filled steel tubular short columns considering the influence of circumferential gap. J. Build. Struct. 2023, 44, 50–63. [Google Scholar]
- Tang, S. Study on Mechanical Properties of Hollow Concrete Filled Steel Tube Members. Ph.D. Thesis, Guangzhou University, Guangzhou, China, 2011. [Google Scholar]
- Liao, F.Y.; Han, L.H.; Tao, Z. Behavior of CFST stub columns with initial concrete imperfection: Analysis and calculations. Thin-Walled Struct. 2013, 70, 57–69. [Google Scholar] [CrossRef]
- Zhao, D.Z. Study on Mechanical Properties of Steel Reinforced High Strength Concrete Filled Steel Tube Composite Columns. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2003. [Google Scholar]
- Yang, H.; Lam, D.; Gardner, L. Testing and analysis of concrete-filled elliptical hollow sections. Eng. Struct. 2008, 30, 3771–3781. [Google Scholar] [CrossRef]
- Dai, X.; Lam, D. Numerical modeling of the axial compressive behavior of short concrete-filled elliptical steel columns. J. Constr. Steel Res. 2010, 66, 931–942. [Google Scholar] [CrossRef]
- Ren, Q.X.; Han, L.H.; Lam, D. Tests on elliptical concrete filled steel tubular (CFST) beams and columns. J. Constr. Steel Res. 2014, 99, 149–160. [Google Scholar] [CrossRef]
- Ji, J.; Xu, Z.C.; Jiang, L.Q.; Liu, Y.C.; Yu, D.Y.; Yang, M.M. Experimental study on compression behavior of H-shaped composite short column with rectangular CFST flanges and honeycombed steel web subjected to axial load. Build. Struct. 2019, 40, 63–73. [Google Scholar]
- Li, J.Z. Study on Axial Compression Performance and Bearing Capacity Calculation Method of Elliptical Concrete Filled Steel Tubular Short Columns with Gap Defects. Ph.D. Thesis, Hefei University of Technology, Hefei, China, 2021. [Google Scholar]
- Wang, J.F.; Cheng, A.L.; Shen, Q.H. Analysis of axial compression performance and stress mechanism of elliptical concrete-filled steel tubular short columns with spherical crown-shaped gap defects. Prog. Steel Build. Struct. 2022, 24, 41–54. [Google Scholar]
- Shen, Q.H.; Wang, J.F.; Li, J.Z. Study on axial compression performance and calculation method of elliptical concrete filled steel tubular short columns with spherical crown gap defects. Eng. Mech. 2022, 39, 141–150. [Google Scholar]
- Ji, J.; Zhang, H.L.; Jiang, L.Q.; Zhang, Y.F.; Yuan, C.Q.; Zhang, Z.B.; Chu, X.; Li, B. Seismic Behaviors of Novel Steel-Reinforced Concrete Composite Frames Prestressed with Bonding Tendons. Buildings 2023, 13, 2124. [Google Scholar] [CrossRef]
- Han, H.; Liao, F.Y. Study on flexural performance of concrete filled steel tubular members with spherical crown gap defects. Prog. Steel Build. Struct. 2018, 20, 67–73+102. [Google Scholar]
- Uenaka, K.; Mizukoshi, M. Lightweight concrete filled steel tubular beam under bending-shear. Structures 2021, 30, 659–666. [Google Scholar] [CrossRef]
- Ji, J.; Li, J.Q.; Jiang, L.Q.; Ren, H.G.; Wang, Q.Q.; Wang, X.; He, L.J.; Zhang, Z.B. Mechanical Behavior of Special-Shaped Reinforced Concrete Composite Columns Encased with GFRP Core Columns. Buildings 2022, 12, 1895. [Google Scholar] [CrossRef]
- Liu, W. Study on the Working Mechanism of Concrete Filled Steel Tube under Local Compression. Ph.D. Thesis, Fuzhou University, Fuzhou, China, 2005. [Google Scholar]
- Guo, X.S. Study on Mechanical Properties of Elliptical Concrete Filled Steel Tubular Short Columns under Axial Compression and Eccentric Compression. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2015. [Google Scholar]
- Wang, J.F.; Xiao, Q.; Sheng, Q.H. Axial compression performance analysis of concrete filled steel tubular short columns with CFRP wrapped with gap defects. Prog. Steel Build. Struct. 2021, 23, 44–53+70. [Google Scholar]
- Zhang, Y.; Wei, Y.; Bai, J.; Zhang, Y.X. Stress-strain model of an FRP-confined concrete filled steel tube under axial compression. Thin-Walled Struct. 2019, 142, 149–159. [Google Scholar] [CrossRef]
- Du, G.F.; Song, X.; Xu, S.P. Experimental study on axial compression performance of concrete-filled steel tubular short columns with built-in steel-reinforced composite L-shaped section. J. Build. Struct. 2013, 34, 82–89. [Google Scholar]
- Ji, J.; Zhang, Z.; Lin, M.; Li, L.Z.; Jiang, L.Q.; Ding, Y.; Yu, K.Q. Structural application of engineered cementitious composites (ECC): A state-of-the-art review. Constr. Build. Mater. 2023, 406, 133289. [Google Scholar] [CrossRef]
- Li, K.S.; Dong, Y.Y.; Du, Y.S. Study on the bending performance of elliptical concrete-filled steel tubular piers under different angle loads. Highway 2023, 68, 140–147. [Google Scholar]
- Ji, J.; He, L.J.; Jiang, L.Q.; Zhang, Y.F.; Liu, Y.C.; Li, Y.H.; Zhang, Z.B. Numerical study on the axial compression behavior of composite columns with steel tube SHCC flanges and honeycombed steel web. Eng. Struct. 2023, 283, 115883. [Google Scholar] [CrossRef]
- Mao, W.J.; Shi, Y.L.; Wang, W.D. Calculation method of axial compression bearing capacity of circular concrete-filled steel tubular members with built-in steel. Prog. Steel Build. Struct. 2021, 23, 37–46. [Google Scholar]
- Tokgoz, S.; Dundar, C.; Karaahmetli, S.; Ozel, R. Research on concrete-filled stainless steel tubular composite columns. Structures 2021, 33, 703–719. [Google Scholar] [CrossRef]
- Ji, J.; Wang, W.C.; Jiang, L.Q.; Ren, H.G.; Wang, Q.Q.; Xuan, W.Y.; Liu, Y.C. Bearing Capacity of UHPC-Filled High-Strength Elliptical Steel Tube Composite Columns with Encased High-Strength H-Shape Steel Subjected to Eccentrical Load. Buildings 2022, 12, 1272. [Google Scholar] [CrossRef]
- Xiao, A.L. Study on Mechanical Behavior and Design Method of Steel Reinforced High Performance Concrete Filled Steel Tube Axial Compression Composite Column. Ph.D. Thesis, Hunan University, Changsha, China, 2009. [Google Scholar]
- Ji, J.; Li, Y.H.; Jiang, L.Q.; Zhang, Y.F.; Liu, Y.C.; He, L.J.; Zhang, Z.B.; Wang, Y. Axial compression behavior of strength-gradient composite stub columns encased CFST with small diameter: Experimental and numerical investigation. Structures 2023, 47, 282–298. [Google Scholar] [CrossRef]
- Zhao, Y.; Zou, R.; Ding, T.; Xiao, J.Z. Experimental study of the shear behaviour of concrete-grout-concrete joints. J. Build. Eng. 2021, 43, 103095. [Google Scholar] [CrossRef]
- Nassiraei, H. Geometrical effects on the LJF of tubular T/Y-joints with doubler plate in offshore wind turbines. Ships Offshore Struct. 2022, 17, 481–491. [Google Scholar] [CrossRef]
- Zhu, T.; Liang, H.; Lu, Y.; Li, W.J.; Zhang, H. Axial behaviour of slender concrete-filled steel tube square columns strengthened with square concrete-filled steel tube jackets. Adv. Struct. Eng. 2020, 23, 1074–1086. [Google Scholar] [CrossRef]
- Luo, Y.P.; Xie, L.P.; Liao, F.Y. Research on detection method of concrete filled steel tube gap defect based on time series analysis theory. Ind. Constr. 2019, 49, 48–53. [Google Scholar]
- Zeng, J.J.; Liang, S.D.; Li, Y.L.; Guo, Y.C.; Shan, G.Y. Compressive behavior of FRP-confined elliptical concrete-filled high strength steel tube columns. Compos. Struct. 2021, 266, 113808. [Google Scholar] [CrossRef]
- Mei, S.; Wang, Y.; Zou, R.; Long, Y.P. Creep of concrete-filled steel tube considering creep-recovery of the concrete core. Adv. Struct. Eng. 2020, 23, 997–1009. [Google Scholar] [CrossRef]
- İpek, S.; Erdoğan, A.; Güneyisi, E.M. Compressive behavior of concrete-filled double skin steel tubular short columns with the elliptical hollow section. J. Build. Eng. 2021, 38, 102200. [Google Scholar] [CrossRef]














| Specimens | 2a × 2b × t × L /mm | fty /MPa | fsy /MPa | fcu /MPa | t /mm | As /mm2 | a/b | dsg /mm | Xsg /% | λ |
|---|---|---|---|---|---|---|---|---|---|---|
| SECT-1 | 400 × 200 × 6 × 800 | 235.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-2 | 400 × 200 × 6 × 800 | 335.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-3 | 400 × 200 × 6 × 800 | 435.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-4 | 400 × 200 × 6 × 800 | 535.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-5 | 400 × 200 × 6 × 800 | 235.0 | 335.0 | 101.3 | 6.0 | 2700 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-6 | 400 × 200 × 6 × 800 | 235.0 | 435.0 | 101.3 | 6.0 | 2700 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-7 | 400 × 200 × 6 × 800 | 235.0 | 535.0 | 101.3 | 6.0 | 2700 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-8 | 400 × 200 × 6 × 800 | 235.0 | 235.0 | 75.9 | 6.0 | 2700 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-9 | 400 × 200 × 6 × 800 | 235.0 | 235.0 | 88.6 | 6.0 | 2700 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-10 | 400 × 200 × 6 × 800 | 235.0 | 235.0 | 113.9 | 6.0 | 2700 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-11 | 400 × 200 × 4 × 800 | 235.0 | 235.0 | 101.3 | 4.0 | 2700 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-12 | 400 × 200 × 8 × 800 | 235.0 | 235.0 | 101.3 | 8.0 | 2700 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-13 | 400 × 200 × 10 × 800 | 235.0 | 235.0 | 101.3 | 10.0 | 2700 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-14 | 400 × 200 × 6 × 800 | 235.0 | 235.0 | 101.3 | 6.0 | 3115 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-15 | 400 × 200 × 6 × 800 | 235.0 | 235.0 | 101.3 | 6.0 | 3520 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-16 | 400 × 200 × 6 × 800 | 235.0 | 235.0 | 101.3 | 6.0 | 3915 | 2.0 | 10.0 | 2.5 | 2.0 |
| SECT-17 | 283 × 283 × 6.4 × 800 | 235.0 | 235.0 | 101.3 | 6.4 | 2700 | 1.0 | 7.1 | 2.5 | 2.0 |
| SECT-18 | 346 × 231 × 6.2 × 800 | 235.0 | 235.0 | 101.3 | 6.2 | 2700 | 1.5 | 8.7 | 2.5 | 2.0 |
| SECT-19 | 447 × 179 × 5.7 × 800 | 235.0 | 235.0 | 101.3 | 5.7 | 2700 | 2.5 | 11.2 | 2.5 | 2.0 |
| SECT-20 | 400 × 200 × 6 × 800 | 235.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 0.0 | 0.0 | 2.0 |
| SECT-21 | 400 × 200 × 6 × 800 | 235.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 6.0 | 1.5 | 2.0 |
| SECT-22 | 400 × 200 × 6 × 800 | 235.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 16.0 | 4.0 | 2.0 |
| SECT-23 | 400 × 200 × 6 × 800 | 235.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 10.0 | 2.5 | 1.5 |
| SECT-24 | 400 × 200 × 6 × 1000 | 235.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 10.0 | 2.5 | 2.5 |
| SECT-25 | 400 × 200 × 6 × 1200 | 235.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 10.0 | 2.5 | 3.0 |
| Specimens | D × t × L /mm | As /mm | fc /MPa | fty /MPa | fsy /MPa | L0/D | /kN | /kN | ||
|---|---|---|---|---|---|---|---|---|---|---|
| AL Xiao [28] | SC-1 | 219 × 4.0 × 876 | 2996 | 43.6 | 337 | 318 | 4 | 3984.71 | 4045.43 | 1.50 |
| SC-2 | 219 × 4.0 × 876 | 3578 | 43.6 | 337 | 303 | 4 | 3884.16 | 4009.87 | 3.14 | |
| SC-3 | 219 × 4.0 × 876 | 4278 | 43.6 | 337 | 308 | 4 | 4455.32 | 4497.03 | 0.93 | |
| SC-5 | 219 × 5.6 × 876 | 3578 | 43.6 | 289 | 303 | 4 | 4153.65 | 4220.82 | 1.59 | |
| SC-8 | 219 × 4.0 × 876 | - | 43.6 | 337 | - | 4 | 3123.38 | 3114.19 | 0.30 | |
| Specimens | 2a × 2b × t × h /mm | fy /MPa | fcu /MPa | dsg /mm | χsg /% | /kN | /kN | ||
|---|---|---|---|---|---|---|---|---|---|
| JZ Li [10] | AC2-S1-LSG10 | 278 × 140 × 6 × 500 | 275 | 58.9 | 10 | 3.6 | 2558.559 | 2418.16 | 5.80 |
| AC2-S1-LSG20 | 278 × 140 × 6 × 500 | 275 | 58.9 | 20 | 7.2 | 2432.16 | 2258.63 | 7.68 | |
| AC2-S1-LSG30 | 278 × 140 × 6 × 500 | 275 | 58.9 | 30 | 10.8 | 2172.91 | 2179.3 | 0.29 | |
| AC1-S2-LSG20 | 278 × 140 × 6 × 500 | 487 | 30.2 | 20 | 7.2 | 2748.864 | 2587.72 | 6.23 | |
| AC2-S2-LSG10 | 278 × 140 × 6 × 500 | 487 | 58.9 | 10 | 3.6 | 3313.991 | 3402.97 | 2.61 | |
| AC2-S2-LSG20 | 278 × 140 × 6 × 500 | 487 | 58.9 | 20 | 7.2 | 3153.748 | 3103.44 | 1.62 | |
| AC2-S2-LSG30 | 278 × 140 × 6 × 500 | 487 | 58.9 | 30 | 10.8 | 3036.264 | 3001.59 | 1.16 | |
| Specimens | fty /MPa | fsy /MPa | fcu /MPa | t /mm | As /mm | a/b | Xsg /% | /kN | /kN | |
|---|---|---|---|---|---|---|---|---|---|---|
| SECT-1 | 235.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 2.5 | 6585.9 | 6542.10 | 0.67 |
| SECT-2 | 335.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 2.5 | 7187.32 | 7095.99 | 1.29 |
| SECT-3 | 435.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 2.5 | 7821.13 | 7649.89 | 2.24 |
| SECT-4 | 535.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 2.5 | 8398.56 | 8203.79 | 2.37 |
| SECT-5 | 235.0 | 335.0 | 101.3 | 6.0 | 2700 | 2.0 | 2.5 | 6883.66 | 6812.10 | 1.05 |
| SECT-6 | 235.0 | 435.0 | 101.3 | 6.0 | 2700 | 2.0 | 2.5 | 7186.76 | 7082.10 | 1.48 |
| SECT-7 | 235.0 | 535.0 | 101.3 | 6.0 | 2700 | 2.0 | 2.5 | 7477.56 | 7352.10 | 1.71 |
| SECT-8 | 235.0 | 235.0 | 75.9 | 6.0 | 2700 | 2.0 | 2.5 | 5538.57 | 5480.77 | 1.1 |
| SECT-9 | 235.0 | 235.0 | 88.6 | 6.0 | 2700 | 2.0 | 2.5 | 6043.07 | 6010.80 | 0.54 |
| SECT-10 | 235.0 | 235.0 | 113.9 | 6.0 | 2700 | 2.0 | 2.5 | 7148.21 | 7069.62 | 1.11 |
| SECT-11 | 235.0 | 235.0 | 101.3 | 4.0 | 2700 | 2.0 | 2.5 | 6183.6 | 6114.12 | 1.14 |
| SECT-12 | 235.0 | 235.0 | 101.3 | 8.0 | 2700 | 2.0 | 2.5 | 7064.91 | 6964.18 | 1.45 |
| SECT-13 | 235.0 | 235.0 | 101.3 | 10.0 | 2700 | 2.0 | 2.5 | 7606.21 | 7380.35 | 4.42 |
| SECT-14 | 235.0 | 235.0 | 101.3 | 6.0 | 3115 | 2.0 | 2.5 | 6696.55 | 6639.63 | 0.86 |
| SECT-15 | 235.0 | 235.0 | 101.3 | 6.0 | 3520 | 2.0 | 2.5 | 6805.29 | 6734.80 | 1.05 |
| SECT-16 | 235.0 | 235.0 | 101.3 | 6.0 | 3915 | 2.0 | 2.5 | 6913.56 | 6827.62 | 1.26 |
| SECT-17 | 235.0 | 235.0 | 101.3 | 6.4 | 2700 | 1.0 | 2.5 | 7279.83 | 7193.12 | 1.21 |
| SECT-18 | 235.0 | 235.0 | 101.3 | 6.2 | 2700 | 1.5 | 2.5 | 6675.33 | 6451.47 | 3.47 |
| SECT-19 | 235.0 | 235.0 | 101.3 | 5.7 | 2700 | 2.5 | 2.5 | 6368.84 | 6206.49 | 2.62 |
| SECT-20 | 235.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 0 | 6999.89 | 6720.13 | 4.16 |
| SECT-21 | 235.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 1.5 | 6713.15 | 6565.85 | 2.24 |
| SECT-22 | 235.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 4.0 | 6404.99 | 6511.98 | 1.64 |
| SECT-23 | 235.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 2.5 | 6788.83 | 6704.59 | 1.24 |
| SECT-24 | 235.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 2.5 | 6505.70 | 6576.80 | 1.01 |
| SECT-25 | 235.0 | 235.0 | 101.3 | 6.0 | 2700 | 2.0 | 2.5 | 6394.60 | 6359.83 | 0.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Ma, L.; Hou, X.; Ji, J.; Zhang, H.; Zhang, Z.; Liang, Y.; Chu, X. Axial Compression Behavior of Elliptical Concrete-Filled Steel Tube Composite Short Columns with Encased Steel Considering Spherical-Cap Gap. Buildings 2024, 14, 350. https://doi.org/10.3390/buildings14020350
Jiang L, Ma L, Hou X, Ji J, Zhang H, Zhang Z, Liang Y, Chu X. Axial Compression Behavior of Elliptical Concrete-Filled Steel Tube Composite Short Columns with Encased Steel Considering Spherical-Cap Gap. Buildings. 2024; 14(2):350. https://doi.org/10.3390/buildings14020350
Chicago/Turabian StyleJiang, Liangqin, Liang Ma, Xiaomeng Hou, Jing Ji, Huiling Zhang, Zhanbin Zhang, Yuan Liang, and Xuan Chu. 2024. "Axial Compression Behavior of Elliptical Concrete-Filled Steel Tube Composite Short Columns with Encased Steel Considering Spherical-Cap Gap" Buildings 14, no. 2: 350. https://doi.org/10.3390/buildings14020350
APA StyleJiang, L., Ma, L., Hou, X., Ji, J., Zhang, H., Zhang, Z., Liang, Y., & Chu, X. (2024). Axial Compression Behavior of Elliptical Concrete-Filled Steel Tube Composite Short Columns with Encased Steel Considering Spherical-Cap Gap. Buildings, 14(2), 350. https://doi.org/10.3390/buildings14020350








