Abstract
The connections of seismic isolation devices for mitigating seismic shocks in the fundamental excitation mode are designed and implemented based on the serial combination of elastomeric isolators, which are primarily elastic, with fluid-based isolators, which are primarily viscous. The energy dissipated in the fluidic isolators represents a significant parameter for ensuring the attenuation degree of the amplitude of the displacement of the system as well as for its energy dissipation capacity as a direct effect on deformability and speed of the heat transfer. For bridges, viaducts, and buildings, families of elastomeric and fluid isolators connected in series are used to enable both analytical and experimental evaluations of the system’s dynamic isolation and energy dissipation capacities. Based on the results obtained from specialized isolation devices from Italy and the numerical and experimental evaluations carried out by ICECON S.A. Bucharest, Romania, this article will address the aforementioned topic.
1. Introduction
The linear viscoelastic connections employed are based on the serial coupling of the elastomeric devices with the equivalent stiffness k with the fluid-based devices having the equivalent viscous damping constant c [1,2,3].
For large displacements permitted during seismic motions [4], which do not compromise the structural functionality and safety of the structure, base isolation solutions using the Maxwell model are adopted [5]. These solutions involve bearing groups with horizontal connections between the superstructure of the building and the supporting base embedded in the ground subjected to seismic motion [5,6].
Each bearing group is constructed as a unit, achieved by serially connecting a linear elastomeric isolator with a linear fluidic device [7,8,9], with the primary function of providing dynamic isolation in the horizontal direction [10,11,12,13].
The computational model that is presented in this paper forms the basis for the design and development of highly efficient base isolation systems [14,15].
The computational relations are derived from the dynamic model of a single degree of freedom system, applicable to a rigid-type structure with translational motions along the three principal orthogonal axes.
Essentially, the approach focuses on a single direction of instantaneous translational motion, with the determination of the displacement parameters, dynamic isolation, and energy dissipation in the fluidic damper [16,17]. For different dissipation devices with distinct values of viscous damping ci, i = 1, …, n, then the compound damping established in [18] can be used.
The novelty of the concept and the results obtained in this study lies in the fact that, based on favorable connections such as total rigidity and compound damping, the designer can choose from the category of CE-marked certified products the most suitable standard dimensions that can ensure a base isolation system with seismic energy isolation and dissipation performance at the values established on efficiency criteria.
2. System Amplitudes
The model of the dynamic system with a Maxwell rheological connection [5], which transmits the seismic kinematic excitation from point O to the receiver point A along the fundamental component of the seismic spectrum, is shown in Figure 1. The viscoelastic Maxwell model, having an elastic component connected in series with a viscous component (E–V), has equivalent viscosity coefficients c [19] and equivalent stiffness coefficients k.
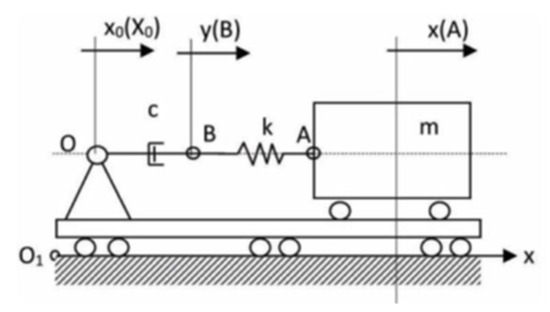
Figure 1.
Dynamic diagram of the equivalent rheological Maxwell model—CKM.
The equivalent dynamic scheme in Figure 1 represents the physical model relative to the reference axis O1X, which is considered fixed. The moving reference point O signifies the point of seismic excitation of the fundamental spectral excitation component (ω, X0) having the pulsation ω = 2π/T0, where T0 represents the fundamental period of the excitation spectral line, and the amplitude X0 corresponding to the acceleration a0 = ω2X0 of the fundamental excitation spectral line (ω, a0) [20,21]. In this case, the seismic excitation following the fundamental, unidirectional spectral component can be expressed by the equation or, in the complex domain, by where .
Depending on the order of the rheological parameters c and k, the deformations in the viscous and elastic media will differ [3,4,6]. This paper focuses on the analysis of the Maxwell dynamic system—CKM.
Based on the dynamic analysis of the system, the parameters for the instantaneous viscous and elastic deformations, as well as the corresponding amplitude values, are determined. In the end, the calculation formulas for the seismic excitation transmissibility and dissipated energy will be presented.
In the moving coordinate system, with the origin in point O, the instantaneous relative displacements concerning the reference point O are x = x(t) and y = y(t) and the instantaneous deformation of the viscous damper with equivalent constant c is h = h(t) = y − x0 [22]. For the entire viscoelastic system (E–V), the instantaneous deformation is d = d(t) = x − x0.
The calculation parameters for the case study are the following: m
The differential equations of relative motion can be written as follows:
or, in the complex formulation, the differential equations of motion can be expressed as follows:
in which
Introducing , , , and in Equation (2), the following system is obtained using and :
The determinant of the unknowns and results in
and from Equation (4) will result in
or in the form of complex functions as follows:
in which
From Equation (7), the following relation can be obtained:
from which
Alternatively, the equations can be expressed in terms of the relative parameters Ω, the dimensionless frequency ratio, and , the damping ratio [17,19], as follows:
in which or is the amplitude of the instantaneous relative displacement of the mass m relative to the moving reference point O.
Also, the amplitude of the instantaneous relative displacement of point B relative to the mobile reference point O can be determined from relation (7), resulting in the following:
From relation (12), B results in
and in relative parameters as follows:
The connection between and results using relations (11) and (14) and has the following form:
Figure 2 shows the variation curves of the relative amplitude . The family of curves is shown in Figure 3.
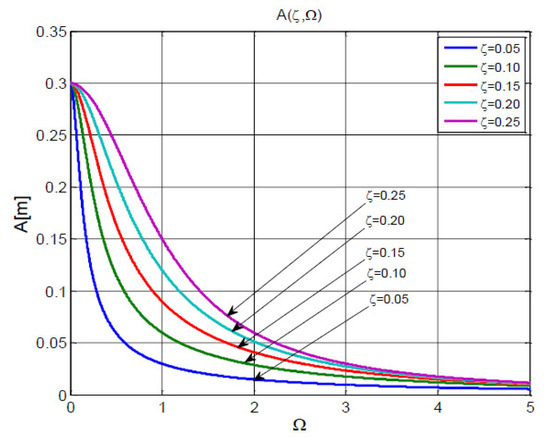
Figure 2.
The parametric curves of variation of the relative amplitude A function of the current variable
and the discrete variable for .
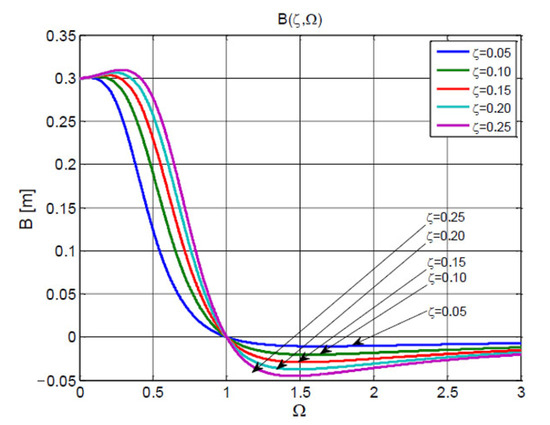
Figure 3.
The parametric curves of variation of the relative amplitude B function of the current variable
and the discrete variable for .
3. The Instantaneous Deformation of the Viscous Equivalent Damper
The instantaneous deformation h(t) = [6,19] of the viscous equivalent damper c results as
and in the complex domain as
resulting in
Introducing Equation (18) in the relation for from Equation (7) it results in
in which D has the relationship from Equation (8).
Thus, becomes
from which
Finally, it results in
From the expression above, Equation (22) can be rewritten in relative parameters as follows:
4. The Maximum Transmitted Force
The maximum transmitted force [1,14,23] is the amplitude of the instantaneous force , with a phase shift between the displacement x0(t) and the force . In this case, the maximum transmitted force is given by the maximum velocity of the viscous deformation, meaning cH0. Thus, it results in the following:
or
5. The Kinematic Transmissibility
For the Maxwell model, the kinematic transmissibility Tc is given by the relation below:
such that
or in relative parameters,
6. The Dissipated Energy
The energy dissipated on the equivalent viscous damper [5,24] c is of the form
in which and are introduced, thus resulting in the following:
For the function of and , the energy dissipated is
or
Figure 4 shows the variation in dissipated energy .
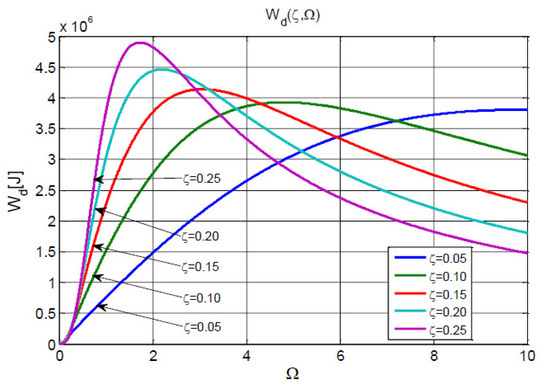
Figure 4.
Energy variation curves for the Wd function of the current variable and the discrete variable for and .
7. Conclusions
Based on the calculation relations established in the case of the linear Maxwell viscoelastic connections, the dynamic isolation system assembly can be evaluated as follows:
- a.
- The amplitude of the total deformation of the fluidic antiseismic systems can be calculated with relation (22) or (23). This is dependent on the amplitude of the first seismic excitation mode, the first order pulsation of the seismic signal spectrum ɷ, the structural sizes of the base isolation system k, c, and the mass m of the building.
- b.
- The maximum force transmitted to the superstructure expressed by is given by relation (25) and is proportional to the amplitude and the dynamic stiffness of the viscoelastic system .
- c.
- The kinematic transmissibility denoted by is directly influenced by the damping c or the fraction of the critical damping as it results from relations (27) and (28).
- d.
- The dissipated energy can be calculated with relation (32), which essentially depends on , , , and k, namely on the excitation factors (, ) and the structure of the insolation system (, k). It is also added that the dissipated energy must be evaluated at the maximum value because the temperature corresponding to the heat transport to the outside can lead to sudden expansions of the piston in the cylinder with mechanical blockages.
Drawing from the computational relationships established in the article, a base isolation system can be specified, comprising elastomeric isolation groups connected in series with fluid dampers, thereby allowing the Maxwell model to be fully defined [25,26,27,28].
The variation curves of parameters such as stiffness, damping, amplitude, transmitted force, and dissipated energy can be analyzed to determine the optimal configuration solution for the base isolation system of buildings subjected to seismic action.
Author Contributions
Conceptualization, P.B.; Methodology, P.B. and P.M.; Writing—original draft preparation, P.B. and P.M.; Writing—review and editing, P.B., P.M., O.T., N.D. and C.F.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yao, D.; Mohit, B.; Murtaza, H. Seismic response of base-isolated buildings: Exploring isolator properties. Asian J. Civ. Eng. 2024, 25, 4197–4209. [Google Scholar]
- Bratu, P. Variety of rheological models used in the isolation of the base for earthquake challenged constructions. ACTA. Napoc. 2020, 63, 119–122. [Google Scholar]
- Bratu, P.; Vasile, O.; Spanu, C.G. The Analyses of Insulation Systems based on Hooke-Voight Kelvin Dynamic Rheological model. J. Vib. Eng. Technol. 2017, 5, 255–262. [Google Scholar]
- Potîrniche, A. Assessments Regarding Effective Configurations of Vibration Isolators Based on Displacements Analysis. J. Vib. Eng. Technol. 2015, 12, 126–131. [Google Scholar]
- Bratu, P.; Tonciu, O.; Dobrescu, C.F.; Vasile, O. The Dynamic Response of the Vibrating System in the Case of the Maxwell Rheological Model. In International Conference on Acoustics and Vibration of Mechanical Structures—2023; Springer: Berlin, Germany, 2024; Volume 302. [Google Scholar] [CrossRef]
- Bratu, P.; Dobrescu, C.-F. Dynamic Response of Zener–Modelled Linearly Viscoelastic Systems under Harmonic Excitation. Symmetry 2019, 11, 1050. [Google Scholar] [CrossRef]
- Ranbeer, T.; Aditya, K.-T. Comparative study on the effectiveness of fluid viscous dampers and base isolation: An approach toward enhancing seismic performance of composite structures. Innov. Infrastruct. Solut. 2023, 8, 267. [Google Scholar]
- Popa, S.A. Analysis of the Performances of Elastomeric Anti-Seismic Devices as Part of the Dynamic Isolation Systems of the Base; Romanian Academy, Institute of Solid Mechanics: București, Romania, 2020. [Google Scholar]
- Dobrescu, C.-F. Seismic Behavior of a Base-Isolated Building with Simultaneous Translational and Rotational Motions During an Earthquake. Buildings 2024, 14, 3099. [Google Scholar] [CrossRef]
- Lopez-Almansa, F.; Piscal, C.M.; Carrillo, J.; Leiva-Maldonado, S.L.; Moscoso, Y.F.M. Survey on Major Worldwide Regulations on Seismic Base Isolation of Buildings. In Advances in Civil Engineering; Publisher Wiley Online: Hoboken, NJ, USA, 2022. [Google Scholar]
- Soluzioni Ingegneristiche Sperimentali Antiseismiche-SISMALAB, Italy; Test Report 00120/2018 for PS 1500/1300 Device; FPC: Milan, Italy, 2018.
- Soluzioni Ingegneristiche Sperimentali Antiseismiche-SISMALAB, Italy; Test Report 000133/2018 for Fluid Viscous Damper 160 kN ± 40 mm; TEC Group: Pleasanton, CA, USA, 2018.
- Bratu, P.; Dobrescu, C.F.; Nitu, M.-C. Dynamic Response Control of Linear Viscoelastic Materials as Resonant Composite Rheological Models. Rom. J. Acoust. Vib. 2023, 20, 73–77. [Google Scholar]
- Vasile, O. Active Vibration Control for Viscoelastic Damping Systems under the Action of Inertial Forces. Rom. J. Acoust. Vib. 2017, 14, 54–58. [Google Scholar]
- Polidor, B.; Stuparu, A.; Popa, S.; Voicu, O.; Iacob, N.; Spânu, G. The dynamic isolation performances analysis of the vibrating equipment with elastic links to a fixed base. ACTA Technol. Napoc. Appl. Math. Mech. Eng. 2018, 61, 23–28. [Google Scholar]
- Bratu, P. Base isolation and dissipation systems subjected to seismic action. In Proceedings of the International Conference. Constructions, Cluj-Napoca, Romania, 9–10 May 2008. [Google Scholar]
- Bratu, P.; Mitu, A.M.; Vasile, O. Dissipation Capacity Evaluation for Neoprene Anti-Seismic Isolators Under Harmonic Dynamic Excitations. Rom. J. Acoust. Vib. 2011, 8, 67–71. [Google Scholar]
- Bratu, P.; Dragomir, C.S.; Dobre, D. Assessment of the Compound Damping of a System with Parallelly Coupled Anti-Seismic Devices. Buildings 2024, 14, 2422. [Google Scholar] [CrossRef]
- Bratu, P. Modal Amortization Rate Equivalent to a Structural System with Elastomer Insulators. Rom. J. Acoust. Vib. 2020, 17, 27–31. [Google Scholar]
- Ciuncanu, M. Test performance evaluation for elastomeric anti-seismic devices on specialized stands with controlled generation excitation functions. In Proceedings of the 22th International Congress on Sound and Vibration, Florance, Italy, 12–16 July 2015. [Google Scholar]
- Murzea, P. Alternative Kinematic Assumptions for the Motions of Structures with Multiple Dynamic Degrees of Freedom Subjected to Seismic Actions. Rom. J. Acoust. Vib. 2014, 11, 53–58. [Google Scholar]
- Potîrniche, A.; Năstac, S. Functional correlations regarding passive isolation of symmetrical systems. ACTA Technol. Napoc. Ser. Appl. Math. Mech. Eng. 2013, 56, 777–785. [Google Scholar]
- D’Amato, M.; Laguardia, R.; Gigliotti, R. Seismic Retrofit of an Existing RC Building with Isolation Devices Applied at Base. Front. Built Environ. 2020, 6, 82. [Google Scholar] [CrossRef]
- Tonciu, O.; Bratu, P. Evaluation of the energetic parameters of viscous dissipation for dynamic systems excited in the harmonic regime. Acta Technol. Napoc. Ser. Appl. Math. Mech. Eng. 2023, 66, 367–374. [Google Scholar]
- Di Egidio, A.; Contento, A. Seimic performance of two rigid blocks coupled through a Maxwell visco-elastic device. Eng. Struct. 2024, 301, 117319. [Google Scholar] [CrossRef]
- Nawaz, Z.; Mohan, S. Performance of low-cost unreinforced elastomeric isolator for masonry building: Experimental investigations and numerical analysis. Structures 2024, 63, 106365. [Google Scholar] [CrossRef]
- Nawaz, Z.; Mohan, S. Development of low-cost base isolation technique using multi-criteria optimization and its application to masonry building. Soil Dyn. Earthq. Eng. 2023, 172, 108024. [Google Scholar] [CrossRef]
- Bratu, P.; Vasile, O. Dynamic Behavior of Vibratory System to Discrete Variation of Viscous Damping in Linear Viscoelastic Material Processing Technologies. In Acoustics and Vibration of Mechanical Structures—AVMS-2023; Springer: Berlin, Germany, 2024; Volume 302, pp. 49–58. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).