Advanced Ensemble Machine-Learning Models for Predicting Splitting Tensile Strength in Silica Fume-Modified Concrete
Abstract
1. Introduction
2. Research Significance
3. Materials and Methods
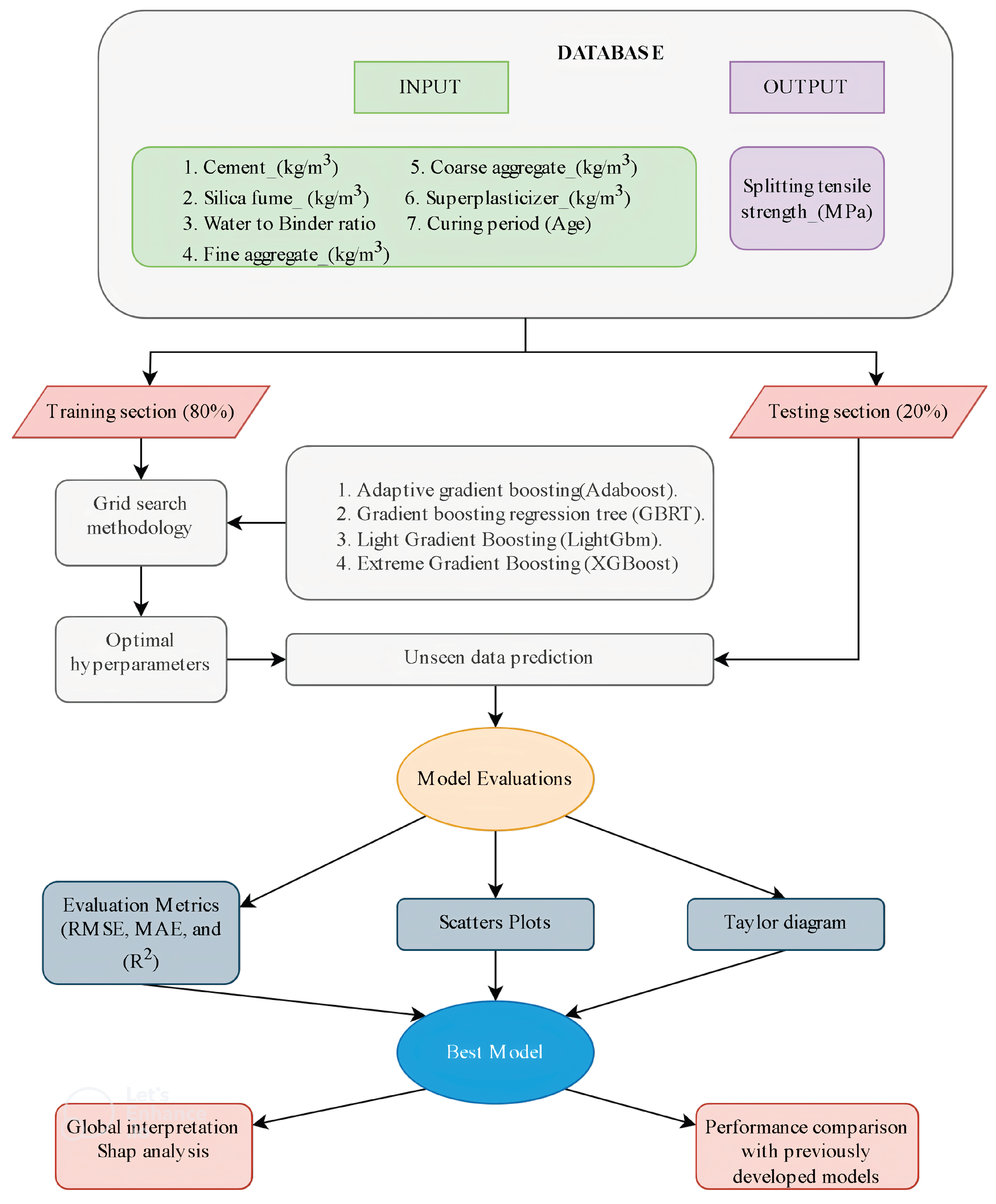
3.1. Research Methodology
3.2. Overview of the Suggested ML Models
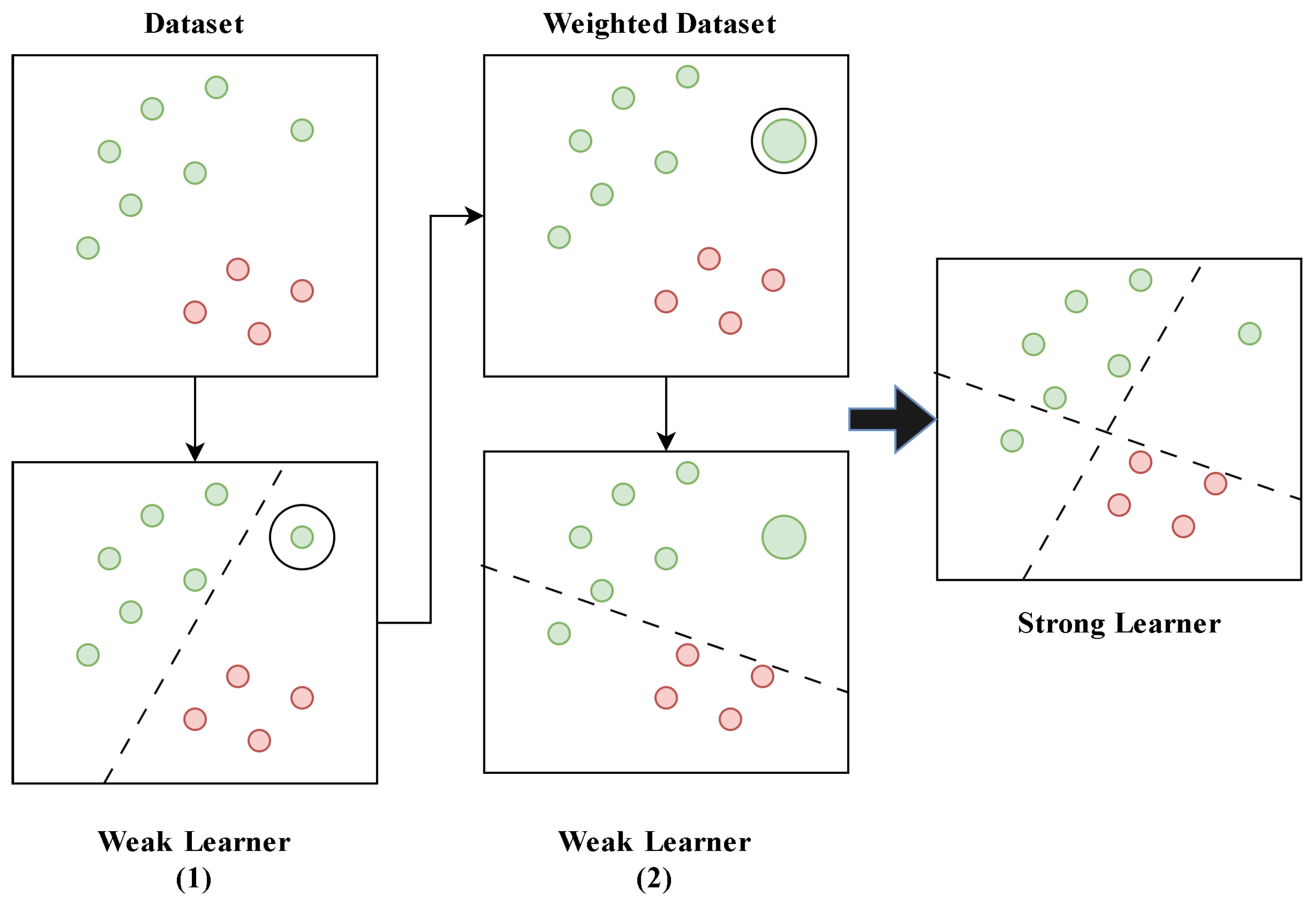
3.2.1. Adaptive Gradient Boosting (AdaBoost)
3.2.2. Gradient Boosting Regression Tree (GBRT)
3.2.3. Light Gradient Boosting (LightGBM)
3.2.4. Extreme Gradient Boosting (XGBoost)
3.3. Data Splitting and Normalization
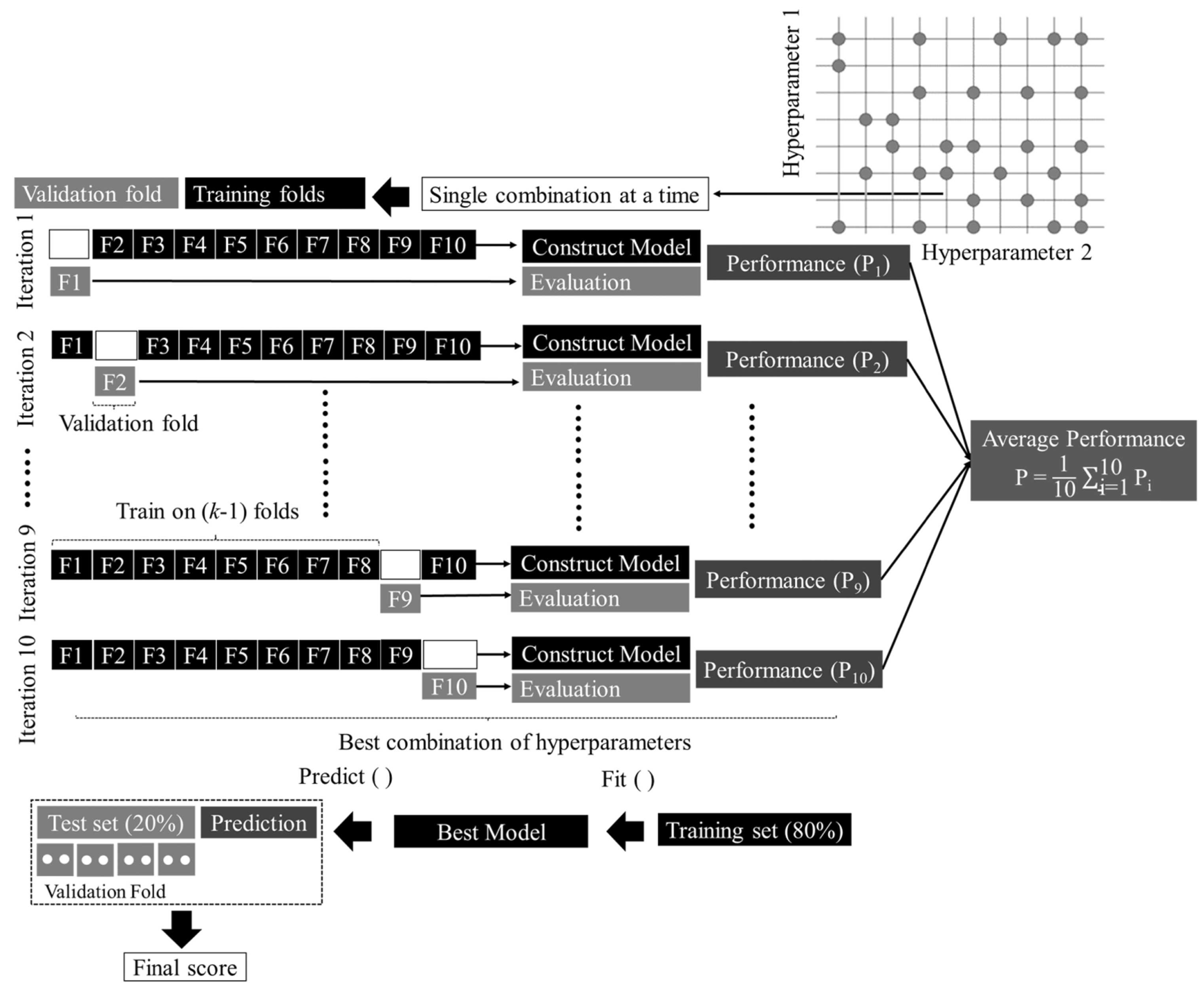
3.4. ML Model Development
3.5. Performance Metrics
4. Database Used
5. Model Results
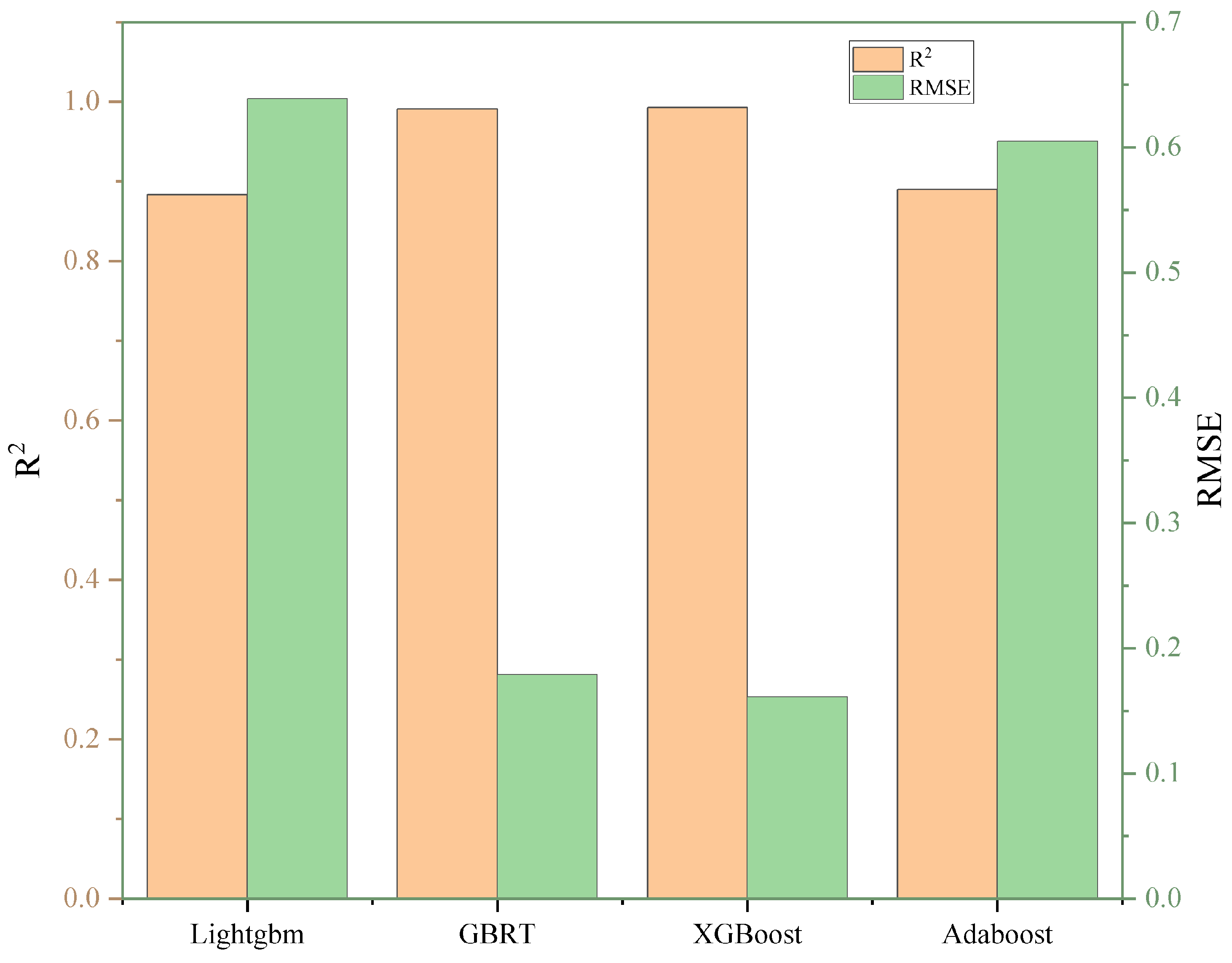
5.1. Statistical Assessment of Models
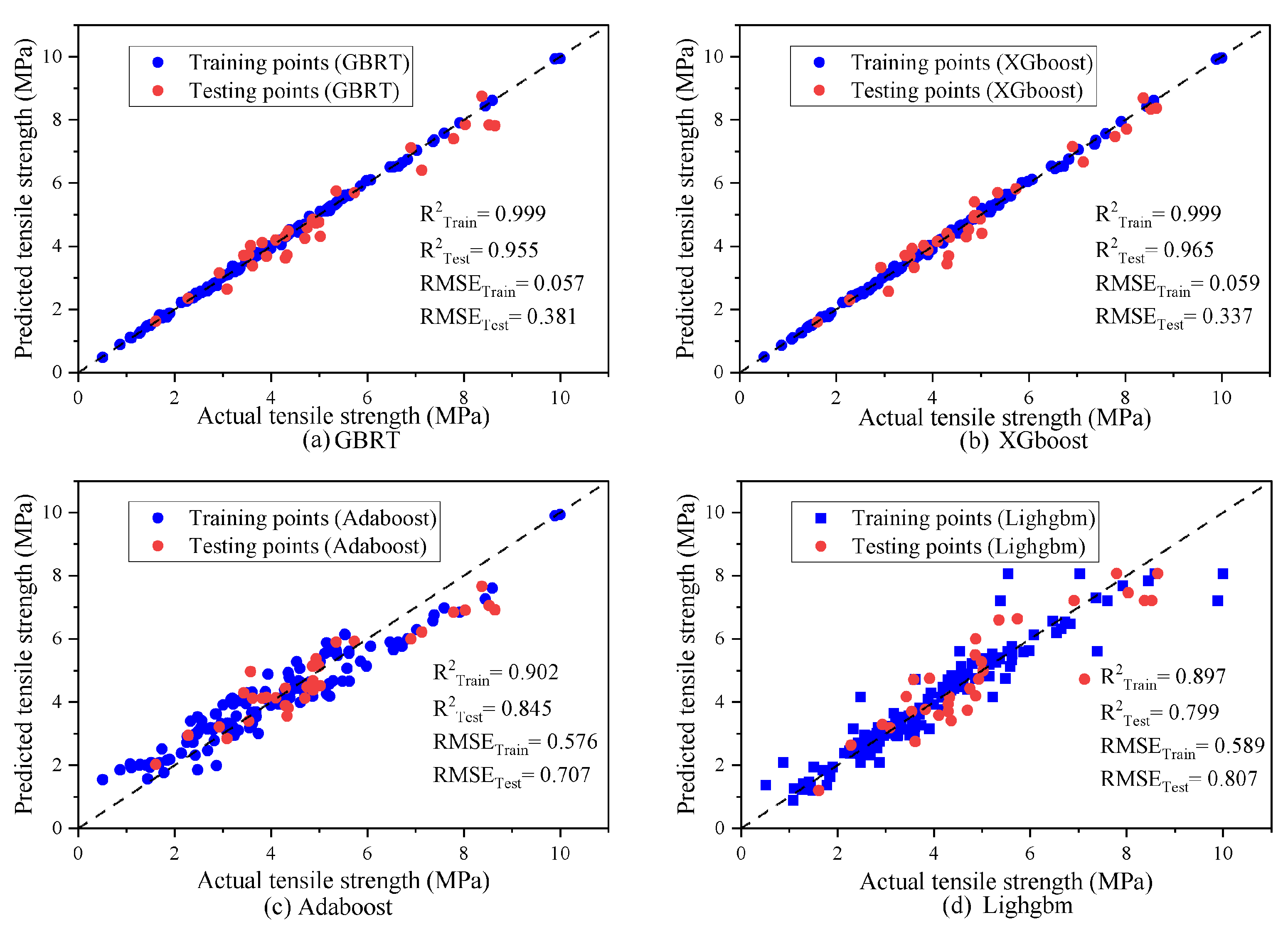
5.2. Cross-Plot
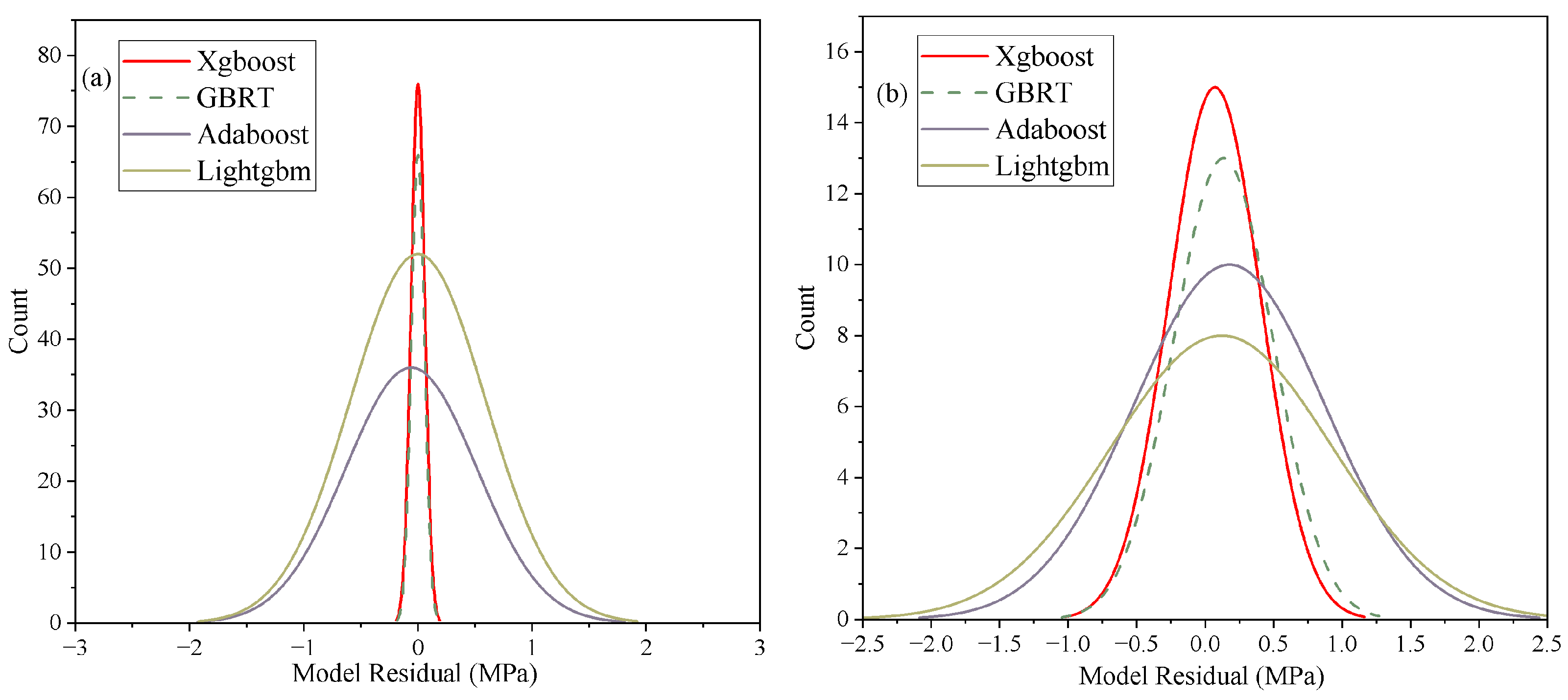
5.3. Histogram of Model Residual Distribution
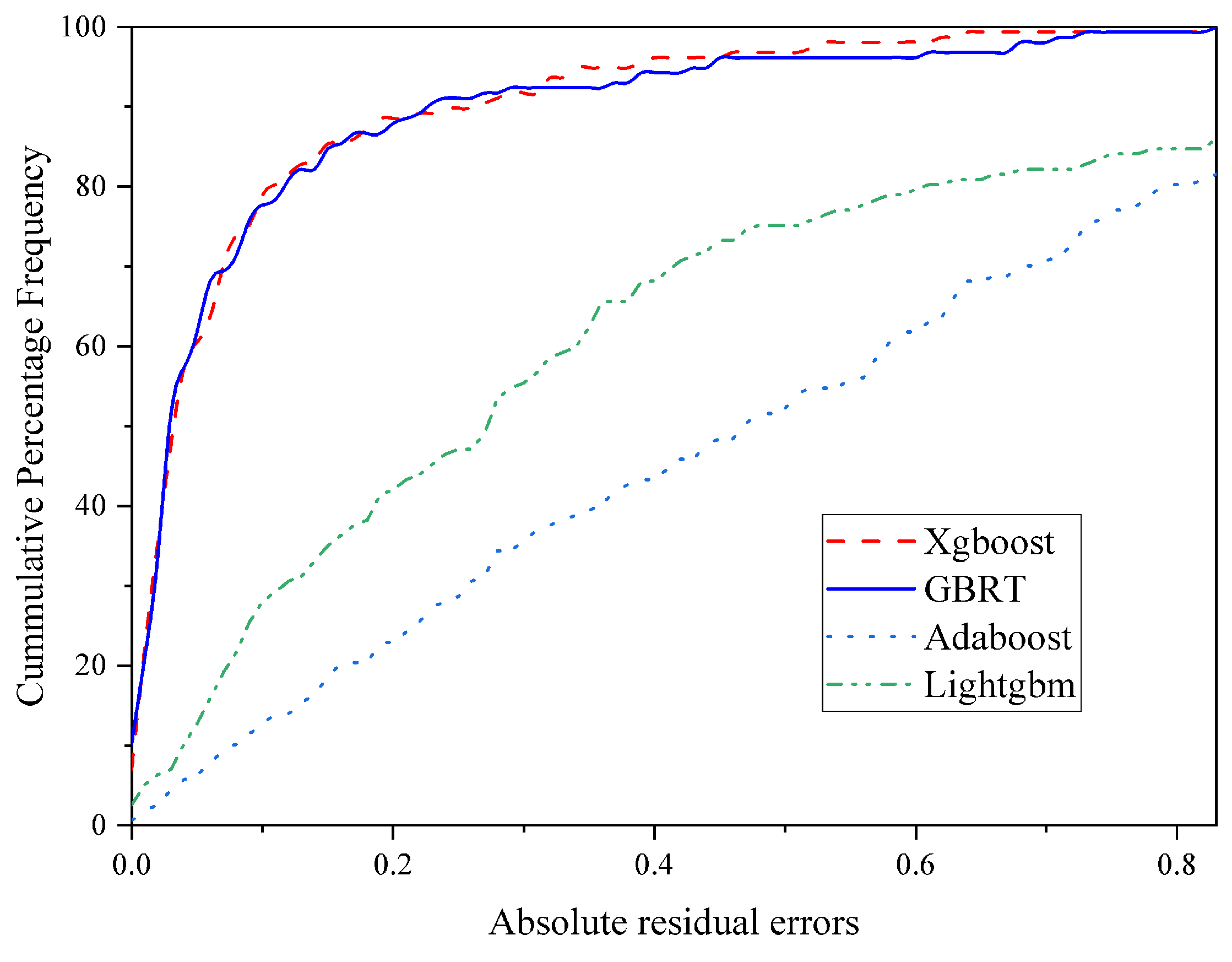
5.4. Cumulative Frequency Plot
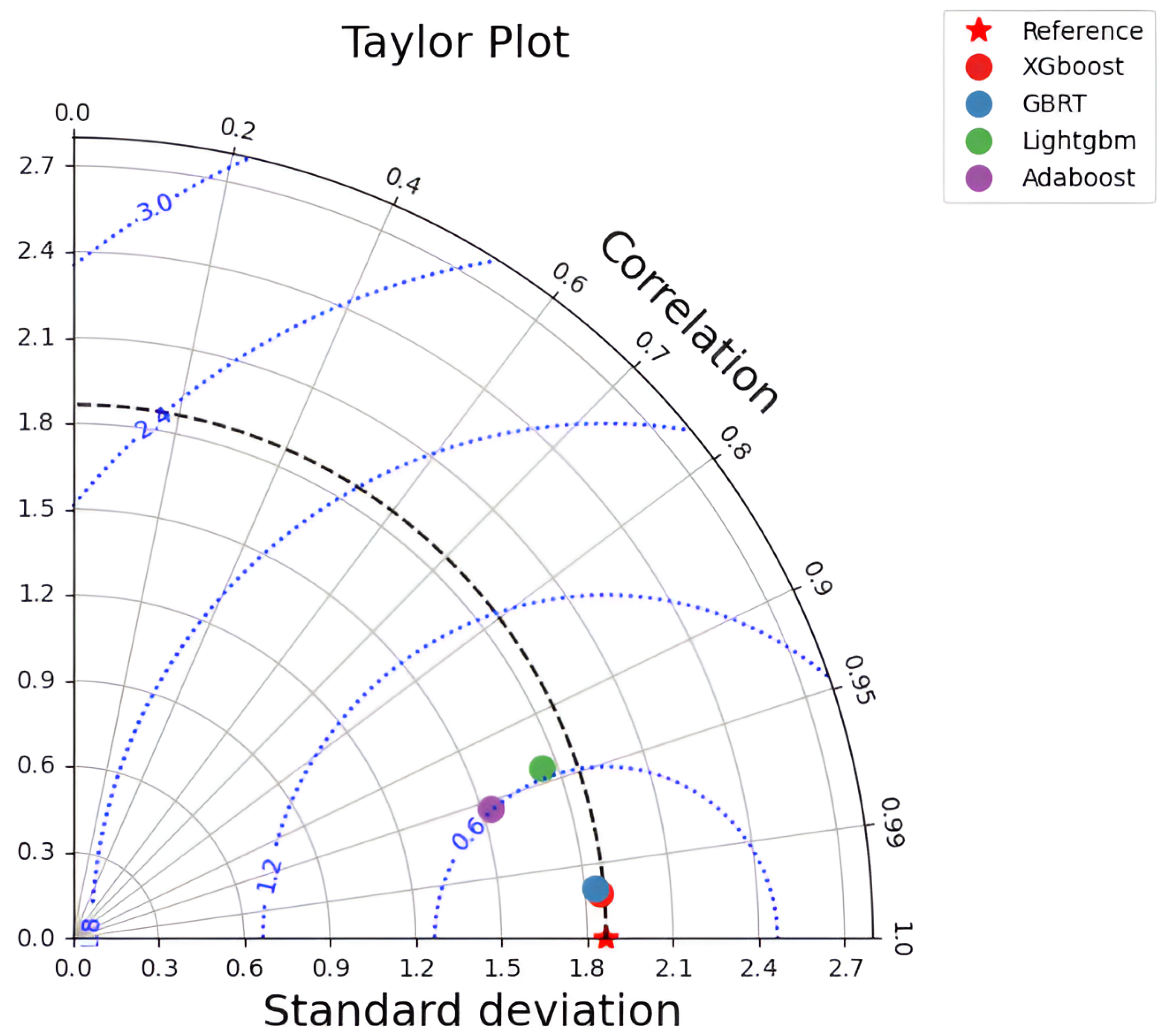
5.5. Taylor Diagram
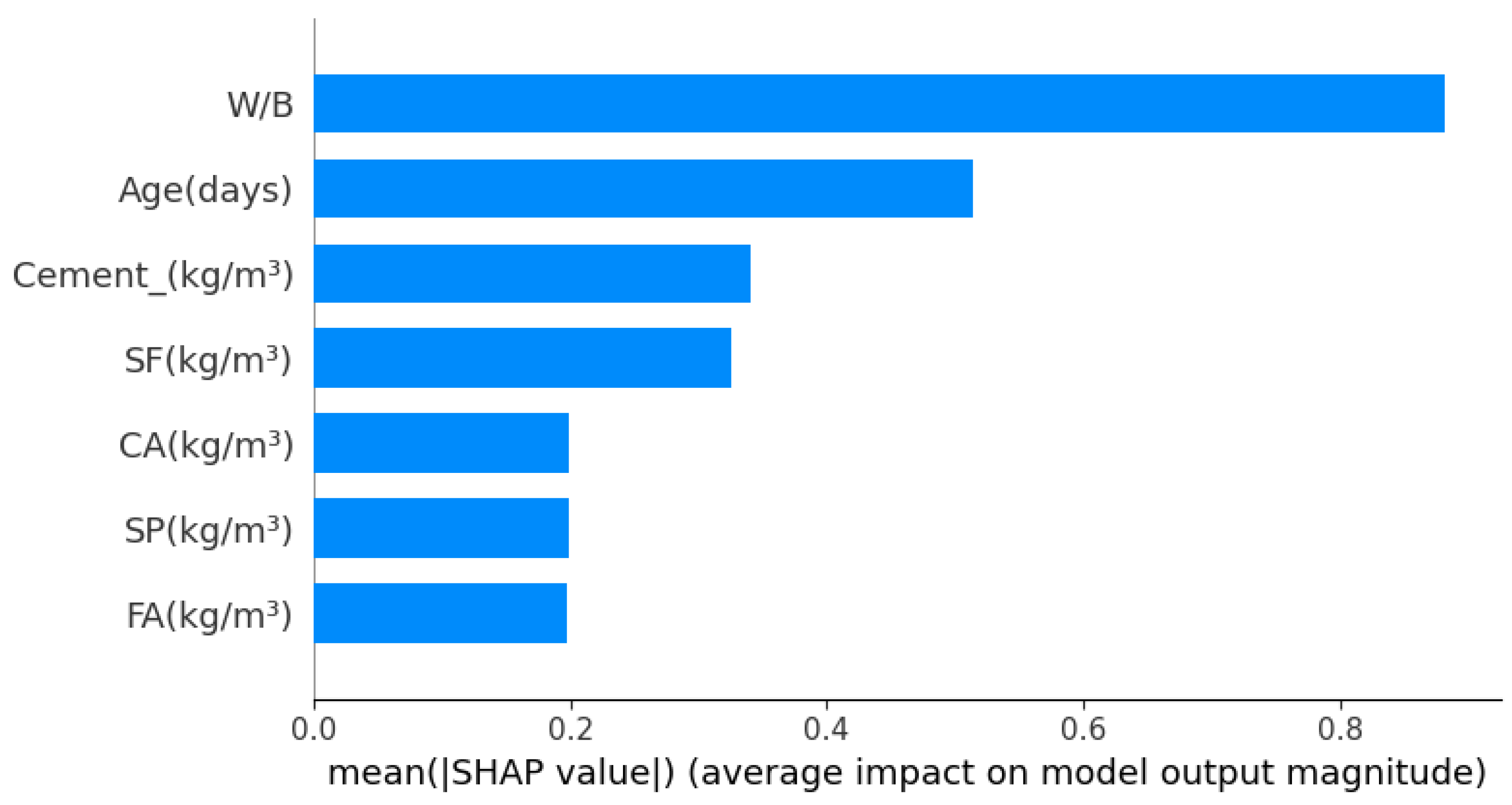
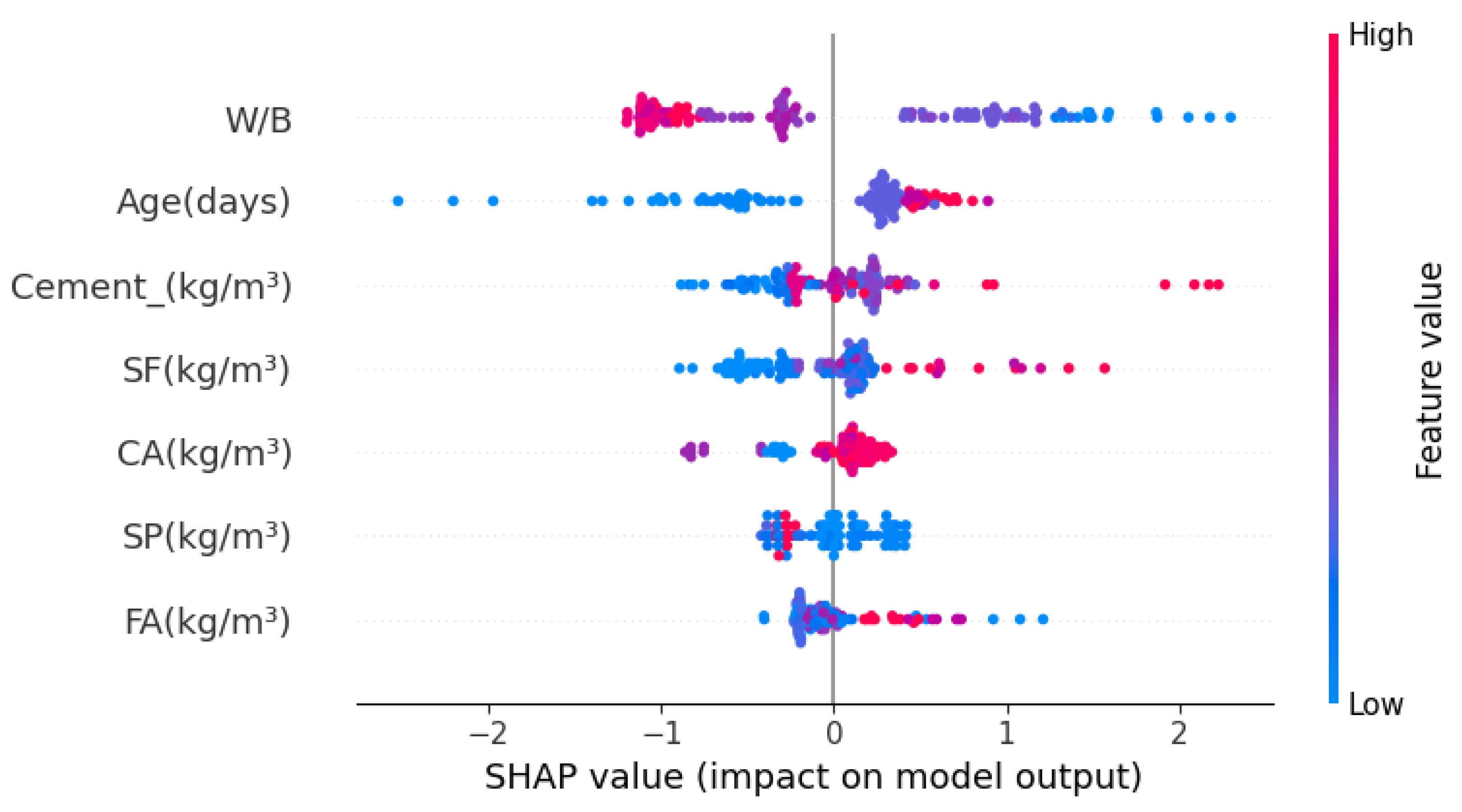
5.6. Feature Importance Analysis
5.7. Comparative Analysis of the XGBoost Model
6. Recommendations for Future Research
7. Conclusions
- The XGBoost and GBRT models demonstrated superior predictive accuracy for SF concrete, with R2 values over 0.955 during testing and low RMSE and MAE values across all phases. They outperformed LightGBM and AdaBoost, with tighter residual distributions and closer alignment to actual data, establishing a clear hierarchy in model performance. Despite being slightly behind in predictive accuracy, LightGBM and AdaBoost still exhibited robust performance, with R2 scores of 0.799 and 0.845 during testing, showcasing their effectiveness in specific scenarios.
- The XGBoost model outperformed previous models like MLPNN, ANFIS, and GEP in predicting SF concrete tensile strength, achieving a superior R2 score of 0.993. This improved accuracy is due to XGBoost’s resilience to noisy data, its ability to capture complex nonlinear relationships, and its computational efficiency.
- The feature importance analysis using SHAP values revealed that the water-to-binder ratio (W/B) and the age of the concrete were the most significant factors influencing the splitting tensile strength.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Singh, R.P.; Vanapalli, K.R.; Cheela, V.R.S.; Peddireddy, S.R.; Sharma, H.B.; Mohanty, B. Fly ash, GGBS, and silica fume based geopolymer concrete with recycled aggregates: Properties and environmental impacts. Constr. Build. Mater. 2023, 378, 131168. [Google Scholar] [CrossRef]
- Qureshi, L.A.; Ali, B.; Ali, A. Combined effects of supplementary cementitious materials (silica fume, GGBS, fly ash and rice husk ash) and steel fiber on the hardened properties of recycled aggregate concrete. Constr. Build. Mater. 2020, 263, 120636. [Google Scholar] [CrossRef]
- Siddique, R. Utilization of silica fume in concrete: Review of hardened properties. Resour. Conserv. Recycl. 2011, 55, 923–932. [Google Scholar] [CrossRef]
- Shelote, K.M.; Bala, A.; Gupta, S. An overview of mechanical, permeability, and thermal properties of silica fume concrete using bibliographic survey and building information modelling. Constr. Build. Mater. 2023, 385, 131489. [Google Scholar] [CrossRef]
- Menéndez, E.; Sanjuán, M.Á.; Recino, H. Study of Microstructure, Crystallographic Phases and Setting Time Evolution over Time of Portland Cement, Coarse Silica Fume, and Limestone (PC-SF-LS) Ternary Portland Cements. Crystals 2023, 13, 1289. [Google Scholar] [CrossRef]
- Wang, Y.S.; Cho, H.K.; Wang, X.Y. Mixture optimization of sustainable concrete with silica fume considering CO2 emissions and cost. Buildings 2022, 12, 1580. [Google Scholar] [CrossRef]
- Biswas, R.K.; Iwanami, M.; Chijiwa, N.; Uno, K. Effect of non-uniform rebar corrosion on structural performance of RC structures: A numerical and experimental investigation. Constr. Build. Mater. 2020, 230, 116908. [Google Scholar] [CrossRef]
- Bai, S.; Li, M.; Kong, R.; Han, S.; Li, H.; Qin, L. Data mining approach to construction productivity prediction for cutter suction dredgers. Autom. Constr. 2019, 105, 102833. [Google Scholar] [CrossRef]
- Ayhan, B.U.; Tokdemir, O.B. Safety assessment in megaprojects using artificial intelligence. Saf. Sci. 2019, 118, 273–287. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, Y.; Wu, D.; Liu, Z.; Zhang, H.; Zhu, M.; Chen, Z.; Sun, J.; Wang, X. An experimental investigation and machine learning-based prediction for seismic performance of steel tubular column filled with recycled aggregate concrete. Rev. Adv. Mater. Sci. 2022, 61, 849–872. [Google Scholar] [CrossRef]
- Nafees, A.; Amin, M.N.; Khan, K.; Nazir, K.; Ali, M.; Javed, M.F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Modeling of mechanical properties of silica fume-based green concrete using machine learning techniques. Polymers 2021, 14, 30. [Google Scholar] [CrossRef]
- Tanyildizi, H.; Şengür, A.; Akbulut, Y.; Şahin, M. Deep learning model for estimating the mechanical properties of concrete containing silica fume exposed to high temperatures. Front. Struct. Civ. Eng. 2020, 14, 1316–1330. [Google Scholar] [CrossRef]
- Nafees, A.; Javed, M.F.; Khan, S.; Nazir, K.; Farooq, F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Predictive modeling of mechanical properties of silica fume-based green concrete using artificial intelligence approaches: MLPNN, ANFIS, and GEP. Materials 2021, 14, 7531. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, Y.; Ma, G.; Nener, B. Mixture optimization for environmental, economical and mechanical objectives in silica fume concrete: A novel frame-work based on machine learning and a new meta-heuristic algorithm. Resour. Conserv. Recycl. 2021, 167, 105395. [Google Scholar] [CrossRef]
- Al-Saraireh, M.A. Predicting compressive strength of concrete with fly ash, metakaolin and silica fume by using machine learning techniques. Lat. Am. J. Solids Struct. 2022, 19, e454. [Google Scholar] [CrossRef]
- Tiwari, N.; Rondinella, F.; Satyam, N.; Baldo, N. Experimental and Machine Learning Approach to Investigate the Mechanical Performance of Asphalt Mixtures with Silica Fume Filler. Appl. Sci. 2023, 13, 6664. [Google Scholar] [CrossRef]
- Zaman, A.; Alyami, M.; Shah, S.; Rehman, M.F.; Hakeem, I.Y.; Farooq, F. Forecasting the strength of micro/nano silica in cementitious matrix by machine learning approaches. Mater. Today Commun. 2023, 37, 107066. [Google Scholar] [CrossRef]
- Zhao, W.; Feng, S.; Liu, J.; Sun, B. An explainable intelligent algorithm for the multiple performance prediction of cement-based grouting materials. Constr. Build. Mater. 2023, 366, 130146. [Google Scholar] [CrossRef]
- Qin, X.; Kaewunruen, S. Eco-friendly design and sustainability assessments of fibre-reinforced high-strength concrete structures automated by data-driven machine learning models. Sustainability 2023, 15, 6640. [Google Scholar] [CrossRef]
- Pak, H.; Paal, S.G. Evaluation of transfer learning models for predicting the lateral strength of reinforced concrete columns. Eng. Struct. 2022, 266, 114579. [Google Scholar] [CrossRef]
- Kumar, P.; Batchu, S.; Kota, S.R. Real-time concrete damage detection using deep learning for high rise structures. IEEE Access 2021, 9, 112312–112331. [Google Scholar] [CrossRef]
- Maherian, M.F.; Baran, S.; Bicakci, S.N.; Toreyin, B.U.; Atahan, H.N. Machine learning-based compressive strength estimation in nano silica-modified concrete. Constr. Build. Mater. 2023, 408, 133684. [Google Scholar] [CrossRef]
- Shariati, M.; Armaghani, D.J.; Khandelwal, M.; Zhou, J.; Khorami, M. Assessment of longstanding effects of fly ash and silica fume on the compressive strength of concrete using extreme learning machine and artificial neural network. J. Adv. Eng. Comput. 2021, 5, 50–74. [Google Scholar] [CrossRef]
- Nagaraju, T.V.; Mantena, S.; Azab, M.; Alisha, S.S.; El Hachem, C.; Adamu, M.; Murthy, P.S.R. Prediction of high strength ternary blended concrete containing different silica proportions using machine learning approaches. Results Eng. 2023, 17, 100973. [Google Scholar] [CrossRef]
- Annlin Jebitha, D.; Ramesh Kannan, M. Numerical Optimization of Mix Proportioning of Self-Compacting Concrete with Silica Fume—A Machine Learning Perspective. In Sustainable Construction Materials: Select Proceedings of ACMM 2021; Springer: Singapore, 2021; pp. 461–468. [Google Scholar]
- Babajanzadeh, M.; Azizifar, V. Compressive strength prediction of self-compacting concrete incorporating silica fume using artificial intelligence methods. Civ. Eng. J. 2018, 4, 1542. [Google Scholar]
- Shah, H.A.; Nehdi, M.L.; Khan, M.I.; Akmal, U.; Alabduljabbar, H.; Mohamed, A.; Sheraz, M. Predicting Compressive and Splitting Tensile Strengths of Silica Fume Concrete Using M5P Model Tree Algorithm. Materials 2022, 15, 5436. [Google Scholar] [CrossRef]
- Topçu, İ.B.; Sarıdemir, M. Prediction of mechanical properties of recycled aggregate concretes containing silica fume using artificial neural networks and fuzzy logic. Comput. Mater. Sci. 2008, 42, 74–82. [Google Scholar] [CrossRef]
- Polikar, R. Ensemble learning. Ensemble Mach. Learn. Methods Appl. 2012, 1–34. [Google Scholar]
- Feng, D.C.; Cetiner, B.; Azadi Kakavand, M.R.; Taciroglu, E. Data-driven approach to predict the plastic hinge length of reinforced concrete columns and its application. J. Struct. Eng. 2021, 147, 04020332. [Google Scholar] [CrossRef]
- Naser, M. Observational analysis of fire-induced spalling of concrete through ensemble machine learning and surrogate modeling. J. Mater. Civ. Eng. 2021, 33, 04020428. [Google Scholar] [CrossRef]
- Soleimani, F. Analytical seismic performance and sensitivity evaluation of bridges based on random decision forest framework. Structures 2021, 32, 329–341. [Google Scholar] [CrossRef]
- Kang, M.C.; Yoo, D.Y.; Gupta, R. Machine learning-based prediction for compressive and flexural strengths of steel fiber-reinforced concrete. Constr. Build. Mater. 2021, 266, 121117. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Misra, S.; Li, H.; He, J. Machine Learning for Subsurface Characterization; Gulf Professional Publishing: Houston, TX, USA, 2019. [Google Scholar]
- Ying, C.; Qi-Guang, M.; Jia-Chen, L.; Lin, G. Advance and prospects of AdaBoost algorithm. Acta Autom. Sin. 2013, 39, 745–758. [Google Scholar]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef]
- Wen, L.; Li, Y.; Zhao, W.; Cao, W.; Zhang, H. Predicting the deformation behaviour of concrete face rockfill dams by combining support vector machine and AdaBoost ensemble algorithm. Comput. Geotech. 2023, 161, 105611. [Google Scholar] [CrossRef]
- Chen, Y.; Jia, Z.; Mercola, D.; Xie, X. A gradient boosting algorithm for survival analysis via direct optimization of concordance index. Comput. Math. Methods Med. 2013, 2013, 873595. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Liang, M.; Chang, Z.; Wan, Z.; Gan, Y.; Schlangen, E.; Šavija, B. Interpretable Ensemble-Machine-Learning models for predicting creep behavior of concrete. Cem. Concr. Compos. 2022, 125, 104295. [Google Scholar] [CrossRef]
- Lin, P.; Ding, F.; Hu, G.; Li, C.; Xiao, Y.; Tse, K.T.; Kwok, K.; Kareem, A. Machine learning-enabled estimation of crosswind load effect on tall buildings. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104860. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Moayedi, H.; Kalantar, B.; Foong, L.K.; Tien Bui, D.; Motevalli, A. Application of three metaheuristic techniques in simulation of concrete slump. Appl. Sci. 2019, 9, 4340. [Google Scholar] [CrossRef]
- Liu, K.; Zou, C.; Zhang, X.; Yan, J. Innovative prediction models for the frost durability of recycled aggregate concrete using soft computing methods. J. Build. Eng. 2021, 34, 101822. [Google Scholar] [CrossRef]
- Tien Bui, D.; Abdullahi, M.M.; Ghareh, S.; Moayedi, H.; Nguyen, H. Fine-tuning of neural computing using whale optimization algorithm for predicting compressive strength of concrete. Eng. Comput. 2021, 37, 701–712. [Google Scholar] [CrossRef]
- Alhakeem, Z.M.; Jebur, Y.M.; Henedy, S.N.; Imran, H.; Bernardo, L.F.; Hussein, H.M. Prediction of ecofriendly concrete compressive strength using gradient boosting regression tree combined with GridSearchCV hyperparameter-optimization techniques. Materials 2022, 15, 7432. [Google Scholar] [CrossRef]
- Wakjira, T.G.; Kutty, A.A.; Alam, M.S. A novel framework for developing environmentally sustainable and cost-effective ultra-high-performance concrete (UHPC) using advanced machine learning and multi-objective optimization techniques. Constr. Build. Mater. 2024, 416, 135114. [Google Scholar] [CrossRef]
- Kuang, F.; Long, Z.; Kuang, D.; Liu, X.; Guo, R. Application of back propagation neural network to the modeling of slump and compressive strength of composite geopolymers. Comput. Mater. Sci. 2022, 206, 111241. [Google Scholar] [CrossRef]
- Peng, Y.; Unluer, C. Analyzing the mechanical performance of fly ash-based geopolymer concrete with different machine learning techniques. Constr. Build. Mater. 2022, 316, 125785. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, K.; Bao, R.; Liu, X. A framework for predicting the carbonation depth of concrete incorporating fly ash based on a least squares support vector machine and metaheuristic algorithms. J. Build. Eng. 2023, 65, 105772. [Google Scholar] [CrossRef]

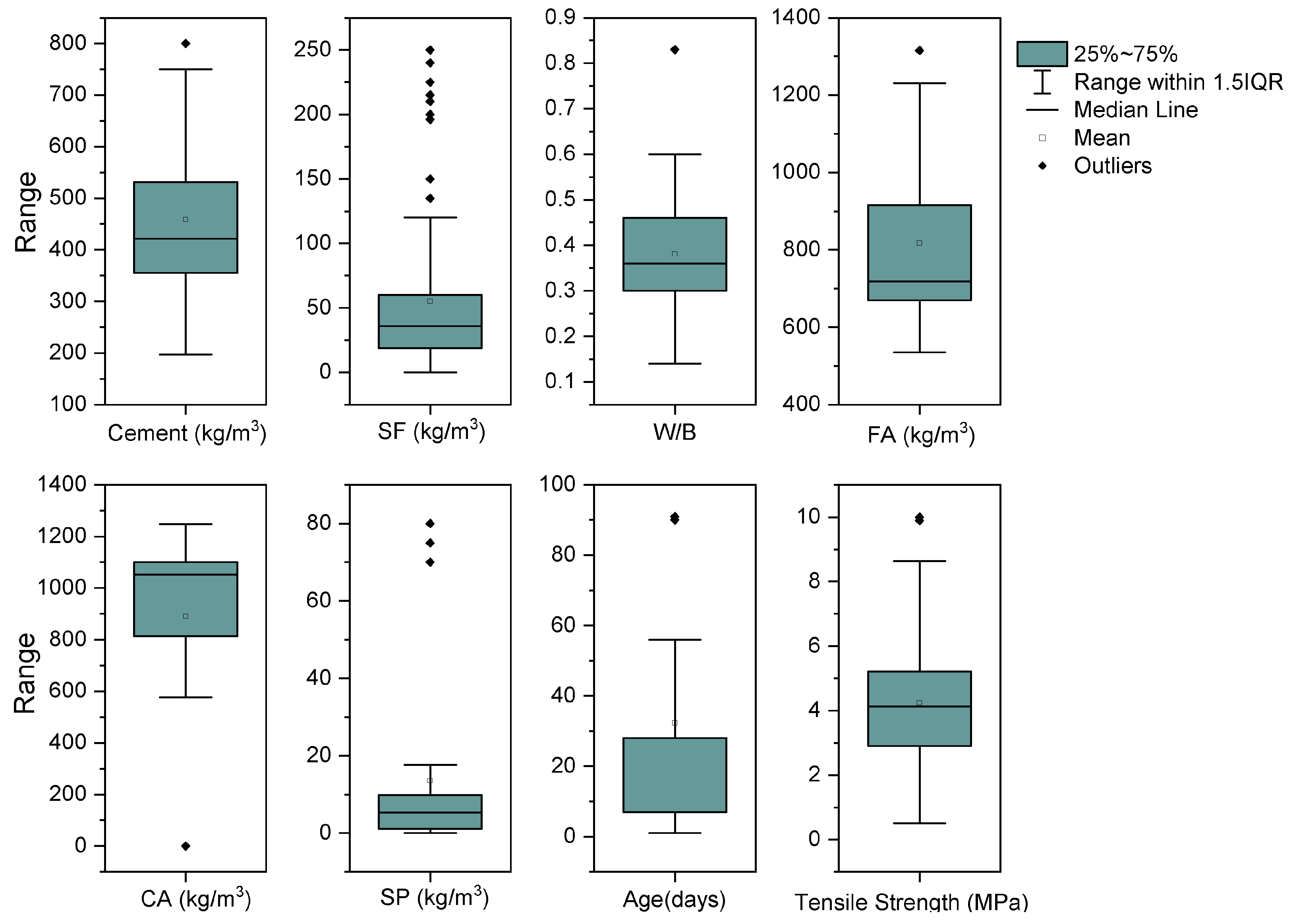

| Model | Learning Rate | Max Depth | Number of Estimators |
|---|---|---|---|
| GBRT | 3.0 | 600 | 0.01 |
| Adaboost | NaN | 50 | 0.50 |
| XGBoost | 3.0 | 500 | 0.01 |
| LightGBM | NaN | 600 | 0.20 |
| Predictor | Cement (kg/m3) | SF (kg/m3) | W/B | FA (kg/m3) | CA (kg/m3) | SP (kg/m3) | Age (Days) | Tensile Strength (MPa) |
|---|---|---|---|---|---|---|---|---|
| Minimum | 197.00 | 0.00 | 0.14 | 535.00 | 0.00 | 0.00 | 1.00 | 0.51 |
| Maximum | 800.00 | 250.00 | 0.83 | 1315.00 | 1248.00 | 80.00 | 91.00 | 10.00 |
| Average | 458.13 | 54.17 | 0.38 | 815.96 | 893.79 | 13.16 | 32.08 | 4.23 |
| Phase | Criteria | LightGBM | GBRT | XGBoost | AdaBoost |
|---|---|---|---|---|---|
| Training | R2 | 0.897 | 0.999 | 0.999 | 0.902 |
| RMSE | 0.589 | 0.057 | 0.059 | 0.576 | |
| MAE | 0.357 | 0.041 | 0.043 | 0.483 | |
| Testing | R2 | 0.799 | 0.955 | 0.965 | 0.845 |
| RMSE | 0.807 | 0.381 | 0.337 | 0.707 | |
| MAE | 0.645 | 0.301 | 0.267 | 0.575 | |
| All | R2 | 0.883 | 0.991 | 0.993 | 0.890 |
| RMSE | 0.639 | 0.179 | 0.161 | 0.605 | |
| MAE | 0.416 | 0.094 | 0.089 | 0.502 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Abdaly, N.M.; Seno, M.E.; Thwaini, M.A.; Imran, H.; Ostrowski, K.A.; Furtak, K. Advanced Ensemble Machine-Learning Models for Predicting Splitting Tensile Strength in Silica Fume-Modified Concrete. Buildings 2024, 14, 4054. https://doi.org/10.3390/buildings14124054
Al-Abdaly NM, Seno ME, Thwaini MA, Imran H, Ostrowski KA, Furtak K. Advanced Ensemble Machine-Learning Models for Predicting Splitting Tensile Strength in Silica Fume-Modified Concrete. Buildings. 2024; 14(12):4054. https://doi.org/10.3390/buildings14124054
Chicago/Turabian StyleAl-Abdaly, Nadia Moneem, Mohammed E. Seno, Mustafa A. Thwaini, Hamza Imran, Krzysztof Adam Ostrowski, and Kazimierz Furtak. 2024. "Advanced Ensemble Machine-Learning Models for Predicting Splitting Tensile Strength in Silica Fume-Modified Concrete" Buildings 14, no. 12: 4054. https://doi.org/10.3390/buildings14124054
APA StyleAl-Abdaly, N. M., Seno, M. E., Thwaini, M. A., Imran, H., Ostrowski, K. A., & Furtak, K. (2024). Advanced Ensemble Machine-Learning Models for Predicting Splitting Tensile Strength in Silica Fume-Modified Concrete. Buildings, 14(12), 4054. https://doi.org/10.3390/buildings14124054







