A Unified Deflection Theory Model for Multi-Tower Self-Anchored Suspension Bridges with Different Tower–Girder and Cable–Girder Connections
Abstract
1. Introduction
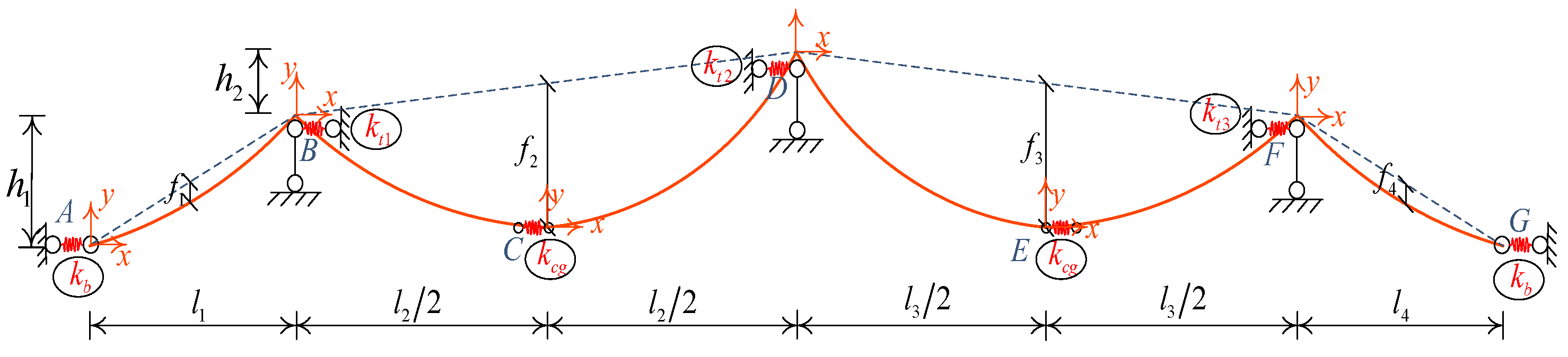
2. Analytical Model for Multi-Tower Suspension Bridges
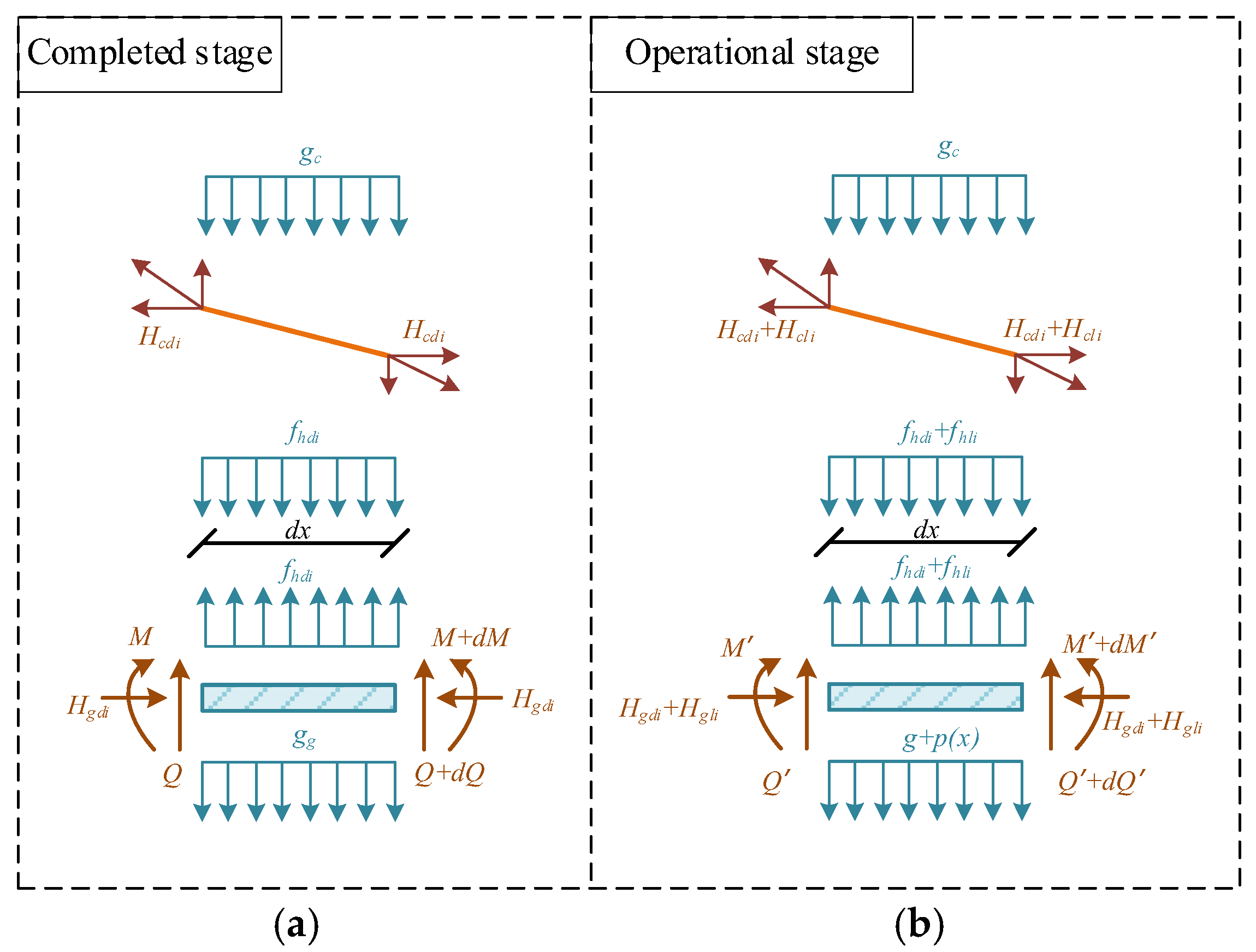
2.1. The Equilibrium Equation of the Main Cable and Girder
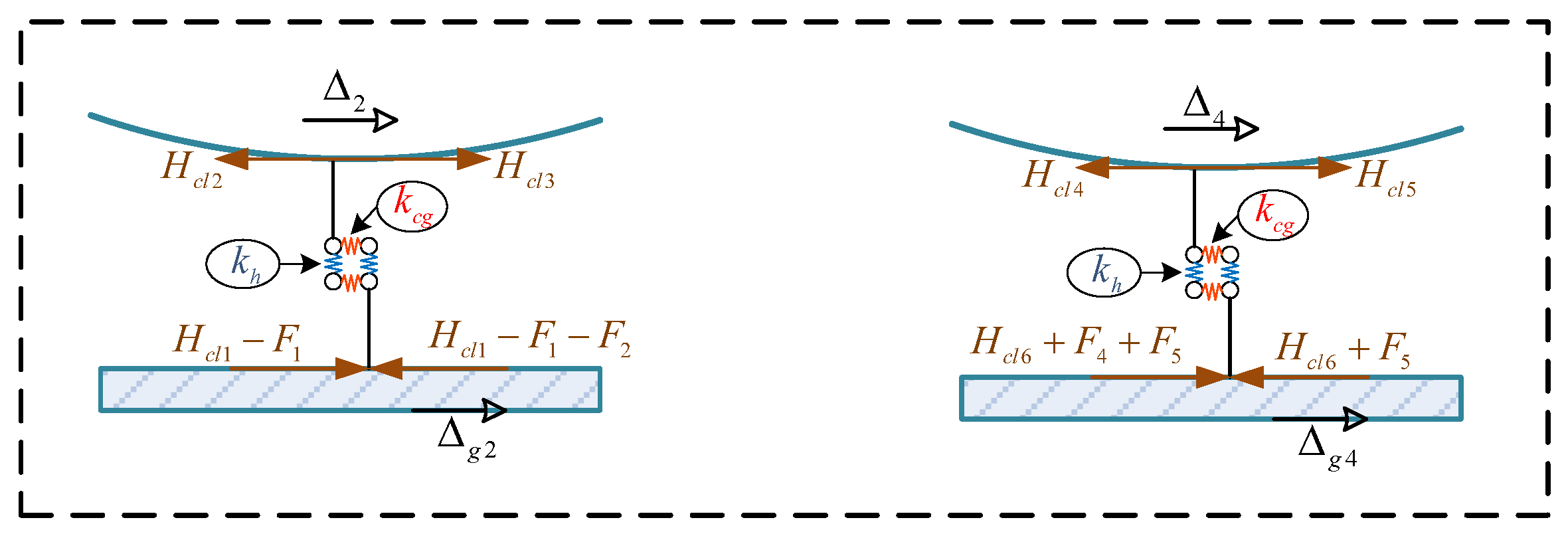
2.2. Consideration of the TGC and CGC
2.3. Compatibility Conditions
2.4. Solution Procedure
3. Validation and Discussions
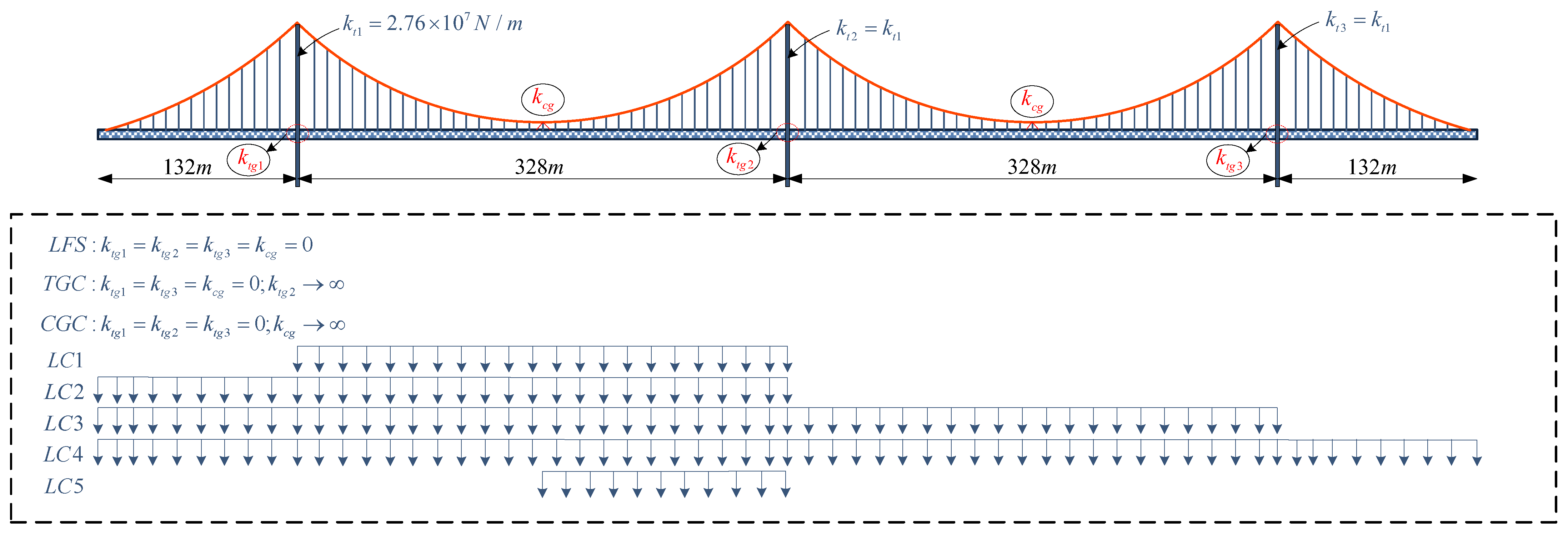
3.1. Numerical Model
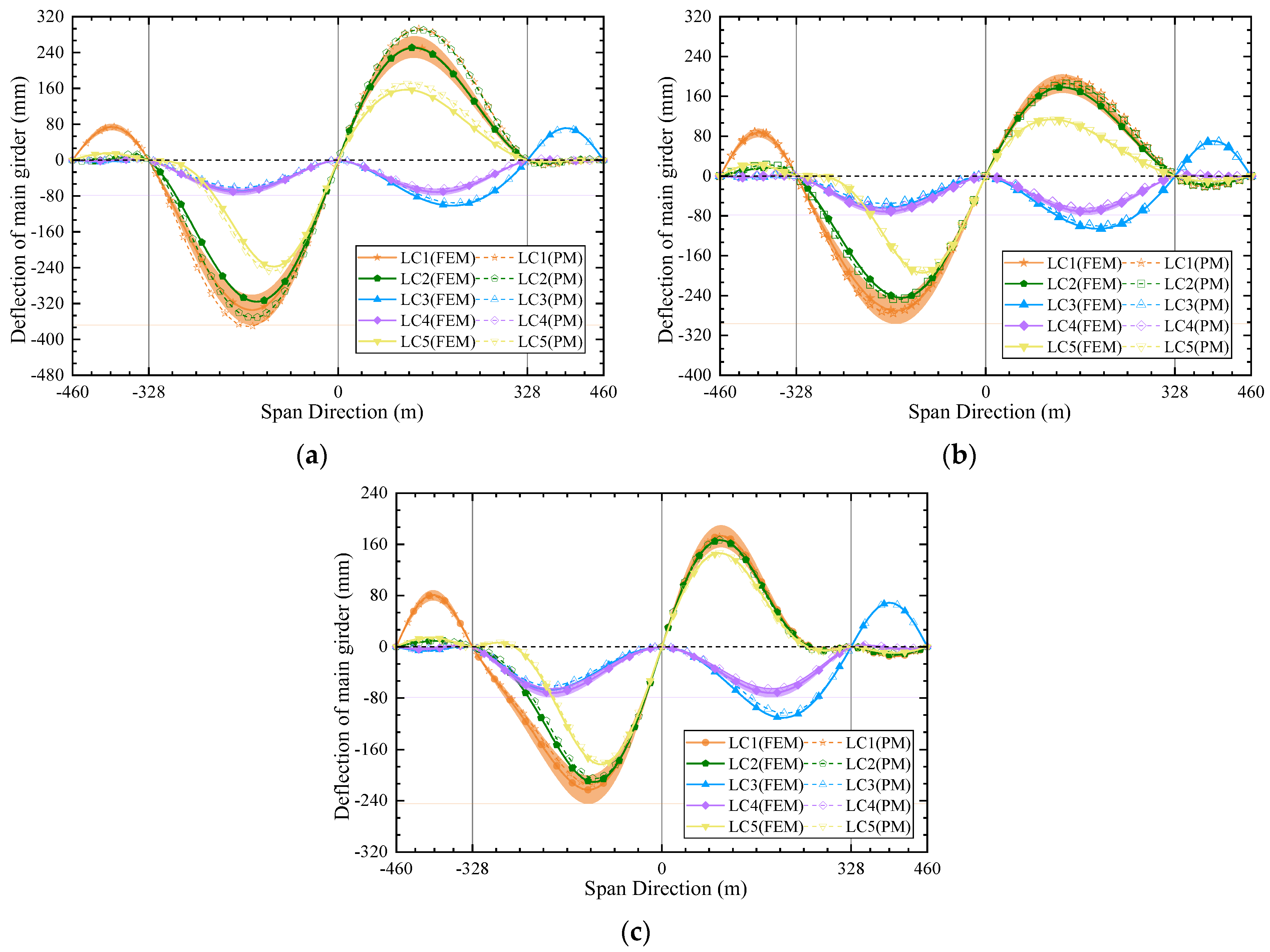
3.2. Deflections of Girder
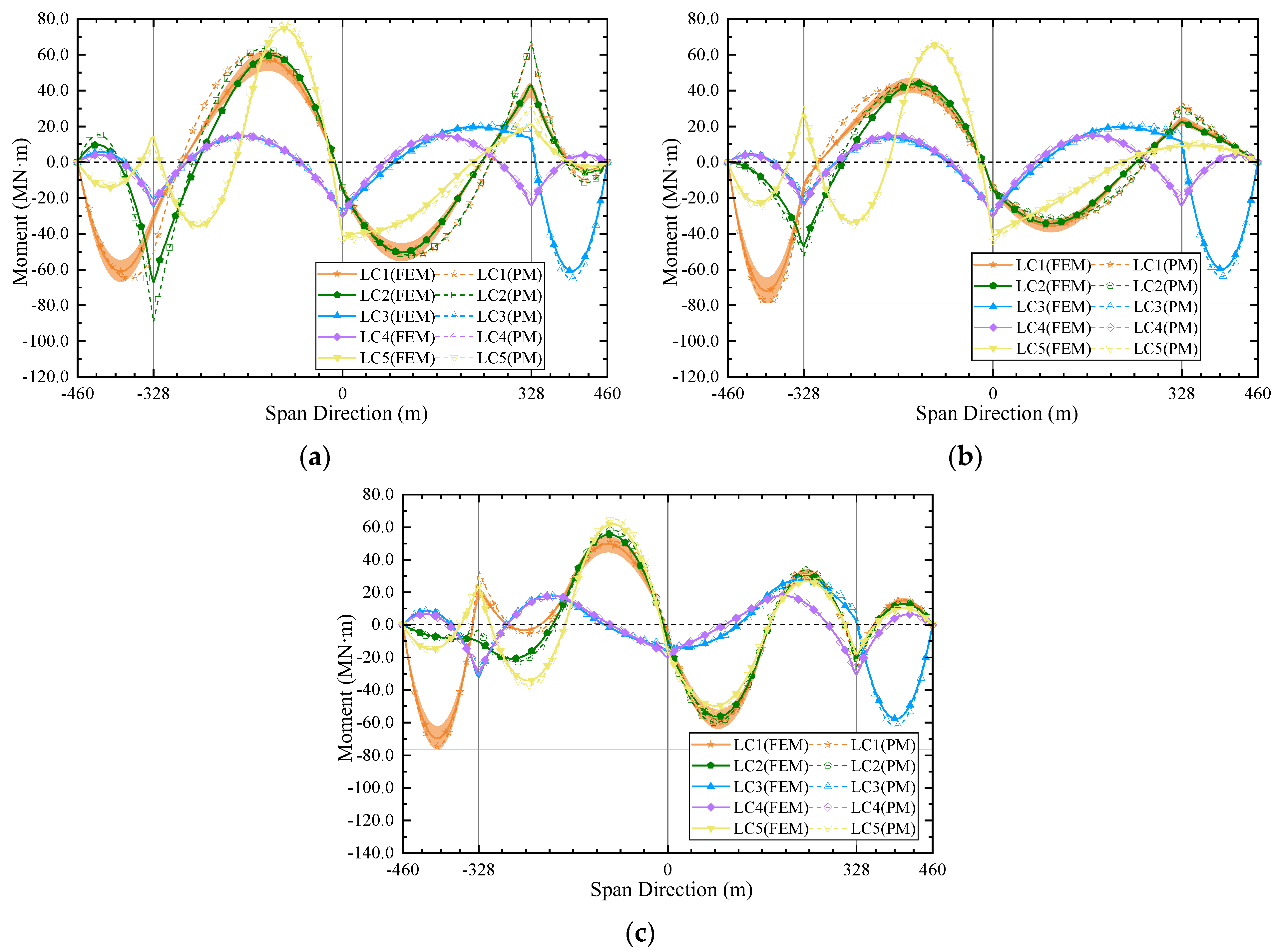
3.3. Moment Distributions of Girder
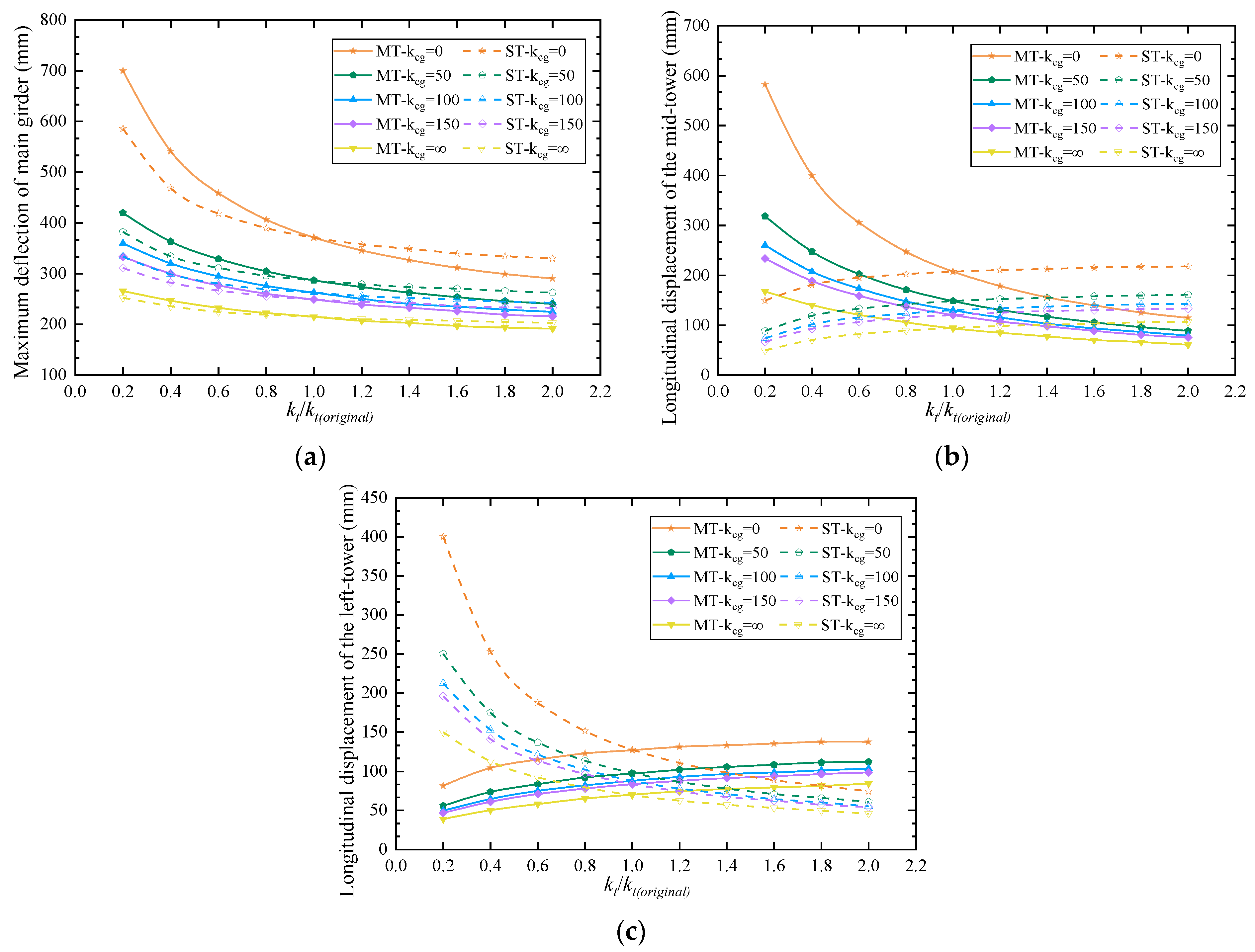
3.4. Longitudinal Displacement of Tower
4. Parametric Studies
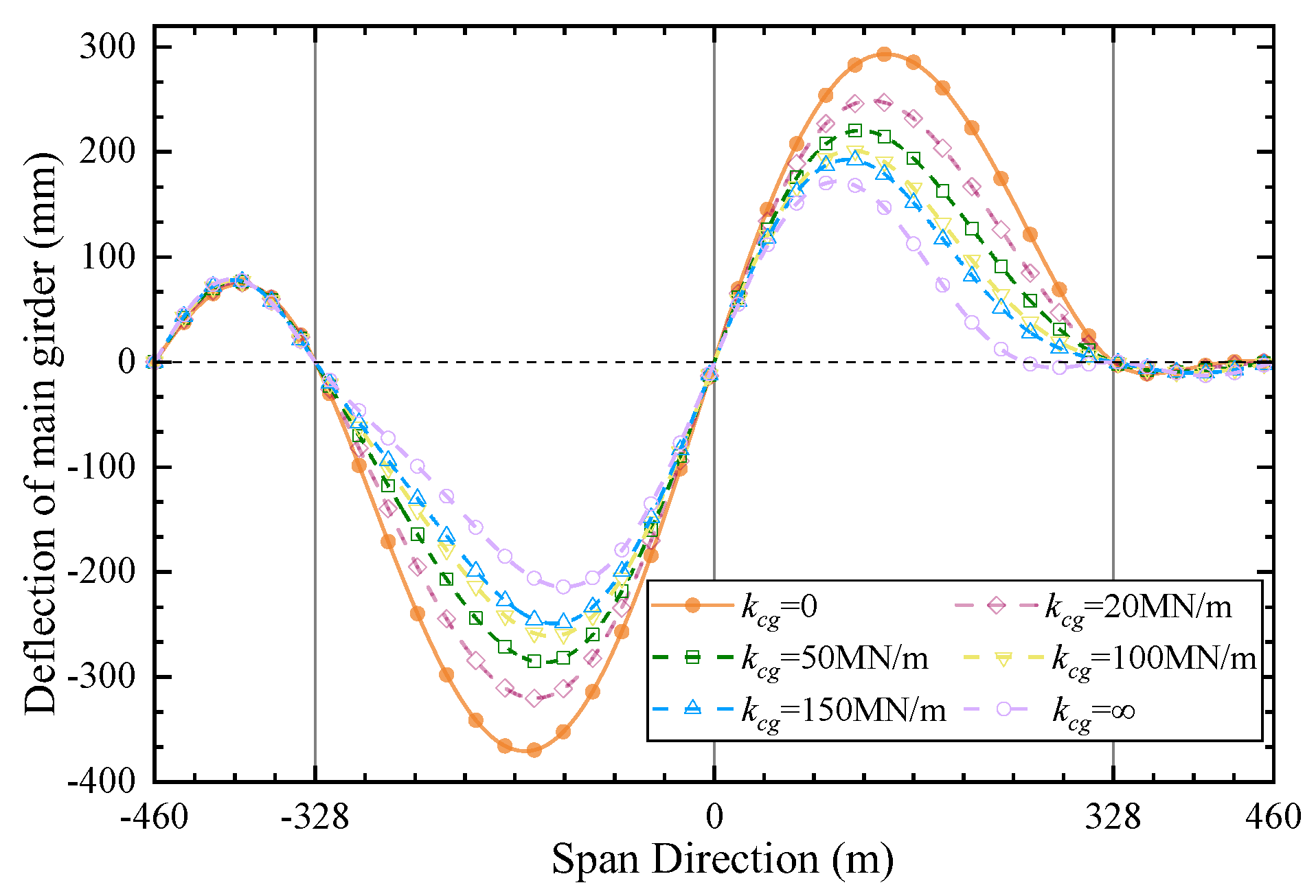
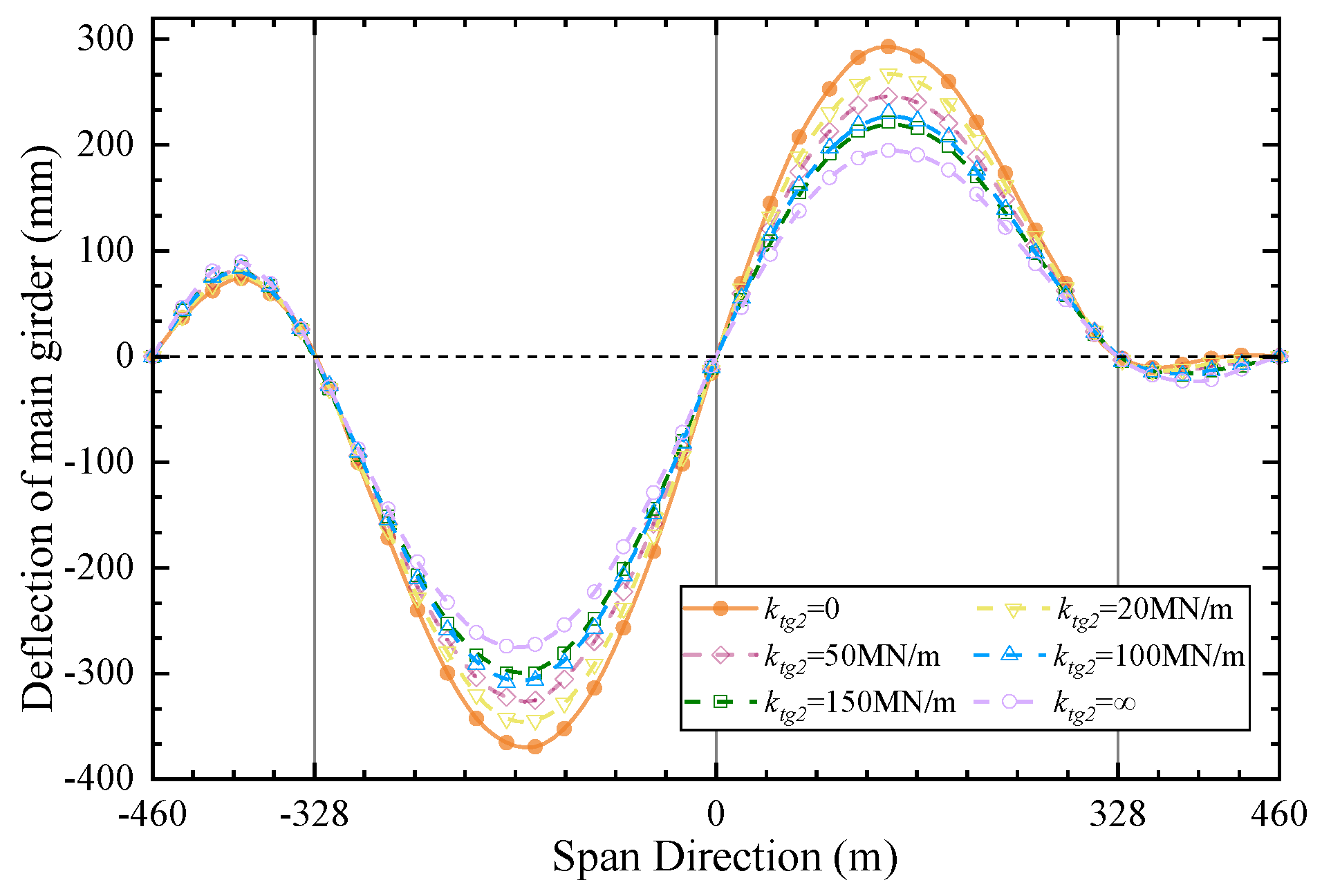
4.1. Stiffness of CGC
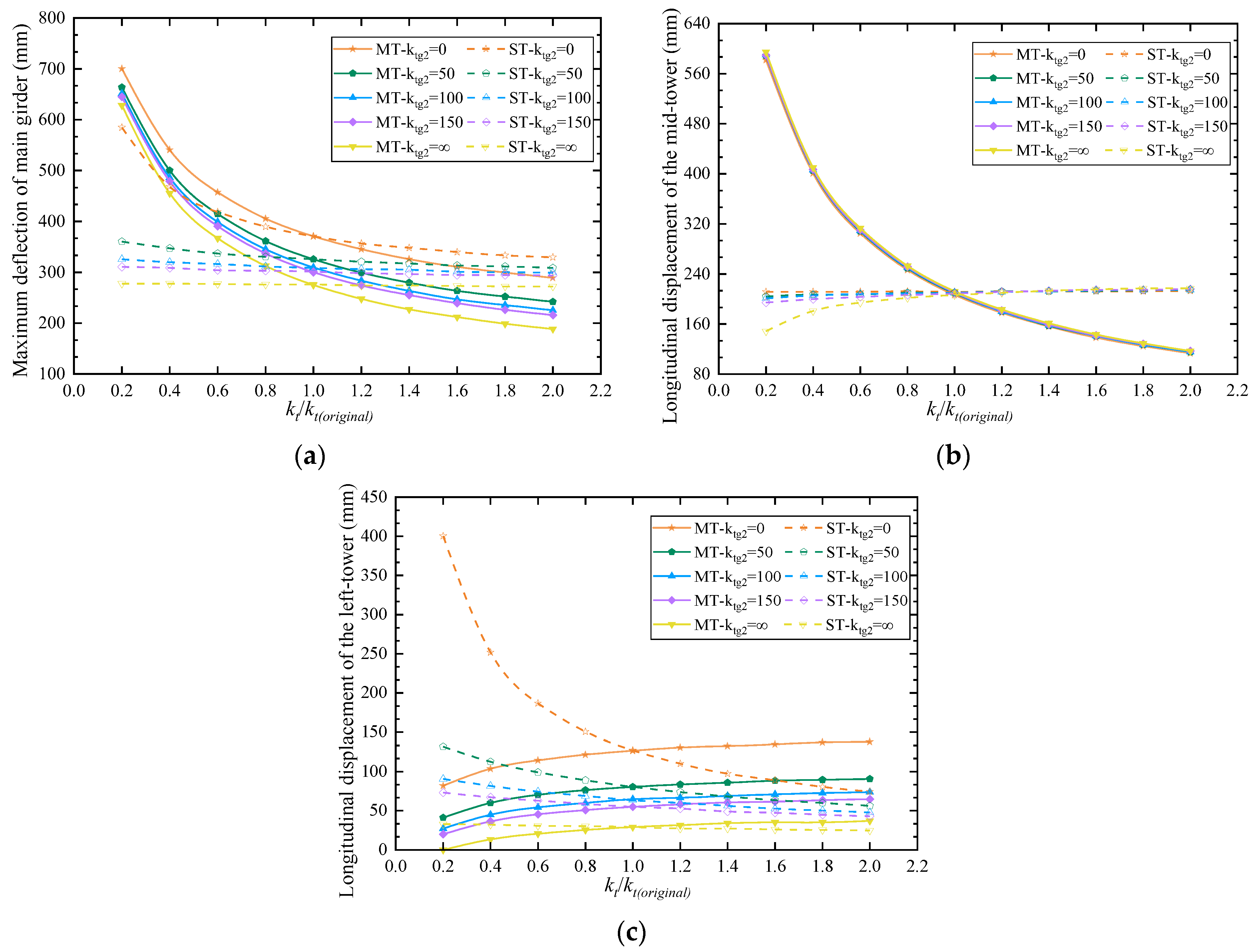
4.2. Stiffness of TGC
5. Conclusions
- A multi-tower self-anchored suspension bridge’s equilibrium differential equation, originally derived from the deflection theory, becomes nonlinear when the stiffness of the towers, TGCs, and CGCs is taken into account. In the substitution beam solution procedure, it was found that the addition of CGCs will not result in the discontinuity of the equivalent axial forces along the two main spans. The analytical model results are almost identical to those of the nonlinear FE analyses with a relative deviation of about 10%. The accuracy is mainly affected by the inclination of the hangers, and the application of TGCs and CGCs can limit this shortcoming.
- By adjusting the main cable’s and girder’s load distribution relationship, the CGC may simultaneously decrease the middle and side towers’ longitudinal displacement. Increasing the stiffness of the CGC will reduce the main girder’s deflection, and the maximum displacement will gradually shift from the mid-span section to the mid-tower section. If the side-tower stiffness is higher, the main beam of the bridge with CGC moves less vertically, which is the same as when the mid-tower toughness is higher.
- The TGC may effectively augment the anchoring effect of the side cable to the side tower by restraining the longitudinal movement of the anchor points. An increase in side-tower stiffness will decrease the main girder’s deflection and increase the mid-tower section’s longitudinal displacement when the TGC stiffness is minimal. As the stiffness of the TGC rises, this action will weaken. While the mid-tower section’s displacement will be somewhat increased due to the TGC, the side tower’s longitudinal displacement will be reduced.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Collings, D. Multiple-span suspension bridges: State of the art. In Proceedings of the Institution of Civil Engineers-Bridge Engineering; Thomas Telford Ltd.: London, UK, 2016; pp. 215–231. [Google Scholar]
- Pan, S.; Cui, Y.; Zhang, Z.; Zhu, W. Behaviour and design of three-tower, self-anchored suspension bridge with a concrete girder. In Proceedings of the Institution of Civil Engineers-Bridge Engineering; Thomas Telford Ltd.: London, UK, 2019; pp. 190–203. [Google Scholar]
- Cheng, J.; Xu, H.; Xu, M. Study on midtower longitudinal stiffness of three-tower four-span suspension bridges with steel truss girders. Struct. Eng. Mech. 2020, 73, 641–649. [Google Scholar]
- Zhang, C.; Wu, S. Effects of Non-Uniform Excitation on Seismic Responses of a Multi-tower Self-Anchored Suspension Bridge. J. Vib. Shock 2015, 34, 7. [Google Scholar]
- Zhang, Q.; Tang, H.; Yang, G. Selection of a structural system for a three-tower suspension bridge of Maanshan Yangtze River Highway Bridge. Struct. Eng. Int. 2012, 22, 139–143. [Google Scholar]
- Xu, F.; Zhang, M.; Wang, L.; Zhang, Z. Self-anchored suspension bridges in China. Pract. Period. Struct. Des. Constr. 2017, 22, 04016018. [Google Scholar] [CrossRef]
- Kang, J.; Hu, J.; Dong, P.; Cao, H.; Qin, S. Parametric Analysis of Dynamic Performance of Triple-tower Self-anchored Suspension Bridge. J. Wuhan Univ. Technol. 2017, 41, 543–548. [Google Scholar]
- Sun, H.T.; Zhang, D.M.; Shao, C.Y. Design of Main Bridge of Binhe Huanghe River Bridge in Yinchuan. Bridge Constr. 2017, 47, 95–100. [Google Scholar]
- Shao, F.; Chen, Z.; Ge, H. Parametric analysis of the dynamic characteristics of a long-span three-tower self-anchored suspension bridge with a composite girder. Adv. Bridge Eng. 2020, 1, 10. [Google Scholar] [CrossRef]
- Yoshida, O.; Okuda, M.; Moriya, T. Structural characteristics and applicability of four-span suspension bridge. J. Bridge Eng. 2004, 9, 453–463. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, C.; Wang, Z.; Liu, Z. An analytical algorithm for reasonable central tower stiffness in the three-tower suspension bridge with unequal-length main spans. Eng. Struct. 2019, 199, 109595. [Google Scholar] [CrossRef]
- General Specifications for the Design of Highway Bridges and Culverts; China Communications Press Co.: Beijing, China, 2015.
- Cao, H.; Qian, X.; Zhou, Y.; Chen, Z.; Zhu, H. Feasible range for midtower lateral stiffness in three-tower suspension bridges. J. Bridge Eng. 2018, 23, 06017009. [Google Scholar] [CrossRef]
- Fukuda, T. Analysis of Multispan Suspension Bridges. J. Struct. Div. 1967, 93, 63–86. [Google Scholar] [CrossRef]
- Chai, S.; Xiao, R.; Li, X. Longitudinal restraint of a double-cable suspension bridge. J. Bridge Eng. 2014, 19, 06013002. [Google Scholar] [CrossRef]
- Gimsing, N.J.; Georgakis, C.T. Cable Supported Bridges: Concept and Design; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hasegawa, K.; Kojima, H.; Sasaki, M.; Takena, K. Frictional resistance between cable and saddle equipped with friction plate. J. Struct. Eng. 1995, 121, 1–14. [Google Scholar] [CrossRef]
- Zhang, Q.; Cheng, Z.; Cui, C.; Bao, Y.; He, J.; Li, Q. Analytical model for frictional resistance between cable and saddle of suspension bridges equipped with vertical friction plates. J. Bridge Eng. 2017, 22, 04016103. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Chen, Z.; Jia, D. Hybrid analytical-numerical method for evaluating the frictional resistance between main cable and saddle. China J. Highw. Transp. 2020, 33, 158–168. [Google Scholar]
- Wang, H.; Li, A.; Zhao, G.; Li, J. Non-linear buffeting response analysis of long-span suspension bridges with central buckle. Earthq. Eng. Eng. Vib. 2010, 9, 259–270. [Google Scholar] [CrossRef]
- Viola, J.M.; Syed, S.; Clenance, J. The new Tacoma Narrows suspension bridge: Construction support and engineering. In Proceedings of the Structures Congress 2005: Metropolis and Beyond, New York, NY, USA, 20 April 2005; pp. 1–12. [Google Scholar]
- Xu, X.; Qiang, S.-Z.; He, S.-H. Influence of central buckle on dynamic behavior and response of long-span suspension bridge under vehicle group excitation. China J. Highw. Transp. 2008, 21, 57–63. [Google Scholar]
- Guo, W.; Li, J.; Xiang, N. Seismic performance of the buckling-restrained brace central buckle for long-span suspension bridges. J. Earthq. Tsunami 2018, 12, 1850015. [Google Scholar] [CrossRef]
- Li, W.; Wang, Y.; Sun, Y.; Wu, H.; Li, P. Effect of structural connections on three-pylon suspension bridges based on analyzing influence lines. J. Harbin Inst. Technol. 2017, 49, 170–174. [Google Scholar]
- Liang, P.; Wu, X.-N.; Li, W.-H.; Xu, Y. Longitudinal Constraint System Optimization for Multi-tower Suspension Bridge. China J. Highw. Transp. 2011, 24, 9. [Google Scholar]
- Zhang, C.; Chen, Y.J.; Fang, Z.Z.; Wu, S.P. Influence law of middle tower on mechanical performance of three-tower self-anchored suspension bridge. Adv. Mater. Res. 2013, 684, 134–138. [Google Scholar] [CrossRef]
- Gwon, S.-G.; Choi, D.-H. Continuum model for static and dynamic analysis of suspension bridges with a floating girder. J. Bridge Eng. 2018, 23, 04018079. [Google Scholar] [CrossRef]
- Jung, M.-R.; Shin, S.-U.; Attard, M.M.; Kim, M.-Y. Deflection theory for self-anchored suspension bridges under live load. J. Bridge Eng. 2015, 20, 04014093. [Google Scholar] [CrossRef]
- Chen, Y.-J.; Wang, S.; Zhong, J.-W.; Lian, F. Study on static analytical method of multi-tower self-anchored suspension bridge. Appl. Sci. 2022, 12, 8499. [Google Scholar] [CrossRef]
- Liu, S.; Chen, Z.; Cao, H.; Shao, C. An Analytical Model for Three-Tower Self-Anchored Suspension Bridges with Longitudinal Tower-Girder Connections. In Proceedings of the Structures; Elsevier: Amsterdam, The Netherlands, 2023; pp. 1455–1467. [Google Scholar]
- Liu, S.; Cao, H.; Chen, Z.; Habib, M.; Zhu, H. Study on Dimensionless Mid-tower Stiffness of Three-Tower Self-Anchored Suspension Bridges Based on an Analytical Approach. In Proceedings of the Structures; Elsevier: Amsterdam, The Netherlands, 2022; pp. 1573–1586. [Google Scholar]
- Cao, H.; Chen, Y.; Li, J.; Liu, S. Static characteristics analysis of three-tower suspension bridges with central buckle using a simplified model. Eng. Struct. 2021, 245, 112916. [Google Scholar] [CrossRef]
- Choi, D.-H.; Gwon, S.-G.; Yoo, H.; Na, H.-S. Nonlinear static analysis of continuous multi-span suspension bridges. Int. J. Steel Struct. 2013, 13, 103–115. [Google Scholar] [CrossRef]
- Irvine, H. Cable Structure (Structural Mechanics); Mit Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Wollmann, G.P. Preliminary analysis of suspension bridges. J. Bridge Eng. 2001, 6, 227–233. [Google Scholar] [CrossRef]




| Item | Deflection | Moment |
|---|---|---|
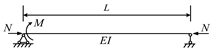 | ||
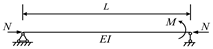 | ||
 |
| Item | Parameter | Value |
|---|---|---|
| Cable | Cross-sectional area | 0.2333 m2 |
| Elastic modulus | 2 × 1011 N/m2 | |
| Girder | Cross-sectional area | 3.5065 m2 |
| Moment of inertia | 7.8483 m4 | |
| Elastic modulus | 2.06 × 1011 N/m2 | |
| Load | Dead load | 745.7 kN/m |
| Live load | 40.32 kN/m |
| Connection Form | Load Case | Left-Side Tower | Mid-Tower Section | Right-Side Tower | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| FEM (mm) | PM (mm) | Error (%) * | FEM (mm) | PM (mm) | Error (%) * | FEM (mm) | PM (mm) | Error (%) * | ||
| LFS | LC1 | 113.91 | 127.28 | 11.74 | −177.96 | −197.58 | 11.02 | 64.89 | 80.30 | 23.75 |
| LC2 | 95.05 | 104.67 | 10.12 | −167.41 | −186.81 | 11.59 | 73.14 | 88.14 | 20.51 | |
| LC3 | 30.14 | 28.43 | 5.67 | 10.57 | 10.87 | 2.84 | −40.75 | −39.30 | 3.56 | |
| LC4 | 21.93 | 20.63 | 5.93 | 0 | 0 | / | −21.93 | −20.63 | 5.93 | |
| LC5 | 58.82 | 63.76 | 8.40 | −102.56 | −110.30 | 7.55 | 44.21 | 48.54 | 9.79 | |
| CGC | LC1 | 71.51 | 69.69 | 2.55 | −97.00 | −95.00 | 2.06 | 25.95 | 25.30 | 2.50 |
| LC2 | 52.40 | 50.98 | 2.71 | −84.50 | −83.13 | 1.62 | 32.50 | 32.15 | 1.08 | |
| LC3 | 26.45 | 25.64 | 3.06 | 12.54 | 11.89 | 5.18 | −39.06 | −37.54 | 3.89 | |
| LC4 | 19.88 | 18.81 | 5.38 | 0 | 0 | / | −19.88 | −18.81 | 5.38 | |
| LC5 | 37.60 | 36.82 | 2.07 | −69.37 | −68.58 | 1.14 | 32.09 | 31.76 | 1.03 | |
| TGC | LC1 | 32.52 | 29.29 | 9.93 | −197.80 | −212.51 | 7.44 | −16.35 | −17.81 | 8.93 |
| LC2 | 6.71 | 6.08 | 9.39 | −188.97 | −202.02 | 6.91 | −15.13 | −16.55 | 9.39 | |
| LC3 | 23.15 | 21.89 | 5.44 | 8.83 | 9.94 | 12.57 | −47.74 | −45.83 | 4.00 | |
| LC4 | 21.93 | 20.63 | 5.93 | 0 | 0 | / | −21.93 | −20.63 | 5.93 | |
| LC5 | 6.11 | 5.72 | 6.38 | −115.27 | −117.24 | 1.71 | −8.47 | −8.82 | 4.13 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, S.; Liao, D.; Zhang, Y.; Shi, J.; Liu, S.; Cao, H. A Unified Deflection Theory Model for Multi-Tower Self-Anchored Suspension Bridges with Different Tower–Girder and Cable–Girder Connections. Buildings 2024, 14, 3945. https://doi.org/10.3390/buildings14123945
Guan S, Liao D, Zhang Y, Shi J, Liu S, Cao H. A Unified Deflection Theory Model for Multi-Tower Self-Anchored Suspension Bridges with Different Tower–Girder and Cable–Girder Connections. Buildings. 2024; 14(12):3945. https://doi.org/10.3390/buildings14123945
Chicago/Turabian StyleGuan, Shiyu, Dinghui Liao, Yi Zhang, Jun Shi, Shuang Liu, and Hongyou Cao. 2024. "A Unified Deflection Theory Model for Multi-Tower Self-Anchored Suspension Bridges with Different Tower–Girder and Cable–Girder Connections" Buildings 14, no. 12: 3945. https://doi.org/10.3390/buildings14123945
APA StyleGuan, S., Liao, D., Zhang, Y., Shi, J., Liu, S., & Cao, H. (2024). A Unified Deflection Theory Model for Multi-Tower Self-Anchored Suspension Bridges with Different Tower–Girder and Cable–Girder Connections. Buildings, 14(12), 3945. https://doi.org/10.3390/buildings14123945






