Statistical Evaluation of Uniform Temperature and Thermal Gradients for Composite Girder of Tibet Region Using Meteorological Data
Abstract
1. Introduction
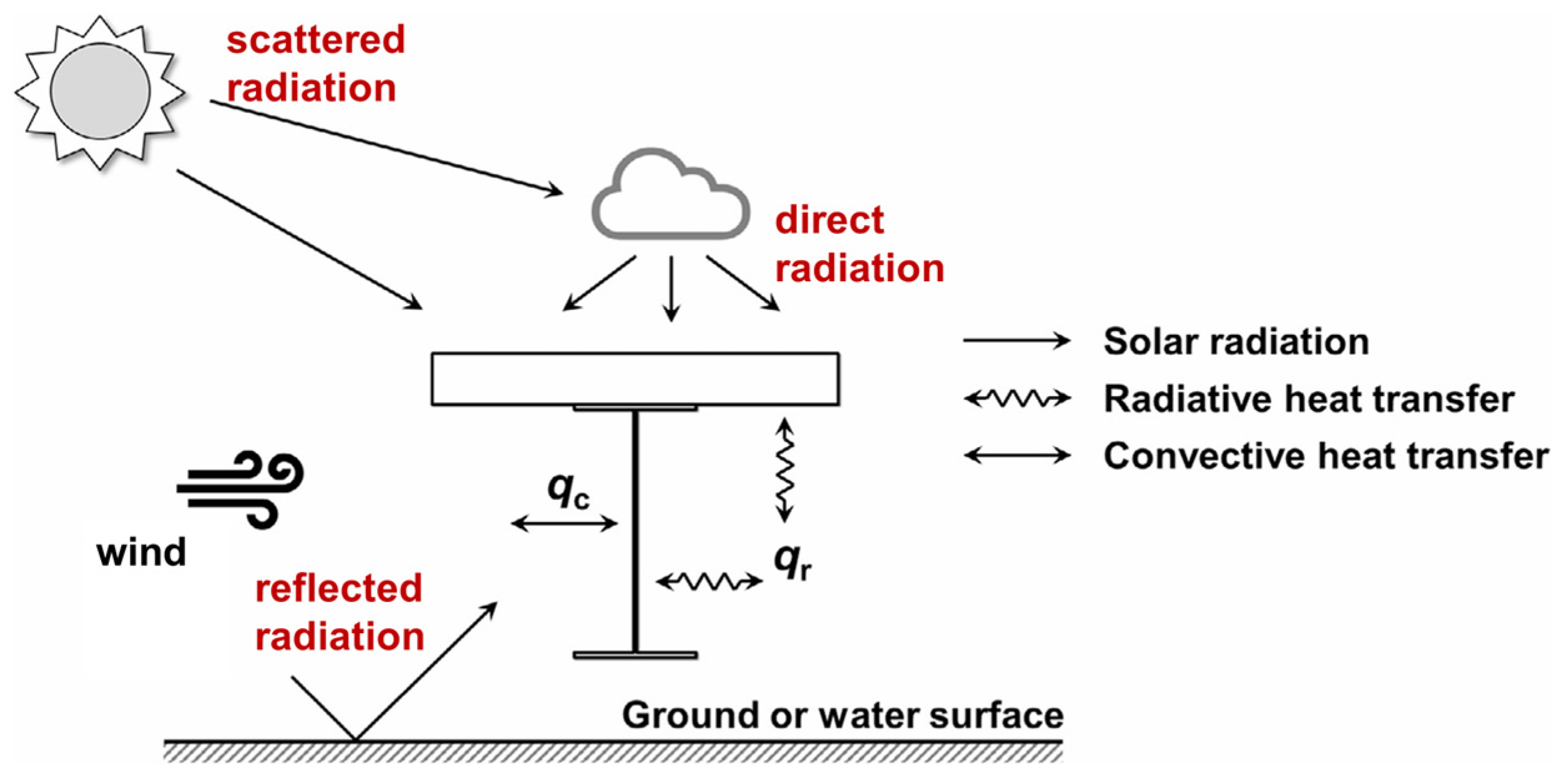
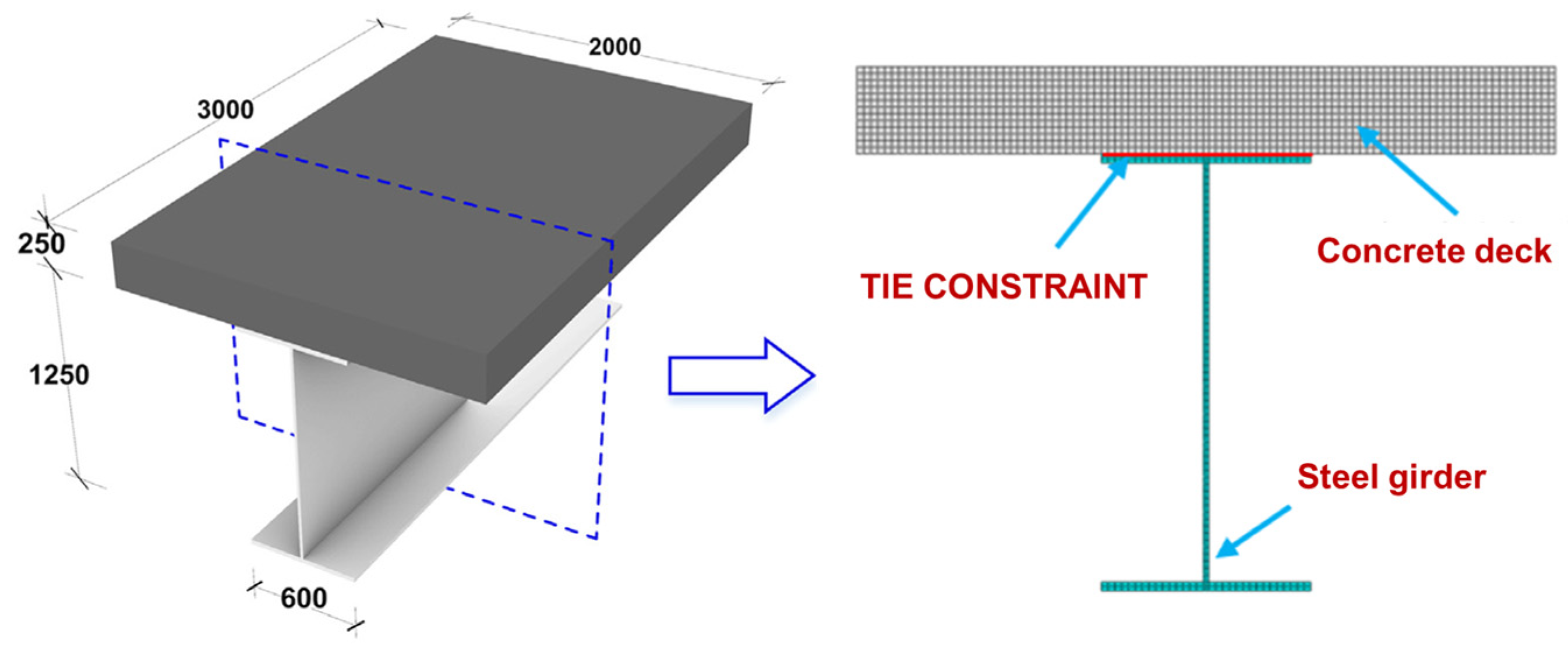
2. Numerical Simulation Method for Temperature Field
3. Temperature Actions on Composite Girder Bridges
3.1. Uniform Temperature
3.2. Thermal Gradient
4. Temperature Action Extremes Based on Meteorological Data
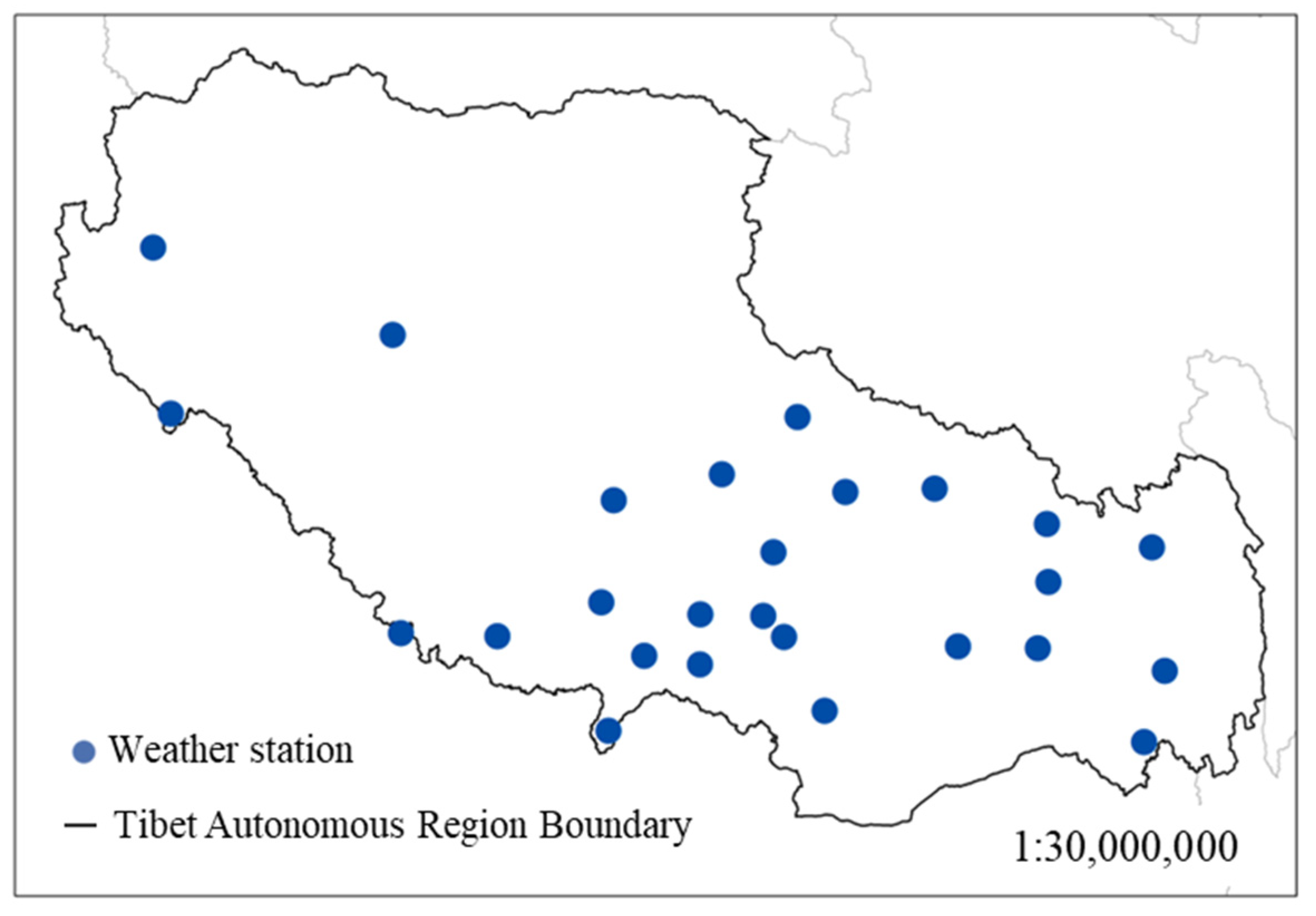
4.1. Historical Meteorological Data Research
4.2. Extreme Meteorological Conditions
4.3. Extreme Value Calculation of Temperature Action
4.3.1. Computational Models
4.3.2. Calculation Results
5. Temperature Actions Extremes Based on Geographic Variation
5.1. Regional Differences in Temperature Actions
5.2. Isotherm Maps of Extreme Temperatures Actions
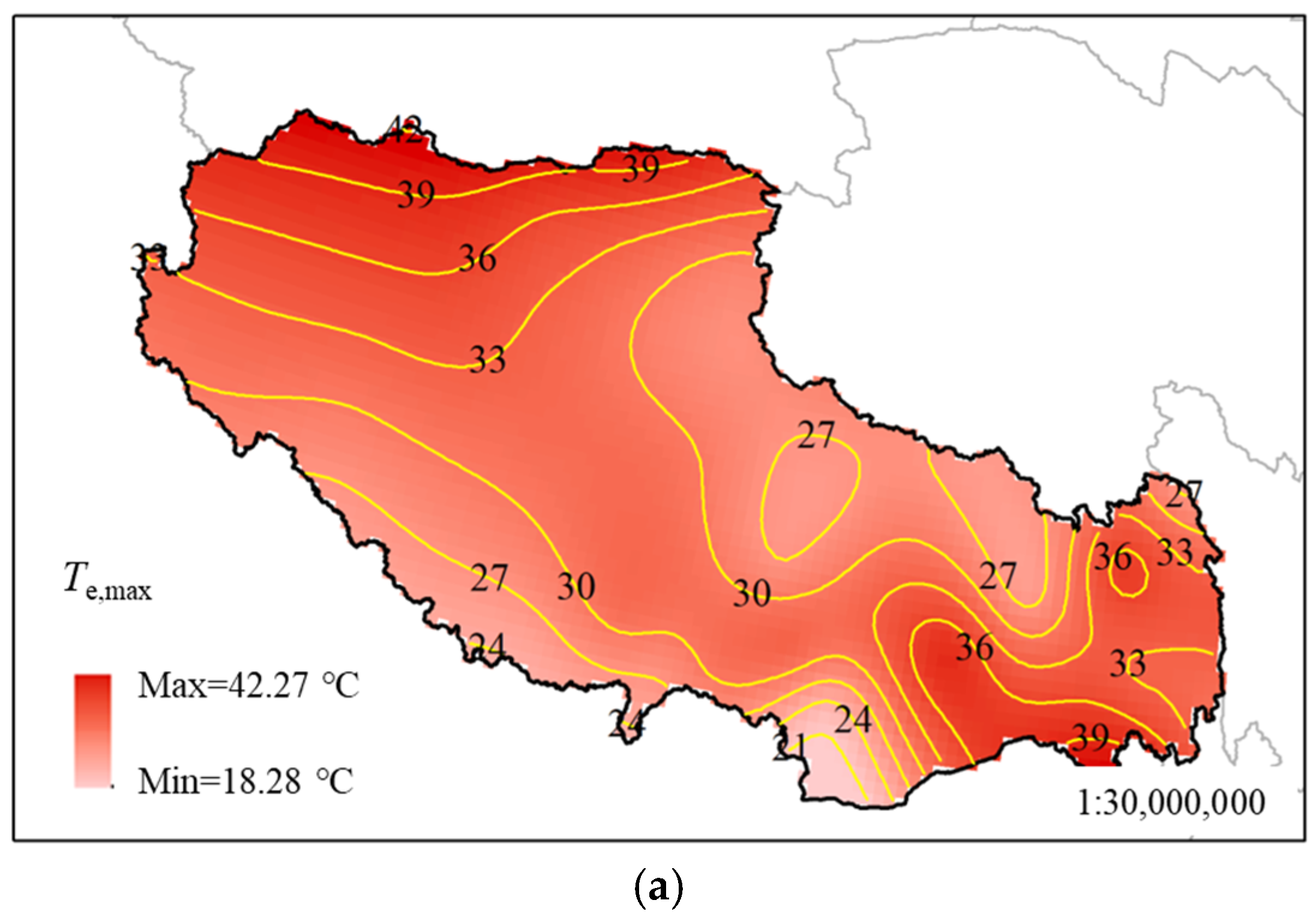
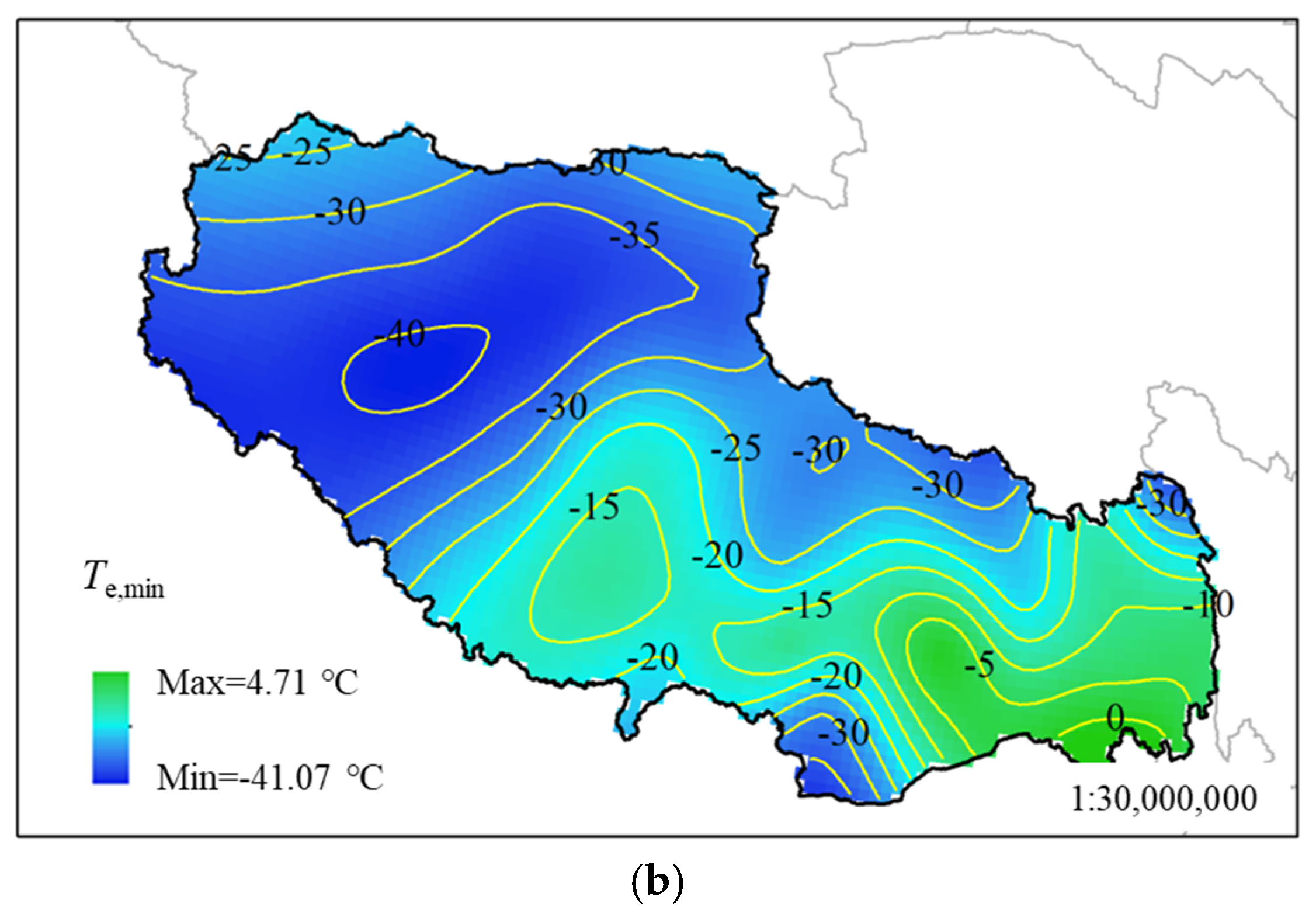
5.2.1. Uniform Temperature
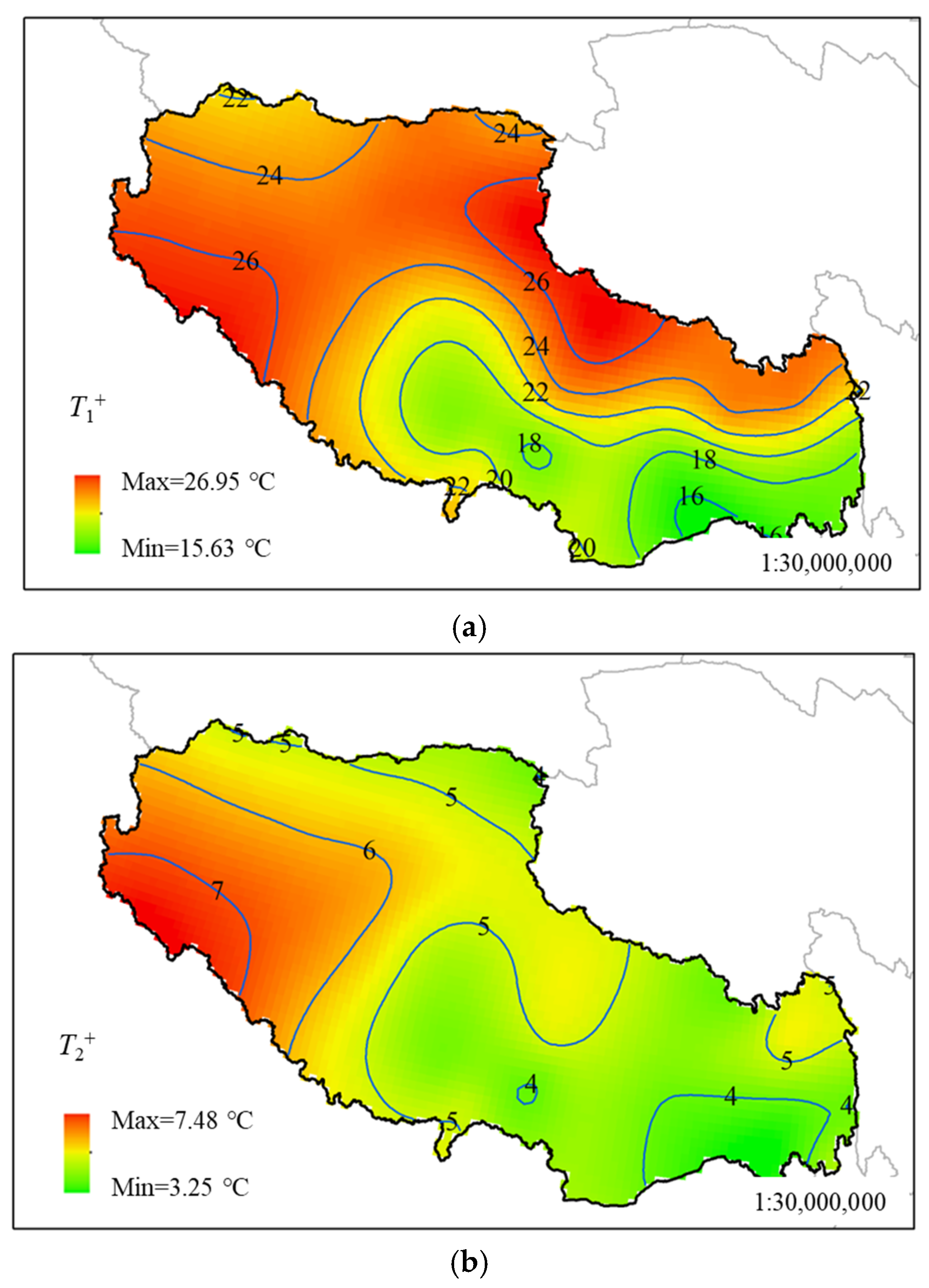
5.2.2. Positive Thermal Gradient
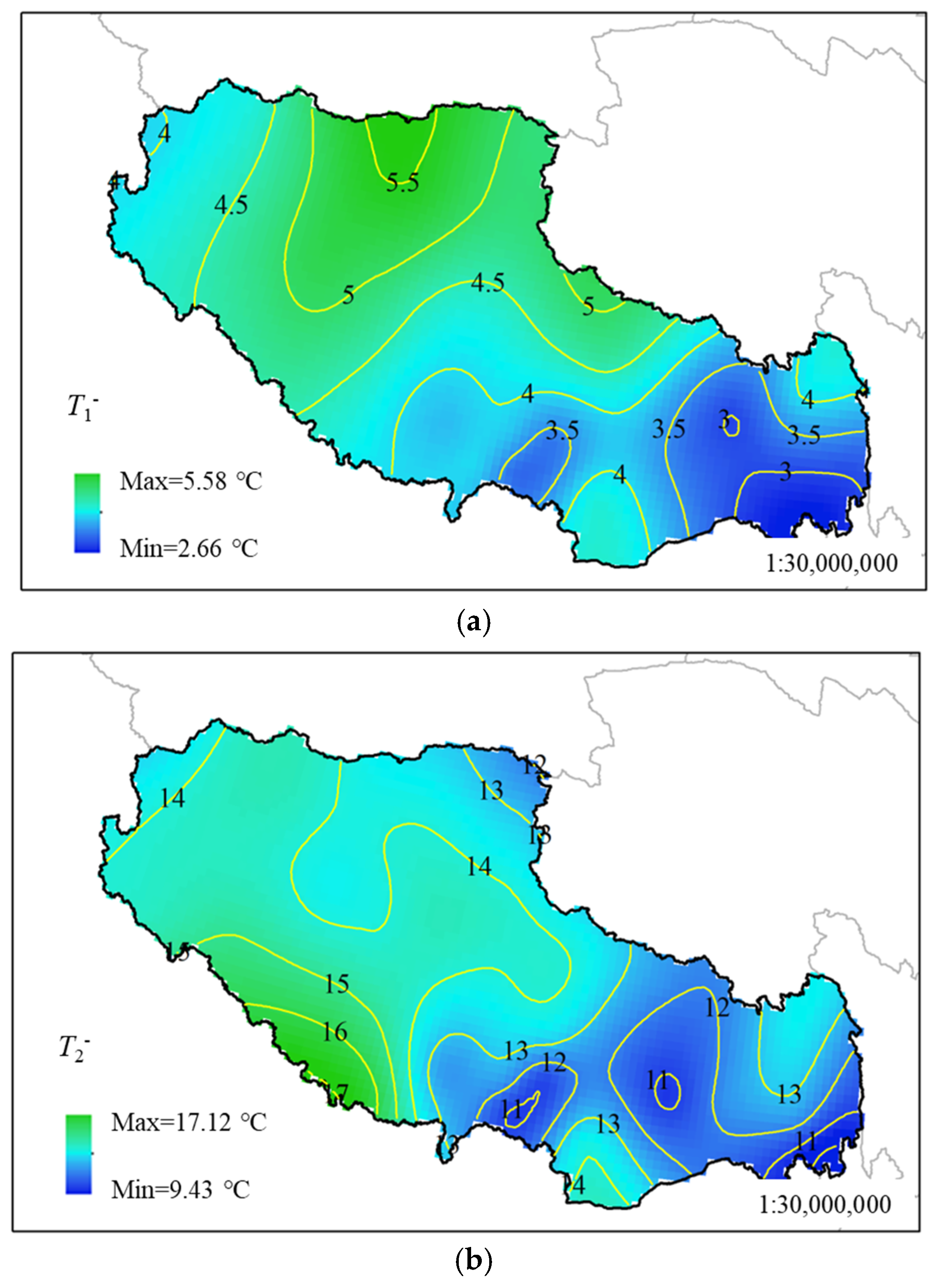
5.2.3. Negative Thermal Gradient
5.3. Comparison of Temperature Effects
6. Conclusions
- (1)
- The temperature action of composite girder bridges in the cold region of the plateau is more unfavorable, and the suggested values in the specification are not safe enough for the design of composite girder bridges in the Tibetan region. The isotherm maps are more detailed and reasonable designs for composite girder bridges in Tibet.
- (2)
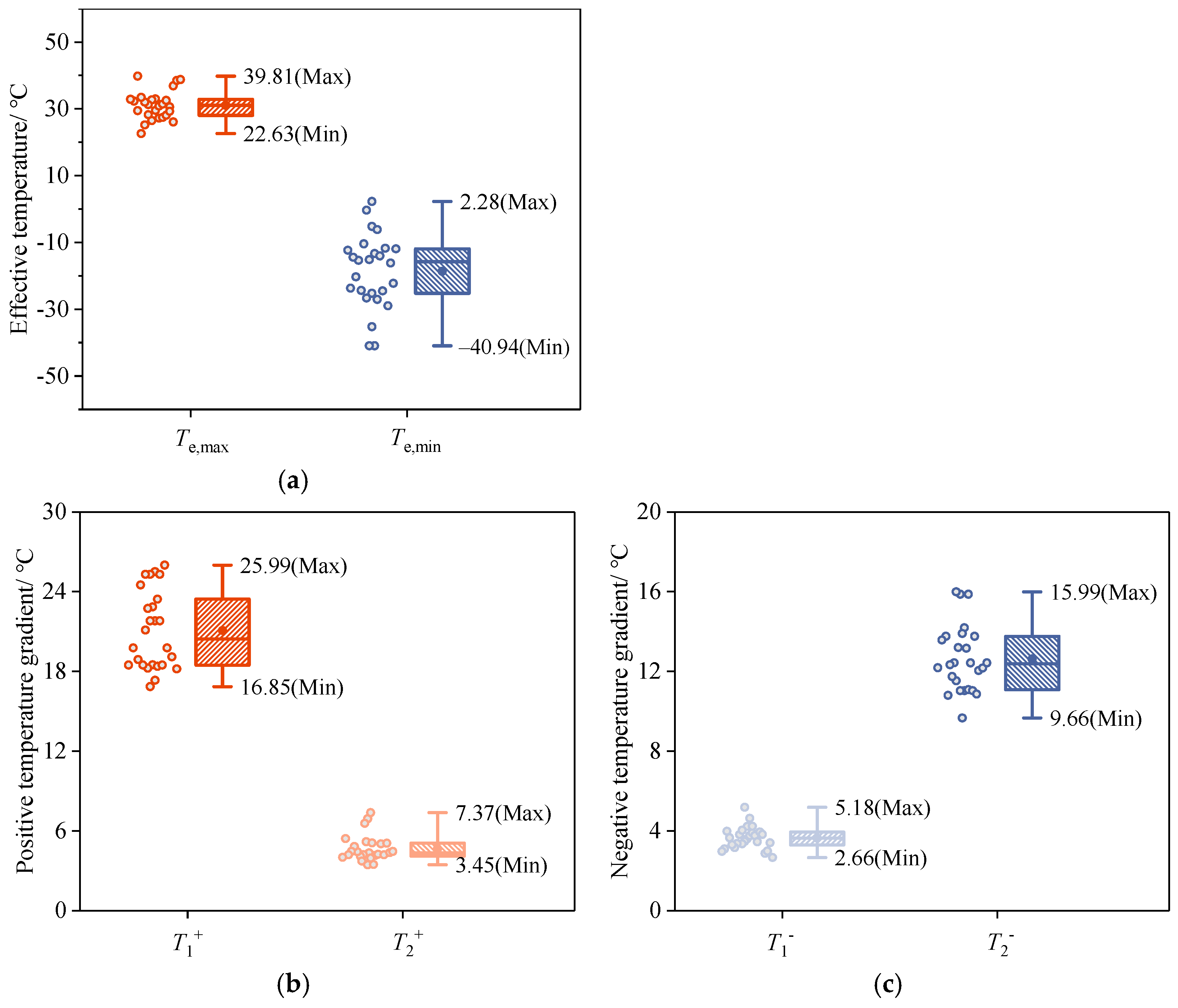
- The uniform temperature of the composite girder is significantly affected by the climatic environment. The maximum and minimum uniform temperatures in Tibet are 18.28~42.27 °C and −41.07~4.71 °C, respectively.
- (3)
- The positive thermal gradient in the Chinese code and the negative thermal gradient in the European code are used to describe the temperature difference characteristics of the composite girders. The values of T1+ and T2+ range from 15.63 °C to 26.95 °C and 3.25 °C to 7.48 °C, respectively. The temperature difference at the top is more significant.
- (4)
- The temperature effects calculated using the most unfavorable values of isotherm maps are more unfavorable than the specification calculations, in which the tensile stress of the concrete reaches 2.91 MPa, with a significant risk of cracking.
- (5)
- The isotherm maps of the temperature action of composite girder bridges in Tibet were obtained from meteorological data and the accuracy of isotherm maps should be verified and improved by placing sensors for long-term structural temperature monitoring.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Liu, J.; Liu, Y.J.; Zhang, C.Y.; Zhao, Q.H.; Lyu, Y. Temperature Action and Effect of Concrete-filled Steel Tubular Bridges: A Review. J. Traffic Transp. Eng. (Engl. Ed.) 2020, 7, 174–191. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.J.; Jiang, L.; Zhang, N. Long-term Field Test of Thermal gradients on the Composite Girder of a Long-span Cable-stayed Bridge. Adv. Struct. Eng. 2019, 22, 2785–2798. [Google Scholar] [CrossRef]
- Kim, S.H.; Park, S.J.; Wu, J.; Won, J.H. Temperature variation in steel box girders of cable-stayed bridges during construction. J. Constr. Steel. Res. 2015, 112, 80–92. [Google Scholar] [CrossRef]
- Elbadry, M.M.; Ghali, A. Temperature Variations in Concrete Bridges. J. Struct. Eng. 1983, 109, 2355–2374. [Google Scholar] [CrossRef]
- Ding, Y.; Zhou, G.; Li, A.; Wang, G. Thermal Field Characteristic Analysis of Steel Box Girder Based on Long-term Measurement Data. Int. J. Steel Struct. 2012, 12, 219–232. [Google Scholar] [CrossRef]
- Zhang, N.; Liu, Y.J.; Liu, J. Temperature Effects of H-shaped Concrete Pylon in Arctic-alpine Plateau Region. J. Traffic Transp. Eng. 2017, 17, 66–77. [Google Scholar]
- Badar, J.; Umar, T.; Akbar, M.; Abbas, N.; Shahzad, Q.; Chen, W.; Arshid, M.U. Innovative Methods to Improve the Seismic Performance of Precast Segmental and Hybrid Bridge Columns under Cyclic Loading. Buildings 2024, 14, 1594. [Google Scholar] [CrossRef]
- The American Association of State Highway and Transportation Officials (AASHTO). AASHTO LRFD Bridge Design Specification; American Association of State Highway and Transportation Officials: Washington, WA, USA, 2012. [Google Scholar]
- EN 1991-1-5; Eurocode 1: Actions on structures-Part 1-5: General Actions-Thermal Actions. European Committee for Standardization (CEN): Brussels, Belgium, 2003.
- TB 10002-2017; National Railway Administration of the People’s Republic of China. Code for Design on Railway Bridge and Culvert. China Railway Publishing House: Beijing, China, 2017.
- Umar, T. Making future floating cities sustainable: A way forward. Proc. Inst. Civ. Eng.-Urban Des. Plan. 2020, 173, 214–237. [Google Scholar] [CrossRef]
- Potgieter, I.C.; Gamble, W.L. Nonlinear Temperature Distributions in Bridges at Different Locations in the United States. PCI J. 1989, 34, 80–103. [Google Scholar] [CrossRef]
- Mirambell, E.; Aguado, A. Temperature and stress distributions in concrete box girder bridges. J. Struct. Eng. 1990, 116, 2388–2409. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.J.; Bai, Y.X. Study on Regional Difference and Zoning of the Thermal gradient Pattern of Concrete Box Girder. China J. Highw. Transp. 2020, 33, 73–84. [Google Scholar]
- Quan, C. Effects of Thermal Loads on Texas Steel Bridges; University of Texas Library: Austin, TX, USA, 2008; Available online: https://www.proquest.com/openview/591e28df629caca6ddb99e845e1a143c/1?pqorigsite=gscholar&cbl=18750 (accessed on 25 November 2024).
- Liu, J.; Liu, Y.; Ma, Z.; Zhang, G.; Lyu, Y. Thermal gradient Action of Steel-concrete Composite Girder Bridge: Action Pattern and Extreme Value Analysis. China J. Highw. Transp. 2022, 35, 269–286. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J. Review on temperature action and effect of steel-concrete composite girder bridge. J. Traffic Transp. Eng. 2020, 20, 42–59. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Liu, J.; Yuan, Z.; Zhang, G.; Ma, Z. Validation of long-term temperature simulations in a steel-concrete composite girder. Structures 2020, 27, 1962–1976. [Google Scholar] [CrossRef]
- Li, Y.; He, S.H.; Liu, P. Effect of Solar Temperature Field on a Sea-crossing Cable-stayed Bridge Tower. Adv. Struct. Eng. 2019, 22, 1867–1877. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.J.; Tang, Z.W.; Zhang, G.J.; Liu, J. Three-dimensional Temperature Field Simulation Method of Truss Arch Rib Based on Sunshine Shadow Recognition. China J. Highw. Transp. 2022, 35, 91–105. [Google Scholar]
- Chen, D.S.; Wang, H.J.; Qian, H.L.; Li, X.Y.; Fan, F.; Shen, S.Z. Experimental and Numerical Investigation of Temperature Effects on Steel Members Due to Solar Radiation. Appl. Therm. Eng. 2017, 127, 696–704. [Google Scholar] [CrossRef]
- Liu, H.B.; Chen, Z.H.; Zhou, T. Theoretical and experimental study on the temperature distribution of H-shaped steel members under solar radiation. Appl. Therm. Eng. 2012, 37, 329–335. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China. JTG D60-2015; General Specifications for Design of Highway Bridges and Culverts. China Communications Press: Beijing, China, 2015; (In Chinese). Available online: https://xxgk.mot.gov.cn/jigou/glj/202006/t20200623_3312312.html (accessed on 25 November 2024).
- Pearson, R.K.; Neuvo, Y.; Astola, J.; Gabbouj, M. Generalized Hampel filters. EURASIP J. Appl. Signal Process 2016, 87, 2016. [Google Scholar] [CrossRef]
- Kehlbeck, F. Effect of Solar Radiation on Bridge Structure; China Railway Publishing House: Beijing, China, 1981. [Google Scholar]
- Hottel, H.C. A Simple Model for Estimating the Transmittance of Direct Solar Radiation Through Clear Atmospheres. Sol. Energy 1976, 18, 129–134. [Google Scholar] [CrossRef]
- Jiang, H.F.; Wen, D.Y.; Li, N.; Ding, Y.; Xiao, J. A New Simulation Method for the Diurnal Variation of Temperature--Sub-sine Simulation. Metro. Disaster Red. Res. 2010, 33, 61–65. [Google Scholar]
- Thapar, V.; Agnihotri, G.; Sethi, V.K. Estimation of Hourly Temperature at a Site and its Impact on Energy Yield of a PV Module. Int. J. Green. Energy 2012, 9, 553–572. [Google Scholar] [CrossRef]
- Zhou, K.; Han, L.-H. Modelling the behaviour of concrete-encased concrete-filled steel tube (CFST) columns subjected to full-range fire. Eng. Struct. 2019, 183, 265–280. [Google Scholar] [CrossRef]



| Characteristics | Steel | Concrete |
|---|---|---|
| Density | 7840 | 2150 |
| Specific heat capacity | 465 | 910 |
| Thermal conductivity | 55 | 2.8 |
| Absorptivity | 0.5 | 0.45 |
| Emittivity | 0.8 | 0.85 |
| Meteorological Station Information | Geographic Information | Uniform Temperature/°C | Positive Gradient/°C | Negative Gradient/°C | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Serial | Station Number | Name of Meteorological Station | Latitude | Longitude | Altitude/m | Te,max | Te,min | T1+ | T2+ | T1− | T2− |
| 1 | 55228 | Shiquan River | 32.3 | 80.05 | 4278.6 | 33.00 | −35.25 | 25.50 | 6.91 | 4.22 | 14.19 |
| 2 | 55248 | Gerze | 32.09 | 84.25 | 4414.9 | 32.69 | −40.94 | 25.30 | 6.56 | 5.18 | 13.90 |
| 3 | 55279 | Bangor | 31.23 | 90.01 | 4700 | 29.53 | −40.94 | 25.30 | 3.45 | 3.60 | 15.87 |
| 4 | 55294 | Amdo | 32.21 | 91.06 | 4800 | 26.51 | −25.24 | 25.30 | 4.34 | 3.47 | 15.87 |
| 5 | 55299 | Nagchu | 31.29 | 92.04 | 4507 | 27.22 | −26.66 | 25.99 | 5.18 | 4.63 | 13.19 |
| 6 | 55437 | Burang | 30.17 | 81.15 | 3900 | 28.26 | −27.07 | 21.80 | 3.90 | 3.76 | 11.03 |
| 7 | 55472 | Shenzha | 30.57 | 88.38 | 4672 | 30.84 | −24.39 | 21.80 | 7.37 | 3.35 | 11.03 |
| 8 | 55493 | Dangxiong | 30.29 | 91.06 | 4200 | 27.42 | −24.51 | 22.85 | 5.09 | 3.90 | 13.16 |
| 9 | 55578 | Shigatse | 29.15 | 88.53 | 3836 | 31.27 | −13.33 | 18.50 | 4.21 | 3.81 | 12.43 |
| 10 | 55585 | Nimu | 29.26 | 90.1 | 3809.4 | 31.45 | −15.15 | 18.24 | 4.14 | 3.76 | 12.42 |
| 11 | 55591 | Lhasa | 29.4 | 91.08 | 3648.9 | 32.02 | −14.03 | 18.38 | 4.09 | 3.36 | 11.08 |
| 12 | 55598 | Tsedang | 29.16 | 91.46 | 3560 | 32.52 | −10.42 | 18.47 | 4.24 | 3.45 | 11.53 |
| 13 | 55655 | Nyalam | 28.11 | 85.58 | 3810 | 33.45 | −11.74 | 18.47 | 4.42 | 3.16 | 9.66 |
| 14 | 55664 | Tingri | 28.38 | 87.05 | 4300 | 25.21 | −15.35 | 21.80 | 5.02 | 4.03 | 15.99 |
| 15 | 55680 | Gyangzê | 28.55 | 89.36 | 4040 | 28.07 | −20.30 | 21.10 | 4.82 | 3.94 | 12.33 |
| 16 | 55681 | Nankazi | 28.58 | 90.24 | 4431.7 | 30.59 | −16.17 | 18.89 | 4.19 | 3.30 | 11.03 |
| 17 | 55696 | Lhunzi | 28.25 | 92.28 | 3860 | 22.63 | −28.96 | 19.76 | 4.46 | 4.23 | 13.76 |
| 18 | 55773 | Pari | 27.44 | 89.05 | 4300 | 29.28 | −14.42 | 19.76 | 5.07 | 3.82 | 13.76 |
| 19 | 56106 | Suo County | 31.53 | 93.47 | 4022.8 | 39.81 | −5.20 | 19.09 | 4.19 | 3.65 | 11.74 |
| 20 | 56116 | Tingqing | 31.25 | 95.36 | 3873.1 | 29.49 | −23.70 | 22.73 | 4.36 | 2.87 | 12.04 |
| 21 | 56137 | Chamdo | 31.09 | 97.1 | 3315 | 36.90 | −11.92 | 24.50 | 5.42 | 3.98 | 13.57 |
| 22 | 56223 | Lhokhorn | 30.45 | 95.5 | 3640 | 26.08 | −22.24 | 23.43 | 4.45 | 2.98 | 12.17 |
| 23 | 56227 | Bomi | 29.52 | 95.46 | 2736 | 32.34 | −12.31 | 18.47 | 3.95 | 3.09 | 12.18 |
| 24 | 56312 | Linzhi | 29.4 | 94.2 | 2991.8 | 38.52 | −0.35 | 17.33 | 4.01 | 3.40 | 10.86 |
| 25 | 56331 | Zuogang | 29.4 | 97.5 | 3780 | 32.87 | −6.13 | 18.18 | 3.73 | 2.97 | 12.42 |
| 26 | 56434 | Qasumi | 28.39 | 97.28 | 2327.6 | 38.79 | 2.28 | 16.85 | 3.46 | 2.66 | 10.80 |
| Temperature Action (°C) | Uniform Temperature | Positive Thermal Gradient | Negative Thermal Gradient | |||
|---|---|---|---|---|---|---|
| Te,max | Te,min | T1+ | T2+ | T1− | T2− | |
| Specification recommended value | 39 | −32 | 25 | 6.7 | 5 | 8 |
| Maximum in Isotherm map | 42.27 | 4.71 | 26.95 | 7.48 | 5.58 | 17.12 |
| Minimum in Isotherm map | 18.29 | −41.07 | 15.63 | 3.25 | 2.66 | 9.43 |
| Stress (MPa) | Maximum Uniform Temperature | Minimum Uniform Temperature | Positive Thermal Gradient | Negative Thermal Gradient |
|---|---|---|---|---|
| Specification recommended value | 0.75 | −1.47 | 2.65 | 1.47 |
| Maximum in Isotherm map | 0.84 | −0.13 | 2.91 | 1.55 |
| Minimum in Isotherm map | 0.39 | −2.01 | 1.77 | 1.13 |
| Stress (MPa) | Maximum Uniform Temperature | Minimum Uniform Temperature | Positive Thermal Gradient | Negative Thermal Gradient |
|---|---|---|---|---|
| Specification recommended value | 0.81 | −1.13 | 11.41 | −8.20 |
| Maximum in Isotherm map | 0.88 | −0.08 | 12.95 | −19.35 |
| Minimum in Isotherm map | 0.43 | −1.47 | 8.03 | −9.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Ma, Z.; Liu, J. Statistical Evaluation of Uniform Temperature and Thermal Gradients for Composite Girder of Tibet Region Using Meteorological Data. Buildings 2024, 14, 3798. https://doi.org/10.3390/buildings14123798
Liu Y, Ma Z, Liu J. Statistical Evaluation of Uniform Temperature and Thermal Gradients for Composite Girder of Tibet Region Using Meteorological Data. Buildings. 2024; 14(12):3798. https://doi.org/10.3390/buildings14123798
Chicago/Turabian StyleLiu, Yujuan, Zhiyuan Ma, and Jiang Liu. 2024. "Statistical Evaluation of Uniform Temperature and Thermal Gradients for Composite Girder of Tibet Region Using Meteorological Data" Buildings 14, no. 12: 3798. https://doi.org/10.3390/buildings14123798
APA StyleLiu, Y., Ma, Z., & Liu, J. (2024). Statistical Evaluation of Uniform Temperature and Thermal Gradients for Composite Girder of Tibet Region Using Meteorological Data. Buildings, 14(12), 3798. https://doi.org/10.3390/buildings14123798






