Horizontal Deformation Control Strategy and Implementation Method of Eccentric Core Tube Structure Based on Construction Error Uncertainty
Abstract
1. Introduction
2. Construction Error Intervention Strategy and Construction Stringing Method
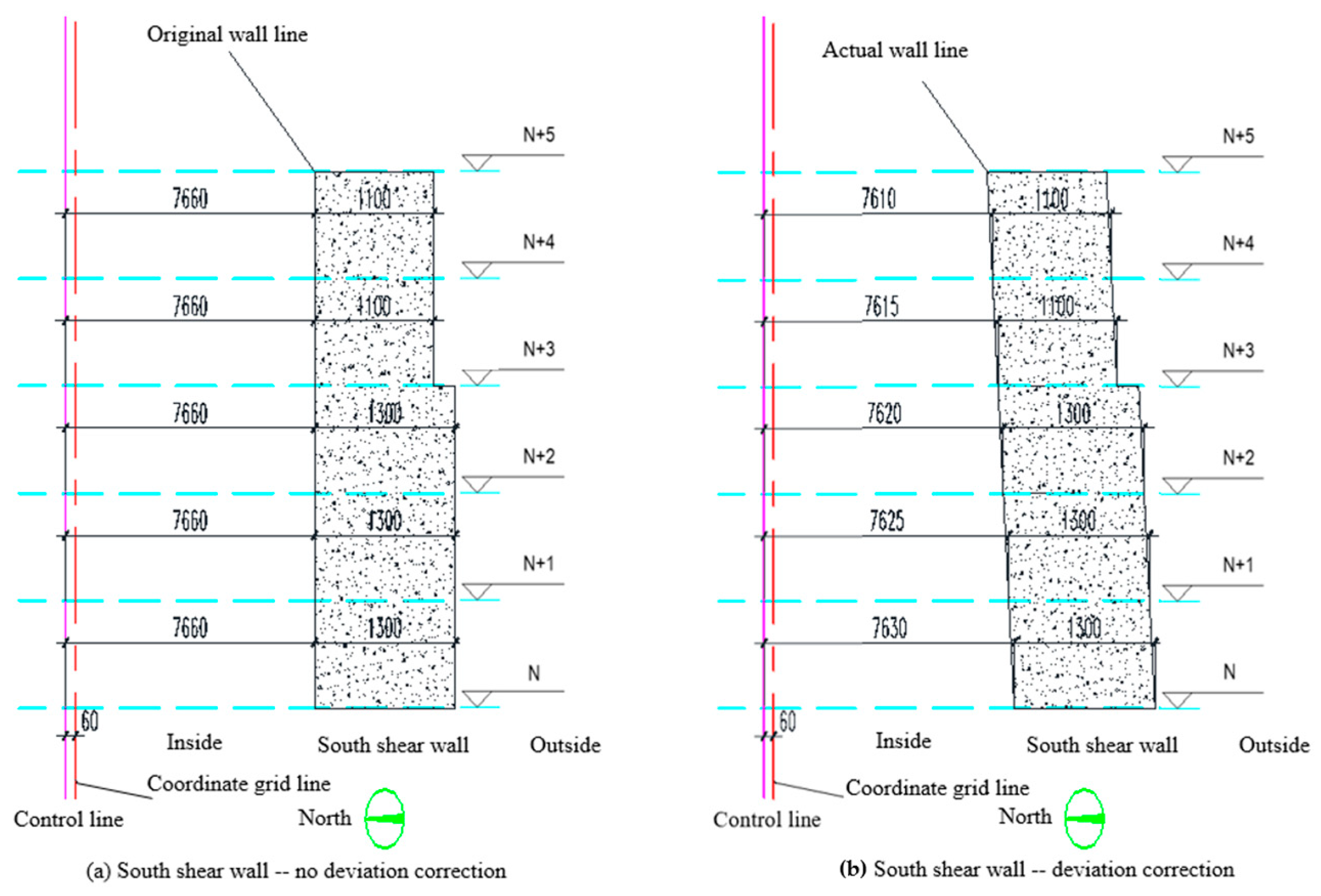
2.1. Construction Error Intervention Strategy
2.2. Implementation Effect Criterion
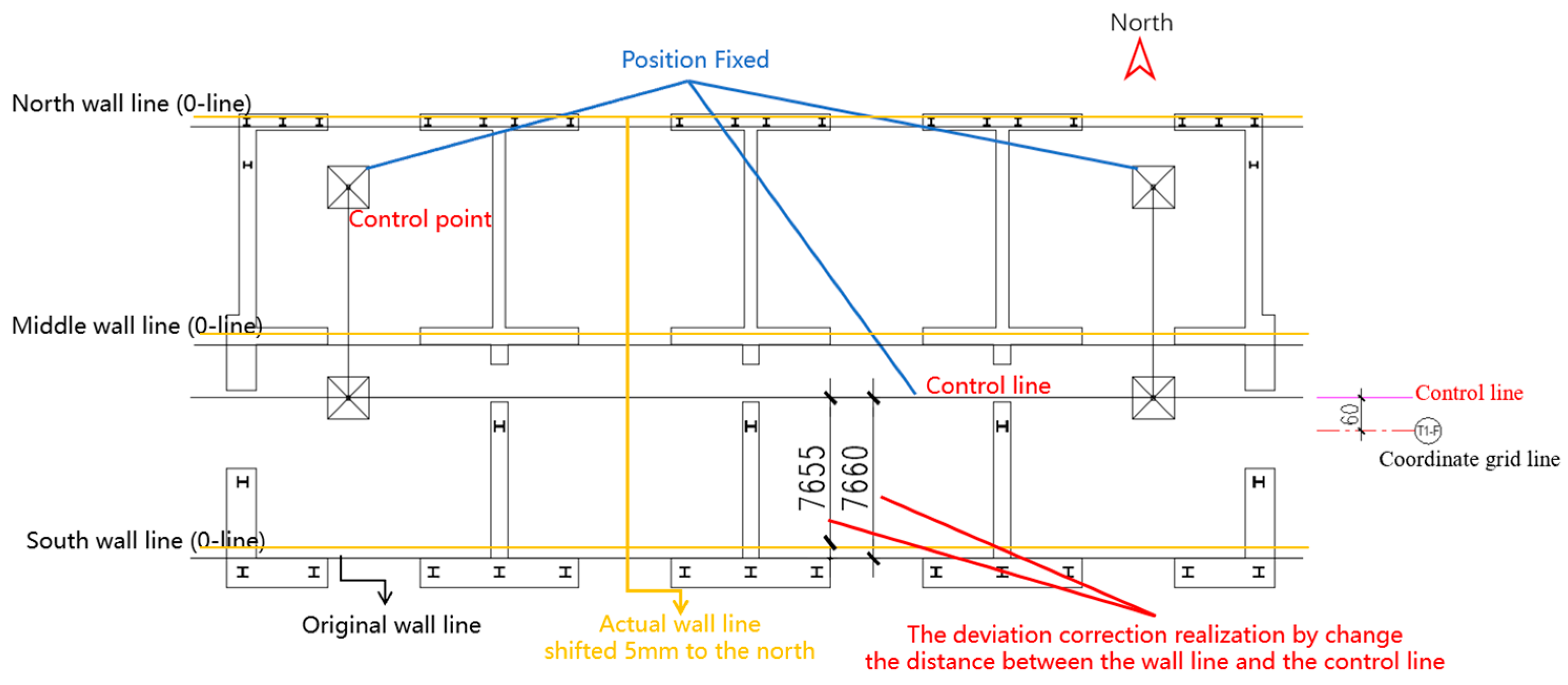
2.3. Construction Stringing Method Based on Construction Error Intervention Strategy
3. Prediction-Construction-Measurement Integration Analysis Theory and Adjusting Process of Pre-Arch Correction Method
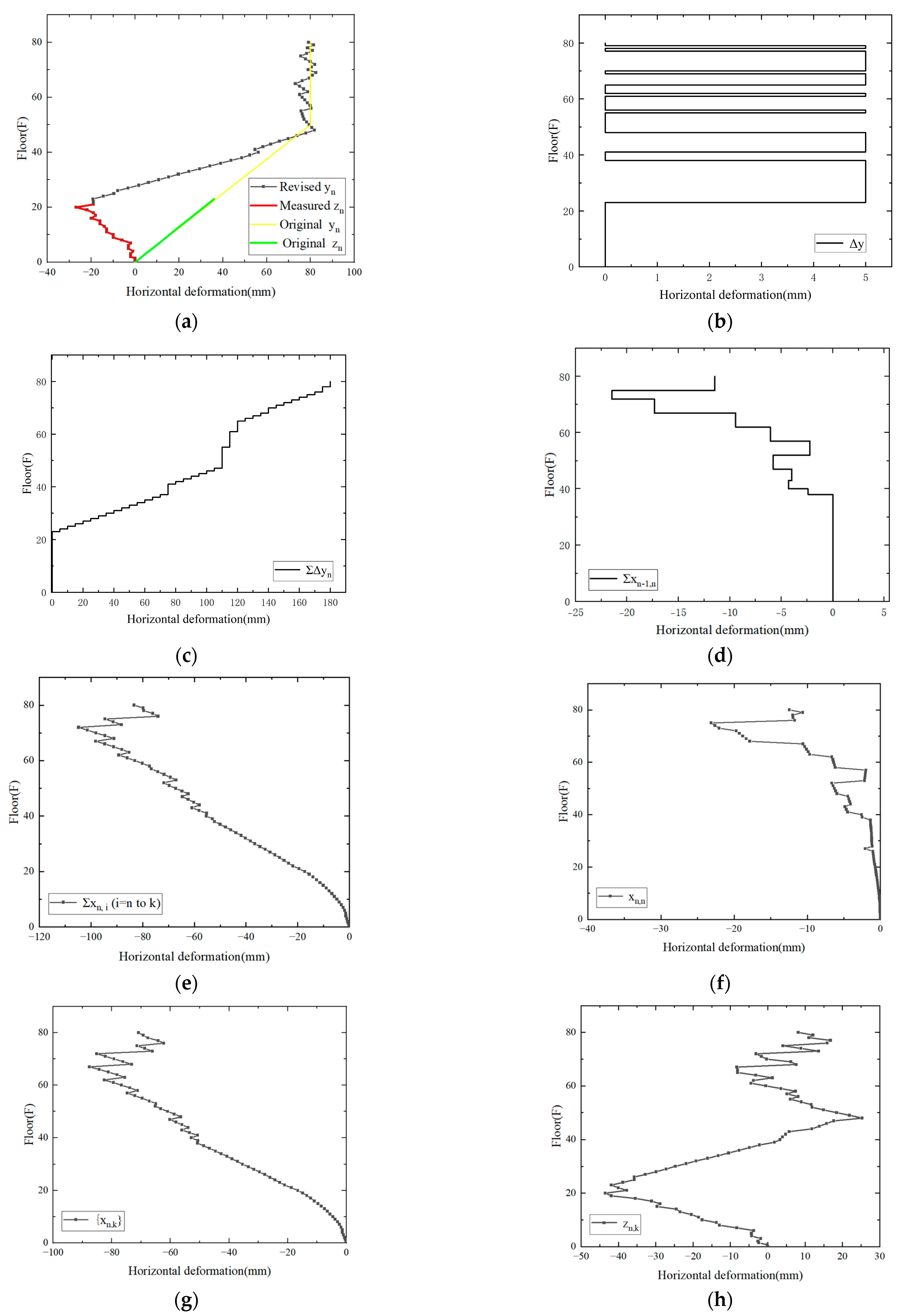
3.1. Prediction-Construction-Measurement Integration Analysis Theory
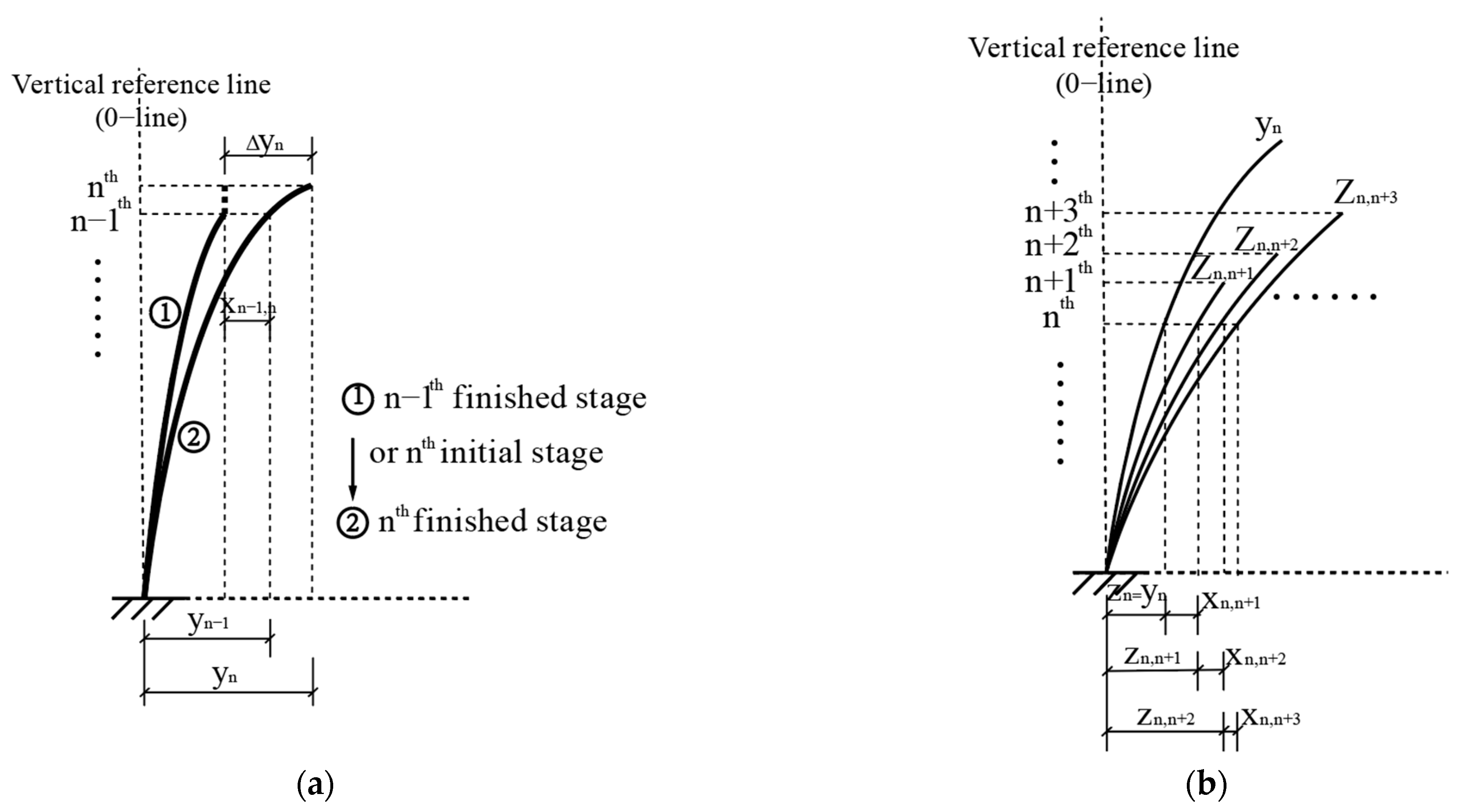
3.1.1. Initial Deformation yn
3.1.2. Deformation Increment {xn,k}
3.1.3. Deviation Correction Value Δyn
3.1.4. Positional Posture zn,k
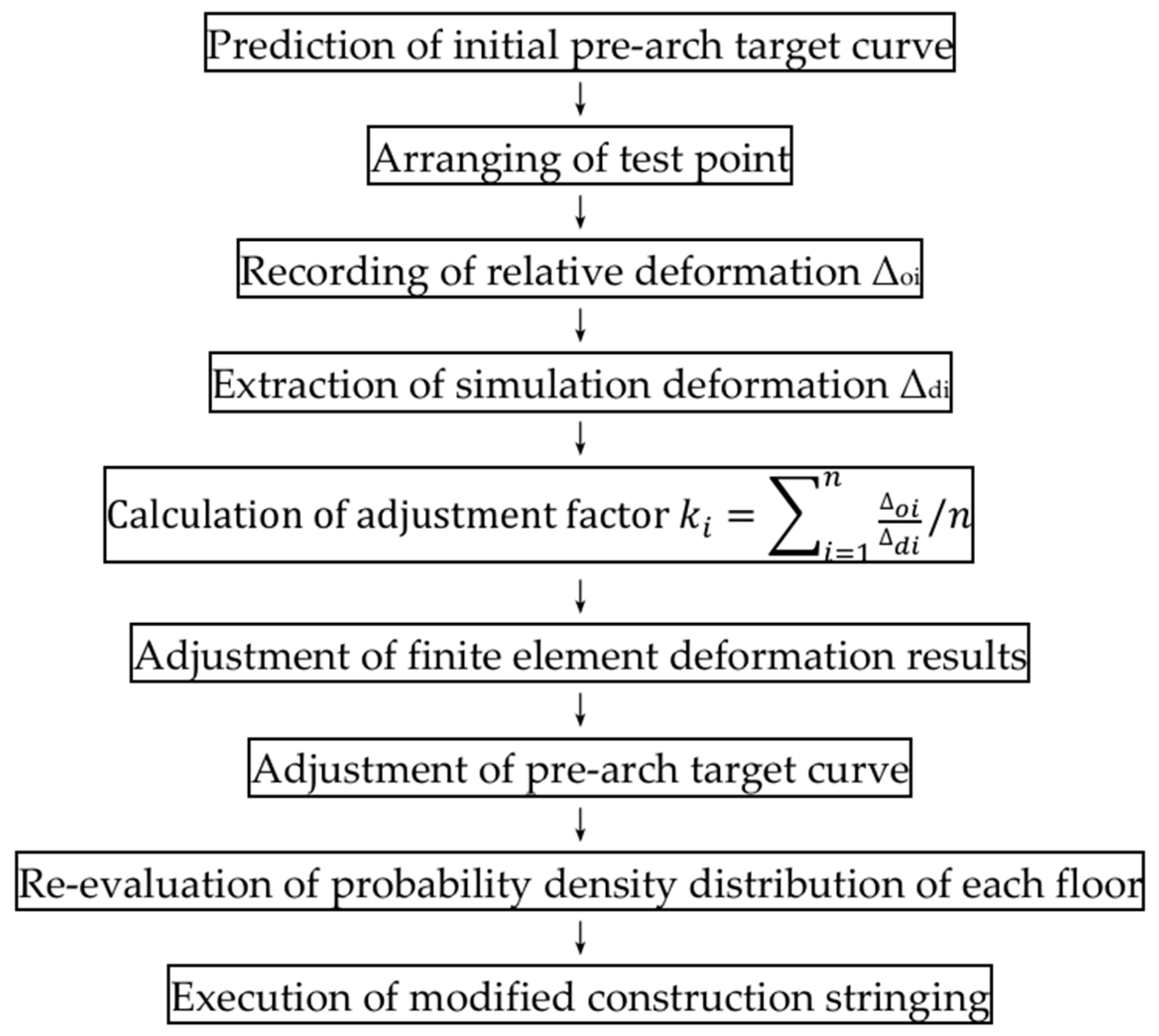
3.2. Adjusting Process of Pre-Arch Correction Method
4. Case Study
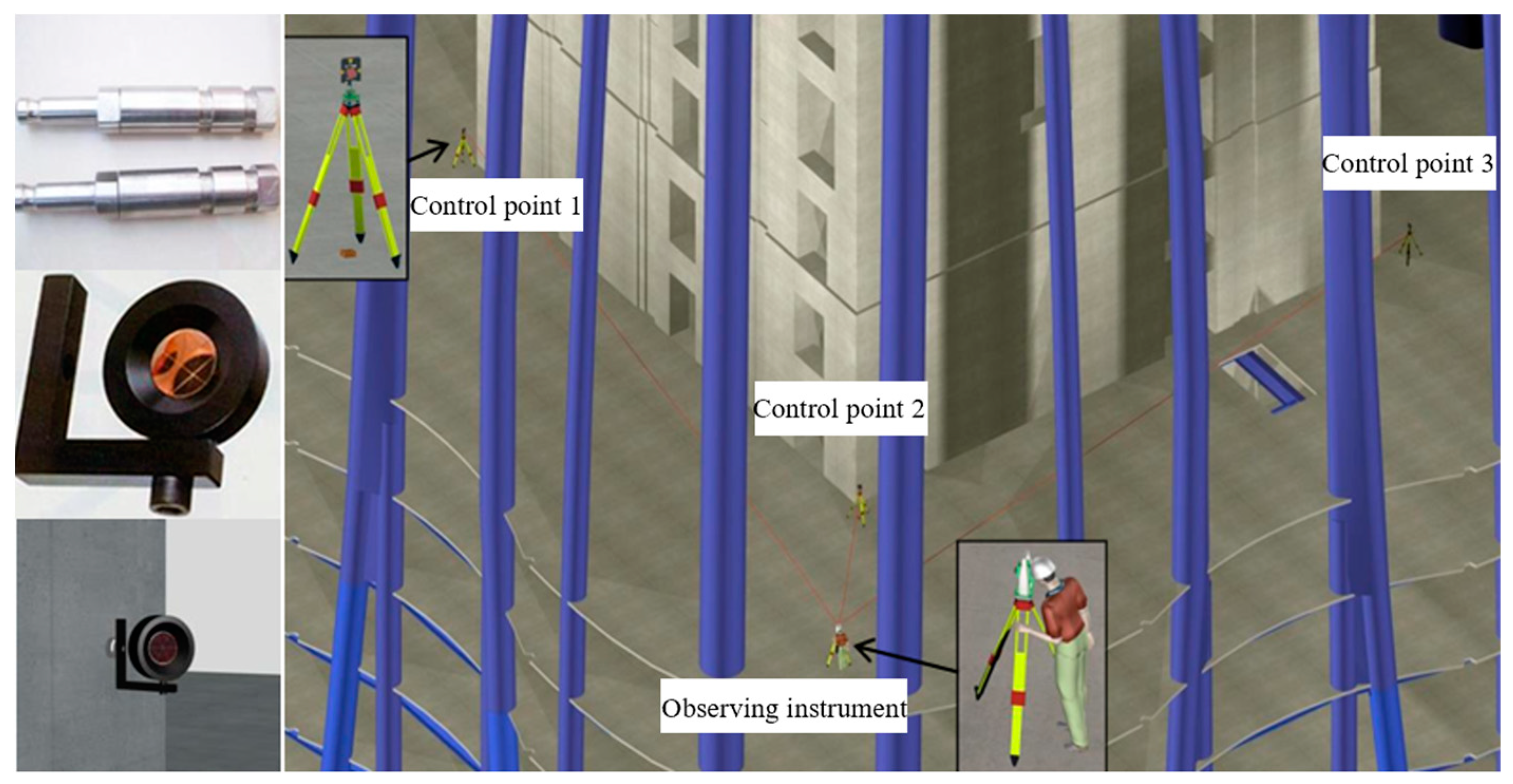
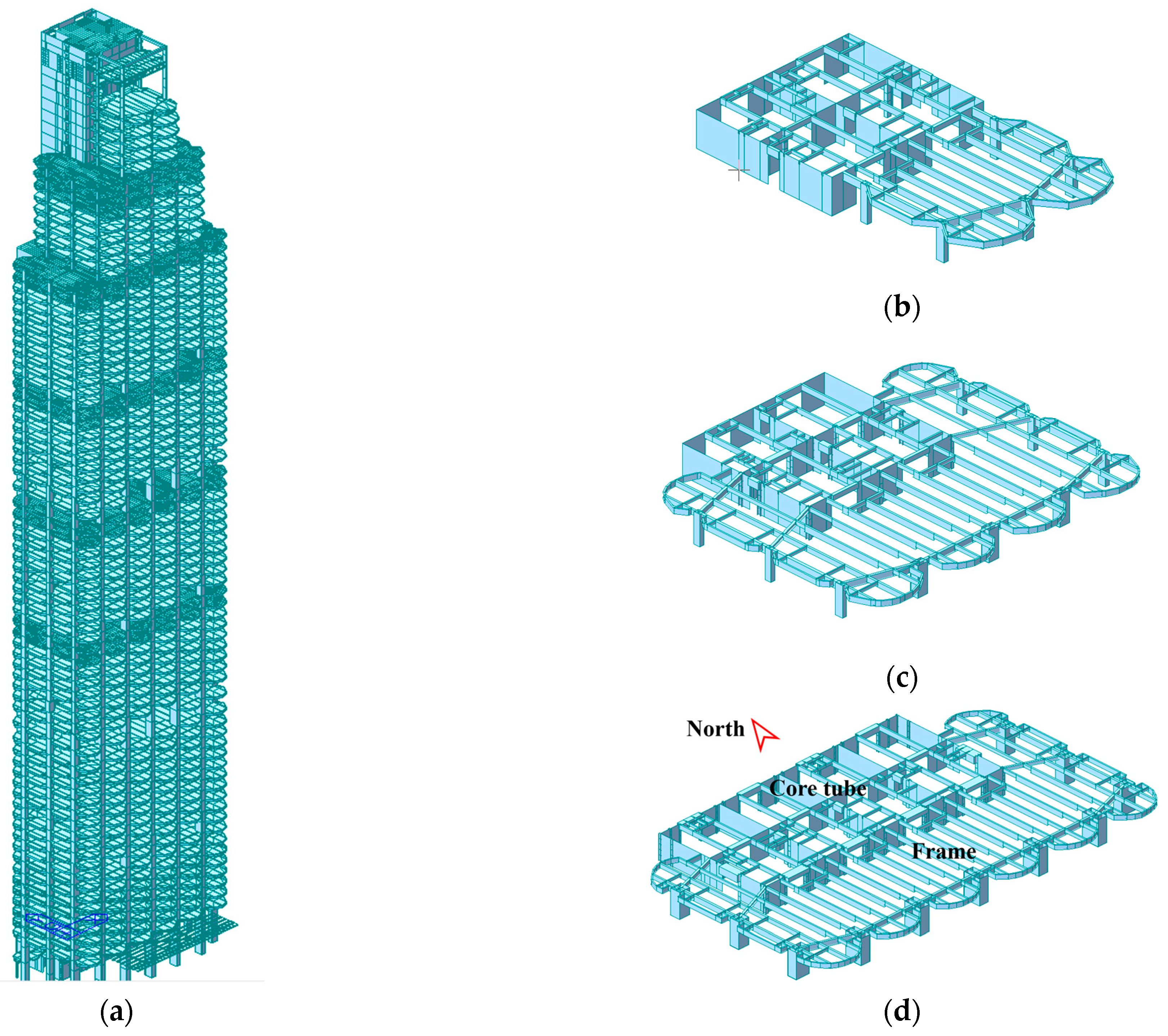
4.1. Project Overview
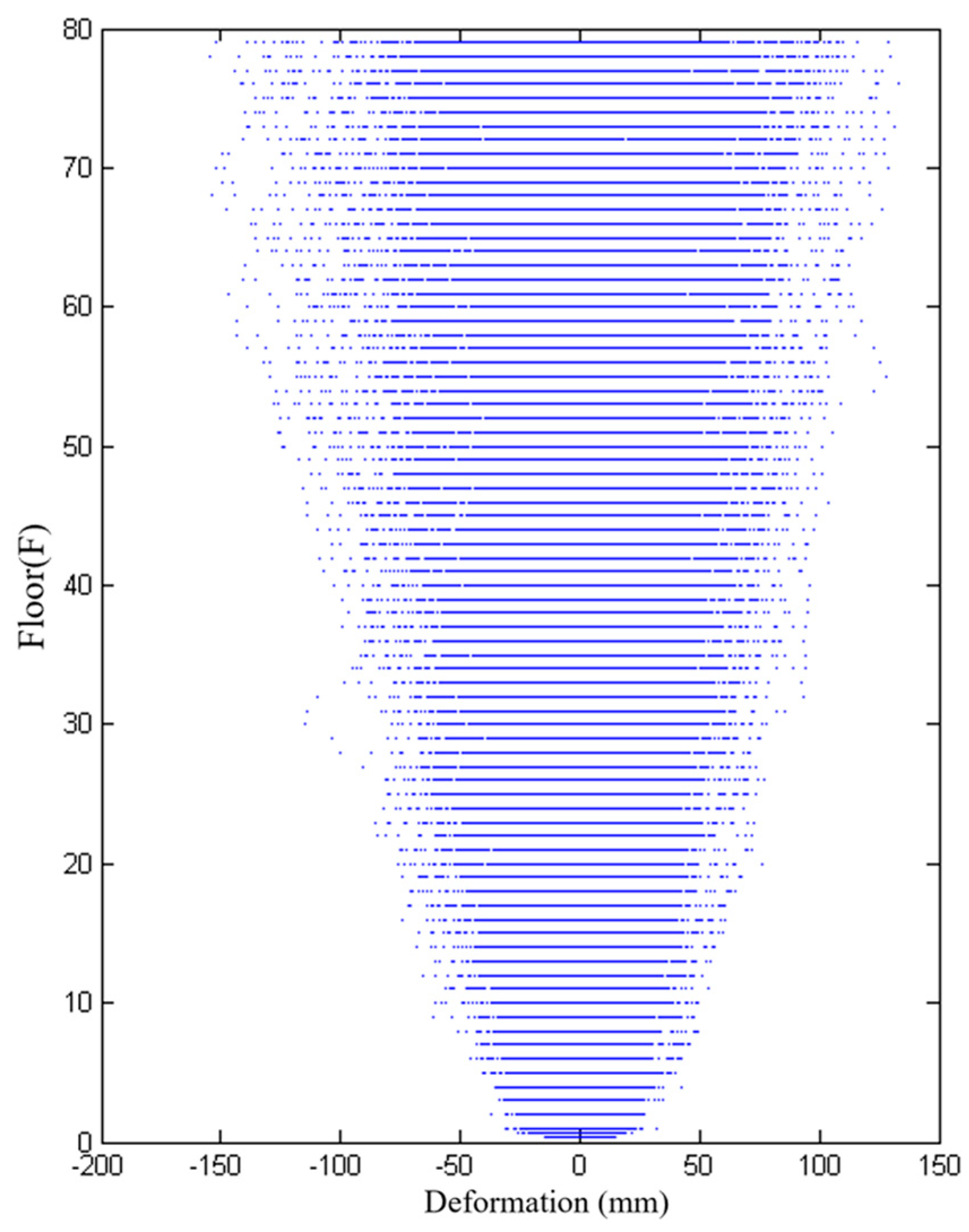
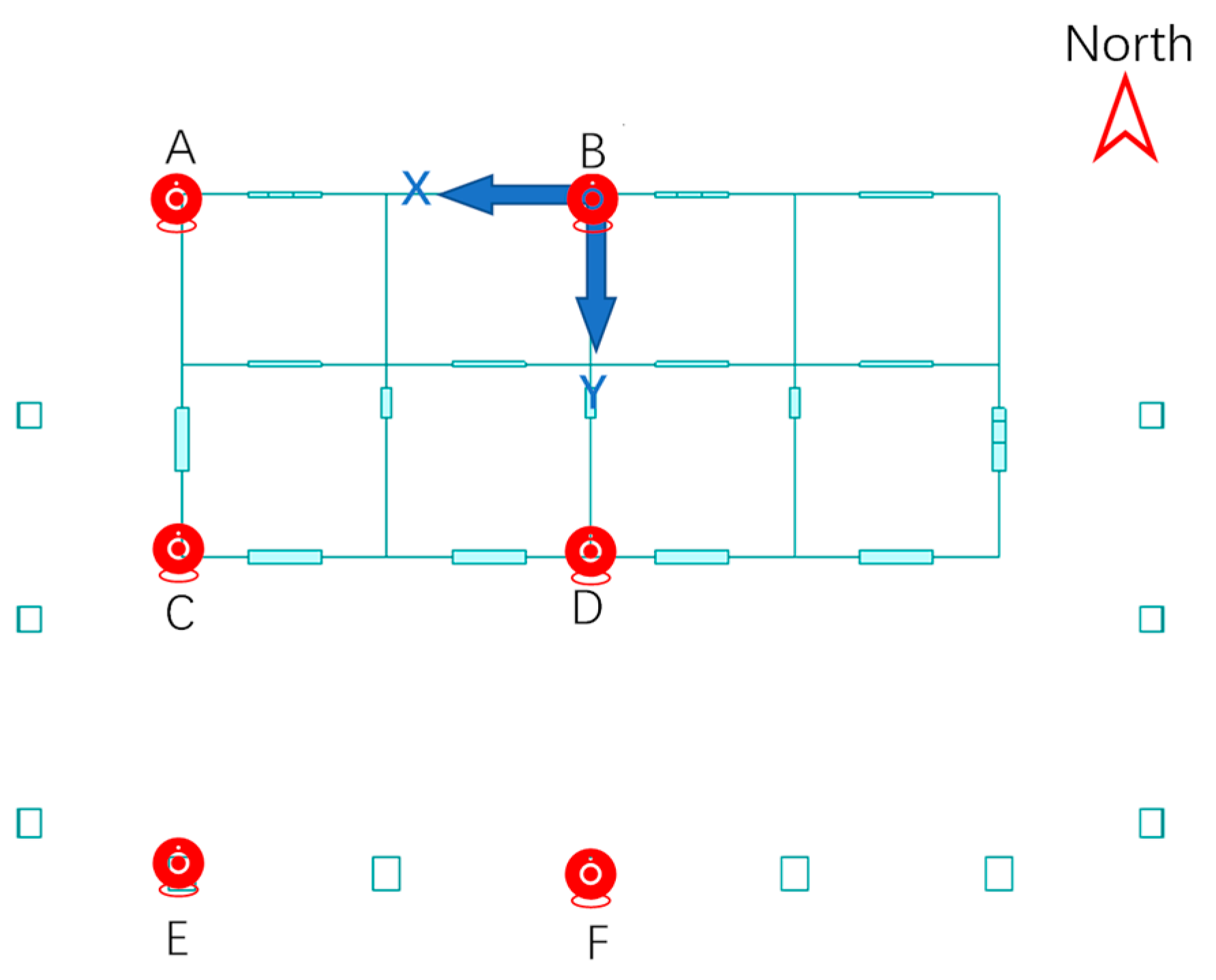
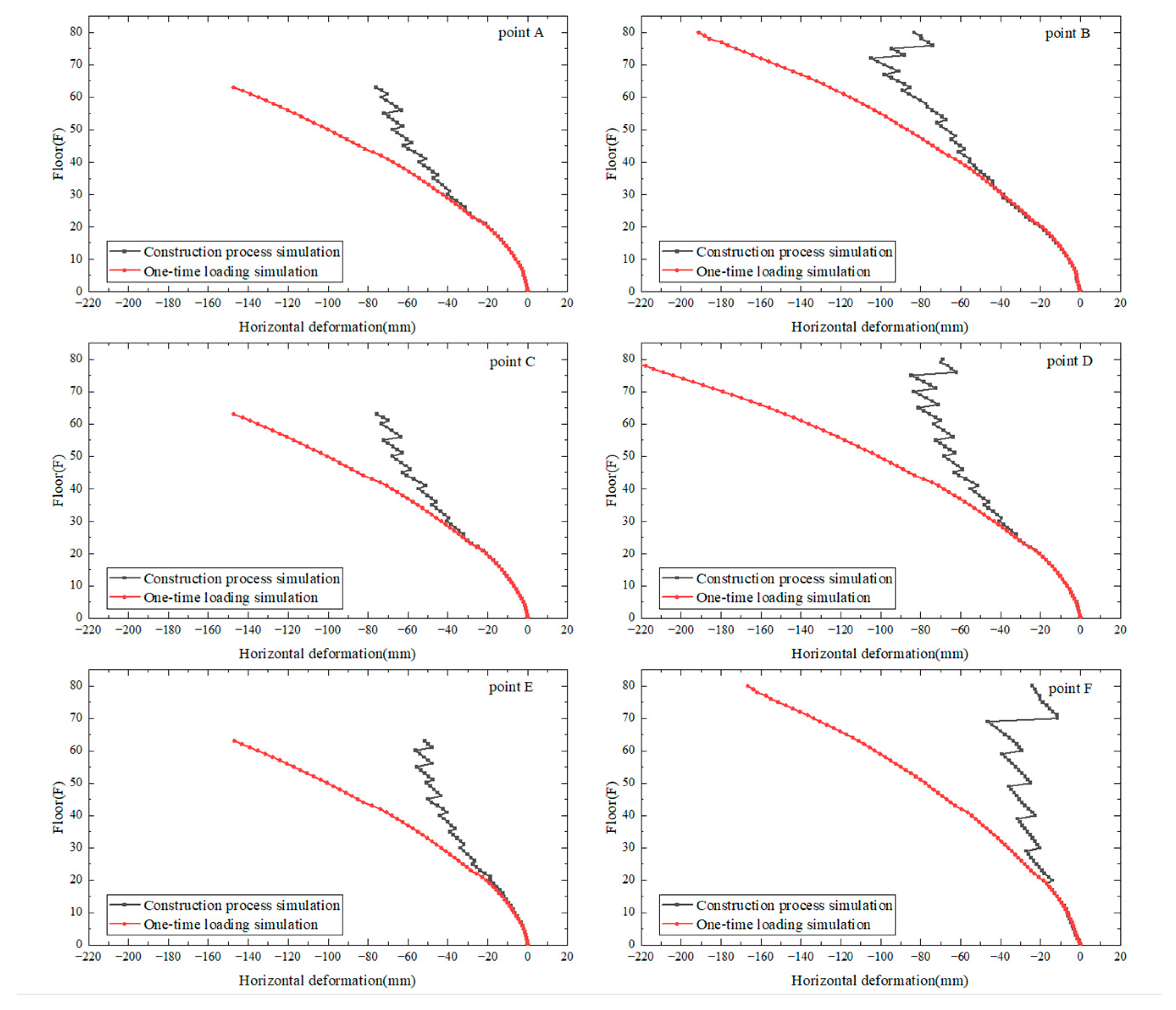
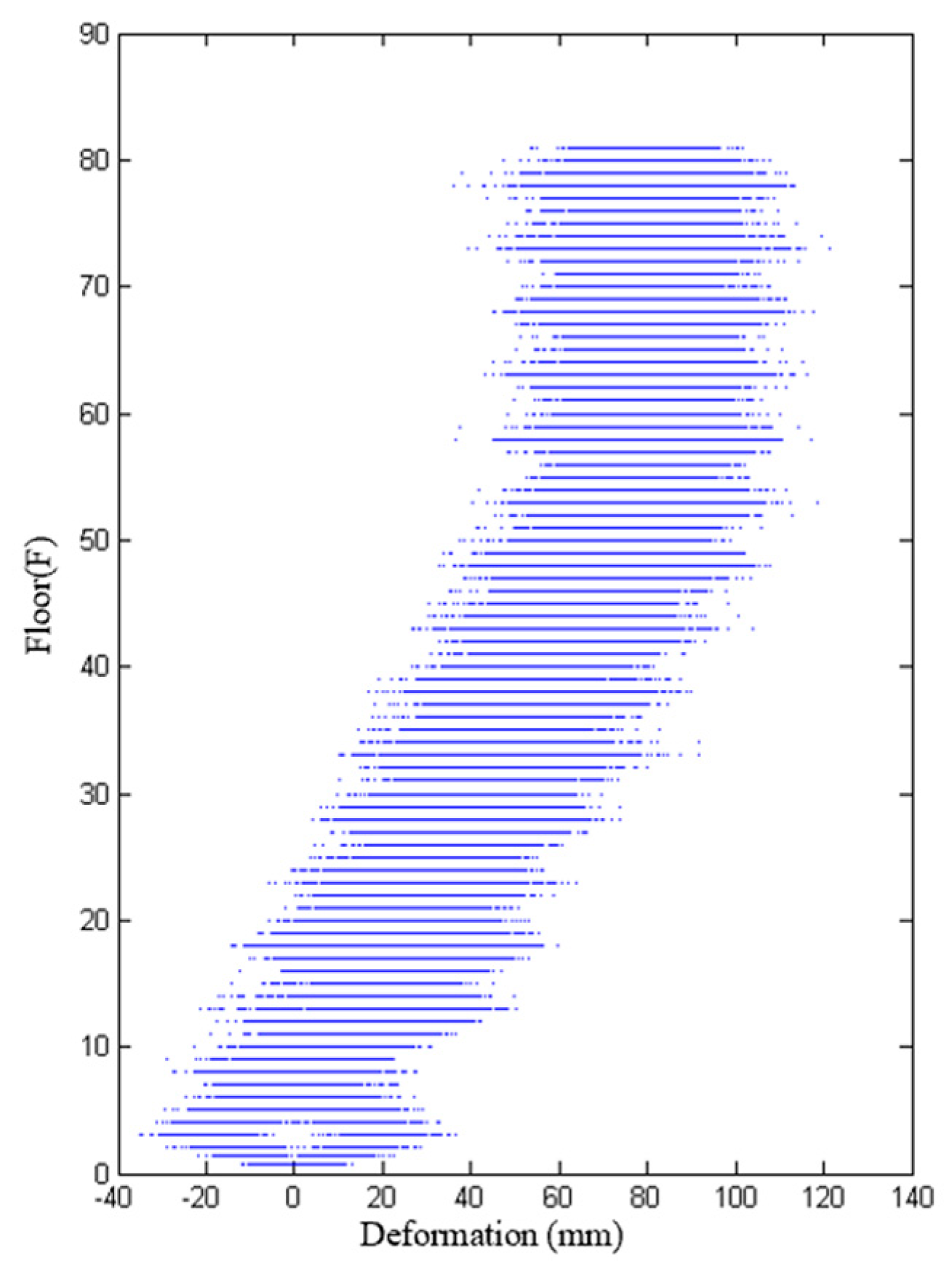
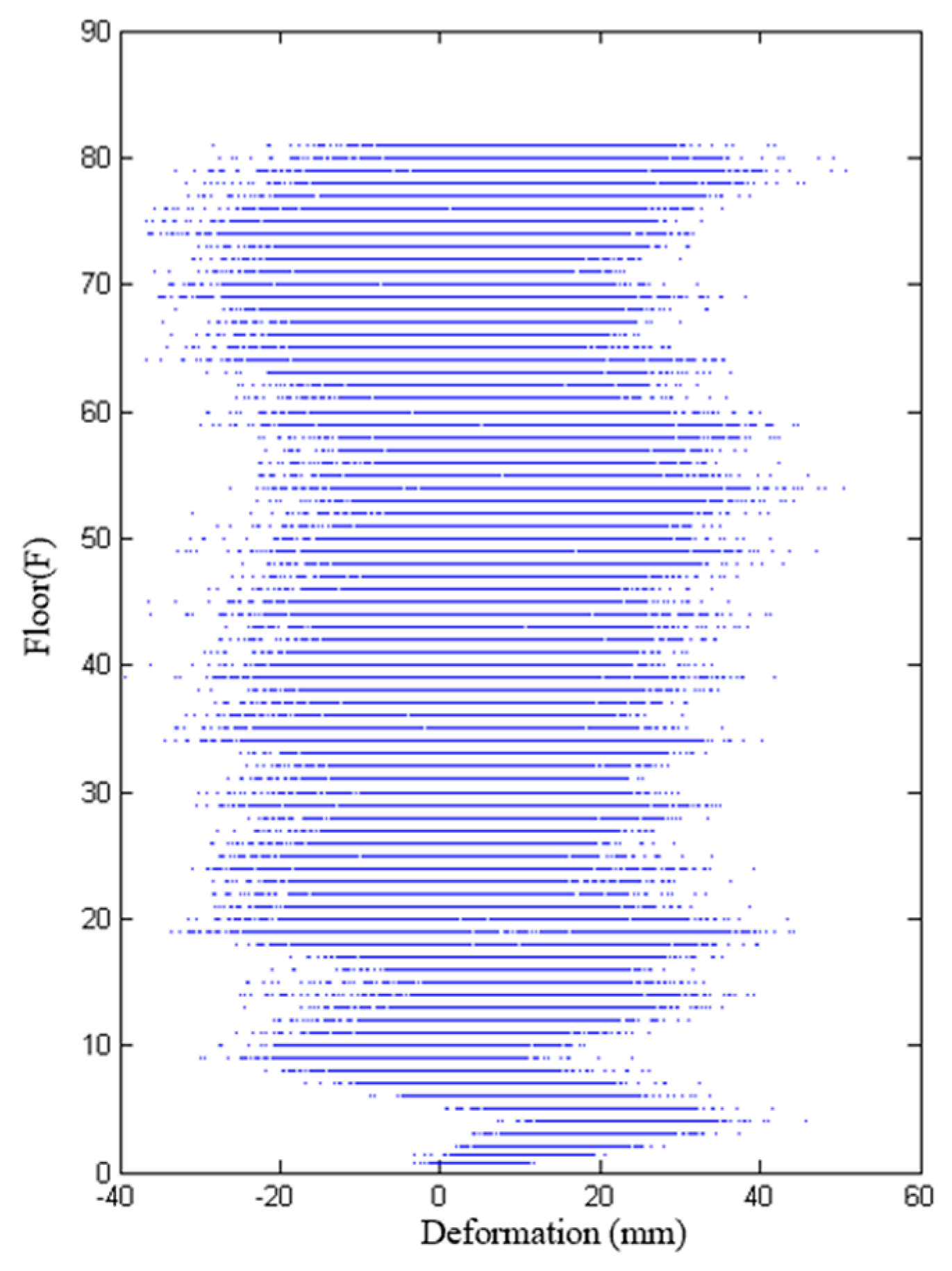
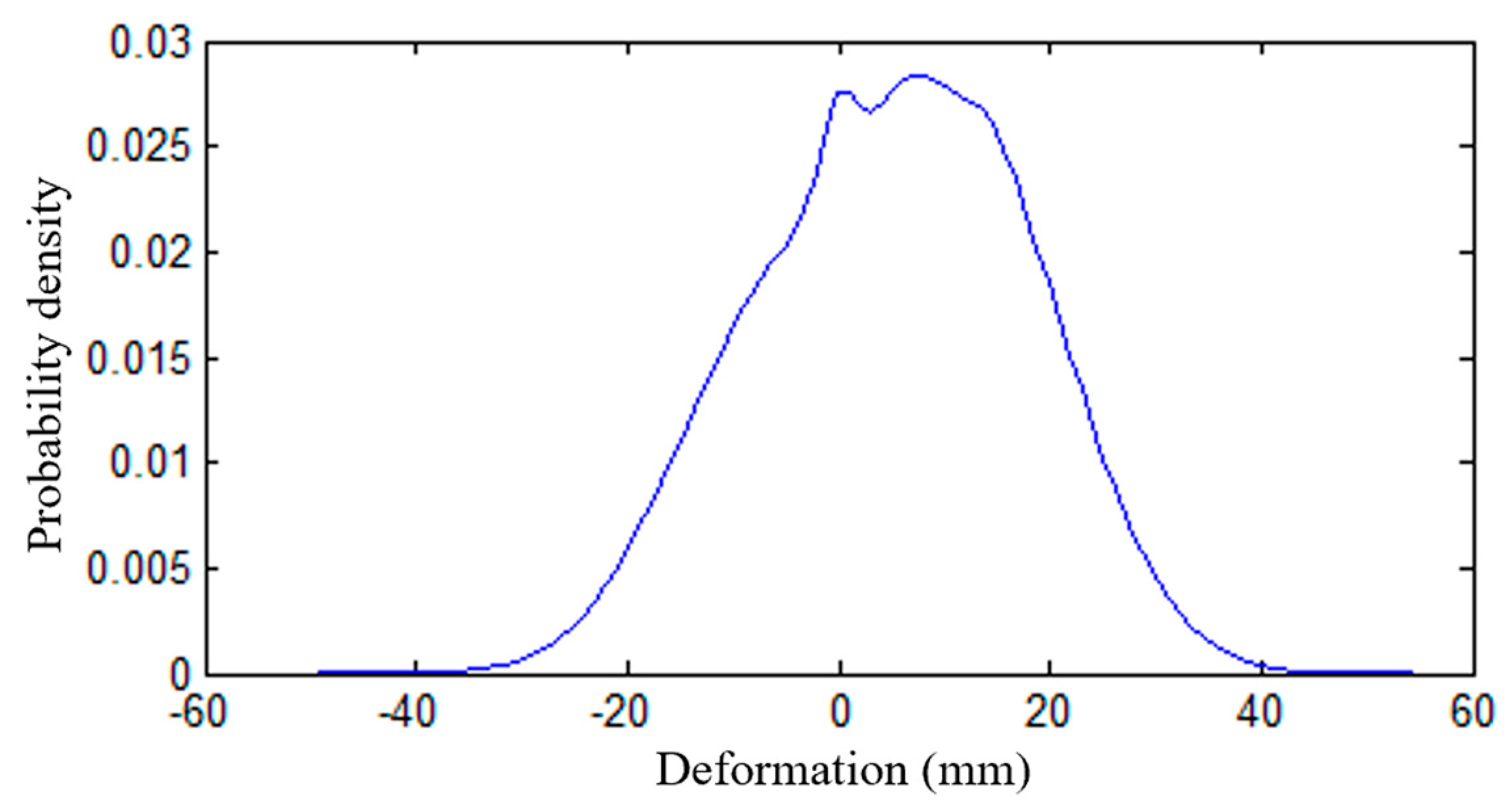
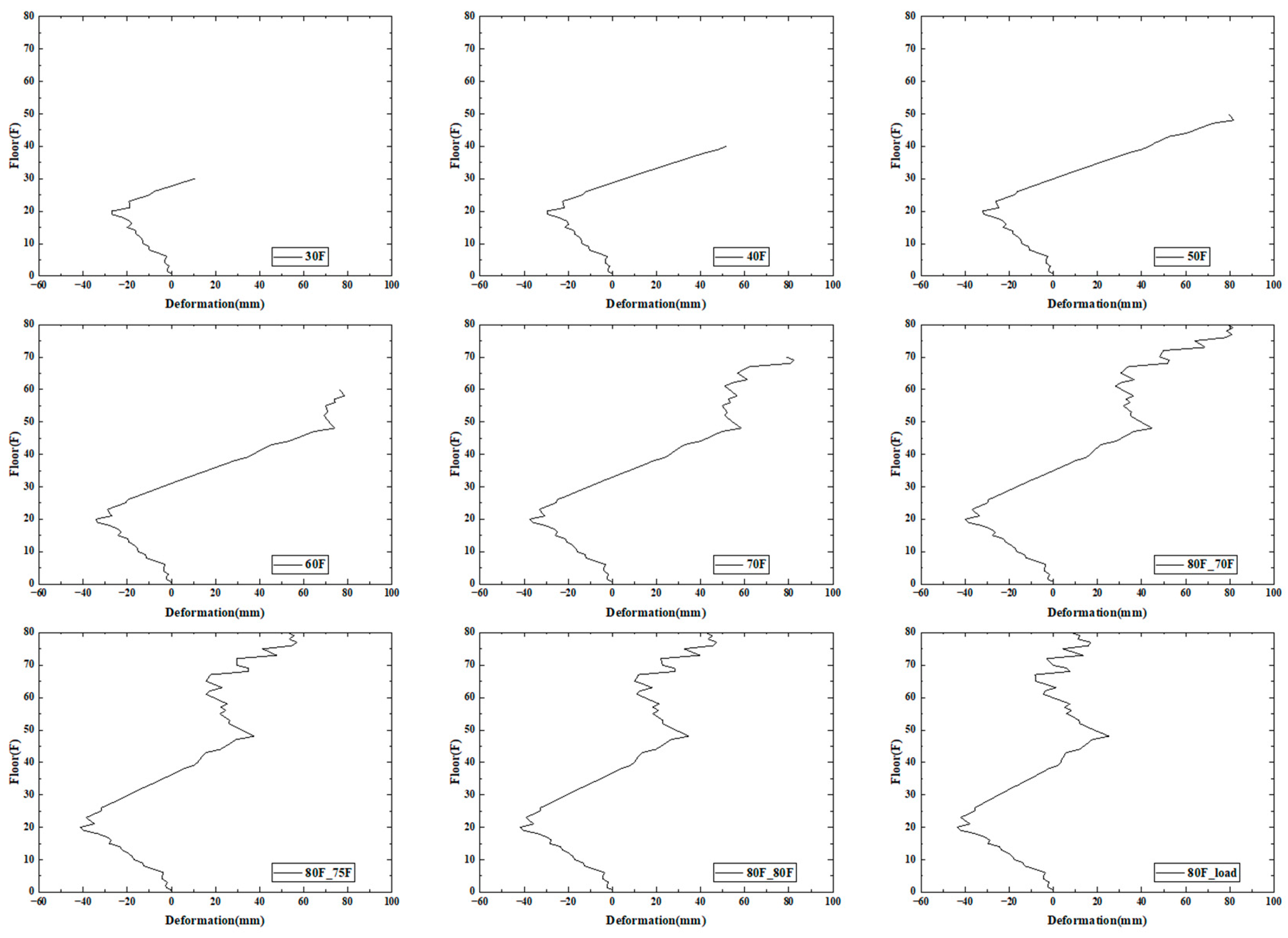
4.2. Horizontal Deformation Results Under Simulation Condition
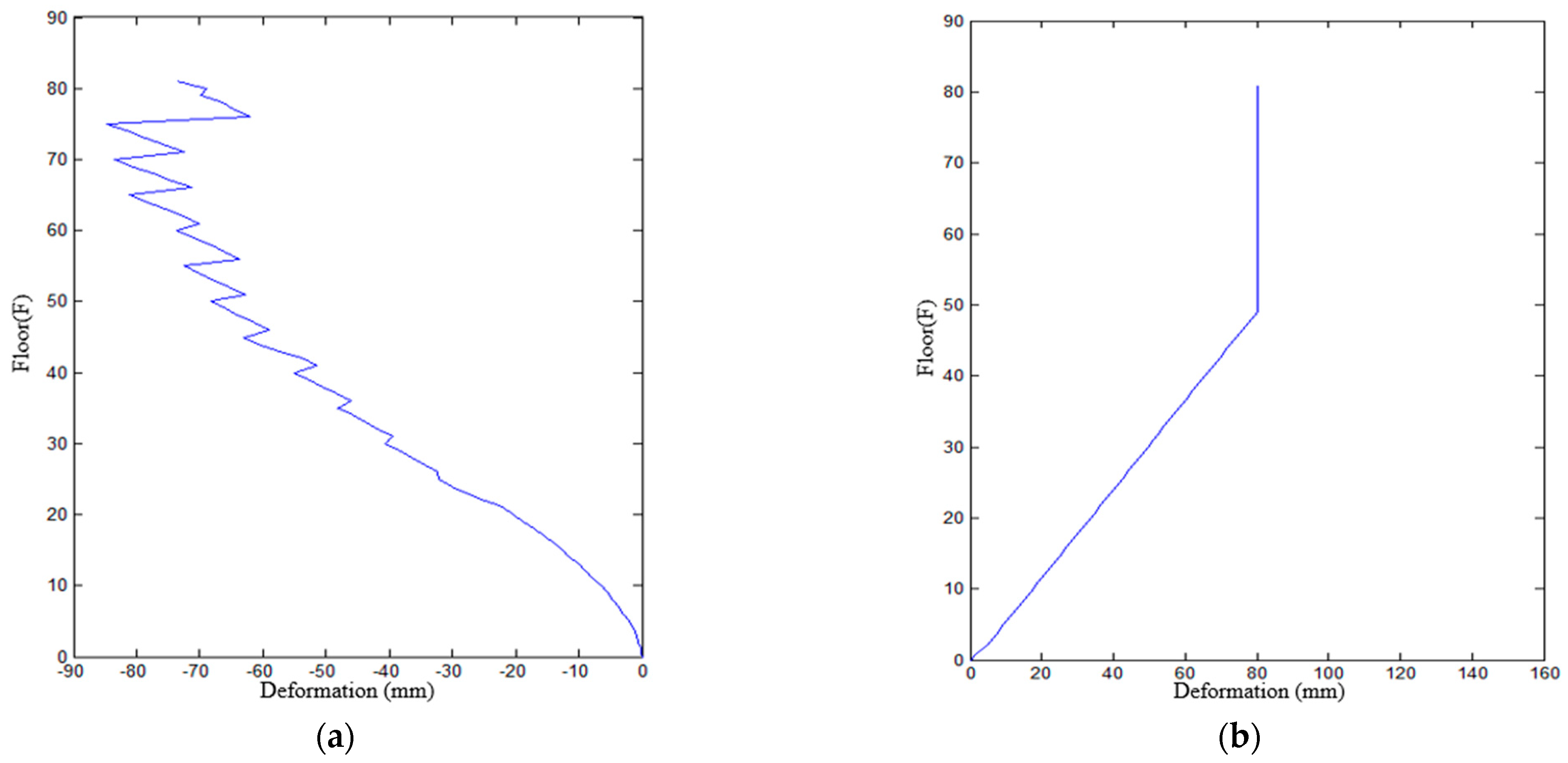
4.3. Initial Determination and Verification of Horizontal Deformation Control Strategy
4.4. Correction of Pre-Arch Target Curve Using Measured Deflection Curve
4.5. Structural Positional Posture Preview After Correction
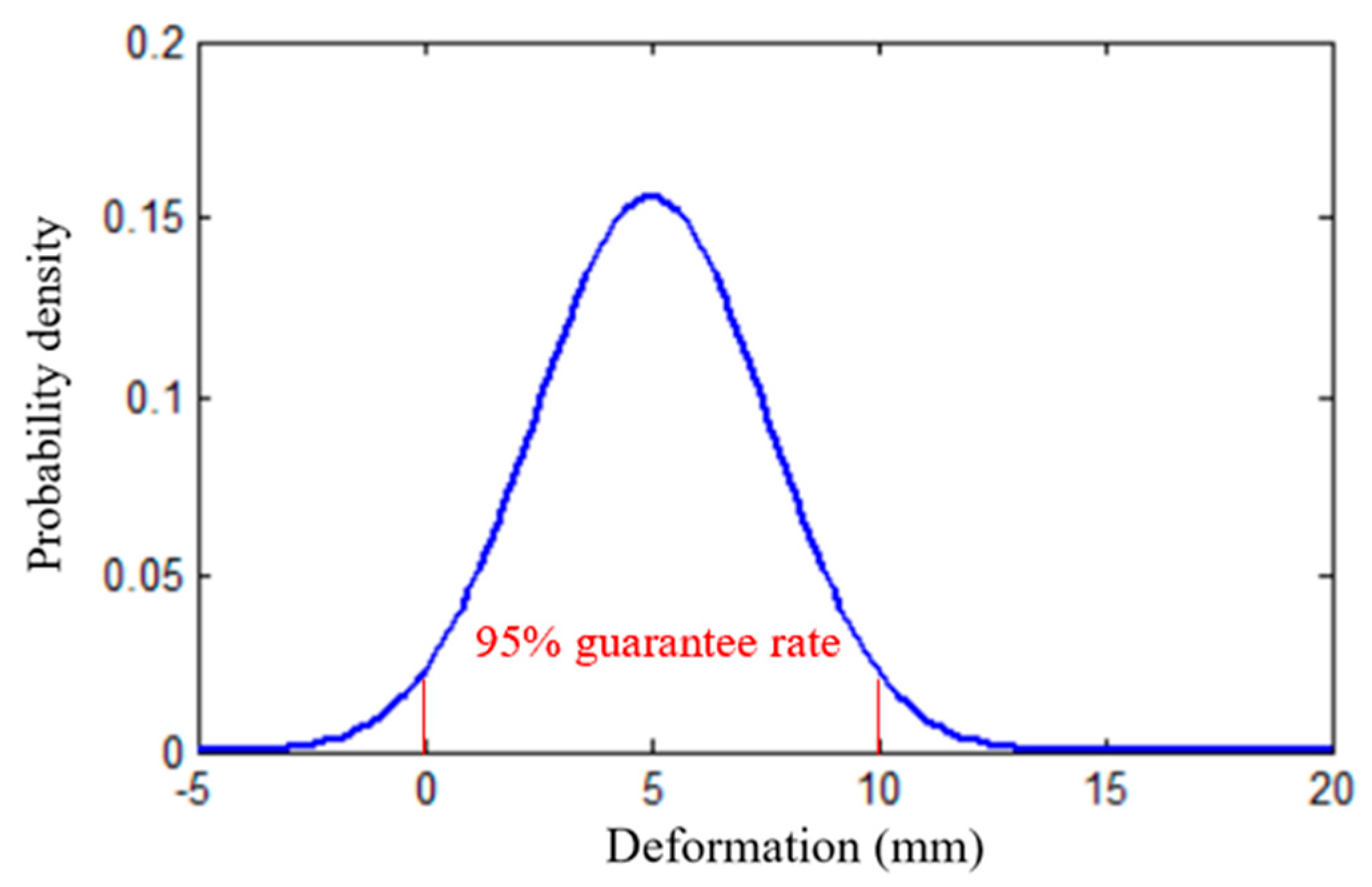
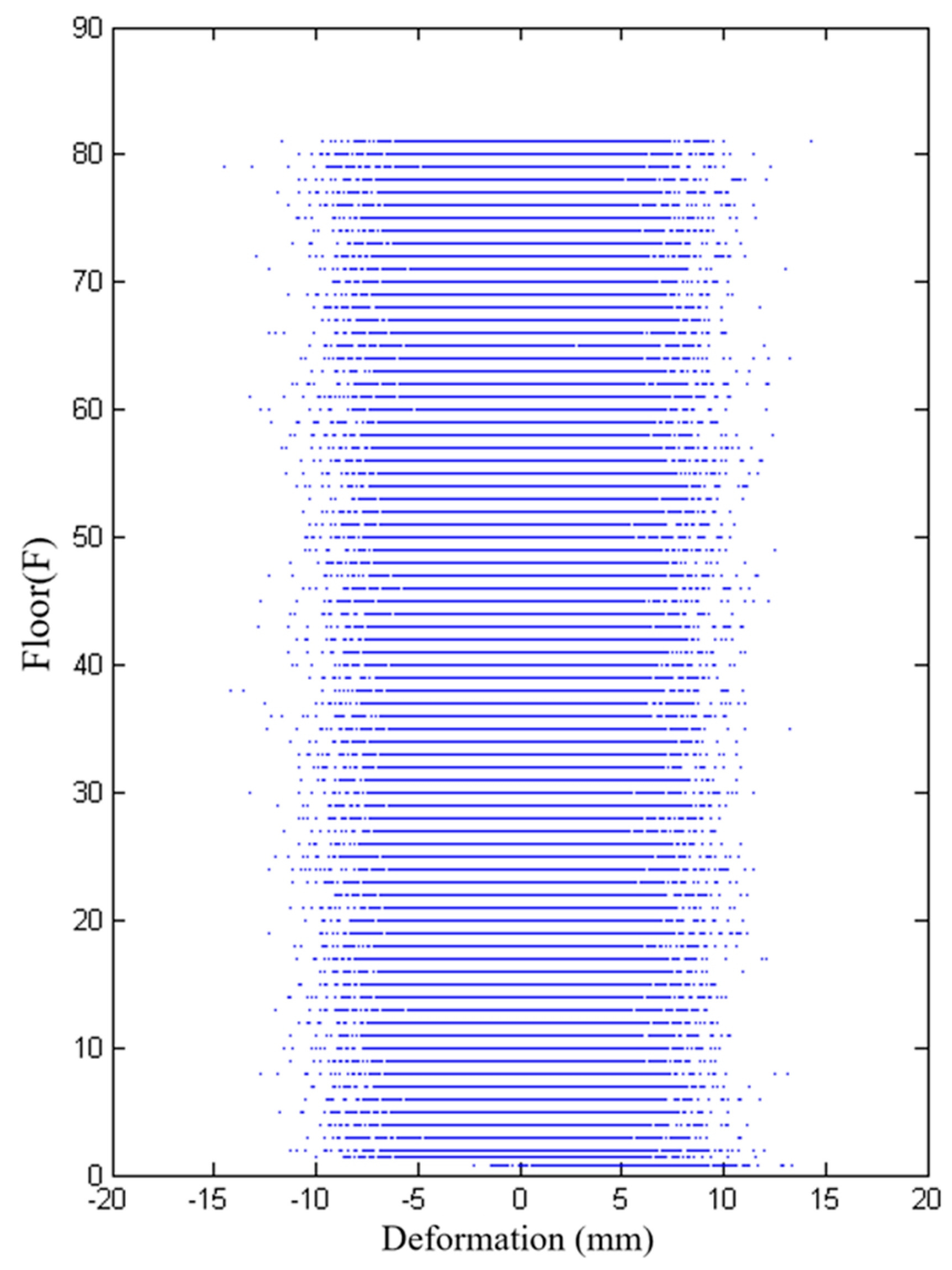
5. Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, W.B.; Hu, H.S.; Wang, R.T.; Gao, Y.C.; Guo, Z.X. Effects of belt trusses on drift control of frame-core tube structures. Eng. Struct. 2024, 304, 117583. [Google Scholar] [CrossRef]
- Li, J.W.; Wang, N.; Zhang, C.X.; Rong, W.H.; Zhao, Y. Research on structural design and key technology of super high-rise China merchants bank headquarters building with off-center core tube. Build. Struct. 2023, 53, 16–24. [Google Scholar]
- Ou, Y.; Chen, B.; Jia, H.; Yin, G.; Cao, J. Simulation Analysis and Application of Super High-rise Tower Construction Process. J. Phys. Conf. Ser. 2022, 2185, 012065. [Google Scholar] [CrossRef]
- Gao, F.; Zhou, H.; Liang, H.; Weng, S.; Zhu, H. Structural deformation monitoring and numerical simulation of a supertall building during construction stage. Eng. Struct. 2019, 209, 110033. [Google Scholar] [CrossRef]
- Porcar, B.; Soutullo, S.; Enríquez, R.; Jiménez, M.J. Quantification of the uncertainties produced in the construction process of a building through simulation tools: A Case Study. J. Build. Eng. 2018, 20, 377–386. [Google Scholar] [CrossRef]
- Jia, H.X.; Zhang, X.Q.; Feng, J. Construction Simulation Analysis of Super High-rise Building Considering: The Concrete Filled Steel Tubular Column Shrinkage and Creep Effect. Build. Struct. 2019, 49, 519–523. [Google Scholar]
- Chen, Z.; Gao, F.; Hu, J.; Liang, H.; Huang, S. Creep and shrinkage monitoring and modelling of CFST columns in a super high-rise under-construction building. J. Build. Eng. 2023, 76, 107282. [Google Scholar] [CrossRef]
- Wang, L.L.; Zhao, X.; Yan, C.Z. Time-dependent vertical shortening prediction for super-tall buildings by using a modified B3 model to consider moisture distribution. Eng. Struct. 2020, 209, 109994. [Google Scholar] [CrossRef]
- Kim, H.S.; Cho, S.H. Column Shortening of Concrete Cores and Composite Columns in a Tall Building. Struct. Des. Tall Spec. Build. 2005, 14, 175–190. [Google Scholar] [CrossRef]
- Xiao, J.; Peng, J.; Cai, C.S.; Bian, H.; Zhang, J. Experimental Study of Shrinkage and Creep Behaviors of Low-Shrinkage and Low-Creep C60 High-Performance Concrete and Parameter Recommendations. J. Mater. Civ. Eng. 2024, 36, 04024218. [Google Scholar] [CrossRef]
- Matiushin, E.; Sizyakov, I.; Shvetsova, V.; Soloviev, V. The Properties and Behavior of Ultra-High-Performance Concrete: The Effects of Aggregate Volume Content and Particle Size. Buildings 2024, 14, 2891. [Google Scholar] [CrossRef]
- GB50204-2015; Code for Quality Acceptance of Concrete Structure Construction. China Architecture & Building Press: Beijing, China, 2015.
- Wu, H.L.; Ding, J.M.; Wang, S.Y.; Yang, B.; Zhang, T.; Geng, Y. Structural design and key technology of eccentric high-rise frame-core tube structures. J. Build. Struct. 2023, 44, 154–165. [Google Scholar]
- Lu, Z.; Zhou, Y.M.; Wang, Y.H.; Wang, Z.; Zhang, F.W. Analysis of horizontal deformation and internal force of super high-riase frame-eccentrical core tube structure considering creep and shrinkage of concrete. Struct. Eng. 2023, 39, 1–8. [Google Scholar]
- Wang, Y.; Zhou, Y.; Zhu, L.; Zhang, T.; Jia, B.; Han, S.; Lu, Z. Horizontal deformation and construction analysis of frame–eccentrical core tube structure. Struct. Des. Tall Spec. Build. 2022, 31, e1943. [Google Scholar] [CrossRef]
- Huang, Y.L. Research on Vertical Time-Varying Characteristics of Super Tall Building Structures During Construction Period; Tongji University: Shanghai, China, 2008. [Google Scholar]
- Liu, F.N. The Analysis and Control Methods of Vertical Deformation of Super High-Rise Frame-Core Wall Structure Under Construction; Dalian University of Technology: Dalian, China, 2018. [Google Scholar]
- Li, P.N.; Qing, R.; Gui, G.Q. Study of differential shortening of steel-concrete hybrid structure vertical members in high-rise residential buildings. Constr. Technol. 2006, 8, 42–45. [Google Scholar]
- Yan, F.; Zhou, J.L.; Wang, D.S.; Zheng, L.; Lang, T. Structural design of Nanjing Greenland Zifeng Mansion Super High-rise Building. Build. Struct. 2007, 37, 20–24. [Google Scholar]
- Zhou, Y.; Luo, X.; Ye, P.; Zhang, W.; Ling, Q.; Du, Z. Bayesian-based prediction and real-time updating of axial deformation in high-rise buildings during construction. Eng. Struct. 2023, 297, 116992. [Google Scholar] [CrossRef]
- Zhou, Y.; Luo, X.; Zhang, W.; Ye, P.; Chen, J.; Du, Z. Improvement of axial deformation prediction in high-rise buildings with field monitoring and adaptive unscented Kalman filter. J. Build. Eng. 2024, 84, 108432. [Google Scholar] [CrossRef]
- Ma, G.Q. Study on the influence of construction error on the reliability of building frame structure. Constr. Budg. 2024, 6, 34–36. [Google Scholar]
- Lim, K.; Kang, J.; Ryu, G.; Koh, K.; Kim, K. Fundamental Design Concepts of a Modular Pier System Using Ultra-High-Performance Concrete for Solving Construction Errors. Buildings 2023, 13, 1816. [Google Scholar] [CrossRef]
- Galvão, N.; Matos, J.C.; Hajdin, R.; Ferreira, L.; Stewart, M.G. Impact of construction errors on the structural safety of a post-tensioned reinforced concrete bridge. Eng. Struct. 2022, 267, 114650. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Xiao, Y.; Zhang, D.; Yin, G.; Ma, X.; Wang, S.; Ai, Q. Horizontal Deformation Control Strategy and Implementation Method of Eccentric Core Tube Structure Based on Construction Error Uncertainty. Buildings 2024, 14, 3384. https://doi.org/10.3390/buildings14113384
Wang H, Xiao Y, Zhang D, Yin G, Ma X, Wang S, Ai Q. Horizontal Deformation Control Strategy and Implementation Method of Eccentric Core Tube Structure Based on Construction Error Uncertainty. Buildings. 2024; 14(11):3384. https://doi.org/10.3390/buildings14113384
Chicago/Turabian StyleWang, Huaping, Yiqing Xiao, Dekai Zhang, Guanghua Yin, Xinxu Ma, Sijiu Wang, and Qiyang Ai. 2024. "Horizontal Deformation Control Strategy and Implementation Method of Eccentric Core Tube Structure Based on Construction Error Uncertainty" Buildings 14, no. 11: 3384. https://doi.org/10.3390/buildings14113384
APA StyleWang, H., Xiao, Y., Zhang, D., Yin, G., Ma, X., Wang, S., & Ai, Q. (2024). Horizontal Deformation Control Strategy and Implementation Method of Eccentric Core Tube Structure Based on Construction Error Uncertainty. Buildings, 14(11), 3384. https://doi.org/10.3390/buildings14113384




