Transfer Learning for Structural Health Monitoring in Bridges That Underwent Retrofitting

Abstract

Bridges are built to last more than 100 years, spanning many human generations. Throughout their lifetime, their service requirements may change, or they age and often suffer a material degradation process that can lead to the need of retrofitting. In bridge engineering, retrofitting refers to the strengthening of existing structures to make them more resistant and to increase the lifespan of bridges. Retrofitting normally increases the stiffness of bridge components, which can cause significant changes in the global modal properties. In the context of structural health monitoring, a classifier trained with datasets before retrofitting will most likely output many outliers after retrofitting, based on the premise that the new observations do not share the same underlying distribution. Therefore, how can long-term monitoring data from one bridge (labeled source domain) be reused to create a classifier that generalizes to the same bridge after retrofitting (unlabeled target domain)? This paper presents a novel approach based on transfer learning in the context of domain adaptation on datasets from two real bridges subjected to retrofit and under-monitoring programs. Based on the assumption that both bridges are undamaged before retrofitting, the results show that transfer learning can support the long-term damage detection process based on a classification using an outlier detection strategy.

1. Introduction

The construction of bridges aims to meet the socioeconomic needs of several human generations, as these structures are engineered to last more than 100 years. However, the service requirements of bridges are prone to change over their lifetime, and the effects of accumulated degradation over the years may result in the need for a retrofit process. In the context of bridge engineering, retrofitting refers to strengthening components after an evaluation structural strength and stiffness of bridge elements to extend their lifespan, ensuring a safe operation as a result of restoring its structural integrity [1].

The retrofit process is often associated with variations in the modal parameters of the bridge due to the structure’s stiffness increase, mainly noticed in the natural frequencies. For instance, a highway bridge in Singapore underwent a retrofit process in 2003, and some components were replaced, leading to a variation in natural frequencies up to $50\%$ while their vibration modes did not show significant changes [2]. The rehabilitation of a concrete bridge located in Italy by replacing the external layer of the pillars with a fiber-reinforced concrete material and steel rebars represents another example of a retrofit process, which restored the material properties of the bridge’s component while preserving its cross-sectional dimensions [3].

In the last decades, structural health monitoring (SHM) has been proposed to support decision-making by bridge owners and authorities [4,5]. The long-term damage detection process often relies on machine learning algorithms to build unsupervised classifiers. An analysis based on unsupervised learning has been the priority as it is not feasible to introduce real damage to bridges due to their high cost and potential safety risks of operating the structures under a damaged condition.

The practical application of machine learning algorithms is not always feasible, as training and test datasets may not share similar underlying distributions due to several reasons [6]. This assumption limits the application of these algorithms to the specific structure they were trained for. For instance, a classifier trained with datasets before retrofit may not be accurate as the new observations obtained after retrofitting may not share the same underlying distribution due to structural changes. Therefore, how can the knowledge contained in the long-term monitoring data of a bridge be generalized to the same bridge after retrofitting? Transfer learning in the context of domain adaptation represents a promising solution in the SHM of bridges, including those bridges that underwent retrofitting. In recent years, the application of transfer learning has received significant attention in bridge SHM [7]. The main idea is to benefit from the existing knowledge of a monitored structure to evaluate another without estimating a new model or classifier.

The traditional analysis assumes the existence of two bridges with unbalanced datasets, i.e., the historical data of the source bridge is well-known, and the target bridge has a reduced amount of datasets. Then, feature-based transfer learning aims to find a new subspace where observations from two bridges in the undamaged condition are properly aligned, as changes in the structural framework of the target bridge often shift the observations. Thus, classifiers trained on a known structure (source) can be generalized to other bridges (target) where there is not enough knowledge about their structural condition [8].

Poole et al. [9] proposed a study on the structural behavior of several bridges, using a normal-correlation alignment method to evaluate features during undamaged conditions. Their approach succeeded in generalizing a classifier for structural evaluation. Specifically, under comparable structural conditions, outliers were highlighted when the features indicated different structural states. Meanwhile, Pan et al. [10] introduced a deep learning model to address the structural damage detection by transferring knowledge between two distinct bridges. A convolutional neural network, which was pretrained using the data of a previously studied bridge, was repurposed to evaluate another bridge’s structural integrity. This strategy reduced the need for extensive labeled data during the training phase and avoided re-estimating the model’s hyperparameters.

This paper proposes transfer learning as a domain adaptation to mitigate the data divergences for the same bridge before and after retrofit, allowing one to reuse previously existing knowledge in a long-term damage detection process. The joint distribution adaptation (JDA) method is carried out using datasets from two railway bridges: the PK 075+317 Bridge in France [11] and the KW51 Bridge in Leuven, Belgium [12]. The authors believe that the retrofit process is one of the most effective uses of SHM and the knowledge contained in the datasets can be reused for the structural assessment of bridges. It is important to note that our aim in this paper is distinct from Poole et al. [9], as knowledge transfer is performed between different moments in time of the same structure.

The structure of this paper is as follows; besides Section 1, the concept of transfer learning is introduced, and a long-term damage detection strategy using domain adaptation in retrofitting is summarize in Section 2. The subsequent Section 3 and Section 4—highlight the application of our proposed methodology in two distinct real bridges as case studies. Section 5 gives a summary of our findings, providing a conclusion and pertinent remarks on our study.

2. Transfer Learning for Long-Term Outlier Detection in the Context of Bridge Retrofitting

2.1. Overview of Transfer Learning for SHM

Transfer learning (or knowledge transfer) can described by the relationship between domains and tasks [13]. Each domain ($\mathcal{D}$) is represented by a feature space ($\mathcal{X}$) comprising damage-sensitive features grouped in the form of observations ($\mathbf{x}$) obtained from the structures with their corresponding probability distributions ($P\left(\mathbf{x}\right)$). The predictive function $f(·)$ applied for the assessment of the structure along with the label space ($\mathcal{Y}$) composed of information about the structural condition represents the task ($\mathcal{T}$) [14].

The definition of transfer learning leverages the knowledge contained in measured datasets despite the inconsistencies between domains (${\mathcal{D}}_s\ne {\mathcal{D}}_t$) and tasks $({\mathcal{T}}_s\ne {\mathcal{T}}_t$). This assumption allow us to use prior knowledge about the source domain (${\mathcal{D}}_s$) and source task (${\mathcal{T}}_s$) to aid in the evaluation of the target domain (${\mathcal{D}}_t$), improving the performance of the target predictive function ($f_t(·)$) consequently [15]. Meanwhile, domain adaptation is a subfield of transfer learning that mainly addresses the differences between the probability distributions ($P\left({\mathbf{x}}_s\right)\ne P\left({\mathbf{x}}_t\right)$), while their domains and tasks are equivalent (${\mathcal{D}}_s={\mathcal{D}}_t$ and ${\mathcal{T}}_s={\mathcal{T}}_t$) [16].

In the context of bridge SHM, the knowledge about structural conditions present in datasets of a known bridge is applied for long-term damage detection in a different bridge. For a successful knowledge transfer between different structures, the bridges should present similarities that motivate the realization of the transfer, an equivalent structural dynamic behavior, for instance.

2.2. Proposed Methodology for Domain Adaptation and Feature Classification

A novel application of transfer learning through domain adaptation is proposed to reuse the knowledge from a bridge before its retrofit to evaluate its structural condition after the retrofit process, assuming the existence of no damage before retrofitting.

As the modal parameters are sensitive to changes in stiffness, the natural frequencies are herein used as damage-sensitive features. The idea is that despite the consequent variations in natural frequencies caused by retrofitting, the historical monitoring data of a given bridge measured before retrofitting can be reused to aid in analyzing its structural integrity after retrofitting.

Figure 1 presents an overview of the methodology proposed in this paper. A bridge in its initial condition (source domain) and after retrofitting (target domain) have their natural frequencies estimated through a monitoring system. In the original feature space, it is assumed the existence of an evident change in the frequencies caused by changes in stiffness after the retrofit is assumed, which directly correlated with changes in the structural dynamic behavior. Afterwards, transfer learning via a domain adaptation method is applied to map features to a subspace where their divergences are mitigated (latent feature space). In this case, the JDA method is applied to estimate a transformation matrix that maps the observations to the latent space.

An outlier damage detection process is performed based on the Mahalanobis squared distance (MSD) [17,18], which is estimated in the original and latent spaces using the source knowledge only and assuming an underlying multivariate Gaussian distribution. The classifier’s performance is evaluated through its accuracy before and after the JDA application. The main idea is to build a classifier capable of correctly evaluating the structural condition through an outlier detection classification despite completing the retrofit process.

2.3. Joint Distribution Adaptation (JDA)

The JDA method [19] proposes a mapping function ($\varphi (·)$) to project the features to a reproducing kernel Hilbert space, where the differences between the joint distributions are mitigated. This often nonlinear mapping function adapts the marginal distributions ($P\left(\varphi \right(\mathbf{X})$) and the class-conditional distributions ($P\left(\varphi \right(\mathbf{X}\left)\right|\mathbf{Y}=c)$) with classes $c=\left\{0,1,\dots ,C\right\}$), allowing the generalization of model/classifier to different structures as a consequence.

Note that the class-conditional distribution is analyzed instead of the conditional distribution. This is a consequence of the lack of knowledge about the labels in the target domain. To address this issue, a base classifier trained with the source knowledge is applied iteratively for the determination of the target pseudo-labels, providing the optimization of the mapping function for the projection of the features as the classifier’s performance improves [20].

A kernel-based distance metric, called maximum mean discrepancy, is applied to evaluate the divergences between the source and target domains. This statistical distance metric measures the average distance between the probability distributions of the features after their embedding through a kernel matrix ($\mathcal{K}$), which avoids the explicit determination of the mapping function [21]. The squared maximum mean discrepancy ($\mathcal{M}$) can be written as:

$$\begin{array}{c}\hfill \mathcal{M}(P\left(\varphi \left({\mathbf{X}}_s\right)\right),P\left(\varphi \left({\mathbf{X}}_t\right)\right))+\mathcal{M}(\left(\varphi \left({\mathbf{X}}_s\right)\right|{\mathbf{Y}}_s),\left(\varphi \left({\mathbf{X}}_t\right)\right|{\mathbf{Y}}_t))=tr\left({\mathcal{W}}^T\mathcal{K}{\mathcal{L}}_c\mathcal{KW}\right)\end{array}$$

(1)

where $\mathcal{W}$ matrix contains the weights applied to perform the feature transformation into a latent space, and $tr(·)$ is the trace function. In addition, the ${\mathcal{L}}_c$ matrix can be described as:

$${\left({\mathcal{L}}_c\right)}_{ij}=\left\{\begin{array}{cc}\frac{1}{n_s^{\left(c\right)}{n}_s^{\left(c\right)}},& x_i,x_j\in {\mathcal{D}}_s^{\left(c\right)}\\ \frac{1}{n_t^{\left(c\right)}{n}_t^{\left(c\right)}},& x_i,x_j\in {\mathcal{D}}_t^{\left(c\right)}\\ \frac{-1}{n_s^{\left(c\right)}{n}_t^{\left(c\right)}},& \left\{\begin{array}{c}{x}_i\in {\mathcal{D}}_s^{\left(c\right)},x_j\in {\mathcal{D}}_t^{\left(c\right)}\\ x_j\in {\mathcal{D}}_s^{\left(c\right)},x_i\in {\mathcal{D}}_t^{\left(c\right)}\end{array}\right.\\ 0,& \mathrm{otherwise}.\end{array}\right.$$

(2)

where ${\mathcal{D}}_s^{\left(c\right)}=\left\{x_i:x_i\in {\mathcal{D}}_s\wedge y\left(x_i\right)=c\right\}$ refers to source features of class c based on their corresponding labels, and ${\mathcal{D}}_t^{\left(c\right)}=\left\{x_j:x_j\in {\mathcal{D}}_t\wedge \widehat{y}\left(x_j\right)=c\right\}$ refers to target features given the class c determined according to their respective pseudo-labels.

It is important to preserve the underlying properties of the features after their mapping to the shared latent space. This constraint can be described by the data variance $({\mathcal{W}}^T\mathcal{K}H\mathcal{KW}$), where H is the centering matrix. Hence, this minimization problem with one constraint to be satisfied can be written as:

$$\underset{{\mathcal{W}}^{\mathit{T}}\mathcal{K}\mathit{H}\mathcal{KW}=\mathit{I}}{min}\sum _{c=0}^{C}tr\left({\mathcal{W}}^T\mathcal{K}{\mathcal{L}}_c\mathcal{KW}\right)+\mu tr\left({\mathcal{W}}^T\mathcal{W}\right)$$

(3)

where $\mathit{I}$ is the identity matrix and $\mu$ is the trade-off parameter. Note that the first term corresponds to the objective function that measures the distance between the joint distributions, and the regularization term described by the second term avoids a possible overfitting. The Lagrange multipliers can be applied to address this minimization problem, resulting into an eigenproblem defined by:

$$\left(\mathcal{K}\sum _{c=0}^C{\mathcal{L}}_c\mathcal{K}+\mu \mathit{I}\right)\mathcal{W}=\mathcal{K}H\mathcal{KW}\lambda$$

(4)

where $\mathcal{W}$ represents the transformation matrix defined by the m smallest eigenvectors, and it is applied with the kernel matrix for the features mapping to the latent space through $Z=\mathcal{K}\mathcal{W}$.

2.4. Classifier: Mahalanobis Squared Distance (MSD)

The MSD is a distance metric for multivariate statistics often applied for outlier detection in SHM analysis [22,23,24]. The traditional methodology estimate the multivariate mean vector $\left(\mathit{\mu }\right)$ and the covariance matrix $\left(\mathbf{\Sigma }\right)$ of the training data from the source domain $\left({\mathbf{X}}_s\right)$. The evaluation of the test data composed by the new observations from the target domain $\left({\mathbf{X}}_t\right)$ investigates whether their patterns differ significantly, indicating structural damage by the presence of outliers. By definition, the MSD or damage index (DI) can be written as [17]:

$$\mathrm{DI}\left(x_t\right)=\left(x_t-\mathit{\mu }\right){\mathbf{\Sigma }}^{-1}{\left(x_t-\mathit{\mu }\right)}^{\top }$$

(5)

In this analysis, a hypothesis test is proposed to ensure the statistical reliability of the structural integrity assessment. Thus, the probability density function of the DIs is investigated if the null or alternative hypotheses are met according to an established threshold value. Formally, the null hypothesis $\left(H_0\right)$ is assumed when the structure is in a healthy condition, while the alternative hypothesis $\left(H_1\right)$ indicates the presence of structural damage.

In the healthy condition, it is assumed that each observation belongs to a Chi-squared distribution $\left({\chi }^2\right)$ by definition, i.e., $\mathrm{DI}\sim {\chi }^2$ [25,26]. Then, it becomes possible to set a threshold value $\left(c\right)$ in agreement with a level of significance $\left(\alpha \right)$ in the form of $c=\mathrm{inv}{F}_{{\chi }^2}\left(1-\alpha \right)$. Therefore, an observation is defined as damaged when its DI equals or exceeds the threshold value, consequently rejecting the null hypothesis. The level of significance is often set to $5\%$, and this value is assumed herein during the analysis.

The transfer learning performance can be evaluated using the overall accuracy of the distance-based classifier estimated. A binary classification is applied in this case, assuming the damaged structural condition is positive while the undamaged condition is negative. Therefore, the accuracy of the classifier can be defined as:

$$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}$$

(6)

where $TP$ and $TN$ represent the number of true positive and true negative when damaged and undamaged conditions are correctly addressed by the classifier, respectively. Meanwhile, $FP$ is the number of false positive and $FN$ is the number of false negative, which are also known as Type I ($FP$) and Type II ($FN$) errors.

3. PK 075+317 Bridge

3.1. Structural Description and Monitoring Datasets

The PK 075+317 Bridge (Figure 2) is a reinforced concrete railway bridge built in the early 1980s in the southeastern region of France. To avoid possible structural problems due to resonance effects, a retrofit process was developed to shift the first natural frequency of the bridge from the excitation frequency resulting from the passage of high-speed trains. Thus, a system composed of bearings and rods was embedded to reinforce the structure and increase the structural stiffness of the bridge consequently [27,28].

The railway bridge’s dynamic monitoring encompassed a comprehensive assessment aimed at evaluating the influence of environmental fluctuations on its modal characteristics. An attempt to determine and quantify the operational improvements made by tightening the rods on the structure’s dynamic behavior (as illustrated in Figure 2) was proposed. It was observed that the frequency of excitation related to the passage of high-speed trains was very close to the first natural frequency of the bridge (4 Hz and 5.85 Hz, respectively). Therefore, the risk of resonance was increased, especially when ballast recharging occurred. To address that concern, the French National Railway Corporation (SNCF) set up a system of rods and bearings (as also seen in Figure 2), which were tightened by torque wrench; that solution added stiffness to increase the frequency and avoid resonance effects. That procedure was carried out in four stages, monitoring each side of the bridge separately. Initially, four rods were tightened, followed by three rods on one side (Lyon). Subsequently, four then three rods on the opposing side (Paris).

A comprehensive monitoring plan was conducted from 23rd to 26th of June, 2003, to investigate the behavior of the bridge before and after the retrofit process. The data acquisition regarding the dynamic behavior of the bridge and local temperature data were obtained using eight accelerometers positioned on the bridge deck (lower face) and an array of temperature gauges, respectively. Note that the PK 075+317 Bridge was only subject to positive temperatures during the monitoring period.

Feature extraction from the collected datasets was performed, and the first four natural frequencies were estimated. Figure 3 illustrates the observations during the monitoring period, with the first 150 observations representing the frequencies before the retrofit and the remaining ones representing the period following the retrofit process. One can observe an evident shift in the first frequency, imposed by the tightening of the system of rods and bearings. From

Table 1. Average natural frequencies estimated before and after retrofitting of the PK 075+317 bridge.

No.	Before Retrofit	After Retrofit	Variation [%]
	f [Hz]	f [Hz]
1	5.85	6.46	+10.43
2	8.73	8.98	+2.86
3	13.10	13.05	−0.38
4	16.81	16.94	+0.77

, it is possible to highlight an average increase of $10.43\%$ in the first natural frequency before and after retrofitting.

Figure 4 shows all observations in the original feature space and their histograms on the main diagonal. The retrofit process primarily affects the first natural frequency as the histograms present a minor overlapping. Additionally, it is possible to notice a variation in the other natural frequencies, potentially due to the challenges addressed during the bridge monitoring process and feature extraction method proposed in the analysis.

3.2. Outlier Detection and Structural Assessment

Figure 5 shows the observations after the JDA method application using a linear kernel to correlate the observations and a trade-off parameter ($\mu$) defined as $1\times {10}^{-3}$. In this case, the observations from the bridge before and after the retrofit were projected from a four-dimensional original space to a two-dimensional latent space $(m=2)$. Overall, the divergences between the joint distributions were adequately mitigated, as highlighted by the overlapping histograms of the two latent features. The classifier with a superimposed Gaussian distribution with a level significance equals to $5\%$ indicates the presence of some outliers, resulting from the dispersion of features in the original space due to the natural frequency estimation process.

Figure 6 indicates the outlier detection (or damage detection) in both feature spaces, in which each observation from target domain (after retrofit) is assigned with a DI. The classifiers in both spaces were defined with training data from the source domain only (before retrofit). The two classifiers in the original and latent feature spaces output an overall accuracy of $3.08\%$ and $94.62\%$, which indicates the advantage of applying transfer learning to mitigate the retrofit effects in the modal parameters. Note there is no indication of damage, so the changes in stiffness should be regarded as normal.

4. The KW51 Bridge

4.1. Structural Description and Monitoring Datasets

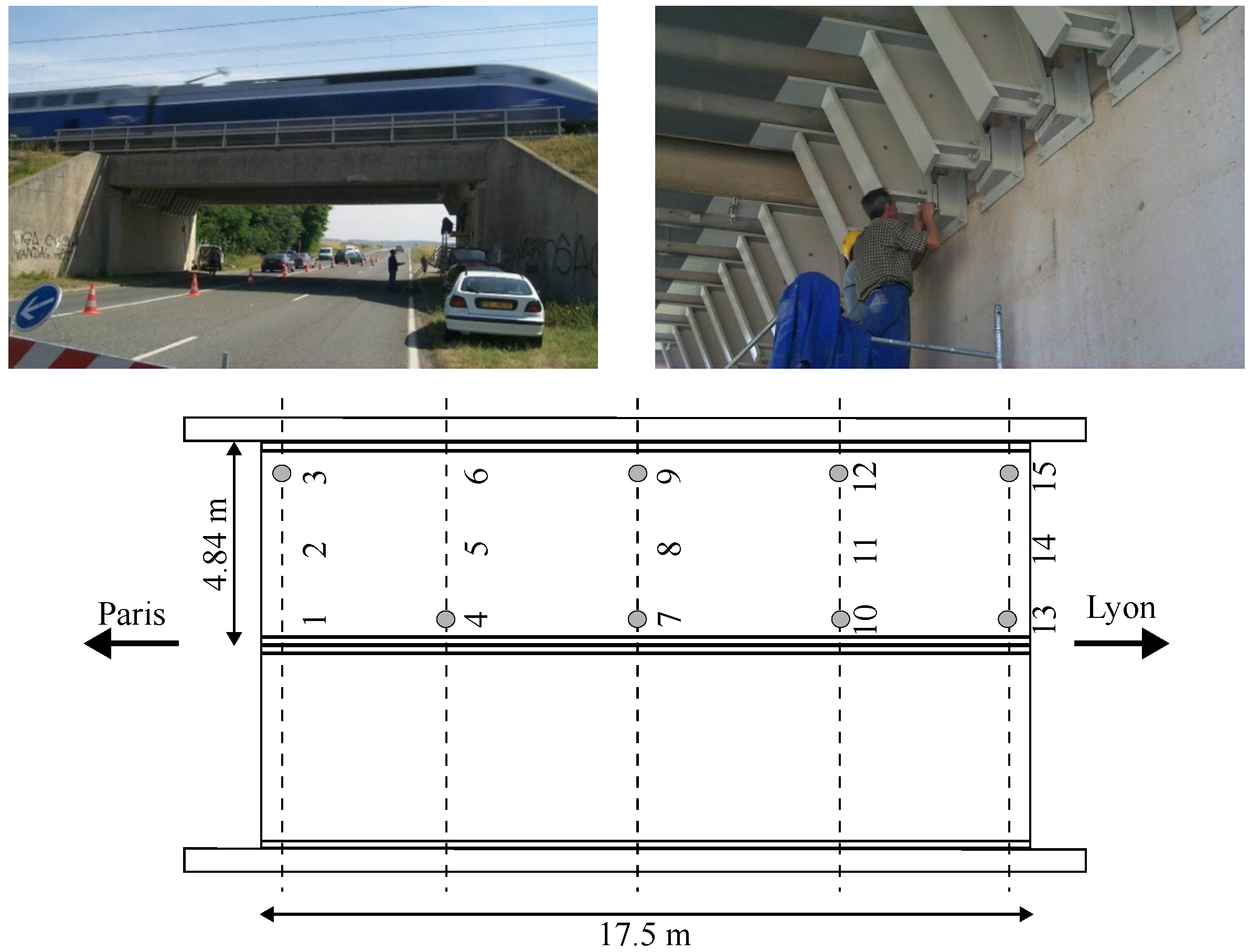
The KW51 Bridge (Figure 7) is a steel bowstring bridge in Leuven, Belgium, with a single span of 115 m that includes two ballasted railway tracks that connect the stations of Herent and Leuven [12].

The bridge underwent an inspection that indicated the necessity for a retrofit plan to address a problem related to its construction. The bolted joints that connected the bridge deck and arches were strengthened by welding a steel box between the structural components to ensure the bridge’s safety and stability.

A long-term monitoring plan was carried out from 2 October 2018, to 15 January 2020, to follow the entire bridge retrofit process. A monitoring system with 12 accelerometers was installed along the bridge to measure its dynamic behavior, as well as other sensors were positioned to collect environmental parameters, including temperature and relative humidity. The datasets were collected in three periods: (i) before the bridge retrofit from 2 October 2018, to 15 May 2019; (ii) while conducting the retrofit from 15 May 2019, to 27 September 2019; and (iii) after completing the retrofit from 27 September 2019, to 15 January 2020.

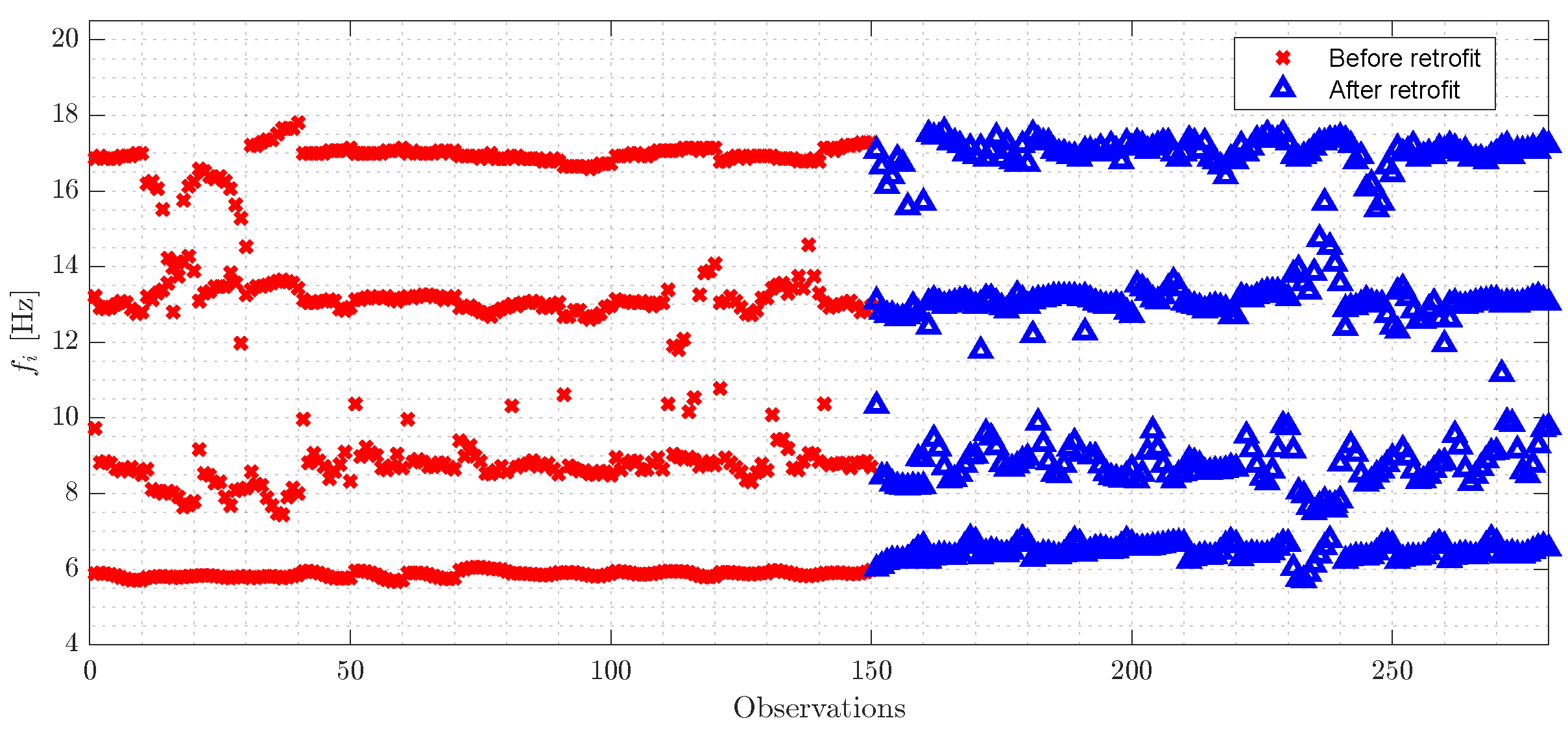
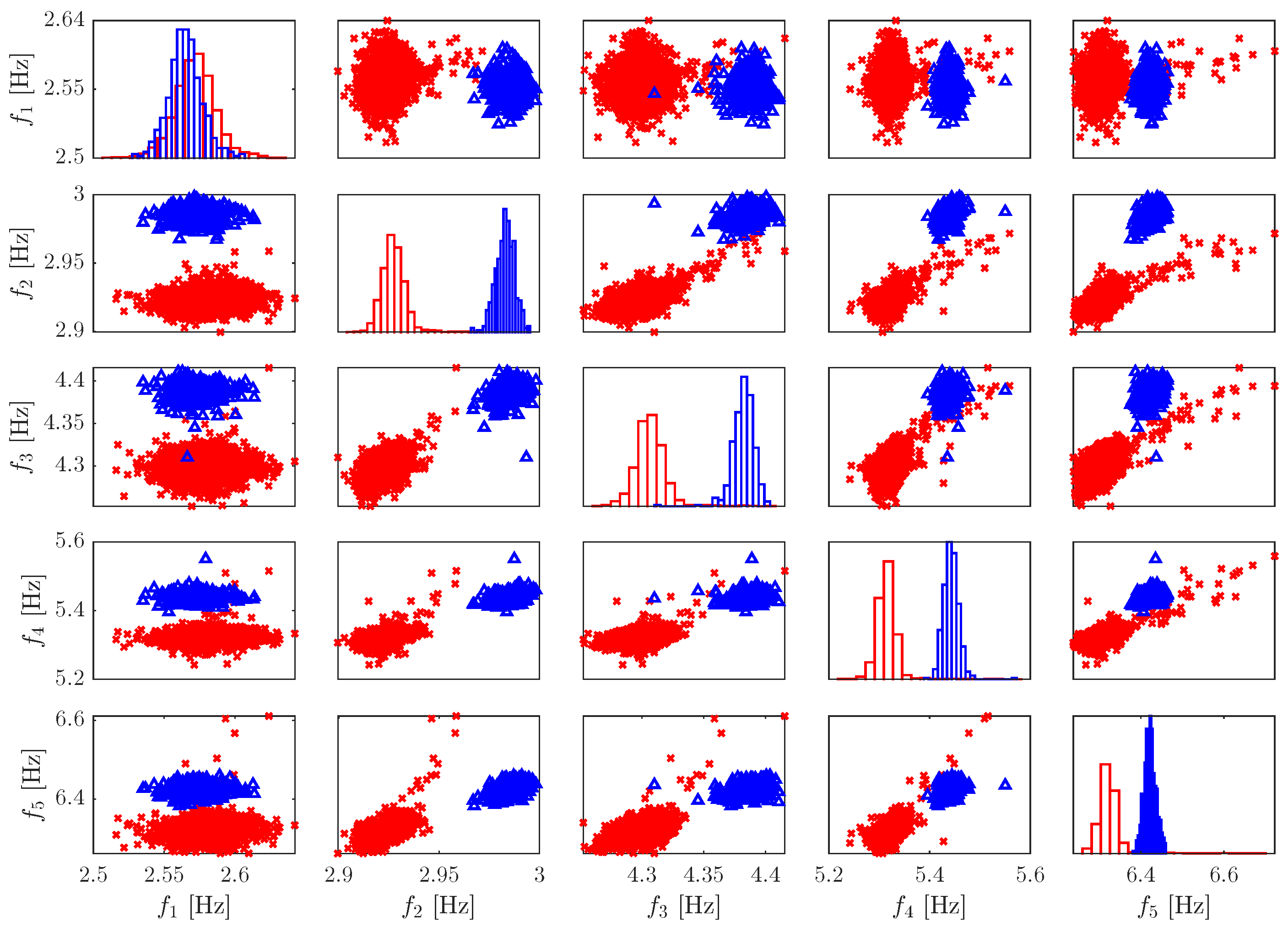
An operational modal analysis was carried out to follow the evolution of the structure’s modal parameters over the monitoring process for the bridge structural assessment. Figure 8 illustrates the 14 natural frequencies estimated in this period. Note that some frequencies are unavailable for some days due to measurement problems. Overall, it can be observed an increase in natural frequencies: (i) before retrofitting due to the effects of negative temperatures as suggested by some peaks in specific frequencies and (ii) after performing the retrofit process due to the increase of permanent stiffness.

In this study, only the bending modes of the bridge are investigated, as the most significant variations in frequencies are present in these modes. Therefore,

Table 2. Average natural frequencies estimated before and after the KW51 bridge retrofit.

No.	Before Retrofit	After Retrofit	Variation [%]
	f [Hz]	f [Hz]
1	2.58	2.57	−0.4
2	2.92	2.98	+2.1
3	4.30	4.39	+2.1
4	5.33	5.44	+2.1
5	6.33	6.42	+1.4

provides an overview of the average of five natural frequencies before and after the retrofit process. A slight yet important variation in some frequencies (maximum of $2.1\%$) can impact the performance of machine learning algorithms, which are often sensitive to changes in the datasets used in the training phase.

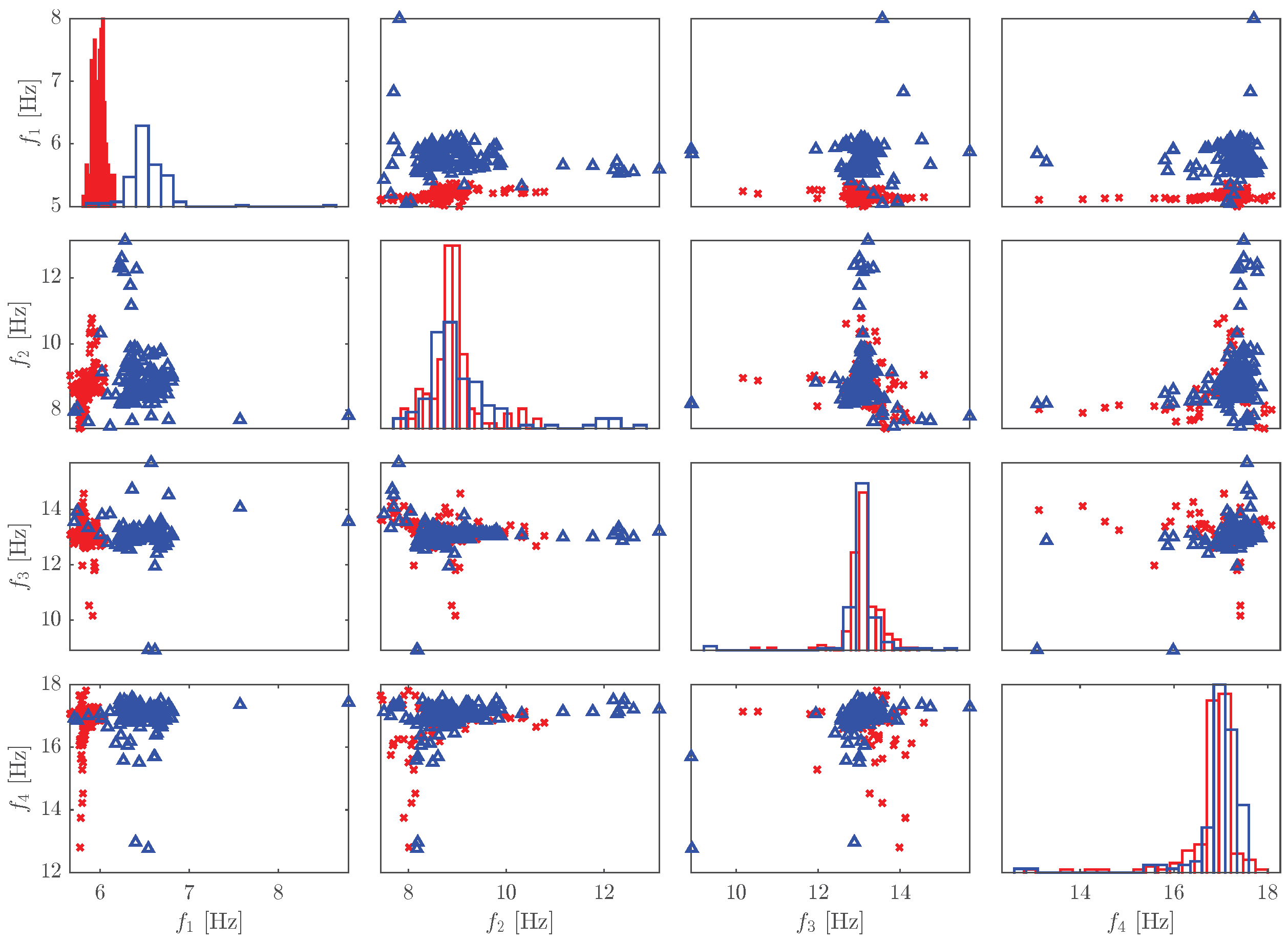
Figure 9 illustrates the natural frequencies in the original space and their corresponding histograms of the bridge before and after its retrofit. On the main diagonal, the histograms highlight the differences between the features extracted from the bridge datasets. In a two-dimensional perspective, the features are not aligned due to frequency variations, and some apparent outliers are present, indicating possible impacts caused by the temperature and by the bridge structural condition that motivated the retrofit.

4.2. Outlier Detection and Structural Assessment

The general concept of transfer learning that preserves a higher proportion of observations from the source domain compared to the target domain is ensured in this analysis, despite the measurement problems that prevented the use of all estimated modes. Therefore, the datasets collected before the retrofit (source domain) have 2582 observations, while the datasets after the retrofit (target domain) have 428 observations.

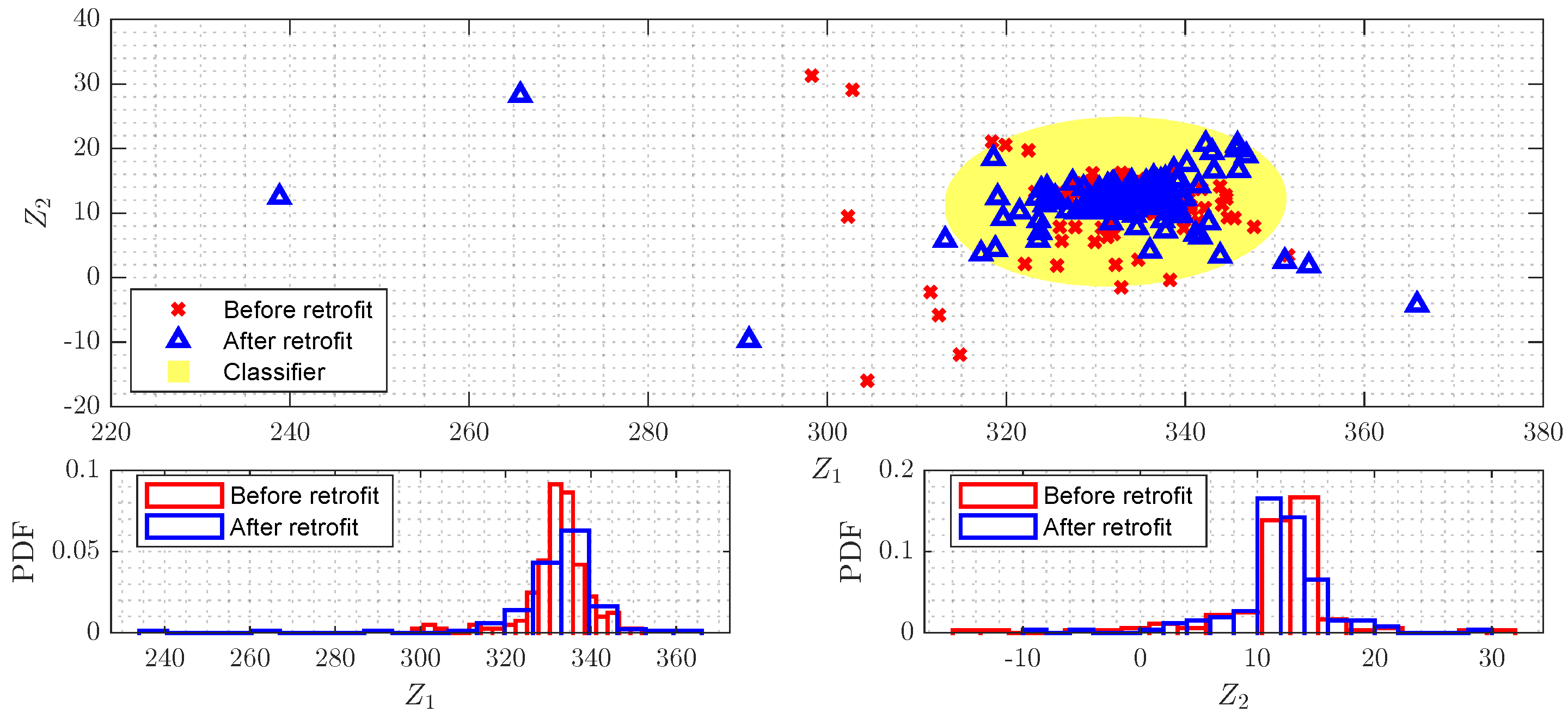
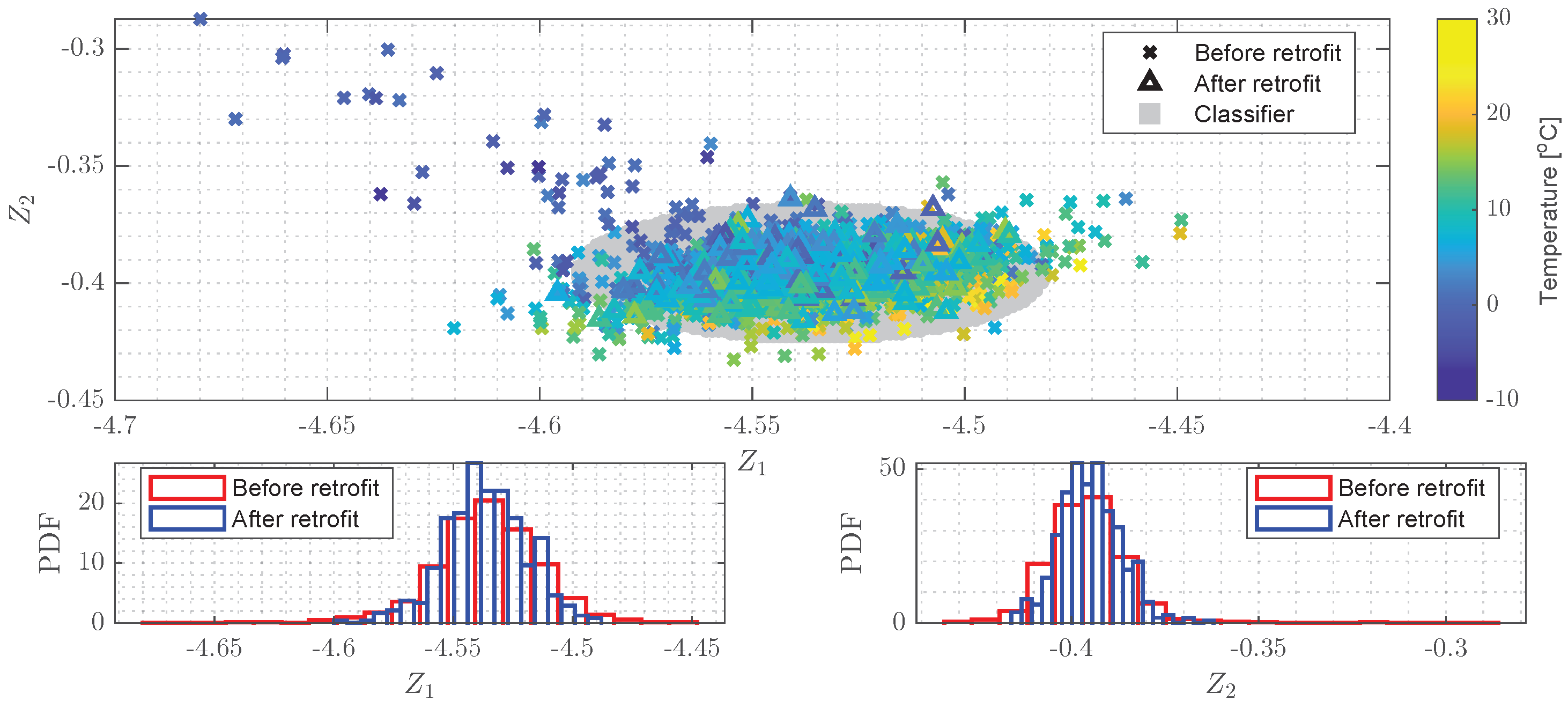
The JDA method is applied for domain adaptation assuming a linear kernel and the regularization parameter ($\mu$) is set to be $1\times {10}^{-4}$. Figure 10 shows the observations in the latent feature space and the decision boundary (threshold) defined by a superimposed Gaussian distribution estimated using the source knowledge only. It is possible to observe that the divergences between the observations from the source and target domains were mitigated in the latent space. The overlap of their histograms indicates the same behavior. The source observations present some outliers in the latent space, evidencing the JDA method preserved the data properties after the features mapping to the latent space.

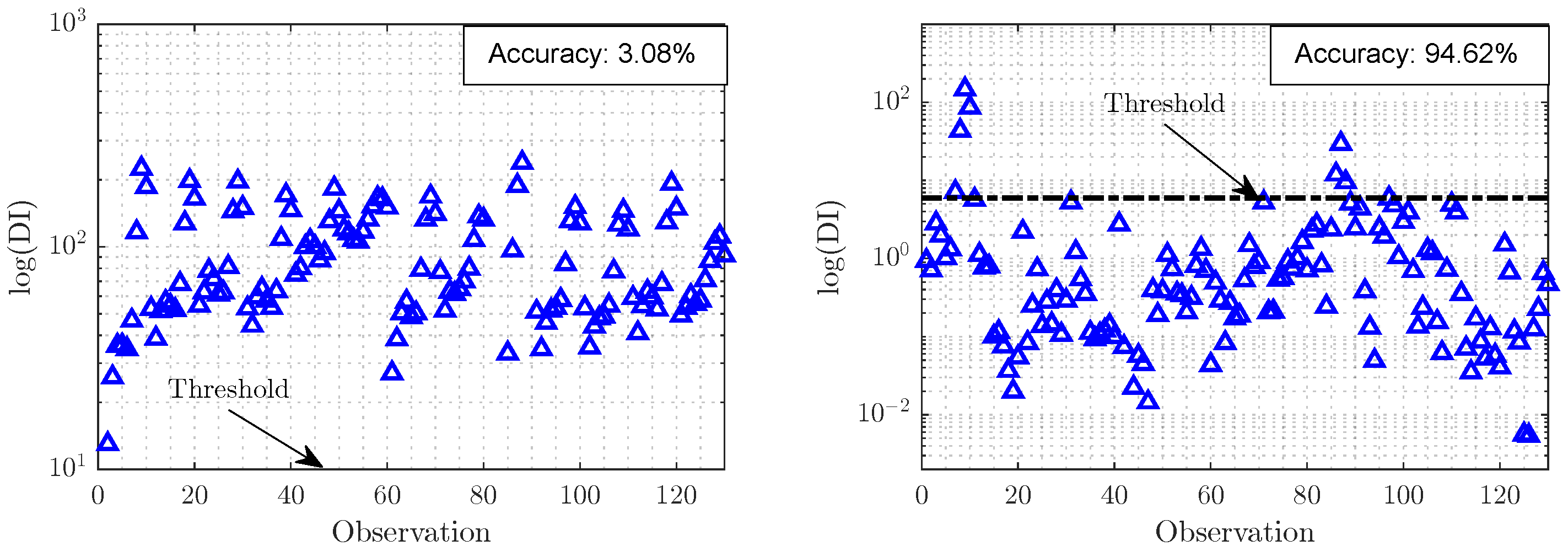
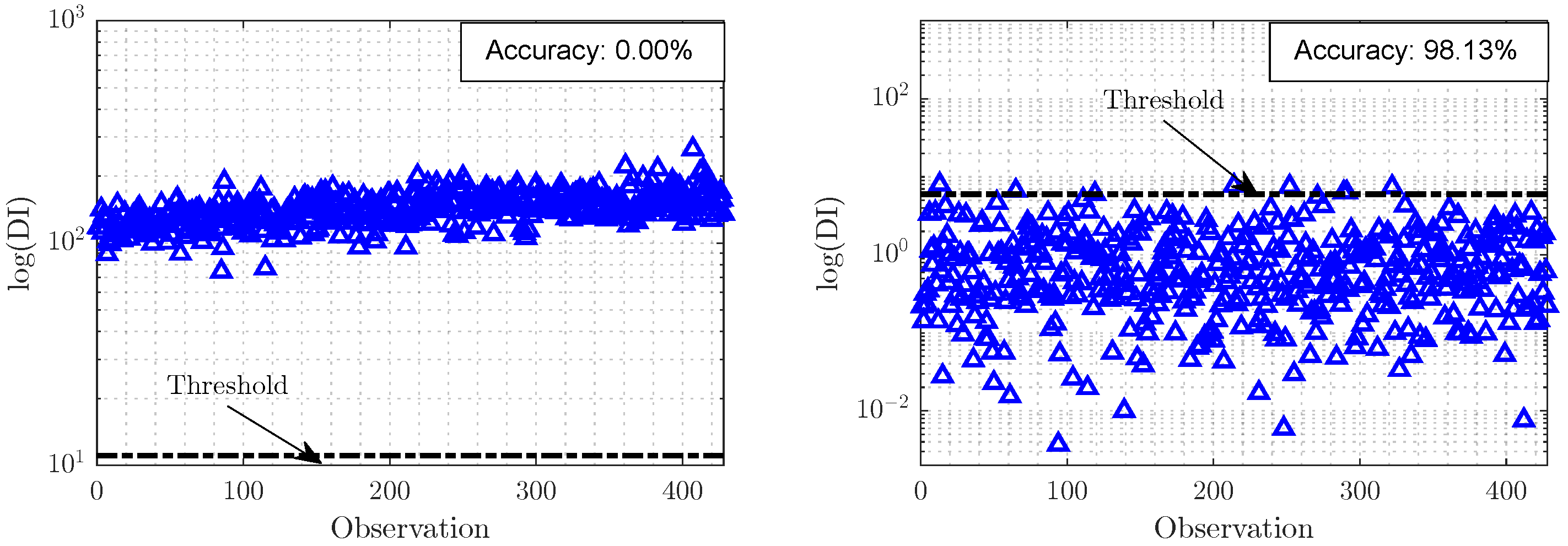
By assuming the presence of outliers could be associated with the presence of damage, Figure 11 presents the DIs estimated by the classifier and its performance in the original and latent feature spaces using the observations from the target domain (after retrofit). Both classifiers were defined with observations from the source domain only (before retrofit). In the original space, the divergences between the observations do not allow a correct evaluation performed by the classifier, which is highlighted by higher values of DIs than the threshold defined for a level of significance of $5\%$. In contrast, the distance-based classifier presents a significant improvement in its performance in the latent feature space, as it could assess the bridge’s structural condition with an accuracy equal to 98.13%, which proves the classifier’s ability to be applied in future decision-making on the bridge condition.

5. Conclusions

The shifts in the damage-sensitive features induced by the retrofit process may challenge the application of long-term damage detection strategies in bridges, as machine learning algorithms may not properly describe structural-related changes in the features occur after the training phase. In a traditional bridge evaluation, the structural knowledge contained in the datasets before retrofitting would not be leveraged in future decision-making on the bridge’s condition, and identifying a new classifier to describe the behavior of the bridge would be necessary.

The possibility of applying transfer learning to assess the structural condition of the PK 075+317 Bridge and KW51 Bridge after the retrofit process was highlighted in this paper. In both cases, possible structural problems justified the retrofitting of the bridge components. The classification in the PK 075+317 Bridge shows an overall accuracy gain from $3.08\%$ to $94.62\%$ after the JDA application. Meanwhile, transfre learning significantly improved the overall classifier accuracy from $0.00\%$ to $98.13\%$ in the KW51 Bridge in Leuven.

Even though the data mapping onto the latent feature space may be challenging to interpret the physical phenomena, the proposed methodology rooted in transfer learning and domain adaptation has the advantage of aligning the monitoring datasets measured before and after retrofitting while keeping their statistical properties. Thus, transfer learning can also be applied to describe the dynamics behavior of structures under retrofit conditions in a lower dimensional space, offering a novel perspective for overcoming monitoring data mismatch in the damage detection process when a bridge is retrofitted.