Ensuring the Safety of Steel Moment Frames Subjected to Uncertain Impacts
Abstract
1. Introduction
1.1. Review of Works Focused on the Research Problem
1.1.1. Type of Loading
1.1.2. Stress–Strain State of Joints and Elements
1.1.3. Taking Account of Soil–Structure Interaction
1.1.4. Studying the Process of Progressive Collapse
1.1.5. The Effect of Initial and Impact-Triggered Imperfections
1.1.6. Other Features
1.2. Purpose and Objectives of the Research Addressed in This Article
- An integral efficiency factor is introduced for safety evaluation purposes (Section 2.2.1). The calculation of the efficiency factor takes into account the random nature of impacts. These impacts are modelled using the approach described in Section 2.1.2, while the effects of an impact on a steel structure are evaluated using the survivability criteria described in Section 2.1.3;
- To calculate the components of the stress–strain state and the stability of a structure at the initial stage, it is proposed to use a quasi-static approach based on the methodology described in Section 2.2.1, with subsequent verification of the result using the dynamic calculation (Section 2.2.2) method. In this case, a multilayered finite element (Section 2.2.3) is constructed to analyse the deformations of steel profiles, which allows for modelling the formation of plastic hinges using a rigid plastic model of the material. The model takes into account the force transfer from the steel moment frame to the deformable soil base, whose part can be removed as a result of an accidental impact (Section 2.2.4);
- The results of the proposed approach are verified experimentally (Section 3.1). A practical case of analysis of a steel moment frame, subjected to impact loading (Section 3.2), is provided and the efficiency of the design solution is evaluated using the integral efficiency factor described in Section 2.2.1.
2. Materials and Methods
2.1. Statement of the Research Problem
2.1.1. General Provisions
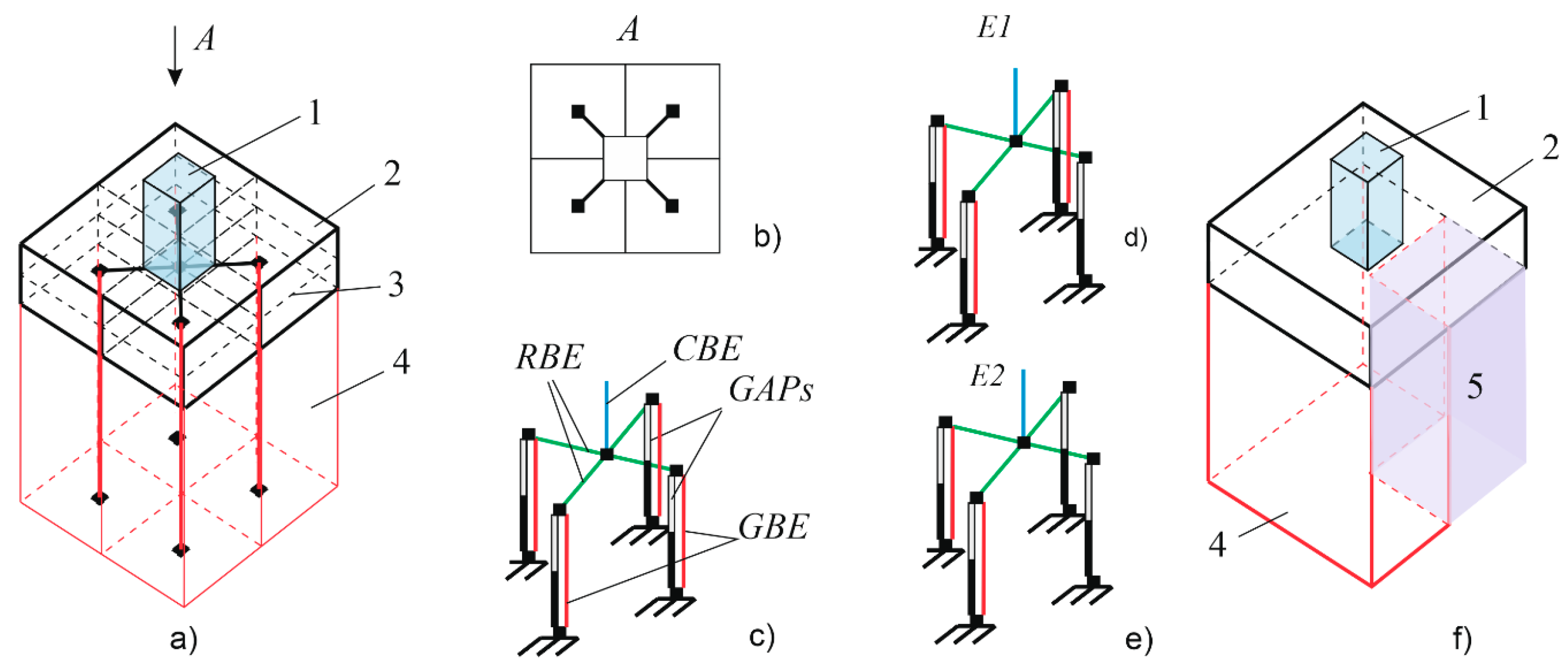
2.1.2. Accidental Impact Generation Procedure
- Generation of arrays of values for vector omponents in the form , ; is the number of potential component values to select from. Here we calculate vector components as ;
- Generation of data array describing the structural elements of a steel moment frame:
- 3.
- Random selection of a structural element from structure ;
- 4.
- Random selection of the third, fourth, or fifth joint from the group of elements listed in the ascending order, starting from ;
- 5.
- The loading of the joint, selected at step 4, using loading values that are randomly selected from the interval at step 1.
2.1.3. Criterial Assessment of Resistance to Progressive Collapse and Survivability of the Structure
- Prevention of any large changes in the geometry of a structural system, taking into account its possible plastic deformation or loss of stability. This condition can be formulated as follows:
- 2.
- For the condition of the absence of cracks as a result of local ruptures of elements, which can be formulated for any (most heavily loaded) cross-section of an element, let n, the most stressed characteristic points of a cross-section, be considered; then,
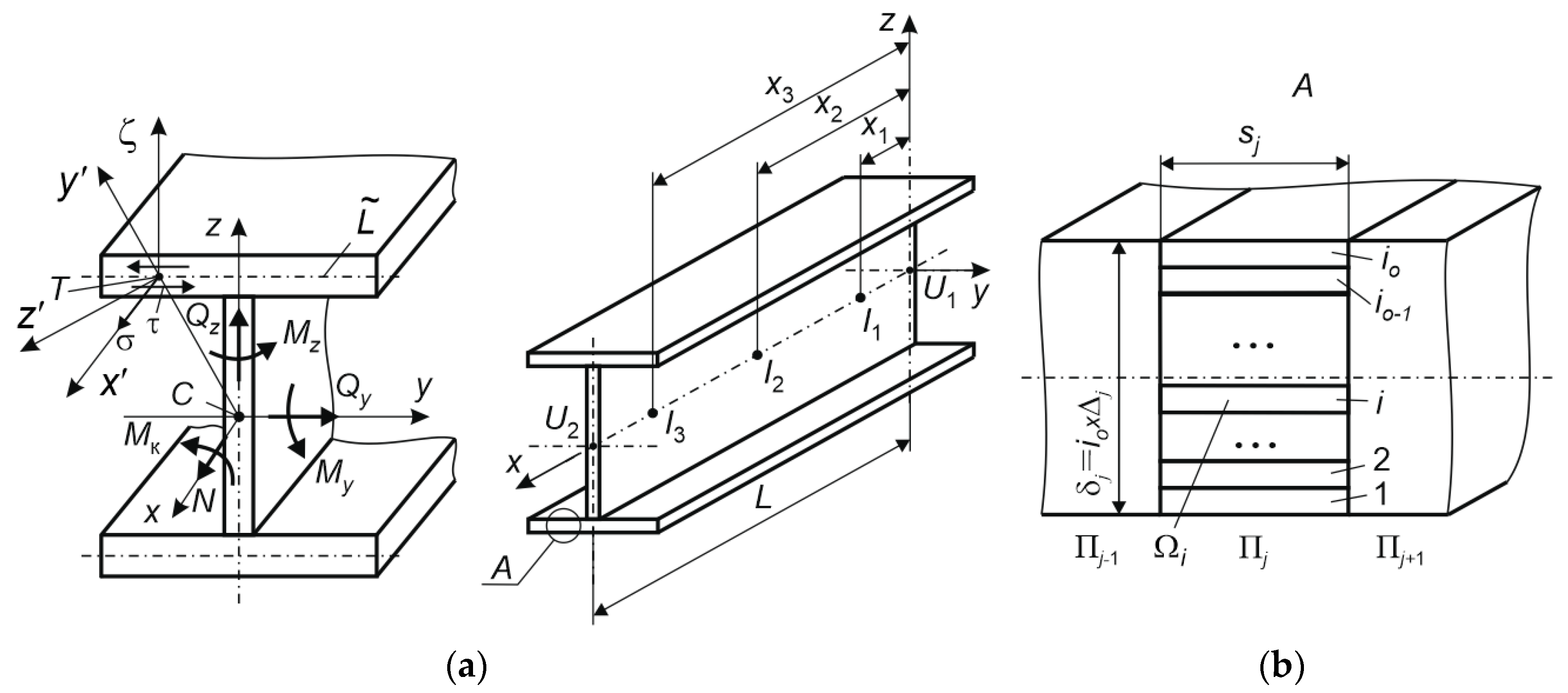
2.2. Method of Dynamic Analysis of Steel Moment Frames Subjected to Impact Loading
2.2.1. Iterative Pattern for Preliminary Strength and Stiffness Evaluation
2.2.2. General Equation of Inelastic Impact Dynamics
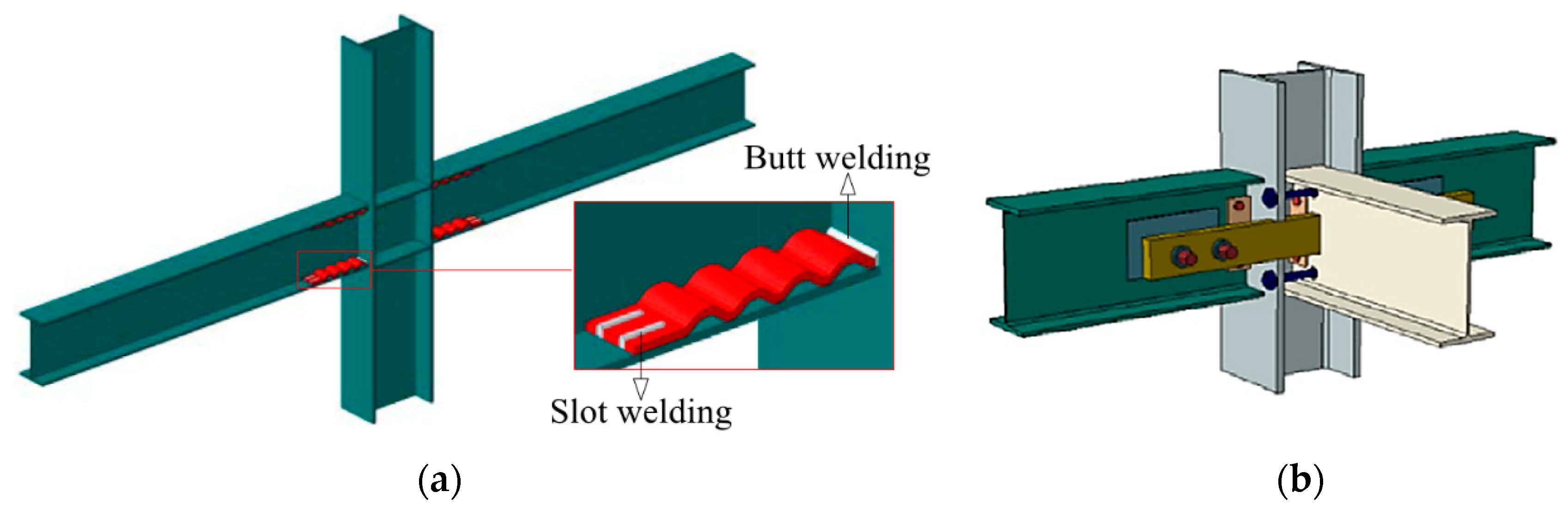
2.2.3. Models of Structural Elements, Loads, and Material Deformations
2.2.4. Modeling Soil-Base Deformations
3. Results
3.1. Experimental Verification of the Calculation Model
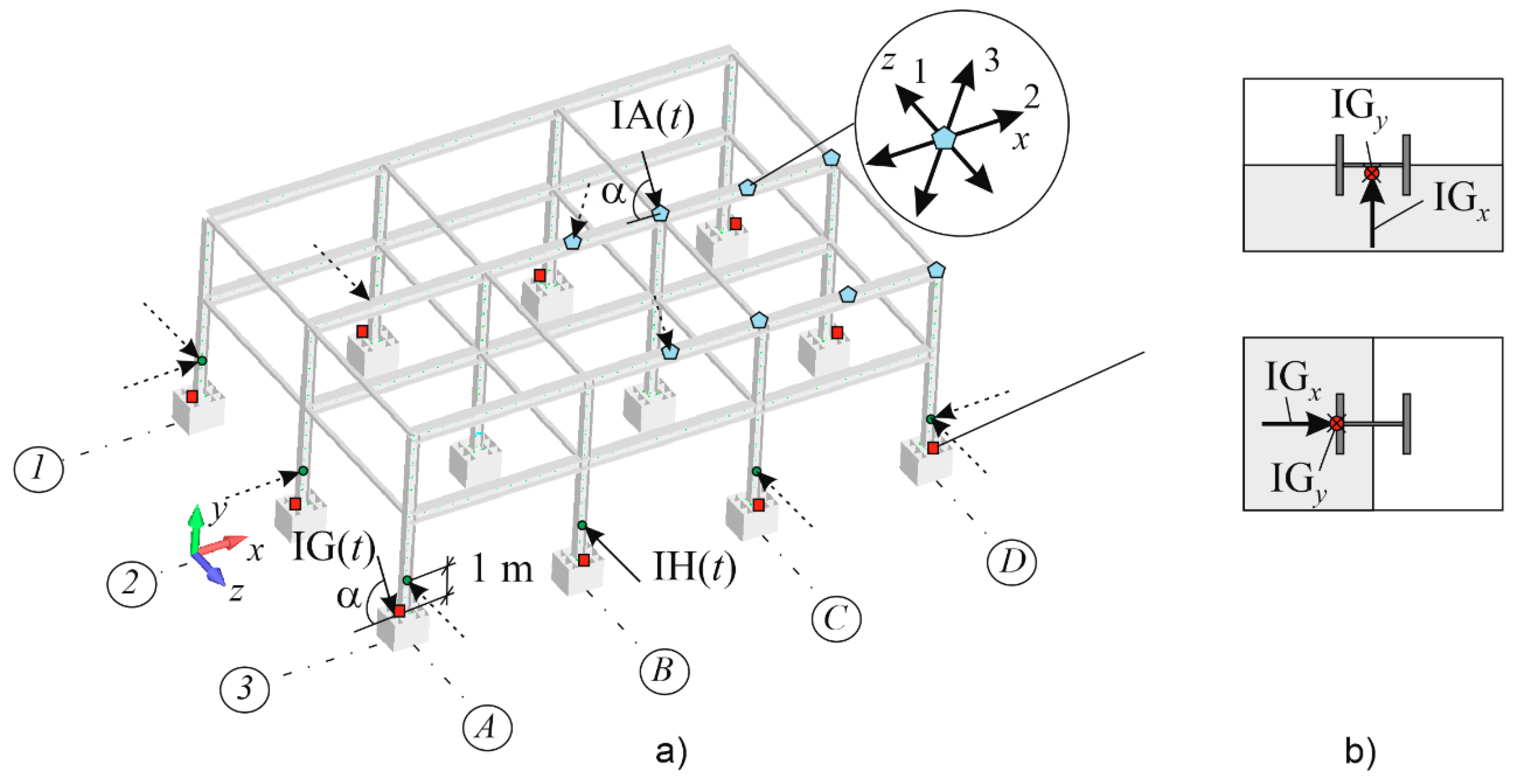
3.2. Example of a Steel-Frame Calculation
3.2.1. Design Input Data
3.2.2. Impact Modeling, Solution Algorithm, and Problem Limitations
- –
- selection of IA loading positions from the set; analysis of the structure in the quasi-static formulation using the methodology described in Section 2.2.3, and verification of limitations. If limitations are violated, then the process is stopped and the system topology is refined or the cross-sections of rods are increased;
- –
- selection of IH loading positions from the set and analysis of the construction obtained at the previous step; verification of limitations. Enhancement of the structural solution, if necessary;
- –
- selection of IG loading positions from the set; verification of limitations with the subsequent enhancement of the design solution, if necessary;
- –
- verification of the solution using the detailed dynamic analysis, in terms of those loads, that require changes in the design.
3.2.3. Results of Calculation and Analysis of Mechanical Safety
4. Discussion and Prospects for Further Research
- –
- consideration of reinforced concrete frames of buildings and structures under accidental impact loads and effects;
- –
- consideration of methods for modelling low-velocity impacts on structures by a heavy mechanical body as a result of the collapse of a prefabricated slab, falling off a destroyed part of the structure on its undamaged part, etc.;
- –
- modelling of accidental thermomechanical effects on structures;
- –
- consideration of reinforced concrete and steel-frame systems subjected to the effects of combined repetitive accidental impacts.
5. Conclusions
- –
- the procedure of generating pulse impacts on a steel moment frame, simulating a high-velocity concentrated impact, which approximates the impact of an absolutely rigid body having a small mass;
- –
- quasi-static and dynamic calculations of steel moment frames, subjected to impact effects, taking into account the physical and geometrical nonlinearity and criteria of resistance to progressive collapse;
- –
- the algorithm for evaluating the effectiveness of the designed structure using the cost minimization criterion while ensuring the required mechanical safety;
- –
- the method for taking into account local damages of the soil base subjected to the impact effect.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Majlesi, A.; Asadi-Ghoozhdi, H.; Bamshad, O.; Attarnejad, R.; Masoodi, A.R.; Ghassemieh, M. On the Seismic Evaluation of Steel Frames Laterally Braced with Perforated Steel Plate Shear Walls Considering Semi-Rigid Connections. Buildings 2022, 12, 1427. [Google Scholar] [CrossRef]
- Xiao, Y. Development of Structural Testing Equipment for Impact and Complex Loading. J. Struct. Integr. Maint. 2021, 6, 1–15. [Google Scholar] [CrossRef]
- Zeinoddin, M. In-Situ Quasi-Static and Dynamic Behavioural Response of Steel Tubular Frames Subjected to Lateral Impact Loads. Lat. Am. J. Solids Struct. 2012, 9, 1–19. [Google Scholar] [CrossRef]
- Wang, H.; Huo, J.; Elchalakani, M.; Liu, Y.; Zhang, S. Dynamic Performance of Retrofitted Steel Beam-Column Connections Subjected to Impact Loadings. J. Constr. Steel. Res. 2021, 183, 106732. [Google Scholar] [CrossRef]
- Chen, K.; Yang, B.; Tan, K.H. Behaviour of Composite Beam-Column Joint with Fin Plate Connection Subjected to Impact Loads. Eng. Struct. 2022, 273, 115143. [Google Scholar] [CrossRef]
- D’Antimo, M.; Latour, M.; Demonceau, J.F. Drop-Weight Impact Tests on Free from Damage Beam to Column Connections. J. Constr. Steel. Res. 2022, 192, 107215. [Google Scholar] [CrossRef]
- Qiao, H.; Luo, C.; Ma, Y.; Chen, Y. Dynamic Effect Analysis of Steel Frame Structure under Impact of Falling Block. J. Vib. Shock. 2021, 40, 8–15. [Google Scholar] [CrossRef]
- Sadeghi, A.; Kazemi, H.; Samadi, M. Reliability and Reliability-Based Sensitivity Analyses of Steel Moment-Resisting Frame Structure Subjected to Extreme Actions. Frat. Integrita Strutt. 2021, 15, 138–159. [Google Scholar] [CrossRef]
- Mirkarimi, S.P.; Mohammadi Dehcheshmeh, E.; Broujerdian, V. Investigating the Progressive Collapse of Steel Frames Considering Vehicle Impact Dynamics. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 4463–4479. [Google Scholar] [CrossRef]
- Sadeghi, A.; Kazemi, H.; Mehdizadeh, K.; Jadali, F. Fragility Analysis of Steel Moment-Resisting Frames Subjected to Impact Actions. J. Build. Pathol. Rehabil. 2022, 7, 26. [Google Scholar] [CrossRef]
- Kou, S.; Zhang, X.; Li, W.; Song, C. Dynamic Response Parameter Analysis of Steel Frame Joints under Blast Loading. Buildings 2022, 12, 433. [Google Scholar] [CrossRef]
- Moon, N.N. Prediction of Blast Loading and Its Impact on Buildings. Master’s Thesis, Department of Civil Engineering, National Institute of Technology, Rourkela, India, 2009. [Google Scholar]
- Wang, H.; Huo, J.; Liu, Y.; Wang, N.; Elchalakani, M. Experimental and Numerical Study on Impact Behavior of Beam-Column Substructures of Steel Frame. Structures 2021, 29, 14–29. [Google Scholar] [CrossRef]
- Stochino, F.; Attoli, A.; Serra, M.; Napoli, A.; Meloni, D.; Mistretta, F. Structural Identification from Operational Modal Analysis: The Case of Steel Structures. Buildings 2023, 13, 548. [Google Scholar] [CrossRef]
- Gusella, F.; Orlando, M.; Peterman, K.D. The Impact of Variability and Combined Loads on Fuses in Braced Frames. Structures 2022, 35, 650–666. [Google Scholar] [CrossRef]
- Wang, H.; Tan, K.H.; Yang, B. Impact Resistance of Steel Frames with Different Beam–Column Connections Subject to Falling-Floor Impact on Various Locations. J. Struct. Eng. 2021, 147, 04021017. [Google Scholar] [CrossRef]
- Sadeghi, A.; Kazemi, H.; Samadi, M. Single and Multi-Objective Optimization of Steel Moment-Resisting Frame Buildings under Vehicle Impact Using Evolutionary Algorithms. J. Build. Pathol. Rehabil. 2021, 6, 21. [Google Scholar] [CrossRef]
- Nakatsuka, S.; Sato, A. Experimental Study on Shallow H-Shaped Steel Column under Combined Loading Condition. In Current Perspectives and New Directions in Mechanics, Modelling and Design of Structural Systems; CRC Press: London, UK, 2022; pp. 900–906. [Google Scholar]
- Brandis, A.; Kraus, I.; Petrovčič, S. Nonlinear Static Seismic Analysis and Its Application to Shallow Founded Buildings with Soil-Structure Interaction. Buildings 2022, 12, 2014. [Google Scholar] [CrossRef]
- Brandis, A.; Kraus, I.; Petrovčič, S. Simplified Numerical Analysis of Soil–Structure Systems Subjected to Monotonically Increasing Lateral Load. Appl. Sci. 2021, 11, 4219. [Google Scholar] [CrossRef]
- Wei, D.; Suizi, J. Restoring Force Model for Composite-Shear Wall with Concealed Bracings in Steel-Tube Frame. Buildings 2022, 12, 1315. [Google Scholar] [CrossRef]
- Forcellini, D. A Novel Framework to Assess Soil Structure Interaction (Ssi) Effects with Equivalent Fixed-Based Models. Appl. Sci. 2021, 11, 10472. [Google Scholar] [CrossRef]
- Qiao, H.; Guo, Z.; Chen, Y.; Zhang, M.; Qiu, H.; Wang, Z. Anti-Progressive Collapse Analysis for Plane Steel Frame under Impact Load. J. Vib. Shock. 2022, 41, 176–184. [Google Scholar] [CrossRef]
- Kumar, A.; Muley, N.; Murnal, P.; Matsagar, V.A. Progressive Collapse Potential of Steel Frames Sustaining Post-Hazard Support-Yielding. In Recent Advances in Computational Mechanics and Simulations; Lecture Notes in Civil Engineering; Springer: Singapore, 2021; Volume 103. [Google Scholar]
- Li, G.Q.; Zhang, J.Z.; Li, L.L.; Jiang, B.H.; Yang, T.C.; Jiang, J. Progressive Collapse Resistance of Steel Framed Buildings under Extreme Events. Adv. Steel Constr. 2021, 17, 318–330. [Google Scholar] [CrossRef]
- Alekseytsev, A.V. Mechanical Safety of Reinforced Concrete Frames under Complex Emergency Actions. Mag. Civ. Eng. 2021, 103, 10306. [Google Scholar] [CrossRef]
- Wei, J.P.; Tian, L.M.; Hao, J.P.; Li, W.; Zhang, C.B.; Li, T.J. Novel Principle for Improving Performance of Steel Frame Structures in Column-Loss Scenario. J. Constr. Steel. Res. 2019, 163, 105768. [Google Scholar] [CrossRef]
- Bregoli, G.; Vasdravellis, G.; Karavasilis, T.L.; Cotsovos, D.M. Static and Dynamic Tests on Steel Joints Equipped with Novel Structural Details for Progressive Collapse Mitigation. Eng. Struct. 2021, 232, 111829. [Google Scholar] [CrossRef]
- Wang, F.; Yang, J.; Wang, X.E.; Azim, I. Study on Progressive Collapse Behaviour of Steel-Framed Substructures with Sheathed CFS Stud Infill Walls. J. Build. Eng. 2021, 42, 102720. [Google Scholar] [CrossRef]
- Qiu, L.; Lin, F.; Wu, K.; Gu, X. Progressive Collapse Resistance of RC T-Beam Cable Subassemblages under a Middle-Column-Removal Scenario. J. Build. Eng. 2021, 42, 102814. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, L.; Lin, K.; Li, Y. Improvement to Composite Frame Systems for Seismic and Progressive Collapse Resistance. Eng. Struct. 2019, 186, 227–242. [Google Scholar] [CrossRef]
- Hadi, M.N.S.; Alrudaini, T.M.S. A New Cable System to Prevent Progressive Collapse of Reinforced Concrete Buildings. In Proceedings of the Structures Congress 2012, Chicago, IL, USA, 29–31 March 2012. [Google Scholar]
- Kiakojouri, F.; De Biagi, V.; Chiaia, B.; Sheidaii, M.R. Strengthening and Retrofitting Techniques to Mitigate Progressive Collapse: A Critical Review and Future Research Agenda. Eng. Struct. 2022, 262, 114274. [Google Scholar] [CrossRef]
- Radwan, M.; Kövesdi, B. Equivalent Geometric Imperfections for Local Buckling of Slender Box-Section Columns. Period. Polytech. Civ. Eng. 2021, 65, 1279–1287. [Google Scholar] [CrossRef]
- Rzeszut, K. Post-Buckling Behaviour of Steel Structures with Different Types of Imperfections. Appl. Sci. 2022, 12, 9018. [Google Scholar] [CrossRef]
- Qu, H.; Huo, J.; Li, A.; Jiang, Y.; Liu, Y. Experimental Study on Impact Behaviour of Steel Plane Tubular Frames. Thin-Walled Struct. 2017, 111, 210–223. [Google Scholar] [CrossRef]
- Alekseytsev, A.V.; Kurchenko, N.S. Safety of Reinforced Concrete Columns: Effect of Initial Imperfections and Material Deterioration under Emergency Actions. Buildings 2023, 13, 1054. [Google Scholar] [CrossRef]
- Oladazimi, A.; Mansour, S.; Hosseinijou, S.A.; Majdfaghihi, M.H. Sustainability Identification of Steel and Concrete Construction Frames with Respect to Triple Bottom Line. Buildings 2021, 11, 565. [Google Scholar] [CrossRef]
- Meshref, A.; El-Dash, K.; Basiouny, M.; El-Hadidi, O. Implementation of a Life Cycle Cost Deep Learning Prediction Model Based on Building Structure Alternatives for Industrial Buildings. Buildings 2022, 12, 502. [Google Scholar] [CrossRef]
- Savin, S.; Kolchunov, V.; Fedorova, N.; Tuyen Vu, N. Experimental and Numerical Investigations of RC Frame Stability Failure under a Corner Column Removal Scenario. Buildings 2023, 13, 908. [Google Scholar] [CrossRef]
- Tamrazyan, A.; Alekseytsev, A. Evolutionary Optimization of Reinforced Concrete Beams, Taking into Account Design Reliability, Safety and Risks during the Emergency Loss of Supports. In Proceedings of the E3S Web of Conferences, Tashkent, Uzbekistan, 18–21 April 2019; Volume 97. [Google Scholar] [CrossRef]
- Construction Regulations SP 22.13330.2016 “Soil Bases of Buildings and Structures”. N.M. Gersevanov NIIOSP—Institute of JSC SIC Construction. Approved: 16.12.2016 Ministry of Construction and Housing and Communal Services of the Russian Federation. Available online: https://meganorm.ru/Index2/1/4293747/4293747631.htm (accessed on 7 June 2023).
- Tamrazyan, A.; Alekseytsev, A.V. Optimization of Reinforced Concrete Beams under Local Mechanical and Corrosive Damage. Eng. Optim. 2022. [Google Scholar] [CrossRef]

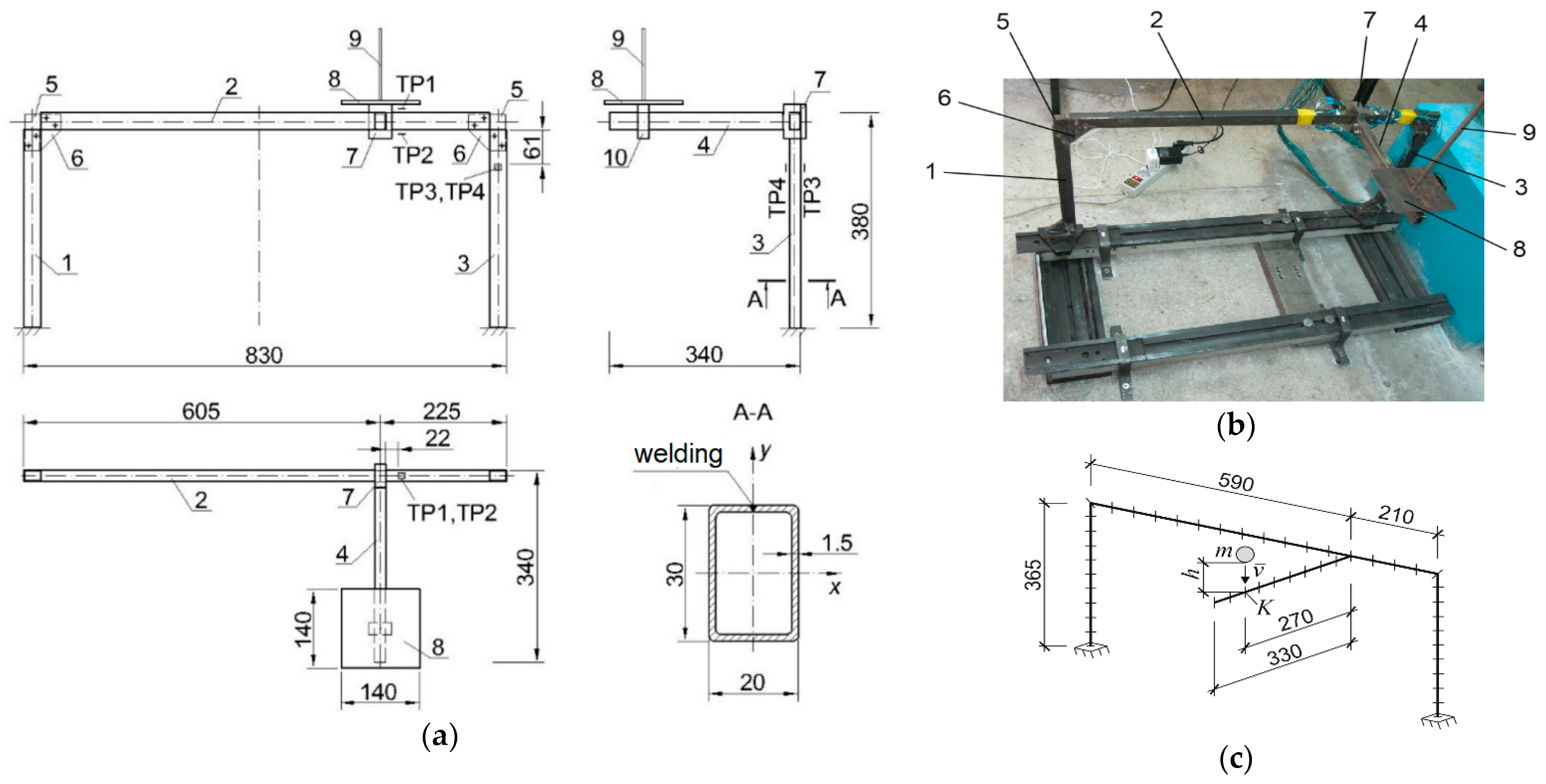




| h0, m | p = Fv, H·s | , MПa | ||
|---|---|---|---|---|
| Calculation | Experiment | Divergence, % | ||
| 0.05 | 48.51 | 55 | 62 | 11 |
| 0.100 | 68.60 | 76 | 83 | 8 |
| 0.15 | 84.01 | 93 | 102 | 9 |
| 0.20 | 97.01 | 107 | 119 | 10 |
| № | Spot of Application, Type of Effect | Condition of Survivability | Structural Changes | |
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| 1 | 1/A, 3/A: IH(t) | Available | - | |
| 2 | 2/A: IH(t) | Not available | ||
| 3 | A/1, A/3: IH(t) | - | Adding braces on the 1st floor of the edge frame | |
| 3a | A/1, A/3: IH(t) | Available | - | |
| 4 | B/1, B/3: IH(t) | Same | - | |
| 5 | 2/A: IG(t) all directions (pиc. 5,b) | Same | - | |
| 6 | 3/A: IG(t) all directions | Same | - | |
| 7 | B/3: IG(t) all directions | Same | - | |
| 8 | 2/D: AG(t), directions | 1 | Not available | Adding braces on the 2nd floor of the edge frame |
| 2 | Same | |||
| 3 | Available | - | ||
| 9…15 | 2/C, 3/C, 3/D, 2/C-D, 2/B-C, 3/C-D, 3/B-C: AG(t), directions | 1 | Available | - |
| 2 | Same | |||
| 3 | Same | - | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alekseytsev, A.V. Ensuring the Safety of Steel Moment Frames Subjected to Uncertain Impacts. Buildings 2023, 13, 2038. https://doi.org/10.3390/buildings13082038
Alekseytsev AV. Ensuring the Safety of Steel Moment Frames Subjected to Uncertain Impacts. Buildings. 2023; 13(8):2038. https://doi.org/10.3390/buildings13082038
Chicago/Turabian StyleAlekseytsev, Anatoly Victorovich. 2023. "Ensuring the Safety of Steel Moment Frames Subjected to Uncertain Impacts" Buildings 13, no. 8: 2038. https://doi.org/10.3390/buildings13082038
APA StyleAlekseytsev, A. V. (2023). Ensuring the Safety of Steel Moment Frames Subjected to Uncertain Impacts. Buildings, 13(8), 2038. https://doi.org/10.3390/buildings13082038