A New Ensemble Prediction Method for Reclaimed Asphalt Pavement (RAP) Mixtures Containing Different Constituents
Abstract
1. Introduction
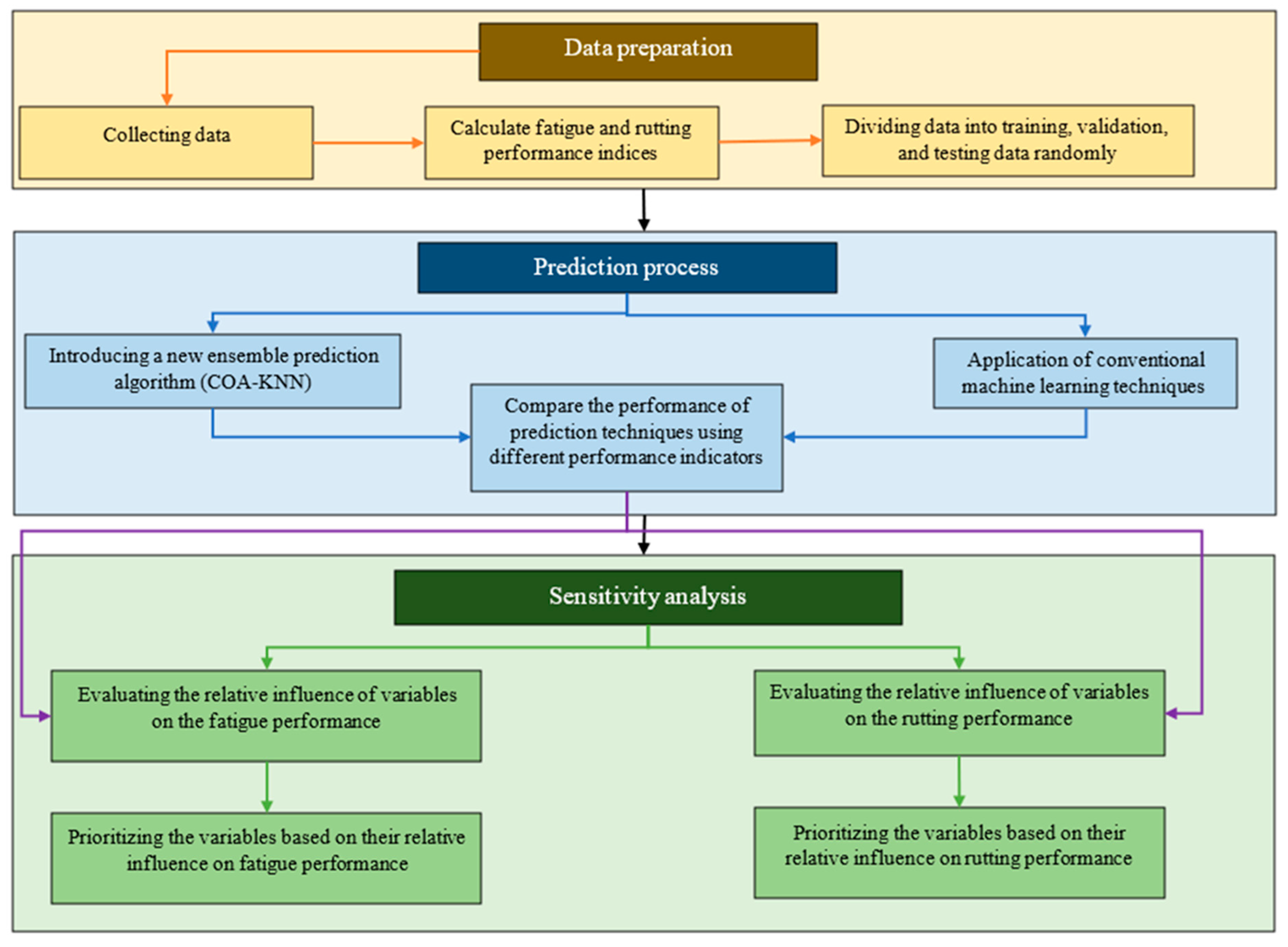
2. Methodology
- The process of data preparation
- The applied algorithms for the prediction procedure
- The description of machine learning performance indicators used to evaluate the accuracy of prediction algorithms
- The methods applied to analyze the effects of the model’s inputs on output variables
2.1. The Data Preparation Process
2.2. Prediction Algorithms
2.2.1. Decision Tree
2.2.2. Random Forest
2.2.3. Gradient Boosting
2.2.4. Multiple Linear Regression
2.2.5. The Proposed Prediction Method (COA-KNN)
2.3. The Evaluation of Algorithms Performance Using the Performance Indicators
2.4. Prioritizing Features on Asphalt Mixture Characteristics
3. Results and Discussion
- The performance of prediction algorithms on fatigue and rutting prediction is analyzed.
- The effects of each variable on fatigue and rutting characteristics are presented, and then the mentioned variables are prioritized based on their effects on the prediction performance.
- The error histogram of the fatigue and rutting models is presented.
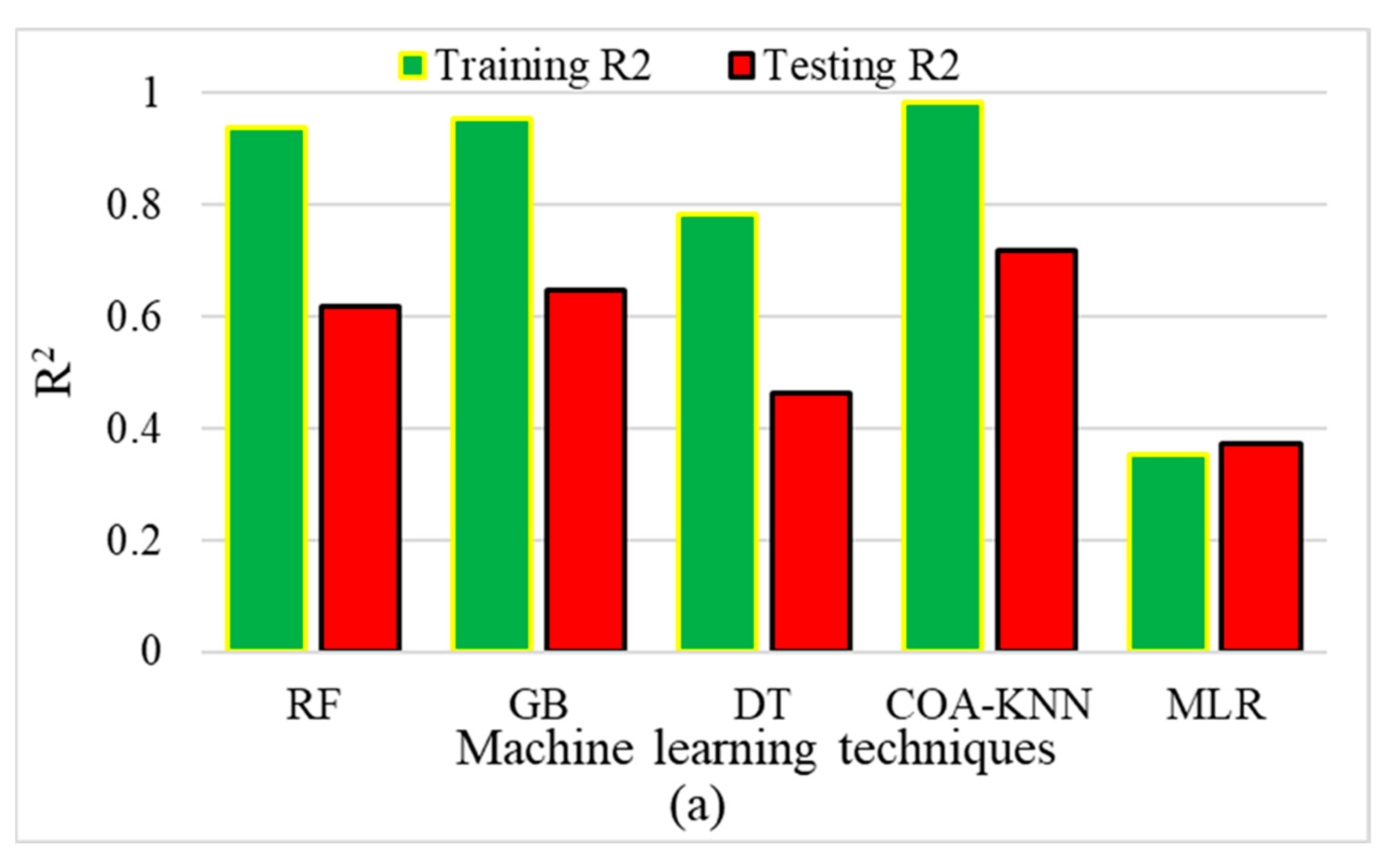
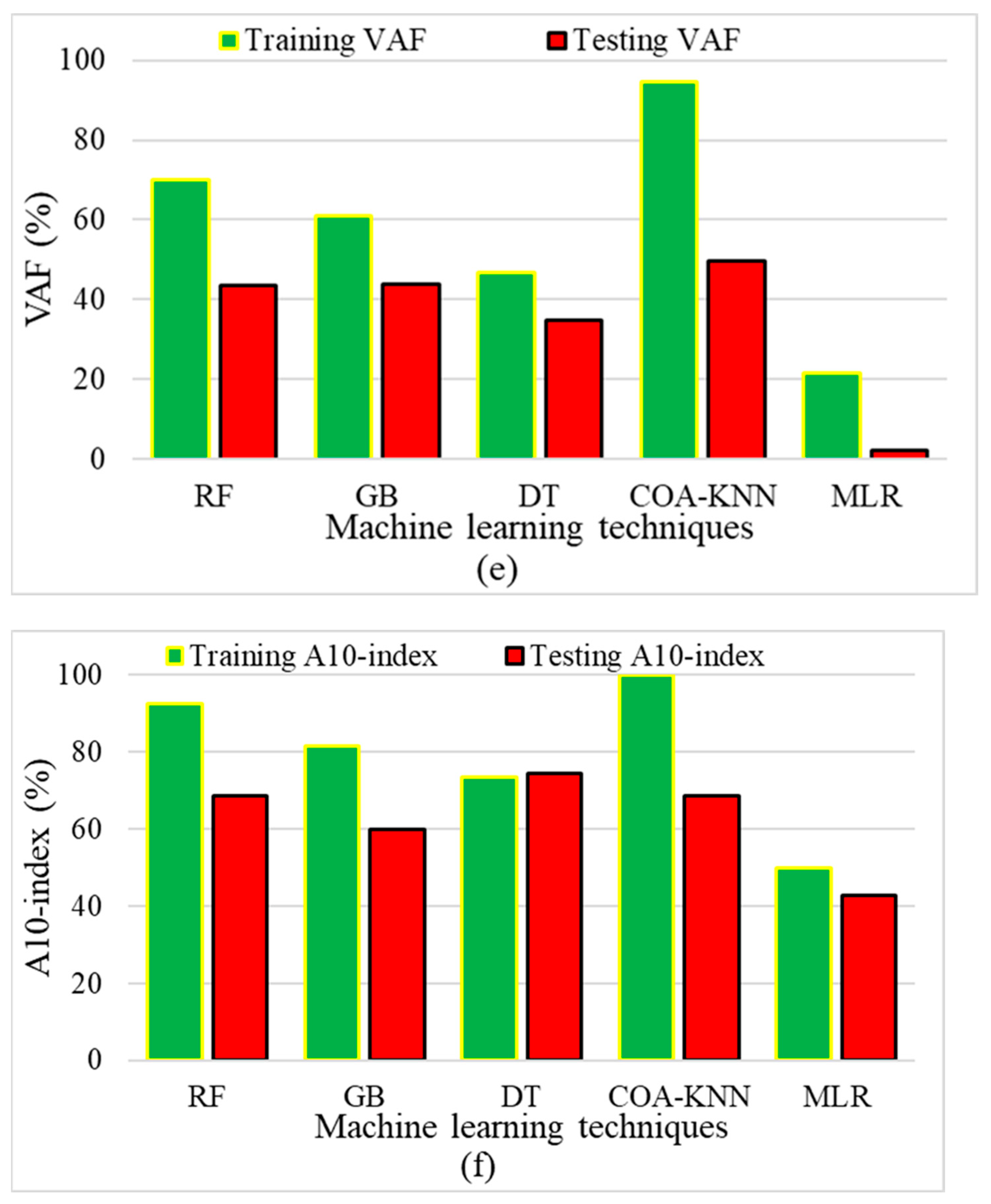
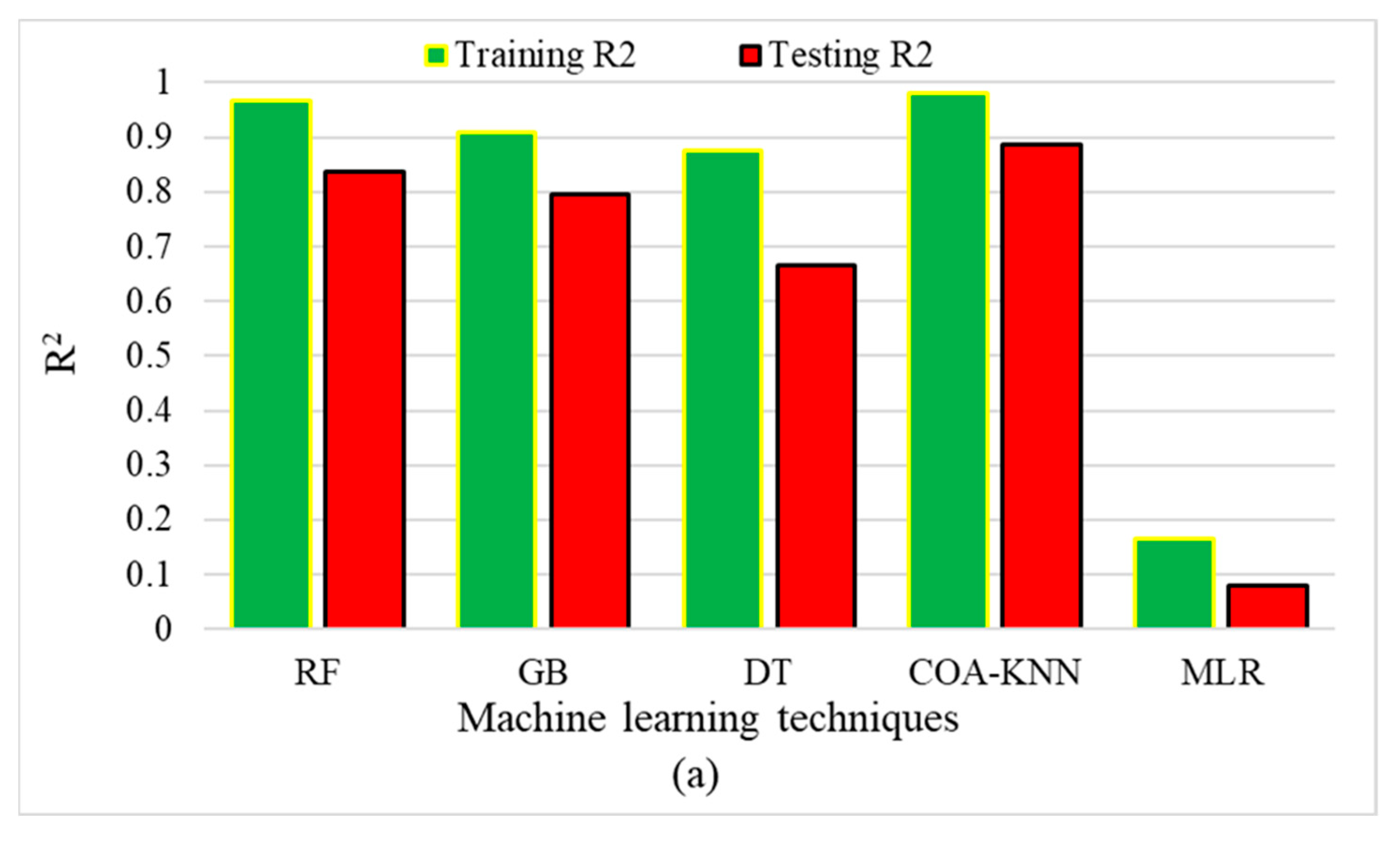
3.1. Performance of Algorithms
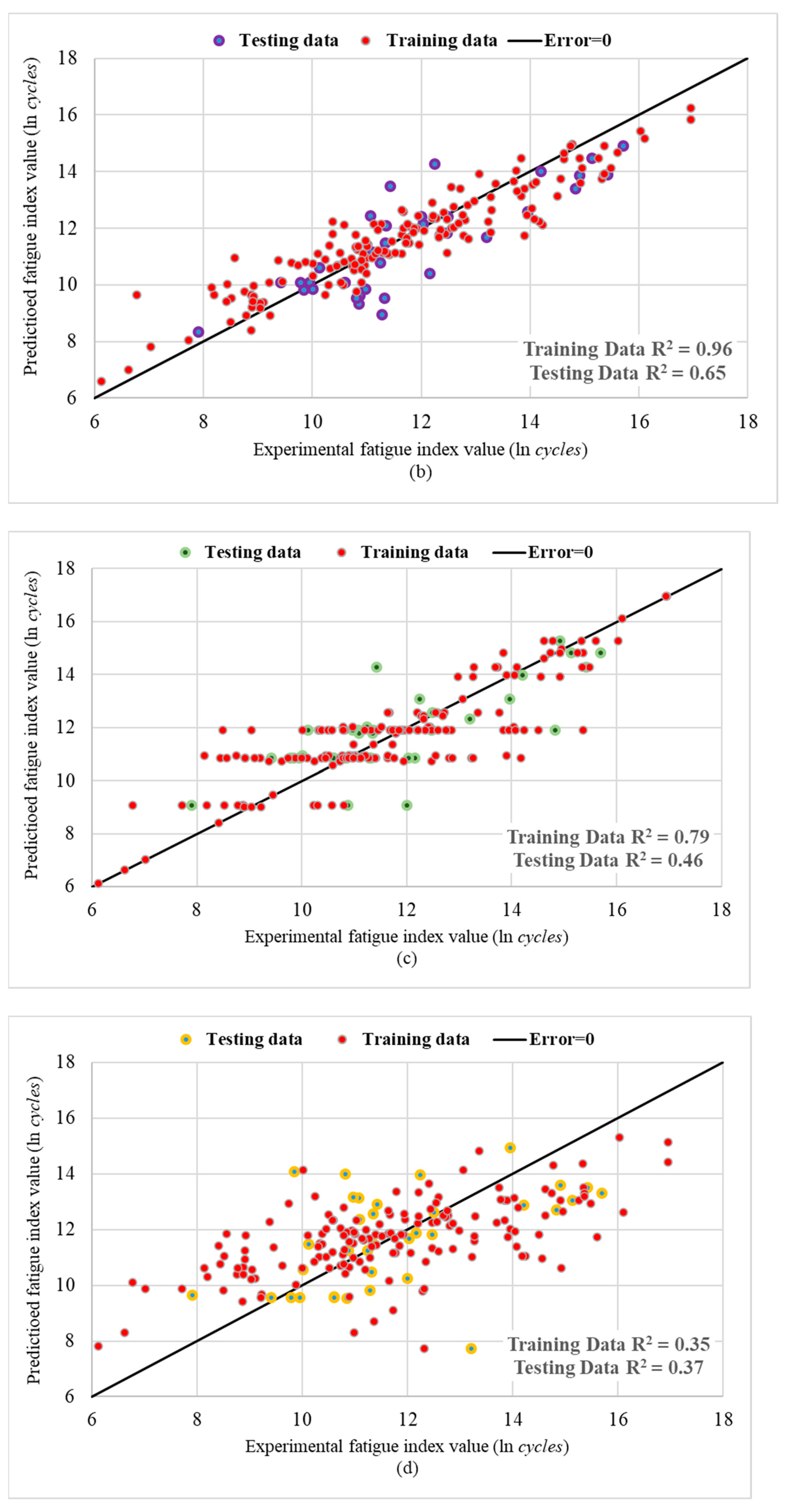
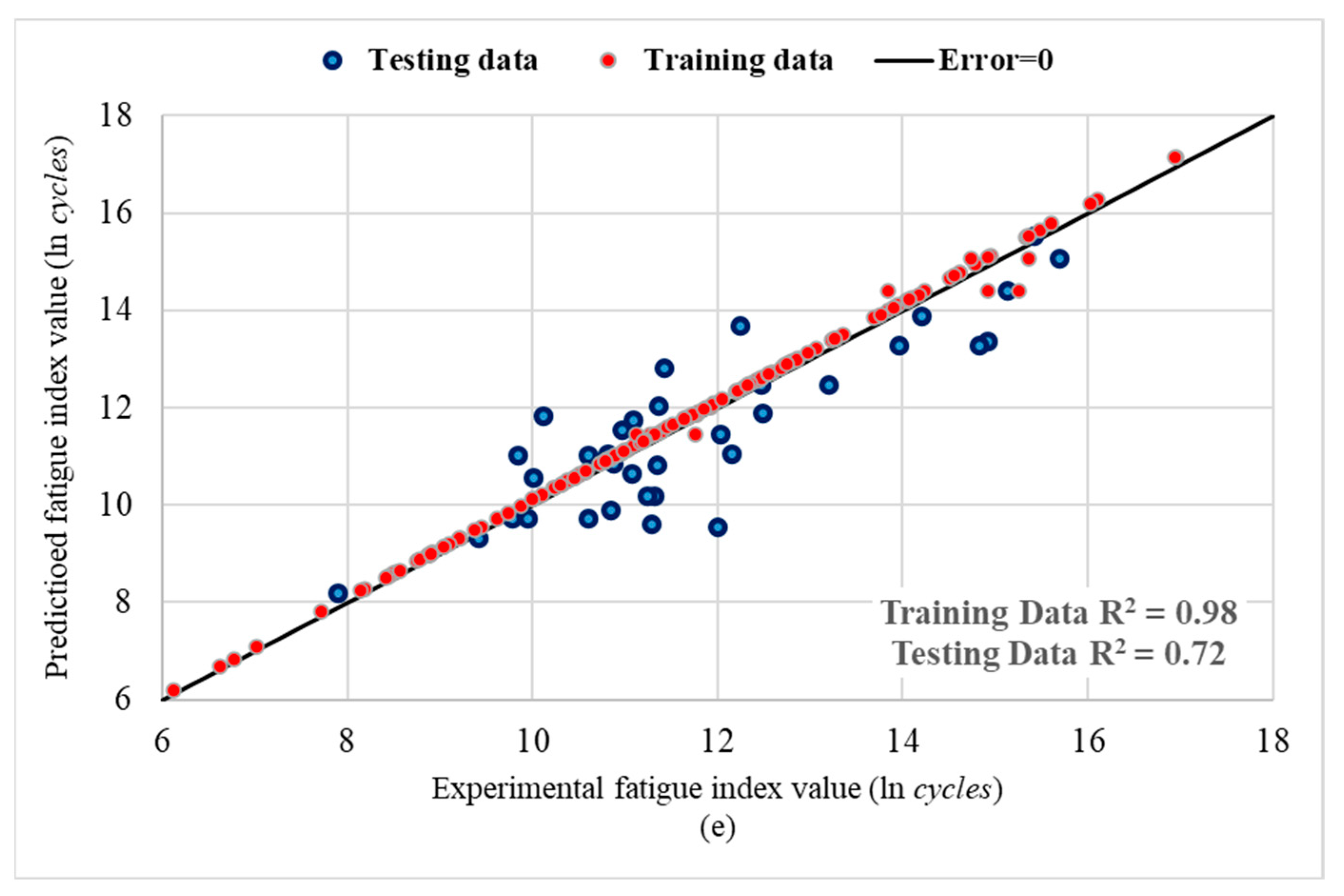
3.1.1. Performance of Machine Learning Algorithms—Fatigue
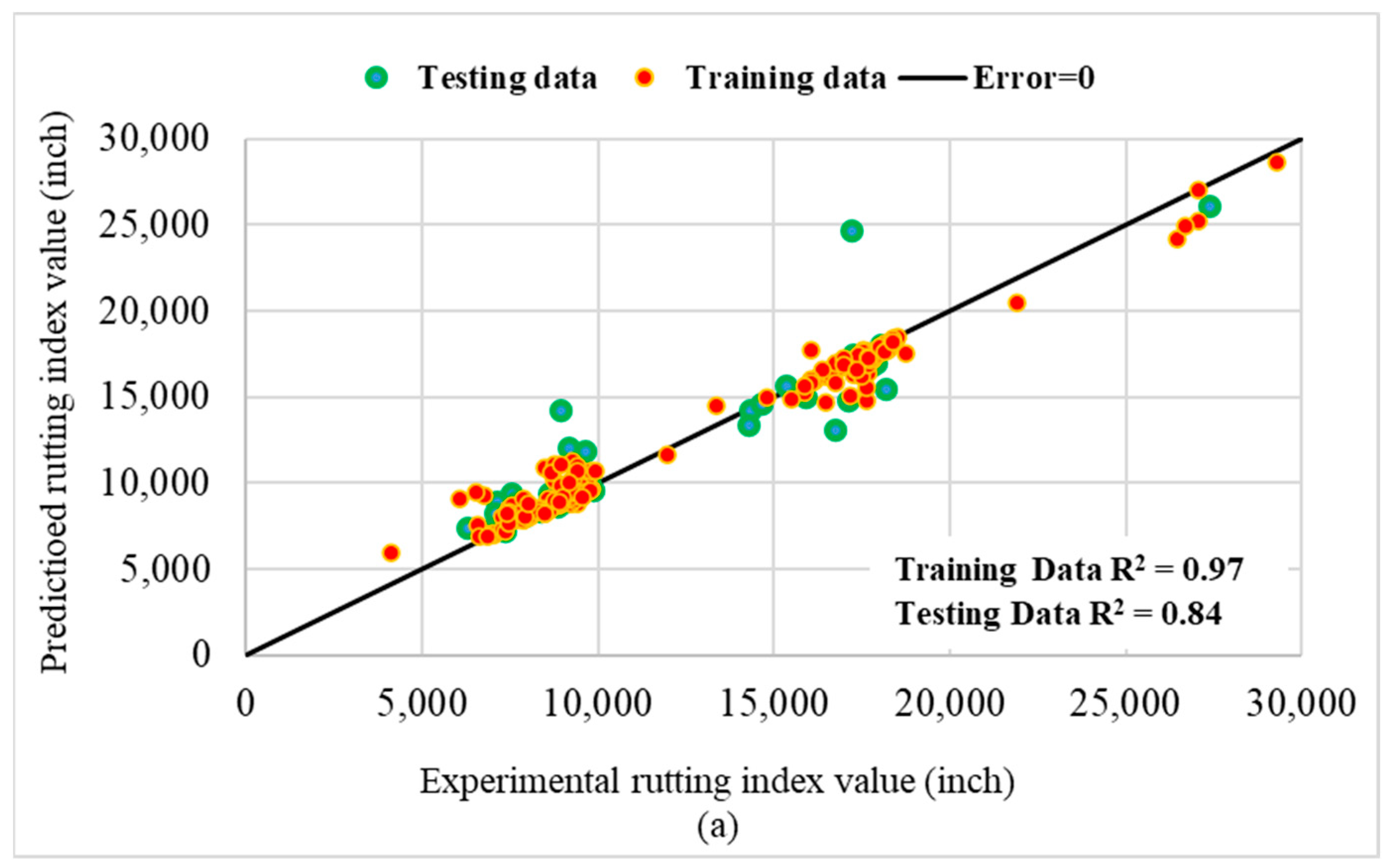
3.1.2. Performance of Machine Learning Algorithms—Rutting
3.2. Relative Influence of Variables
3.2.1. Fatigue Input Feature Performance
3.2.2. Rutting Input Feature Performance
3.3. Error Histogram
3.3.1. Accuracy of the Machine Learning Methods—Fatigue Prediction
3.3.2. Accuracy of the Machine Learning Methods—Rutting Prediction
4. Conclusions
- The R2 values of COA-KNN test data are 0.07, 0.10, 0.26, and 0.35 more than that of the gradient boosting, random forest, decision tree, and multiple linear regression, respectively, in the fatigue performance prediction.
- Applying COA-KNN to the fatigue database reduces the MAE test data by 0.01, 0.02, 0.04, and 0.07 ln (cycles) compared to gradient boosting, random forest, decision tree, and multiple linear regression, respectively.
- COA-KNN MAPE test data are 0.04%, 0.11%, 0.21%, and 0.38% lower than gradient boosting, random forest, decision tree, and multiple linear regression, respectively, in fatigue performance prediction.
- The MSE test data obtained using COA-KNN for fatigue prediction are 0.01, 0.01, 0.03, and 0.03 (ln (cycles))2 lower than gradient boosting, random forest, decision tree, and multiple linear regression, respectively.
- The R2 values of test data attained using COA-KNN for rutting performance are 0.050, 0.091, 0.222, and 0.806 more than random forest, gradient boosting, decision tree, and multiple linear regression, respectively.
- The MAE COA-KNN test data are 361.44, 890.44, 897.21, and 3123.89 inches lower than random forest, gradient boosting, decision tree, and multiple linear regression, respectively, in rutting performance prediction.
- Replacing COA-KNN on the fatigue database with random forest, decision tree, gradient boosting, and multiple linear regression can reduce the MAPE test data by 1.44%, 5.06%, 5.70%, and 22.60%, respectively.
- The MSE test data of COA-KNN are 1297190, 2506610, 7206180, and 19897280 inches2 less than the random forest, gradient boosting, decision tree, and multiple linear regression, respectively, for the rutting database.
- Considering the performance indicators, COA-KNN outperforms the other conventional algorithms in fatigue and rutting predictions. Moreover, random forest and gradient boosting methods had an appropriate accuracy, compared to other methods, in both datasets.
- Based on the importance weights of random forest and gradient boosting, the most effective features on fatigue performance of asphalt mixes containing RAP are the total binder content in the mix, the virgin binder content, and the intermediate-temperature PG of the virgin binder, respectively.
- According to the ranking of the variables on the rutting characteristic, the PG span of the virgin binder, total binder content, and the coarse-to-fine aggregate ratio are the most effective parameters on the rutting damage of recycled asphalt pavements.
- One of the limitations of this study is to apply a limited number of machine learning algorithms. Hence, it is recommended that other machine learning techniques, such as artificial neural networks or Gaussian Processes [108], will be applied to predict rutting and fatigue in future studies, and their performance will be compared with the proposed method in the current investigation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| RAP | Reclaimed asphalt pavement |
| COA-KNN | Coyote Optimization Algorithm and K-Nearest Neighbor |
| RF | Random Forest regression |
| GB | Gradient Boosting regression |
| DT | Decision Tree regression |
| MLR | Multiple Linear Regression |
| GHG | Global Greenhouse Gas |
| HMA | Hot Mix Asphalt |
| ANN | Artificial Neural Networks |
| BBO | Biogeography-Based Optimization algorithm |
| RRI | Rutting Resistance Index |
| PG | Performance Grade |
| RD | Rut Depth |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MSE | Mean Squared Error |
| NMAS | Nominal Maximum Aggregate Size |
| RAS | Reclaimed Asphalt Shingles |
| CR | Crumbed Rubber |
References
- Jahanbakhsh, H.; Karimi, M.M.; Jahangiri, B.; Nejad, F.M. Induction Heating and Healing of Carbon Black Modified Asphalt Concrete under Microwave Radiation. Constr. Build. Mater. 2018, 174, 656–666. [Google Scholar] [CrossRef]
- Karimi, M.M.; Jahanbakhsh, H.; Jahangiri, B.; Moghadas Nejad, F. Induced Heating-Healing Characterization of Activated Carbon Modified Asphalt Concrete under Microwave Radiation. Constr. Build. Mater. 2018, 178, 254–271. [Google Scholar] [CrossRef]
- Naseri, H.; Waygood, E.O.D.; Wang, B.; Patterson, Z.; Daziano, R.A. A Novel Feature Selection Technique to Better Predict Climate Change Stage of Change. Sustainability 2021, 14, 40. [Google Scholar] [CrossRef]
- Jahanbakhsh, H.; Karimi, M.M.; Naseri, H.; Nejad, F.M. Sustainable Asphalt Concrete Containing High Reclaimed Asphalt Pavements and Recycling Agents: Performance Assessment, Cost Analysis, and Environmental Impact. J. Clean. Prod. 2020, 244, 118837. [Google Scholar] [CrossRef]
- Karimi, M.M.; Amani, S.; Jahanbakhsh, H.; Jahangiri, B.; Alavi, A.H. Induced Heating-Healing of Conductive Asphalt Concrete as a Sustainable Repairing Technique: A Review. Clean. Eng. Technol. 2021, 4, 100188. [Google Scholar] [CrossRef]
- Kamali, Z.; Karimi, M.M.; Dehaghi, E.A.; Jahanbakhsh, H. Using Electromagnetic Radiation for Producing Reclaimed Asphalt Pavement (RAP) Mixtures: Mechanical, Induced Heating, and Sustainability Assessments. Constr. Build. Mater. 2022, 321, 126315. [Google Scholar] [CrossRef]
- Xing, C.; Li, M.; Liu, L.; Lu, R.; Liu, N.; Wu, W.; Yuan, D. A Comprehensive Review on the Blending Condition between Virgin and RAP Asphalt Binders in Hot Recycled Asphalt Mixtures: Mechanisms, Evaluation Methods, and Influencing Factors. J. Clean. Prod. 2023, 398, 136515. [Google Scholar] [CrossRef]
- Praticò, F.G.; Giunta, M.; Mistretta, M.; Gulotta, T.M. Energy and Environmental Life Cycle Assessment of Sustainable Pavement Materials and Technologies for Urban Roads. Sustainability 2020, 12, 704. [Google Scholar] [CrossRef]
- Diab, A.; Sangiorgi, C.; Ghabchi, R.; Zaman, M.; Wahaballa, A.M. Warm Mix Asphalt (WMA) Technologies: Benefits and Drawbacks—A Literature Review. In Functional Pavement Design; CRC Press: Boca Raton, FL, USA, 2017; pp. 1145–1154. [Google Scholar] [CrossRef]
- Abdollahi, S.F.; Karimi, M.M.; Jahanbakhsh, H.; Tabatabaee, N. Cracking Performance of Rubberized RAP Mixtures with Sasobit. Constr. Build. Mater. 2022, 319, 126090. [Google Scholar] [CrossRef]
- Ziari, H.; Aliha, M.R.M.; Moniri, A.; Saghafi, Y. Crack Resistance of Hot Mix Asphalt Containing Different Percentages of Reclaimed Asphalt Pavement and Glass Fiber. Constr. Build. Mater. 2020, 230, 117015. [Google Scholar] [CrossRef]
- Yousefi, A.; Behnood, A.; Nowruzi, A.; Haghshenas, H. Performance Evaluation of Asphalt Mixtures Containing Warm Mix Asphalt (WMA) Additives and Reclaimed Asphalt Pavement (RAP). Constr. Build. Mater. 2021, 268, 121200. [Google Scholar] [CrossRef]
- Jahanbakhsh, H.; Hosseini, P.; Nejad, F.M.; Habibi, M. Intermediate Temperature Fracture Resistance Evaluation of Cement Emulsified Asphalt Mortar. Constr. Build. Mater. 2019, 197, 1–11. [Google Scholar] [CrossRef]
- Behbahani, H.; Ayazi, M.J.; Moniri, A. Laboratory Investigation of Rutting Performance of Warm Mix Asphalt Containing High Content of Reclaimed Asphalt Pavement. Pet. Sci. Technol. 2017, 35, 1556–1561. [Google Scholar] [CrossRef]
- Colbert, B.; You, Z. The Determination of Mechanical Performance of Laboratory Produced Hot Mix Asphalt Mixtures Using Controlled RAP and Virgin Aggregate Size Fractions. Constr. Build. Mater. 2012, 26, 655–662. [Google Scholar] [CrossRef]
- Tran, N.H.; Taylor, A.; Willis, R. Effect of Rejuvenator on Performance Properties of HMA Mixtures with High RAP and RAS Contents. NCAT Rep. 2012, 1, 5–12. [Google Scholar]
- Izaks, R.; Haritonovs, V.; Klasa, I.; Zaumanis, M. Hot Mix Asphalt with High RAP Content. Procedia Eng. 2015, 114, 676–684. [Google Scholar] [CrossRef]
- Guduru, G.; Goli, A.K.; Matolia, S.; Kuna, K.K. Chemical and Performance Characteristics of Rejuvenated Bituminous Materials with High Reclaimed Asphalt Content. J. Mater. Civ. Eng. 2021, 33, 04020434. [Google Scholar] [CrossRef]
- Miró, R.; Valdés, G.; Martínez, A.; Segura, P.; Rodríguez, C. Evaluation of High Modulus Mixture Behaviour with High Reclaimed Asphalt Pavement (RAP) Percentages for Sustainable Road Construction. Constr. Build. Mater. 2011, 25, 3854–3862. [Google Scholar] [CrossRef]
- Behnood, A.; Daneshvar, D. A Machine Learning Study of the Dynamic Modulus of Asphalt Concretes: An Application of M5P Model Tree Algorithm. Constr. Build. Mater. 2020, 262, 120544. [Google Scholar] [CrossRef]
- Garbowski, T.; Pożarycki, A. Multi-Level Backcalculation Algorithm for Robust Determination of Pavement Layers Parameters. Inverse Probl. Sci. Eng. 2017, 25, 674–693. [Google Scholar] [CrossRef]
- Sarkhani Benemaran, R.; Esmaeili-Falak, M.; Javadi, A. Predicting Resilient Modulus of Flexible Pavement Foundation Using Extreme Gradient Boosting Based Optimised Models. Int. J. Pavement Eng. 2022, 1–20. [Google Scholar] [CrossRef]
- Esmaeili-Falak, M.; Benemaran, R.S. Ensemble Deep Learning-Based Models to Predict the Resilient Modulus of Modified Base Materials Subjected to Wet-Dry Cycles. Geomech. Eng. 2023, 32, 583–600. [Google Scholar]
- Ghasemi, P.; Aslani, M.; Rollins, D.K.; Williams, R.C. Principal Component Neural Networks for Modeling, Prediction, and Optimization of Hot Mix Asphalt Dynamics Modulus. Infrastructures 2019, 4, 53. [Google Scholar] [CrossRef]
- Behnood, A.; Mohammadi Golafshani, E. Predicting the Dynamic Modulus of Asphalt Mixture Using Machine Learning Techniques: An Application of Multi Biogeography-Based Programming. Constr. Build. Mater. 2021, 266, 120983. [Google Scholar] [CrossRef]
- Kaloush, K.E.; Witczak, M.W. Development of a Permanent to Elastic Strain Ratio Model for Asphalt Mixtures; Development of the 2002 Guide for the Design of New and Rehabilitated Pavement Structures. NCHRP 1-37 A, Inter Team Technical Report; Scientific Research Publishing: Wuhan, China, 2000. [Google Scholar]
- Ullah, S.; Tanyu, B.F.; Zainab, B. Development of an Artificial Neural Network (ANN)-Based Model to Predict Permanent Deformation of Base Course Containing Reclaimed Asphalt Pavement (RAP). Road Mater. Pavement Des. 2021, 22, 2552–2570. [Google Scholar] [CrossRef]
- Majidifard, H.; Jahangiri, B.; Rath, P.; Urra Contreras, L.; Buttlar, W.G.; Alavi, A.H. Developing a Prediction Model for Rutting Depth of Asphalt Mixtures Using Gene Expression Programming. Constr. Build. Mater. 2021, 267, 120543. [Google Scholar] [CrossRef]
- Mogawer, W.S.; Austerman, A.J.; Bonaquist, R. Determining the Influence of Plant Type and Production Parameters on Performance of Plant-Produced Reclaimed Asphalt Pavement Mixtures. Transp. Res. Rec. 2012, 2268, 71–81. [Google Scholar] [CrossRef]
- Elkashef, M.; Williams, R.C. Improving Fatigue and Low Temperature Performance of 100% RAP Mixtures Using a Soybean-Derived Rejuvenator. Constr. Build. Mater. 2017, 151, 345–352. [Google Scholar] [CrossRef]
- Mogawer, W.; Austerman, A.; Mohammad, L.; Kutay, M.E. Evaluation of High RAP-WMA Asphalt Rubber Mixtures. Road Mater. Pavement Des. 2013, 14, 129–147. [Google Scholar] [CrossRef]
- Valdés, G.; Pérez-Jiménez, F.; Miró, R.; Martínez, A.; Botella, R. Experimental Study of Recycled Asphalt Mixtures with High Percentages of Reclaimed Asphalt Pavement (RAP). Constr. Build. Mater. 2011, 25, 1289–1297. [Google Scholar] [CrossRef]
- Nabizadeh, H.; Haghshenas, H.F.; Kim, Y.R.; Aragão, F.T.S. Effects of Rejuvenators on High-RAP Mixtures Based on Laboratory Tests of Asphalt Concrete (AC) Mixtures and Fine Aggregate Matrix (FAM) Mixtures. Constr. Build. Mater. 2017, 152, 65–73. [Google Scholar] [CrossRef]
- Bonicelli, A.; Calvi, P.; Martinez-Arguelles, G.; Fuentes, L.; Giustozzi, F. Experimental Study on the Use of Rejuvenators and Plastomeric Polymers for Improving Durability of High RAP Content Asphalt Mixtures. Constr. Build. Mater. 2017, 155, 37–44. [Google Scholar] [CrossRef]
- Mogawer, W.S.; Booshehrian, A.; Vahidi, S.; Austerman, A. Evaluating the Effect of Rejuvenators on the Degree of Blending and Performance of High RAP, RAS, RAP/RAS Mixtures. Assoc. Asph. Paving Technol. AAPT 2013, 82, 403–436. [Google Scholar] [CrossRef]
- Tran, N.; Xie, Z.; Julian, G.; Taylor, A.; Willis, R.; Robbins, M.; Buchanan, S. Effect of a Recycling Agent on the Performance of High-RAP and High-RAS Mixtures: Field and Lab Experiments. J. Mater. Civ. Eng. 2017, 29, 04016178. [Google Scholar] [CrossRef]
- Abreu, L.P.F.; Oliveira, J.R.M.; Silva, H.M.R.D.; Fonseca, P.V. Recycled Asphalt Mixtures Produced with High Percentage of Different Waste Materials. Constr. Build. Mater. 2015, 84, 230–238. [Google Scholar] [CrossRef]
- Cooper, S.B.; Rouge, B. Characterization of Hma Mixtures Containing High Recycled Asphalt Pavement Content with Crumb Rubber Additives; Louisiana State University and Agricultural & Mechanical College: Baton Rouge, LA, USA, 2008. [Google Scholar]
- Bueche, N.; Dumont, A.G.; Vanelstraete, A.; De Visscher, J.; Vansteenkiste, S.; Vervaecke, F.; Gaspar, L.; Thogersen, F. Laboratory and Alt-Evaluation of High Stiffness Underlayers With High Percentage of Re-Use as Developed in the NR2C-Project. In Proceedings of the 4th Eurasphalt and Eurobitume Congress, Copenhagen, Denmark, 21–23 May 2008. [Google Scholar]
- Büchler, S.; Falchetto, A.C.; Walther, A.; Riccardi, C.; Wang, D.; Wistuba, M.P. Wearing Course Mixtures Prepared with High Reclaimed Asphalt Pavement Content Modified by Rejuvenators. Transp. Res. Rec. 2018, 2672, 96–106. [Google Scholar] [CrossRef]
- Sabouri, M. Evaluation of Performance-Based Mix Design for Asphalt Mixtures Containing Reclaimed Asphalt Pavement (RAP). Constr. Build. Mater. 2020, 235, 117545. [Google Scholar] [CrossRef]
- Arshadi, A.; Steger, R.; Ghabchi, R.; Zaman, M.; Hobson, K.; Commuri, S. Performance Evaluation of Plant-Produced Warm Mix Asphalts Containing RAP and RAS. Asph. Paving Technol. Assoc. Asph. Paving Technol.-Proc. Tech. Sess. 2017, 86, 403–425. [Google Scholar] [CrossRef]
- Daniel, J.S.; Mogawer, W.S. Determining the Effective PG Grade of Binder in RAP Mixes; The New England Transportation Consortium: Concord, NH, USA, 2010. [Google Scholar]
- Tavakol, M.; Hossain, M.; Heptig, B. Minimum Virgin Binder Content Needed in Recycled Superpave Mixtures to Resist Fatigue Cracking and Moisture Damage. J. Mater. Civ. Eng. 2018, 30, 04018126. [Google Scholar] [CrossRef]
- Vahidi, S.; Mogawer, W.S.; Booshehrian, A. Effects of GTR and Treated GTR on Asphalt Binder and High-RAP Mixtures. J. Mater. Civ. Eng. 2014, 26, 721–727. [Google Scholar] [CrossRef]
- Pasetto, M.; Giacomello, G.; Pasquini, E. Effectiveness of Rejuvenators for Asphalt Mixtures with High Reclaimed Asphalt Pavement Content in Cold Climates. In Proceedings of the International Symposium on Asphalt Pavement & Environment, Padua, Italy, 11–13 September 2019; pp. 3–13. [Google Scholar]
- Ozer, H.; Al-Qadi, I.; Kanaan, A.; Lippert, D. Performance Characterization of Asphalt Mixtures at High Asphalt Binder Replacement with Recycled Asphalt Shingles. Transp. Res. Rec. 2013, 2371, 105–112. [Google Scholar] [CrossRef]
- Haghshenas, H.; Nabizadeh, H.; Kim, Y.-R.; Santosh, K. Research on High-RAP Asphalt Mixtures with Rejuvenators and WMA Additives; University of Nebraska: Lincoln, NE, USA, 2019. [Google Scholar]
- Sabahfar, N.; Ahmed, A.; Aziz, S.R.; Hossain, M. Cracking Resistance Evaluation of Mixtures with High Percentages of Reclaimed Asphalt Pavement. J. Mater. Civ. Eng. 2017, 29, 06016022. [Google Scholar] [CrossRef]
- Ahmed, A. Evaluation of Cracking Potential of Superpave Mixtures with High Reclaimed Asphalt Pavement Content. Master’s Thesis, Kansas State University, Manhattan, KS, USA, 2015. [Google Scholar]
- Cong, P.; Zhang, Y.; Liu, N. Investigation of the Properties of Asphalt Mixtures Incorporating Reclaimed SBS Modified Asphalt Pavement. Constr. Build. Mater. 2016, 113, 334–340. [Google Scholar] [CrossRef]
- Mogawer, W.S.; Fini, E.H.; Austerman, A.J.; Booshehrian, A.; Zada, B. Performance Characteristics of High Reclaimed Asphalt Pavement Containing Bio-Modifier. Road Mater. Pavement Des. 2016, 17, 753–767. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, C.; Chen, T.; Zhang, W.; Yao, K.; Fan, C.; Liang, M.; Guo, C.; Yao, Z. Evaluation on the Mechanical Performance of Recycled Asphalt Mixtures Incorporated with High Percentage of RAP and Self-Developed Rejuvenators. Constr. Build. Mater. 2021, 269, 121337. [Google Scholar] [CrossRef]
- Ma, T.; Ding, X.; Zhang, D.; Huang, X.; Chen, J. Experimental Study of Recycled Asphalt Concrete Modified by High-Modulus Agent. Constr. Build. Mater. 2016, 128, 128–135. [Google Scholar] [CrossRef]
- Kocak, S.; Kutay, M.E. Use of Crumb Rubber in Lieu of Binder Grade Bumping for Mixtures with High Percentage of Reclaimed Asphalt Pavement. Road Mater. Pavement Des. 2017, 18, 116–129. [Google Scholar] [CrossRef]
- Baaj, H.; Ech, M.; Tapsoba, N.; Sauzeat, C.; Di Benedetto, H. Thermomechanical Characterization of Asphalt Mixtures Modified with High Contents of Asphalt Shingle Modifier (ASM®) and Reclaimed Asphalt Pavement (RAP). Mater. Struct./Mater. Constr. 2013, 46, 1747–1763. [Google Scholar] [CrossRef]
- Hossain, M.; Musty, H.Y.; Sabahfer, N. Use of High-Volume Reclaimed Asphalt Pavement (RAP) for Asphalt Pavement Rehabilitation Due to Increased Highway Truck Traffic from Freight Transportation; University of Nebraska: Lincoln, NE, USA, 2012. [Google Scholar]
- Sanchez, X.; Tighe, S.L. Steps towards the Detection of Reclaimed Asphalt Pavement in Superpave Mixtures. Road Mater. Pavement Des. 2019, 20, 1201–1214. [Google Scholar] [CrossRef]
- Ozer, H.; Al-Qadi, I.L.; Carpenter, S.H.; Aurangzeb, Q.; Roberts, G.L.; Trepanier, J. Evaluation of RAP Impact on Hot-Mix Asphalt Design and Performance. Asph. Paving Technol. Assoc. Asph. Paving Technol. Proc. Tech. Sess. 2009, 78, 317–348. [Google Scholar]
- Safi, F.R.; Al-Qadi, I.L.; Hossain, K.; Ozer, H. Total Recycled Asphalt Mixes: Characteristics and Field Performance. Transp. Res. Rec. 2019, 2673, 149–162. [Google Scholar] [CrossRef]
- Zhu, J.; Ma, T.; Fan, J.; Fang, Z.; Chen, T.; Zhou, Y. Experimental Study of High Modulus Asphalt Mixture Containing Reclaimed Asphalt Pavement. J. Clean. Prod. 2020, 263, 121447. [Google Scholar] [CrossRef]
- Boriack, P.; Katicha, S.W.; Flintsch, G.W. Laboratory Study on Effects of High Reclaimed Asphalt Pavement and Binder Content. Transp. Res. Rec. J. Transp. Res. Board 2014, 2445, 64–74. [Google Scholar] [CrossRef]
- Pérez-martínez, M.; Marsac, P.; Gabet, T.; Hammoum, F.; Lopes, M.; Pouget, S. Durability Analysis of Different Warm Mix Asphalt Containing Reclaimed Asphalt Pavement. In Proceedings of the XXVth WRC Seoul Seoul, Seoul, Republic of Korea, 2–6 November 2015; pp. 1–15. [Google Scholar]
- Xie, Z.; Tran, N.; Julian, G.; Taylor, A.; Blackburn, L.D. Performance of Asphalt Mixtures with High Recycled Contents Using Rejuvenators and Warm-Mix Additive: Field and Lab Experiments. J. Mater. Civ. Eng. 2017, 29, 04017190. [Google Scholar] [CrossRef]
- Tran, N.; Taylor, A.; Turner, P.; Holmes, C.; Porot, L. Effect of Rejuvenator on Performance Characteristics of High RAP Mixture. Road Mater. Pavement Des. 2017, 18, 183–208. [Google Scholar] [CrossRef]
- Al-Qadi, I.L.; Qazi, A.; Carpenter, S.H. Impact of High RAP Content on Structural and Performance Properties of Asphalt Mixtures; Research Report FHWA-ICT-12-002; University of Illinois, Urbana-Champaign: Champaign, IL, USA, 2012; pp. 1–107. [Google Scholar]
- Daneshvar, D.; Behnood, A. Estimation of the Dynamic Modulus of Asphalt Concretes Using Random Forests Algorithm. Int. J. Pavement Eng. 2020, 23, 250–260. [Google Scholar] [CrossRef]
- Huang, Y.H. Pavement Analysis and Design (Second Edition); Pearson: London, UK, 2004; ISBN 0131424734. [Google Scholar]
- European Standard EN 12697-24; Bituminous Mixtures—Test Methods for Hot Mix Asphalt—Part 24: Resistance to Fatigue. British Standards Institution: London, UK, 2005.
- Silva, H.M.R.D.; Oliveira, J.R.M.; Jesus, C.M.G. Are Totally Recycled Hot Mix Asphalts a Sustainable Alternative for Road Paving? Resour. Conserv. Recycl. 2012, 60, 38–48. [Google Scholar] [CrossRef]
- Zaumanis, M.; Arraigada, M.; Wyss, S.A.; Zeyer, K.; Cavalli, M.C.; Poulikakos, L.D. Performance-Based Design of 100% Recycled Hot-Mix Asphalt and Validation Using Traffic Load Simulator. J. Clean. Prod. 2019, 237, 117679. [Google Scholar] [CrossRef]
- Pradyumna, T.A.; Mittal, A.; Jain, P.K. Characterization of Reclaimed Asphalt Pavement (RAP) for Use in Bituminous Road Construction. Procedia Soc. Behav. Sci. 2013, 104, 1149–1157. [Google Scholar] [CrossRef]
- Cooper, S.B.; Mohammad, L.N.; Elseifi, M.A. Laboratory Performance of Asphalt Mixtures Containing Recycled Asphalt Shingles, Reclaimed Asphalt Pavement, and Recycling Agents. J. Mater. Civ. Eng. 2017, 29, D4016001. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Sahoo, U.C. Influence of Softer Binder and Rejuvenator on Bituminous Mixtures Containing Reclaimed Asphalt Pavement (RAP) Material. Int. J. Transp. Sci. Technol. 2021, 11, 46–59. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Sahoo, U.C. Evaluation of Recycled Asphalt Mixtures Rejuvenated with Madhuca Longifolia (Mahua) Oil. Int. J. Pavement Res. Technol. 2021, 14, 43–53. [Google Scholar] [CrossRef]
- Celauro, C.; Bernardo, C.; Gabriele, B. Production of Innovative, Recycled and High-Performance Asphalt for Road Pavements. Resour. Conserv. Recycl. 2010, 54, 337–347. [Google Scholar] [CrossRef]
- Maupin, G.W.; Diefenderfer, S.D.; Gillespie, J.S. Evaluation of Using Higher Percentages of Recycled Asphalt Pavement in Asphalt Mixes in Virginia; Virginia Transportation Research Council: Charlottesville, VA, USA, 2008. [Google Scholar]
- Widyatmoko, I. Mechanistic-Empirical Mixture Design for Hot Mix Asphalt Pavement Recycling. Constr. Build. Mater. 2008, 22, 77–87. [Google Scholar] [CrossRef]
- Hill, B.; Behnia, B.; Buttlar, W.G.; Reis, H. Evaluation of Warm Mix Asphalt Mixtures Containing Reclaimed Asphalt Pavement through Mechanical Performance Tests and an Acoustic Emission Approach. J. Mater. Civ. Eng. 2013, 25, 1887–1897. [Google Scholar] [CrossRef]
- Vargas, A. Evaluation of the Use of Reclaimed Asphalt Pavement in Stone Matrix Asphalt Mixtures. Master’s Thesis, Auburn University, Auburn, AL, USA, 2007. [Google Scholar]
- Pradhan, S.K.; Sahoo, U.C. Effectiveness of Pongamia Pinnata Oil as Rejuvenator for Higher Utilization of Reclaimed Asphalt (RAP) Material. Innov. Infrastruct. Solut. 2020, 5, 92. [Google Scholar] [CrossRef]
- Gedafa, D.S.; Berg, A.; Karki, B.; Saha, R.; Melaku, R.S. Cracking and Rutting Performance of Field and Laboratory HMA Mixes. In Proceedings of the Airfield and Highway Pavements 2019: Testing and Characterization of Pavement Materials—Selected Papers from the International Airfield and Highway Pavements Conference 2019, Chicago, IL, USA, 18 July 2019; pp. 12–19. [Google Scholar] [CrossRef]
- Aurangzeb, Q.; Al-Qadi, I.L.; Pine, W.J.; Trepanier, J.S.; Abuawad, I.M. Thermal Cracking Potential in Asphalt Mixtures with High RAP Contents. In Proceedings of the 7th RILEM International Conference on Cracking in Pavements, Delft, The Netherlands, 20–22 June 2012; Springer: Berlin/Heidelberg, Germany, 2012; Volume 4, pp. 1271–1280. [Google Scholar] [CrossRef]
- Al-Saffar, Z.H.; Yaacob, H.; Mohd Satar, M.K.I.; Mohd Usak, S.N.; Jaya, R.P.; Hassan, N.A.; Radeef, H.R.; Warid, M.N.M. Evaluating the Performance of Reclaimed Asphalt Pavement Incorporating PelletRAP as a Rejuvenator. In Proceedings of the 4th National Conference on Wind & Earthquake Engineering, Putrajaya, Malaysia, 16–17 October 2020; IOP Publishing: Bristol, UK, 2021; Volume 682. [Google Scholar] [CrossRef]
- Kim, S.; Shen, J.; Myung Jeong, M. Effects of Aggregate Size on the Rutting and Stripping Resistance of Recycled Asphalt Mixtures. J. Mater. Civ. Eng. 2018, 30, 04017280. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Sahoo, U.C. Effectiveness of Polanga Oil as Rejuvenator for Asphalt with High RAP Content. In Proceedings of the Airfield and Highway Pavements 2019: Testing and Characterization of Pavement Materials—Selected Papers from the International Airfield and Highway Pavements Conference 2019, Chicago, IL, USA, 18 July 2019; pp. 114–126. [Google Scholar] [CrossRef]
- Jamal; Hafeez, I.; Yaseen, G.; Aziz, A. Influence of Cereclor on the Performance of Aged Asphalt Binder. Int. J. Pavement Eng. 2020, 21, 1309–1320. [Google Scholar] [CrossRef]
- Al-Saffar, Z.H.; Yaacob, H.; Mohd Satar, M.K.I.; Putra Jaya, R. The Tailored Traits of Reclaimed Asphalt Pavement Incorporating Maltene: Performance Analyses. Int. J. Pavement Eng. 2020, 23, 1800–1813. [Google Scholar] [CrossRef]
- Zhang, W.; Shen, S.; Wu, S.; Mohammad, L.N. Prediction Model for Field Rut Depth of Asphalt Pavement Based on Hamburg Wheel Tracking Test Properties. J. Mater. Civ. Eng. 2017, 29, 04017098. [Google Scholar] [CrossRef]
- Rau, C.S.; Wu, S.C.; Chien, P.C.; Kuo, P.J.; Chen, Y.C.; Hsieh, H.Y.; Hsieh, C.H. Prediction of Mortality in Patients with Isolated Traumatic Subarachnoid Hemorrhage Using a Decision Tree Classifier: A Retrospective Analysis Based on a Trauma Registry System. Int. J. Environ. Res. Public Health 2017, 14, 1420. [Google Scholar] [CrossRef] [PubMed]
- Naseri, H.; Shokoohi, M.; Jahanbakhsh, H.; Karimi, M.M. A Novel Soft Computing Approach to Better Predict Flexible Pavements Roughness. SSRN 4191842. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4191842 (accessed on 2 May 2023).
- Wei, Z.; Meng, Y.; Zhang, W.; Peng, J.; Meng, L. Downscaling SMAP Soil Moisture Estimation with Gradient Boosting Decision Tree Regression over the Tibetan Plateau. Remote Sens. Environ. 2019, 225, 30–44. [Google Scholar] [CrossRef]
- Naseri, H.; Jahanbakhsh, H.; Moghadas Nejad, F. Developing a Novel Machine Learning Method to Predict the Compressive Strength of Fly Ash Concrete in Different Ages. AUT J. Civ. Eng. 2019, 4, 423–436. [Google Scholar] [CrossRef]
- Pierezan, J.; Maidl, G.; Massashi Yamao, E.; dos Santos Coelho, L.; Cocco Mariani, V. Cultural Coyote Optimization Algorithm Applied to a Heavy Duty Gas Turbine Operation. Energy Convers. Manag. 2019, 199, 111932. [Google Scholar] [CrossRef]
- Naseri, H.; Ehsani, M.; Golroo, A.; Moghadas Nejad, F. Sustainable Pavement Maintenance and Rehabilitation Planning Using Differential Evolutionary Programming and Coyote Optimisation Algorithm. Int. J. Pavement Eng. 2021, 23, 2870–2887. [Google Scholar] [CrossRef]
- Thanh Noi, P.; Kappas, M. Comparison of Random Forest, k-Nearest Neighbor, and Support Vector Machine Classifiers for Land Cover Classification Using Sentinel-2 Imagery. Sensors 2017, 18, 18. [Google Scholar] [CrossRef]
- Naseri, H.; Shokoohi, M.; Jahanbakhsh, H.; Golroo, A.; Gandomi, A.H. Evolutionary and Swarm Intelligence Algorithms on Pavement Maintenance and Rehabilitation Planning. Int. J. Pavement Eng. 2022, 23, 4649–4663. [Google Scholar] [CrossRef]
- Naseri, H.; Jahanbakhsh, H.; Hosseini, P.; Moghadas Nejad, F. Designing Sustainable Concrete Mixture by Developing a New Machine Learning Technique. J. Clean. Prod. 2020, 258, 120578. [Google Scholar] [CrossRef]
- Naseri, H.; Hosseini, P.; Jahanbakhsh, H.; Hosseini, P.; Gandomi, A.H. A Novel Evolutionary Learning to Prepare Sustainable Concrete Mixtures with Supplementary Cementitious Materials. Environ. Dev. Sustain. 2022, 25, 5831–5865. [Google Scholar] [CrossRef]
- Naseri, H.; Jahanbakhsh, H.; Khezri, K.; Shirzadi Javid, A.A. Toward Sustainability in Optimizing the Fly Ash Concrete Mixture Ingredients by Introducing a New Prediction Algorithm. Environ. Dev. Sustain. 2022, 24, 2767–2803. [Google Scholar] [CrossRef]
- Naseri, H.; Jahanbakhsh, H.; Foomajd, A.; Galustanian, N.; Karimi, M.M.; Waygood, E.O.D. A Newly Developed Hybrid Method on Pavement Maintenance and Rehabilitation Optimization Applying Whale Optimization Algorithm and Random Forest Regression. Int. J. Pavement Eng. 2022, 1–13. [Google Scholar] [CrossRef]
- Mrówczyński, D.; Gajewski, T.; Garbowski, T. Sensitivity Analysis of Open-Top Cartons in Terms of Compressive Strength Capacity. Materials 2023, 16, 412. [Google Scholar] [CrossRef]
- Sreedhar, S.; Coleri, E. Effects of Binder Content, Density, Gradation, and Polymer Modification on Cracking and Rutting Resistance of Asphalt Mixtures Used in Oregon. J. Mater. Civ. Eng. 2018, 30, 04018298. [Google Scholar] [CrossRef]
- FHA. Administration Superpave Fundamentals; FHA: Washington, DC, USA, 2008. [Google Scholar]
- Taher, B.M.; Mohamed, R.K.; Mahrez, A. A Review on Fatigue and Rutting Performance of Asphalt Mixes. Sci. Res. Essays 2011, 6, 670–682. [Google Scholar]
- Golalipour, A.; Jamshidi, E.; Niazi, Y.; Afsharikia, Z.; Khadem, M. Effect of Aggregate Gradation on Rutting of Asphalt Pavements. Procedia Soc. Behav. Sci. 2012, 53, 440–449. [Google Scholar] [CrossRef]
- Ahmed, M.A.; Attia, M.I.E. Impact of Aggregate Gradation and Type on Hot Mix Asphalt Rutting In Egypt. Int. J. Eng. Res. Appl. (IJERA) 2013, 3, 2249–2258. [Google Scholar]
- Garbowski, T. Stochastic Model Reduction Applied to Inverse Analysis. In Proceedings of the VI International Conference on Adaptive Modeling and Simulation ADMOS 2013, Lisbon, Portugal, 3–5 June 2013. [Google Scholar]
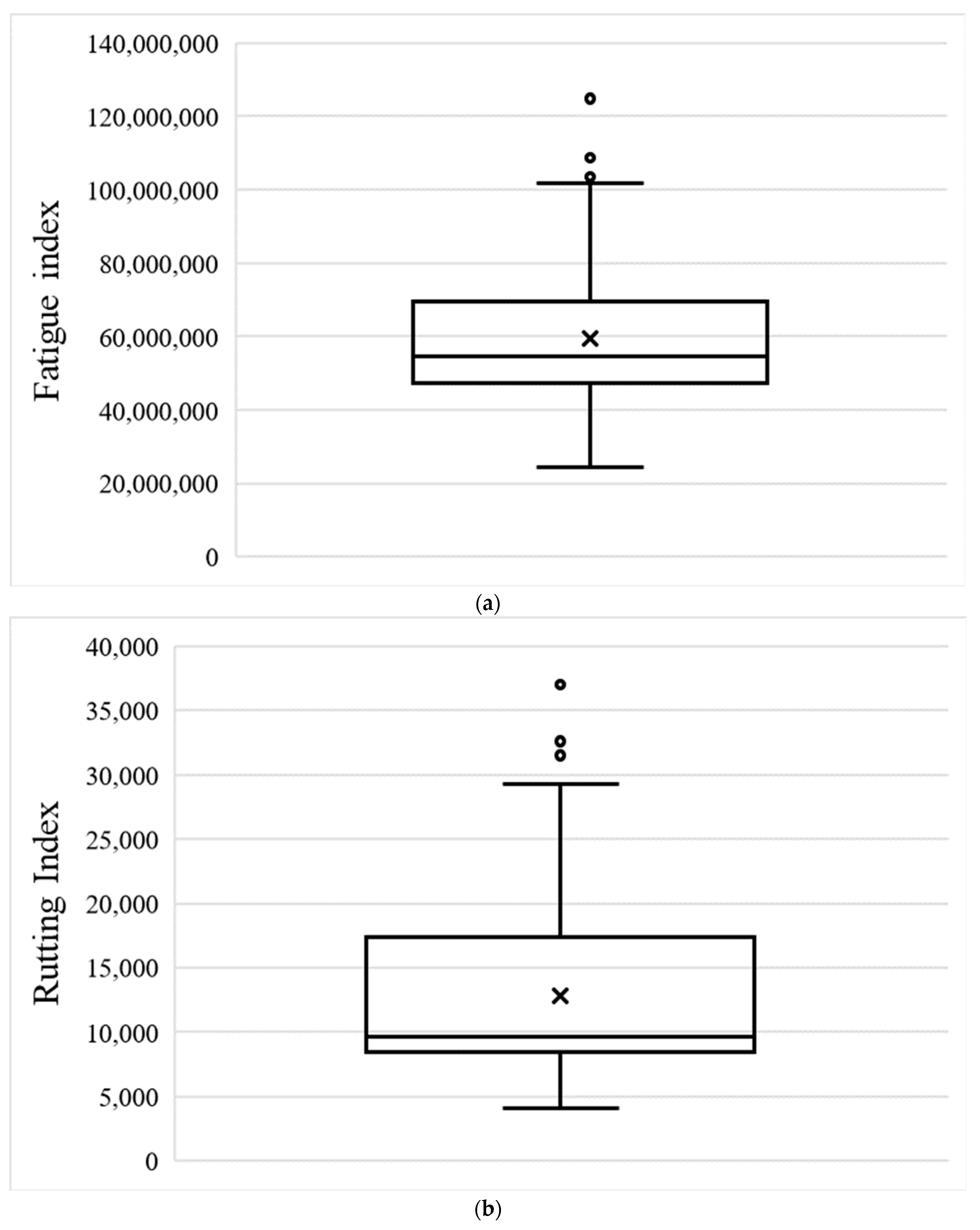






| Variable | Type | Description | Data | Pearson Correlation with Ln (Nf) | Maximum | Minimum | Average | Variance | Standard Error | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|
| Nf | Fatigue Index | Calculated fatigue index | Training | - | 0.91 | |||||
| Testing | - | 0.14 | ||||||||
| Ln (Nf) | Fatigue Index | Ln of Calculated fatigue index | Training | 1 | 18.64 | 17.01 | 17.84 | 0.31 | 0.02 | −0.01 |
| Testing | 1 | 18.50 | 17.25 | 17.89 | 0.29 | 0.05 | −0.10 | |||
| Temperature | Test Condition | Dynamic modulus test temperature (°C) | Training | 0.005 | 25.00 | 4.00 | 19.41 | 3.15 | 0.25 | 6.72 |
| Testing | 0.005 | 25.00 | 15.00 | 19.89 | 2.30 | 0.39 | 1.70 | |||
| RAP | RAP | RAP content (%) | Training | −0.292 | 100.00 | 0.00 | 31.76 | 21.95 | 1.75 | 1.20 |
| Testing | −0.384 | 70.00 | 0.00 | 30.74 | 18.68 | 3.16 | −0.31 | |||
| PGSpan | Binder | Span of PG of binder | Training | 0.232 | 98.00 | 62.00 | 86.47 | 9.28 | 0.74 | 0.39 |
| Testing | 0.127 | 98.00 | 62.00 | 87.71 | 8.76 | 1.48 | 0.60 | |||
| PGInter | Binder | Intermediate-temperature PG of binder | Training | −0.246 | 40.00 | 10.00 | 22.92 | 4.67 | 0.37 | 1.90 |
| Testing | −0.278 | 37.00 | 10.00 | 22.43 | 5.46 | 0.92 | 0.90 | |||
| Rejuvenator | Rejuvenator | Rejuvenator content (%) | Training | 0.052 | 13.80 | 0.00 | 1.30 | 3.25 | 0.26 | 4.45 |
| Testing | 0.010 | 12.00 | 0.00 | 1.45 | 3.16 | 0.53 | 3.87 | |||
| ACVirgin | Volumetric | Virgin asphalt content (%) | Training | 0.326 | 6.74 | 0.00 | 3.69 | 1.31 | 0.10 | 0.48 |
| Testing | 0.397 | 8.00 | 1.00 | 3.62 | 1.29 | 0.22 | 2.98 | |||
| ACRAP | Volumetric | RAP asphalt content (%) | Training | −0.117 | 7.90 | 0.00 | 4.27 | 1.93 | 0.15 | 0.98 |
| Testing | −0.245 | 8.90 | 0.00 | 4.39 | 1.99 | 0.34 | 1.61 | |||
| ACTotal | Volumetric | Total asphalt content (%) | Training | 0.366 | 8.00 | 3.70 | 5.32 | 0.76 | 0.06 | 0.54 |
| Testing | 0.428 | 8.00 | 4.00 | 5.28 | 0.75 | 0.13 | 3.54 | |||
| NMAS | Gradation | Nominal maximum aggregate size (mm) | Training | −0.217 | 20.00 | 4.75 | 13.62 | 3.55 | 0.28 | −0.13 |
| Testing | −0.145 | 20.00 | 4.75 | 13.87 | 3.56 | 0.60 | −0.01 | |||
| Fine agg. | Gradation | Aggregate smaller than 4.75 mm (%) | Training | 0.215 | 93.00 | 6.10 | 57.54 | 13.17 | 1.05 | 0.68 |
| Testing | −0.148 | 76.80 | 33.90 | 56.07 | 11.90 | 2.01 | −0.97 | |||
| Course agg./Fine agg. | Gradation | Aggregate larger than 4.75 mm/Aggregate smaller than 4.75 mm | Training | 0.149 | 13.29 | 0.06 | 1.69 | 1.39 | 0.11 | 31.89 |
| Testing | −0.214 | 3.31 | 0.51 | 1.47 | 0.74 | 0.12 | 0.24 |
| Variable | Type | Description | Data | Pearson Correlation with RRI | Maximum | Minimum | Average | Variance | Standard Error | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|
| RRI | Rutting Index | Calculated rutting index | Training | 1 | 37,007.90 | 4094.49 | 12,767.91 | 5666.04 | 450.77 | 1.88 |
| Testing | 1 | 27,401.60 | 6305.51 | 12,577.05 | 4975.55 | 853.30 | 0.23 | |||
| RAP | RAP | RAP content (%) | Training | 0.008 | 100.00 | 0.00 | 36.04 | 24.97 | 1.99 | 0.56 |
| Testing | −0.058 | 100.00 | 0.00 | 35.96 | 18.27 | 3.13 | 3.70 | |||
| PGSpan | Binder | Span of PG of binder | Training | −0.146 | 98.00 | 62.00 | 82.66 | 9.38 | 0.75 | −0.26 |
| Testing | −0.096 | 98.00 | 68.00 | 84.50 | 8.04 | 1.38 | 0.13 | |||
| PGHigh | Binder | High-temperature PG of binder | Training | −0.084 | 76.00 | 46.00 | 60.24 | 7.87 | 0.63 | −0.29 |
| Testing | −0.030 | 76.00 | 46.00 | 60.74 | 8.18 | 1.40 | −0.01 | |||
| Rejuvenator | Rejuvenator | Rejuvenator content (%) | Training | −0.091 | 15.00 | 0.00 | 1.88 | 3.40 | 0.27 | 2.08 |
| Testing | −0.081 | 9.28 | 0.00 | 0.84 | 2.41 | 0.41 | 7.55 | |||
| ACVirgin | Volumetric | Virgin asphalt content (%) | Training | −0.038 | 8.00 | 0.00 | 3.89 | 1.38 | 0.11 | 0.71 |
| Testing | −0.124 | 5.70 | 0.51 | 3.75 | 1.01 | 0.17 | 2.33 | |||
| ACRAP | Volumetric | RAP asphalt content (%) | Training | 0.063 | 7.90 | 0.00 | 3.94 | 1.85 | 0.15 | 0.59 |
| Testing | −0.265 | 6.20 | 0.00 | 4.55 | 1.31 | 0.22 | 6.97 | |||
| ACTotal | Volumetric | Total asphalt content (%) | Training | −0.191 | 8.00 | 3.70 | 5.54 | 0.76 | 0.06 | 0.64 |
| Testing | −0.402 | 6.60 | 4.00 | 5.40 | 0.61 | 0.10 | 0.04 | |||
| NMAS | Gradation | Nominal maximum aggregate size (mm) | Training | 0.091 | 25.00 | 4.75 | 14.69 | 5.27 | 0.42 | −0.47 |
| Testing | 0.346 | 25.00 | 4.75 | 13.41 | 3.79 | 0.65 | 1.85 | |||
| Fine agg. | Gradation | Aggregate smaller than 4.75 mm (%) | Training | 0.087 | 88.90 | 10.00 | 53.74 | 16.63 | 1.32 | −0.51 |
| Testing | −0.130 | 93.00 | 25.20 | 52.16 | 15.40 | 2.64 | 0.32 | |||
| Course agg./Fine agg. | Gradation | Aggregate larger than 4.75 mm /Aggregate smaller than 4.75 mm | Training | −0.212 | 9.00 | 0.12 | 1.10 | 0.95 | 0.08 | 29.89 |
| Testing | −0.085 | 2.97 | 0.08 | 1.11 | 0.69 | 0.12 | 1.21 |
| Random Forest | Gradient Boosting | Average | ||||||
|---|---|---|---|---|---|---|---|---|
| Input Features | Importance Weight | Ranking | Input Features | Importance Weight | Ranking | Input Features | Importance Weight | Ranking |
| ACTotal | 0.214 | 1 | ACTotal | 0.313 | 1 | ACTotal | 0.264 | 1 |
| ACVirgin | 0.167 | 2 | RAP | 0.123 | 2 | ACVirgin | 0.132 | 2 |
| PGInter | 0.116 | 3 | PGInter | 0.105 | 3 | PGInter | 0.110 | 3 |
| Temperature | 0.091 | 4 | ACVirgin | 0.097 | 4 | RAP | 0.104 | 4 |
| PGSpan | 0.086 | 5 | Temperature | 0.086 | 5 | Temperature | 0.088 | 5 |
| RAP | 0.085 | 6 | ACRAP | 0.078 | 6 | ACRAP | 0.076 | 6 |
| ACRAP | 0.074 | 7 | NMAS | 0.049 | 7 | PGSpan | 0.067 | 7 |
| Course agg./Fine agg. | 0.051 | 8 | PGSpan | 0.047 | 8 | Course agg./Fine agg. | 0.048 | 8 |
| Fine agg. | 0.048 | 9 | Course agg./Fine agg. | 0.044 | 9 | NMAS | 0.043 | 9 |
| NMAS | 0.038 | 10 | Fine agg. | 0.032 | 10 | Fine agg. | 0.040 | 10 |
| Rejuvenator | 0.031 | 11 | Rejuvenator | 0.024 | 11 | Rejuvenator | 0.027 | 11 |
| Random Forest | Gradient Boosting | Average | ||||||
|---|---|---|---|---|---|---|---|---|
| Input Features | Importance Weight | Ranking | Input Features | Importance Weight | Ranking | Input Features | Importance Weight | Ranking |
| PGSpan | 0.253 | 1 | PGSpan | 0.299 | 1 | PGSpan | 0.276 | 1 |
| Course agg./Fine agg. | 0.154 | 2 | ACTotal | 0.184 | 2 | ACTotal | 0.164 | 2 |
| ACTotal | 0.145 | 3 | RAP | 0.136 | 3 | Course agg./Fine agg. | 0.132 | 3 |
| ACRAP | 0.140 | 4 | Course agg./Fine agg. | 0.110 | 4 | RAP | 0.114 | 4 |
| RAP | 0.092 | 5 | Fine agg. | 0.096 | 5 | ACRAP | 0.092 | 5 |
| Fine agg. | 0.060 | 6 | PGHigh | 0.071 | 6 | Fine agg. | 0.078 | 6 |
| PGHigh | 0.051 | 7 | ACRAP | 0.045 | 7 | PGHigh | 0.061 | 7 |
| ACVirgin | 0.050 | 8 | ACVirgin | 0.042 | 8 | ACVirgin | 0.046 | 8 |
| NMAS | 0.049 | 9 | Rejuvenator | 0.011 | 9 | NMAS | 0.028 | 9 |
| Rejuvenator | 0.006 | 10 | NMAS | 0.006 | 10 | Rejuvenator | 0.008 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghavami, S.; Alipour, Z.; Naseri, H.; Jahanbakhsh, H.; Karimi, M.M. A New Ensemble Prediction Method for Reclaimed Asphalt Pavement (RAP) Mixtures Containing Different Constituents. Buildings 2023, 13, 1787. https://doi.org/10.3390/buildings13071787
Ghavami S, Alipour Z, Naseri H, Jahanbakhsh H, Karimi MM. A New Ensemble Prediction Method for Reclaimed Asphalt Pavement (RAP) Mixtures Containing Different Constituents. Buildings. 2023; 13(7):1787. https://doi.org/10.3390/buildings13071787
Chicago/Turabian StyleGhavami, Sadegh, Zeynab Alipour, Hamed Naseri, Hamid Jahanbakhsh, and Mohammad M. Karimi. 2023. "A New Ensemble Prediction Method for Reclaimed Asphalt Pavement (RAP) Mixtures Containing Different Constituents" Buildings 13, no. 7: 1787. https://doi.org/10.3390/buildings13071787
APA StyleGhavami, S., Alipour, Z., Naseri, H., Jahanbakhsh, H., & Karimi, M. M. (2023). A New Ensemble Prediction Method for Reclaimed Asphalt Pavement (RAP) Mixtures Containing Different Constituents. Buildings, 13(7), 1787. https://doi.org/10.3390/buildings13071787







