A Study on the Applicability and Accuracy of the Discrete Element Method for Plates Based on Parameter Sensitivity Analysis
Abstract
1. Introduction
2. Basic Theory of the DEM for a Plate
2.1. The Model of the DEM for a Plate
2.2. Calculation of Internal Forces in Contact Elements
3. Theory of Parameter Sensitivity Analysis
3.1. Single-Parameter Sensitivity Analysis
3.2. Multi-Parameter Sensitivity Analysis
3.2.1. Full Factorial Method
3.2.2. Orthogonal Design Method
4. Parameter Sensitivity Analysis
4.1. Influences of Single-Parameter Changes
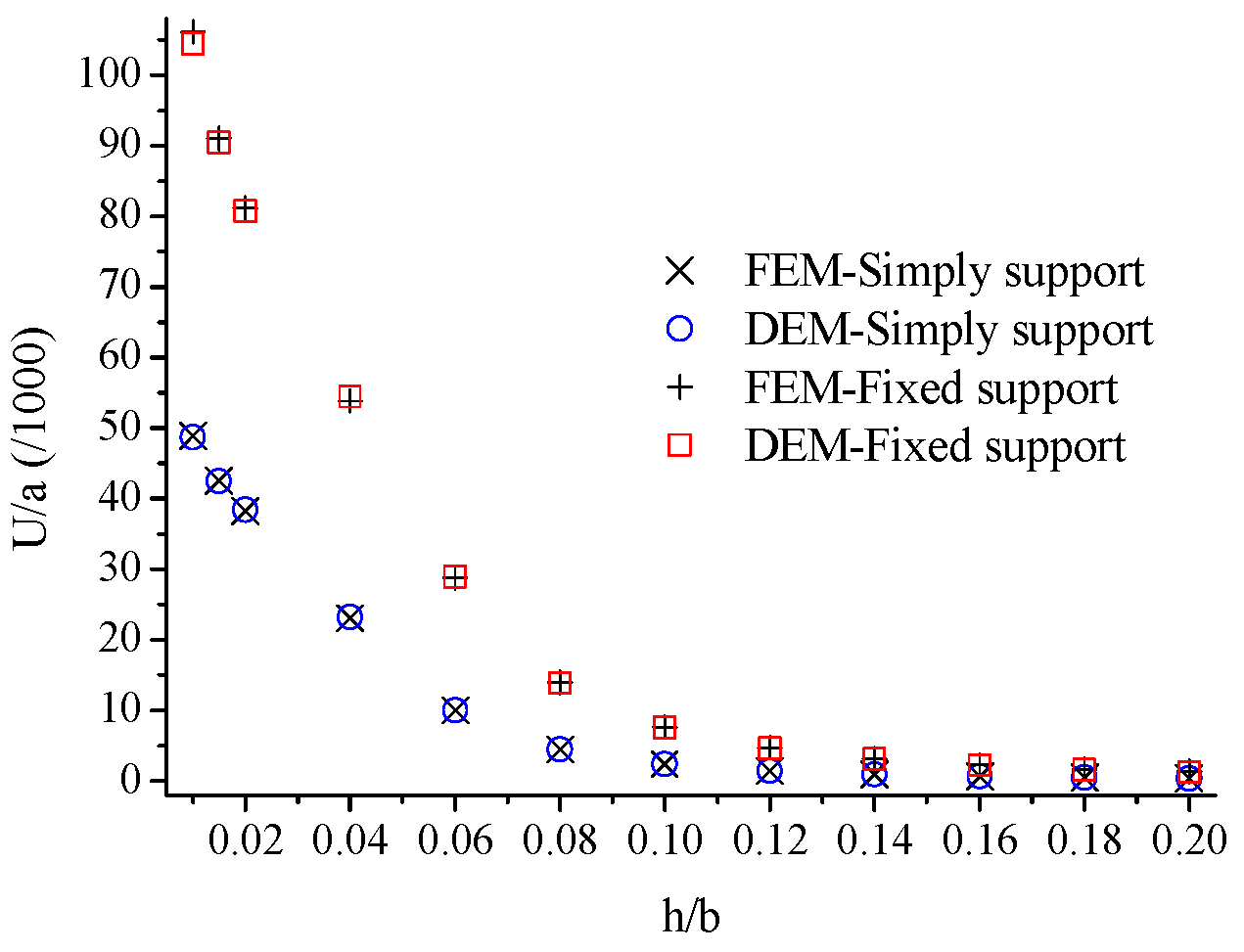
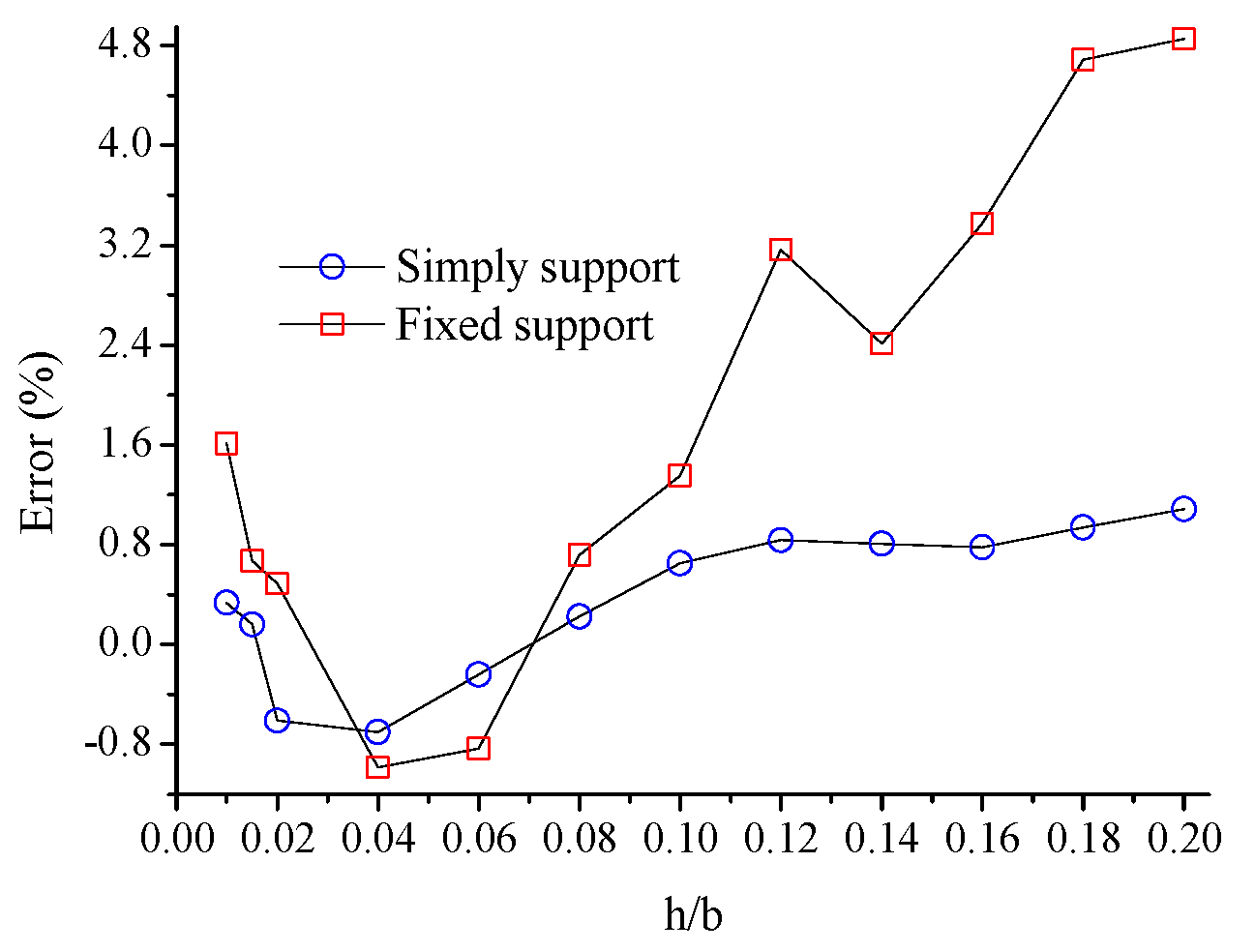
4.1.1. Thickness-to-Width Ratio
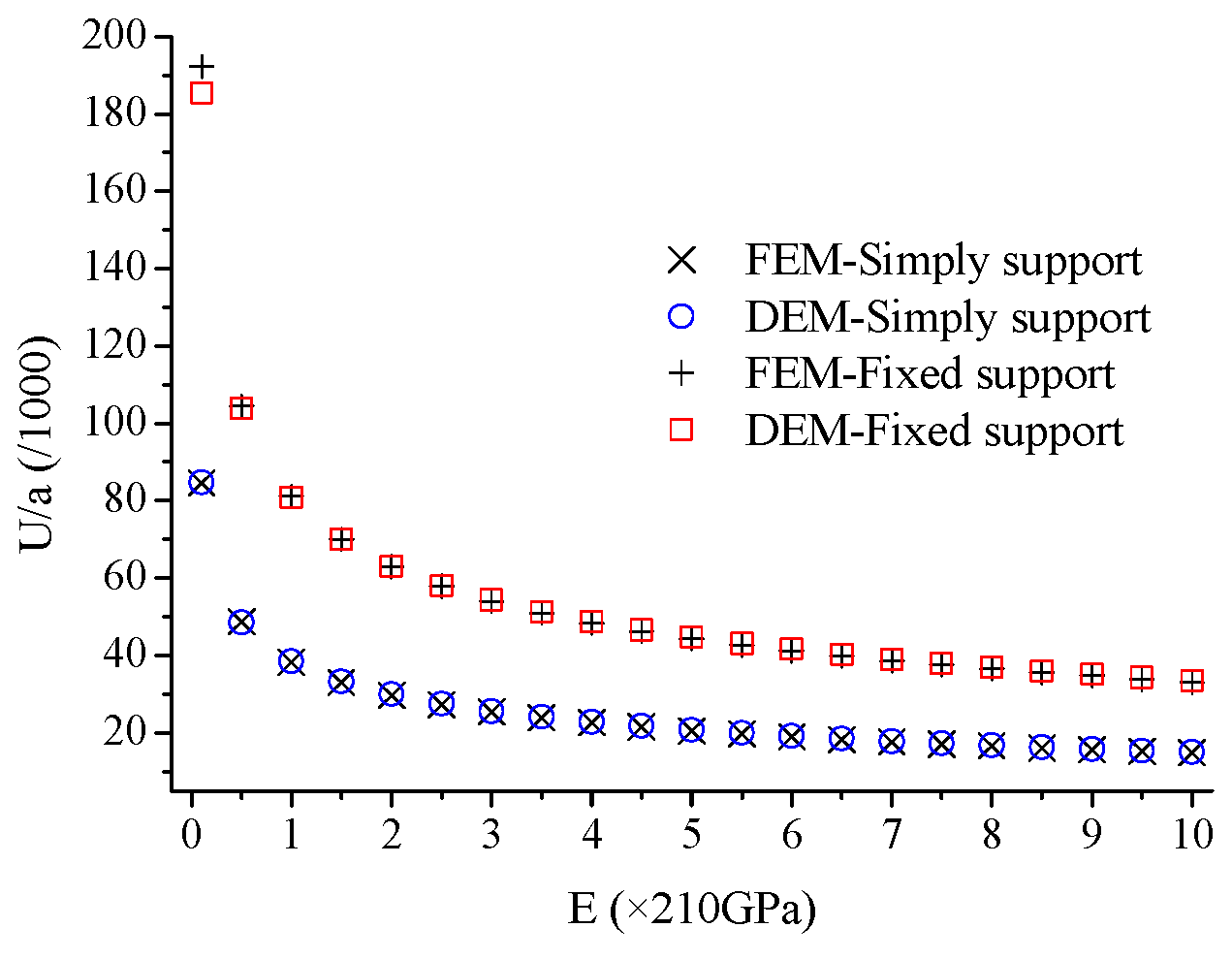
4.1.2. Elastic Modulus
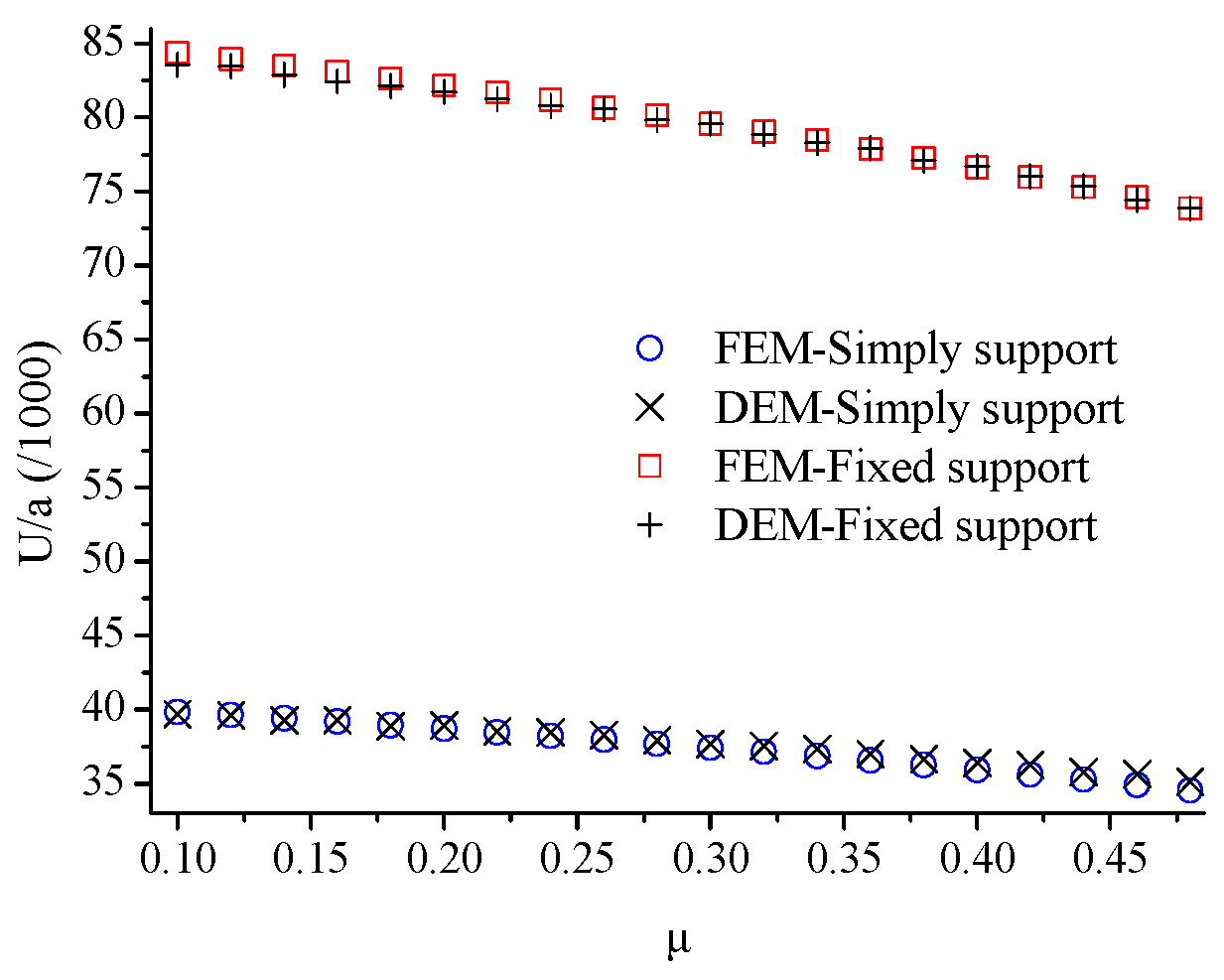
4.1.3. Poisson’s Ratio
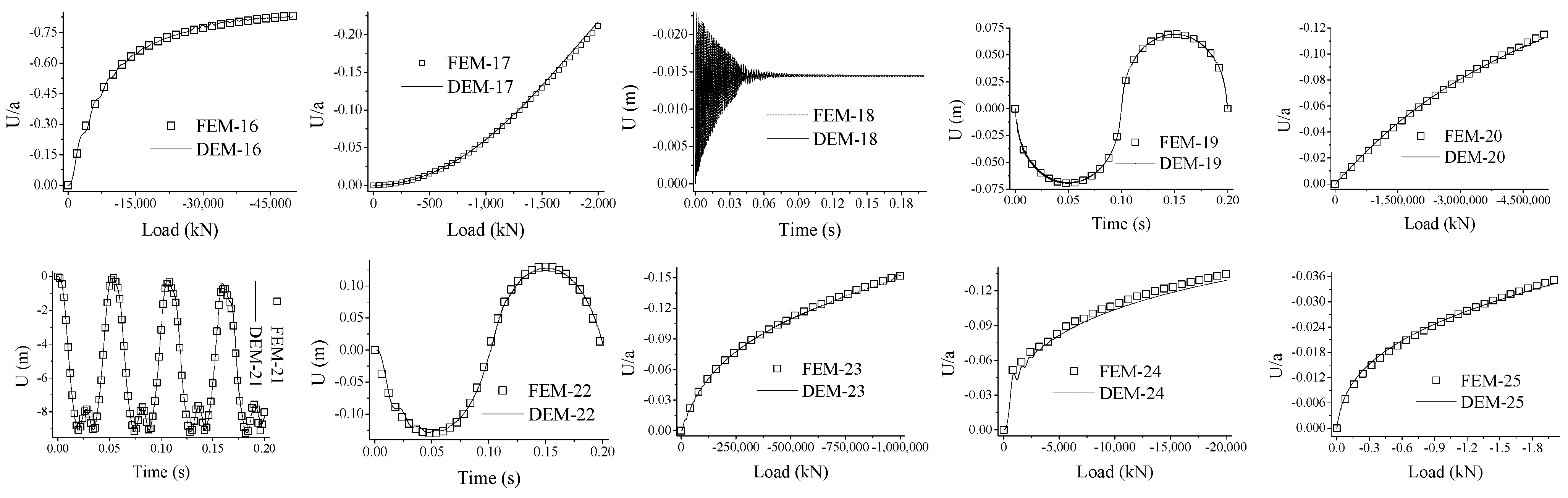
4.2. Influences of Multi-Parameter Changes
4.2.1. Boundary Conditions
4.2.2. Plate Dimensions
4.2.3. Form of Loading
4.2.4. Thickness-to-Width Ratio
4.2.5. Elastic Modulus
4.2.6. Poisson’s Ratio
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bourada, M.; Bouadi, A.; Bousahla, A.A.; Senouci, A.; Bourada, F.; Tounsi, A.; Mahmoud, S.R. Buckling behavior of rectangular plates under uniaxial and biaxial compression. Struct. Eng. Mech. 2019, 70, 113–123. [Google Scholar]
- Bohinc, U.; Brank, B.; Ibrahimbegovics, A. Discretization error for the Discrete Kirchhoff plate finite element approximation. Comput. Methods Appl. Mech. Eng. 2014, 269, 415–436. [Google Scholar] [CrossRef]
- Nguyen-Xuan, H. A polygonal finite element method for plate analysis. Comput. Struct. 2017, 188, 45–62. [Google Scholar] [CrossRef]
- Kikis, G.; Dornisch, W.; Klinkel, S. Adjusted approximation spaces for the treatment of transverse shear locking in isogeometric Reissner-Mindlin shell analysis. Comput. Methods Appl. Mech. Eng. 2019, 354, 850–870. [Google Scholar] [CrossRef]
- Enshaeian, A.; Rofooei, F. Geometrically nonlinear rectangular simply supported plates subjected to a moving mass. Acta Mech. 2014, 225, 595–608. [Google Scholar] [CrossRef]
- Kovalenko, M.D.; Abrukov, D.A.; Menshova, I.V.; Kerzhaev, A.P.; Yu, G.M. Exact solutions of boundary value problems in the theory of plate bending in a half-strip: Basics of the theory. Z. Für Angew. Math. Und Phys. 2019, 70, 98. [Google Scholar] [CrossRef]
- Papkov, S.; Banerjee, J.R. A New Method for Free Vibration Analysis of Triangular Isotropic and Orthotropic Plates of Isosceles Type Using an Accurate Series Solution. Mathematics 2023, 11, 649. [Google Scholar] [CrossRef]
- Belinha, J.; Aires, M. Elastoplastic Analysis of Plates with Radial Point Interpolation Meshless Methods. Appl. Sci. 2023, 12, 12842. [Google Scholar] [CrossRef]
- Morse, L.; Mallardo, V.; Sharif-Khodaei, Z.; Aliabadi, F.M.H. Shape Optimisation of Assembled Plate Structures with the Boundary Element Method. Aerospace 2022, 9, 381. [Google Scholar] [CrossRef]
- Burman, E.; Hansbo, P.; Larson, M.G. A simple approach for finite element simulation of reinforced plates. Finite Elem. Anal. Des. 2023, 142, 51–60. [Google Scholar] [CrossRef]
- Trinh, M.C.; Jun, H. A higher-order quadrilateral shell finite element for geometrically nonlinear analysis. Eur. J. Mech. A-Solids 2021, 89, 104283. [Google Scholar] [CrossRef]
- Lee, C.; Lee, D.H.; Lee, P.S. The strain-smoothed MITC3+ shell element in nonlinear analysis. Comput. Struct. 2022, 265, 106768. [Google Scholar] [CrossRef]
- Wu, B.; Pagani, A.; Filippi, M.; Chen, W.Q.; Carrera, E. Large-deflection and post-buckling analyses of isotropic rectangular plates by Carrera Unified Formulation. Int. J. Non-Linear Mech. 2019, 116, 18–31. [Google Scholar] [CrossRef]
- Rezaiee, P.M.; Arabie, E.; Masoodi, A.R. A triangular shell element for geometrically nonlinear analysis. Acta Mech. 2018, 229, 323–342. [Google Scholar] [CrossRef]
- Ansarir, R.; Hasrati, E.; Shakouri, A.H. Nonlinear large deformation analysis of shells using the variational differential quadrature method based on the six-parameter shell theory. Int. J. Non-Linear Mech. 2018, 106, 130–143. [Google Scholar] [CrossRef]
- Onkar, A.K. Nonlinear buckling analysis of damaged laminated composite plates. J. Compos. Mater. 2019, 53, 3111–3126. [Google Scholar] [CrossRef]
- Ko, Y.; Leep, S.; Bathe, K.J. The MITC4+ shell element in geometric nonlinear analysis. Comput. Struct. 2017, 185, 1–14. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Timsina, K.; Krishna, C.G.; Meguro, K. Sociotechnical Evaluation of the Soft Story Problem in Reinforced Concrete Frame Buildings in Nepal. J. Perform. Constr. Facil. 2021, 35, 04021019. [Google Scholar] [CrossRef]
- Christy, D.L.; Pillai, T.M.M.; Nagarajan, P. Analysis of Brick Masonry Wall using Applied Element Method. In Proceedings of the International Conference on Recent Advances in Materials, Mechanical and Civil Engineering, Hyderabad, India, 1–2 June 2017. [Google Scholar]
- Le, B.D.; Dau, F.; Charles, J.L. Modeling damages and cracks growth in composite with a 3D discrete element method. Compos. Part B Eng. 2016, 91, 615–630. [Google Scholar] [CrossRef]
- Kumar, R.; Rommel, S.; Jauffres, D. Effect of packing characteristics on the discrete element simulation of elasticity and buckling. Int. J. Mech. Sci. 2016, 110, 14–21. [Google Scholar] [CrossRef]
- Mathews, A.K.; Khan, A.; Sharma, B.; Kumar, S.; Kumar, R. A numerical investigation of granular shock waves over a circular cylinder using the discrete element method. J. Fluid Mech. 2022, 936, A11. [Google Scholar] [CrossRef]
- Ye, J.H.; Qi, N. Progressive collapse simulation based on DEM for single-layer reticulated domes. J. Constr. Steel Res. 2017, 128, 721–731. [Google Scholar]
- Ye, J.H.; Xu, L.L. Member Discrete Element Method for Static and Dynamic Responses Analysis of Steel Frames with Semi-Rigid Joints. Appl. Sci. 2017, 7, 714. [Google Scholar] [CrossRef]
- Ye, J.H.; Zhang, M. Buckling behavior of single-layer reticulated shells based on member discrete element method. J. Build. Struct. 2019, 40, 50–57. (In Chinese) [Google Scholar]
- Qi, N.; Ye, J.H. Nonlinear Dynamic Analysis of Space Frame Structures by Discrete Element Method. Appl. Mech. Mater. 2014, 638–640, 1716–1719. [Google Scholar] [CrossRef]
- Xu, L.L.; Ye, J.H. DEM Algorithm for Progressive Collapse Simulation of Single-Layer Reticulated Domes under Multi-Support Excitation. J. Earthq. Eng. 2017, 23, 18–45. [Google Scholar] [CrossRef]
- Xu, Q.; Ye, J.H. An adaptively coupled DEM–FEM algorithm for geometrical large deformation analysis of member structures. Comput. Part. Mech. 2019, 7, 947–959. [Google Scholar] [CrossRef]
- Guo, F.; Ye, J.H. Contact Model and Elastic Deformation Analysis of Plate Structure Based on the Discrete Element Method. Arch. Appl. Mech. 2022, 92, 2513–2523. [Google Scholar] [CrossRef]
- Borgonovo, E. A Methodology for Determining Interactions in Probabilistic Safety Assessment Models by Varying One Parameter at a Time. Risk Anal. 2010, 30, 385–399. [Google Scholar] [CrossRef]
- Proppe, C. Local reliability based sensitivity analysis with the moving particles method. Reliab. Eng. Syst. Saf. 2021, 207, 107269. [Google Scholar] [CrossRef]
- Frey, H.C.; Patil, S.R. Identification and review of sensitivity analysis methods. Risk Anal. 2010, 22, 553–578. [Google Scholar] [CrossRef]
- Kamal, M.; Inel, M. Correlation between Ground Motion Parameters and Displacement Demands of Mid-Rise RC Buildings on Soft Soils Considering Soil-Structure-Interaction. Buildigs 2021, 11, 125. [Google Scholar] [CrossRef]
- Cavaliere, P.; Perrone, A.; Marsano, D.; Primavera, V. Hydrogen-Based Direct Reduction of Iron Oxides Pellets Modeling. Steel Res. Int. 2023, 94, 2200791. [Google Scholar] [CrossRef]
- Batou, A. A sensitivity-based one-parameter-at-a-time model updating method. Mech. Syst. Signal Process. 2019, 122, 247–255. [Google Scholar] [CrossRef]
- Zhang, M.; Yu, L.; Xu, X. New Sensitivity Analysis Methods for Complex Modal Parameters in Asymmetrical Damped System. AIAA J. 2021, 59, 3165–3172. [Google Scholar] [CrossRef]
- Wang, B.H.; Deng, C. Investigation of the effect of humidity at both electrode on the performance of PEMFC using orthogonal test method. Int. J. Hydrogen Energy 2019, 44, 13737–13743. [Google Scholar] [CrossRef]
- Zhang, K.; Lu, Z.; Cheng, L. A new framework of variance based global sensitivity analysis for models with correlated inputs. Struct. Saf. 2015, 55, 1–9. [Google Scholar] [CrossRef]



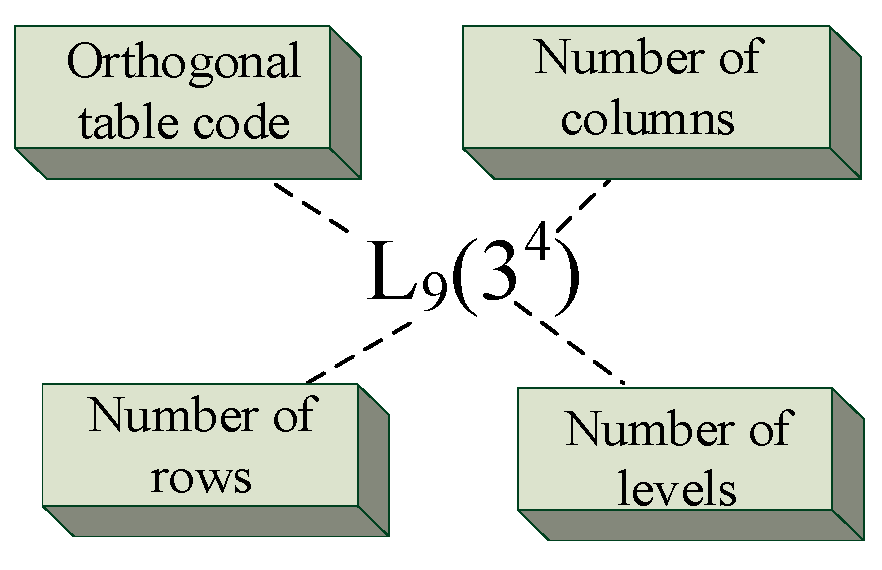






| Operating Combination | Parameter | |||
|---|---|---|---|---|
| A | B | C | D | |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 | 2 |
| 3 | 1 | 3 | 3 | 3 |
| 4 | 2 | 1 | 2 | 3 |
| 5 | 2 | 2 | 3 | 1 |
| 6 | 2 | 3 | 1 | 2 |
| 7 | 3 | 1 | 3 | 2 |
| 8 | 3 | 2 | 1 | 3 |
| 9 | 3 | 3 | 2 | 1 |
| Boundary | Fixed | Simply | Displacement Tracking Point | Position of Line Load | Position of Point Load |
|---|---|---|---|---|---|
| Cantilever plate | AB | \ | C | CD | C |
| Two adjacent edges | AB | AD | C | CD | C |
| Two opposite edges | AB | CD | E | FG | E |
| Three edges | AB | AD, BC | H | CD | H |
| Four edges | AB, CD | BC, AD | E | FG | E |
| Material | E (GPa) | μ | Material | E (GPa) | μ |
|---|---|---|---|---|---|
| Alloy steel | 206 | 0.25–0.3 | Cast steel | 175 | 0.31–0.34 |
| Lead | 170 | 0.42 | Aluminum alloy | 71 | 0.3 |
| Rolled aluminum | 69 | 0.32–0.36 | Concrete | 14–23 | 0.1–0.18 |
| Nylon | 2.83 | 0.4 | Rubber | 0.00784 | 0.48 |
| Parameters | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 | |
|---|---|---|---|---|---|---|
| 1 | Boundary conditions | Cantilever plate | Two adjacent | Two opposite | Three edges | Four edges |
| 2 | Plate dimensions (m) | 0.3 × 0.3 | 1.2 × 0.6 | 2 × 2 | 4 × 1 | 10 × 10 |
| 3 | Form of loading | Uniformly distributed | Line load | Concentrated load | Impact | Harmonic |
| 4 | Thickness-to-width ratio | 0.01 | 0.04 | 0.1 | 0.16 | 0.2 |
| 5 | Elastic modulus (GPa) | 0.005 | 50 | 100 | 150 | 200 |
| 6 | Poisson’s ratio | 0.1 | 0.24 | 0.3 | 0.4 | 0.48 |
| Operating Combination | Boundary | Dimension | Form of Loading | h/b | E | μ | Error * |
|---|---|---|---|---|---|---|---|
| Y (%) | |||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.239 |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 0.918 |
| 3 | 3 | 3 | 3 | 3 | 3 | 3 | 1.063 |
| 4 | 4 | 4 | 4 | 4 | 4 | 4 | −2.342 |
| 5 | 5 | 5 | 5 | 5 | 5 | 5 | 2.002 |
| 6 | 1 | 2 | 3 | 4 | 5 | 1 | 0.838 |
| 7 | 2 | 3 | 4 | 5 | 1 | 2 | 1.359 |
| 8 | 3 | 4 | 5 | 1 | 2 | 3 | 3.102 |
| 9 | 4 | 5 | 1 | 2 | 3 | 4 | 4.212 |
| 10 | 5 | 1 | 2 | 3 | 4 | 5 | 2.805 |
| 11 | 1 | 3 | 5 | 2 | 4 | 1 | 0.187 |
| 12 | 2 | 4 | 1 | 3 | 5 | 2 | 0.474 |
| 13 | 3 | 5 | 2 | 4 | 1 | 3 | 2.762 |
| 14 | 4 | 1 | 3 | 5 | 2 | 4 | 1.623 |
| 15 | 5 | 2 | 4 | 1 | 3 | 5 | 0.424 |
| 16 | 1 | 4 | 2 | 5 | 3 | 1 | 0.460 |
| 17 | 2 | 5 | 3 | 1 | 4 | 2 | −2.884 |
| 18 | 3 | 1 | 4 | 2 | 5 | 3 | −1.736 |
| 19 | 4 | 2 | 5 | 3 | 1 | 4 | 0.865 |
| 20 | 5 | 3 | 1 | 4 | 2 | 5 | 1.747 |
| 21 | 1 | 5 | 4 | 3 | 2 | 1 | −2.652 |
| 22 | 2 | 1 | 5 | 4 | 3 | 2 | 1.538 |
| 23 | 3 | 2 | 1 | 5 | 4 | 3 | 0.546 |
| 24 | 4 | 3 | 2 | 1 | 5 | 4 | 4.121 |
| 25 | 5 | 4 | 3 | 2 | 1 | 5 | 2.559 |
| Mean value1 ** (%) | 0.875 | 1.811 | 1.642 | 2.154 | 2.154 | 0.875 | |
| Mean value2 ** (%) | 1.435 | 0.718 | 2.213 | 1.922 | 2.008 | 1.435 | |
| Mean value3 ** (%) | 1.842 | 0.980 | 1.794 | 1.572 | 1.540 | 1.842 | |
| Mean value4 ** (%) | 2.633 | 2.100 | 1.703 | 1.845 | 1.753 | 2.633 | |
| Mean value5 ** (%) | 1.907 | 2.903 | 1.539 | 1.198 | 1.834 | 1.907 | |
| Range *** (%) | 1.757 | 2.184 | 0.674 | 0.956 | 0.614 | 1.757 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, F.; Ye, J. A Study on the Applicability and Accuracy of the Discrete Element Method for Plates Based on Parameter Sensitivity Analysis. Buildings 2023, 13, 1567. https://doi.org/10.3390/buildings13061567
Guo F, Ye J. A Study on the Applicability and Accuracy of the Discrete Element Method for Plates Based on Parameter Sensitivity Analysis. Buildings. 2023; 13(6):1567. https://doi.org/10.3390/buildings13061567
Chicago/Turabian StyleGuo, Fei, and Jihong Ye. 2023. "A Study on the Applicability and Accuracy of the Discrete Element Method for Plates Based on Parameter Sensitivity Analysis" Buildings 13, no. 6: 1567. https://doi.org/10.3390/buildings13061567
APA StyleGuo, F., & Ye, J. (2023). A Study on the Applicability and Accuracy of the Discrete Element Method for Plates Based on Parameter Sensitivity Analysis. Buildings, 13(6), 1567. https://doi.org/10.3390/buildings13061567






