Bayesian Model-Updating Implementation in a Five-Story Building
Abstract
1. Introduction
2. BI in Finite Element Model Updating (FEMU)
2.1. Likelihood Function
Identity Matrix as a Covariance Matrix
3. Experimental Program
3.1. Test Building
3.2. Test and Data Collection
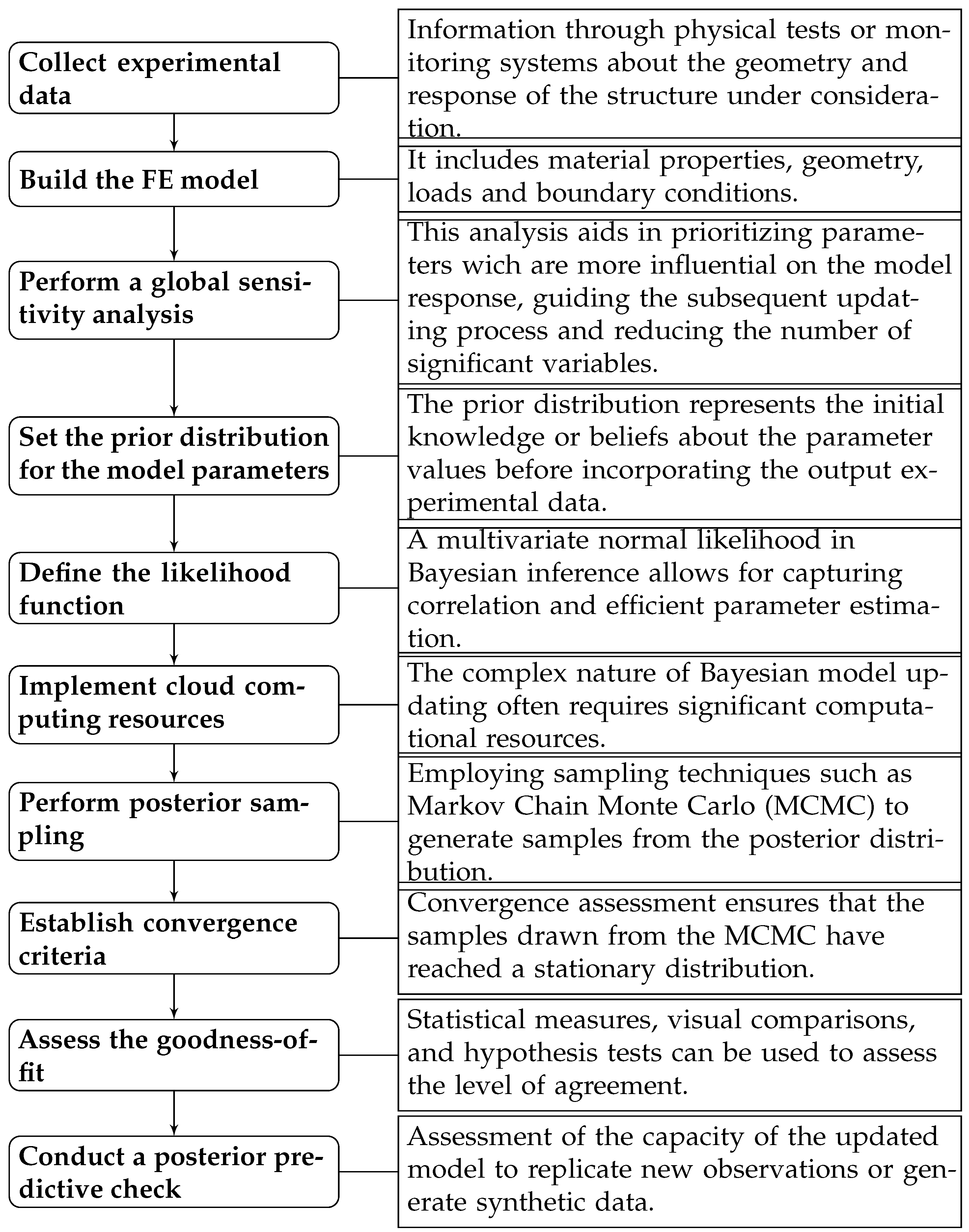
4. Methodology
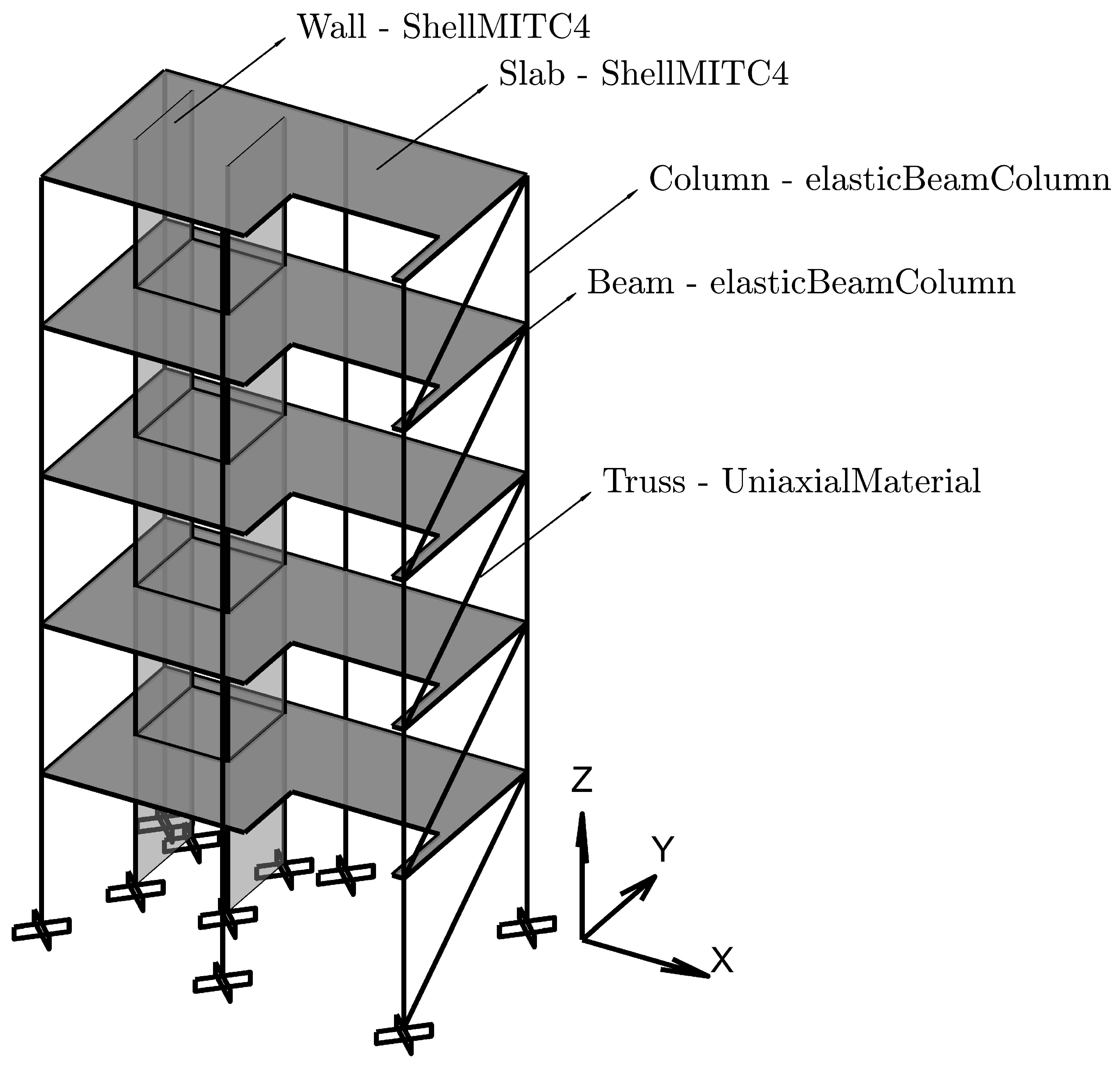
4.1. Modeling of the Structure
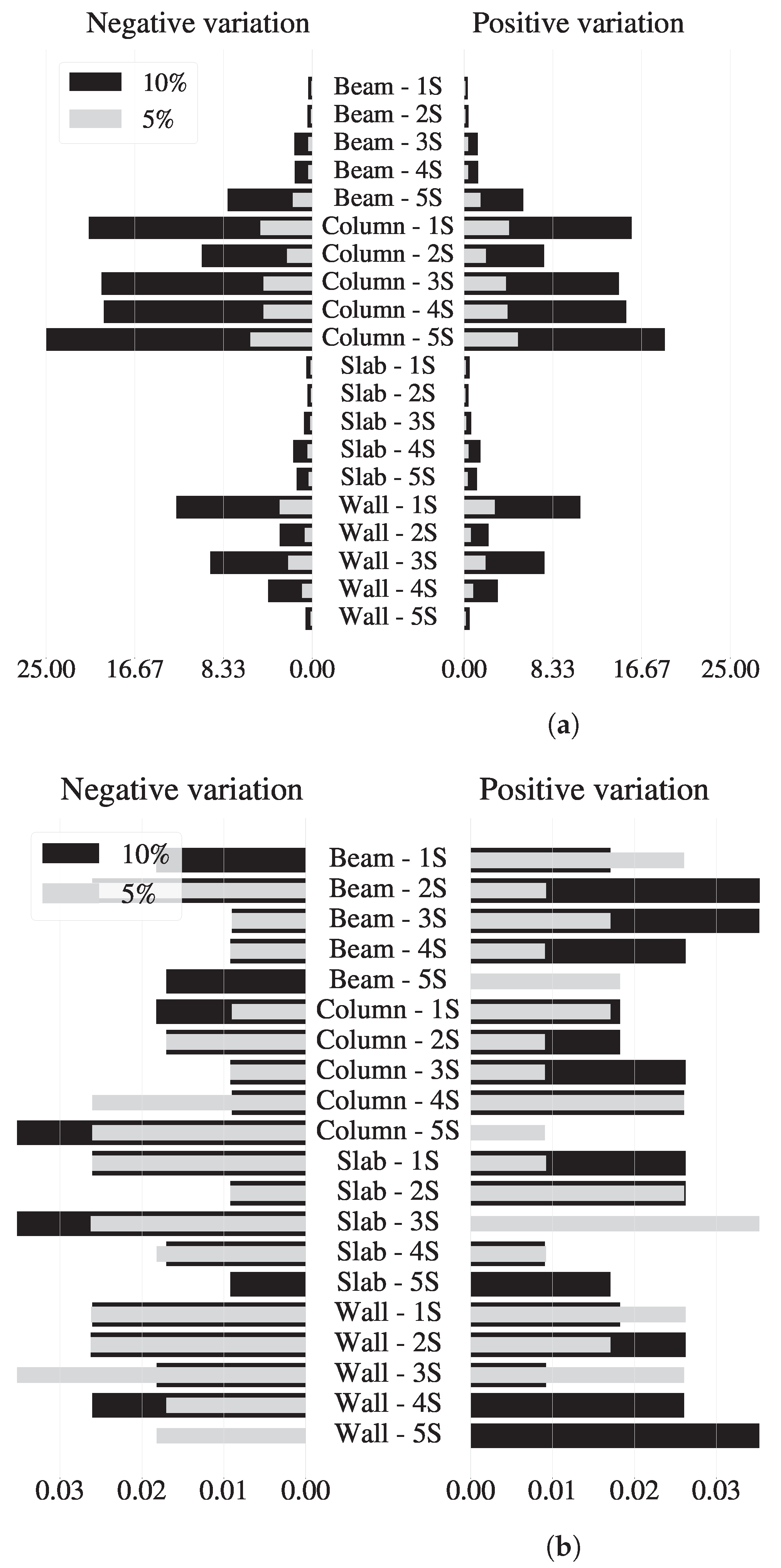
4.2. Global Sensitivity Analysis
4.3. Bayesian Updating Algorithm
4.3.1. Likelihood Function Estimation
4.3.2. Posterior Sampling
4.4. Cloud Computing as Alternative
5. Results and Discussions
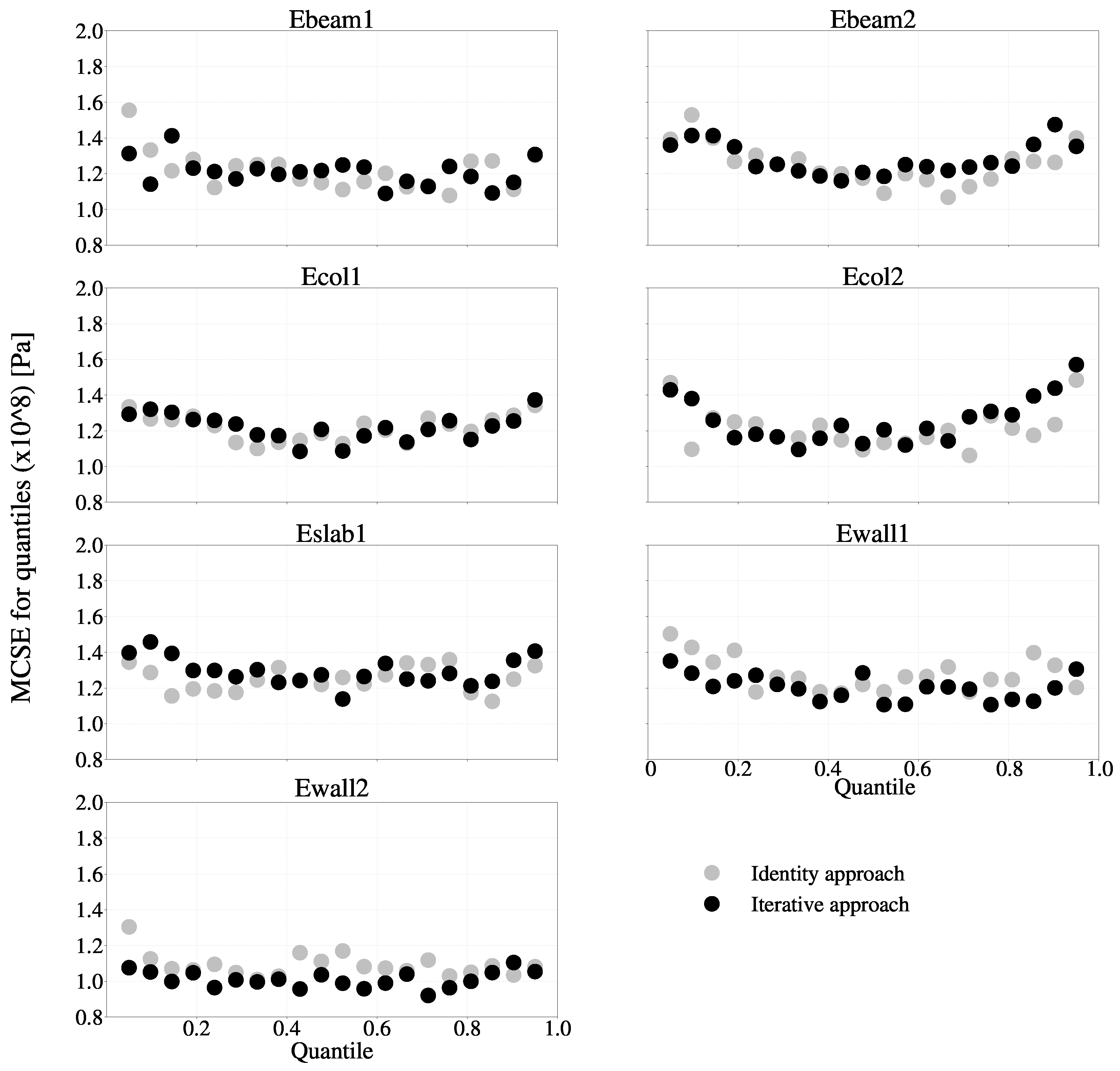
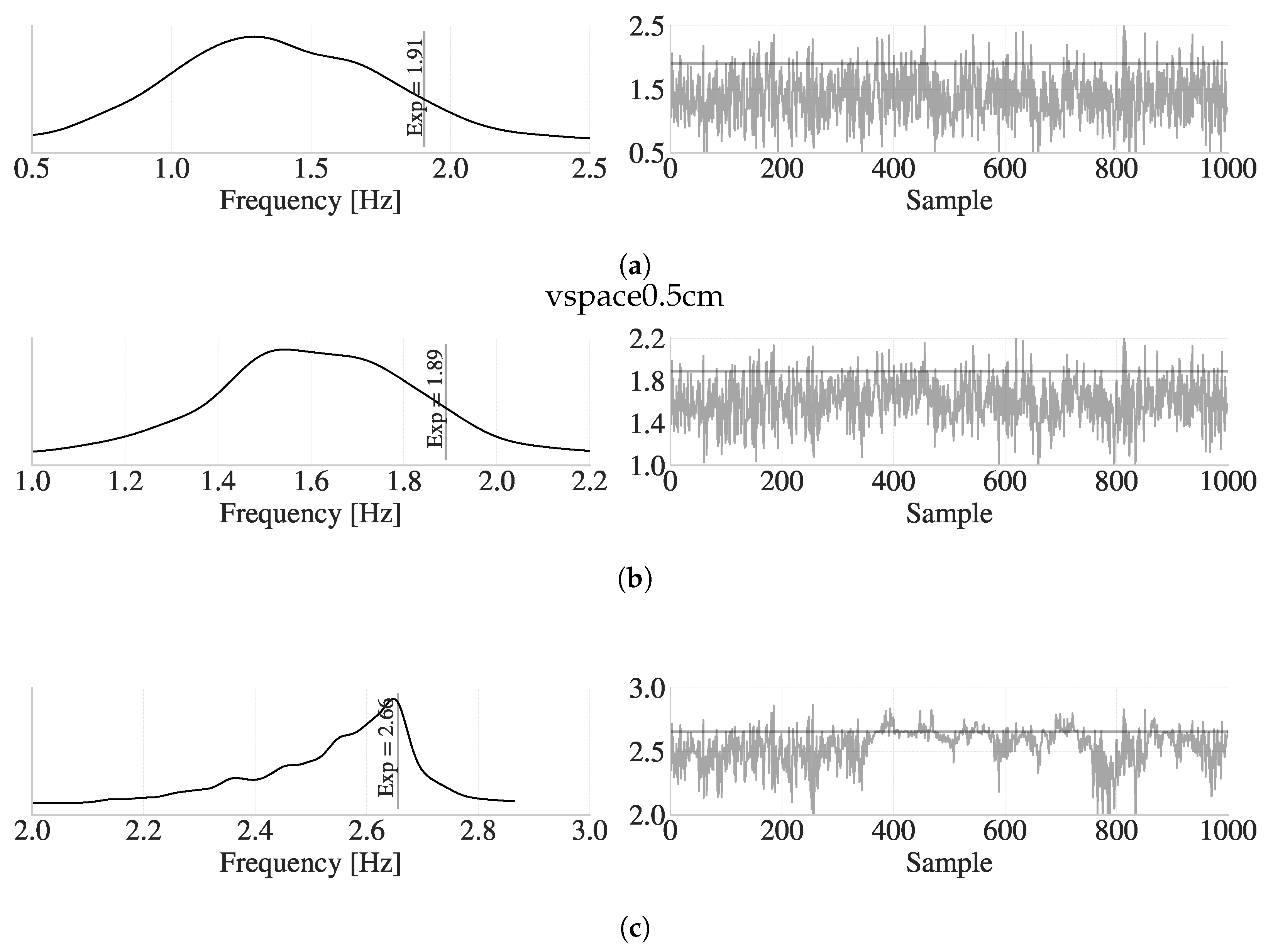
5.1. Convergence Criteria
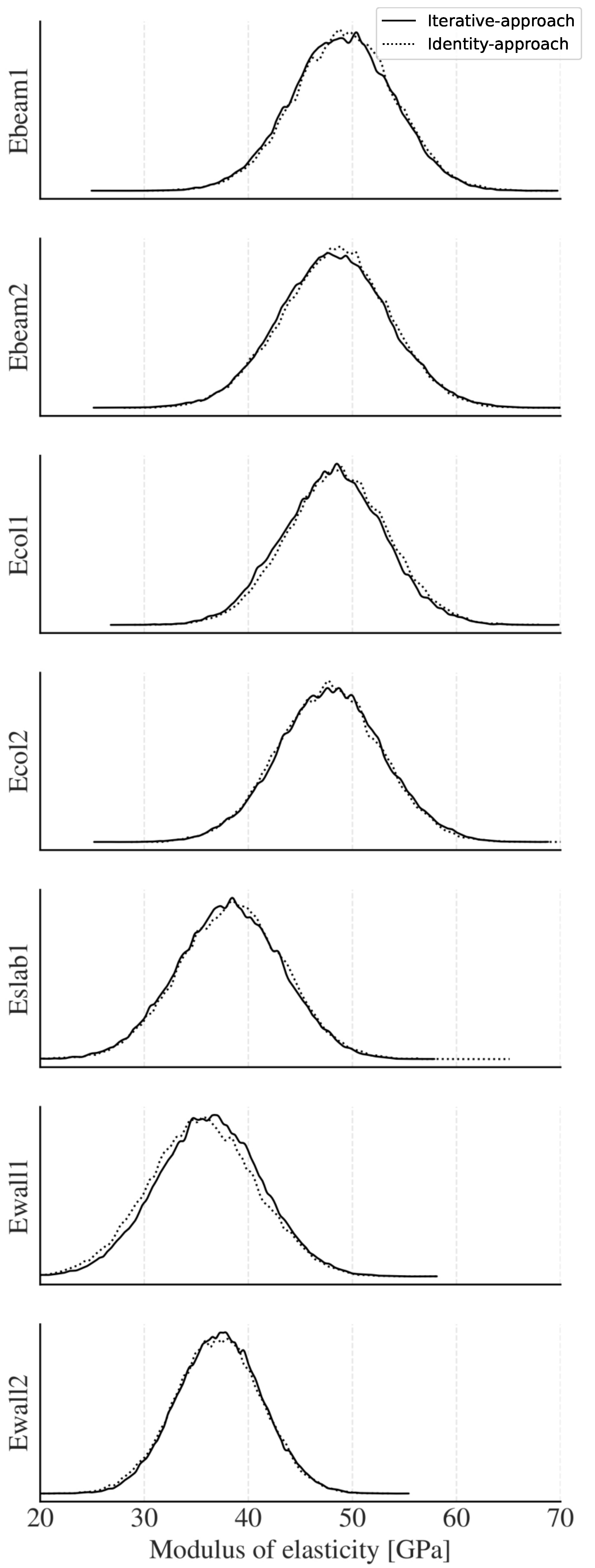
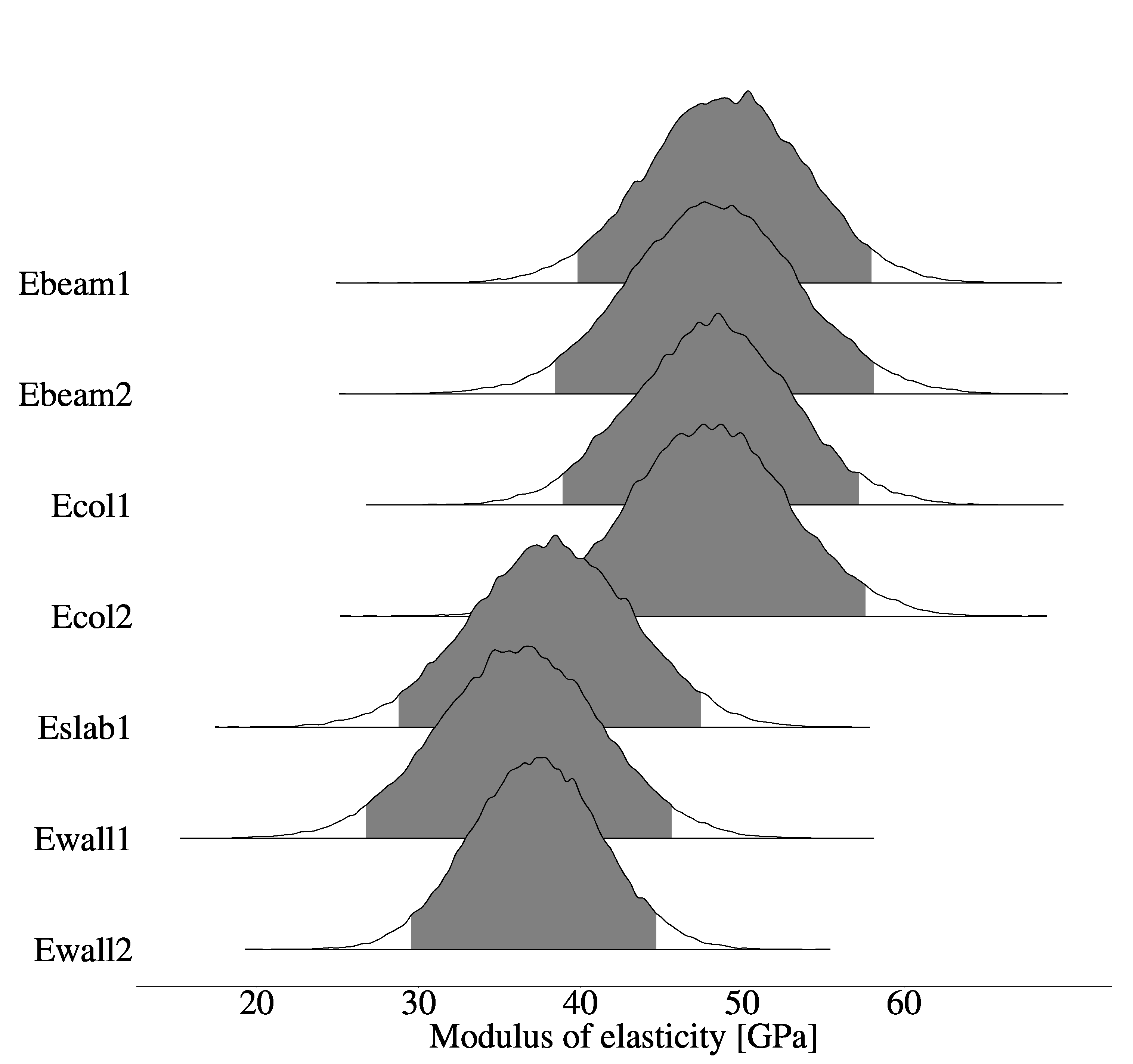
5.2. Numerical Evaluation of the Model Updating
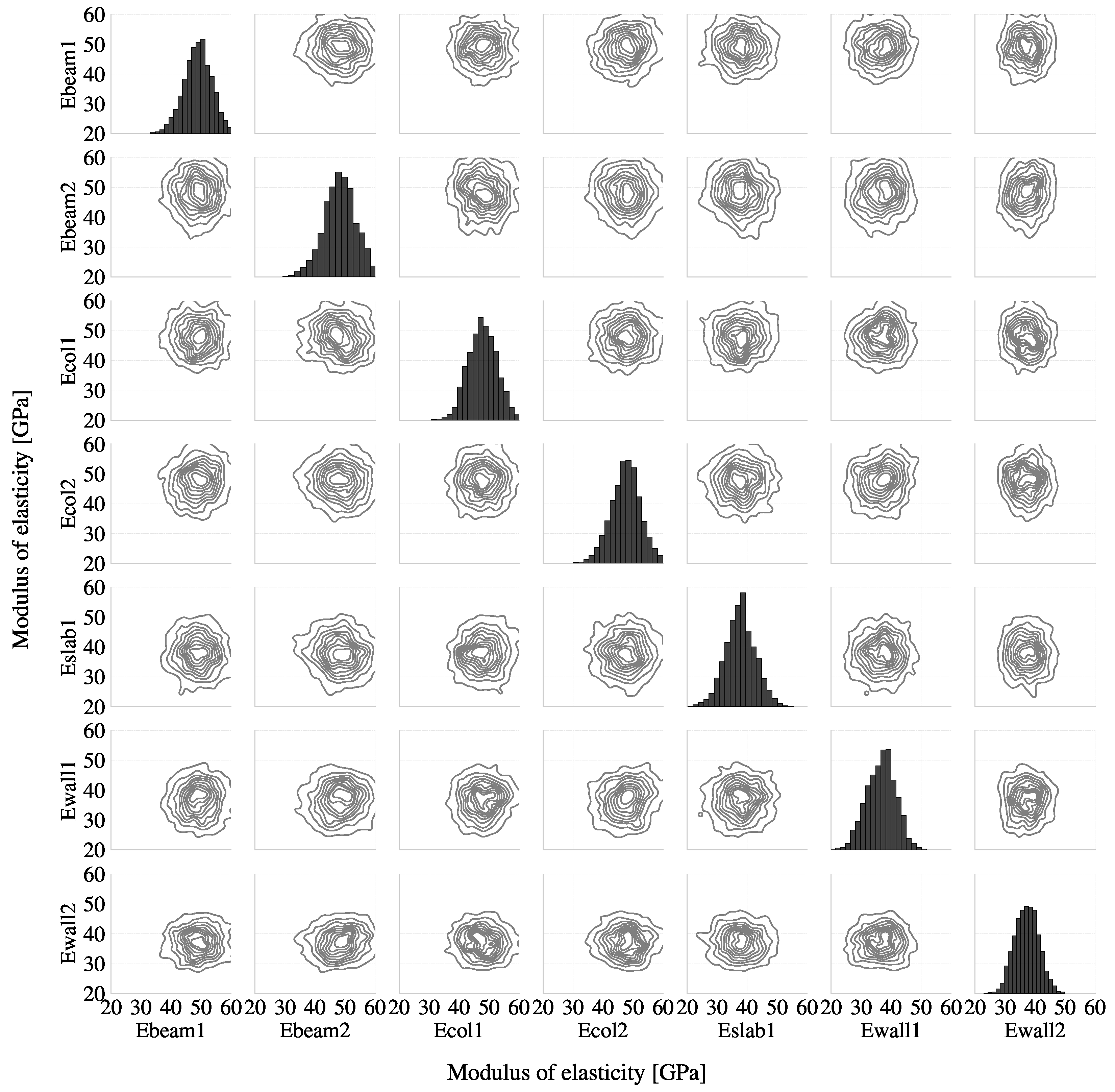
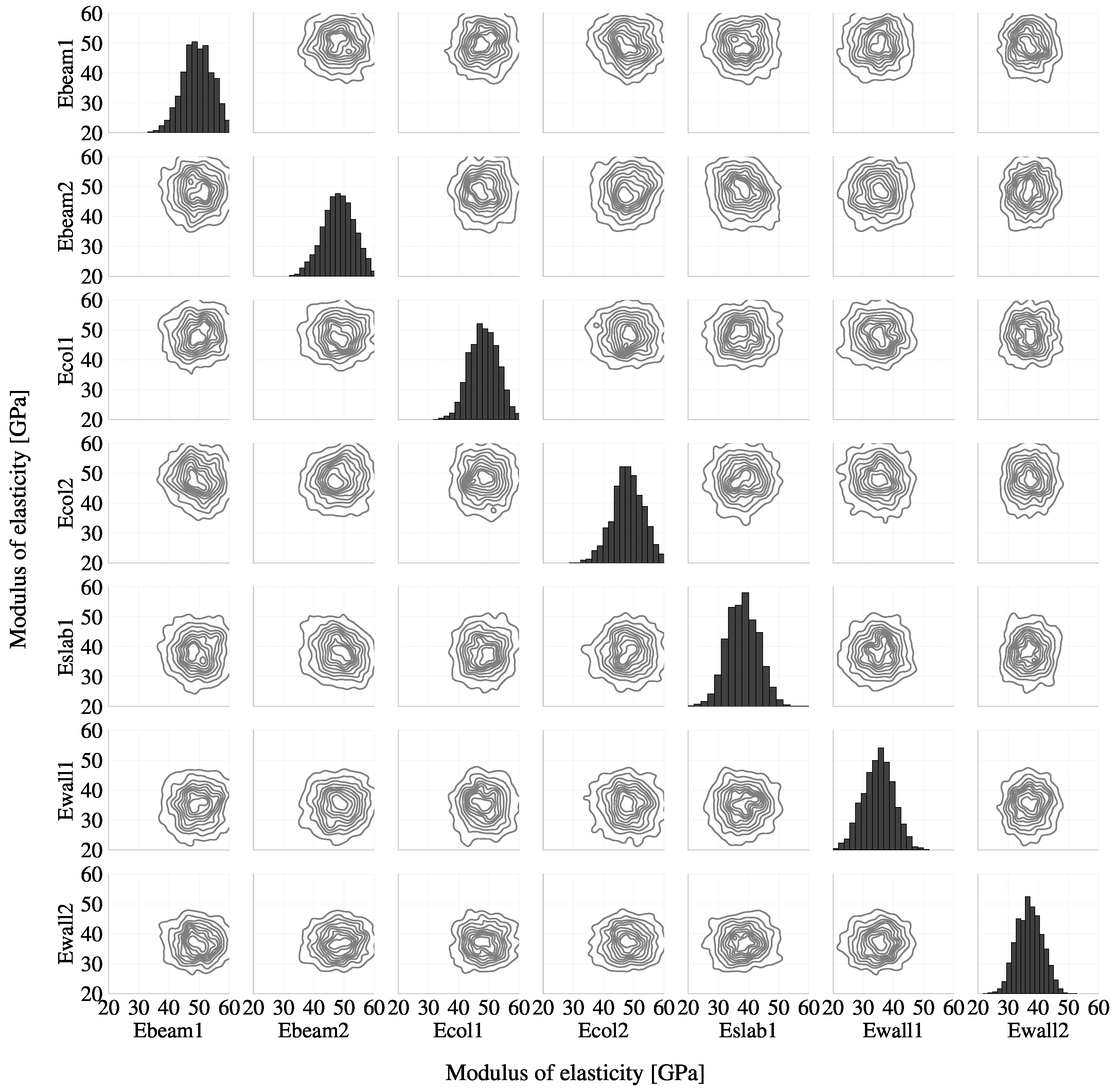
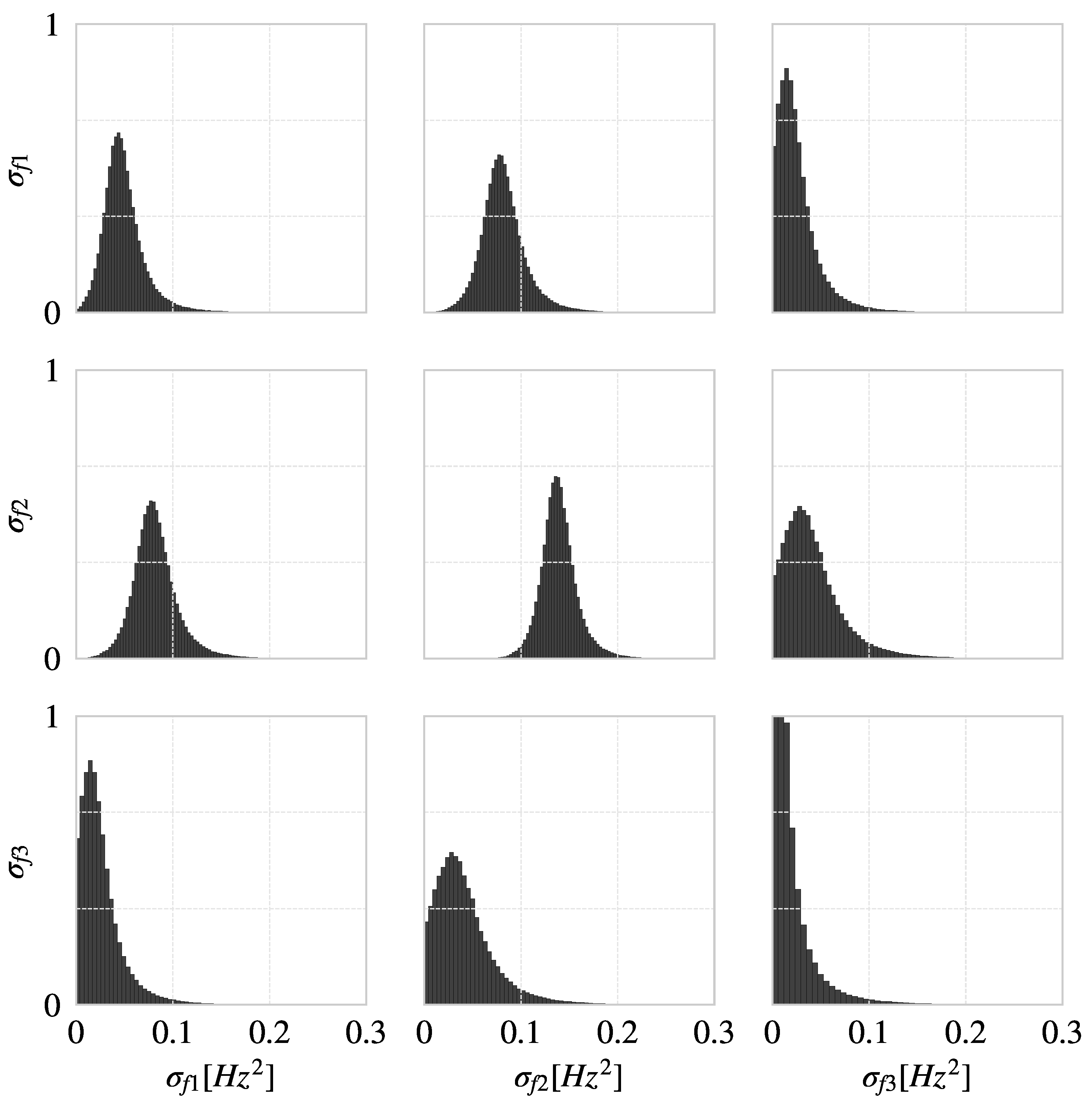
5.3. Covariance Matrix Analysis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Armstrong, C.G. Modelling requirements for finite-element analysis. Comput.-Aided Des. 1994, 26, 573–578. [Google Scholar] [CrossRef]
- Shan, S.; Wang, G.G. Survey of modeling and optimization strategies to solve high-dimensional design problems with computationally-expensive black-box functions. Struct. Multidiscip. Optim. 2010, 41, 219–241. [Google Scholar] [CrossRef]
- Zárate, B.A.; Caicedo, J.M. Finite element model updating: Multiple alternatives. Eng. Struct. 2008, 30, 3724–3730. [Google Scholar] [CrossRef]
- Jagota, V.; Sethi, A.P.S.; Kumar, K. Finite element method: An overview. Walailak J. Sci. Technol. (WJST) 2013, 10, 1–8. [Google Scholar]
- Rios, J.M. Uncertainty in Structural Dynamic Models. Ph.D. Thesis, Swansea University, Swansea, UK, 2005. [Google Scholar]
- Igusa, T.; Buonopane, S.; Ellingwood, B. Bayesian analysis of uncertainty for structural engineering applications. Struct. Saf. 2002, 24, 165–186. [Google Scholar] [CrossRef]
- Bulleit, W.M. Uncertainty in structural engineering. Pract. Period. Struct. Des. Constr. 2008, 13, 24–30. [Google Scholar] [CrossRef]
- Gomez, D.; Dyke, S.J.; Rietdyk, S. Structured uncertainty for a pedestrian-structure interaction model. J. Sound Vib. 2020, 474, 115237. [Google Scholar] [CrossRef]
- Vailati, M.; Monti, G.; Khazna, M.; Realfonzo, R.; De Iuliis, M. Probabilistic seismic response analysis of existing masonry structures. In Brick and Block Masonry; CRC Press: Boca Raton, FL, USA, 2016; pp. 2489–2498. [Google Scholar] [CrossRef]
- Zellner, A. Bayesian and non-Bayesian approaches to statistical inference and decision-making. J. Comput. Appl. Math. 1995, 64, 3–10. [Google Scholar] [CrossRef]
- Briggs, A.H.; Weinstein, M.C.; Fenwick, E.A.; Karnon, J.; Sculpher, M.J.; Paltiel, A.D. Model parameter estimation and uncertainty analysis: A report of the ISPOR-SMDM Modeling Good Research Practices Task Force Working Group-6. Med. Decis. Mak. 2012, 32, 722–732. [Google Scholar] [CrossRef] [PubMed]
- Hoang, T.V.; Matthies, H.G. An efficient computational method for parameter identification in the context of random set theory via Bayesian inversion. Int. J. Uncertain. Quantif. 2021, 11, 1–18. [Google Scholar] [CrossRef]
- Sehgal, S.; Kumar, H. Structural dynamic model updating techniques: A state of the art review. Arch. Comput. Methods Eng. 2016, 23, 515–533. [Google Scholar] [CrossRef]
- Loyola, M. Big data in building design: A review. J. Inf. Technol. Constr. 2018, 23, 259–284. [Google Scholar]
- Beck, J.L.; Katafygiotis, L.S. Updating models and their uncertainties. I: Bayesian statistical framework. J. Eng. Mech.-Proc. ASCE 1998, 124, 455–462. [Google Scholar] [CrossRef]
- Katafygiotis, L.S.; Beck, J.L. Updating models and their uncertainties. II: Model identifiability. J. Eng. Mech. 1998, 124, 463–467. [Google Scholar] [CrossRef]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Bayes, T. LII. An essay towards solving a problem in the doctrine of chances. By the late Rev. Mr. Bayes, FRS communicated by Mr. Price, in a letter to John Canton, AMFR S. In Philosophical Transactions of the Royal Society of London; Royal Society of London: London, UK, 1763; pp. 370–418. [Google Scholar]
- Swinburne, R. Bayes’ Theorem. Mind 2004, 113, 591–596. [Google Scholar] [CrossRef]
- Denison, D.G.; Holmes, C.C.; Mallick, B.K.; Smith, A.F. Bayesian Methods for Nonlinear Classification and Regression; John Wiley & Sons: Hoboken, NJ, USA, 2002; Volume 386. [Google Scholar]
- MacLehose, R.F.; Hamra, G.B. Applications of Bayesian methods to epidemiologic research. Curr. Epidemiol. Rep. 2014, 1, 103–109. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, G. Bayesian methods for dealing with missing data problems. J. Korean Stat. Soc. 2018, 47, 297–313. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, C.; Guo, B. Transfer-learning guided Bayesian model updating for damage identification considering modeling uncertainty. Mech. Syst. Signal Process. 2022, 166, 108426. [Google Scholar] [CrossRef]
- Zhang, E.; Feissel, P.; Antoni, J. A comprehensive Bayesian approach for model updating and quantification of modeling errors. Probabilistic Eng. Mech. 2011, 26, 550–560. [Google Scholar] [CrossRef]
- Argyris, C.; Papadimitriou, C.; Panetsos, P.; Tsopelas, P. Bayesian model-updating using features of modal data: Application to the metsovo bridge. J. Sens. Actuator Netw. 2020, 9, 27. [Google Scholar] [CrossRef]
- Ghurye, S.; Olkin, I. A characterization of the multivariate normal distribution. Ann. Math. Stat. 1962, 33, 533–541. [Google Scholar] [CrossRef]
- Tong, Y.L. The Multivariate Normal Distribution; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Srivastava, M.S. Some tests concerning the covariance matrix in high dimensional data. J. Jpn. Stat. Soc. 2005, 35, 251–272. [Google Scholar] [CrossRef]
- Srivastava, M.S.; Kollo, T.; von Rosen, D. Some tests for the covariance matrix with fewer observations than the dimension under non-normality. J. Multivar. Anal. 2011, 102, 1090–1103. [Google Scholar] [CrossRef]
- Birke, M.; Dette, H. A note on testing the covariance matrix for large dimension. Stat. Probab. Lett. 2005, 74, 281–289. [Google Scholar] [CrossRef]
- Fisher, T.J. On testing for an identity covariance matrix when the dimensionality equals or exceeds the sample size. J. Stat. Plan. Inference 2012, 142, 312–326. [Google Scholar] [CrossRef]
- Yan, W.J.; Katafygiotis, L.S. A novel Bayesian approach for structural model updating utilizing statistical modal information from multiple setups. Struct. Saf. 2015, 52, 260–271. [Google Scholar] [CrossRef]
- Zhang, X.; Boscardin, W.J.; Belin, T.R. Sampling correlation matrices in Bayesian models with correlated latent variables. J. Comput. Graph. Stat. 2006, 15, 880–896. [Google Scholar] [CrossRef]
- Chen, M.C.; Pantoli, E.; Wang, X.; Astroza, R.; Ebrahimian, H.; Hutchinson, T.C.; Conte, J.P.; Restrepo, J.I.; Marin, C.; Walsh, K.D.; et al. Full-scale structural and nonstructural building system performance during earthquakes: Part I–specimen description, test protocol, and structural response. Earthq. Spectra 2016, 32, 737–770. [Google Scholar] [CrossRef]
- Pantoli, E.; Chen, M.C.; Hutchinson, T.C.; Astroza, R.; Conte, J.P.; Ebrahimian, H.; Restrepo, J.I.; Wang, X. Landmark data set from the building nonstructural components and systems (BNCS) project. Earthq. Spectra 2016, 32, 1239–1259. [Google Scholar] [CrossRef]
- Astroza, R.; Ebrahimian, H.; Conte, J.P.; Restrepo, J.I.; Hutchinson, T.C. Influence of the construction process and nonstructural components on the modal properties of a five-story building. Earthq. Eng. Struct. Dyn. 2016, 45, 1063–1084. [Google Scholar] [CrossRef]
- Gutierrez, M. Bayesian Finite Element Model Parameter and Covariance Estimation. Master’s Thesis, Universidad de los Andes, Santiago, Chile, 2020. [Google Scholar]
- Persson, B. Poisson’s ratio of high-performance concrete. Cem. Concr. Res. 1999, 29, 1647–1653. [Google Scholar] [CrossRef]
- Ashton, G.; Hübner, M.; Lasky, P.D.; Talbot, C.; Ackley, K.; Biscoveanu, S.; Chu, Q.; Divakarla, A.; Easter, P.J.; Goncharov, B.; et al. BILBY: A user-friendly Bayesian inference library for gravitational-wave astronomy. Astrophys. J. Suppl. Ser. 2019, 241, 27. [Google Scholar] [CrossRef]
- Goodman, J.; Weare, J. Ensemble samplers with affine invariance. Commun. Appl. Math. Comput. Sci. 2010, 5, 65–80. [Google Scholar] [CrossRef]
- Mirza, S.A.; MacGregor, J.G. Probabilistic study of strength of reinforced concrete members. Can. J. Civil Eng. 1982, 9, 431–448. [Google Scholar] [CrossRef]
- Nowak, A.S.; Szerszen, M.M. Calibration of design code for buildings (ACI 318): Part 1—Statistical models for resistance. Struct. J. 2003, 100, 377–382. [Google Scholar] [CrossRef]
- Pinto, F.; Toledo, J.; Birrell, M.; Bazaez, R.; Hernandez, F.R.A. Uncertainty Quantification in Constitutive Models of Highway Bridge Components: Seismic Bars and Elastomeric Bearings. Materials 2023, 16, 1792. [Google Scholar] [CrossRef] [PubMed]
- Vehtari, A.; Gelman, A.; Simpson, D.; Carpenter, B.; Bürkner, P.C. Rank-normalization, folding, and localization: An improved for assessing convergence of MCMC (with Discussion). Bayesian Anal. 2021, 16, 667–718. [Google Scholar] [CrossRef]
- Kruschke, J. Doing Bayesian Data Analysis: A Tutorial with R, JAGS, and Stan; Academic Press: Waltham, MA, USA, 2014. [Google Scholar] [CrossRef]
- Kampenes, V.B.; Dybå, T.; Hannay, J.E.; Sjøberg, D.I. A systematic review of effect size in software engineering experiments. Inf. Softw. Technol. 2007, 49, 1073–1086. [Google Scholar] [CrossRef]



| Element | Average [MPa] | Average [GPa] |
|---|---|---|
| Columns and walls | 57.2 | 32.6 |
| Slabs and beams | 51.7 | 33.1 |
| Group | Element | Previous Nomenclature | New Nomenclature |
|---|---|---|---|
| 1 | Beam—1st Story | Ebeam1 | Ebeam1 |
| Beam—2nd Story | Ebeam2 | ||
| 2 | Beam—3rd Story | Ebeam3 | Ebeam2 |
| Beam—4th Story | Ebeam4 | ||
| Beam—5th Story | Ebeam5 | ||
| 3 | Column—1st Story | Ecol1 | Ecol1 |
| Column—2nd Story | Ecol2 | ||
| 4 | Column—3rd Story | Ecol3 | Ecol2 |
| Column—4th Story | Ecol4 | ||
| Column—5th Story | Ecol5 | ||
| 5 | Slab—1st Story | Eslab1 | Eslab1 |
| Slab—2nd Story | Eslab2 | ||
| Slab—3rd Story | Eslab3 | ||
| Slab—4th Story | Eslab4 | ||
| Slab—5th Story | Eslab5 | ||
| 6 | Wall—1st Story | Ewall1 | Ewall1 |
| Wall—2nd Story | Ewall2 | ||
| 7 | Wall—3rd Story | Ewall3 | Ewall2 |
| Wall—4th Story | Ewall4 | ||
| Wall—5th Story | Ewall5 |
| Prior Distributions | |||
|---|---|---|---|
| Parameters | Type of Distribution | Mean [MPa] | Std. Dev. [MPa] |
| Ebeam1 | LogNormal | 35,000 | 9700 |
| Ebeam2 | LogNormal | 35,000 | 9700 |
| Ecol1 | LogNormal | 35,000 | 9700 |
| Ecol2 | LogNormal | 35,000 | 9700 |
| Eslab1 | LogNormal | 35,000 | 9700 |
| Ewall1 | LogNormal | 35,000 | 9700 |
| Ewall2 | LogNormal | 35,000 | 9700 |
| Mean [GPa] | SD [GPa] | HDI 3% [GPa] | HDI 97% [GPa] | |
|---|---|---|---|---|
| Ebeam1 | 48.93 | 4.87 | 39.75 | 57.99 |
| Ebeam2 | 48.16 | 5.27 | 38.39 | 58.18 |
| Ecol1 | 48.14 | 4.88 | 38.90 | 57.23 |
| Ecol2 | 47.92 | 5.03 | 38.60 | 57.68 |
| Eslab1 | 38.19 | 5.00 | 28.75 | 47.48 |
| Ewall1 | 36.23 | 5.03 | 26.74 | 45.66 |
| Ewall2 | 37.25 | 4.05 | 29.50 | 44.72 |
| Mean [GPa] | SD [GPa] | HDI 3% [GPa] | HDI 97% [GPa] | |
|---|---|---|---|---|
| Ebeam1 | 49.22 | 4.86 | 40.01 | 58.25 |
| Ebeam2 | 48.29 | 5.15 | 38.43 | 57.79 |
| Ecol1 | 48.55 | 4.85 | 39.28 | 57.54 |
| Ecol2 | 47.76 | 4.96 | 38.59 | 57.25 |
| Eslab1 | 38.38 | 5.04 | 28.63 | 47.50 |
| Ewall1 | 35.55 | 5.17 | 25.84 | 45.34 |
| Ewall2 | 37.08 | 4.15 | 29.20 | 44.77 |
| Ebeam1 | Ebeam2 | Ecol1 | Ecol2 | Eslab1 | Ewall1 | Ewall2 | |
|---|---|---|---|---|---|---|---|
| Ebeam1 | 1 | −0.01629 | 0.01 | 0.02 | 0.000633 | 0.009928 | 0.007501 |
| Ebeam2 | −0.000538 | 1 | 0.016919 | −0.003235 | −0.005969 | 0.00827 | 0.004841 |
| Ecol1 | 0.020662 | 0.005784 | 1 | −0.002967 | 0.020706 | −0.007723 | 0.021349 |
| Ecol2 | 0.019176 | 0.012743 | −0.007397 | 1 | 0.006645 | −0.001015 | −0.01976 |
| Eslab1 | 0.008815 | −0.02366 | 0.017139 | 0.034489 | 1 | 0.012989 | 0.010983 |
| Ewall1 | −0.003382 | 0.006759 | 0.026454 | 0.005082 | 0.022536 | 1 | 0.017236 |
| Ewall2 | −0.004593 | 0.003377 | 0.024154 | 0.010754 | −0.00095 | −0.011894 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hurtado, O.D.; Ortiz, A.R.; Gomez, D.; Astroza, R. Bayesian Model-Updating Implementation in a Five-Story Building. Buildings 2023, 13, 1568. https://doi.org/10.3390/buildings13061568
Hurtado OD, Ortiz AR, Gomez D, Astroza R. Bayesian Model-Updating Implementation in a Five-Story Building. Buildings. 2023; 13(6):1568. https://doi.org/10.3390/buildings13061568
Chicago/Turabian StyleHurtado, Oscar D., Albert R. Ortiz, Daniel Gomez, and Rodrigo Astroza. 2023. "Bayesian Model-Updating Implementation in a Five-Story Building" Buildings 13, no. 6: 1568. https://doi.org/10.3390/buildings13061568
APA StyleHurtado, O. D., Ortiz, A. R., Gomez, D., & Astroza, R. (2023). Bayesian Model-Updating Implementation in a Five-Story Building. Buildings, 13(6), 1568. https://doi.org/10.3390/buildings13061568




_Mei.png)




