Damage Estimation of Full-Scale Infilled RC Frames under Pseudo-Dynamic Excitation by Means of Output-Only Modal Identification
Abstract
1. Introduction
2. Output-Only Modal Identification and Pseudo-Dynamic Loading
2.1. Specimens and Setup
2.2. Loading Sequence and Dynamic Identification
3. Experimental Results
4. Model Development
5. Numerical vs. Experimental Results
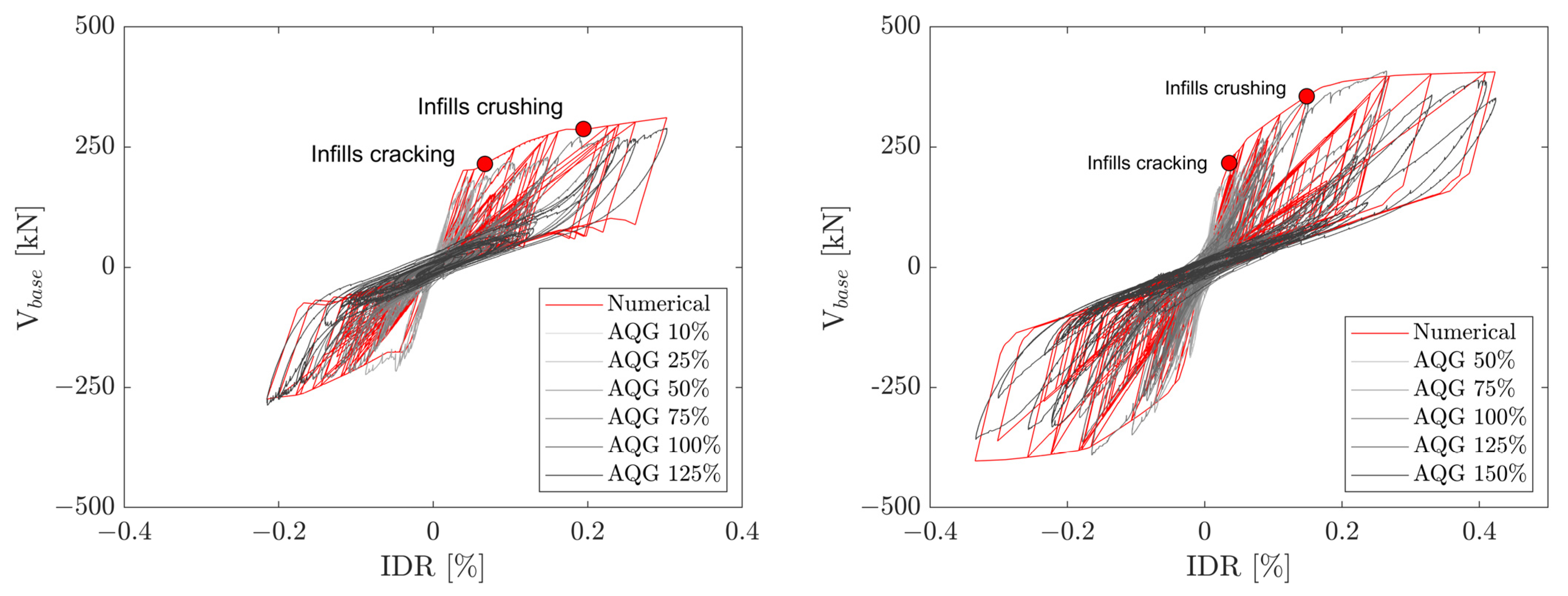
5.1. Performance Curves and Damage
5.2. Modal Properties
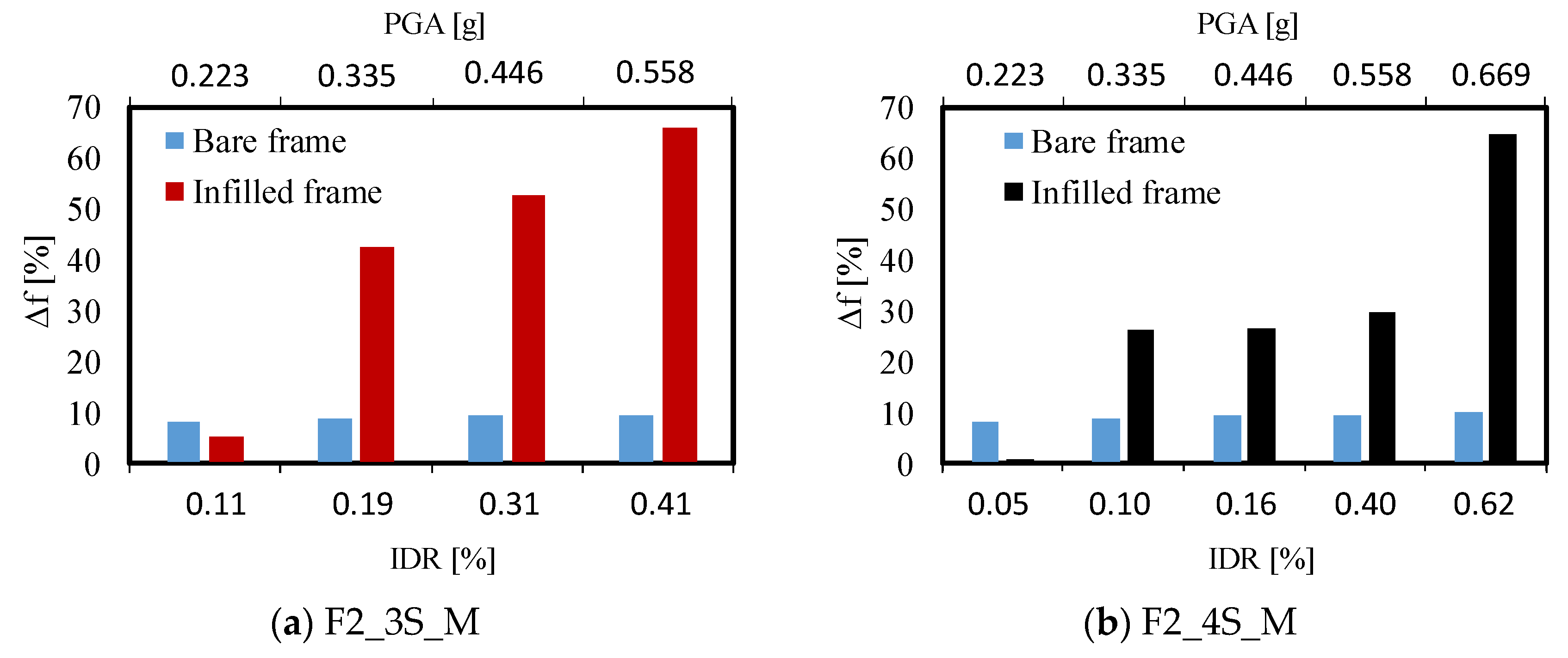
5.3. Frequency Variation for Increasing Damage Level
6. Conclusions
- The fundamental frequency of the bare frame (i.e., structural component) is in the ratio 1 to 4 (25%) with respect to the fundamental frequency of the infilled frame in the undamaged configuration for the first in-plane mode and 4 to 5 (about 80%) in the first out-of-plane mode;
- Output-only modal identification tests that were output for the first in-plane mode attested that the experimental damage occurred in infill walls at the end of the loading sequences for a PGA = 0.558–0.669 g (IDR = 0.41–0.62%), consisting of the crushing of bricks and classified as DL2-DL2/DL3, produced a variation in the fundamental frequency of the infilled RC frames of about 60% with respect to the undamaged configuration;
- For the first out-of-plane mode, modal identification test records from the two tests show that a DL2 damage to infill walls caused a reduction of fundamental frequency of about 20%;
- The FE model has shown to predict the experimental static and dynamic performance of tested specimens before and after damage with a good degree of accuracy, slightly underestimating the experimental fundamental frequencies ranging between 2% and 10%;
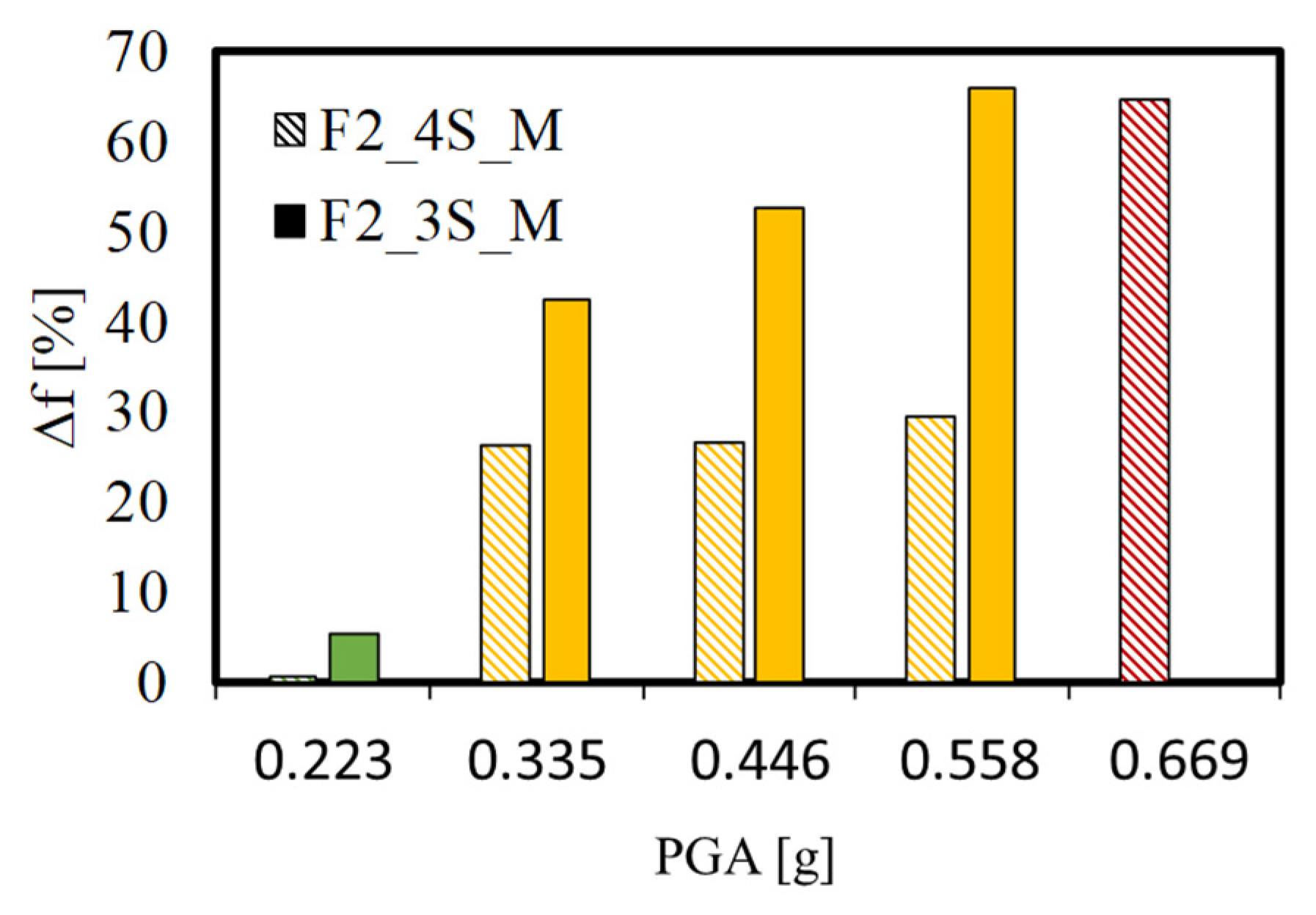
- The numerical nonlinear analyses allowed the assessment of the contribution of structural and non-structural damage to the overall frequency variations. The analysis results confirmed that the different boundary conditions of infill walls affected the frequency variation in RC frames subjected to the same ground shaking. In detail, greater frequency variations are associated with the three-sided boundary condition with respect to the four-sided one. However, in both cases, a significant variation of frequency due to seismic damage is observed for a PGA = 0.335 g (IDR = 0.10–0.19%);
- For the tested specimens, the maximum frequency variation due to structural damage is 10% of the bare frame undamaged frequency for a PGA = 0.669 g.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dolce, M.; Papa, F.; Pizza, A.G. DPCM 8/8/2014. Manuale per La Compilazione Della Scheda Di 1° Livello Di Rilevamento Danno, Pronto Intervento e Agibilità per Edifi Ci Ordinari Nell’emergenza Post-Sismica (AeDES). Seconda Edizione. 2014; pp. 1–121. Available online: https://www.protezionecivile.gov.it/it/pubblicazione/manuale-la-compilazione-della-scheda-di-primo-livello-di-rilevamento-di-danno-pronto-intervento-e-agibilita-edifici-ordinari-nellemergenza-post (accessed on 10 March 2023).
- NZSEE. The Seismic Assessment of Existing Buildings–Tecnichal Guidelines for Engineering Assessments—Part B; Ministry of Business Innovation and Employment: Wellington, New Zealand, 2017. [Google Scholar]
- Xu, J.G.; Feng, D.C.; Mangalathu, S.; Jeon, J.S. Data-Driven Rapid Damage Evaluation for Life-Cycle Seismic Assessment of Regional Reinforced Concrete Bridges. Earthq. Eng. Struct. Dyn. 2022, 51, 2730–2751. [Google Scholar] [CrossRef]
- Varriano, N.; Rainieri, C.; Gargaro, D.; Fabbrocino, G.; Cardillo, A. The Role of Dynamic Testing in Rapid Screening of Seismic Vulnerability of Strategic Reinforced Concrete Buildings Il Ruolo Delle Prove Dinamiche Nella Valutazione Speditiva Di Vulnerabilità Sismica Di Edifici Strategici in Cemento Armato; Pisa University Press: Pisa, Italy, 2019; pp. 12–21. [Google Scholar]
- Rainieri, C.; Fabbrocino, G. Operational Modal Analysis of Civil Engineering Structures. In Operational Modal Analysis of Civil Engineering Structures; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Rainieri, C.; Rosati, I.; Cieri, L.; Fabbrocino, G. Development of the Digital Twin of a Historical Structure for SHM Purposes. In European Workshop on Structural Health Monitoring; Lecture Notes in Civil Engineering; Springer: Cham, Switerland, 2023; Volume 254, pp. 639–646. [Google Scholar] [CrossRef]
- Marra, A.; Trizio, I.; Fabbrocino, G.; Savini, F. Digital Models for E-Conservation: The HBrIM of a Bridge along the Aterno River. SCIRES-IT-Sci. Res. Inf. Technol. 2021, 11, 83–96. [Google Scholar] [CrossRef]
- Rainieri, C.; Notarangelo, M.A.; Fabbrocino, G. Experiences of Dynamic Identification and Monitoring of Bridges in Serviceability Conditions and after Hazardous Events. Infrastructures 2020, 5, 86. [Google Scholar] [CrossRef]
- Rainieri, C.; Marra, A.; Fabbrocino, G. On the Estimation of the Fundamental Modal Properties of Italian Historical Masonry Towers. Ing. Sismica 2014, 31, 4–16. [Google Scholar]
- Rosati, I.; Fabbrocino, G.; Rainieri, C. A Discussion about the Douglas-Reid Model Updating Method and Its Prospective Application to Continuous Vibration-Based SHM of a Historical Building. Eng. Struct. 2022, 273, 115058. [Google Scholar] [CrossRef]
- Lorenzoni, F.; Casarin, F.; Modena, C.; Caldon, M.; Islami, K.; da Porto, F. Structural Health Monitoring of the Roman Arena of Verona, Italy. J. Civ. Struct. Health Monit. 2013, 3, 227–246. [Google Scholar] [CrossRef]
- Zanon, P.; Bursi, O.S.; Erlicher, S.; Zonta, D.; Clemente, P.; Indirli, M. Intervention Scenarios on the Basilica of San Gaudenzio Dome in Novara. In Proceedings of the International Seventh Seminar on Seismic Isolation, Passive Energy Dissipation and Active Control of Vibrations of Structures, Assisi, Italy, 2–5 October 2001; pp. 19–20. [Google Scholar]
- Chiorino, M.A.; Ceravolo, R.; Spadafor, A.; Zanotti Fragonara, L.; Abbiati, G. Dynamic Characterization of Complex Masonry Structures: The Sanctuary of Vicoforte. Int. J. Archit. Herit. 2011, 5, 296–314. [Google Scholar] [CrossRef]
- Sabia, D.; Aoki, T.; Cosentini, R.M.; Lancellotta, R. Model Updating to Forecast the Dynamic Behavior of the Ghirlandina Tower in Modena, Italy. J. Earthq. Eng. 2015, 19, 1–24. [Google Scholar] [CrossRef]
- Altunişik, A.C.; Karahasan, O.Ş.; Genç, A.F.; Okur, F.Y.; Günaydin, M.; Kalkan, E.; Adanur, S. Modal Parameter Identification of RC Frame under Undamaged, Damaged, Repaired and Strengthened Conditions. Meas. J. Int. Meas. Confed. 2018, 124, 260–276. [Google Scholar] [CrossRef]
- Günaydin, M.; Adanur, S.; Altunişik, A.C.; Mosallam, A.; Sevim, B. Dynamic Characteristics Monitoring Changes of Damaged and Retrofitted RC Buildings. Exp. Tech. 2022, 46, 457–484. [Google Scholar] [CrossRef]
- Inci, P.; Goksu, C.; Tore, E.; Ilki, A. Effects of Seismic Damage and Retrofitting on a Full-Scale Substandard RC Building-Ambient Vibration Tests. J. Earthq. Eng. 2022, 26, 5747–5774. [Google Scholar] [CrossRef]
- Goksu, C.; Inci, P.; Demir, U.; Yazgan, U.; Ilki, A. Field Testing of Substandard RC Buildings through Forced Vibration Tests. Bull. Earthq. Eng. 2017, 15, 3245–3263. [Google Scholar] [CrossRef]
- Durmazgezer, E.; Yucel, U.; Ozcelik, O. Damage Identification of a Reinforced Concrete Frame at Increasing Damage Levels by Sensitivity-Based Finite Element Model Updating. Bull. Earthq. Eng. 2019, 17, 6041–6060. [Google Scholar] [CrossRef]
- Del Vecchio, C.; Di Ludovico, M.; Verderame, G.M.; Prota, A. Pseudo-Dynamic Tests on Full-Scale Two Storeys RC Frames with Different Infill-to-Structure Connections. Eng. Struct. 2022, 266, 114608. [Google Scholar] [CrossRef]
- Naeim, F.; Kelly, J.M. Design of Seismic Isolated Structures: From Theory to Practice; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Cardone, D.; Perrone, G. Developing Fragility Curves and Loss Functions for Masonry Infill Walls. Earthq. Struct. 2015, 9, 257–279. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal Identification of Output-Only Systems Using Frequency Domain Decomposition. Smart Mater. Struct. 2001, 10, 441–445. [Google Scholar] [CrossRef]
- McKenna, F. Open System for Earthquake Engineering Simulation. Available online: http://opensees.berkeley.edu (accessed on 10 March 2023).
- De Risi, M.T.; Ricci, P.; Verderame, G.M. Modelling Exterior Unreinforced Beam-Column Joints in Seismic Analysis of Non-Ductile RC Frames. Earthq. Eng. Struct. Dyn. 2017, 46, 899–923. [Google Scholar] [CrossRef]
- Kyriakides, N.; Chrysostomou, C.Z.; Kyriakides, N.C.; Kotronis, P.; Georgiou, E. Derivation of Fragility Curves for Rc Frames Retrofitted with Rc Infill Walls Based on Full-Scale Pseudodynamic Testing Results Engineer: Civil Engineering and Geomatics Innovative Research on Heritage View Project Incorporation of End-of-Life Tyre Produc. In Proceedings of the VII European Congress on Computational Methods in Applied Sciences and Engineering, Crete Island, Greece, 5–10 June 2016; pp. 5–10. [Google Scholar]
- Panagiotakos, T.B.; Fardis, M.N. Seismic Response of Infilled RC Frame Structures. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996; pp. 1–8. [Google Scholar]
- Verderame, G.M.; Ricci, P.; De Risi, M.T.; Del Gaudio, C. Experimental Assessment and Numerical Modelling of Conforming and Non-Conforming RC Frames with and without Infills. J. Earthq. Eng. 2022, 26, 573–614. [Google Scholar] [CrossRef]


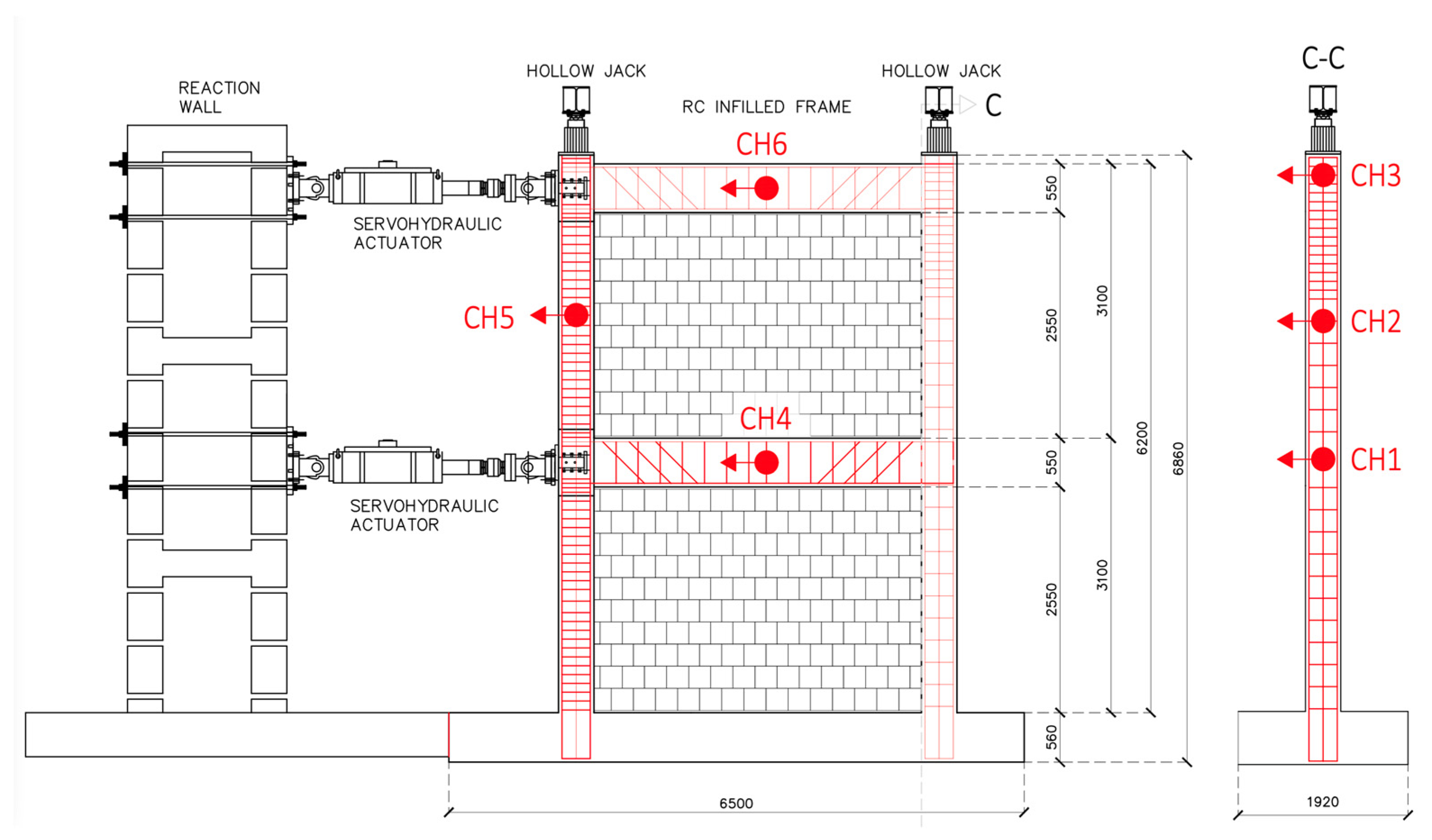


| Test ID | Infill Walls | Notes |
|---|---|---|
| F2_3S_M | Connected to the frame with a mortar on three sides, with a gap between the upper beam and the wall | After a pseudo-dynamic test, the infill walls are demolished and re-built |
| F2_4S_M | Connected to the frame on four sides with mortar | The frame is the same as those of previous test, with new infill walls |
| Intensity [%] | PGA [g] | F2_3S_M | F2_4S_M |
|---|---|---|---|
| 0 | - | OMA | OMA |
| 10 | 0.045 | - | - |
| 25 | 0.112 | - | - |
| 50 | 0.223 | - | - |
| 75 | 0.335 | - | - |
| 100 | 0.446 | - | - |
| 125 | 0.558 | OMA + OMA without infill walls | - |
| 150 | 0.669 | - | OMA |
| Earthquake Intensity [%] | PGA [g] | [-] | Test Description |
|---|---|---|---|
| 10 | 0.045 | - | Intensity 10%. Peak Interstorey Drift 0.01%. No Damage (DL0) |
| 25 | 0.112 | - | Intensity 25%. Peak Interstorey Drift 0.01%. No Damage (DL0) |
| 50 | 0.223 | 0.143 | Intensity 50%. Peak Interstorey Drift 0.11%. Infill-frame separation and light diagonal cracking of infill (DL0/DL1) |
| 75 | 0.335 | 0.175 | Intensity 75%. Peak Interstorey Drift 0.19%. Light diagonal cracking of infill (DL1) |
| 100 | 0.446 | 0.125 | Intensity 100%. Peak Interstorey Drift 0.31%. Significant diagonal cracking of infill and crushing of corners (DL2) |
| 125 | 0.558 | 0.135 | Intensity 125%. Peak Interstorey Drift 0.41%. Crushing of some bricks (DL2) |
| Earthquake Intensity [%] | PGA [g] | [-] | Test Description |
|---|---|---|---|
| 10 | 0.045 | - | Intensity 10%. Peak Interstorey Drift 0.01%. No Damage (DL0) |
| 25 | 0.112 | - | Intensity 25%. Peak Interstorey Drift 0.01%. No Damage (DL0) |
| 50 | 0.223 | 0.206 | Intensity 50%. Peak Interstorey Drift 0.05%. Infill-frame separation (DL0/DL1) |
| 75 | 0.335 | 0.166 | Intensity 75%. Peak Interstorey Drift 0.10%. Light diagonal cracking of infill (DL1) |
| 100 | 0.446 | 0.178 | Intensity 100%. Peak Interstorey Drift 0.16%. Significant diagonal cracking of infill (DL2) |
| 125 | 0.558 | 0.153 | Intensity 125%. Peak Interstorey Drift 0.40%. Significant diagonal cracking of infill and column cracking due to infill action (DL2) |
| 150 | 0.669 | 0.100 | Intensity 150%. Peak Interstorey Drift 0.62%. Wide diagonal cracking of infill and crushing of some bricks (DL2/DL3) |
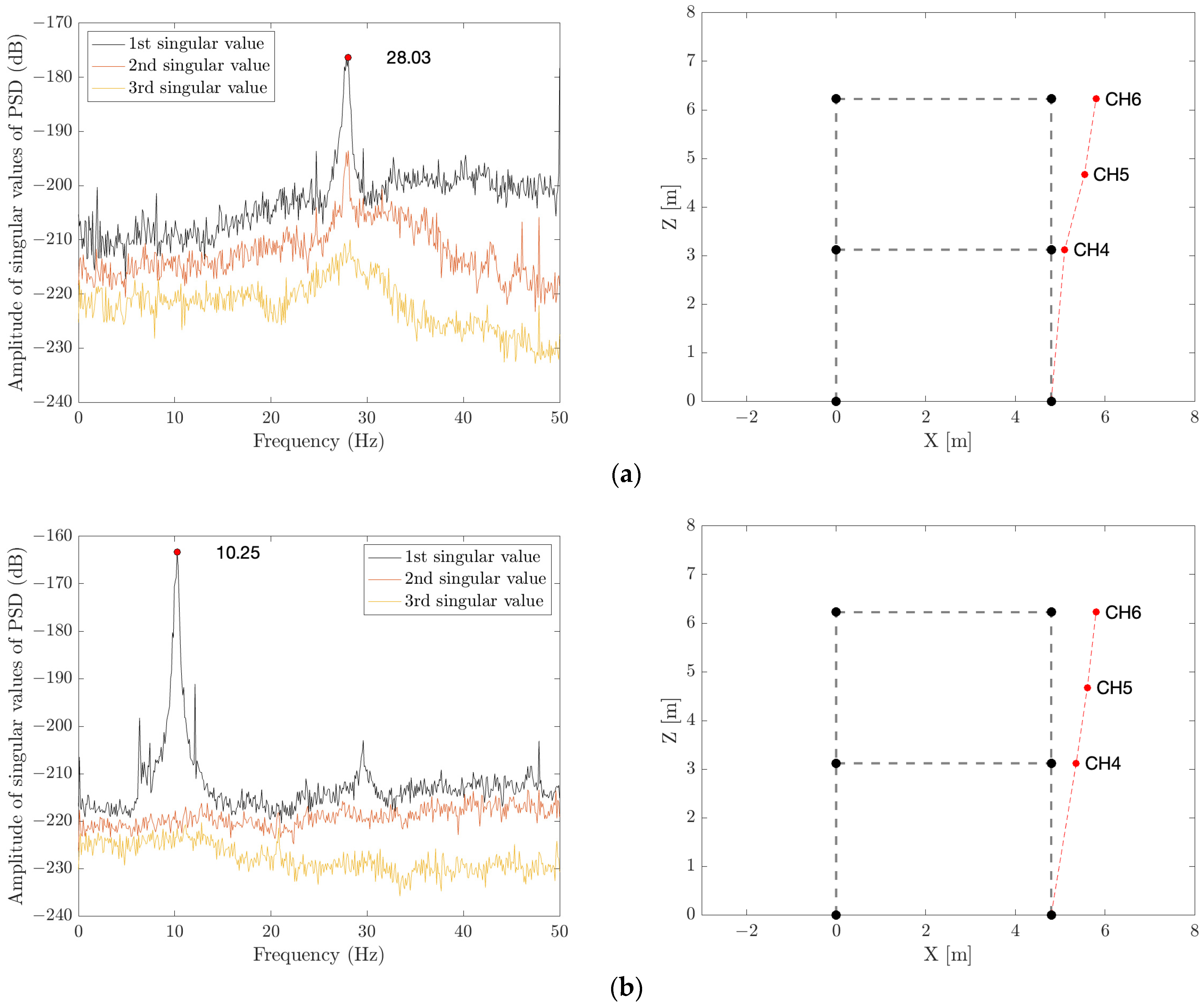
| ID | Configuration | IP 1st Frequency [Hz] | Frequency Variation [%] | Mode Shape | Peak Drift [%] | Observed Damage | Damage Level |
|---|---|---|---|---|---|---|---|
| F2_3S_M | Undamaged | 25.4 | - | 1.00;0.78;0.59 | 0.41 | Significant diagonal cracking of infill and crushing of corners | DL2 |
| Damaged | 9.5 | −63 | 1.00;0.82;0.53 | ||||
| Bare | 6.5 | −74 | 1.00;0.83;0.50 | ||||
| F2_4S_M | Undamaged | 28.0 | - | - | 0.62 | Diagonal cracking of infills and crushing of some bricks | DL2/DL3 |
| Damaged | 10.2 | −63 | 1.00;0.81;0.56 |
| ID | Configuration | OOP 1st Frequency [Hz] | Frequency Variation [%] | Mode Shape | Peak Drift [%] | Observed Damage | Damage Level |
|---|---|---|---|---|---|---|---|
| F2_3S_M | Undamaged | 3.4 | - | 1.00;0.10;0.03 | 0.41 | Significant diagonal cracking of infill and crushing of corners | DL2 |
| Damaged | 2.6 | −23 | 1.00;0.70;0.11 | ||||
| Bare | 2.6 | −23 | - | ||||
| F2_4S_M | Undamaged | 2.8 | - | - | 0.62 | Diagonal cracking of infills and crushing of some bricks | DL2/DL3 |
| Damaged | 2.3 | −19 | 1.00;0.69;0.12 |
| Backbone Point | ||
|---|---|---|
| Cracking | 0.04 | |
| Pre-peak | 0.17 | |
| Peak | 0.49 | |
| Residual | 4.41 |
| Backbone of Infills | K [MPa] | F [kN] |
|---|---|---|
| Cracking | K1 = GLt/H | Fcr = τcrLt |
| Peak | K2 = 0.03K1 | Fpeak = 1.3Lt |
| Post-Peak | K3 = -0.01K1 | Fu = 0.1Fpeak |
| ID | Configuration | Experimental Frequency [Hz] | Numerical Frequency [Hz] | Δ [%] |
|---|---|---|---|---|
| F2_3S_M | Undamaged | 25.4 | 24.9 | −2 |
| Damaged | 9.5 | 8.5 | −10 | |
| Bare | 6.5 | 6.3 | −4 | |
| F2_4S_M | Undamaged | 27.8 | 27.4 | −1 |
| Damaged | 10.2 | 9.7 | −5 |
| Configuration | Earthquake Intensity [%] | PGA [g] | IDR [%] | Numerical Frequency [Hz] | Frequency Variation [%] | Numerical Damage | Experimental DL |
|---|---|---|---|---|---|---|---|
| Bare frame | 0 | 0.000 | - | 6.90 | - | - | - |
| 50 | 0.223 | 0.05 | 6.33 | −8.3 | - | DL0 | |
| 75 | 0.335 | 0.10 | 6.30 | −8.7 | - | DL0 | |
| 100 | 0.446 | 0.16 | 6.26 | −9.3 | - | DL0 | |
| 125 | 0.558 | 0.40 | 6.25 | −9.3 | - | DL0 | |
| 150 | 0.669 | 0.62 | 6.20 | −10.1 | - | DL0 | |
| Infilled frame F2_3S_M | 0 | 0.000 | - | 24.9 | - | - | - |
| 50 | 0.223 | 0.11 | 23.6 | −5.2 | Infills first cracking | DL0/DL1 | |
| 75 | 0.335 | 0.19 | 14.3 | −42.5 | - | DL1 | |
| 100 | 0.446 | 0.31 | 11.8 | −52.6 | Infill crushing | DL2 | |
| 125 | 0.558 | 0.41 | 8.5 | −65.9 | - | DL2 | |
| Infilled Frame F2_4S_M | 0 | 0.000 | - | 27.4 | - | - | - |
| 50 | 0.223 | 0.05 | 27.2 | −0.7 | Infill first cracking | DL0/DL1 | |
| 75 | 0.335 | 0.10 | 20.2 | −26.3 | - | DL1 | |
| 100 | 0.446 | 0.16 | 20.1 | −26.6 | - | DL2 | |
| 125 | 0.558 | 0.40 | 19.3 | −29.6 | Infill crushing | DL2 | |
| 150 | 0.669 | 0.62 | 9.7 | −64.6 | - | DL2/DL3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lubrano Lobianco, A.; Del Zoppo, M.; Rainieri, C.; Fabbrocino, G.; Di Ludovico, M. Damage Estimation of Full-Scale Infilled RC Frames under Pseudo-Dynamic Excitation by Means of Output-Only Modal Identification. Buildings 2023, 13, 948. https://doi.org/10.3390/buildings13040948
Lubrano Lobianco A, Del Zoppo M, Rainieri C, Fabbrocino G, Di Ludovico M. Damage Estimation of Full-Scale Infilled RC Frames under Pseudo-Dynamic Excitation by Means of Output-Only Modal Identification. Buildings. 2023; 13(4):948. https://doi.org/10.3390/buildings13040948
Chicago/Turabian StyleLubrano Lobianco, Alessandro, Marta Del Zoppo, Carlo Rainieri, Giovanni Fabbrocino, and Marco Di Ludovico. 2023. "Damage Estimation of Full-Scale Infilled RC Frames under Pseudo-Dynamic Excitation by Means of Output-Only Modal Identification" Buildings 13, no. 4: 948. https://doi.org/10.3390/buildings13040948
APA StyleLubrano Lobianco, A., Del Zoppo, M., Rainieri, C., Fabbrocino, G., & Di Ludovico, M. (2023). Damage Estimation of Full-Scale Infilled RC Frames under Pseudo-Dynamic Excitation by Means of Output-Only Modal Identification. Buildings, 13(4), 948. https://doi.org/10.3390/buildings13040948









