Abstract
The development of Structural Health Monitoring (SHM) and Non-Destructive Testing (NDT) techniques has rapidly evolved and matured over the past few decades. Advances in sensor technology have facilitated deploying SHM systems for large-scale structures and local NDT of structural members. Although both methods have been successfully applied to identify structural damage in various systems, Environmental and Operational Condition (EOC) variations can influence sensor measurements and mask damage signatures in the structural response. EOCs include environmental conditions, such as temperature, humidity, and wind, as well as operational conditions, such as mass loading, vibration, and boundary conditions. The effect of EOCs can significantly undermine the reliability and robustness of damage assessment technologies and limit their performance. Thus, successful SHM and NDT systems can compensate for changing EOCs. This paper provides a state-of-the-art review of the effects of EOCs on SHM and NDT systems. It presents recent developments in advanced sensing technology, signal processing, and analysis techniques that aim to eliminate the masking effect of EOC variations and increase the damage sensitivity and performance of SHM and NDT systems. The paper concludes with current research challenges, trends, and recommendations for future research directions.
1. Introduction
The early 1980s marked the beginning of vibration-based structural monitoring for civil infrastructure. Monitoring the health of structures was primarily based on modal characteristics, and acquired data, such as frequency, mode shapes, mode curvature, and the dynamic flexibility matrix [1,2,3,4], were correlated with damage. For the functioning of modern society, it is vital to maintain structures in a safe and reliable condition during their service lives [5,6]. Accordingly, the health of a structure can be defined as the present ability of a system to perform its intended function safely and cost-effectively against the anticipated risks during its service life. To ensure structural integrity, SHM systems have been developed for periodic health assessment [7] and employed for various structures, such as buildings [8,9,10,11,12,13], cultural heritage structures [14,15,16,17], bridges [18,19,20,21,22,23,24], underground structures [25,26], dams [27], offshore structures [28,29,30,31,32,33], wind turbines [34,35,36,37,38], ships [39,40,41,42], and aerospace infrastructure [43,44,45,46].
An SHM system comprises various components, including networks, data transmission systems, data acquisition and processing units, damage identification algorithms, and decision-making procedures [47,48,49]. Depending on the application, various SHM methods have been developed and investigated [42,50,51,52,53,54].
SHM can be classified into two primary approaches: passive SHM and active SHM [55]. In passive techniques, different operational parameters are passively measured, and the results are interpreted to determine the state of the structure’s health. While passive methods can be successful for specific applications, they lack accuracy, and damage might stay undetected [56,57]. On the other hand, active SHM enables the direct and targeted detection and evaluation of structural damage resulting in more reliable and accurate health assessment. By comparison, this approach to SHM is similar to non-destructive evaluation (NDE) [58], except that active SHM takes a step further and employs permanent sensors to allow for continuous on-demand structural health assessment [59,60]. The configuration of active and passive SHM systems is illustrated in Figure 1.
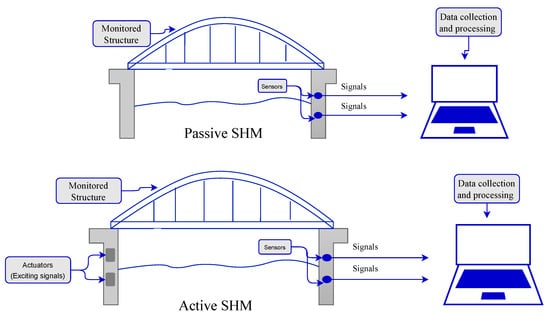
Figure 1.
Passive and active SHM systems.
SHM methods can be implemented utilizing different types of sensors, such as accelerometers [61,62], vibrating wire transducers [63], fiber optic sensors [64], linear variable differential transformer (LVDT) [65], strain gauges [66], load cells [67], temperature sensors [68], acoustic emission sensors [69], an inclinometer (slope indicator) [70], a tiltmeter [71], antenna sensors [72], Resonant(LC)/Resistor–Capacitor(RC) circuit sensors [73,74], and Micro-Electro-Mechanical System sensors (MEMS) [75]. MEMS and LC/RC circuit sensors can be employed in active and passive SHM approaches. On the other hand, antenna sensors are limited to passive SHM systems.
Using numerical tools, measured data in an SHM system can be converted into meaningful information that can detect damage and indicate its location and severity [76]. Some methods include Finite Difference Techniques [77], the Finite Element Method [78], Perturbation Techniques [79], the Boundary Element Method [80], and the Spectral Finite Element Method [81]. Mathematical models in SHM are described by partial differential equations (PDEs) that are emanated using assumptions regarding the behavior of field variables. Generally, in both cases of hyperbolic and elliptic PDEs, obtaining an analytical solution is challenging; hence, numerical techniques are required. The Weighted Residual Technique (WRT) was developed to indicate the most suitable numerical method. Various numerical techniques and their applications in SHM are presented in Table 1.

Table 1.
Numerical methods and their applications in SHM.
As a result of technological advancements in the Internet of Things (IoT), this tool enables SHM to be incorporated into the Internet for continuous data tracking regardless of time or location [95,96].
SHM approaches vary based on the monitoring objective, site, system conditions, available sensing equipment, expert knowledge, and budget. As such, various SHM approaches have been developed that consider one of the following items:
- The type of measured data, such as vibration [97] or static response measurements [98].
- The type of damage signatures, such as modal strain energy, precursor transformation, modal flexibility-based deflection and curvature, Kolmogorov–Smirnov (KS) statistical test distance, and model residual errors [99,100,101].
- The monitored section of the structure, such as the entire system or subspace identification [102].
- The type of data analysis algorithm used, such as neural networks and machine-learning-based algorithms. A detailed list and description of these algorithms are presented in Section 4 [103].
It has been demonstrated that SHM technology can provide significant economic and life-safety benefits [104,105]. Nevertheless, due to the multidisciplinary characteristics of SHM technologies, using SHM in real-world applications is still challenging and demands ongoing research [106,107]. Challenges in SHM include insufficient data from existing structures [108], cost restrictions [109,110], a large variety of systems, and the effects of EOCs. Since the 1980s, a considerable volume of research on SHM has been conducted. Over 20,000 papers have been published in the last two decades (according to a Google Scholar search on “structural health monitoring” completed in March 2023). Figure 2 displays the number of papers published between 2003 and 2023 with the words “structural health monitoring” or “environmental and operational conditions” in the title. A breakdown of various EOCs investigated for SHM applications, including temperature, wind, humidity, boundary conditions, and mass loading, is presented in Figure 3. SHM methods can generally be classified as local or global methods. Figure 4 displays various methods divided into global and local approaches.
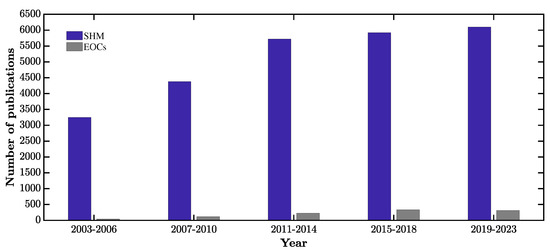
Figure 2.
Number of publications with SHM or EOCs in their title.
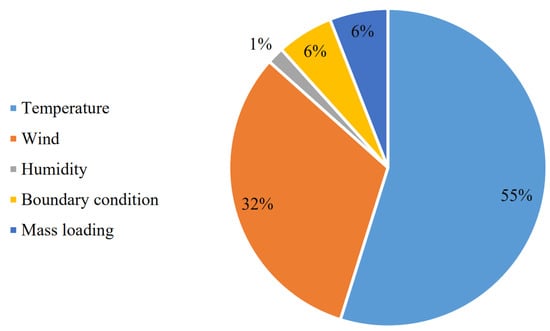
Figure 3.
Breakdown of various EOCs studied for SHM.
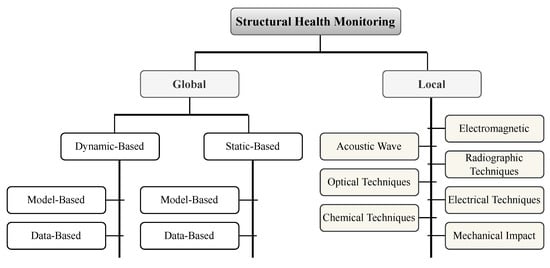
Figure 4.
Classification of SHM methods.
Compared to SHM methods, NDT techniques are generally one-time evaluations carried out manually or semi-manually to assess the condition of a material or a structure. They are typically used to detect hidden damage or map deterioration and identify its underlying cause within a structure. NDT applications are often operated contactless to avoid damage to the material integrity and functioning of the system under assessment. Various NDT techniques are implemented into routinely scheduled inspection and maintenance operations for the continuous monitoring and management of civil structures and also play an integral role in SHM systems [111]. The selection of suitable NDT technology depends on various factors, including the type and physical properties of the material or structure, the desired parameters, assessment aims, available expert knowledge, and budget restrictions. Often, it is necessary to use a combination of different types of NDT methods. By integrating multiple techniques, additional parameters can be evaluated and added to the measurement process, which in turn enhances accuracy [112,113]. Significant challenges in NDE are noise exposure, and analysis and interpretation of measurement data, which often require expert knowledge [54,114,115,116]. Commonly used NDT methods are eddy-current, ultrasonic, acoustic emission, laser scanning, and ground penetration radar (GPR) technologies. As such, laser scanning is a remote sensing technology that utilizes focused pulses of coherent light. Distances are calculated by measuring the transmission of light beams reflected from structures. The availability of a large quantity of data allows for detailed assessment. The scans generated by point clouds contain data of all collected points from the material or structure being tested and are typically transformed into precise and highly detailed 3D maps. These cloud maps include valuable information that can reveal structural characteristics and help identify the extent of possible deterioration. Over time, applying this technique can provide a clear picture of damage progression [117,118]. Due to these capabilities, laser scanning has become increasingly popular for NDT and SHM applications [119,120].
GPR is often used for civil engineering applications due to its affordability and rapid processing, particularly for defect inspections where cracks and voids could threaten concrete and masonry integrity [121]. This method requires a balance between penetration depth and the desired solution. For instance, a higher resolution is achieved with a higher operating frequency and a lower penetration depth [122].
A significant challenge in SHM and NDT arises from varying environmental and operational conditions. EOCs can mask the signature of damage in the structural responses in both passive and active assessment techniques. Variations in EOCs may cause a more significant impact on structures than damage-induced changes. By overlooking these influences, damage detection accuracy may be affected and lead to unreliable conclusions. Some common EOCs are described below:
- Environmental conditions
- -
- Temperature: Due to temperature-related expansion and contraction of materials, the dynamic properties of a structure can change. The findings of several studies have been reported on the influences of temperature changes on signal measurements from SHM systems [123,124].
- -
- Humidity: Due to the absorption of moisture, material properties can be altered, potentially leading to false damage features and incorrect damage identifications [125].
- -
- Wind: Wind-induced vibration plays a critical and influential role in SHM systems of long-span bridges. Li et al. [126] studied the effects of wind excitation on damage assessment.
- Operational conditions
- -
- Mass loading: Mass loadings, such as traffic, can introduce challenges to SHM techniques as another operational variable. Several papers on SHM have studied the effects of mass loading on the measured signals from SHM systems [127,128].
- -
- Marine growth in offshore structures: Offshore structures are known to be adversely affected by marine growth. The roughened surfaces can increase the drag coefficient of the structure. Moreover, this phenomenon causes changing mass loads to the structures. Therefore, this challenge should be considered in SHM systems of marine structures [129].
EOCs can influence various material and structural properties, such as stiffness and boundary conditions, as well as vibration characteristics, including natural frequencies, mode shapes, and damping. Temperature affects material and vibration properties in several ways, including solar radiation, day-night alternations, and seasonal shifts. Generally, structures are simultaneously exposed to different EOCs. Temperature variations can cause significant and slow changes in stress, leading to fast-loading changes in structures such as TV towers [130].
A comparative analysis was conducted using a weigh-in-motion roadway scale on the consequences of thermal stresses and traffic loads on a steel bridge. It was reported that thermal stresses are significantly more influential than stresses induced by traffic [131]. Vibration properties of in-service structures can change over time as EOCs vary. Therefore, it is necessary to compensate for these variables in SHM measurements. Table 2 summarizes the effects of typical types of damage and EOCs on the properties of composite materials, including stiffness, mass, damping, conductivity, and boundary conditions. As can be seen, damage and EOCs can have similar effects on the material properties, leading to false damage identifications. Recent studies considering the impact of EOCs on laser scanning and GPR testing are presented in Table 3.

Table 2.
Relationship between environmental conditions and local properties of composite material: (∘) average, (+) strong, and (−) weak influence; (N) Notch, (FC) Fiber crack, (MC) Matrix crack, (Dl) Delamination, (Dt) Dirt, (T) Temperature, (M) Moisture, (ER) Electromagnetic Radiation and (ML) Mechanical Load [58].

Table 3.
Examples of studies considering the effects of EOCs on NDE using laser scanning and GPR techniques.
2. Effects of Varying EOCs in SHM
As outlined above, varying EOCs have a significant effect on damage signatures and have been recognized by the research community as a major concern for the reliability and accuracy of current SHM systems [140]. Environmental conditions include temperature, wind, and humidity. Seasonal changes are a crucial factor causing various environmental changes. Mass loadings, such as permanent loads, ship impact, highway, traffic, and railway loads, are examples of operational conditions. Figure 5 provides an overview of the mechanisms by which various EOCs can influence modal properties.
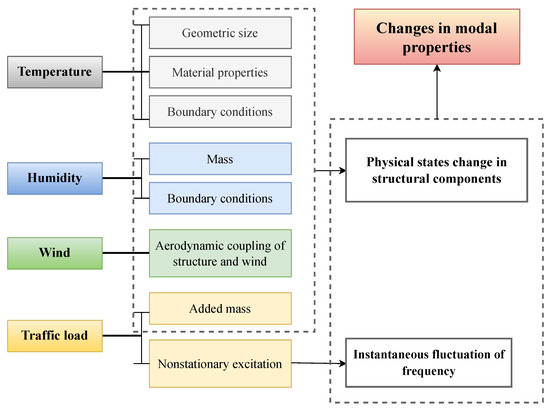
Figure 5.
Influence mechanisms of EOCs on modal properties [141].
Civil structures under EOCs often exhibit inherent non-stationary dynamic responses, and quasi-static signals can obscure any shifts in the measured structural response due to damage. As a result, any occurrence or progression of a structural fault or a variation in performance malfunction can be challenging to detect. Sohn [142] stated that some SHM methods neglect the considerable effect of changing EOCs. Indeed, the confounding effects resulting from EOCs represent one of the main obstacles to the widespread application of SHM in the industry. Hence, to ensure accurate and reliable condition monitoring, it is therefore essential to consider the effects of EOCs. Some reviews on several potential solutions for dealing with the critical effects of variations in EOCs on structural responses can be found in [143,144,145,146]. The following sections address the effect of different EOCs in SHM systems.
2.1. Temperature
The temperature sensitivity of structural responses is the most widely studied aspect of EOCs on damage-sensitive features [147,148]. SHM systems are continuously subjected to various temperature-induced effects, such as seasonal transitions, day-night shifts, and solar radiation. Temperature and structural responses are strongly correlated [149,150]. As such, the temperature can significantly affect the dynamic response of structures. This is due to its effects on the stiffness of elements and their potential impact on a system’s material properties and boundary conditions. A comprehensive review of the relationship between ambient temperature and vibration properties of long-span bridges was published by Zhou and Yi [151]. Under the same damage scenarios, temperature variations can increase the severity of structural damage. In an experimental study, Farrar et al. [152] anticipated a reduction in the stiffness of girders’ elements and natural frequencies as a result of the inflicted damage trend. Although the actual observed outcomes were not as expected, the girder’s natural frequency rose for the first two faults before decreasing. It was found that the initial rise in the girder’s frequency was caused due to ambient temperature changes in the laboratory. Xia et al. [153] developed a novel technique based on structural vibration variations versus the structure’s non-uniform temperature field to quantify the environmental effects on the structural vibration characteristics. The authors used thermodynamic models to estimate the temperature of various system elements at different times. This enabled the analysis of the structure’s natural frequencies through FE analysis. The authors repeated the procedures at different times to calculate the variation in the frequencies. They observed a significant linear correlation between the recorded natural frequencies rather than the air or surface temperatures. Zhou and Sun [154] addressed the mechanisms of temperature-induced changes in mid-span and girder length deflection through plane geometries. They analyzed a cable-stayed bridge using FE analysis based on recorded field measurements from the case study. Kromanis et al. [155] conducted research aiming to understand bridge behavior under variations in environmental conditions by analyzing long-term records. Data from the Cleddau Bridge was used to analyze thermal effects in steel box-girder bridges, and numerical models were developed to estimate the forces at the supports resulting from bearing movements. The authors demonstrated the importance of considering a spectrum of temperature distribution cases that exceed those in design codes for the purposes of evaluating thermal effects in a reliable manner.
The temperature has been reported to influence wave propagation within materials. Roy et al. [156] studied the effect of ambient temperature on structural wave propagation. Numerical simulations and analytical models were used to compensate for the effect of temperature on piezo-sensor responses. This method only requires a small set of baseline sensor data for estimating unknown model parameters, making it efficient and practical for structural condition monitoring. Moreover, the proposed method was shown to be capable of damage localization. Schubert et al. [157] investigated the effects of structural features and damage on the propagation and measurement of Lamb waves in combination with environmental conditions. An analysis of changes in sensor responses caused by reflections and interactions with stiffness discontinuities, unrelated and related to damage, was carried out using the local temporal coherence technique. As the report indicates, even in a climate-controlled laboratory environment, the effects of varying EOCs are inevitable.
Not only does temperature affect structural responses, but it can also affect deployed sensors’ characteristics, resulting in misleading sensor readings. For instance, Ai et al. [158] reported that temperature affected electromechanical admittance responses. Moreover, they observed different behaviors of electromechanical admittance signatures in surface-bonded and inside-embedded PZT transducers. Hoshyarmanesh et al. [159] found that elevated temperature can affect the impedance signals obtained from piezoelectric wafers. As such, a rise in temperature was found to lead to a slight decrease in the number of anti-resonance peaks and the actual impedance amplitude. Moreover, piezo films exhibited an increase in permittivity and capacitance of piezo-sensor networks due to rising temperatures.
Statistical distance metrics have been employed for detecting damage in structures under severe environmental variations. For instance, Deraemaeker and Worden [160] discussed using Mahalanobis squared distance of multivariate feature vectors obtained from damaged and healthy structures for robust novelty detection under significant environmental variability. Studies found a significant correlation between the structural response and the ambient temperature in concrete dams. For instance, Kang et al. [161] developed a dam health monitoring approach using recorded air temperatures for simulating temperature effects using kernel extreme learning machines. The proposed model examined recorded data of a concrete gravity dam, and it was shown to be practical for concrete dam behavior prediction. Caspani et al. [162] presented an approach to evaluate the efficacy of an SHM system accounting for temperature compensation. A primary focus of the study was on condition-state parameters describing the long-term response trend of pre-stressed concrete bridges, such as shrinkage and creep effects. An equation was developed for estimating the uncertainty associated with the long-term response trend of measurements with temperature compensation. The study showed that the recorded signals, model uncertainties, initiation time, and monitoring period affected the condition-state uncertainty.
Some techniques rely on historical data to construct a baseline against which the abnormal behavior of a structure can be pinpointed. Thus, a baseline is obtained based on the expected behavior of a healthy system subjected to varying temperature effects. For instance, Yue and Aliabadi [163] proposed a data-driven approach to reconstruct temperature baselines that can be applied to various structures with identical materials. According to the experiments, temperature effects on the phase and amplitude of guided wave measurements can be recognized as a dimensionless compensation factor. The researchers used a stiffened panel and a simple flat plate as case studies. They employed the extracted compensation factors to reconstruct baselines at different temperatures for guided wave measurements in these structures. Detecting and locating the damage was efficiently and accurately performed by taking advantage of the extracted temperature compensation factors. Mariani et al. [164] proposed a novel compensation approach to address both phase and velocity changes due to temperature variation. The proposed method reduced the residual signal from a set baseline and enabled more satisfactory damage detection performance than the typical baseline signal stretch technique. Aiming to address the effects of temperature, Salmanpour et al. [165] developed an approach based on baseline signal stretch with an improved minimum residual to derive a signal correction over an extensive range of temperatures. In addition to the technique’s application to a baseline comparison, they analyzed the efficacy and accuracy of the method for damage detection and localization through experiments on aluminum and carbon fiber-reinforced polymer panels. Yarnold et al. [166,167] developed a quantitative structural assessment technique based on responses induced by temperature variations, termed the Temperature-Based Structural Identification (TBSI) method. This approach can be used to assess the effects of thermal-induced strains on global displacements and member forces. A crucial aspect of this input-output relationship is its sensitivity to factors that pose modeling challenges, such as continuity and boundary conditions. Hence, it is highly beneficial for model updating. The method exploits the correlation between the boundary, the captured transfer function, and continuity conditions. It was found to be capable of detecting both linear and nonlinear behavior and is highly efficient in capturing signal patterns for long periods. Figure 6 shows the process of TBSI and general temperature-based SHM.
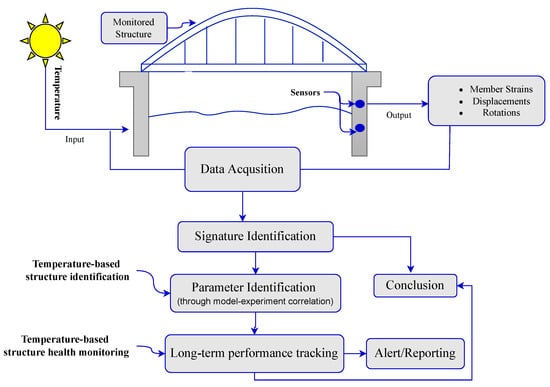
Figure 6.
SHM system based on TBSI technique.
New sensor arrays have been developed for compensating the effect of the temperature signature on sensors’ data. For instance, Dhingra et al. [168] developed a sensor for SHM at different temperatures based on Bragg grating (BG). As both the temperature and strain increase simultaneously, a direct proportionality relationship was observed in the Bragg wavelength. The results demonstrated the improved capability of the presented sensor. Such sensor arrays are often equipped with software to interpret the recorded data. For instance, Lambinet and Khodaei [169] developed a software platform for acquiring ultrasonic guided waves for the SHM of industrial-scale composite fuselage panels. The authors developed an SHM measurement platform and evaluated it under varying EOCs using a variety of sensors and sensor networks. The platform was found to be simple to operate, reliable, and scalable to large sub-components with handling protocols and optimized information acquisition. Other researchers employed numerical techniques to interpret the sensor array’s data without developing specific software. For instance, Bastani et al. [170] proposed a novel method using sensor arrays and statistical metric analysis to identify signal changes resulting from environmental variations and/or damage. The results were expected to show that environmental variations affect the output signals of different row sensors similarly. However, changes caused by damage did not affect all row and column sensors similarly. Hence, statistical metrics analysis was developed to identify environmental disturbances resulting from damage detection. This method was shown to be reliable in identifying damage through experimental validations.
Sensing technologies must be designed to withstand harsh environmental conditions. Sensors must resist high temperatures over sustained periods, as in sodium-cooled fast reactors, requiring specialized developments and evaluations. Laffont et al. [171] studied the development of temperature-resistant wavelength-multiplexed fiber Bragg gratings, which are increasingly used in nuclear power plant instrumentation, particularly for components exposed to high temperatures and radiation levels. Gao et al. [172] developed a PZT-based Lamb waves SHM strategy for long-term aircraft storage tanks under cryogenic conditions. This work performed a series of tests to identify the durability of PZT-epoxy sensor systems and the functionality of the NDT method under cryogenic conditions in long-term storage tanks. Experimental results indicated that the developed SHM technology was practical at cryogenic and room temperatures under high strain and long-term operation.
2.2. Wind
Bridge systems with long spans are particularly susceptible to wind loads, and as such, high winds can significantly affect these structures. Wind loads are defined by two main features, wind speed, and wind direction. These loadings influence the aerodynamic coupling between the structure and wind, modal parameters, and response amplitude. During strong winds or typhoons, wind-induced vibrations contribute more energy to a system than damping, causing it to flutter or buffet.
As the number of bridge systems across seas and rivers has grown in recent decades, there has been a large increase in research work addressing bridge wind engineering issues [173,174]. Studies found that high wind conditions have a complex effect on dynamic structural properties [129,175,176,177]. In general, in high winds, it is difficult to accurately identify a bridge’s modal parameters, and their estimates are subject to a substantial degree of uncertainty. A decrease in wind velocity was found to cause a reduction in the modal damping and the natural frequency of a suspension bridge. A quadratic function can be designated as the vertical amplitude of the bridge’s response to the wind speed. Moreover, the damping ratio depends on the vibration amplitude [178,179]. Advancements in NDT and SHM technologies have emerged as an option to equip in situ information platforms to study the wind resistance of long-span bridges. Weijtjens et al. [180] discussed how vibration measurements could assist operators in making more informed decisions on the structural health of their equipment. They found that wind conditions like wind speed and turbulence affect turbine vibration levels. Additionally, the authors investigated the interaction between loads and tower dynamics. Li et al. [181] investigated the wind-induced response of an air-supported structure. They reported that the equivalent static wind load technique based on the fundamentals of maximum displacement equivalence could be used to calculate wind-induced displacement responses. According to the study, the recommended approach is practical for wind resistance design; however, displacement responses were slightly higher than actual responses. During six tropical cyclones, Wang and Ni [182] collected field measurements of wind influence on a supertall structure. Field measurements were used to determine the dynamic properties of the system. This study provided practical information for wind-resistant designs and considered the wind effects on the SHM of skyscrapers. Zhou and Sun [183] investigated the influence of high winds on vibrational signals and changes in the modal parameters of a sea-crossing cable-stayed bridge system. The authors reported that most of the vehicles crossing the bridge are heavy-load container trucks. This work was defined as field evidence for the performance evaluation and the wind-resistant design of bridge systems in identical operational conditions considering wind effects. Zhu et al. [184] conducted a computational fluid dynamics study on a full-scale bridge. The simulated varying wind condition satisfied the characteristic of field data. This approach was shown to be adequately practical in bridge studies under fluctuating wind conditions.
Li et al. [185] studied the dependence of the modal shapes, modal frequencies, and associated damping ratios on wind velocity and temperature. The study employed nonlinear PCA (NLPCA) and ANN techniques. According to numerical results, the modal parameters pre-processed by NLPCA were capable of retaining the majority of the characteristics of the original signals. The damping ratios and the pre-processed modal frequency were also influenced by wind velocity and temperature. The ANN regression models showed the fine mapping of the relationship between modal frequency and environmental factors and damping ratios. Wang et al. [186] proposed a Bayesian probabilistic approach for characterizing wind-induced responses of high-rise structures. This approach enabled accounting for the uncertainty in the monitored responses. Tsai and Alipour [187] monitored a cantilever traffic signal structure under different wind conditions. They proposed a data-driven algorithm for wind-excited structures based on the long-term monitoring data of this structure.
2.3. Humidity
Humidity [188,189] is another environmental factor affecting SHM systems. Effects of variations in humidity can be reflected in changes in boundary conditions and structural mass. A slow process of changes occurs as the moisture content increases, and the structural frequencies tend to be reduced as a consequence.
Xia et al. [190] found that humidity has a relatively small impact on stiffness in long-span structures. Zhou et al. [114] monitored a 600 m high supertall building with an active tuned mass damper over two years. The structure underwent five typhoons and ambient environmental factors. The authors indicated that ambient humidity has limited effects on the modal parameters of the structure. In 2001, based on observing a bi-linear distribution of modal frequencies of the Z-24 bridge centered around the freezing point, Peeters and De Roeck [191] found that ambient moisture content changed the effect of temperature on the structure.
Kullaa [192] conducted experimental research for distinguishing between sensor fault, structural damage, and EOCs in SHM. They considered temperature and humidity as the main environmental factors. Bekas et al. [193] developed a novel lightweight diagnostic film for metal and composite structures. The film provided durable and reliable performance in withstanding the variable harsh humidity and temperature. He et al. [194] introduced a frequency-modified method for continuous beam bridges considering environmental effects. The proposed technique can eliminate the effects of humidity and temperature on structural responses. He et al. [195] proposed a reliability assessment approach for bridge structures. This method is capable of eliminating temperature and humidity effects. Dong et al. [196] developed multifunctional cementitious composites with integrated self-sensing based on conductive graphene nanoplates and silicone hydrophobic powders. This piezoresistive cementitious composite containing a novel cement-based sensor showed less sensitivity to moisture than conventional cement-based sensors.
2.4. Mass Loading
Mass loadings are primarily due to changing traffic, resulting in added mass and non-stationary excitations acting on a structure. Traffic loads are typically subject to daily or weekly fluctuations. As mass increases, natural frequencies decrease, as can be inferred from an equivalent spring-mass model. A non-stationary excitation primarily affects the stiffness of a system due to amplitude changes in vibrations that cause random fluctuations [197]. The temporal variability of traffic loads particularly affects bridges. The interaction between bridges and vehicles can be characterized by a time-variant oscillating system. Accordingly, each identified modal parameter corresponds to this system. Since mass is recognized as the most significant consequence of crossing vehicles, its effects on the bridge structure have been investigated by the SHM community in recent decades [198,199].
Short-span bridges are significantly more affected by traffic-induced mass variations than stiffness changes caused by environmental conditions. For middle to long-span bridges, due to the mass ratio between the vehicle and the overall bridge structure, traffic-induced variations of natural frequencies are insignificant. Accordingly, lighter bridges are more affected by variations in mass. The modal variations induced by traffic can be considered to arise in dynamic and static forms [200,201]. The dynamic modal changes induced by traffic are not linear and may tend to decrease as the load increases. However, in the case of static variations, they are shown to be directly correlated with mass. This effect makes vibration-based monitoring challenging for in-service bridges since the determined variations in the modal parameters of a bridge may represent the response of the interaction between a crossing vehicle and the healthy bridge. Several variables characterize the vehicle-bridge loading, such as vehicle velocity, vehicle weight, bridge weight, the number of vehicles, and other EOCs [202,203,204].
Rahim [205] developed a method for detecting and identifying damage severity under the effects of different loading conditions. The author extracted the structure’s natural frequencies and used Principal Component Analysis (PCA) as a feature-reduction technique. The PCs were used as input for an ANN model to predict various damage severity levels under the effects of different loading variables. It was found that nonlinear PCA and kernel Gaussian PCA can improve the chance of detecting damage and reduce false negative damage detection. Wang et al. [206] evaluated the dynamic responses of vehicles on a long-span bridge using a monitoring-based approach considering the effects of random traffic and wind loads. Several factors contributing to vehicle vibration were investigated, including road roughness, bridge vibration, and wind loads. According to the results, bridge vibration was the primary contributing factor to the vertical vehicle vibration, while wind forces and bridge vibration were the dominant factors contributing to the lateral and torsional vibration of the vehicle, respectively. The presented monitoring-based approach offers the possibility of estimating the dynamic responses of a moving vehicle on a bridge with high reliability, regardless of its operational condition. In addition, the method provides real-time information that can be used to assess the serviceability and safety of the structure.
Since lightweight structures may be affected by mass loading, such as heavy contact sensors, Sarrafi et al. [207] recommended using digital video cameras to rapidly collect high-density spatial data. The practicality of performing non-contact video measurements was demonstrated by the researchers for structural damage detection. Operational deflection shapes and derived resonant frequencies were used to perform the first level of SHM, i.e., detecting the presence of damage.
In summary, EOC variations can significantly impact the accuracy of SHM systems. Temperature, wind, humidity, and mass-loading effects are all factors that can alter the behavior of a structure, making it difficult to acquire reliable data from monitoring sensors and obtain accurate monitoring results. For instance, temperature variations can result in structural expansion or contraction, leading to changes in the structure’s mechanical characteristics, such as natural frequency and mode shapes. Wind can cause structural vibrations, which can impact the accuracy of the sensors and can lead to false systems estimations. Humidity and mass-loading effects can induce changes in the structure’s weight due to loading and unloading, resulting in changes in the sensors’ reading and the SHM system’s reliability. It has also been argued that sensors can render misleading data when affected by EOC changes. Therefore, the future trend leans more toward developing robust sensors that are less sensitive to EOC changes. It was also noted that sensor arrays could be employed to cancel out any effects from EOC. However, such a sensor network requires software explicitly developed for real-time interpretation of recorded data. Alternatively, numerical techniques may serve offline data analysis for interpreting data recorded from such sensor networks.
Most studies focus on evaluating the effect of EOC on long-term structural condition monitoring, and likewise, the developed techniques are primarily designed for monitoring large-scale structures over a long period. However, it was argued that EOC variations could affect wave propagation within materials. This implies that one needs to consider these effects when interpreting NDE techniques’ results. This demands more work performed in this area in the future.
While mass loading can decrease the natural frequencies of a structure, cold temperatures can have an elevating effect. While the former is a dynamic effect, the latter effect usually stays static over short-term monitoring. Therefore, the interaction of different EOC factors can complicate the monitoring of a structure. As another example, high humidity can affect the structure’s weight and response to wind loads. These interactions can create complex patterns of behavior that require sophisticated analysis techniques. As such, it is essential to carefully consider EOCs when designing and deploying health monitoring systems to ensure their accuracy and reliability in real-world applications.
3. Sensing Technologies
SHM and NDT systems typically involve a sensor network or a single sensor that measures various structural, material, or environmental quantities. These sensor readings thereby reflect either the structural behavior, material properties, or external factors, such as EOCs, that can affect the sensor measurements or behavior of the system. Detecting damage requires sensor data that are sensitive to the damage to provide a direct correlation to the health of the structure. A sensor that is robust to variations in EOCs can be of significant advantage in accurately and reliably detecting damage in structures. An overview of the typical EOCs affecting civil infrastructure and the sensors suitable for measuring these effects in SHM systems is provided in Table 4. In general, sensors convert parameters of a physical nature to electronic signals. These physical parameters can be acceleration, strain, light, humidity, temperature, pressure, or moisture. Sensing techniques can be divided into conventional and advanced sensing technologies depending on their stage of development and establishment status. Examples of conventional sensors used for SHM systems and NDT are strain gauges, accelerometers, ultrasonic transducers, eddy current sensors, and temperature gauges [208].

Table 4.
Typical EOCs and appropriate sensors for SHM systems [141].
As compared to conventional methods, advanced sensing techniques rely on emerging technologies based on multi-physics and include more complex system setups and data analysis methodologies [209]. In recent decades, a wide variety of advanced sensing technologies have been developed based on different physical working principles. As many of these techniques are relatively new technologies for most civil engineering applications, many of them are currently used only for research or on a small scale in the field or pilot projects. Application examples of advanced sensing systems are the monitoring of infrastructure [210,211], electricity and water distribution systems [212], and transportation systems [213].
The advantages of advanced sensing systems include
- suitability for continuous monitoring,
- capability for remote sensing,
- less sensitivity to EOC variations,
- more accuracy and reliability,
- automatability,
- less labor intensivity,
- more cost-effectiveness.
Selecting the most appropriate sensor based on the system requirements and limitations depends on assessing specific sensor characteristics, such as (1) susceptibility to damage, (2) susceptibility to noise, (3) susceptibility to variations in the EOC, (4) susceptibility to chemical influences, (5) susceptibility to mechanical influences, (6) measurement accuracy, (7) error-proneness, and (8) cost. Advanced sensing technologies used for SHM systems and NDT can be grouped as follows:
- Fiber optic sensing technologies: These sensors are already widely applied in several areas due to their benefits, such as small size, corrosion resistance, high precision, flexibility, lightweight, and anti-electromagnetic interference property [214,215]. Fibre optic sensors include Fibre Bragg grating (FBG) sensors [216], polymer optical fiber sensors [217], and Rayleigh scattering distributed sensors [218].
- Electrochemical sensors: the three main types of these sensors are (1) potentiometric sensors [219,220] (2) amperometric sensors [221,222] and (3) conductometric sensors [223,224].
- Wireless monitoring via wireless sensors: In recent decades, the development of wireless sensor technologies has been based on advancements in microelectromechanical systems (MEMS) technology, digital electronics, and wireless communications [225,226,227]. The two main subsystems of this system are (1) Portable Inspection and Maintenance Strategy (PIMS) [228,229] and (2) Portable Data Acquisition Strategy (PDAs) [230].
- Remote-sensing technologies: remote-sensing technologies can be divided into five main groups, including (1) mathematical morphology-based methods [231], (2) object-oriented methods Li et al. [232], (3) edge detection-based methods [233], (4) road information-based methods [234] and (5) statistics-based methods [235].
The development of next-generation sensing techniques as a result of recent advancements in sensing and robotic technology is outperforming conventional and advanced sensors. Next-generation measurement technology for SHM has grown in response to the need for automated and efficient sensing systems. Robotic sensors, cloud services, wireless sensors, GPS, drones, machine vision, smartphones, and high-speed cameras are examples of next-generation sensors that are employed to monitor various systems.
While advanced sensing technologies that are insensitive to EOCs and sensitive to damage are crucial for reliable damage detection in structures, some gaps still need to be addressed. One of the main challenges is the high cost and complexity of these sensing technologies rendering them difficult to implement on a large scale. Additionally, some advanced sensing technologies require calibration and elaborate maintenance work, which can be time-consuming and expensive. Another challenge is the lack of standardization in sensing techniques, which makes it difficult to compare and evaluate different technologies. Furthermore, the performance of these sensors can be affected by the structure’s material properties, making it challenging to apply the same technology to different types of systems. Overall, more research and development are needed to address these gaps and provide advanced sensing technology that is more accessible and practical for widespread implementation in SHM applications.
4. Data Analysis for EOC Compensation
Sensor measurements typically undergo a process of data acquisition, signal conditioning, data transfer, data storage, signal processing, and data interpretation for damage detection. Over the years, a variety of data analysis techniques have been introduced and are constantly being further advanced. Rapid advances and innovations in artificial intelligence (AI) and data mining have led to the transformation and renewal of data analysis methodologies for SHM and NDT technology. Although traditional signal processing methods are used to execute and test models and hypotheses on datasets, regardless of the volume of data, AI techniques, including deep learning, are operated to detect hidden patterns in large data sets [236].
Swarm intelligent algorithms are widely used for structural optimization and compensating for EOCs. These algorithms include genetic algorithm (GA), Moth Flame Optimization (MFO), and Whale Optimization Algorithm (WOA) [237,238]. Novel algorithm developments have focused on data analysis techniques that can compensate for the effects of EOC variations. These algorithms can be classified into two main groups based on the available data type, i.e., (1) input-output and (2) output-only methods. The input usually refers to information about varying EOCs, such as temperature variations. The output relates to structural response characteristics containing damage-sensitive features, such as natural frequencies or mode shape data. While input–output methods aim to establish a map between the input and output data, output-only methods rely only on the available information about the structural response. Examples of data analysis algorithms used for EOC compensation are described below [239,240,241].
- Support vector machine (SVM): SVM is an algorithm for analyzing data relations. The technique is beneficial for pattern recognition and can be used for regression analysis [242,243,244].
- Artificial neural network (ANN): ANN is an input and output method. Using historical data, it approximates the nonlinear function between inputs and outputs with high accuracy [245,246,247].
- Machine learning (ML): ML algorithms can be input–output or output-only algorithms. They can interpret signals or images to analyze, inspect, and examine material integrity [248,249,250].
- Genetic algorithm (GA): GA provides an effective solution to both constrained and unconstrained optimization problems by mimicking the process of biological evolution through natural selection. Several individual solutions are modified repeatedly by the algorithm [251,252].
- Autoregressive-exogenous (ARX): An ARX model simulates datasets. Existing structural vibration data are fitted to the model, and observations are removed. Using ARX(n, m), the current system output is defined as a function of n previous outputs and m previous inputs [253,254].
- Linear regression (LR): The LR model is one of the most popular and straightforward regression analysis methods. A linear relationship exists between temperature and structural response. The structural response can be calculated using temperature data from a single point [255,256].
- Principal component analysis (PCA): As a multivariate statistical analysis technique, PCA can reduce the data dimension. High-dimensional related variables are thereby transformed into low-dimensional uncorrelated variables [257,258].
- Swarm intelligent algorithms: By discovering different combinations of values, these algorithms assist in improving fitness functions in combinatorial and numerical optimization problems [259,260].
- Auto-associative neural network (AANN): AANN is an ANN structure with the same input and output layer. The program is typically used to simulate a nonlinear PCA process and solve problems related to feature extraction, pattern recognition, and dimensionality reduction [261,262].
- Variational mode decomposition (VMD): VMD is a time-frequency analysis strategy for analyzing non-stationary and nonlinear signals based on decomposing the original signal into several sets of intrinsic mode functions (IMF) [53,263].
Table 5 presents recent papers on input–output and output-only data analysis techniques considering temperature variations.
Damage-detection strategies for health monitoring can be categorized into model-based and data-based methods [264]. In model-based approaches, damage detection techniques are based on initial physics models of a structure. Here, damage can be identified by updating the initial properties of the structure and comparing these with real properties. Data-based techniques, on the other hand, are based on structural measurements. The effects of EOC variations can be considered using both approaches. Table 6 presents recent research on model-based and data-based damage detection methods that use vibration data and compensate for temperature effects. For static-based ways that compensate for the effects of EOCs, Table 6 presents two developed approaches. The first method is based on temperature-removed responses. This method can efficiently analyze the results of other factors, such as traffic load; it may, however, lead to the loss of critical information. The second method is based on temperature-induced responses and can apply the excitation by temperature in structure identification. In this approach, a uniform temperature field can cause challenges in accurately obtaining the model input. Furthermore, the nonlinear relationship between structural characteristics and temperature responses can cause model uncertainty.

Table 6.
Examples of data analysis techniques considering EOCs.

Table 5.
Recent papers on data analysis algorithms considering temperature variations.
Table 5.
Recent papers on data analysis algorithms considering temperature variations.
| Ref(s). | Input-Output | Output-Only | Type | Description |
|---|---|---|---|---|
| [265] | ✓ | SVM | A novel SVM was proposed that gradually tunes the kernel parameter and determines the necessity of model updating. | |
| [266] | ✓ | SVM | Genetic algorithm, grid-search, and partial swarm optimization were presented for damage detection based on SVM. | |
| [267] | ✓ | ANN | An ANN was evaluated for predicting the modal parameters accurately; additionally, the model error of the ANN was validated as an indicator for detecting anomalous structural functions. | |
| [268] | ✓ | ANN | A damage detection approach under temperature variation was developed using a sensor-clustering-based time-series analysis combined with ANNs. | |
| [269] | ✓ | ARX | A long-term continuous SHM system was presented to perform under seismic and environmental excitation. The application of ARX was for modal identification under seismic excitation. | |
| [270] | ✓ | LR | A model to separate temperature influence from structural strain responses was addressed. A tied arch bridge was employed in the case study, and LR mapped the strain responses with temperature. | |
| [271] | ✓ | LR | Regressive analysis was used to determine the experiential regressive equation based on the correlating factors between temperature and structural response. Moreover, the influence of temperature was separated from the response. | |
| [272] | ✓ | GA | GA was employed for structural damage identification considering the effect of varying temperatures. | |
| [273] | ✓ | MFO | A damage identification method was proposed based on the MFO and SVM. | |
| [274] | ✓ | WOA | A damage identification method was developed based on the WOA compensating for the noises. | |
| [275] | ✓ | AANN | A multilayer ANN, which resembles an AANN while employing temperature variables alongside frequencies, was studied for identifying patterns in frequencies of undamaged structures under changing temperatures. | |
| [276] | ✓ | Kernel PCA (KPCA) | A data normalization method based on the KPCA method was proposed to enhance damage detection sensitivity under changing temperatures and reduce false warnings resulting from these alternations. | |
| [277] | ✓ | EMD | A feature extraction approach for determining the temperature influences on structural responses was proposed where EMD and some other techniques were employed for mode decomposition. |
Data analysis techniques developed for structural health monitoring under EOC often require a threshold to be set for identifying any abnormal behavior of the structure. One challenge with these methods is the lack of a robust dynamic threshold-setting strategy for differentiating between normal and abnormal behavior of the structure. This is mainly because historical data, on which a static threshold is usually based, might not cover the entire spectrum of EOC changes over the monitored period. Therefore, false positives/negatives may occur in the process of structural condition monitoring. Accordingly, future work needs to focus on techniques that rely on developing dynamic threshold-setting strategies. As a result, by creating a dynamic threshold setting, these techniques can be made baseline-independent.
On the other hand, most of these techniques rely upon a predictive model whose prediction error is taken as a damage-sensitive feature. Nonetheless, real-time condition monitoring of structures demands non-predictive-based models that do not need to be trained a priori. These methods will facilitate online condition monitoring of targeted systems without requiring any predictive models to be developed in advance.
5. Conclusions and Discussion
This paper comprehensively reviewed recent developments in SHM and NDT methods considering EOC variations, including temperature, moisture, wind, and traffic loads. Background information on SHM and NDT technology was provided, and uncertainty challenges of EOCs for civil infrastructure assessment were discussed. To provide the reader with an overview of the latest research on sensing technologies and data analysis algorithms capable of EOC compensation, tables are provided summarizing research findings and discussing advantages and disadvantages.
The significance of understanding the challenges associated with EOC variations in developing SHM methods for monitoring complex systems, automotive, civil infrastructures, and mechanical systems is evident. Below, we summarize challenges and future research recommendations related to the compensation of EOC variations.
- -
- Most researchers have developed compensation techniques and strategies for temperature effects. However, in actual practice, the effects of other EOC variations, such as traffic or wind loads, are unavoidable in SHM systems. Thus, studying and developing compensation techniques for other EOC factors is critical.
- -
- SHM methods have not been adequately examined in practice for the effects of moisture and applied loads. In order to achieve accurate monitoring, these key variations need to be addressed.
- -
- Baseline-free methods only employ the current recorded signals for damage identification. These techniques apply the signal energy or amplitude to detect system damage. However, EOC variations can affect current recorded signals’ features (e.g., amplitude). Baseline-free methods can be integrated with EOC compensation techniques and strategies to increase the efficiency of these methods.
- -
- With the applications of AI, ML, and Deep Learning (DL) algorithms, more advanced damage detection techniques have been proposed to tackle the effects of EOC variations on SHM and NDT methods. ML has shown promise in addressing the drawbacks associated with current NDT methods. AI algorithms can potentially make SHM and NDT techniques simple, time-efficient, and affordable. Nevertheless, addressing the limitations of the input dataset is required for training and algorithm accuracy.
- -
- Last but not least, based on our literature review, only minor work has been conducted on the combined effects of EOC factors on SHM techniques. This research area needs to be given special attention in future work.
The presented study will be useful to researchers working on a significant bottleneck issue of in-service assessment of civil structures subjected to varying EOC.
Author Contributions
Conceptualization: A.K. and S.H.; methodology: A.K. and S.H.; software: A.K.; validation: A.K., S.H., M.M. and U.D.; formal analysis: A.K.; investigation: A.K. and S.H.; resources: A.K. and S.H.; data curation: A.K.; writing—original draft preparation: A.K. and S.H.; writing—review and editing: S.H., M.M. and U.D.; visualization: A.K. and S.H.; supervision: U.D.; project administration: U.D.; funding acquisition: U.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Senyurek, V. Detection of cuts and impact damage at the aircraft wing slat by using Lamb wave method. Measurement 2015, 67, 10–23. [Google Scholar] [CrossRef]
- Kim, S.; Frangopol, D.M. Optimal planning of structural performance monitoring based on reliability importance assessment. Probabilistic Eng. Mech. 2010, 25, 86–98. [Google Scholar] [CrossRef]
- Taha, M.R.; Noureldin, A.; Lucero, J.; Baca, T. Wavelet transform for structural health monitoring: A compendium of uses and features. Struct. Health Monit. 2006, 5, 267–295. [Google Scholar] [CrossRef]
- Ni, Y.; Wong, K.; Xia, Y. Health checks through landmark bridges to sky-high structures. Adv. Struct. Eng. 2011, 14, 103–119. [Google Scholar] [CrossRef]
- Gatti, M. Structural health monitoring of an operational bridge: A case study. Eng. Struct. 2019, 195, 200–209. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, M.S.; Boashash, B.; Sodano, H.; Inman, D.J. 1-D CNNs for structural damage detection: Verification on a structural health monitoring benchmark data. Neurocomputing 2018, 275, 1308–1317. [Google Scholar] [CrossRef]
- Moreno-Gomez, A.; Perez-Ramirez, C.A.; Dominguez-Gonzalez, A.; Valtierra-Rodriguez, M.; Chavez-Alegria, O.; Amezquita-Sanchez, J.P. Sensors used in structural health monitoring. Arch. Comput. Methods Eng. 2018, 25, 901–918. [Google Scholar] [CrossRef]
- Yan, K.; Zhang, Y.; Yan, Y.; Xu, C.; Zhang, S. Fault diagnosis method of sensors in building structural health monitoring system based on communication load optimization. Comput. Commun. 2020, 159, 310–316. [Google Scholar] [CrossRef]
- Bulajić, B.Đ.; Todorovska, M.I.; Manić, M.I.; Trifunac, M.D. Structural health monitoring study of the ZOIL building using earthquake records. Soil Dyn. Earthq. Eng. 2020, 133, 106105. [Google Scholar] [CrossRef]
- Rahmani, M.; Todorovska, M.I. Structural health monitoring of a 32-storey steel-frame building using 50 years of seismic monitoring data. Earthq. Eng. Struct. Dyn. 2021, 50, 1777–1800. [Google Scholar] [CrossRef]
- Ongbali, S.; Afolalu, S.; Oladipupo, S.; Akra, S.; Bello, K. Building structural health monitoring: A tool for building collapse mitigation. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2021; Volume 1036, p. 012028. [Google Scholar] [CrossRef]
- Bakkar, A.R.; Elyamani, A.; El-Attar, A.G.; Bompa, D.V.; Elghazouli, A.Y.; Mourad, S.A. Dynamic Characterisation of a Heritage Structure with Limited Accessibility Using Ambient Vibrations. Buildings 2023, 13, 192. [Google Scholar] [CrossRef]
- Pan, H.; Wu, J.; Fu, J. Monitoring of Wind Effects on a Super-Tall Building under a Typhoon. Buildings 2023, 13, 47. [Google Scholar] [CrossRef]
- Barsocchi, P.; Bartoli, G.; Betti, M.; Girardi, M.; Mammolito, S.; Pellegrini, D.; Zini, G. Wireless sensor networks for continuous structural health monitoring of historic masonry towers. Int. J. Archit. Herit. 2021, 15, 22–44. [Google Scholar] [CrossRef]
- Saisi, A.; Gentile, C.; Guidobaldi, M. Post-earthquake continuous dynamic monitoring of the Gabbia Tower in Mantua, Italy. Constr. Build. Mater. 2015, 81, 101–112. [Google Scholar] [CrossRef]
- Zini, G.; Betti, M.; Bartoli, G. A pilot project for the long-term structural health monitoring of historic city gates. J. Civ. Struct. Health Monit. 2022, 12, 537–556. [Google Scholar] [CrossRef]
- Alaggio, R.; Aloisio, A.; Antonacci, E.; Cirella, R. Two-years static and dynamic monitoring of the Santa Maria di Collemaggio basilica. Constr. Build. Mater. 2021, 268, 121069. [Google Scholar] [CrossRef]
- Hassani, S.; Mousavi, M.; Sharif-Khodaei, Z. Smart bridge monitoring. In The Rise of Smart Cities; Elsevier: Amsterdam, The Netherland, 2022; pp. 343–372. [Google Scholar] [CrossRef]
- Zhang, L.; Qiu, G.; Chen, Z. Structural health monitoring methods of cables in cable-stayed bridge: A review. Measurement 2021, 168, 108343. [Google Scholar] [CrossRef]
- Ni, Y.; Wang, Y.; Zhang, C. A Bayesian approach for condition assessment and damage alarm of bridge expansion joints using long-term structural health monitoring data. Eng. Struct. 2020, 212, 110520. [Google Scholar] [CrossRef]
- Ngeljaratan, L.; Moustafa, M.A. Structural health monitoring and seismic response assessment of bridge structures using target-tracking digital image correlation. Eng. Struct. 2020, 213, 110551. [Google Scholar] [CrossRef]
- Fitzgerald, P.C.; Malekjafarian, A.; Bhowmik, B.; Prendergast, L.J.; Cahill, P.; Kim, C.W.; Hazra, B.; Pakrashi, V.; OBrien, E.J. Scour damage detection and structural health monitoring of a laboratory-scaled bridge using a vibration energy harvesting device. Sensors 2019, 19, 2572. [Google Scholar] [CrossRef]
- Wang, H.; Mao, J.X.; Xu, Z.D. Investigation of dynamic properties of a long-span cable-stayed bridge during typhoon events based on structural health monitoring. J. Wind Eng. Ind. Aerodyn. 2020, 201, 104172. [Google Scholar] [CrossRef]
- Vagnoli, M.; Remenyte-Prescott, R.; Andrews, J. Railway bridge structural health monitoring and fault detection: State-of-the-art methods and future challenges. Struct. Health Monit. 2018, 17, 971–1007. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, P.; Zhou, C.; Huang, Y.; Zhang, L. Structural health monitoring of underground structures in reclamation area using fiber bragg grating sensors. Sensors 2019, 19, 2849. [Google Scholar] [CrossRef] [PubMed]
- Sham, W.L. Spatial Deformation Estimation and Long Term Structural Health Monitoring in Underground Engineering. Ph.D. Thesis, Nanyang Technological University, Singapore, 2012. [Google Scholar] [CrossRef]
- Hong, K.; Wang, H.; Yuan, B.; Wang, T. Multiple Defects Inspection of Dam Spillway Surface Using Deep Learning and 3D Reconstruction Techniques. Buildings 2023, 13, 285. [Google Scholar] [CrossRef]
- O’Shea, M.; Murphy, J. Design of a BIM integrated structural health monitoring system for a historic offshore lighthouse. Buildings 2020, 10, 131. [Google Scholar] [CrossRef]
- Bao, C.; Hao, H.; Li, Z. Vibration-based structural health monitoring of offshore pipelines: Numerical and experimental study. Struct. Control Health Monit. 2013, 20, 769–788. [Google Scholar] [CrossRef]
- Chandrasekaran, S. Structural Health Monitoring with Application to Offshore Structures; World Scientific: Singapore, 2019. [Google Scholar] [CrossRef]
- Haeri, M.H.; Lotfi, A.; Dolatshahi, K.M.; Golafshani, A.A. Inverse vibration technique for structural health monitoring of offshore jacket platforms. Appl. Ocean. Res. 2017, 62, 181–198. [Google Scholar] [CrossRef]
- Zhu, J. Review on Structural Health Monitoring of Offshore Platform. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 2014, p. 012019. [Google Scholar] [CrossRef]
- Zhou, L.; Huang, P.; Chi, S.; Li, M.; Zhou, H.; Yu, H.; Cao, H.; Chen, K. Structural health monitoring of offshore wind power structures based on genetic algorithm optimization and uncertain analytic hierarchy process. Ocean. Eng. 2020, 218, 108201. [Google Scholar] [CrossRef]
- Li, M.; Kefal, A.; Oterkus, E.; Oterkus, S. Structural health monitoring of an offshore wind turbine tower using iFEM methodology. Ocean. Eng. 2020, 204, 107291. [Google Scholar] [CrossRef]
- Nielsen, J.S.; Tcherniak, D.; Ulriksen, M.D. A case study on risk-based maintenance of wind turbine blades with structural health monitoring. Struct. Infrastruct. Eng. 2021, 17, 302–318. [Google Scholar] [CrossRef]
- Hubbard, P.G.; Xu, J.; Zhang, S.; Dejong, M.; Luo, L.; Soga, K.; Papa, C.; Zulberti, C.; Malara, D.; Fugazzotto, F.; et al. Dynamic structural health monitoring of a model wind turbine tower using distributed acoustic sensing (DAS). J. Civ. Struct. Health Monit. 2021, 11, 833–849. [Google Scholar] [CrossRef]
- Chung, W.C.; Pestana, G.R.; Kim, M. Structural health monitoring for TLP-FOWT (floating offshore wind turbine) tendon using sensors. Appl. Ocean. Res. 2021, 113, 102740. [Google Scholar] [CrossRef]
- Gómez Muñoz, C.Q.; García Márquez, F.P.; Hernández Crespo, B.; Makaya, K. Structural health monitoring for delamination detection and location in wind turbine blades employing guided waves. Wind Energy 2019, 22, 698–711. [Google Scholar] [CrossRef]
- Yan, H.; Wei, D.; Wang, X.B.; Chen, Y.X.; Meng, X.W. Research of structural health monitoring system for stinger of large deep water pipe-laying ship. Ocean. Eng. 2019, 171, 361–376. [Google Scholar] [CrossRef]
- Sabatino, S.; Frangopol, D.M. Structural Health Monitoring Planning of Ship Structures in a Life-Cycle Perspective. In Life-Cycle of Engineering Systems; CRC Press: Boca Raton, FL, USA, 2016; pp. 1927–1933. [Google Scholar] [CrossRef]
- Decò, A.; Frangopol, D.M. Real-time risk of ship structures integrating structural health monitoring data: Application to multi-objective optimal ship routing. Ocean. Eng. 2015, 96, 312–329. [Google Scholar] [CrossRef]
- Karvelis, P.; Georgoulas, G.; Kappatos, V.; Stylios, C. Deep machine learning for structural health monitoring on ship hulls using acoustic emission method. Ships Offshore Struct. 2021, 16, 440–448. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Structural health monitoring (SHM) of aerospace composites. In Polymer Composites in the Aerospace Industry; Elsevier: Amsterdam, The Netherland, 2020; pp. 491–558. [Google Scholar] [CrossRef]
- Elahi, H. The investigation on structural health monitoring of aerospace structures via piezoelectric aeroelastic energy harvesting. Microsyst. Technol. 2021, 27, 2605–2613. [Google Scholar] [CrossRef]
- Royon, M.; Jamon, D.; Blanchet, T.; Royer, F.; Vocanson, F.; Marin, E.; Morana, A.; Boukenter, A.; Ouerdane, Y.; Jourlin, Y.; et al. Sol–Gel Waveguide-Based Sensor for Structural Health Monitoring on Large Surfaces in Aerospace Domain. Aerospace 2021, 8, 109. [Google Scholar] [CrossRef]
- Ahmed, S.; Nauman, S.; Khan, Z.M. Development of TPU/CNPs flexible composite strain sensors using Additive Manufacturing (AM) for Structural Health Monitoring (SHM) of aerospace components. In Proceedings of the 2021 International Bhurban Conference on Applied Sciences and Technologies (IBCAST), Islamabad, Pakistan, 12–16 January 2021; pp. 47–54. [Google Scholar] [CrossRef]
- Goyal, D.; Pabla, B. The vibration monitoring methods and signal processing techniques for structural health monitoring: A review. Arch. Comput. Methods Eng. 2016, 23, 585–594. [Google Scholar] [CrossRef]
- Tokognon, C.A.; Gao, B.; Tian, G.Y.; Yan, Y. Structural health monitoring framework based on Internet of Things: A survey. IEEE Internet Things J. 2017, 4, 619–635. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Experimental validation of cost-effective vision-based structural health monitoring. Mech. Syst. Signal Process. 2017, 88, 199–211. [Google Scholar] [CrossRef]
- Yu, H.; Chen, X.; Ren, M.; Liu, Q.; Yang, K.; Chang, K.; Wu, Q.; Zhan, J. An online pipeline structural health monitoring method based on the spatial deformation fitting. IEEE Trans. Ind. Electron. 2021, 69, 7383–7393. [Google Scholar] [CrossRef]
- Aung, T.L.; Ma, N.; Kishida, K.; Guzik, A. Advanced Structural Health Monitoring Method by Integrated Isogeometric Analysis and Distributed Fiber Optic Sensing. Sensors 2021, 21, 5794. [Google Scholar] [CrossRef]
- Hassani, S.; Mousavi, M.; Gandomi, A.H. A mode shape sensitivity-based method for damage detection of structures with closely-spaced eigenvalues. Measurement 2022, 190, 110644. [Google Scholar] [CrossRef]
- Hassani, S.; Mousavi, M.; Gandomi, A.H. Damage detection of composite laminate structures using VMD of FRF contaminated by high percentage of noise. Compos. Struct. 2022, 286, 115243. [Google Scholar] [CrossRef]
- Hassani, S.; Mousavi, M.; Gandomi, A.H. Minimizing Noise Effects in Structural Health Monitoring Using Hilbert Transform of the Condensed FRF. Struct. Health Monit. 2021. [Google Scholar] [CrossRef]
- Liu, Y.; Nayak, S. Structural health monitoring: State of the art and perspectives. JOM 2012, 64, 789–792. [Google Scholar] [CrossRef]
- Lackner, M.A.; Rotea, M.A. Passive structural control of offshore wind turbines. Wind Energy 2011, 14, 373–388. [Google Scholar] [CrossRef]
- Capineri, L.; Bulletti, A. Ultrasonic guided-waves sensors and integrated structural health monitoring systems for impact detection and localization: A review. Sensors 2021, 21, 2929. [Google Scholar] [CrossRef]
- Hassani, S.; Mousavi, M.; Gandomi, A.H. Structural Health Monitoring in Composite Structures: A Comprehensive Review. Sensors 2022, 22, 153. [Google Scholar] [CrossRef]
- Amer, A.; Kopsaftopoulos, F.P. Statistical guided-waves-based structural health monitoring via stochastic non-parametric time series models. Struct. Health Monit. 2022, 21, 1139–1166. [Google Scholar] [CrossRef]
- Feng, T.; Aliabadi, M. Structural Integrity Assessment of Composites Plates with Embedded PZT Transducers for Structural Health Monitoring. Materials 2021, 14, 6148. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Fu, Y.; Chow, R.; Spencer, B.F.; Park, J.W.; Mechitov, K. Development of a high-sensitivity wireless accelerometer for structural health monitoring. Sensors 2018, 18, 262. [Google Scholar] [CrossRef]
- Ma, Z.; Choi, J.; Yang, L.; Sohn, H. Structural displacement estimation using accelerometer and FMCW millimeter wave radar. Mech. Syst. Signal Process. 2023, 182, 109582. [Google Scholar] [CrossRef]
- Modares, M.; Waksmanski, N. Overview of structural health monitoring for steel bridges. Pract. Period. Struct. Des. Constr. 2013, 18, 187–191. [Google Scholar] [CrossRef]
- Pevec, S.; Donlagić, D. Multiparameter fiber-optic sensors: A review. Opt. Eng. 2019, 58, 072009. [Google Scholar] [CrossRef]
- Petchmaneelumka, W.; Mano, P.; Riewruja, V. Linear variable differential transformer temperature compensation technique. Sens. Mater. 2018, 30, 2171–2181. [Google Scholar] [CrossRef]
- Lei, X.; Sun, L.; Xia, Y. Lost data reconstruction for structural health monitoring using deep convolutional generative adversarial networks. Struct. Health Monit. 2021, 20, 2069–2087. [Google Scholar] [CrossRef]
- Gkantou, M.; Muradov, M.; Kamaris, G.S.; Hashim, K.; Atherton, W.; Kot, P. Novel electromagnetic sensors embedded in reinforced concrete beams for crack detection. Sensors 2019, 19, 5175. [Google Scholar] [CrossRef]
- Abdulkarem, M.; Samsudin, K.; Rokhani, F.Z.; Rasid, M.F.A. Wireless sensor network for structural health monitoring: A contemporary review of technologies, challenges, and future direction. Struct. Health Monit. 2020, 19, 693–735. [Google Scholar] [CrossRef]
- Ono, K. Review on structural health evaluation with acoustic emission. Appl. Sci. 2018, 8, 958. [Google Scholar] [CrossRef]
- Zhuang, Y.; Chen, Y.; Zhu, C.; Gerald, R.E.; Tang, Y.; Huang, J. A high-resolution 2-D fiber optic inclinometer for structural health monitoring applications. IEEE Trans. Instrum. Meas. 2020, 69, 6544–6555. [Google Scholar] [CrossRef]
- Bianchi, S.; Biondini, F.; Rosati, G.; Anghileri, M.; Capacci, L.; Cazzulani, G.; Benedetti, L. Structural Health Monitoring of Two Road Bridges in Como, Italy. In Proceedings of the International Conference of the European Association on Quality Control of Bridges and Structures; Springer: Berlin/Heidelberg, Germany, 2021; pp. 390–399. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, G.Y.; Marindra, A.M.; Sunny, A.I.; Zhao, A.B. A review of passive RFID tag antenna-based sensors and systems for structural health monitoring applications. Sensors 2017, 17, 265. [Google Scholar] [CrossRef]
- Mustafa, M.; Rizwan, M.; Kashif, M.; Khan, T.; Waseem, M.; Annuk, A. LC Passive Wireless Sensor System Based on Two Switches for Detection of Triple Parameters. Sensors 2022, 22, 3024. [Google Scholar] [CrossRef]
- Deivasigamani, A.; Daliri, A.; Wang, C.H.; John, S. A review of passive wireless sensors for structural health monitoring. Mod. Appl. Sci. 2013, 7, 57. [Google Scholar] [CrossRef]
- Di Nuzzo, F.; Brunelli, D.; Polonelli, T.; Benini, L. Structural Health Monitoring System With Narrowband IoT and MEMS Sensors. IEEE Sens. J. 2021, 21, 16371–16380. [Google Scholar] [CrossRef]
- Hassani, S.; Shadan, F. Using incomplete FRF measurements for damage detection of structures with closely-spaced eigenvalues. Measurement 2022, 188, 110388. [Google Scholar] [CrossRef]
- Kumar, S.; Chakraborty, S.K. Response analysis of structural building excited by seismic waves using finite difference method. Int. J. Struct. Eng. 2015, 6, 123–139. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method for Solid and Structural Mechanics; Elsevier: Amsterdam, The Netherland, 2005. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Non-Linear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- Aliabadi, M.H. The Boundary Element Method, Volume 2: Applications in Solids and Structures; John Wiley & Sons: Hoboken, NJ, USA, 2002; Volume 2. [Google Scholar]
- Ostachowicz, W.M. Damage detection of structures using spectral finite element method. Comput. Struct. 2008, 86, 454–462. [Google Scholar] [CrossRef]
- Carrino, S.; Nicassio, F.; Scarselli, G.; Vitolo, R. Finite difference model of wave motion for structural health monitoring of single lap joints. Int. J. Solids Struct. 2019, 161, 219–227. [Google Scholar] [CrossRef]
- Piccolo, V.; Chiappini, A.; Vaccari, A.; Lesina, A.C.; Ferrari, M.; Deseri, L.; Perry, M.; Zonta, D. Finite difference analysis and experimental validation of 3D photonic crystals for structural health monitoring. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2017, Portland, OR, USA, 26–29 March 2017; Volume 10168, pp. 403–411. [Google Scholar] [CrossRef]
- Ahmad, Z.; Vivar-Perez, J.; Gabbert, U. Semi-analytical finite element method for modeling of lamb wave propagation. CEAS Aeronaut. J. 2013, 4, 21–33. [Google Scholar] [CrossRef]
- Thorsson, S.I.; Xie, J.; Marek, J.; Waas, A.M. Matrix crack interacting with a delamination in an impacted sandwich composite beam. Eng. Fract. Mech. 2016, 163, 476–486. [Google Scholar] [CrossRef]
- He, J.; Ran, Y.; Liu, B.; Yang, J.; Guan, X. A fatigue crack size evaluation method based on lamb wave simulation and limited experimental data. Sensors 2017, 17, 2097. [Google Scholar] [CrossRef] [PubMed]
- Kuna, M. Finite elements in fracture mechanics. Solid Mech. Its Appl. 2013, 201, 153–192. [Google Scholar] [CrossRef]
- Chen, H.P.; Wang, K.L.; Tee, K.F. Structural health monitoring utilizing dynamic perturbation method. In Proceedings of the 3rd International Conference on Dynamics, Vibration and Control (ICDVC-2010), Hangzhou, China, 12–14 May 2010. [Google Scholar]
- Zou, F.; Benedetti, I.; Aliabadi, M. A boundary element model for structural health monitoring using piezoelectric transducers. Smart Mater. Struct. 2013, 23, 015022. [Google Scholar] [CrossRef]
- Li, J.; Khodaei, Z.S.; Aliabadi, M. Boundary element modelling of ultrasonic Lamb waves for structural health monitoring. Smart Mater. Struct. 2020, 29, 105030. [Google Scholar] [CrossRef]
- Li, J.; Sharif Khodaei, Z.; Aliabadi, F.M. A boundary element model for structural health monitoring based on the S0 lamb wave mode. In Proceedings of the Key Engineering Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2018; Volume 774, pp. 625–631. [Google Scholar] [CrossRef]
- Lucena, R.; Dos Santos, J. Structural health monitoring using time reversal and cracked rod spectral element. Mech. Syst. Signal Process. 2016, 79, 86–98. [Google Scholar] [CrossRef]
- Mesnil, O.; Imperiale, A.; Demaldent, E.; Baronian, V.; Chapuis, B. Simulation tools for guided wave based structural health monitoring. In Proceedings of the AIP Conference Proceedings; AIP Publishing LLC: New York, NY, USA, 2018; Volume 1949, p. 050001. [Google Scholar] [CrossRef]
- Sepehry, N.; Shamshirsaz, M.; Bakhtiari Nejad, F. Low-cost simulation using model order reduction in structural health monitoring: Application of balanced proper orthogonal decomposition. Struct. Control Health Monit. 2017, 24, e1994. [Google Scholar] [CrossRef]
- Hannan, M.A.; Hassan, K.; Jern, K.P. A review on sensors and systems in structural health monitoring: Current issues and challenges. Smart Struct. Syst. 2018, 22, 509–525. [Google Scholar] [CrossRef]
- Scuro, C.; Sciammarella, P.F.; Lamonaca, F.; Olivito, R.S.; Carni, D.L. IoT for structural health monitoring. IEEE Instrum. Meas. Mag. 2018, 21, 4–14. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y.; Tan, X. Review on Vibration-Based Structural Health Monitoring Techniques and Technical Codes. Symmetry 2021, 13, 1998. [Google Scholar] [CrossRef]
- Kralovec, C.; Schagerl, M. Review of structural health monitoring methods regarding a multi-sensor approach for damage assessment of metal and composite structures. Sensors 2020, 20, 826. [Google Scholar] [CrossRef]
- Farhangdoust, S.; Mehrabi, A. Health monitoring of closure joints in accelerated bridge construction: A review of non-destructive testing application. J. Adv. Concr. Technol. 2019, 17, 381–404. [Google Scholar] [CrossRef]
- Catbas, F.N.; Gul, M.; Burkett, J.L. Conceptual damage-sensitive features for structural health monitoring: Laboratory and field demonstrations. Mech. Syst. Signal Process. 2008, 22, 1650–1669. [Google Scholar] [CrossRef]
- Roy, K.; Bhattacharya, B.; Ray-Chaudhuri, S. ARX model-based damage sensitive features for structural damage localization using output-only measurements. J. Sound Vib. 2015, 349, 99–122. [Google Scholar] [CrossRef]
- Shokravi, H.; Shokravi, H.; Bakhary, N.; Rahimian Koloor, S.S.; Petr, M. Health monitoring of civil infrastructures by subspace system identification method: An overview. Appl. Sci. 2020, 10, 2786. [Google Scholar] [CrossRef]
- Tang, Z.; Chen, Z.; Bao, Y.; Li, H. Convolutional neural network-based data anomaly detection method using multiple information for structural health monitoring. Struct. Control Health Monit. 2019, 26, e2296. [Google Scholar] [CrossRef]
- Cao, Y.; Miraba, S.; Rafiei, S.; Ghabussi, A.; Bokaei, F.; Baharom, S.; Haramipour, P.; Assilzadeh, H. Economic application of structural health monitoring and internet of things in efficiency of building information modeling. Smart Struct. Syst. Int. J. 2020, 26, 559–573. [Google Scholar] [CrossRef]
- Rose Enid Teresa, A.; Stella, S.; Goutham Priya, M.; Gajalakshmi, P.; Revathy, J. Road Bridges Across Cooum and Adyar Rivers in Chennai City—Need for Structural Health Monitoring. In Advances in Construction Materials and Sustainable Environment; Springer: Berlin/Heidelberg, Germany, 2022; pp. 281–294. [Google Scholar] [CrossRef]
- Wu, R.T.; Jahanshahi, M.R. Data fusion approaches for structural health monitoring and system identification: Past, present, and future. Struct. Health Monit. 2020, 19, 552–586. [Google Scholar] [CrossRef]
- Gordan, M.; Ismail, Z.; Ghaedi, K.; Ibrahim, Z.; Hashim, H.; Ghayeb, H.H.; Talebkhah, M. A brief overview and future perspective of unmanned aerial systems for in-service structural health monitoring. Eng. Adv. 2021, 1, 9–15. [Google Scholar] [CrossRef]
- Ling, Y.; Mahadevan, S. Integration of structural health monitoring and fatigue damage prognosis. Mech. Syst. Signal Process. 2012, 28, 89–104. [Google Scholar] [CrossRef]
- Cantero-Chinchilla, S.; Beck, J.L.; Chiachío, M.; Chiachío, J.; Chronopoulos, D.; Jones, A. Optimal sensor and actuator placement for structural health monitoring via an efficient convex cost-benefit optimization. Mech. Syst. Signal Process. 2020, 144, 106901. [Google Scholar] [CrossRef]
- Villacorta, J.J.; Del-Val, L.; Martínez, R.D.; Balmori, J.A.; Magdaleno, Á.; López, G.; Izquierdo, A.; Lorenzana, A.; Basterra, L.A. Design and Validation of a Scalable, Reconfigurable and Low-Cost Structural Health Monitoring System. Sensors 2021, 21, 648. [Google Scholar] [CrossRef]
- Zhang, T.; Zhu, J.; Xiong, Z.; Zheng, K.; Wu, M. A New Drive-by Method for Bridge Damage Inspection Based on Characteristic Wavelet Coefficient. Buildings 2023, 13, 397. [Google Scholar] [CrossRef]
- Tayeh, B.; Hadzima-Nyarko, M.; Riad, M.Y.R.; Hafez, R.D.A. Behavior of Ultra-High-Performance Concrete with Hybrid Synthetic Fiber Waste Exposed to Elevated Temperatures. Buildings 2023, 13, 129. [Google Scholar] [CrossRef]
- Dackermann, U.; Elsener, R.; Li, J.; Crews, K. A comparative study of using static and ultrasonic material testing methods to determine the anisotropic material properties of wood. Constr. Build. Mater. 2016, 102, 963–976. [Google Scholar] [CrossRef]
- Zhou, K.; Li, Q.S.; Zhi, L.H.; Han, X.L.; Xu, K. Investigation of modal parameters of a 600-m-tall skyscraper based on two-year-long structural health monitoring data and five typhoons measurements. Eng. Struct. 2023, 274, 115162. [Google Scholar] [CrossRef]
- Krause, M.; Dackermann, U.; Li, J. Elastic wave modes for the assessment of structural timber: Ultrasonic echo for building elements and guided waves for pole and pile structures. J. Civ. Struct. Health Monit. 2015, 5, 221–249. [Google Scholar] [CrossRef]
- Hassani, S.; Mousavi, M.; Dackermann, U. Johansen cointegration of frequency response functions contaminated with nonstationary colored noise for structural damage detection. J. Sound Vib. 2023, 552, 117641. [Google Scholar] [CrossRef]
- Mukupa, W.; Roberts, G.W.; Hancock, C.M.; Al-Manasir, K. A review of the use of terrestrial laser scanning application for change detection and deformation monitoring of structures. Surv. Rev. 2017, 49, 99–116. [Google Scholar] [CrossRef]
- Dackermann, U.; Smith, W.A.; Alamdari, M.M.; Li, J.; Randall, R.B. Cepstrum-based damage identification in structures with progressive damage. Struct. Health Monit. 2019, 18, 87–102. [Google Scholar] [CrossRef]
- Yuan, M.; Fang, Z.; Xiao, P.; Tong, R.; Zhang, M.; Huang, Y. An FPGA-Based Laser Virtual Scale Method for Structural Crack Measurement. Buildings 2023, 13, 261. [Google Scholar] [CrossRef]
- Chen, S.E. Laser scanning technology for bridge monitoring. Laser Scanner Technol. 2012, 71. [Google Scholar] [CrossRef]
- Daniels, D.J. Ground Penetrating Radar; IET: Stevenage, UK, 2004; Volume 1. [Google Scholar] [CrossRef]
- Tešić, K.; Baričević, A.; Serdar, M. Non-destructive corrosion inspection of reinforced concrete using ground-penetrating radar: A review. Materials 2021, 14, 975. [Google Scholar] [CrossRef]
- Lanza di Scalea, F.; Salamone, S. Temperature effects in ultrasonic Lamb wave structural health monitoring systems. J. Acoust. Soc. Am. 2008, 124, 161–174. [Google Scholar] [CrossRef]
- Raghavan, A.; Cesnik, C.E. Effects of elevated temperature on guided-wave structural health monitoring. J. Intell. Mater. Syst. Struct. 2008, 19, 1383–1398. [Google Scholar] [CrossRef]
- Bremer, K.; Wollweber, M.; Weigand, F.; Rahlves, M.; Kuhne, M.; Helbig, R.; Roth, B. Fibre optic sensors for the structural health monitoring of building structures. Procedia Technol. 2016, 26, 524–529. [Google Scholar] [CrossRef]
- Li, S.; Laima, S.; Li, H. Cluster analysis of winds and wind-induced vibrations on a long-span bridge based on long-term field monitoring data. Eng. Struct. 2017, 138, 245–259. [Google Scholar] [CrossRef]
- Schommer, S.; Nguyen, V.H.; Maas, S.; Zürbes, A. Model updating for structural health monitoring using static and dynamic measurements. Procedia Eng. 2017, 199, 2146–2153. [Google Scholar] [CrossRef]
- Dackermann, U.; Li, J.; Samali, B. Identification of member connectivity and mass changes on a two-storey framed structure using frequency response functions and artificial neural networks. J. Sound Vib. 2013, 332, 3636–3653. [Google Scholar] [CrossRef]
- Martinez-Luengo, M.; Kolios, A.; Wang, L. Structural health monitoring of offshore wind turbines: A review through the Statistical Pattern Recognition Paradigm. Renew. Sustain. Energy Rev. 2016, 64, 91–105. [Google Scholar] [CrossRef]
- Pirner, M.; Fischer, O. Long-time observation of wind and temperature effects on TV towers. J. Wind Eng. Ind. Aerodyn. 1999, 79, 1–9. [Google Scholar] [CrossRef]
- Helmicki, A.; Hunt, V.; Shell, M.; Lenett, M.; Turer, A.; Dalal, V.; Aktan, A. Multidimensional performance monitoring of a recently constructed steel-stringer bridge. In Proceedings of the 2nd International Workshop on Structural Health Monitoring, Stanford, CA, USA, 8–10 September 1999; pp. 408–416. [Google Scholar]
- Endsley, A.; Brooks, C.; Harris, D.; Ahlborn, T.; Vaghefi, K. Decision support system for integrating remote sensing in bridge condition assessment and preservation. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2012, San Diego, CA, USA, 12–15 March 2012; Volume 8345, pp. 1181–1195. [Google Scholar] [CrossRef]
- An, Y.K.; Park, B.; Sohn, H. Complete noncontact laser ultrasonic imaging for automated crack visualization in a plate. Smart Mater. Struct. 2013, 22, 025022. [Google Scholar] [CrossRef]
- Cao, X.; Rembe, C. Non-contact damage detection under operational conditions with multipoint laservibrometry. Sensors 2020, 20, 732. [Google Scholar] [CrossRef]
- Barnes, C.L.; Trottier, J.F. Phenomena and conditions in bridge decks that confound ground-penetrating radar data analysis. Transp. Res. Rec. 2002, 1795, 57–61. [Google Scholar] [CrossRef]
- Hing, C.C.; Halabe, U.B. Nondestructive testing of GFRP bridge decks using ground penetrating radar and infrared thermography. J. Bridge Eng. 2010, 15, 391–398. [Google Scholar] [CrossRef]
- Khamzin, A.K.; Varnavina, A.V.; Torgashov, E.V.; Anderson, N.L.; Sneed, L.H. Utilization of air-launched ground penetrating radar (GPR) for pavement condition assessment. Constr. Build. Mater. 2017, 141, 130–139. [Google Scholar] [CrossRef]
- Calhoon, T.; Zegeye, E.; Velasquez, R.; Calvert, J. Using Falling Weight Deflectometer (FWD) and Ground Penetrating Radar (GPR) to monitor the effects of seasonal moisture variation on the structural capacity of pavements. Constr. Build. Mater. 2022, 351, 128831. [Google Scholar] [CrossRef]
- Zatar, W.; Nguyen, T.T.; Nguyen, H. Environmental effects on condition assessments of concrete structures with ground penetrating radar. J. Appl. Geophys. 2022, 203, 104713. [Google Scholar] [CrossRef]
- Chen, H.P. Structural Health Monitoring of Large Civil Engineering Structures; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar] [CrossRef]
- Hassani, S.; Dackermann, U. A Systematic Review of Advanced Sensor Technologies for Non-Destructive Testing and Structural Health Monitoring. Sensors 2023, 23, 2204. [Google Scholar] [CrossRef]
- Sohn, H. Effects of environmental and operational variability on structural health monitoring. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2007, 365, 539–560. [Google Scholar] [CrossRef]
- Bao, Y.; Tang, Z.; Li, H.; Zhang, Y. Computer vision and deep learning–based data anomaly detection method for structural health monitoring. Struct. Health Monit. 2019, 18, 401–421. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to Machine Learning and Deep Learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Bado, M.F.; Casas, J.R. A review of recent distributed optical fiber sensors applications for civil engineering structural health monitoring. Sensors 2021, 21, 1818. [Google Scholar] [CrossRef]
- Perera, R.; Torres, L.; Ruiz, A.; Barris, C.; Baena, M. An EMI-based clustering for structural health monitoring of NSM FRP strengthening systems. Sensors 2019, 19, 3775. [Google Scholar] [CrossRef]
- Liu, Y.; Yekani Fard, M.; Chattopadhyay, A. A Statistical Approach to Investigate Temperature Effects on Guided Wave Based Structural Health Monitoring. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 20th AIAA/ASME/AHS Adaptive Structures Conference 14th AIAA, Honolulu, HI, USA, 23–26 April 2012; p. 1787. [Google Scholar] [CrossRef]
- Kita, A.; Cavalagli, N.; Ubertini, F. Temperature effects on static and dynamic behavior of Consoli Palace in Gubbio, Italy. Mech. Syst. Signal Process. 2019, 120, 180–202. [Google Scholar] [CrossRef]
- Antunes, R.A.; Cortez, N.E.; Gianesini, B.M.; Vieira Filho, J. Modeling, simulation, experimentation, and compensation of temperature effect in impedance-based SHM systems applied to steel pipes. Sensors 2019, 19, 2802. [Google Scholar] [CrossRef]
- Chen, Y.; Xue, X. Advances in the structural health monitoring of bridges using piezoelectric transducers. Sensors 2018, 18, 4312. [Google Scholar] [CrossRef]
- Zhou, G.D.; Yi, T.H. A summary review of correlations between temperatures and vibration properties of long-span bridges. Math. Probl. Eng. 2014, 2014, 638209. [Google Scholar] [CrossRef]
- Farrar, C.R.; Baker, W.; Bell, T.; Cone, K.; Darling, T.; Duffey, T.; Eklund, A.; Migliori, A. Dynamic Characterization and Damage Detection in the I-40 Bridge over the Rio Grande; Technical report; Los Alamos National Lab.: Los Alamos, NM, USA, 1994. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, Y.L.; Wei, Z.L.; Zhu, H.P.; Zhou, X.Q. Variation of structural vibration characteristics versus non-uniform temperature distribution. Eng. Struct. 2011, 33, 146–153. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, L. Insights into temperature effects on structural deformation of a cable-stayed bridge based on structural health monitoring. Struct. Health Monit. 2019, 18, 778–791. [Google Scholar] [CrossRef]
- Kromanis, R.; Kripakaran, P.; Harvey, B. Long-term structural health monitoring of the Cleddau bridge: Evaluation of quasi-static temperature effects on bearing movements. Struct. Infrastruct. Eng. 2016, 12, 1342–1355. [Google Scholar] [CrossRef]
- Roy, S.; Lonkar, K.; Janapati, V.; Chang, F.K. A novel physics-based temperature compensation model for structural health monitoring using ultrasonic guided waves. Struct. Health Monit. 2014, 13, 321–342. [Google Scholar] [CrossRef]
- Schubert, K.J.; Brauner, C.; Herrmann, A.S. Non-damage-related influences on Lamb wave–based structural health monitoring of carbon fiber–reinforced plastic structures. Struct. Health Monit. 2014, 13, 158–176. [Google Scholar] [CrossRef]
- Ai, D.; Lin, C.; Luo, H.; Zhu, H. Temperature effect on electromechanical admittance–based concrete structural health monitoring. Struct. Health Monit. 2020, 19, 661–692. [Google Scholar] [CrossRef]
- Hoshyarmanesh, H.; Ghodsi, M.; Kim, M.; Cho, H.H.; Park, H.H. Temperature effects on electromechanical response of deposited piezoelectric sensors used in structural health monitoring of aerospace structures. Sensors 2019, 19, 2805. [Google Scholar] [CrossRef]
- Deraemaeker, A.; Worden, K. A comparison of linear approaches to filter out environmental effects in structural health monitoring. Mech. Syst. Signal Process. 2018, 105, 1–15. [Google Scholar] [CrossRef]
- Kang, F.; Liu, X.; Li, J. Temperature effect modeling in structural health monitoring of concrete dams using kernel extreme learning machines. Struct. Health Monit. 2020, 19, 987–1002. [Google Scholar] [CrossRef]
- Caspani, V.F.; Tonelli, D.; Poli, F.; Zonta, D. Designing a Structural Health Monitoring System Accounting for Temperature Compensation. Infrastructures 2022, 7, 5. [Google Scholar] [CrossRef]
- Yue, N.; Aliabadi, M. A scalable data-driven approach to temperature baseline reconstruction for guided wave structural health monitoring of anisotropic carbon-fibre-reinforced polymer structures. Struct. Health Monit. 2020, 19, 1487–1506. [Google Scholar] [CrossRef]
- Mariani, S.; Heinlein, S.; Cawley, P. Compensation for temperature-dependent phase and velocity of guided wave signals in baseline subtraction for structural health monitoring. Struct. Health Monit. 2020, 19, 26–47. [Google Scholar] [CrossRef]
- Salmanpour, M.; Sharif Khodaei, Z.; Aliabadi, M. Guided wave temperature correction methods in structural health monitoring. J. Intell. Mater. Syst. Struct. 2017, 28, 604–618. [Google Scholar] [CrossRef]
- Yarnold, M.T. Temperature-Based Structural Identification and Health Monitoring for Long-Span Bridges; Drexel University: Philadelphia, PA, USA, 2013. [Google Scholar]
- Yarnold, M.T.; Moon, F.L.; Emin Aktan, A. Temperature-based structural identification of long-span bridges. J. Struct. Eng. 2015, 141, 04015027. [Google Scholar] [CrossRef]
- Dhingra, I.; Kaur, G.; Kaler, R. Design and analysis of fiber Bragg grating sensor to monitor strain and temperature for structural health monitoring. Opt. Quantum Electron. 2021, 53, 1–9. [Google Scholar] [CrossRef]
- Lambinet, F.; Khodaei, Z.S. Measurement platform for structural health monitoring application of large scale structures. Measurement 2022, 190, 110675. [Google Scholar] [CrossRef]
- Bastani, A.; Amindavar, H.; Shamshirsaz, M.; Sepehry, N. Identification of temperature variation and vibration disturbance in impedance-based structural health monitoring using piezoelectric sensor array method. Struct. Health Monit. 2012, 11, 305–314. [Google Scholar] [CrossRef]
- Laffont, G.; Cotillard, R.; Roussel, N.; Desmarchelier, R.; Rougeault, S. Temperature resistant fiber Bragg gratings for on-line and structural health monitoring of the next-generation of nuclear reactors. Sensors 2018, 18, 1791. [Google Scholar] [CrossRef]
- Gao, D.; Wu, Z.; Yang, L.; Zheng, Y.; Yin, W. Structural health monitoring for long-term aircraft storage tanks under cryogenic temperature. Aerosp. Sci. Technol. 2019, 92, 881–891. [Google Scholar] [CrossRef]
- Chen, J.; Chajes, M.J.; Shenton, H.W., III. Impact of Wind Load Characteristics on Computed Bridge Stay-Cable Forces Used for Bridge Health Monitoring. J. Bridge Eng. 2023, 28, 04023007. [Google Scholar] [CrossRef]
- Ye, X.W.; Sun, Z.; Lu, J. Prediction and early warning of wind-induced girder and tower vibration in cable-stayed bridges with machine learning-based approach. Eng. Struct. 2023, 275, 115261. [Google Scholar] [CrossRef]
- Li, H.N.; Ren, L.; Jia, Z.G.; Yi, T.H.; Li, D.S. State-of-the-art in structural health monitoring of large and complex civil infrastructures. J. Civ. Struct. Health Monit. 2016, 6, 3–16. [Google Scholar] [CrossRef]
- Xu, Y.L.; Xia, Y. Structural Health Monitoring of Long-Span Suspension Bridges; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Chen, Z.; Zhou, X.; Wang, X.; Dong, L.; Qian, Y. Deployment of a smart structural health monitoring system for long-span arch bridges: A review and a case study. Sensors 2017, 17, 2151. [Google Scholar] [CrossRef]
- Zhang, Q.; Fan, L.; Yuan, W. Traffic-induced variability in dynamic properties of cable-stayed bridge. Earthq. Eng. Struct. Dyn. 2002, 31, 2015–2021. [Google Scholar] [CrossRef]
- Abe, M.; Fujino, Y.; Yanagihara, M.; Sato, M. Monitoring of Hakucho Suspension Bridge by ambient vibration measurement. In Proceedings of the Nondestructive Evaluation of Highways, Utilities, and Pipelines IV; Aktan, A.E., Gosselin, S.R., Gosselin, S.R., Eds.; SPIE: Cergy Pontoise, France, 2000; Volume 3995, pp. 237–244. [Google Scholar] [CrossRef]
- Weijtjens, W.; Verbelen, T.; Capello, E.; Devriendt, C. Vibration based structural health monitoring of the substructures of five offshore wind turbines. Procedia Eng. 2017, 199, 2294–2299. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Chu, Q.; Xue, S.; He, Y. Wind-induced response monitoring of large-span air-supported membrane structure coal-shed under the influence of typhoons. Thin-Walled Struct. 2022, 181, 109951. [Google Scholar] [CrossRef]
- Wang, Y.W.; Ni, Y.Q. Full-scale monitoring of wind effects on a supertall structure during six tropical cyclones. J. Build. Eng. 2022, 45, 103507. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, L. Effects of high winds on a long-span sea-crossing bridge based on structural health monitoring. J. Wind Eng. Ind. Aerodyn. 2018, 174, 260–268. [Google Scholar] [CrossRef]
- Zhu, L.; McCrum, D.; Sweeney, C.; Keenahan, J. Full-scale computational fluid dynamics study on wind condition of the long-span Queensferry Crossing Bridge. J. Civ. Struct. Health Monit. 2023, 1–18. [Google Scholar] [CrossRef]
- Li, H.; Li, S.; Ou, J.; Li, H. Modal identification of bridges under varying environmental conditions: Temperature and wind effects. Struct. Control Health Monit. 2010, 17, 495–512. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Ni, Y.; Xu, X. Bayesian probabilistic assessment of occupant comfort of high-rise structures based on structural health monitoring data. Mech. Syst. Signal Process. 2022, 163, 108147. [Google Scholar] [CrossRef]
- Tsai, L.W.; Alipour, A. Structural health monitoring and fatigue life reliability assessment of a flexible structure in extreme wind. J. Civ. Struct. Health Monit. 2023, 1–15. [Google Scholar] [CrossRef]
- Mu, H.Q.; Yuen, K.V. Modal frequency-environmental condition relation development using long-term structural health monitoring measurement: Uncertainty quantification, sparse feature selection and multivariate prediction. Measurement 2018, 130, 384–397. [Google Scholar] [CrossRef]
- Ramos, L.F.; Marques, L.; Lourenço, P.B.; De Roeck, G.; Campos-Costa, A.; Roque, J. Monitoring historical masonry structures with operational modal analysis: Two case studies. Mech. Syst. Signal Process. 2010, 24, 1291–1305. [Google Scholar] [CrossRef]
- Xia, Y.; Hao, H.; Zanardo, G.; Deeks, A. Long term vibration monitoring of an RC slab: Temperature and humidity effect. Eng. Struct. 2006, 28, 441–452. [Google Scholar] [CrossRef]
- Peeters, B.; De Roeck, G. One-year monitoring of the Z24-Bridge: Environmental effects versus damage events. Earthq. Eng. Struct. Dyn. 2001, 30, 149–171. [Google Scholar] [CrossRef]
- Kullaa, J. Distinguishing between sensor fault, structural damage, and environmental or operational effects in structural health monitoring. Mech. Syst. Signal Process. 2011, 25, 2976–2989. [Google Scholar] [CrossRef]
- Bekas, D.G.; Sharif-Khodaei, Z.; Aliabadi, M.F. An innovative diagnostic film for structural health monitoring of metallic and composite structures. Sensors 2018, 18, 2084. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Wang, W.; Zhang, X. Frequency modification of continuous beam bridge based on co-integration analysis considering the effect of temperature and humidity. Struct. Health Monit. 2019, 18, 376–389. [Google Scholar] [CrossRef]
- He, X.; Tan, G.; Chu, W.; Zhang, S.; Wei, X. Reliability Assessment Method for Simply Supported Bridge Based on Structural Health Monitoring of Frequency with Temperature and Humidity Effect Eliminated. Sustainability 2022, 14, 9600. [Google Scholar] [CrossRef]
- Dong, W.; Li, W.; Zhu, X.; Sheng, D.; Shah, S.P. Multifunctional cementitious composites with integrated self-sensing and hydrophobic capacities toward smart structural health monitoring. Cem. Concr. Compos. 2021, 118, 103962. [Google Scholar] [CrossRef]
- Chang, K.; Kim, C.; Borjigin, S. Variability in bridge frequency induced by a parked vehicle. Smart Struct. Syst. 2014, 13, 75–79. [Google Scholar] [CrossRef]
- Farreras-Alcover, I.; Chryssanthopoulos, M.K.; Andersen, J.E. Regression models for structural health monitoring of welded bridge joints based on temperature, traffic and strain measurements. Struct. Health Monit. 2015, 14, 648–662. [Google Scholar] [CrossRef]
- Guo, T.; Chen, Y.W. Field stress/displacement monitoring and fatigue reliability assessment of retrofitted steel bridge details. Eng. Fail. Anal. 2011, 18, 354–363. [Google Scholar] [CrossRef]
- Saidin, S.S.; Kudus, S.A.; Jamadin, A.; Anuar, M.A.; Amin, N.M.; Ya, A.B.Z.; Sugiura, K. Vibration-based approach for structural health monitoring of ultra-high-performance concrete bridge. Case Stud. Constr. Mater. 2023, 18, e01752. [Google Scholar] [CrossRef]
- Svendsen, B.T.; Øiseth, O.; Frøseth, G.T.; Rønnquist, A. A hybrid structural health monitoring approach for damage detection in steel bridges under simulated environmental conditions using numerical and experimental data. Struct. Health Monit. 2023, 22, 540–561. [Google Scholar] [CrossRef]
- OBrien, E.J.; Cantero, D.; Enright, B.; González, A. Characteristic dynamic increment for extreme traffic loading events on short and medium span highway bridges. Eng. Struct. 2010, 32, 3827–3835. [Google Scholar] [CrossRef]
- Kim, C.W.; Kawatani, M.; Hao, J. Modal parameter identification of short span bridges under a moving vehicle by means of multivariate AR model. Struct. Infrastruct. Eng. 2012, 8, 459–472. [Google Scholar] [CrossRef]
- Deng, L.; Cai, C. Development of dynamic impact factor for performance evaluation of existing multi-girder concrete bridges. Eng. Struct. 2010, 32, 21–31. [Google Scholar] [CrossRef]
- Rahim, S. Investigating the Effect of Variable Mass Loading in Structural Health Monitoring from a Machine Learning Perspective. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2018. [Google Scholar]
- Wang, H.; Mao, J.X.; Spencer, B.F., Jr. A monitoring-based approach for evaluating dynamic responses of riding vehicle on long-span bridge under strong winds. Eng. Struct. 2019, 189, 35–47. [Google Scholar] [CrossRef]
- Sarrafi, A.; Mao, Z.; Niezrecki, C.; Poozesh, P. Vibration-based damage detection in wind turbine blades using Phase-based Motion Estimation and motion magnification. J. Sound Vib. 2018, 421, 300–318. [Google Scholar] [CrossRef]
- Rocha, H.; Semprimoschnig, C.; Nunes, J.P. Sensors for process and structural health monitoring of aerospace composites: A review. Eng. Struct. 2021, 237, 112231. [Google Scholar] [CrossRef]
- Soman, R.; Wee, J.; Peters, K. Optical fiber sensors for ultrasonic structural health monitoring: A review. Sensors 2021, 21, 7345. [Google Scholar] [CrossRef]
- Braunfelds, J.; Senkans, U.; Skels, P.; Janeliukstis, R.; Salgals, T.; Redka, D.; Lyashuk, I.; Porins, J.; Spolitis, S.; Haritonovs, V.; et al. FBG-based sensing for structural health monitoring of road infrastructure. J. Sens. 2021, 2021. [Google Scholar] [CrossRef]
- Sharma, V.B.; Singh, K.; Gupta, R.; Joshi, A.; Dubey, R.; Gupta, V.; Bharadwaj, S.; Zafar, M.I.; Bajpai, S.; Khan, M.A.; et al. Review of structural health monitoring techniques in pipeline and wind turbine industries. Appl. Syst. Innov. 2021, 4, 59. [Google Scholar] [CrossRef]
- Chen, J.; Feng, X.; Xiao, S. An iterative method for leakage zone identification in water distribution networks based on machine learning. Struct. Health Monit. 2021, 20, 1938–1956. [Google Scholar] [CrossRef]
- Ravet, F.; Briffod, F.; Goy, A.; Rochat, E. Mitigation of geohazard risk along transportation infrastructures with optical fiber distributed sensing. J. Civ. Struct. Health Monit. 2021, 11, 967–988. [Google Scholar] [CrossRef]
- Min, R.; Liu, Z.; Pereira, L.; Yang, C.; Sui, Q.; Marques, C. Optical fiber sensing for marine environment and marine structural health monitoring: A review. Opt. Laser Technol. 2021, 140, 107082. [Google Scholar] [CrossRef]
- Sivasuriyan, A.; Vijayan, D.; LeemaRose, A.; Revathy, J.; Gayathri Monicka, S.; Adithya, U.; Jebasingh Daniel, J. Development of smart sensing technology approaches in structural health monitoring of bridge structures. Adv. Mater. Sci. Eng. 2021, 2021, 2615029. [Google Scholar] [CrossRef]
- Adhreena, M.; Hafizi, Z. A Review on the Application of Fiber Bragg Grating Sensors in Bolted Joints Health Monitoring. In Technological Advancement in Instrumentation & Human Engineering: Selected Papers from ICMER 2021; Springer: Singapore, 2022; pp. 655–667. [Google Scholar] [CrossRef]
- Chu, P.L. CHAPTER 2—Recent Development of a Polymer Optical Fiber and its Applications. In Guided Wave Optical Components and Devices; Pal, B.P., Ed.; Academic Press: Burlington, MA, USA, 2006; pp. 27–40. [Google Scholar] [CrossRef]
- Gowshikan, A.; Kariyawasam, K.; Xu, X.; Kechavarzi, C.; de Battista, N.; Ferdinando, N.; Acikgoz, S.; Gunawardana, N.; Ranasinghe, M. A Review on the Advances in Distributed Fibre Optic Sensing Technology for Structural Health Monitoring. In Proceedings of the 12th International Conference on Structural Engineering and Construction Management: Proceedings of the ICSECM 2021; Springer: Singapore, 2022; pp. 145–159. [Google Scholar] [CrossRef]
- Jendrlin, M.; Radu, A.; Zholobenko, V.; Kirsanov, D. Performance modelling of zeolite-based potentiometric sensors. Sens. Actuators B Chem. 2022, 356, 131343. [Google Scholar] [CrossRef]
- Kulapina, E.; Kulapina, O.; Cherdakova, E.; Ankina, V. Potentiometric Sensors Sensitive to Some Cephalosporin Antibiotics: Properties and Applications. J. Anal. Chem. 2022, 77, 963–973. [Google Scholar] [CrossRef]
- Sobhanie, E.; Roshani, A.; Hosseini, M. Microfluidic systems with amperometric and voltammetric detection and paper-based sensors and biosensors. In Carbon Nanomaterials-Based Sensors; Elsevier: Amsterdam, The Netherland, 2022; pp. 275–287. [Google Scholar] [CrossRef]
- Beck, L.; Barker, A.; Carew, P.; Instruments, K. Novel Bare Amperometric Sensors to Provide Accurate Stabilized Bromine Dosing in Cooling Towers; KUNTZE: Meerbusch, Germany, 2022. [Google Scholar]
- Neri, G. New Applications of Conductometric Gas Sensors: Quo Vadis? In Proceedings of the AISEM Annual Conference on Sensors and Microsystems; Springer: Berlin/Heidelberg, Germany, 2023; pp. 147–152. [Google Scholar] [CrossRef]
- Vázquez-López, A.; Bartolomé, J.; Cremades, A.; Maestre, D. High-performance room-temperature conductometric Gas sensors: Materials and strategies. Chemosensors 2022, 10, 227. [Google Scholar] [CrossRef]
- Sofi, A.; Regita, J.J.; Rane, B.; Lau, H.H. Structural health monitoring using wireless smart sensor network–An overview. Mech. Syst. Signal Process. 2022, 163, 108113. [Google Scholar] [CrossRef]
- Komarizadehasl, S.; Lozano, F.; Lozano-Galant, J.A.; Ramos, G.; Turmo, J. Low-cost wireless structural health monitoring of bridges. Sensors 2022, 22, 5725. [Google Scholar] [CrossRef]
- Hao, X.H.; Yuen, K.V.; Kuok, S.C. Energy-aware versatile wireless sensor network configuration for structural health monitoring. Struct. Control Health Monit. 2022, 29, e3083. [Google Scholar] [CrossRef]
- Abner, M.; Wong, P.K.Y.; Cheng, J.C. Battery lifespan enhancement strategies for edge computing-enabled wireless Bluetooth mesh sensor network for structural health monitoring. Autom. Constr. 2022, 140, 104355. [Google Scholar] [CrossRef]
- Le, T.C.; Luu, T.H.T.; Nguyen, H.P.; Nguyen, T.H.; Ho, D.D.; Huynh, T.C. Piezoelectric Impedance-Based Structural Health Monitoring of Wind Turbine Structures: Current Status and Future Perspectives. Energies 2022, 15, 5459. [Google Scholar] [CrossRef]
- Adekola, O.; Lamond, J.; Adelekan, I.; Bhattacharya-Mis, N.; Ekinya, M.; Bassey Eze, E.; Ujoh, F. Towards adoption of mobile data collection for effective adaptation and climate risk management in Africa. Geosci. Data J. 2022. [Google Scholar] [CrossRef]
- Li, H.; Greenhalgh, S.; Liu, B.; Liu, X.; Hao, Q.; Chen, Y. A Generalized Seismic Attenuation Compensation Operator Optimized by 2-D Mathematical Morphology Filtering. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Li, Z.; Li, E.; Samat, A.; Xu, T.; Liu, W.; Zhu, Y. An Object-Oriented CNN Model Based on Improved Superpixel Segmentation for High-Resolution Remote Sensing Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 4782–4796. [Google Scholar] [CrossRef]
- Xia, L.; Chen, J.; Luo, J.; Zhang, J.; Yang, D.; Shen, Z. Building Change Detection Based on an Edge-Guided Convolutional Neural Network Combined with a Transformer. Remote Sens. 2022, 14, 4524. [Google Scholar] [CrossRef]
- Shao, S.; Xiao, L.; Lin, L.; Ren, C.; Tian, J. Road Extraction Convolutional Neural Network with Embedded Attention Mechanism for Remote Sensing Imagery. Remote Sens. 2022, 14, 2061. [Google Scholar] [CrossRef]
- Ji, W.; Liu, Y. Research on Quantitative Evaluation of Remote Sensing and Statistics Based on Wireless Sensors and Farmland Soil Nutrient Variability. Comput. Intell. Neurosci. 2022, 2022. [Google Scholar] [CrossRef] [PubMed]
- Olson, D.L. Data mining in business services. Serv. Bus. 2007, 1, 181–193. [Google Scholar] [CrossRef]
- Luo, J.; Huang, M.; Lei, Y. Temperature Effect on Vibration Properties and Vibration-Based Damage Identification of Bridge Structures: A Literature Review. Buildings 2022, 12, 1209. [Google Scholar] [CrossRef]
- Hassani, S.; Dackermann, U. A Systematic Review of Optimization Algorithms for Structural Health Monitoring and Optimal Sensor Placement. Sensors 2023, 23, 3293. [Google Scholar] [CrossRef]
- Erazo, K.; Sen, D.; Nagarajaiah, S.; Sun, L. Vibration-based structural health monitoring under changing environmental conditions using Kalman filtering. Mech. Syst. Signal Process. 2019, 117, 1–15. [Google Scholar] [CrossRef]
- Baptista, F.G.; Budoya, D.E.; De Almeida, V.A.; Ulson, J.A.C. An experimental study on the effect of temperature on piezoelectric sensors for impedance-based structural health monitoring. Sensors 2014, 14, 1208–1227. [Google Scholar] [CrossRef]
- Barbosh, M.; Singh, P.; Sadhu, A. Empirical mode decomposition and its variants: A review with applications in structural health monitoring. Smart Mater. Struct. 2020, 29, 093001. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, W.; Su, G. A Novel Support-Vector-Machine-Based Grasshopper Optimization Algorithm for Structural Reliability Analysis. Buildings 2022, 12, 855. [Google Scholar] [CrossRef]
- Lei, J.; Cui, Y.; Shi, W. Structural damage identification method based on vibration statistical indicators and support vector machine. Adv. Struct. Eng. 2022, 25, 1310–1322. [Google Scholar] [CrossRef]
- Dackermann, U.; Yu, Y.; Niederleithinger, E.; Li, J.; Wiggenhauser, H. Condition assessment of foundation piles and utility poles based on guided wave propagation using a network of tactile transducers and support vector machines. Sensors 2017, 17, 2938. [Google Scholar] [CrossRef]
- Ding, Z.; Li, J.; Hao, H. Simultaneous identification of structural damage and nonlinear hysteresis parameters by an evolutionary algorithm-based artificial neural network. Int. J. Non-Linear Mech. 2022, 142, 103970. [Google Scholar] [CrossRef]
- Albahri, A.; Alnoor, A.; Zaidan, A.; Albahri, O.; Hameed, H.; Zaidan, B.; Peh, S.; Zain, A.; Siraj, S.; Masnan, A.; et al. Hybrid artificial neural network and structural equation modelling techniques: A survey. Complex Intell. Syst. 2022, 8, 1781–1801. [Google Scholar] [CrossRef]
- Dackermann, U.; Li, J.; Samali, B. Dynamic-based damage identification using neural network ensembles and damage index method. Adv. Struct. Eng. 2010, 13, 1001–1016. [Google Scholar] [CrossRef]
- Furuya, S.; Sanaee, A.; Georgescu, S.; Townsend, J.; Rasmussen, B.; Chow, P.; Snelling, D.; Goto, M. Imagification technology and deep learning accelerating defect detection in non-destructive testing for wind turbine blades. Fujitsu Sci. Tech. J. 2019, 55, 23–29. [Google Scholar]
- Yu, Y.; Dackermann, U.; Li, J.; Niederleithinger, E. Wavelet packet energy–based damage identification of wood utility poles using support vector machine multi-classifier and evidence theory. Struct. Health Monit. 2019, 18, 123–142. [Google Scholar] [CrossRef]
- Kot, P.; Muradov, M.; Gkantou, M.; Kamaris, G.S.; Hashim, K.; Yeboah, D. Recent advancements in non-destructive testing techniques for structural health monitoring. Appl. Sci. 2021, 11, 2750. [Google Scholar] [CrossRef]
- Ismail, Z.; Mustapha, S.; Tarhini, H. Optimizing the placement of piezoelectric wafers on closed sections using a genetic algorithm–Towards application in structural health monitoring. Ultrasonics 2021, 116, 106523. [Google Scholar] [CrossRef] [PubMed]
- Hassan, H.; Tallman, T.N. Failure prediction in self-sensing nanocomposites via genetic algorithm-enabled piezoresistive inversion. Struct. Health Monit. 2020, 19, 765–780. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, J.; Shen, Y.; Karkera, B.; Croxford, A.J.; Wilcox, P.D. Defect detection in guided wave signals using nonlinear autoregressive exogenous method. Struct. Health Monit. 2022, 21, 1012–1030. [Google Scholar] [CrossRef]
- Meixedo, A.; Santos, J.; Ribeiro, D.; Calçada, R.; Todd, M.D. Online unsupervised detection of structural changes using train–induced dynamic responses. Mech. Syst. Signal Process. 2022, 165, 108268. [Google Scholar] [CrossRef]
- Vieira, M.; Henriques, E.; Snyder, B.; Reis, L. Insights on the impact of structural health monitoring systems on the operation and maintenance of offshore wind support structures. Struct. Saf. 2022, 94, 102154. [Google Scholar] [CrossRef]
- Li, Y.; Bao, T.; Gao, Z.; Shu, X.; Zhang, K.; Xie, L.; Zhang, Z. A new dam structural response estimation paradigm powered by deep learning and transfer learning techniques. Struct. Health Monit. 2022, 21, 770–787. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, Á.; Caetano, E. Vibration based structural health monitoring of an arch bridge: From automated OMA to damage detection. Mech. Syst. Signal Process. 2012, 28, 212–228. [Google Scholar] [CrossRef]
- Cao, S.; Guo, N.; Xu, C. Robust damage localization in plate-type structures by using an enhanced robust principal component analysis and data fusion technique. Mech. Syst. Signal Process. 2022, 162, 108091. [Google Scholar] [CrossRef]
- Das, S.; Saha, P. Performance of swarm intelligence based chaotic meta-heuristic algorithms in civil structural health monitoring. Measurement 2021, 169, 108533. [Google Scholar] [CrossRef]
- Jiang, S.; Zhao, L.; Du, C. Structural deformation prediction model based on extreme learning machine algorithm and particle swarm optimization. Struct. Health Monit. 2022, 21, 2786–2803. [Google Scholar] [CrossRef]
- Guerrisi, G.; Del Frate, F.; Schiavon, G. Satellite On-Board Change Detection via Auto-Associative Neural Networks. Remote Sens. 2022, 14, 2735. [Google Scholar] [CrossRef]
- Entezami, A.; De Michele, C.; Arslan, A.N.; Behkamal, B. Detection of partially structural collapse using long-term small displacement data from satellite images. Sensors 2022, 22, 4964. [Google Scholar] [CrossRef]
- Ji, X.; Tian, Z.; Song, H.; Liu, F. Structural performance degradation identification of offshore wind turbines based on variational mode decomposition with a Grey Wolf Optimizer algorithm. Ocean Eng. 2022, 256, 111449. [Google Scholar] [CrossRef]
- Moallemi, A.; Burrello, A.; Brunelli, D.; Benini, L. Model-based vs. data-driven approaches for anomaly detection in structural health monitoring: A case study. In Proceedings of the 2021 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Scotland, UK, 17–20 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Anaissi, A.; Khoa, N.L.D.; Rakotoarivelo, T.; Alamdari, M.M.; Wang, Y. Adaptive online one-class support vector machines with applications in structural health monitoring. ACM Trans. Intell. Syst. Technol. TIST 2018, 9, 1–20. [Google Scholar] [CrossRef]
- Gui, G.; Pan, H.; Lin, Z.; Li, Y.; Yuan, Z. Data-driven support vector machine with optimization techniques for structural health monitoring and damage detection. KSCE J. Civ. Eng. 2017, 21, 523–534. [Google Scholar] [CrossRef]
- Wang, C.; Xiao, J.; Zhang, C.; Xiao, X. Structural health monitoring and performance analysis of a 12-story recycled aggregate concrete structure. Eng. Struct. 2020, 205, 110102. [Google Scholar] [CrossRef]
- Kostić, B.; Gül, M. Vibration-based damage detection of bridges under varying temperature effects using time-series analysis and artificial neural networks. J. Bridge Eng. 2017, 22, 04017065. [Google Scholar] [CrossRef]
- Xiang, Z.-Q.; Pan, J.-W.; Wang, J.-T.; Chi, F.-D. Improved approach for vibration-based structural health monitoring of arch dams during seismic events and normal operation. Struct. Control Health Monit. 2022, 29, e2955. [Google Scholar] [CrossRef]
- Duan, Y.F.; Li, Y.; Xiang, Y.Q. Strain-temperature correlation analysis of a tied arch bridge using monitoring data. In Proceedings of the 2011 International Conference on Multimedia Technology, Hangzhou, China, 26–28 July 2011; pp. 6025–6028. [Google Scholar] [CrossRef]
- Liang, Z.; Zhang, J.; Cao, J.; Zhou, J. Separating temperature effect from state monitoring of concrete bridges. In Proceedings of the Health Monitoring of Structural and Biological Systems 2009; SPIE: Cergy Pontoise, France, 2009; Volume 7295, pp. 809–817. [Google Scholar] [CrossRef]
- Huang, M.S.; Gül, M.; Zhu, H.P. Vibration-Based Structural Damage Identification under Varying Temperature Effects. J. Aerosp. Eng. 2018, 31, 04018014. [Google Scholar] [CrossRef]
- Huang, M.; Lei, Y.; Li, X.; Gu, J. Damage Identification of Bridge Structures Considering Temperature Variations-Based SVM and MFO. J. Aerosp. Eng. 2021, 34, 04020113. [Google Scholar] [CrossRef]
- Huang, M.; Wan, Z.; Cheng, X.; Xu, Z.; Lei, Y.; Pan, D. Two-stage damage identification method based on fractal theory and whale optimization algorithm. Adv. Struct. Eng. 2022, 25, 2364–2381. [Google Scholar] [CrossRef]
- Gu, J.; Gul, M.; Wu, X. Damage detection under varying temperature using artificial neural networks. Struct. Control Health Monit. 2017, 24, e1998. [Google Scholar] [CrossRef]
- Lim, H.J.; Kim, M.K.; Sohn, H.; Park, C.Y. Impedance based damage detection under varying temperature and loading conditions. NDT E Int. 2011, 44, 740–750. [Google Scholar] [CrossRef]
- Zhu, Y.; Ni, Y.Q.; Jesus, A.; Liu, J.; Laory, I. Thermal strain extraction methodologies for bridge structural condition assessment. Smart Mater. Struct. 2018, 27, 105051. [Google Scholar] [CrossRef]
- Ren, Y.; Qiu, L.; Yuan, S.; Fang, F. Gaussian mixture model–based path-synthesis accumulation imaging of guided wave for damage monitoring of aircraft composite structures under temperature variation. Struct. Health Monit. 2019, 18, 284–302. [Google Scholar] [CrossRef]
- Fendzi, C.; Rebillat, M.; Mechbal, N.; Guskov, M.; Coffignal, G. A data-driven temperature compensation approach for Structural Health Monitoring using Lamb waves. Struct. Health Monit. 2016, 15, 525–540. [Google Scholar] [CrossRef]
- Moaveni, B.; Behmanesh, I. Effects of changing ambient temperature on finite element model updating of the Dowling Hall Footbridge. Eng. Struct. 2012, 43, 58–68. [Google Scholar] [CrossRef]
- Su, J.; Xia, Y.; Zhu, L.; Zhu, H.; Ni, Y. Typhoon-and temperature-induced quasi-static responses of a supertall structure. Eng. Struct. 2017, 143, 91–100. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).