Nonlinear Dynamic Analysis of the Wind–Train–Bridge System of a Long-Span Railway Suspension Truss Bridge
Abstract
1. Introduction
2. Long-Span Suspension Bridge Analysis
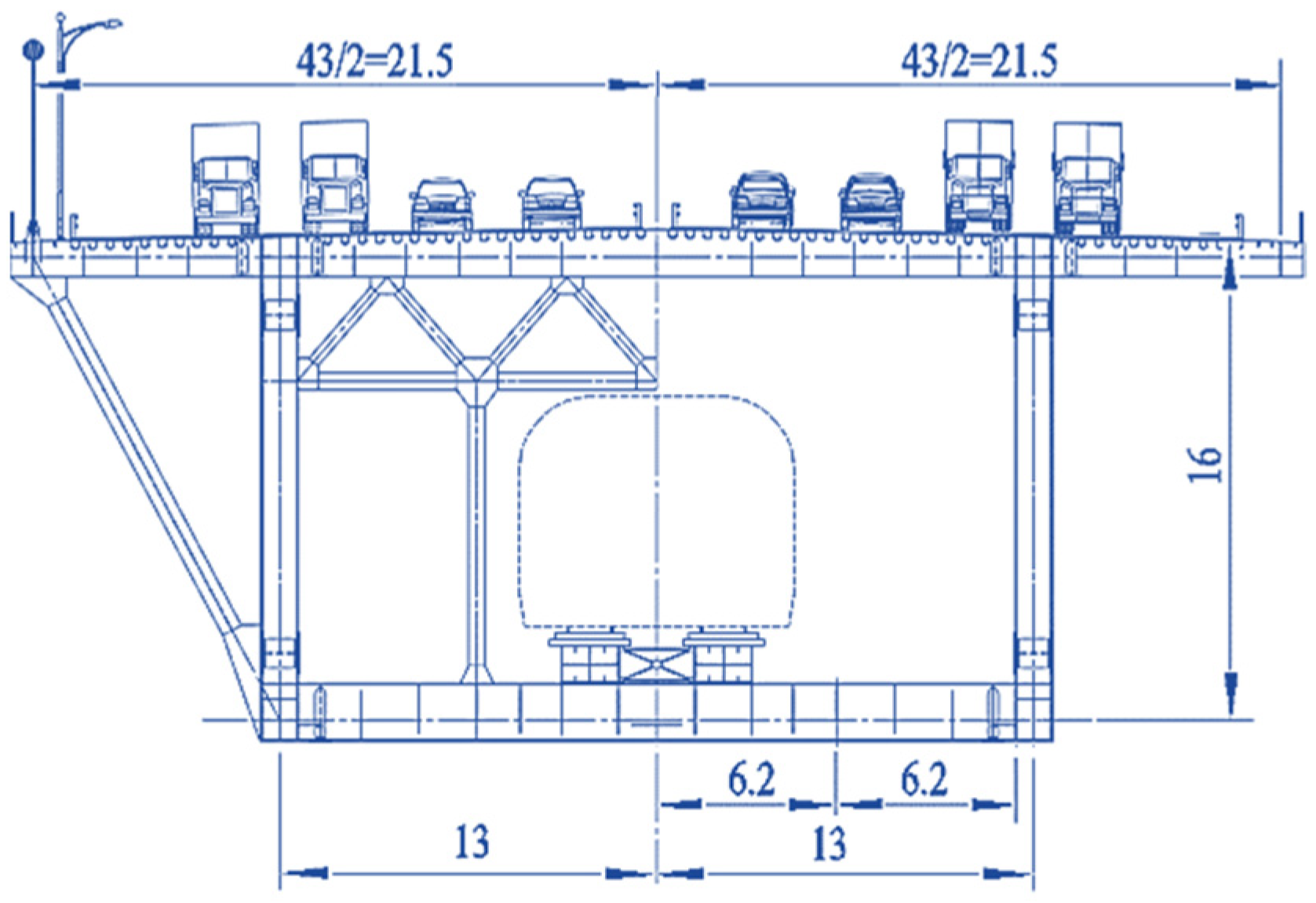
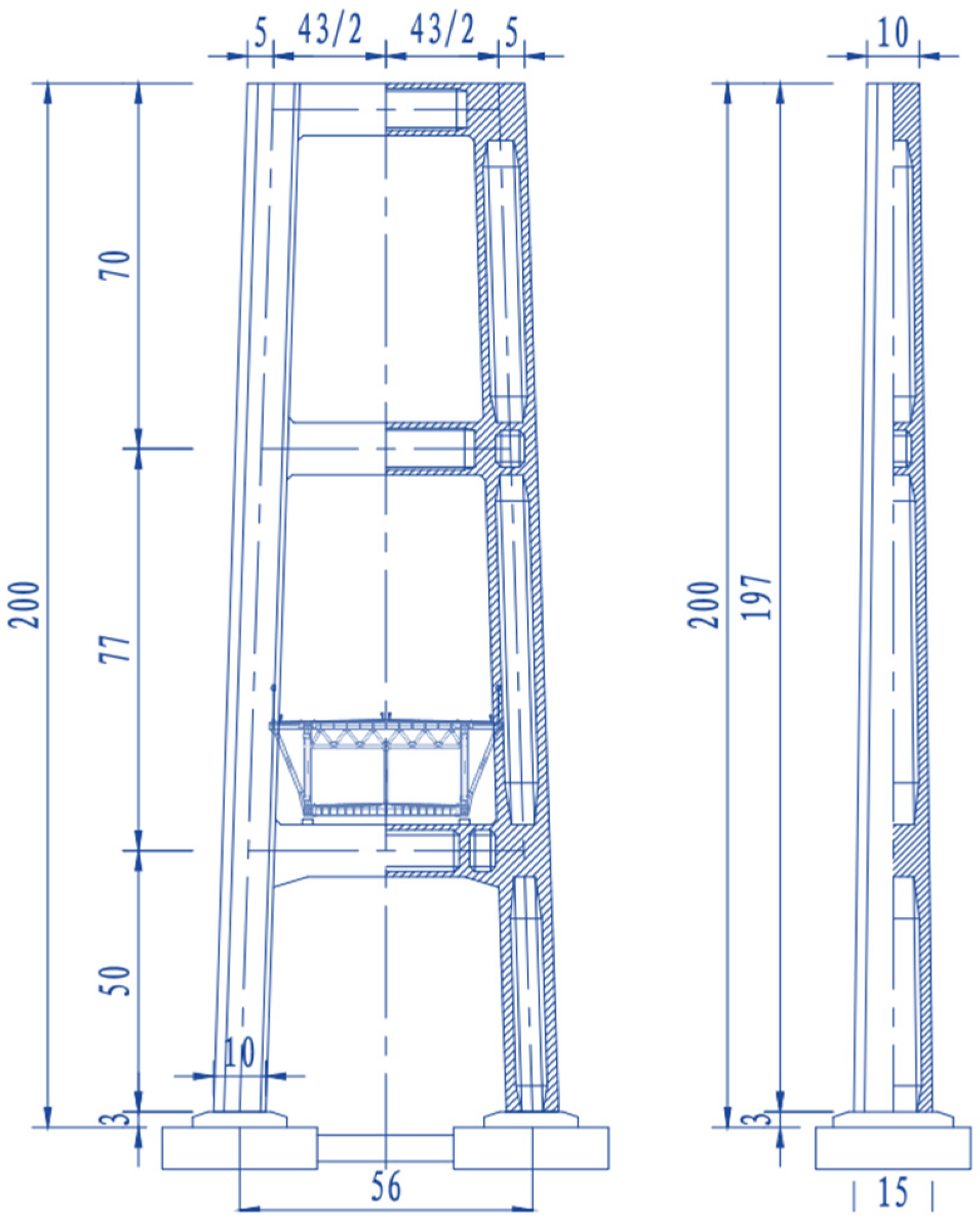
2.1. Bridge Model
2.2. Geometric Nonlinearity
- Influence of the weight sag of the main cable
- Influence of the initial internal force of the cable
- Influence of a large displacement of the structure
2.3. Bridge Modal Analysis
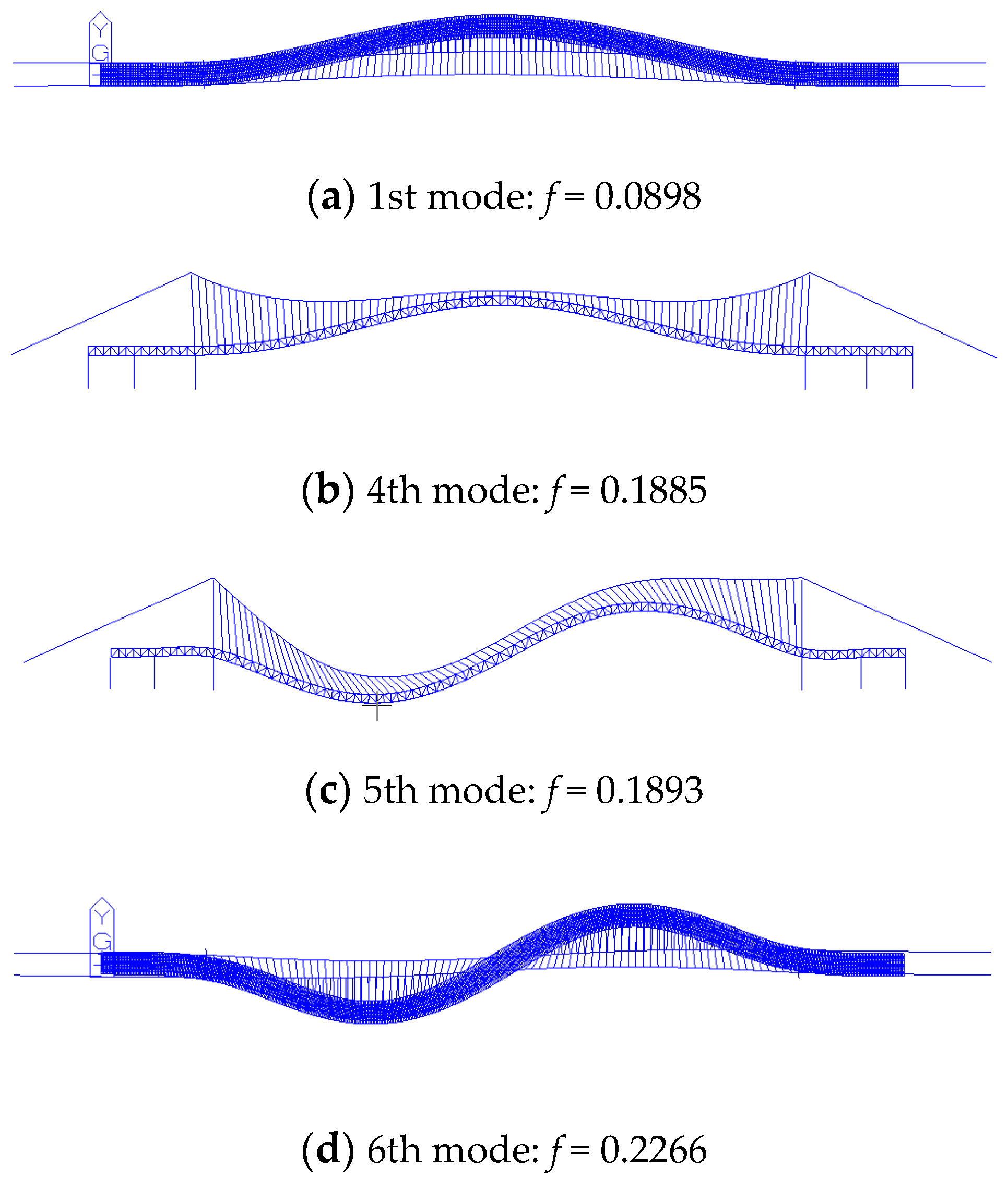
- The structural internal forces caused by weight and dead load are applied to the cables of the suspension bridge, and the elastic modulus of the suspension bridge is iteratively calculated and corrected by the Ernst formula. The first 50th natural frequencies and vibration modes of the bridge are solved by the subspace iteration method. It can be seen from the calculation results that the first 50th natural frequencies of the suspension bridge are very close, varying between 0.0898 Hz and 1.3563 Hz. The first 10th vibration frequencies and the main vibration mode characteristics are listed in Table 2, and the schematic diagram of some vibration modes is shown in Figure 5. The first mode of the bridge is the lateral vibration of the main girder, with a corresponding frequency of 0.0898 Hz. The vertical vibration of the main girder appears in the fourth mode, with a frequency of 0.1885 Hz. The first torsional of the main girder appears in the 10th mode of the structure at a frequency of 2.3720 Hz. Through finite element modeling and natural vibration analysis, it can be seen that the natural frequencies of the bridge are very low, and it is prone to vibrate due to the excitation of external vehicle loads and wind loads.
3. Wind–Train–Bridge Interaction Model
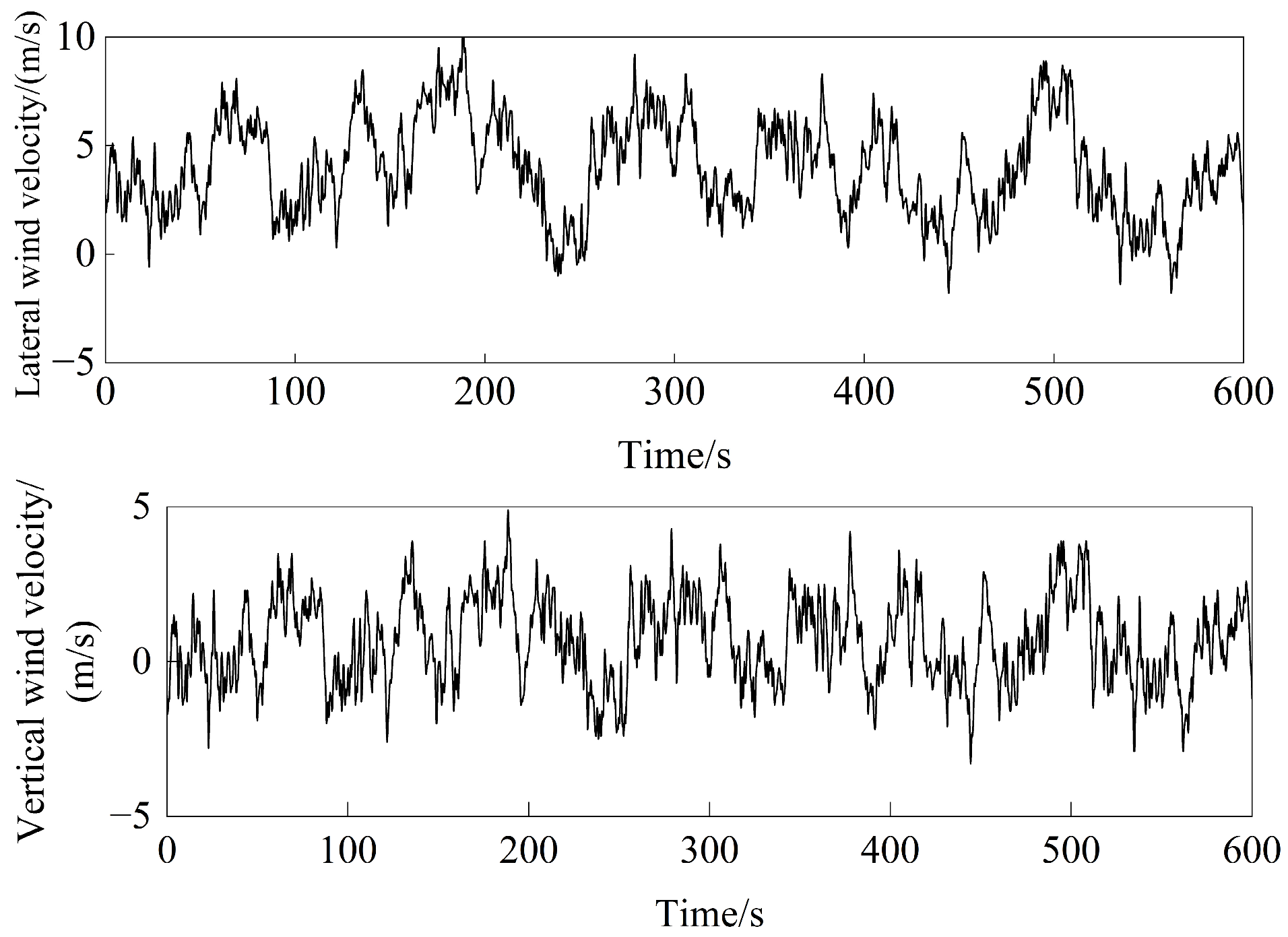
3.1. Wind Loads Model
3.2. Train Model
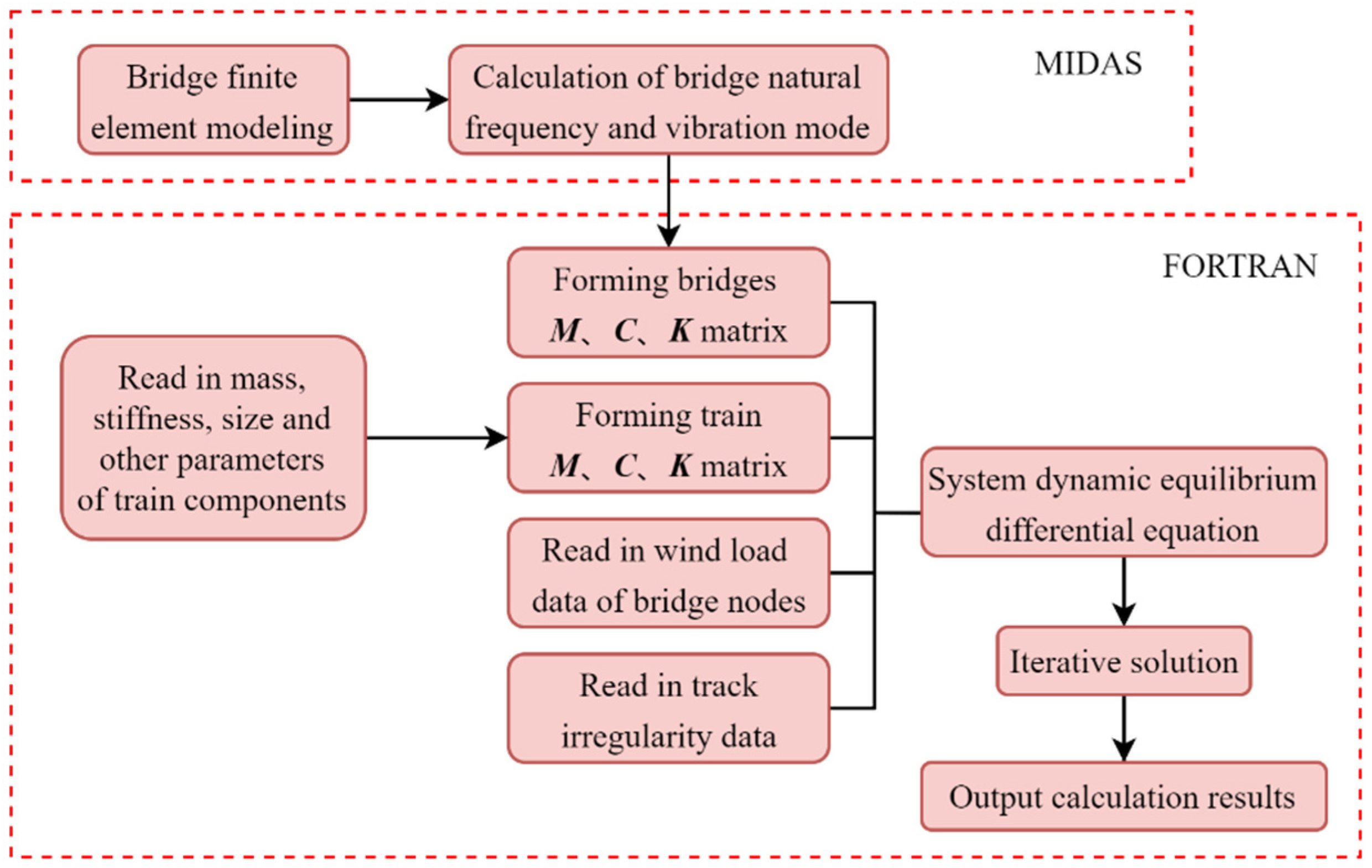
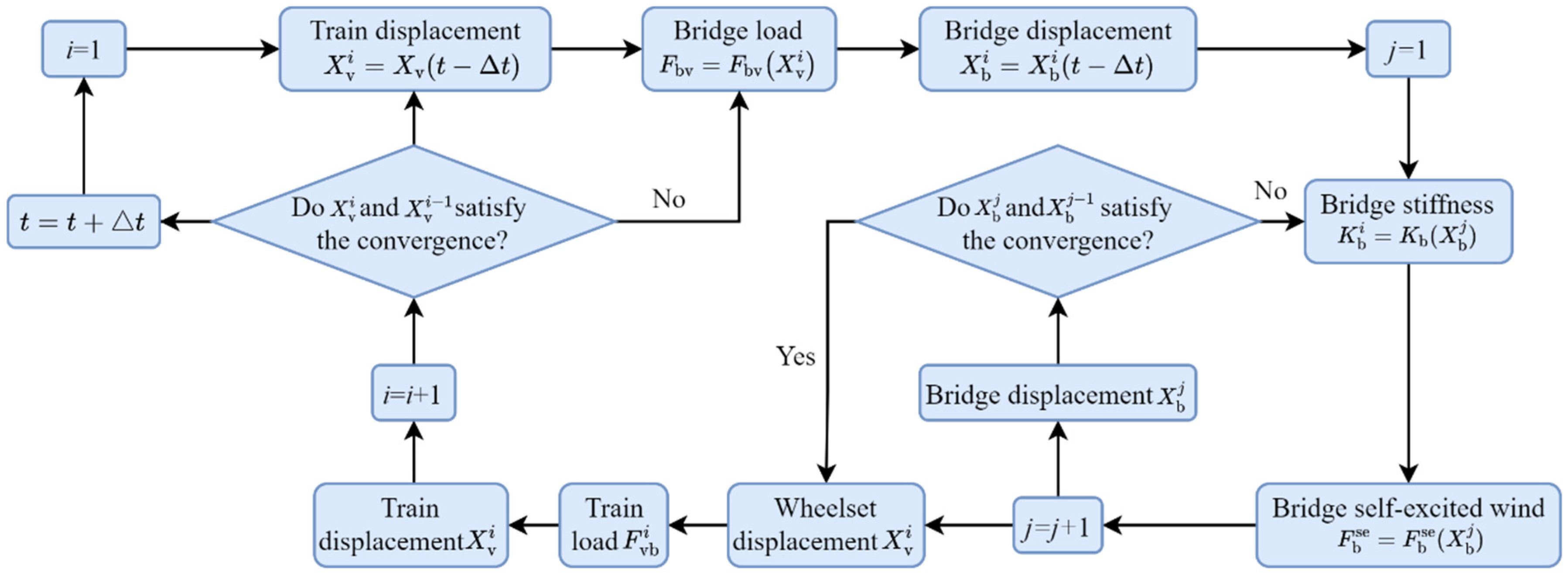
3.3. Wind–Train–Suspension Bridge System Calculation
4. Wind–Train–Bridge Coupling Vibration Calculation
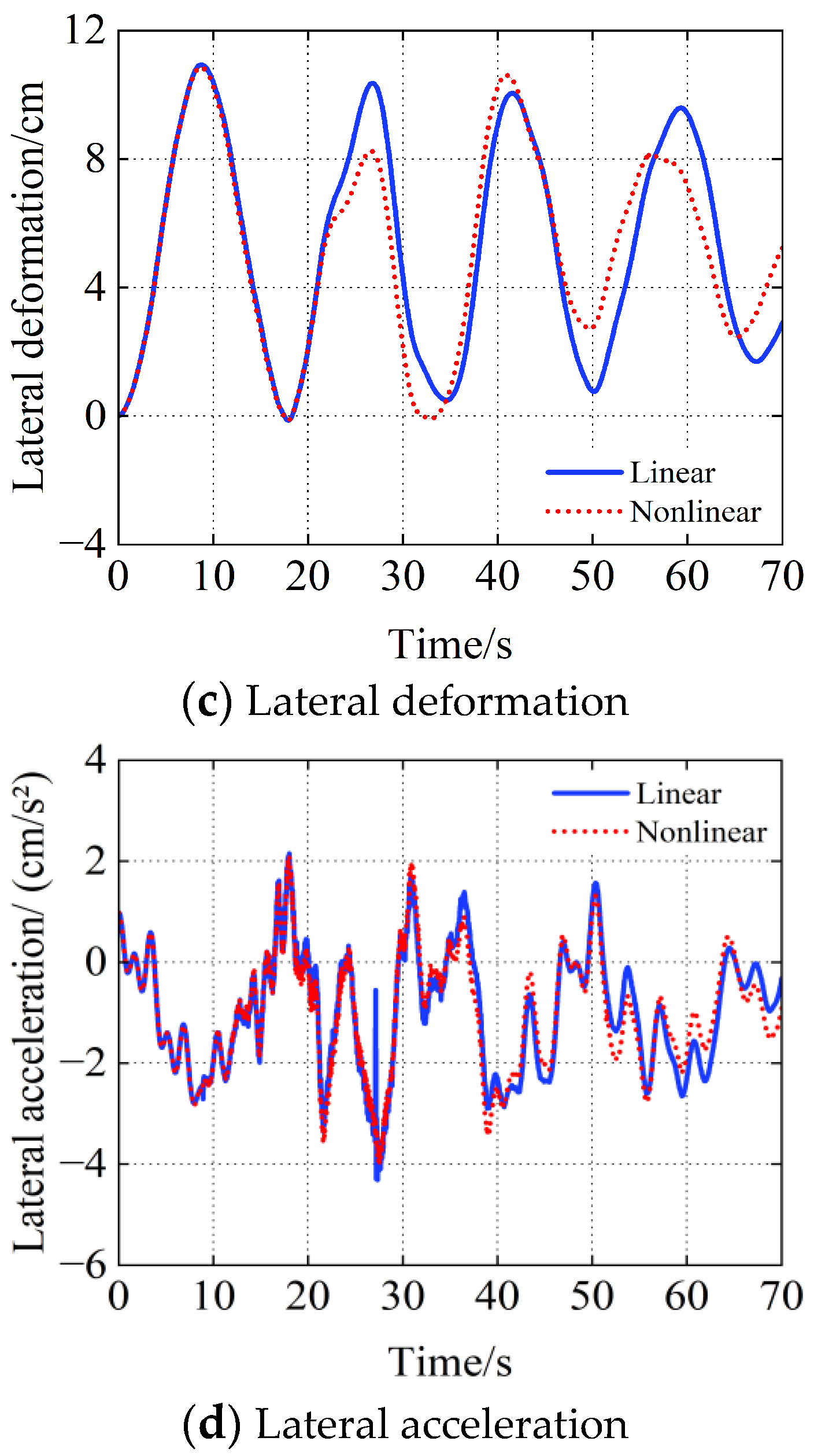
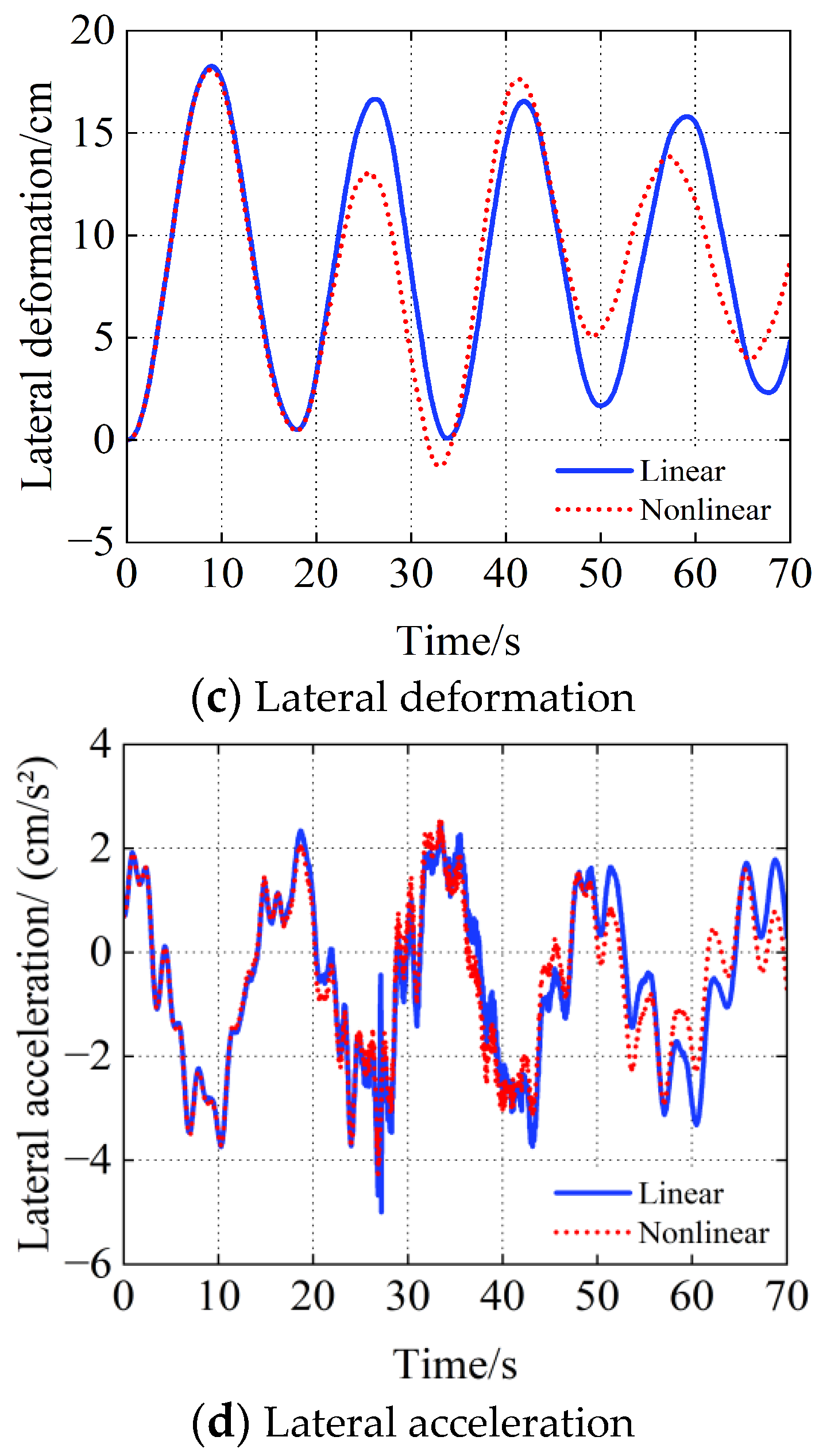
4.1. Analysis of the Nonlinear Influence of the Large Displacement of the Structure
- As the first lateral vibration mode of the bridge structure is symmetrical, the maximum lateral deflection occurs at point ➃, which is in the middle of the main span of the bridge. Since the first vertical mode of the bridge is the antisymmetric vibration, the maximum vertical displacement occurs, therefore, at points ➂ and ➄ in the middle of the 1/4 span. The calculation results keep the same with the vibration tendency of the bridge, which shows that the calculation program has good reliability.
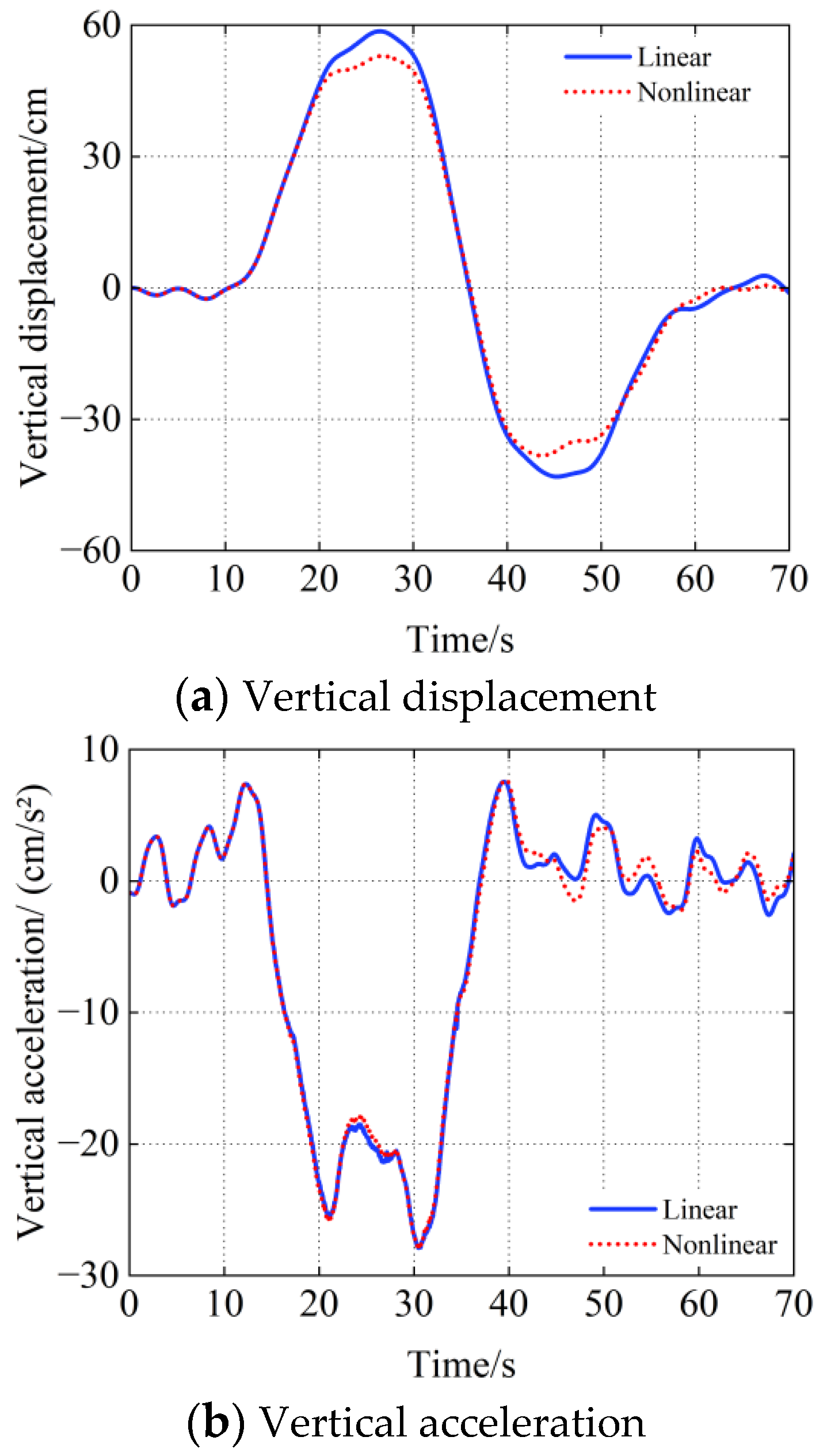
- The large displacement nonlinear factor has little effect on the changing tendency of the displacement and acceleration time history curves of the suspension bridge.
- After considering the nonlinear factors of the suspension bridge structure, the displacements and accelerations of the bridge will be significantly smaller than the linear ones. The maximum difference of lateral deformation is 2.53%, and the vertical displacement is 9.62%, which indicates that when the large displacement effect of the structure is considered, the total stiffness of the structure increases due to the existence of geometric stiffness, and the vibration responses are slightly lower than that when nonlinear factors are not considered.
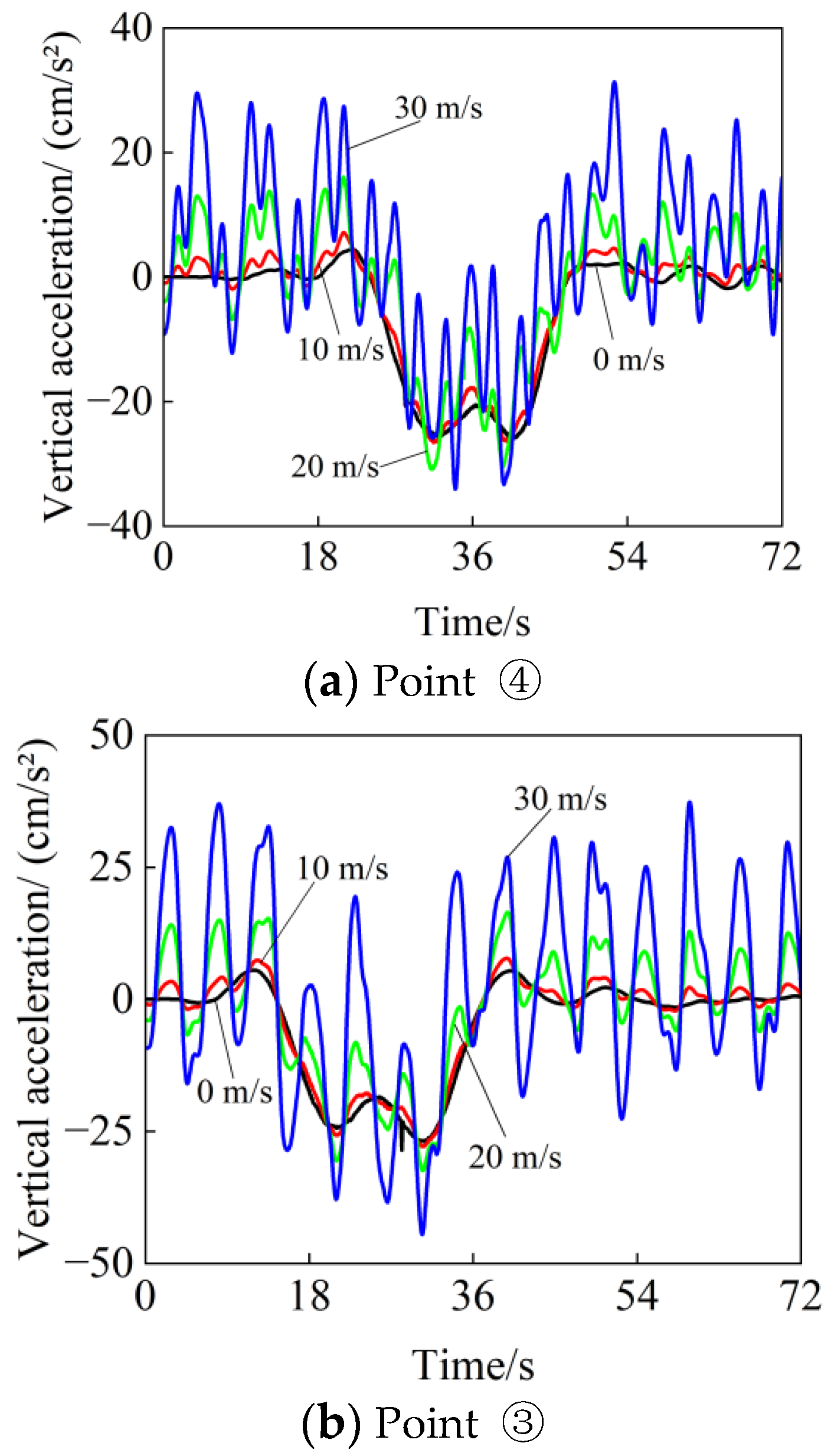
- Compared with the change in acceleration time history curves of each node in Figure 13 and Figure 14, the bridge displacement curves are more obviously changed. Since the first mode of the bridge is lateral, the lateral mode appears more frequently in the first 50th vibration modes. It can be found from the comparison between b and d that the lateral vibration acceleration of the bridge changes more obviously.
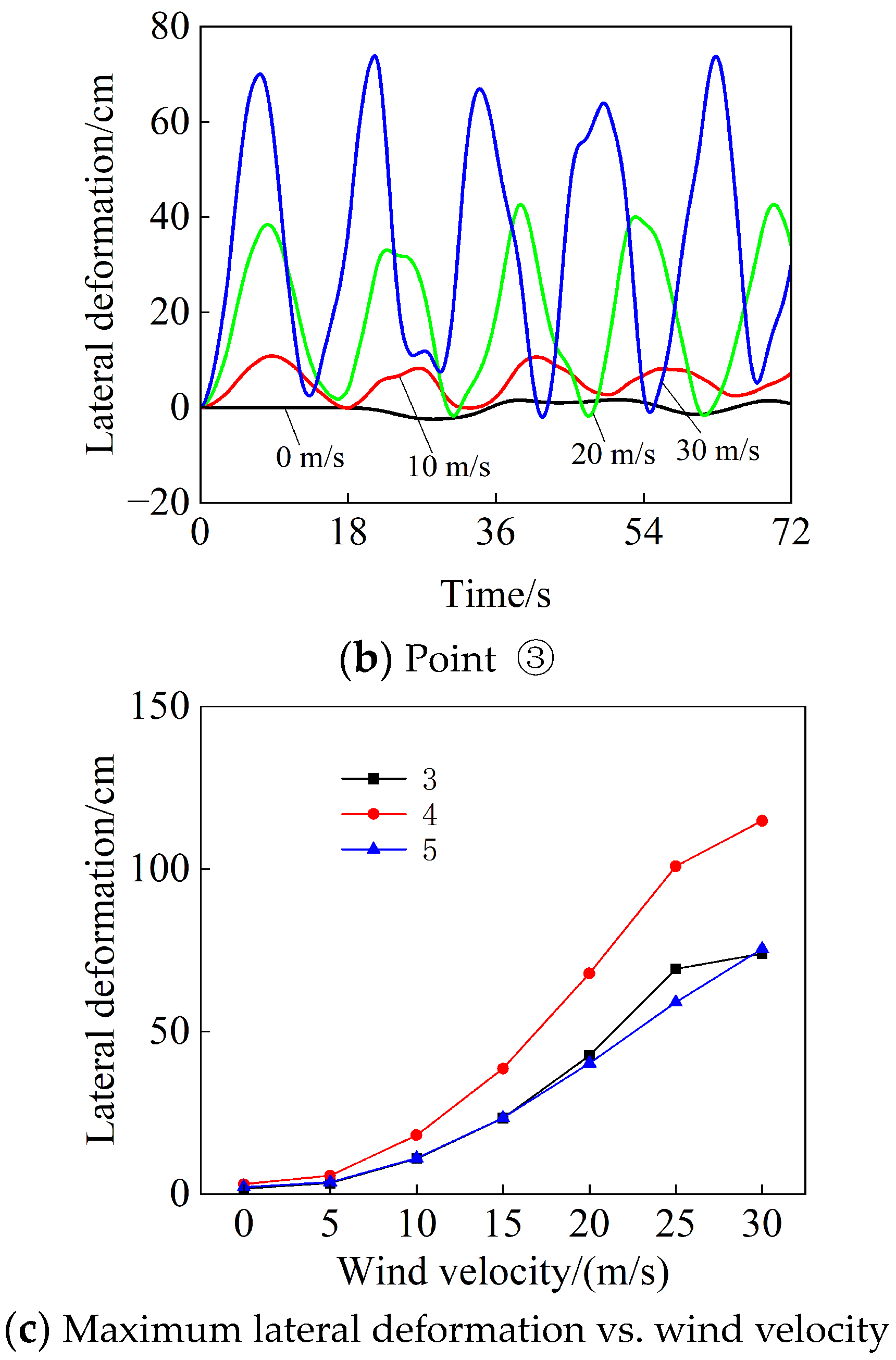
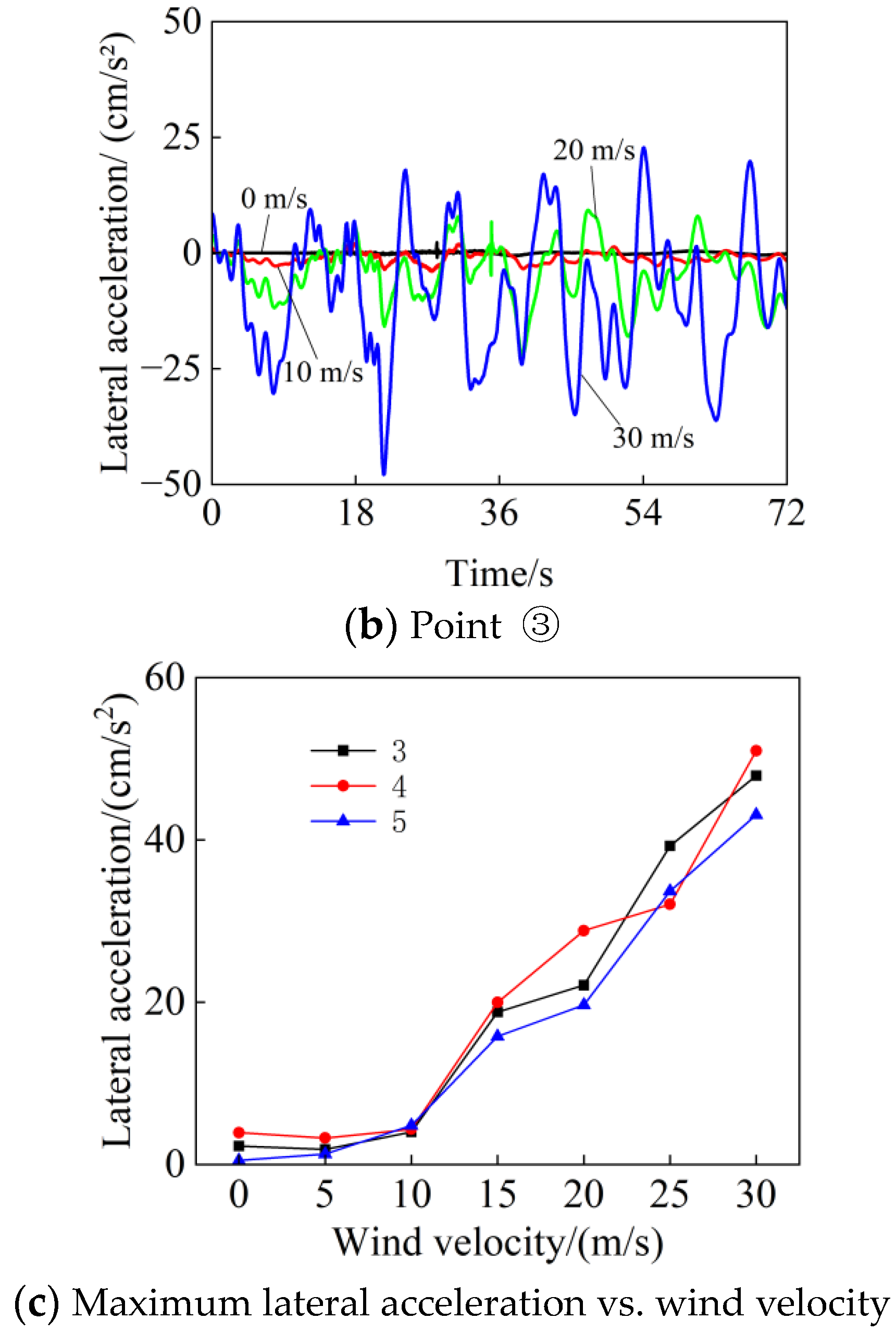
4.2. Analysis of the Influence of Wind Velocity Changes
- The vertical displacement time history curves of the bridge and the changing tendency of the maximum with the wind velocity are plotted in Figure 17. It can be seen that when the wind velocity is small (≤20 m/s), the vertical displacement of the bridge is not very sensitive to the wind loads. The time history curves of vertical displacement under different wind velocities in Figure 17a,b are close. The maximum vertical displacement of the bridge decreases slightly due to the wind loads. The maximum vertical displacement of the bridge at point ➂ and point ➃ is 39.8 cm and 53.5 cm, respectively, without wind load. However, when the wind velocity increases to 20 m/s, the maximum vertical displacement of the bridge decreases to 35.2 cm and 53.0 cm, which can reflect the lift effect of the wind loads. However, when the wind velocity exceeds 20 m/s, the suspension bridge appears buffeted under the effect of the wind loads and the vertical vibration will intensify. The maximum vertical displacement of some nodes will show an increasing tendency, which can be clearly seen in Figure 17c.
4.3. Comprehensive Analysis of Wind Velocity and Train Speed
- The vertical displacement of the bridge is mainly caused by the weight of the train, and the train speed and the average wind velocity have little influence on it.
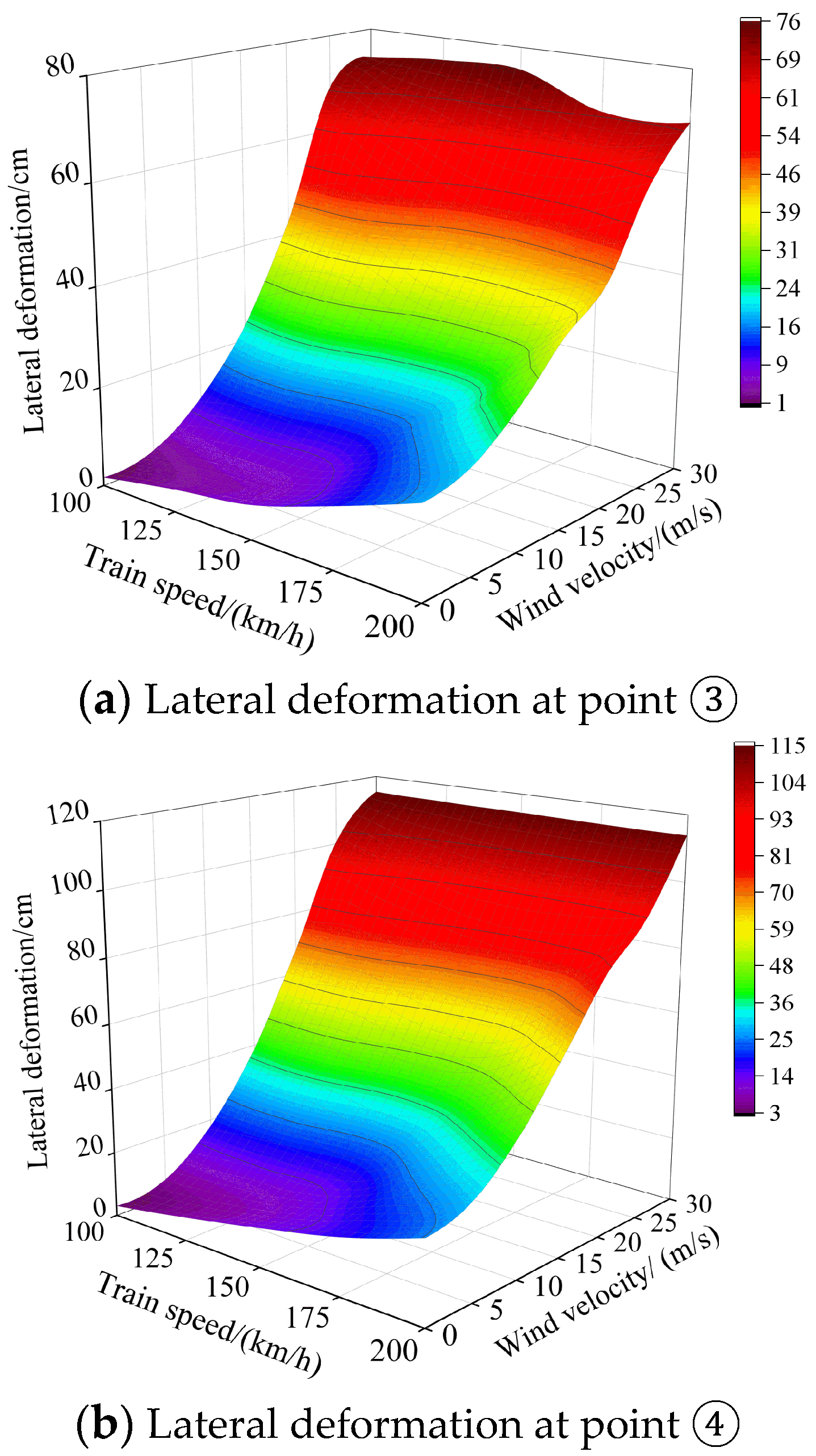
- When the wind loads are not considered, the maximum lateral deformation of the bridge under the action of the train loads is 25.34 cm, while under the action of wind loads, the lateral deformation increases greatly, and its maximum value reaches 114.8 cm.
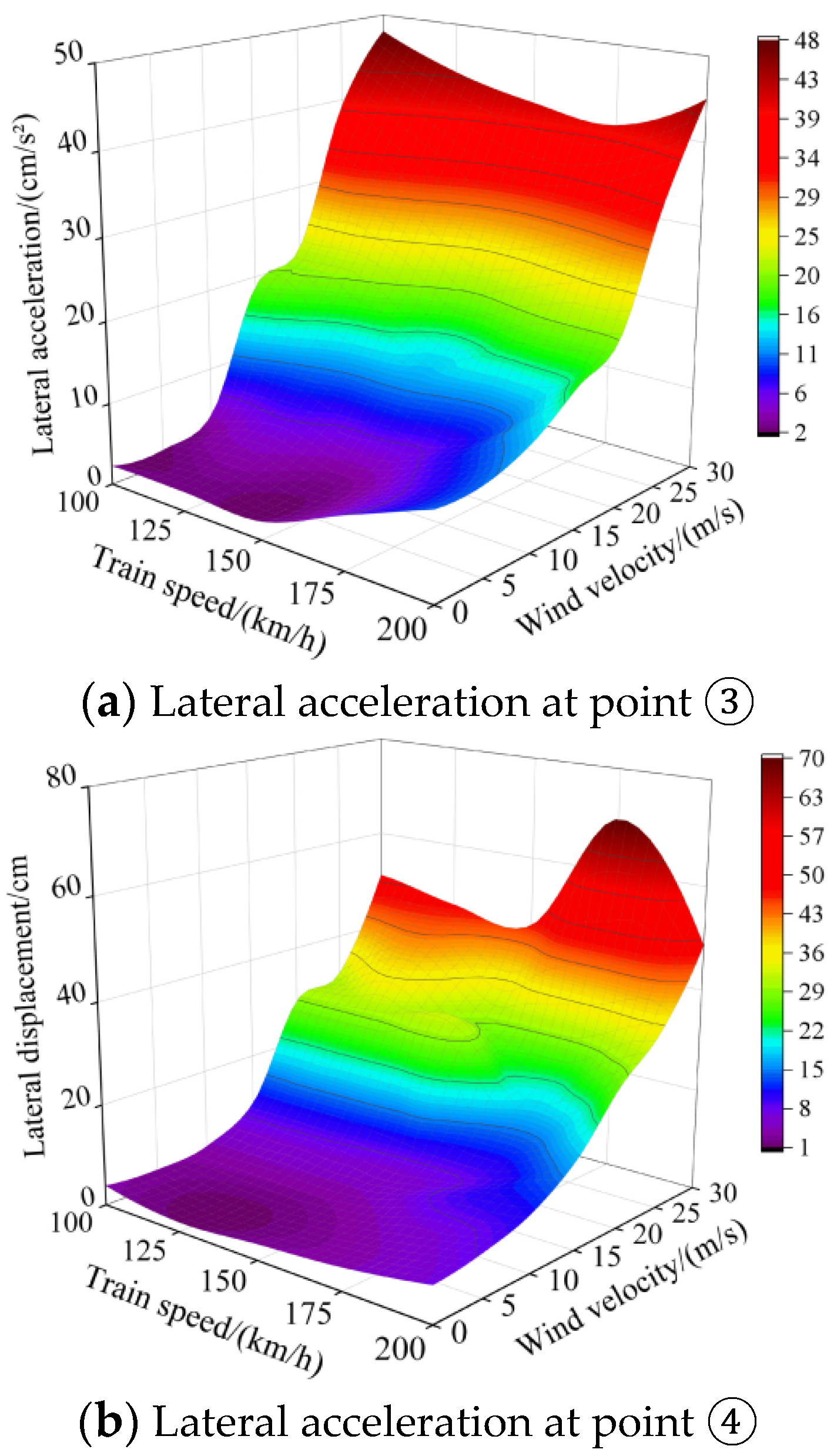
- Wind velocity and train speed have a great influence on both the vertical acceleration and lateral acceleration of the bridge.
5. Conclusions
- The large displacement nonlinear factor of the structure does not affect the changing tendency of the displacement and acceleration time history curves of the bridge, but it will reduce the calculated value more than those under the linear factors. The error in the vibration acceleration of the bridge is smaller than that of the displacement when considering the large nonlinear displacement of the structure.
- (1)
- The suspension bridge’s natural frequency is very low; it is very sensitive to wind loads and it is easy to produce wind–train–bridge coupling vibration. When the wind velocity is small, the vertical displacement of the bridge is mainly affected by the gravitational force loading of the vehicle; when the wind velocity is large (≥20 m/s), the buffeting effect of the bridge caused by the wind will induce a large vertical displacement.
- (2)
- The changes in train speed and average wind velocity have a great influence on the maximum bridge displacement. The vertical and lateral accelerations of the bridge increase sharply with the wind velocity, and the bridge vibration caused by wind loads far exceeds the train’s effect.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, W.W.; Xia, H.; Karoumi, R.; Zhang, T.; Li, X.Z. Aerodynamic effect of wind barriers and running safety of trains on high-speed railway bridges under cross wind. Wind Struct. 2015, 20, 213–236. [Google Scholar] [CrossRef]
- Liu, Q.K.; Zheng, Y.F.; Liu, X.B.; Ma, W.Y. Wind loads, wind induced vibrations and control of cables of cable-stayed bridges. Eng. Mech. 2015, 32, 1–7. [Google Scholar] [CrossRef]
- Zhang, T.; Guo, W.W.; Xia, H. Aerodynamic characteristics of vehicle-bridge system under crosswinds and effect of wind barriers. J. China Railw. Soc. 2013, 35, 102–106. [Google Scholar]
- Zhang, M.; Zhang, N.; Xia, H. Analysis on wind-vehicle-bridge dynamic interaction for long-span railway suspension bridge. China Railw. Sci. 2013, 34, 14–21. [Google Scholar]
- Zhang, N.; Xia, H.; Guo, W.W. Vehicle-bridge interaction analysis under high-speed trains. J. Sound Vib. 2008, 309, 407–425. [Google Scholar] [CrossRef]
- Li, Y.L.; Qian, Y.Z.; Zhu, J.; Huang, X. Longitudinal vibration characteristics of a long-span highway suspension bridge under stochastic wind and traffic loads. China J. Highw. Transp. 2021, 34, 93–104. [Google Scholar]
- Li, Y.L.; Xu, X.Y.; Yan, N.J.; Deng, J.T.; Xiang, H.Y. Comparison of wind-vehicle-bridge coupling vibration characteristics of three-line and three-tower suspension bridge. J. Traffic Transp. Eng. 2015, 15, 17–25. [Google Scholar]
- Li, Y.L.; Dong, S.F.; Zang, Y.; Qiang, S.Z. Coupling vibration of wind-vehicle-bridge system for long-span road-rail suspension bridge and resistant-wind criterion of running train. Eng. Mech. 2012, 29, 114–120. [Google Scholar]
- Li, Y.L.; Qiang, S.Z.; Liao, H.L.; Xu, Y.L. Dynamics of wind–rail vehicle–bridge systems. J. Wind Eng. Ind. Aerod. 2005, 3, 483–507. [Google Scholar] [CrossRef]
- Guo, W.H.; Hong, X.M.; Chen, C.X. Coupled vibration of train and bridge under high-speed trains passing each other in crosswind. China Railw. Sci. 2020, 41, 48–56. [Google Scholar]
- Montenegro, P.A.; Barbosa, D.; Carvalho, H.; Calçada, R. Dynamic effects on a train-bridge system caused by stochastically generated turbulent wind fields. Eng. Struct. 2020, 211, 110430. [Google Scholar] [CrossRef]
- Wang, Z.J.; Tang, T.F.; Guo, X.R.; Zou, Y.F. Influence of wind attack angle on aerodynamic characteristics and coupled vibration of vehicle-bridge system. J. Railw. Sci. Eng. 2022, 19, 752–759. [Google Scholar]
- Liu, Q.J. Coupled vibration research of wind-vehicle-bridge of light rail-cum-road suspension bridges. J. Wuhan Univ. Technol. 2014, 36, 107–113. [Google Scholar]
- Li, X.Z.; Liu, D.J.; Jin, Z.B. Analysis of train-track-bridge coupled vibration of a railway long-span suspension bridge. Steel Constr. 2010, 25, 6–12+71. [Google Scholar]
- Zhai, J.P.; Li, M.; Zhang, J.Y.; Lv, F.M. Influence of bridge height on passing performance of high speed trains under crosswind. Comput. Aided Eng. 2013, 22, 1–8. [Google Scholar]
- Han, W.S.; Chen, A.R. Time-domain buffeting analysis of cable-stayed bridge considering pylon wind field. Eng. Mech. 2007, 24, 123–128. [Google Scholar]
- Zhang, N.; Tian, Y.; Xia, H. A train-bridge dynamic interaction analysis method and its experimental validation. Engineering 2016, 2, 528–536. [Google Scholar] [CrossRef]
- Olmos, J.M.; Astiz, M.Á. Non-linear vehicle-bridge-wind interaction model for running safety assessment of high-speed trains over a high-pier viaduct. J. Sound Vib. 2018, 419, 63–89. [Google Scholar] [CrossRef]
- Xiong, Z.L.; Zhu, J.; Zheng, K.F.; Zhang, W.; Li, Y.L.; Wu, M.X. Framework of wind-traffic-bridge coupled analysis considering realistic traffic behavior and vehicle inertia force. J. Wind Eng. Ind. Aerod. 2020, 205, 104322. [Google Scholar] [CrossRef]
- Bao, Y.L.; Li, Y.L.; Ding, J.J. A case study of dynamic response analysis and safety assessment for a suspended monorail system. Int. J. Environ. Res. Public Health 2016, 13, 1121. [Google Scholar] [CrossRef]
- Wu, W.H.; Chen, C.C.; Chen, Y.C.; Lai, G.; Huang, C.M. Tension determination for suspenders of arch bridge based on multiple vibration measurements concentrated at one end. Measurement 2018, 123, 254–269. [Google Scholar] [CrossRef]
- Bonopera, M.; Liao, W.C.; Perceka, W. Experimental–theoretical investigation of the short-term vibration response of uncracked prestressed concrete members under long-age conditions. Structures 2022, 35, 260–273. [Google Scholar] [CrossRef]
- Wang, S.Q.; Ma, Q.; Ren, Y.R.; Yang, Z. Dynamic interaction analysis on wind-train-bridge system of long-span railway suspension bridge. J. Railw. Sci. Eng. 2017, 14, 1241–1248. [Google Scholar]
- Zhou, Z.H.; Liu, R.T.; Zhu, Z.H.; Gong, W.; Yu, Z.W. Train passing analysis on large-span railway suspension bridge based on ANSYS-MATLAB co-simulation. J. Traffic Transp. Eng. 2021, 21, 117–128. [Google Scholar]
- Xu, L.P.; Huo, X.J. Study on stiffness of super-long span rail-cum-road suspension bridge under live load. Railw. Eng. 2021, 61, 5–8+37. [Google Scholar]
- Guan, Q.H.; Li, J.W.; Liu, J.X. Influence of wind-resistant cable on nonlinear areostatic instability mode of long-span pedestrian suspension bridge. Highw. Traffic Sci. Technol. 2022, 39, 103–110. [Google Scholar]
- Zhang, X.J.; Sun, L.L.; Ying, F.B. Three-dimensional nonlinear aerostatic stability analysis of long-span suspension bridges under skew wind. Adv. Struct. Eng. 2022, 25, 2547–2557. [Google Scholar] [CrossRef]
- Shan, Q.W.; Zhang, L.L.; Yan, Z.C.; Yang, J.X. Aerostatic stability analysis of streamline box girder suspension bridge under non-uniform wind. J. Civ. Environ. Eng. 2022, 44, 117–125. [Google Scholar]
- Almutairi, N.B.; Hassan, M.F.; Abdel-Rohman, M.; Terro, M. Control of suspension bridge nonlinear vibrations due to moving loads. J. Eng. Mech. 2006, 132, 659–670. [Google Scholar] [CrossRef]
- Nino, S.D.; Luongo, A. Nonlinear aeroelastic in-plane behavior of suspension bridges under steady wind flow. Appl. Sci. 2020, 10, 1689. [Google Scholar] [CrossRef]
- Boonyapinyo, V.; Lauhatanon, Y.; Lukkunaprasit, P. Nonlinear aerostatic stability analysis of suspension bridges. Eng. Struct. 2005, 28, 793–803. [Google Scholar] [CrossRef]
- Liu, J.S.; Wang, F.; Yang, Y.; Liu, R.H. Nonlinear flutter analysis for a long-span suspension bridge. Shock Vib. 2021, 2021, 1–20. [Google Scholar] [CrossRef]
- Choi, D.H.; Gwon, S.G.; Yoo, H.; Na, H.S. Nonlinear static analysis of continuous multi-span suspension bridges. Int. J. Steel Struct. 2013, 13, 103–105. [Google Scholar] [CrossRef]
- Petrini, F.; Bontempi, F. Estimation of fatigue life for long span suspension bridge hangers under wind action and train transit. Struct. Infrastruct. Eng. 2011, 7, 491–507. [Google Scholar] [CrossRef]
- Yao, Y. Computer Aided Design of Bridge Engineering; Chongqing University Press: Chongqing, China, 2019. [Google Scholar]
- Tang, M.L.; Shen, R.L.; Qiang, S.Z. Analytic theories and software development of spatial non-linearity static and dynamic of long-span suspension bridge. Bridge Constr. 2000, 1, 9–12. [Google Scholar]
- Pan, Y.R. Nonlinear Analysis Theory Method for Suspension Bridge Structure; Science Press: Beijing, China, 2006. [Google Scholar]
- Zhao, H.X.; Zhang, W.M.; Jiang, X.F.; Liu, Z. Calculation method of equivalent elastic modulus of cable sag effect based on catenary. J. China Foreign Highw. 2020, 40, 62–66. [Google Scholar]
- Liu, Z.X.; Sun, Y. Compuation Solid Mechanics, 2nd ed.; Shanghai Jiao Tong University Press: Shanghai, China, 2010. [Google Scholar]
- Xu, H.T.; Liao, H.L.; Li, M.S.; He, Y. Wind tunnel test study of sectional model of baling river bridge. World Bridges 2009, 4, 30–33. [Google Scholar]
- Guo, W.W.; Xiao, H.; De Roeck, G. Dynamic characteristics and coupling vehicle-bridge vibration analysis of the high speed railway Sesia bridge in Italy. J. Vib. Shock 2013, 32, 82–88. [Google Scholar]
- Xia, H.; Zhang, N.; Guo, W.W. Coupling Vibration of Train-Bridge System; Science Press: Beijing, China, 2014. [Google Scholar]




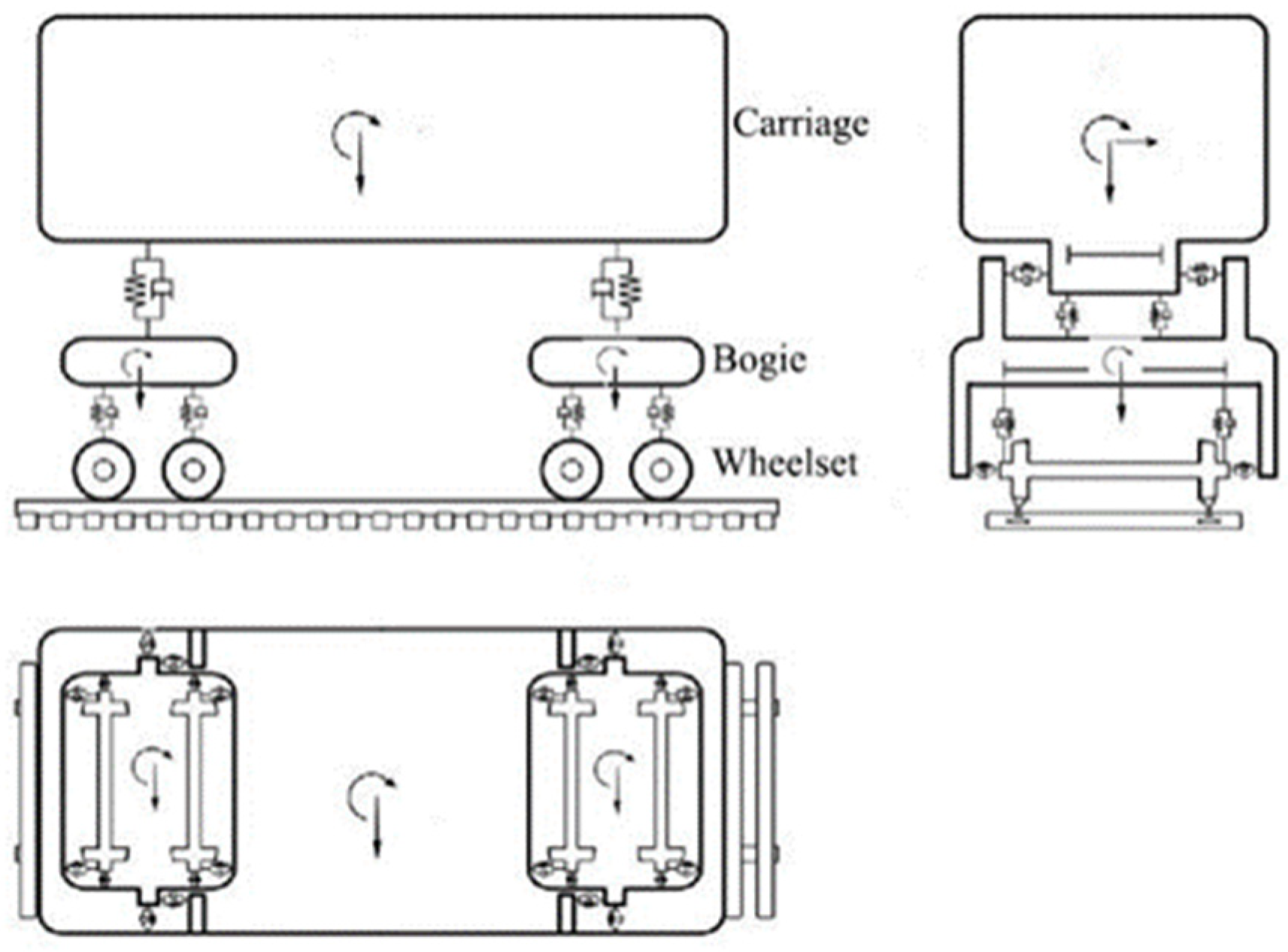










| Bridge structures | Main cable | Suspension cables | Bridge towers | Bridge piers | Stiffening beams | Highway/railway bridge deck |
| FEM types | Link elements (tension only) | Link elements (tension only) | Beam elements | Beam elements | Beam elements | Plate elements (with different thicknesses) |
| Mode Shape | Frequency (Hz) | Mode Shape Characteristics |
|---|---|---|
| 1 | 0.0898 | Lateral symmetrical vibration of the main beam and main cable, half-wave |
| 2 | 0.1784 | The vibration of the main cable, half-wave |
| 3 | 0.1804 | Lateral vibration of the main cable, half-wave |
| 4 | 0.1885 | Vertically symmetrical vibration of the main beam, half-wave |
| 5 | 0.1893 | Vertical antisymmetric vibration of the main beam, whole-wave |
| 6 | 0.2266 | Lateral antisymmetric vibration of the main beam, whole-wave |
| 7 | 0.3174 | lateral vibration of the main cable, whole-wave |
| 8 | 0.3235 | Vertical symmetrical vibration of the main beam, whole-wave and half-wave |
| 9 | 0.3312 | Lateral vibration of the main cable, whole-wave |
| 10 | 0.3720 | Torsional symmetrical vibration of the main beam, accompanied by lateral vibration, half-wave |
| Node Location | ➀ | ➁ | ➂ | ➃ | ➄ | |
|---|---|---|---|---|---|---|
| Calculation Conditions | ||||||
| Linear calculation results | Vertical displacement/cm | 0.13 | 2.10 | 58.62 | 40.29 | 59.68 |
| Lateral deformation/cm | 0.40 | 0.44 | 11.13 | 18.56 | 11.28 | |
| Torsional displacement/(×10−3/(°)) | 1.17 | 0.37 | 3.94 | 7.08 | 52.22 | |
| Vertical acceleration/(cm/s2) | 0.15 | 2.33 | 27.93 | 26.88 | 28.78 | |
| Lateral acceleration/(cm/s2) | 2.46 | 1.07 | 4.19 | 4.56 | 4.91 | |
| Torsional acceleration/(×10−3/(°/s2)) | 4.66 | 2.33 | 25.45 | 36.50 | 25.61 | |
| Nonlinear calculation results | Vertical displacement/cm | 0.13 | 2.01 | 52.98 | 37.93 | 52.72 |
| Lateral deformation/cm | 0.39 | 0.43 | 10.85 | 18.09 | 11.00 | |
| Torsional displacement/(×10−3/(°)) | 1.16 | 0.36 | 3.93 | 7.03 | 51.33 | |
| Vertical acceleration/(cm/s2) | 0.15 | 2.30 | 27.91 | 26.63 | 27.97 | |
| Lateral acceleration/(cm/s2) | 2.45 | 1.04 | 4.01 | 4.35 | 4.82 | |
| Torsional acceleration/(×10−3/(°/s2)) | 4.66 | 2.29 | 25.37 | 36.50 | 25.73 | |
| Nonlinear difference | Vertical displacement (%) | 0 | 4.3 | 9.6 | 5.9 | 11.7 |
| Lateral deformation (%) | 2.5 | 2.3 | 2.5 | 2.5 | 2.5 | |
| Torsional displacement (%) | 0.3 | 1.1 | 0.4 | 0.7 | 1.5 | |
| Vertical acceleration (%) | 0 | 1.3 | 0.1 | 0.9 | 2.8 | |
| Lateral acceleration (%) | 0.4 | 2.8 | 4.3 | 4.6 | 1.8 | |
| Torsional acceleration (%) | 0 | 1.7 | 0.3 | 0 | −0.5 |
| Wind Velocity (m/s) | 0 | 5 | 10 | 15 | 20 | 25 | 30 | |
|---|---|---|---|---|---|---|---|---|
| Node Responses | ||||||||
| Point ➂ | Vertical displacement/cm | 53.5 | 53.1 | 53.0 | 53.1 | 53.0 | 55.0 | 63.5 |
| Lateral deformation/cm | 1.7 | 3.4 | 10.9 | 23.3 | 42.6 | 69.3 | 73.9 | |
| Vertical acceleration/(cm/s²) | 5.5 | 26.8 | 27.9 | 30.0 | 32.4 | 37.9 | 44.6 | |
| Lateral acceleration/(cm/s²) | 2.3 | 1.9 | 4.0 | 18.8 | 22.1 | 39.3 | 47.9 | |
| Point ➃ | Vertical displacement/cm | 39.8 | 39.3 | 37.9 | 36.3 | 35.2 | 32.6 | 30.3 |
| Lateral deformation/cm | 3.0 | 5.7 | 18.1 | 38.6 | 67.9 | 100.8 | 114.8 | |
| Vertical acceleration/(cm/s²) | 4.5 | 25.6 | 26.6 | 28.4 | 30.9 | 30.3 | 34.1 | |
| Lateral acceleration/(cm/s²) | 3.9 | 3.3 | 4.4 | 19.9 | 28.8 | 32.1 | 51.0 | |
| Point ➄ | Vertical displacement/cm | 53.8 | 53.0 | 52.7 | 5 2.9 | 53.3 | 58.3 | 71.7 |
| Lateral deformation/cm | 2.1 | 3.6 | 11.0 | 3.4 | 40.2 | 59.0 | 75.5 | |
| Vertical acceleration/(cm/s²) | 5.5 | 27.0 | 28.0 | 29.3 | 31.2 | 34.9 | 48.0 | |
| Lateral acceleration/(cm/s²) | 0.5 | 1.3 | 4.8 | 19.4 | 19.6 | 33.7 | 43.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Wan, X.; Guo, M.; Qiao, H.; Zhang, N.; Ye, Q. Nonlinear Dynamic Analysis of the Wind–Train–Bridge System of a Long-Span Railway Suspension Truss Bridge. Buildings 2023, 13, 277. https://doi.org/10.3390/buildings13020277
Wang S, Wan X, Guo M, Qiao H, Zhang N, Ye Q. Nonlinear Dynamic Analysis of the Wind–Train–Bridge System of a Long-Span Railway Suspension Truss Bridge. Buildings. 2023; 13(2):277. https://doi.org/10.3390/buildings13020277
Chicago/Turabian StyleWang, Shaoqin, Xing Wan, Minghao Guo, Hong Qiao, Nan Zhang, and Qing Ye. 2023. "Nonlinear Dynamic Analysis of the Wind–Train–Bridge System of a Long-Span Railway Suspension Truss Bridge" Buildings 13, no. 2: 277. https://doi.org/10.3390/buildings13020277
APA StyleWang, S., Wan, X., Guo, M., Qiao, H., Zhang, N., & Ye, Q. (2023). Nonlinear Dynamic Analysis of the Wind–Train–Bridge System of a Long-Span Railway Suspension Truss Bridge. Buildings, 13(2), 277. https://doi.org/10.3390/buildings13020277








