Abstract
Eccentrically braced frames are renowned for their capacity to absorb seismic forces while offering greater adaptability. These frames incorporate bracings that are joined to the beams with an intentional offset, forming a connection within the beams. Nevertheless, there are drawbacks associated with implementing these beam connections when renovating frames. This paper seeks to enhance the design approach by introducing an eccentric link within the column of a composite structure. Eccentric braced frames (EBFs) are hybrid systems that offer both ductility in moment resisting frames (MRFs) and lateral stiffening in the concentrically braced system. The study examines composite frames with 5, 10, and 15 stories using eccentric X- and V-type bracings with an eccentricity of 0.5 m and 1 m. Three different earthquake zones are considered, based on Indian seismic code provisions: zone 3, zone 4, and zone 5. The structures are analyzed computationally by nonlinear time history analyses. The lateral load-resisting behavior of the structure with the same eccentricity in beam links and column links is compared. Then, the structure is subjected to a pushover analysis to study the performance characteristics such as capacity curve, lateral displacement, inter-storey drift, and plastification of the structure. As anticipated, compared to conventional moment resisting frames (MRFs) and concentrically braced frames (CBFs), eccentrically braced frames have better energy dissipation. Furthermore, the behavior of X-braced column links is found to be similar to the performance of beam links, but V-braced frames showed better performance in column link frames than in beam link frames. Also, the increase of the link length played a major role in the ductility of the frames.
1. Introduction
Today, high-rise steel–concrete composite buildings are commonly used due to their ability to handle heavy loads and their high strength-to-weight ratio. Structural systems that are subjected to seismic conditions often use braced frames, which can be either concentric braced frames (CBFs) or eccentric braced frames (EBFs), in addition to moment resisting frames (MRFs) for better performance. The use of reduced beam sections (RBSs) in MRFs, which take advantage of a rotational moment of inertia, has been studied by [1,2] to enhance their ductility. The effect of semirigid connections on the performance of the frames, as well as the optimization of MRFs without losing the lateral stiffness of the structure under seismic conditions, has also been studied by [3,4]. Previous research [5,6,7] has shown that the concentric braced-X type performs better under seismic conditions in CBFs. Five different types of CBF bracing systems under seismic loading conditions were studied by [8] and found to exhibit good ductility at various heights. Previous studies have examined the use of EBFs in which one end of the bracing is connected to the column concentrically and the other end is connected to the beam using K- and V-types of bracing (Figure 1). The braces are connected to the beam with an eccentricity, creating a link in the beam between the two braces. The EBF is a hybrid system that combines the benefits of both the MRF and CBF, providing lateral stiffening and ductility to the structure under lateral loads. Previous studies have only considered the location of eccentric links in either the vertical or horizontal beams.
Researchers [5,9] have conducted similar studies on composite frames. They observed that the beam link undergoes inelastic rotation, increasing the ductility of the frames. The length of the link determines the extent of inelastic rotation, which can occur due to shear, flexure, or a combination of shear and flexure. All the aforementioned studies were conducted on a 2-dimensional frame system, either experimentally or analytically. The design approach for the linked column frames according to the theory of plastic mechanism control (TPMC) was developed and studied by [10].
The failure of a structural floor system under a lateral load is often caused by plastic deformation of the beam link, either by shear or flexure. Limited literature exists regarding the unique features encountered in the analysis of the EBF. However, a new approach involving active links in the column segments between braces and columns can be used to study the ductility factor and stiff elastic mechanism during extreme cyclic overloads. Placing the link in the columns instead of the beams offers advantages during construction, particularly when retrofitting structures with vertical bracings or creating openings for architectural purposes.
Extensive research has been conducted on the behavior of EBFs with beam links. The link behavior and recommended limitations to the AISC manual for EBF link length were investigated by [11]. They studied the limitations of the link length and arrived at a formula to calculate it based on the behavior of the link as a shear link, moment link, or combined shear and moment yielding during plastic hinge formation in the structural system. The inverted braced frames with zipper struts were studied by [12], while the real-time failure of column links in an electric dust catcher was examined by [13]. The behavior of long links subjected to cyclic loading in EBFs, which showed a large inelastic rotation higher than 0.02 radians, as described in the AISC for bending criteria, was analyzed by [14,15].
The plastic hinge formation in an MRF is scattered throughout the building, as discovered by [8,16]. The formation starts with beams and progresses to the columns before the collapse. In contrast, braced frames start with bracing and then transfer to the beam and column. CBFs perform better than MRFs in resisting lateral displacements. The different types of EBF with beam links were experimentally and analytically studied by [17,18] and it was concluded that such systems offer higher ductility and better lateral displacement resistance under seismic loading. Research in the literature [5,6,19,20,21,22,23,24,25,26] explains the collapse performance of steel CBF and EBF structures, which assisted the optimized design of concentrically braced frames. Some authors used a force-based design approach, while others used a displacement-based design approach.
The column links are employed to improve the buildings’ structural integrity and enhance their seismic resistance. In particular, the proposed design approach provides flexibility in architectural design, construction efficiency, and compliance with building codes. This paper introduces a novel approach for eccentric braces with links in columns. By leveraging the column splice connection locations, it is possible to enable the construction of the column link within the structure. The analysis of column links in 3-dimensional steel concrete composite frames with X- and V-type bracing systems across buildings with 5, 10, and 15 stories is a unique contribution to the field. Previous works by [18,22,27,28,29] have solely focused on vertical links, whereas this study emphasizes the provision of eccentric column links.
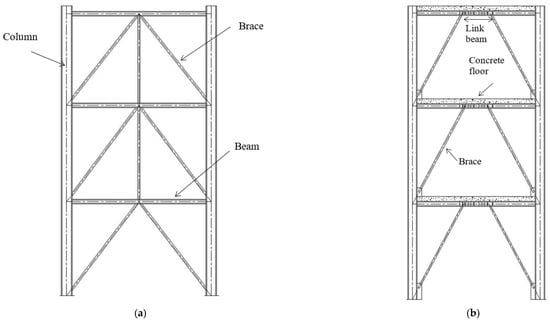
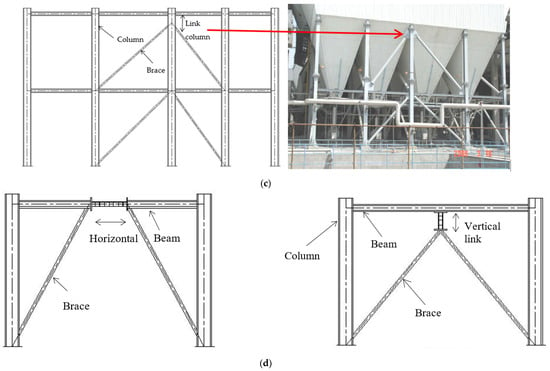
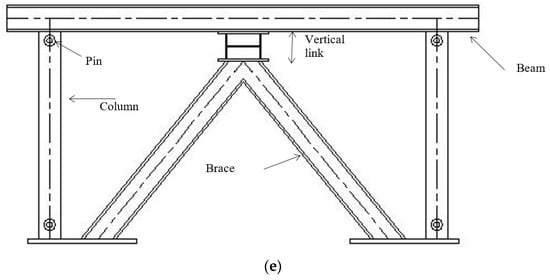
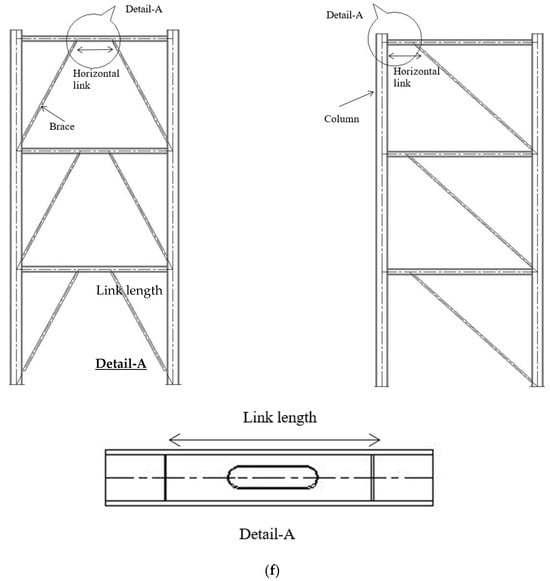
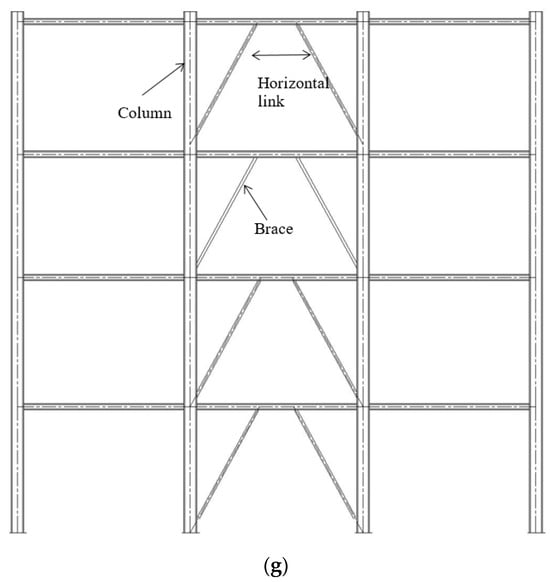





Figure 1.
Various concentric and eccentric bracing types from the literature. (a) Yang et al. [12]; (b) Tengfei et al. [9]; (c) Tong et al. [13]; (d) Caprili et al. [27]; (e) Bouwkamp et al. [17]; (f) Erfani et al. [28]; (g) Nassani et al. [5].
2. Analytical Model
The typical structural plan of 35 m × 25 m with five bays spaced at 7 m and 5 m along the X-direction and Y-direction, respectively, with a 3 m storey height, is considered in this study. In Figure 2, there is a display of the 3-dimensional (3-D) model and plan of the structure. The center bay of the frames is equipped with bracings for symmetric arrangement to prevent torsional effects in the structure caused by eccentricity between the center of mass and the center of rigidity and to improve lateral resistance [20]. This study examines various structural systems, with the loadings as given in Table 1 in a single MRF system and a dual MRF system with bracings according to Indian standards for the seismic design of buildings [30].
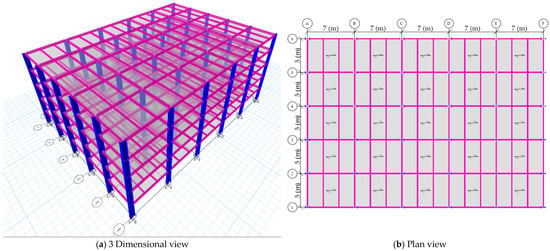
Figure 2.
Five-storey moment resisting frame (MRF) structure.

Table 1.
Seismic Considerations of the Structure.
The bracings are designed as buckling restrained bracings. Additionally, the study investigates MRF configurations with X- and V-type CBF (XBR and VBR) as well as MRF setups with X- and V-type EBFs that have eccentricities of 0.5 m and 1.0 m in both beams (BXBR, BVBR) and columns (CXBR, CVBR), as illustrated in Figure 3. Table 2 presents an analysis of 5-, 10-, and 15-storey structures using MRFs, CBFs, and EBFs as well as XBRFs and VBRFs, with links incorporated in both beams and columns. These different models enable us to draw conclusions regarding the performance of the structure with links in the columns and emphasize the significance of eccentrically braced frames as the structure’s height increases.
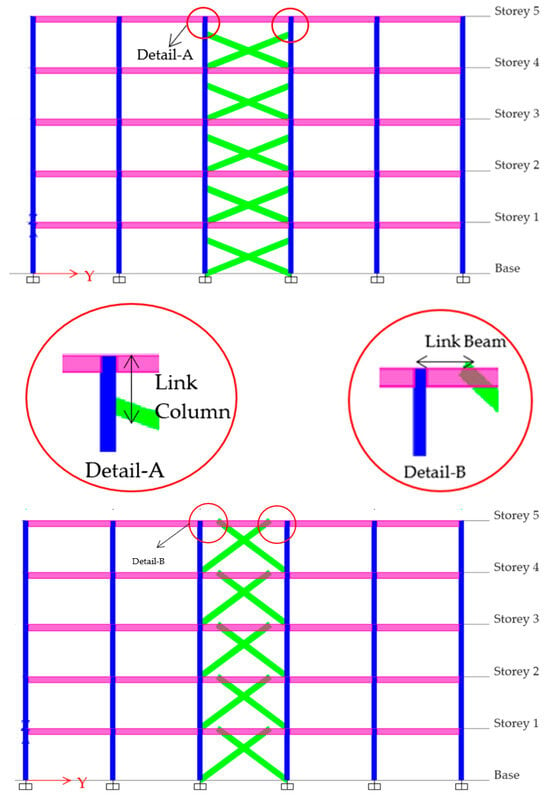
Figure 3.
Elevation view of column links in five-storey V- and X-braced frames.

Table 2.
Fundamental period (seconds) of vibration for three modes of braced and unbraced frames.
For the structures of 5, 10, and 15 stories, the eccentricity of the links is altered by 0.5 m and 1.0 m from the centerline of the column work points to the brace-beam work points in beam link locations and brace-column work points in the column link locations. The following loading patterns are considered: (i) dead load (DL), which includes the self-weight of the concrete slab and the structural steel elements according to Indian standards for loadings [30,31,32]; (ii) superimposed dead load due to flooring of 0.4 kN/m2; (iii) live load (LL) of 3.0 kN/m2; and (iv) seismic loads based on the building location on medium or stiff soil. Table 1 lists the remaining seismic parameters that are used for the analysis of the structure. These parameters are important for accurately determining the base shear of the structure using the equivalent static approach outlined in [30].
To ensure the foundation of the structure is strong, medium-stiff and soft soil types, specifically of Type II classification, are considered. The structure is a steel–concrete composite, with a deck slab serving as the floor slabs. It is a commonly used choice in seismic zones for its cost-effectiveness and performance. It has been classified as a special moment resisting frame (SMRF) with bracings. The composite deck slab acts as a diaphragm, allowing better dissipation of lateral displacement across all frames. The response reduction factor is considered as per the codified provisions for the SMRF system.
ETABS v 2018 [33] software was used to analyze the structure, considering seismic loads for both nonlinear static and dynamic analysis. The steel grade used was E350, while M30 was used for the concrete. The structure was designed to include both gravity and seismic load cases, with load combinations defined according to Indian standard [30,31,32,34]. Initially, the structure was analyzed as an MRF with static load cases, and the members were designed to withstand the effects of the worst load combinations.
2.1. Nonlinear Analysis
According to [30], linear dynamic analysis is only suitable for structures with a height of less than 15 m that are located in Zone II. As the structure being studied in this paper is taller than 15 m and falls under Zones III, IV, and V, the recommended nonlinear dynamic analysis methods in accordance with [30] are the response spectrum method, modal time history method, and time history method. Consequently, in this investigation, a time-history analysis is carried out.
Investigating the response of structures to seismic loads in a sequential manner can be achieved using nonlinear dynamic analysis. In this process, the structure is analyzed under seismic excitations in three distinct zones: Zone 3, 4, and 5. To obtain the necessary time history data for these zones, three different locations in India—Chamoli, Uttarkashi, and Bhuj—were selected, as depicted in Figure 4.
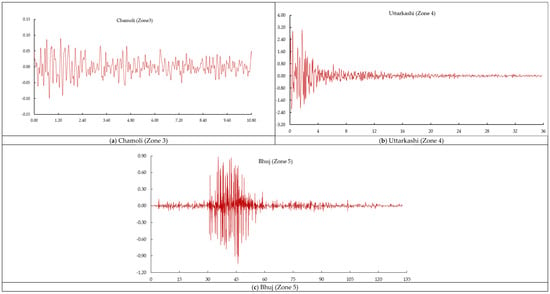
Figure 4.
Time history data for Zone 3, Zone 4, and Zone 5 in India.
The data on the earthquake ground motion are sourced from the strong motion center. The base shear is scaled to ensure its validity in both static and dynamic load cases. To obtain the necessary time history data for these zones, three different locations in India—Chamoli, Uttarkashi, and Bhuj—were selected, as depicted in Figure 4.
In this study, to determine the performance parameters of a structure, a non-linear dynamic procedure, i.e., displacement-controlled pushover analysis, as recommended by [35] is performed. This analysis helped us to obtain the various performance characteristics like the capacity curve, ductility demand, and inter storey drift ratio. The recommended target displacement is 4% of the building’s total height, according to the American Technology Council [36]. To perform the pushover analysis, ETABS [33] software was employed, and auto hinges were assigned to beams and columns by the American Society of Civil Engineers [37,38]. For beams and columns, the hinges were placed at the ends of the member, and for braces, they were positioned at the center of the member. The structure was then pushed in the X direction until the target displacement was achieved. The pushover analysis was conducted on moment-resisting braced frames with 0.5- and 1.0-m beam links and column links. The capacity curve, sequence of failure, ductile capacity, ultimate load level, and deflection of the structure at the point of failure were meticulously observed.
The examination of recorded time history data has yielded information on inter-storey drift ratios, storey drifts, storey displacements, and storey shears. To delve deeper into the performance of the analyzed structures, a modal analysis was conducted to identify different mode shapes. Table 2 presents the fundamental periods of the first three modes for both frames with bracing and frames without bracing.
After analyzing Table 2, it was discovered that the period for 5-, 10-, and 15-storey MRFs is greater than that of the concentric and eccentric braced frames. This indicates that braced frames are more rigid than unbraced frames. In addition, it was determined that structures with a column link are stiffer than those with a beam link in the case of V-braced frames. But in the case of X-braced frames, beam links are stiffer than column links. The length of the link and its placement in either the beam or column also had a significant impact on the time period. When the link is longer and in the column, it results in a shorter time period compared to a beam link with the same length in the case of V-braced frames, whereas in the case of X-braced frames, it is observed to be a higher time period.
Regardless of how the eccentrically or concentrically braced frames are connected within the structural system, the X-braced frames are stiffer than the V-braced frames. However, the V-braced frames are stiffer if the link is in the columns than if the link is in the beams.
The validity of this model is confirmed by comparing it with the base reaction of the analysis through manual calculations. The critical column design is then checked using manual calculations, which only vary by approximately 0.19%. The outcomes of nonlinear time history and pushover analysis for both braced and unbraced frames with the beam link and column link are compared.
2.2. Design Guidelines by the AISC 341-16 [39], EC3 [40], EC8 [41] and IS 1893:2016 [30]
The American Institute of Steel Construction [39], European Codes of Practice [40,41], and Indian Seismic Code [30] recommend using EBFs in all seismic zones for high ductility behavior. The limits on the length of link with or without link stiffeners are given in the American standards [39]. According to the codified standards [39], one end of the brace should be connected to one end of the link created in the beam or column. The eccentricities should be less than the beam depth, and the brace connection should provide elastic deformation through shear or flexural yielding.
Moreover, according to [37,42], link lengths can be categorized as short, intermediate, or long. This study only focuses on the short and intermediate links. As stated in Cl.F. 3.4a, Figure 5 illustrates the rotation angle of the link, assuming that the total storey drift is equal to the design storey drift. It is worth noting that the link rotation angle must not exceed certain limitations.
For links 1.6 Mp/Vp length or less, the link rotation angle = 0.08 rad.
For links 2.6 Mp/Vp length or greater, the link rotation angle = 0.02 rad.
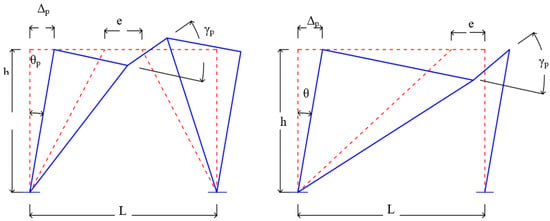
Figure 5.
Link rotation angle.
Linear interpolation between the above values if the link length is between 1.6 Mp/Vp and 2.6 Mp/Vp. When the link length is less or equal to 1.6 Mp/Vp, it satisfies the requirements of moderately ductile members.
Link length ratio (ϸ),
where Mp—plastic moment capacity, Vp—plastic shear capacity, e—eccentricity.
ϸ = (e Vp)/Mp
To classify the links in the beams and columns into the shear and intermediate link category, specific eccentricity measures are employed. This paper considers the eccentricities of 0.5 m and 1.0 m. The type of classification is given in Table 3.

Table 3.
Classification of link.
The 5-, 10-, and 15-storey buildings are analyzed using ETABS [33] software by varying the link distance X- and V-bracings. The impact of the link distance on the beam and column is studied, and the analytical results are investigated.
3. Performance under Seismic Loadings
3.1. Storey Displacement
To ensure optimal performance of a structure, the storey displacement must meet the acceptable limits recommended by the code for service requirements. If a building’s displacement is larger, it is more ductile. Figure 6, Figure 7 and Figure 8 illustrate a comparison of storey displacement for 5-, 10-, and 15-storey buildings with braced and unbraced frames.
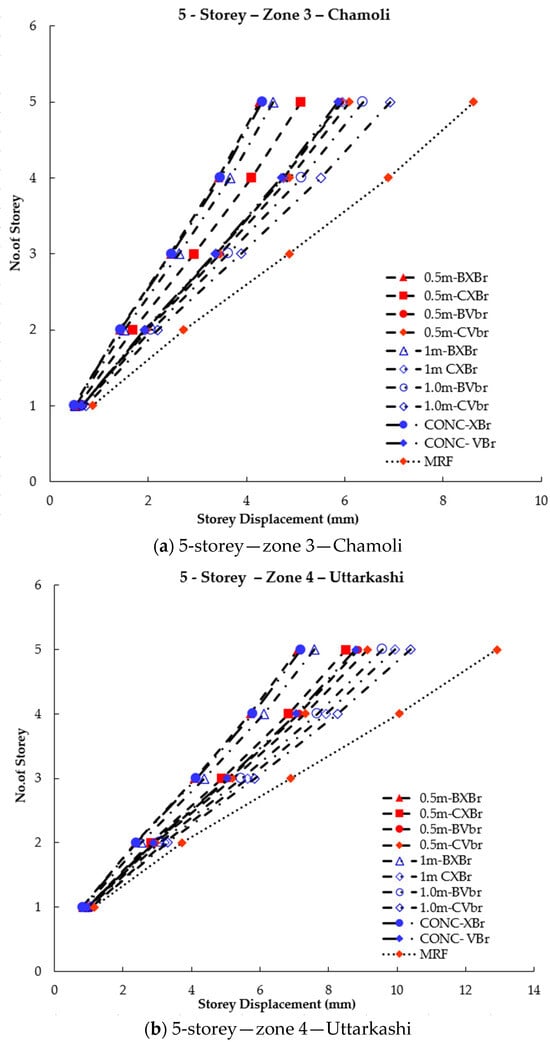
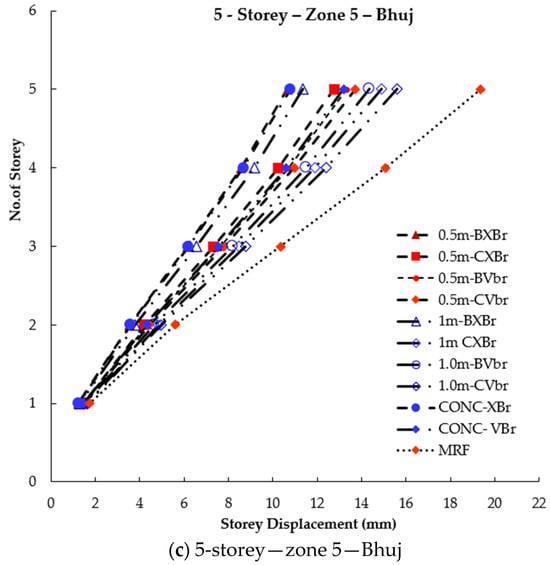
Figure 6.
Storey displacement of 5-storey braced and unbraced frames under seismic effect.
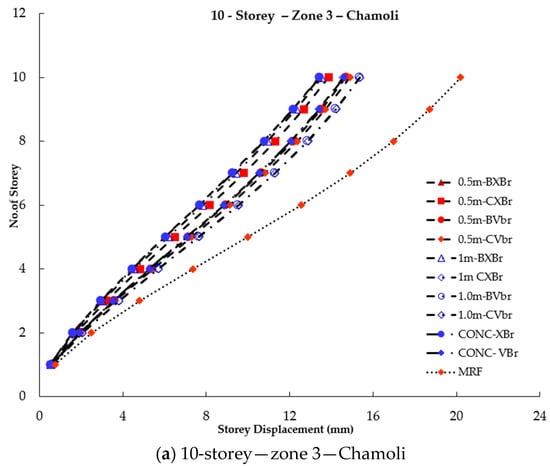
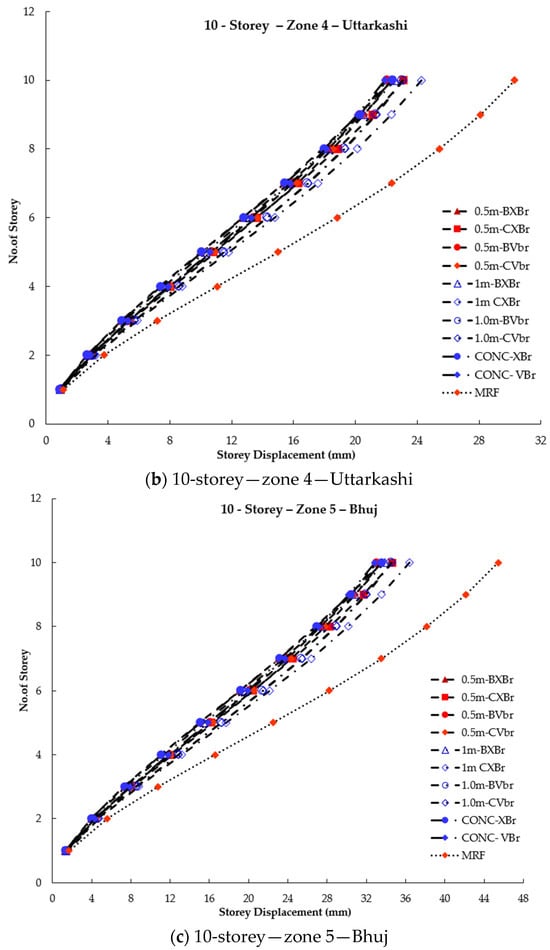
Figure 7.
Storey displacement of 10-storey braced and unbraced frames under seismic effect.
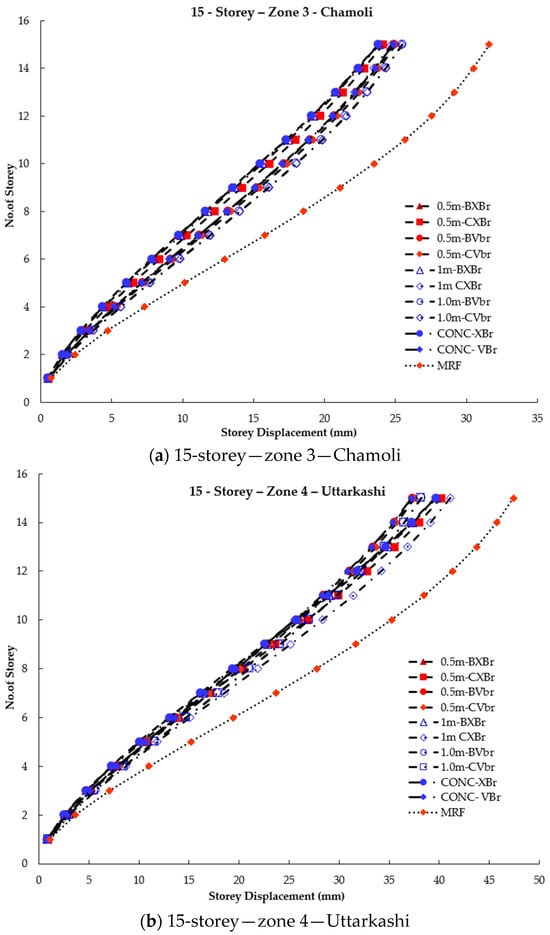
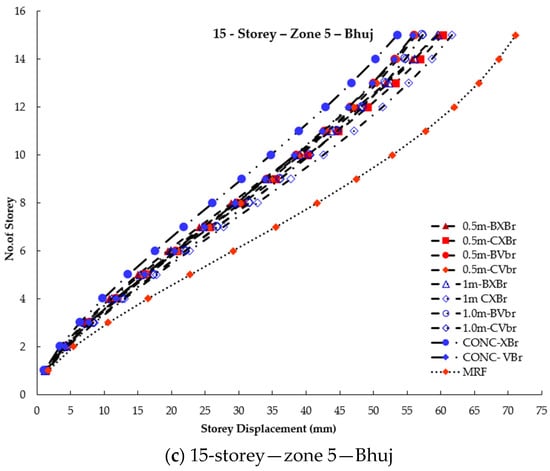
Figure 8.
Storey displacement of 15-storey braced and unbraced frames under seismic effect.
It can be inferred that an MRF has higher storey displacement, which can be reduced by 50% by providing concentric X- or V-type bracing. With the introduction of beam links, regardless of bracing type, the storey displacement is almost the same as that of the CBF. When eccentric column links are introduced in X-bracing, the storey displacement is 10% higher than that of beam links but still lower than that of the MRF. It is also evident that beam links and column links perform similarly in all three zones for V-bracing. Therefore, in V-type bracing, the presence of links in beams or columns results in similar storey displacement.
Based on the data, it was observed that column links with a length of 0.5 m exhibited lower storey displacements compared to those with a length of 1 m. This suggests that the lateral resisting capacity of the structure is affected by the eccentric distances. Therefore, to ensure the building performs as intended, it is recommended to use link lengths that are less than twice the depth of the connecting beam.
3.2. Inter-Storey Drift Ratio
The inter-storey drift ratio is the ratio between the storey drift and its corresponding storey height. By providing column links, it is observed that the drift ratio is reduced, similar to the reduction in storey displacements, regardless of the considered cases. The reduction in percentage is higher in zone 3 compared to zone 4 and zone 5. However, increasing the link length drastically increases the drift ratio, indicating that column links make the structure more ductile, allowing for larger displacements. However, this can lead to the plastification of members and promote the collapse of the entire structure. Using a minimum 0.5-m column link results in a lower drift, making the structure more rigid and reducing the displacement between consecutive stories, keeping all members in the elastic stage.
Column links reduce the drift ratio, similar to the X-bracing system. In lower zones, shorter column links reduce drift, while in higher zones, they do not perform well. It is not advisable to use links in higher zones for X-bracing. The percentage reduction is the same for both zone 3 and zone 4. Conversely, in zone 5, drifts slightly increase, but within 5%.
For V-type bracing, it is preferable to use column links in higher zones, contrary to the X-type bracing system. Therefore, providing suitable links with proper eccentricity can prevent failure and ensure the desirable performance of the structure.
3.3. Base Shear
The diagram in Figure 9 shows the time periods when the structure experiences maximum base shear. The base shear capacity of 0.5-m beam links and column links performs similarly in X-bracing. However, 1 m column links exhibit reduced base shear, similar to the storey shear. This implies that the structure becomes less rigid when links are introduced in columns with greater eccentricity, and vice versa. Regardless of the location of bracings in the structure, beam links, or column links, the base shear capacity remains unchanged. Comparing the results, it is concluded that the base shear capacity is greater for a link length of 0.5 m. Therefore, it is advisable to provide less eccentricity between the bracings to improve the base shear capacity of the structure.
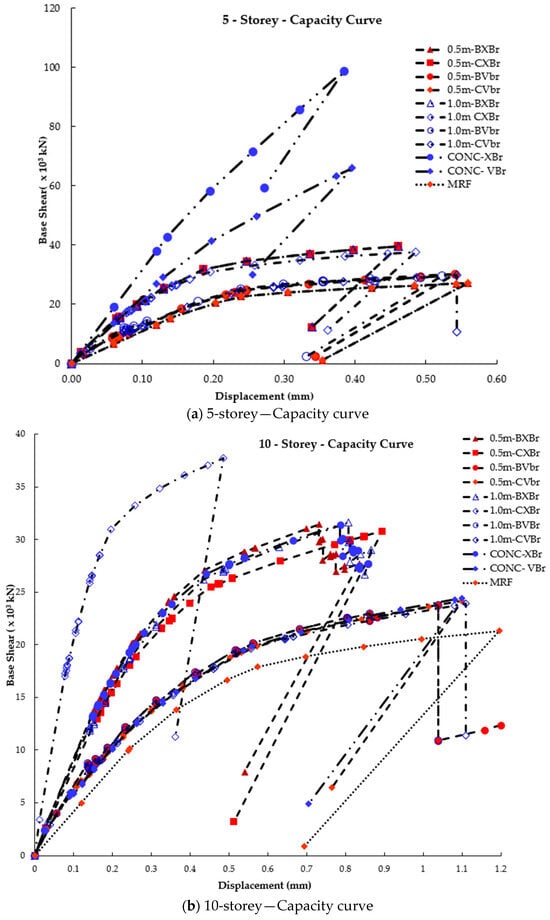
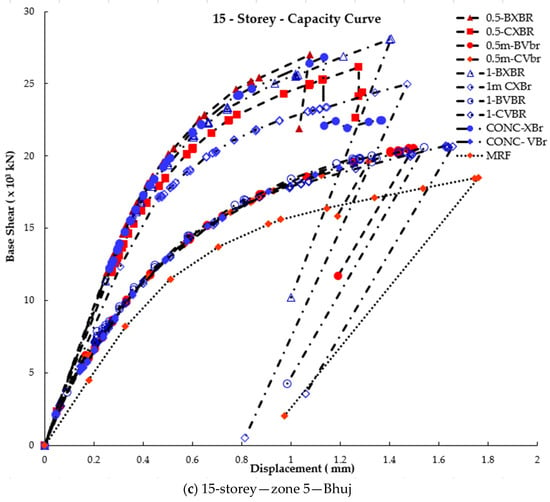
Figure 9.
Capacity curve for braced and unbraced frames from pushover analysis.
In low-rise buildings, the V-braced frames exhibit better displacement resistance than the X-braced frames. Similarly, in this study, the V-braced frames perform better in lower zones (as seen in Figure 6, Figure 7, Figure 8 and Figure 9). It is also noted that in taller structures, the X-braced frames demonstrate superior performance in terms of displacement criteria. The X-braced frames display smaller displacements in this study, similar to the results of the author [5].
3.4. Capacity Curve
By analyzing push load cases, hinges were incorporated into structural elements to achieve the desired target displacement. The base shear ultimately fell within the target range, as seen in Figure 9 for both braced and unbraced frames. The unbraced frames’ capacity curve in Figure 9 was bilinear, indicating that it was in the elastic stage with a linear slope. As the seismic load increased, certain columns and beams transitioned to the inelastic stage, causing a shift in the slope of the capacity curve. EBFs and MRFs showed more ductile behaviors, with EBFs featuring beam and column links of similar lengths behaving similarly and exhibiting greater ductility. Bracing improved ductility, with V-braced frames proving more effective than X-braced frames.
With an increase in the number of stories, the frames exhibited an enhanced capacity to withstand higher seismic forces. In particular, V-braced frames with column links exhibited a greater capacity for dissipating energy, and the formation of hinges resulted in a redistribution of moments within the frames. Currently, V-braced beam links are the primary option for dissipating energy in frames exposed to significant seismic forces. Nevertheless, in unavoidable situations, column links outperform beam links. Consequently, column links can also be employed in tall buildings to attain improved performance parameters.
4. Plastic Hinge Formation
Overall, beam links in eccentric braced frames contribute to the earthquake resilience of structures by improving energy dissipation, ductility, and overall seismic performance, while also offering design flexibility and cost-effectiveness.
Based on the results from the pushover analyses, it is evident that column links have a higher yield point than beam links. Delay in the failure of the structure by better moment redistribution as well as the enhanced ductility and dissipation of column links are the added benefits of using column links over beam links. Figure 10, Figure 11 and Figure 12 illustrate the formation of plastic hinges in braced frames with both beam and column links for 10 and 15 stories. Hinge formation is determined to be scattered in an MRF [8], with hinges forming throughout the building. In MRFs, hinge formation begins with beams and progresses to columns before collapse. However, in braced frames, hinge formation starts with the bracings and is then transferred to the beams and columns.
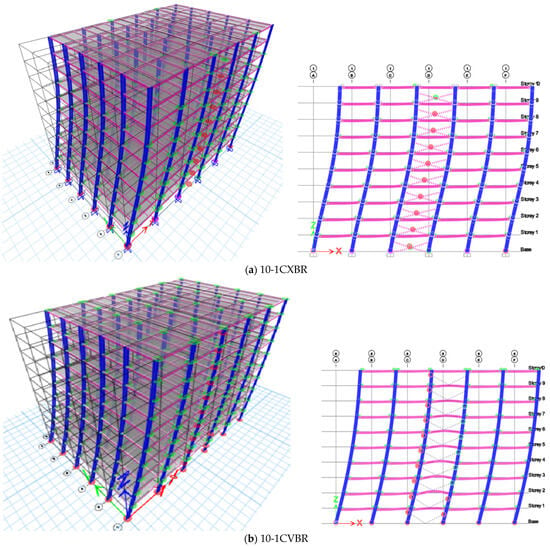
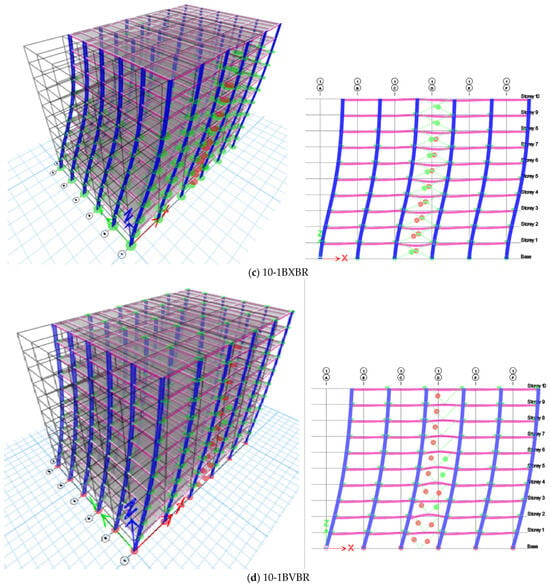
Figure 10.
Plastic hinge formation of 10-storey for 1 m column links, beam links in X- and V-braced frames.
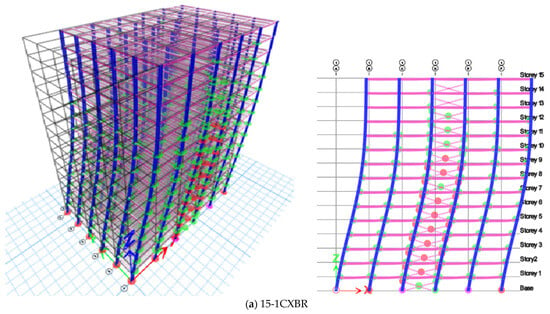
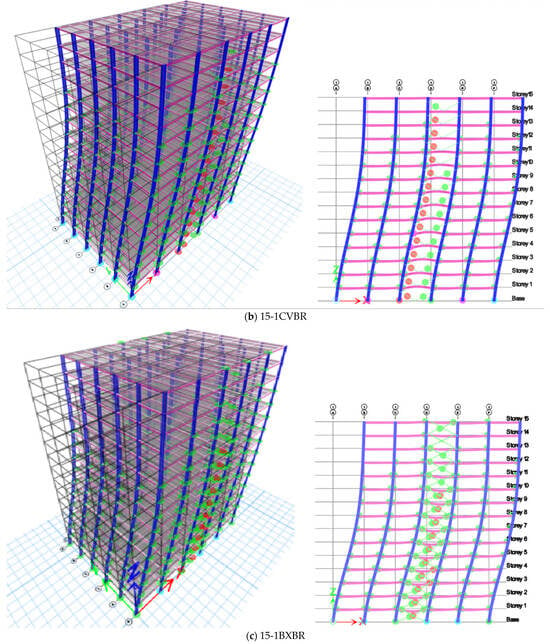
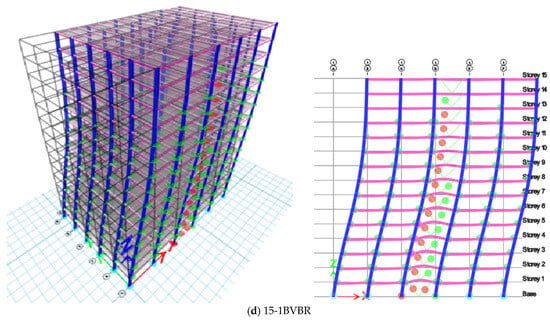
Figure 11.
Plastic hinge formation of 15-storey for 1 m column links, beam links in X- and V-braced frames.
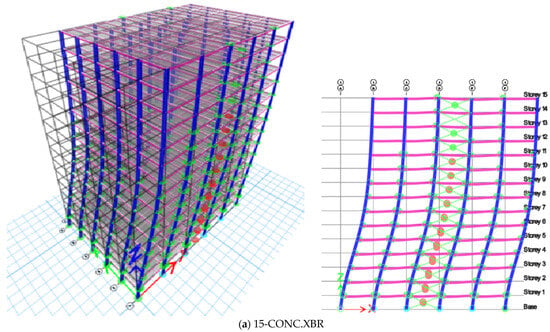
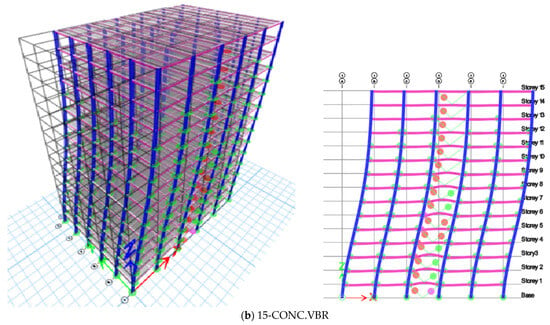
Figure 12.
Plastic hinge formation of 15-storey for concentric X- and V-braced frames.
The 5-storey MRF, CBF, and EBF behave similarly. The CBF is preferred for lower-storey structures that are subjected to heavy loads and experience higher base shear. The MRF showed better performance, and it is an economical option when the height of the building is less than 15 m. On the other hand, when the number of stories is greater, it leads to an increase in the seismic demand of the structure, which also increases the weight of the structure in the case of an MRF. The dual system of an MRF with braces can address the seismic demand; however, better ductility can be achieved by employing the links in the structure.
In this study, the formation of hinges for an EBF was found to be very similar to the [8] study of CBFs. In X- and V-braced frames, hinges initially form in the braces, followed by hinges forming in the beams and columns, respectively. The columns suddenly collapsed into V-braced frames with beam links rather than column links. In 10-storey X- and V-braced frames, column failure was not observed, and the frames performed well. For the 15-storey building with beam and column links, the sequence of hinge formation was similar to the 10-storey building, but the column hinge reached its ultimate state in the column link case, while the ultimate yield state of the column was not attained in the X-braced beam link structure. The column is non-composite. Therefore, the steel column tends to promote the development of a hinge mechanism similar to that observed with beam links, rather than exhibiting brittleness.
The hinge formation in the 15-storey building is similar to the 10-storey V-braced frames. Hinges initially formed in the braces, followed by the beams and columns. In the 15-storey building, the V-braced frames perform better when linked to the columns rather than the beams. As the height of the building increases, the structural capacity decreases, even when the sequence of hinge formation remains the same. Figure 12 shows that the CBF is stiffer but has lower ductility compared to the EBF, which has higher ductility and energy dissipation characteristics. This makes the EBF the preferred choice for a performance-braced design.
5. Concluding Remarks and Recommendations
This study delves into the impact of link columns in eccentrically braced frames, drawing comparisons with moment-resisting frames when subjected to seismic conditions. The investigation encompasses X-braced and V-braced frames, each featuring eccentric beam and column connections with standard eccentricities of 0.5 m and 1.0 m. Models of composite frames are scrutinized across typical building heights of 5, 10, and 15 stories, subject to three distinct seismic scenarios in accordance with the Indian code. Key findings include:
- The length of the connections significantly influences the performance of V-braced frames compared to X-braced frames.
- The categorization of eccentric connections as either shear or intermediate links plays a pivotal role in determining the structure’s lateral displacement and energy dissipation.
- The column link length of 0.5 m showed a stiffness reduction of 5% when compared with the beam link of the same length. However, when the number of stories increased, the difference was less than 1%. Additionally, when the column link length is increased to 1.0 m, the stiffness reduction is increased by 15% in low-rise buildings and <5% in high-rise buildings.
- The eccentric X-braced frames are stiffer when compared with the V-braced frames when the link is in the beams. When the links are in the columns, the V-braced frames are stiffer than the X-braced frames.
- In the case of column links, lateral deformation is observed to be approximately 10% greater than that of beam links but 30% less than in moment-resisting frames (MRFs), consistently falling within the recommended displacement limits specified by ATC 40 and AISC 341.
- The lateral deformation of the MRF is controlled by braced frames, and X-braced frames offer more stiffness against lateral deformation compared with V-braced frames. The EBF with a link beam and link column is not effectively utilized in low-rise buildings. The 1.0-m eccentric link column in V-braced frames can be used for better performance in high-rise buildings when compared with the 1.0-m link beam in V-braced and X-braced frames.
Consequently, link columns can be an alternative design approach where installing link beams is impractical, including retrofitting projects that share similarities with the eccentric placement of dampers in bracing systems. The characterization of beam–column connections is not employed in the structure. It is worth noting that the study does not explore the cost-effectiveness of this structural approach. Further research is also essential to explore the degradation of link column members and their overall impact on the performance of composite frames featuring column links.
Author Contributions
Conceptualization, Data curation, Formal analysis, Investigation, Methodology, C.R.G., Project administration, B.G.A.G. and K.D.T., Supervision, B.G.A.G., Visualization, B.G.A.G. and K.D.T., Validation, Writing—original draft, B.G.A.G., Writing—review and editing, K.D.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alonso-Rodríguez, A.; Tsavdaridis, K.D. Effect of Rotational Inertia on Building Response to Earthquakes via a Closed-Form Solution. Mech. Based Des. Struct. Mach. 2021, 51, 1842–1855. [Google Scholar] [CrossRef]
- Tabar, A.M.; Alonso-Rodriguez, A.; Tsavdaridis, K.D. Building Retrofit with Reduced Web (RWS) and Beam (RBS) Section Limited-Ductility Connections. J. Constr. Steel Res. 2022, 197, 107459. [Google Scholar] [CrossRef]
- Boushehri, K.; Tsavdaridis, K.D.; Cai, G. Seismic Behaviour of RWS Moment Connections to Deep Columns with European Sections. J. Constr. Steel Res. 2019, 161, 416–435. [Google Scholar] [CrossRef]
- Wang, Z.; Tsavdaridis, K.D. Optimality Criteria-Based Minimum-Weight Design Method for Modular Building Systems Subjected to Generalised Stiffness Constraints: A Comparative Study. Eng. Struct. 2022, 251, 113472. [Google Scholar] [CrossRef]
- Nassani, D.E.; Hussein, A.K.; Mohammed, A.H. Comparative Response Assessment of Steel Frames With Different Bracing Systems Under Seismic Effect. Structures 2017, 11, 229–242. [Google Scholar] [CrossRef]
- Hassanzadeh, A.; Gholizadeh, S. Collapse-Performance-Aided Design Optimization of Steel Concentrically Braced Frames. Eng. Struct. 2019, 197, 109411. [Google Scholar] [CrossRef]
- Rahimi, A.; Maheri, M.R. The Effects of Steel X-Brace Retrofitting of RC Frames on the Seismic Performance of Frames and Their Elements. Eng. Struct. 2020, 206, 110149. [Google Scholar] [CrossRef]
- Patil, D.M.; Sangle, K.K. Seismic Behaviour of Different Bracing Systems in High Rise 2-D Steel Buildings. Structures 2015, 3, 282–305. [Google Scholar] [CrossRef]
- Tengfei, L.; Su, M.; Sui, Y. Hybrid Simulation Tests of High-Strength Steel Composite K-Eccentrically Braced Frames. Steel Compos. Struct. 2021, 38, 1–15. [Google Scholar] [CrossRef]
- Montuori, R.; Nastri, E.; Piluso, V.; Pisapia, A. Design Procedure for Failure Mode Control of Linked Column Frames. Eng. Struct. 2023, 296, 116937. [Google Scholar] [CrossRef]
- Popov, E.P.; Malley, J.O. Design of Links and Beam to Column Connections for Eccenrically Braced Steel Frames. National Science Foundation and American Iron and Steel Institute: Washington, DC, USA; p. 1983.
- Yang, C.-S.; Leon, R.T.; DesRoches, R. Pushover Response of a Braced Frame with Suspended Zipper Struts. J. Struct. Eng. 2008, 134, 1619–1626. [Google Scholar] [CrossRef]
- Tong, G.S.; Pi, Y.L.; Bradford, M. Buckling Failure of an Unusual Braced Steel Frame Supporting an Electric Dust-Catcher. Eng. Fail. Anal. 2009, 16, 2400–2407. [Google Scholar] [CrossRef]
- Shayanfar, M.A.; Barkhordari, M.A.; Rezaeian, A.R. Experimental behaviour of cyclic behaviour of composite vertical links in eccentrically braced frames. Steel Compos. Struct. 2011, 12, 13–29. [Google Scholar] [CrossRef]
- Danesh, F.; Faridalam, M. Behavior of Link-to-Column Connections in Eccentrically Braced Frames. In Proceedings of the 15th World Conference of Earthquake Engineering, Lisboa, Portugal, 24–28 September 2012; p. 9. [Google Scholar]
- D’Aniello, M.; La Manna Ambrosino, G.; Portioli, F.; Landolfo, R. Modelling Aspects of the Seismic Response of Steel Concentric Braced Frames. Steel Compos. Struct. 2013, 15, 539–566. [Google Scholar] [CrossRef]
- Bouwkamp, J.; Vetr, M.G.; Ghamari, A. An Analytical Model for Inelastic Cyclic Response of Eccentrically Braced Frame with Vertical Shear Link (V-EBF). Case Stud. Struct. Eng. 2016, 6, 31–44. [Google Scholar] [CrossRef]
- Junda, E.; Leelataviwat, S.; Doung, P. Cyclic Testing and Performance Evaluation of Buckling-Restrained Knee-Braced Frames. J. Constr. Steel Res. 2018, 148, 154–164. [Google Scholar] [CrossRef]
- Mohammadrezapour, E.; Danesh, F. Experimental Investigation of Bolted Link-to-Column Connections in Eccentrically Braced Frames. J. Constr. Steel Res. 2018, 147, 236–246. [Google Scholar] [CrossRef]
- Kumar, M.S.; Senthilkumar, R.; Sourabha, L. Seismic Performance of Special Concentric Steel Braced Frames. Structures 2019, 20, 166–175. [Google Scholar] [CrossRef]
- Shoeibi, S.; Gholhaki, M.; Kafi, M.A. Simplified Force-Based Seismic Design Procedure for Linked Column Frame System. Soil Dyn. Earthq. Eng. 2019, 121, 87–101. [Google Scholar] [CrossRef]
- Yao, Z.; Wang, W.; Fang, C.; Zhang, Z. An Experimental Study on Eccentrically Braced Beam-through Steel Frames with Replaceable Shear Links. Eng. Struct. 2020, 206, 110185. [Google Scholar] [CrossRef]
- Kabir, H.; Aghdam, M. A robust Bézier based solution for nonlinear vibration and post-buckling of random checkerboard graphene nano-platelets reinforced composite beams. Compos. Struct. 2019, 212, 184–198. [Google Scholar] [CrossRef]
- Nguyen, D.D.; Nguyen, M.N.; Duc, N.D.; Rungamornrat, J.; Bui, T.Q. Enhanced Nodal Gradient Finite Elements with New Numerical Integration Schemes for 2D and 3D Geometrically Nonlinear Analysis. Appl. Math. Model. 2021, 93, 326–359. [Google Scholar] [CrossRef]
- Bert, C.W.; Malik, M. Differential Quadrature: A Powerful New Technique for Analysis of Composite Structures. Compos. Struct. 1997, 39, 179–189. [Google Scholar] [CrossRef]
- Šabatka, L.; Wald, F.; Kabeláč, J.; Kolaja, D.; Pospíšil, M. Structural Analysis and Design of Steel Connections Using Component-Based Finite Element Model. J. Civ. Eng. Archit. 2015, 9, 1–7. [Google Scholar] [CrossRef]
- Caprili, S.; Mussini, N.; Salvatore, W. Experimental and Numerical Assessment of EBF Structures with Shear Links. Steel Compos. Struct. 2018, 28, 123–138. [Google Scholar] [CrossRef]
- Erfani, S.; Vakili1a, A.; Akrami, V. Numerical Investigation on the Flexural Links of Eccentrically Braced Frames with Web Openings. Steel Compos. Struct. 2021, 38, 381–397. [Google Scholar]
- Li, T.; Shi, Q.; Wang, X.; Ye, C. Study on the Seismic Behavior of Eccentrically Braced Steel Frames of Replaceable Shear Links with Web Opening. J. Phys. Conf. Ser. 2020, 1637, 012036. [Google Scholar] [CrossRef]
- IS 1893:2016; Part-I-2016 Criteria for Earthquake Resistant Design of Structures, Part 1: General Provisions and Buildings. Bureau of Indian Standards: New Delhi, India, 2016; pp. 1–44.
- IS 875; Part 1 Code of Practice for Design Loads (Other than Earthquake) for Buildings and Structures. Part 1: Dead Loads-Unit Weights of Building Materials and Stored Materials (Second Revision). Bureau of Indian Standards: New Delhi, India, 1989.
- IS 875; Part 2 Code of Practice for Design Loads (Other than Earthquake) for Buildings and Structures, Part 2: Imposed Loads. Bureau of Indian Standards: New Delhi, India, 1987; p. 18.
- ETABS: Analysis and Design; Computer and Structure Inc.: Berkeley, CA, USA, 2018.
- IS:800; Indian Standard Code of Practice for General Construction in Steel. Bureau of Indian Standards: New Delhi, India, 2007.
- Naughton, D.T.; Tsavdaridis, K.D.; Maraveas, C.; Nicolaou, A. Pushover Analysis of Steel Seismic Resistant Frames with Reduced Web Section and Reduced Beam Section Connections. Front. Built Environ. 2017, 3, 59. [Google Scholar] [CrossRef]
- ATC-40; Seismic Evaluation and Retrofit of Concrete Buildings. Applied Technology Council: Redwood City, CA, USA, 1996.
- ASCE 41; Seismic Evaluation and Retrofit of Existing Buildings. ASCE: Reston, VA, USA, 2013; ISBN 9780784412855.
- Pekelnicky, R.; Hagen, G. A Summary of Significant Updates in ASCE 41-17. In Proceedings of the 2017 SEAOC Convention Proceedings, San Diego, CA, USA, 13–15 September 2017; Volume 1. [Google Scholar]
- AISC 341-16; Seismic Provisions for Structural Steel Buildings Supersedes the Seismic Provisions for Structural Steel Buildings. AISC: Chicago, IL, USA, 2016.
- EN 1993-1-8; Eurocode 3: Design of Steel Structures. CEN: Brussels, Belgium, 2011; Volume 8.
- EN 1994-1-1; Design of Composite Steel and Concrete Structures—Part 1-1: General Rules and Rules for Buildings Eurocode. CEN: Brussels, Belgium, 2011.
- Lin, X.; Okazaki, T.; Nakashima, M. Bolted Beam-to-Column Connections for Built-up Columns Constructed of H-SA700 steel. J. Constr. Steel Res. 2014, 101, 469–481. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).