Carbon Emissions of Assembly Buildings Constrained by Flexible Resource: A Study on Cost Optimization

Abstract

The construction industry is a high-energy-consumption industry. Nearly 40% of global carbon emissions derive from the construction industry. Prefabricated assembly technology is an effective means of carbon emission reduction, but the incremental cost of prefabricated components is much more expensive than that of cast-in-place components. It is not conducive for enterprises to choose prefabricated assembly technology to decrease emissions. Most of the current studies focus on the carbon-reduction effect of prefabricated assembled buildings, and there are fewer studies related to the impact of cost factors on enterprises’ participation in building carbon reduction. The cost factor will affect the choice of prefabricated assembly technology to reduce carbon emissions. Therefore, it is necessary to analyze the relationship between carbon emissions and costs in prefabricated buildings. Aiming at this problem, this paper proposes a dual-objective method to optimize cost and carbon emissions by using the improved optimization algorithm to solve the problem. Through the analysis of actual cases, the results show that when the prefabrication rate is 35–40%, enterprises can obtain a better carbon-emission-reduction effect by appropriately increasing the cost. When the prefabrication rate is higher than 40%, the carbon-reduction effect that can be obtained by greatly increasing the cost is limited. Therefore, when enterprises decide a prefabrication range of 35–40%, they are able to obtain the maximum carbon-reduction effect with the minimum cost. This study can provide a reference for the government to formulate relevant policies with energy conservation and emission reductions in prefabricated buildings and also can provide a reference for enterprises to make decisions between carbon emission reduction and cost.

1. Introduction

The construction industry is listed as one of the largest consumers of energy, with serious waste in terms of resources [1]. The industry consumes 36% of global energy consumption, and its carbon emissions have reached up to 40% of global carbon emissions [2,3,4]. According to the relevant research on global carbon emissions, construction is a major industry contributing to emissions, which indicates a great potential for reducing carbon emissions [5,6,7]. The Paris Agreement set a goal for carbon neutrality by 2050 [8], while China has announced that it aims to peak its carbon emissions before 2030 and achieve carbon neutrality before 2060 [9,10,11]. For China to achieve its target, it is critical to reduce the carbon footprint derived from the construction industry. With the rapid development of China’s urbanization, the construction area has maintained an annual growth rate of 3% to 5% in the past ten years [12], which increases the pressure of carbon emission reduction. Enterprises have outdated construction technology, serious waste of materials and energy in the production process, and insufficient investment in technology, which make the huge carbon-emission-reduction potential of the construction industry untapped. Since the 21st century, modern construction technology has developed towards green construction, with low energy consumption and low pollution. In this trend, prefabricated buildings have gained attention. The prefabricated building (Precast Concrete (PC) building) is to transfer manyon-site operations to the factory instead of the traditional construction process [13]. The components and accessories are fabricated in the factory, transported to the construction site, then installed in a standardized connection method to complete the building. Compared with traditional cast-in-place buildings, prefabricated buildings have greatly improved the utilization efficiency of building materials, construction equipment, and labor. They reduce construction waste and material waste [14], improve construction quality [15], increase production safety [16,17], and make the energy-saving and emission-reduction effect better [18]. The wide use of PC buildings is an effective method for carbon emission reductions in the whole life cycle of buildings [19]. In 1976, the U.S. Congress passed the National Industrial Housing Construction and Safety Act. In the same year, a series of strict industry norms and standards were issued, which are still in use today. Europe is the birthplace of prefabricated construction, and the road to industrialization of construction began as early as the 17th century. Various professional precast construction systems and product series standards have been formed. In Japan’s first five-year housing plan formulated in 1965, the “Five-Year Plan for New Housing Construction”, it was pointed out that the ratio of industrialized housing should reach 15%. After 1975, the Japanese government issued two codes, “Industrialized Housing Performance Certification Regulations” and “Industrialized Housing Performance Certification Technical Standards”, which played a decisive role in improving the industrialization level of Japanese housing. China proposed the “ACTION PLAN FOR CARBON DIOXIDE PEAKING BEFORE 2030”, developing low-carbon building materials and green construction, and vigorously uses prefabricated buildings to strengthen green design and green construction. By 2025, the proportion of new prefabricated buildings will be greater than 30% [20], with reference to “The 15th-FIVE-YEAR PLAN”. These policies have also strongly pushed the development of low-carbon buildings.

Hao et al. [21] proposed to use building information modeling (BIM) technology to simulate and evaluate instead of building physical facilities and measured the carbon emissions of prefabricated buildings. The results show that prefabricated assembly technology is able to reduce building carbon emissions. Ji et al. [22] relied on Luban software to simulate prefabricated assembly construction technology and cast-in-place construction technology. The results show that in the construction process, compared with cast-in-place technology, the prefabricated assembly technology is more environmentally friendly. Based on BIM technology and a carbon-emission calculation model, Ding et al. [23] measured the carbon emissions of prefabricated buildings in the materialization stage and compared them with cast-in-place technology. Hence, they concluded that the carbon emissions of prefabricated components were decreased by 20.11% per unit volume, compared to cast-in-place components. The carbon emission reduction effect is remarkable. The above studies show that prefabricated buildings have high potential for energy saving and emission reduction. However, in recent years, it has been found that not all prefabricated components have a better carbon-reduction effect than prefabricated components. Teng et al. [24] conducted research on 12 factors that affect the carbon emissions of prefabricated buildings and found that prefabricated buildings do not promise to reduce carbon emissions without using energy-efficient materials. Du et al. [25] found that in the prefabricated building supply chain, technical factors play the most important role in carbon reduction. Jeong et al. [26] found that although the new prefabricated column improved the production efficiency, the carbon emission of the prefabricated column would be higher than that of the traditional one, which is the result of increasing the material. Du et al. [27] measured the carbon emissions of buildings based on three prefabrication scenarios and found that prefabricated transverse members had the most significant carbon-reduction effect. Chippagiri et al. [28] proposed that prefabrication technology can effectively contribute about 30% in reduced carbon emissions. Pan et al. [17] suggested that using well-proven methods and materials contributed to the high capital cost. Jingke et al. [29] proposed that the average incremental cost is highly linearly correlated with the prefabrication rate, which ranged from 237 CNY/m² to 437 CNY/m² in Mainland China.

The above studies show that prefabrication technology is an effective means to reduce carbon emissions in buildings, and an appropriate increase in prefabrication rate reduces the overall carbon emissions of buildings. However, these studies do not consider that prefabricated assembly technology in China is relatively outdated. Increasing the prefabrication rate will lead to a sharp rise in construction costs. The rising cost blocks the way when companies try to achieve carbon emission reduction in buildings by increasing the prefabrication rate. Therefore, this paper proposes to optimize the two goals between carbon emission and cost by means of dual-objective optimization. Combined with engineering examples, the relationship between prefabrication rate, carbon emission, and cost is analyzed, so that enterprises can create both economic and environmental benefits and increase the enthusiasm of enterprises to reduce carbon emissions by using prefabricated assembly technology. This study can provide a reference for the government to formulate relevant policies with energy conservation and emission reduction of prefabricated buildings, and also can provide a reference for enterprises to make decisions between carbon emission reduction and cost. In this paper, the impact of different prefabrication rates on building carbon emissions and construction costs is analyzed through dual-objective optimization, and the maximum environmental benefits are obtained with the minimum economic cost. It improves the motivation of enterprises to use prefabricated components for carbon emission reduction and provides reference for the decision-making of enterprises and government.

2. Problem Description

The minimum cost and carbon emissions of construction projects are two important indicators for evaluating the profitability and greenness of engineering projects. In the resource-constrained project scheduling problem (RCPSP), each problem has a single cost and demand for resources. The multimode resource-constrained project scheduling problem (MRCPSP) is a form of RCPSP in which each problem has a finite number of costs—resource modes—and each feasible mode is associated with its specific cost; the allocation of resources is in one-to-one correspondence [30]. At present, in the field of MRCPSP, the main area of study is renewable resources (machinery, equipment, labor, etc.) or non-renewable resources (raw materials, funds, etc.) under the constraints of the weight relationship, so that each feasible mode has a specific cost and resource demand. The carbon emission/cost trade-off problem (CECTP) can also be classified as a special form of MRCPSP.

During the implementation of engineering projects, different prefabrication conditions will affect the carbon emissions and costs of the building. In general, as the prefabrication rate increases, carbon emissions decrease and costs increase. Conversely, reducing the prefabrication rate will increase carbon emissions and reduce costs. For engineering projects, managers need a balance between the minimization of carbon emissions and construction costs. The conflicting goals of carbon emissions and cost cannot be minimized simultaneously under resource constraints. The role of dual-objective optimization is that under the current resource constraints, the two objectives can achieve a relatively balanced minimum value. Through a series of simulation analysis, managers can appropriately increase the prefabrication rate and cost to greatly reduce carbon emissions, or appropriately reduce the prefabrication rate and increase a small part of carbon emissions to greatly reduce costs. Finally, we take into account both economic and environmental benefits. To achieve these goals, the first step is to establish carbon emissions, the lowest-cost objective function, and constraints for each target. The current resource constraints are solved by a dual-objective optimization algorithm, a series of optimal solutions that meet the constraints is used. Common solution algorithms include genetic algorithms, particle swarm optimization, and simulated annealing algorithms. The optimal solution is obtained to make two objectives reach the relatively lowest equilibrium state under the constraints. Finally, the optimal set of solutions is found to inform the managers’ decisions.

Before establishing a carbon emission–cost dual-objective optimization model, this paper considers the following factors that can directly affect building carbon emissions and construction costs:

• The impact of carbon trading on costs:

Carbon trading, in brief, means that one party to the contract obtains carbon emission allowances by purchasing from the other party, and the buyer uses the purchased allowances for industries that exceed the standard to achieve carbon-emission-reduction goals. When considering the objective function of cost, the impact of carbon trading on construction costs needs to be considered. There is currently no mandatory limit for its quota, since carbon trading in China’s construction industry is in its infancy. The quota is temporarily considered based on the carbon emissions when it is fully cast in place. The reduced carbon emissions can be used for carbon trading, so that companies can make profits. According to the National Carbon Emissions Trading Market’s figure, the average price of China’s carbon trading market in 2021, is about 59 CNY CO₂/t. When the carbon emission is lower than the quota, the indicators below the quota can be sold; otherwise, the indicators need to be purchased to meet the corresponding carbon emission standards.

• Requirements for precast rate:

China’s prefabrication rate for industrialized buildings is limited to not less than 20% [31], but requirements vary from region to region across the country. For instance, the standard in Beijing and Shanghai is not less than 40%, which is the highest in China. In some areas, only the assembly rate is required, and the prefabrication situation can be adjusted according to the actual local conditions.

• Incremental relationship between prefabricated components and cast-in-place components:

Due to the difference in structural design and construction methods, the volume of prefabricated components per unit area is higher than that of cast-in-place components. When establishing the optimization model, it is necessary to convert the volume of the prefabricated or cast-in-place component by its adjustment factor into the same component for modeling. The volume of components in a unit building area shall not be lower than that of fully cast-in-place components and not higher than that of fully prefabricated components.

3. Model Establishment

3.1. Objective Function

3.1.1. Objective Function of Carbon Emission

Calculate the carbon emissions of structural components according to the carbon emission coefficient method in the raw material production stage, the transportation stage, and the component processing and on-site installation stages [32], and the carbon emission objective function is shown in the below formula.

$$MinT={\displaystyle \sum }_{i=1}^n{x}_i\times p_{xei}+y_i\times p_{yei}$$

(1)

where T denotes carbon emissions of the overall structural components of the building (CO₂/kg); x_i denotes volume of the i-th cast-in-place component (m³); p_xei denotes carbon emission coefficient of the i-th cast-in-place component (CO₂ kg/m³); y_i denotes volume of the i-th prefabricated element (m³); p_yei denotes carbon emission factor of the i-th prefabricated element (CO₂ kg/m³).

3.1.2. Objective Function of Cost

The cost of prefabricated components includes the supply cost and the installation cost of components. The cost of cast-in-place components includes material, labor, and equipment usage fee. The cost measurement model of structural components is obtained by adding up various costs of each component. According to the relevant rules of “Carbon trading management methods (trial implementation)” in China, this study assumes that the overall carbon emission of a building is lower than that of a fully cast-in-place building, which can be considered as carbon saving. The constructed model is as follows.

When T ≥ L:

$$MinC={\displaystyle \sum }_{i=1}^n{x}_i\times c_{xdi}+y_i\times c_{ydi}+\left(T-L\right)\times C_t$$

(2)

When T < L:

$$MinC={\displaystyle \sum }_{i=1}^n{x}_i\times c_{xdi}+y_i\times c_{ydi}+\left(L-T\right)\times C_t$$

(3)

where C denotes total cost of components (CNY); x_i denotes volume of the i-th cast-in-place component (m³); Cxdi denotes cost of the i-th cast-in-place component (CNY/m³); yi denotes volume of the i-th prefabricated element (m³); Cydi denotes cost of the i-th prefabricated element (CO₂ CNY/m³); L denotes carbon emissions of cast-in-place components (CO₂/kg); T denotes carbon emissions of the overall structural components of the building (CO₂/kg); Ct denotes carbon trading price (CO₂ CNY/kg).

3.2. Restrictions

According to the design requirements of the building, there are certain restrictions on the structural components within the unit building area. In general, the material consumption of prefabricated components increases compared with cast-in-place components, and the influence of this part of the increment on the volume of structural components per unit area should be considered. The volume change will affect the change in carbon emissions and cost. The prefabrication rate constraints are formulated according to the actual situation, as shown in the following formula.

Restrictions on the volume of each member within a unit area, according to the actual data of the project, are considered.

$$x_i\times h_i+y_i=v_{yi}$$

(4)

$$0\le x_i\le v_{xi}$$

(5)

$$0\le y_i\le v_{yi}$$

(6)

Restrictions on precast rate [31]

$$\frac{{\sum }_{i=1}^n{y}_i}{{\sum }_{i=1}^n{x}_i+y_i}\ge PR$$

(7)

where x_i denotes volume of the i-th cast-in-place component (m³); h_i denotes adjustment factor of the i-th cast-in-place component, that is, the ratio of the same prefabricated component to the cast-in-place component of the same building; v_yi denotes volume of the i-th component, which, per unit building area, completely applies prefabricated construction (m³); v_xi denotes volume of the i-th component, which, per unit building area, completely applies cast-in-place construction (m³); y_i denotes volume of the i-th prefabricated element (m³); n denotes all kinds of components; PR denotes prefabrication rate, which is the ratio of the total volume of prefabricated components to the total volume of the overall structural components of the building.

The insulation of the two components not only affects the energy consumption of the building during its use, but also has an impact on the carbon emissions and the cost of the building life cycle. At present, there are few studies related to the insulation performance of two components and, therefore, relatively accurate constraints cannot be presented. With more relevant studies, the effects of insulation performance on carbon emissions and costs can be considered in subsequent studies.

4. Algorithm Improvement

For solving dual-objective optimization problems, common methods include exact algorithms, heuristic algorithms, and evolutionary algorithms. Heuristic algorithms are commonly used with the benefits of being faster and more efficient, including traditional genetic algorithm (GA) [33,34,35,36], simulated annealing (SA) [37], ant colony optimization (ACO) [38], and particle swarm optimization (PSO) [39,40], as well as the mean gray wolf optimization (MGWO), which appeared in recent years, Non-Dominated Sorting Whale Optimization Algorithm (NSWOA), Multi-Objective Artificial Bee Colony (MOABC), etc. Among these algorithms, the genetic algorithm is the most widely used.

The single-objective genetic algorithm can be easily modified to solve the dual-objective Pareto solution set algorithm. The genetic algorithm can search in all areas of the solution set space, which can transform the non-continuous, discrete, and multidimensional space problems into the operation of the genetic algorithm, display the non-dominated Pareto solutions of each target, and finally find its frontier solution set. Especially in dual-objective optimization, it is not necessary to set the weights of each objective in advance, which reduces the influence of subjective factors on the results. Therefore, genetic algorithm and its series of algorithms have become the mainstream algorithms for solving dual-objective and multi-objective problems in recent years.

The NSGA-II algorithm is a branch of the traditional genetic algorithm. The algorithm uses the spatial crowding degree to fully cover the feasible solutions and gradually finds the optimal solution through Pareto frontier sorting. The quality of the parent population and the offspring population and the efficiency of the algorithm are important factors that affect the effectiveness of the NSGA-II algorithm [41].

The current NSGA-II algorithm usually chooses the roulette method or the tournament method when solving dual objectives. Although it enriches the diversity of the next-generation population to a certain extent, its strong randomness makes the quality of the generated new-generation population hard to guarantee. The crossover operator and mutation operator also have problems, such as freedom and anisotropy, which lead to the unstable quality of the generated offspring population and the result falling into local optimum. Therefore, this section proposes to improve the selection method, genetic operator, and mutation operator to improve the quality of the population and make the optimization effect of dual objectives better.

4.1. Selection Operator Improvements

In the traditional tournament method or roulette method, although individuals are randomly selected, when the population is large, there will be repetitions between individuals, which will reduce the quality of the next generation generated by the selected population for crossover mutation. In response to this problem, this study proposes to use the Stochastic universal sampling (SUS) method to improve the roulette method.

The principle of roulette wheel selection (RWS) is to reflect the fitness value of an individual into the roulette wheel. The resulting offspring has better fitness.

Assuming that there are six individuals, the respective fitness values from 1 to 6 are (0.311 0.528 0.162 0.794 0.166 0.602), and the roulette wheel corresponding to their fitness is shown in Figure 1. If you want to select n individuals, you need to operate n times, and the area pointed by the pointer is the individual represented.

Using the roulette method to select n individuals requires running the wheel n times, which affects the efficiency of the algorithm. SUS is an improvement to this problem. For example, if n individuals are selected, SUS can generate equally spaced pointer positions only once and then select n individuals. The specific steps of the improved selection method are given as follows:

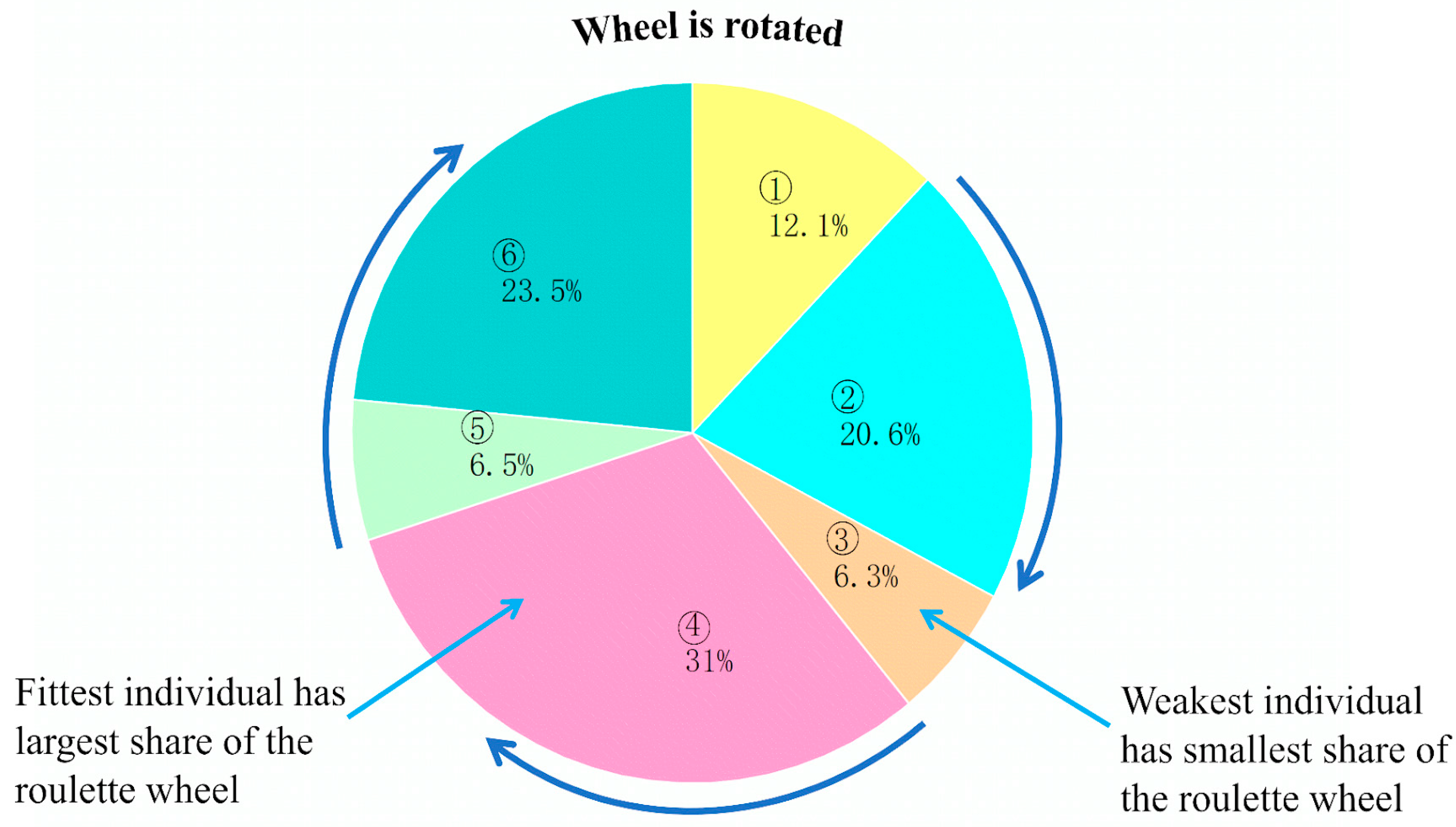
• Step 1: Calculate pointer spacing D = f/n, where f is the fitness value;
• Step 2: Randomly generate the starting point of the pointer, Start = (A random number between 0 and P);
• Step 3: Determine the position of each pointer, Pointers = (Start + I ×D) (where I ∈ (0,n − 1));
• Step 4: Select the required n individuals according to the pointer position.

For instance, six individuals’ fitness values are 0.311, 0.528, 0.162, 0.794, 0.166, 0.602, respectively, and the total fitness value of six individuals’ fitness values, f = 2.563. Assuming that six individuals are selected, the selection steps are as follows:

• Step 5: Calculate pointer spacing, D = f/n = 2.563/6 = 0.4272
• Step 6: Assuming the position of the initial pointer, Start = 3
• Step 7: Calculate the position of each pointer:

Pointers = (3 + 0.311 × 0.3 + 0.528 × 1.3 + 0.162 × 2.3 + 0.794 × 3.3 + 0.166 × 4.3 + 0.602 × 5) = (3, 3.528, 3.324, 5.382, 3.664, 6.01). Finally, the individual in the area corresponding to the pointer can be found through the program.

4.2. Crossover Operator Improvement

The NSGA-II algorithm usually uses single-point crossover or multipoint crossover operator to perform crossover operation. This crossover method makes the chromosomes of gene recombination appear as coding duplication, which reduces the quality of the new population. For this problem, this paper proposes to use partial matching crossover (PMX) to improve single-point crossover, so that no duplicate genes appear in chromosomes and the quality of the population after gene recombination is improved. The specific steps are as follows:

• Step 1: Select the initial population, assuming that the population list 1 and list 2 are as follows.

list 1: [5 9 4 2 3 0 8 7 6 1]

list 2: [5 7 8 6 9 2 4 3 1 0]

• Step 2: Randomly generate a vector length smaller than the parent through the program, such as

p = 2.

list 1: [5 9] [4 2 3 0 8 7 6 1]

list 2: [5 7] [8 6 9 2 4 3 1 0]

• Step 3: Crossover the randomly selected vector to the last digit of the gene.

list 1: [5 9] [8 6 9 2 4 3 1 0]

list 2: [5 7] [4 2 3 0 8 7 6 1]

• Step 4: Revised, the three steps above performed the single-point crossover operation and the fourth step performed partial matching crossover for the individuals after the single-point crossover. Keep the genes after single-point crossover unchanged, search for duplicate values in the unexchanged genes, and then find the corresponding position in the previous generation of individuals to reproduce in situ. In this example, the second and fifth elements 9 in list 1 are repeated after the single-point crossover, and the fifth element 3 in the original position of list 1 before the crossover is found to reproduce. After reproduction, it is found that element 3 is repeated and it needs to be reproduced again, and finally, element 7 is found. In the same way, the repeated element 7 in list 2 also needs to be reproduced, which is the same as the method of list 1 and it also needs to be reproduced twice. The result after reproduction is as follows.

list 1: [5 9] [8 6 7 2 4 3 1 0]

list 2: [5 7] [4 2 9 0 8 7 6 1]

The improved crossover operator avoids gene duplication, improves the quality of offspring, and makes the solution set better.

4.3. Mutation Operator Improvement

The mutation operation of a genetic algorithm is based on probability, and a certain gene in an individual is mutated through a certain probability. Traditional genetic operators include mutation operators, such as bit-flip mutation and crossover mutation. The traditional mutation operator is distributed around the in situ and the gene to be mutated is searched in a small range, which can easily make the algorithm fall into local optimum, and the final optimization effect is not significant. This section proposes to use Gaussian mutation operators to enrich the diversity of population individuals, so that the algorithm does not easily fall into local optimum.

Gaussian mutation (GM) is a new vector generated using a random vector that obeys a normal distribution as the in-place vector. This mutation method not only improves the quality of the population and improves the accuracy of optimization but also enables the genetic algorithm to jump out of the local optimum in the search. A better global search makes the algorithm run more efficiently. The Gaussian probability density formula is as follows [42].

$$f\left(x\right)=\frac{1}{\sqrt{2\Pi }\sigma }exp\left(-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}\right)$$

(8)

where μ is expected value of a normal distribution; σ is standard deviation of the distribution. In this study, μ and σ are set to 0 and 1, respectively.

5. Algorithm Design

5.1. Principle of NSGA-Ⅱ Algorithm

NSGA (Non-dominated Sorting Genetic Algorithms) is one of the genetic algorithms. Compared with the traditional genetic algorithm, the concept of non-dominated sorting is introduced, and hierarchical non-dominated sorting is used to make individuals with higher fitness genetics [43,44]. The probability of reaching the next generation is even greater. Deb et al. [45] proposed NSGA-II (Fast Non-dominated Sorting Genetic Algorithms) with elite strategy. The basic idea is to perform non-dominated sorting on the population to classify the population and calculate the crowded distance of the population to maintain the population. The diversity of an approximate solution is obtained when the termination condition is reached. The algorithm reduces the computational complexity and can preserve the diversity of the population. Based on the elite retention strategy, while expanding the population, it prevents the loss of elite individuals. Compared with the traditional genetic algorithm, it runs faster and has better convergence. The basic process framework of the NSGA-II algorithm is shown in Figure 2.

Similar to NSGA, the main implementation specifications of NSGA-II are provided as follows:

• (1) Generation of initial population and offspring population

A population n(t) with a set number of chromosomes n is randomly generated, and the initial population is sorted by non-dominated classification, through selection, crossover, and variation to generate a descendant population.

• (2) Generation of populations after the second generation

Starting from the second generation, the parent population and the offspring are merged to obtain a population with 2n individuals. Non-dominant sorting is performed on the merged population. At the same time, the crowded distance between individuals needs to be calculated. The dominant principle is used to select individuals to generate the next generation of populations.

• (3) Algorithm termination judgment

After executing the first two steps, check whether the termination conditions are met. If so, output the optimal solution; otherwise, continue to execute the above steps.

5.2. Improved NSGA-Ⅱ Algorithm

In Section 4, the existing problems of the traditional algorithm and the improved methods are introduced in detail, mainly by improving the selection method, the crossover operator, and the mutation operator to optimize the offspring population and generate a high-quality population. The biggest feature of NSGA-II is to use the spatial crowded distance to conduct an omnidirectional search for the solution under the constraints, so as to find the optimal solution at the frontier. The improved population is of higher quality, and it is easier to find a higher-quality Pareto frontier solution to improve the final optimization result. The specific steps are as follows.

• Step 1: Initialize the population N(n) with the number of individuals n, gen = 0, the total G, and the value of each individual conforms to the constraints of the model.
• Step 2: Sort the population non-dominantly and find the Pareto frontier solution set.
• Step 3: Use the improved method in Section 4.2 to select the parent population, use the fitness function to measure the pros and cons of the individual, and select the better individual to generate the offspring population W(t).
• Step 4: Using partial matching crossover and Gaussian mutation operator to perform crossover and mutation operations on W(t), a population Q(n) is obtained.
• Step 5: Combine W(t) and Q(t) to obtain a population R(t) with a population size of 2n.
• Step 6: Perform non-dominated sorting on R(t) and sort according to rank. Individuals with the same rank are sorted according to their fitness from large to small, and the first n individuals are selected as the next-generation population N (gen + 1).
• Step 7: Repeat the operations from the second step to the sixth step until the generation is greater than the maximum G, then stop the operation and output the value.

6. Case Study

6.1. Determination of Carbon Emissions and Cost Parameters

The project for case1 study is located in Liaoning Province, with 34 floors, 2.9 m high per floor, and a single building area of 22,862.69 m². The project for case2 study is located in Zhejiang Province, with 18 floors, 2.8 m high per floor, and a single building area of 8964 m². The project for case2 study is located in Guangdong Province, with two floors, 3.5 m high per floor, and a single building area of 1040 m². In the design stage of three projects, the increment of prefabricated components and cast-in-place components of the project was analyzed and simulated, and a list of quantities of the two components per unit area was obtained, as shown in

Table 1. List of quantities for structural components.

Material Component		Concrete (m3/m2)			Steel (kg/m3)			Steel (kg/m2)			Mold (m2/m2)
Case		1	2	3	1	2	3	1	2	3	1	2	3
Column	Prefab	0.130	0.113	0.049	120	104	102	15.6	14	4.998	1.08	0.97	1.05
	Cast-In-Place	0.120	0.105	0.045	125	110	95	15	13.1	4.275	1.00	0.88	1.01
Girder	Prefab	0.100	0.087	0.05	150	131	129	15	12.8	6.45	0.89	0.76	0.45
	Cast-In-Place	0.090	0.079	0.046	167	146	143	15	13	6.578	0.80	0.70	0.41
Board	Prefab	0.100	0.087	0.060	110	95	92	11	9.4	5.52	1.00	0.85	0.51
	Cast-In-Place	0.090	0.079	0.054	111	97	95	10	8.8	5.13	0.90	0.79	0.54
Wall	Prefab	0.080	0.07	0.12	120	105	122	9.6	8.4	14.64	0.80	0.7	0.10
	Cast-In-Place	0.080	0.07	0.12	125	109	127	10	8.8	15.24	0.80	0.7	0.10
Stairs	Prefab	0.020	0.018	0.01	90	81	85	1.8	1.6	0.85	0.20	0.18	0.10
	Cast-In-Place	0.020	0.018	0.01	80	72	76	2	1.44	0.76	0.20	0.18	0.10

.

In the measurement of carbon emissions, the activities that produce the difference in production of the two components are considered. The carbon emissions’ measurement for both components includes the carbon emissions from all activities during the raw material production, raw material and component transportation, component processing, and installation phases. According to the engineering quantity list per unit area, the carbon emission of prefabricated components per unit area and unit volume is measured in combination with the carbon emission factor method. The measured results are shown in

Table 2. Carbon emissions of each component.

Processing Methods Component	Prefab (CO2 kg/m3)			Cast-In-Place (CO2 kg/m3)			Prefab (CO2kg/m2)			Cast-In-Place (CO2kg/m2)
Case	1	2	3	1	2	3	1	2	3	1	2	3
Column	500.04	440.22	431.42	535.04	467.92	458.56	65.00	49.74	21.14	64.2	49.13	20.64
Girder	565.14	480.9	471.28	607.69	569.48	558.09	50.86	41.84	23.57	54.69	44.99	25.67
Board	479.36	417.58	409.23	512.98	442.89	434.03	47.94	36.33	24.55	46.17	34.99	23.43
Wall	518.45	453.65	444.58	536.06	468.96	459.58	41.48	31.76	53.35	42.88	32.83	55.15
Stairs	400.61	361.73	354.50	458.33	414.12	405.84	8.01	6.511	3.55	9.17	7.45	4.06

.

Costs include the cost of raw materials, auxiliary materials, and components consumed in the production process of components; amortization fees or rental fees for turnover materials; usage fees or rental fees for construction machinery and transportation tools; wages and bonuses paid to production workers, allowances of the nature of wages, etc., and all expenses incurred during construction organization and management. Further, it includes the impact of carbon emissions trading prices on component costs. According to the local carbon emission trading price, the carbon trading prices of the three cases are 14.63 CNY/co₂t, 52.78 CNY/co₂t and 74.12 CNY/co₂t, respectively, and the cost of the main components is shown in

Table 3. Cost of each component (m³/CNY).

Component Case		Column	Girder	Board	Wall	Stairs
1	Prefab	4436	4171	3175	4236	3092
	Cast-In-Place	1398	1559	1320	1575	1370
2	Prefab	4585	4659	4021	4569	4148
	Cast-In-Place	1445	1741	1671	1699	1838
3	Prefab	4930	4519	3890	4540	3530
	Cast-In-Place	1554	1689	1617	1688	1564

.

6.2. Model Establishing and Solving

According to the method in Section 3 and the data in Section 6.1, the carbon emission-cost dual-objective optimization model is established, and then it is solved according to the improved NSGA-II algorithm in Section 5. Local policies require the assembly rate to be no less than 50% in three cases, and there are no clear requirements for the prefabrication rate. The prefabrication rate is not less than 20%, according to China’s “Industrialized Building Evaluation Standard”, and the model is established with a building area of 100 m² according to the method in Section 3. The number of iterations is 200 and the number of populations is 300. The Pareto frontier diagram after the optimization is shown in Figure 3.

The Pareto solutions in Figure 3 satisfy the constraints and are the result of the trade-off between the two objectives. From the perspective of the solved optimal population, when the prefabrication rate is in a range of 35% to 40%, by adjusting the prefabrication situation, a better carbon-reduction effect can be obtained on the premise of increasing a small amount of cost. When the prefabrication rate is 40–50%, the impact of a substantial increase in the cost on the overall carbon emission reduction of the building is weakened. When the prefabrication rate is higher than 50%, to obtain a better carbon-reduction effect, the cost needs to be greatly increased, and the carbon-reduction effect is the weakest. The carbon emissions of individual solutions tend to be the same, but the costs are different. The specific data changes are shown in

Table 4. Comparison of objective function values of Pareto optimal solution sets under different prefabrication rates (Case(1) Case(2) Case(3)).

Case (1)
Solution Number	35% ≤ PR ≤ 40%		40% ≤ PR ≤ 50%		50% ≤ PR ≤ 60%
	CO2/kg	Cost/CNY	CO2/kg	Cost/CNY	CO2/kg	Cost/CNY
1	21,405.42	88,080.61	21,336.22	93,853.74	21,267.56	106,311.6
2	21,405.42	88,080.61	21,326.84	94,488.22	21,258.07	108,547.5
3	21,399.63	88,549.59	21,323.25	94,924.01	21,254.47	109,195.6
4	21393.39	88,904.89	21,318.66	95,482.5	21,253.79	109,887.7
5	21,381.52	89,491.56	21,317.22	95,877.21	21,246	110,805.6
6	21,381.45	90,067.24	21,306.68	98,065.6	21,244.92	111,239.6
7	21,375.37	90,591.67	21,304.3	98,907.15	21,242.02	111,649.6
8	21,361.41	90,678.79	21,299.97	99,497.52	21,238.74	11,2346.6
9	21,359.61	91,219.65	21,297.58	100,070.1	21,235.63	112,820
10	21,355.09	91,619.5	21,296.39	100,323.9	21,233.99	113,559.8
11	21,352.31	92,219.93	21,293.73	100,719.8	21,228.44	114,697.2
12	21,342.33	92,772.25	21,292.64	101,199.2	21,225.6	11,5331.7
13	21,338.42	93,336.47	21,289.11	101,812.6	21,220.63	116,070
14			21,285.74	102,436.4	21,218.05	116,658.5
15			21,282.8	103,161.5	21,217.74	117,131.7
16			21,281.38	103,438.9	21,214.96	117,379.4
17			21,278.55	103,913.2	21,214.12	117,872.5
18			21,276.85	104,596.5	21,210.27	118,334.9
19			21,272.16	105,435.4	21,207.1	118,986.9
20			21,272.11	105,444.3
21			21,269.3	106,077.5
Case (2)
Solution Number	35% ≤ PR ≤ 40%		40% ≤ PR ≤ 50%		50% ≤ PR ≤ 60%
	CO2/kg	Cost/CNY	CO2/kg	Cost/CNY	CO2/kg	Cost/CNY
1	16,602.24	98,584.14	16,551.5	110,131.97	16,525.56	120,317.52
2	16,607.9	98,060.06	16,556.01	109,282.56	16,525.56	120,317.52
3	16,612.12	97,685.44	16,556.24	108,866.58	16,526.18	119,829.63
4	16,614.63	97,207.39	16,557.83	108,454.89	16,526.8	119,325.12
5	16,620.16	97,037.34	16,559.01	108,174.19	16,528.15	118,714.01
6	16,623.57	96,635.62	16,565.55	106,753.72	16,528.8	118,177.95
7	16,631.7	95,858.59	16,566.33	106,238.39	16,529.11	117,620.51
8	16,634.45	95,478.21	16,567.64	106,150.79	16,530.09	116,838.05
9	16,639.89	94,982.78	16,568.54	105,574.55	16,531.1	116,412.19
10	16,642.12	94,732.9	16,571.72	105,033.09	16,531.76	115,674.13
11	16,651.62	94,356.45	16,573.02	104,544.22	16,532.64	115,318.3
12	16,657.77	93,981.65	16,577.29	103,796.67	16,533.05	114,926.11
13	16,678.28	93,128.06	16,578.61	103,050.43	16,534.71	114,561.35
14	16,659.62	93,633.91	16,580.08	102,619.07	16,535.94	114,283.03
15	16,685.06	92,700.67	16,580.34	102,315.13	16,537.21	113,938.91
16	16,694.98	92,243.69	16,582.11	102,041.3	16,538.28	113,651.73
17	16,709.69	91,524.65	16,584.72	101,603.88	16,541.24	113,013
18	16,719.52	91,109.94	16,587.14	101,153.27	16,542.72	112,503.05
19	16,719.52	91,109.94	16,592.91	10,0641.74	16,544.08	112,240.5
20			16,595.69	99,699.83	16,551	110,848.22
21			16,597.53	99,366.72
Case (3)
Solution Number	35% ≤ PR ≤ 40%		40% ≤ PR ≤ 50%		50% ≤ PR ≤ 60%
	CO2/kg	Cost/CNY	CO2/kg	Cost/CNY	CO2/kg	Cost/CNY
1	12,795.25	72,712.57	12,661.18	77,418.01	12,621.88	86,671.82
2	12,773.54	73,276.82	12,656.76	77,441.21	12,621.03	86,918.29
3	12,761.54	73,504.08	12,654.88	77,845.11	12,620.8	87,091.2
4	12,739.02	73,636.25	12,653.61	78,216.09	12,619.55	87,439.58
5	12,721.35	73,924.12	12,651.35	78,468.9	12,619.05	87,852.52
6	12,709.43	74,118.92	12,650.52	78,637.57	12,616.56	88,431.36
7	12,700.45	74,852.8	12,649.98	78,983.97	12,615.82	88,795.8
8	12,697.53	75,081.87	12,649.05	79,059.65	12,615.02	89,090.96
9	12,687.1	75,346.38	12,642.14	79,704.56	12,613.87	89,744.3
10	12,680.8	75,691.11	12,641.3	80,052.81	12,612.62	90,377.25
11	12,677.08	76,069.06	12,640.41	80,325.04	12,609.91	91,248.27
12	12,671.7	76,434.38	12,640	80,655.42	12,609.62	91,760.12
13	12,663.15	76,691.65	12,639.49	80,801.29	12,609.57	92,065.52
14	12,661.27	76,990.67	12,638.24	81,114.03	12,607.43	92,558.71
15			12,637.55	81,436.05	12,607.24	92,979.5
16			12,636.98	81,474.49	12,606.15	93,486.78
17			12,635.71	81,933.67	12,604.74	94,108.97
18			12,634.4	82,478.35	12,604.17	94,457.95
19			12,633.25	82,782.7	12,603.82	94,674.42
20			12,632.21	83,197.97	12,602.87	95,025.05
21			12,629.02	84,284.16
22			12,627.63	84,839.62
23			12,626.99	84,951.18
24			12,625.79	85,439.21
25			12,624.98	85,830.62
26			12,624.57	85,996.64

.

7. Conclusions

In this paper, two goals of carbon emission and cost are firstly modeled by means of dual-objective optimization, and the impact of relevant status quo on these two goals is considered in the model. Secondly, in the solution of the model, this paper analyzes the shortcomings of the traditional NSGA-II algorithm and makes related improvements. Finally, the relationship between carbon emissions, cost, and prefabrication rate is analyzed based on actual examples. The conclusions are drawn as follows:

• Carbon emission and cost are two conflicting goals, and dual-objective optimization can make them reach a balanced state, creating both economic and environmental benefits. When establishing a dual-objective model, the impact of carbon trading on component costs needs to be considered.
• The traditional NSGA-II algorithm has the problem of low quality of the parent and offspring population. This paper proposes to optimize the population by improving the selection method, crossover operator and mutation operator, and redesigning the algorithm.
• From the case, after the dual-objective optimization, by increasing a small amount of cost, a better carbon-reduction effect is achieved when the prefabrication rate is 35–40%. When the prefabrication rate is greater than 40%, for a better carbon emission reduction effect, you need to increase the cost significantly.
• For enterprises, when the prefabrication rate is between 35% and 40%, the maximum environmental benefit can be obtained at the minimum economic cost. Enterprises can make more reasonable decisions based on the optimal solution set after optimization and the actual engineering situation. For the government, when the prefabrication rate is between 35% and 40%, popularizing prefabricated buildings for energy saving and emission reduction can improve the enthusiasm of enterprises to reduce carbon emissions. In addition, the government can refer to the optimal solution set to establish building carbon reduction policies that make it easier for companies to implement.
• The difference in insulation performance was not considered in this study because the insulation properties of cast-in-place and prefabricated components have been less studied. Insulation performance can have an impact on the carbon emission and cost during the use of the building. Therefore, the impact of insulation performance of different members on the overall cost and carbon emission reduction of the building can be considered in subsequent studies.