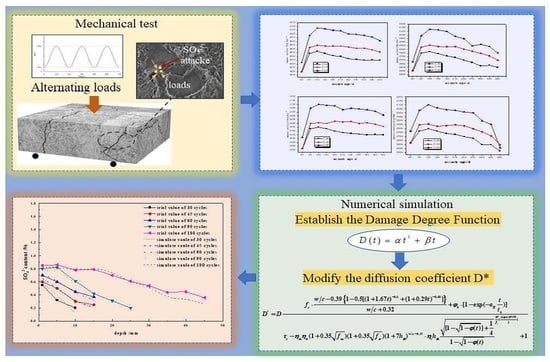
Numerical Simulation of Concrete Attacked by Sulfate under Drying–Wetting Cycles Coupled with Alternating Loads

Abstract

Concrete structures such as rigid pavements, tunnels, and runways at airports are usually subject to fatigue traffic loading during their service life. Research on the aftereffects of drying–wetting cycles coupled with alternating loads on concrete erosion in saline–alkali and coastal areas is of considerable practical importance. For this study, we utilized specimens of dimensions 100 mm × 100 mm × 400 mm with strength ratios of C30, C40, and C50. We incubated the concrete samples in a 24 h/24 h drying–wetting cycle with sodium sulfate solutions of different concentrations as we applied alternating loads. We conducted ultrasonic wave velocity tests every 30 days from the 60th day of the experiment to determine the change in the sound velocity of the concrete over the course of 360 days. In addition, we examined the invasion depth of SO₄²⁻ with time. Based on the change in sound velocity, we developed the damage degree function, and we modified the diffusion coefficient of SO₄²⁻ in concrete in accordance with the coupling of drying–wetting cycles and alternating loads. We conducted a simulation on SO₄²⁻ penetration depth, and the results were in reasonable agreement with those obtained by experimental testing.

1. Introduction

An external sulfate attack on concrete structures is one of the primary causes of structural deterioration [1,2,3,4,5]. Infiltrations of sulfate into concrete constructions produce expansion products such as ettringite and gypsum when it reacts with the hydration products produced by the cement [6,7,8]. Expansion products fill pores and initially increase the strength of the concrete structures [9]. However, later in time, the excessive gypsum and ettringite in the concrete eventually lead to cracking and expansion, and the service life is greatly reduced [10,11]. Concrete that is exposed to drying–wetting cycling conditions is more seriously damaged by sulfate than concrete in a persistently moist environment [12,13,14]. Moreover, concrete buildings, particularly road structures, are not only attacked by sulfate ions in the environment but are also subject to traffic loads during their service life [15]. The combined effect of alternating loads caused by traffic flow and cyclic sulfate attacks caused by tides and precipitation is increasingly challenging the durability and service life of roads, bridges, and buildings in eastern coastal areas, and the same problem is also occurring in the Gansu and Qinghai provinces in Western China [16]. Consequently, studying how sulfate affects concrete under drying–wetting cycles coupled with alternating loads is of paramount practical importance.

Initially, researchers studied sulfate attack by directly soaking concrete specimens in sulfate solutions without any other operations. However, continuous immersion in a sulfate solution does not simulate real road conditions. The authors of [17,18,19,20,21] investigated the durability, functional performance, and damage process of concrete subjected to sulfate attacks under drying–wetting cycles and bending loads. Both drying–wetting cycles and loads could cause concrete that is exposed to sulfate-rich environments to be damaged. Variations in the testing conditions have led to differing understandings of how drying–wetting cycles and loading affect the deterioration of concretes. According to Gao and colleagues [7], the maximum stress level of the flexural load determines whether drying–wetting cycles or flexural loads are the influential factors that dictate the outcome of sulfate attacks on concrete. Liu [22] found that fatigue loads can lead to an acceleration of a sulfate attack by causing cracks and sulfate migration, which leads to more SO₄²⁻ entering the pore solution and a greater expansion force. Additionally, the cations of sulfate and the sulfate solution of different concentrations also impact the promotion effect of drying–wetting cycles and loads on sulfate attacks [23,24,25].

The development of computer technology has made possible numerical simulations of concrete performance decay under complex environments [24,26]. Researchers have constructed a variety of mathematical models to study the sulfate erosion of concrete [27,28,29,30,31]. Yin [32] developed a coupled chemical–mechanical damage constitutive model to describe the erosion process from sulfate diffusion evolution in concrete to volume expansion caused by reaction products to mechanical and chemical damage. Based on Li’s [33] model, sulfate diffusion inside concrete is simulated, along with strength degradation as a result of an external sulfate attack and drying–wetting cycles. Current research on the sulfate attack of concrete has focused on concrete subjected to drying–wetting cycles and loads. However, the loads during the experiments or model are mainly static or compressive cyclic loads. However, concrete structures, such as pavements and bridge decks, are subject to alternating loads. Until now, few studies have focused on models of concrete attacked by sulfate under drying–wetting cycles coupled with alternating loads.

For this study, we conducted long-term sulfate attack tests of concrete by independently using a concrete sulfate attack test device under drying–wetting cycles coupled with alternating loads. We subjected concrete samples with varying sulfate concentrations, alternating loads stress levels, and erosion times to ultrasonic nondestructive testing. We established a damage degree function based on the change in the wave velocity, and we corrected the diffusion coefficient of SO₄²⁻ in concrete under the coupling of drying–wetting cycles and alternating loads based on the established damage degree function. Based on a concrete model of sulfate erosion constructed by predecessors, we discussed and verified the related numerical simulation.

2. Materials and Methods

2.1. Materials

In this study, we used Chinese-standard early-strength Portland cement (P.C 42.5 R) produced by HaiLuo Co., Ltd. Baoji City, Shaanxi province, China; the mineralogical composition of the cement is shown in

Table 1. Chemical composition of cement (wt%).

SiO2	Al2O3	Fe2O3	CaO	MgO	SO3	Na2Oeq	LOSS	f-CaO
21.01	4.55	2.99	62.4	1.79	2.93	0.58	3.14	0.61

. We used nature limestone with a maximum size of 25 mm as coarse aggregate and river sand with a fineness modulus of 2.6. The technical performance indicators of the coarse aggregate are shown in

Table 2. Aggregate performance.

Density (kg/m3)	Crushing Value (%)	Water Absorption (%)	Elongated Particle Content (%)
2699	9.41	1.37	3.6

. We used the polycarboxylic acid water-reducing agent produced by Shaanxi JiaoKe New Material Co., Ltd. of Xi’an, China as the concrete admixture. We used running water to mix the above materials.

2.2. Concrete Mixing Ratio

According to the JGJ 55-2011 specification for the mix proportion design of ordinary concrete, we cast 100 mm × 100 mm × 400 mm concrete specimens, and the water–cement ratios of the concrete specimens were 0.55, 0.40, and 0.28 with design strength grades of C30, C40, and C50, respectively. We prepared a total of 27 specimens. Three specimens made up each group for each water–cement ratio and Na₂SO₄ solution concentration. We demolded all the specimens after 24 h and cured them for 28 d in a standard curing tank at a temperature of 20 ± 2 °C and 95% relative humidity. The concrete mixing ratio is listed in

Table 3. Concrete proportion and performance.

Strength Grade	Water (kg/m3)	Cement (kg/m3)	Fine Aggregate (kg/m3)	Coarse Aggregate (kg/m3)	Water Reducer (%)	w/c
C50	145	518	506	1281	1.4	0.28
C40	202	505	593	1150	/	0.40
C30	193	357	691	1159	/	0.55

.

2.3. Testing Methods

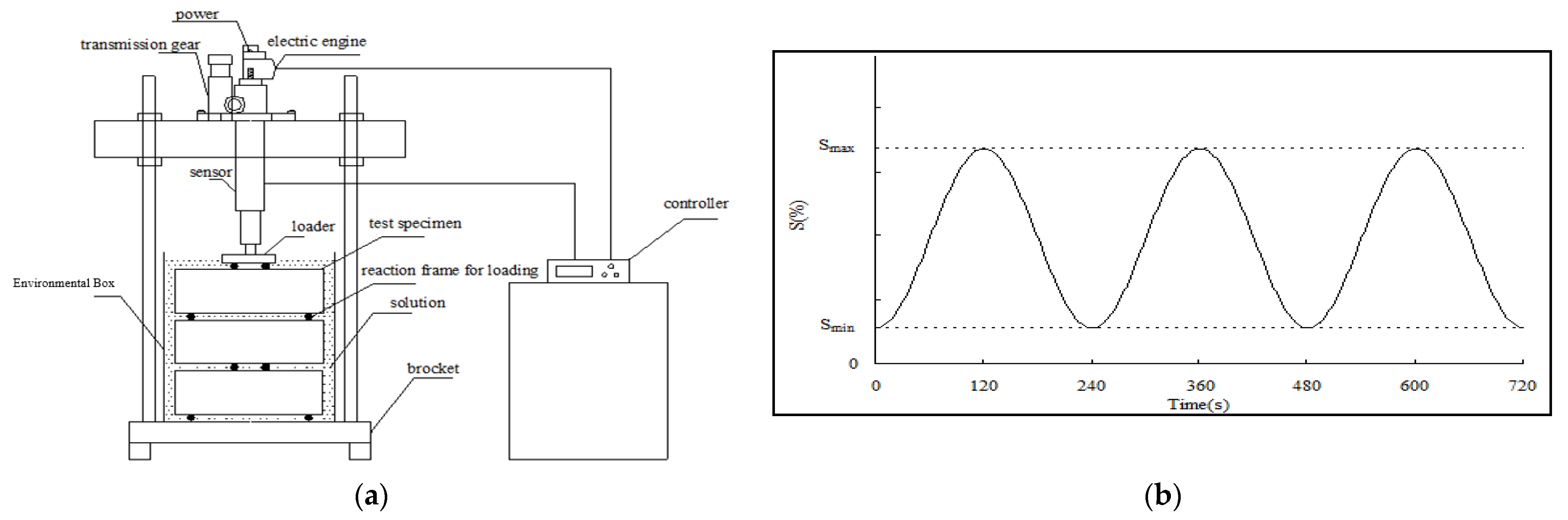
2.3.1. Experiment on Sulfate Attack of Concrete under Drying–Wetting Cycles Coupled with Alternating Loads

The erosion solution was a Na₂SO₄ solution with mass concentrations of 0, 5, and 10%. Before the exposure experiments, we covered the specimens with epoxy resin on all four surfaces except for the two smaller opposite surfaces (100 × 100) to ensure the infiltration direction of SO₄²⁻. After immersion in a sodium sulfate solution for 24 h at room temperature, we allowed the concrete specimens to dry in the air for 24 h. We repeated the drying–wetting cycle until we reached a predetermined time. Figure 1 shows the test device for the sulfate attack of concrete under drying–wetting cycles coupled with alternating loads. The loading frequency of the alternating load was 400 times/day. We stressed the alternating loads at a maximum of 0.5 and 0.7 and a minimum of 0.2 based on the ultimate stress of structural failure. Figure 2 illustrates the schematic diagram and load spectrum of the attack test device.

2.3.2. Sulfate Concentration Test

After an attack period, we used a drill to obtain powder from different depths of the concrete, and we passed the powder through a 0.08 mm sieve. We obtained 5 g of powder and dissolved it in 100 mL of deionized water. We then added diluted hydrochloric acid (6 mol/L) to the solution and boiled it. We filtered the solution after cooling. After dissolving the filtrate to 200 mL and boiling it, we stirred 10 mL of 10% barium chloride solution into the solution. After a full reaction, we left the solution to stand for 4 h and then filtered it. We wrapped the precipitate in filter paper and placed it in a crucible. This was assigned a weight of m₁. We then heated the crucible in a high-temperature furnace to 800 °C. After heating, the organic matter in the filter evaporated into a gas, and we dissolved the remaining ash in acid. Then, we removed the crucible and cooled it to room temperature, and we recorded the new weight as m₂. The sulfate ion content can be calculated according to Equation (1), whereby the powder from the same depth of three specimens as a group and the average SO₄²⁻ concentration of a group is the result.

$$\begin{array}{cc}{W}_{{\mathrm{SO}}_4^{2-}}& =1.2\times \frac{0.343\times (m_2-m_1)}{m}\times 100\%\hfill \\ & =0.4116\times \frac{(m_2-m_1)}{m}\times 100\%\hfill \end{array}$$

(1)

where m is the weight of the powder (g); m₁ is the weight of the crucible (g); m₂ is the weight of the crucible with precipitate contained (g); 0.343 is the conversion coefficient of barium sulfate to sulfur trioxide; and 1.2 is the conversion coefficient of sulfur trioxide to sulfate ions.

3. Analysis, Mathematical Derivation, and Simulation

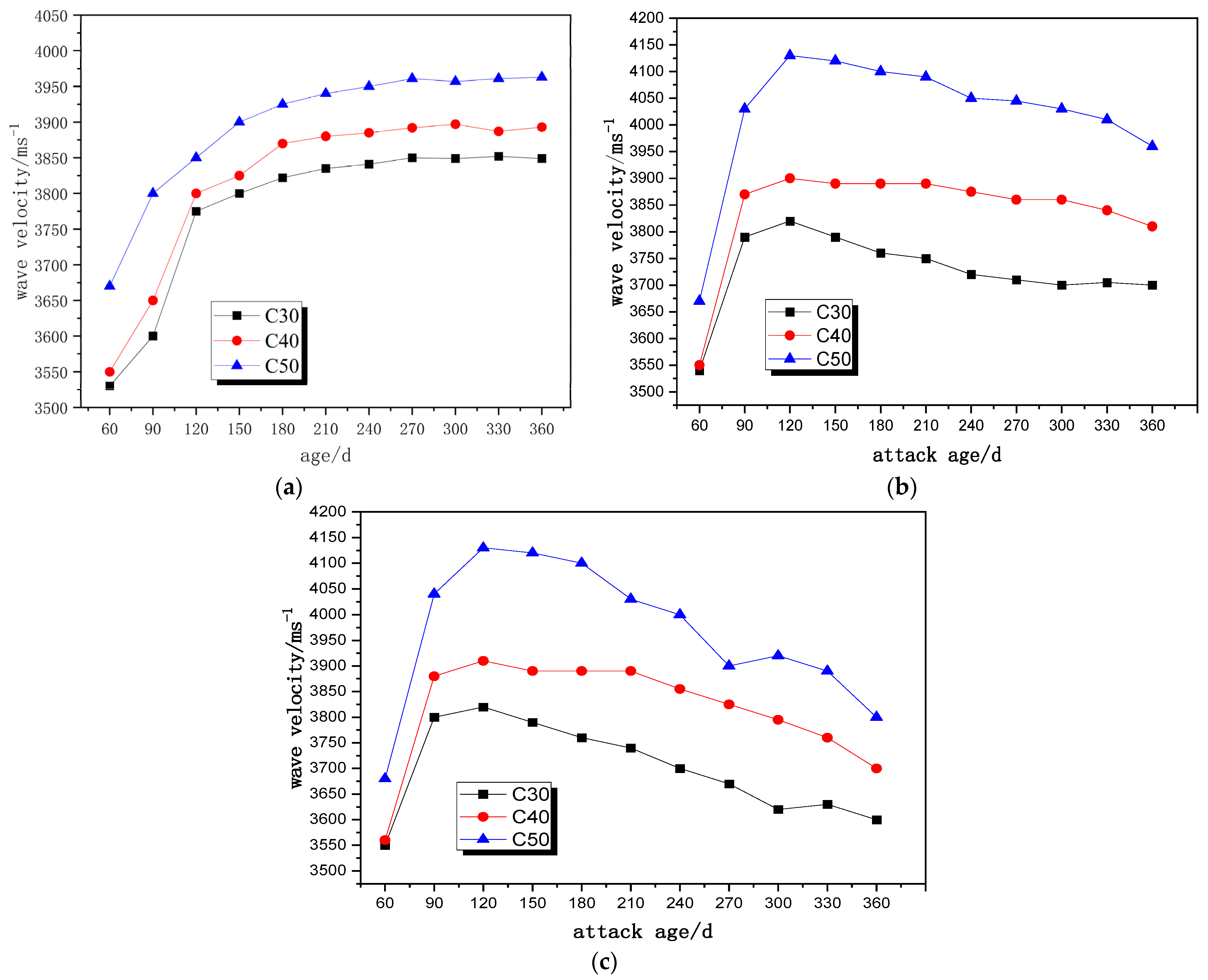
3.1. Ultrasonic Wave Velocity Test

Figure 3 and Figure 4 show the wave velocity curves of concrete subjected to a sulfate attack under drying–wetting cycles coupled with alternating loads. The wave velocity changed over time for concrete with different strength grades, but generally increased during inception and then decreased. This occurred because the attack products had a filling effect on the concrete structure during the early stages of the attack, resulting in increased compactness. The wave velocities of the C30, C40, and C50 corroded concretes generally peaked at about 120 days under drying–wetting cycles and alternating loads, and the highest wave velocities of the C50 corroded concrete exceeded 4100 ms⁻¹. In the period prior to 120 days, the density of the concrete continuously increased under the combined action of the hydration of raw materials and attack products, and the wave velocity curve showed an upward trend. If the attack time exceeded 120 days, the wave velocity curve of the concrete began to decrease; at this time, internal cracks appeared in the concrete and damage occurred, which reduced the performance of the concrete. Figure 5 shows the microstructure of the C30 concrete at the attack age of 120 d and 360 d. The structure of the concrete was dense at the early stage of the attack. However, when the attack age was 360 d, obvious cracks were present in the structure because the expansion product’s ettringite gradually increased.

As shown in Figure 3 and Figure 4, when no sulfate attack occurred, the wave velocity increased at an early curing age and then tended to plateau. When the concrete suffered a sulfate attack, the wave velocity first increased and then decreased. As the alternating loads’ stress level remained the same for the concrete of different strength grades, the wave velocity decreased faster under drying–wetting cycles with a higher sulfate concentration (10%) compared to concrete with a lower sulfate concentration (0% and 5%). Figure 3a and Figure 4b both demonstrate that, when the sulfate concentration was high, the load stress level had little impact on the wave velocity, and alternating loads played a minimal role in this process. Nevertheless, by comparing Figure 3c with Figure 4c, we can see that, when the sulfate concentration was maintained at a high level, the 360 d wave velocity of the concrete of each strength grade when alternating loads were applied was greater at low stress levels (0.5–0.2) than at high stress levels (0.7–0.2). In the presence of high stress-level alternating loads, the 360 d wave velocities of the corroded concrete C30, C40, and C50 were very similar to one another. Thus, coupling the drying–wetting cycles with high sulfate concentrations and alternation loading with high stress accelerated concrete corrosion by sulfate and severely damaged the concrete.

Figure 5 shows the appearance of the C30 concrete at 60 d, 180 d, and 360 d when it suffered a 5% sulfate attack and the alternating loads were stressed at a maximum of 0.7 and a minimum of 0.2. From Figure 5, it can be seen that the surface of the concrete gradually peeled as the attack age grew. When the attack age is 180 d, the surface of the concrete becomes loose and porous. The surface of the concrete peeled off in a large area at 360 d. At the same time, under the action of alternating load, microcracks also appear in the concrete, as shown in Figure 6. Sulfate corrosion causes the concrete surface to become loose, and alternating loads cause microcracks to sprout and expand. The original defects evolve from an independent state to a connected state, eventually leading to the failure of the concrete.

3.2. Establishment of Damage Degree Function

The damage degree is the ratio between the change value of any characteristic parameter value and the initial value of concrete and can be expressed as

$$d=\frac{\Delta R}{R_0}$$

(2)

where $d$ is the degree of damage, $\Delta R$ is the change value of the characterization parameters (ultrasonic wave velocity, strength, mass, dynamic elastic modulus, etc.), and $R_0$ is the characterization parameter of concrete without damage.

In accordance with this formula, the change function relation of the concrete damage degree function $D(t)$ with time t can be determined from the test results of the concrete sound velocity change shown in Figure 3 and Figure 4.

$$D(t)=\alpha t^2+\beta t$$

(3)

where $\alpha$ and $\beta$ are fitting coefficients.

Equation (3) illustrates the overall change law for concrete subjected to a sulfate attack under the coupling of drying–wetting cycles and alternating loads. In the early stages of the attack, however, the porosity of the concrete decreased and the compactness increased without any damage to the structure. Thus, a correlation coefficient for material damage evolution is defined as $\eta (t)$. $\eta (t)$ consists of two major parts: the enhancement function $f_E(t)$ of the concrete in the early stage of erosion under cement hydration and the filling of the sulfate attack products, and the damage function $D(t)$ for the concrete at the late attack stage subjected to alternating loads.

In this way, the concrete damage caused by a sulfate attack under the coupling of drying–wetting cycles and alternating loads can be more deeply understood.

According to damage theory and the definition of the material damage evolution correlation coefficient, the dynamic modulus of concrete that was affected by a sulfate attack under drying–wetting cycles coupled with alternating loads can be expressed as

$$E_d=E_0\eta (t)$$

(4)

where $E_d$ is the dynamic modulus of the concrete after a sulfate attack, $E_0$ is the initial dynamic modulus of the concrete, and $\eta (t)$ is the correlation coefficient for the material damage evolution.

The dynamic modulus of concrete is usually considered as

$$E=\frac{\rho (1+\nu )(1-2\nu )}{1-\nu }{V}^2$$

(5)

where $\rho$ is the concrete density, $\nu$ is Poisson’s ratio of concrete, and $V$ is the ultrasonic wave velocity.

Thus,

$$\eta (t)=\frac{(1+\nu )(1-2\nu )}{E_0(1-\nu )}\rho V^2(t)$$

(6)

Determining the relationship between the damage evolution coefficient and the time curve is possible by measuring the change in ultrasonic wave velocity after loading and eroding of the concrete specimens. $\eta (t)$ is the comprehensive damage function consisting of the reinforcement effect of the attack product filling and the failure effect of the expansion stress and the alternating loads. The enhancement function was denoted as $f_E(t)$; thus,

$$\eta (t)=f_E(t)[1-D(t)]$$

(7)

$f_E(t)$ and $D(t)$ must meet the following conditions:

$$\left\{\begin{array}{ll}0<f_E(t)\le {\phi }_0,& f_E\left(0\right)=0\\ 0\le D(t)\le 1-{\phi }_0,& D\left(0\right)=0\end{array}\right.$$

(8)

where ${\phi }_0$ is the initial porosity of the concrete.

The following hypotheses are proposed in accordance with phenomenological theory and the above conditions [34]:

$$\{\begin{array}{l}{f}_E(t)={\phi }_0\cdot [1-\exp (-a_E\frac{t}{t_0})]\\ D(t)=(1-{\phi }_0)\cdot [1-\exp (-a_D\frac{t}{t_0})]\end{array}$$

(9)

where $a_E$ and $a_D$ are fitting coefficients.

Therefore,

$$\eta (t)={\phi }_0\cdot [1-\exp (-a_E\frac{t}{t_0})]\left\{1-(1-{\phi }_0)\cdot [1-\exp (-a_D\frac{t}{t_0})]\right\}$$

(10)

We used the test data shown in Figure 3 and Figure 4 to fit $\eta (t)$, and the results are shown in

Table 4. Fitting parameters for maximum stress level 0.7 and minimum stress level 0.2.

	${\mathit{a}}_{\mathit{E}}$				${\mathit{a}}_{\mathit{D}}$
	w/c				w/c
Concentration	0.28	0.40	0.55	R2	0.28	0.40	0.55	R2
5%	0.0742	0.0541	0.0741	0.9632	0.1647	0.5789	0.0468	0.9125
10%	0.1325	0.0698	0.1362	0.9421	1.2465	0.4621	0.6987	0.9368

and

Table 5. Fitting parameters for maximum stress level 0.5 and minimum stress level 0.2.

	${\mathit{a}}_{\mathit{E}}$				${\mathit{a}}_{\mathit{D}}$
	w/c				w/c
Concentration	0.28	0.40	0.55	R2	0.28	0.40	0.55	R2
5%	0.0734	0.0612	0.0816	0.9457	0.1467	0.5814	0.0519	0.9632
10%	0.1065	0.0715	0.1679	0.9682	1.3914	0.4139	0.7145	0.9528

. R² is the coefficient of determination. The relationship between the damage function and time can be determined by substituting the fitting parameters under different conditions into Equation (9).

3.3. Concrete Porosity Correction Based on Damage Degree

The most fundamental reason for the reduction in durability caused by damage to concrete structures is the initiation and expansion of microcracks within concrete structures during their service life. By taking the damage degree of the concrete as an increasing function of the equivalent porosity of concrete, the correction process of the diffusion coefficient can be simplified, and the calculation efficiency of the SO₄²⁻ transport equation can be increased. If SO₄²⁻ attacks concrete, the pore structure will not only become gradually dense with cement hydration, but it will also gradually fill with the expansion products produced by SO₄²⁻. In instances where the expansion force produced by the expansion product exceeds the tensile strength of the concrete pores, microcracks will form within the concrete, and these microcracks will gradually expand with the action of alternating loads until cracks appear in the concrete. The porosity of concrete is a time function of concrete hydration and damage and is expressed as

$$\phi (t)=D(t)+{\phi }_w$$

(11)

where $\phi (t)$ is the time-dependent porosity of the concrete subject to a sulfate attack under drying–wetting cycles coupled with alternating loads, $D(t)$ is the damage function of concrete with time, and ${\phi }_w$ is the porosity of concrete under hydration, which can be expressed as

$${\phi }_w=f_c\cdot \frac{w/c-0.39h_{\alpha }}{w/c+0.32}$$

(12)

$$f_c={[\frac{{\rho }_c}{{\rho }_s}(\frac{s}{c})+\frac{{\rho }_c}{{\rho }_w}(\frac{w}{c})+\frac{{\rho }_c}{{\rho }_a}(\frac{a}{c})]}^{-1}$$

(13)

$$h_{\alpha }=1-0.5[{(1+1.67t)}^{-0.6}+{(1+0.29t)}^{-0.48}]$$

(14)

where $f_c$ is the volume fraction of the cement in the concrete; $h_{\alpha }$ is the hydration degree of the cement; $t$ is the hydration time of the cement; ${\rho }_c$, ${\rho }_s$, ${\rho }_w$, and ${\rho }_a$ are the density of the cement, sand, water, and air, and $c$, $s$, $w$, and $a$ are the quality of the cement, sand, water, and air, respectively.

By substituting Equations (12)–(14) into (11), the change in concrete porosity due to cement hydration and damage can be calculated:

$$\phi (t)=f_c\cdot \frac{w/c-0.39\left\{1-0.5[{(1+1.67t)}^{-0.6}+{(1+0.29t)}^{-0.48}]\right\}}{w/c+0.32}+{\phi }_0\cdot [1-\exp (-a_D\frac{t}{t_0})]$$

(15)

3.4. Modification of the SO₄²⁻ Diffusion Coefficient D*

Because concrete is a porous medium structure, the diffusion of SO₄²⁻ in concrete is different from that in pure liquid, and the diffusion coefficient is influenced by the internal porosity and the tortuosity degree of the concrete. Fick’s law assumes a constant diffusion coefficient, so the diffusion coefficient of SO₄²⁻ must be corrected to establish the transport model of SO₄²⁻ transport in the concrete with accuracy. The effective diffusion coefficient of SO₄²⁻ in concrete can be expressed as [35]

$$D^{*}=D\frac{\phi (t)}{\tau }$$

(16)

where $D^{*}$ is the effective diffusion coefficient of SO₄²⁻, m²/s; $D$ is the diffusion coefficient of SO₄²⁻ in solution, m²/s; and $\phi (t)$ is the porosity of concrete, %.

Following the determination of the relationship between concrete porosity and time in Section 3.3, fitting the equation relating concrete tortuosity to time is necessary.

The tortuosity degree is defined as the ratio of the shortest path of diffusing ions to the effective transport path, and the tortuosity degree of the concrete under stress can be described as follows [36]:

$${\tau }_c{}^{\sigma }={\tau }_c-{\tau }_c{}^{\frac{\sigma }{f_t}[\frac{sign(\sigma )+1}{2}]}+1$$

(17)

where ${\tau }_c{}^{\sigma }$ is the concrete torsional degree under the stress condition; ${\tau }_c$ is the initial torsional degree of the concrete under the no stress condition; $\sigma$ is the stress of the concrete; $f_t$ is the maximum tensile stress of the concrete; and $sign(\sigma )$ can be described as follows:

$$sign(\sigma )=\left\{\begin{array}{ccc}\hfill 1& \hfill \sigma >0,& under tensile stress\hfill \\ \hfill 0& \hfill \sigma =0,& no stress\hfill \\ \hfill -1& \hfill \sigma <0,& under sterss\hfill \end{array}\right.$$

(18)

A relationship between the initial tortuosity degree of the concrete and the aggregate shape coefficient, the water–cement ratio, and the volume ratio of the sand and stone of concrete exists and can be expressed as [37]

$${\tau }_c={\eta }_{sa}{\eta }_{st}(1+0.35\sqrt{f_{sa}})(1+0.35\sqrt{f_{st}}){\tau }_{cp}$$

(19)

$${\tau }_{cp}={\omega }_{wc}{\eta }_r{h}_{\alpha }\frac{\sqrt{[1-\sqrt{1-\phi (t)}]+\frac{1}{4}}}{1-\sqrt{1-\phi (t)}}$$

(20)

$${\omega }_{wc}={(1+7h_{\alpha })}^{w/c-0.35}$$

(21)

where ${\tau }_c$ is the tortuosity degree of SO₄²⁻ transmission in concrete; ${\eta }_{sa}$ and ${\eta }_{st}$ are the shape coefficients of sand and stone particles, respectively, and generally are 1.368 and 1.087; $f_{sa}$ and $f_{st}$ are the volume ratio of sand and stone, respectively, %; ${\tau }_{cp}$ is the tortuosity degree of hardened cement paste; ${\omega }_{wc}$ is the correction coefficient for the influence of the water–cement ratio on the tortuosity degree of hardened cement paste; ${\eta }_r$ is the shape factor of the cement particles; $h_{\alpha }$ is the hydration degree of the cement; and $\phi (t)$ is the time-dependent porosity of the concrete, %.

In accordance with fracture mechanics theory, we know the following [7]:

$$\frac{\sigma }{f_t}=\sqrt{\frac{\tan [\frac{\pi D_0}{2}]}{\tan [\frac{\pi D(t)}{2}]}}$$

(22)

where $D_0$ is the damage corresponding to the peak stress of the concrete and $D(t)$ is the corresponding damage after the plastic deformation of the concrete.

By combining Equations (19)–(24), we can obtain the relation function of the concrete’s overall tortuosity degree with time:

$$\begin{array}{c}{\tau }_c{}^{\sigma }={\tau }_c-{\eta }_{sa}{\eta }_{st}(1+0.35\sqrt{f_{sa}})(1+0.35\sqrt{f_{st}}){(1+7h_{\alpha })}^{w/c-0.35}\\ \cdot {\eta }_r{h}_{\alpha }{\frac{\sqrt{[1-\sqrt{1-\phi (t)}]+\frac{1}{4}}}{1-\sqrt{1-\phi (t)}}}^{\frac{\sigma }{f_t}[\frac{sign(\sigma )+1}{2}]}+1\end{array}$$

(23)

Clearly, the tortuosity degree of the concrete is also a function of porosity.

Therefore, the effective diffusion coefficient of SO₄²⁻ in concrete is denoted as

$$D^{*}=D\frac{\begin{array}{l}{f}_c\cdot \frac{w/c-0.39\left\{1-0.5[{(1+1.67t)}^{-0.6}+{(1+0.29t)}^{-0.48}]\right\}}{w/c+0.32}\\ +{\phi }_0\cdot [1-\exp (-a_E\frac{t}{t_0})]\end{array}}{\begin{array}{c}{\tau }_c-{\eta }_{sa}{\eta }_{st}(1+0.35\sqrt{f_{sa}})(1+0.35\sqrt{f_{st}}){(1+7h_{\alpha })}^{w/c-0.35}\\ \cdot {\eta }_r{h}_{\alpha }{\frac{\sqrt{[1-\sqrt{1-\phi (t)}]+\frac{1}{4}}}{1-\sqrt{1-\phi (t)}}}^{\frac{\sigma }{f_t}[\frac{sign(\sigma )+1}{2}]}+1\end{array}}$$

(24)

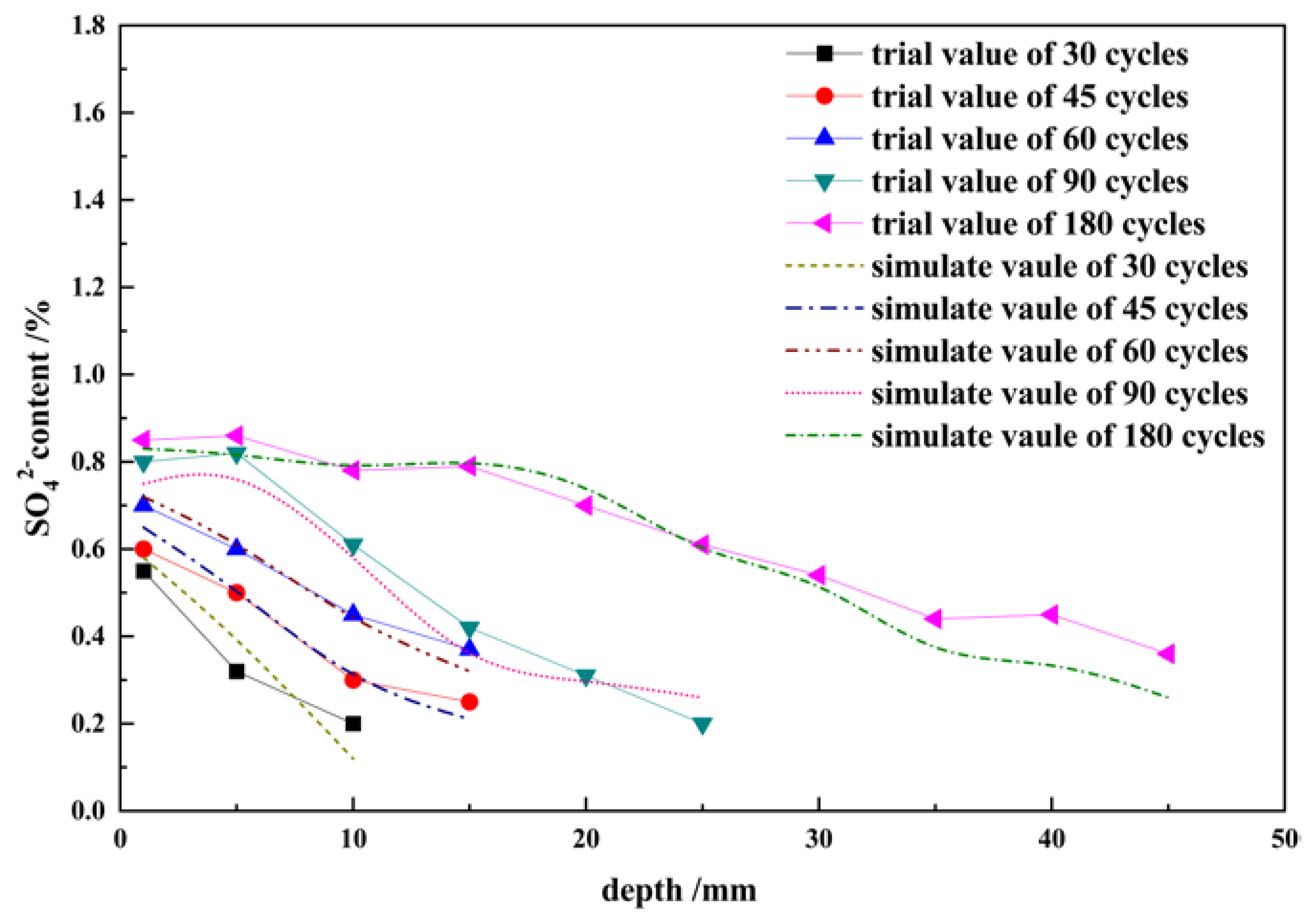
3.5. Simulation of SO₄²⁻ Distribution in Concrete under Drying–Wetting Cycles Coupled with Alternating Loads

We numerically simulated the distribution of SO₄²⁻ in concrete attacked by sulfate under the drying–wetting cycles coupled with alternating loads. The SO₄²⁻ transport–reaction model in concrete can be described as follows [38]:

$$\left\{\begin{array}{l}\frac{\partial C}{\partial t}=D^{*}\frac{{\partial }^{2}C(x,t)}{\partial x^2}-k_v\cdot c_{{\mathrm{Ca}}^{2+}}\cdot c\\ \\ C(x,0)=C_0,[x\in 0,L] \hspace{0.17em}\mathrm{Initial} \mathrm{conditions}\\ C(0,t)=C_s,[0<t<T] \mathrm{Boundary} \mathrm{conditions}\end{array}\right.$$

(25)

$k_v$ is the rate of the sulfate ion consumption, 3.05 × 10⁻⁸ m³·mol⁻¹·s⁻¹; $c_{{\mathrm{Ca}}^{2+}}$ is the concentration of the calcium ions in the solution, 21.25 mol/m³; and $c$ is the concentration of the sulfate ions consumed in the matrix.

We conducted tests to determine the amount of SO₄²⁻ in concrete with a water–cement ratio of 0.28, maximum stress level of 0.5, and minimum stress level of 0.2. We set the drying–wetting cycles system to 24 h of wetting and 24 h of drying, and the sulfate attack concentration was 5%.

Figure 7 illustrates a comparison between the simulation and test results. We found a reasonable agreement between the calculated and experimental results. In the early phases of the sulfate attack, the test results of the surface SO₄²⁻ were slightly larger than the simulation figures, which occurred because of the rapid evaporation of water at the early stages of the attack, resulting in excessive SO₄²⁻ remaining on the surface. The concrete’s surface layer gradually spalled off with the increase in the drying–wetting cycles, resulting in a lower SO₄²⁻ content in the late stage of erosion than in the simulated condition.

4. Conclusions

(1)

As demonstrated by the ultrasonic wave velocity test, the drying–wetting cycles played an important part in the attack process of concrete induced by sulfate with a low sulfate concentration. The effect of the drying–wetting cycles with a high sulfate concentration coupled with the alternating loads with a high stress level caused the concrete to deteriorate faster and to a higher degree under sulfate attack.

(2)

We constructed a damage degree function of the concrete attacked by sulfate under drying–wetting cycles coupled with alternating loads using ultrasonic wave velocity testing and the concept of the relative elastic modulus, and we determined the key coefficients $a_D$ and $a_E$ by fitting the results.

(3)

In relation to the damage degree function, we modified the change function of the concrete porosity under drying–wetting cycles and alternating loads. Additionally, we modified the diffusion coefficient of SO₄²⁻ in conjunction with the concept of tortuosity. We numerically simulated the distribution of SO₄²⁻ in concrete, and the calculated results fitted well with the experimental data.

(4)

The model for the prediction of concrete sulfate attack depth under drying–wetting cycles coupled with alternating loads was developed. This model considers the effect of traffic loading and provides a complement to the study of the damage theory of concrete in complex environments.