Initial Shape Analysis and Experimental Study of Air-Supported Membrane Structure Considering Cable–Membrane Contact
Abstract
1. Introduction
2. Establishment of Contact Model
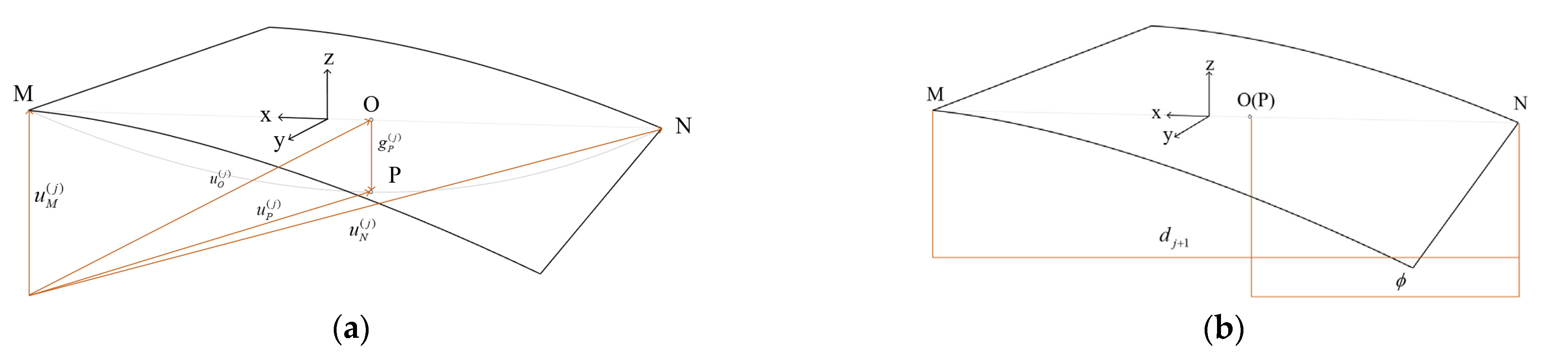
2.1. Point-Surface Contact Pair
2.2. Contact State
2.3. Contact Algorithm
2.4. Numerical Method
3. Numerical Simulation
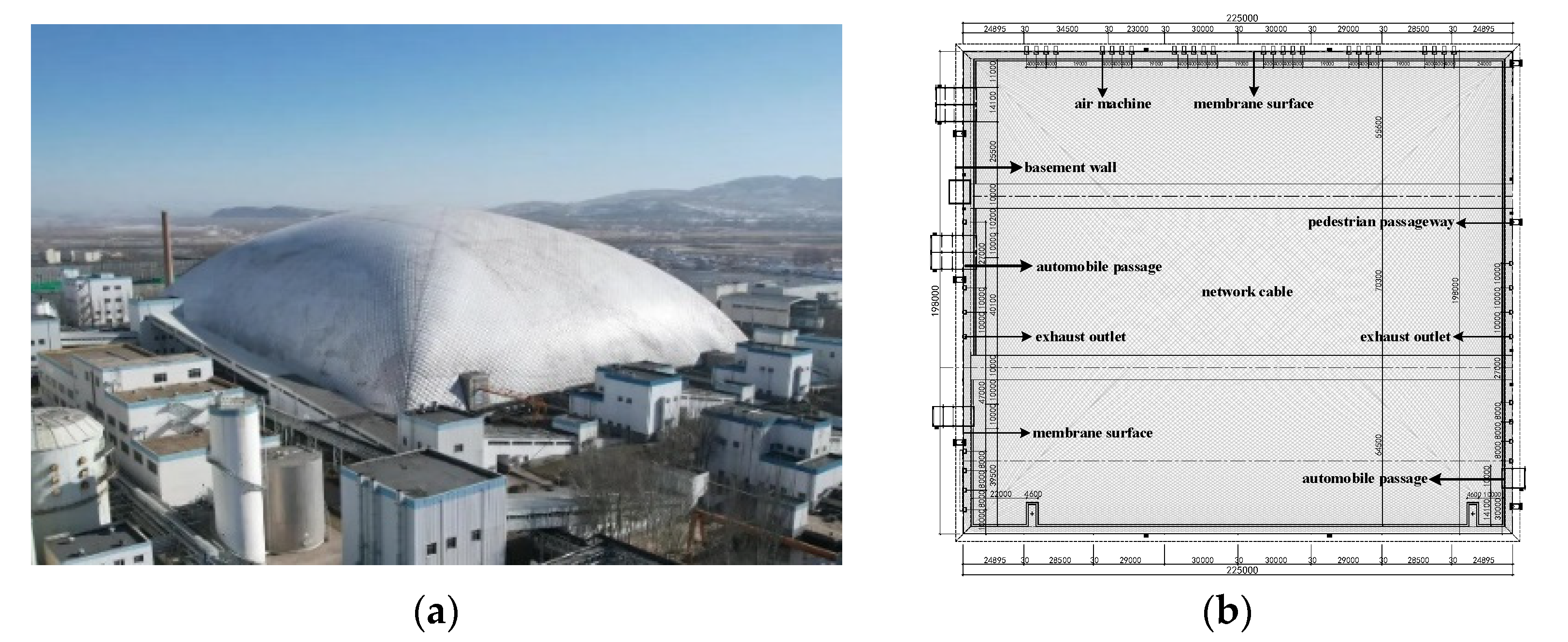
3.1. Model Simplification
3.2. Parameter Setting
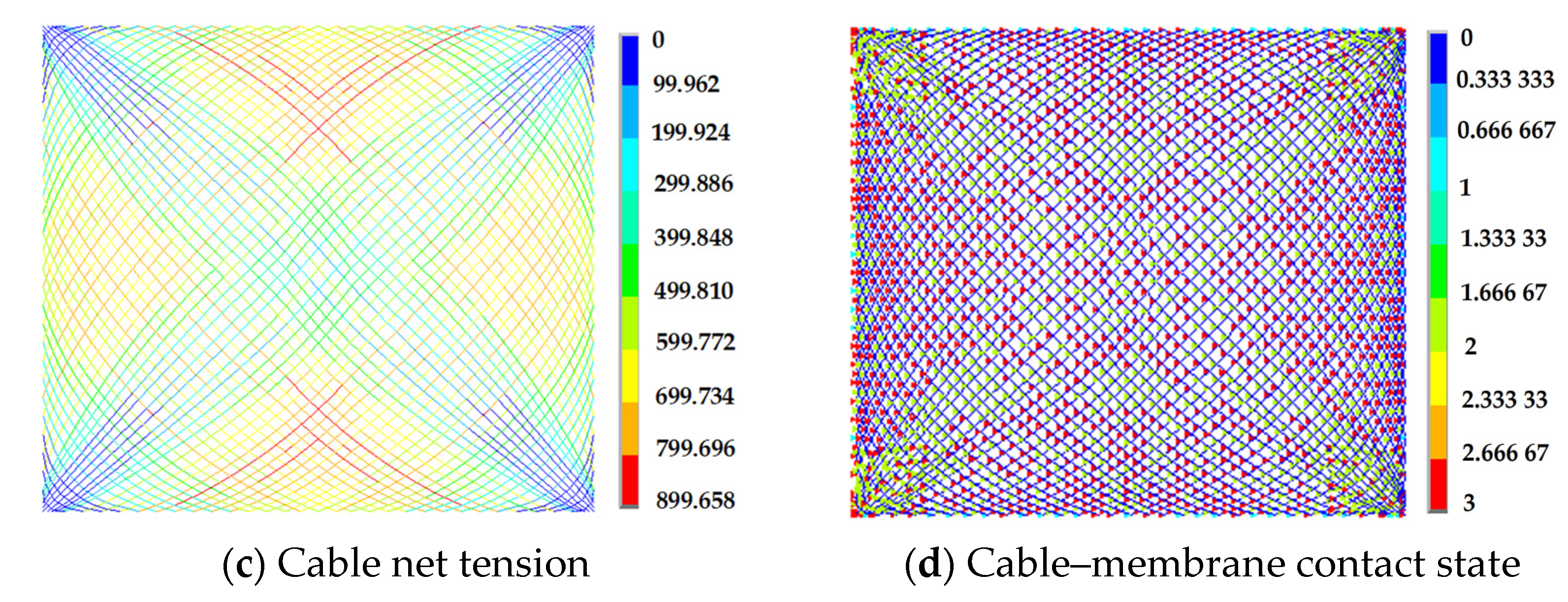
3.3. Analysis of Simulation Results
4. Experimental Verification
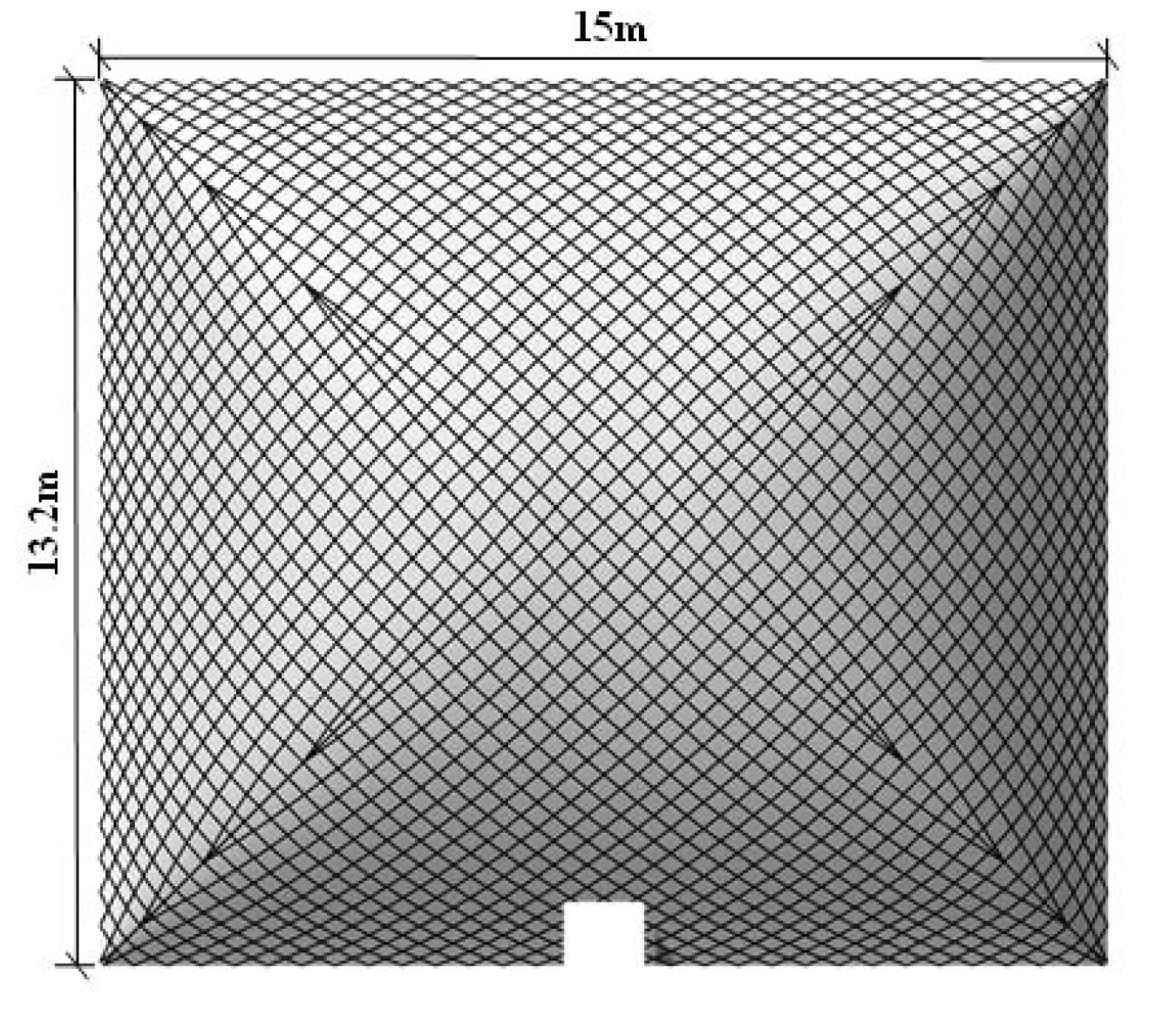
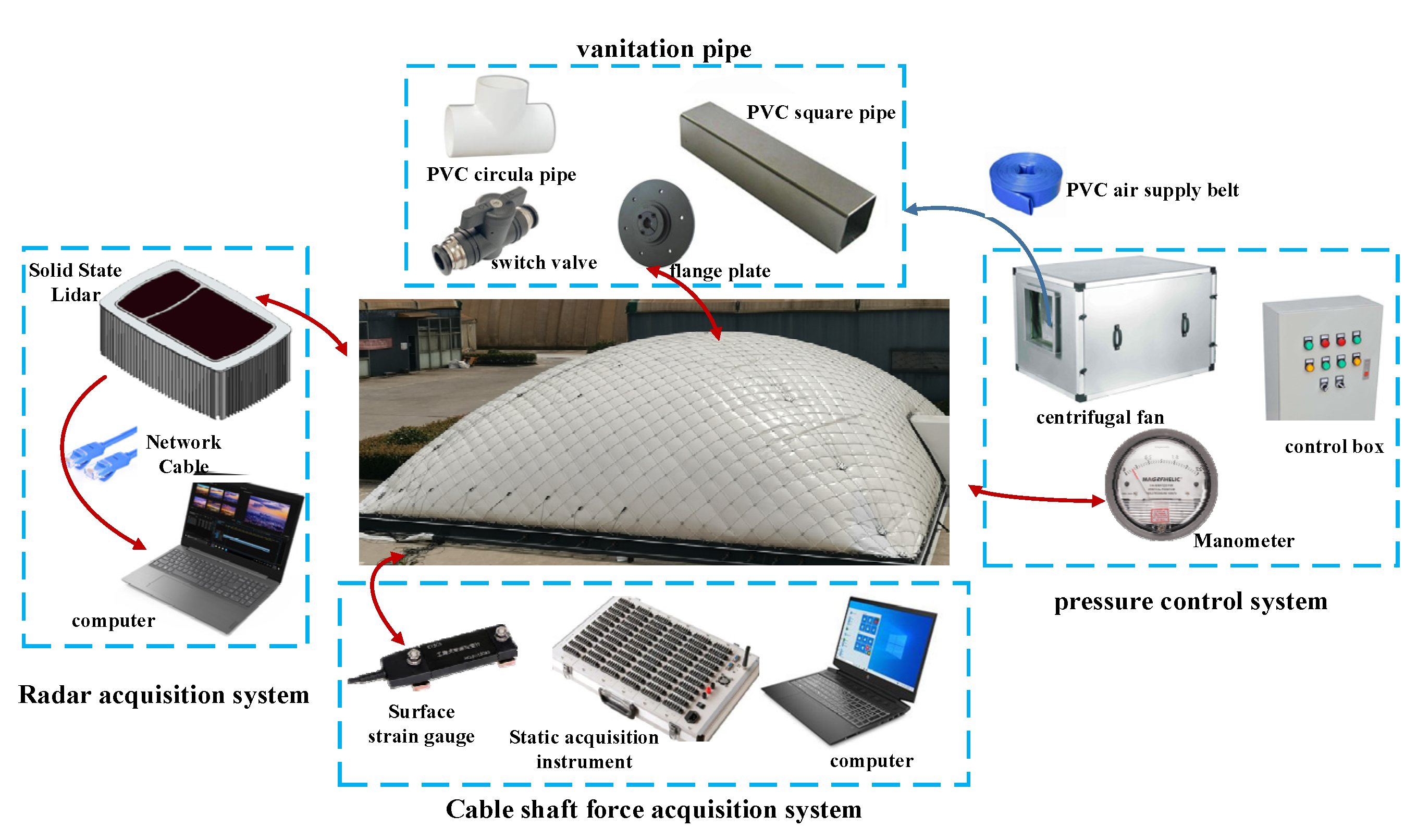
4.1. Model Design and Installation
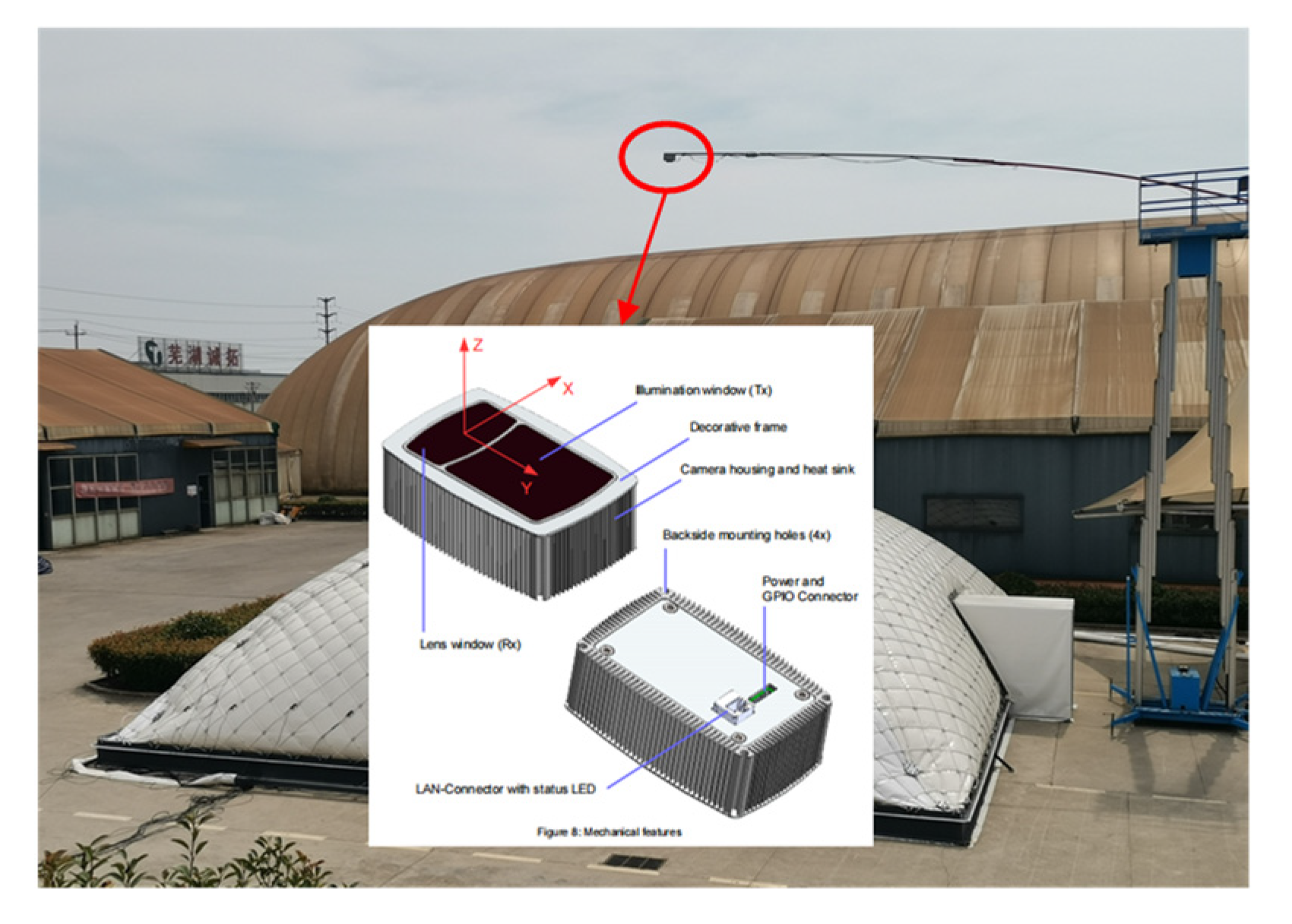
4.2. Measuring Instrument
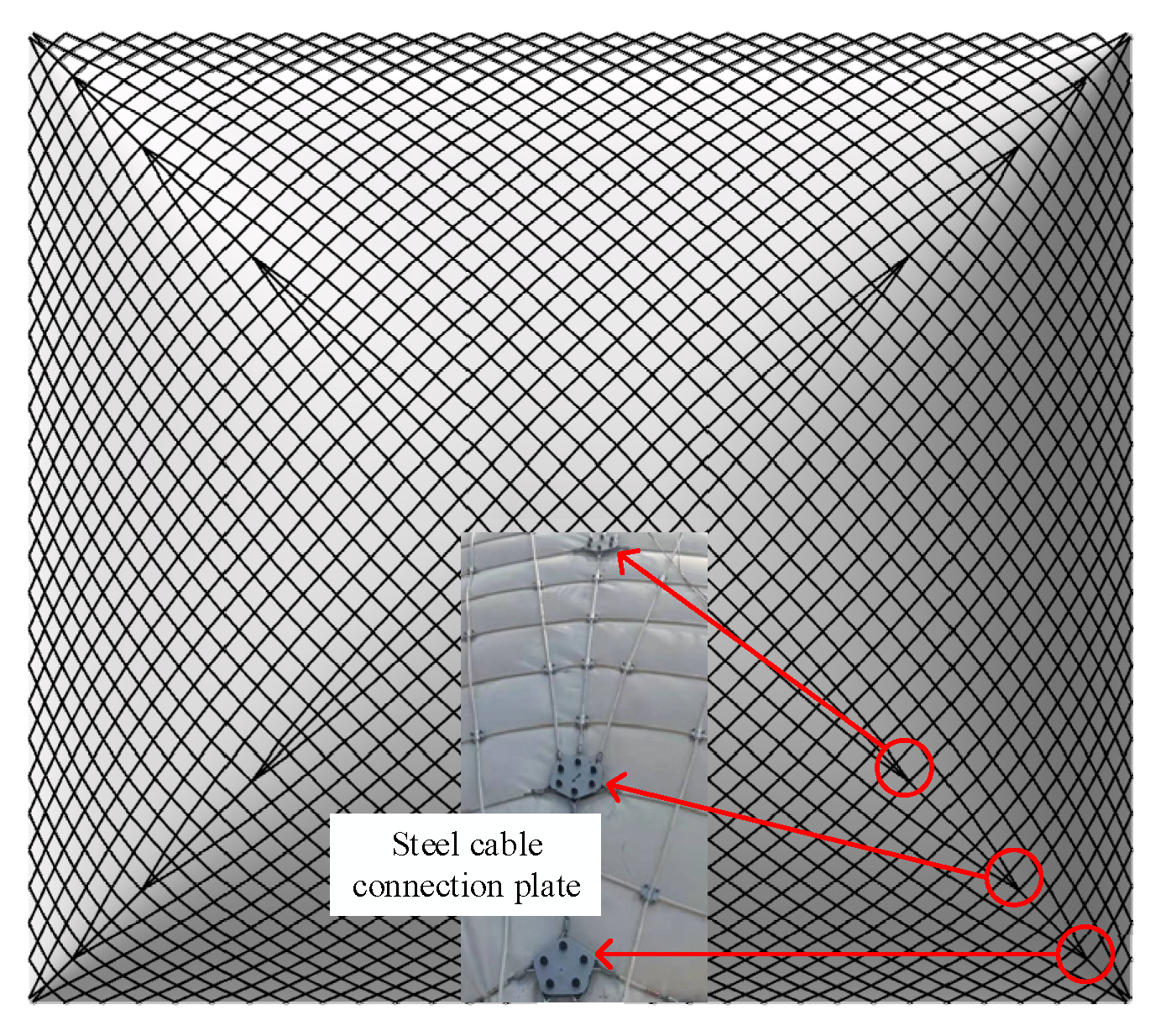
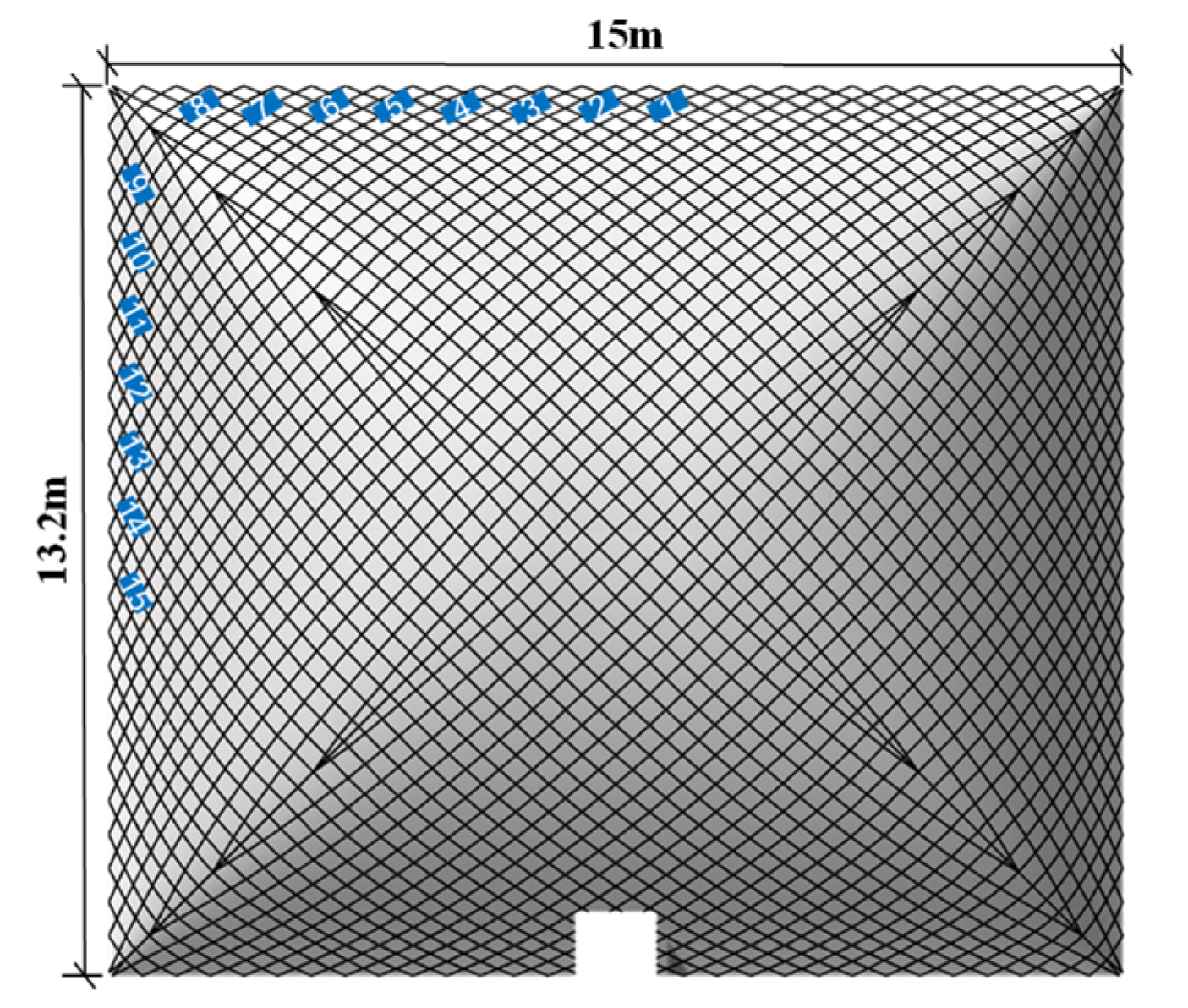
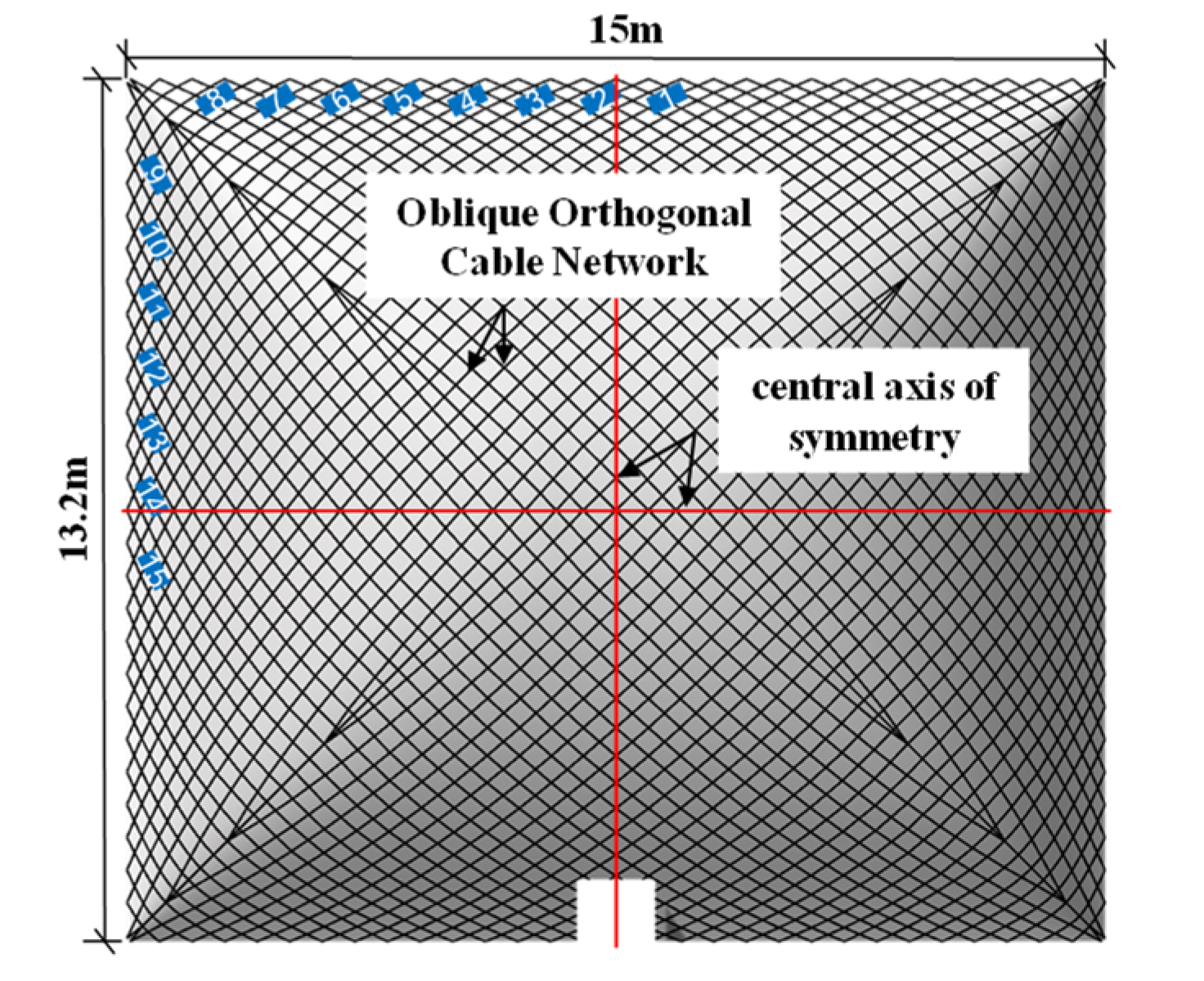
4.3. Measurement Point Arrangement
4.4. Test Process
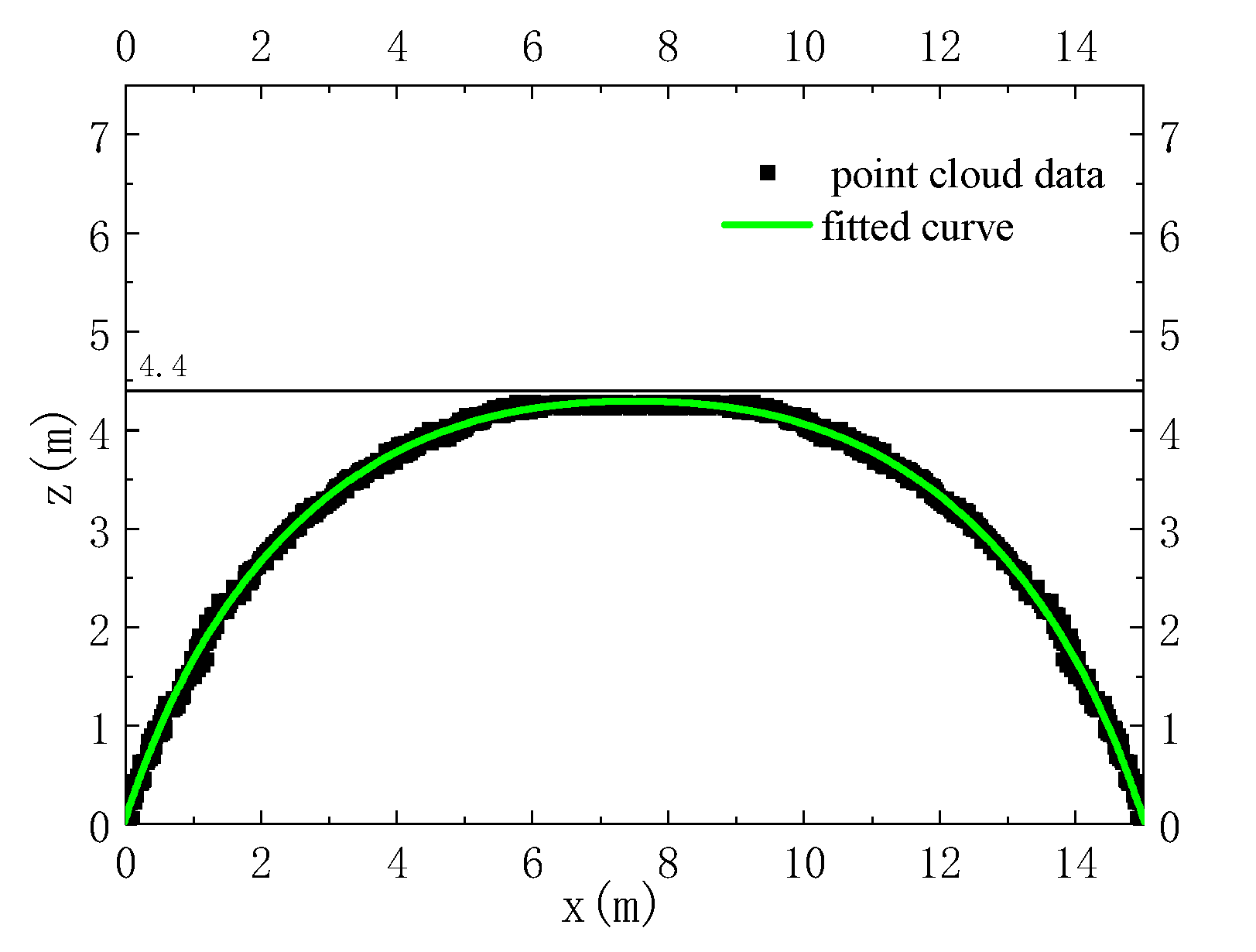
4.5. Test Results
5. Comparative Analysis of Results
5.1. Comparison of the Tensile Force
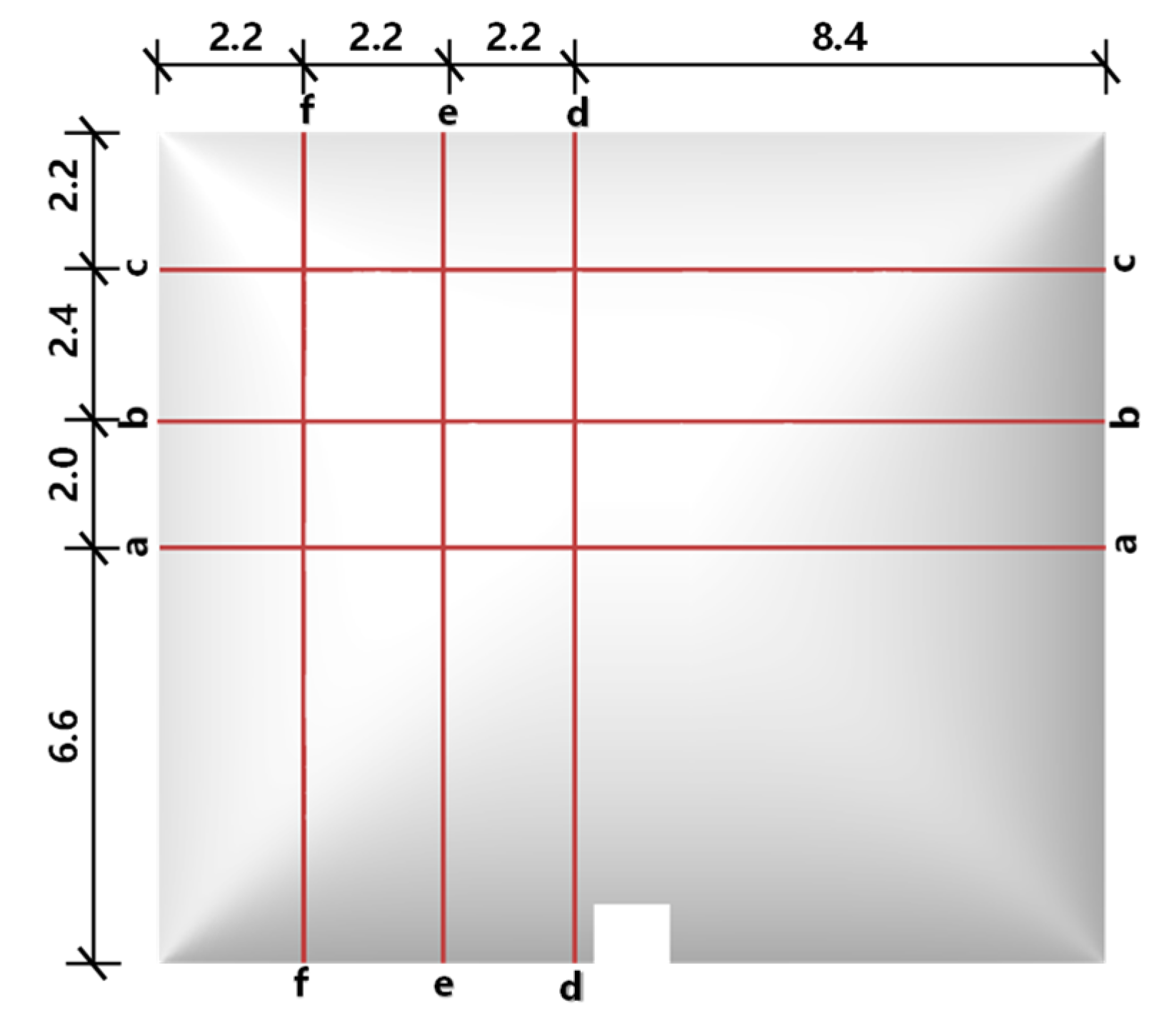
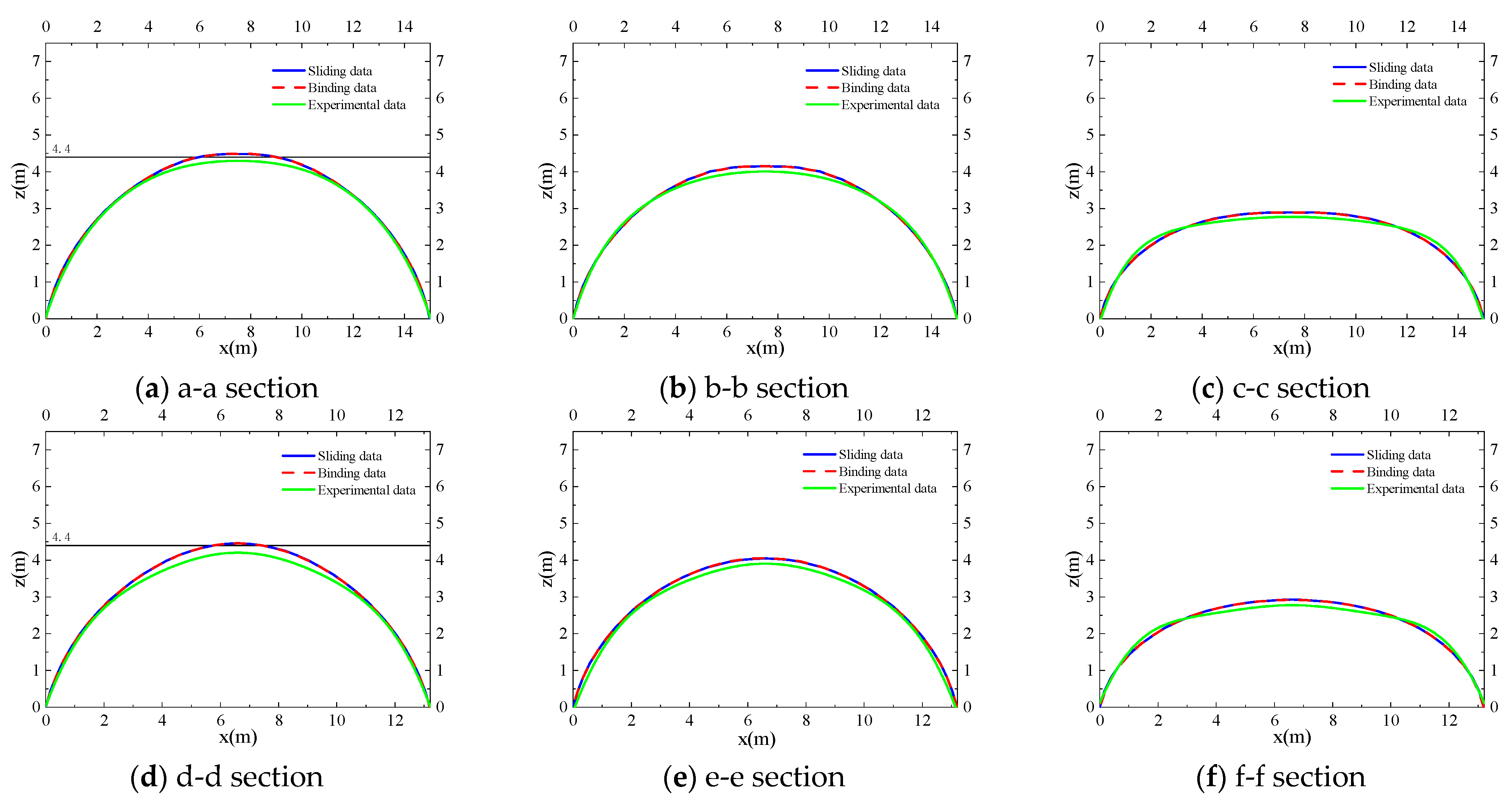
5.2. Comparison of Sections
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kromoser, B.; Huber, P. Pneumatic formwork systems in structural engineering. Adv. Mater. Sci. Eng. 2016, 2016, 4724036. [Google Scholar] [CrossRef]
- Yin, Y.; Chen, W.; Hu, J.; Zhao, B.; Wang, Q. In-situ measurement of structural performance of large-span air-supported dome under wind loads. Thin-Walled Struct. 2021, 169, 108476. [Google Scholar] [CrossRef]
- Xu, Y.; Guan, F.-L. Structure design and mechanical measurement of inflatable antenna. Acta Astronaut. 2012, 76, 13–25. [Google Scholar] [CrossRef]
- Europe-China Today. 2020. Available online: https://www.ectoday.eu/ (accessed on 5 January 2023).
- Bell, L. Pneumatic membrane structures for space and terrestrial applications. In Proceedings of the 11th Biennial ASCE Aerospace Division International Conference on Engineering, Science, Construction, and Operations in Challenging Environments, Long Beach, CA, USA, 3–5 March 2008; pp. 1–8. [Google Scholar]
- Li, X.; Zhang, Z.; Xue, S.; He, Y. Experimental and simulation analysis of the initial shape of a large-span air-supported membrane structure. Thin-Walled Struct. 2022, 178, 109491. [Google Scholar] [CrossRef]
- Bonet, J.; Wood, R.D.; Mahaney, J.; Heywood, P. Finite element analysis of air supported membrane structures. Comput. Methods Appl. Mech. Eng. 2000, 190, 579–595. [Google Scholar] [CrossRef]
- Mokin, N.A.; Kustov, A.A.; Trushin, S.I. Numerical simulation of an air-supported structure in the air flow. Textiles composites and inflatable structures VIII. In Proceedings of the VIII International Conference on Textile Composites and Inflatable Structures, Barcelona, Spain, 9–11 October 2017; CIMNE; pp. 383–393. [Google Scholar]
- Schek, H.J. The force density method for form finding and computations of general networks. Comput. Methods Appl. Mech. Eng. 1974, 12, 115–134. [Google Scholar] [CrossRef]
- Wan, Z.; Ohlbrock, P.O.; D’Acunto, P.; Cao, Z.; Fan, F.; Schwartz, J. A form-finding approach for the conceptual design of air-supported structures using 3D graphic statics. Comput. Struct. 2021, 243, 106401. [Google Scholar] [CrossRef]
- Matumura, T.K. Finite Element Analysis of Cable Reinforced Membrane Structures with the Use of Bendable-Element; IASS International Symposium’97 on Sell & Spatial Structures: Singapore, 1997; pp. 567–576. [Google Scholar]
- Lshii, K. Form finding analysis in consideration of cutting patterns of membrane structures. Int. J. Space Struct. 1999, 14, 105–119. [Google Scholar]
- Yong, S.C.; Wang, S. The influence of cable sliding on the performance of membrane structure. In Proceedings of the 10th National Conference on Structural Engineering, Nanjing, China, 1 October 2001; Chinese Society of Mechanics: Beijing, China, 2001; pp. 674–682. (In Chinese). [Google Scholar]
- Ju, F.; Choo, Y.S. Super element approach to cable passing through multiple pulleys. Int. J. Solids Struct. 2005, 42, 3533–3547. [Google Scholar] [CrossRef]
- Noguchi, H.; Kawashima, T. Meshfree Analyses of Cable-reinforced Membrane Structures by ALE–EFG Method. Eng. Anal. Bound. Elem. 2004, 28, 443–451. [Google Scholar] [CrossRef]
- He, Y.; Zhu, M.; Zhao, Y.; Li, X. Influence of different cable–membrane connection models on wind-induced responses of an air supported membrane structure with orthogonal cable net. Thin-Walled Struct. 2022, 180, 109840. [Google Scholar] [CrossRef]
- Okamoto, N.; Nakazawa, M. Finite element incremental contact analysis with various frictional conditions. Int. J. Numer. Methods Eng. 1979, 14, 337–357. [Google Scholar] [CrossRef]
- Mijar, A.R.; Arora, J.S. Review of formulations for elastostatic frictional contact problems. Struct. Multidiscip. Optim. 2000, 20, 167–189. [Google Scholar] [CrossRef]
- Chen, J.S.; Wang, H.P. New boundary condition treatments in meshfree computation of contact problems. Comput. Methods Appl. Mech. Eng. 2000, 187, 441–468. [Google Scholar] [CrossRef]
- Yin, L.; Zhou, H.L.; Lü, Y.F. Form-finding and wind loading analysis of air-supported membrane structures. Ind. Constr. 2013, 43 (Suppl. 1), 349–353. [Google Scholar]
- Belytschko, T.; Neal, M.O. Contact-impact by the pinball algorithm with penalty and Lagrangian methods. Int. J. Numer. Methods Eng. 1991, 31, 547–572. [Google Scholar] [CrossRef]
- Cuomo, M.; Ventura, G. Complementary energy approach to contact problems based on consistent augmented Lagrangian formulation. Math. Comput. Model. 1998, 28, 185–204. [Google Scholar] [CrossRef]
- Gould, N.I.M. On the convergence of a sequential penalty function method for constrained minimization. SIAM J. Numer. Anal. 1989, 26, 107–128. [Google Scholar] [CrossRef]
- Wang, X.M. ANSYS Structural Dynamic Analysis and Application; People’s Communications Press: Beijing, China, 2011. [Google Scholar]
- Li, Z.; Zhang, Y.; Zhang, Y. Experimental study on friction coefficient between cable and membrane. Build. Struct. 2010, 40, 107–110. (In Chinese) [Google Scholar]
















| Along the Long Side | Along the Short Side | ||
|---|---|---|---|
| Measuring Point | Cable Tension(kN) | Measuring Point | Cable Tension(kN) |
| 1 | 0.595 | 9 | 0.549 |
| 2 | 0.626 | 10 | 0.595 |
| 3 | 0.722 | 11 | 0.659 |
| 4 | 0.746 | 12 | 0.621 |
| 5 | 0.742 | 13 | 0.674 |
| 6 | 0.660 | 14 | 0.689 |
| 7 | 0.492 | 15 | 0.604 |
| 8 | 0.427 | - | - |
| Measuring Point | Test | Sliding Contact | Binding Contact | ||
|---|---|---|---|---|---|
| Tension (kN) | Tension (kN) | Error (%) | Tension (kN) | Error (%) | |
| 1 | 0.595 | 0.641 | 7.75 | 0.672 | 13.00 |
| 2 | 0.626 | 0.660 | 5.48 | 0.818 | 30.60 |
| 3 | 0.722 | 0.759 | 5.06 | 0.853 | 18.16 |
| 4 | 0.746 | 0.768 | 2.99 | 0.924 | 23.89 |
| 5 | 0.742 | 0.768 | 3.46 | 0.806 | 8.58 |
| 6 | 0.660 | 0.719 | 8.95 | 0.815 | 23.46 |
| 7 | 0.492 | 0.527 | 7.10 | 0.685 | 39.31 |
| 8 | 0.427 | 0.476 | 11.47 | 0.476 | 11.47 |
| 9 | 0.549 | 0.596 | 8.62 | 0.796 | 44.94 |
| 10 | 0.595 | 0.625 | 5.02 | 0.736 | 23.77 |
| 11 | 0.659 | 0.692 | 4.95 | 0.880 | 33.61 |
| 12 | 0.621 | 0.653 | 5.23 | 0.669 | 7.78 |
| 13 | 0.674 | 0.700 | 3.84 | 0.710 | 5.31 |
| 14 | 0.689 | 0.730 | 5.91 | 0.903 | 31.00 |
| 15 | 0.604 | 0.661 | 9.48 | 0.817 | 35.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhang, Z.; Xue, S.; He, Y.; Zhao, Y. Initial Shape Analysis and Experimental Study of Air-Supported Membrane Structure Considering Cable–Membrane Contact. Buildings 2023, 13, 184. https://doi.org/10.3390/buildings13010184
Li X, Zhang Z, Xue S, He Y, Zhao Y. Initial Shape Analysis and Experimental Study of Air-Supported Membrane Structure Considering Cable–Membrane Contact. Buildings. 2023; 13(1):184. https://doi.org/10.3390/buildings13010184
Chicago/Turabian StyleLi, Xiongyan, Zhen Zhang, Suduo Xue, Yanli He, and Yanguo Zhao. 2023. "Initial Shape Analysis and Experimental Study of Air-Supported Membrane Structure Considering Cable–Membrane Contact" Buildings 13, no. 1: 184. https://doi.org/10.3390/buildings13010184
APA StyleLi, X., Zhang, Z., Xue, S., He, Y., & Zhao, Y. (2023). Initial Shape Analysis and Experimental Study of Air-Supported Membrane Structure Considering Cable–Membrane Contact. Buildings, 13(1), 184. https://doi.org/10.3390/buildings13010184






