Mechanical Properties on Various FRP-Reinforced Concrete in Cold Regions
Abstract
1. Introduction
2. Experimental Methods and Procedures
2.1. Raw Materials
2.2. Specimen Preparation
2.3. Testing Method and Loading Process
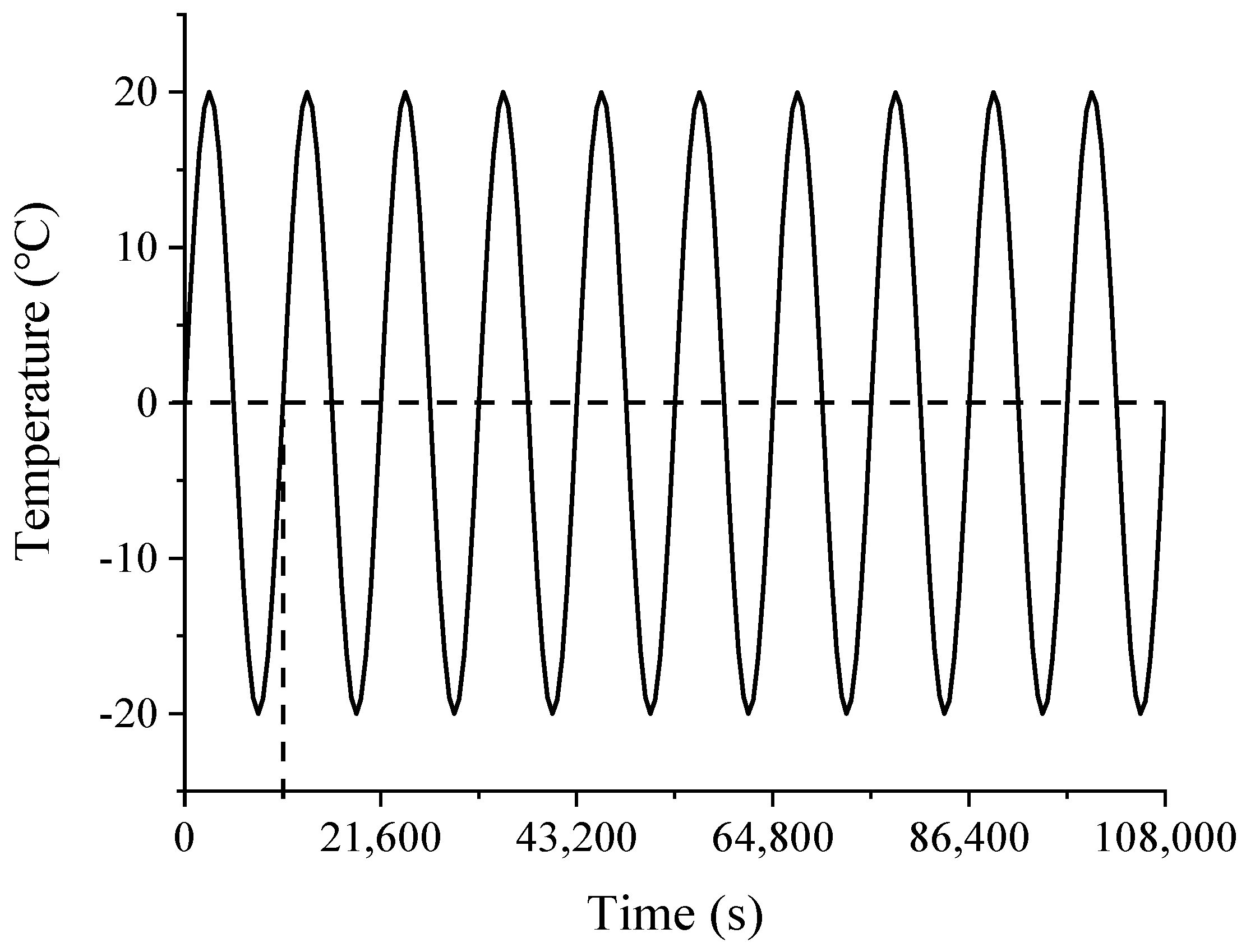
2.3.1. Freeze–Thaw Cycle
2.3.2. Mechanical Tests
3. Results and Discussion
3.1. Damage Morphology of 100 Freeze–Thaw Cycles
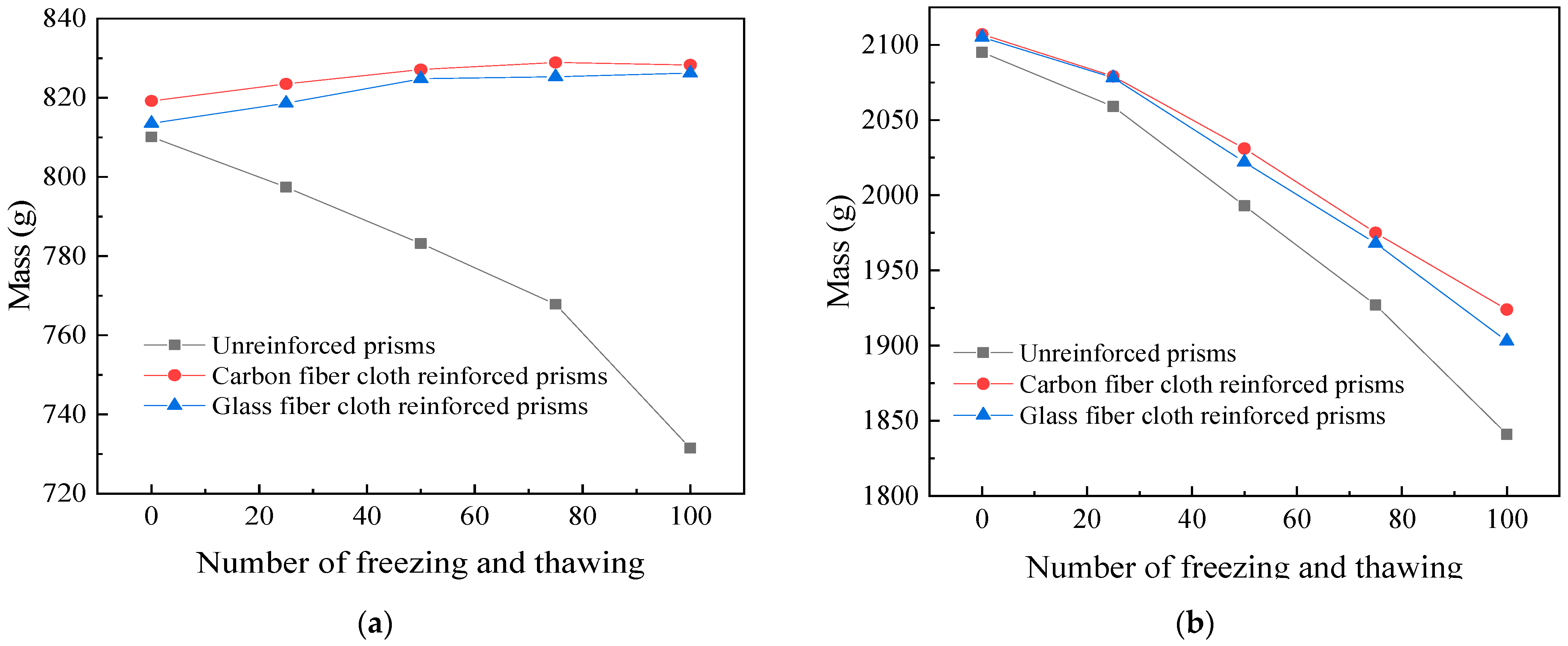
3.2. Weight Variation
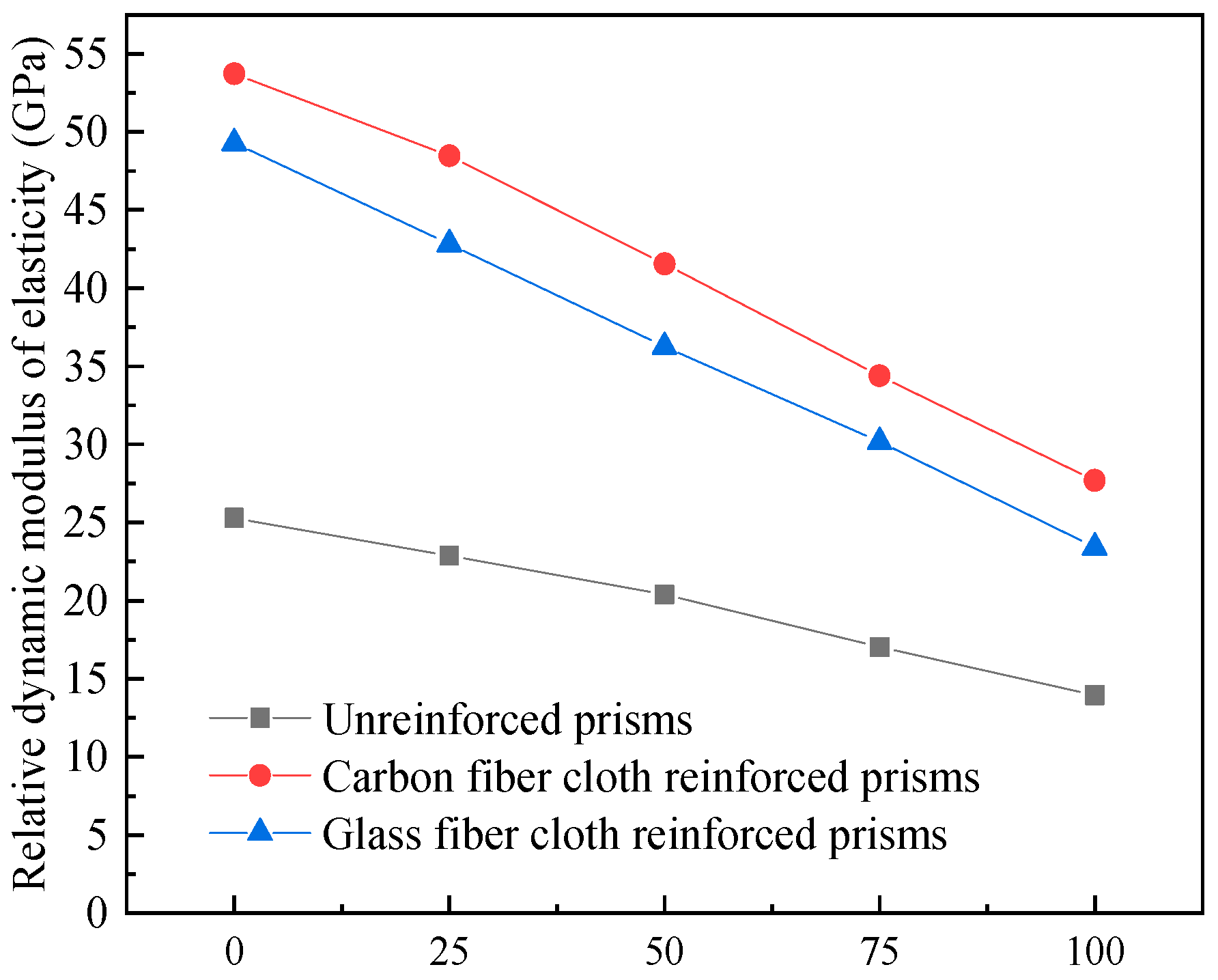
3.3. Changes in Elastic Modulus
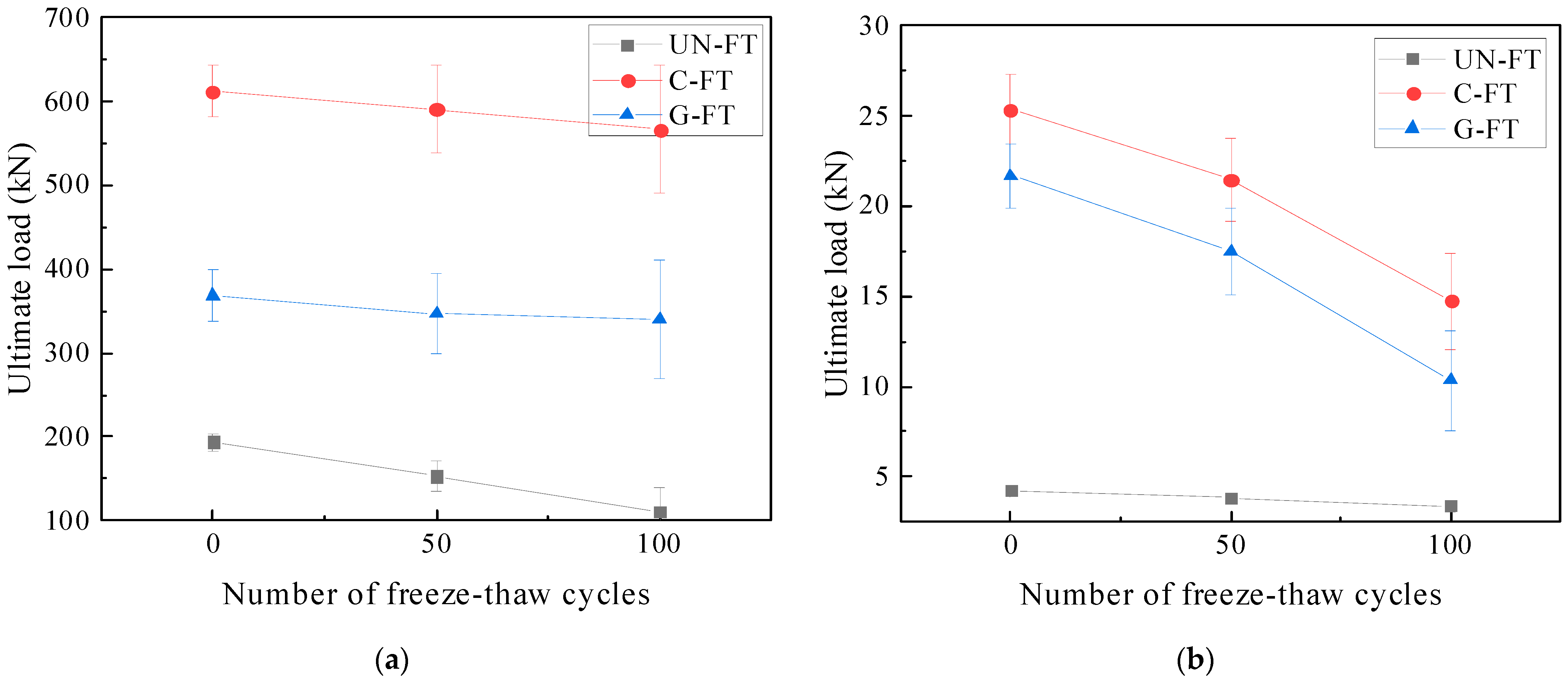
3.4. Compressive and Flexural Strength
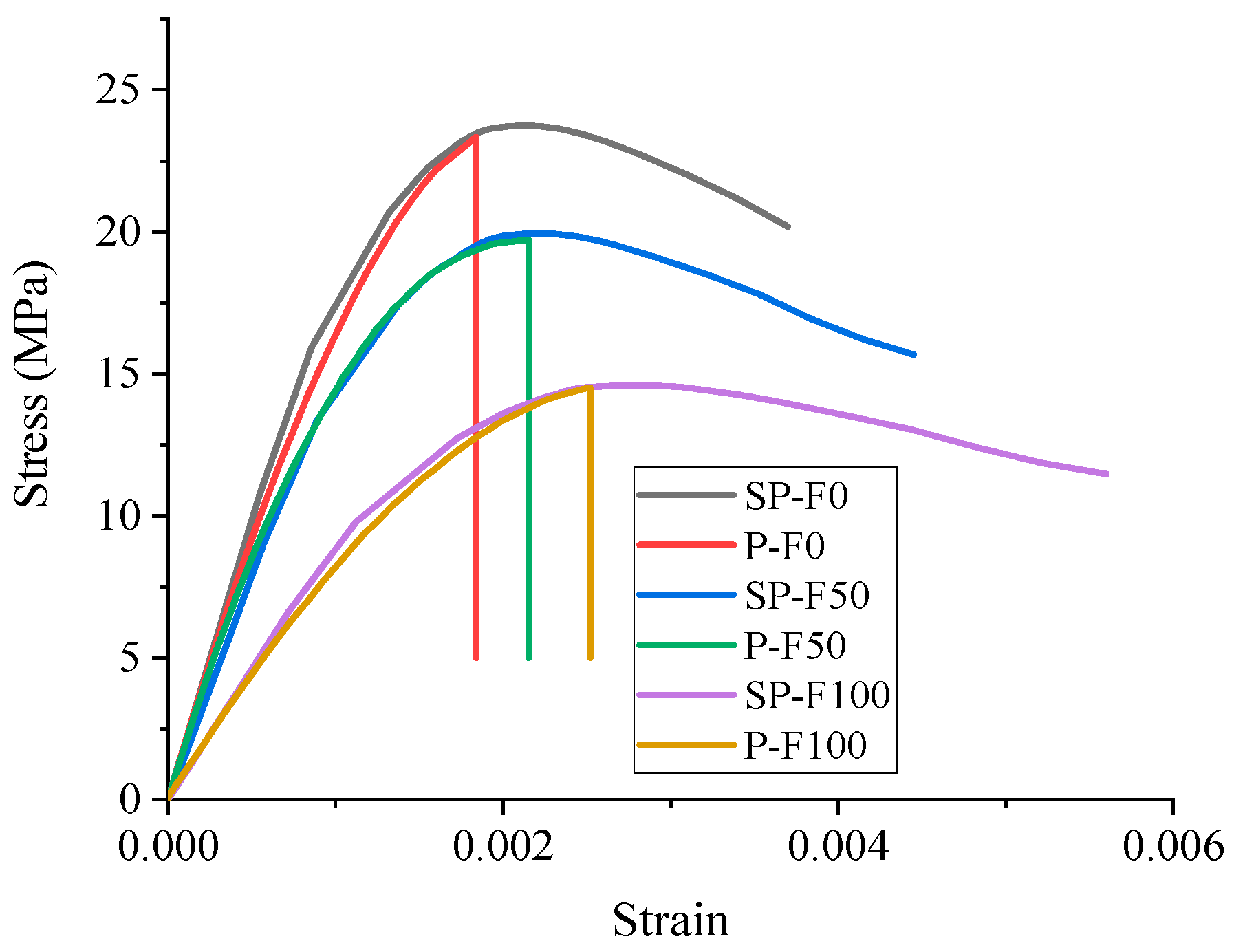
3.5. Load Displacement or Stress–Strain Analysis
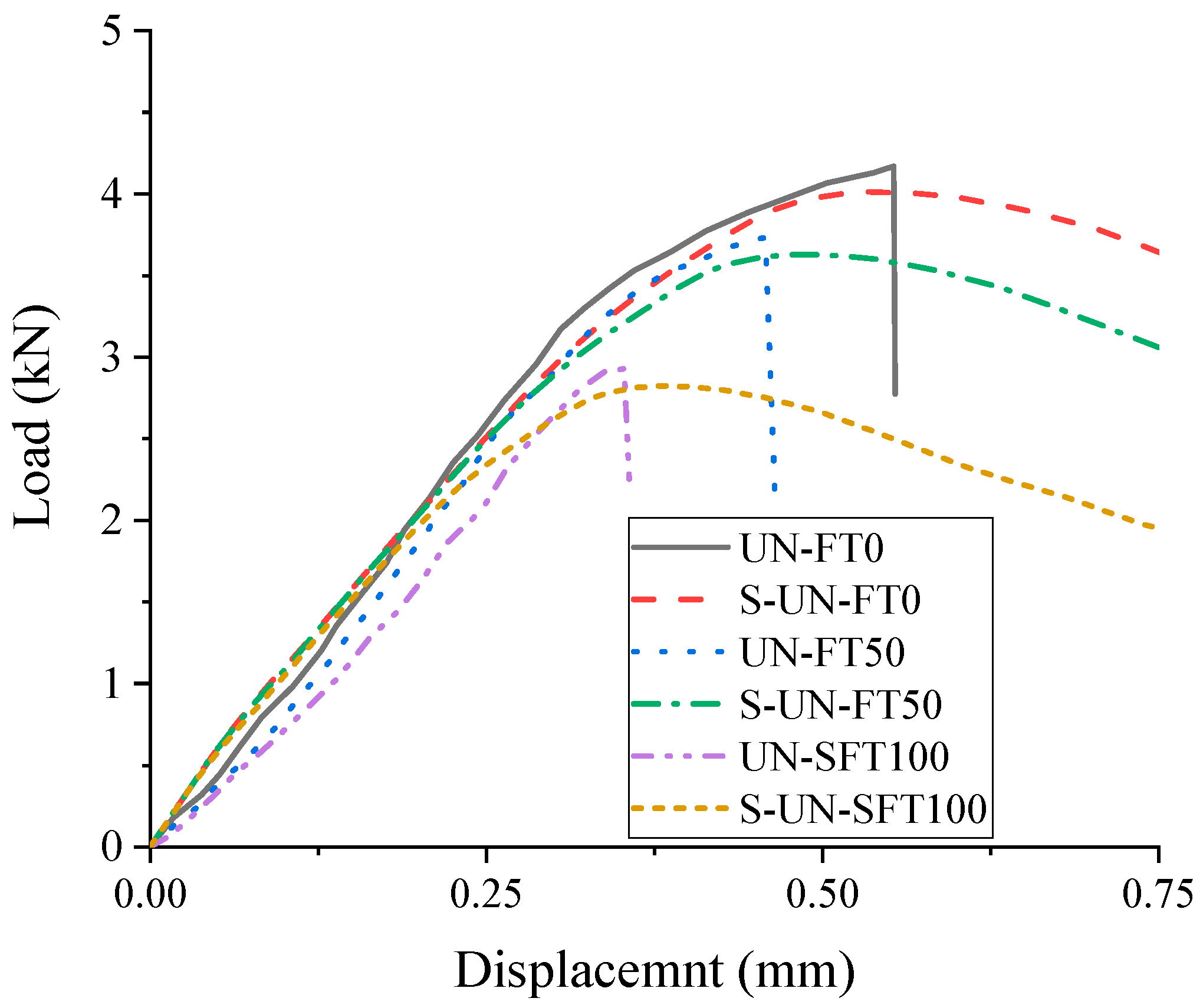
3.5.1. Load Displacement Curve of Prismatic Specimen
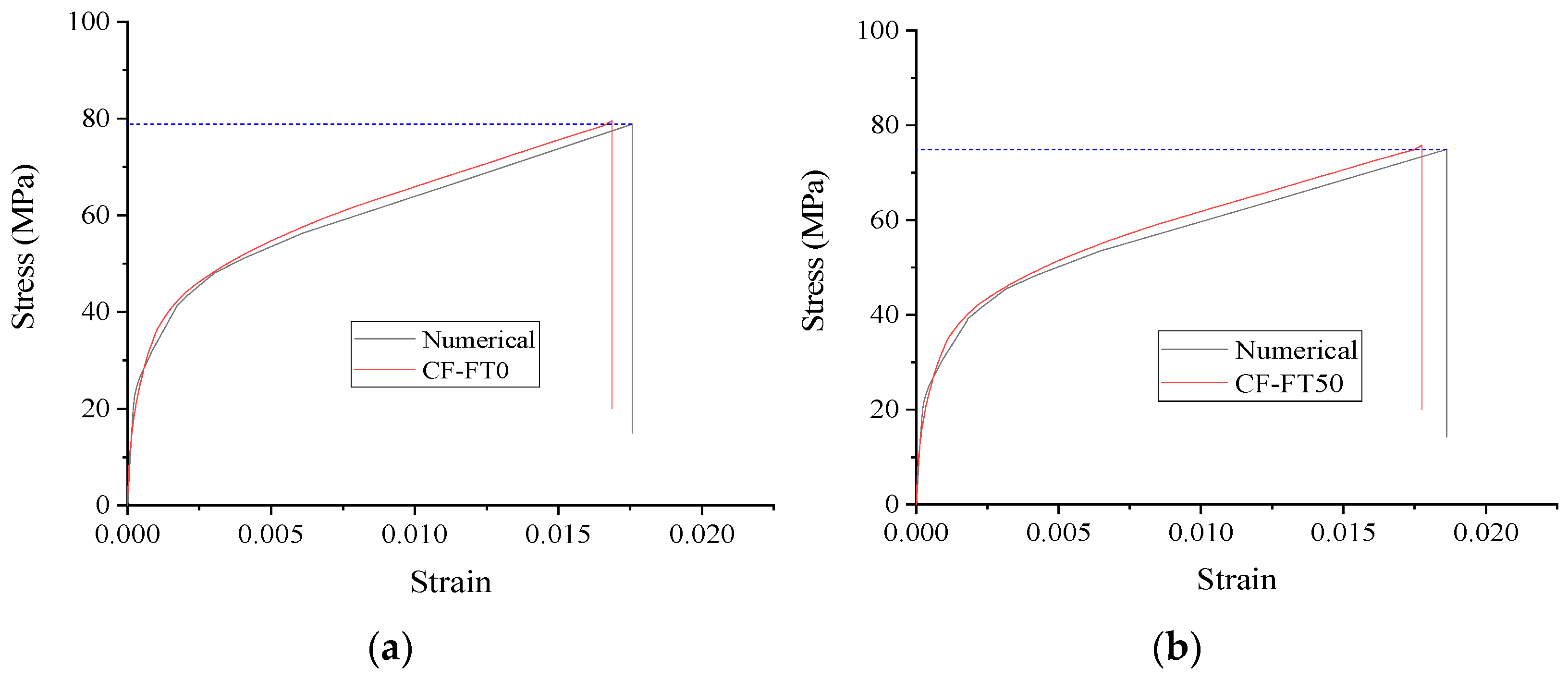
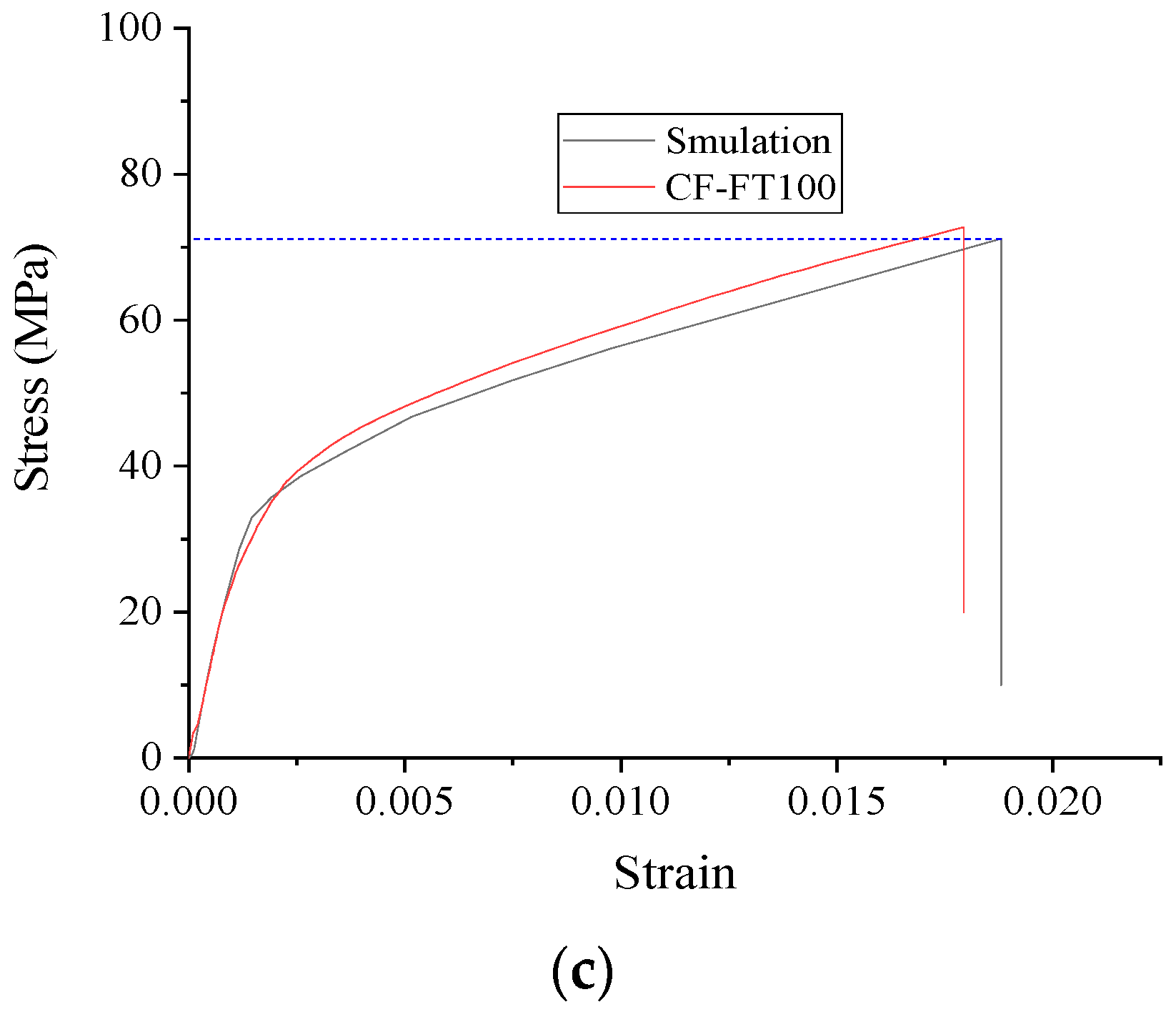
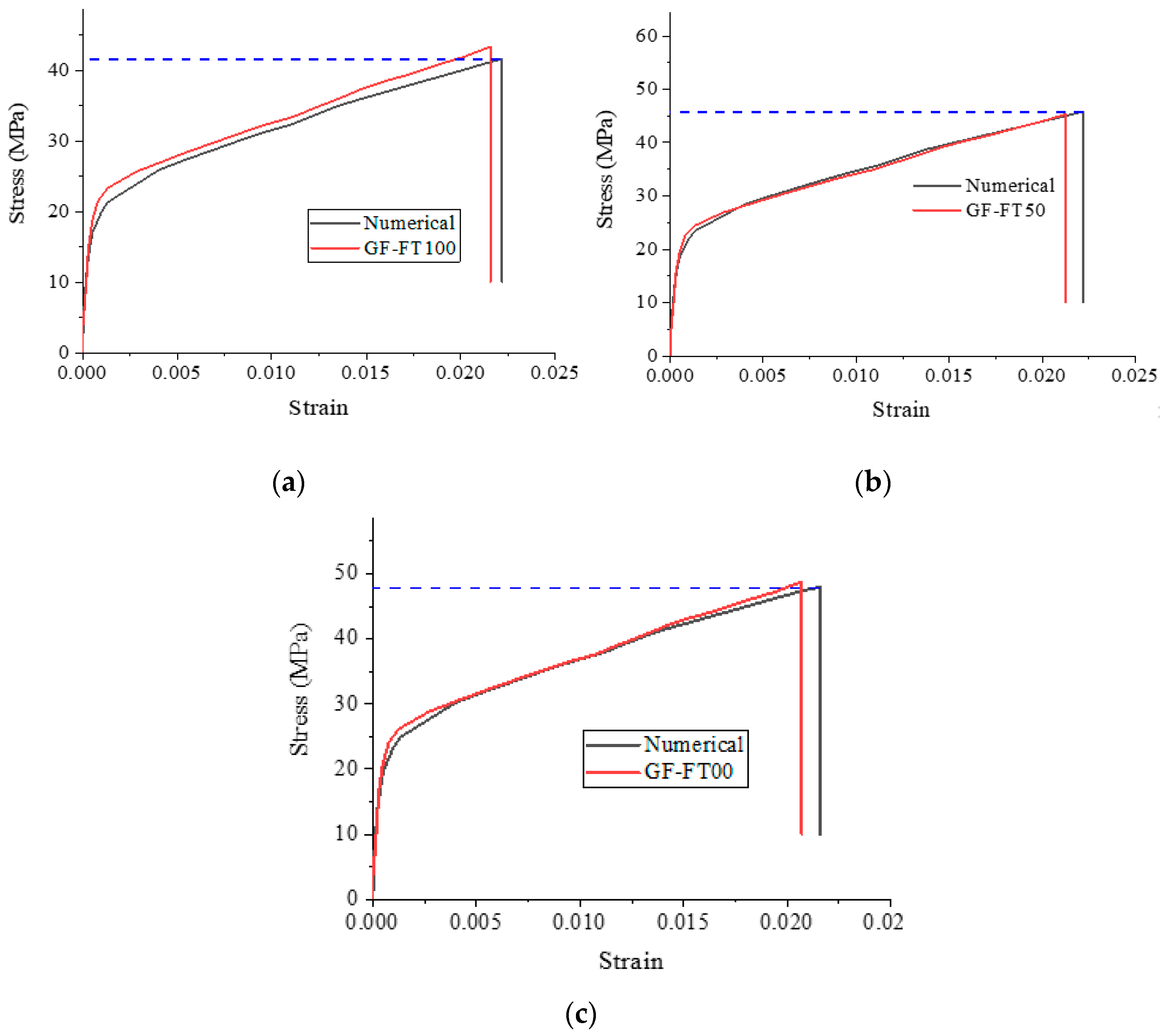
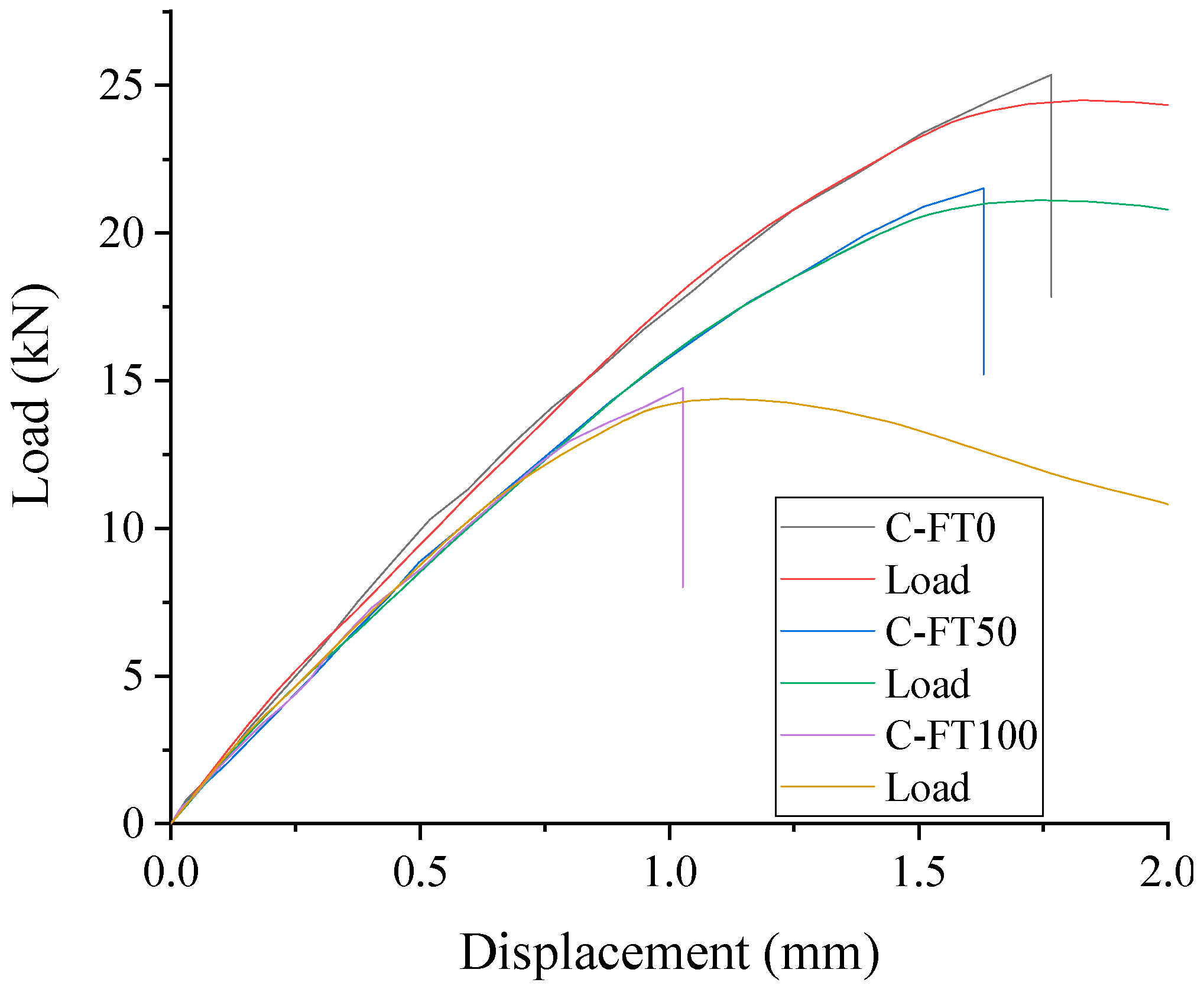
3.5.2. Stress–Strain Relationship for Cylindrical Specimens
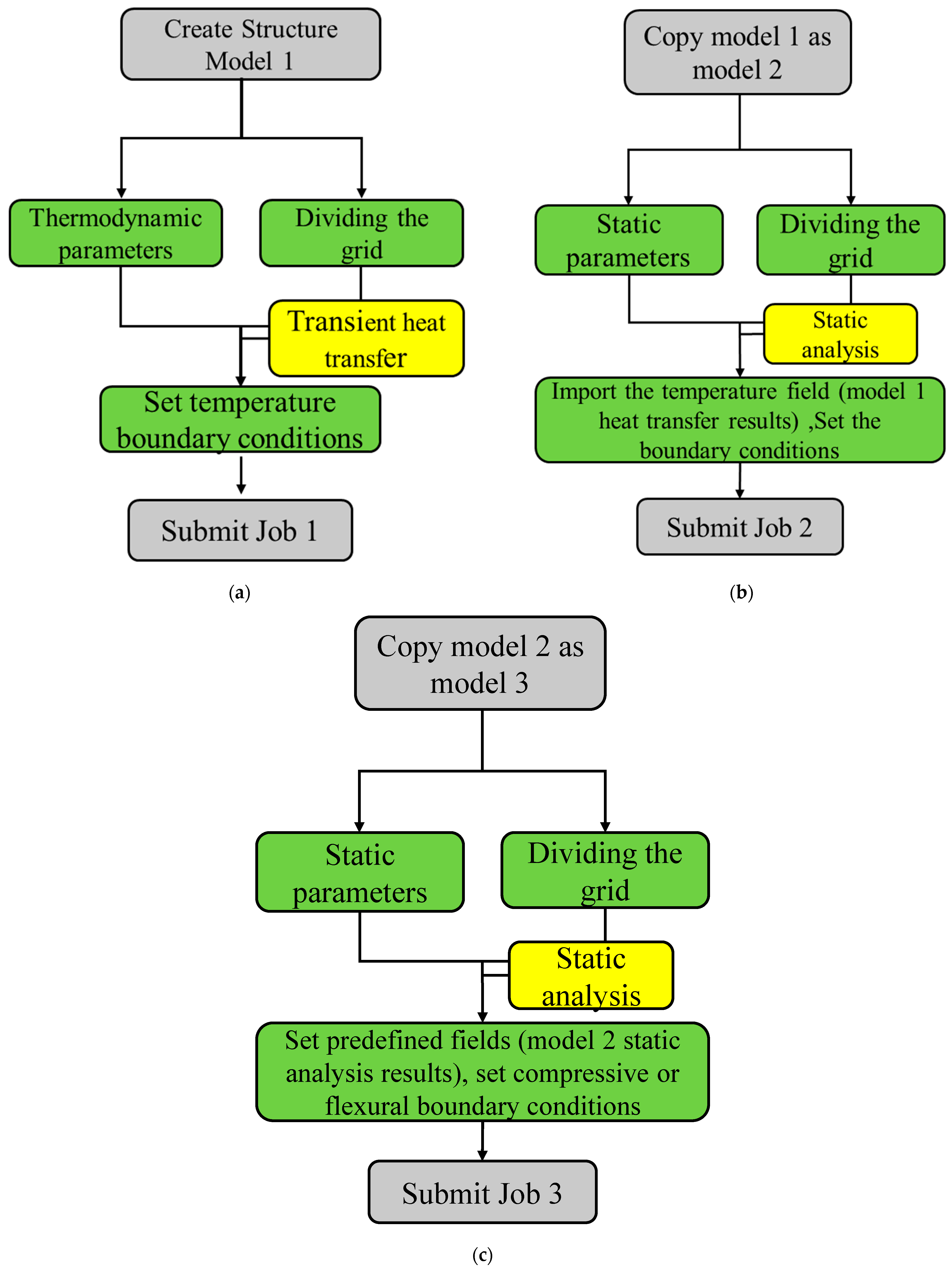
4. Finite Element Simulation
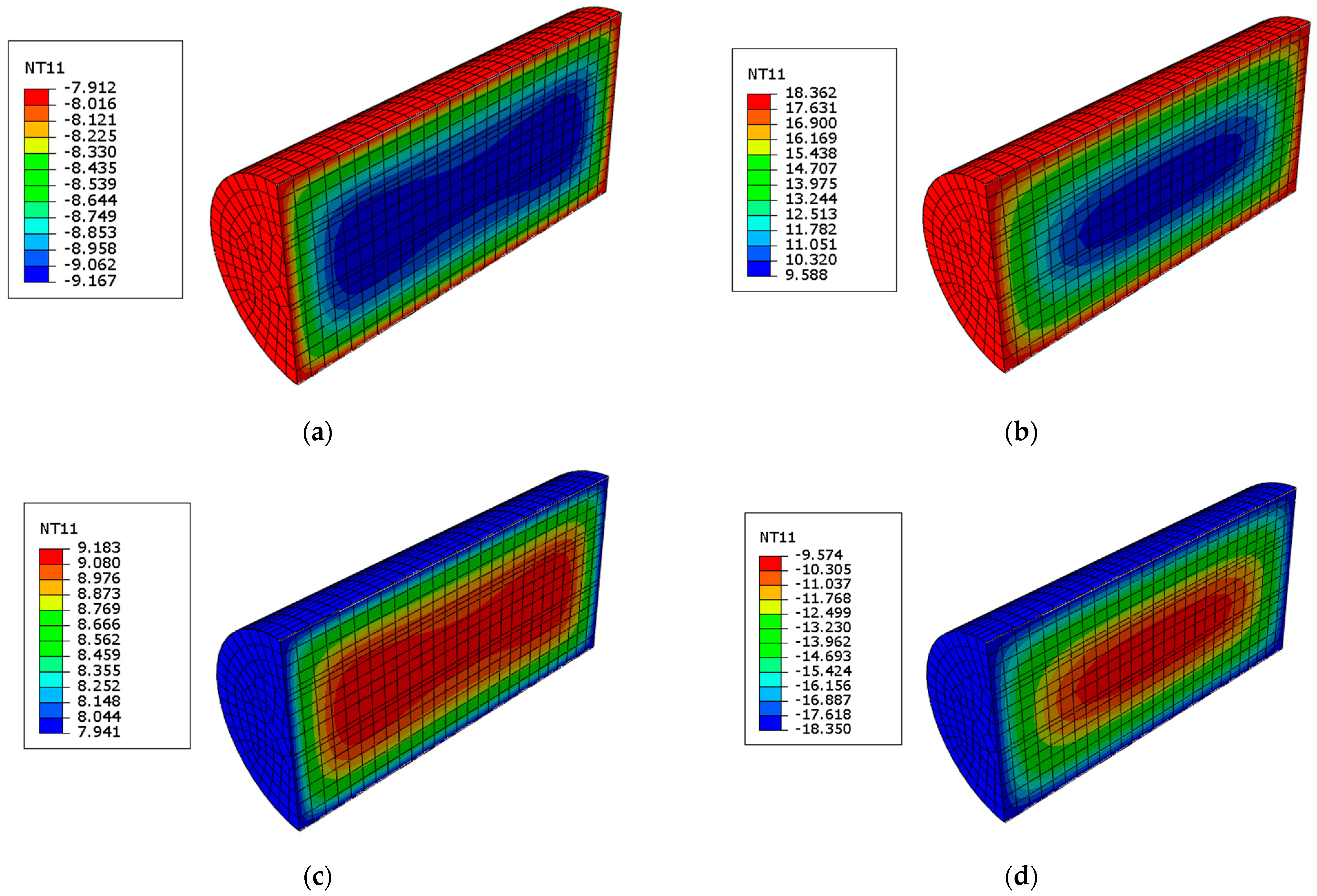
4.1. Thermodynamic Parameters
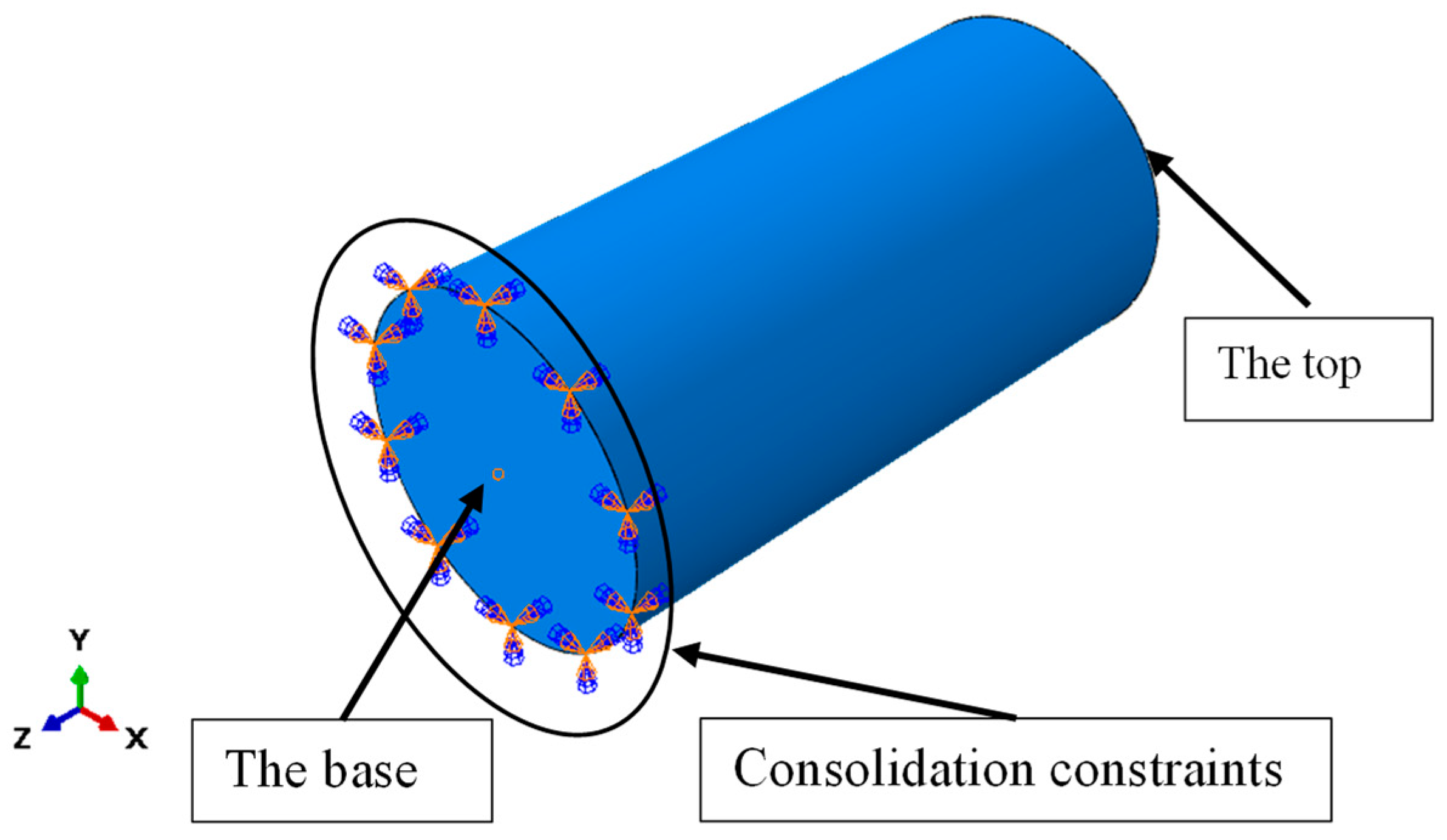
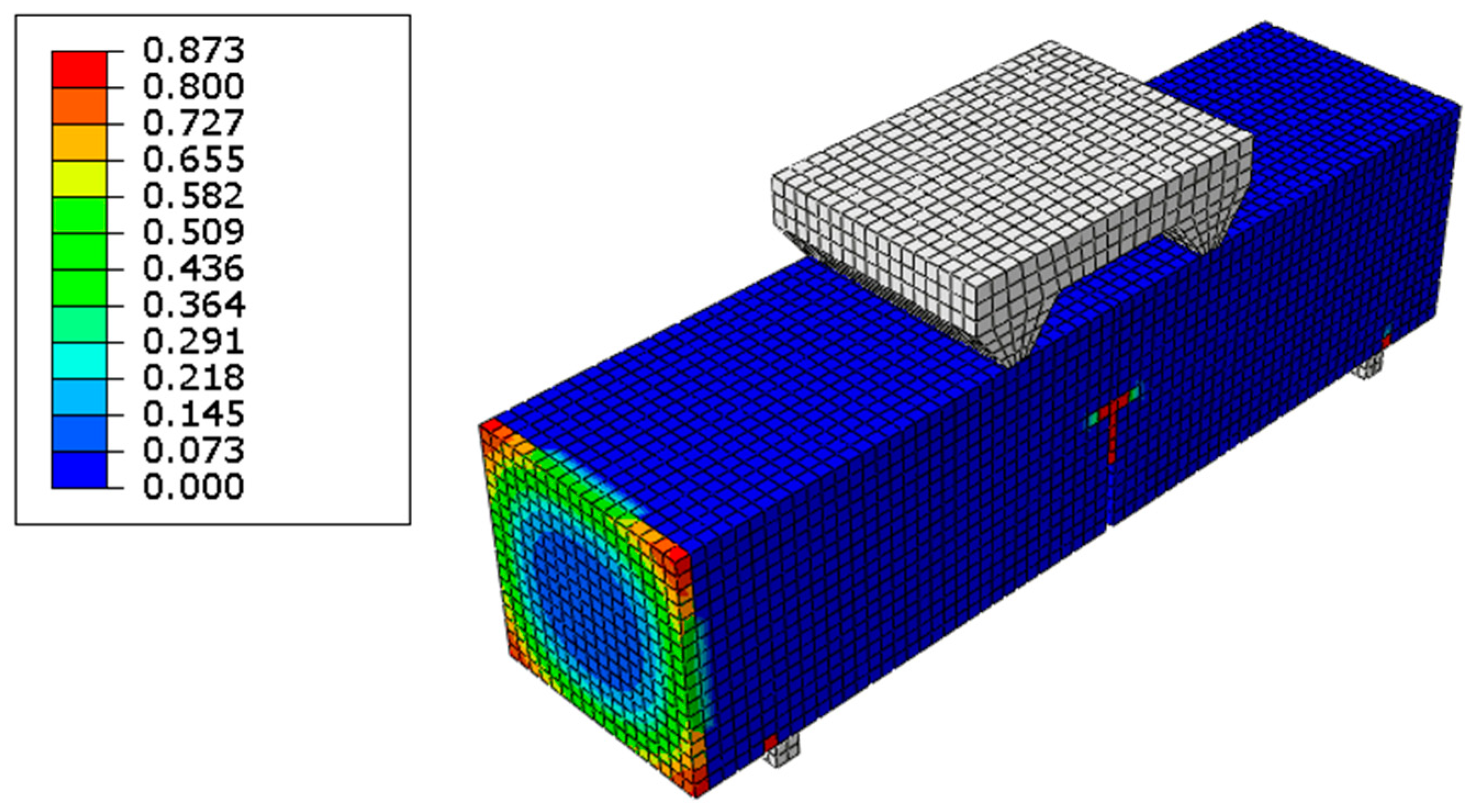
4.2. Numerical Simulation of Axial Pressure
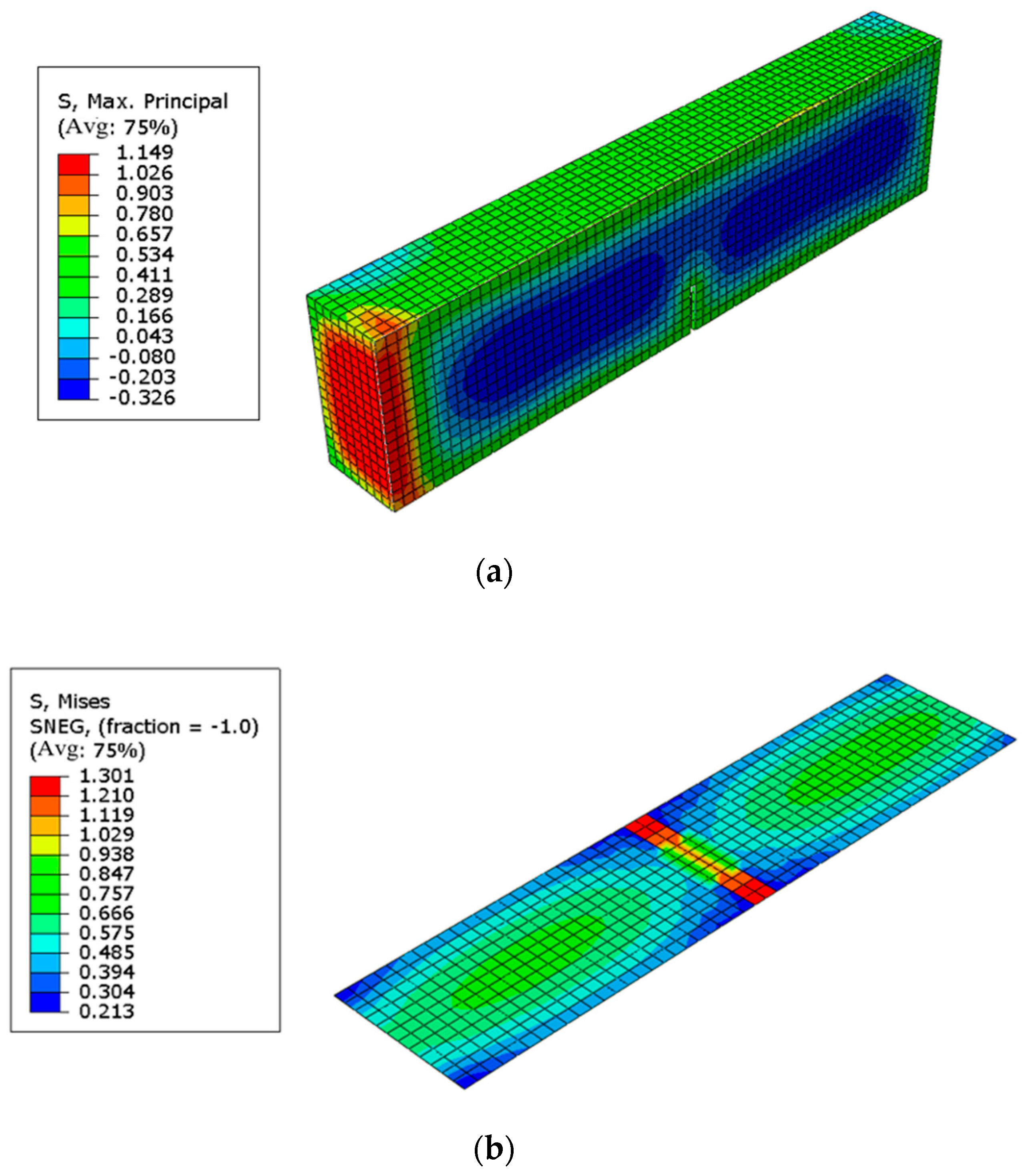
4.3. Numerical Simulation of Flexural Resistance
5. Conclusions
- The morphological analysis can observe the surface of the CFRP- and GFRP-reinforced concrete prisms, and the specimens are still severely damaged. Especially at the junction of FRP and concrete, the bonding fails, and cracks at the interface can be clearly observed. There is also a difference in the freezing resistance of the specimens by different reinforcement methods.
- The weight test reveals that the weight of a standard concrete cylinder decreases by 9.7% after 100 freeze–thaw cycles. The weights of CFRP- and GFRP-reinforced concrete cylinders increase by 1.1% and 1.58%, respectively. The weights of concrete prisms without reinforcement, CFRP reinforcement, and GFRP reinforcement after 100 freeze–thaw cycles decrease by 12.13%, 8.7%, and 9.6%, respectively. This indicates that FRP materials differ significantly in the frost resistance of FRP-reinforced concrete types under freeze–thaw cycles.
- The compressive and flexural strengths and relative dynamic modulus of elasticity of the two specimens are used to compare the frost resistance of concrete with different reinforcement methods in cold regions. The modulus of elasticity of unreinforced, CFRP-reinforced, and GFRP-reinforced concrete prisms decreases by 44.9%, 48.5%, and 52.5% after 100 freeze–thaw cycles, respectively. However, the percentage reduction in elastic modulus is very similar for the three specimens. The compressive strength of unreinforced, CFRP-reinforced, and GFRP-reinforced concrete cylinders is reduced by 27.6%, 7.4%, and 8% after 100 freeze–thaw cycles.
- The axial compressive stress–strain curve and bending of the load–displacement curve of FRP-reinforced concrete are studied in a cold zone environment. Two FEA models are established utilizing finite elements under the action of different numbers of freeze–thaw cycles. The axial stress–strain curve and the load–displacement curve under bending load are calculated and compared with the experimental values. The results show that the modified finite element model can have a good prediction effect.
- This paper evaluates the frost resistance of specimens under different reinforcement techniques in terms of bearing capacity and weight change. Future research can be conducted on the adhesive interface between FRP material and concrete, and finite elements can help to study the change in the adhesive interface in freeze–thaw and further analyze the mechanism of the FRP material’s influence on the frost resistance of concrete.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moghaddam, H.; Samadi, M.; Pilakoutas, K.; Mohebbi, S. Axial compressive behaviour of concrete actively confinedby metal strips, part A: Experimental study. Mater. Struct. 2010, 43, 1369–1381. [Google Scholar] [CrossRef]
- Yan, L.; Chouw, N. Behavior and analytical modeling of natural flax fibre reinforced polymer tube confined plain concrete and coir fibre reinforced concrete. J. Compos. Mater. 2013, 47, 2133–2148. [Google Scholar] [CrossRef]
- Orbanich, C.J.; Dominguez, P.N.; Ortega, N.F. Strength-ening and repair of concrete foundation beams with carbon fibre composite materials. Mater. Struct. 2012, 45, 1693–1704. [Google Scholar] [CrossRef]
- Yan, L.; Chouw, N. Dynamic and static properties of flax fibre reinforced polymer tube confined coir fibre rein-forced concrete. J. Compos. Mater 2014, 48, 1595–1610. [Google Scholar] [CrossRef]
- Yue, Q.; Yang, Y. Overview of durability research on fiber reinforced composite strengthened structures. J. Build. Struct. 2009, 30, 8–15. [Google Scholar]
- Ji, Y.; Kim, Y.J. Effects of sulfuric acid on durability characteristics of CFRP composite sheets. J. Mater. Civ. Eng. 2017, 29, 04017159. [Google Scholar] [CrossRef]
- Institute of Construction Research, Ministry of Metallurgical Industry. Proceedings of the First Academic Conference of China Academic Exchange Society on Fiber Reinforced Plastic Concrete Structures; Building Research Institute of the Ministry of Metallurgical Industry Press: Chengdu, China, 2000; pp. 5–13. [Google Scholar]
- Jahami, A.; Temsah, Y.; Khatib, J.; Baalbaki, O.; Kenai, S. The behavior of CFRP strengthened RC beams subjected to blast loading. Mag. Civ. Eng. 2021, 103, 10309. [Google Scholar] [CrossRef]
- Masmoudi, R.; Zaidi, A.; Gérard, P. Transverse thermal expansion of FRP bars embedded in concrete. J. Compos. Constr. 2005, 9, 377–387. [Google Scholar] [CrossRef]
- Li, C.; Guo, R.; Xian, G.; Li, H. Effects of elevated temperature, hydraulic pressure and fatigue loading on the property evolution of a carbon/glass fiber hybrid rod. Polym. Test. 2020, 90, 106761. [Google Scholar] [CrossRef]
- Xian, G.; Guo, R.; Li, C.; Wang, Y. Mechanical performance evolution and life prediction of prestressed cfrp plate exposed to hygrothermal and freeze-thaw environments. Compos. Struct. 2022, 293, 115719. [Google Scholar] [CrossRef]
- Zhong, Y.; Cheng, M.; Zhang, X.; Hu, H.; Cao, D.; Li, S. Hygrothermal durability of glass and carbon fiber reinforced composites–A comparative study. Compos. Struct. 2019, 211, 134–143. [Google Scholar] [CrossRef]
- Li, B.Q.; Zhou, Y.X. Research progress of fiber composite reinforced concrete structures. J. Water Resour. Constr. Eng. 2016, 14, 85–90. [Google Scholar]
- Wang, Q.; Lu, C. Experimental study on the frost resistance of CFRP-reinforced reinforced concrete beams under chloride ion attack. Sichuan Constr. Sci. Res. 2012, 38, 118–120+142. [Google Scholar]
- Ji, Y.; Kim, Y.J.; Jia, Y. Performance characterization of plain and CFRP-bonded concrete subjected to sulfuric acid. Mater. Des. 2021, 197, 109176. [Google Scholar] [CrossRef]
- Lu, Z.; Li, J.; Xie, J.; Huang, P.; Xue, L. Durability of flexurally strengthened RC beams with prestressed CFRP sheet under wet–dry cycling in a chloride-containing environment. Compos. Struct. 2021, 255, 112869. [Google Scholar] [CrossRef]
- Attari, N.; Youcef, Y.S.; Amziane, S. Seismic performance of reinforced concrete beam–column joint strengthening by frp sheets. Structures 2019, 20, 353–364. [Google Scholar] [CrossRef]
- Xiong, G.J.; Jiang, X.; Liu, J.W.; Chen, L. A way for preventing tension delamination of concrete cover in midspan of FRP strengthened beams. Constr. Build. Mater. 2007, 21, 402–408. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Pleveris, N. Strengthening of of RC beams with epoxy bonded fibre composite materials. Mater. Struct. 1992, 25, 201–211. [Google Scholar] [CrossRef]
- Hasan, M.; Okuyama, H.; Sato, Y.; Ueda, T. Stress-strain model of concrete damaged by freezing and thawing cycles. J. Adv. Concr. Technol. 2004, 2, 89–99. [Google Scholar] [CrossRef]
- Huang, L.; Ke, M.; Si, Z.; Du, X.; Wang, Z. Study on uniaxial compression fine view damage of freeze-thaw damaged concrete. J. Appl. Mech. 2021, 38, 1400–1407. [Google Scholar]
- Zhang, Y.; Zheng, S.; Pei, P. Freeze-thaw damage model for reinforced concrete columns. Eng. Mech. 2019, 36, 78–86. [Google Scholar]
- Zheng, S.; Yang, L.; Ji, J.; Pei, P.; Huang, Y.; Wang, B. Seismic performance of freeze-thaw RC beams with numerical simulation method. J. Vib. Eng. 2021, 34, 889–898. [Google Scholar] [CrossRef]
- Griffis, C.A.; Masumura, R.A.; Chang, C.I. Thermal response of graphite epoxy composite subjected to rapid heating. J. Compos. Mater. 1981, 15, 427–442. [Google Scholar] [CrossRef]
- Wang, X.; Cha, X.; Zhu, Y. Calculation method of fire resistance performance of GFRP reinforced concrete beams. J. Build. Struct. 2014, 35, 119–127. [Google Scholar] [CrossRef]
- Zhou, Y. Dynamic Numerical Simulation Analysis of Concrete under Freeze-Thaw Environment; Dalian University of Technology: Dalian, China, 2019. [Google Scholar] [CrossRef]
- Gandage, A.S.; Ram, V.V.; Vasan, A.; Sivakumar, M.V.N.; Yaswanth, A.B. Effect of perlite on thermal conductivity of self compacting concrete. In Proceedings of the 2nd Transportation Research Group of India Conference, Agra, India, 12–15 December 2013. [Google Scholar]
- Albostan, U. Implementation of Coupled Thermal and Structural Analysis Methods for Reinforced Concrete Structures; Middle East Technical University: Ankara, Turkey, 2013. [Google Scholar]
- Dong, S.; Liu, G.; Zhan, T.; Yao, Y.; Ni, L. A thermal conductivity prediction model of cement-based grouts for ground source heat pump. Int. Commun. Heat Mass Transf. 2022, 135, 106079. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, Y.; Xi, Y. Modeling the effect of temperature gradient on moisture and ionic transport in concrete. Cem. Concr. Compos. 2020, 106, 103454. [Google Scholar] [CrossRef]
- Bisby, L.A. Fire Behavior of Fiber-Reinforced Polymers (FRP) Reinforced or Confined Concrete; Queen’s University: Kingston, ON, Canada, 2003. [Google Scholar]
- Xue, J.Y.; Zhang, F.L.; Zhao, H.T.; Xie, Q.F.; Sui, Y.; Wu, Z. Numerical simulation of the bonding performance of carbon fiber cloth with wood interface. J. Xi’an Univ. Archit. Technol. (Nat. Sci. Ed.) 2013, 45, 305–310. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Q.F.; Huang, Y.H.; Yang, Y.X.; Lin, J.H. Numerical simulation of bonding performance of GFRP composites with brick interface. Eng. Mech. 2007, 5, 119–124. [Google Scholar]
- Li, L.; Wang, B.; Hubler, M.H. Durability and mechanical property improvement of ultra-high performance concrete with carbon nanofibers. Cem. Concr. Compos. 2022, 131, 104592. [Google Scholar] [CrossRef]
- Jin, Y. Study on Temperature Field and Temperature Effect of CFRP Reinforced Concrete Box Girder under Solar Radiation; Lanzhou Jiaotong University: Lanzhou, China, 2015. [Google Scholar]










| SO3 /% | Cl /% | Desulfurization Gypsum/% | Fly Coal Ash/% | Loss of Ignition/% | Setting Time/min | Flexural Strength/MPa | Compressive Strength/MPa | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Initial Condensation | Final Condensation | 3 d | 28 d | 3 d | 28 d | |||||
| 2.8 | 0.053 | 6.5 | 9 | 4.46 | 185 | 230 | 5.4 | 5.4 | 28.6 | 42.5 |
| Materials | Tensile Strength/MPa | Modulus of Elasticity/GPa | Elongation at Break/% |
|---|---|---|---|
| GFRP | 2450~2550 | 75~85 | 2.25~2.35 |
| CFRP | 3470~3570 | 250~270 | 1.68~1.78 |
| Epoxy resin adhesive | 52.3~56.3 | 2.5~2.9 | 2.20~2.30 |
| Number of Freezing and Thawing | Unreinforced Specimen Number | Glass-Fiber-Reinforced Specimen Number | Carbon-Fiber-Reinforced Specimen Number | |||
|---|---|---|---|---|---|---|
| Prism | Cylindrical | Prism | Cylindrical | Prism | Cylindrical | |
| 0 times | P-F0 | C-F0 | PG-F0 | CG-F0 | PC-F0 | CC-F0 |
| 50 times | P-F50 | C-F50 | PG-F50 | CG-F50 | PC-F50 | CC-F50 |
| 100 times | P-F100 | C-F100 | PG-F100 | CG-F100 | PC-F100 | CC-F100 |
| Materials | Water | Cement | Medium Sand | 5–10 mm Gravel | 10–20 mm Gravel |
|---|---|---|---|---|---|
| Content/(kg/m3) | 209.0 | 387.0 | 635.0 | 350.7 | 818.3 |
| Materials | λ W/(m·K) | ρ kg/m3 | c J/(kg·°C) |
|---|---|---|---|
| CFRP [24] | 1.4 | 1600 | 1250 |
| GFRP [25] | 0.35 | 2000 | 1100 |
| Concrete [26] | 1.28 | 2500 | 960 |
| Parameters | Expansion Angle | Eccentricity | fc0/fb0 | k | Viscosity Coefficient | Modulus of Elasticity | Poisson’s Ratio | Expansion Coefficient |
|---|---|---|---|---|---|---|---|---|
| Concrete [24] | 20 | 0.1 | 1.15 | 0.7 | 1 × 10−5 | 20,680 | 0.1 | 1 × 10−5 |
| CFRP [29] | - | - | - | - | - | 97,800 | 0.28 | −0.1 × 10−6 |
| GFRP [25] | - | - | - | - | - | 93,750 | 0.3 | −0.1 × 10−6 |
| Number | Compressive Strength (MPa) | Peak Strain | ||||
|---|---|---|---|---|---|---|
| Experimental Result | Simulation Result | Error | Experimental Result | Simulation Result | Error | |
| C-F0 | 23.34 | 23.74 | 0.017 | 0.00212 | 0.0021 | 0.009 |
| C-F50 | 19.73 | 19.94 | 0.011 | 0.00215 | 0.0022 | 0.023 |
| C-F100 | 14.52 | 14.60 | 0.006 | 0.00262 | 0.00277 | 0.057 |
| CC-F0 | 79.56 | 78.83 | 0.009 | 0.01687 | 0.0176 | 0.043 |
| CC-F50 | 75.77 | 74.89 | 0.012 | 0.01776 | 0.0186 | 0.047 |
| CC-F100 | 72.72 | 71.15 | 0.022 | 0.01793 | 0.0188 | 0.049 |
| CG-F0 | 48.77 | 48.00 | 0.016 | 0.02069 | 0.0216 | 0.044 |
| CG-F50 | 45.36 | 45.80 | 0.010 | 0.02128 | 0.0222 | 0.043 |
| CG-F100 | 43.35 | 41.63 | 0.040 | 0.02157 | 0.0230 | 0.066 |
| Number | Ultimate Load | Peak Displacement | ||||
|---|---|---|---|---|---|---|
| Experimental Result | Simulation Result | Error | Experimental Result | Simulation Result | Error | |
| P-F0 | 4.169 | 4.014 | 0.037 | 0.553 | 0.537 | 0.029 |
| P-F50 | 3.734 | 3.632 | 0.027 | 0.458 | 0.484 | 0.057 |
| P-F100 | 2.928 | 2.825 | 0.035 | 0.353 | 0.381 | 0.079 |
| PC-F0 | 25.35 | 24.485 | 0.034 | 1.766 | 1.827 | 0.034 |
| PC-F50 | 21.508 | 21.107 | 0.018 | 1.630 | 1.740 | 0.067 |
| PC-F100 | 14.751 | 14.388 | 0.024 | 1.027 | 1.107 | 0.077 |
| PG-F0 | 21.60 | 21.54 | 0.002 | 1.84 | 2.00 | 0.086 |
| PG-F50 | 17.40 | 17.53 | 0.007 | 1.52 | 1.63 | 0.072 |
| PG-F100 | 10.34 | 9.90 | 0.042 | 0.92 | 0.97 | 0.054 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C.; Ji, Y.; Zou, Y.; Zhou, J.; Tian, Y.; Xing, Z. Mechanical Properties on Various FRP-Reinforced Concrete in Cold Regions. Buildings 2023, 13, 138. https://doi.org/10.3390/buildings13010138
Lu C, Ji Y, Zou Y, Zhou J, Tian Y, Xing Z. Mechanical Properties on Various FRP-Reinforced Concrete in Cold Regions. Buildings. 2023; 13(1):138. https://doi.org/10.3390/buildings13010138
Chicago/Turabian StyleLu, Chenxuan, Yongcheng Ji, Yunfei Zou, Jieying Zhou, Yuqian Tian, and Zhiqiang Xing. 2023. "Mechanical Properties on Various FRP-Reinforced Concrete in Cold Regions" Buildings 13, no. 1: 138. https://doi.org/10.3390/buildings13010138
APA StyleLu, C., Ji, Y., Zou, Y., Zhou, J., Tian, Y., & Xing, Z. (2023). Mechanical Properties on Various FRP-Reinforced Concrete in Cold Regions. Buildings, 13(1), 138. https://doi.org/10.3390/buildings13010138







