On the Seismic Behavior of Masonry Infilled Frame Structures
Abstract
1. Introduction
2. Behaviour of Masonry Infill Walls
2.1. Failure Modes
2.1.1. On Masonry Infill Wall
- Purely Flexural. It is identified as the case in which frame and infill wall cooperate as a unique element during a low loading phase. Since it does not reach a failure state from this behaviour, the mode is not considered as a primary failure mechanism.
- Sliding Shear. This failure occurs from the shear failure on the bed joint layer of the masonry infill wall. It is one of the most important failure modes, which decreases the stiffness of the panel and may create local deficiencies on the frame, but not an ultimate failure because the panel maintain some lateral strength capacity for the infilled frame. The mode occurs in masonry walls with a weak mortar joint and a strong frame.Multiple Sliding Shear. This mode is a special case of the previous one. While the single sliding shear is usually observed for an individual layer located near the middle of the panel, for the case of multiple sliding, the formations are distributed along the height of the panel, creating fewer local problems in the RC frame.
- Diagonal Compression. Occurs from the crushing of the infill. It may be located on the central region, and it is associated with slender infill walls and out-of-plane buckling.
- Corner Crushing. Crushing by compression located on one or more corners of the masonry panel, with probability of occurrence for weak infills within frames with strong members and weak joints.
- Diagonal Cracking. It is the formation of cracks along the infill compression strut, or also in the horizontal layer along the panel’s half height. It is common to occur together with sliding shear, corner crushing, or frame failure modes.
- Out-of-Plane. It is characterised by a more destructive and spectacular failure compared to in-plane failures. Seismic action does not occur perfectly aligned to the building directions. Therefore, the failure often occurs with a combination of in-plane and out-of-plane forces, with initial cracking caused by in-plane forces that weaken the wall substantially. Masonry walls, as infills for frame structures, due to the interaction with the bounding frame can develop out-of-plane resistance through the arching mechanism, which is mainly dependent on the slenderness of the wall, on the compressive strength of the masonry and on the support conditions. The risk for this type of failure can be greatly reduced by decreasing distances between supports, use of proper floor-to-ceiling supports, and attachment between walls and frames, however the available knowledge in this regard is still limited, especially for non-pure out-of-plane failure considering prior in-plane damage.
- Frame Failure. An obvious possibility for the failure is the formation of plastic hinges in the columns, or shear failure in the beam-column joints or columns. It can be caused by either a weak frame or weak joints with a strong infill. The failure induced by the infill walls may arise from a number of factors. The increase of stiffness and the forces introduced by the infills can elevate the axial stresses on columns (both in tension and compression). The diagonal truss of the infill creates a concentration region where the wall transfers some of the stress near the joints, resulting in increased shear stresses on both columns and the beams. In such a scenario the joints may fail, causing the failure of the system. The flexural and shear demands may increase even more if a short column is formed by an infill shear failure or by the existence of openings.
2.1.2. Structural Implications
3. Design Codes and Recommendations
3.1. Concepts and Ductility
3.2. Infilled Structures
- Structural isolation by creating gaps between the masonry wall and the frame to allow free deformation by the frame. Some national codes adopting this philosophy are a Russian code (SNIP-II-7-81 1996 [13]), or an old New Zealand code (NZS1170.5 1995 [14], replaced later by the 2004 version [15]). It has some disadvantages regarding fire protection, thermal and sound insulation, or higher vulnerability for out-of-plane collapses during an earthquake. The advantages are mainly a better control of the structural behavior, in terms of stiffness, brittle failures, and undesirable effects created by irregular placement of infills.
- Use of the infill wall’s characteristics to reduce costs of construction and improve the comfort and seismic behavior of the buildings. Codes following this philosophy, such as the European one (CEN 2003 [12]), recommend some procedures to achieve realistic natural frequencies, stiffness and seismic design loads, to avoid irregularities, to account for openings, provisions of out-of-plane collapses, etc.
- Mandatory reinforcement of the masonry infill walls that is proposed from the International Building Code (ICC 2003 [16]). Infill masonry walls are permitted during design, but they must follow some stricter rules on their construction in order to improve their quality and control of the assumed conditions during the design of structures.
| Country & References | D | Natural Period | Min. Force (%) | Irregularity | K | Drift | Infill | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frame | Inf | Plan | Elev. | σi | Ki | O | OOP | |||||
| Greece (EAK 2000; nGCI 2012) [22,23] | - | - | - | - | - | - | - | - | - | - | - | - |
| USA (ICC 2003) [16] | N | X | N | N | N | N | X | N | N | N | N | N |
| USA (MSJC 2011) [24] | - | - | - | - | - | - | Y | - | Y | Y | Y | Y |
| India (IS1893-Part1 2002) [25] | Y | N | N | N | Y | X | N | N | N | N | N | |
| Israel (SI-413 1995) [26] | Y | 25 | N | Y | Y | 1.15 | N | Y | N | N | N | |
| Italy (NTC08 2008) [27] | - | - | - | - | - | - | - | - | - | - | - | - |
| Mexico (Mexican-Code 2004) [28] | - | - | - | - | - | - | - | - | Y | Y | - | Y |
| Nepal (NBC-105 1994; NBC-201 1994) [29,30] | Y | 25 | N | Y | Y | 2 | Y | Y | N | Y | Y | |
| New Zealand (NZS 2004) [15] | - | - | - | - | - | - | N | - | - | - | - | - |
| Philippines (NSCP 1992) [31] | Y | N | N | N | N | 1.5 | N | N | N | N | N | |
| Russia (SNIP-II-7-81 1996) [13] | - | - | - | - | - | - | - | - | - | - | - | - |
| Venezuela (COVENIN-2002 1988) [32] | Y | Rayleigh formula (*ray) | 25 | N | N | N | X | N | N | N | N | N |
| Only standard (FEMA 1998) [33] | Y | X | N | N | N | N | X | Y | Y | Y | Y | Y |
| Albania (KTP-N2-89 1989) [34] | Y | N | N | N | N | 1.2–1.5 | N | N | N | N | N | |
| Algeria (RPA 1988) [35] | Y | 25 | N | N | N | 1.42 | N | N | N | N | N | |
| Bulgaria (BGSC 1987) [36] | Y | X | N | N | N | Y | 1.5–3.0 | N | N | N | N | N |
| Canada (CSA-S304.1 2004) [37] | - | - | - | - | - | - | Y | - | Y | Y | N | - |
| China (GBJ-11 1989) [38] | Y | X | N | N | N | N | X | Y | N | N | N | N |
| Colombia (NSR 1998) [39] | Y | 25 | 100 | N | N | X | Y | N | N | N | N | |
| 25 | 100 | N | N | X | Y | N | N | N | N | |||
| Costa Rica (CFIA 1986) [40] | Y | N | N | Y | Y | X | Y | N | N | N | N | |
| Egypt (ECP 1988) [41] | Y | 25 | 100 | N | N | 2 | N | N | N | N | N | |
| Ethiopia (ESCP-1 1983) [42] | Y | 25 | 100 | N | N | 1.25Y | NNN | YNY | N | N | N | |
| Europe (CEN 2003) [12] | Y | 50–65 | N | Y | Y | 1.2 | Y | N | N | Y | Y | |
| France (AFPS 1990) [43] | Y | N | N | N | N | X | N | N | N | N | N | |
4. Lessons from Earthquakes
4.1. Recent Earthquakes in Europe
Observed Damages
- RC buildings with 3 up to 6 storeys, with masonry infill walls, exhibited the larger damages.
- Ground storeys without wall infills, used for commerce/services, can be decisive for the building behaviour and performance.
- Higher level of damage occurred at the lower storeys in both structural and non-structural elements.
- Poor reinforcement detailing in the beam-column joints resulted in the formation of plastic hinges in the columns prior to beams.
- Several collapses and buildings marked for demolition were due to shear failure of the columns, designed as slender columns.
- Non-structural elements with very poor performance caused major economic losses and some deaths.
- A great number of failures of masonry infill walls (due to in-plane actions) was recorded and detachments of the exterior panels in façade’s masonry walls, as well.
- Most damages on the buildings come from non-structural elements, such as infill walls.
- Building collapses occurred from irregularities in plan or in elevation from both structural and/or non-structural elements.
- Structural damages are mainly present in columns, walls and beam-column joints due to insufficient shear capacity.
4.2. Seismic Performance
5. Experimental Work
6. Numerical Modelling
6.1. Macro-Modelling
6.1.1. In-Plane Models
6.1.2. Out-Plane Models
6.2. Micro-Modelling
6.3. Reinforced Concrete Models
6.3.1. Concrete Material
6.3.2. Steel Material
7. Final Remarks
7.1. Earthquake Lessons
- Stirrups and hoops (inadequate quantity and detailing),
- Detailing (bond, anchorage and lap-splices),
- Inadequate capacity and failure (shear, flexural),
- Inadequate shear capacity of the joints,
- Strong-beam weak-column mechanism,
- Short-column mechanism,
- Structural irregularities (in plan or in elevation: torsion, soft-storey, etc.),
- Pounding,
- Damages in structural secondary elements (cantilevers, stairs, etc.), and
- Damages in non-structural elements.
7.2. Structural Codes
- Dynamic analysis on irregular buildings,
- Empirical formulas to compute the natural period of the structure,
- Minimum seismic design ratio for the structural elements, preventing the resistance of the structure to be decided by brittle infill walls,
- Recommendations regarding irregularities in plan and in elevation,
- Lower response by reducing factors for structures with infill walls compared to bare-frame structures, in order to compensate for increased uncertainties and the decrease of ductility of the building,
- Limitation of deformations to control damage,
- Specifications for wall slenderness to prevent out-of-plane collapses,
- Suggestions regarding openings, and
- Suggestions regarding retrofitting of the walls.
7.3. Experimental Work
- Wall aspect-ratio (height/length)—Decrease of aspect-ratio leads to an increase of the ultimate capacity.
- Boundary conditions of frame-infill—Initial stiffness is not affected; The presence of gaps decreases substantially the ultimate capacity of the frame.
- Gaps on infill-frame interface—Masonry still contributes to the horizontal strength of the system, but the efficiency is affected.
- Wall stiffness—Stiffer walls allow higher load carrying capacity; Building stiffness does not increase linearly with the number of walls.
- Openings on the walls—They decrease the ultimate capacity; Openings near edges reduce more the load capacity of the wall compared to centered openings; (usually) they increase the ductility of the system.
- Reinforcement of masonry wall (i.e., mesh reinforcement)—Increases both initial stiffness and ultimate capacity.
- Gravity loading on columns—Higher level of vertical loading leads to an increase of stiffness and resistance of the system due to increased confinement of the wall.
- Frame stiffness—Stiffer frames lead to higher ultimate capacity of the system, offering better confinement and contact between frame and infill.
- Bonding quality between wall and frame—Affects the ultimate capacity of the system.
- Position of infill—Eccentricity of the wall relative to the panel middle leads to out-of-plane bending effects, reducing both initial stiffness and ultimate capacity of the system.
- Horizontal bond beam and other retrofitting strategies –capable of increasing the ductility of the system.
7.4. Numerical Modelling
7.5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Silva, V. Development of Open Models and Tools for Seismic Risk Assessment: Application to Portugal. Ph.D. Thesis, University of Aveiro, Aveiro, Portugal, 2013. [Google Scholar]
- MunichRe. Topics Geo: Natural Catastrophes 2011 Analyses, Assessments, Positions; 2012 Issue, MunichRe: Munich, Germany, 2012. [Google Scholar]
- Dias-Oliveira, J. Seismic Assessment of Existing Concrete Buildings. Master’s Thesis, University of Aveiro, Aveiro, Portugal, 2013. [Google Scholar]
- Fardis, M. Seismic Design, Assessment and Retrofitting of Concrete Buildings: Based on EN-Eurocode 8; Geotechnical, Geological and Earthquake Engineering; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Kritikos, A.I.; Ntasis, G.D.; Zitouniatis, D.G.; Lemonis, M.E.; Asteris, P.G. Lateral response evaluation of steel frame structures with masonry infills. In Proceedings of the 6th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2017), Rhodes Island, Greece, 15–17 June 2017. [Google Scholar]
- Lemonis, M.E.; Asteris, P.G.; Zitouniatis, D.G.; Ntasis, G.D. Modeling of the lateral stiffness of masonry infilled steel moment-resisting frames. Struct. Eng. Mech. 2019, 70, 421–429. [Google Scholar]
- Crisafulli, F.J. Seismic Behaviour of Reinforced Concrete Structures with Masonry Infills. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 1997. [Google Scholar]
- El-Dakhakhni, W.W. Experimental and Analytical Seismic Evaluation of Concrete Masonry-Infilled Steel Frames Retrofitted Using GFRP Laminates. Ph.D. Thesis, Drexel University, Philadelphia, PA, USA, 2002. [Google Scholar]
- El-Dakhakhni, W.W.; Elgaaly, M.; Hamid, A.A. Three-strut model for concrete masonry-infilled steel frames. ASCE J. Struct. Eng. 2003, 129, 177–185. [Google Scholar] [CrossRef]
- Asteris, P.G.; Kakaletsis, D.J.; Chrysostomou, C.Z.; Smyrou, E. Failure modes of infilled frames. Electron. J. Struct. Eng. 2011, 11, 11–20. [Google Scholar]
- Shing, P.B.; Mehrabi, A.B. Behaviour and analysis of masonry-infilled frames. Prog. Struct. Eng. Mater. 2002, 4, 320–331. [Google Scholar] [CrossRef]
- CEN. Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2003. [Google Scholar]
- SNIP-II-7-81; Building Code on Construction in Seismic Areas. The Ministry for Construction of Russia: Moscow, Russia, 1996.
- NZS1170.5; Code of Practice for the Design of Concrete Structures, Part 1. Standards Association of New Zealand: Wellington, New Zealand, 1995.
- NZS:1170.5:2004; Structural Design Actions Part 5: Earthquake Actions. Standards New Zealand: Wellington, New Zealand, 2004.
- ICC. IBC—International Building Code; International Code Council: Reston, VA, USA, 2003. [Google Scholar]
- Chronopoulos, M.; Chronopoulos, P. Recent Greek provisions for RC structures with urm infills. Open Constr. Build. Technol. J. 2012, 6, 92–112. [Google Scholar] [CrossRef][Green Version]
- Nazief, M. Finite Element Characterization of the Behaviour of Masonry Infill Shear Walls with and without Openings. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2014. [Google Scholar]
- Kaushik, H.B.; Rai, D.C.; Jain, S.K. Code approaches to seismic design of masonry-infilled reinforced concrete frames: A state-of-the-art review. Earthq. Spectra 2006, 22, 961–983. [Google Scholar] [CrossRef]
- FEMA. NEHRP Commentary on the Guidelines for the Seismic Rehabilitation of Buildings; FEMA-274; Applied Technology Council: Washington, DC, USA, 1997.
- FEMA. Prestandard and Commentary for the Seismic Rehabilitation of Buildings; Federal Emergency Management Agency: Washington, DC, USA, 2000.
- EAK. Greek Seismic Code; Earthquake Planning and Protection Organization: Athens, Greece, 2000.
- New Greek Code (nGCI). Interventions (and Redesign) of Existing RC Structures; Earthquake Planning and Protection Organization: Athens, Greece, 2012.
- MSJC. Building Code Requirements and Specification for Masonry Structures; Structural Engineering Institute of the American Society of Civil Engineers: Reston, CA, USA, 2011. [Google Scholar]
- IS1893-Part 1; Part I: Criteria for Earthquake Resistant Design of Structures -General Provisions and Buildings. Bureau of Indian Standards: New Delhi, India, 2002.
- SI-413; Design Provisions for Earthquake Resistance of Structures. The Standards Institution of Israel: Tel-Aviv, Israel, 1995.
- NTC08; Approvazione delle Nuove Norme Tecniche per le Costruzioni. Gazzetta Ufficiale N. 29. Ministero delle Infrastrutture: Rome, Italy, 2008.
- Mexican-Code. Complementary Technical Norms for Design and Construction of Masonry Structures; Mexico City Building Code Ltd.: Mexico City, Mexico, 2004. [Google Scholar]
- NBC-105; Nepal National Building Code for Seismic Design of Buildings in Nepal. Ministry of Housing and Physical Planning, Department of Buildings: Kathmandu, Nepal, 1994.
- NBC-201; Nepal National Building Code for Mandatory Rules of Thumb for Reinforced Concrete Buildings with Masonry Infill. Ministry of Housing and Physical Planning, Department of Buildings: Kathmandu, Nepal, 1994.
- NSCP. National Structural code of Philippines, 4th ed.; The Board of Civil Engineering of the Professional Regulation Commission: Manila, Philippines, 1992.
- COVENIN-2002; Regulations for Earthquake-Resistant Buildings. Comision de Normas Industriales: Caracas, Venezuela, 1988.
- FEMA. Evaluation of Earthquake Damaged Concrete and Masonry Wall Buildings: Basic Procedures Manual; Federal Emergency Management Agency: Washington, DC, USA, 1998.
- KTP-N2-89; Earthquake Resistant Design Regulations. Seismological Center, Academy of Sciences of Albania, Department of Design, Ministry of Construction: Tirana, Albania, 1989.
- RPA. Algerian Earthquake Resistant Regulations; Ministry of Town-Planning and Construction: Algiers, Algeria, 1988.
- BGSC. Code for Design of Buildings and Structures in Seismic Regions; Bulgarian Academy of Science Committee of Territorial and Town System at the Council of Ministers: Sofia, Bulgaria, 1987. [Google Scholar]
- CSA-S304.1; Design of Masonry Structures S304.1-04. Canadian Standards Association: Mississauga, ON, Canada, 2004.
- GBJ-11; Seismic Design Code for Buildings and Structures. Building Industry Press: Beijing, China, 1989.
- NSR. Colombian Standards for Seismic Resistant Design and Construction; Associación Colombiana de Ingeniería Sísmica: Bogota, Colombia, 1998. [Google Scholar]
- CFIA. Seismic Code of Costa Rica; Federal College of Engineers and Architects of Costa Rica: San Jose, Costa Rica, 1986.
- ECP. Regulations for Earthquake Resistant Design of Buildings in Egypt; Egyptian Society for Earthquake Engineering: Cairo, Egypt, 1988. [Google Scholar]
- ESCP-1; Code of Practice for Loading. Ministry of Urban Development and Housing: Addis Ababa, Ethiopia, 1983.
- AFPS. Recommendations for the Redaction of Rules Relative to the Structures and Installations Built in Regions Prone to Earthquakes; French Association of Earthquake Engineering: Paris, France, 1990. [Google Scholar]
- EM-DAT. OFDA/DRED International Disaster Database; Universitá Catholique de Louvain: Brussels, Belgium, 2013; Available online: www.emdat.be (accessed on 5 May 2020).
- Daniell, J. CATDAT Global Socio-Economic Databases, 2009–2012; Digital Database: Karlsruhe, Germany, 2013. [Google Scholar]
- GEMECD. Consulted in 2014. Global Earthquake Model—Earthquake Consequences Database. Available online: http://gemecd.org/ (accessed on 26 June 2022).
- Rodrigues, H.; Romão, X.; Costa, A.; Arêde, A.; Varum, H.; Guedes, J.; Vicente, R.; Costa, A.; Paupério, E. Sismo de l’aquila de 6 de Abril de 2009. Ensinamentos para Portugal. In Proceedings of the 8th National Congress of Seismology and Seismic Engineering (SISMICA 2010), Aveiro, Portugal, 20–23 October 2010. [Google Scholar]
- Vicente, R.; Rodrigues, H.; Costa, A.; Varum, H.; Mendes-da Silva, J. Masonry enclosure walls: Lessons learnt from the recent abruzzo earthquake. In Proceedings of the 14th European Conference on Earthquake Engineering 2010, Ohrid, North Macedonia, 30 August–3 September 2010. [Google Scholar]
- Romão, X. Deterministic and Probabilistic Methods for Structural Seismic Safety Assessment. Ph.D. Thesis, University of Oporto, Oporto, Portugal, 2013. [Google Scholar]
- Barbosa, A.; Fahnestock, L.; Fick, D.; Gautam, D.; Soti, R.; Wood, R.; Moaveni, B.; Stavridis, A.; Olsen, M.; Rodrigues, H. Performance of medium-to-high rise reinforced concrete frame buildings with masonry infill in the 2015 gorkha, nepal, earthquake. Earthq. Spectra 2017, 33, 197–218. [Google Scholar] [CrossRef]
- De Luca, F.; Woods, G.E.D.; Galasso, C.; D’Ayala, D. RC infilled building performance against the evidence of the 2016 EEFIT Central Italy post-earthquake reconnaissance mission: Empirical fragilities and comparison with the FAST method. Bull. Earthq. Eng. 2018, 16, 2943–2969. [Google Scholar] [CrossRef]
- Mavroulis, S.; Andreadakis, E.; Spyrou, N.; Antoniou, V.; Skourtsos, E.; Papadimitriou, P.; Kasssaras, I.; Kaviris, G.; Tselentis, G.; Voulgaris, N.; et al. UAV and GIS based rapid earthquake-induced building damage assessment and methodology for EMS-98 isoseismal map drawing: The June 12, 2017 Mw 6.3 Lesvos (Northeastern Aegean, Greece) earthquake. Int. J. Disaster Risk Reduct. 2019, 37, 101169. [Google Scholar] [CrossRef]
- Vlachakis, G.; Vlachaki, E.; Lourenço, P.B. Learning from failure: Damage and failure of masonry structures, after the 2017 Lesvos earthquake (Greece). Eng. Fail. Anal. 2020, 117, 104803. [Google Scholar] [CrossRef]
- Gurbuz, T.; Cengiz, A.; Kolemenoglu, S.; Demir, C.; Ilki, A. Damages and Failures of Structures in İzmir (Turkey) during the October 30, 2020 Aegean Sea Earthquake. J. Earthq. Eng. 2022. Available online: https://www.tandfonline.com/doi/abs/10.1080/13632469.2022.2086186 (accessed on 26 June 2022). [CrossRef]
- Bilgin, H.; Shkodrani, N.; Hysenlliu, M.; Ozmen, H.; Isik, E.; Harirchian, E. Damage and performance evaluation of masonry buildings constructed in 1970s during the 2019 Albania earthquakes. Eng. Fail. Anal. 2022, 131, 105824. [Google Scholar] [CrossRef]
- Macabuag, J.; Altheim, C.; Thorvaldsdottir, S.; Perks, D. Damage assessments by International Engineers following the Albania earthquake of November 2019. Int. J. Disaster Risk Reduct. 2022, 72, 2022. [Google Scholar] [CrossRef]
- Lulić, L.; Ožić, K.; Kišiček, T.; Hafner, I.; Stepinac, M. Post-Earthquake Damage Assessment—Case Study of the Educational Building after the Zagreb Earthquake. Sustainability 2021, 13, 6353. [Google Scholar] [CrossRef]
- Uroš, M.; Šavor Novak, M.; Atalić, J.; Sigmund, Z.; Baniček, M.; Demšić, M.; Hak, S. Post-earthquake damage assessment of buildings—Procedure for conducting building inspections. Građevinar 2020, 72, 1089–1115. [Google Scholar] [CrossRef]
- Ricci, P.; De Luca, F.; Verderame, G.M. 6th April 2009 l’aquila earthquake, Italy: Reinforced concrete building performance. Bull. Earthq. Eng. 2011, 9, 285–305. [Google Scholar] [CrossRef]
- Mosalam, K.M.; Gunay, M.S. Chapter 23: Seismic analysis and design of masonry-infilled frames. In Structural and Geotechnical Engineering; Kunnath, S.K., Ed.; Encyclopaedia of Life Support Systems (EOLSS) Publishers: Oxford, UK, 2012. [Google Scholar]
- Estêvão, J. Efeitos da Ação Sísmica no Comportamento de Edifícios de Betão Armado com Alvenarias de Enchimento. Ph.D. Thesis, Technical University of Lisbon, Lisbon, Portugal, 2012. [Google Scholar]
- Hamburger, R.O.; Meyer, J.D. The performance of steel-frame buildings with infill masonry walls in the 1906 San Francisco earthquake. Earthq. Spectra 2006, 22, S43–S67. [Google Scholar] [CrossRef]
- Tiedemann, H. A statistical evaluation of the importance of non-structural damage to buildings. In Proceedings of the 7th World Conference on Earthquake Engineering, Istanbul, Turkey, 8–13 September 1980; Volume 6, pp. 617–624. [Google Scholar]
- Carino, N.J.; Chung, R.M.; Lew, H.S.; Taylor, A.W.; Walton, W.D. 1994 Northridge Earthquake: Performance of Structures, Lifelines and Fire Protection Systems; NIST SP 862; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1994.
- Watanabe, F. Behavior of reinforced concrete buildings during the hyougoken-nanbu earthquake. Cem. Concr. Compos. 1997, 19, 203–211. [Google Scholar] [CrossRef]
- Tezcan, S.S.; Ipek, M. A reconnaissance report: 1995 dinar, turkey, earthquake. Eng. Struct. 1996, 18, 906–916. [Google Scholar] [CrossRef]
- Jain, S.K.; Murty, C.V.; Arlekar, J. Some observations on engineering aspects of the Jabalpur earthquake of 22 May 1997. Spec. Earthq. 1997, 32, 1–21. [Google Scholar]
- Adalier, K.; Aydingun, O. Structural engineering aspects of the June 27, 1998 adana-ceyhan (Turkey) earthquake. Eng. Struct. 2001, 23, 343–355. [Google Scholar] [CrossRef]
- Bruneau, M. Building damage from the marmara, turkey earthquake of August 17, 1999. J. Seismol. 2002, 6, 357–377. [Google Scholar] [CrossRef]
- Sezen, H.; Whittaker, A.S.; Elwood, K.J.; Mosalam, K.M. Performance of reinforced concrete buildings during the august 17, 1999 kocaeli, turkey earthquake, and seismic design and construction practise in Turkey. Eng. Struct. 2003, 25, 103–114. [Google Scholar] [CrossRef]
- Elenas, A. Athens earthquake of 7 September 1999: Intensity measures and observed damages. ISET J. Earthq. Technol. 2003, 40, 77–97. [Google Scholar]
- Naeim, F.; Lew, M.; Huang, S.C.; Lam, H.K.; Carpenter, L.D. The performance of tall buildings during the 21 september 1999 chi-chi earthquake, Taiwan. Struct. Des. Tall Build. 2000, 9, 137–160. [Google Scholar] [CrossRef]
- Tsai, K.C.; Hsiao, C.P.; Bruneau, M. Overview of building damages in 921 chi-chi earthquake. Earthq. Eng. Eng. Seismol. 2000, 2, 93–108. [Google Scholar]
- Yin, P. Building Performance in the Taiwan Earthquake: A Review of Nantou County; Department of Public Works, Bureau of Engineering: Los Angeles, CA, USA, 2000.
- Humar, J.M.; Lau, D.; Pierre, J.-R. Performance of buildings during the 2001 bhuj earthquake. Can. J. Civ. Eng. 2001, 28, 979–991. [Google Scholar] [CrossRef]
- Sato, T.; Hamada, M.; Hayasi, Y.; Hisada, Y.; Kato, T.; Katta, V.; Lakhina, G.S.; Malik, J.N.; Miyashita, K.; Mori, J.J.; et al. A Comprehensive Survey of the 26 January 2001 Earthquake (Mw 7.7) in the State of Gujarat, India; Grant-in-Aid for Specially Promoted Research Provided by the Japanese Ministry of Education, Culture, Sports, Science and Technology; Hirosaki University: Hirosaki, Japan, 2001. [Google Scholar]
- Sinha, R.; Shaw, R.; Goyal, A.; Saita, J.; Choudhury, M.; Arai, H.; Jaiswal, K.; Pribadi, K.; Arya, A.S. The Bhuj Earthquake of January 26, 2001: Consequences and Future Challenges; Department of Civil Engineering, Indian Institute of Technology Bombay: Mumbai, India; Earthquake Disaster Mitigation Research Center: Kyoto, Japan, 2001. [Google Scholar]
- Tanvir Wasti, S.; Özcebe, G. Seismic Assessment and Rehabilitation of Existing Buildings; Springer: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Doĝangü, A. Performance of reinforced concrete buildings during the May 1, 2003 bingöl earthquake in turkey. Eng. Struct. 2004, 26, 841–856. [Google Scholar] [CrossRef]
- Kaplan, H.; Yilmaz, S.; Binici, H.; Yazar, E.; Çetinkaya, N. May 1, 2003 turkey-bingöl earthquake: Damage in reinforced concrete structures. Eng. Fail. Anal. 2004, 11, 279–291. [Google Scholar] [CrossRef]
- Goto, Y.; Hamada, M.; Aydan, O.; Unjoh, S.; Sugano, T.; Nakajima, H.; Tomita, T.; Takeuchi, M.; Furukawa, N.; Wong, S.F.; et al. The Damage Induced by Sumatra Earthquake and Associated Tsunami of December 26, 2004; Japan Society of Civil Engineers: Tokyo, Japan, 2005. [Google Scholar]
- Saatcioglu, M.; Ghobarah, A.; Nistor, I. Effects of the December 26, 2004 Sumatra earthquake and tsunami on physical infrastructure. ISET J. Earthq. Technol. 2005, 42, 79–94. [Google Scholar]
- Sinadinovki, C. The event of 26th of December 2004—The biggest earthquake in the world in the last 40 years. Bull. Earthq. Eng. 2006, 4, 131–139. [Google Scholar] [CrossRef]
- Kaushik, H.B.; Jain, S.K. Impact of great december 26, 2004 sumatra earthquake and tsunami on structures in port blair. J. Perform. Constr. Facil. 2007, 21, 128–142. [Google Scholar] [CrossRef]
- Zhao, B.; Taucer, F.; Rossetto, T. Field investigation on the performance of building structures during the 12 May 2008 Wenchuan earthquake in China. Eng. Struct. 2009, 31, 1707–1723. [Google Scholar] [CrossRef]
- Mohyeddin-Kermani, A.; Goldsworthy, H.M.; Gad, E.F. The behaviour of RC frames with masonry infill in Wenchuan earthquake. In Proceedings of the Australian Earthquake Engineering Society Conference, Ballarat, Australia, 21–23 November 2008. [Google Scholar]
- Eberhard, M.O.; Baldridge, S.; Marshall, J.; Mooney, W.; Rix, G.J. The MW 7.0 Haiti Earthquake of January 12, 2010; Technical Report, USGS-2010-1048; U.S. Geological Survey: Reston, VA, USA, 2010.
- DesRoches, R.; Comerio, M.; Eberhard, M.; Mooney, W.; Rix, G.J. Overview of the 2010 haiti earthquake. Earthq. Spectra 2011, 27, 1–21. [Google Scholar] [CrossRef]
- Kato, H.; Tajiri, S.; Mukai, T. Preliminary Reconnaissance Report of the Chile Earthquake 2010; Building Research Institute: Tsukuba, Japan, 2010. [Google Scholar]
- Cole, G.L.; Dhakal, R.P.; Turner, F.M. Building pounding damage observed in the 2011 christchurch earthquake. Earthq. Eng. Struct. Dyn. 2012, 41, 893–913. [Google Scholar] [CrossRef]
- Ismail, N.; Griffith, M.; Ingham, J. Performance of masonry buildings during the 2010 Darfield (New Zealand) earthquake. In Proceedings of the 11th North American Masonry Conference (NAMC), Minneapolis, MN, USA, 5–8 June 2011. [Google Scholar]
- Takewaki, I.; Murakami, S.; Fujita, K.; Yoshitomi, S.; Tsuji, M. The 2011 off the pacific coast of tohoku earthquake and response of high-rise buildings under long-period ground motions. Soil Dyn. Earthq. Eng. 2001, 31, 1511–1528. [Google Scholar] [CrossRef]
- Thomas, F.G. The strength of brickwork. Struct. Eng. 1953, 31, 44–46. [Google Scholar]
- Ockleston, A.J. Load tests on a three story reinforced concrete buildings in johannesburg. Struct. Eng. 1955, 33, 304–322. [Google Scholar]
- Benjamin, J.R.; Williams, H.A. Behavior of one-storey walls containing opening. J. Am. Concr. Inst. 1958, 30, 605–618. [Google Scholar]
- Benjamin, J.R.; Williams, H.A. The behavior of one-storey brick shear walls. ASCE J. Strucructural Div. 1959, 124, 669–708. [Google Scholar]
- Wood, R.H. The stability of tall buildings. Proc. Inst. Civ. Eng. 1958, 11, 69–102. [Google Scholar] [CrossRef]
- Sachanski, S. Analysis of the arthquake resistance of frame buildings taking into consideration the carrying capacity of the filling masonry. In Proceedings of the 2nd World Conference on Earthquake Engineering, Tokyo, Japan, 11–18 July 1960; Volume 3, pp. 2127–2141. [Google Scholar]
- Holmes, M. Steel frames with brickwork and concrete infilling. Proc. Inst. Civ. Eng. 1961, 2, 473–478. [Google Scholar] [CrossRef]
- Holmes, M. Combined loading on infilled frames. Proc. Inst. Civ. Eng. 1963, 25, 31–38. [Google Scholar] [CrossRef]
- Jorquera, L.G. Estudio experimental sobre la resistencia de muros de albãnileria sometidos a cargas horizontales. Rev. IDIEM 1964, 3, 193–222. [Google Scholar]
- Stafford-Smith, B. Behavior of square infilled frames. ASCE J. Struct. Div. 1966, 92, 381–403. [Google Scholar] [CrossRef]
- Esteva, L. Behavior under alternating loads of masonry diaphragms framed by reinforced concrete members. In Proceedings of the International Symposium on the Effects of Repeated Loading of Materials and Structures, RILEM, Mexico City, Mexico, 15–17 September 1966. [Google Scholar]
- Polyakov, S.V. On the Interaction between Masonry Filler Walls and Enclosing Frame When Loaded in the Plane of a Wall; Translation of Earthquake Engineering Research Institute; Earthquake Engineering Research Institute: San Francisco, CA, USA, 1967; pp. 36–42. [Google Scholar]
- Yorulmaz, M.; Sozen, M.A. Behavior of Single-Story Reinforced Concrete Frames with Filler Walls; Technical Report, Structural Research Series No. 337; University of Illinois at Urbana: Champaign, IL, USA, 1968. [Google Scholar]
- Stafford-Smith, B. Model test results of vertical and horizontal loading of infilled frames. ACI J. 1968, 65, 618–625. [Google Scholar]
- Trigo, J.T. Estruturas de Painéis sob a Acção de Solicitações Horizontais; National Laboratory for Civil Engineering (LNEC): Lisbon, Portugal, 1968. [Google Scholar]
- Mallick, D.V.; Severn, R.T. Dynamic characteristics of infilled frames. Inst. Civ. Eng. 1968, 39, 261–287. [Google Scholar] [CrossRef]
- Stafford-Smith, B.; Carter, C. A method of analysis for infilled frames. Proc. Inst. Civ. Eng. 1969, 44, 31–48. [Google Scholar] [CrossRef]
- Fiorato, A.E.; Sozen, M.A.; Gamble, W.L. An Investigation of the Interaction of Reinforced Concrete Frames with Masonry Filler Walls; Technical Report UILU-ENG; Deptartment of Civil Engineering of University of Illinois: Champaign, IL, USA, 1970; pp. 70–100. [Google Scholar]
- Bonvalet, C. Influence des remplissages dans les bâtiments a ossatures soumis aux efforts horizontaux dûs aux vents et aux seismes. L’ITBTP 1970, 276, 86–107. [Google Scholar]
- Fiorato, A.E.; Sozen, M.A.; Gamble, W.L. Behavior of Five-Storey Reinforced Concrete Frames with Filler Walls; Interim Report to the Department of Defence Office of Secretary of the Army, Office of Civil Defense: Urbana, IL, USA, 1970.
- Chandrasekaran, A.R.; Chandra, B. Experimental study of infilled frames. In Proceedings of the 4th Symposium on Earthquake Engineering (SEE), Roorkee, India, 14–16 November 1970; pp. 75–80. [Google Scholar]
- Mallick, D.V.; Garg, R.P. Effect of openings on the lateral stiffness of infilled frames. Proc. Inst. Civ. Eng. 1971, 49, 193–209. [Google Scholar] [CrossRef]
- Mainstone, R.J. On the stiffnesses and strengths of infilled frames. Inst. Civ. Eng. 1971, IV, 57–90. [Google Scholar]
- Dawson, R.V. An Analytical and Experimental Study of the Lateral Load Response of Framed Structures before and after the Inclusion of Infill Walls. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 1972. [Google Scholar]
- Dawson, R.V.; Ward, M.A. Dynamic response of framed structures with infill walls. In Proceedings of the 5th World Conference on Earthquake Engineering (5WCEE), Rome, Italy, 25–29 June 1973. [Google Scholar]
- Abdul-Kadir, M.R. The Structural Behaviour of Masonry Infill Panels in Framed Structures. Ph.D. Thesis, Civil Engineering, University of Edinburgh, Edinburgh, UK, 1974. [Google Scholar]
- Leuchars, J.M.; Scrivener, J.C. Masonry infill panels subjected to cyclic in-plane loading. Bull. N. Z. Natl. Soc. Earthq. Eng. 1976, 9, 122–131. [Google Scholar] [CrossRef]
- Klingner, R.E.; Bertero, V.V. Infilled Frames in Earthquake-Resistant Construction; Report EERC/76-32; Earthquake Engineering Research Center, University of California at Berkeley: Berkeley, CA, USA, 1976. [Google Scholar]
- Klingner, R.E.; Bertero, V.V. Earthquake Resistance of Infilled Frames; American Society of Civil Engineers: Reston, VA, USA, 1978. [Google Scholar]
- Jurina, L. Pareti in muratura soggette ad azioni sismiche. Costruire 1977, 100, 1–46. [Google Scholar]
- Liauw, T.C.; Lee, S.W. On the behaviour and the analysis of multi-storey infilled frames subjected to lateral loading. Proc. Inst. Civ. Eng. 1977, 63, 641–656. [Google Scholar]
- Kahn, L.F.; Hanson, R.D. Infilled walls for earthquake strengthening. ASCE J. Struct. Div. 1979, 105, 283–296. [Google Scholar] [CrossRef]
- Liauw, T.C. An effective structural system against earthquakes—Infilled frames. In Proceedings of the 7th World Conference on Earthquake Engineering (WCEE), Istanbul, Turkey, 8–13 September 1980. [Google Scholar]
- Liauw, T.C.; Kwan, K.H. New development in research of infilled frames. In Proceedings of the 8th World Conference on Earthquake Engineering, San Francisco, CA, USA, 21–28 July 1984; Volume 4, pp. 623–630. [Google Scholar]
- Parducci, A.; Mezzi, M. Repeated horizontal displacements of infilled frames having different stiffness and connection systems—Experimental analysis. In Proceedings of the 7th World Conference on Earthquake Engineering (7WCEE), Istanbul, Turkey, 8–13 September 1980; Volume 5, pp. 193–196. [Google Scholar]
- Wei, L.; Wu, Q.; Tion, J.; Dai, G. Inelastic earthquake response analysis of brick infilled frames. In Proceedings of the 7th World Conference on Earthquake Engineering (7WCEE), Istanbul, Turkey, 8–13 September 1980; pp. 307–314. [Google Scholar]
- Brokken, S.T.; Bertero, V.V. Studies on Effects of Infills in Seismic Resistant R/C Construction; Report No UCB/EERC-81/12; Earthquake Engineering Research Center, University of California at Berkeley: Berkeley, CA, USA, 1981. [Google Scholar]
- Bertero, V.V.; Brokken, S. Infills in seismic resistant building. ASCE J. Struct. Eng. 1983, 109, 1337–1361. [Google Scholar] [CrossRef]
- Žarnić, R.; Tomazevic, M. Study of the Behavior of Masonry Infilled Reinforced Concrete Frames Subjected to Seismic Loading—Part One; Report ZRMK/IKPI-84/04; Institute for Testing and Research in Materials and Structures: Ljubljana, Yugoslavia, 1984. [Google Scholar]
- Žarnić, R.; Tomazevic, M. Study of the Behavior of Masonry Infilled Reinforced Concrete Frames Subjected to Seismic Loading—Part Two; Report ZRMK/IKPI-85/02; Institute for Testing and Research in Materials and Structures: Ljubljana, Yugoslavia, 1985. [Google Scholar]
- McBride, R.T. The Behavior of Masonry Infilled Steel Frames Subjected to Racking. Master’s Thesis, University of New Brunswick, Fredericton, NB, Canada, 1984. [Google Scholar]
- Yong, T.C. Shear Strength of Masonry Infilled Panels in Steel Frames. Master’s Thesis, University of New Brunswick, Fredericton, NB, Canada, 1984. [Google Scholar]
- Amos, K.A. The Shear Strength of Masonry Infilled Steel Frames. Master’s Thesis, University of New Brunswick, Fredericton, NB, Canada, 1985. [Google Scholar]
- Richardson, J. The Influence of Initial Gaps on Infilled Frame Behavior. Master’s Thesis, University of New Brunswick, Fredericton, NB, Canada, 1986. [Google Scholar]
- Yanev, B.; McNiven, H.D. An Experimental Program for Studying the Dynamic Response of a Steel Frame with a Variety of Infill Partitions; Report No UCB/EERC-85/16; Earthquake Engineering Mechanics, ASCE: Berkeley, CA, USA, 1985; Volume 119, pp. 1376–1386. [Google Scholar]
- Dawe, J.L.; Young, T.C. An investigation of factors influencing the behavior of masonry infill in steel frames subjected to in-plane shear. In Proceedings of the 7th International Brick Masonry Conference, Melbourne, Australia, 17–20 February 1985; Volume 2, pp. 803–814. [Google Scholar]
- Liauw, T.C.; Kwan, K.H. Static and cyclic behaviors of multistory infilled frames with different interface conditions. J. Sounds Vib. 1985, 99, 275–283. [Google Scholar] [CrossRef]
- Govindan, P.; Lakshmipathy, M.; Santhakumar, A.R. Ductility of infilled frames. ACI J. 1986, 86, 567–576. [Google Scholar]
- Govindan, P.; Lakshmipathy, M.; Santhakumar, A.R. Effect of openings in infilled frames subjected to lateral reversal cyclic load. In Proceedings of the 8th European Conference on Earthquake Engineering, Lisbon, Portugal, 7–12 September 1986. [Google Scholar]
- Stylianidis, K. Cyclic behaviour of infilled RC frames. In Proceedings of the 8th International Brick and Block Masonry Conference, Dublin, Ireland, 19–21 September 1988. [Google Scholar]
- Žarnić, R.; Tomazevic, M. An experimentally obtained method for evaluation of the behaviour of masonry infilled r/c frames. In Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo/Kyoto, Japan, 2–9 August 1988; Volume 6, pp. 162–168. [Google Scholar]
- Moghaddam, H.; Dowling, P.; Ambraseys, N. Shaking table study of brick masonry infilled frames subjected to seismic excitations. In Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo, Japan, 2–9 August 1988; Volume 8, pp. 913–918. [Google Scholar]
- Dawe, J.L.; Seah, C.K. Behaviour of masonry infilled steel frames. J. Can. Soc. Civ. Eng. 1989, 16, 865–876. [Google Scholar] [CrossRef]
- Dawe, J.L.; Seah, C.K. Out-of-plane resistance of concrete masonry infilled panels. J. Can. Soc. Civ. Eng. 1989, 16, 854–864. [Google Scholar] [CrossRef]
- Dawe, J.L.; Schriver, A.B.; Sofocleous, C. Masonry infilled steel frames subjected to dynamic load. Can. J. Civ. Eng. 1989, 16, 877–885. [Google Scholar] [CrossRef]
- Schmidt, T. Experiments on the nonlinear behavior of masonry infilled reinforced concrete frames. Annu. J. Concr. Struct. 1989, 4, 185–194. [Google Scholar]
- Valiasis, T.; Stylianidis, K.C. Masonry infilled r/c frames under horizontal loading: Experimental results. Eur. Earthq. Eng. 1989, 3, 10–20. [Google Scholar]
- Vintzeleou, E.; Tassios, T.P. Seismic behaviour and design of infilled R.C. frames. Int. J. Earthq. Eng. Eng. Seismol. 1989, 3, 22–28. [Google Scholar]
- Manos, G.C.; Mpoufidis, D.; Demosthenous, M.; Triamataki, M. Influence of masonry infill panels on the response of r. c. structures subjected to lateral loads. In Proceedings of the 5th North American Masonry Conference, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 3–6 June 1990; Volume 1, pp. 93–104. [Google Scholar]
- Žarnić, R. Inelastic Response of R/C Frames with Masonry Infill. Ph.D. Thesis, University of Ljubljana, Ljubljana, Slovenia, 1992. [Google Scholar]
- Liauw, T.C.; Kwan, K.H. Experimental study of shear wall and infilled frame on shake-table. In Proceedings of the 10th World Conference on Earthquake Engineering, Madrid, Spain, 19–24 July 1992; Volume 5, pp. 2659–2663. [Google Scholar]
- Manos, G.C.; Yasin, B.; Valiasis, T. Small scale model simulation of the cyclic behavior of infill brick panels. In Proceedings of the 6th North American Masonry Conference, Philadelphia, PA, USA, 6–9 June 1993; Volume 1, pp. 359–370. [Google Scholar]
- Mander, J.B.; Nair, B.; Wojtkhowski, K.; Ma, J. An Experimental Study of the Seismic Performance of Brick Infilled Frames with and without Retrofit; Report, Technical Report NCEER-93-0001; University at Buffalo: Buffalo, NY, USA, 1993. [Google Scholar]
- Angel, R.; Abrams, D.; Shapiro, D.; Uzarski, J.; Webster, M. Behavior of Reinforced Concrete Frames with Masonry Infills; Civil Engineering Studies, Structural Research Series No. 589, UILU-ENG; Deptartment of Civil Engineering, University of Illinois: Champaign, IL, USA, 1994; pp. 94–2005. [Google Scholar]
- Mehrabi, A.B.; Shing, P.B.; Schuller, M.P.; Noland, J.L. Performance of Masonry-Infilled R/C Frames under in-Plane Lateral Loads; Report No. CU/SR-94-6; Deptartment of Civil, Environmental, and Architectural Engineering, University of Colorado: Denver, CO, USA, 1994. [Google Scholar]
- Ishibashi, K.; Hastumata, H. Nonlinear Finite Element Analysis of Confined Masonry Walls; Individual Studies; Participants at the International Institute of Seismology and Earthquake Engineering: Tsukuba, Japan, 1994; Volume 30, pp. 293–308. [Google Scholar]
- Gergely, P.; White, R.N.; Mosalam, K.M. Evaluation and modelling of infilled frames. In Proceedings of the NCEER Workshop on Seismic Response of the Masonry Infills, San Francisco, CA, USA, 4–5 February 1994; pp. 1–56. [Google Scholar]
- Bashandy, T.; Rubiano, N.R.; Klingner, R.E. Evaluation and Analytical Verification of Infilled Frame Test Data; Report 95-1; Department of Civil Engineering, University of Texas: Austin, TX, USA, 1995. [Google Scholar]
- Mehrabi, A.B.; Shing, P.B.; Schuller, M.P.; Noland, J. Experimental evaluation of masonry-infilled RC frames. ASCE J. Struct. Eng. 1996, 122, 228–237. [Google Scholar] [CrossRef]
- Negro, P.; Verzeletti, G. Effect of infills on the global behavior of r/c frames: Energy considerations from pseudodynamic tests. Earthq. Eng. Struct. Dyn. 1996, 25, 753–773. [Google Scholar] [CrossRef]
- Durrani, A.J.; Haider, S. Seismic response of RC frames with unreinforced masonry infills. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996; Elsevier: Oxford, UK, 1996. [Google Scholar]
- Mosalam, K.M.; White, R.N.; Gergely, P. Static response of infilled frames using quasi-static experimentation. ASCE J. Struct. Eng. 1997, 123, 1462–1469. [Google Scholar] [CrossRef]
- Al-Chaar, G.K. Nonductile Behavior of Reinforced Concrete Frames with Masonry Infill Panels Subjected to in-Plane Loading. Ph.D. Thesis, University of Illinosis, Champaign, IL, USA, 1998. [Google Scholar]
- Al-Chaar, G.K.; Issa, M.; Sweeney, S. Behavior of masonry-infilled nonductile reinforced concrete frames. ASCE J. Struct. Eng. 2002, 128, 1055–1063. [Google Scholar] [CrossRef]
- Pires, F.; Rodrigues, J.; Campos-Costa, A. Experimental study of the behavior under horizontal actions of repaired masonry infilled RC frames. In Proceedings of the 11th European Conference on Earthquake Engineering, Paris, France, 6–11 September 1998. [Google Scholar]
- Chiou, Y.J.; Tzeng, J.C.; Liou, Y.W. Experimental and analytical study of masonry infilled frames. ASCE J. Struct. Eng. 1999, 125, 1109–1117. [Google Scholar] [CrossRef]
- Flanagan, R.D.; Bennett, R.M. In-plane behaviour of structural clay tile infilled frames. ASCE J. Struct. Eng. 1999, 125, 590–599. [Google Scholar] [CrossRef]
- Flanagan, R.D.; Bennett, R.M. Bidirectional behavior of structural clay tile infilled frames. ASCE J. Struct. Eng. 1999, 125, 236–244. [Google Scholar] [CrossRef]
- Buonopane, S.G.; White, R.N. Pseudodynamic testing of masonry infilled reinforced concrete frame. ASCE J. Struct. Eng. 1999, 125, 578–589. [Google Scholar] [CrossRef]
- Fardis, M.N.; Bousias, S.N.; Franchioni, G.; Panagiotakos, T.B. Seismic response and design of rc structures with plan-eccentric masonry infills. Earthq. Eng. Struct. Dyn. 1999, 28, 173–191. [Google Scholar] [CrossRef]
- Combescure, D.; Pegon, P. Application of the local to global approach to the study of infilled frame structures under seismic loading. In Proceedings of the 12th World Conference in Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Lafuente, M.; Molina, A.; Genatios, C. Seismic-resistant behavior of minor reinforced concrete frames with masonry infilled frames lateral response of infilled frames. In Proceedings of the 12 WCEE, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Dukuze, A. Behaviour of Reinforced Concrete Frames Infilled with Brick Masonry Panels. Ph.D. Thesis, University of New Brunswick, Fredericton, NB, Canada, 2000. [Google Scholar]
- Murty, C.V.; Jain, S.K. Beneficial influence of masonry infill walls on seismic performance of RC frame buildings. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 2000. [Google Scholar]
- Calvi, G.M.; Bolognini, D. Seismic response of reinforced concrete frames infilled with weakly reinforced masonry panels. J. Earthq. Eng. 2001, 5, 153–185. [Google Scholar] [CrossRef]
- Žarnić, R.; Gostič, S.; Crewe, A.; Taylor, C. 2001. Shaking table tests of 1:4 reduced-scale models of masonry infilled reinforced concrete frame buildings. Earthq. Eng. Struct. Dyn. 2001, 30, 819–834. [Google Scholar] [CrossRef]
- Felice, G.; Giannini, R. Out-of-plane seismic resistance of masonry walls. J. Earthq. Eng. 2001, 5, 253–271. [Google Scholar] [CrossRef]
- Lee, H.S.; Woo, S.-W. Effect of masonry infills on seismic performance of a 3-storey R/C frame with non-seismic detailing. Earthq. Eng. Struct. Dyn. 2002, 31, 353–378. [Google Scholar] [CrossRef]
- Pinto, A.V.; Verzeletti, G.; Molina, J.; Varum, H.; Pinho, R.; Coelho, E. Pseudo-Dynamic Tests on Non-Seismic Resisting RC Frames (Bare and Selective Retrofit Frames); Joint Research Centre: Ispra, Italy, 2002. [Google Scholar]
- Canbay, E.; Ersoy, U.; Ozcebe, G. Contribution of reinforced concrete infills to seismic behavior of structural systems. ACI Struct. J. 2003, 100, 637–643. [Google Scholar]
- Cavaleri, L.; Fossetti, M.; Papia, M. Effect of vertical loads on lateral response of infilled frames. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- El-Dakhakhni, W.W.; Hamid, A.A.; Elgaaly, M. Seismic retrofit of concrete-masonry-infilled steel frames with glass fiber-reinforced polymer laminates. J. Struct. Eng. 2004, 130, 1343–1352. [Google Scholar] [CrossRef]
- Moghaddam, H.A. Lateral load behavior of masonry infilled steel frames with repair and retrofit. ASCE J. Struct. Eng. 2004, 130, 56–63. [Google Scholar] [CrossRef]
- Yàñez, F.; Astroza, M.; Holmberg, A.; Ogaz, O. Behavior of confined masonry shear walls with large openings. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Negro, P.; Molina, F.; Magonette, G. Full scale psd tesing of a torsionally unbalanced three-storey non-seismic RC frame. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Molina, F.; Bauchet, P.; Magonette, G.; Hubert, O.; Negro, P. Bidirectional pseudodynamic technique for testing a three storey reinforced concrete building. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; Volume 75. [Google Scholar]
- Molina, F.; Bauchet, P.; Magonette, G.; Hubert, O.; Negro, P. Full scale bidirectional psd testing of the torsionally unbalanced spear structure: Method, algorithm and experimental set-up. In Proceedings of the International Workshop on SPEAR Project, Ispra, Italy, 4–5 April 2005; Volume 75. [Google Scholar]
- Colangelo, F. Pseudo-dynamic seismic response of reinforced concrete frames infilled with non-structural brick masonry. Earthq. Eng. Struct. Dyn. 2005, 34, 1219–1241. [Google Scholar] [CrossRef]
- Dolce, M.; Cardone, D.; Ponzo, F.C.; Valente, C. Shaking table tests on reinforced concrete frames without and with passive control systems. Earthq. Eng. Struct. Dyn. 2005, 34, 1687–1717. [Google Scholar] [CrossRef]
- Santhi, M.H.; Knight, G.M.S.; Muthumani, K. Evaluation of seismic performance of gravity load designed reinforced concrete frames. J. Perform. Constr. Facil. 2005, 19, 277–282. [Google Scholar] [CrossRef]
- Santhi, M.H.; Knight, G.M.S.; Muthumani, K. Evaluation of seismic response of soft-storey infilled frames. Comput. Concr. 2005, 2, 423–437. [Google Scholar] [CrossRef]
- Hashemi, A.; Mosalam, K.M. Shake-table experiment on reinforced concrete structure containing masonry infill wall. Earthq. Eng. Struct. Dyn. 2006, 35, 1827–1852. [Google Scholar] [CrossRef]
- Huang, C.; Tuan, Y.; Hsu, R. Nonlinear pushover analysis of infilled concrete frames. Earthq. Eng. Eng. Vib. 2006, 5, 245–255. [Google Scholar] [CrossRef]
- Erdem, I.; Akyuz, U.; Ersoy, U.; Ozcebe, G. An experimental study on two different strengthening techniques for RC frames. Eng. Struct. 2006, 28, 1843–1851. [Google Scholar] [CrossRef]
- Kakaletsis, D.J.; Karayannis, C.G. Experimental investigation of infilled r/c frames with eccentric openings. Struct. Eng. Mech. 2007, 26, 231–250. [Google Scholar] [CrossRef]
- Kakaletsis, D.J.; Karayannis, C.G. Influence of masonry strength and openings on infilled R/C frames under cycling loading. J. Earthq. Eng. 2008, 12, 197–221. [Google Scholar] [CrossRef]
- Griffith, M.C.; Vaculik, J.; Lam, N.T.K.; Wilson, J.; Lumantarna, L. Cyclic testing of unreinforced masonry walls in two-way bending. Earthq. Eng. Struct. Dyn. 2007, 36, 801–821. [Google Scholar] [CrossRef]
- Anil, O.; Altin, S. An experimental study on reinforced concrete partially infilled frames. Eng. Struct. 2007, 29, 449–460. [Google Scholar] [CrossRef]
- Corte, D.C.; Fiorino, L.; Mazzolani, F.M. Lateral-loading tests on a real RC building including masonry infill panels with and without FRP strengthening. ASCE J. Mater. Civ. Eng. 2008, 20, 419–431. [Google Scholar] [CrossRef]
- Arulselvan, S.; Subramanian, K. Experimental investigation on three dimensional RC infilled frame—RC plane frame interactions with slab for seismic resistance. Am. J. Appl. Sci. 2008, 5, 328–333. [Google Scholar] [CrossRef]
- Blackard, B.; Willam, K.; Mettupalayam, S. Experimental observations of masonry infilled reinforced concrete frames with openings. In Proceedings of the ACI Fall 2009 Convention, New Orleans, LA, USA, 8–11 November 2009; pp. 199–221. [Google Scholar]
- Subramanian, K.; Jayaguru, C. Lateral behavior of partially infilled reinforced concrete frames with masonry inserts. J. Civ. Eng. Res. Pract. 2009, 6, 1–10. [Google Scholar] [CrossRef]
- Okuyucu, D.; Sevil, T.; Canbay, E. Shear behavior of hollow brick infill wall panels strengthened by precast reinforced concrete panels and steel fiber reinforced plaster. A preliminary study for RC frame strengthening. In Proceedings of the WCCE-ECCE-TCCE Joint Conference, Istanbul, Turkey, 22–24 June 2009. [Google Scholar]
- Stavridis, A. Analytical and Experimental Study of Seismic Performance of Reinforced Concrete Frames Infilled with Masonry Walls. Ph.D. Thesis, University of California at Berkeley, Berkeley, CA, USA, 2009. [Google Scholar]
- Pujol, S.; Fick, D. The test of a full-scale three story RC structure with masonry infill walls. Eng. Struct. 2010, 32, 3112–3121. [Google Scholar] [CrossRef]
- Moghaddam, H.A.; Goudarzi, N. Transverse resistance of masonry infills. ACI Struct. J. 2010, 107, 461–467. [Google Scholar]
- Tasnimi, A.A.; Mohebkhah, A. Investigation on the behavior of brick-infilled steel frames with openings, experimental and analytical approaches. Eng. Struct. 2011, 33, 968–980. [Google Scholar] [CrossRef]
- Komaraneni, S.; Rai, D.C.; Singhal, V. Seismic behavior of framed masonry panels with prior damage when subjected to out-of-plane loading. Earthq. Spectra 2011, 27, 1077–1103. [Google Scholar] [CrossRef]
- Mohammadi, M.; Akrami, V.; Mohammadi-Ghazi, R. Methods to improve infilled frame ductility. J. Struct. Eng. 2011, 137, 646–653. [Google Scholar] [CrossRef]
- Mohammadi, M.; Mahalleh, R.M.G. A new infilled steel frame with engineering properties. Proc. Inst. Civ. Eng. Struct. Build. 2012, 165, 15–25. [Google Scholar] [CrossRef]
- Misira, I.S.; Ozcelik, O.; Girginb, S.C.; Kahramanc, S. Experimental work on seismic behavior of various types of masonry infilled RC frames. Struct. Eng. Mech. 2012, 44, 763–774. [Google Scholar] [CrossRef]
- Stavridis, A.; Koutromanos, I.; Shing, P.B. Shake-table tests of a three-story reinforced concrete frame with masonry infill walls. Earthq. Eng. Struct. Dyn. 2012, 41, 1089–1108. [Google Scholar] [CrossRef]
- Kurt, G.; Kurc, E.; Binici, O.; Canbay, B. Performance examination of two seismic strengthening procedures by pseudodynamic testing. J. Struct. Eng. 2012, 138, 31–41. [Google Scholar] [CrossRef]
- Kakaletsis, D.J. Rotations of RC members of infilled frames at yielding and ultimate. Open Constr. Build. Technol. J. 2012, 6, 50–62. [Google Scholar] [CrossRef][Green Version]
- Stylianidis, K.C. Experimental investigation of masonry infilled R/C frames. Open Constr. Build. Technol. 2012, 6, 194–212. [Google Scholar] [CrossRef]
- Zovkic, J.; Sigmund, V.; Guljaš, I. Cyclic testing of a single bay reinforced concrete frames with various types of masonry infill. Earthq. Eng. Struct. Dyn. 2013, 42, 1131–1149. [Google Scholar] [CrossRef]
- Pereira, M. Avaliação do Desempenho das Envolventes dos Edifícios Face à Acção dos Sismos. Ph.D. Thesis, University of Minho, Braga, Portugal, 2013. [Google Scholar]
- Dubey, S.; Kute, S. Experimental investigation on the ultimate strength of partially infilled and steel-braced reinforced concrete frames. Int. J. Adv. Struct. Eng. 2013, 5, 15. [Google Scholar] [CrossRef][Green Version]
- Markulak, D.; Radi’c, I.; Sigmund, V. Cyclic testing of single bay steel frames with various types of masonry infill. Eng. Struct. 2013, 51, 267–277. [Google Scholar] [CrossRef]
- Fang, M.-J.; Wang, J.-F.; Li, G.-Q. Shaking table test of steel frame with alc external wall panels. J. Constr. Steel Res. 2013, 80, 278–286. [Google Scholar] [CrossRef]
- Ali, H. Half Scale Three-Storey Infilled RC Building. A Comparison of Experimental and Numerical Models. Ph.D. Thesis, Rose School, University of Pavia, Pavia, Italy, 2013. [Google Scholar]
- Mansouri, A.; Marefat, M.S.; Khanmohammadi, M. Experimental evaluation of seismic performance of low-shear strength masonry infills with openings in reinforced concrete frames with deficient seismic details. Struct. Des. Tall Spec. Build. 2014, 23, 1190–1210. [Google Scholar] [CrossRef]
- Dubey, S.K.; Kute, S. An experimental investigation on the ultimate strength of epoxy-repaired braced partial infilled RC frames. Int. J. Adv. Struct. Eng. 2014, 6, 3. [Google Scholar] [CrossRef][Green Version]
- Kauffman, A.; Memari, A.M. Performance evaluation of different masonry infill walls with structural fuse elements based on in-plane cyclic load testing. Buildings 2014, 4, 605–634. [Google Scholar] [CrossRef]
- Morandi, P.; Hak, S.; Magenes, G. In-plane experimental response of strong masonry infills. In Proceedings of the 9th International Masonry Conference, Guimarães, Portugal, 7–9 July 2014. [Google Scholar]
- Rastogi, G.; Moin, K.; Abbas, S. Nonlinear response of a 1:4 scale model of 3-storey reinforced concrete frame with partially masonry infill walls. Int. J. Innov. Res. Sci. Eng. Technol. 2014, 3, 14768–14775. [Google Scholar]
- Essa, A.; Badr, M.; El-Zanaty, A.H. Effect of infill wall on the ductility and behavior of high strength reinforced concrete frames. Hous. Build. Natl. Res. Cent. 2014, 10, 258–264. [Google Scholar]
- Mainstone, R.J.; Weeks, G.A. The influence of bounding frame on the racking stiffness and strength of brick walls. In Proceedings of the 2nd International Brick Masonry Conference, Building Research Establishment, Watford, UK, 12–15 April 1970; pp. 165–171. [Google Scholar]
- Varum, H. Seismic Assessment, Strengthening and Repair of Existing Buildings. Ph.D. Thesis, University of Aveiro, Aveiro, Portugal, 2003. [Google Scholar]
- Asteris, P.G.; Antoniou, S.T.; Sophianopoulos, D.; Chrysostomou, C.Z. Mathematical macromodeling of infilled frames: State of the art. ASCE J. Struct. Eng. 2011, 137, 1508–1517. [Google Scholar] [CrossRef]
- Asteris, P.G.; Cotsovos, D.; Chrysostomou, C.Z.; Mohebkhah, A.; Al-Chaar, G.K. Mathematical micromodeling of infilled frames: State of the art. Eng. Struct. 2013, 56, 1905–1921. [Google Scholar] [CrossRef]
- Polyakov, S.V. Masonry in Framed Buildings. Gosudalst-Vennoe’stvo Literature po Straitel’ stuv i Arkitecture, Moscow, Russia; Cairns, G.L., Translator; Building Research Station: Watford, UK, 1956. [Google Scholar]
- Stafford-Smith, B. Lateral stiffness of infilled frames. ASCE J. Struct. Div. 1962, 88, 183–199. [Google Scholar] [CrossRef]
- Hendry, A. Structural Brickwork; Macmillan: London, UK, 1981. [Google Scholar]
- Tassios, T.P. Masonry infill and R/C walls under cyclic actions (an invited state-of-the-art report). In Proceedings of the 3rd International Symposium on Wall Structures, Warsaw, Poland, 1–3 June 1984. [Google Scholar]
- Liauw, T.C.; Kwan, K.H. Nonlinear behaviour of non-integral infilled frames. Comput. Struct. 1984, 18, 551–560. [Google Scholar]
- Decanini, L.D.; Fantin, G.E. Modelos simplificados de la mamposteria incluida en porticos. caracteristicas de rigidez y resistencia lateral en estado limite. Jorn. Argent. De Ing. Estruct. 1986, 2, 817–836. [Google Scholar]
- Paulay, T.; Priestley, M.J.N. Seismic Design of Reinforced Concrete and Masonry Buildings, 1st ed.; Wiley-Interscience: New York, NY, USA, 1992. [Google Scholar]
- Durrani, A.J.; Luo, Y.H. Seismic retrofit of flat-slab buildings with masonry infills. In Proceedings of the NCEER Workshop on Seismic Response of Masonry Infills, San Francisco, CA, USA, 4–5 February 1994. [Google Scholar]
- Hendry, A.W. Structural Masonry, 2nd ed.; Macmillan Press: London, UK, 1998. [Google Scholar]
- Flanagan, R.D.; Bennett, R.M. In-plane analysis of masonry infill materials. Pract. Period. Struct. Des. Constr. ASCE 2001, 6, 176–182. [Google Scholar] [CrossRef]
- Amato, G.; Fossetti, M.; Cavaleri, L.; Papia, M. An updated model of equivalent diagonal strut for infill panels. In Eurocode 8, Perspectives from the Italian Standpoint Workshop; Doppiavoce: Napoli, Italy, 2009; pp. 119–128. [Google Scholar]
- Tabeshpour, M.R. Masonry Infills in Structural Frames (Handbook, Part 18); FadakIsatis Publisher: Tehran, Iran, 2009. [Google Scholar]
- Parchuri, C.P.; Kaushik, H.B. Use of rc shear walls in strengthening of open ground story RC buildings. In Proceedings of the 8th International Conference on Structural Dynamics, Leuven, Belgium, 4–6 July 2011. [Google Scholar]
- Pradhan, P.M.; Pradhan, P.L.; Maskey, R.K. A review on partial infilled frames under lateral loads. J. Sci. Eng. Technol. 2012, 8, 142–152. [Google Scholar] [CrossRef]
- Stafford-Smith, B. Methods for predicting the lateral stiffness and strength of multi-storey infilled frames. Build. Sci. 1967, 2, 247–257. [Google Scholar] [CrossRef]
- Liauw, T.C.; Kwan, K.H. Plastic theory of infilled frames with finite interface shear strength. Proc. Inst. Civ. Eng. 1983, 75, 707–723. [Google Scholar] [CrossRef]
- Liauw, T.C.; Kwan, K.H. Plastic theory of non-integral infilled frames. Proc. Inst. Civ. Eng. 1983, 75, 379–396. [Google Scholar] [CrossRef]
- Bazan, E.; Meli, R. Seismic analysis of structures with masonry walls. In Proceedings of the 7th World Conference on Earthquake Engineering, Istanbul, Turkey, 8–13 September 1980; Volume 5, pp. 633–640. [Google Scholar]
- Thiruvengadam, V. On the natural frequencies of infilled frames. J. Earthq. Eng. Struct. Dyn. 1985, 13, 401–419. [Google Scholar] [CrossRef]
- Doudoumis, I.N.; Mitsopoulou, E.N. Non-linear analysis of multistorey infilled frames for unilateral contact conditions. In Proceedings of the 8th European Conference on Earthquake Engineerings, Lisbon, Portugal, 7–12 September 1986; Volume 3, pp. 63–70. [Google Scholar]
- Syrmakezis, C.A.; Vratsanou, V.Y. Influence of infill walls to R.C. frames response. In Proceedings of the Eighth European Conference on Earthquake Engineering, Lisbon, Portugal, 7–12 September 1986; Volume 3, pp. 47–53. [Google Scholar]
- Chrysostomou, C.Z. Effects of Degrading Infill Walls on the Nonlinear Seismic Response of Two-Dimensional Steel Frames. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 1991. [Google Scholar]
- Chrysostomou, C.Z.; Gergely, P.; Abel, J.F. A six-strut model for nonlinear dynamic analysis of steel infilled frames. Int. J. Struct. Stab. Dyn. 2002, 2, 335–353. [Google Scholar] [CrossRef]
- Hamburger, R.O.; Chakradeo, A.S. Methodology for seismic-capacity evaluation of steel-frame buildings with infill unreinforced masonry. In Proceedings of the National Earthquake Conference, Memphis, TN, USA, 2–5 May 1993; Central U.S. Earthquake Consortium: Memphis, TN, USA, 1993; Volume II, pp. 173–191. [Google Scholar]
- Saneinejad, A.; Hobbs, B. Inelastic design of infilled frames. ASCE J. Struct. Eng. 1995, 121, 634–650. [Google Scholar] [CrossRef]
- Crisafulli, F.J.; Carr, A.J. Proposed macro-model for the analysis of infilled frame structures. Bull. N. Z. Soc. Earthq. Eng. 2007, 40, 69–77. [Google Scholar] [CrossRef]
- Smyrou, E. Implementation and Verification of a Masonry Panel Model for Nonlinear Dynamic Analysis of Infilled RC Frames. Master’s Thesis, Rose School, Pavia, Italy, 2006. [Google Scholar]
- SeismoSoft. SeismoStruct (Version 100)—A Computer Programme for Static and Dynamic Nonlinear Analysis of Framed Structures. Help Documentation of the Program. 2012. Available online: http://www.seismosoft.com/ (accessed on 26 June 2022).
- Asteris, P.G. Lateral stiffness of brick masonry infilled plane frames. ASCE J. Struct. Eng. 2003, 129, 1071–1079. [Google Scholar] [CrossRef]
- Giannakas, A.; Patronis, D.; Fardis, M. The influence of the position and the size of openings to the elastic rigidity of infill walls. In Proceedings of the 8th Hellenic Concrete Conference, Kavala, Greece, 27–29 May 1987; pp. 49–56. [Google Scholar]
- El-Dakhakhni, W.W. Non-Ninear Finite Element Modeling of Concrete Masonry-Infilled Steel Frame. Master’s Thesis, Drexel University, Philadelphia, PA, USA, 2000. [Google Scholar]
- El-Dakhakhni, W.W.; Elgaaly, M.; Hamid, A.A. Finite element modeling of concrete masonry-infilled steel frame. In Proceedings of the 9th Canadian Masonry Symposium, University of New Brunswick, Fredericton, NB, Canada, 4–6 June 2001. [Google Scholar]
- ANSYS Software, Version 14.5; ANSYS-Inc.: Canonsburg, PA, USA, 2012.
- Asteris, P.G. Finite element micro-modeling of infilled frames. Electron. J. Struct. Eng. 2008, 8, 1–11. [Google Scholar]
- Kadysiewski, S.; Mosalam, K.M. Modeling of Unreinforced Masonry Infill Walls Considering in-Plane and Out-of-Plane Interaction; Report, PEER Technical Report 2008/102; University of California, Berkeley: Berkeley, CA, USA, 2009. [Google Scholar]
- Hashemi, S.A.; Mosalam, K.M. Seismic Evaluation of Reinforced Concrete Buildings Including Effects of Infill Masonry Walls; PEER 2007/100; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2007. [Google Scholar]
- Rodrigues, H.; Varum, H.; Costa, A. Simplified macro-model for infill masonry panels. J. Earthq. Eng. 2010, 14, 390–416. [Google Scholar] [CrossRef]
- Yekrangnia, M.; Asteris, P.G. Multi-strut macro-model for masonry infilled frames with openings. J. Build. Eng. 2020, 32, 101683. [Google Scholar] [CrossRef]
- Timoshenko, S.; Woinowsky, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Drydale, R.G.; Essawy, A.S. Out-of-plane bending of concrete block walls. ASCE J. Struct. Div. 1988, 114, 121–133. [Google Scholar] [CrossRef]
- Haseltine, B.A. Design of laterally loaded wall panels. Br. Ceram. Soc. 1976, 5, 115–126. [Google Scholar]
- Haseltine, B.A.; West, H.W.H.; Tutt, J.N. Design of walls to resist lateral loads. Struct. Eng. 1977, 55, 422–430. [Google Scholar]
- Hendry, A.W. The lateral strength of unreinforced brickwork. Struct. Eng. 1973, 51, 43–50. [Google Scholar]
- Klingner, R.E.; Rubiano, N.R.; Bashandy, T.R.; Sweeney, S.C. Evaluation and analytical verification of shaking table data from infilled frames. Part 2: Out-of-plane behavior. In Proceedings of the 7th North American Masonry Conference, University of Notre Dame, South Bend, IN, USA, 2–5 June 1996. [Google Scholar]
- Sobaih, M.; Abdin, M.M. Seismic analysis of infilled reinforced concrete frames. Comput. Struct. 1988, 30, 457–464. [Google Scholar] [CrossRef]
- Fardis, M.N.; Calvi, G.M. Effects of infills on the global response of reinforced concrete frames. In Proceedings of the 10th European Conference on Earthquake Engineering, Vienna, Austria, 28 August–2 September 1994; Volume 3, pp. 2331–2336. [Google Scholar]
- Negro, P.; Colombo, A. Irregularities induced by non-structural masonry panels in framed buildings. Eng. Struct. 1997, 19, 576–585. [Google Scholar] [CrossRef]
- Fardis, M.N.; Panagiotakos, T.B. Seismic design and response of bare and masonry-infilled reinforced concrete buildings. part ii: Infilled structures. J. Earthq. Eng. 1997, 1, 475–503. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Erki, M.A.; Quenneville, J.H.P. Seismic design and analysis of masonry-infilled frames. Can. J. Civ. Eng. 1995, 22, 576–587. [Google Scholar] [CrossRef]
- Balendra, T.; Huang, X. Overstrength and ductility factors for steel frames designed according to bs 5950. ASCE J. Struct. Eng. 2003, 129, 1019–1035. [Google Scholar] [CrossRef]
- Crowley, H.; Pinho, R. Simplified equations for estimating the period of vibration of existing buildings. In Proceedings of the First European Conference on Earthquake Engineering And Seismology, Geneva, Switzerland, 3–8 September 2006. [Google Scholar]
- Perera, R. Performance evaluation of masonry-infilled RC frames under cyclic loading based on damage mechanics. Eng. Struct. 2005, 27, 1278–1288. [Google Scholar] [CrossRef]
- Reflak, J.; Fajfar, P. Elastic analysis of infilled frames using substructures. In Proceedings of the 6th Canadian Conference on Earthquake Engineering, Toronto, ON, Canada, 12–14 June 1991; pp. 285–292. [Google Scholar]
- Chrysostomou, C.Z.; Asteris, P.G. On the in-plane properties and capacities of infilled frames. Eng. Struct. 2012, 41, 385–402. [Google Scholar] [CrossRef]
- Rodrigues, H.; Varum, H.; Costa, A. A non-linear masonry infill macro-model to represent the global behaviour of buildings under cyclic loading. Int. J. Mech. Mater. Des. 2008, 4, 123–135. [Google Scholar] [CrossRef]
- Muratović, A.; Ademović, N. Influence of masonry infill on reinforced concrete frame structures’ seismic response. Coupled Syst. Mech. 2015, 4, 173–189. [Google Scholar] [CrossRef]
- Mallick, D.V.; Severn, R.T. The behaviour of infilled frames under static loading. Proc. Inst. Civ. Eng. 1967, 38, 639–656. [Google Scholar] [CrossRef]
- Goodman, R.E.; Taylor, R.L.; Brekke, T.L. A model for the mechanics of jointed rock. ASCE J. Soil Mech. Found. Div. 1968, 94, 637–659. [Google Scholar] [CrossRef]
- King, G.J.W.; Pandey, P.C. The analysis of infilled frames using finite elements. Proc. Inst. Civ. Eng. 1978, 65, 749–760. [Google Scholar] [CrossRef]
- Kost, G.; Weaver, W.; Barber, R.B. Nonlinear dynamic analysis of frames with filler panels. ASCE J. Struct. Div. 1974, 100, 743–757. [Google Scholar] [CrossRef]
- Axley, J.M.; Bertero, V.V. Infill Panels: Their Influence on Seismic Response of Buildings; Report UCB/EERC-79/28; University of California at Berkeley: Berkeley, CA, USA, 1979. [Google Scholar]
- Rivero, C.; Walker, W. An analytical study of the interaction of frames and infill masonry walls. In Proceedings of the 8th World Conference on Earthquake Engineering, San Francisco, CA, USA, 21–28 July 1984; Volume 4, pp. 591–598. [Google Scholar]
- Dhanasekar, M.; Page, A.W. Influence of brick masonry infill properties on the behaviour of infilled frames. Proc. Inst. Civ. Eng. 1986, 2, 593–605. [Google Scholar]
- El-Haddad, M.H. Finite element analysis of infilled frames considering cracking and separation phenomena. Comput. Struct. 1991, 41, 439–447. [Google Scholar] [CrossRef]
- Rots, J.G. Smeared and discrete representations of localized fracture. Int. J. Fract. 1991, 51, 45–59. [Google Scholar] [CrossRef]
- Lotfi, H.R.; Shing, P.B. Interface model applied to fracture of masonry structures. J. Struct. Eng. 1994, 120, 63–80. [Google Scholar] [CrossRef]
- Lourenço, P.B. Computational Strategies for Masonry Structures. Ph.D. Thesis, Delft University, Delft, The Netherlands, 1996. [Google Scholar]
- Mehrabi, A.B.; Shing, P.B. Finite element modeling of masonry-infilled RC frames. ASCE J. Struct. Eng. 1997, 123, 604–613. [Google Scholar] [CrossRef]
- Singh, H.; Paul, D.K.; Sastry, V.V. Inelastic dynamic response of reinforced concrete infilled frames. Comput. Struct. 1998, 69, 685–693. [Google Scholar] [CrossRef]
- Chiou, Y.J.; Tzeng, J.C.; Hwang, S.C. Discontinuous deformation analysis for reinforced concrete frames infilled with masonry walls. Struct. Eng. Mech. 1998, 6, 201–215. [Google Scholar] [CrossRef]
- Dawe, J.L.; Seah, C.K.; Liu, Y. A computer model for predicting infilled frame behavior. Can. J. Civ. Eng. 2001, 28, 133–148. [Google Scholar] [CrossRef]
- Asteris, P.G. Closure to ‘lateral stiffness of brick masonry infilled plane frames’ by P. G. Asteris. ASCE J. Struct. Eng. 2005, 131, 523–524. [Google Scholar] [CrossRef]
- Zhuge, Y.; Hunt, S. Numerical simulation of masonry shear panels with distinct element approach. J. Struct. Eng. Mech. 2003, 15, 477–493. [Google Scholar] [CrossRef]
- Basiouny, W.; Ghobarah, A. Modeling of masonry infill panels for dynamic analysis. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Al-Chaar, G.K.; Mehrabi, A.B.; Manzouri, T. Finite Element Interface Modeling and Experimental Verification of Masonry-Infilled R/C Frames; Masonry Society: Longmont, CO, USA, 2008. [Google Scholar]
- Stavridis, A.; Shing, P.B. Finite-element modeling of nonlinear behavior of masonry-infilled RC frames. ASCE J. Struct. Eng. 2010, 136, 285–296. [Google Scholar] [CrossRef]
- Koutromanos, I. Numerical Analysis of Masonry-Infilled Reinforced Concrete Frames Subjected to Seismic Loads and Experimental Evaluation of Retrofit Techniques. Ph.D. Thesis, University of California at San Diego, San Diego, CA, USA, 2011. [Google Scholar]
- Koutromanos, I.; Stavridis, A.; Shing, P.B.; Willam, K. Numerical modeling of masonry-infilled RC frames subjected to seismic loads. Comput. Struct. 2011, 89, 1026–1037. [Google Scholar] [CrossRef]
- D’Ayala, D.; Worth, J.; Riddle, O. Realistic shear capacity assessment of infill frames: Comparison of two numerical procedures. Eng. Struct. 2009, 31, 1745–1761. [Google Scholar] [CrossRef]
- Ellul, F.; D’Ayala, D. Realistic Fe models to enable push-over nonlinear analysis of masonry infilled frames. Open Constr. Build. Technol. J. 2012, 6, 213–235. [Google Scholar] [CrossRef]
- Taylor, R.L. FEAP—A Finite Element Analysis Program, Version 8.1; University of California at Berkeley: Berkeley, CA, USA, 2007. [Google Scholar]
- Cavaleri, L.; Zizzo, M.; Asteris, P.G. Residual out-of-plane capacity of infills damaged by in-plane cyclic loads. Eng. Struct. 2020, 209, 109957. [Google Scholar] [CrossRef]
- Penelis, G.G.; Kappos, A.J. Earthquake-Resistant Concrete Structures; Report, E & Fn Spon (Chapman & Hall): London, UK, 1997. [Google Scholar]
- Karsan, I.D.; Jirsa, J.O. Behavior of concrete under compressive loadings. ASCE J. Struct. Div. 1969, 95, 2543–2563. [Google Scholar] [CrossRef]
- Blakeley, R.W.G.; Park, R. Prestressed concrete sections with cyclic flexure. ASCE J. Struct. Div. 1973, 99, 1717–1742. [Google Scholar] [CrossRef]
- Yankelevsky, D.Z.; Reinhardt, H.W. Model for cyclic compressive behavior of concrete. J. Struct. Eng. Mech. 1987, 113, 228–240. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. ASCE J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Popovic, S. A numerical approach to the complete stress-strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Martínez-Rueda, J.E.; Elnashai, A.S. Confined concrete model under cyclic load. Mater. Struct. 1997, 30, 139–147. [Google Scholar] [CrossRef]
- Yu, H.S. Inelastic Modeling of Reinforcing Bars and Blind Analysis of the Benchmark Tests on Beam-Column Joints under Cyclic Loading. Master’s Thesis, Rose School, Pavia, Italy, 2006. [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curve by Three Parameters; Report; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943.
- Dafalias, Y.F.; Popov, E.P. Plastic internal variables formalism of cyclic plasticity. ASCE J. Struct. Eng. 1976, 43, 645–651. [Google Scholar] [CrossRef]
- Popov, E.P.; Petersson, H. Cyclic metal plasticity: Experiments and theory. ASCE J. Struct. Eng. 1978, 104, 1371–1388. [Google Scholar] [CrossRef]
- Santhanam, T.K. Model for mild steel in inelastic frame analysis. ASCE J. Struct. Eng. 1979, 105, 199–220. [Google Scholar] [CrossRef]
- Tseng, N.T.; Lee, G.C. Simple plasticity model of two-surface type. ASCE J. Struct. Eng. 1983, 109, 795–810. [Google Scholar] [CrossRef]
- Cofie, N.G.; Krawinkler, H. Uniaxial cyclic stress-strain behavior of structural steel. ASCE J. Struct. Eng. 1985, 111, 1105–1120. [Google Scholar] [CrossRef]
- Ma, S.Y.M.; Bertero, V.V.; Popov, E.P. Experimental and Analytical Studies on Hysteretic Behavior of Reinforced Concrete Rectangular and T-Beams; Report; Earthquake Engineering Research Center, University of California at Berkeley: Berkeley, CA, USA, 1976. [Google Scholar]
- Elnashai, A.S.; Izzuddin, B.A. Modeling of material non-linearities in steel structures subjected to transient dynamic loading. Earthq. Eng. Struct. Dyn. 1993, 22, 509–532. [Google Scholar] [CrossRef]
- Menegotto, M.; Pinto, P.E. Method of Analysis for Cyclically Loaded RC Plane Frames Including Changes in Geometry and Non-Elastic Behaviour of Elements under Combined Normal Force and Bending; International Association for Bridge and Structural Engineering: Zurich, Switzerland, 1973. [Google Scholar]
- Filippou, F.C.; Popov, E.P.; Bertero, V.V. Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints; Report, UCB/EERC-83/19; Earthquake Engineering Research Center, University of California at Berkeley: Berkeley, CA, USA, 1983. [Google Scholar]
- Schmidt, T. An approach of modelling masonry infilled frames by the f.e. method and a modified equivalent strut method. Annu. J. Concr. Concr. Struct. 1989, 4, 171–180. [Google Scholar]
- Dolšek, M.; Fajfar, P. The effect of masonry infills on the seismic response of a four-storey reinforced concrete frame—A deterministic assessment. Eng. Struct. 2008, 30, 1991–2001. [Google Scholar] [CrossRef]
- Sattar, S.; Liel, A. Seismic performance of nonductile reinforced concrete frames with masonry infill walls—I: Development of a strut model enhanced by finite element models. Earthq. Spectra 2016, 32, 795–818. [Google Scholar] [CrossRef]
- Stavridis, A.; Martin, J.; Bose, S. Updating the asce-41 provisions for infilled RC frames. In Proceedings of the SEAOC Convention, San Diego, CA, USA, 12–15 September 2017. [Google Scholar]
- Lourenço, P.B.; Leite, J.C.; Paulo-Pereira, M.F. Masonry infills and earthquakes. In Proceedings of the 11th Canadian Masonry Symposium, Toronto, ON, Canada, 31 May–3 June 2009. [Google Scholar]
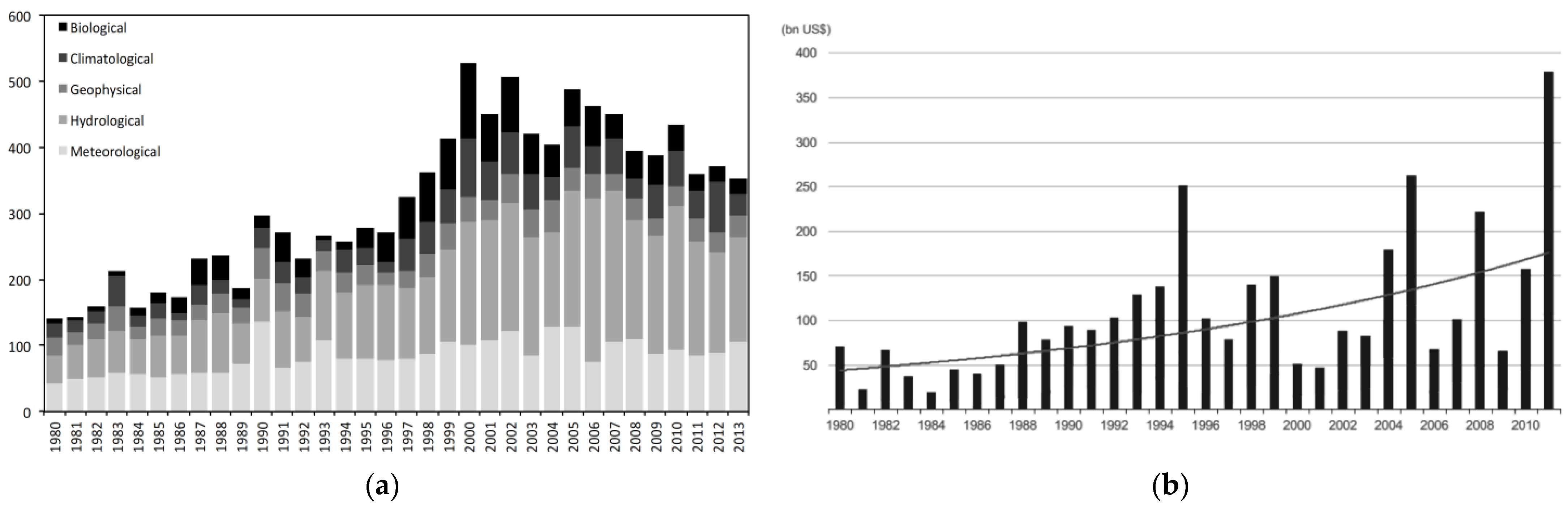

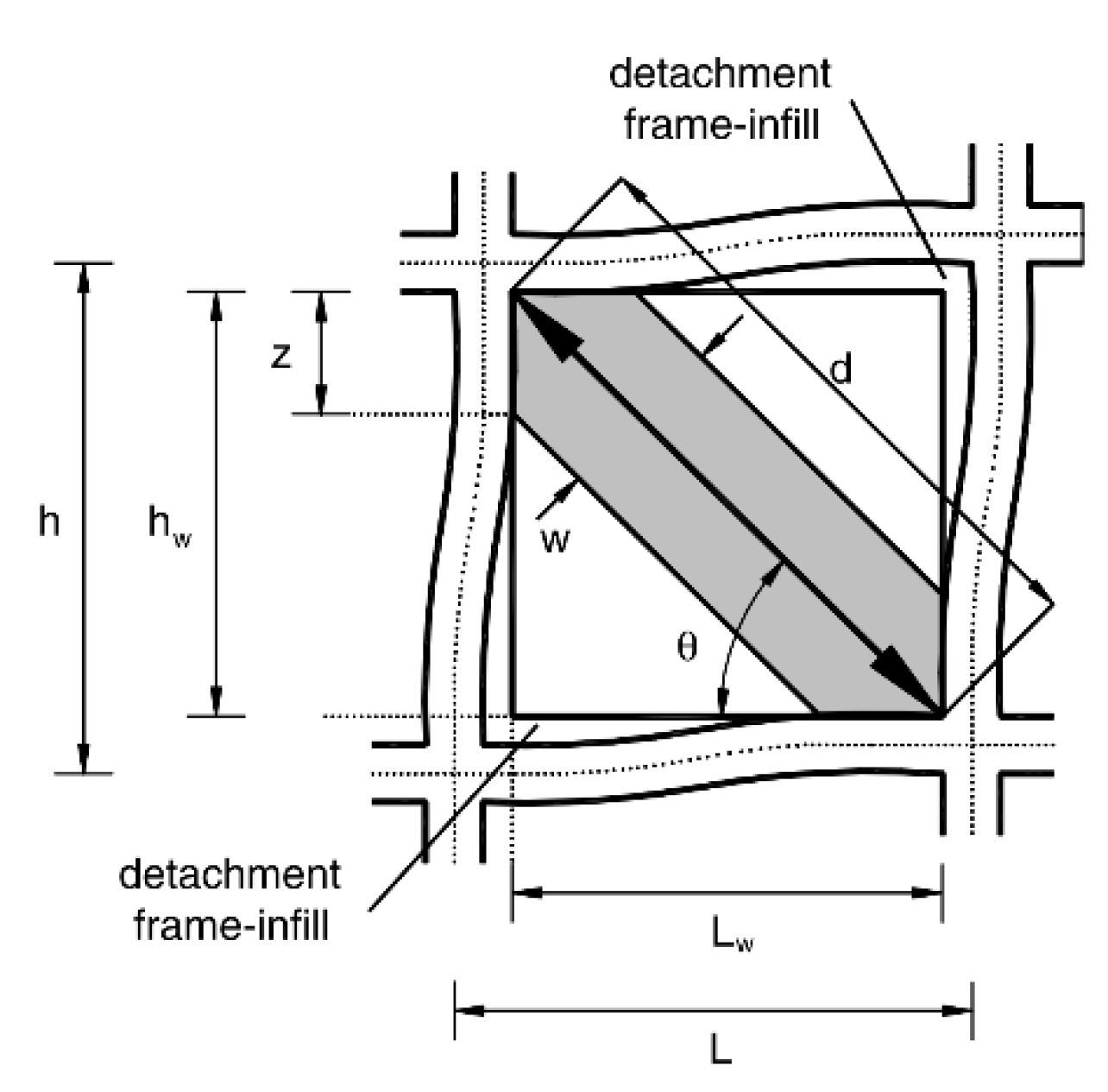
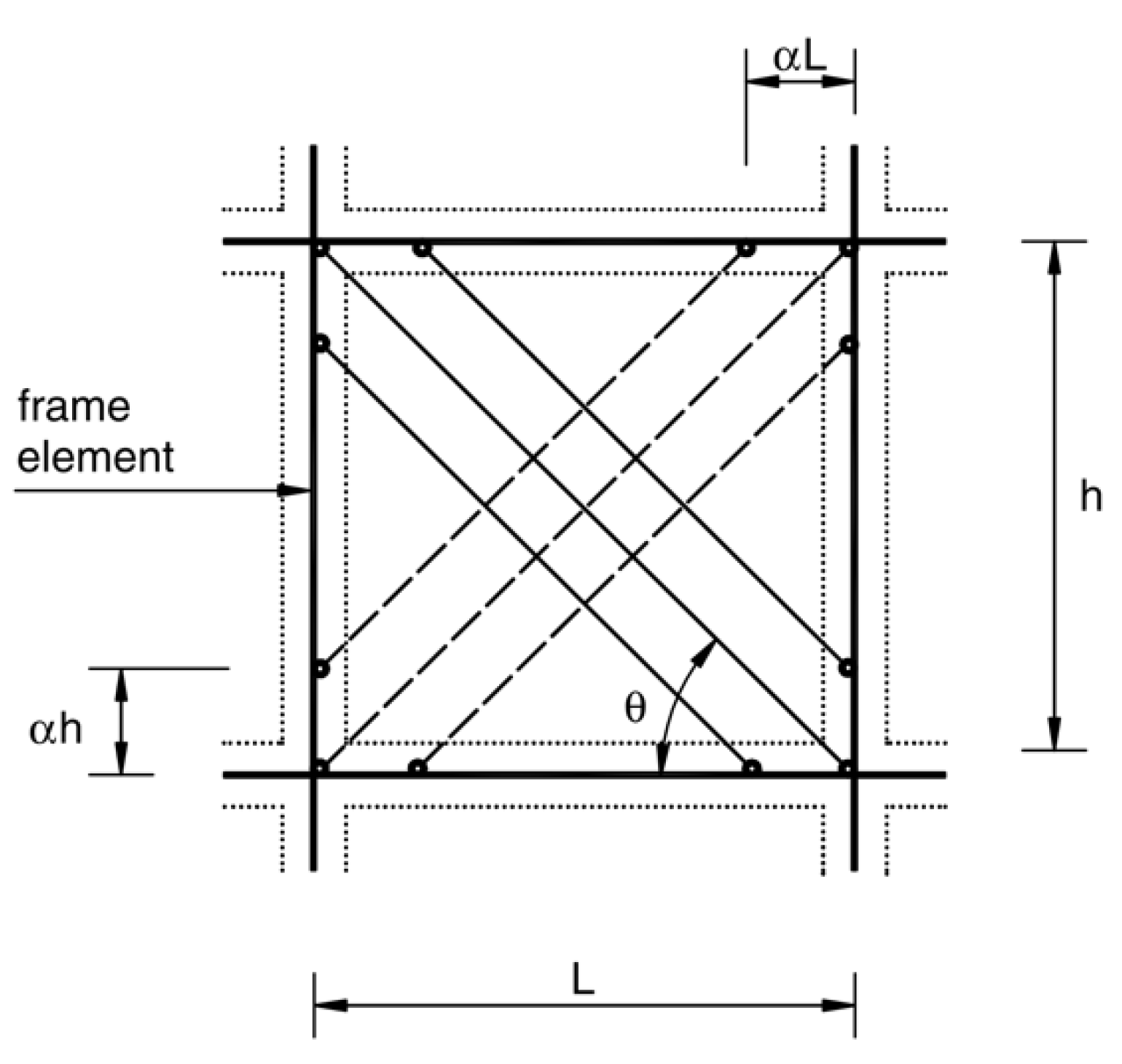
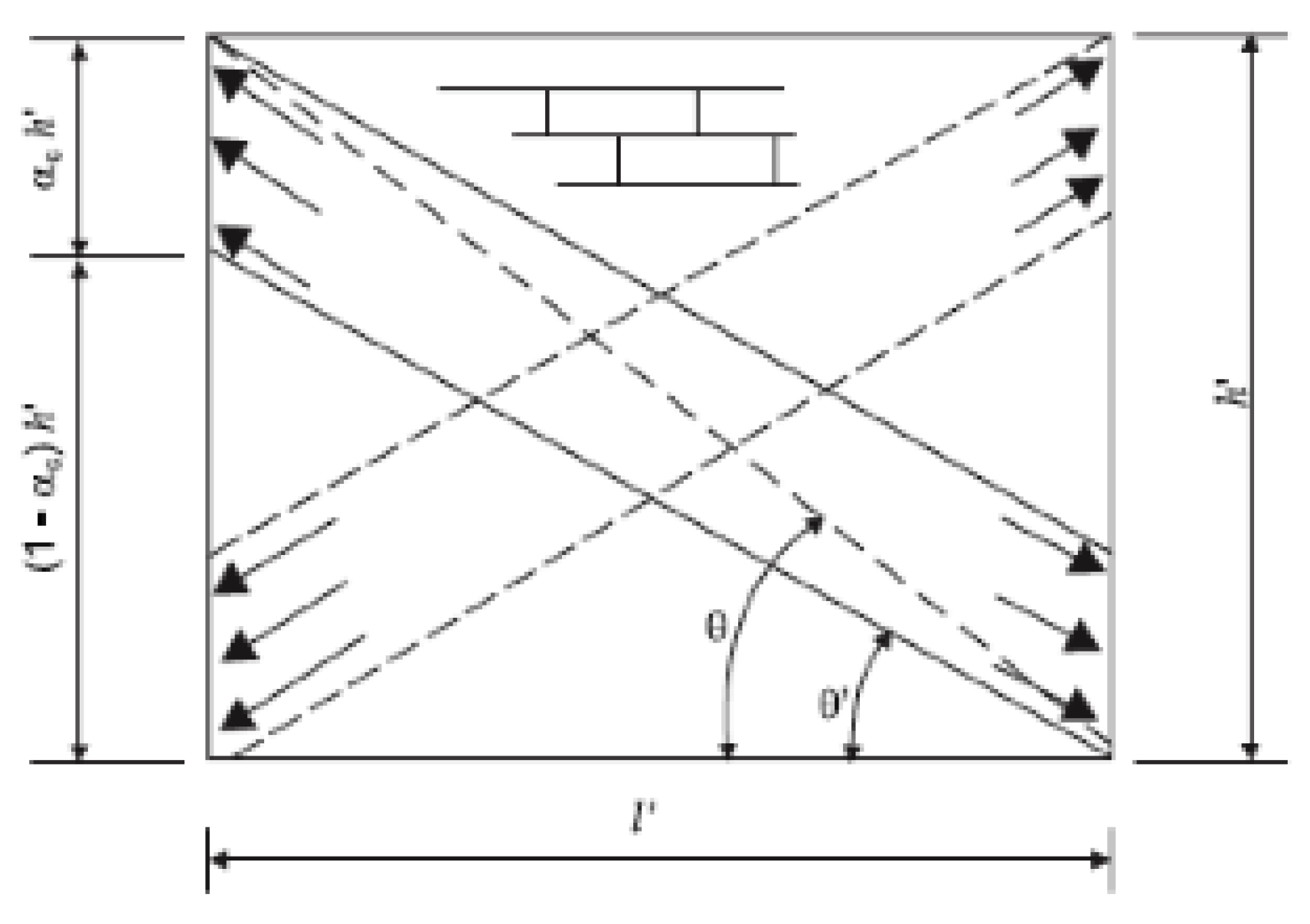
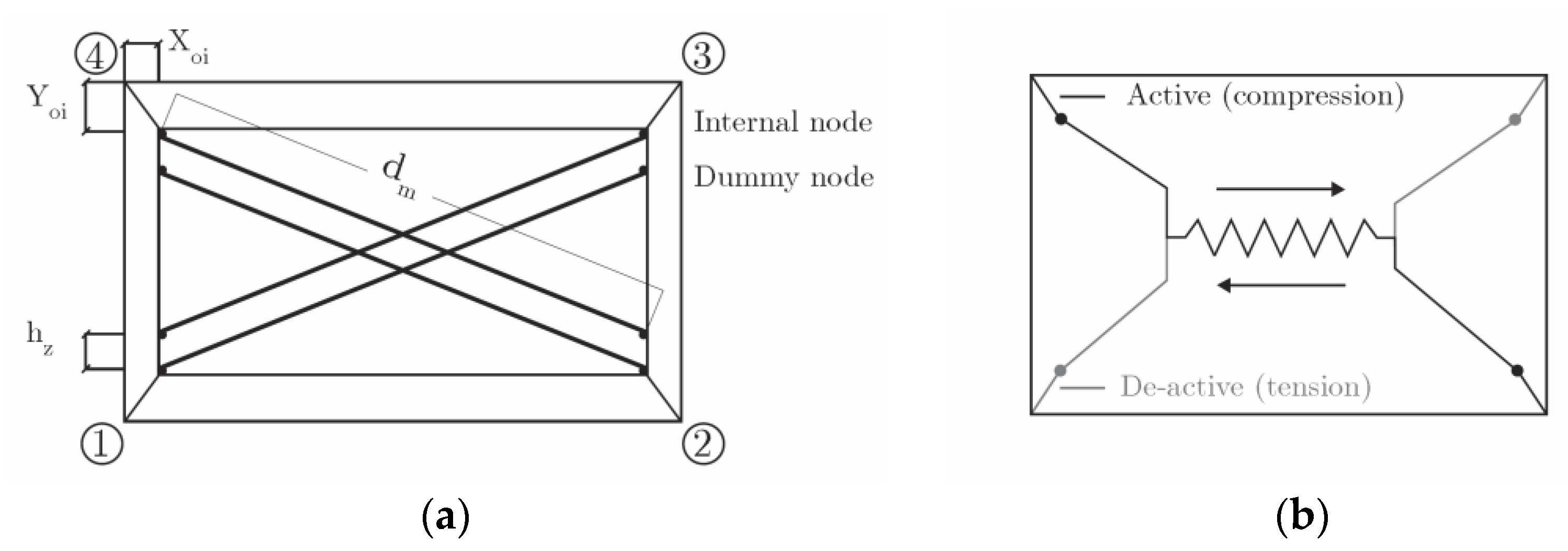
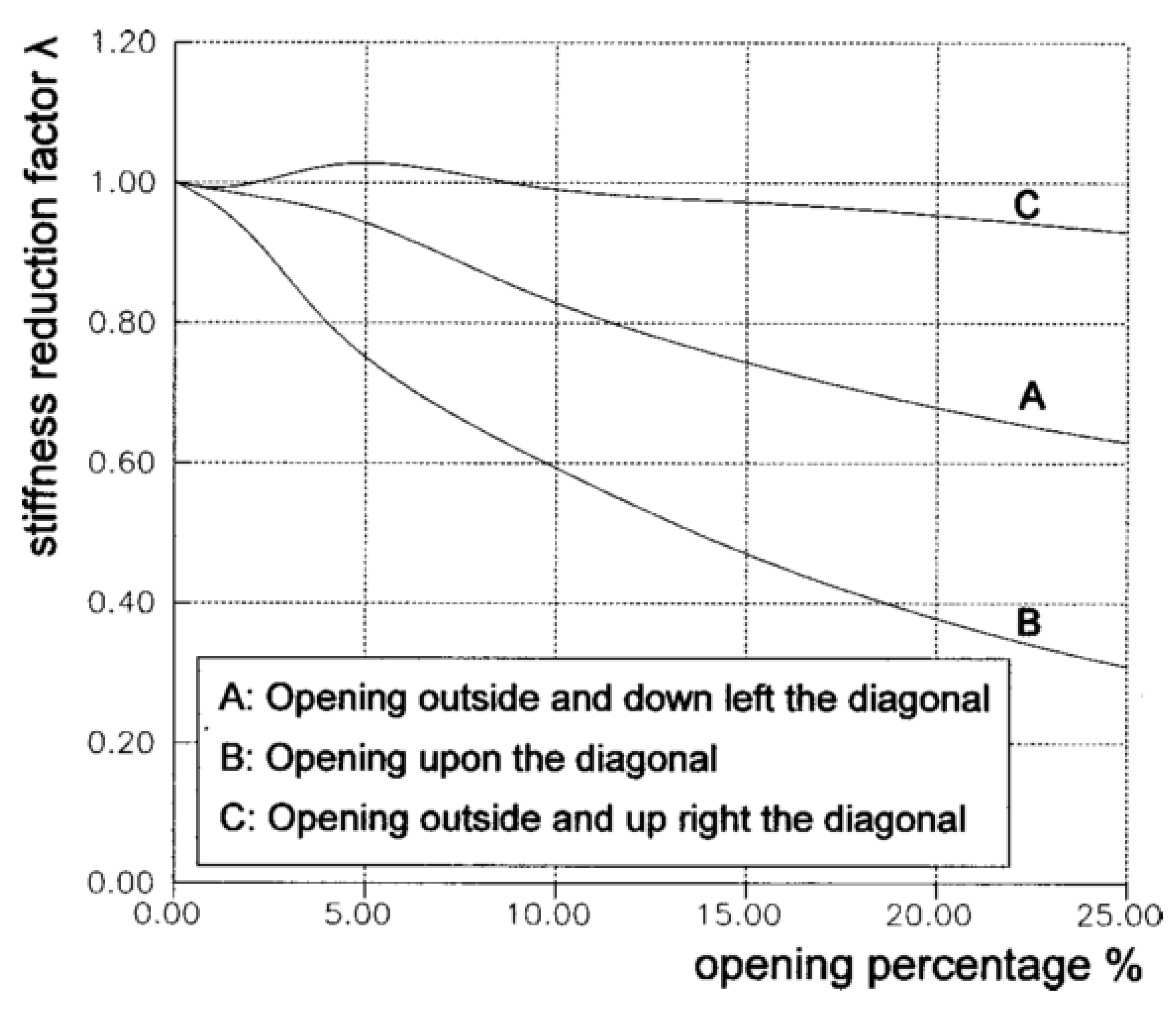
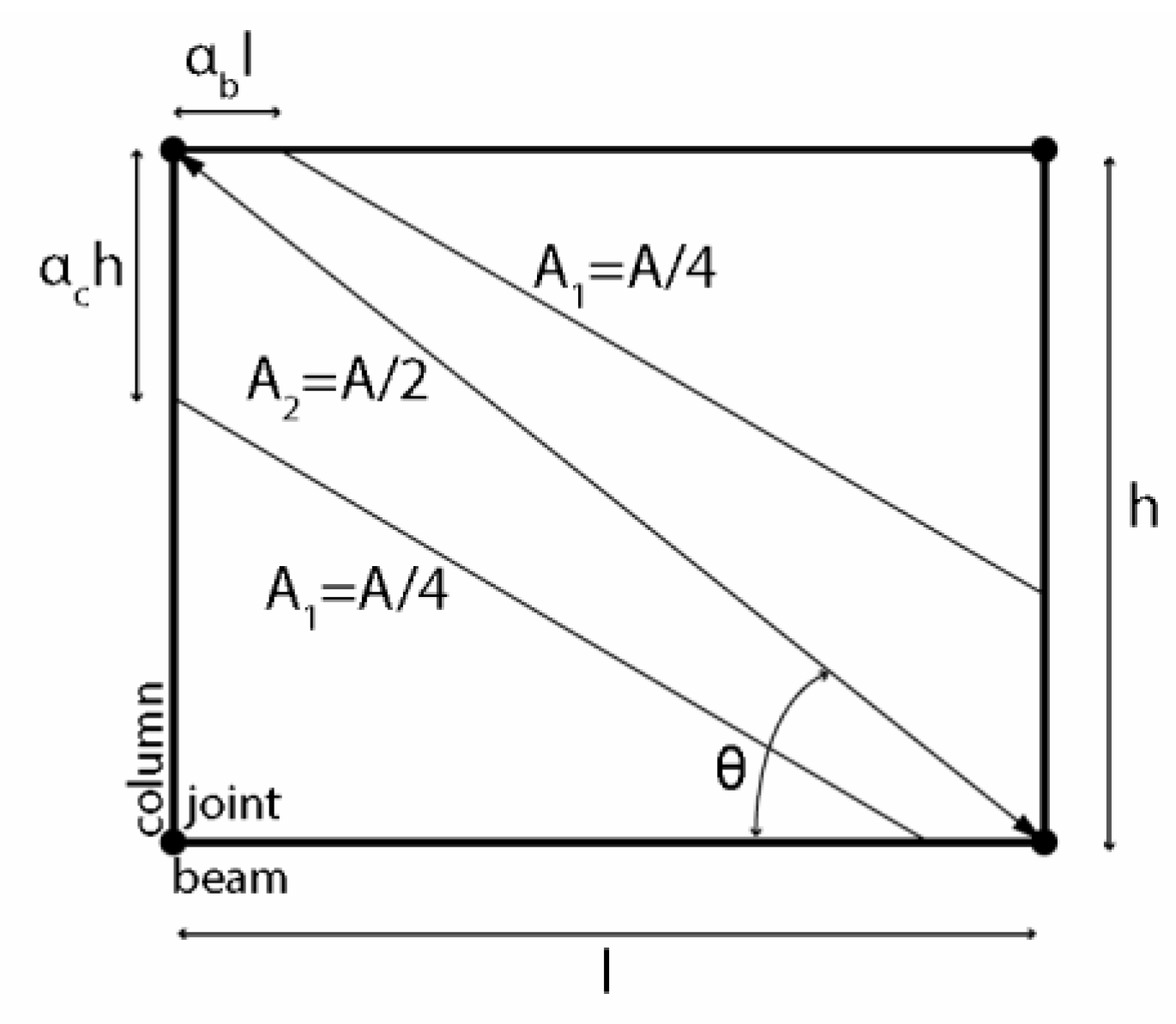
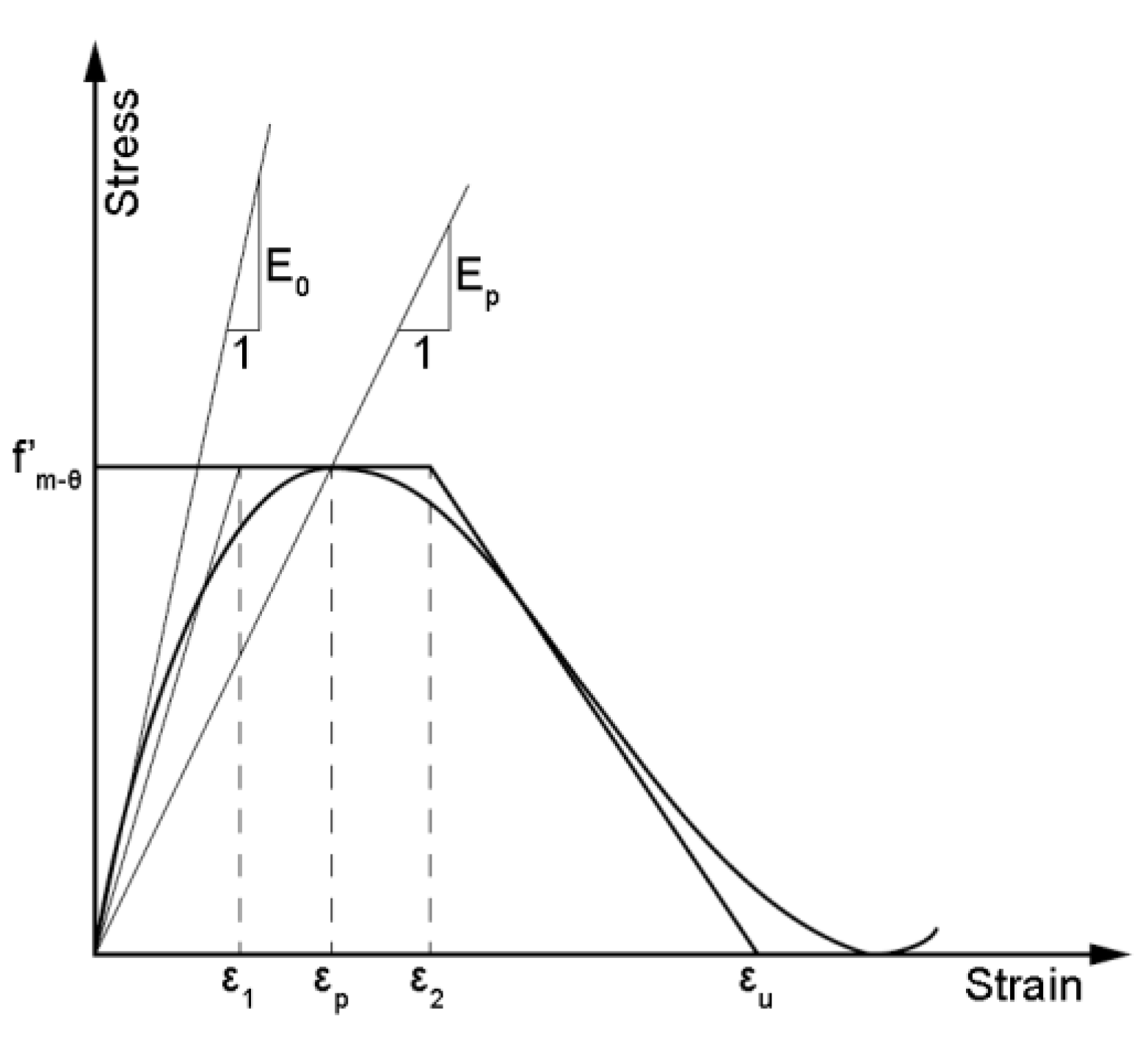
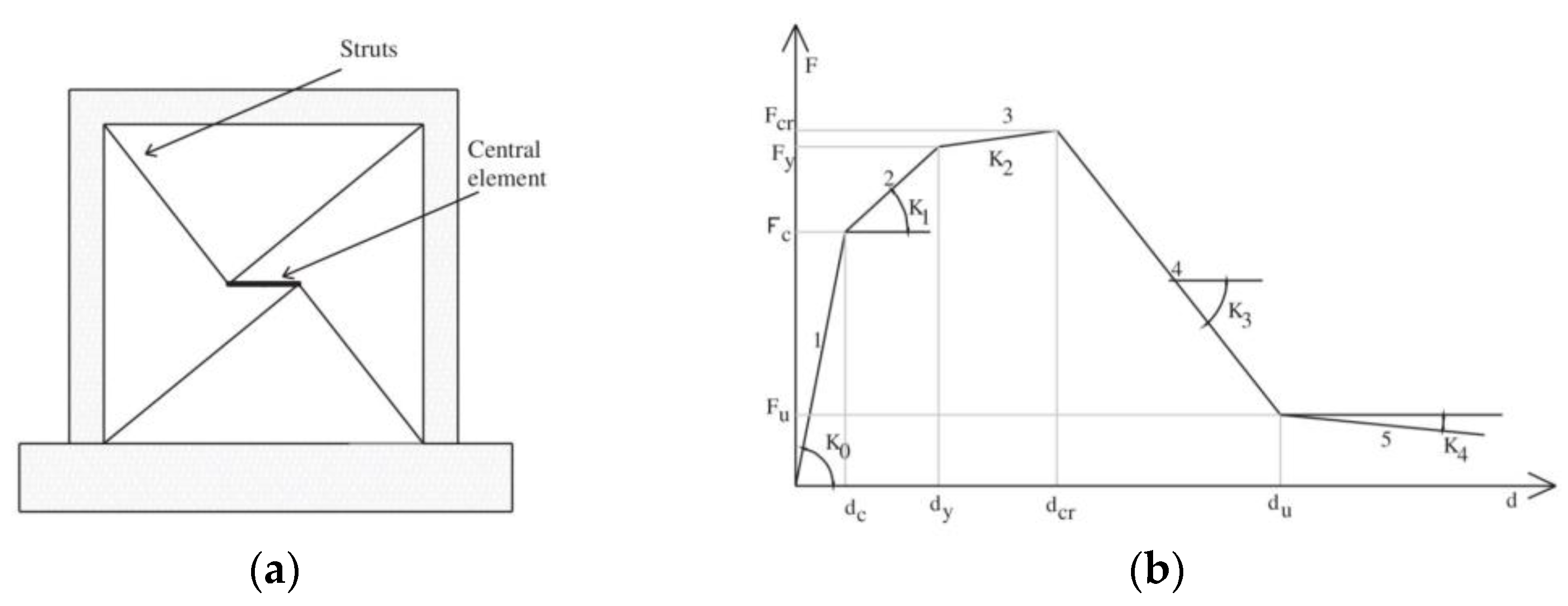



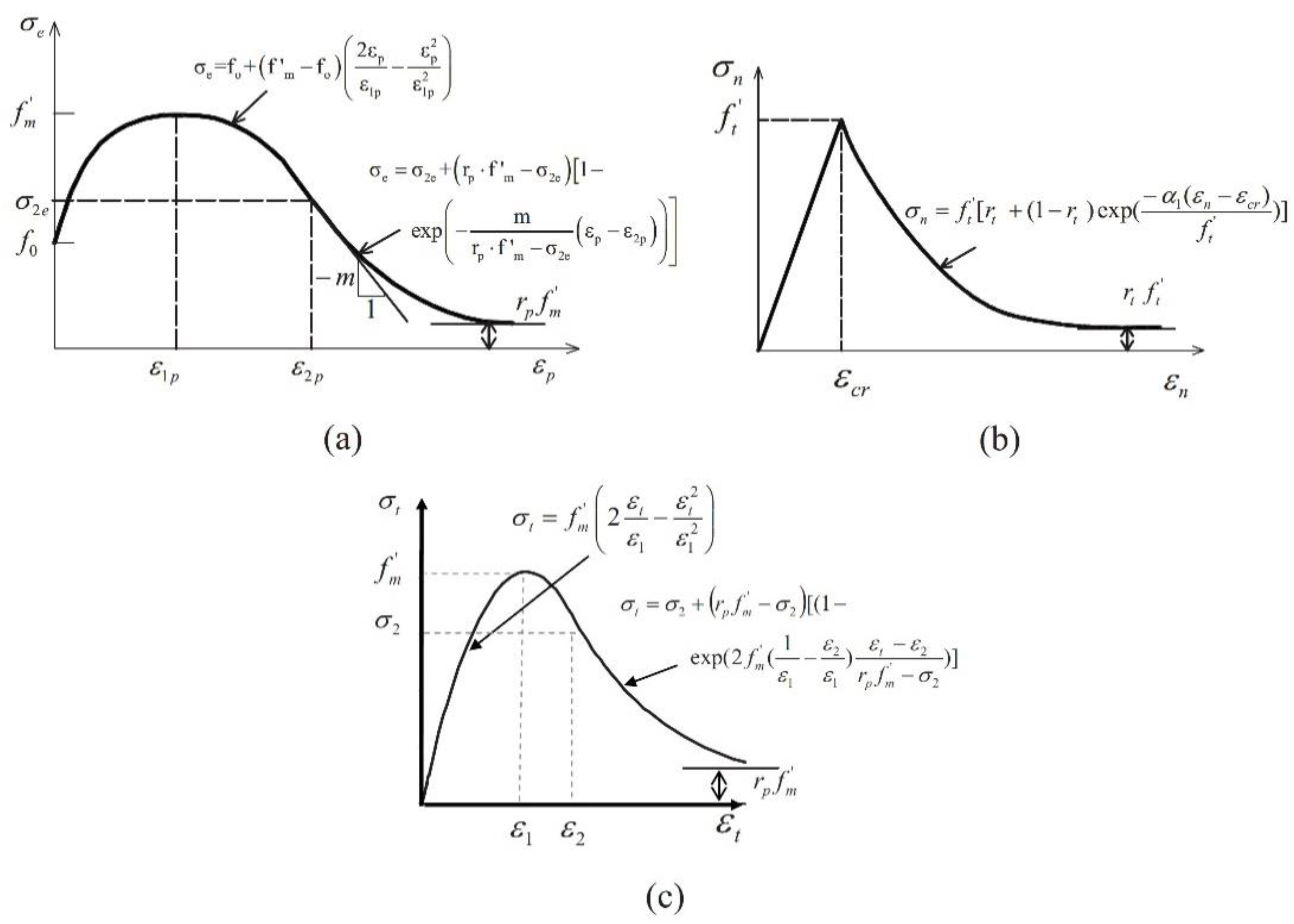
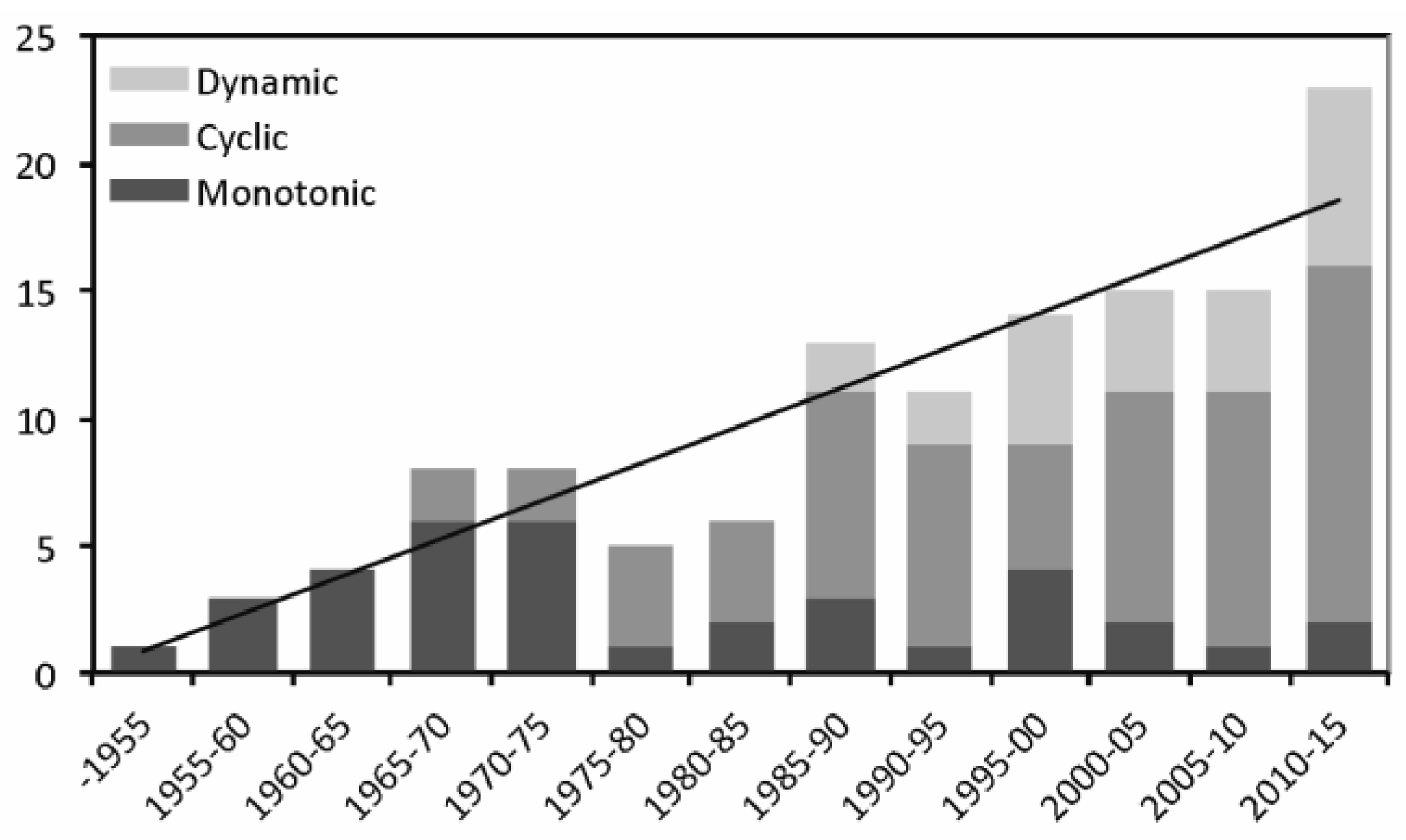
| Advantages | Disadvantages |
|---|---|
| Structure protection for low and medium earthquakes | Degradation of stiffness, strength, and energy dissipation capacity |
| Higher stiffness | Stiffness irregularity in height (soft-storey) and in plan (torsion) |
| Higher strength | Strength irregularity in height (weak-storey) |
| Reduction of lateral resisting contribution from the columns | Concentration of shear in columns beams and joints |
| Reduction of deformations on the structure | Increase of axial loads on columns |
| Higher energy dissipation capacity | Higher stress demand due to higher frequencies, especially on the foundations |
| Weak Infill | Strong Infill | |
|---|---|---|
| Weak Frame | Shear Sliding Diagonal Cracking Frame Failure | |
| Strong Members Weak Joints | Corner crushing | Shear Sliding Diagonal Cracking Frame Failure |
| Strong frame | Corner crushing |
| City, Country | Year | Mw | Deaths | Losses |
|---|---|---|---|---|
| San Francisco, USA | 1906 | 7.8 | 3.425 | USD8000 M |
| Guatemala City, Guatemala | 1976 | 7.5 | 23.000 | >USD750 M |
| Northridge, USA | 1994 | 6.7 | 58 | >USD50,000 M |
| Kobe, Japan | 1995 | 6.8 | 6.434 | >USD100,000 M |
| Dinar, Turkey | 1995 | 6.2 | 90 | USD250 M |
| Jabalpur, India | 1997 | 6 | 39 | |
| Adana-Ceyhan, Turkey | 1998 | 5.9 | 145 | USD1000 M |
| Athens, Greece | 1999 | 6 | 143 | USD3000 M |
| Kocaeli, Turkey | 1999 | 7.5 | 17.127 | USD23,000 M |
| Chi-Chi, Taiwan | 1999 | 7.6 | 2.416 | USD9200 M |
| Gujarat, India | 2001 | 7.7 | 20.000 | >USD10,000 M |
| Bingöl, Turkey | 2003 | 6.4 | 176 | |
| Sumatra, Indonesia | 2004 | 9.2 | 280.000 | >USD10,000 M |
| Sichuan, China | 2008 | 8 | 62.664 | >USD100,000 M |
| L’Aquila, Italy | 2009 | 6.3 | 308 | USD10,000 M |
| Haiti | 2010 | 7 | 300.000 | USD8000 M |
| Maule, Chile | 2010 | 8.8 | 525 | USD30,000 M |
| Christchurch, New Zealand | 2011 | 6.3 | 181 | USD20,000 M |
| Tohoku, Japan | 2011 | 9 | 15.800 | USD300,000 M |
| Lorca, Spain | 2011 | 5.1 | 9 | USD99 M |
| Bologna, Italy | 2012 | 6.1 | 26 | USD13,000 M |
| Nepal | 2015 | 7.8 | 8964 | USD10,000 |
| Central Italy | 2016 | 6.2 | 297 | USD71,000 |
| Northeastern Aegean, Greece | 2017 | 6.3 | 2 | |
| Albania | 2019 | 6.4 | 51 | USD12,000 M |
| Zagreb, Croatia | 2020 | 5.5 | 1 | USD11,500 M |
| Author, Year | Scale | Type | Wall | Frame | Wall | Tests |
|---|---|---|---|---|---|---|
| Thomas (1953) [93] | M | IP | Steel | B, C | ||
| Ockleston (1955) [94] | 1 | M | IP | RC | B | |
| Benjamin and Williams (1958, 1959) [95,96] | 1–1/8 | M | IP | RC | C | 20 |
| Wood (1958) [97] | M | IP | Steel | |||
| Sachanski (1960) [98] | 1 | M | IP, O | RC | B, C | 31 |
| Holmes (1961) [99] | 1 | M | IP | RC | B, C | |
| Holmes (1963) [100] | 1 | M | IP | Steel | B | 13 |
| Jorquera (1964) [101] | 1 | M | IP | RC | B | |
| Stafford-Smith (1966) [102] | M | IP | RC | B | ||
| Esteva (1966) [103] | C | IP | RC | B, C | 7 | |
| Polyakov (1967) [104] | M | IP | RC | B | ||
| Yorulmaz and Sozen (1968) [105] | 1/8 | M | IP | RC | B | 7 |
| Stafford-Smith (1968) [106] | <1 | M | IP | Steel | B, C | 3 |
| Trigo (1968) [107] | <1 | M | IP | RC | B, C | |
| Mallick and Severn (1968) [108] | C | IP | Steel | |||
| Stafford-Smith and Carter (1969) [109] | IP | RC | B | |||
| Fiorato et al. (1970) [110] | 1/8 | M, C | IP, O | RC | B | 3 (27) |
| Bonvalet (1970) [111] | 1 | M | IP | Steel | B | |
| Fiorato et al. (1970) [112] | 1/8 | M | IP | RC | B | |
| Chandrasekaran and Chandra (1970) [113] | C | IP | ||||
| Mallick and Garg (1971) [114] | <1 | M | IP, O | Steel | C | |
| Mainstone (1971) [115] | 1–1/6 | M | IP | Steel | B | |
| Dawson (1972); Dawson and Ward (1974) [116,117] | <1 | M | IP | Steel | C | 6 |
| Abdul-Kadir (1974) [118] | <1 | M | IP, O | RC | B | |
| Leuchars and Scrivener (1976) [119] | ½ | C | IP | RC | B, C | 3 |
| Klingner and Bertero (1976, 1978) [120,121] | ½ | C | IP | RC | B, C | 5 |
| Jurina (1977) [122] | ½ | C | IP | RC | B | 5 |
| Liauw and Lee (1977) [123] | M | IP, O | Steel | 4 | ||
| Kahn and Hanson (1979) [124] | C | IP | RC | C | 5 | |
| Liauw (1980); Liauw and Kwan (1984) [125,126] | <1 | M | IP | Steel | C | 3 |
| Parducci and Mezzi (1980) [127] | 2/3 | C | IP | RC | B | 8 |
| Wei et al. (1980) [128] | ½ | M, C | IP | RC | B, C | 9 |
| Brokken and Bertero (1981) [129] | 1/3 | C | IP | RC | B, C | 18 |
| Bertero and Brokken (1983) [130] | ||||||
| Žarnić and Tomazevic (1984,1985) [131,132] | 1/3 | C | IP | RC | C | 8 |
| McBride (1984); Yong (1984) [133,134] | 1 | M | IP | Steel | C | 34 |
| Amos (1985); Richardson (1986) [135,136] | ||||||
| Yanev and McNiven (1985) [137] | C | IP | Steel | |||
| Dawe and Young (1985) [138] | M | IP | Steel | C | ||
| Liauw and Kwan (1985) [139] | <1 | M, C | IP, O | RC | ||
| Govindan et al. (1986,1986) [140,141] | ¼ | C | IP | RC | B | 4 |
| Stylianidis (1988) [142] | 1/3 | C | IP | RC | B | 18 |
| Žarnić and Tomazevic (1988) [143] | 1/2–1/3 | C | IP | RC | B | 28 |
| Moghaddam et al. (1988) [144] | <1 | D | IP, OP | Steel | B | 4 |
| Dawe and Seah (1989) [145] | 1 | M | IP, O | Steel | C | 28 |
| Dawe and Seah (1989) [146] | 1 | M | OP, O | Steel | C | 9 |
| Dawe et al. (1989) [147] | 1/3 | ST | IP | Steel | B | 10 |
| Schmidt (1989) [148] | C | IP | RC | B | ||
| Valiasis and Stylianidis (1989) [149] | 1/3 | C | IP | RC | B | 24 |
| Vintzeleou and Tassios (1989) [150] | RC | |||||
| Manos et al. (1990) [151] | ST | IP, O | RC | B | ||
| Žarnić (1992) [152] | 1/2 | C | IP | RC | B | 1 |
| Žarnić (1992) [152] | 1/3 | M | IP | RC | B | 3 |
| Liauw and Kwan (1992) [153] | 1/3 | ST | IP, OP | RC | B, C | 2 |
| Manos et al. (1993) [154] | 1/3–1/9 | C | IP | RC | C | |
| Mander et al. (1993) [155] | <1 | C | IP, OP | Steel | B | 3 |
| Angel et al. (1994) [156] | 1 | C | IP, OP | RC | B, C | 7 |
| Mehrabi et al. (1994) [157] | 1/2 | M, C | IP | RC | B | 14 |
| Angel et al. (1994) [156] | 1 | C, M | IP, OP | RC | B, C | 8 |
| Ishibashi and Hastumata (1994) [158] | 1 | M, C | IP | RC | B | 19 |
| Gergely et al. (1994) [159] | <1 | C | IP | Steel | C | |
| Bashandy et al. (1995) [160] | 1/2 | ST | IP, OP | RC | B | 8 (58) |
| Mehrabi et al. (1996) [161] | 1/2 | M | IP, O | RC | C | 12 |
| Negro and Verzeletti (1996) [162] | 1 | D | IP | RC | B | 2 |
| Durrani and Haider (1996) [163] | C | IP | RC | B | ||
| Crisafulli (1997) [7] | 3/4 | M | IP | RC | B | 2 |
| Mosalam et al. (1997) [164] | C | IP, O | Steel | C | ||
| Al-Chaar (1998); Al-Chaar et al. (2002) [165,166] | 1/2 | C | IP | RC | B, C | 2 |
| Pires et al. (1998) [167] | 2/3 | C | IP, O | RC | B | 9 |
| Chiou et al. (1999) [168] | 1 | M | IP | RC | B | |
| Flanagan and Bennett (1999) [169] | <1 | M | IP, O | Steel | B | 8 |
| Flanagan and Bennett (1999) [170] | <1 | C | IP, OP | Steel | B | |
| Buonopane and White (1999) [171] | 1/2 | D | IP, O | RC | B | 1 |
| Fardis et al. (1999) [172] | 1 | ST | IP, OP | RC | B | 1 |
| Buonopane and White (1999) [171] | 1/2 | D | IP, O | Steel | B | 4 |
| Combescure and Pegon (2000) [173] | 1/1.5 | C | IP, O | RC | B | 9 |
| Lafuente et al. (2000) [174] | 1/2 | C | IP | RC | B | 10 |
| Dukuze (2000) [175] | 1/3 | M | IP | RC | B | 23 |
| Murty and Jain (2000) [176] | 1/2.7 | C | IP | RC | B | 12 |
| Calvi and Bolognini (2001) [177] | 1 | C, M | IP, OP | RC | B | |
| Žarnić et al. (2001) [178] | 1/4 | D | IP, OP | RC | B | 2 |
| Felice and Giannini (2001) [179] | M | OP | ||||
| Lee and Woo (2002) [180] | 1/5 | ST | IP, O | RC | C | 5 |
| Pinto et al. (2002) [181] | 1 | C, D | IP, O | RC | B | 7 |
| Canbay et al. (2003) [182] | 1/3 | C | IP | RC | C | |
| Cavaleri et al. (2004) [183] | 1/2 | M, C | IP | RC | B | 3 |
| El-Dakhakhni et al. (2004) [184] | 1 | C | IP, O | Steel | C | 2 |
| Moghaddam (2004) [185] | <1 | C | IP | RC | B, C | 5 |
| Yàñez et al. (2004) [186] | 1 | C | IP, O | RC | B, C | 16 |
| Negro et al. (2004); Molina et al. (2004) [187,188] | 1 | D | IP | RC | B | 1 |
| Molina et al. (2005) [189] | ||||||
| Colangelo (2005) [190] | 1/2 | C | IP | RC | B | 11 |
| Dolce et al. (2005) [191] | 1/3.3 | ST | IP | RC | B | 3 |
| Santhi et al. (2005) [192,193] | 1/3 | ST | IP | RC | B | 2 |
| Hashemi and Mosalam (2006) [194] | 3/4 | ST | IP | RC | B | 1 |
| Huang et al. (2006) [195] | <1 | C | IP, O | RC | B | 6 |
| Erdem et al. (2006) [196] | 1/3 | C | IP | RC | B | 2 |
| Kakaletsis and Karayannis (2007, 2008) [197,198] | 1/3 | C | IP, O | RC | B | 8 |
| Griffith et al. (2007) [199] | 1 | C | OP | - | B | 8 |
| Anil and Altin (2007) [200] | 1/3 | C | IP, O | RC | C | 9 |
| Corte et al. (2008) [201] | 1 | C | IP, OP | RC | B | 2 |
| Arulselvan and Subramanian (2008) [202] | 1/5 | C | IP | RC | B | 1 |
| Blackard et al. (2009) [203] | 2/3 | C | IP, O | RC | B | 4 |
| Subramanian and Jayaguru (2009) [204] | 1/3 | C | IP, O | RC | B | |
| Okuyucu et al. (2009) [205] | 1/3 | M | IP | RC | B, C | 46 |
| Stavridis (2009) [206] | 1/3–2/3 | C, D | IP, OP, O | RC | B | |
| Pujol and Fick (2010) [207] | 1 | D | IP | RC | B, C | 1 |
| Moghaddam and Goudarzi (2010) [208] | M | OP | B | |||
| Tasnimi and Mohebkhah (2011) [209] | 1 | C | IP, O | Steel | B | 6 |
| Komaraneni et al. (2011) [210] | 1/2 | C, ST | IP, OP | RC | B | 3 |
| Mohammadi et al. (2011) [211] | 1/3 | C | IP | Steel | B | 8 |
| Mohammadi and Mahalleh (2012) [212] | ||||||
| Asteris et al. (2011) [10] | 1/3 | C | IP, O | RC | B | 10 |
| Misira et al. (2012) [213] | 1/2 | C | IP | RC | B | 3 |
| Stavridis et al. (2012) [214] | 2/3 | SK | IP, O | RC | B | 14 |
| Kurt et al. (2012) [215] | 1/2 | S | IP | RC | C | 2 |
| Kakaletsis (2012) [216] | 1/3 | C | IP, O | RC | B | 15 |
| Stylianidis (2012) [217] | 1/3 | C | IP | RC | B | 48 |
| Zovkic et al. (2013) [218] | 1/2.5 | C | IP | RC | B, C | 9 |
| Pereira (2013) [219] | 1 | C | IP, OP | RC | B | 8 |
| Dubey and Kute (2013) [220] | <1 | M | IP, O | RC | C | 7 |
| Markulak et al. (2013) [221] | <1 | C | IP | Steel | B, C | 9 |
| Fang et al. (2013) [222] | 1 | ST | IP, OP | Steel | C | 1 |
| Ali (2013) [223] | 1/2 | D | IP, O | RC | B | 1 |
| Mansouri et al. (2014) [224] | 1/2 | C | IP, O | RC | B | 6 |
| Dubey and Kute (2014) [225] | <1 | C | IP | RC | C | 14 |
| Kauffman and Memari (2014) [226] | 1/4 | M, C | IP | - | B | 12 |
| Morandi et al. (2014) [227] | 1 | C | IP, OP, O | RC | B | 5 |
| Rastogi et al. (2014) [228] | 3/4 | D | IP, O | RC | B | 7 |
| Essa et al. (2014) [229] | 1/2 | C | IP | RC | B | 4 |
| Micro-Modelling | Macro-Modelling |
|---|---|
| Simplified |
| Allow a representation of the global behaviour of the infill masonry panels and of their influence in the building’s response |
| Usually modelled as an equivalent strut |
| Lower computational cost |
|
| Reference | Formulae |
|---|---|
| [99] | |
| [235] | for square infill infill side’s ratio 5/1 |
| [109] | |
| [230] | |
| [115] | |
| [120] | |
| [236] | |
| [237] | |
| [238] | |
| [239] | |
| [240] | |
| [241] | |
| [242] | |
| [243] | |
| [244] | |
| [245] | |
| [246] | |
| [247] | W* for partially infilled walls |
| h/l | Moderate | Severe |
|---|---|---|
| ≤21 | 0.7 | 0.4 |
| >21 | Requires repair | |
| Author, Year | Strut | Capability |
|---|---|---|
| Polyakov (1956) [235] | 1 | Concept |
| Holmes (1961) [99] | 1 | Ultimate strength |
| Stafford-Smith (1962) [236] | 1 | Effective width of equivalent strut |
| Stafford-Smith and Carter (1969) [109] | 1 | Stiffness, strength |
| Mainstone and Weeks (1970) [231] | 1 | Stiffness, strength |
| Mainstone (1971) [115] | 1 | Stiffness, strength |
| Klingner and Bertero (1976) [120] | 1 | Stiffness, strength, hysteretic response |
| Liauw and Kwan (1984) [238] | 1 | Stiffness, strength |
| Syrmakezis and Vratsanou (1986) [255] | 5 | Frame-infill interaction, strength stiffness |
| Žarnić and Tomazevic (1988) [143] | 1 | Stiffness, strength |
| Schmidt (1989) [334] | 2 | Frame-infill (FI) interaction, strength, stiffness |
| Chrysostomou (1991) [255] | 3 | FI interaction, stiffness, strength degradation |
| Saneinejad and Hobbs (1995) [258] | 1 | Non-linear force-displacement response |
| Crisafulli (1997) [7] | 2 | FI interaction, compressive and shear strength |
| Flanagan and Bennett (1999) [170] | 1 | Stiffness, crushing strength |
| El-Dakhakhni et al. (2003) [9] | 3 | FI interaction, corner crushing strength |
| Dolšek and Fajfar (2008) [335] | 1 | Non-linear force-disp. response, post-peak |
| Stavridis (2009) [206] | ||
| Kadysiewski and Mosalam (2009) [268] | 1 | In-plane and out-of-plane interaction |
| Rodrigues et al. (2010) [270] | 1 | Non-linear behaviour, strength degradation |
| Sattar and Liel (2016) [336] | ||
| Stavridis et al. (2017) [337] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dias-Oliveira, J.; Rodrigues, H.; Asteris, P.G.; Varum, H. On the Seismic Behavior of Masonry Infilled Frame Structures. Buildings 2022, 12, 1146. https://doi.org/10.3390/buildings12081146
Dias-Oliveira J, Rodrigues H, Asteris PG, Varum H. On the Seismic Behavior of Masonry Infilled Frame Structures. Buildings. 2022; 12(8):1146. https://doi.org/10.3390/buildings12081146
Chicago/Turabian StyleDias-Oliveira, João, Hugo Rodrigues, Panagiotis G. Asteris, and Humberto Varum. 2022. "On the Seismic Behavior of Masonry Infilled Frame Structures" Buildings 12, no. 8: 1146. https://doi.org/10.3390/buildings12081146
APA StyleDias-Oliveira, J., Rodrigues, H., Asteris, P. G., & Varum, H. (2022). On the Seismic Behavior of Masonry Infilled Frame Structures. Buildings, 12(8), 1146. https://doi.org/10.3390/buildings12081146









