Abstract
The main strength and elastic properties of structural timber products, such as glued laminated timber (glulam; GLT) and cross-laminated timber (CLT), are usually described via load-bearing models, which use the tensile properties parallel to the grain of the base material boards and finger joints as input parameters. These load-bearing models assume that the strength-graded boards will retain their full dimensions in the final product. In some applications or use cases, however, the structural timber products are split lengthwise, e.g., split/resawn glulam, or comprise a random share of in width randomly lengthwise split lamellas. As a result of splitting, the material properties assigned to these boards during the grading process in their full cross-sections are no longer valid. Examples of such structural timber products are the novel flex_GLT-beams which are cut out from large dimensional multi-laminated timber panels. In the following paper, the bending properties and system effects of resawn glulam and flex_GLT-beams are described by means of a 3D stochastic-numerical beam model that uses probabilistic models to create the input values for unsplit and split boards as well as finger joints. The models are successfully validated by our own tests and tests from literature and applied in numerous parameter studies.
1. Introduction
Timber is a naturally grown material featuring large uncertainties in its properties. These uncertainties can be identified on the scales of species, growing regions, and individual trees, as well as between and within timber members. In the manufacturing of structural timber products, additional scales need to be considered, e.g., the scale of production and that of producers; see Fink et al. [1]. To assign a specific set of properties to timber, it first needs to be graded. In the course of this, only some properties are directly controlled by the grading process, while the majority of properties are only indirectly controlled. In most cases, however, the properties are assigned based on relationships from probabilistic models (Köhler [2]). In the course of such grading processes, eigenfrequency or ultrasonic runtime, together with density measurements, are standard parameters in today’s machine grading facilities. The modulus of elasticity itself is well correlated with the strength properties parallel to the grain, in particular with the tensile parallel to the grain and bending strength; however, these strength properties are additionally determined by local, morphological characteristics of timber, in particular knots, which are found to occur with some regularity (e.g., [3,4]). With a focus on the scale of timber, in particular of boards, the uncertainty in corresponding properties can be separated into uncertainties (i) between boards (variation of average properties) and (ii) within boards (variation of local properties). This kind of separation can be well represented by a so-called two-level hierarchical model, which has already been successfully used for similar applications in previous investigations (e.g., [2,5,6,7,8,9]).
The strength and elastic properties of structural timber products, such as glued laminated timber (glulam; GLT) and cross-laminated timber (CLT), are preferably regulated by so-called “load bearing models”, which use the tensile properties parallel to the grain of the base material boards and finger joints as input parameters (see, e.g., EN 14080 [10] for glulam and ON B 1995-1-1 [11], Annex K for CLT). These load-bearing models are developed on the basis of experimental investigations and/or probabilistic numerical simulations (e.g., [3,7,8,12]). All of these models use knot indicators as surrogates for the influence of local growth characteristics on the mechanical properties of the base material and also the laminated products made from it. Furthermore, in these probabilistic numerical simulations, linear, unidirectionally laminated timber products such as glulam, featuring principally a serial, sub-parallel structure, are represented two-dimensionally by lamellas which are further separated in board segments and segments with finger joints. Consequently, only the discrete variation of local growth characteristics such as knots in the longitudinal direction but with no variation of them in the width and thickness direction are considered. By this means, it is possible to mirror common production processes, for example, those for glulam, where the cross-section of strength graded boards, to which the strength grading refers, (nearly) is fully retained in the final structural timber product.
Some structural timber products, however, feature a fixed or random share of lengthwise split lamellas within their cross-section, such as resawn glulam or girders cut out from CLT in large dimensional CLT panels. Due to the lengthwise splitting of the lamellas, the profile of strength and elastic properties, which were assigned during grading of the base material in full cross-section, becomes invalid. This is because of altered natural growth characteristics and the change of proportions in the dimension of local growth characteristics (macroscopic flaws; e.g., knots and knot clusters) to the residual board cross-sections. This also has a corresponding major influence on the input parameters for the load-bearing models and/or the relationships contained therein. EN 14081-1 [13], for example, limits the allowable reduction of cross-sections after grading without losing the assigned strength grade by ≤ 5 mm and ≤ 10 mm, respectively, below and above board widths of 100 mm. Figure 1 shows the effect of splitting as an influence on the distribution and magnitude of macroscopic flaws along the board qualitatively, represented here by knots and knot clusters, exemplarily for one board split in width into three equally wide pieces. The areas marked in red represent the weak zones (WZ) within the board which are usually represented by large knots or knot clusters; the areas in green usually represent smaller intermediate knot zones (IZ), and the areas in yellow represent timber free from knots. These marked areas and their distribution mirror the natural growth structure of branches in trees.
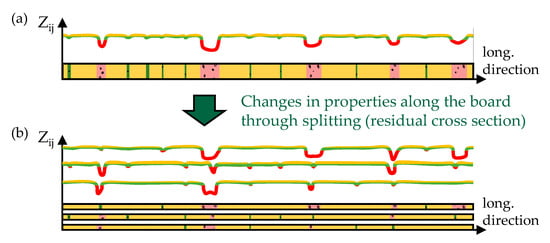
Figure 1.
Qualitative changes in properties (e.g., the tensile strength) along a single board strength graded in full cross-section (a) and when split lengthwise into three equal pieces (b).
Residual board cross-sections of this kind, which are random in width, also occur to some extent in a novel structural timber product with the name “flex_GLT”, which is thoroughly investigated within the research project FFG BRIDGE “flex_GLT-CLT-beams” (No. 877111). The production steps and their intermediary products are illustrated in Figure 2. In a first step, strength-graded boards are finger jointed to endless lamellas, which are glued side by side to endless single-layer solid wood panels (SWPs, see Figure 2a). These SWPs are subsequently cut to the required width (Figure 2b) and glued together unidirectionally to multi-layer large dimensional solid wood panels (Figure 2c). From these multi-layer panels, two different types of beams, i.e., beams with two different orientations of the lamellas in respect to the main or primary loaded axes, can be produced. For type A, the panel thickness equals the beam width, and the depth is flexible and only dependent on the placement of the cuts (Figure 2d1,e1). For type B, the panel thickness is equivalent to the beam depth, and the width can be chosen in a relatively flexible manner (Figure 2d2,e2). Depending on the type of the flex_GLT-beam, the boards/lamellas are loaded edgewise (type A) or flatwise (type B). Within this contribution, the focus is set on flex_GLT beam type B, whereby the models and findings presented hereafter are not restricted to this type.
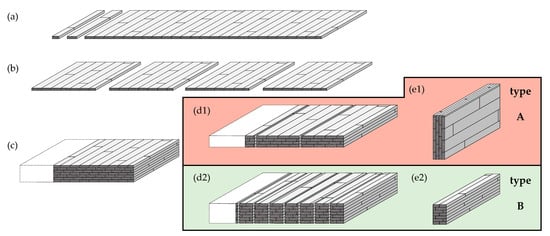
Figure 2.
Production of flex_GLT beams: (a) finger jointing and edge bonding of strength graded boards to single-layer solid wood panels (SWPs); (b) splitting of SWPs to required width; (c) face gluing and pressing of SWPs to unidirectionally oriented, large dimensional multi-layer panels; (d1,d2) cut out of flex_GLT-beam elements of (e1) type A and (e2) type B.
Production parameters, such as the width of the raw material boards/lamellas, the width of the multi-layer panels and of the flex_GLT-beams, together with the overall accuracy in production, particularly in the laying process, have an influence on the overlap of the board edges in neighbouring layers and on the share of lengthwise split boards. Figure 3 shows some possible overlap patterns in flex_GLT-beam cross-sections. For a specific board width and by assuming a perfectly accurate laying process, the overlap of edge-bonds, i.e., board/lamella edges, can be adjusted between no overlap to a maximum of one-half of the board width by the adequate setting of the width of the large dimensional multi-layer panel (see Figure 3a,c). In the case of no overlap and a beam width equal to or less than the board width, special cases of flex_GLT-beams occur, mirroring conventional glulam (Figure 3a1) and resawn glulam with one or two cuts (Figure 3a2,a3).
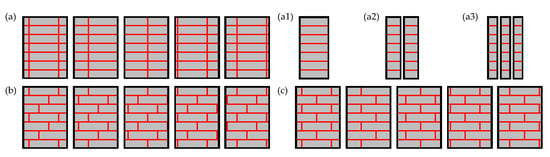
Figure 3.
Some possible cross-section patterns in flex_GLT type B beams for specific board, raw panel, and beam widths: (a) beam width greater than board width and aligned board edges; (a1) beam width equal to the board width {conventional glulam}; (a2) beam width approximately one-half of the board width {resawn glulam with one cut}; (a3) beam width approximately one-third of the board width {resawn glulam with two cuts}; (b) beam width greater than the board width and an overlap at the board edges of one-third of the board width; (c) beam width greater than the board width and an overlap at the board edges of one-half of the board width.
The current European product standard for glulam EN 14080 [10] provides regulations for the illustrated special cases of resawn glulam (Figure 3a2,a3). One possible approach when following the standard is to consider the splitting process during the grading of the boards by setting higher requirements on knot indicators or by grading virtually split boards. Alternatively, the characteristic bending strength of resawn glulam, fm,s,k, can be calculated as a function of the characteristic bending strength of glulam in full cross-section, fm,g,k, the characteristic tensile strength of the boards, ft,0,l,k, and the number of cuts; see Equation (1). This equation is applicable for 18 MPa ≤ ft,0,l,k ≤ 30 MPa and in compliance with specific geometric boundary conditions; EN 14080 [10] also regulates the mean modulus of elasticity parallel to the grain of resawn glulam, E0,s,mean, based on E0,g,mean, the mean modulus of elasticity parallel to the grain of glulam in full cross-section.
Equation (1) is based on experimental investigations from Cleason [14] and Crocetti [15], where only glulam beams of higher strength classes (GL32 acc. to EN 14080 [10]) were split and tested. Viguier et al. [16] and Kastner et al. [17] also investigated lower glulam strength classes (GL24h acc. to EN 14080 [10]) for both unsplit and split conditions. From the results of all these investigations, it can be concluded that decreasing bending strength and the modulus of elasticity parallel to the grain has no influence on the bending properties of resawn glulam from single cuts. Possible reasons for the obvious uncertainties in outcomes so far available are the limited number of tests per series and investigations on resawn glulam. With respect to resawn glulam from two cuts, no research or publications whatsoever are known to the authors.
No regulations, standards, load-bearing models, or experimental investigations are currently available for the more general cases of flex_GLT type B (Figure 3a–c). In contrast to split glulam, layers in flex_GLT type B beams can feature multiple edge bonded boards. New models are needed in order to analyse and quantify the influence of the arbitrary reduced boards/lamellas within the beam cross-section as well as possible system and size effects on the load bearing capacity of flex_GLT type B beams. First, a probabilistic board model for unsplit and length-wise split boards is derived. Secondly, a novel three-dimensional probabilistic-numerical beam model is developed, which is tailored for flex_GLT-beams.
Viguier et al. [16] investigated the change of the bending strength due to lengthwise splitting of boards and characterized resawn glulam beams based on their results. Apart from the work of Viguier et al. [16], no other numerical or probabilistic investigations are known to the authors dealing with this matter. One reason for this research gap might be the lack of information on the distribution of knots and knot clusters in the width direction of boards, which serve as surrogates for local growth characteristics in timber. Furthermore, the new probabilistic board model represents timber in a manner different from that in previous models (i) by classifying board sections explicitly in three different knot zones, (ii) by treating lengths of and distances between these zones randomly and not by a fixed increment, and (iii) by also incorporating the effects of width and splitting of boards and their statistical distributions and moments in the modelling of geometric and knot parameters.
The probabilistic board model is presented in Section 2 as a basis for the probabilistic numerical beam model in Section 3. Both chapters are structured in a typical manner, mirroring sections “Material and Methods”, “Results”, and “Discussion”. Section 4 is dedicated to resawn glulam beams, and Section 5 is dedicated to flex_GLT type B beams. Finally, conclusions are made in Section 6.
2. Probabilistic Board Model
2.1. Board Databases
The physical and geometric properties within the probabilistic board model are represented as random variables based on distribution models. For the validation of the distribution models used and the estimation of corresponding distribution parameters, the main statistics and relationships of two databases on boards for the glulam production were analysed. The databases originate from two research projects named “INTELLIWOOD” (Schickhofer and Augustin [18]) and “separate” (Kastner et al. [17]). The databases contain knot data (position and dimension), other technological parameters, such as the annual ring width or radial distance to the pith, and physical properties such as the dynamic modulus of elasticity based on eigenfrequency measurements, moisture content, density at the reference moisture content of uref = 12%, and the modulus of elasticity and strength in tension parallel to the grain, {EDYN,F; ρ12; Et,0,b; ft,0,b}. The tensile test was carried out in accordance with EN 408 [19], and the results were corrected to a moisture content of uref = 12% and a board width of wb,ref = 150 mm, in line with EN 384 [20]. Measurements for the dynamic modulus of elasticity only, based on the ultrasonic runtime, are available in the database from the “INTELLIWOOD” project. To achieve comparable results and a uniform data representation, these measurements were converted to values representative of the dynamic modulus of elasticity based on eigenfrequency by means of the linear regression model based on data from Fink and Kohler [21], as given in Equation (2).
Overall, the two databases comprise more than 1000 Norway spruce (Picea abies) timber boards of Central Europe provenience (see Table 1).

Table 1.
Test data from two board databases: overview of main- and sub-series, nominal grading classes, quantities, and dimensions based on Schickhofer and Augustin [18] and Kastner et al. [17].
Based on the dynamic modulus of elasticity calculated from eigenfrequency measurements, as one major indicating parameter in the grading process, the boards were divided into two groups, GI and GII, which can be approximately allocated to the strength classes T14 and T24 according to EN 338 [22]. Hereby, T14 represents the common quality of boards used for glulam of strength class GL24 as well as CLT, whereas T24 would allow production of GL32, the highest glulam strength class according to EN 14080 [10]. The dynamic modulus of elasticity is also further used in the new probabilistic board model; it stands for the global mechanical potential of the board material. Similar to previous investigations, knot parameters serve as surrogates for the general influence of local growth characteristics on the mechanical properties of timber. The knot data used to calculate the knot parameters comprises all boards from group GI and GII. However, the tensile properties parallel to the grain, ft,0,b and Et,0,loc,12,b, are available only for a subset of the boards from Schickhofer and Augustin [18] and Kastner et al. [17]; see Table 2.

Table 2.
Mechanical properties of groups GI and GII; results taken from Schickhofer and Augustin [18] and Kastner et al. [17].
2.2. Model Specifications
The probabilistic board model aims to achieve a generic representation of the distribution and magnitude of global and local growth characteristics in structural timber. The focus here is on the softwood species Norway spruce (Picea abies) because of the extensive data available and the dominance in the use of the species as the base material for laminated structural timber products such as glulam and CLT. As mentioned above, such products are usually characterized by means of the tensile properties parallel to the grain of the timber boards and of the finger joints, joining boards, and board segments lengthwise. As the tensile properties are influenced to a great extent by knots and knot clusters, the probabilistic model aims to represent these local growth characteristics realistically and treats them as surrogates for others, such as reaction wood, local grain deviations caused by broken treetops or bark inclusions, to name only a few. Analogously to the typical hierarchical structure of branches in trees, boards are further separated into weak zones (WZ), intermediate knot zones (IZ), and knot-free zones (CW) in the longitudinal direction. The geometric parameters are illustrated in Figure 4.
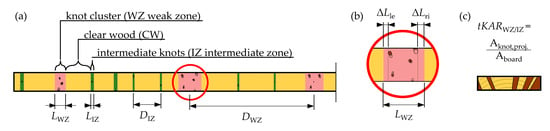
Figure 4.
Definition of geometric parameters (a); detail of the length of knot zones (b); definition of tKAR (c).
In most probabilistic approaches, the length of WZ (LWZ) is kept constant, mostly at LWZ = 150 mm, and the distance between weak zones (DWZ) only is varied discretely with LWZ as an increment. In previous probabilistic board models, knots or knot clusters under a certain threshold of the knot parameter tKAR (tension/total Knot Area Ratio, see Figure 4b) are usually neglected, and no differentiation is made in WZ and IZ (e.g., [3,7,8]). In contrast to these references but similar to the investigations in Brandner [9], the lengths of the weak and intermediate knot zones (LWZ and LIZ) as well as the distances between (DWZ and DIZ) are modelled as continuous variables, and the occurrence of weak and intermediate knot zones is represented by two interlaced alternating renewal (AR) processes. Hereby, the length of knot zones (see Figure 4b) is defined by the outer distance of knots or knot clusters plus an additional length taking the local grain deviation caused by the knots into account. Olsson et al. [24] stated that local grain distortions in the vicinity of knots begin to decay after a distance in the longitudinal direction of approximately 1.5-times the adjacent knot diameter. Based on this investigation and the assumption of a gradual decrease of the grain distortions, the additional length was fixed at 1.0-times the diameter of the knot at the margin of the knot zone to account for the influence of knots on the mechanical properties. This dimension corresponds to the distance of the centre of gravity from the knot’s outside diameter when assuming a simplified triangularly decaying influence of the local grain deviation. As the length of knot zones is kept random, for the distinction between WZ and IZ, no fixed value is possible; instead, the product LWZ × tKARWZ, as some measure for the “knot intensity”, was introduced, and products of LWZ × tKARWZ ≥ 2.0 were regarded as weak zones and otherwise as intermediate knot zones. Figure 5a shows the principle of the employed two-level probabilistic hierarchical model as well as the definition of the corresponding equi-correlation. This hierarchical model describes local properties represented by the random variable Zij of a specific board segment i in board j as a sum of the average value of the same property Yj of board j and the local deviation from this average value represented by Xij. This model can be directly inferred from the hierarchical material structure of timber as a natural raw material. It allows the separating of the total variation σZ2 in (i) the variation between the individual boards, σY2, and (ii) the variation within a single board, σX2; see, for example, Ditlevsen and Källsner [6].
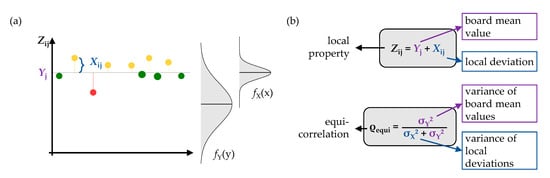
Figure 5.
Two-level probabilistic hierarchical model (a) as well as the formal definitions of its main components (b).
This probabilistic hierarchical approach, wherever applicable, was further applied to characterize the physical properties and geometrical parameters. In total, there are six random variables X = {LWZ; LIZ; DWZ; DIZ; tKARWZ; tKARIZ} necessary to describe the position, dimension, and magnitude of knot zones. Each variable is characterized by a representative statistical distribution model, its corresponding distribution parameters, its equi-correlation, and its correlations to other random variables. The statistical models are selected based on physical constraints and their correspondence to data. All statistical calculations were realized within Mathematica [25]. Figure 6 shows the plots of the correlation between the global (mean) board properties as well as histograms with the selected statistical distribution models. The lengths of knot zones, LWZ and LIZ, are described by a lognormal distribution. Similar to Fink et al. [26], the distances between knot zones, DWZ and DIZ, are assumed to be gamma distributed. A beta distribution is chosen for the measures of the magnitudes of knot zones, tKARWZ and tKARIZ, which are by default restricted to the interval {0; 1}.
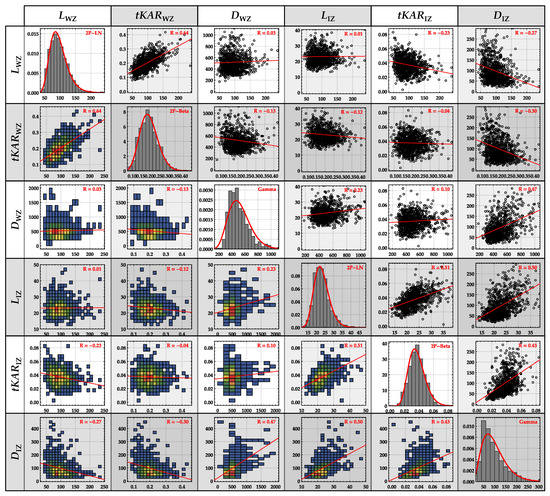
Figure 6.
Simplified linear regressions and correlations together with histograms and corresponding density functions of assumed statistical distribution models of global (mean) board properties X = {LWZ; LIZ; DWZ; DIZ; tKARWZ; tKARIZ} of all boards in the databases.
For simplification and first indication, the correlations and calibrated linear models in Figure 6 are derived from empirical data without considering the corresponding marginal distributions of the random variables. Within the probabilistic board model, however, the correlation structure between the random variables representing the geometric parameters and their individual distribution models is approximated by means of a Gaussian copula. A total of 15 pairwise combinations are necessary for the 6 geometric parameters there to fully describe all correlations between these random variables. The calculation of this common correlation matrix, however, may lead to an invalid non-positive semidefinite matrix. In these cases, the correlation matrix was adjusted to a positive semidefinite matrix, following the methodology in Ref. [27].
The statistics and parameters for all random variables were determined from the datasets, as introduced earlier in Section 2.1. In order to describe the dependency of these six geometric parameters from resawing (lengthwise splitting of boards), the changes in the geometric parameters from splitting all boards virtually in width direction into {2; 3; 5; 8} equally wide pieces are analysed. Figure 7 shows exemplarily the expected (average) functional relationships for the variables LWZ and tKARWZ. Hereby, the separation ratio ηs as the ratio between the residual and the original board width and the board with ratio ηw = wb/wb,ref as the ratio between the original board width and the reference board width are introduced. The reference width was set with wb,ref = 150 mm in accordance with EN 338 [22] and ON EN 1995-1-1 [28].
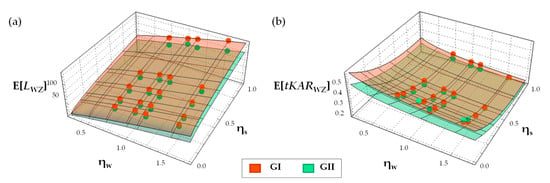
Figure 7.
Expected (average) functional relationships of LWZ (a) and tKARWZ (b).
The principle regression model to describe all random variables in dependency of board width ratio ηw and the separation ratio ηs is given in Equation (3). The regression coefficients, together with reference values and standard deviation of the error term from the regression models to describe the expected values, E(X), the coefficients of variation, COV(X), and the equi-correlation coefficients, ρequi(X), are listed in Table 3 and for modelling the correlation between the variables, ρ(Xi,Xi+1), in Table 4.
with
| βij | regression coefficients (−) |
| board width ratio factor (−) , with ; see Table 3 and Table 4 | |
| separation ratio factor (−); , with ; see Table 3 and Table 4 | |
| board width (mm) | |
| residual board width (mm) | |
| error term; (−) | |
| reference value (mm); (%); (−) |

Table 3.
Regression coefficients, standard deviations of the error term, and reference values of the regression models for the description of the expected values, coefficients of variation, and equi-correlation coefficients for all six geometric variables and reference values of GI and GII.

Table 4.
Regression coefficients, standard deviations of the error term, and reference values of the regression models for the correlation functions and reference values of GI and GII.
The resulting distributions for the global (mean) board properties from the previously stated models are compared to the empirical data from the databases by means of PP-Plots in Figure 8. The plots include data/model predictions and the corresponding 95% confidence intervals (based on empiric quantiles of 500 randomly chosen distributions) for group GI (T14), the separation ratios of ηs = {1; 1/2; 1/3} as well as the board widths wb = {110; 150; 170; 230} mm. Clear deviations from the empirical data are observed for the group of 230 mm wide boards. These deviations might be caused by the small sample size for the 230 mm wide boards compared to that of the other board widths. Apart from this, the probabilistic board model represents the six geometric board parameters of unsplit as well as lengthwise split boards in a quite satisfactory manner. Similar results or approximations of the empiric data are achieved with the model for GII (T24).
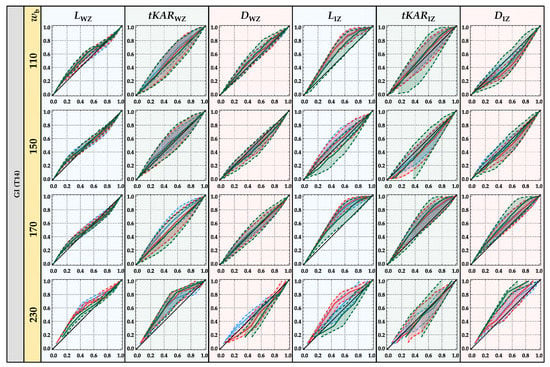
Figure 8.
PP-Plots of model prediction (incl. 95% confidence interval) vs. empirical data from database for global (mean) board properties of unsplit boards (ηs = 1 in green) and lengthwise split boards (ηs = 1/2 in red; ηs = 1/3 in blue).
2.3. Board Generation Process
Figure 9 shows the board generation process schematically by means of the probabilistic board model presented in previous Section 2.2. First, based on the input parameters, the board width, the separation ratio, and the strength class, together with the main statistics and parameters of the marginal distributions, are calculated. In the next step, the six-dimensional copula is formulated, and a random vector Yj with the correlated mean values for the six geometric parameters of a specific board is generated. Following this, local deviations Xij from the global (mean) board properties are calculated for LWZ, tKARWZ, and DWZ for the first alternating renewal process (ARN 1). The positioning and characterization of the intermediate knot zones within the distance to the next WZ follows as a sub-process in the second alternating renewal process ARN 2. ARN 1 and ARN 2 are repeated until a board of predefined overlength is fully characterized. Boards with a length of 20 m are created, and the first 4 m are discarded. The virtual board is then cut from the remaining 16 m. This process ensures a random start at the beginning of each virtual board, despite the board generation process always starting with a weak zone.
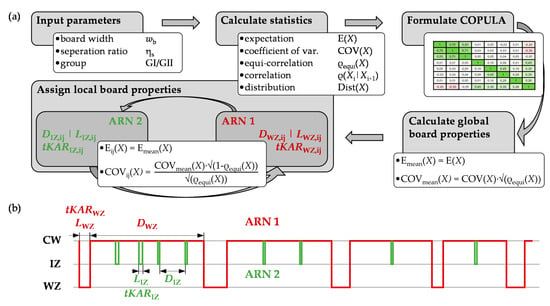
Figure 9.
Board generation process (a) supported by two interlaced alternating renewal (AR) processes responsible for the assignment of local board properties (b).
2.4. Board Mechanical Properties
The regression models from Fink et al. [26], as given in principle for Equation (4), apply for the allocation of mechanical properties to each individual board section, i.e., the local tensile properties parallel to the grain. The regression coefficients for these models are summarized in Table 5.

Table 5.
Coefficients and standard deviations of the error term for the regression model in Equation (4) for Y = {ft,0,ij; Et,0,ij} in (MPa); from Fink et al. [26].
Similar to Fink et al. [26], a correlation of ρ = 0.8 was applied between the error terms of the strength and the modulus of elasticity. In line with the findings in Colling [12] and by following the two-level hierarchical model, the error term was separated into two parts. For the error terms of the strength and the modulus of elasticity, this was done by means of the following equi-correlation coefficients, which were set to account for the different homogeneities in knot and knot-free zones with ρequi,WZ = 0.45, ρequi,IZ = 0.70, and ρequi,CW = 0.90. Although Brandner [29] gave a slightly higher equi-correlation of the WZ for the modulus of elasticity than for the tensile strength parallel to the grain, no differentiation has been made here for the sake of simplification.
The main statistics for the dynamic modulus of elasticity based on eigenfrequency, EDYN,F, as indicating a property for the strength in the grading process and for the average board potential in the virtual board generation process, see Equation (5), are given in Table 6. The comparison of EDYN,F from boards before and after lengthwise splitting based on data from Kastner et al. [17] and recently conducted own tests (see Section 2.5.2) shows that the mean value approximately remains the same, i.e., is independent of the splitting process, whereas the coefficient of variation increases with a decreasing separation ratio; see Equation (5).

Table 6.
Parameters for the dynamic modulus of elasticity.
2.5. Validation of the Probabilistic Board Model
2.5.1. Boards with a Full Cross-Section
The validation of the probabilistic board model is performed by comparing the main statistics together with the various influences of the geometric parameters, i.e., width and length effects, as calculated from simulated board data with experimental data from the literature. These size effects (e.g., width and length) in timber engineering are described via power regression models (e.g., refs. [10,28,30]). Therefore, 1.5 × 104 timber boards were virtually generated for each width wb = {100; 150; 200; 250} mm and both groups GI and GII. The main statistics of the tensile strength and modulus of elasticity in tension parallel to the grain determined from these boards are summarized in Table 7. The results are calculated with a test length according to EN 408 [19] of nine times the width for the determination of the tensile strength and five times the width for the determination of the modulus of elasticity in tension parallel to the grain.

Table 7.
Main statistics of the tensile strength ft,0,b and modulus of elasticity in tension Et,0,b parallel to the grain in (MPa) calculated from 1.5 × 104 simulated boards for each width and group, considering a test length of lb = 9 × wb and lb = 5 × wb, respectively, for ft,0,b and Et,0,b according to EN 408 [19].
In both groups, the average modulus of elasticity in tension parallel to the grain is 500 MPa lower than assigned to the strength classes T14 and T24 in EN 338 [22]. A similar outcome is reported in Fink et al. [26], whose models were also applied here for the allocation of mechanical properties to board segments. An influence of the width of the boards on the modulus of elasticity was not observed.
The mean values of tensile strength and modulus of elasticity are also almost constant, i.e., independent of wb. Slightly increasing 5%-quantile values of the tensile strengths are observed because of decreasing variation with increasing width. This can be well argued, at least qualitatively, on the basis of the natural growing process for branches in softwood trees and their transformation when worked as boards in standard sawing processes (see Figure 10). For the influence of the width, a power coefficient of kw,9b,05 = 0.10 for GI and kw,9b,05 = 0.06 for GII with respect to the reference length of lb,ref = 9 × wb can be found. Burger [31] found similar coefficients of kw,9b,05 = 0.13 and kw,9b,05 = 0.07, respectively, for the visual grading classes S10 and S13 according to ON DIN 4074-1 [23].
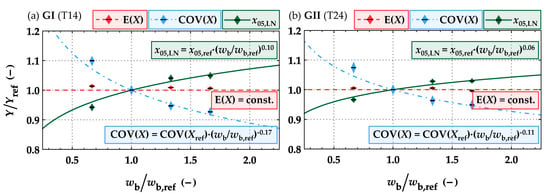
Figure 10.
Influence of the width on main statistics Y = {E(X); COV(X); x05,LN} of the tensile strength parallel to the grain of boards (X = ft,0,b) at the reference length lref = 9 × wb relative to the statistics at reference width of wb,ref = 150 mm; analysis based on virtually generated boards for GI (a) and GII (b).
As the reference length according to EN 408 [19] is directly coupled with the width, i.e., lb,ref = 9 × wb, this width effect represents a combined width and length effect. A more pronounced width effect is observed in the case of a fixed reference testing length. Figure 11 shows a comparison between the tensile strength of boards with a width of wb = {100; 150; 200; 250} mm and a length of lb = {2.0; 4.0} m and the tensile strength of boards featuring a reference width of wb,ref = 150 mm and a length of lb,ref = {2.0; 4.0} m. Given a constant reference length, the power coefficients for adjusting the 5%-quantile of the tensile strength parallel to the grain to the reference width results in kw,2|4m,05 = 0.25 and kw,2|4 m,05 = 0.20, respectively, for GI and GII. EN 384 [20] states a power coefficient kw,EN384 = 0.20 for adjustment acc. to the width of the board, but no length effects are considered. Therefore, the power coefficients found based on fixed board lengths of lb = {2.0; 4.0} m are largely in line with the power coefficient of the width correction function stated in EN 384 [20].
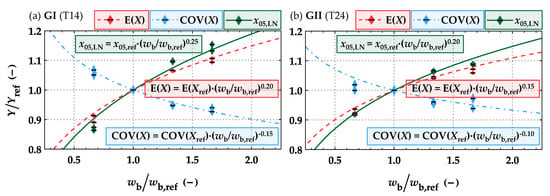
Figure 11.
Influence of the width on the main statistics Y = {E(X); COV(X); x05,LN} of the tensile strength parallel to the grain of boards (X = ft,0,b) featuring a length of lb = {2.0; 4.0} m relative to the statistics at a reference width of wb,ref = 150 mm and lb,ref = {2.0; 4.0} m; analysis based on virtually generated boards for GI (a) and GII (b).
In addition to the board width, the board length also has an influence on the tensile properties. Table 8 summarizes the main statistics of the tensile strength and modulus of elasticity in tension parallel to the grain of 150 mm wide boards, i.e., of boards at reference width wb,ref according to EN 338 [22], EN 384 [20], and ON EN 1995-1-1 [28], for different lengths and for both groups GI and GII. As expected, with increasing length decreasing tensile strengths are observed. The modulus of elasticity in tension parallel to the grain remains unaffected; i.e., there are no trends in mean values nor coefficients of variation given.

Table 8.
Main statistics of the tensile strength ft,0,b and modulus of elasticity in tension Et,0,b parallel to the grain in (MPa) calculated from 1.5 × 104 simulated boards for each length and group, featuring a width of wb = 150 mm according to EN 338 [22].
Figure 12 shows the influence of length on the main statistics of the tensile strength parallel to the grain of boards featuring widths of wb = {100; 150; 200; 250} mm and a length of lb = {900; 1350; 1800; 2000; 2250; 4000} mm relative to their corresponding reference length of lb,ref = 9 × wb. By means of power regression models based on the characteristic (5%-quantile) tensile strength values for group GI and GII, respectively, power coefficients kl,05 = 0.15 and kl,05 = 0.11 are found. Fink [7] reports a comparable dependency of the characteristic tensile strength parallel to the grain on length with kl,05 = 0.15 for L25 and kl,05 = 0.10 for L40. Brandner and Schickhofer [32] calculated power coefficients in dependence on the variation of the tensile strength of the boards. They proposed kl,05 = 0.13 and kl,05 = 0.21, respectively, for boards with coefficients of variation for the tensile strength parallel to the grain in the range of COV(ft,0,b) = 25 ± 5% and COV(ft,0,b) = 35 ± 5%. In line with the outcomes here, they and Brandner [29] and Brandner and Schickhofer [32] also report on higher power coefficients for the length effect on the mean values of the tensile strength parallel to the grain. This is because of the coefficient of variation COV(ft,0,b), which also slightly but constantly decreases with the increasing length of the boards; see Figure 12.
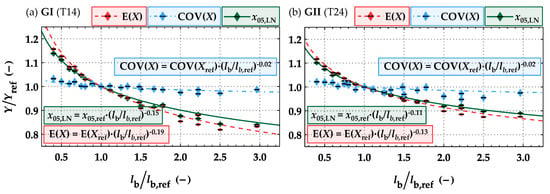
Figure 12.
Influence of the length on the main statistics Y = {E(X); COV(X); x05,LN} of the tensile strength parallel to the grain of boards (X = ft,0,b) relative to the statistics at a reference length lb,ref = 9 × wb; analysis based on virtually generated boards for GI (a) and GII (b).
The probabilistic board model presented here is able to predict in overall terms the tensile strength parallel to the grain of boards and to depict width and length effects within a plausible range as found in experimental investigations in the literature (e.g., [7,31,32]). As shown above, the size effects are partially dependent on the different testing lengths anchored in EN 408 [19]. A uniform reference length and width are needed for further use of tensile properties in load-bearing models. This can be achieved either by a fixed testing length or by correction functions. The former European glulam standard EN 1194 [30], for example, provided power functions for the correction of the tensile strength of boards to a reference width of wb,ref = 150 mm and length of lb,ref = 2 m with power coefficients of kw,EN1194 = 0.05 and kl,EN1194 = 0.10 irrespective of the board strength class. Such regulations are missing in the current product standard for GLT EN 14080 [10]. Based on these observations, the tensile strength of boards within load-bearing models is always referenced to a length of lb,ref = 2.0 m in the following.
2.5.2. Boards in Split Condition
A comparison between simulated data, test data from the literature, and also from additionally conducted own test series is made for validation of the new probabilistic board model. This also applies in the context of the prediction quality for lengthwise split boards, whereby the splitting process takes place after grading the boards in full cross-section. Boards of various widths wb = {100; 150; 200; 250} mm and lengths lb = {2000; 4000} mm were generated for the simulated data (each combination with 1.5 × 10⁴ realizations). These boards were subsequently split virtually lengthwise given the separation ratios ηs = {1; 2/3; 1/2; 1/3; 1/4; 1/8}. Figure 13 shows the results based on simulated data as main statistics of the tensile strength parallel to the grain of split boards relative to that of boards of full cross-section, i.e., ηs = 1.
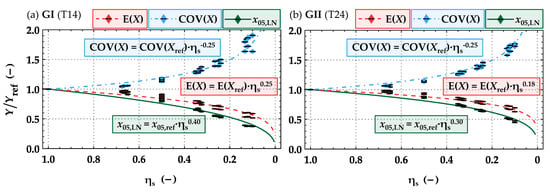
Figure 13.
Influence of lengthwise splitting on the main statistics Y = {E(X); COV(X); x05,LN} of the tensile strength parallel to the grain of boards (X = ft,0,b) relative to the statistics of full cross-section properties; analysis based on virtually generated boards for GI (a) and GII (b).
Compared to the properties of unsplit boards, with decreasing residual width, i.e., smaller ηs, the mean value of the tensile strength parallel to the grain decreases while the coefficient of variation increases. This observation is even more pronounced in the case of boards in the lower strength class GI (T14), but it is less noticeable for GII (T24). Viguier et al. [16] investigated the influence of splitting boards lengthwise on the edgewise bending strength. For boards of strength class C24, according to EN 338 [22] ηs = {1/2; 1/3}, reductions to 78% and 57% of the characteristic bending strength at full cross-section were reported. Reductions to 83% and 75% were found for boards of strength class C40 and with the same separation ratios. Similar reductions are observed for the characteristic values in the current investigations on the tensile strength parallel to the grain.
The results from the tensile parallel to the grain tests conducted on unsplit and split boards from Kastner et al. [17] (strength class T14.5 according to EN 338 [22]) are summarised in Table 9, and a comparison with the model predictions is shown in Figure 14a. The same tendencies are generally observed in the test and simulated data, i.e., with decreasing separation ratios, there is a decrease in the mean and 5%-quantile values and an increase in the coefficient of variation.

Table 9.
Results from the tensile tests parallel to the grain on boards for different separation ratios; data taken from Kastner et al. [17] and own investigations (see Scherfler [33] for further details).
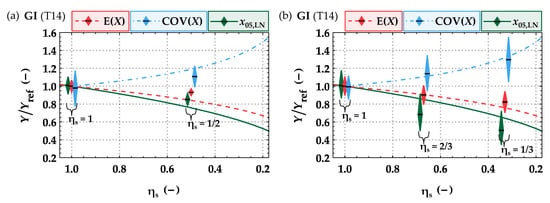
Figure 14.
Model predictions vs. the main statistics Y = {E(X); COV(X); x05,LN} from test results (X = ft,0,b) relative to properties of boards at full width with 95% CI assuming X ~ LN; data taken from (a) Kastner et al. [17] and (b) own investigations (see Scherfler [33] for further details).
To further validate the model, additional tests were carried out on Norway spruce (Picea abies) boards with dimensions wb × tb × lb = 165 × 30 × 4000 mm3 and of nominal strength class T14+ according to EN 338 [22]. In total, 108 boards were delivered. Half of them, randomly selected, remained in their full width, and the other half were split lengthwise to obtain boards featuring ηs = {1/3; 2/3}. The dynamic modulus of elasticity based on eigenfrequency, the density, as well as the positions and dimensions of knots were determined for each individual piece and for split boards before and after splitting. All were subsequently tested together in tension parallel to the grain until failure at a free span of 3180 mm. For both groups of unsplit and split boards, the main statistics and distribution characteristics of the dynamic modulus of elasticity and the density determined from boards at full cross-section are almost identical (see Scherfler [33] for further details).
The main statistics gathered from test results are summarized in Table 9 and compared to the model predictions in Figure 14b. The model outcomes show tendencies comparable to the test results. The mean values for the tensile strength parallel to the grain generally decrease with decreasing separation ratios, while the variation is increased, and the 5%-quantiles, thus, also decrease. An increase in the variation of the modulus of elasticity was also observed within the simulated boards. The reduction of the mean modulus of elasticity as found from current tests was neither detected in Kastner et al. [17] nor in simulated boards.
Some additional comments on current tests: although T14 according to EN 338 [22] was ordered, the delivered material seems to be composed of two groups of strength classes with a significant number of boards, which have every appearance of belonging to much higher strength grades. This circumstance is visible in the high mean tensile strength for the declared strength class T14 according to EN 338 [22] and in the unexpectedly high variation. Since the model for split boards was developed for material featuring a common variation COV(ft,0,l) ≅ 30%, discrepancies between data from simulations and tests have to be expected.
As the possibilities for validating the probabilistic model for split boards are relatively limited due to the small number of experimental investigations and the uncertainties accompanying them, an implicit validation will be conducted later by comparing the outcomes of the probabilistic numerical glulam model with test data gathered from resawn glulam beams; see Section 4.
2.6. Probabilistic Characterization of Finger Joints and Distances of Finger Joints
As an intermediary, product boards or board segments are joined to an endless lamella via finger joints. These endless lamellas are subsequently cut into pieces of the required length. The properties of finger joints and their overall mechanical potential depend on the properties of the two boards/segments that are joined by them. In addition, the execution conditions, the machinery, and other production process-related parameters also play a major role. These influences are assumed to be sufficiently well controlled and are thus not given further consideration. Following the regulations in, e.g., EN 14080 [10], finger joints must be placed in zones free of knots (as surrogates for local grain deviations) and at a sufficient distance from these to avoid possible negative influences from local grain deviations on the performance of the finger joints. This circumstance also needs to be considered in the modelling process. The required characteristic bending and tensile strengths of the finger joints in relation to the characteristic tensile strength parallel to the grain of boards according to EN 14080 [10] are given in Equations (6)–(8).
Regarding the assignment of mechanical properties to finger joints, the approach in Fink [7] is to use a specific tKAR-value in combination with the strength model for the weak knot zones (WZ). Based on tests, he proposed tKARFJ = 0.20. Following his procedure, the tensile strength of finger joints is defined as the minimum of weak zones in both boards calculated at the joint zone with tKARFJ = 0.20. The modulus of elasticity is approximated as the average value of the module of elasticity from clear wood zones of both boards; see Equation (9).
The statistics of the tensile strength of the finger joints are shown in Table 10, and the histograms with overlaid lognormal density functions in Figure 15 for both groups GI and GII. In Table 10, the results for the finger joints are also compared with the tensile strengths parallel to the grain of simulated boards featuring wb = 150 mm and lb = 2 m. The requirements with respect to the strength of finger joints in Equation (8) are fulfilled for both groups. The strength ratios ft,FJ,05,LN/ft,0,b,05,LN are 1.46 for GI and 1.08 for GII. The finger joint tensile strength overall is within the range found in the literature ([34,35]).

Table 10.
Main statistics of the tensile strength parallel to the grain (ft,FJ) of 1.5 × 104 simulated finger joints and of the tensile strength parallel to the grain (ft,0,b) of 1.5 × 104 simulated boards featuring wb = 150 mm and lb = 2 m.
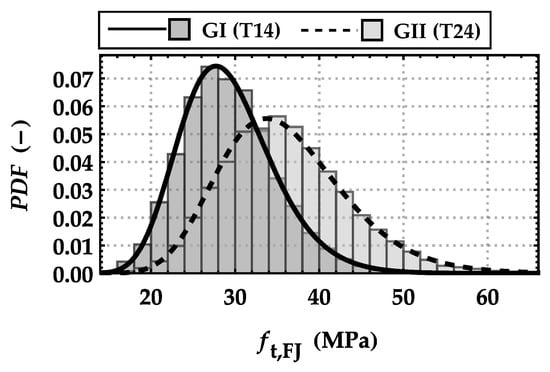
Figure 15.
Histograms together with calibrated lognormal density functions of the finger joint tensile strength parallel to the grain ft,FJ in (MPa) for both groups GI and GII.
The edge effects at finger joints, derived from non-uniform pressure distribution along the width of boards during the production of finger joints and, in particular, with respect to split boards, are not relevant for the products discussed here, i.e., flat finger joint profiles (flanges running parallel to the board’s side faces) are assumed. The increasing influence of grain deviations on the tensile strength of finger joints in split boards is considered via the higher variation in the dynamic modulus of elasticity. For a separation ratio of ηs = 1/10, approximately 10% lower characteristic finger joint tensile strengths are observed from simulations.
The positioning of the finger joints plays an essential role within the probabilistic models. In previous investigations, the positions of the finger joints were randomly chosen based on a normal distribution (ND(4.3; 0.76) in Fink [7] and Fink et al. [26] and ND(4.62; 0.67) Frese [8], Ehlbeck and Colling [36] and Blaß et al. [37]). The approach within this contribution is based on the current production processes. Hereby, a board length of 4 m, a common dimension at least in Austria, is chosen, and the finger joints are placed within a knot-free zone (CW) as close as possible to the board ends. The finger joints with a length of 20 mm were thereby placed in the middle of a knot-free zone with a minimal length of 90 mm. This was done to implement the regulation regarding the minimal distance of knots from the finger joints in EN 14080 [10]. The distribution of distances between the finger joints dFJ for different separation ratios ηs = {1; 1/2; 1/3; 1/8} and base materials are shown in Figure 16.
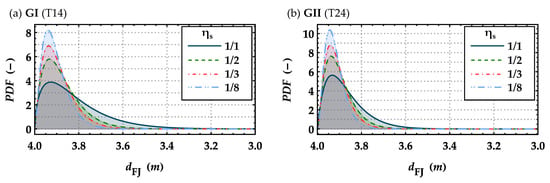
Figure 16.
Calibrated beta density functions {0;4} for representing the distances between finger joints dFJ placed in boards as well as lengthwise split boards featuring different separation ratios of ηs = {1; 1/2; 1/3; 1/8}, assuming a reference board length of lb = 4 m for base material of (a) GI (T14) and (b) GII (T24); for each setting 1.5 × 104 simulations.
The average distance between finger joints is almost independent of the separation ratio and amounts dFJ,mean = 3.86 m for GI (T14) and dFJ,mean = 3.90 m for GII (T24). The variation of the distance between the finger joints decreases with increasing separation ratios. There is no plausible reason why this should occur in real production. In the real production line, the boards are finger jointed to lamellas in full cross-section and are subsequently split lengthwise. Therefore, the distances between finger joints should be independent of the separation ratio. In the presented model, the individual boards are generated in split condition and must be joined subsequently. The observed deviations due to the positioning of the finger joints in the already split board are negligible. The current approach, however, delivers more plausible and realistic board lengths or distances between finger joints dFJ than previous models and depends only on the original board length as the input parameter.
3. Probabilistic Numerical Beam Model
3.1. Principles of the Probabilistic Numerical Model
In order to examine the load-bearing behaviour of virtually generated flex_GLT and glulam beams by means of four-point-bending tests in accordance with EN 408 [19], a stochastic finite-element model was developed within the FE software package Ansys [38]. The test setup is shown in Figure 17. The load is applied at the third points of the test span. The width of the load introductions and supports is 0.5 times the beam depth.
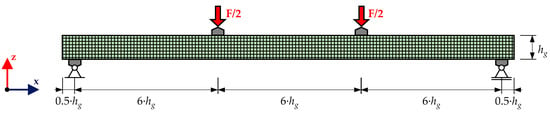
Figure 17.
Test setup of four-point-bending tests in accordance with EN 408 [19] within the FE software package Ansys [38].
All necessary geometric parameters and material properties are provided by individual input files. Figure 18 shows exemplarily a part of one virtually generated flex_GLT beam (hg = 360 mm; wg = 150 mm) consisting of tb = 30 mm thick and wb = 100 mm wide lamellas, its elements, and the distribution of local material properties tKARij, ft,0,ij and Et,0,ij.

Figure 18.
Exemplary representation of one flex_GLT beam type B part as implemented in stochastic FE-analysis: (a) board segment type {CW—Clear wood; IZ—Intermediate knot zone; WZ—Weak zone; FJ—Finger joints}; (b) modulus of elasticity in tension parallel to the grain (x-axis); (c) tKAR-value; (d) tensile strength parallel to the grain (x-axis).
The element size/increment in the longitudinal direction of the beam (x-axis) was set to le = 10 mm. This relatively small value was chosen to realistically depict the morphology of the timber boards within the new probabilistic board model. This represents measures for the extension and magnitude of knots and knot-free zones by random variables. One element per lamination/lamella was used in the direction of the beam depth (z-axis) and width (y-axis). The length of the finger joints was set to 20 mm, which corresponds to two elements. For the board segments and finger joints 8-noded elements of type SOLID185 were used to model the orthotropic behaviour (Ex = Et,0,ij; Ey = Ez = 300 MPa; Gxy = Gxz = G0 = 650 MPa; Gyz = Gzy = G90 = 100 MPa). Similar to Fink et al. [26], differences in the material properties and behaviour as regards to tension and compression parallel to the grain with respect to elastic and strength properties are not considered. Hence, a prior yielding within the bending–compression zone is excluded, and only failures within the bending–tension zone are considered. The contact between the individual lamellas within and between layers was treated as being rigid. This narrow and side face bonding was realized by means of surface contact elements (TARGET170 and CONA174). For the load introduction and support plates, solid three-dimensional elements (SOLID186) with isotropic material behaviour (ES = 1010 MPa) were used. In contrast to the contact formulation between the individual layers of the beam, the contact between the beam and the load introductions and supports was modelled as rigid contact in compression and with a small tangential (y- and x-direction) stiffness to prevent an influence of stiff load introductions on the load-bearing behaviour of the beam.
3.2. Beam Generation and Simulation Process
The beam generation and simulation process is schematically shown in Figure 19.
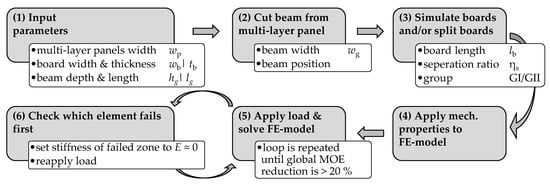
Figure 19.
Beam generation and simulation process.
The beam generation process is directly linked to the necessary production steps of flex_GLT beams (see Figure 2). First, the geometry of the multi-layer panel is created based on the input parameters wp, hp = hg, lp = lg. The cross-section pattern (number of layers and overlap at the board edges; see Figure 3) is calculated based on the multi-layer panel width wp, the board width wb, and the board thickness tb. At this point, it is possible to choose whether the first board of the first solid wood panel (Figure 2a) is arbitrarily reduced in width or not. In the second step, the beam featuring a width of wb is cut from the multi-layer panel. The cutting position with respect to the multi-layer width can be either a fixed value or chosen arbitrarily. With these two randomized generation steps, it is possible to ensure that all possible cross-section patterns are covered within the stochastic process. In the next step, boards featuring a length of lb are generated based on the cross-section pattern of the beam and joined via finger joints. In the course of this, the finger joints are placed in knot-free zones (CW) as close to the board ends as possible, thus mirroring current industrial glulam production lines; see also Section 2.6. To ensure a random distribution of finger joints within the beam, an arbitrary starting position within the first board is chosen.
The total set of mechanical properties is subsequently passed on to the FE-program. In Ansys [38], a load of fixed magnitude, Ftest, is applied, and the resulting local stresses are calculated. Based on the mean tensile stress in each element, the degree of utilization in tension parallel to the grain is calculated. The stiffness of the corresponding zone {WZ, IZ, CW, or FJ} within the beam containing the FE-element with the highest utilization ratio in tension is set to zero. This process is repeated until the global modulus of elasticity in bending (MOE) is reduced by more than 20% from that of the totally intact beam. The maximal load Fmax,I for the glulam beam in each load step i, is calculated based on the utilization ratios in tension parallel to the grain of each element.
The bending strength fm,g of the glulam beam is derived from the ultimate load Fult of all load cycles assuming linear-elastic material behaviour; see Equation (10).
3.3. Validation of the Probabilistic Numerical Beam Model on Glulam
Glulam beams with a width of wg = 150 mm and depths hg = {280; 600; 900} mm were simulated for validation of the probabilistic numerical beam model (each combination with 103 realizations). The length of the boards used was fixed with lb = 4 m, a common dimension widely used in Austria. Therefore, the characteristic tensile strengths of the simulated boards at a reference length of lb,ref = 2 m (see EN 1194 [30]) are ft,0,b,05,LN = 14.3 MPa for GI and ft,0,b,05,LN = 23.4 MPa for GII. The results for the bending properties of the simulated glulam beams virtually tested in bending are summarized in Table 11. Histograms, together with calibrated lognormal density functions of the bending strengths, are shown in Figure 20. The lognormal distributions clearly represent the simulated data in a satisfactory manner. It can be observed from a glance at the main statistics that the mean values of the bending strengths and the coefficients of variation decrease with increasing beam depth. The reduction in the 5%-quantiles of the bending strengths provides good confirmation of the size (depth) effect kh = (hg/600)0.10 as anchored in EN 14080 [10] as well as the depth effect kh = 1.19–− 3.73 × 10−4 × h + 1.04 × 10−7 × h2 for 300 ≤ hg ≤ 1800 mm as proposed in Frese and Blaß [39]. The 5%-quantiles of the bending strength fm,g,05,LN = 21.2 MPa for the GLT beams built up with boards from GI is below the characteristic value as anchored for GL24h according to EN 14080 [10]; also, the mean value of the modulus of elasticity Em,0,g,mean = 10,450 MPa is lower than regulated (Em,0,g,mean = 11,500 MPa). Similar results are reported in the contexts of strength and modulus of elasticity in bending in Fink [7]. One reason for the lower strength value in the simulations presented here might be the coefficient of variation with COV(ft,0,b) ≈ 31% (and 30% in Fink [7]), which is lower than usually found in other studies. For the effect of homogenization of material properties, however, this coefficient of variation is of utmost importance, i.e., the higher the coefficient of variation, the higher the possible effects in homogenization (see [34,40]). Blaß et al. [37], for example, simulated glulam beams of class GL24h built up of boards featuring a tensile strength parallel to the grain of ft,0,b,k = 14.4 MPa and a COV(ft,0,b) = 41.7% and reached the stipulated bending strength.

Table 11.
Main statistics for the bending strength fm,g and the modulus of elasticity Em,0,g as calculated from the data of 103 simulated glulam beams for each setting for a width of wg = 150 mm, various depths and base material GI (T14) and GII (T24).
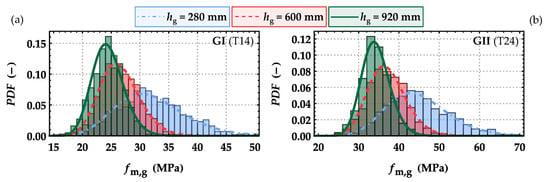
Figure 20.
Histograms together with calibrated lognormal density functions of the bending strength fm,g based on simulated glulam beams of width wg = 150 mm and various depths built up from base material (a) GI (T14) and (b) GII (T24); for each setting 103 simulations.
The bending strength of fm,g,05,LN,ref = 29.9 MPa for glulam beams simulated with boards of the higher strength class GII (T24) are well in line with the load bearing model given in EN 14080 [10], which implicitly considers less variation in the tensile properties of boards of higher strength class.
With regard to the modulus of elasticity in bending of glulam beams, EN 14080 [10] states 5% higher mean values than for the base board material. This was not observed in the simulated data. The mean values remain constant at all investigated depths, whereas, due to homogenization effects, the coefficient of variation decreases significantly with greater beam depths. Brandner and Schickhofer [41] present probabilistic models which allow the distribution and statistics of elastic and shear modules of laminated timber members to be characterized. These statistical models also incorporate the serial and parallel systems within glulam beams. In line with the findings here, they propose not considering any increase in the mean value of the modulus of elasticity in bending of glulam beams in comparison to that of the boards, i.e., Em,g,mean = Et,0,l,mean is concluded.
Overall, the probabilistic numerical beam model is capable of predicting the bending strength and the modulus of elasticity of glulam beams. The presented bending properties and size effects are within a plausible range as found in the literature.
4. Resawn Glulam Beams
4.1. Glulam in Split Condition
In order to analyse the influence of splitting glulam beams on the properties of the remaining cross-sections, the probabilistic model for lengthwise split boards, presented in Section 2, was combined with the probabilistic numerical model for glulam beams in Section 3. Glulam beams of different widths, depths, degrees of separation (one or two cuts separating each beam in equally wide split beams, i.e., ηs = 1/2 or 1/3), and board strength classes were simulated for this purpose. The results for the bending strength fm,g of all simulated parameter combinations (103 for each combination) are summarized in Table 12. The relative bending strength of resawn glulam also varies with the beam width and depth. These deviations are of relatively minor significance compared to the influence of the number of cuts (separation ratio ηs). The absolute mean and 5%-quantile values of the bending strength of the beams are dependent on the beam width. These consequences from the testing lengths as anchored in EN 408 [19] are directly linked to the board width and the influence of the board length on the tensile strength parallel to the grain, as already discussed in Section 2. The former European glulam standard EN 1194 [30] included a reference width of wb,ref = 150 mm and a reference length of lb,ref = 2 m. In cases of deviating board dimensions, the characteristic tensile strength parallel to the grain can be adjusted via two multiplicative coupled power models with power coefficients of kw,EN1194 = 0.05 and kl,EN1194 = 0.10 for all strength classes. Regulations of this kind are lacking in the current standard EN 14080 [10]. Making use of these former provisions or fixing a representative reference testing length, for example, lb,ref = 2 m (e.g., in EN 408 [19]), would be a necessity for correctly depicting the bending strength of glulam and for further reducing uncertainties in the load bearing models.

Table 12.
Main statistics of the bending strength fm,g from 103 simulated glulam beams and resawn glulam {1 cut; 2cuts} for each parameter setting featuring various widths wg = {100; 150; 200} mm, depths hg = {280; 600} mm and base material GI (T14) and GII (T24).
Figure 21 shows the influence of resawing glulam beams on the main statistics of the bending strength relative to that of glulam beams in full cross-section (ηs = 1). With a decreasing separation ratio ηs, i.e., an increasing number of lengthwise cuts, the relative mean values of the bending strength decrease, and the coefficients of variation increase. These effects are more pronounced in the lower glulam strength class. One reason for this is the higher coefficients of variation in the physical properties of the boards, in particular in their tensile strength parallel to the grain.
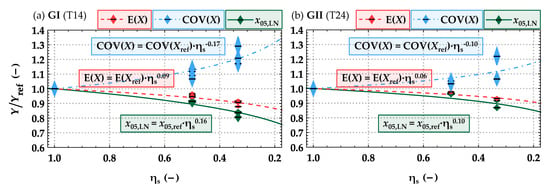
Figure 21.
Influence of lengthwise splitting on the main statistics Y = {E(X); COV(X); x05,LN} of the bending strength (X = fm,g) of resawn glulam beams relative to the statistics of the bending strength of glulam beams with full cross-section; outcomes for glulam beams built up of virtually generated boards of GI (a) and GII (b).
The results for the modulus of elasticity Em,g of all simulated parameter combinations (103 for each combination) are summarized in Table 13. Similar to the bending strength, the MOE of resawn glulam relative to the unsplit glulam varies slightly with the beam width and depth. These deviations are minor compared to the influence of the number of cuts (separation ratio ηs).

Table 13.
Main statistics of the modulus of elasticity Em,g from 103 simulated glulam beams and resawn glulam {1 cut; 2cuts} for each parameter setting featuring various widths wg = {100; 150; 200} mm, depths hg = {280; 600} mm and base material GI (T14) and GII (T24).
Figure 22 shows the development of the main statistics for the modulus of elasticity in bending from resawn glulam beams relative to that of glulam beams in full cross-section (ηs = 1). Constant mean values together with increasing coefficients of variation and consequently slightly reduced 5%-quantile values are observed for decreasing separation ratios. The constant mean values Em,g,mean are in line with the results reported in Viguier et al. [16] and Crocetti [15].
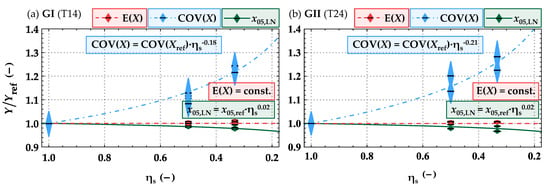
Figure 22.
Influence of lengthwise splitting on the main statistics Y = {E(X); COV(X); x05,LN} of the modulus of elasticity (X = Em,g) of resawn glulam relative to the statistics of the modulus of elasticity of glulam with full cross-section; glulam beams built up of virtually generated boards of GI (a) and GII (b).
In addition to the changes in physical properties, the failure mechanism of glulam and resawn glulam were also analysed. Figure 23 shows the relative shares of the causes of failure at the peak load (Fmax) for glulam and split glulam, classified in weak zones (WZ; knot clusters), intermediate zones (IZ; intermediate knots), clear wood zones (CW; zones without knots), and finger joint failures (FJ), for both groups GI and GII. In general, the relative share of finger joint failures is higher for GII (T24) than for GI (T14). This can be explained by the lower ratio between the tensile strength of the finger joints and the tensile strength parallel to the grain of the board material (see Section 2.6). This circumstance is also well known from other investigations ([7,26,37,39]). The lengthwise splitting of the glulam beams does not affect the properties of the finger joints. Thus the ratio of FJ failures is decreasing for resawn glulam with an increasing number of cuts.
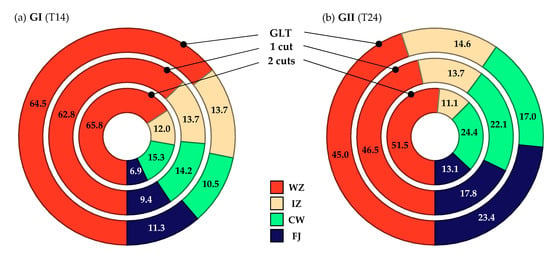
Figure 23.
Mean values of the relative shares of the causes of failures (Fmax), classified according to the types of board segments in {CW—Clear wood; IZ—Intermediate knot zone; WZ—Weak zone; FJ—finger joint}, for glulam and resawn glulam beams built up of virtually generated boards of GI (a) and GII (b).
4.2. Comparison with Previous Investigations
Only a few experimental investigations are known to the authors that provide mechanical properties of resawn glulam beams. These investigations mostly comprise only a limited number of tests per series (n ≤ 20), which commonly leads to considerable uncertainties in relative comparisons between the properties of resawn and unsplit glulam beams. This uncertainty can be seen as one potential reason for partly inconsistent results, as already discussed in Section 1 and as illustrated by the dimensions of the 95% confidence intervals in Figure 24. This figure summarizes test results from experimental investigations of Cleason [14], Crocetti [15], Viguier et al. [16] and Kastner et al. [17] and compares them to the predictions of the new probabilistic numerical beam model, as presented in Section 4.1. This comparison is again made based on relative values.
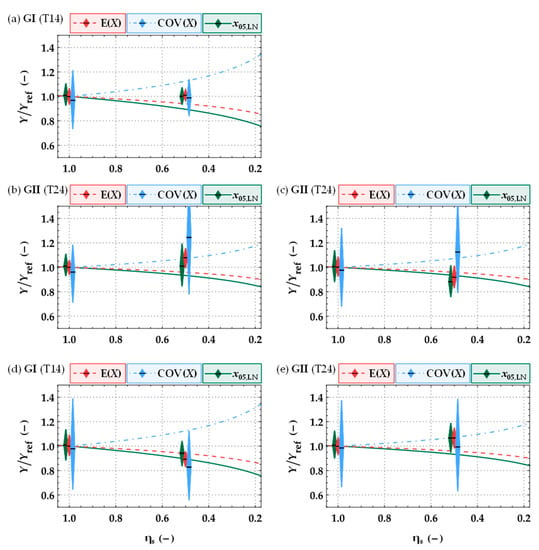
Figure 24.
Main statistics Y = {E(X); COV(X); x05,LN} of the bending strength from split vs. unsplit glulam beams (X = fm,g) based on model predictions (dashed lines; GI or GII) and from test results taken from literature together with 95% CI assuming X ~ LN; (a) Kastner et al. [17]—GL24h, 170 × 160|80 × 160 mm2 (number of tests: 35 full|78 1-cut); (b) Crocetti [15]—GL30h, 90 × 180|40 × 180 mm2 (number of tests: 16 full|# 16 1-cut); (c) Cleason [14]—GL28c, 90 × 225|40 × 225 mm2 (number of tests: 16 full|# 16 1-cut); (d) Viguier et al. [16]—GL24h, 170 × 400|80 × 400 mm2 (number of tests: 16 full|# 16 1-cut); (e) Viguier et al. [16]—GL28h, 170 × 400|80 × 400 mm2 (number of tests: 16 full|# 16 1-cut).
The tendencies resulting from the splitting process, the decreasing mean and 5%-quantile values, and the increasing coefficients of variation as described above, are, in general, to a majority extent, consistent with the experimental investigations found in the literature. The comparisons are rather promising when also considering the circumstances that the glulam properties from tests are only represented by two different board material qualities in the probabilistic numerical investigations presented here, these being GI and GII. However, there are also two investigations (Kastner et al. [17] and GL28h in Viguier et al. [16]), which conclude that there is no influence from splitting on the bending strength statistics. It must be noted here, however, that all these previous investigations focused only on resawn glulam beams based on single lengthwise cuts. Experimental investigations with two cuts (ηs = 1/3) are, unfortunately, not known to the authors.
4.3. Modeling the Bending Strength of Resawn Glulam Beams
4.3.1. Model Based on the Tensile Strength Parallel to the Grain of Split Boards
The load-bearing model for glulam in bending describes the characteristic bending strength of glulam beams in relationship to the characteristic tensile strength parallel to the grain of boards and finger joints. By analogy, one possible approach for characterizing the bending strength of resawn glulam beams is via the tensile strength parallel to the grain of the lengthwise split boards. For better comparability between the board properties at various dimensions, a reference length of lb,ref = 2 m is applied, as formerly anchored in EN 1194 [30]. Figure 25a shows the characteristic (5%-quantile) bending strength of all simulated glulam beams (see Table 12) related to the reference depth hg,ref = 600 mm according to EN 14080 [10] vs. the characteristic bending strength estimated via the load-bearing model in EN 14080 [10], {1} Brandner and Schickhofer [34] {2} and the new proposed model {3} in Equation (11), which is based on the simulation results.
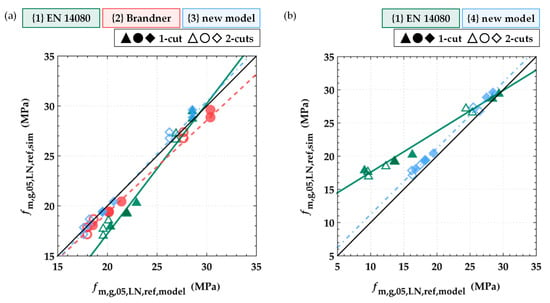
Figure 25.
(a) Results of simulated characteristic (5%-quantile) bending strength values (hg,ref = 600 mm) vs. the characteristic (5%-quantile) bending strengths according to the load bearing model in EN 14080 [10] {1}, Brandner and Schickhofer [34] {2} and Equation (11) {3} based on the characteristic (5%-quantile) tensile strength parallel to the grain of full and split boards with lb,ref = 2 m; (b) results of simulated characteristic (5%-quantile) bending strength values for split glulam beams (hg,ref = 600 mm) vs. the characteristic (5%-quantile) bending strengths according to the model for resawn glulam beams in Equation (1) from EN 14080 [10] {1} and the new model in Equation (12) {4}.
The currently anchored load-bearing model {1} significantly overestimates the characteristic bending strength of resawn glulam beams built up of GI, i.e., in the case of lower strength glulam beams. By contrast, model {2} leads to slightly overestimated characteristic bending strength values for the higher strength classes, e.g., resawn glulam beams built up of GII board material. Apart from these general observations, one overall disadvantage of this approach is that the tensile strength parallel to the grain of the split boards is required as an input parameter. This strength value is usually not available or unknown, apart from in the models presented here for the two strength classes, GI (T14) and GII (T24) (see Section 2.5.2).
4.3.2. Model Based on the Bending Strength of Glulam Beams and the Tensile Strength Parallel to the Grain at Full Cross-Sections
The second approach is to estimate the characteristic bending strength of resawn glulam from the characteristic bending strength of the unsplit glulam beams and the characteristic tensile strength parallel to the grain of the board material used to build up the glulam beams. This approach is currently anchored in EN 14080 [10]. Figure 25b shows the comparison between the characteristic bending strengths of the simulated resawn glulam beams and the stipulated formula in EN 14080 [10] {1} as given in Equation (1) as well as the new proposal as formulated in Equation (12) {4}.
Equation (1) from EN 14080 [10] is based on experimental results from tests on glulam of higher strength classes (see [14,15]). This circumstance might be the reason for the observed larger deviations at lower glulam strength classes. The new proposal in Equation (12) covers the influence of resawing on the characteristic bending strength of glulam also for lower strength classes. It gives an intentionally slightly conservative estimate with a widely constant bias.
Table 14 provides a comparison between the characteristic bending strengths of resawn glulam according to the current regulations (EN 14080 [10]), see Equation (1), and the new proposal in Equation (12). Whereas the outcomes for resawn glulam beams based on GL32h according to Equations (1) and (12) are relatively close, the new proposed model in Equation (12) allows, on the one hand, the production of resawn glulam beams also based on GL24h and, on the other hand, much more economical use of the outstanding natural building material timber in the form of resawn glulam beams.

Table 14.
Comparison of the characteristic bending strengths in (MPa) of resawn glulam beams according to the current regulations in EN 14080 [10] and the new proposed model in Equation (12).
5. Investigations on Flex_GLT Beams of Type B
5.1. System and Size Effects in the Context of Bending Strength
5.1.1. General Background and Overview on the Reasons for System and Size Effects in flex_GLT Type B Beams
Due to the production method for flex_GLT type B beams, different system and/or size effects may occur with respect to the bending strength. The flex_GLT beams in Figure 26 show exemplarily some possibilities for activating these effects. As already mentioned in Section 3.2, the first residual width of the first board within the lowest layer (SWP) is chosen arbitrarily, and the positioning of the boards’ edges in the other layers is only dependent on the multi-layer panel width and thus are constant. Therefore, all possible cross-section patterns are represented within the stochastic generation process.
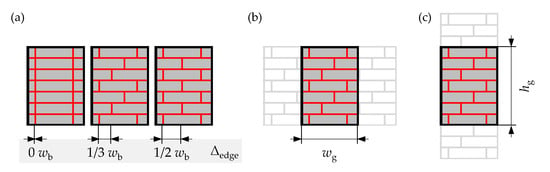
Figure 26.
Possibilities to activate system and size effects in flex_GLT type B beams: (a) the positioning (alignment) of board edges between the layers; (b) the number of parallel acting members within the bending-tension zone (width effect); (c) the number of layers (depth effects).
The first possible influence on the bending strength comes from the positioning or alignment of the board edges between the layers within the cross-section (Figure 26a). The second effect in Figure 26b accounts for the number of boards/lamellas in the bending-tension zone activating parallel system effects. The last effect in Figure 26c addresses the number of layers within the cross-section, well-known as the depth effect from conventional glulam. The mentioned possibilities and consequent effects on the bending strength of flex_GLT type B beams are presented and discussed in the following.
5.1.2. Positioning of Board Edges between the Layers
To analyse the influence of the positioning/alignment of the board edges between the layers on the bending strength of flex_GLT type B beams, 3 different overlaps Δedge = {0; 33; 50} mm between the board edges of the neighbouring layers were investigated. All investigated beams featured a depth of hg = 360 mm and a width of wg = 150 mm. As the base material for building up the flex_GLT type B beams, boards of group GI (T14), featuring cross-section dimensions of wb = 100 mm and tb = 30 mm, were used. Given that the absolute overlap measures as given above correspond to {0; 1/3; 1/2} times the board width, where half the board width is the maximum possible overlap. The results of 103 simulations per setting are shown as boxplots in Figure 27. Based on these outcomes, there is no significant influence from the overlap as a parameter on the distribution and main statistics of the bending strength of flex_GLT type B beams, neither on the mean nor on the 5%-quantile level.
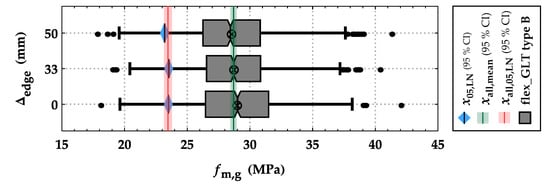
Figure 27.
Boxplots together with mean and 5%-quantile values of the bending strength fm,g of flex_GLT type B beams with dimension hg = 360 mm and wg = 150 mm featuring different overlaps of Δedge = {0; 33; 50} mm = {0; 1/3; 1/2} × wb between the board edges of the neighbouring layers built up from boards of group GI (T14) with dimensions of wb = 100 mm and tb = 30 mm.
5.1.3. Influence of Beam width (Parallel System Effect)
Depending on the beam width wg relative to the board/lamella width wb a certain average number of boards will act together in a parallel system within the bending–tension zone of the flex_GLT type B beams. This circumstance enables load sharing between adjacent boards and load redistribution after the occurrence of partial failures. Figure 28 shows boxplots illustrating the distribution and main statistics of the bending strength of randomly built-up flex_GLT type B beams featuring a depth of hg = 360 mm and width of wg = {50; 100; 150; 250; 500} mm. As a baseline, conventional glulam beams of similar depth and width wg = 100 mm were generated, built up with the same boards of group GI (T14) and a dimension of wb = 100 mm and tb = 30 mm. In addition to the width ratio wg/wb, the average number of parallel acting boards (nb,all) and the average number of boards with a full cross-section (nb,full) are stated.
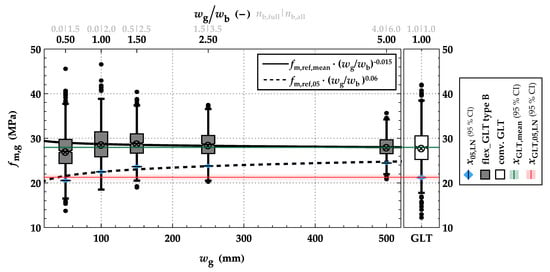
Figure 28.
Boxplots together with mean and 5%-quantile values of the bending strength fm,g of flex_GLT type B beams featuring a depth of hg = 360 mm and different beam widths wg = {50; 100; 150; 250; 500} mm and conventional glulam (reference) of similar depth and width wg = 100 mm built up from boards of group GI (T14) with dimensions of wb = 100 mm and tb = 30 mm.
The average bending strength stays almost constant for ratios of wg/wb ≥ 1.00, whereas at higher beam widths, the coefficient of variation decreases, and therefore, the bending strength fm,g,05 increases. Significantly reducing mean and 5%-quantile values are observed at ratios wg/wb < 1.00. This reduction is of similar magnitude as found for resawn glulam resulting from one cut in Section 4.1. This “change in system” or “kink” also becomes visible in the number of boards within the lowest layer of the randomly built-up flex_GLT type B beams (see Figure 29). At a ratio of wg/wb < 1.00, the cross-section consists of only split boards.
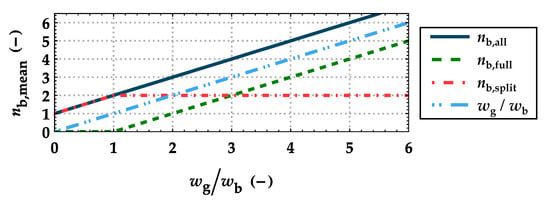
Figure 29.
Average numbers of boards acting in parallel in the bending–tension zone of flex_GLT type B beams in dependence on the width ratio wg/wb: total number of boards (nb,all); number of boards in full cross-section (nb,full); number of lengthwise split boards (nb,split).
Following the outcomes, flex_GLT type B beams featuring the same ratio as conventional glulam (wg/wb = 1.00) have approximately a 6% higher characteristic (5%-quantile) bending strength than conventional glulam. Although flex_GLT beams of this kind comprise a certain share of lengthwise split boards, which are characterized by a lower tensile strength, the already present parallel system effects at this ratio (mean number of boards nb,all = 2) counteract this reduction and result in a higher bending strength.
The observations made generally of approximately constant mean values and the decreasing coefficient of variation with an increasing number of parallel acting boards/lamellas in the bending-tension zone of the bending strength of flex_GLT type B beams featuring wg/wb ≥ 1.00 are consistent with the theoretical statistical background (see Ref. [9]).
5.1.4. Influence of Beam Depth (Depth Effect)
The influence of the beam depth on the bending strength is well-known in conventional glulam beams and has been frequently discussed in the literature (e.g., [7,8,12,37,39,42]). The aim of this section is to discuss potential differences between the depth effect of conventional glulam beams and that of flex_GLT type B beams, which feature a certain share of lengthwise split lamellas.
Figure 30 shows the distribution of the bending strength of flex_GLT type B beams featuring a width of wg = 150 mm and various depths of hg = {210; 360; 600} mm built up from boards of group GI (T14) and GII (T24) with cross-section dimensions of wb = 100 mm and tb = 30 mm. Similar to conventional glulam, the bending strength decreases with increasing depth. For flex_GLT beams of type B power coefficients of kh,mean = 0.22 for the mean values and kh,05 = 0.14 for the 5%-quantile values were found. The latter is within the range kh,05 = 0.10–0.20 commonly found for conventional glulam (see [10,12,34,37,43]).
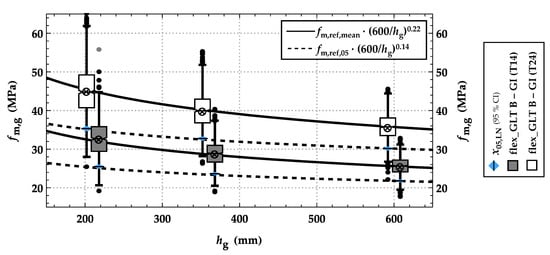
Figure 30.
Boxplots together with mean and 5%-quantile values of the bending strength fm,g for flex_GLT type B beams, featuring a width of wg = 150 mm and various beam depths (hg = {210; 360; 600} mm), built up from boards of group GI (T14) and GII (T24) with dimensions wb = 100 mm and tb = 30 mm.
5.2. Prediction of the Bending Strength of Flex_GLT Type B Beams
Similar to glulam and CLT, one possible approach to characterize the mechanical properties of flex_GLT type B beams is via a relationship to the tensile strength parallel to the grain of the boards and finger joints used. In the following, it is assumed that the characteristic tensile strength of the finger joints fulfils the minimum requirements, for example, as outlined in Equation (6). As a consequence, the load-bearing model for glulam (alike) beams in bending concentrates on the characteristic tensile strength parallel to the grain of the board material used. For better comparability between the characteristic tensile strength parallel to the grain of boards at various dimensions, a reference length of lb,ref = 2 m applies, as anchored in EN 1194 [30]. Figure 31a shows the characteristic bending strength of all simulated flex_GLT type B beams and test data from Sieder and Brandner [44], all referred together to a reference depth hg,ref = 600 mm by means of a power coefficient of kh,05 = 0.14 (power law model), vs. the characteristic bending strength estimated via the load bearing models for glulam in bending as given in EN 14080 [10] {1}, Brandner and Schickhofer [34] {2} and the new load bearing model developed here {3}, which is based on the simulation results and represents an adoption of models {1} and {2}; see Equation (13). In addition to the model in Section 4.3.1 (Equation (11)), the factor ksys,w,flexB is introduced, which accounts for system effects as a consequence of parallel acting adjacent lamellas in the bending-tension zone of flex_GLT beams type B; see Equation (14).
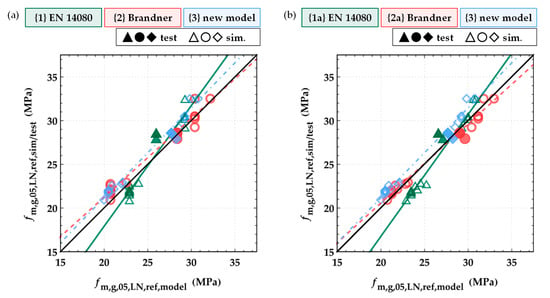
Figure 31.
Characteristic (5%-quantile) bending strength values calculated from simulated and tested flex_GLT type B beams taken from Sieder and Brandner [44] (hg,ref = 600 mm) vs. the characteristic bending strength values according to (a) the load bearing model in EN 14080 [10] {1}, Brandner and Schickhofer [34] {2} and Equation (13) {3} based on the characteristic tensile strength parallel to the grain of boards with lb,ref = 2 m and the characteristic bending strength of the finger joints; (b) the load bearing models EN 14080 [10] {1a}, Brandner and Schickhofer [34] {2a} and Equation (13) {3}, based on the characteristic (5%-quantile) tensile strength parallel to the grain of boards with lb,ref = 2 m and the characteristic (5%-quantile) bending strength of the finger joints, multiplied by ksys,w,flexB; see Equation (14).
The models {1} and {2} are developed for conventional glulam and therefore are not intended for the prediction of system effects caused by parallel acting lamellas in the bending–tension zone. Both models underestimate the characteristic (5%-quantile) bending strength of flex_GLT type B beams. The new model in Equation (13) {3}, which additionally accounts for the number of parallel acting lamellas in the bending–tension zone via the factor ksys,w,flexB, delivers a more homogeneous prediction.
In Figure 31b, models {1} and {2} are also multiplied with ksys,w,flexB. This modification leads to a better agreement between the models {1a} and {2a} and the outcomes from simulated and tested beams. Overall, the load-bearing model for flex_GLT type B beams as given in Equations (11) and (13) can be successfully validated by the test data as presented in Sieder and Brandner [44] (see Table 15). The base board material features a very high coefficient of variation with COV = 43.2% and a tensile strength (5%-quantile) parallel to the grain of ft,0,b,05,LN = 16.0 MPa, which results in a relatively high bending strength (5%-quantile) of the flex_GLT type B beams built up from it. This emphasizes the necessity of considering the coefficient of variation of the base material properties as part of load-bearing models for glulam beams and other structural timber products acting as composites.

Table 15.
Results of tensile tests parallel to the grain on boards, flatwise bending tests on finger joints, and bending tests on two series of flex_GLT type B beams from Sieder and Brandner [44].
6. Summary and Conclusions
The new probabilistic board model presented here allows not only the representation of timber boards in the context of their global and local growth characteristics and also their local and global properties in tension parallel to the grain in the longitudinal direction, but it further enables quantifying the impact of lengthwise splitting after grading on the residual cross-section’s properties. This is of particular relevance for boards graded and classified in full cross-section according to EN 14081-1 [13], which are then and in subsequent production processes regularly or arbitrarily reduced in their width to an extent greater than currently permitted in EN 14081-1 [13].
The probabilistic board model was validated with data from both the literature and our own experiments. Based on simulated tensile tests on boards with full cross-section, power regression models were derived. These allow the influence of the board length on the tensile strength parallel to the grain to be quantified. Power coefficients for these regression models and for the correction of the characteristic (5%-quantile) values of kl,05 = 0.15 and kl,05 = 0.11, respectively, for the lower (GI/T14) and the higher strength class (GII/T24), were found. Additionally, the influence of lengthwise splitting of boards on the tensile properties parallel to the grain was evaluated, and functions to calculate the tensile strength of arbitrarily in width reduced boards were presented.
These possibilities of the board model are also a prerequisite for the characterization of unidirectionally and orthogonally laminated timber products featuring, to a certain extent, boards that are arbitrarily reduced in width, as focused in the ongoing FFG BRIDGE research project “flex_GLT-CLT-beams” (No. 877111). Based on this new probabilistic board model, a probabilistic numerical beam model for glulam and glulam-like products has been set up under the name of flex_GLT beams. This model was successfully validated for the previously defined flex_GLT type B beams. Furthermore, it was also applied for the quantification of the effect of resawing on the bending properties of glulam beams. In the case of regularly resawn glulam beams, the simulations (i) demonstrate the possibility of quantifying glulam beams of this kind even when built up of boards from lower strength classes, (ii) rating the model in Equation (1) from EN 14080 [10] as conservative for low and suitable for higher glulam strength classes, and (iii) serve as the basis for the new proposed load-bearing model for glulam and glulam-like products in bending as formulated in Equation (12). The main conclusions concerning resawn glulam are that the bending properties of glulam from lower strength classes can also be quantified, and the model for bending strength of twice resawn glulam (with two cuts) is also within a plausible range; it should be noted that no other investigations dealing with resawn glulam beams from two cuts are known to the authors.
In the framework of the parameter studies that were conducted, the depth effect on the characteristic (5%-quantile) bending strength of glulam as anchored in EN 14080 [10] with a power coefficient of kh = 0.10 was also re-evaluated and very largely confirmed.
Based on the statistics from simulations, the bending strength of glulam beams was also dependent on the width of the glulam beam. This is due to the different testing lengths of boards when following the regulations in EN 408 [19], where the free test length is a function of the board width and the well-known length effect on the tensile strength parallel to the grain in structural timber. The former European glulam standard EN 1194 [30] specified a reference length of lb,ref = 2 m for the tensile strength parallel to the grain of boards independent of the board width. A correction function was provided for cases of deviating test lengths. Regulations of this kind are missing in the current standard EN 14080 [10]. New provisions in the former regulation could be of value here. These would include a fixed reference length for boards and/or length correction functions for their tensile strength parallel to the grain. This would reduce the uncertainties associated with the current load-bearing model for glulam in bending. Furthermore, incorporating the coefficient of variation for the tensile strength parallel to the grain of the base material as an input parameter in the load-bearing models is highly recommended. This would increase the reliability of glulam beams and make better and more explicit use of the base material homogenization potential featuring higher variability in its tensile properties parallel to the grain. In the current version of EN 14080 [10], the influence of the coefficient of variation for the tensile strength parallel to the grain of the base material is somehow considered implicitly. A higher COV(ft,0,b) for lower board strength classes and vice versa for the higher board strength classes is assumed. This is not visible either to the producer or the engineers.
EN 14080 [10] also states that the mean value of the modulus of elasticity in bending of glulam is 1.05 times higher than the modulus of elasticity in tension parallel to the grain of the base material, and the MOE should be reduced by 500 MPa for resawn glulam. Neither of these effects was observed in the simulated bending test. In the case of resawn glulam, this was not observed for either one or for two cuts. Based on these results, the recommendation can be made that these regulations should be revised.
The main difference between conventional glulam and flex_GLT type B is the presence of one or more board cross-sections in the beam element with an arbitrarily reduced width. In conventional glulam, however, the width of the beam is equal to the width of the board. For flex_GLT type B beams, the influence of (i) the positioning of the board edges, (i) the beam depth, and (iii) beam width was analysed and quantified. Additionally, in Equation (13), a load-bearing model for bending was proposed based on the simulations and was successfully validated with test results. Furthermore, a factor ksys,w,flexB (see Equation (14)) was introduced, which proved to be suitable for adapting the existing load-bearing models of glulam in such a manner as to enable their use also for the prediction of the characteristic bending strength of flex_GLT type B beams. Based on the simulated and the experimental bending tests and with the aim of also providing at least to some extent a safety margin in the regulation of the new product, minimal geometric requirements are defined for flex_GLT type B beams; see Figure 32.
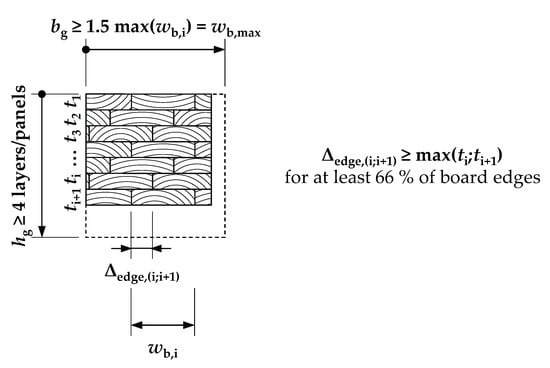
Figure 32.
Requirements on the cross-section of flex_GLT type B beams.
Flex_GLT type B beams should be comprised of at least four layers, in a manner similar to the former definition of glulam (see EN 1194 [30]). As for conventional glulam, also for the characteristic bending strength of flex_GLT type B beams, the depth effect should be considered by means of a power regression model with a power coefficient of kh,05,flexB = 0.14. Despite no influence having been found on the bending strength from the positioning of the board edges, it is proposed that no less than 66% of all board edges should be offset by at least one times the greatest thickness of the adjacent layers. Although it was shown that with a beam width equal to the board width, the parallel system effects outweigh the loss in tensile strength parallel to the grain of boards due to the arbitrary lengthwise splitting, to be on the safe side, the minimum flex_beam type B width wg should be at least 1.5 times the maximum width of boards wb,max used to build up flex_GLT beams. This regulation is a precautionary measure to make sure at least one board is always present in the bending tension zone in its full cross-section.
In addition to the current regulations for conventional glulam, due to the specifics of flex_GLT type B beams, a width effect was introduced, which allows incorporating the number of parallel acting boards in the bending tension zone of the beams. This width effect, which represents a system effect in real terms, is based on the width ratio of the beam to board width (wg/wb). For the characteristic bending strength of the beams, it is given as ksys,w,flexB = (wg/wb)0.06. Due to the fact that no influence on the positioning of the board edges was found, this system effect should also be applicable for conventional block glued glulam beams.
The new probabilistic board model presented here allows for the first time a consistent description of the position and magnitude of knot zones. In addition, a model for the tensile properties parallel to the grain for lengthwise split boards was presented as well as a novel three-dimensional probabilistic numerical beam model. These have been successfully validated for glulam, resawn glulam, and flex_GLT type B beams. Furthermore, the new model was used to describe the bending properties, size, and system effects of glulam and revealed the possibility of producing resawn glulam beams from lower strength classes. In addition, the bending properties of the novel product flex_GLT type B were characterized, the influence of arbitrary in width reduced boards was analysed, and functions for size and system effects were presented.
Author Contributions
Conceptualization, R.S.; methodology, R.S.; validation, R.S.; writing—Original draft preparation, R.S.; writing—review and editing, R.B.; supervision, R.B.; project administration, R.B.; funding acquisition, R.S. and R.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been funded by the Austrian Research Promotion Agency (FFG) within the research project “flex_GLT-CLT-beams”, grant number 877111. The support from the commercial partners Stora Enso Wood Products GmbH and Henkel Central Eastern Europe GmbH is thankfully acknowledged.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors are grateful for the support of the commercial partners, Stora Enso Wood Products GmbH and Henkel Central Eastern Europe GmbH. This publication is supported by TU Graz Open Access Publishing Fund.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fink, G.; Kohler, J.; Brandner, R. Application of European design principles to cross laminated timber. Eng. Struct. 2018, 171, 934–943. [Google Scholar] [CrossRef]
- Köhler, J. Reliability of Timber Structures. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2007. [Google Scholar]
- Ehlbeck, J.; Colling, F.; Görlacher, R. Einfluss keilgezinkter Lamellen Biegefestigkeit Brettschichtholztraeger: Eingangsdaten fuer das Rechenmodell. Holz als Roh-und Werkstoff 1985, 43, 369–373. [Google Scholar] [CrossRef]
- Isaksson, T. Modelling the Variability of Bending Strength in Structural Timber: Length and Load Configuration Effects. Ph.D. Thesis, Lund Institute of Technology, Lund, Sweden, 1999. [Google Scholar]
- Källsner, B.; Ditlevsen, O. Lengthwise bending strength variation of structural timber. In Proceedings of the IUFRO—Timber Engineering, Sydney, Australia, 5–7 July 1994; p. 9. [Google Scholar]
- Ditlevsen, O.; Källsner, B. System effects influencing the bending strength of timber beams. In Proceedings of the IFIP 8th WG 7.5 Working Conference on Reliability and Optimization of Structural Systems, Krakow, Poland, 11–13 May 1998. [Google Scholar]
- Fink, G. Influence of Varying Material Properties on the Load-Bearing Capacity of Glued Laminated Timber. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2014. [Google Scholar]
- Frese, M. Computergestützte Verfahren zur Pragmatischen Beurteilung der Tragwiderstände von Brettschichtholz: Zusammenfassung Exemplarischer Simulationsstudien; Habilitation; KIT Scientific Publishing: Karlsruhe, Germany, 2016. [Google Scholar]
- Brandner, R. Stochastic Modelling in Timber Engineering; Habilitation, Graz University of Technology: Graz, Austria, 2018. [Google Scholar]
- EN 14080:2013; Timber Structures—Glued Laminated Timber and Glued Solid Timber—Requirements. European Committee for Standardization: Brussels, Belgium, 2013.
- ON B 1995-1-1:2019; Eurocode 5: Bemessung und Konstruktion von Holzbauten: Teil 1-1: Allgemeines—Allgemeine Regeln und Regeln für den Hochbau. Austrian Standards Institute: Vienna, Austria, 2019.
- Colling, F. Tragfähigkeit von Biegeträgern aus Brettschichtholz in Abhängigkeit von den Festigkeitsrelevan-Ten Einflussgrößen. Ph.D. Thesis, Universität Fridericiana zu Karlsruhe, Karlsruhe, Germany, 1990. [Google Scholar]
- EN 14081-1:2016; Timber Structures—Strength Graded Structural Timber with Rectangular Crosssection: Part 1: General Requirements. European Committee for Standardization: Brussels, Belgium, 2016.
- Cleason, T. Hallfasthet hos “Klycbalkar”; 2003. [Google Scholar]
- Crocetti, R. Strength of Split Glulam Beams; 2009. [Google Scholar]
- Viguier, J.; Boquet, J.-F.; Dopeux, J.; Bléron, L.; Dubois, F.; Aubert, S. Strength Grading of Split Glulam Beams; International Network on Timber Engineering Research: Bath, UK; Lehrstuhl für Ingenieurholzbau und Baukonstruktionen, Universität Karlsruhe: Karlsruhe, Gemany, 2014. [Google Scholar]
- Kastner, E.; Schickhofer, G.; Brandner, R.; Unterwieser, H. Untersuchung der Auswirkung des Längsweisen Auftrennens auf das Mechanische Potenzial von Brettschichtholzlamellen und Daraus Aufgebauten Brettschichtholzträgern, Hinsichtlich Ihrer Festigkeit und Steifigkeit; Graz University of Technology: Graz, Austria, 2011. (In German) [Google Scholar]
- Schickhofer, G.; Augustin, M. Project Intelliwood: Working Package 3: ‘Strength Correspondence’; Report LR 9808/4; Institut für Holzbau und Holztechnologie, Technische Universität Graz: Graz, Austria, 2001. [Google Scholar]
- EN 408:2012; Timber Structures—Structural Timber and Glued Iaminated Timber—Determination of Some Physical and Mechanical Properties. European Committee for Standardization: Brussels, Belgium, 2012.
- EN 384:2016; Structural Timber—Determination of Characteristic Values of Mechanical Properties and Density. European Committee for Standardization: Brussels, Belgium, 2016.
- Fink, G.; Kohler, J. Zerstörungsfreie Versuche zur Ermittlung des Elastizitätsmodules von Holzbrettern; Eth Zürich: Zürich, Switzerland, 2012. [Google Scholar]
- EN 338:2016; Structural Timber—Strength Classes. European Committee for Standardization: Brussels, Belgium, 2016.
- ON DIN 4074-1:2012; Sortierung von Holz nach der Tragfähigkeit: Teil 1: Nadelschnittholz. Austrian Standards Institute: Vienna, Austria, 2012.
- Olsson, A.; Briggert, A.; Oscarsson, J. Increased yield of finger jointed structural timber by accounting for grain orientation utilizing the tracheid effect. Eur. J. Wood Prod. 2019, 77, 1063–1077. [Google Scholar] [CrossRef] [Green Version]
- Wolfram Research, Inc. Mathematica; Wolfram Research, Inc.: Champaign, IL, USA, 2021. [Google Scholar]
- Fink, G.; Frangi, A.; Köhler, J. Modelling the bending strength of glued laminated timber—Considering the natural growth characteristics. In Proceedings of the 46th Meeting, International Council for Research and Innovation in Building and Construction, Working Commission W18—Timber Structures, Vancouver, BC, Canada, 26–29 August 2013; Lehrstuhl für Ingenieurholzbau und Baukonstruktionen, Universität Karlsruhe: Karlsruhe, Gemany, 2013; pp. 211–225. [Google Scholar]
- Rebonato, R.; Jaeckel, P. The Most General Methodology to Create a Valid Correlation Matrix for Risk Management and Option Pricing Purposes; Quantitative Research Centre of the NatWest Group: Edinburgh, Scotland, UK, 2011. [Google Scholar]
- ON EN 1995-1-1:2019; Eurocode 5: Design of timber structures—Part 1-1: General-Common Rules and Rules for Buildings (Consolidated Version). Austrian Standards Institute: Vienna, Austria, 2019.
- Brandner, R. Stochastic System Actions and Effects in Engineered Timber Products and Structures. Ph.D. Thesis, Verlag der Technischen Universität Graz, Graz, Austria, 2013. [Google Scholar]
- EN 1194:1999; Timber Structures—Glued Laminated Timber—Strength Classes and Determination of Characteristic Values. European Committee for Standardization: Brussels, Belgium, 1999.
- Burger, N. Einfluß der Holzabmessungen auf die Festigkeit von Schnittholz unter Zugbeanspruchung in Faserrichtung. Ph.D. Thesis, Shaker-Verlag, München, Germany, 1998. [Google Scholar]
- Brandner, R.; Schickhofer, G. Length Effects on Tensile Strength in Timber Members With and Without Joints. In Materials and Joints in Timber Structures: Recent Developments of Technology; Aicher, S., Reinhardt, H.-W., Garrecht, H., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 751–760. ISBN 978-94-007-7810-8. [Google Scholar]
- Scherfler, J. Versuchstechnische Ermittlung des Längsweisen Auftrennens auf die Zugeigenschaften von Festigkeitssortierten Brettern; Masterprojekt; Technische Universität Graz: Graz, Austria, 2022. [Google Scholar]
- Brandner, R.; Schickhofer, G. Glued laminated timber in bending: Thoughts, experiments, models and verification. In Proceedings of the 11th World Conference on Timber Engineering, Trentino, Italy, 20–24 June 2010. [Google Scholar]
- Riberholt, H. Nordic Glulam—Mechanical Properties; 2008. [Google Scholar]
- Ehlbeck, J.; Colling, F. Biegefestigkeit von Brettschichtholz in Abhängigkeit von Dichte, Elastizitätsmodul, Festigkeit und Keilzinkungen der Lamellen, der Lage der Keilzinkungen sowie von der Trägerhöhe.: Teil A; Karslruher Untersuchungen; Universität Fridericiana Karlsruhe: Karlsruhe, Germany, 1987. [Google Scholar]
- Blaß, H.J.; Frese, M.; Glos, P.; Denzler, J.K.; Linsenmann, P.; Ranta-Maunus, A. Zuverlässigkeit von Fichten-Brettschichtholz mit Modifiziertem Aufbau; Technische Informationsbibliothek u. Universitätsbibliothek; Universitätsverlag: Hannover, Karlsruhe, 2008; ISBN 9783866442511. [Google Scholar]
- Ansys®. Ansys Mechanical; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Frese, M.; Blaß, H.J. Bending Strength of Spruce Glulam New Models for the Characteristic Bending Strength. In Proceedings of the 41th Meeting, International Council for Research and Innovation in Building and Construction, Working Commission W18—Timber Structures, St. Andrews, NB, Canada, 24–28 August 2008. [Google Scholar]
- Brandner, R.; Schickhofer, G. Glued laminated timber in bending: New aspects concerning modelling. Wood Sci. Technol. 2008, 42, 401–425. [Google Scholar] [CrossRef]
- Brandner, R.; Schickhofer, G. Probabilistic models for the modulus of elasticity and shear in serial and parallel acting timber elements. Wood Sci. Technol. 2015, 49, 121–146. [Google Scholar] [CrossRef]
- Sieder, R.; Brandner, R. A new probabilistic approach to model the tensile properties of split spruce boards and its application in engineered timber products. In Proceedings of the INTER 8th Meeting, Online, 16–19 August 2021. [Google Scholar]
- Colling, F. Brettschichtholz unter Biegebeanspruchung: STEP 3: Holzbauwerke nach Eurocode 5: Grundlagen, Entwicklungen, Ergänzungen; Informationsdienst Holz: Düsseldorf, Germany, 1995. [Google Scholar]
- Sieder, R.; Brandner, R. Tensile properties of lengthwise split boards and their application in engineered timber products. In Proceedings of the PhD Seminiar Stuttgart, Online, 11 March 2022. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).