A Novel Framework for Optimizing Indoor Illuminance and Discovering Association of Involved Variables

Abstract

The associations between various design variables affecting the visual performance of responsive facade systems are investigated in this study. First, we propose a data-driven approach to study practical aspects of illuminance optimization for responsive facades. In this approach, the hourly indoor illuminance data are combined with the location information to generate an objective function. This function is then utilized to evaluate the visual performance of responsive facade systems by matching a variety of facade angle movements to hourly sunshine patterns. Next, statistical tests were deployed to evaluate the role of design variables in different scenarios. The results provide detailed information about the design variables and their effects on visual comfort at 0.05 significant levels. On average, facade angles, facade configurations, facade orientations, and facade locations were significant in 100%, 41%, 87%, and 45% of different possible combinations of scenarios/variables, respectively.

1. Introduction

A building facade system is one of the most important contributors to occupant comfort [1]. The performance of building facades contributes to 17 percent of occupants’ visual comfort and 58 percent of occupants’ thermal comfort [2,3]. Traditional facades, as static systems, are incapable of altering their performance over time in response to frequent variations in weather [4,5,6]. The performance of dynamic facades developed by advanced technologies can improve the limited response of static facades [7,8,9]. Facade systems have the potential to change their function, features, and behavior over time in response to repeated weather changes using advanced control technologies [10]. If the design variables for a responsive facade system are optimized for specific objectives, such as improved occupant visual comfort [11], the system can perform optimally. Occupants’ visual comfort optimization is not a straightforward process [12]. The number of variables involved and the complexity of interactions among the variables make the optimization problem a difficult task for designers [13,14].

In the design process, three types of design variables must be considered: active design variables, passive design variables, and environmental variables [13]. Active design variables such as louver angles, the facade porosity, and facade granularity can adjust the response to external stimuli and interior elements [9]. In contrast, passive design variables remain constant in response to external stimuli and interior elements, including infiltration, window-to-wall ratio, glazing types, and wall insulation [15]. Furthermore, parametric study of environmental variables such as climate zones, building locations, facade orientations, and facade configurations can be implemented to develop multiple design scenarios [14].

Limited past studies developed mathematical models that incorporate active, passive, and environmental variables to optimize visual comfort in responsive facades [13,14,15]. However, no study has investigated the impact of the design variables and their associations with the optimization function in responsive facades.

In this study, we present a double stage framework for investigating the associations between various design variables affecting the visual performance of responsive facade systems. First, we focused on louver adaptation angles in horizontal and vertical facade configuration. An objective function for obtaining optimal indoor illuminance is introduced, utilizing hourly adaptation angles. Compared to the previous objective functions, the proposed function can support all possible occupant activities with the required illuminance ranges. Moreover, the proposed function can deliver an optimal solution even when multiple activities are conducted in the room in different timeframes. The brute force search algorithm is implemented to decide the optimum hourly angles for various facade configurations, orientations, and locations/climates. To find the maximum indoor illuminance, the proposed optimization function is calculated for increments of the facade variables and time.

In the second stage, a proposed three-step framework is implemented to investigate the associations of various design variables with the optimal solution affecting the visual performance of responsive facade systems. The three main steps of the proposed framework are (1) defining scenarios, (2) performing statistical tests, and (3) evaluating the test results, which determines the association of the variables with the optimal solution.

Since the proposed framework yields the optimum angles as its main outcome, the optimum angles are inputted in a facade control system. This potentially could not only improve control latency, but also reduce computational cost. However, it should be explicitly noted that the cost of the hardware and required computational power were not considered in this study and would vary depending on the building specifications.

2. Materials and Methods

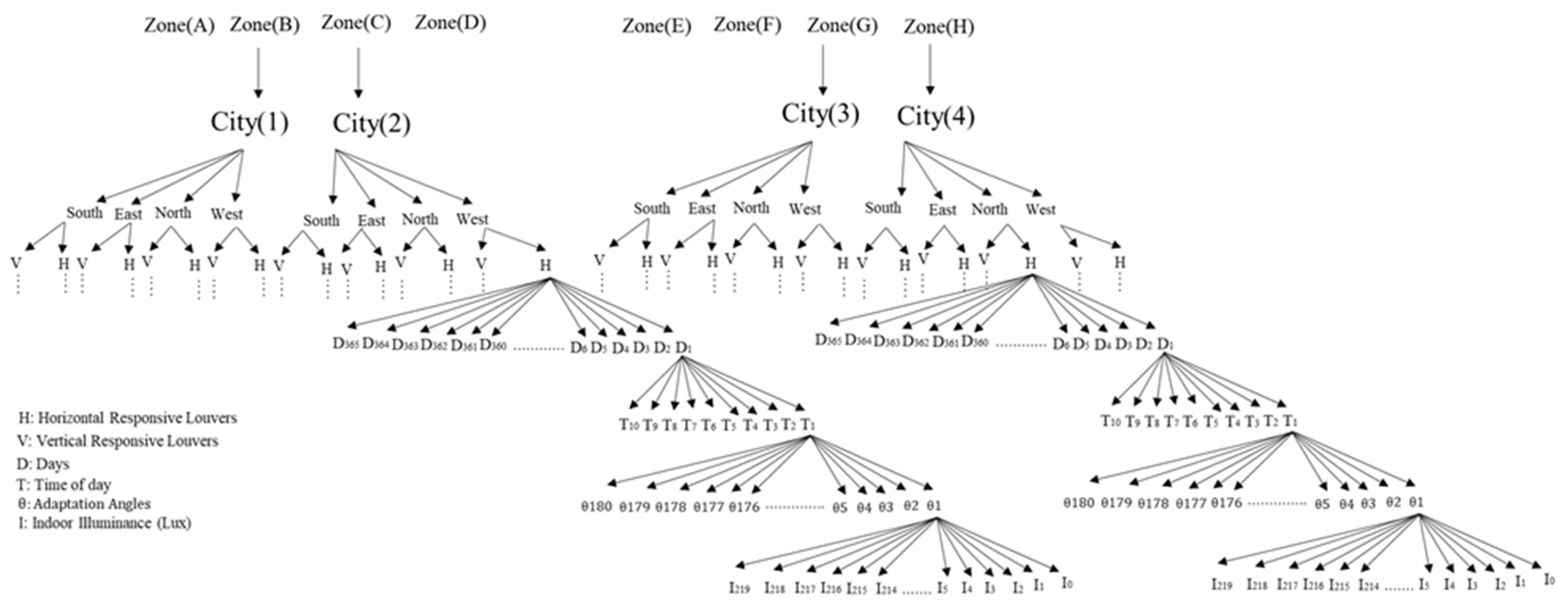
2.1. Experimental Settings

A typical office room was designed using Rhinoceros version 6.0 developed by Robert McNeel & Associates (Seattle, WA, USA). The dimensions of the designed office were 4.0 m wide, 9.0 m deep, and 3.0 m high. The typical daylight zone is about 7.0 m deep from the window wall in common office spaces [16]. The thickness of walls, ceiling, and flooring elements are 0.15 m, 0.12 m, and 0.12 m, respectively. The depth of the office was chosen to be larger than the typical depth so that the effect of daylight remains visible for all variables [17]. Natural light was considered as the only source of light in the office room, with no artificial lighting inside. This simulated office room had a window opening of 2.6 m width and 3.6 m length. The window was made from double-glazed, clear glass with a visible light transmittance of 76% that was installed on the small side of the office room. The window-to-wall ratio before applying the responsive facade system was 78% (floor area = 36.0 m² and window area = 9.36 m² representing a 26% glazing to floor ratio).

Using the Grasshopper modeling tool, a responsive facade system was simulated parametrically and applied to the office window. The simulated office room could be rotated to face the four main cardinal directions (N, W, S, E) in order to create various design scenarios.

The horizontal and vertical louver angles were able to be rotated hourly from −90 degrees to +90 degrees in response to daylight patterns during the day. Horizontal and vertical louvers moved in a clockwise direction from −90 degrees to +90 degrees. The movement of louvers was divided into 60 steps with increments of 3 degrees. The designed facades considered for simulation consisted of 7 horizontal and 7 vertical louvers with dimensions of 3 m × 0.26 m × 0.18 m, as shown in Figure 1. The distances between louvers in the horizontal configuration were 0.40 m and in the vertical configuration were 0.50 m when louvers were fitted on 0 degrees. It is assumed that the louvers were built from diffuse metal provided by DIVA, which corresponds to Radiance parameters of 0.9 specularity, 0.175 roughness, and 0.175 reflectance (RGB) in the DIVA plug-in.

The DIVA daylight-modeling plug-in was utilized to measure indoor illuminance and its corresponding visual metric of Useful Daylight Illuminance (UDI). The DIVA is one of Grasshopper’s plug-ins, which assists Grasshopper in conducting sustainability simulations, such as daylight analysis. Radiance is the core of the DIVA engine and was previously validated by other researchers [18,19,20,21,22,23,24,25]. It has been proven by Reinhart and Walkenhorst that Radiance-based simulation methods are able to efficiently and accurately model complicated daylighting elements [18]. It has also been demonstrated by Ng et al. [18] that Radiance can be used to predict the internal illuminance with a high degree of accuracy. Additionally, Yoon et al. [19] have stated that Radiance is validated computational software and is well known to provide reliable prediction results under various sky conditions. Furthermore, Reinhart and Andersen have shown that translucent materials can be modeled in Radiance with even higher accuracy than was demonstrated earlier [20,21,22,23,24,25].

A grid-based metric of indoor illuminance was developed by defining 220 sensors located over a horizontal grid surface with a height of 0.8 m from the office floor, which was within the average height of a work surface in an office. In both directions of the surface, sensors were spaced approximately every 0.43 m apart. The interior of the office room was simulated using standard Radiance materials that included a generic floor with 20% reflectance, a generic ceiling with 70% reflectance, generic interior walls with 50% reflectance, and generic furniture with 50% reflectance.

It was assumed that the office would be occupied daily from 8:00 a.m. to 6:00 p.m. without daylight savings time. IESNA’s new Lighting Measurement IES LM-83-12 was in agreement with the occupancy schedule [17]. It was assumed that six workspaces would be occupied during occupancy hours. The occupants would be performing regular office work, including working on computers. The clear sky with the sun was assumed as sky conditions. Typical annual meteorological data provided as an EnergyPlus Weather File (EPW) by the U.S. Department of Energy were utilized for the selected cities/climate zones. Three design scenarios were considered: (1) no louvers/no shade, (2) fixed horizontal and vertical louvers with zero-degree angle, and (3) responsive horizontal and vertical louvers with hourly optimum angles, as shown in Figure 2. These scenarios were repeated parametrically for four facade orientations (N, W, S, E) and different facade locations/climate zones.

Four cities from different climate zones in the United States, namely, Miami (FL), Phoenix (AZ), Boston (MA), and Milwaukee (WI), were selected using K-cluster analysis along with an elbow method [26,27]. Annual meteorological data of the selected cities were adopted to simulate the hourly indoor illuminance associated with the multiple scenarios considered. Based on the ASHRAE classification, Miami and Phoenix represent the very Hot-Humid (1A) and Hot-Dry (2B) climates, respectively. Boston and Milwaukee represent Cool-Humid (5A) and Cold-Humid (6A) climates, respectively [28].

Hourly indoor illuminances were calculated at 220 predefined sensors for every 8760 h of a year, while the responsive louver angles were parametrically changed incrementally from −90 to +90°. The measurements were repeated for four facade orientations, horizontal and vertical facade configurations, and four cities/climate zones. The simulations ran 37,843,200 times to calculate and stored raw indoor illuminance values at 8,325,504,000.

The stored output data of the DIVA plug-in were transferred and stored in the Postgres-SQL database. Then, R software was utilized to apply the brute force search algorithm based on the proposed objective function to find the optimum louver angles [29,30,31]. After calculating indoor illuminance, UDI is calculated as a metric, which represents both indoor illuminance level and discomfort glare in one scheme, as widely utilized in the field. Figure 3 shows the flow and execution of the data in the simulation.

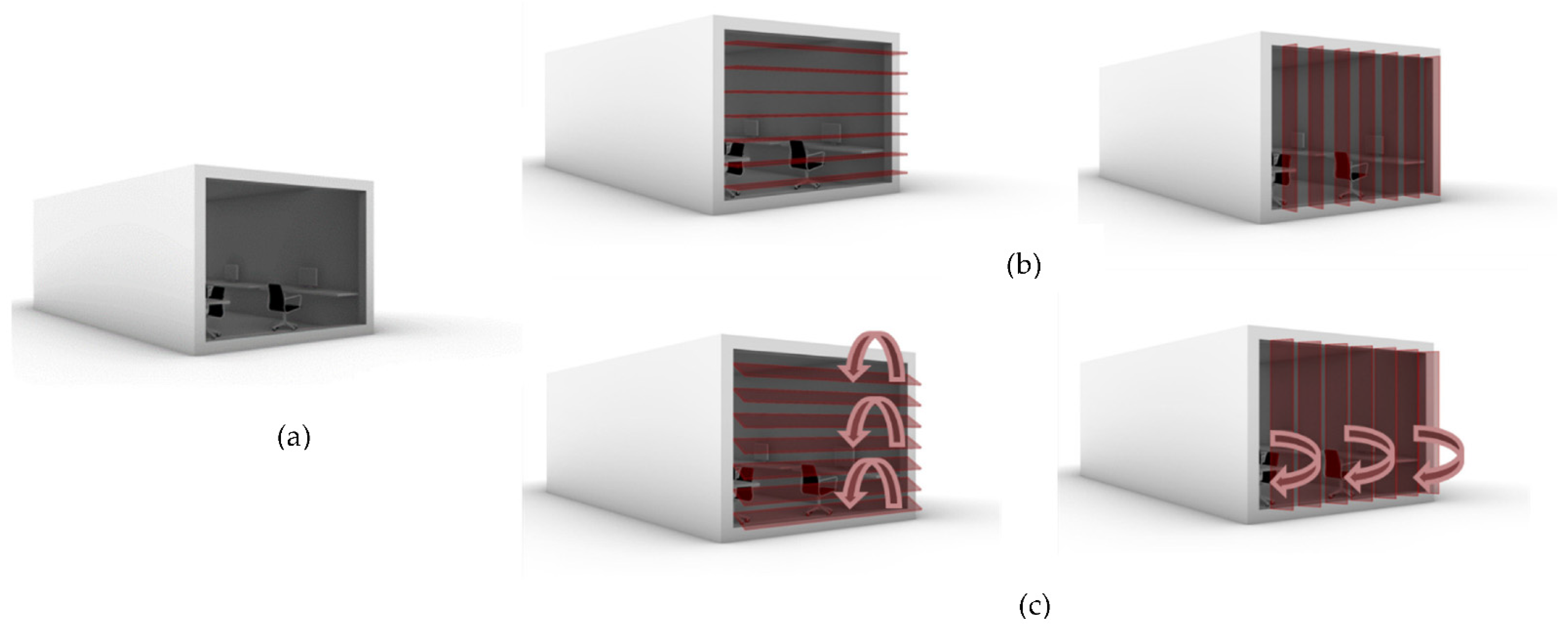
2.2. The Proposed Framework—Stage 1

The UDI is a measure of the annual light quantity accessible in a certain interior space. The annual average of UDI may be used to evaluate the annual performance of a facade. The UDI metric, which depends on both active and passive variables, is considered as a dependent variable for establishing an objective function [28,29,30,31]. The UDI is calculated not only as lower and upper thresholds but also as a useful value depending on the range of illuminance. The lower and upper thresholds and the useful value of UDI are denoted as UDI_underlit, UDI_overlit, and UDI_useful, respectively [32]. In general, UDI is defined as a weighted average as follows [30]:

$$\mathrm{UDI}=\frac{{{\displaystyle \sum }}_{\mathrm{i}}\left({\mathrm{wf}}_{\mathrm{i}}·{\mathrm{t}}_{\mathrm{i}}\right)}{{{\displaystyle \sum }}_{\mathrm{i}}\left({\mathrm{t}}_{\mathrm{i}}\right)}$$

(1)

where t_i is the time when the illuminance E is calculated, and wf_i is the weighting factor, which depends on the range of the calculated illuminance E. It should be noted that the weighting factor wf_i is selected based on the range of the calculated illuminance E. For instance, as shown below, for the upper threshold, UDI_overlit is calculated as below after wf_i is selected depending on how the illuminance E value compares to the upper limit of illuminance specified in standards:

$${\mathrm{UDI}}_{\mathrm{overall}}{\mathrm{with}\mathrm{wf}}_{\mathrm{i}}=\left\{\begin{array}{l}1\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}\mathrm{E}>{\mathrm{E}}_{\mathrm{Upper}\mathrm{limit}}\\ 0\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}\mathrm{E}\le {\mathrm{E}}_{\mathrm{Upper}\mathrm{limit}}\end{array}\right.$$

(2)

In a similar way, the lower threshold UDI_underlit is calculated as:

$${\mathrm{UDI}}_{\mathrm{Usefull}}{\mathrm{with}\mathrm{wf}}_{\mathrm{i}}=\left\{\begin{array}{l}1\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}{\mathrm{E}}_{\mathrm{Lower}\mathrm{limit}}<\mathrm{E}\le {\mathrm{E}}_{\mathrm{Upper}\mathrm{limit}}\\ 0\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}\mathrm{E}\le {\mathrm{E}}_{\mathrm{Lower}\mathrm{limit}}\vee \mathrm{E}>{\mathrm{E}}_{\mathrm{Upper}\mathrm{limit}}\end{array}\right.$$

(3)

Similarly, UDI_useful is calculated as:

$${\mathrm{UDI}}_{\mathrm{Underlit}}{\mathrm{with}\mathrm{wf}}_{\mathrm{i}}=\left\{\begin{array}{l}1\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}{\mathrm{E}}_{\mathrm{Daylight}}<{\mathrm{E}}_{\mathrm{Lowelimit}}\\ 0\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}{\mathrm{E}}_{\mathrm{Daylight}}\ge {\mathrm{E}}_{\mathrm{Lower}\mathrm{limit}}\end{array}\right.$$

(4)

To optimize indoor illuminance, an objective function is established in the following general form as:

$${\mathrm{Obj}}_{\mathrm{general}}={{\displaystyle \int }}_{\mathrm{X}}\mathrm{F}\left(\mathrm{Active}\mathrm{variables},\mathrm{Passive}\mathrm{variables},\mathrm{Environmental}\mathrm{variables}\right)\mathrm{dx}$$

(5)

In this study, an objective function with active variables that can adapt the hourly daylight pattern is proposed. The illuminance includes the useful, overlit, and underlit ranges as the function constraints. These constraints divide interior space into three zones with three different levels of indoor illuminance appropriate for three distinct human activities. The goal of the proposed objective function is to increase the area of useful range for the different human activities and to decrease the area of undesirable ranges.

Two configurations of responsive facades, facades with horizontal louvers and facades with vertical louvers, were considered. The selected configurations are the most influential among various types of responsive facades with high visual performance in facade orientations [33,34,35,36].

Let $S=\left\{s_1,\dots ,s_j\right\}$ represent a specific set of human activities in a desired range of illuminance. H = {h₁, h₂, …, h_k} denotes hour of the day, and $\mathrm{E}\left(\mathrm{x},\mathsf{\theta }\right)$ indicates the indoor illuminance for a specific point x located in the room for a louver angle of $\mathsf{\theta }$. Then, depending on whether or not the value of $\mathrm{E}\left(\mathrm{x},\mathsf{\theta }\right)$ lays on one of the desired ranges, a new indication function ${\mathrm{I}}_{\left(\mathrm{x},\mathsf{\theta }\right)}$ is calculated for a specific point of x in the room and louver angle $\mathsf{\theta }$ by using Equation (3):

$$\mathrm{I}{\left(\mathrm{x},\mathsf{\theta }\right)}_{\mathrm{j}}=\left\{\begin{array}{cc}1\hfill & \hfill \mathrm{when} \mathrm{E}\left(\mathrm{x},\mathsf{\theta }\right) \mathrm{is} \mathrm{in} \mathrm{the} \mathrm{range} \mathrm{of} \mathrm{activity} \mathrm{j}\\ 0\hfill & \hfill \mathrm{otherwise}\end{array}\right.$$

(6)

It should be noted that ${\mathrm{I}}_{\left(\mathrm{x},\mathsf{\theta }\right)}$ indicates some indoor illuminance since it is based on the value of $\mathrm{E}\left(\mathrm{x},\mathsf{\theta }\right)$. Depending on the importance of the human activities, which correspond to the illuminance ranges defined in $S$, a weighting factor W may be defined in a matrix form as:

$$\mathrm{W}=\left[\begin{array}{ccc}{\mathrm{w}}_{11}& \cdots & {\mathrm{w}}_{1\left|\mathrm{s}\right|}\\ ⋮& \ddots & ⋮\\ {\mathrm{w}}_{\left|\mathrm{H}\right|1}& \cdots & {\mathrm{w}}_{\left|\mathrm{H}\right|\left|\mathrm{s}\right|}\end{array}\right]$$

(7)

The rows of the weighting factor are associated with the different human activities as defined in $S$. Thus, there are as many columns as the numbers of human activities as defined in $S$ and denoted by $\left|S\right|$. The weighting factors of columns are associated with the different hours of the day as defined in H and denoted by |H| for which $\mathrm{E}\left(\mathrm{x},\mathsf{\theta }\right)$ is calculated. The hours considered were from 8:00 a.m. to 6:00 p.m.

For a given hour of h, the weighting factors associated with the human activities are obtained by calculating a weighted average of values of the indication function ${\mathrm{I}}_{\left(\mathrm{x},\mathsf{\theta }\right)}$ for the entire points in the room. As shown in Equation (8), the weighted average can be considered as a new indoor illuminance function and be presented as a new metric, sAUDI_h:

$${\mathrm{sAUDI}}_{\mathrm{h}}\left(\mathrm{x},\mathsf{\theta }\right)={{\displaystyle \int }}_{\mathrm{x}\in \mathrm{X}} \frac{{{\displaystyle \sum }}_{\mathrm{j}=1}^{\left|\mathrm{s}\right|}{\mathrm{w}}_{\mathrm{hj}}\mathrm{I}{\left(\mathrm{x},\mathsf{\theta }\right)}_{\mathrm{j}}}{{\mathrm{N}}_{\mathrm{X}}}\mathrm{dx}$$

(8)

where ${\mathrm{N}}_{\mathrm{X}}$ denotes the total number of points in the room.

The final objective function, AUDI, which is a function of the point x, the louvre angle $\mathsf{\theta }$, and the hour h, is computed by adding the calculated sAUDI_h for all the hours, as presented in Equation (9):

$$\mathrm{AUDI}\left(\mathrm{x},\mathsf{\theta },\mathrm{h}\right)={{\displaystyle \int }}_{\mathrm{h}\in \mathrm{H}}{\mathrm{sAUDI}}_{\mathrm{h}}\mathrm{dh}$$

(9)

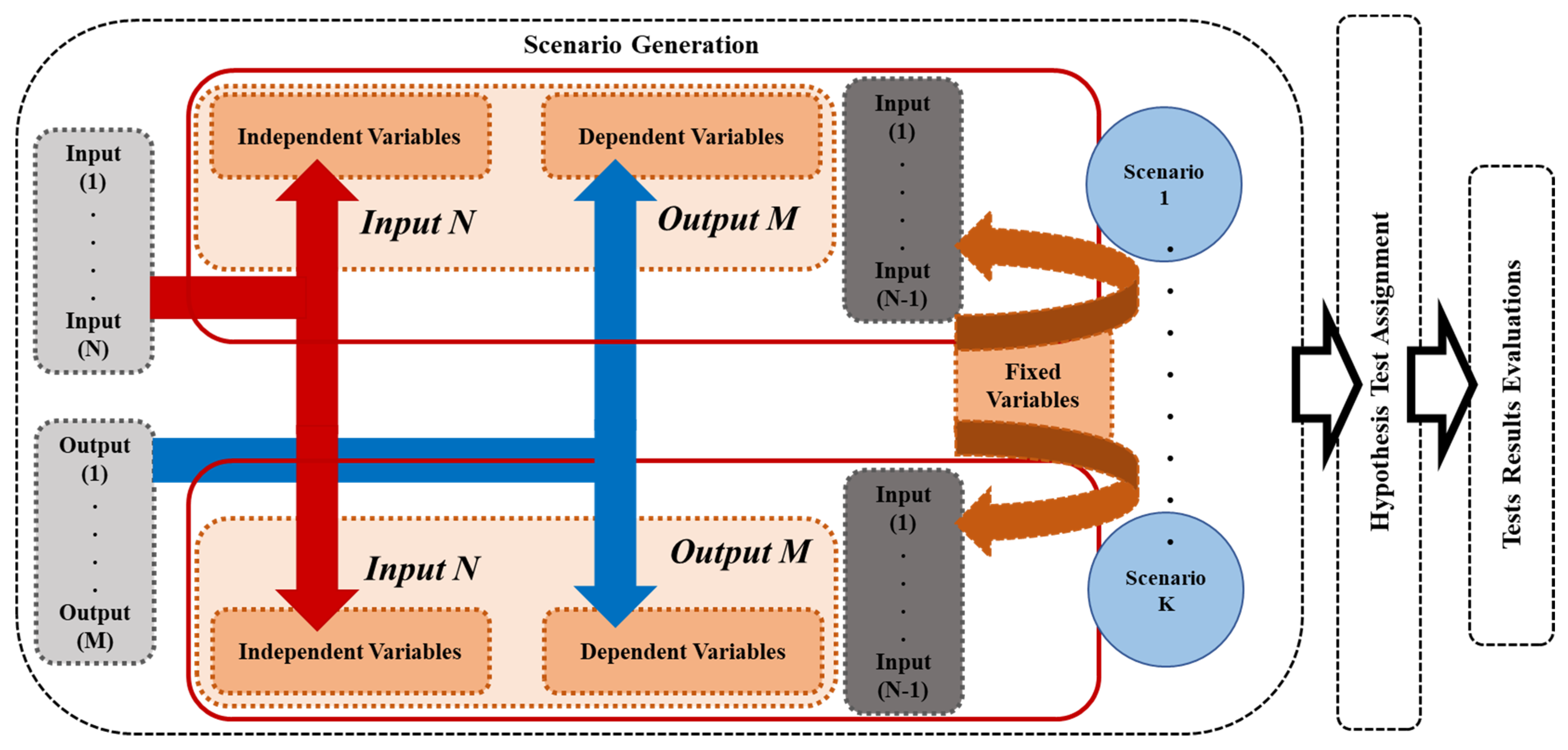
2.3. The Proposed Framework—Stage 2

While the first stage of the framework aims to find the optimum angle by using Equation (6), the second stage investigates the role of various input variables in the optimum daylight illuminance. There are three steps in this stage, entitled scenario generation, hypothesis test assignment, and hypothesis test conduction and evaluation, as shown in Figure 4. The scenario generation step includes the following:

• A dependent variable is selected from the visual comfort and maximum visual comfort calculations of Equation (9).
• An independent variable is chosen from active variables or environmental variables.
• Other input variables are fixed at specific values.

As an example, in order to investigate whether the office orientation impacts the values of the maximum visual comfort, the office orientation and the maximum hourly visual comfort are considered as the independent variable and dependent variables, respectively.

Each design scenario needs a specific statistical test based on the type of the independent and dependent variables. Therefore, the second step assigns a statistical test from the list of available statistical tests based on the different experimental settings (scenarios) and the type of the dependent and independent variables. The statistical tests available for this step include ANOVA, the Kruskal–Wallis, and Chi-squared [37,38,39].

Finally, the third step evaluates the results of the statistical test based on the obtained p-value, which measures the difference between the involved populations in the conducted test. A p-value greater than 0.05 indicates statistical insignificance. Thus, if the p-value calculated was below 0.05, the result was considered as statistically significant.

All statistical analyses were carried out using R v.3.4.0 [40]. The complete list of the variables is provided in

Table 1. Experimental settings for scenario generation.

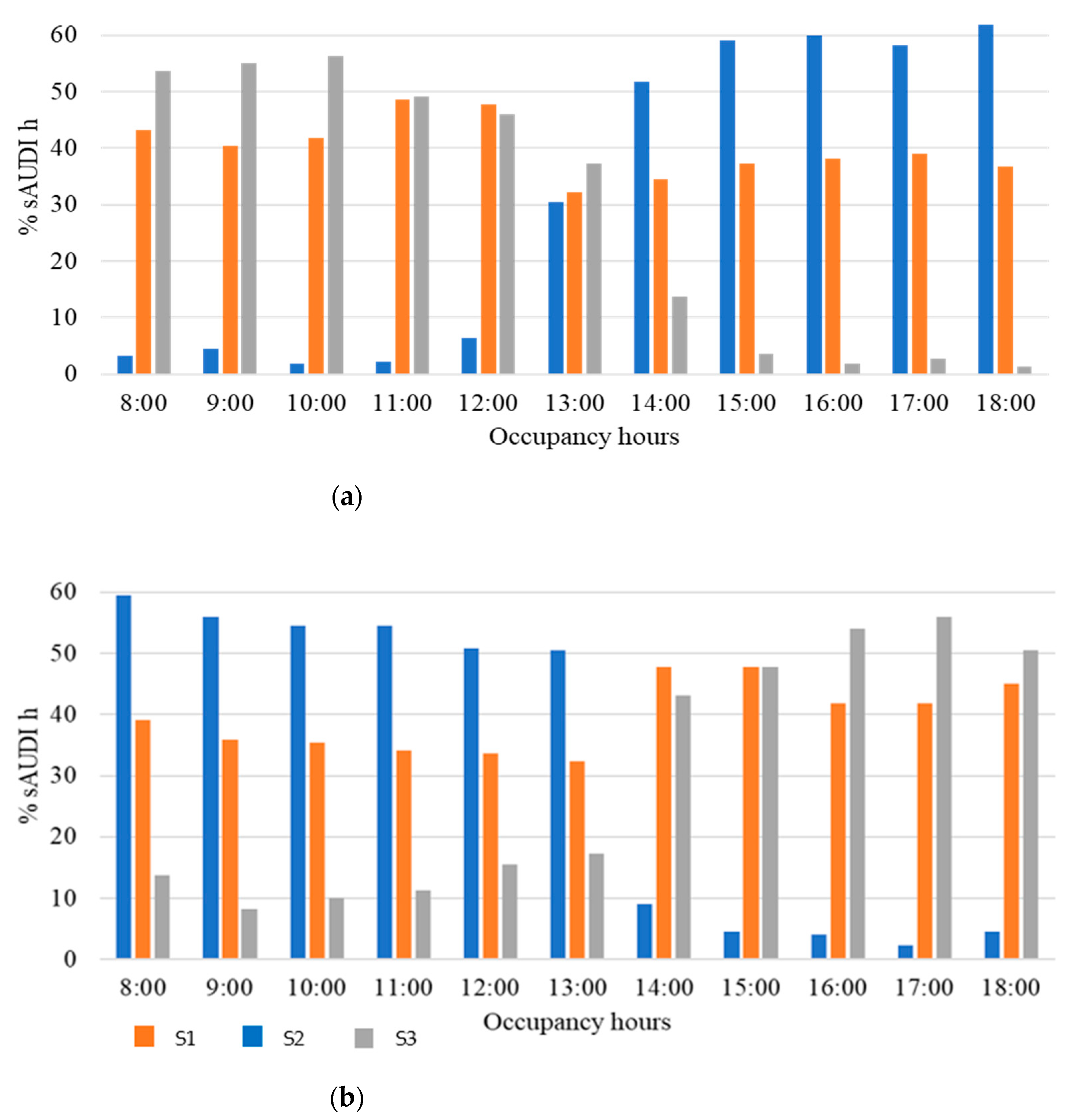
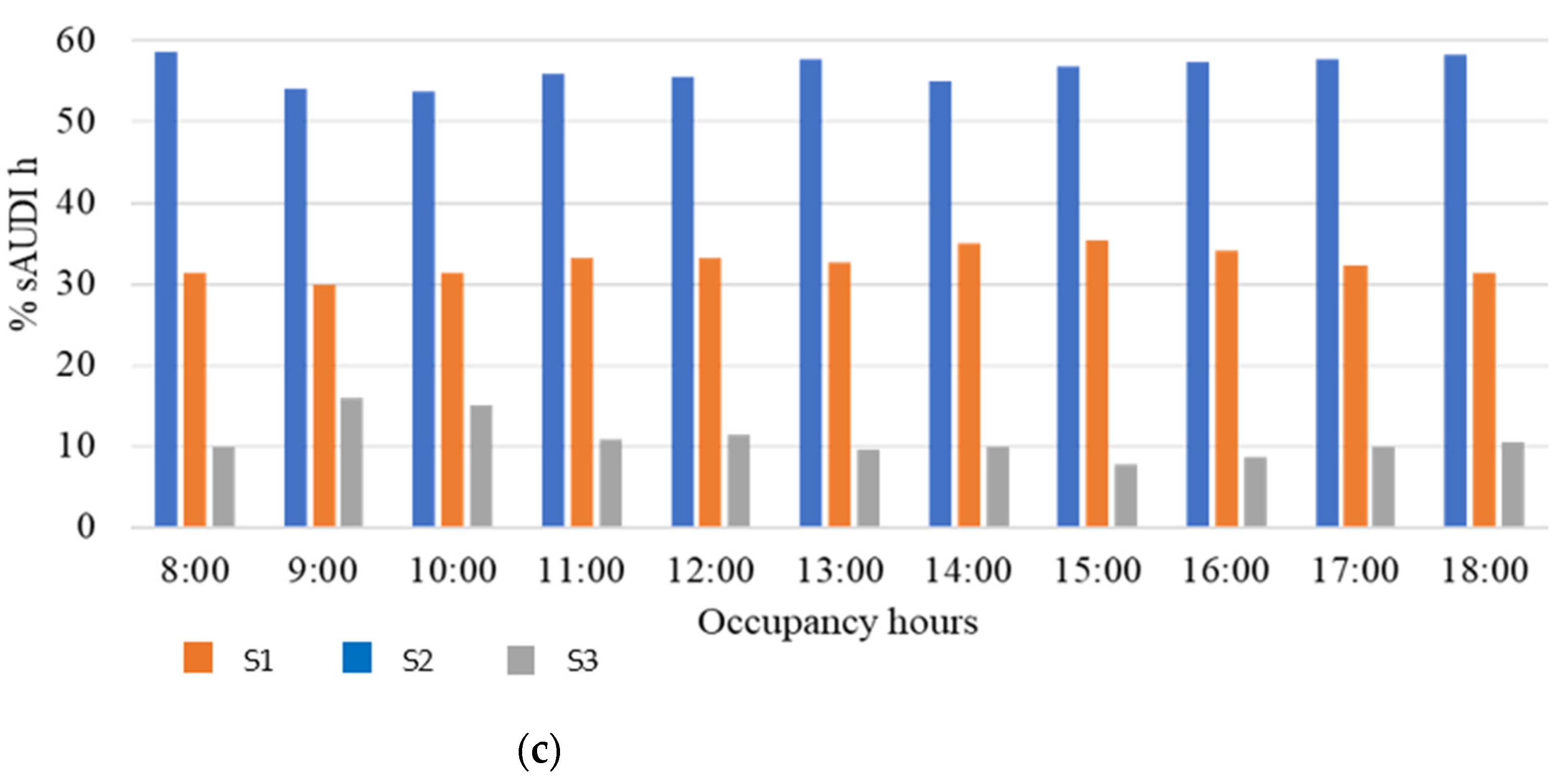
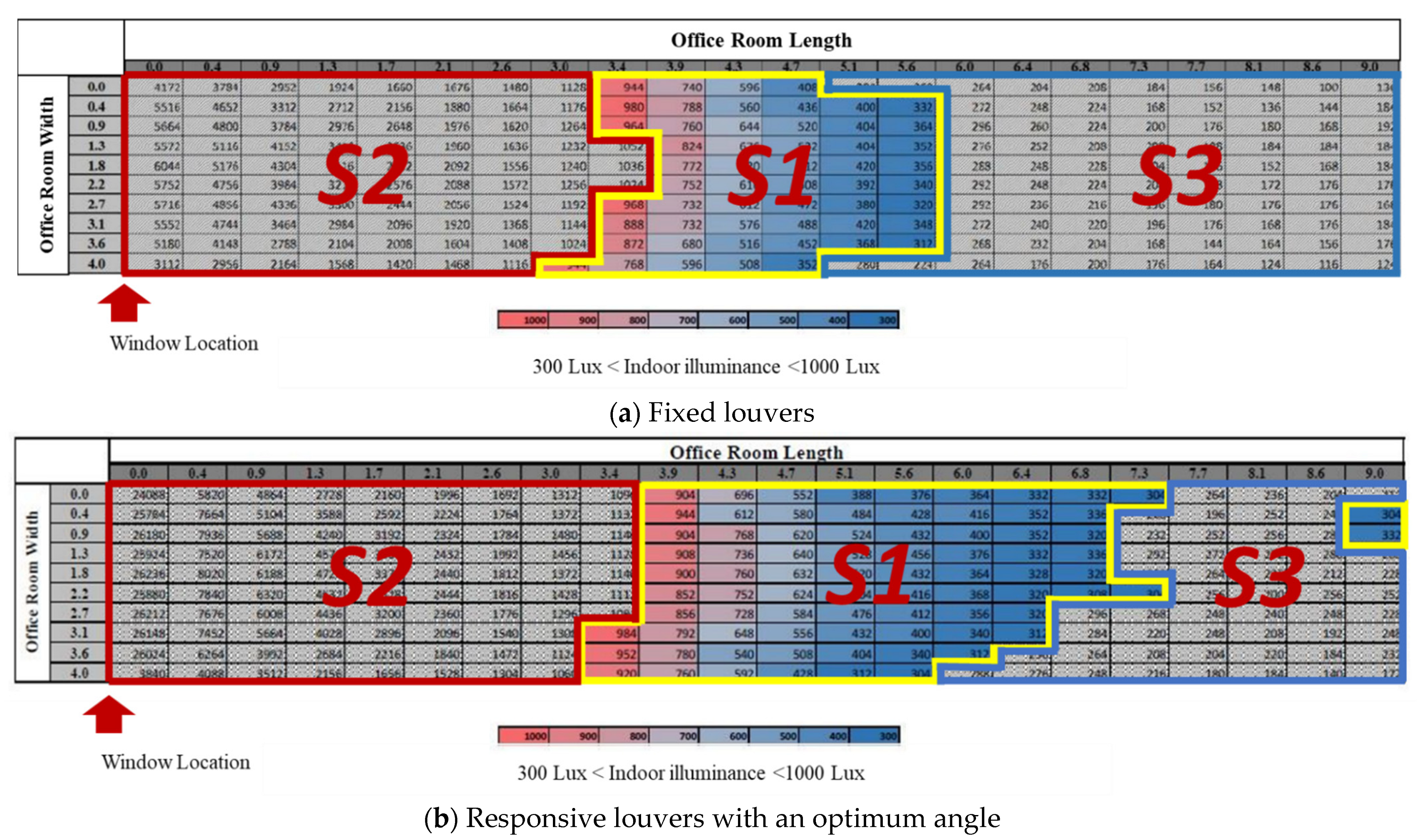
Independent Variable	Dependent Variable	Fixed Variables	Assigned Test	Scenarios
Fixed facade and Responsive facade with Adaptation angle	Visual comfort metric—UDIh	City Rotational Motion Orientation Month of the year	One-way ANOVA	384
Horizontal louvers and Vertical louvers	Visual comfort metric—UDIh	City Orientation Month of the year	One-way ANOVA	192
Building orientation	Max visual comfort	City Rotational Motion Month of the year	Kruskal–Wallis	96
Positive angles and negative angles	Max visual comfort	City Rotational Motion Orientation	Chi squared	32

. Using the statistical tests presented in Table 1, the impacts of several independent variables on visual comfort were investigated. These independent variables include adaptation angles, type of rotational motion of the louvers (horizontal or vertical), orientations of responsive facade systems, and the range of the rotational angles of the louvers’ motion. Some of the independent variables mentioned are active variables and others are environmental.

3. Results

The percentage values of the indoor illuminance function %sAUDI_h for the three different human activities of $s_1$, $s_2$, and $s_3$ associated with the three different illuminance ranges and for both horizontal and vertical louvers on two specific days of 21 June and 21 December are presented in

Table 2. Hourly optimum angles and the associated sAUDI_h for three different human activities of $s_1$, $s_2$, and $s_3$ and four facade orientations calculated for 21 June-Phoenix-Horizontal louvers.

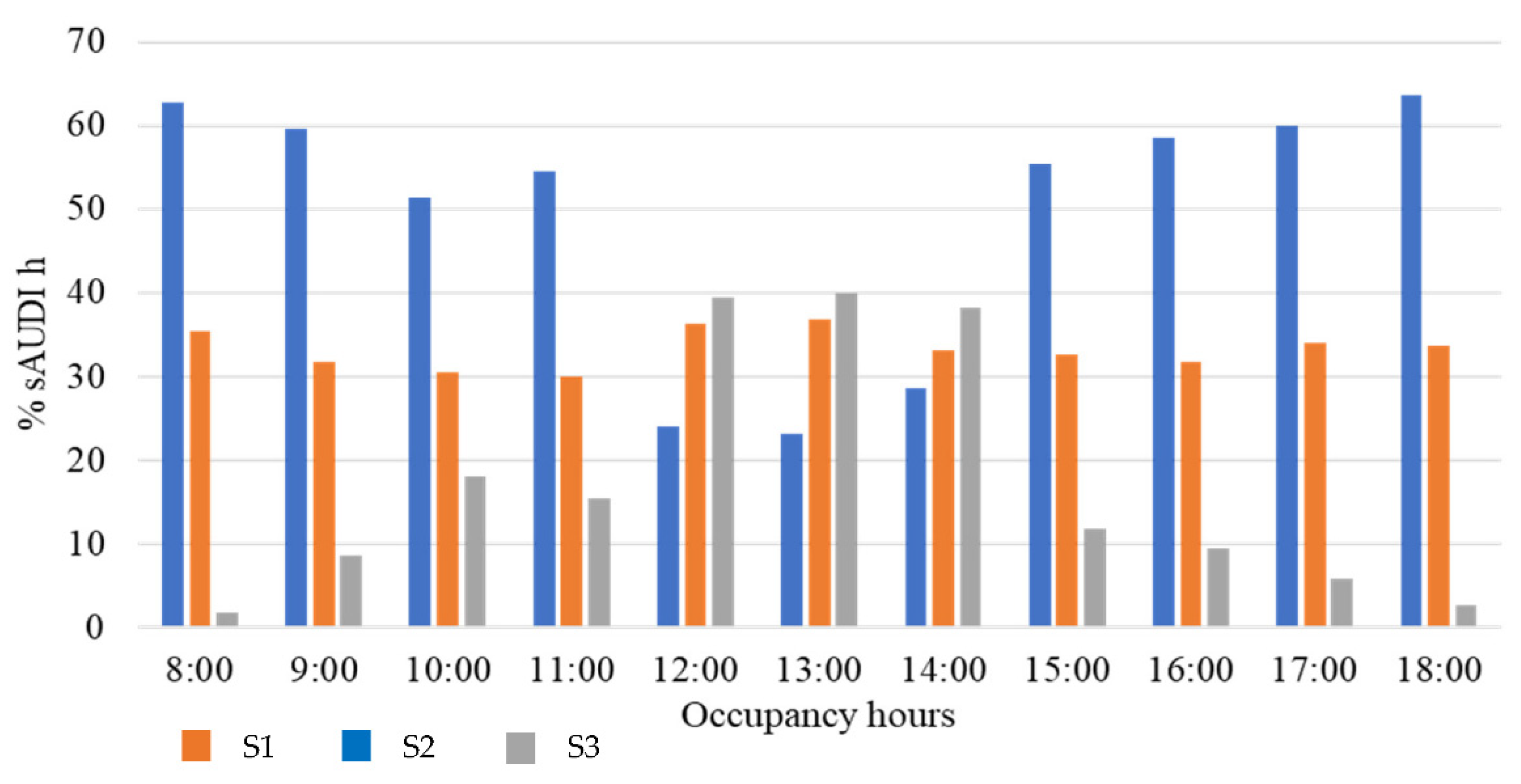
June-21st-Horizontal Facade-Phoenix
Orientations		South				East				North				West
		%sAUDIh				%sAUDIh				%sAUDIh				%sAUDIh
Hours	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3
8:00	43	35.455	62.727	1.818	75	43.182	3.182	53.636	−46	31.364	58.636	10.000	−49	39.091	59.545	13.64
9:00	40	31.818	59.545	8.636	80	40.455	4.545	55.000	−43	30.000	54.091	15.909	−46	35.909	55.909	8.182
10:00	40	30.455	51.364	18.182	−53	41.818	1.818	56.364	−43	31.364	53.636	15.000	−46	35.455	54.545	10.000
11:00	44	30.000	54.545	15.455	−60	48.636	2.273	49.091	−40	33.182	55.909	10.909	−44	34.091	54.545	11.364
12:00	32	36.364	24.091	39.545	−63	47.727	6.364	45.909	−46	33.182	55.455	11.364	−46	33.636	50.909	15.455
13:00	−32	36.818	23.182	40.000	−60	32.273	30.455	37.273	−44	32.727	57.727	9.545	−46	32.273	50.455	17.273
14:00	−26	33.182	28.636	38.182	46	34.545	51.818	13.636	−46	35.000	55.000	10.000	60	47.727	9.091	43.182
15:00	46	32.727	55.455	11.818	43	37.273	59.091	3.636	−46	35.455	56.818	7.727	63	47.727	4.545	47.727
16:00	46	31.818	58.636	9.545	43	38.182	60.000	1.818	−46	34.091	57.273	8.636	86	41.818	4.091	54.091
17:00	43	34.091	60.000	5.909	49	39.091	58.182	2.727	−43	32.273	57.727	10.000	−77	41.818	2.273	55.909
18:00	43	33.636	63.636	2.727	49	36.818	61.818	1.364	−43	31.364	58.182	10.455	−43	45.000	4.545	50.455

,

Table 3. Hourly optimum angles and the associated sAUDI_h for three different human activities of s₁, s₂, and s₃ and four facade orientations calculated for 21 June-Phoenix-Vertical louvers.

June-21st-Vertical Facade-Phoenix
Orientations			South				East				North				West
		%sAUDIh				%sAUDIh				%sAUDIh				%sAUDIh
Hours	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3
8:00	−32	26.818	54.545	18.636	66	43.636	4.545	51.818	34	26.818	52.273	20.909	69	27.273	55.909	16.818
9:00	−12	26.818	47.727	25.455	80	41.364	2.273	56.364	32	25.909	47.727	26.364	69	27.273	50.909	21.818
10:00	−26	26.818	46.818	26.364	−89	40.909	5.909	53.182	32	26.818	46.818	26.364	−77	27.273	50.000	22.727
11:00	14	25.909	41.818	32.273	83	31.818	23.182	45.000	29	27.727	47.273	25.000	−80	26.818	48.636	24.545
12:00	46	25.455	46.364	28.182	75	25.455	38.636	35.909	32	26.364	46.818	26.818	77	26.818	47.273	25.909
13:00	−32	25.455	44.091	30.455	−57	25.455	47.273	27.273	32	27.273	48.182	24.545	69	25.455	47.273	27.273
14:00	−34	26.818	43.636	29.545	83	28.636	45.455	25.909	−26	28.182	46.818	25.000	52	26.818	44.545	28.636
15:00	29	27.727	47.273	25.000	86	29.545	48.182	22.273	0	28.182	47.273	24.545	−80	31.364	24.091	44.545
16:00	14	28.182	47.273	24.545	77	30.909	49.091	20.000	−3	27.727	47.273	24.545	89	35.909	10.000	54.091
17:00	17	28.182	51.818	20.000	−77	30.909	52.273	16.818	−40	28.182	53.182	18.636	−66	39.545	4.091	56.364
18:00	−37	27.273	51.818	20.909	−66	27.273	57.727	15.000	−40	27.273	55.455	17.273	−57	42.273	3.182	54.545

,

Table 4. Hourly optimum angles and the associated sAUDI_h for three different human activities of $s_1$, $s_2$, and $s_3$ and four facade orientations calculated for 21 December-Phoenix-Horizontal louvers.

December-21st-Horizontal Facade-Phoenix
Orientations			South				East				North				West
		%sAUDIh				%sAUDIh				%sAUDIh				%sAUDIh
Hours	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3
8:00	89	0.000	100.000	0.000	−89	0.000	100.000	0.000	89	0.000	100.000	0.000	−89	0.000	100.000	0.000
9:00	49	28.182	52.273	19.545	46	35.455	30.000	34.545	12	35.455	64.545	0.000	80	37.727	60.909	1.364
10:00	0	31.818	20.000	48.182	89	30.909	22.727	46.364	0	40.455	59.545	0.000	90	37.727	57.727	4.545
11:00	3	41.818	3.182	55.000	43	30.000	51.364	18.636	3	41.818	55.000	3.182	86	35.455	54.091	10.455
12:00	14	41.818	2.727	55.455	49	31.818	52.273	15.909	−37	40.000	59.545	0.455	−49	37.273	59.545	3.182
13:00	43	45.455	5.909	48.636	46	34.545	63.182	2.273	0	39.545	51.364	9.091	−49	34.091	58.636	7.273
14:00	14	41.818	3.182	55.000	46	35.000	60.909	4.091	−40	39.545	60.455	0.000	−46	31.364	50.909	17.727
15:00	0	41.818	2.727	55.455	46	35.909	62.727	1.364	−40	39.091	60.909	0.000	83	30.909	25.909	43.182
16:00	0	31.364	20.455	48.182	52	35.455	64.545	0.000	0	35.909	57.273	6.818	83	32.273	15.000	52.727
17:00	52	27.727	55.000	17.273	−86	30.455	60.000	9.545	12	30.455	60.000	9.545	−49	35.000	28.182	36.818
18:00	89	0.000	100.000	0.000	−89	0.000	100.000	0.000	89	0.000	100.000	0.000	−89	0.000	100.000	0.000

and

Table 5. Hourly optimum angles and the associated sAUDI_h for three different human activities of $s_1$, $s_2$, and $s_3$ and four facade orientations calculated for 21 December-Phoenix-Vertical louvers.

Orientations			South				East				North				West
		%sAUDIh				%sAUDIh				%sAUDIh				%sAUDIh
Hours	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3
8:00	89	0.000	100.000	0.000	89	0.000	100.000	0.000	89	0.000	100.000	0.000	89	0.000	100.000	0.000
9:00	1	31.364	56.818	11.818	−37	35.000	47.273	17.727	−43	26.818	72.273	0.909	60	25.455	72.727	1.818
10:00	17	33.182	16.818	50.000	72	31.364	24.091	44.545	20	30.000	62.273	7.727	83	28.182	64.545	7.273
11:00	−3	44.545	3.182	52.273	57	27.727	34.545	37.727	12	31.818	58.182	10.000	69	27.727	63.182	9.091
12:00	−46	44.091	5.000	50.909	−80	28.182	50.909	20.909	20	32.273	53.182	14.545	−63	27.727	54.545	17.727
13:00	52	41.818	3.636	54.545	−80	28.636	55.000	16.909	14	32.273	54.545	13.182	89	27.727	55.455	16.818
14:00	43	45.000	4.545	50.455	66	28.636	50.909	20.455	0	30.909	51.818	17.273	54	26.364	52.273	21.364
15:00	−9	42.273	2.273	55.455	86	28.182	54.545	17.273	−9	28.636	54.091	17.273	−60	27.273	31.818	40.909
16:00	−29	34.545	15.909	49.545	86	29.091	59.545	11.364	−12	28.636	59.545	11.818	57	30.000	0.055	44.545
17:00	46	26.818	57.727	15.455	−89	23.182	65.455	11.364	32	22.727	65.455	11.818	−40	32.273	46.818	20.909
18:00	89	0.000	100.000	0.000	89	0.000	100.000	0.000	89	0.000	100.000	0.000	89	0.000	100.000	0.000

. The three different human activities of s₁, s₂, and s₃ associated with the three different illuminance ranges are introduced in Equation (7).

$$S=\{\begin{array}{ccc}{s}_1& \mathrm{where}& \hfill 300\mathrm{Lux}\le \mathrm{E}\left(\mathrm{x},\mathsf{\theta }\right)\le 1000\mathrm{Lux}\\ s_2& \mathrm{where}& \hfill \mathrm{E}\left(\mathrm{x},\mathsf{\theta }\right)\le 300\mathrm{Lux}\\ s_3& \mathrm{where}& \hfill 1000\mathrm{Lux}\le \mathrm{E}\left(\mathrm{x},\mathsf{\theta }\right)\end{array}$$

(10)

As shown in Table 2, at 12:00 p.m. on 21 June, the percentage value of sAUDI_h associated with the target range of $s_1$ (where illuminance is between 300 Lux and 1000 Lux) is calculated as 36%. This value indicates that 36% of the working space area had the desired indoor illuminance (as specified for $s_1$ human activity) if an optimum angle of −32 degrees was chosen for south-facing horizontal louvers for that specific time of the year.

The hourly optimum angles and sAUDI_h associated with ranges $s_1$, $s_2$, and $s_3$ for all the locations investigated including Miami, Phoenix, Boston, and Milwaukee on 21 June for the entire facade orientations are shown in

Table 6. The hourly optimum angles and their associated %sAUDI_h on 21 June in Miami−Horizontal Louvers.

June−21st-Horizontal Facade-Miami
Orientations			South				East				North				West
		%sAUDIh				%sAUDIh				%sAUDIh				%sAUDIh
Hours	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3
8:00	37	33.64	64.09	2.27	−86	43.63	4.54	51.81	−43	29.54	62.72	7.72	−52	35.00	64.54	0.45
9:00	49	33.64	60.45	5.90	80	40.45	5.00	54.54	−43	31.81	52.27	15.90	−43	35.90	60.45	3.63
10:00	46	30.00	57.27	12.72	−63	45.45	1.36	53.18	−46	29.54	56.81	13.63	−49	35.00	53.18	11.81
11:00	43	29.55	50.90	19.54	−57	49.54	1.81	48.63	−46	31.36	52.72	15.90	−46	35.00	50.00	15.00
12:00	46	28.64	56.81	14.54	−57	35.45	23.63	40.90	−43	30.45	55.90	13.63	−46	30.90	55.45	13.63
13:00	−32	35.00	24.54	40.	−75	36.36	22.72	40.90	29	32.27	28.18	39.54	60	38.18	19.54	42.27
14:00	43	29.09	51.81	19.09	46	28.63	30.45	40.90	−49	29.54	57.27	13.18	69	31.36	24.54	44.09
15:00	49	30.91	66.81	22.72	46	33.18	63.63	3.18	−43	30.90	60.00	9.09	63	34.09	54.00	41.81
16:00	43	30.91	59.54	9.54	54	36.81	59.54	3.63	43	29.54	55.90	14.54	−54	45.90	68.18	48.63
17:00	32	29.55	70.00	0.45	54	29.09	70.90	3.18	−32	29.54	70.00	0.04	−46	30.90	59.09	0.00
18:00	37	30.00	69.54	0.45	72	30.45	69.09	3.63	43	30.00	70.00	0.00	−46	37.27	53.18	3.63

,

Table 7. The hourly optimum angles and their associated %sAUDI_h on 21 June in Miami-Vertical louvers.

June-21st-Vertical Facade-Miami
Orientations			South				East				North				West
		%AUDIh				%AUDIh				%AUDIh				%AUDIh
Hours	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3
8:00	32	26.82	55.00	18.18	80	40.00	13.63	46.36	17	25.91	55.00	19.09	77	26.81	60.00	13.18
9:00	6	27.27	46.81	25.90	−80	41.36	2.72	55.90	34	26.82	48.18	25.00	−60	27.72	52.72	19.54
10:00	−29	25.45	50.00	24.54	−80	32.27	22.27	45.45	26	25.91	47.27	26.81	−69	26.36	50.90	22.72
11:00	3	25.45	42.27	32.27	89	25.91	33.18	40.90	6	25.45	43.18	31.36	69	25.90	46.81	27.27
12:00	−20	23.18	47.27	29.54	54	23.64	46.36	30.00	32	23.64	49.54	26.81	−77	24.09	50.90	25.00
13:00	3	23.64	43.18	33.18	−89	23.64	43.63	32.72	34	24.09	45.90	30.00	−26	23.18	45.00	31.81
14:00	32	22.72	46.36	30.90	−54	22.73	46.81	30.45	40	22.73	46.81	30.45	52	22.27	46.81	30.90
15:00	−20	24.55	50.45	25.00	−72	25.45	54.54	20.00	0	25.00	49.09	25.90	52	23.63	46.81	29.54
16:00	17	25.45	50.90	23.63	77	28.64	51.36	20.00	−40	25.91	52.72	21.36	86	25.90	30.45	43.63
17:00	−32	19.55	65.90	14.54	−54	19.09	69.54	11.36	0	19.09	64.54	16.36	60	19.54	66.36	14.09
18:00	34	20.45	65.45	14.09	57	20.45	65.90	13.63	−3	22.27	60.45	17.27	54	26.36	54.54	19.09

,

Table 8. The hourly optimum angles and their associated %sAUDI_h on 21 June in Boston-Horizontal louvers.

June-21st-Horizontal Facade-Boston
Orientations			South				East				North				West
		%sAUDIh				%sAUDIh				%sAUDIh				%sAUDIh
Hours	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3
8:00	46	32.27	60.45	7.27	75	41.82	3.18	55.00	−43	33.18	56.81	10.00	−46	38.63	60.90	0.00
9:00	43	31.36	54.09	14.54	−86	41.36	3.18	55.45	−46	34.09	59.09	6.81	−46	38.63	56.81	4.54
10:00	40	30.45	49.54	20.00	−60	45.45	5.90	48.63	−46	35.00	59.54	5.45	−43	36.81	59.09	4.09
11:00	−29	32.27	31.81	35.90	-63	36.82	22.72	40.45	−43	39.55	60.00	0.00	−43	37.72	59.09	3.18
12:00	−26	37.73	22.27	40.00	46	32.73	51.36	15.90	−46	36.36	59.54	4.54	−49	35.00	49.09	15.90
13:00	−26	35.00	27.27	37.72	46	36.36	55.45	8.18	−46	39.55	59.54	0.00	−46	35.45	49.09	15.45
14:00	46	31.82	52.27	15.90	46	36.36	55.45	8.18	−43	37.27	61.81	3.18	63	45.00	10.45	44.54
15:00	40	31.36	50.45	18.18	43	37.73	60.00	2.27	−46	33.64	58.63	6.81	60	43.63	2.72	53.63
16:00	43	32.27	57.27	10.45	46	38.64	59.54	1.81	−46	33.64	59.54	4.54	−80	41.81	4.09	54.09
17:00	40	33.18	60.45	6.36	49	39.55	0.00	60.45	−40	30.45	58.63	10.90	−43	45.45	5.00	49.54
18:00	40	32.27	67.72	0.00	52	34.09	0.00	65.54	−40	28.64	59.54	11.81	−43	44.09	6.81	49.09

,

Table 9. The hourly optimum angles and their associated %sAUDI_h on 21 June in Boston−Vertical louvers.

June-21st-Vertical Facade-Boston
Orientations			South				East				North				West
		%sAUDIh				%sAUDIh				%sAUDIh				%sAUDIh
Hours	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3
8:00	46	38.64	60.90	0.00	−49	42.73	4.54	52.72	32	27.73	51.81	20.45	−86	27.27	54.54	18.18
9:00	46	35.64	56.81	45.45	80	41.82	4.54	53.63	37	28.64	51.81	19.54	86	29.09	50.90	20.00
10:00	43	36.82	59.09	4.09	−86	34.09	20.90	45.00	23	28.64	49.54	21.81	−69	29.54	50.90	19.54
11:00	43	37.73	59.09	3.18	−72	30.00	34.54	35.45	6	30.91	49.09	20.00	−83	29.09	51.81	19.09
12:00	49	35.00	49.09	15.90	63	28.64	46.36	25.00	0	29.09	46.81	24.09	80	28.18	47.27	24.54
13:00	46	35.45	49.09	15.45	−86	30.91	48.63	20.45	−34	30.91	49.09	20.00	−54	28.18	48.18	23.63
14:00	−63	45.00	2.72	53.63	−86	30.00	49.09	20.09	6	29.09	51.36	19.54	72	29.54	30.45	40.00
15:00	60	43.64	4.09	54.09	−86	30.45	49.09	20.45	−23	27.73	47.27	25.00	75	32.72	16.81	50.45
16:00	80	41.82	5.00	49.54	−89	30.00	50.90	19.09	29	28.64	51.36	20.00	-80	39.09	3.63	57.27
17:00	43	45.45	6.81	49.09	−72	30.00	54.09	15.90	29	27.27	45.90	26.81	49	42.27	3.18	54.54
18:00	43	44.09	10.45	49.09	−66	25.91	60.90	1.31	17	27.73	44.54	27.72	-46	40.00	5.90	54.09

,

Table 10. The hourly optimum angles and their associated %sAUDI_h on 21 June in Milwaukee-Horizontal louvers.

June−21st-Horizontal Facade-Milwaukee
Orientations		South				East				North				West
		%sAUDIh				%sAUDIh				%sAUDIh				%sAUDIh
Hours	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3
8:00	43	30.45	59.09	10.45	-69	43.64	1.81	54.54	40	31.45	59.09	10.45	−46	35.91	61.81	2.27
9:00	40	30.00	51.81	18.18	−69	40.91	0.00	59.09	43	31.00	51.81	18.18	−46	35.45	56.36	8.18
10:00	40	31.36	49.54	19.09	−63	45.00	3.18	51.81	43	32.36	49.54	19.09	−43	38.18	59.09	2.72
11:00	43	31.36	50.45	18.18	−60	35.91	22.27	41.81	40	31.36	50.45	18.18	−43	38.18	59.09	2.72
12:00	−26	34.55	27.72	37.72	49	33.18	51.36	15.45	−26	35.55	27.72	37.72	−49	35.45	53.18	11.36
13:00	−26	32.73	30.90	36.36	46	35.91	56.81	7.27	−26	33.73	30.90	36.36	−46	34.09	51.36	14.54
14:00	40	32.73	50.90	16.36	46	38.18	60.45	1.36	40	33.73	50.90	16.36	60	35.45	24.09	40.45
15:00	40	31.36	54.09	14.54	49	41.36	58.18	0.06	40	32.36	54.09	14.54	66	45.00	5.00	50.00
16:00	43	32.73	59.54	7.72	49	41.82	58.18	0.00	43	33.73	59.54	7.72	83	43.64	3.63	52.72
17:00	40	34.09	60.09	5.00	49	39.09	60.90	0.01	40	35.09	60.90	5.00	43	46.82	5.45	47.72
18:00	40	33.64	65.45	0.00	52	35.91	63.18	0.00	40	34.64	65.45	0.00	46	41.82	5.43	52.72

and

Table 11. The hourly optimum angles and their associated %sAUDI_h on 21 June in Milwaukee−Vertical louvers.

June-21st-Vertical Facade-Milwaukee
Orientations		South				East				North				West
		%sAUDIh				%sAUDIh				%sAUDIh				%sAUDIh
Hours	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3	Opt. Angle	s1	s2	s3
8:00	−34	25.45	54.09	20.45	−90	40.45	10.00	49.54	32	25.45	52.27	22.27	−80	25.91	54.54	19.54
9:00	−34	25.91	49.09	25.00	−89	40.00	6.36	53.63	9	27.73	46.81	25.45	−69	27.27	50.90	21.81
10:00	−40	28.18	46.81	26.81	−77	35.91	14.54	49.54	14	29.55	48.18	22.27	−75	29.09	51.36	19.54
11:00	43	29.09	44.09	30.00	49	29.55	41.81	28.63	14	30.00	50.00	20.00	−86	29.55	51.36	19.09
12:00	34	28.64	41.36	29.54	−83	29.09	45.45	25.45	12	30.91	50.45	18.63	89	29.09	50.90	20.00
13:00	32	28.18	42.27	24.54	−75	30.45	49.54	20.00	12	30.00	50.90	19.09	−80	28.18	47.27	24.54
14:00	29	29.09	46.36	20.45	77	31.82	51.81	16.36	6	30.45	52.72	16.81	−43	28.64	45.45	25.90
15:00	34	29.09	50.45	16.36	77	31.36	52.72	15.90	−20	29.55	54.09	16.36	−89	33.18	20.00	46.81
16:00	34	28.64	55.00	14.54	−69	32.27	53.63	14.09	−9	29.55	55.00	15.45	−83	39.55	3.18	57.27
17:00	−40	28.18	57.27	19.54	−69	30.45	55.45	14.09	−29	27.73	56.81	15.45	46	42.27	5.90	51.81
18:00	−37	27.27	53.18	7.27	−57	25.00	60.90	14.09	40	26.36	45.45	28.18	66	37.73	5.45	56.81

.

Figure 5 shows the percentage values of sAUDI_h associated with ranges $s_1$, $s_2$, and $s_3$for a south-orientated office in Phoenix on 21 June when the responsive louvers were set at an optimum angle of 32 degrees. Furthermore, the percentage values of sAUDI_h on 21 June associated with ranges $s_1$, $s_2$, and $s_3$ are illustrated in Figure 6a–c for four facade orientations (N, W, S, E).

Additionally, the visual representation of the estimated indoor illuminance in the office considered is depicted in Figure 7. It is observed that the area which experiences the targeted illuminance range s₁ increases as a responsive facade with an optimum angle is utilized as opposed to a fixed louver system.

To examine the significance of the optimum adaptation angle (as an active variable) on the maximum visual comfort, 384 scenarios were generated. One-way ANOVA statistical tests were performed, and the results are shown in Table 6. The p-values less than 0.05 demonstrate significant differences between the facade of fixed louvers of a 0-degree angle (base case) and the vast majority of the responsive facades of horizontal configuration for all orientations examined in the city of Phoenix. This suggests that applying the optimal adaptation angles to the responsive facade of horizontal configuration leads to more desirable indoor illuminance for the majority of cases. The p-value of greater than 0.05 in

Table 12. Significant differences between fixed facade (FF) and responsive facade (RF) with horizontal louvers.

Month	City	Type	Orientation	Mean_FF	SD_FF	Mean_RF	Mean_Rf	p-Value	T-Statistic	Significant
January	Phoenix	Horizontal	South	0.33	0.06	0.35	0.35	0.001	−4.970	Yes
February	Phoenix	Horizontal	South	0.31	0.05	0.34	0.34	0.004	−3.660	Yes
Macrh	Phoenix	Horizontal	South	0.27	0.02	0.35	0.35	0.002	4.130	Yes
April	Phoenix	Horizontal	South	0.30	0.03	0.32	0.32	0.000	−5.810	Yes
May	Phoenix	Horizontal	South	0.31	0.03	0.33	0.33	0.002	4.210	Yes
June	Phoenix	Horizontal	South	0.28	0.02	0.33	0.33	0.000	−6.360	Yes
July	Phoenix	Horizontal	South	0.29	0.02	0.33	0.33	0.000	−8.580	Yes
August	Phoenix	Horizontal	South	0.28	0.06	0.31	0.31	0.000	−5.230	Yes
September	Phoenix	Horizontal	South	0.28	0.02	0.34	0.34	0.005	−3.590	Yes
October	Phoenix	Horizontal	South	0.26	0.08	0.32	0.32	0.001	4.690	Yes
November	Phoenix	Horizontal	South	0.31	0.10	0.33	0.33	0.007	−3.480	Yes
December	Phoenix	Horizontal	South	0.33	0.06	0.36	0.36	0.057	−2.280	Yes

suggests that there were no significant differences between the responsive facade with optimum adaption angles and the responsive facade with fixed louvers of a 0-degree angle. This case is associated with the month of December for the south orientation and suggests that for this specific time of the year, and for such an orientation, applying optimum adaptation angles does not lead to more desirable indoor illuminance as compared to the fixed facade.

A similar approach was used for the responsive facade of vertical configurations for the city of Phoenix for all main orientations. It was observed that applying optimum adaptation angles led to more desirable indoor illuminance for facades of vertical configuration.

One-way ANOVA statistical tests were conducted for four cities of Miami, Phoenix, Boston, and Milwaukee in both horizontal and vertical layouts.

To evaluate the significance of rotation direction of the louver angle, both optimum positive and negative adaption angles were considered as the independent variables. Different orientations and cities were considered for both positive and negative adaptation angles to generate 32 scenarios for both horizontal and vertical louvers. Then, Chi-squared tests were utilized. The results for Phoenix are shown in

Table 13. Significant differences between positive and negative optimum adaptation angles in the city of Phoenix.

City	Type	Orientation	Statistic	p-Value	Significant
Phoenix	Horizontal	North	140.01	3 × 10−32	Yes
Phoenix	Vertical	North	139.38	4 × 10−32	Yes
Phoenix	Horizontal	West	139.62	3 × 10−32	Yes
Phoenix	Vertical	West	139.62	3 × 10−32	Yes
Phoenix	Horizontal	South	139.93	3 × 10−32	Yes
Phoenix	Vertical	South	139.99	3 × 10−32	Yes
Phoenix	Horizontal	East	139.93	3 × 10−32	Yes
Phoenix	Vertical	East	140.02	3 × 10−32	Yes

, which demonstrates that Chi-squared tests delivered significantly low p-values (p < 0.05), indicating there were significant differences between the optimum positive and negative adaptation angles for both horizontal and vertical louvers in all four facade orientations.

To study the role of horizontal versus vertical louvers, 192 distinct scenarios were considered and one-way ANOVA tests were performed. The results are shown in

Table 14. Significant differences between horizontal and vertical louvers for the months of January, February, June, July, November, and December.

Month	City	Orientation	Mean Imp_H	SD Imp_H	Mean Imp_V	SD hmp_V	p-Value	T-Statistic	Significant
January	Phoenix	South	5.66	3.32	36.70	42.02	0.0445	−2.329	Yes
February	Phoenix	South	9.37	8.12	18.51	9.58	0.0258	−2.414	Yes
March	Phoenix	South	26.51	20.01	13.30	7.05	0.0604	2.065	No
April	Phoenix	South	7.61	5.24	12.31	7.02	0.0779	−1.857	No
May	Phoenix	South	5.96	5.82	6.64	4.18	0.7449	−0.330	No
June	Phoenix	South	20.59	12.57	6.89	4.94	0.0033	3.515	Yes
July	Phoenix	South	13.65	6.11	8.95	4.64	0.0461	2.122	Yes
August	Phoenix	South	17.73	23.74	11.88	5.58	0.4220	0.831	No
September	Phoenix	South	23.12	20.38	14.87	8.43	0.2362	1.240	No
October	Phoenix	South	30.18	34.00	11.27	8.83	0.1009	1.786	No
November	Phoenix	South	9.87	13.33	27.39	17.95	0.0179	−2.599	Yes
December	Phoenix	South	10.75	11.50	29.27	20.69	0.0362	−2.346	Yes

, providing different ranges of p-values depending on month of the year. Thus, the difference between horizontal and vertical louvers is significant for only those months of the year when the p-value is below 0.05. For the remaining months, the difference was found to be insignificant.

To determine the significance of the four key orientations of building facades, 96 scenarios were considered that included both horizontal and vertical louvers. Kruskal–Wallis tests were applied to the scenarios and the results are shown in

Table 15. Significant differences among different building orientations including south-facing, north-facing, east-facing, and west-facing in Phoenix.

Month	City	Type	T-Statistic	p-Value	Significant
January	Phoenix	Horizontal	28.19	3 × 10−6	Yes
February	Phoenix	Horizontal	28.79	2 × 10−6	Yes
March	Phoenix	Horizontal	26.78	7 × 10−6	Yes
April	Phoenix	Horizontal	34.89	1 × 10−7	Yes
May	Phoenix	Horizontal	32.95	3 × 10−7	Yes
June	Phoenix	Horizontal	34.61	1 × 10−7	Yes
July	Phoenix	Horizontal	35.86	8 × 10−8	Yes
August	Phoenix	Horizontal	35.86	4 × 10−6	Yes
September	Phoenix	Horizontal	30.62	1 × 10−6	Yes
October	Phoenix	Horizontal	16.19	1 × 10−3	Yes
November	Phoenix	Horizontal	26.31	8 × 10−6	Yes
December	Phoenix	Horizontal	23.46	3 × 10−5	Yes

, which shows significant differences for all four facade orientations. The tests were repeated for four different cities, and similar results were achieved.

4. Conclusions

In this study, we developed an objective function and a data-driven approach to investigate the contribution of different design variables to the visual performance of responsive facades. A computer model of an office with specific responsive facades (in the form of louvers) was constructed as an architectural space. For a specific hour of a day, the louvers were set to a specific adaptation angle, and a simulation was conducted to estimate the indoor illuminance. For the same selected hour, the simulation was repeated for a range of different adaptation angles to estimate the associated indoor illuminance. The data collected on indoor illuminance were fed into the proposed objective function to deliver the optimum adaptation angle for the selected hour. This process was repeated for all hours of a day and all days of a year. The study was also repeated for several design variables, including the location of the office, orientation of the office, and the facade’s configuration being vertical or horizontal.

Statistical tests were implemented to investigate the significance of the design variables on the visual comfort under different scenarios. In limited cases, and under specific circumstances, some design variables were found to be insignificant.

The results of this study indicate that obtaining and deploying optimum adaptation angles could lead to significantly desired levels of visual comfort. Implementing the proposed approach could help designers achieve higher levels of visual comfort, although the specifics of the design variables (such as location, orientation, and facade configuration) must be considered during the design process.