Detailed Structural Characterization of Existing RC Buildings for Seismic Exposure Modelling of the Lisbon Area
Abstract
:1. Introduction
2. Lisbon RC Building Stock
2.1. Characteristics of RC Buildings
- (i)
- transition buildings or mixed masonry-RC buildings, built until the beginning of 1950.
- (ii)
- first phase RC buildings, built before the introduction of seismic resistance codes, until around 1958.
- (iii)
- second phase RC buildings, built between around 1958 and 1983.
- (iv)
- modern RC buildings, built after 1983.
2.2. Census Data
2.3. Benfica and Alvalade Parishes as Representative of the Lisbon Building Stock
3. Exposure Model for the Lisbon Residential RC Building Stock
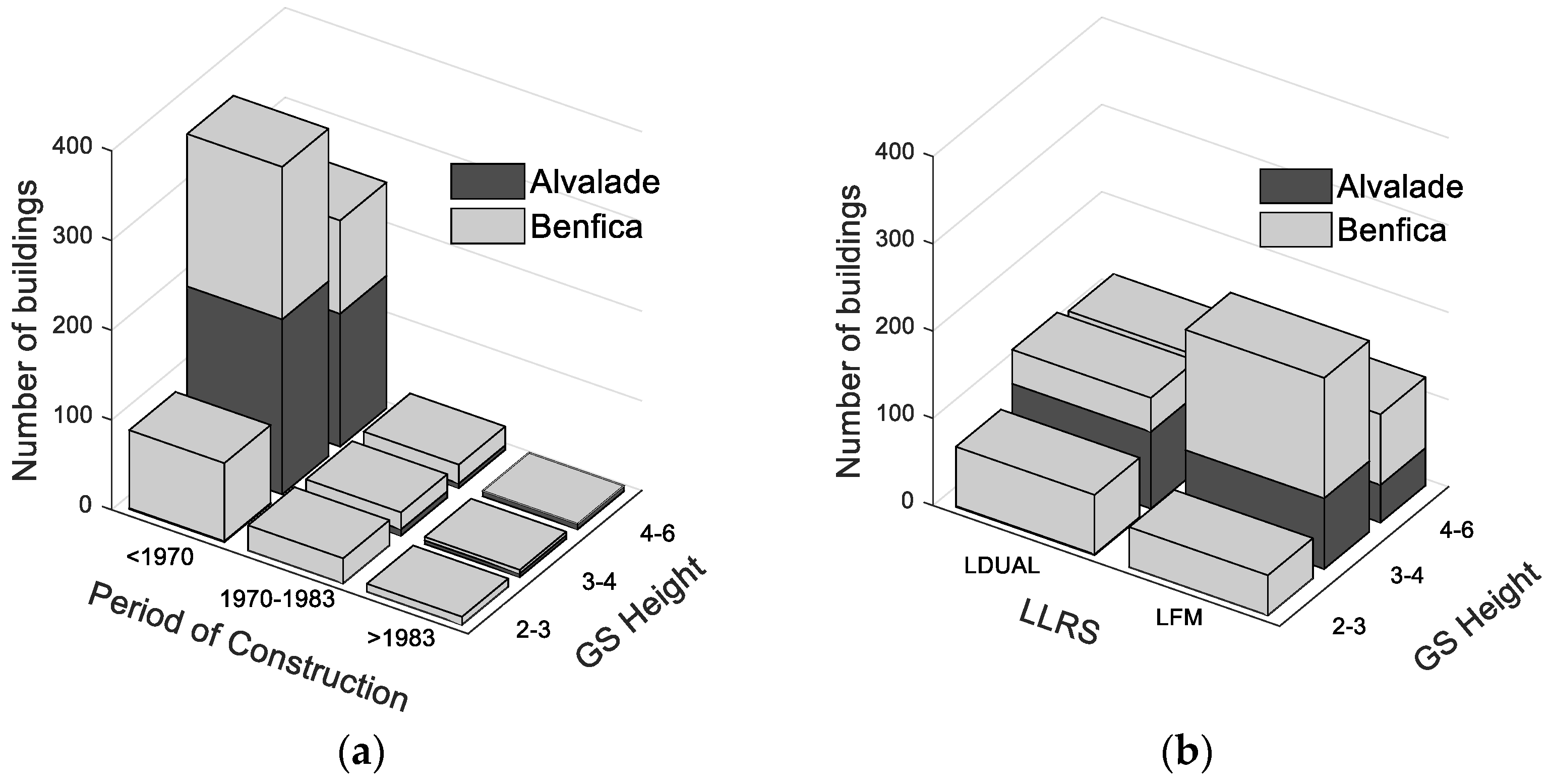
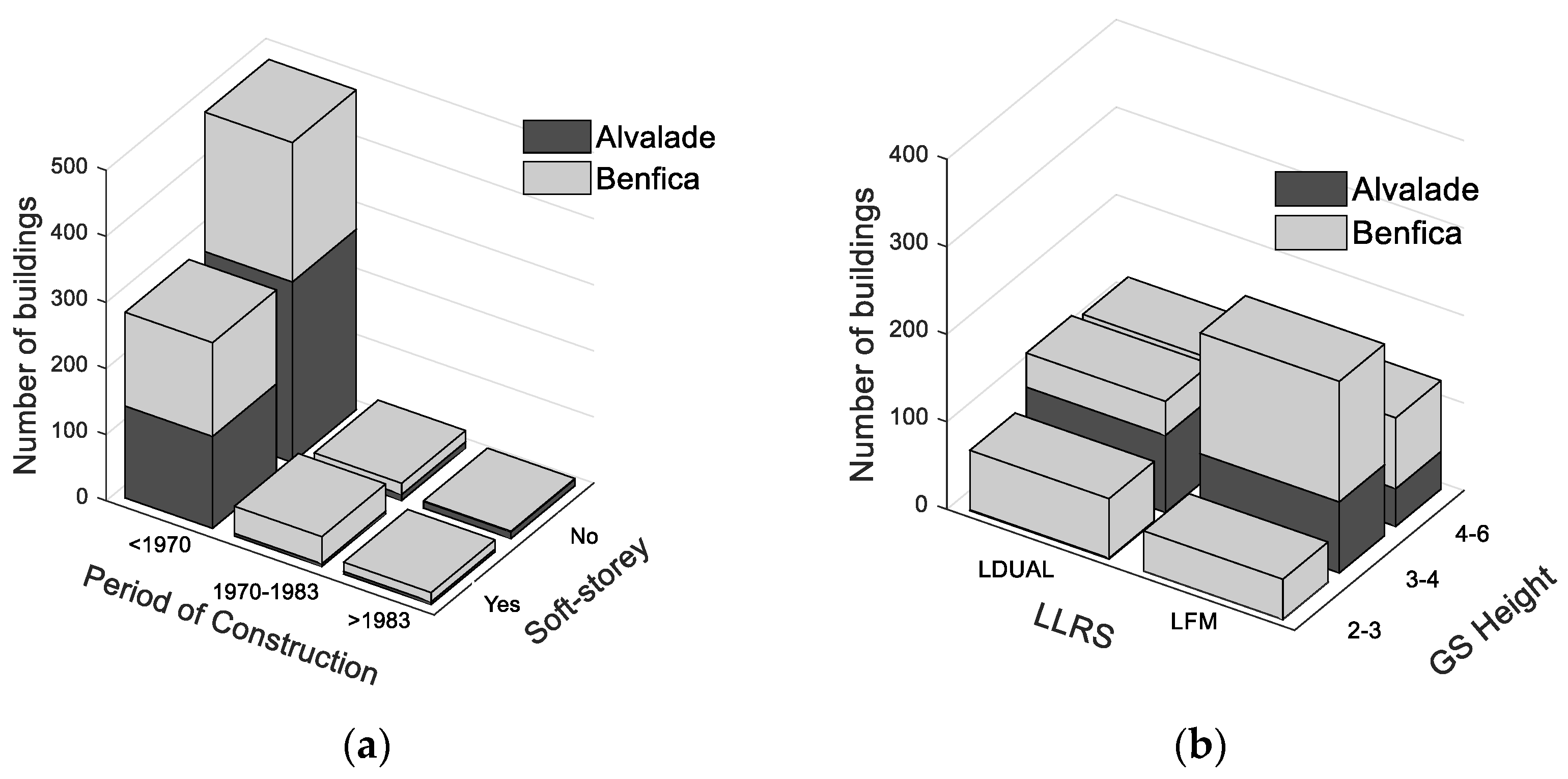
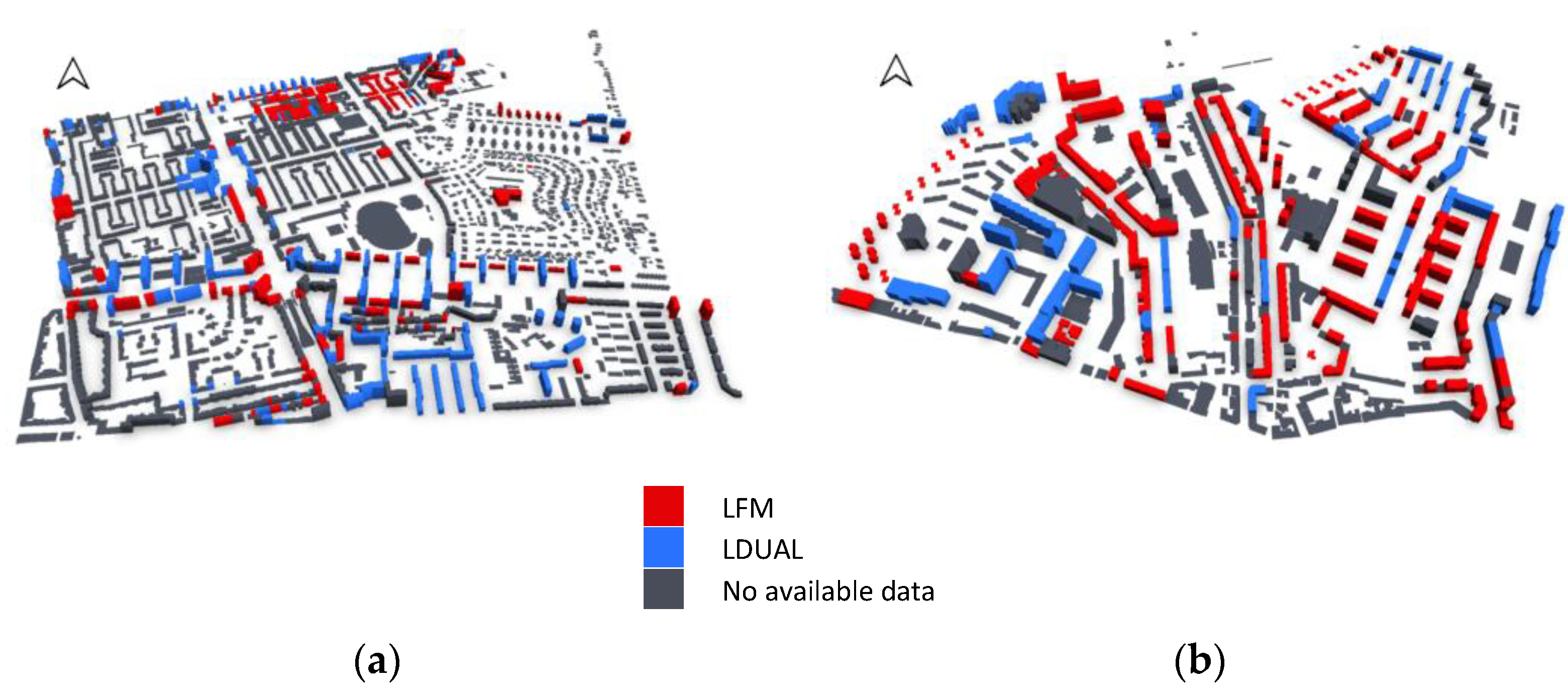
3.1. Buildings Taxonomies
3.2. RC Exposure Model
4. Structural Characterization
4.1. Construction Material
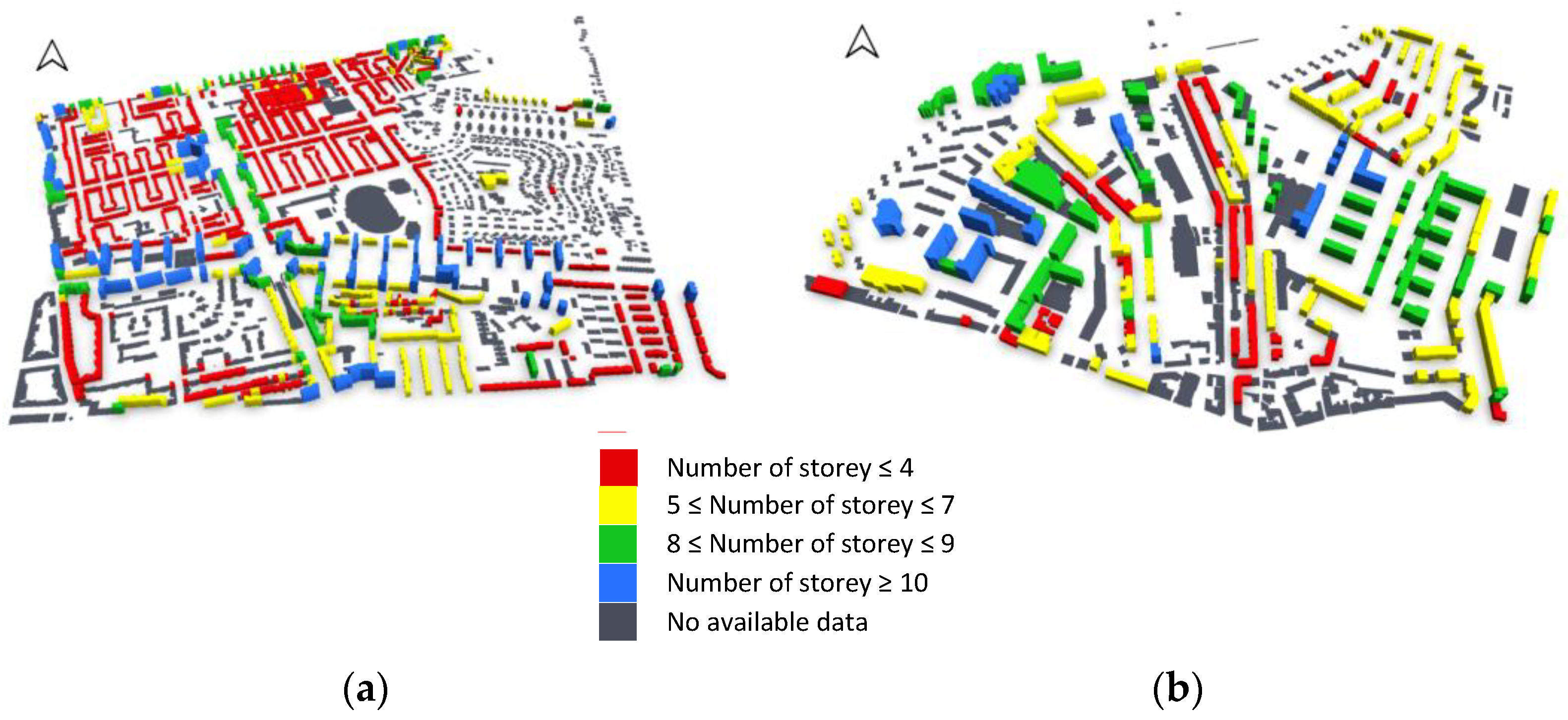
4.2. Storey Heights
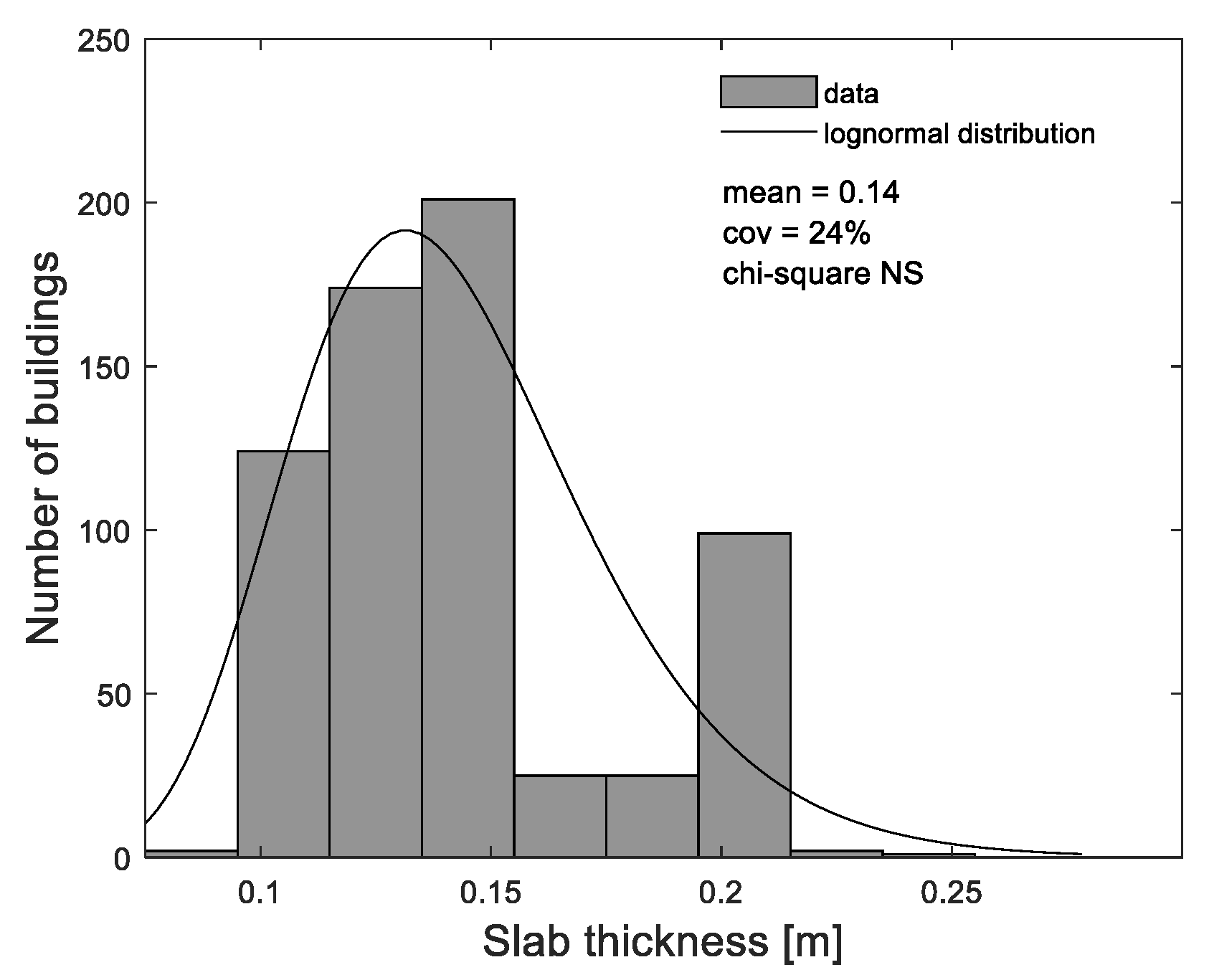
4.3. Slab Thickness
4.4. Elements′ Cross-Section
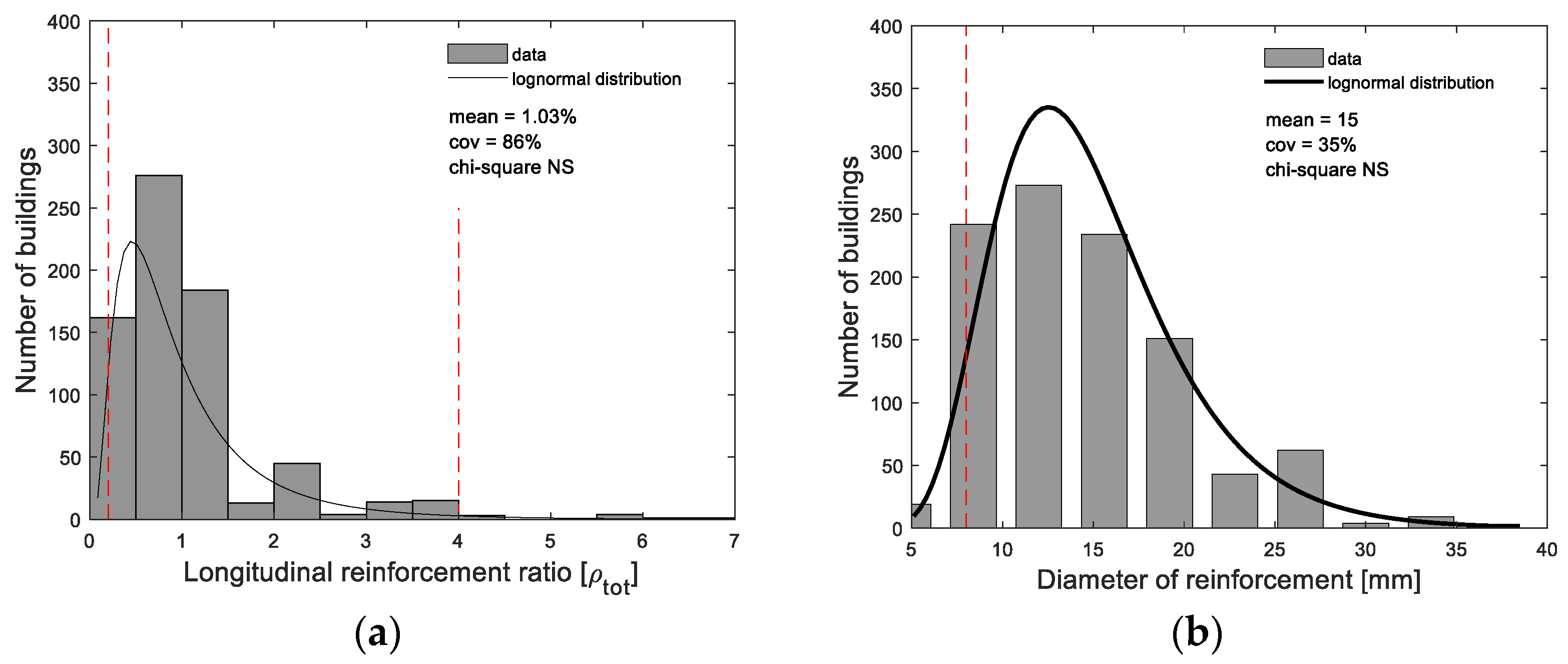
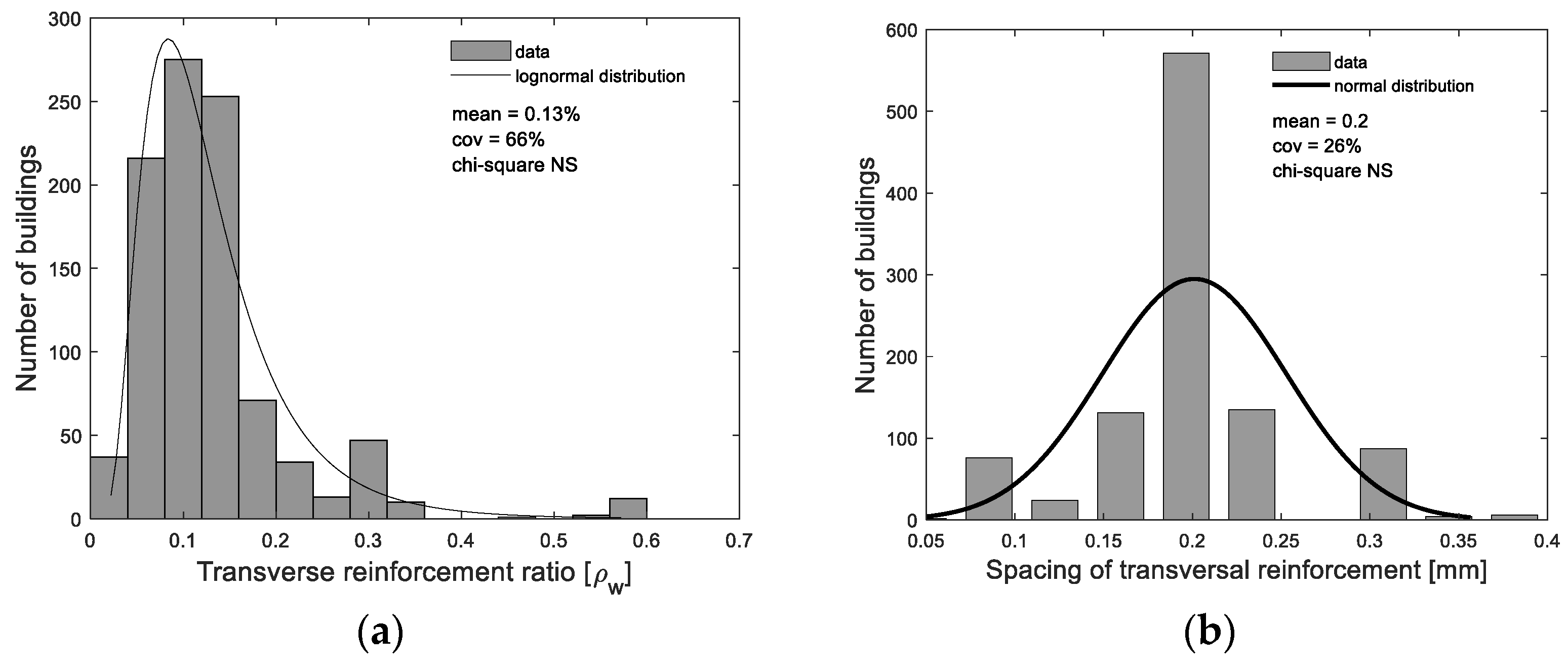
4.5. Reinforcement Details
4.5.1. Columns
4.5.2. RC Walls
4.5.3. Beams
4.5.4. Discussion of Results—Reinforcement for Vertical Structural Elements
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Borges, J.F.; Fitas, A.J.S.; Bezzeghoud, M.; Teves-Costa, P. Seismotectonics of Portugal and its adjacent Atlantic area. Tectonophysics 2001, 331, 373–387. [Google Scholar] [CrossRef]
- Lamego, P.; Lourenço, P.B.; Sousa, M.L.; Marques, R. Seismic vulnerability and risk analysis of the old building stock at urban scale: Application to a neighbourhood in Lisbon. Bull. Earthq. Eng. 2017, 15, 2901–2937. [Google Scholar] [CrossRef]
- Gago, A.; Proença, J. Parque Escolar: Reforço Sísmica de Edificios Escolares; Diário da República: Lisbon, Portugal, 2011; ISBN 9789899610668. [Google Scholar]
- RSCCS. Regulamento de Segurança das Construções Contra os Sismos, Decreto-Lei n.o 41658 de 31 de Maio de 1958; Diário da República: Lisbon, Portugal, 1958. [Google Scholar]
- RSEP. Regulamento de Solicitações em Edifícios e Pontes (RSEP). Decreto n.o 44041 de 18 de Novembro; Diário da República: Lisbon, Portugal, 1961. [Google Scholar]
- REBA-67/76. Regulamento de Estruturas de Betão Armado; Diário da República: Lisbon, Portugal, 1967. [Google Scholar]
- RSA. Regulamento de Segurança e Acções para Estruturas de Edifícios e Pontes. Decreto-Lei n.o 235/83; Diário da República: Lisbon, Portugal, 1983. [Google Scholar]
- CEN. NP EN 1992-1-1: Eurocódigo 2—Projecto de Estruturas de Betão; Parte 1-1: Regras Gerais e Regras Para Edifícios; CEN: Brussels, Belgium, 2004. [Google Scholar]
- CEN. NP EN 1998-1: Eurocódigo 8—Projecto de Estruturas Para Resistência Aos Sismos. Parte 1: Regras Gerais, Acções Sísmicas e Regras Para Edifícios; CEN: Brussels, Belgium, 2010. [Google Scholar]
- Costa, R.; Providência, C. Avaliação e Reabilitação Sísmicas de Edifícios de Betão Armado; ENGEBOOK: Porto, Portugal, 2019; ISBN 9789898927774. [Google Scholar]
- Saraiva, J.P.; Appleton, J. Avaliação da Capacidade Sísmica de Edifícios de Betão Armado de Acordo com o Eurocódigo 8—Parte 3. 4as Jorn. Port. Eng. Estruturas 2006, 1980, 1–15. [Google Scholar]
- Caruso, C.; Bento, R.; Castro, J.M. A contribution to the seismic performance and loss assessment of old RC wall-frame buildings. Eng. Struct. 2019, 197, 109369. [Google Scholar] [CrossRef]
- Couto, R.; Requena-García-Cruz, M.V.; Bento, R.; Morales-Esteban, A. Seismic capacity and vulnerability assessment considering ageing effects. Case study: Three local Portuguese RC buildings. Bull. Earthq. Eng. 2020, 19, 6591–6614. [Google Scholar] [CrossRef]
- Appleton, J. Tipificação do Parque Construído. In Sismos e Edifícios; Orion: London, UK, 2008. [Google Scholar]
- Oliveira, C.S.; Gaspar, J.; Correia, F. Levantamento do Parque Habitacional de Lisboa. Vol. 1—Ficha-inquérito. Apuramento de Resultados na Zona da Alameda D. Afonso Henriques, Freguesias de Alto do Pina, S. João de Deus e S. Jorge de Arroios. Report; LNEC: Lisboa, Portugal, 1985. [Google Scholar]
- Couto, R.; Sousa, I.; Bento, R.; Castro, J.M. Chapter 2. Seismic vulnerability assessment of RC structures: Research and practice at building level. In Seismic Vulnerability Assessment of Civil Engineering Structures at Multiple Scales. From Single Buildings to Large-Scale Assessment; Ferreira, T.M., Rodrigues, H., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; ISBN 9780128240724. [Google Scholar]
- Grigoratos, I.; Monteiro, R.; Ceresa, P.; Di Meo, A.; Faravelli, M.; Borzi, B. Crowdsourcing Exposure Data for Seismic Vulnerability Assessment in Developing Countries. J. Earthq. Eng. 2021, 25, 835–852. [Google Scholar] [CrossRef]
- Pittore, M.; Wieland, M.; Fleming, K. Perspectives on global dynamic exposure modelling for geo-risk assessment. Nat. Hazards 2017, 86, 7–30. [Google Scholar] [CrossRef]
- Pavić, G.; Hadzima-Nyarko, M.; Bulajić, B.; Jurković, Ž. Development of seismic vulnerability and exposure models-A case study of Croatia. Sustainability 2020, 12, 973. [Google Scholar] [CrossRef] [Green Version]
- Grünthal, G. European Macroseismic Scale 1998; European Seismological Commission: Luxembourg, 1998; Volume 15. [Google Scholar]
- Rojahn, C.; Sharpe, R.L.; Scholl, R.E.; Kiremidjian, A.S.; Nutt, R.V. ATC-13 Earthquake Damage Evaluation Datas for California; Redwood City, CA, USA, 1985. Available online: https://www.atcouncil.org/pdfs/atc13.pdf (accessed on 15 December 2021).
- Rojahn, C.; Scawthorn, C.; Anagnos, T.; Wong, K.; Poland, C.D. Rapid Visual Screening of Buildings for Potential Seismic Hazards, Handbook, FEMA 154; CreateSpace Independent Publishing Platform: Redwood City, CA, USA, 2002. [Google Scholar]
- FEMA. FEMA 178—NEHRP Handbook for the Seismic Evaluation of Existing Buildings; FEMA: Washington, DC, USA, 1992.
- Kircher, C.A.; Whitman, R.V.; Holmes, W.T. HAZUS Earthquake Loss Estimation Methods. Nat. Hazards 2006, 7, 45–59. [Google Scholar] [CrossRef]
- Jaiswal, K.; Wald, D.; Porter, K. A global building inventory for earthquake loss estimation and risk management. Earthq. Spectra 2010, 26, 731–748. [Google Scholar] [CrossRef]
- Pitilakis, K.; Franchin, P.; Khazai, B.; Wenzel, H. SYNER-G: Systemic seismic vulnerability and risk assessment of complex urban, utility, lifeline systems and critical facilities: Methodology and Applications. In Geotechnical, Geological and Earthquake Engineering; Springer: Berlin/Heidelberg, Germany, 2014; Volume 31, ISBN 9789401788342. [Google Scholar]
- World Housing Encyclopedia (WHE). Available online: https://www.world-housing.net (accessed on 15 December 2021).
- Brzev, S.; Scawthorn, C.; Charleson, A.W.; Allen, L.; Greene, M.; Jaiswal, K.; Silva, V. GEM Building Taxonomy Version 2.0. GEM Tech. Rep. 2013, 2, 188. [Google Scholar] [CrossRef]
- Riga, E.; Fotopoulou, S.; Karatzetzou, A.; Apostolaki, S.; Ntafloukas, K.; Pitilakis, K. Towards the development of a seismic risk model for greece. In Proceedings of the International Conference on Natural Hazards and Infrastructure, Chania, Greece, 23–16 June 2019. [Google Scholar]
- Ferreira, T.M.; Rodrigues, H.; Vicente, R. Seismic vulnerability assessment of existing reinforced concrete buildings in urban centers. Sustainability 2020, 12, 1996. [Google Scholar] [CrossRef] [Green Version]
- Salazar, L.G.F.; Ferreira, T.M. Seismic vulnerability assessment of historic constructions in the downtown of Mexico City. Sustainability 2020, 12, 1276. [Google Scholar] [CrossRef] [Green Version]
- Wieland, M.; Pittore, M.; Parolai, S.; Begaliev, U.; Yasunov, P.; Tyagunov, S.; Moldobekov, B.; Saidiy, S.; Ilyasov, I.; Abakanov, T. A multiscale exposure model for seismic risk assessment in Central Asia. Seismol. Res. Lett. 2015, 86, 210–222. [Google Scholar] [CrossRef] [Green Version]
- Dolce, M.; Prota, A.; Borzi, B.; da Porto, F.; Lagomarsino, S.; Magenes, G.; Moroni, C.; Penna, A.; Polese, M.; Speranza, E.; et al. Seismic Risk Assessment of Residential Buildings in Italy; Springer: Amsterdam, The Netherlands, 2021; Volume 19, ISBN 0123456789. [Google Scholar]
- Kechidi, S.; Abarca, A.; Marques, M.; Castro, J.M.; Monteiro, R. On the seismic risk assessment of the residential buildings in Northern Algeria. In Proceedings of the 12th Canadian Conference on Earthquake Engineering, Quebec City, QC, Canada, 17–20 June 2019; pp. 1–8. [Google Scholar]
- Silva, V.; Crowley, H.; Varum, H.; Pinho, R.; Sousa, L. Investigation of the characteristics of Portuguese regular moment-frame RC buildings and development of a vulnerability model. Bull. Earthq. Eng. 2015, 13, 1455–1490. [Google Scholar] [CrossRef]
- Vicente, R.; Ferreira, T.M.; Maio, R. Seismic risk mitigation of old urban centres: Characterizationand seismic vulnerability assessment of the Ribeirinha neighborhood of Faro, Portugal. Territorium 2015, 22, 283–290. [Google Scholar] [CrossRef] [Green Version]
- Furtado, A.; Costa, C.; Arêde, A.; Rodrigues, H. Geometric characterisation of Portuguese RC buildings with masonry infill walls. Eur. J. Environ. Civ. Eng. 2015, 20, 396–411. [Google Scholar] [CrossRef]
- Bal, I.E.; Crowley, H.; Pinho, R.; Gülay, F.G. Detailed assessment of structural characteristics of Turkish RC building stock for loss assessment models. Soil Dyn. Earthq. Eng. 2008, 28, 914–932. [Google Scholar] [CrossRef]
- Meral, E. Evaluation of Structural Properties of Existing Turkish RC Building Stock. Iran. J. Sci. Technol.—Trans. Civ. Eng. 2019, 43, 445–462. [Google Scholar] [CrossRef]
- Ozmen, H.B.; Inel, M.; Senel, S.M.; Kayhan, A.H. Load carrying system characteristics of existing turkish rc building stock. Int. J. Civ. Eng. 2015, 13, 76–91. [Google Scholar] [CrossRef]
- Rodrigues, H.; Sousa, R.; Vitorino, H.; Batalha, N.; Varum, H.; Fernandes, P. Characterisation of Portuguese RC Precast Industrial Building Stock. Adv. Civ. Eng. 2020, 2020, 7517205. [Google Scholar] [CrossRef]
- Arquivo Municipal de Lisboa Obra n 33461—Folha 23. In Process. 25114-DAG-PG-1959; Lisbon Municipial Archive: Lisboa, Portugal, 1959.
- Appleton, J. The Seismic Mega-Earthquakes in the XXI Century or the Seismic Vulnerability of Lisbon Constructions. In Reducing the Seismic Vulnerability of the Building Stock; SPES, GECo: Lisbon, Portugal, 2001. [Google Scholar]
- Celarec, D.; Ricci, P.; Dolšek, M. The sensitivity of seismic response parameters to the uncertain modelling variables of masonry-infilled reinforced concrete frames. Eng. Struct. 2012, 35, 165–177. [Google Scholar] [CrossRef]
- Mucedero, G.; Perrone, D.; Monteiro, R. Nonlinear static characterisation of masonry-infilled RC building portfolios accounting for variability of infill properties. Bull. Earthq. Eng. 2021, 19, 2597–2641. [Google Scholar]
- Verderame, G.M.; de Luca, F.; Ricci, P.; Manfredi, G. Preliminary analysis of a soft-storey mechanism after the 2009 L’Aquila earthquake. Earthq. Eng. Struct. Dyn. 2011, 40, 925–944. [Google Scholar] [CrossRef] [Green Version]
- Ruiz-Pinilla, J.G.; Adam, J.M.; Pérez-Cárcel, R.; Yuste, J.; Moragues, J.J. Learning from RC building structures damaged by the earthquake in Lorca, Spain, in 2011. Eng. Fail. Anal. 2016, 68, 76–86. [Google Scholar] [CrossRef]
- REBAP. Regulamento de Estruturas de Betão Armado e Pré-Esforçado. Decreto-Lei n.o 349-C/83 de 30 de Julho; Diário da República: Lisbon, Portugal, 1983. [Google Scholar]
- Instituto Nacional de Estatística. Censos 2011 Resultados Definitivos; Instituto Nacional de Estatística: Lisboa, Portugal, 2012; Volume 26.
- JFA História da Freguesia. Available online: https://www.jf-alvalade.pt/alvalade/historia/ (accessed on 20 December 2021).
- Santos, J. Espaços de Mediação Infraestrutural: Interpretação e Projeto Na produção do Urbano no Território Metropolitano de Lisboa”, Prémio Metrópoles Ciência 2016; Faculdade de Arquitectura de Lisboa: Lisboa, Portugal, 2016. [Google Scholar]
- JFB História da Freguesia. Available online: https://www.jf-benfica.pt/freguesia/junta-de-freguesia/ (accessed on 20 December 2021).
- AML Área Metropolitana de Lisboa—Atas do Seminário “Área Metropolitana de Lisboa-Ambiente Urbano e Riscos”; AML: Lisbon, Portugal, 2013.
- Kohrangi, M.; Bazzurro, P.; Vamvatsikos, D. Seismic risk and loss estimation for the building stock in Isfahan. Part I: Exposure and vulnerability. Bull. Earthq. Eng. 2021, 19, 1709–1737. [Google Scholar] [CrossRef]
- Pittore, M.; Haas, M.; Megalooikonomou, K.G. Risk-oriented, bottom-up modeling of building portfolios with faceted taxonomies. Front. Built Environ. 2018, 4, 41. [Google Scholar] [CrossRef]
- Tzitzikas, Y. Faceted Taxonomy-Based Sources; Springer: Heidelberg, Germany, 2009. [Google Scholar]
- Roeslin, S.; Ma, Q.T.M.; García, H.J. Damage assessment on buildings following the 19th september 2017 puebla, Mexico earthquake. Front. Built Environ. 2018, 4, 72. [Google Scholar] [CrossRef]
- Allen, L.; Brzev, S.; Charleson, A.W.; Scawthorn, C.; Silva, V. GEM Building Taxonomy—An open global building classification system. In Proceedings of the New Zealand Society for Earthquake Engineering Technical Conference & AGM, Rotorua, New Zealand, 10–12 April 2015. [Google Scholar]
- Crowley, H.; Despotaki, V.; Silva, V.; Pitilakis, D.; Pitilakis, K.; Rodrigues, D.; Pitilakis, K.; Pitilakis, D.; Hancilar, U.; Bursi, O.; et al. D26.1 Taxonomy of European Residential, Commercial, Industrial Buildings and Industrial Plants. 2017. Available online: DOCUMENTS/DELIVERABLES/SERA_D26.1_Taxonomy_Buildings_Industry (accessed on 20 December 2021).
- Martins, L.; Silva, V. Development of a fragility and vulnerability model for global seismic risk analyses. Bull. Earthq. Eng. 2021, 19, 6719–6745. [Google Scholar] [CrossRef]
- Grigoratos, I.; Monteiro, R.; Ceresa, P.; Di Meo, A.; Faravelli, M.; Borzi, B. Seismic Vulnerability Assessment of the Urban Building Environment in Nablus—Palestine. Int. J. Archit. Herit. 2018, 12, 1196–1215. [Google Scholar]
- Kechidi, S.; Castro, J.M.; Monteiro, R.; Marques, M.; Yelles, K.; Bourahla, N.; Hamdache, M. Development of Exposure Datasets for Earthquake Damage and Risk Modelling: The Case Study of Northern Algeria; Springer: Amsterdam, The Netherlands, 2021; Volume 19. [Google Scholar]
- De Sousa, R.R.; Costa, A.C.; Costa, A.G. Metodologia Para a Avaliação da Segurança Sísmica de Edifícios Existentes Baseada em Análises de Fiabilidade Estrutural; LNEC: Lisbon, Portugal, 2019. [Google Scholar]
- CEN. NP EN 1998-3: Eurocódigo 8—Projecto de Estruturas Para Resistência ao Sismo. Parte 3: Avaliação e Reabilitação de Edifícios; CEN: Brussels, Belgium, 2017. [Google Scholar]
- Peres, R.; Couto, R.; Sousa, I.; Castro, J.; Bento, R. Modelling and evaluation of brittle shear effects on the seismic performance and loss assessment of RC buildings. Eng. Struct. 2011, 9, 1137–1155. [Google Scholar]
- Priestley, M.J.N.; Seible, F.; Verma, R.; Xiao, Y. Seismic Shear Strength of Reinforced Concrete Columns; University of California: San Diego, CA, USA, 1993. [Google Scholar]
- Pujol, S. Drift Capacity of Reinforced Concrete Columns Subjected to Displacement Reversals; Purdue University: West Lafayette, IN, USA, 2002. [Google Scholar]
- Sezen, H. Seismic Behaviour and Modeling of Reinforced Concrete Building Columns; University of California: Berkeley, CA, USA, 2002. [Google Scholar]
- Elwood, K.; Moehle, J.P. Shake Table Tests and Analytical Studies on the Gravity Load Collapse of Reinforced Concrete Frames; University of California: Berkeley, CA, USA, 2003. [Google Scholar]
- Elwood, K.J.; Moehle, J.P. Drift capacity of reinforced concrete columns with light transverse reinforcement. Earthq. Spectra 2005, 21, 71–89. [Google Scholar] [CrossRef]
- Sezen, H.; Moehle, J. Strength and Deformation Capacity of Reinforced Concrete Columns with Limited Ductility. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Aslani, H.; Miranda, E. Probabilistic Earthquake Loss Estimation and Loss Disaggregation in Buildings; Stanford University: Stanford, CA, USA, 2005. [Google Scholar]
- Zhu, L.; Elwood, K.J.; Haukaas, T. Classification and Seismic Safety Evaluation of Existing Reinforced Concrete Columns. J. Struct. Eng. 2007, 133, 1316–1330. [Google Scholar] [CrossRef]
- Leborgne, M.R. Modeling the Post Shear Failure Behavior of Reinforced Concrete Columns; University of Texas: Austin, TX, USA, 2012. [Google Scholar]
- LeBorgne, M.R.; Ghannoum, W.M. Calibrated analytical element for lateral-strength degradation of reinforced concrete columns. Eng. Struct. 2014, 81, 35–48. [Google Scholar] [CrossRef]
- Wibowo, A.; Wilson, J.L.; Lam, N.T.K.; Gad, E.F. Drift performance of lightly reinforced concrete columns. Eng. Struct. 2014, 59, 522–535. [Google Scholar] [CrossRef]
- Wilson, J.L.; Lam, N.T.K.; Gad, E.F. Hazard Identification and Behaviour of Reinforced Concrete Framed Buildings in Regions of Lower Seismicity. In Proceedings of the 10th Pacific Conference on Earthquake Engineering, Sydney, Australia, 6–8 November 2015; pp. 6–8. [Google Scholar]


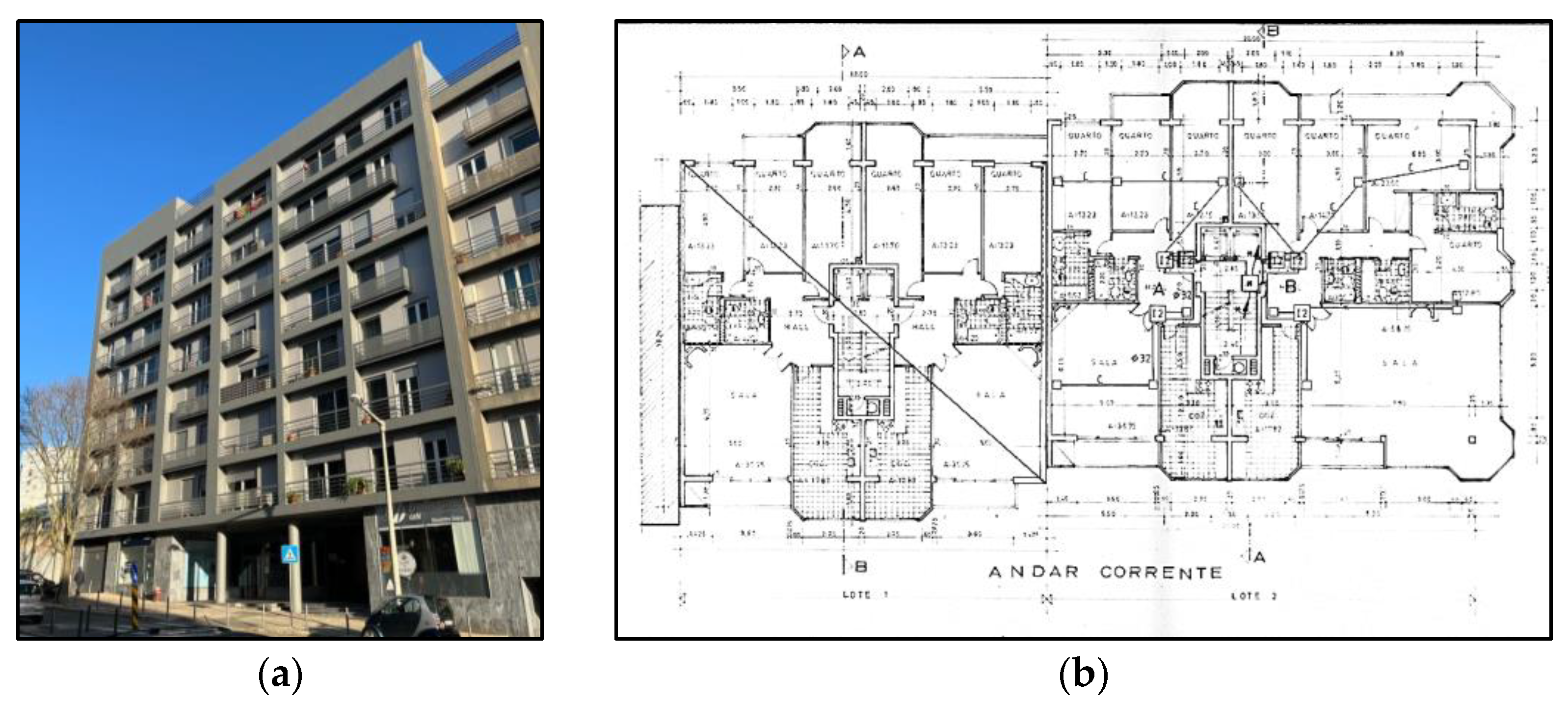
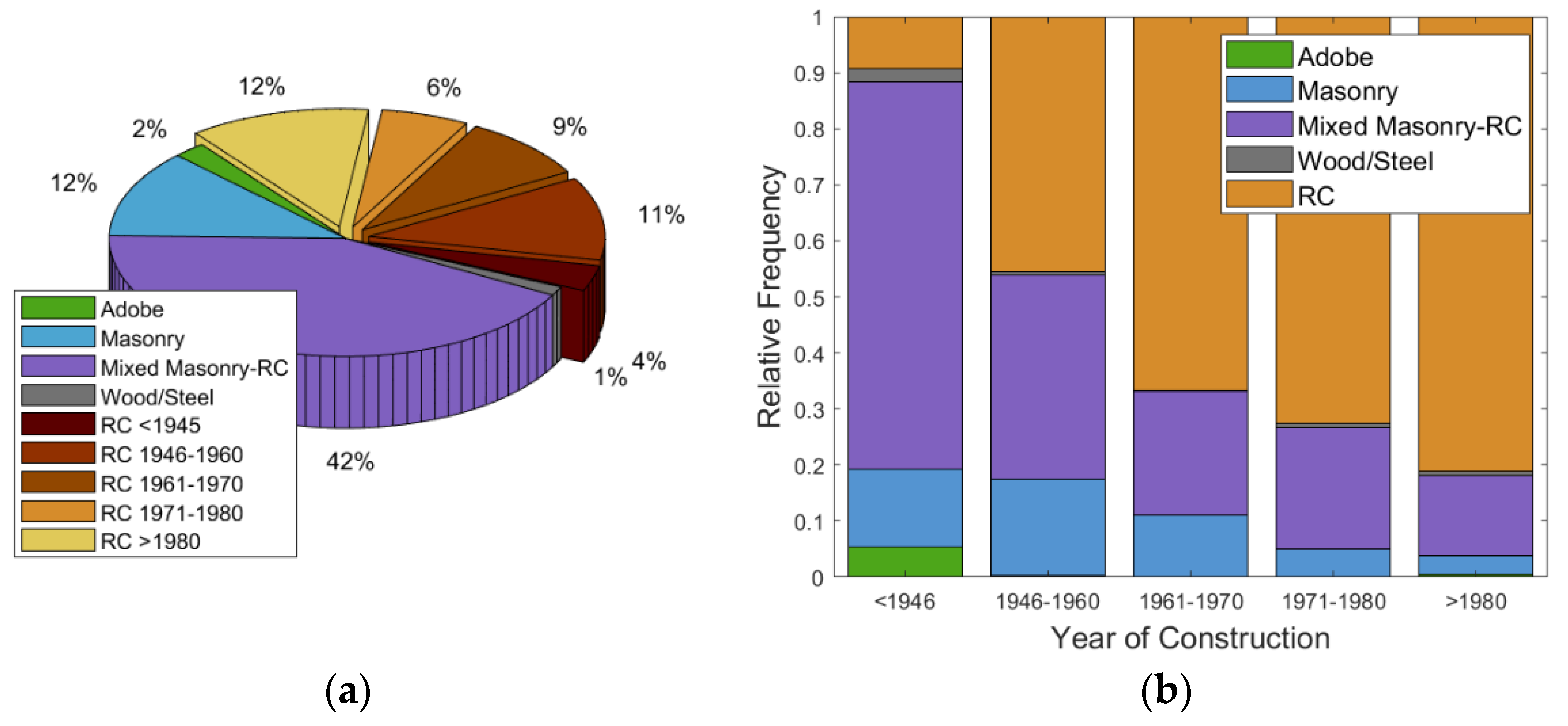
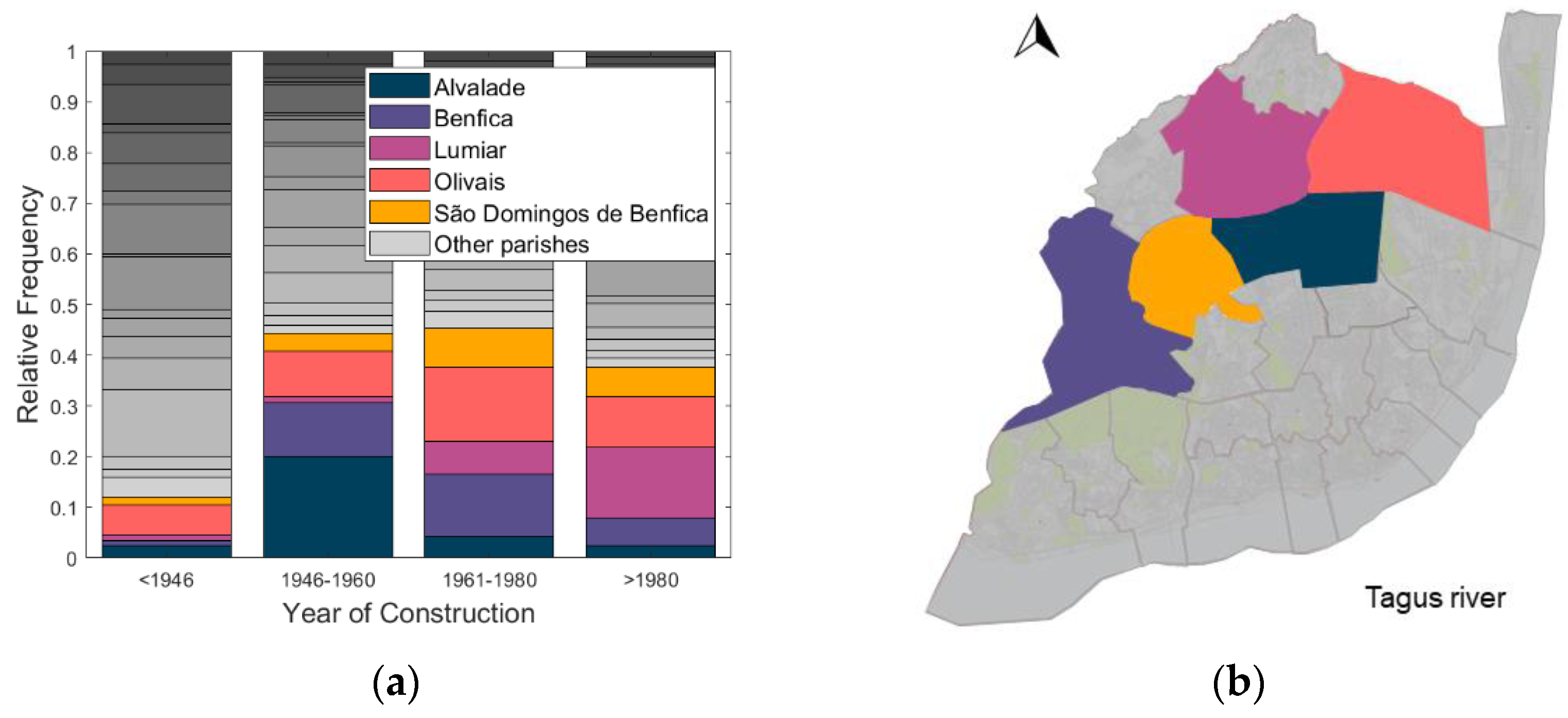

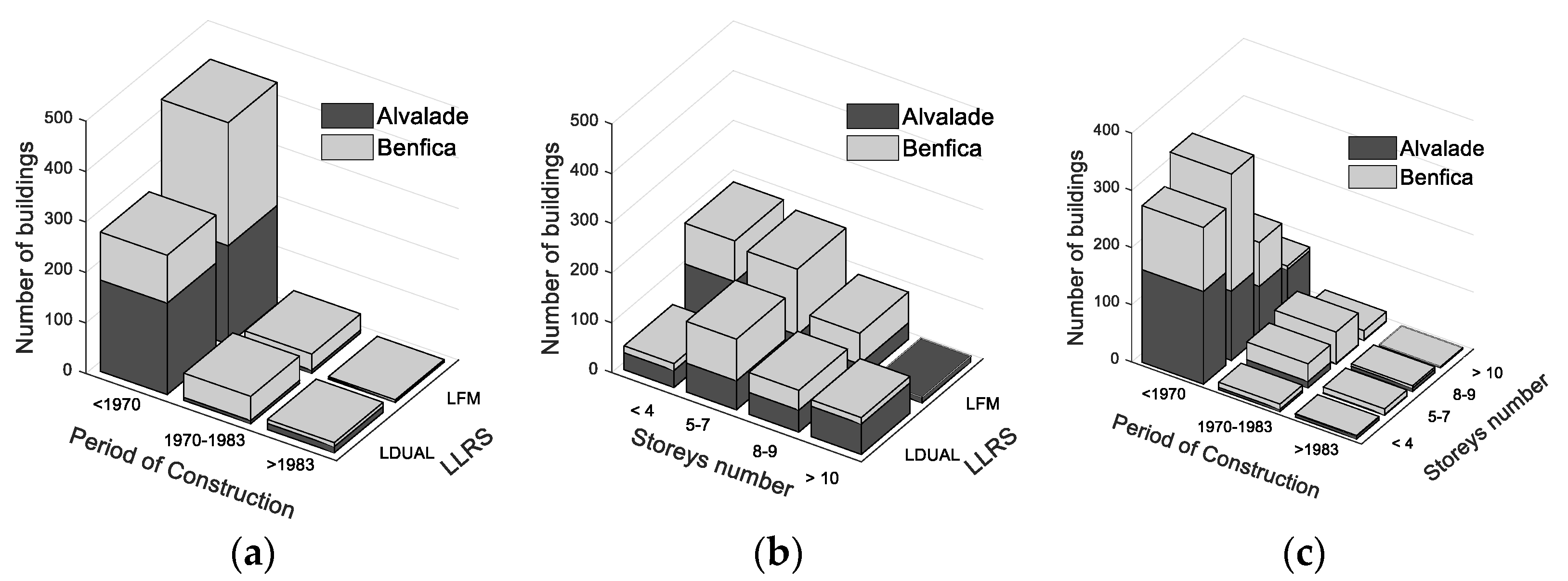

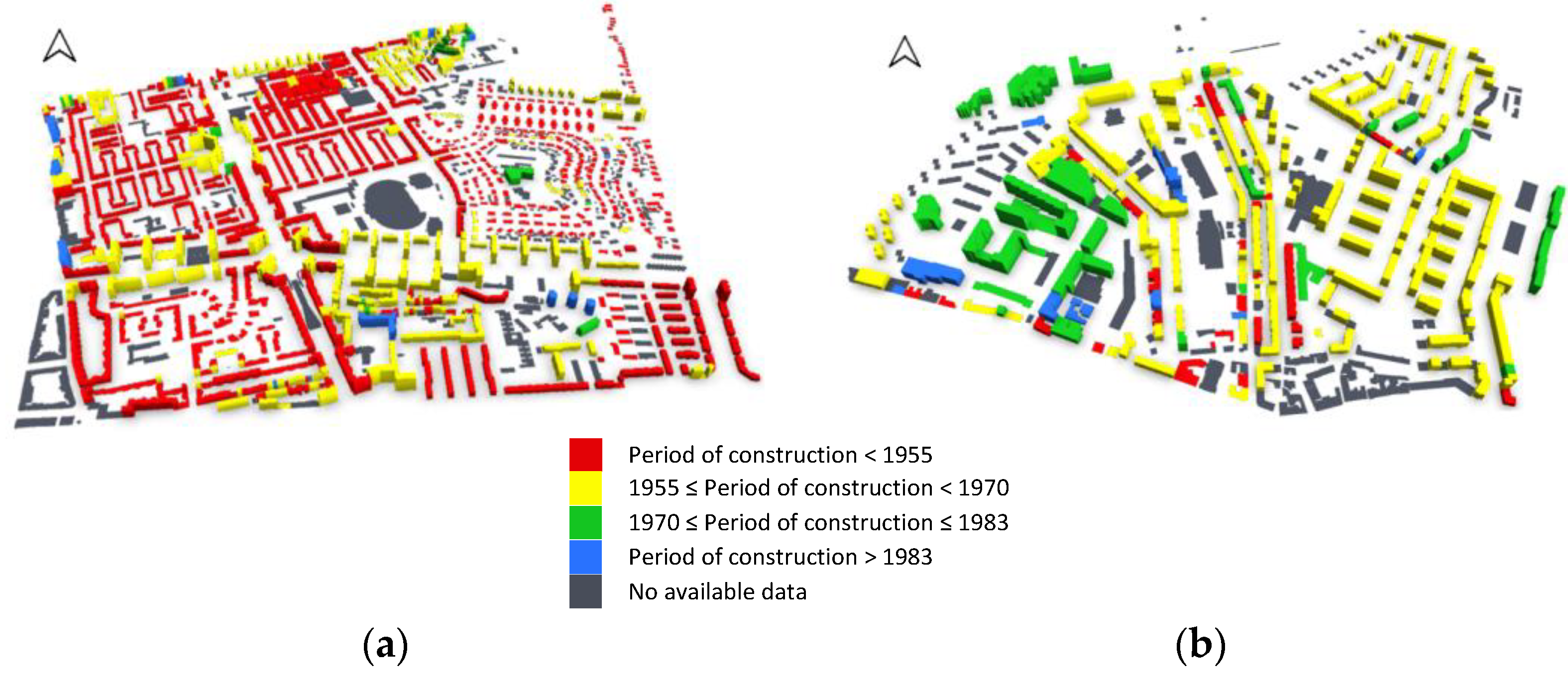


| Typology | Period of Construction | Codes | Remarks |
|---|---|---|---|
| 1st phase RC building | End of 40′s–Beginning of 60′s | RPEBA (1918) RBA (1935) |
|
| 2nd phase RC building | Beginning of 60′s–End of 70′s | RSCCS (1958) RSEP (1961) REBA (1967) |
|
| Modern RC buildings | Beginning of 80′s | RSA (1983) REBAP (1983) RBLH (1971) CEN (1990) |
|
| Attribute | Level 1 | Level 2 | ||||
|---|---|---|---|---|---|---|
| 1. Material of lateral load-resisting system | Concrete, reinforced CR | CR | Cast-in-place concrete | CIP | ||
| 2. Lateral load resisting system | Dual frame-wall system | LDUAL | Non-ductile | DNO | ||
| Ductile, low | DUCL | |||||
| Moment Frame | LFM | Ductile, medium | DUCM | |||
| Ductile, high | DUCH | |||||
| 3. Date of construction or retrofit | Upper and lower bound for the date of construction or retrofit | YBET | ||||
| 4. Height | Number of storeys above ground | H | Range of number of storeys above ground | HBET | ||
| Height of ground floor level above ground | HF | Range of height of ground floor level above ground | HFBET | |||
| 5. Regular or irregular | Regular structure | IRRE | ||||
| Irregular structure | IRIR | |||||
| Category | Attribute |
|---|---|
| General information | Project number, building year, type of occupation (residential, commercial, service, or mixed). |
| Global structural characteristics | Floors number, ground and regular floors height, materials, structure type, RC classes, type of configuration (LFM or LDUAL), slab type and thickness. |
| Specific structural characteristics of RC elements (columns, walls, and beams) | Detailed structural cross-sections, longitudinal and transverse rebar, and RC elements data. |
| Irregularities | Soft-s and/or plan or height irregularities (and the respective floor). |
| Attribute | Benfica | Alvalade |
|---|---|---|
| Façade | Masonry infills walls (as single or double plans) | Masonry infills walls (as single or double plans) |
| Façade coating | Marble, Limestone and Evinel (as wall tile) | No data available |
| Roof | Marseille and Lusa (as roof tile) | Marseille and Lusa (as roof tile) |
| Interior Walls | Masonry infills walls | Masonry infills walls |
| Pavement floor | Hydraulic, ceramic, and stone (as floor tile) and wood parquet | Ceramic and stone (as floor tile) |
| Soft-storey | Present, mainly, in buildings built prior to the 1970s with a decrease for the subsequent years. In total, 46% of the RC buildings are characterized by a soft-storey | Present, mainly, in buildings built prior to the 1970s. In total, 34% of the RC buildings are characterized by a soft-storey |
| Structure type | Reinforced concrete | Reinforced concrete |
| Concrete | B225 | B180, B225, C20/25 and C40 |
| Steel rebars | A40 (usually as smooth bars until 1970s and ribbed afterwards) | A40 (usually as smooth bars and ribbed afterwards) and S235 |
| Foundation | Pad footing (casually with strap beam) | Pad footing |
| Areas | Sample Size | Storey | Probabilistic Distribution | Mean (m) | COV (%) | Min. (m) | Max. (m) | Χ2 Test |
|---|---|---|---|---|---|---|---|---|
| Alvalade | 303 | Ground | Lognormal | 3.89 | 19 | 2.80 | 6.00 | NS * |
| Regular | Lognormal | 3.03 | 4 | 2.70 | 4.00 | NS * | ||
| Benfica | 400 | Ground | Lognormal | 3.54 | 21 | 2.50 | 5.40 | NS * |
| Regular | Lognormal | 2.86 | 10 | 2.10 | 4.00 | NS * | ||
| Total | 703 | Ground | Lognormal | 3.69 | 21 | 2.50 | 6.00 | NS * |
| Regular | Lognormal | 2.93 | 8 | 2.10 | 4.00 | NS * |
| Areas | Sample Size | Probabilistic Distribution | Mean (m) | COV (%) | Min. (m) | Max. (m) | Χ2 Test |
|---|---|---|---|---|---|---|---|
| Alvalade | 246 | Lognormal | 0.12 | 27 | 0.08 | 0.40 | NS * |
| Benfica | 408 | Lognormal | 0.15 | 20 | 0.10 | 0.20 | NS * |
| Total | 654 | Lognormal | 0.14 | 24 | 0.08 | 0.40 | NS * |
| LLRS | Number of Storeys | Sample Size | Mode (m) | Probabilistic Distribution | Mean (m) | COV (%) | Min. (m) | Max. (m) | Χ2 Test |
|---|---|---|---|---|---|---|---|---|---|
| LFM | <4 | 199 | 0.30 | Lognormal | 0.46 | 39 | 0.20 | 1.10 | NS * |
| 5–7 | 293 | 0.60 | Gamma | 0.57 | 32 | 0.25 | 1.20 | NS * | |
| 8–9 | 146 | 0.40 | Weibull | 0.57 | 36 | 0.20 | 1.00 | NS * | |
| >10 | 13 | 0.55 | Lognormal | 0.72 | 25 | 0.55 | 1.00 | NS * | |
| LDUAL | <4 | 43 | 0.60 | Beta | 0.53 | 35 | 0.20 | 0.80 | NS * |
| 5–7 | 178 | 0.80 | Gamma | 0.58 | 40 | 0.20 | 1.25 | NS * | |
| 8–9 | 108 | 0.35 | Lognormal | 0.69 | 52 | 0.35 | 2.60 | NS * | |
| >10 | 46 | 0.90 | Gamma | 0.71 | 34 | 0.40 | 1.20 | NS * |
| LLRS | Number of Storeys | Sample Size | Mode (m) | Probabilistic Distribution | Mean (m) | COV (%) | Min. (m) | Max. (m) | Χ2 Test |
|---|---|---|---|---|---|---|---|---|---|
| LFM | <4 | 199 | 0.30 | Lognormal | 0.31 | 33 | 0.15 | 0.75 | NS * |
| 5–7 | 293 | 0.20 | Lognormal | 0.27 | 32 | 0.20 | 0.60 | NS * | |
| 8–9 | 146 | 0.20 | Lognormal | 0.30 | 35 | 0.15 | 0.80 | NS * | |
| >10 | 13 | 0.30 | NA * | 0.30 | 45 | 0.17 | 0.70 | NA * | |
| LDUAL | <4 | 43 | 0.20 | Lognormal | 0.27 | 42 | 0.20 | 0.80 | 1% |
| 5–7 | 178 | 0.25 | Lognormal | 0.29 | 27 | 0.20 | 0.55 | NS * | |
| 8–9 | 108 | 0.20 | Lognormal | 0.29 | 31 | 0.18 | 0.60 | NS * | |
| >10 | 46 | 0.40 | Lognormal | 0.40 | 32 | 0.20 | 0.70 | NS * |
| Parish | RC Elements | Dimension | Sample Size | Probabilistic Distribution | Mean (m) | COV (%) | Min. (m) | Max. (m) | Χ2 Test |
|---|---|---|---|---|---|---|---|---|---|
| Alvalade | Walls | No available data | |||||||
| Beams | Depth | 98 | Lognormal | 0.53 | 21 | 0.30 | 0.90 | NS * | |
| Width | 98 | Lognormal | 0.27 | 30 | 0.15 | 0.50 | 10% | ||
| Benfica | Walls | Depth | 163 | Lognormal | 2.00 | 31 | 1.60 | 4.00 | NS * |
| Width | 163 | Lognormal | 0.24 | 15 | 0.18 | 0.40 | NS * | ||
| Beams | Depth | 432 | Lognormal | 0.48 | 25 | 0.25 | 1.00 | NS * | |
| Width | 432 | Lognormal | 0.24 | 28 | 0.10 | 0.50 | 10% | ||
| LLRS | Period of Const. | Sample Size | Mode (%) | Probabilistic Distribution | Mean (%) | COV (%) | Min (%) | Max (%) | Χ2 Test |
|---|---|---|---|---|---|---|---|---|---|
| LFM | <1970 | 335 | 0.77 | Lognormal | 0.98 | 80 | 0.13 | 5.63 | NS * |
| 1970–1983 | 60 | 1.13 | Lognormal | 1.32 | 94 | 0.18 | 3.85 | NS * | |
| >1983 | 6 | 0.13 | NA * | 0.93 | 79 | 0.13 | 2.15 | NA * | |
| LDUAL | <1970 | 197 | 0.23 | Lognormal | 0.98 | 99 | 0.21 | 6.62 | NS * |
| 1970–1983 | 56 | 0.57 | Lognormal | 1.21 | 81 | 0.43 | 4.46 | 1% | |
| >1983 | 20 | 0.52 | NA * | 0.96 | 51 | 0.52 | 2.06 | NA * |
| LLRS | Period of Const. | Sample Size | Mode (%) | Probabilistic Distribution | Mean (%) | COV (%) | Min (%) | Max (%) | Χ2 Test |
|---|---|---|---|---|---|---|---|---|---|
| LFM | <1970 | 327 | 0.14 | Lognormal | 0.12 | 66 | 0.02 | 0.69 | NS * |
| 1970–1983 | 59 | 0.19 | Lognormal | 0.21 | 68 | 0.03 | 0.57 | NS * | |
| >1983 | 6 | 0.03 | NA * | 0.11 | 84 | 0.03 | 0.28 | NA * | |
| LDUAL | <1970 | 201 | 0.07 | Lognormal | 0.11 | 52 | 0.02 | 0.46 | NS * |
| 1970–1983 | 45 | 0.05 | Lognormal | 0.14 | 48 | 0.05 | 0.33 | NS * | |
| >1983 | 18 | 0.28 | NA * | 0.21 | 39 | 0.07 | 0.28 | NS * |
| Reinforcement Ratio | Period of Const. | Sample Size | Mode | Probabilistic Distribution | Mean (%) | COV (%) | Min (%) | Max (%) | Χ2 Test |
|---|---|---|---|---|---|---|---|---|---|
| Longitudinal | <1970 | 97 | 0.08 | Lognormal | 0.33 | 96 | 0.02 | 1.75 | NS * |
| 1970–1983 | 43 | 0.20 | Weibull | 0.63 | 61 | 0.06 | 1.48 | NS * | |
| >1983 | 11 | 1.17 | NA * | 0.78 | 53 | 0.61 | 1.17 | NA * | |
| Transverse | <1970 | 97 | 0.12 | Gamma | 0.14 | 96 | 0.01 | 0.90 | NS * |
| 1970–1983 | 43 | 0.23 | NA * | 0.19 | 23 | 0.11 | 0.27 | NA * | |
| >1983 | 11 | 0.23 | NA * | 0.29 | 71 | 0.23 | 0.90 | NA * |
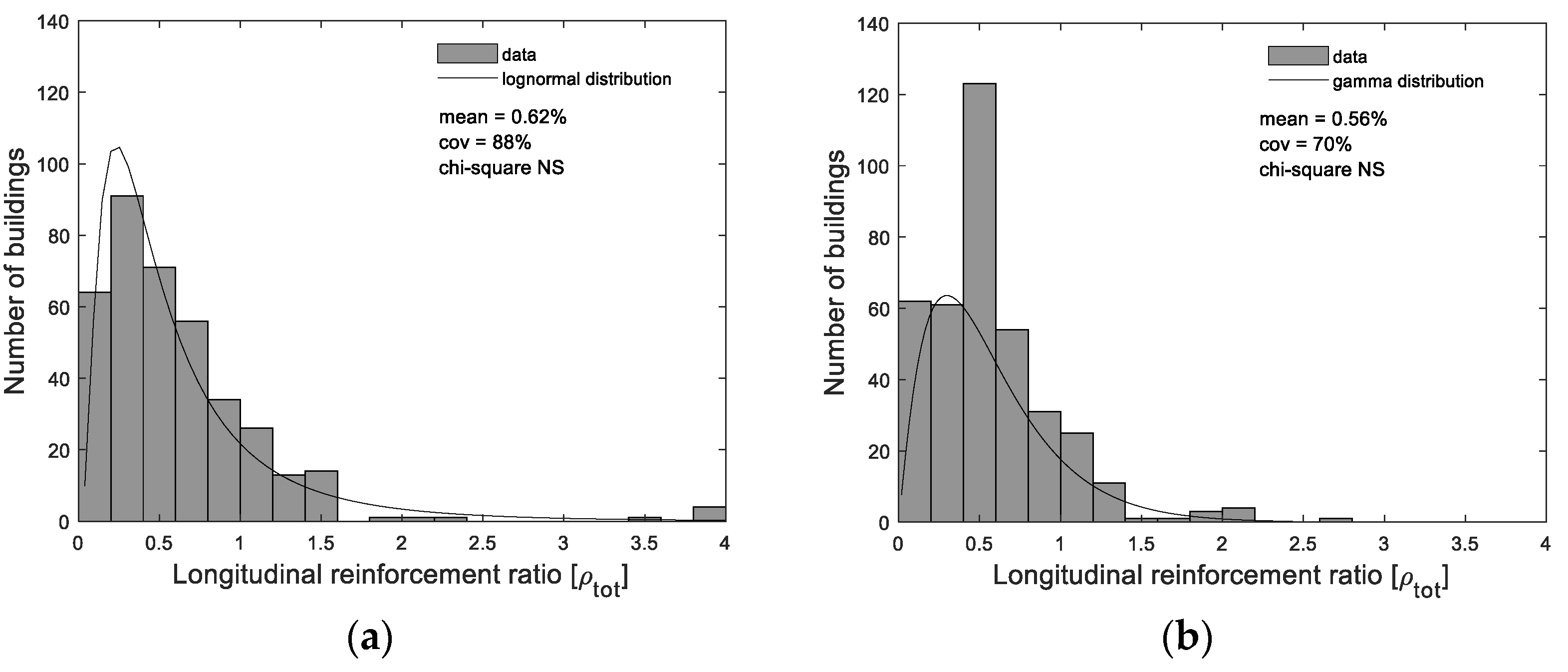
| Type | Sample Size | Mode ρtot (%) | Probabilistic Distribution | Mean ρtot (%) | Coefficient of Variation (%) | Min.ρtot (%) | Max.ρtot (%) | Chi-Square Test (%) | |
|---|---|---|---|---|---|---|---|---|---|
| Alvalade | Edge | 66 | 0.30 | Lognormal | 0.64 | 69 | 0.06 | 2.37 | 1 |
| Interior | 60 | 0.43 | Lognormal | 0.78 | 56 | 0.12 | 2.11 | 1 | |
| Benfica | Edge | 413 | 0.13 | Gamma | 0.62 | 92 | 0.04 | 3.91 | NS * |
| Interior | 415 | 0.10 | Gamma | 0.52 | 71 | 0.06 | 2.73 | NS * |
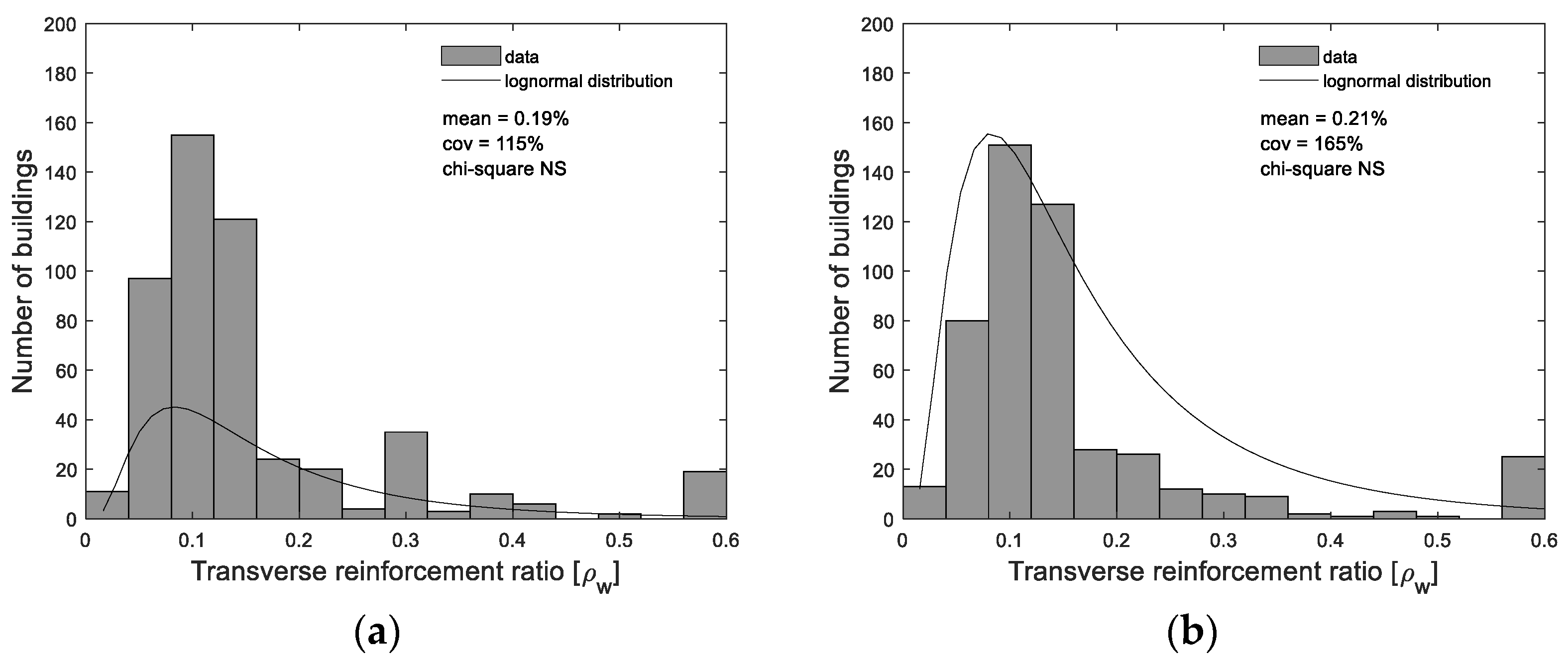
| Type | Sample Size | Mode ρw (%) | Probabilistic Distribution | Mean ρw (%) | Coefficient of Variation (%) | Min. ρw (%) | Max. ρw (%) | Chi-Square Test (%) | |
|---|---|---|---|---|---|---|---|---|---|
| Alvalade | Edge | 66 | 0.10 | Lognormal | 0.19 | 98 | 0.01 | 3.28 | NS * |
| Interior | 60 | 0.21 | Lognormal | 0.25 | 97 | 0.04 | 5.81 | NS * | |
| Benfica | Edge | 413 | 0.14 | Lognormal | 0.20 | 78 | 0.02 | 1.58 | NS * |
| Interior | 415 | 0.14 | Lognormal | 0.20 | 97 | 0.03 | 1.68 | NS * |
| Model | Sample Size | Longitudinal Reinforcement Ratio ρtot (%) | Transverse Reinforcement Ratio ρw (%) | ||
|---|---|---|---|---|---|
| Range | Mean | Range | Mean | ||
| Priestley et al. (1993) [66] | 86 columns | N.A. | 0.16< ρw <1.31 | N.A. | |
| Pujol et al. (1999) [67] | 92 columns | 0.5 < ρtot < 5.1 | N.A. | 0.0< ρw <1.64 | N.A. |
| Sezen (2002); Elwood and Moehle (2003, 2005); Sezen and Moehle (2004) [68,69,70,71] | 50 columns | 1 < ρtot < 4 | 2.3 | 0.10 < ρw <0.65 | 0.3 |
| Aslani and Miranda (2005) [72] | 92 columns | 0.9 < ρtot < 4 | 2.4 | 0.05< ρw <0.7 | 0.25 |
| Zhu et al. (2007) [73] | 125 columns | 1.2 < ρtot < 3.3 | 2.27 | 0.06< ρw <2.2 | 0.55 |
| Leborgne (2012); LeBorgne and Ghannoum (2014) [74,75] | 32 columns | 1.3 < ρtot < 3.8 | 2.44 | 0.07< ρw <1.41 | 0.36 |
| Wibowo et al. (2014); Wilson et al. (2015) [76,77] | 31 columns | 0.56 < ρtot < 4 | 2.01 | 0.07< ρw <0.38 | 0.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xavier, V.; Couto, R.; Monteiro, R.; Castro, J.M.; Bento, R. Detailed Structural Characterization of Existing RC Buildings for Seismic Exposure Modelling of the Lisbon Area. Buildings 2022, 12, 642. https://doi.org/10.3390/buildings12050642
Xavier V, Couto R, Monteiro R, Castro JM, Bento R. Detailed Structural Characterization of Existing RC Buildings for Seismic Exposure Modelling of the Lisbon Area. Buildings. 2022; 12(5):642. https://doi.org/10.3390/buildings12050642
Chicago/Turabian StyleXavier, Válter, Rita Couto, Ricardo Monteiro, José Miguel Castro, and Rita Bento. 2022. "Detailed Structural Characterization of Existing RC Buildings for Seismic Exposure Modelling of the Lisbon Area" Buildings 12, no. 5: 642. https://doi.org/10.3390/buildings12050642
APA StyleXavier, V., Couto, R., Monteiro, R., Castro, J. M., & Bento, R. (2022). Detailed Structural Characterization of Existing RC Buildings for Seismic Exposure Modelling of the Lisbon Area. Buildings, 12(5), 642. https://doi.org/10.3390/buildings12050642









