Experimental Investigation of h-Type Supporting System for Excavation beneath Existing Underground Space

Abstract

A double-row pile support system combined with existing and additional support piles offers an effective solution for further excavation beneath existing underground space. A large-scale test chamber was therefore built to simulate the whole construction process of underground space extension. Several parallel tests are conducted through observation, data monitoring, and analysis to study the influence of several parameters on an h-type support system containing double-row piles. The relevant parameters include pile row spacing, pile length ratio, pile-head constraint, and in-service foundation pile. The tests reveal that a significant load-transfer effect is generated between the pile rows, and increasing the spacing between pile rows within a certain range can lead to a more reasonable distribution of bending moments and pile force. The displacement of the pile top and its rate of increase are directly proportional to excavation depth, and additional excavation to the bottom of the back-row piles tends to be a critical point, after which the deformation will be significant. The stability of the system varies inversely with the reduction in pile length ratio, but is positively related to the existing pile-head constraint. Furthermore, in-service foundation piles can result in increased bending moments and reduced displacement of the pile top. Finally, the rationality of the model test results was verified according to the numerical simulation and the stability of the double-row piles support system was calculated.

1. Introduction

As a result of rapid urbanization in developing countries such as China, clustered urban buildings face intense demand for underground space. Underground story supplementation beneath existing buildings is one way to meet this demand. In this approach, it is particularly important to choose an appropriate type of support system for excavation with respect to the proper protection of buildings, underground pipelines, and surrounding facilities.

The code for the conversion and extension of existing underground spaces in Shanghai, China introduces two types of retaining structure [1]. The first uses longer additional support row piles installed on the outside existing support-row piles of the building to form a long and short double-row pile support system. The second, inversely, is a newly added longer pile row installed inside the existing support pile row. This second approach is called an h-type double-row pile-supported structure in reference to its visual appearance, which is schematically shown in Figure 1.

1.1. Previous Research

Since the design of the support piles is governed by bearing capacity and deformation, research on the mechanical performance of double-row piles is extensive. Phillip et al. concluded that the arrangement of double-row piles had a significant influence on the deformation of retaining structures [2]. Masatoshi proposed an analytical solution for double-row piles by comparing the results from theoretical calculation and model tests [3]. Zheng et al. established an orthogonal model test based on double-row piles, studied its law of deformation, and compared it with corresponding numerical simulation analysis [4]. Based on the measured data and finite element numerical analysis, the displacement law of a double-row pile support system was also studied in practice [5,6]. Taiyari et al. studied the efficiency of various meta-heuristic optimization algorithms in the optimization design of the pile wall’s retaining system [7]. Ayasrah et al. studied the influence of tunnel construction on adjacent pile foundation by numerical simulation [8]. Iwasaki et al. obtained the pile ultimate load capacity and creep load characteristics, based on full-scale short and long-term load tests [9]. Poulos et al. used the finite element method and boundary element method to study the response of the pile foundations caused by excavation [10].

In urban regions, another important issue with double-row piles involves the earth pressure calculation. A large body of literature examines this problem. For instance, Yu et al. analyzed the displacement and bending moment distribution characteristics of double-row piles through in situ testing of a double-row pile support system in soft clay, and they examined the earth pressure transfer effect between the rows [11]. Tang et al. used numerical approaches and large-scale model tests to investigate the law of evolution of stress and deformation and proposed a prediction method of earth pressure on the backs of existing support piles [12]. Jacazz et al. used Finite element software to calculate the earth pressure for the retaining wall near the bedrock and analyzed the stress and deformation laws of the earth fill behind the wall [13,14,15,16,17]. Liu et al. and Fang et al. proposed theoretical models based on the characteristics of the soil pressure distribution of double-row piles [18,19].

There are many previous scholars who have conducted research based on related directions. Issa et al. introduced and further applied a method to support decision makers to distinguish various deep excavation support systems (DESSs) in construction projects [20]. Oliveira et al. and Sainea-Vargas et al. conducted case analyses on the adjacent construction based on geotechnical engineering [21,22]. In order to meet the minimum damage requirements of nearby buildings, Aswathy et al. proposed a solid and economic support scheme [23]. Mitew-Czajewska et al. conducted a parametric study of finite element modelling of deep excavation [24]. Support selection and environmental impact issues based on adjacent excavation were studied by Szabowicz et al.; Dmochowski et al.; and Mitew-Czajewska et al. [25,26,27]. Bryson et al. proposed a method to help select the stiffness of an excavation support system [28]. Fourie et al. compared the results of limit equilibrium methods with those of finite element studies based on the predictions of embedding depth and maximum bending moment [29]. Lam et al. developed a new apparatus for centrifuge model testing of deep excavations in soft clay soils, in order to better understand the mechanisms of soil excavation [30]. Leung et al. introduced the centrifuge model test results of deep excavation without support in dense sandy land [31]. Ooi et al. determined the reasonable method of estimating the bending moment from inclinometer data [32]. Wyjadłowski et al. carried out methods and technical analysis based on a building excavation and construction process [33]. Popielski et al. used the finite element method to model the structure-soil coupling and verified its rationality [34].

However, little research has focused on the issue of parameters influencing the working performance of retaining structures. Bose et al. and On et al. established finite element models to analyze the influence of spacing of the double-row piles and excavation depth on the working behavior of retaining structures [35,36]. Liu et al. and Ren et al. established finite element models based on engineering examples to investigate the influence of the row spacing, pile length ratio, and cantilever length of primary support piles on the mechanical deformation and working performance of multi-stage support systems [37,38]. Bolton et al. illustrated aspects of the collapse of a rigid cantilever retaining wall embedded in over-consolidated clay through five centrifugal model tests [39]. Moormann measured and analyzed the retaining wall and ground movement of all excavations [40]. Osman et al. proposed a new design method based on plastic theory [41].

1.2. Research Priority of This Paper

Most research on further excavation beneath existing underground space suffers from a limited spatial focus on adding new support piles outside existing support piles. The advantage of such a support system is its relative simplicity, but the demands and constraints of the construction site cannot be overlooked. The working conditions of urban central areas include complex surrounding environments close to buildings, intricate networks of underground pipelines, fragile surrounding facilities, and business operations that require continued normal operations. The h-type double-row pile support system adds support piles inside the existing support framework, making it a valid approach in a complex building environment. Construction space is limited, and the operational technology is complicated; however, it does avoid the constraints of external environmental conditions. The h-type double-row pile support system is often applied in practice, but few theoretical studies have focused on this technique. This study uses a large-scale chamber test system to research the effect of various parameters on the excavation process of the h-type double-row pile support system, including pile row spacing, pile length ratio, pile-head constraint, and whether an in-service foundation pile exists. The test configuration is designed to accurately investigate the influence of various parameters on the performance of the support system, and to provide a reference framework for the engineering projects that adopt this system.

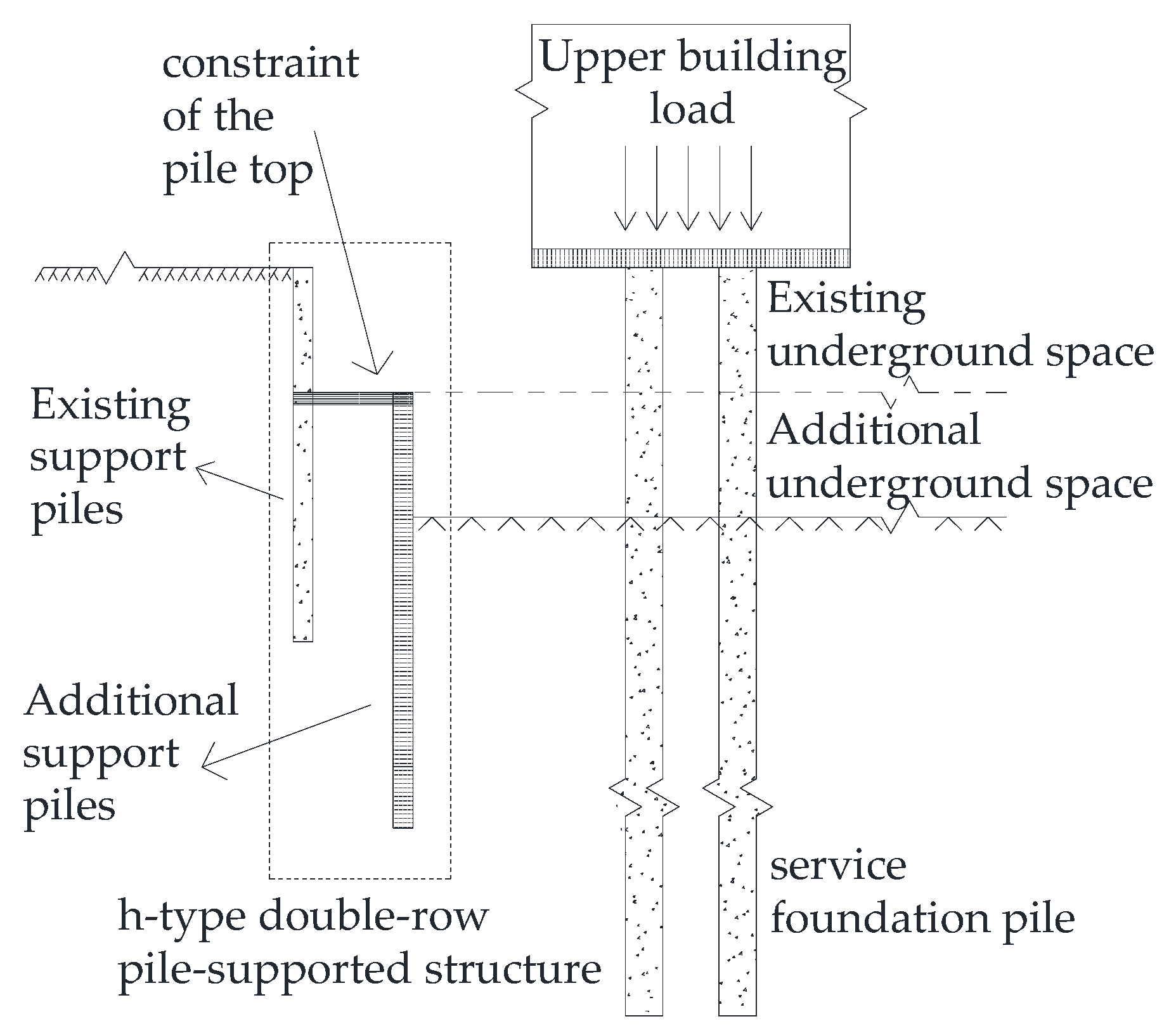
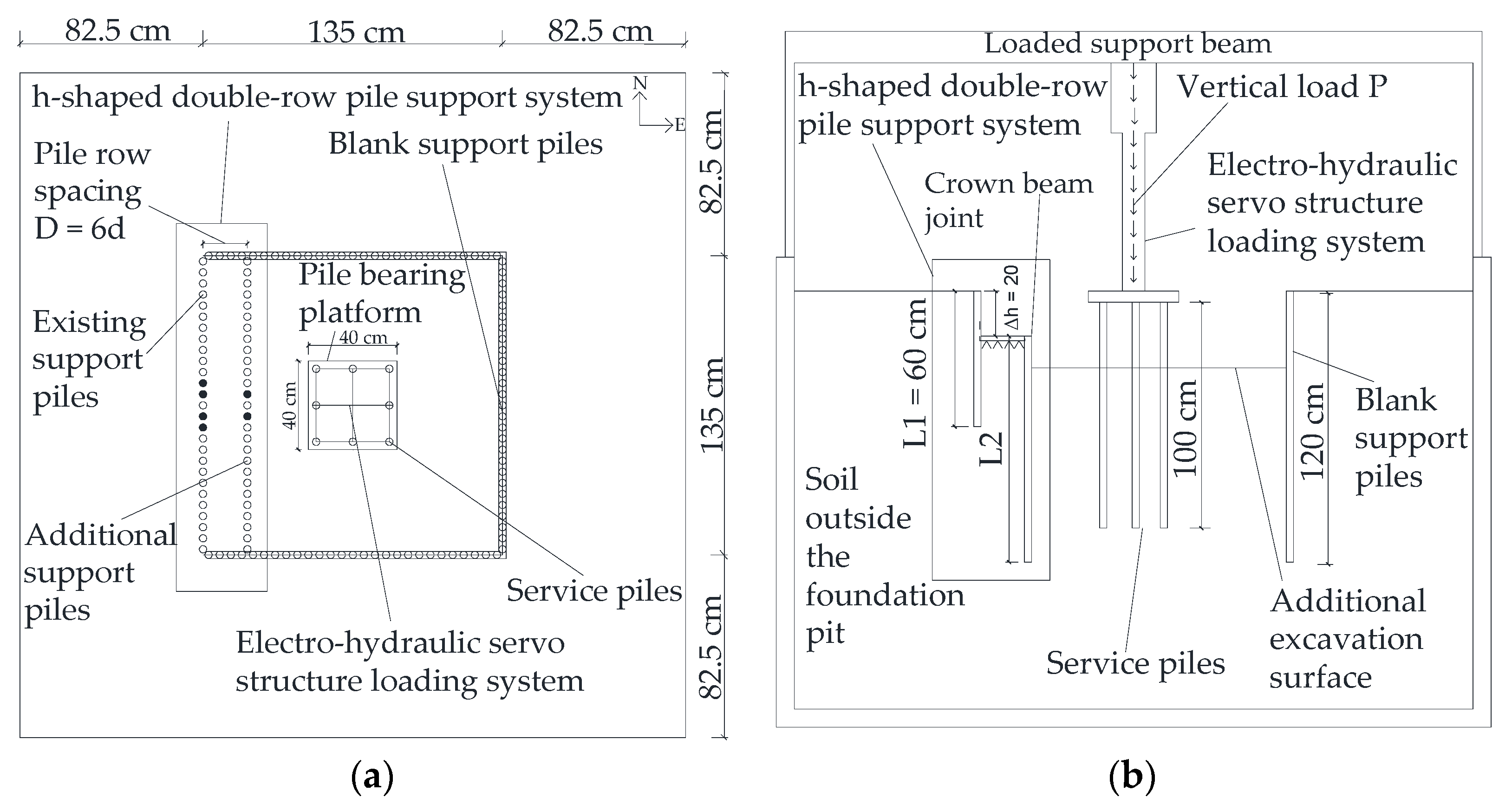
2. Test Arrangement

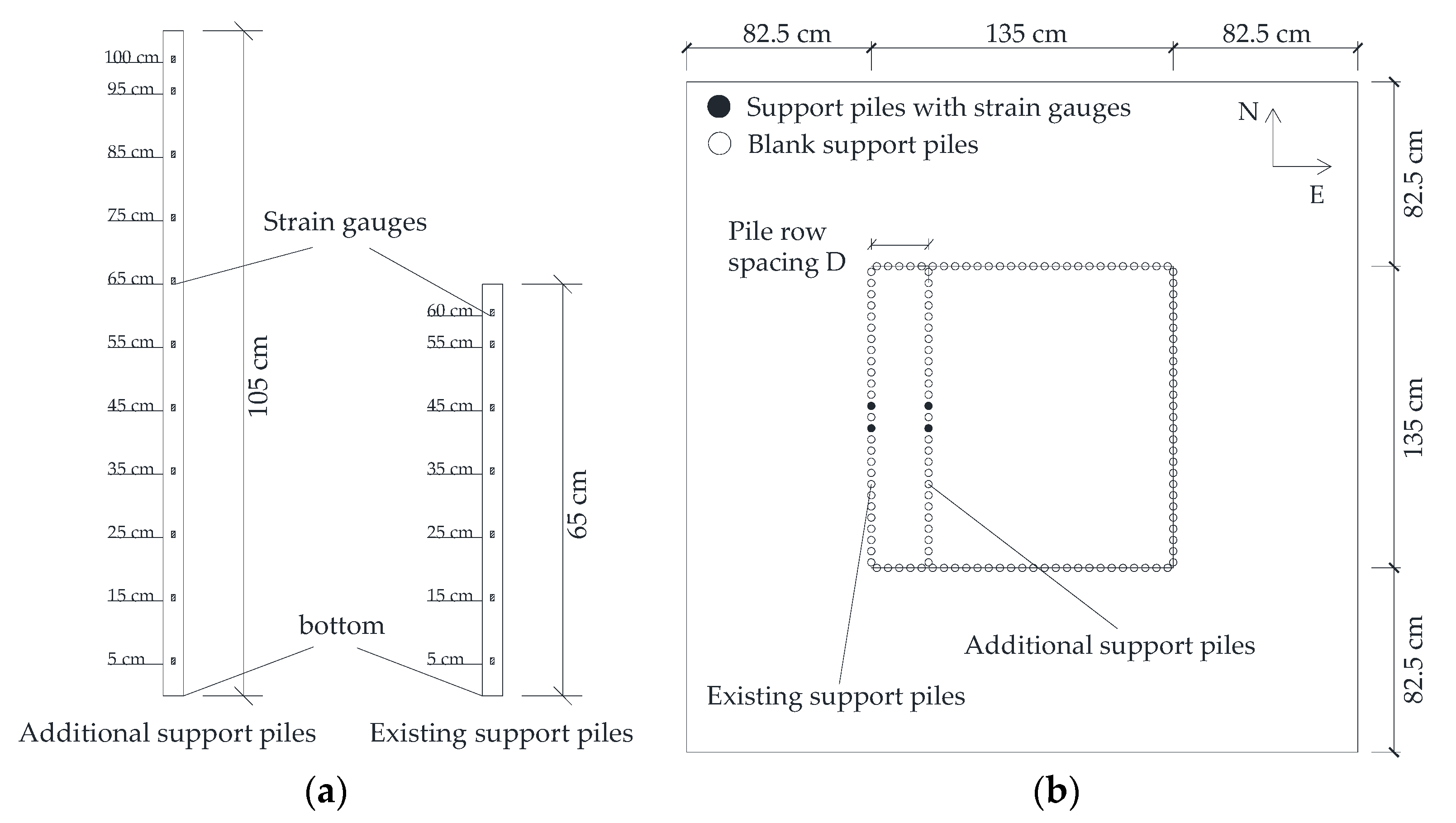
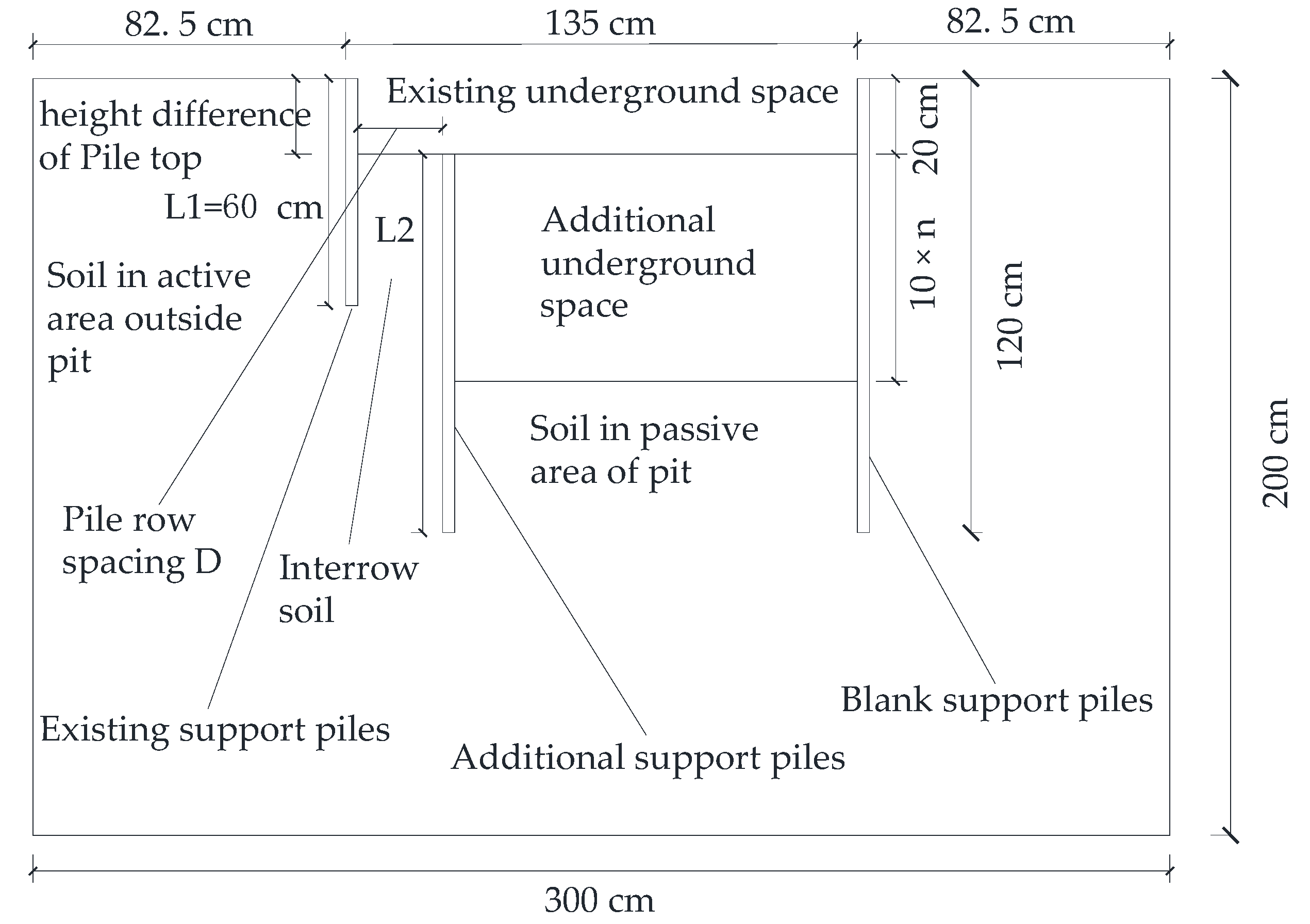
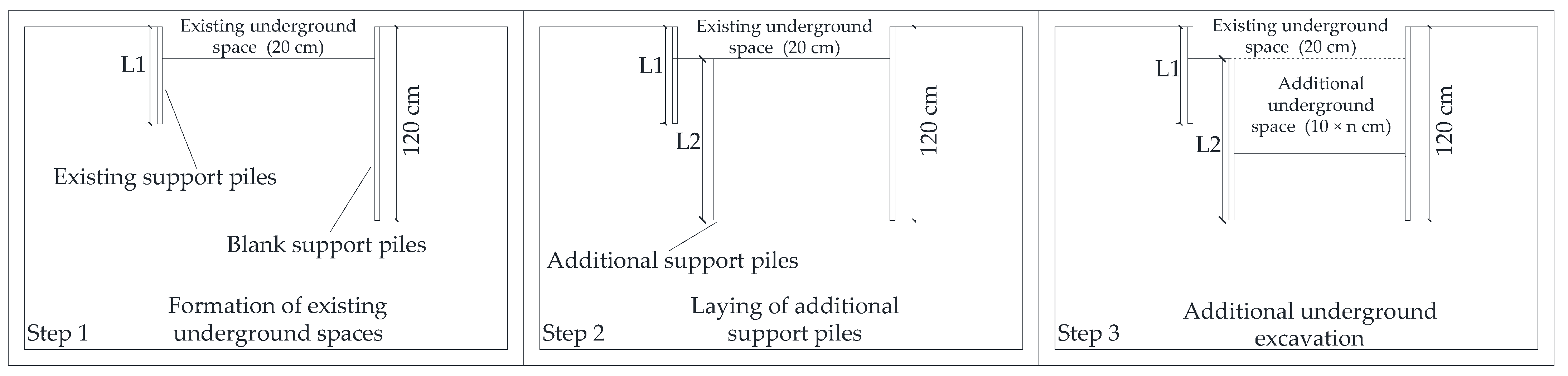
2.1. Test Preparation

The test was carried out at Zhejiang Sci-Tech University (ZSTU), and the test model was selected from a particular project in Zhejiang [42], designed to create additional underground space to meet parking space requirements. Although the project was ultimately not started due to the needs of subway construction, the safety issues surrounding its secondary excavation support remain worthy of exploration. The selection of test materials and their size is based on the actual engineering deep-excavation size, existing and additional support pile length, diameter, elastic modulus, and other measured engineering data. The scale ratio between the actual size and the physical model was 250:1. In addition, the chamber was made of steel that was 3 m in width, 3 m in length, and 2 m in height, and plastic film was laid around and at the bottom of the chamber to improve the boundary effect in the test process. Deep excavation in the testing process was arranged in the middle position of the chamber plane. Above the excavation face sits the steel channel mobile platform and the loaded support beam. Pile strain data were transmitted to the data collection system through the data transmission line. The main instrument devices and materials are shown in Figure 2.

Polyvinyl chloride (PVC) model pipes used in the test had lengths of 0.6 m and 1 m in existing and added piles, respectively. The pile diameter and elastic modulus were 32 mm and 2 GPa, respectively, and the elastic modulus similarity ratio was C_E = 30/2 = 15. The bending moment similarity was calculated as C_M = C_EC_L³ = 234,375, pile stress similarity as C_σ = C_E = 15, and line displacement similarity as C_δ = C_L = 25. Local silty soil was used. After first sieving, the soil showed low cohesion value and natural moisture content. Parameters of this silty soil are shown in

Table 1. Measured values of soil parameters.

Description /	Unit Weight ρ: g/cm3	Water Content ω: %	Cohesion c: kPa	Friction Angle Φ: deg
Silt	15.8	5	2	24

after a series of laboratory tests, including direct shear tests.

Two existing support piles and two additional support piles for measurement were set up with lengths of 65 cm and 105 cm, respectively. The top of the pile was excavated 5 cm to assist the arrangement of the measuring system. The strain gauge point arrangement is shown in Figure 3a. Figure 3b shows the plane layout of the piles, where the east, south, and north planes are blank supporting piles. The westward inner and outer sides consist of additional and existing support piles with 5 cm center-to-center distance in the same row. The distance between the rows, which have 27 piles each, is D. The test pile is blackened in Figure 3b and is arranged on both sides of the central pile to avoid the influence of the spatial effect of deep excavation on the measurement [43].

The process of making model piles is taken from Yu et al. [44]. First, the PVC piles were split as a whole. Then, strain gauges were attached to the inner wall, and shielded cables were connected along the inner wall and extended to the pile heads. Finally, two separate parts of PVC pipes were stuck together with high-strength glue. To remove the soil plug, the same trial piles were first applied to push in and pull out several times at the target pile position, before the formal piles were installed.

Pile strain was collected via two high-speed static strain gauges, which had 120 accesses to log data with a resolution of 0.1 με. In addition, the temperature drift was 1 × 10⁻⁶/24 h, and the connection mode was 1/2 bridge. Horizontal displacement of pile top was measured via dial gauge, with a range and accuracy of 10 mm and 0.01 mm, respectively. Pile length and space dimensions are shown in Figure 4.

2.2. Experimental Scheme

The test scheme with the pile row spacing as the parameter is shown in

Table 2. Test scheme (taking pile spacing as parameter) (unit: cm).

Number	L1	L2	h	D	Existing Excavation	Additional Excavation
T1	65	105	20	4d	20	10 × n
T2	65	105	20	6d	20	10 × n
T3	65	105	20	8d	20	10 × n
T4	65	105	20	10d	20	10 × n
T5	65	105	20	12d	20	10 × n
T6	65	105	20	4d	20	10 × n
T7	0	105	/	/	0	10 × n
T8	65	0	/	/	20	10 × n

. A total of eight groups are set up: five formal groups, T1–T5; one repeated experimental group, T6; and two control groups, T7 and T8. The variable set in the formal group is pile row spacing D, which is set to 4d, 6d, 8d, 10d, and 12d (d = 3.2 cm), in turn. In addition, ‘h’ in Table 2 means the height difference of pile top in the adjacent row.

The procedure of deep excavation can be divided into three steps, as described in Figure 5. Step 1 aims to form the existing underground space through standing for 30 min after placing the existing supporting pile, then excavating 20 cm downward and standing for 72 h. During Step 2, an h-type double-row pile support system is formed by placing additional support piles. The specific operation includes statically pressing the new support piles inside the existing support piles, after the soil stabilizes. In the final step, the additional excavation is conducted after stability of the deformation (specified as 30 min), until final failure of the support system. In addition, excavation depth is kept at 10 cm and the excavation face should be kept smoothed each time, similar to the stage of filling soil. The ‘rain method’ was implemented to ensure soil uniformity. In addition, the control group received only excavation until failure of the support system after arranging the row piles.

The test scheme with parameters, including pile length ratio, pile top constraint, and in-service foundation pile (whether existing or not), is shown in

Table 3. Test scheme (other parameters). (unit: cm).

Number	L1	L2	h	D	P(N)	Pile Top Constraint	Existing Excavation	Additional Excavation
N1	65	125	20	6d	240	NO	20	10 × n
N2	65	105	20	6d	240	NO	20	10 × n
N3	65	85	20	6d	240	NO	20	10 × n
N4	65	65	20	6d	240	NO	20	10 × n
N5	65	105	20	6d	240	YES	20	10 × n
N6	65	65	20	6d	240	YES	20	10 × n

. A total of six groups are set up, including four formal groups, N1–N4. The variable set in the formal groups, N1–N4, is the additional support pile length L2, which is set to 125 cm, 105 cm, 85 cm, and 65 cm, respectively. In addition, the row spacing, height difference of the pile top, length of the existing support piles, and vertical load of the service foundation piles are kept the same to investigate the influence of pile length ratio on the h-type double-row pile support system. Control groups N5 and N6 increase the pile top constraint compared to formal groups N2 and N4 to study this effect. At the same time, the effect of the service foundation piles on the system can be observed by comparing N2 and T2.

The plane and section drawings of the chamber for investigating the effect of service foundation piles are shown in Figure 6a,b. A cap whose size is 40 cm × 40 cm is arranged in the middle of the chamber, and the upper part is connected with the electro-hydraulic servo structure loading system. The eight holes distributed in the lower portion are vertically fixed with the PVC pipes, effectively limiting their relative movement. At the same time, the loading instrument uniformly transfers the load to the eight foundation piles through the cap.

3. Observed Performance and Discussion

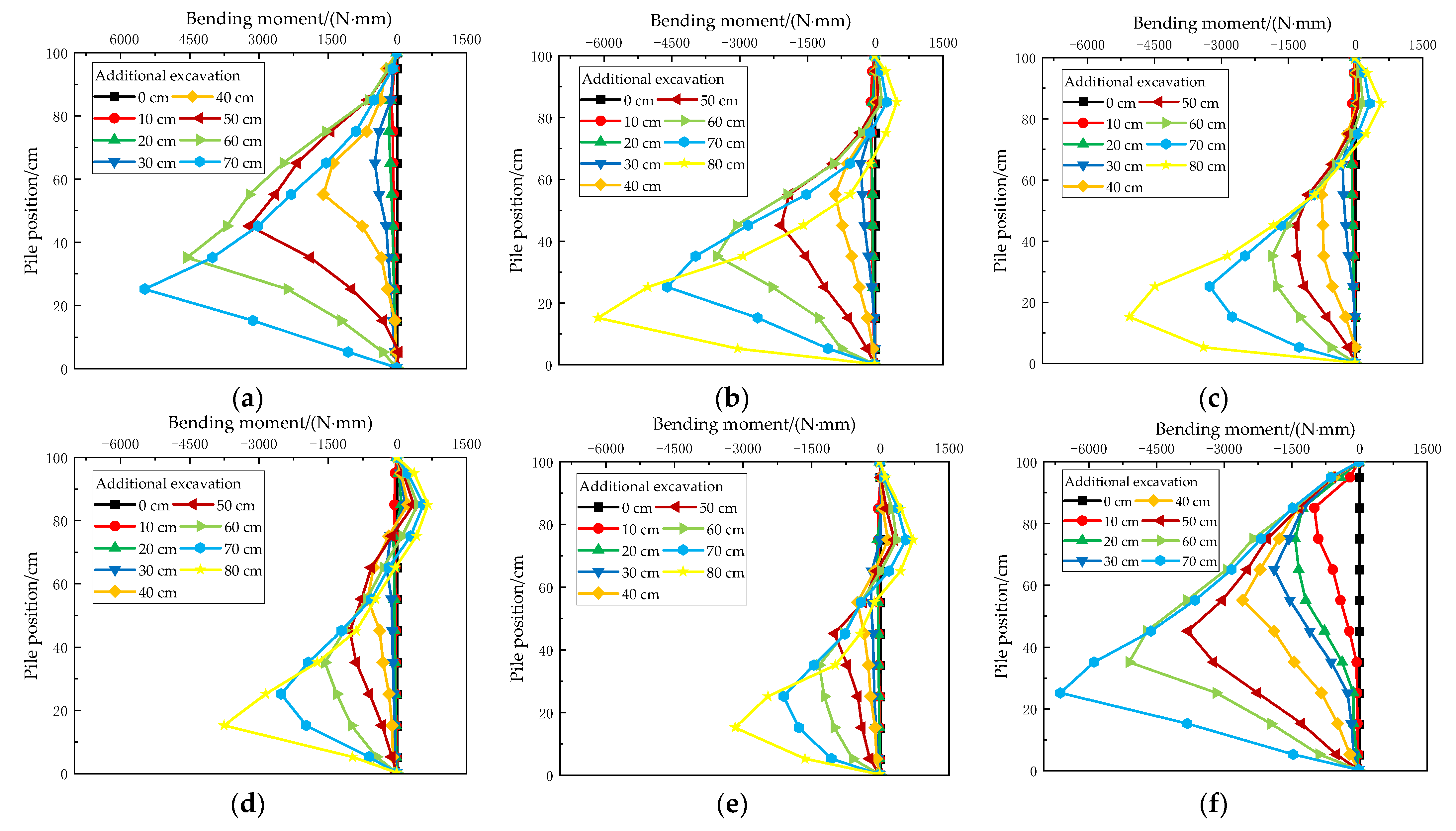
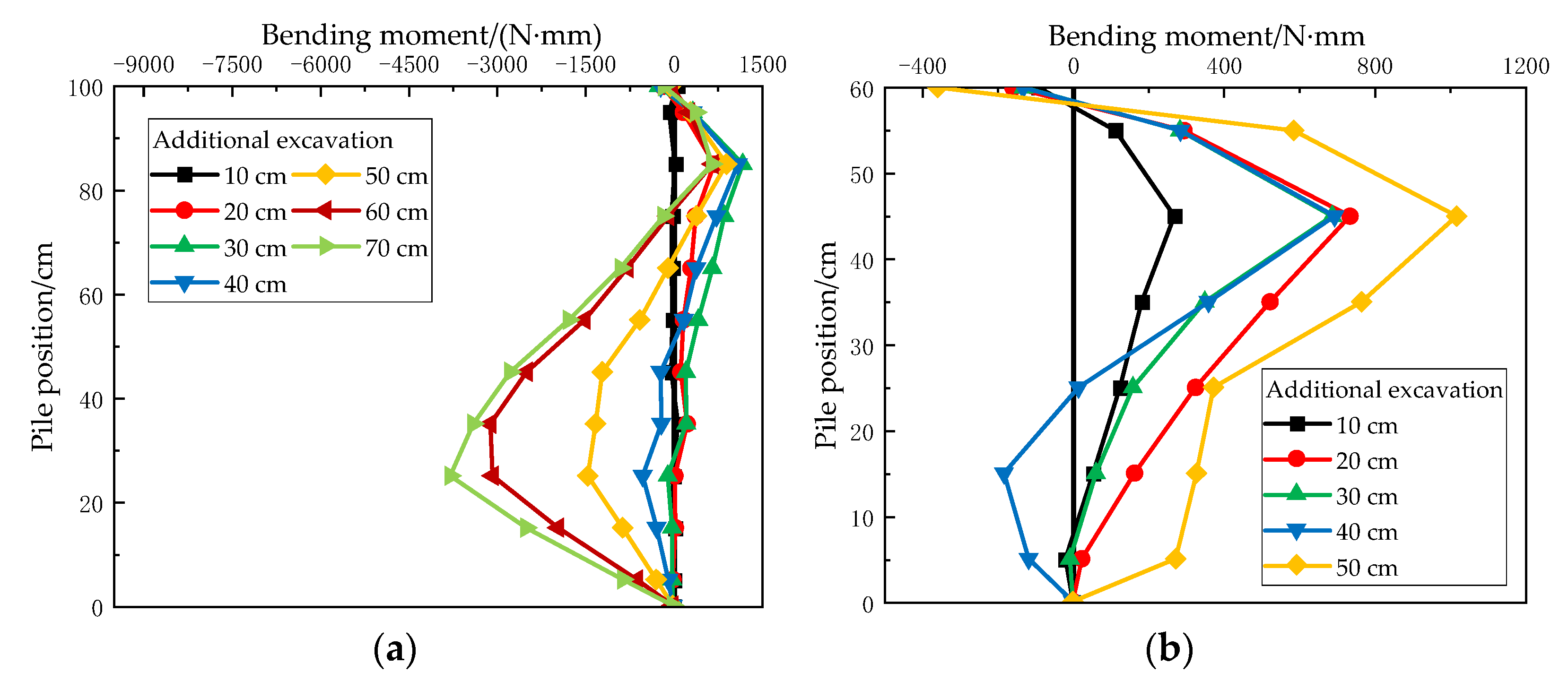
3.1. Influence and Effect of Pile Row Spacing

Figure 7 shows the comparison of the bending moment distribution of the additional support piles with different excavation depths. From Figure 7a–e, it can be seen that the maximum negative bending moment of the piles increases with excavation. The final maximum value appears at 10 cm below the excavation face. In addition, the law of bending moment development is similar to that of the control group T7, and the peak values are all less than T7, indicating that the mechanical characteristics of the additional support piles of the h-type double-row pile support system are similar to those of the single row cantilever pile, and that the existing support piles share the stress of the overall support system. Moreover, note that there is a positive bending moment on the upper part of the piles, and the peak value and its range increase with excavation. The reason for this is that the soil in the active area of inter-row differentiation increases with excavation, and the instability of the back-row piles transfers the soil pressure outside the deep excavation, which then applies on the upper part of the additional piles, making the positive bending moment of the upper lateral tension of the pile body increase continuously. An abrupt increase in the variability of the increase in the bending moment occurs after the additional excavation reaches 40 cm. This is due to the excavation depth to the bottom of the existing piles, which is the critical point of tilting instability. The slip surface of the soil behind the existing support piles then shows accelerated development, and the squeezed piles and the inter-row soil transfer to the additional support piles.

Figure 8 shows a comparison of the bending moment distribution of the existing support piles with different excavation depths, which exhibits an overall S-shape. From Figure 8a–e, observe that the bending moment decreases slightly with the increased excavation depth when the excavation depth is less than 40 cm, and the peak position remains unchanged. Considering that the slip surface between rows has not developed rapidly when the excavation depth is small, the soil exerts back pressure on the existing support piles. The bending moment of the piles changes greatly when the excavation depth is more than 40 cm, the negative bending moment peak continues to decrease, and the position moves upward. The reason for this is that the additional support piles have a sharing effect on the existing supporting piles, and better cooperativity is achieved with an increased excavation depth. The turning point of the bending moment from negative to positive focuses at a pile position of 15–25 cm. In addition, the peak of the positive bending moment is still much smaller than its negative counterpart at the end of the additional excavation. At the same time, the positive bending moment appears in the lower part of the pile and gradually increases with excavation. The reason for this is that the soil in the active area differentiated from the soil between the rows is insufficient to embed the existing support piles, and the slip surface development of the soil between the rows induces a large displacement of the existing support piles, leading to the instability of the existing support piles. Under the combined action of the slip soil outside the deep excavation and the compressed soil above the row, a positive bending moment at the lower part of the pile is generated. In addition, the corresponding peak value of the bending moment is small when the spacing between piles is large, because the increased soil thickness between the piles enhances the back pressure on the existing support piles, such that the force of the existing support piles is stable.

Compared with Figure 8a–e, the deformation of the bending moment of group T8’s single row piles is in the shape of a ‘drum belly’, which has the characteristic that the positive bending moment disappears and the negative bending moment increases rapidly with excavation. In addition, the bending moment of the final collapse is 62.5% larger than the maximum value of the existing piles in the double-row pile support system. It is important to focus on the value of the additional excavation depths at failure, which for the single row is 20 cm and for the back row is 80 cm.

Figure 9a shows the relationship between the pile top displacement of the additional support piles and the excavation depth. Note that the pile top displacement is proportional to the excavation depth, and the growth rate of the pile top displacement increases with the development of the excavation. Meanwhile, the pile top displacement of the formal test group is smaller than that of the control group T7, indicating that the h-type double-row pile retaining system has a promoting effect on the deformation and displacement control of the additional support piles. With increased pile spacing, the pile top displacement first decreases and then increases, depending on the influence of the soil state. Moreover, the pile spacing of 10d seems to be the turning point beyond which the soil state is altered. In the process of changing the pile spacing from 4d to 12d, the displacement of the existing support piles’ top first decreases and then increases.

Figure 9b shows the relationship between the pile top displacement of the existing support piles and the excavation depth. Observe that the pile top displacement of the control group T8 is significantly larger than that of the formal test group; that is, the system also promotes deformation control of the existing support piles. In addition, note from Figure 9a,b that the interaction effect of existing additional double-row piles observably improves the overall stability of the retaining structure. The pile top displacement of the existing support piles decreases with the increase in row spacing, which is due to increased soil back pressure between the rows, improving the embedded effect of the pile; furthermore, the influence of deep excavation on its disturbance is tiny because it is far from the test excavation. Meanwhile, a comparison between the two figures shows that there is no clear difference in the displacement of the top of the two piles in the early stage. The displacement of the pile top increases significantly after the additional excavation reaches 40 cm, and the displacement growth rate of the existing support pile is greater than that of the additional support pile.

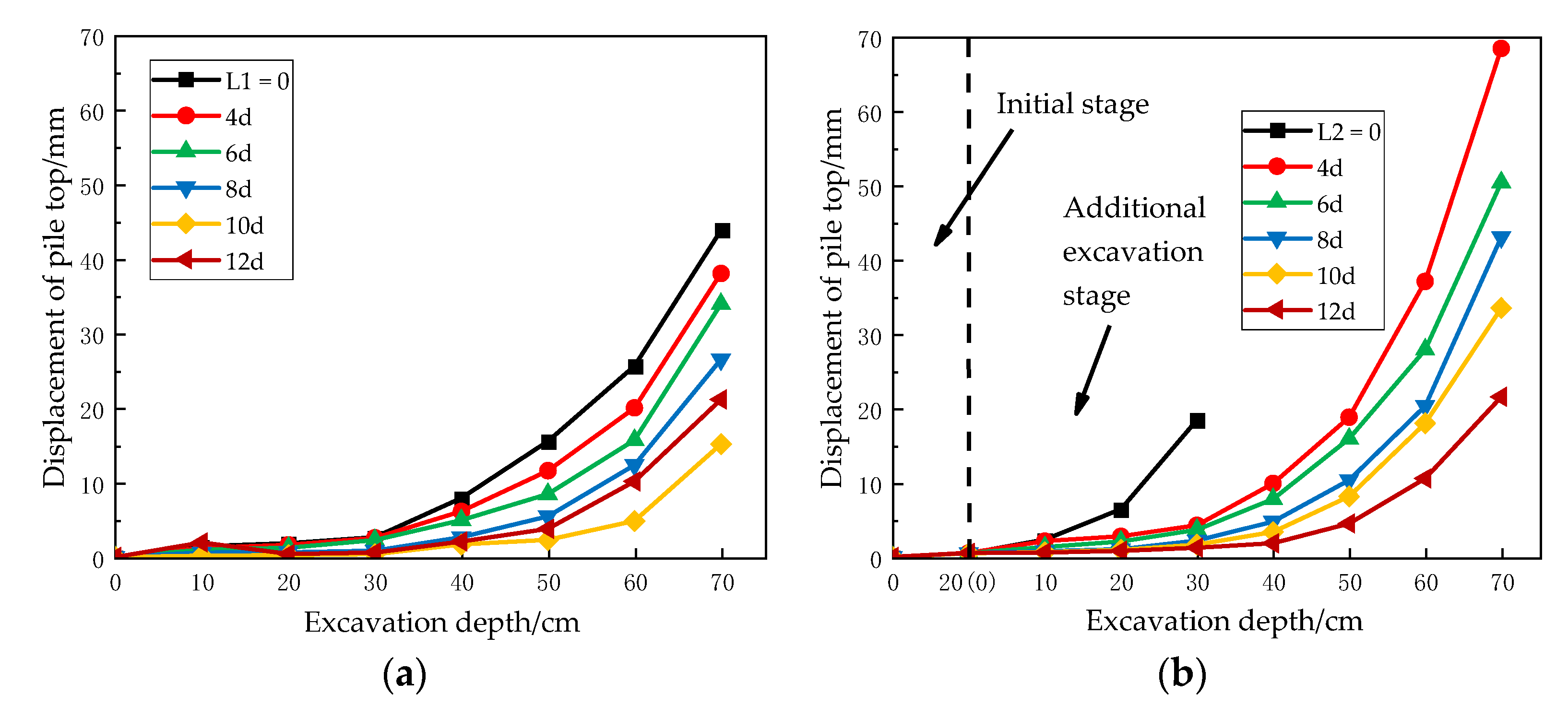
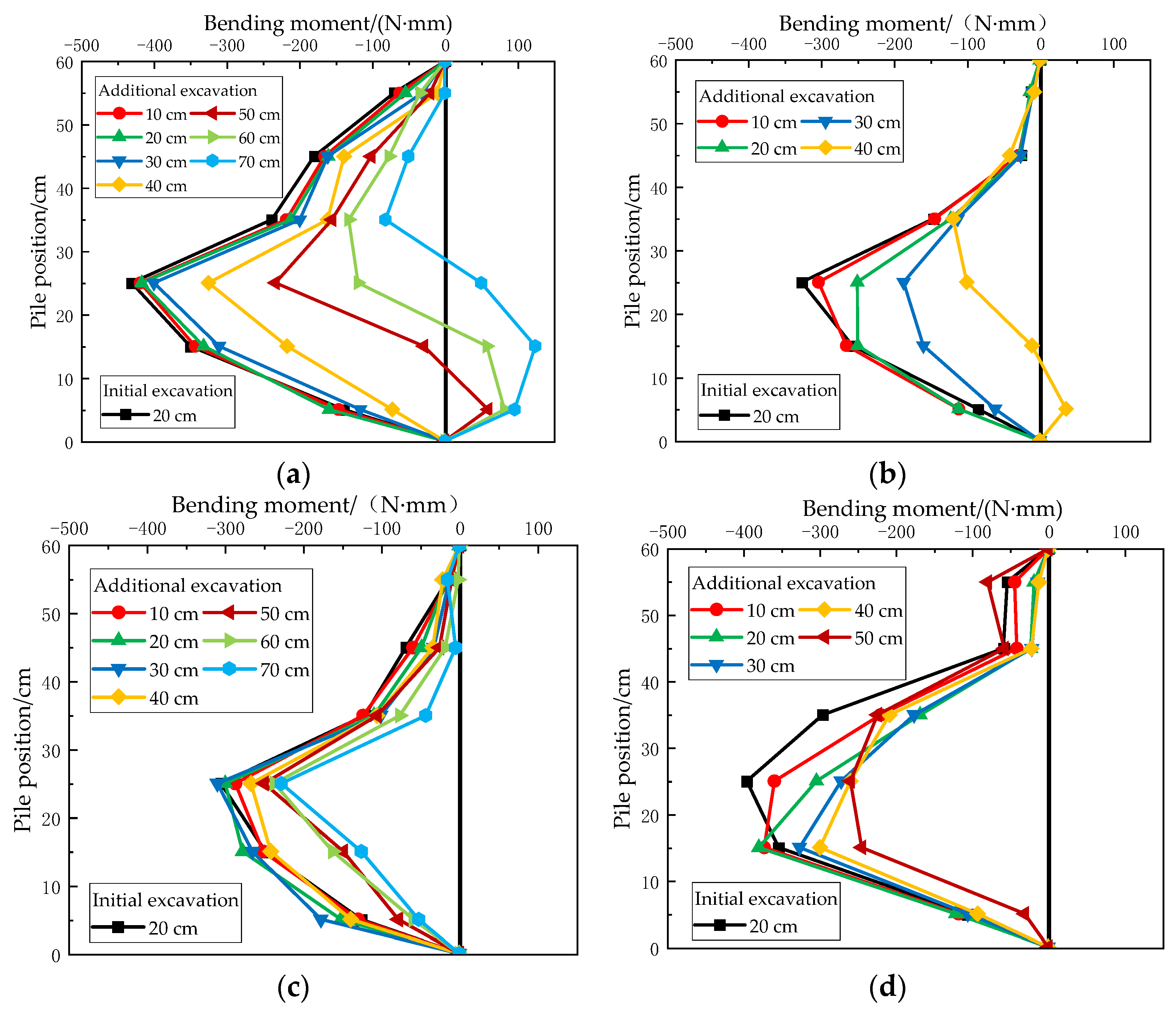
3.2. Influencing Effect of Pile Length Ratio

Figure 10 shows the bending moment comparison of the additional support piles under different additional excavation conditions in the N1–N4 tests. First, in the process of decreasing the pile length ratio (L2/L1), the overall stability of the support system continues to weaken, and the maximum practicable excavation depth of the system even decreases to 40 cm in the N4 test. Shortening the additional support piles is generally harmful to the embedded effect and weakens the overall stability of the support system. Second, at the same additional excavation stage, the peak value of the negative bending moment gradually decreases and shows an accelerated decreasing trend with decreased pile length ratio.

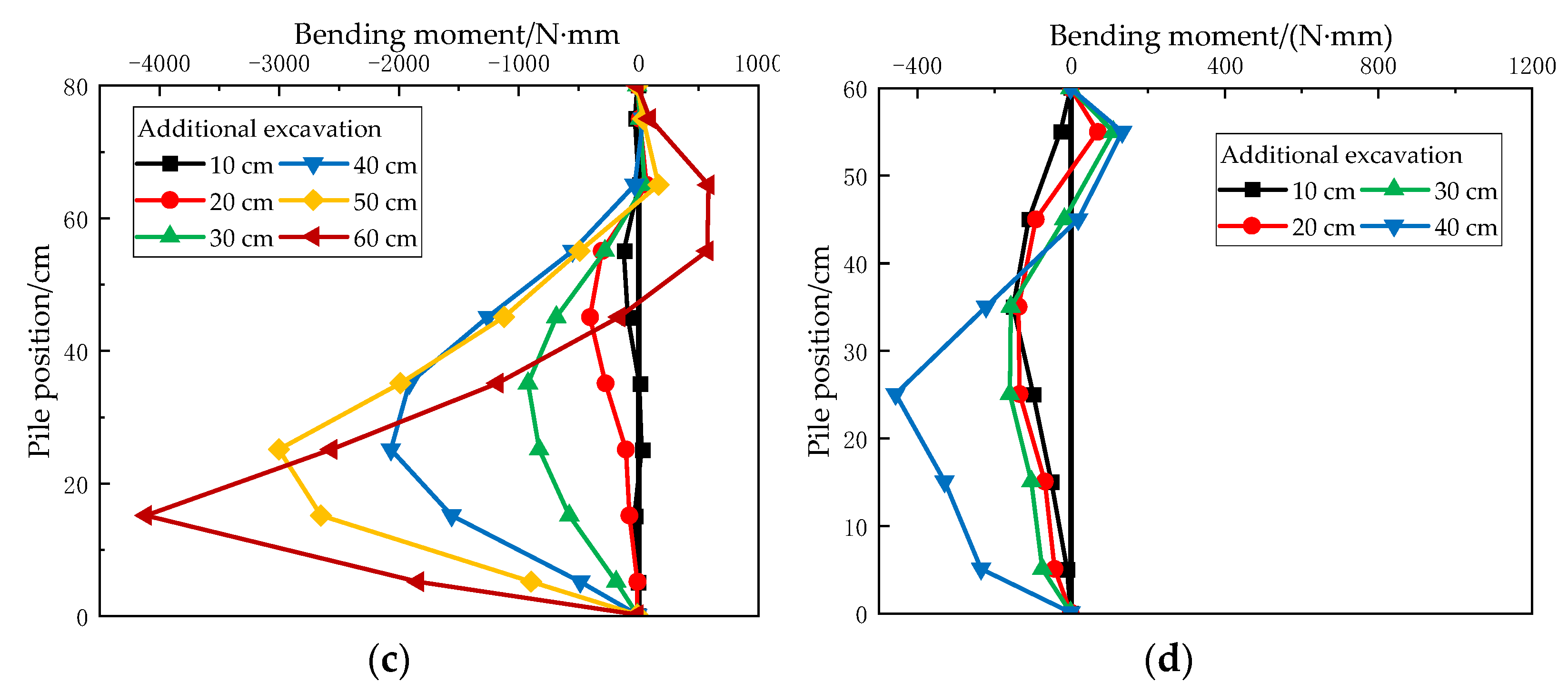
3.3. Influencing Effect of Pile-Head Constraint

Figure 11 shows the bending moment variation of additional support piles with pile top constraints. By comparing Figure 11a with Figure 10b, observe that the negative bending moment peak of N5 decreases as a whole, and the positive bending moment’s region and peak expand sharply. Meanwhile, almost all negative bending moments of N6 evolve into positive bending moments by comparing Figure 11b with Figure 10d. Thus, it can be concluded that the existence of a pile top constraint will make the negative bending moment area and peak value of the additional support piles decrease as a whole, evolving into a positive bending moment.

Figure 12 is the bending moment variation of existing support piles with pile top constraints. Comparison of a,c and b,d in Figure 12 indicates that the state of the whole support system is more stable after increasing the pile top constraint, which shows that the bending moment changes in each adjacent stage in the process of additional excavation and are smaller. The specific reason for this is that the pile top constraint plays the role of force transmission between two rows of piles and improves the integrity of the support system.

3.4. Influencing Effect of Service Foundation Pile

Figure 13a indicates that there is no significant difference in the maximum bending moment between the two groups of tests when the excavation depth is small. The two groups of tests show a clear differentiation after the excavation reaches 50 cm; the peak of N2 begins to be greater than T2. In addition, the gap between the two increased with excavation depth. Figure 13b shows that, with progressing excavation, the displacement of the pile top increases gradually, while the displacement of the pile top in N2 is always less than in T2. In summary, the existence of the service foundation pile can increase the bending moment of the additional support piles and reduce the displacement of the pile top.

3.5. Validity Research

Based on the previous model tests, a PLAXIS finite element calculation model is developed and the reasonableness of the results of the model tests is discussed. In which the present structural model takes the small strain soil hardening model, the soil parameters are shown in

Table 4. Soil parameter values of finite element.

Parameter	γunsat	E50ref	Eoedref	Eurref	C	φ	γ0.7	G0ref	Rinter
Value	15.8	6000	3000	18 × 103	2	24	1 × 10−3	54 × 103	0.7

and the basic model of the test is referred to the setup of the N2 test in the model test. The effect of the soil outside the right side of the pit was not considered and an additional 60 cm of excavation was selected as the data collection and analysis stage. The final reduction coefficient of the stability of the h-type double-row pile-supported structure in this section is the ratio of the soil strength to the soil strength when the numerical calculation process is not convergent. It is defined as the safety factor ΣMsf, which can be regarded as the safety factor Fs of deep excavation stability.

The characteristics of the bending moment curves of the finite element model for each additional excavation stage are more or less the same as compared with the measured data, as can be seen in Figure 14a. Secondly, as can be seen from Figure 14b, the peak bending moment variation trends are the same for both phases, and the difference at the maximum moment differentiation does not exceed 15%, so it can be considered that this finite element model and the N2 test situation are basically in line with each other, and it also verifies the reasonableness of the model test results.

3.6. Safety and Stability Analysis

Based on the finite element model, the strength reduction analysis is carried out at the stages of 40 cm and 60 cm excavation. The displacement of the pile top changes with the safety factor, as shown in Figure 15. According to the previous definition, the safety factors of the two excavation stages are Fs = 1.455 and Fs = 1.039, respectively. At the same time, it can be seen from the diagram that the displacement of the top of the existing support piles is greater than that of the additional support piles, which is in line with the actual model test. In Figure 15, the acceleration position of curve growth is defined as the displacement mutation, and the increment of ΣMsf is defined as the displacement mutation position to the calculation non-convergence position. This increment area can be regarded as the sensitive area of the retaining system for soil strength. It is easy to obtain that the sensitive areas in Figure 15a and Figure 15b are 0.1 and 0.01 respectively.

3.7. Discussion

In general, increasing the pile spacing within a certain range can increase the positive bending moment of the upper part of the additional support piles and decrease the negative bending moment of the lower part, such that the bending moment distribution of the pile is more reasonable and the stress state of the pile is optimized. Meanwhile, the mechanism of loading transfers from the existing piles to additional piles through inter-row soil does exist in a double-row pile support system. The comparison of the single-row piles test groups with the double-row piles test groups in Figure 8 implies that the front piles play an important bearing role in the double-row pile support system, which becomes more helpful after the failure of the back piles. Therefore, cooperation of the double-row piles support system can be reasonably applied through the transfer path of force of pile–row–pile in the test, such that the double-row pile support system can continue to work until the additional excavation reaches 80 cm after the failure of the back-row piles, rather than the overall failure of the system when the additional excavation reaches just 20 cm, as in group T8. These characteristics are quite consistent with the phenomenon of the double-row pile test carried out by Yu et al., and verify the reliability of the conclusions of this test [44].

The pile spacing of 10d seems to be the turning point beyond which soil state is altered. In the process of changing the pile spacing from 4d to 10d, the existing support piles’ embedding effect is strengthened by the soil anti-pressure, and the force transmitted to the additional support piles by the inter-row soil is relatively reduced, which means that displacement of the pile top is reduced. At the same time, the soil in the active area increases with differentiation of the inter-row soil, and when the pile spacing increases to a turning point, the pile top displacement does not decrease, but instead increases (12d). This is different from the regular pattern of ordinary double-row piles studied by Tang et al. [12]. The displacement of the front-row piles’ top increases with the increase of the pile spacing in the ordinary double-row piles system, and there is no inflection point, which reflects the difference between the ordinary double-row piles system and the h-type double-row piles system. This inflection point phenomenon may be further studied in the future.

A comparison of the displacement of the existing and additional support piles’ top illustrates some of the principles. First, it is verified that the excavation of the 40 cm layer is a critical point in the test. Second, it can be preliminarily concluded that the existing support pile is in a state of dumping destruction, due to the weak pile length and embedded effect after the excavation depth reaches the bottom of the existing support pile. This phenomenon is completely different from the ordinary double-row piles support system [12]. When the ordinary double-row piles support system is excavated to about half of the height of the front-row piles, the front-row piles will be destroyed by tilting, and the whole system is forced by the back-row piles. When the h-type double-row piles support system is excavated to the bottom of the back-row, due to factors such as short pile length, the back-row piles are first in the state of dumping and destruction, and the front row piles are extruded through the soil between the rows.

As for pile length ratio, with the increase of the additional pile length, the overall embedded depth of the piles increases, and the embedded stability of the soil in the passive area of the pit on the additional support piles increases. Therefore, the development of the slip surface between the rows and the soil outside the pit is relatively slow, and the displacement of the support system in the whole direction of the pit decreases. Besides, in the double-row piles support system without pile top constraint, the deformation coordination between the double-row piles is completely realized by the inter-row soil. After the pile top constraint is arranged between the existing and additional double-row piles, the front and rear double-row piles are connected as a whole, eliminating the relatively independent state between the double-row piles, which will undoubtedly have a great influence on the overall stress and deformation state of the system. The mechanism for the changes arising from the presence or absence of service foundation piles is that the service foundation pile limit the displacement of the pile top, on the basis of hindering the horizontal displacement of the soil in the passive zone of the excavation via using the soil in the passive zone as the medium, which also leads to an increased maximum bending moment of the pile. Previous researchers have not conducted theoretical mechanistic discussions based on these parameters, and these discussions will hopefully provide some insight into subsequent studies.

Section 3.5 and Section 3.6 verify the rationality of the model test results, according to the numerical simulation. Among them, the strength reduction method is adopted to calculate the stability of the h-type double-row piles support system, which has smaller limitations than the traditional limit equilibrium method [45] and is more convenient for calculation. According to the change of safety factor in the two stages of excavation, it can be seen that the overall stability and safety of deep excavation decrease with the increase of excavation depth. According to the sensitive domain values of 0.1 and 0.01 in the diagram, it can also be found that with the increase of excavation depth, the safety and stability of deep excavation decreases, which is then easily damaged by external interference.

4. Conclusions

This paper reports a series of parameter-related parallel tests conducted in a large-scale test chamber to better understand the influence of key parameters on the h-type double-row pile support system. The findings are summarized as follows:

• Increasing pile spacing within a certain range can increase the positive bending moment of the upper part of the additional support piles and decrease the negative bending moment of the lower part, such that the bending moment distribution of the pile is more reasonable, and the stress state of the pile is optimized. When the spacing between piles is large, the increase in soil thickness between piles enhances the back pressure on the existing support piles, such that the force of the existing support piles is stable. In addition, the front piles play an important bearing role in the double-row pile support system, which is more helpful after failure of the back piles;
• The additional excavation of the 40 cm layer is a critical point in the test. It can be preliminarily concluded that the existing support pile is in a state of dumping destruction after the additional excavation depth reaches the bottom of the existing support pile (40 cm). In addition, the pile top displacement is proportional to the excavation depth, and the growth rate of the pile top displacement increases with increasing excavation. Meanwhile, the interaction effect of the h-type double-row pile support system can significantly improve the overall stability of the retaining structure, which can promote the deformation and displacement control of the additional and existing support piles. Moreover, it is verified that row spacing of 10d appears to be the turning point beyond which the soil state is altered;
• In the process of decreasing the pile length ratio (L2/L1), the overall stability of the support system continues to weaken. It can be concluded that the existence of a pile top constraint will make the negative bending moment area and the peak value of the additional support piles decrease as a whole, evolving into a positive bending moment. In addition, it is observed that the state of the whole support system is more stable after increasing the pile top constraint. The existence of the service foundation pile can increase the bending moment of the additional support piles and reduce displacement of the pile top;
• The study verified the rationality of the model test results according to the numerical simulation and calculated the stability of the double-row piles support system. It can be seen that the overall stability and safety of deep excavation decrease with the increase of excavation depth, which is easily damaged by external interference;
• The influence of service foundation piles on the double-row pile support system is related to many factors, including the number of foundation piles, layout of foundation piles, size design of foundation piles, distance between foundation piles and retaining wall, and the load on the pile top. Currently, research on the influencing effect of parameter adjustments is lacking, and more work needs to be carried out on this topic. Research work based on this issue is, in our opinion, a worthwhile direction.