Seismic Analysis of Baffle-Reinforced Elevated Storage Tank Using Finite Element Method

Abstract

The sloshing phenomenon is an important field of fluid dynamics in liquid storage tanks under earthquake excitation. When the sloshing frequency gets close to the liquid tank’s natural frequency, the resulting resonance could lead to instability and even damage to structures, followed by catastrophic economic losses and environmental damages. As passive control devices, baffles are a place for liquid energy dissipation. This study uses annular and horizontal baffles to evaluate the baffles’ relative effectiveness on the elevated storage tanks’ dynamic response. The analysis results are compared with those of elevated storage tanks with no baffles. The flexible and rigid storage tank analysis is examined here, where half of the tank height is filled with liquid. The structural interaction between the liquid, the (horizontal and annular) baffle, and the elevated storage tank affected by seismic action are investigated using Abaqus software. The results confirm that using the baffles, the maximum base shear force in flexible and rigid elevated storage tanks decreases as much as 26.43% and 31.90%, respectively, and the maximum hydrodynamic pressure reduction in the tank is 50.1%.

1. Introduction

Surface waves and the turbulence generated in the free surface of liquid induced by earthquakes exert considerable dynamic forces on the tank’s structure. As the liquid tanks are considered important elements of urban systems, oil industry, maritime industry, and aerospace systems, devices that reduce turbulence, the consequent environmental damages and economic losses are crucial in designing these structures. Generally, slosh amplitude depends on the amplitude and frequency of tank motion, liquid-fill depth, liquid properties, and tank geometry [1].

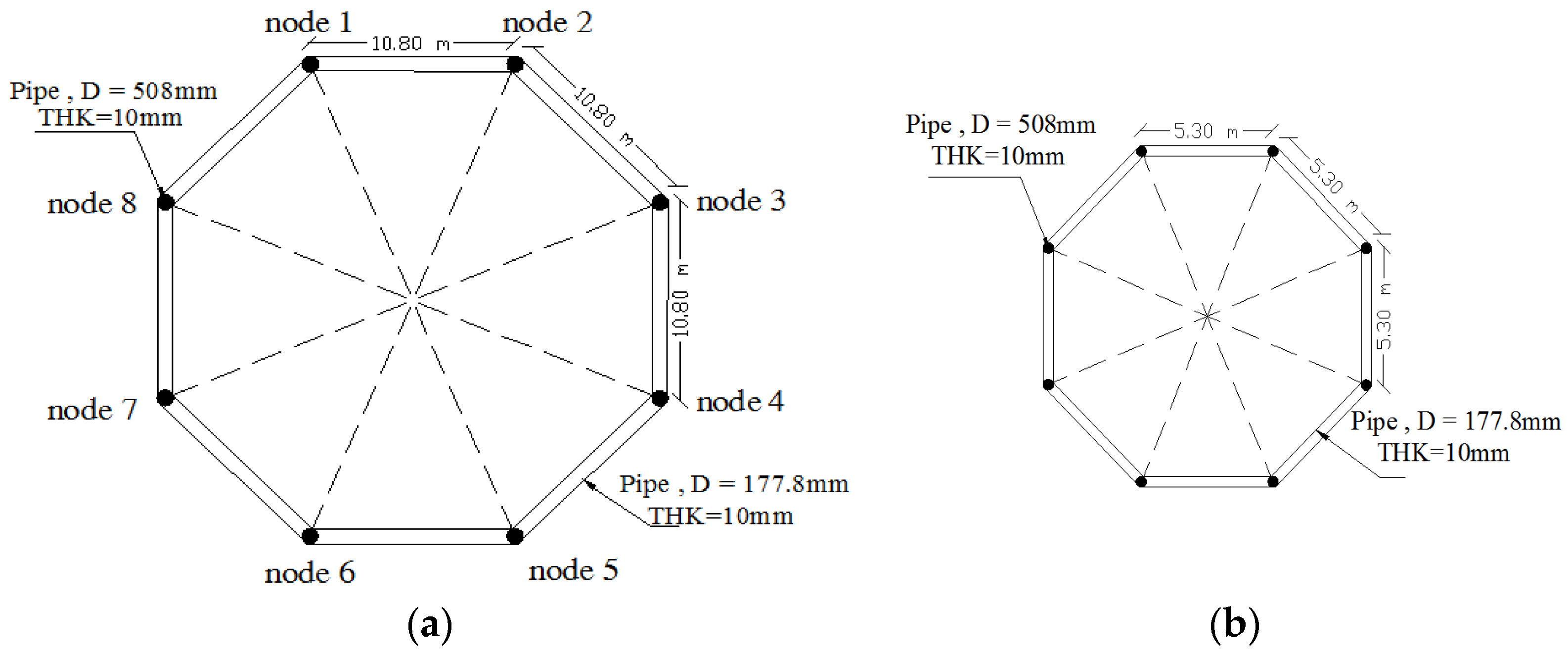
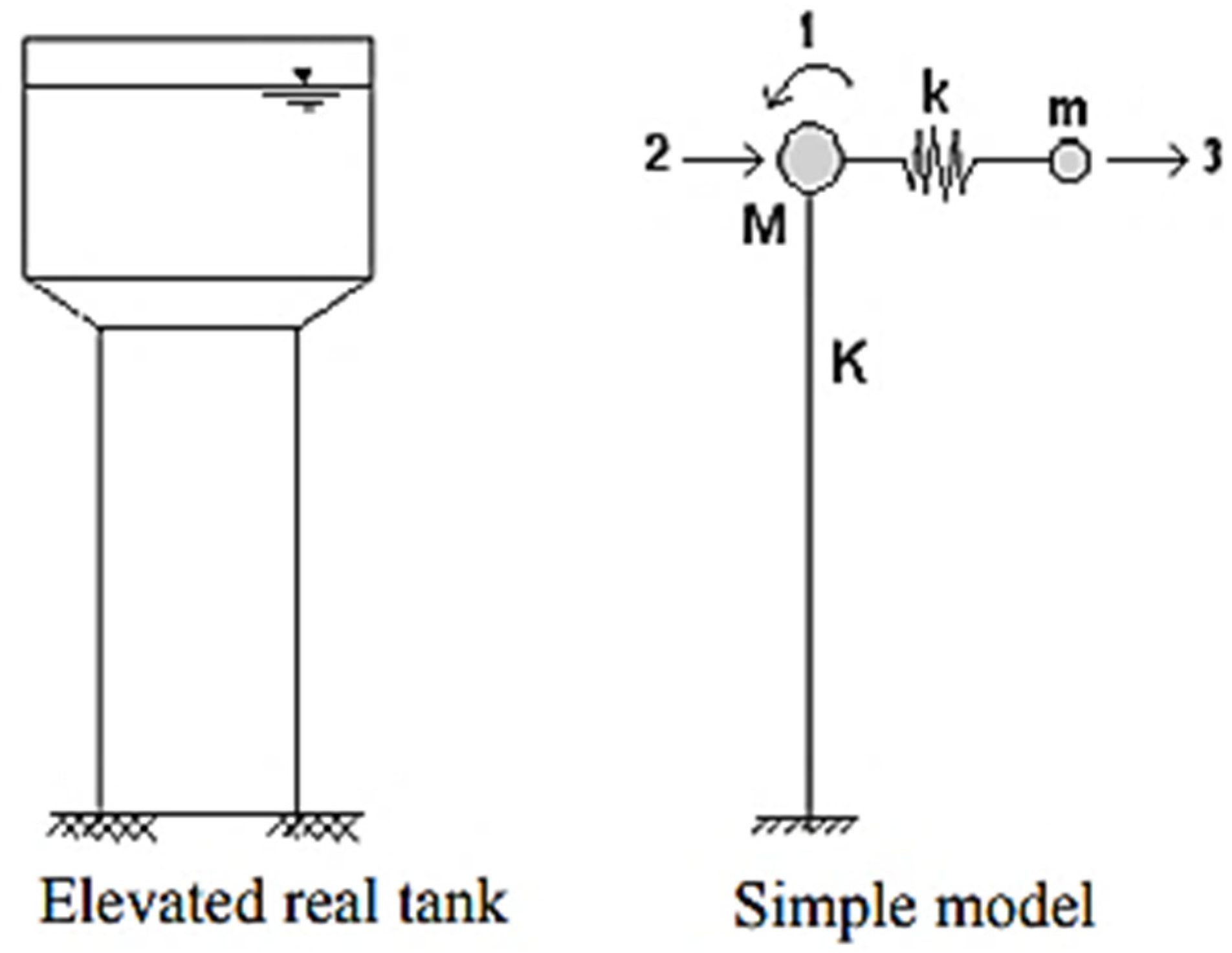
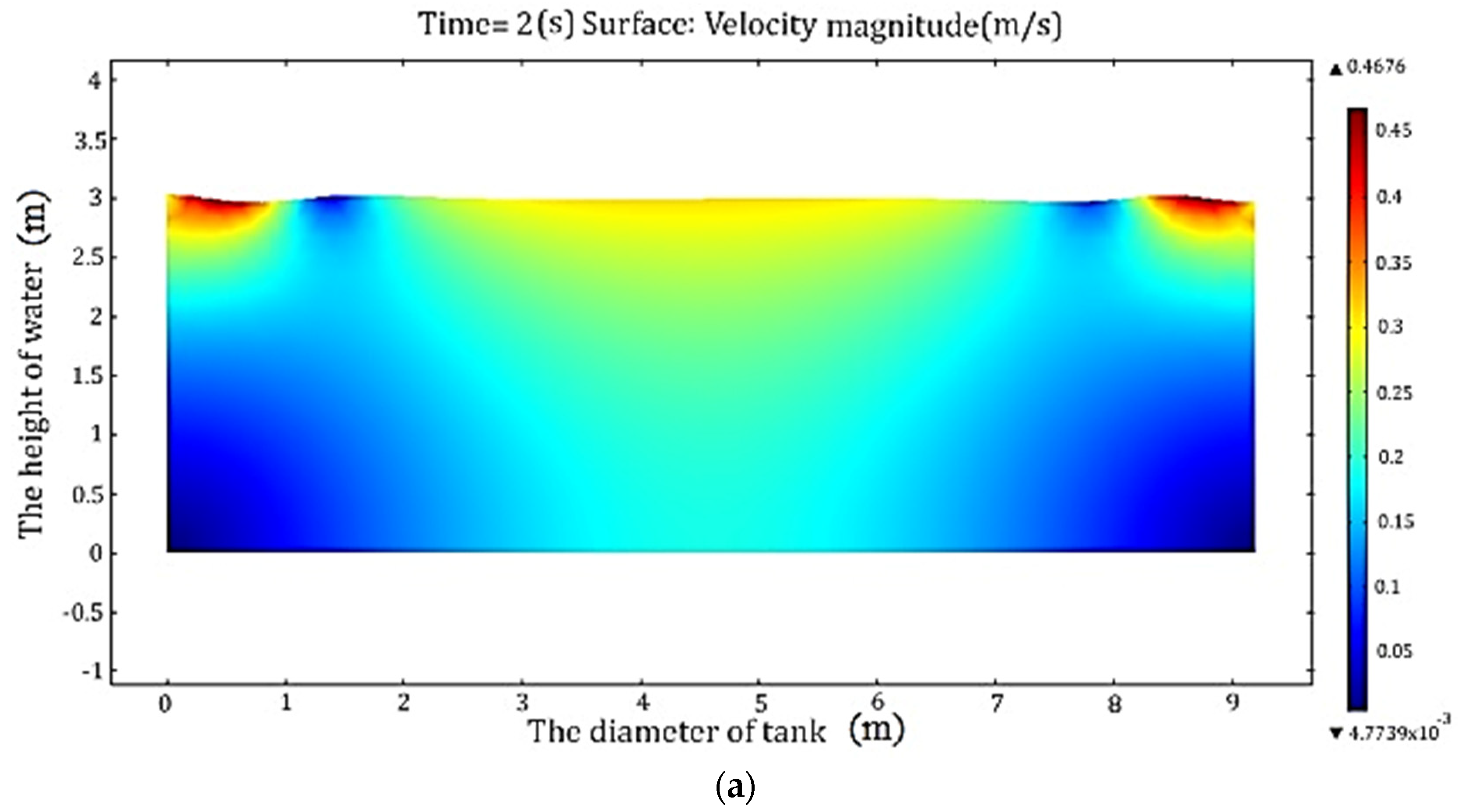
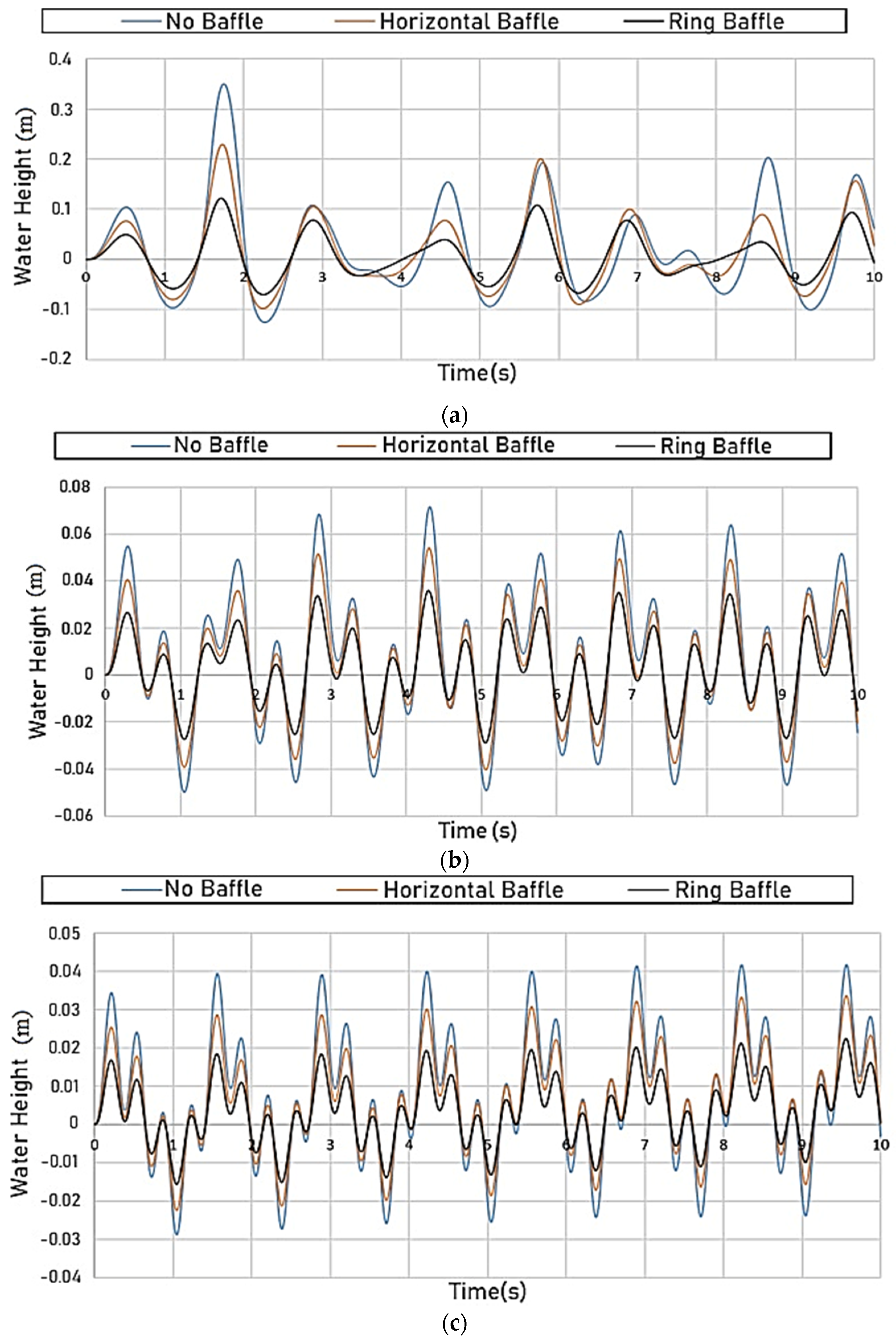
When fluid damping is insufficient for reducing sloshing, as the viscosity of fluid is near resonance, baffles can be effective as tools for reducing the impact of dynamic loads [2]. Preventing the creation of an oscillating fluid mode using baffles dates back to the studies on fuel tanks in the National American Space and Aviation Center in the 1960s by Silveria et al. [3] and Abrahamson et al. [4]. Since then, valuable experimental and analytical studies about sloshing liquid have been published, including Miles [5], Welt and Modi [6], and Faltinsen [7,8]. Today, most researchers focus on using numerical methods such as finite element and boundary element analysis of sloshing events. In recent years, Biswal et al. investigated nonlinear sloshing in cylindrical and rectangular tanks with a baffle in the two-dimensional case using the finite element method [9]. Pal and Bhattacharya examined the numerical scheme for the analysis of liquids sloshing in a tank partially filled with liquid under earthquake excitation and validated the results using experimental data [10]. The study showed that utilizing a baffle considerably reduces the sloshing pressure. Curadelli et al. examined the dynamic response of an elastic spherical tank partially filled with liquid and subjected to a horizontal ground motion [11]. In their study, the baffle was used for liquid sloshing damping. They showed that the blade damper could effectively reduce liquid and tank hydrodynamic load fluctuations, and the blade could hardly improve the tank simultaneously. Askari and Daneshmand [12] and Askari et al. [13] studied the effect of baffles on the dynamic properties of a cylindrical tank partially filled with liquid. Xue and Lin developed a 3D numerical model to examine the liquid sloshing in a prismatic tank under conditions close to resonant frequency excitation [14]. The numerical experiments proved that the developed 3D numerical model was robust in handling fluid–structure interaction and the ring baffle was an effective tool in reducing violent sloshing amplitude. Wang et al. obtained the liquid sloshing’s natural frequencies and mode shapes in a rigid cylindrical container with multiple baffles of the same inner radius using a semi-analytical approach [15]. They observed that the natural frequencies increased with the rise in the inner radius of the baffles. The uppermost baffle effects on natural frequencies and modes were much more significant than the other baffles. Goudarzi and Sabbagh-Yazdi conducted an experimental and analytical investigation of hydrodynamic damping resulting from lower and upper mounted vertical baffles and horizontal baffles in partially filled rectangular tanks [16]. According to the experimental results, horizontal baffles were most effective in all aspect ratios of the tanks. However, the horizontal baffles’ efficiency decreased as the liquid depths declined; but this is not the case in vertical baffles. Hasheminejad and Aghabeigi investigated the effects of surface-piercing or bottom-mounted vertical baffles on two-dimensional liquid sloshing characteristics in a half-full nondeformable horizontal cylindrical container with an elliptical cross-section [17]. The surface-piercing vertical baffle effectively reduced the antisymmetric sloshing frequencies, especially for lower-aspect-ratio tanks and higher modes. On the other hand, the bottom-mounted baffle greatly influenced the higher antisymmetric slosh modes only when its tip approached the liquid’s free surface. Increasing the vertical baffle extensions did not affect the symmetric modes, while it decreased the antisymmetric natural sloshing frequencies for both surface-piercing and bottom-mounted baffles. The result was in contrast with the horizontal side baffles, for which a boundless increase was observed in all the natural sloshing frequencies with the increasing baffle length. In addition, increasing the tank aspect ratio led to an overall decrease in natural frequencies for all three baffle configurations. Hasheminejad et al. examined a two-dimensional semi-analytic model based on the linear potential theory for transient sloshing in laterally excited horizontal annular containers for three common baffle configurations, a pair of liquid-surface-touching horizontal side baffles, a central surface-piercing vertical baffle, and a bottom-mounted vertical baffle [18]. The study showed that an increase in the baffle length for the tank with a pair of surface-touching side baffles led to a notable decrease in the upper bounds of the lateral force and moment coefficients. Goudarzi and Danesh established a finite volume-based estimate of hydrodynamic damping caused by vertical baffles in a rectangular tank subjected to seismic excitation [19]. Nayak and Biswal studied the influence of a submerged block on the impulsive and convective sloshing liquid response in a tank [20]. They systematically quantified the ground motion’s frequency content on the liquid tank’s nonlinear dynamic response. Shamsoddini et al. applied the incompressible SPH method, particle shifting algorithms, turbulence viscosity calculations, and free surface particle detectors for free surface flow modeling [21]. The results showed that the used algorithm effectively specifies free surface problems to simulate liquid sloshing phenomena with the aim of vertical and horizontal baffle effects on the control and damping of liquid sloshing. They showed that the horizontal and vertical baffle size and the horizontal baffle base position played a major role in sloshing fluctuation damping. Shamsoddini and Abolpur studied the effects of baffles on water sloshing at the time of liquid tank transportation [22]. They used the Incompressible Smoothed Particle Hydrodynamics (ISPH) numerical method to model the phenomenon. They approved the ability of the present algorithm for simulating shallow water sloshing by comparing it with experimental data. The results showed that the number of baffles has a major role in sloshing fluctuation damping. Wang et al. studied the effects of multiple porous baffles on the liquid sloshing problem in the horizontal rectangular, annular, or elliptical annular tanks by using the isogeometric boundary element (IGABEM), which coupled the Boundary Element Method (BEM) with the isogeometric boundary based on Non-Uniform Rational B Splines (NURBS). In this research, the effects of the tank’s geometry, liquid filling level, and the baffle’s parameters with various lengths, submergence depths, number of baffles, and porosities on the sloshing characteristics were discussed [23]. Guan et al. used the nonlinear Boundary Element Method (BEM) with Green’s theorem based on the potential in a three-dimensional tank under horizontal excitation and roll excitation to investigate the effect of different baffles on the sloshing phenomenon [24]. Their research showed that the horizontal baffle is more effective when the tank is under a roll excitation, while the vertical baffle is more effective in reducing the sloshing amplitude when the tank is under a horizontal harmonic excitation. Hajimehrabi et al. [25] investigated the effects of baffles on the seismic behavior of concrete cylindrical tanks. Three types of tanks with different aspect ratios, including short, medium, and tall structures, were examined under nine earthquake ground motions. Seismic fragility curves and the bending moment of the tank wall at the base were calculated. They concluded that although using baffles decreases the sloshing wave height, it results in a minor increase in the base bending moment of the tank wall. Cho et al. [26] investigated the dynamic response characteristics of the cylindrical-baffled liquid storage tank, which was subjected to a vertical acceleration at boosting concerning the number of baffles. They concluded that introducing baffles to the partially filled liquid tank remarkably decreases the maximum values of displacement and effective stress at both the bottom plate and baffles. Hosseinzadeh et al. [27] studied the annular baffle effects as anti-sloshing damping devices to reduce fluid wave sloshing height in steel storage tanks typically used in oil and petrochemical complexes during an earthquake. They confirmed significant effects of the annular baffles in reducing the fluid wave sloshing height as sloshing-dependent variable dampers.

Previous literature has reported the effect of the baffle and tank shape on seismic behavior without considering the tank body’s flexibility and rigidity. In this study, the effect of horizontal and annular baffles as passive control on the dynamic response of elevated storage tanks was investigated flexibly and rigidly by connecting flexible tower modes using the finite element method. Indeed, such a solution may be cheaper than conventional [28,29] and innovative [30,31] passive control strategies. The codes were written in Abaqus software, and the analysis of fluid and structure interaction was performed in three-dimensional mode using no baffle and baffle-equipped cases. Subsequently, horizontal and annular tanks were investigated under the effect of earthquake forces.

2. The Case Study

This study considered a cylindrical steel-elevated storage tank (9.2 m in diameter, 6 m in height, and 0.02 m in thickness). The elevated storage tank was mounted on the frame structure, where the frame’s peripheral beams attached its columns in 14.25, 25.5, and 34.35 m above ground. The container system tank was a bracing frame consisting of beams and columns located on a conical frustum’s lateral surface. The base and top radii of the conical frustum were 13 and 4.6 m, respectively. In this study, two types of horizontal and annular baffles were used (i.e., the horizontal baffle was 1.80 m long, 1.80 m wide, and 0.005 m thick, and in the annular baffles, the baffle ring had a width of 1.80 m and a thickness of 0.005 m). Figure 1 shows the schematic view of an elevated storage tank half-filled with fluid and equipped with a baffle, and Figure 2 shows the arrangement of columns and beams in the tower. In addition,

Table 1. Profile sections tank tower (mm).

Diagonal	Area	Thickness	Steel Pipes
139.70	26.40	6.30	Bracing
177.80	52.70	10	Beam
508	156	10	Column

presents the details of the tower sections used in this study.

3. Numerical Modeling

Abaqus software was used to model the elevated storage tank. The physical characteristics and modeling of rigid and flexible tanks were the same for both cases. The difference here was that in the rigid elevated storage tank, the truss tower connected to the bottom of a cylindrical tank was defined as relatively rigid. An algorithm in Abaqus software defines the rigid connection to the tank and the bottom of the tower. Meanwhile, COMSOL Multiphysics software was used to model the sloshing in the tank where this software has a moving mesh feature to model the fluid sloshing phenomenon accurately.

The convergence test’s importance is such that critical areas are identified after the completion of the first analysis and evaluation of stress values and damage model in the mesh model. It was intended to achieve the optimal mesh size in critical areas by changing the mesh due to the sensitivity of the results to the defined mesh and the need to consider the time phases of the analysis and the optimal time spent. This optimal size for the mesh was shaped once the larger size affected the quantity and quality of the results, whereas the smaller size did not alter the response. In this study, concerning the water–structure interaction, the size of meshes from 30 cm to 3 cm was examined (see

Table 2. The examined mesh sizes from 30 cm to 3 cm.

Stress	Mesh Size (cm)	Model Name
34.89	30	A30
35.13	20	A20
35.64	10	A10
35.69	5	A5
35.69	3	A3

). As shown in Table 2, a mesh size of 10 cm was accurate enough as the stress did not change significantly, and therefore, a mesh size of 10 cm was selected.

Figure 3 shows the motion of the mesh inside the tank using the software. To this end, conditions of tanks equipped with baffles and definitions of baffles coded using MATLAB software were used in COMSOL. Finally, a software output was imported to Abaqus and located under the horizontal and vertical seismic excitation spectrum.

3.1. Boundary Conditions

3.1.1. Boundary Conditions for the Fluid

There are two types of boundaries in the fluid model domain: three solid walls modeled with slip conditions and one free boundary (the top boundary) [32,33]. Using Navier–Stokes equations, the slip boundary condition is:

$$u.n=0$$

(1)

where $n={\left(nx,ny\right)}^{\mathrm{T}}$ is the normal boundary vector. In this boundary, the fluid is free to move on the top boundary, and the stress in the surrounding environment is neglected; therefore, the stress continuity condition on the free boundary is:

$$\left(-pI+\mathsf{\eta }\left(\nabla \mathrm{u}+{\left(\nabla \mathrm{u}\right)}^{\mathrm{T}}\right)\right).n=-p_{0}n$$

(2)

where $p_0$ is the surrounding (constant) pressure and η is fluid viscosity. For this model, $p_0=0$, without the loss of generality.

3.1.2. Boundary Conditions for the Mesh

To follow the motion of liquid with the moving mesh, it is necessary to (at least) couple the mesh motion to the fluid motion, which is normal to the surface. For this type of free surface motion, it is crucial not to couple the mesh motion in the tangential direction with the fluid motion. Therefore, the boundary condition for the mesh equations on the free surface is:

$${\left(x_t.y_t\right)}^T.n=u.n$$

(3)

where n is the boundary normal and ${\left(x_t.y_t\right)}^T$ is the mesh velocity. The moving mesh must be free near the wall in a tangential direction for the fluid’s motion and the mesh’s motion to follow each other. In the moving mesh interface, the global coordinate system specifies the boundary condition and sets the mesh displacement to zero in the x-direction. The mesh is fixed at the bottom of the tank. A similar result can be obtained by setting the mesh displacements to zero in both the x and y directions.

3.2. The Governing Equations of Fluid Behavior

The structure of the tank is modeled using fluid motion by incompressible Navier–Stokes equations. Because the liquid has a free surface, the ALE (Arbitrary Lagrangian–Eulerian) technique is well suited for addressing such models. Surface tension effects are ignored in this model. The model describes the fluid dynamics using incompressible Navier–Stokes expressed using the following equations:

$$\rho \frac{\partial u}{\partial t}+\rho u.\nabla u-\nabla .\left(-pI+\mathsf{\eta }\left(\nabla u+{\left(\nabla u\right)}^{\mathrm{T}}\right)\right)=F$$

(4)

$$\nabla u=0$$

(5)

where ρ is the density, $u=\left(u,v\right)$ is the fluid velocity, p is the pressure, I is the unit diagonal matrix, η is the viscosity, and F is the volume force. The force exerted by the gravity vector is expressed as:

$$Fx=\rho gsin\left(\mathsf{\phi }\max \ast sin\left(2\pi \omega t\right)\right)$$

(6)

$$Fy=-\rho gcos\left(\mathsf{\phi }\max \ast \sin \left(2\mathsf{\pi }\mathsf{\omega }\mathrm{t}\right)\right)$$

(7)

where φ max is the vertical angle of the tank. These equations can be solved by defining the free motion of deformed meshes. The fluid considered in this study was water with a density of 1000 kg/m³.

In turbulence issues, the fluid can be considered incompressible and nonviscous. A practical method for fluid modeling in ABAQUS/Explicit is to use the Newtonian shear viscosity model and the US-UP linear equation. The bulk functions act as correction parameters for fluid incompressibility constraints. As the turbulence of the fluid inside the water tank is free and unconstrained, the bulk modulus can be considered two to three times smaller than the actual value, and the fluid can still behave in an incompressible way. The shear viscosity acts as a corrective parameter to neutralize the shear modes that cause mesh failure. Because water is a nonviscous fluid, the shear viscosity of the fluid must be considered small. High shear viscosity results in highly rigid responses. The value of suitable viscosity can be calculated based on the value of the bulk modulus. The properties of the water are given in

Table 3. Properties of the water.

	Variable	Value
1	Density (kg/m3)	1000
2	Viscosit (N·s/m3)	0.001
3	Sound velocity in water (m/s)	1450
4	Curve slope	0

.

3.3. Loading Protocol

In the dynamic analysis, Koyna’s (1967) ground acceleration, Kobe, and Cape Mendocino were applied to the rigid elevated storage tank without a baffle. The results obtained from maximum base shear are shown in

Table 4. Maximum base shear of the tanks (kN).

Earthquake Name	Horizontal Base Shear	Vertical Base Shear
Koyna	125	172
Kobe	90	124
Cape Mendocino	110	128

. A detailed study of the base shear of tanks illustrated that the maximum base shears values were obtained in the Koyna earthquake. According to Table 4, only the quake-induced earthquake results are discussed below.

Figure 4 shows the Koyna (1967) ground acceleration used for dynamic analysis of elevated storage tanks (with horizontal and annular baffles and with no baffle) in this study. In this study, a tank state that is half full of liquid was considered.

The natural frequency of the water tank was calculated as a result of interaction between stored water and the structure with respect to the following calculation. Figure 5 shows the representative model of the elevated tank with respect to the interaction between stored water and the structure.

The stiffness and mass matrices of the system are:

$$K_s=\left[\begin{array}{ccc}{K}_{\theta }& K_{\theta \delta }& 0\\ K_{\theta \delta }& K+k& -k\\ 0& -k& k\end{array}\right]$$

(8)

$$M_s=\left[\begin{array}{ccc}0& 0& 0\\ 0& M& 0\\ 0& 0& m\end{array}\right]$$

(9)

where $k$ is the stiffness associated with the convective mass; $K$ is the lateral stiffness of the structure; $K_{\theta }$ is the flexural stiffness of the structure; $K_{\theta \delta }$ is the rotational transition stiffness; $M$ is the mass of the structure; and $m$ is the convective mass associated with the mobile water.

Resolving the eigenvalues problem $\left|K_s-{\omega }^2{M}_s\right|=0$,

$${\omega }^4\left(Mm\right)-{\omega }^2\left(Mk+Km+km\right)+Kk=0$$

The variable $K_A$ is defined as $K_A=K+k$,

$${\omega }^2=\frac{+\left(Mk+K_{A}m\right)\mp \sqrt{{\left(Mk+K_{A}m\right)}^2-4\left(Mm\right)Kk}}{2Mm}$$

(10)

$${\omega }^2=\frac{1}{2}\left[\left(\frac{k}{m}+\frac{K_A}{M}\right)\mp \sqrt{{\left(\frac{k}{m}+\frac{K_A}{M}\right)}^2-4\frac{K}{M}}\frac{k}{m}\right]$$

(11)

By defining the following parameters

$$\sqrt{\frac{k}{m}}=W_a\mathrm{frequency}\mathrm{of}\mathrm{vibration}\mathrm{of}\mathrm{the}\mathrm{water}$$

(12)

$$\sqrt{\frac{K}{M}}=W_e\mathrm{frequency}\mathrm{of}\mathrm{vibration}\mathrm{of}\mathrm{the}\mathrm{structure}$$

(13)

$$\sqrt{\frac{K_A}{M}}=W^2{}_{ea}\mathrm{frequency}\mathrm{of}\mathrm{vibration}\mathrm{of}\mathrm{the}\mathrm{structure}\text{-}\mathrm{water}\mathrm{coupling}$$

(14)

subsequently,

$$W=\sqrt{\frac{1}{2}}\left[\left(W^2{}_a+W^2{}_{ea}\right)\mp \sqrt{{\left(W^2{}_a+W^2{}_{ea}\right)}^2-4W^2{}_e{W}^2{}_a}\right]$$

(15)

where $W$ is the frequency of vibration of the water–structure system. Equation (15) allows the analysis of 2 particular cases of the interaction that exists between stored water and the structure.

4. Results and Discussion

The analysis results of hydrodynamic pressure on the baffle, sloshing amplitude and frequency, and base shear areas are as follows.

4.1. Hydrodynamic Pressure

Earthquakes cause liquid sloshing in the tank, resulting in increased wall pressure compared to the hydrostatic pressure of the wall, which is considered equal to the hydrodynamic pressure. To investigate the baffle’s effect in the tank on the hydrodynamic pressure, fluid velocity, and sloshing in different parts, the cross-sectional detail of the tank is shown in Figure 6. According to Figure 5, the tank’s hydrodynamic pressure is compared at points 1 and 12 without a baffle.

The hydrodynamic pressure in the tank with no baffles and with baffles are presented in Figure 7 and Figure 8, respectively.

The results in Figure 6 show that the maximum hydrodynamic pressure is decreased to 50.1% in the tank equipped with a baffle, compared to the tank without a baffle.

Figure 7 indicates that the hydrodynamic pressure in the left and right baffles is the same, almost equal to that pressure at points 12 and 1. This confirms that using baffles in the tank leads to an equal distribution of hydrodynamic pressure.

4.2. Sloshing of the Fluid Surface

The two-dimensional diagrams of fluctuations on the tank’s fluid surface with/without baffles are provided at 2, 5, and 6 s in Figure 9, Figure 10 and Figure 11. Each graph shows the surface sloshing of the fluid at a specific time, where the horizontal axis shows the diameter of the tank and the vertical axis represents the height of fluid in the tank. These graphs show that fluid motion is active above the baffle in the tank equipped with a baffle, while the motion below the baffle is considerably weakened. In addition, the vortex created around the baffle is evident, which leads to fluid energy loss.

The effect of baffles on the sloshing of fluid surface diagrams for tanks equipped with/without baffles is illustrated in Figure 12, which compares the sloshing changes at points 6 and 7. These comparisons represent the reduction in maximum sloshing of the fluid surface down to 16.20% for the tank equipped with baffles.

4.3. Sloshing Fluid Velocity

The effect of utilizing baffles on changes in fluid velocity in the tanks with/without baffles is shown in Figure 13, which compares the changes in fluid velocity at points 6 and 7. These comparisons indicate a reduction in maximum fluid velocity oscillation to 12.77% in the tank equipped with a baffle compared to the tank without a baffle.

4.4. Evaluating the Effect of the Baffle on the Frequency Content

The effect of baffles on the frequency content of the tank is investigated, as shown in Figure 14. Changes in the fluid surface height are shown at frequencies ω = 1~4 Hz for the three cases: a tank with no baffle, a tank with a horizontal baffle, and a tank with an annular baffle. In

Table 5. Decrease in the fluid surface height at different frequencies with the baffle.

Frequency (Hz)	No Baffle (m)	Maximum Reduction (%)	Horizontal Baffle (m)	Maximum Reduction (%)	Annular Baffle (m)
1	0.350	34.57	0.229	65.14	0.122
2	0.072	25	0.054	50	0.036
3	0.042	19.05	0.034	47.62	0.022
4	0.031	25.80	0.023	54.84	0.014

, the fluid surface sloshing height reductions at frequencies 1 to 4 Hz are compared in the cases with baffles (horizontal and annular) and with no baffles. According to the figures and tables, using a baffle decreases the height of free-surface turbulence in the tank. Meanwhile, the results confirm that the annular baffle leads to more reduction in the free-surface turbulence height than the horizontal baffle. It is noteworthy to mention that the effect depends entirely on the frequency content of the applied load.

4.5. Shear Force in a Rigid and Flexible Elevated Storage Tank

Baffles affect the hydrodynamic force exerted on rigid walls of the tank, thus affecting the shear forces. The shear force in the tank support is shown in Figure 15 for the three cases, including the rigid tank without a baffle, the rigid tank with a horizontal baffle, and the rigid tank with an annular baffle, following the ground acceleration record. Figure 16 depicts the maximum base shear forces comparison for the three cases.

Figure 17 demonstrates the stress in the rigid elevated storage tank equipped with an annular baffle, analyzed using Abaqus software.

Table 6. Base shear (KN) maximum percentage reduction in a rigid elevated storage tank.

Node	No Baffle	Horizontal Baffle	Maximum Reduction (%)	Annular Baffle	Maximum Reduction (%)
Node 1	125.30	118.81	5.18	98.28	21.56
Node 2	87.72	81.37	7.24	65.17	25.71
Node 3	82.60	74.55	9.75	59.67	27.76
Node 4	30.56	28.19	7.76	26.31	13.91
Node 5	130.34	123.29	5.41	88.75	31.90
Node 6	89.60	83.71	6.57	69.42	22.52
Node 7	88.51	79.52	10.16	68.24	22.90
Node 8	31.14	28.65	8.00	26.37	15.32

summarizes the shear forces in all investigated nodes in a rigid elevated storage tank. The results show that the maximum base shear force declines to 31.9% in the rigid tank equipped with an annular baffle compared to the no baffle tank. This reduction for the tank with the horizontal baffle equals 10.16%.

Figure 18 shows the shear force in the flexible tank for the three cases, including the tank with no baffle, the tank with a horizontal baffle, and the tank with an annular baffle. A comparison of the maximum base shear forces is also provided for the three cases in Figure 19.

Figure 20 shows the stress in a flexible elevated storage tank with a horizontal baffle resulting from Abaqus software.

Table 7. Base shear (KN) maximum percentage reduction in a flexible elevated storage tank.

Node	No Baffle	Horizontal Baffle	Maximum Reduction (%)	Annular Baffle	Maximum Reduction (%)
Node 1	141.92	137.50	3.11	117.51	17.20
Node 2	103.38	100.73	2.56	89.96	12.98
Node 3	77.40	72.81	5.93	60.37	22.00
Node 4	38.98	37.74	3.18	35.42	9.13
Node 5	144.20	139.62	3.18	118.11	18.09
Node 6	104.80	102.11	2.57	90.25	13.88
Node 7	80.37	75.45	6.12	59.13	26.43
Node 8	39.32	38.08	3.15	35.51	9.69

summarizes the shear forces in all investigated nodes in a flexible elevated storage tank. The results show that the maximum base shear force declines to 26.43% in the flexible tank equipped with an annular baffle, compared to the tank with no baffles. This reduction equals 6.12% for the tank with a horizontal baffle.

5. Conclusions

In this study, to examine the baffle’s effects on elevated storage tanks’ dynamic response, both flexible and rigid tanks are considered connected to a flexible tower. The code writing is performed for the moving fluid in the tank with baffles. The codes are written in Abaqus software, and the analysis of fluid and structure interaction is performed in three-dimensional mode using no baffle and baffle-equipped cases. Horizontal and annular tanks are investigated under the effect of earthquake forces. The results of the analysis show that:

(1)

A baffle creates a place for energy dissipation in the tank. It divides the fluid mass into several smaller subdivisions in the tank and reduces the mass flow oscillation. On the other hand, the oscillating motion of steamy fluid forms a vortex around the blade by oscillating the baffle mounted on the tank wall, and the vortex is associated with fluid energy dissipation.

• Compared to the horizontal baffle, the annular baffle is more capable and effective in reducing the oscillation parameters. This is because of the expansion of the cylindrical tank with annular blades instead of merely focusing on its walls. The walls absorb and dissipate the energy.

(2)

Compared to the tank with no baffles, the oscillation parameters, including amplitude oscillatory waves, oscillating velocity, and hydrodynamic pressure, decrease in the tank equipped with baffles.

• Mounting baffles on an elevated storage tank reduces the maximum amplitude of oscillations in the fluid surface to 16.20%.
• Horizontal and annular baffles reduce the vertical component of the fluid velocity and decrease the oscillations’ velocity in the tank.
• Compared to the tank with no baffle, the maximum rate of fluid velocity is reduced to 12/0.77% for the tank equipped with a baffle.
• Mounting baffles on the tank effectively reduces the hydrodynamic pressure. A baffle mounted on the elevated storage tank reduces the maximum rate of hydrodynamic pressure to 50.1%.

(3)

The results show that by installing a baffle on the tank, the height of the fluid surface at different frequencies is reduced. The maximum values of this reduction for the annular and horizontal baffles reach 65.11% and 34.57%, respectively.

(4)

Depending on the type of baffle (horizontal or annular), the baffle on the tank reduces the base shear forces.

• The maximum base shear force reduction in rigid elevated storage tanks equipped with annular and horizontal baffles compared to the tank without baffles is 32.9% and 10.16%, respectively.

The maximum base shear force reduction in flexible elevated storage tanks equipped with annular and horizontal baffles compared to the tank without baffle is 26.43% and 9.61%, respectively.