Study on Wind Loads of Different Height Transmission Towers under Downbursts with Different Parameters
Abstract
:1. Introduction
2. Wind Load Model and Parameters
2.1. Wind Field Model
2.1.1. Boundary Layer Wind
2.1.2. Downburst
Mean Wind
Turbulent Wind
3. Transmission Tower Model Parameters
4. Calculation Results and Analysis
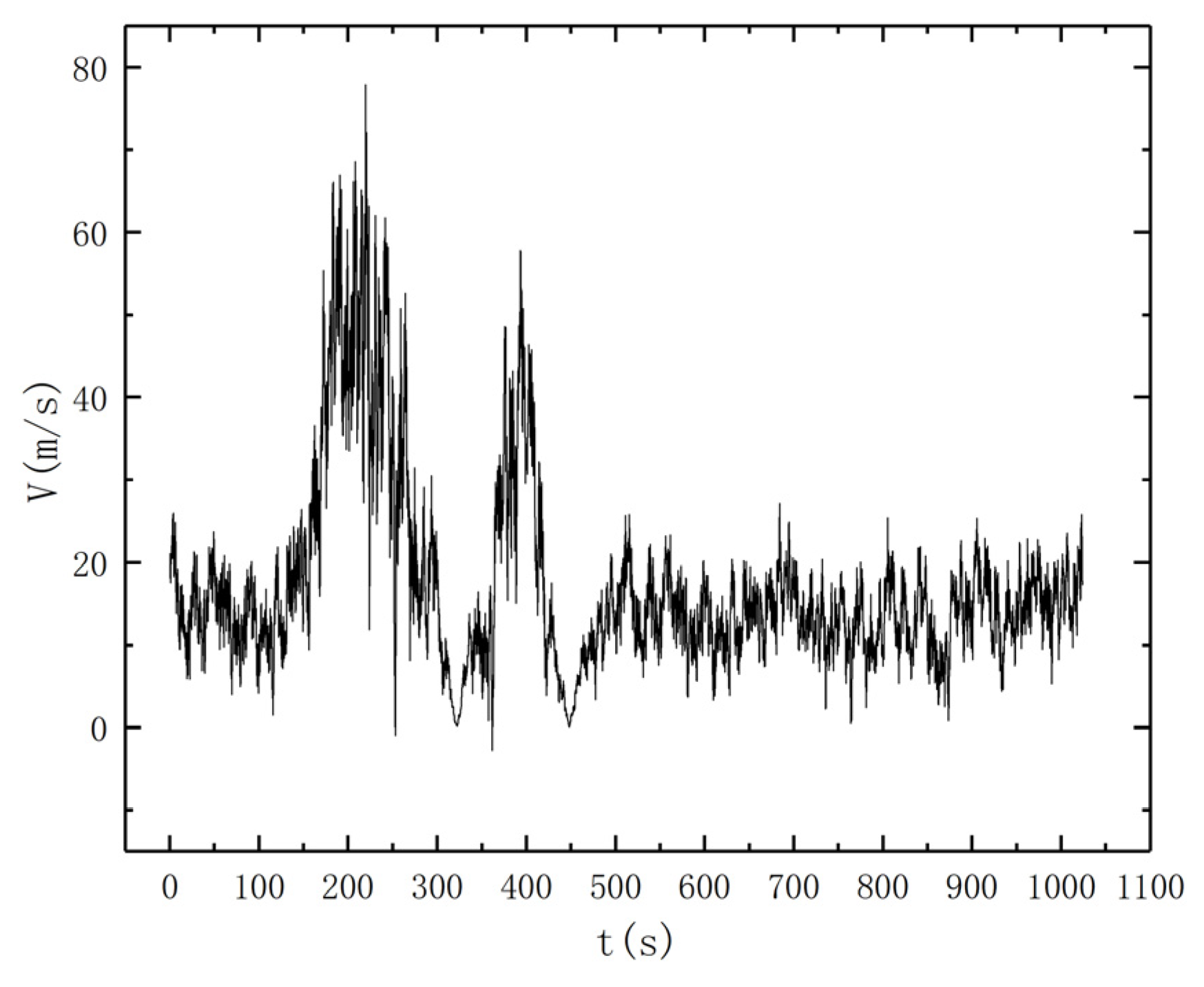
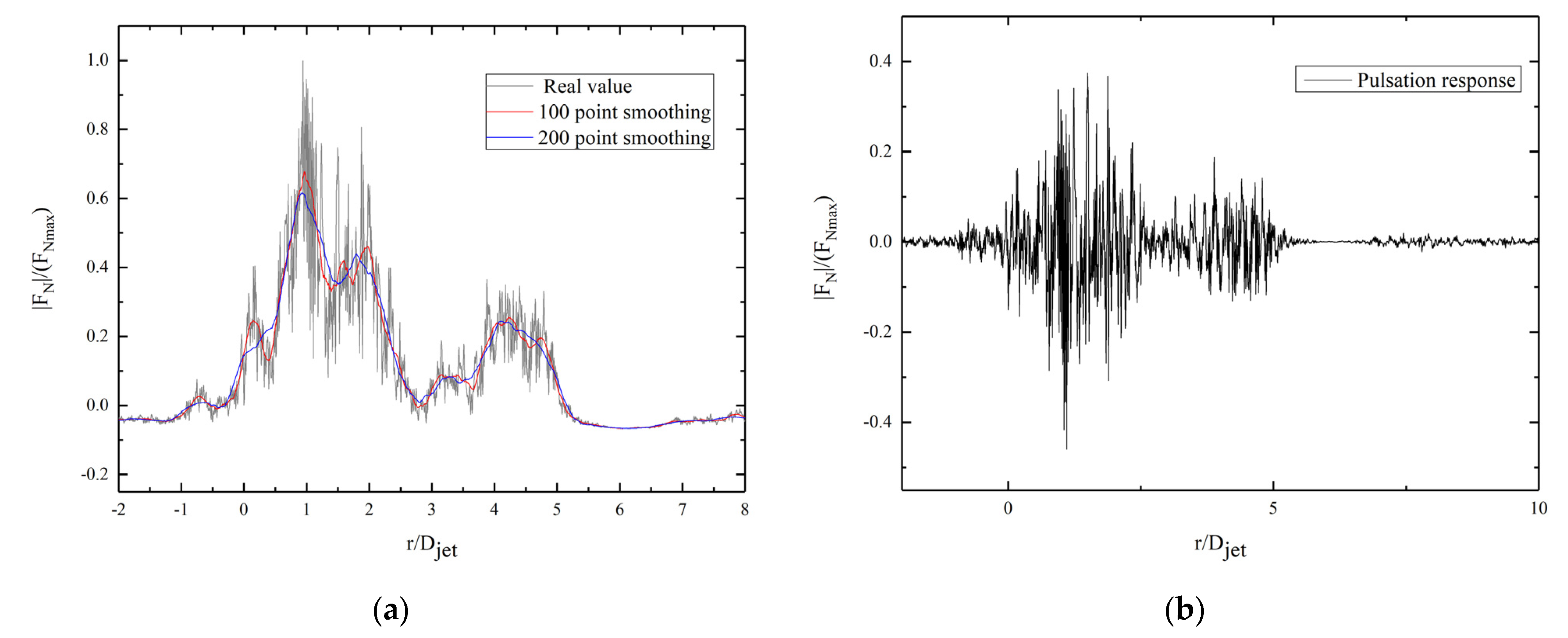
4.1. Wind Field Parameter Analysis
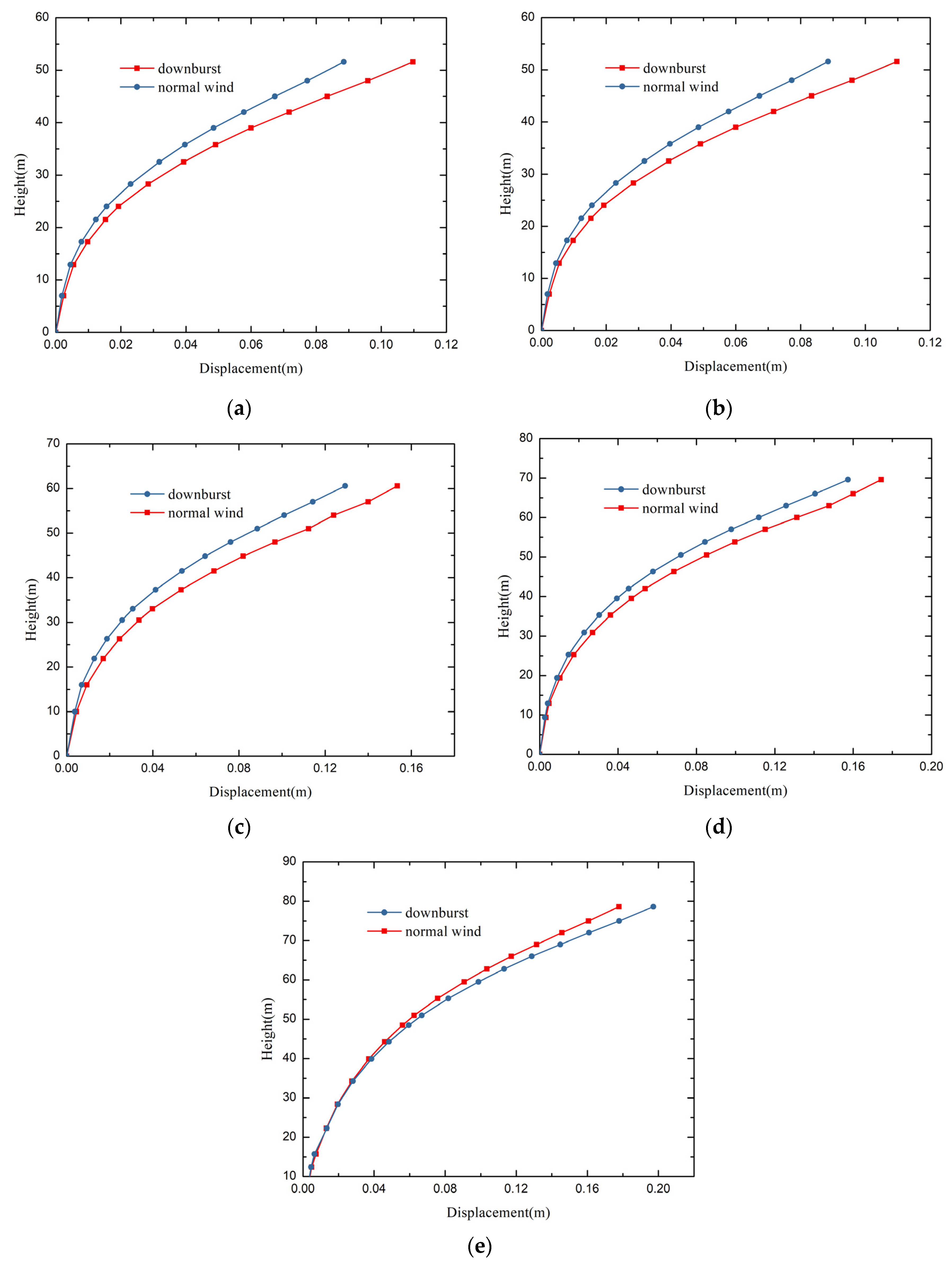
4.2. Comparison of the Effects of Downburst and Ordinary Boundary Wind
4.2.1. Static Response
4.2.2. Dynamic Response
4.3. Comparison of the Effects of Unsteady and Steady Downburst
5. Conclusions
- (1)
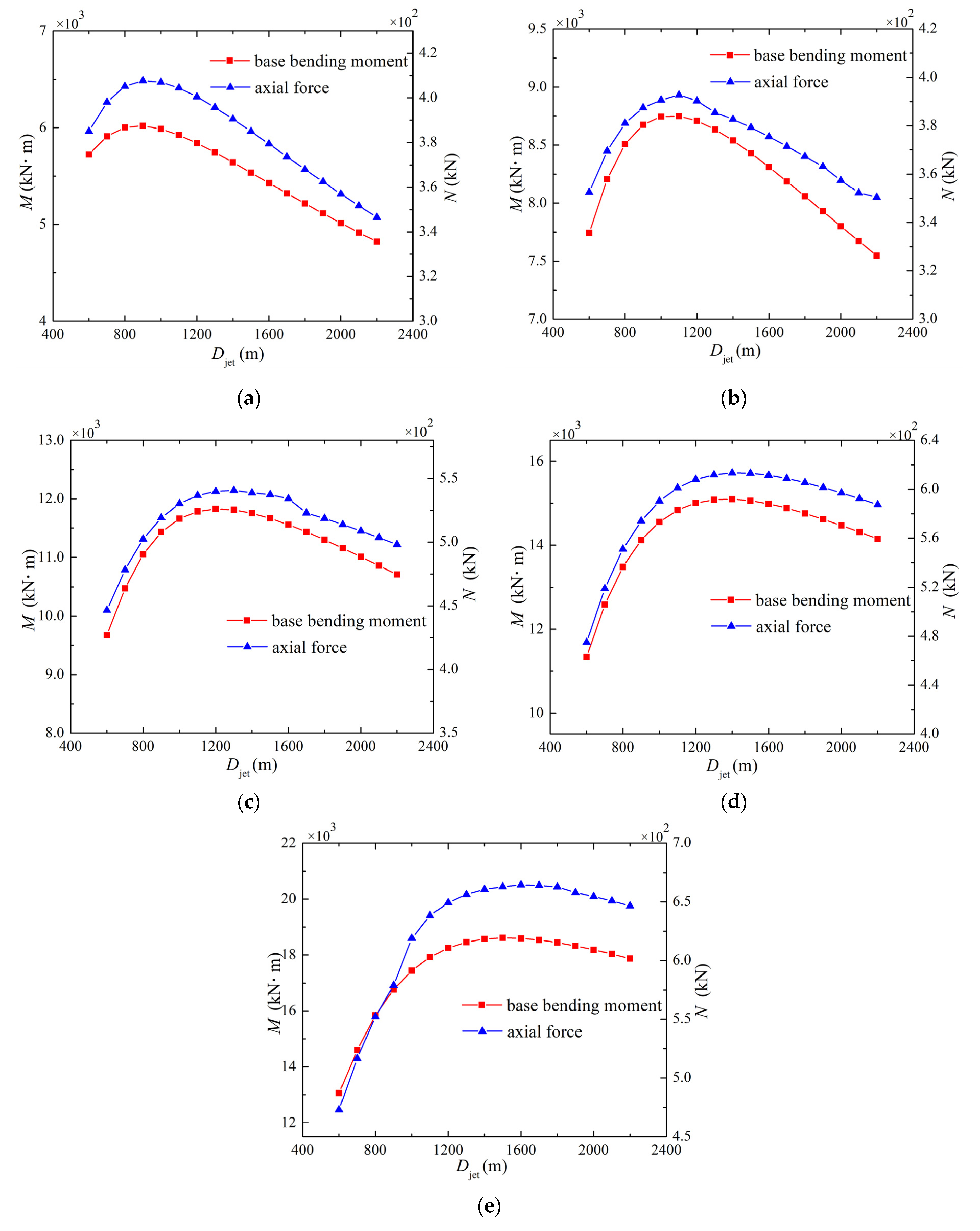
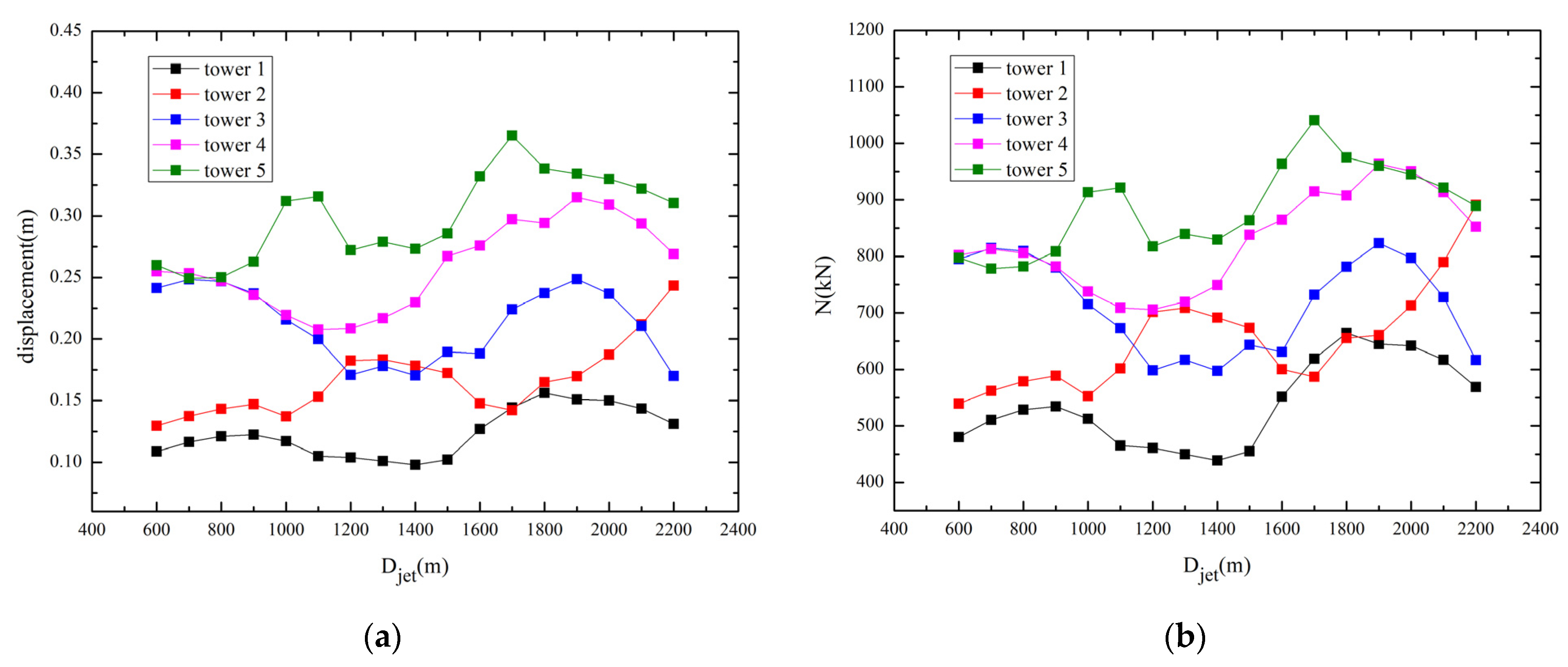
- When the transmission tower was located near r = 0.9–1.0 Djet, the impact of the downburst wind load was the greatest.
- (2)
- The wind load on the transmission tower first increased and then decreased with an increase in the downburst jet diameter. The jet diameter had similar effects on transmission towers of different tower heights, but the most unfavorable jet diameters of transmission towers with different tower heights were different. When r/Djet = 1.0, the most unfavorable jet diameters corresponding to towers with H = 45.5, 54.5, 63.5, 72.5 and 81.5 m were 900, 1100, 1300, 1400 and 1600 m, respectively.
- (3)
- When the height of the transmission tower was small, the downburst wind was more damaging to the transmission tower than the normal wind. The response ratio of the transmission tower under two types of wind fields was about 1.1 to 1.4. In the design, it is necessary to consider the effect of the downburst wind. When the transmission tower was taller, the normal wind was slightly more damaging to the transmission tower than the downburst. The response ratio of the transmission tower under two types of wind fields was about 0.91–1.01, and the effect of violent downburst wind was not considered.
- (4)
- Under the action of the moving downburst wind field, the response of the transmission tower did not change significantly with the change of storm parameters. Compared with the static wind field, the Djet corresponding to the most unfavorable load increased.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Haitham, A.; Amal, E.; Ayman, E.A.; Ashraf, E.D. Review on dynamic and quasi-static buffeting response of transmission lines under synoptic and non-synoptic winds. Eng. Struct. 2016, 112, 23–46. [Google Scholar]
- Wang, Z.; Wu, Y.; Fang, Z. Downburst wind field characteristics under moving effect. J. Vib. Shock 2019, 38, 32–38. [Google Scholar]
- Sun, Q.; Wu, J.; Wang, D.; Sun, X. Analysis of the Quasi-Static Buffeting Responses of Transmission Lines to Moving Downburst. Comput. Modeling Eng. Sci. 2020, 124, 287–302. [Google Scholar] [CrossRef]
- Holmes, J.D.; Hangan, H.M.; Schroeder, J.L.; Letchford, C.W.; Orwig, K.D. A forensic study of the Lubbock-Reese downdraft of 2002. Wind Struct. 2008, 11, 137–152. [Google Scholar] [CrossRef]
- Mohamed, D.; Ashraf, E.D. Critical Parameters and Configurations Affecting the Analysis and Design of Guyed Transmission Towers under Downburst Loading. Pract. Period. Struct. Des. Constr. 2017, 22, 04016017. [Google Scholar]
- Yang, F.; Zhang, H.; Yang, J.; Dang, H.; Liu, J. Bearing Capacity Analysis and Load Values of Transmission Towers Under Thunderstorm Downburst. Proc. CSEE 2014, 34, 4179–4186. [Google Scholar]
- Dempsey, D.; White, H.B. Wind wreak havoc on lines. TD World Mag. 1996, 48, 32–42. [Google Scholar]
- Savory, E.; Parke, G.A.R.; Zeinoddini, M.; Toy, N.; Disney, P. Modelling of tornado and microburst-induced wind loading and failure of a lattice transmission tower. Eng. Struct. 2001, 23, 365–375. [Google Scholar] [CrossRef]
- Chen, L.; Letchford, C.W. A deterministic-stochastic hybrid model of downbursts and its impact on a cantilevered structure. Eng. Struct. 2004, 26, 619–629. [Google Scholar] [CrossRef]
- Shehata, A.Y.; El Damatty, A.A.; Savory, E. Finite element modeling of transmission line under downburst wind loading. Finite Elem. Anal. Des. 2005, 42, 71–89. [Google Scholar] [CrossRef]
- Shehata, A.Y.; El Damatty, A.A. Behavior of guyed transmission line structures under downburst wind loading. Wind Struct. 2007, 10, 249–268. [Google Scholar] [CrossRef]
- Shehata, A.Y.; Nassef, O.; El Damatty, A.A. A coupled finite element-optimization technique to determine critical microburst parameters for transmission towers. Finite Elem. Anal. Des. 2008, 45, 1–12. [Google Scholar] [CrossRef]
- Chay, M.T.; Albermani, F.; Wilson, R. Wind loads on transmission line structures in simulated downbursts. Eng. Struct. 2006, 28, 240–254. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.L. Zhang, H.J. Two case studies on structural analysis of transmission towers under downburst. Wind Struct. 2016, 22, 685–701. [Google Scholar] [CrossRef]
- Damatty, A.E.; Hamada, A.; Elawady, A. Development of Critical Load Cases Simulating the Effect of Downbursts and Tornados on Transmission Line Structures. In Proceedings of the Eighth Asia-Pacific Conference on Wind Engineering, Chennai, India, 10–14 December 2013. [Google Scholar]
- Ji, B.; Qu, W.; Wang, L.; Zhao, E. Elastic-plastic buckling collapse analysis of transmission tower under downburst. China Saf. Sci. J. 2014, 24, 90–95. [Google Scholar]
- Wang, F.Y.; Xu, Y.L.; Qu, W.L. Multi-Scale Failure Analysis of Transmission Towers Under Downburst Loading. Int. J. Struct. Stab. Dyn. 2018, 18, 1850029. [Google Scholar] [CrossRef]
- Damatty, E.; Elawady, A. Critical load cases for lattice transmission line structures subjected to downbursts: Economic implications for design of transmission lines. Eng. Struct. 2018, 159, 213–226. [Google Scholar] [CrossRef]
- Elawady, A.; Aboshosha, H.; Damatty, E. Amal Aero-elastic response of transmission line system subjected to downburst wind: Validation of numerical model using experimental data. Wind Struct. 2018, 27, 71–88. [Google Scholar]
- Wood, G.S.; Kwok, K.C.S.; Motteram, N.A.; Fletcher, D.F. Physical and numerical modelling of thunderstorm downbursts. J. Wind Eng. Ind. Aerodyn. 2001, 89, 535–552. [Google Scholar] [CrossRef]
- Holmes, J.D.; Oliver, S.E. An empirical model of a downburst. Eng. Struct. 2000, 22, 1167–1172. [Google Scholar] [CrossRef]
- Hamada, A.; Damatty, A.A.E. Behaviour of guyed transmission line structures under tornado wind loading. Comput. Struct. 2011, 89, 986–1003. [Google Scholar] [CrossRef]
- Fang, Z.; Li, Z.; Wang, Z. Study on effect of storm movement on wind field characteristics of downburst. J. Build. Struct. 2019, 40, 166–174. [Google Scholar]
- Andi, X.; Massimiliano, B.; Giovanni, S. A general-purpose analytical model for reconstructing the thunderstorm outflows of travelling downbursts immersed in ABL flows. J. Wind Eng. Ind. Aerodyn. 2020, 207, 104373. [Google Scholar]

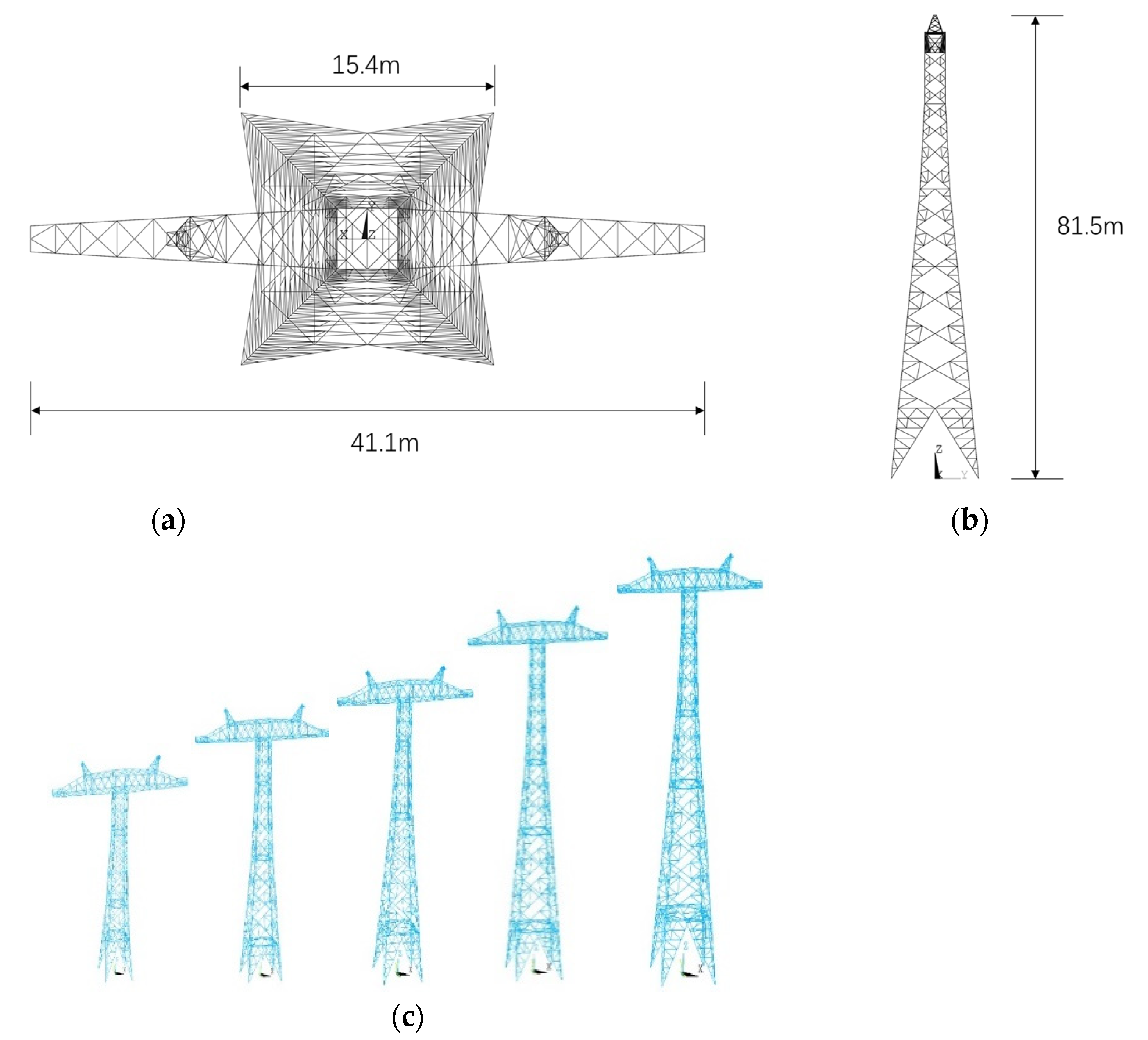



| Tower Number | 1 | 2 | 3 | 4 | 5 |
| Nominal Height (m) | 39 | 48 | 57 | 66 | 75 |
| Tower Height (m) | 45.5 | 54.5 | 63.5 | 72.5 | 81.5 |
| As/A | ≤0.1 | 0.2 | 0.3 | 0.4 | 0.5 | >0.6 |
| b/a ≤ 1 | 1.0 | 0.85 | 0.66 | 0.50 | 0.33 | 0.15 |
| b/a = 2 | 1.0 | 0.90 | 0.75 | 0.60 | 0.45 | 0.30 |
| Tower Number | Downburst (m) | Boundary Layer Wind (m) | Ratio |
|---|---|---|---|
| 1 | 6019.8 | 4150.2 | 1.45 |
| 2 | 8749.3 | 6403.1 | 1.37 |
| 3 | 13,229.2 | 10,162.3 | 1.3 |
| 4 | 15,735.1 | 13,404.5 | 1.17 |
| 5 | 18,597.6 | 18,234.9 | 1.01 |
| Tower Number | Downburst (m) | Boundary Layer Wind (m) | Ratio |
|---|---|---|---|
| 1 | 385.1 | 281.8 | 1.36 |
| 2 | 441.7 | 354.0 | 1.25 |
| 3 | 522.9 | 460.1 | 1.14 |
| 4 | 572.9 | 529.9 | 1.08 |
| 5 | 570.5 | 621.1 | 0.92 |
| Tower Height (m) | Downburst (m) | Boundary Layer Wind (m) | Ratio |
|---|---|---|---|
| 45.5 | 0.0752 | 0.0636 | 1.18 |
| 54.5 | 0.1097 | 0.0885 | 1.24 |
| 63.5 | 0.1535 | 0.1293 | 1.18 |
| 72.5 | 0.1643 | 0.1573 | 1.11 |
| 81.5 | 0.1778 | 0.1972 | 0.91 |
| Tower Height (m) | Downburst (kN) | Boundary Layer Wind (kN) | Ratio |
|---|---|---|---|
| 45.5 | 378.5 | 298.9 | 1.26 |
| 54.5 | 441.7 | 369.6 | 1.19 |
| 63.5 | 522.9 | 448.8 | 1.16 |
| 72.5 | 562.9 | 503.8 | 1.11 |
| 81.5 | 570.5 | 581.8 | 0.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yang, F.; Wang, Y.; Fang, Z. Study on Wind Loads of Different Height Transmission Towers under Downbursts with Different Parameters. Buildings 2022, 12, 193. https://doi.org/10.3390/buildings12020193
Wang Z, Yang F, Wang Y, Fang Z. Study on Wind Loads of Different Height Transmission Towers under Downbursts with Different Parameters. Buildings. 2022; 12(2):193. https://doi.org/10.3390/buildings12020193
Chicago/Turabian StyleWang, Zhisong, Fei Yang, Yujie Wang, and Zhiyuan Fang. 2022. "Study on Wind Loads of Different Height Transmission Towers under Downbursts with Different Parameters" Buildings 12, no. 2: 193. https://doi.org/10.3390/buildings12020193
APA StyleWang, Z., Yang, F., Wang, Y., & Fang, Z. (2022). Study on Wind Loads of Different Height Transmission Towers under Downbursts with Different Parameters. Buildings, 12(2), 193. https://doi.org/10.3390/buildings12020193





