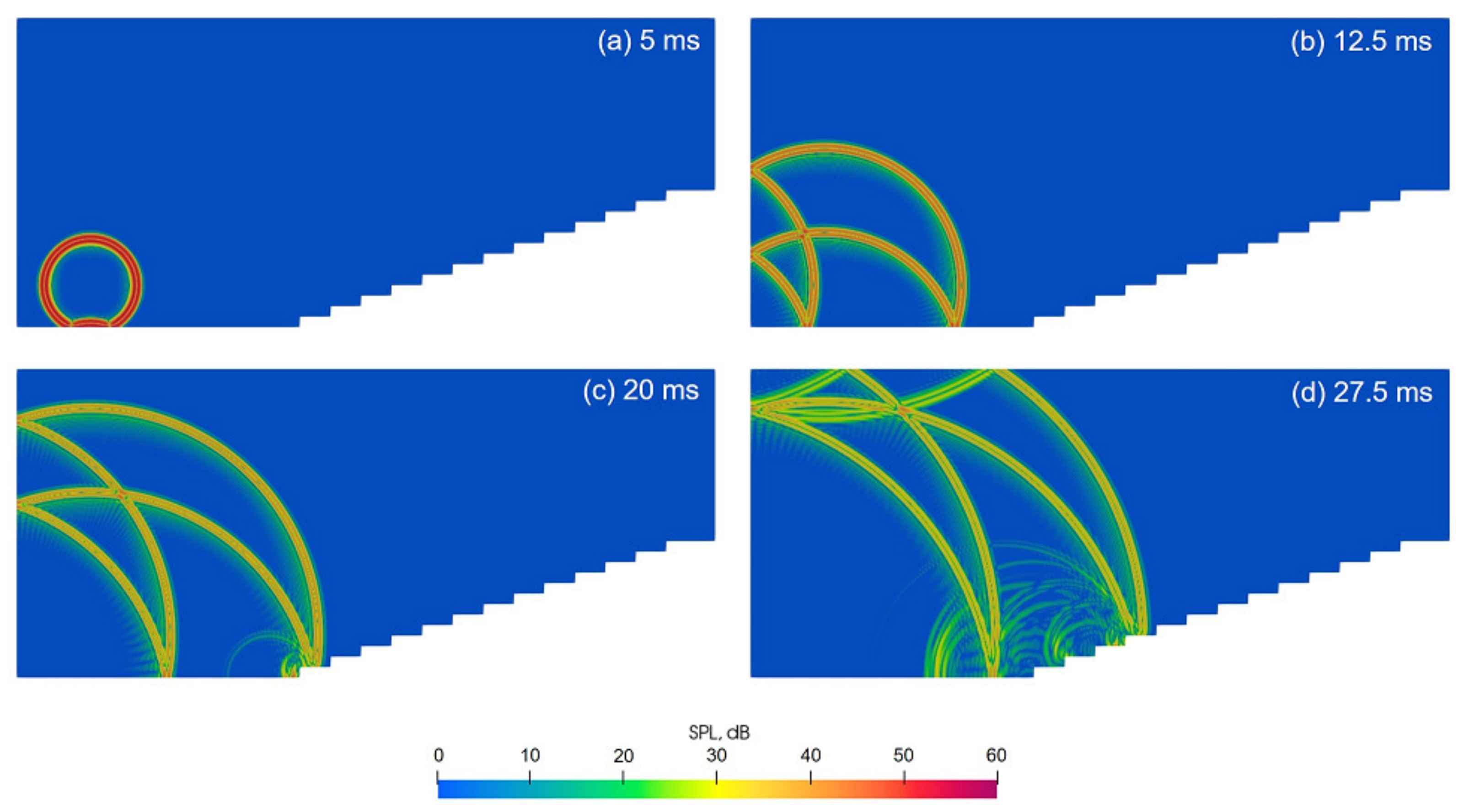
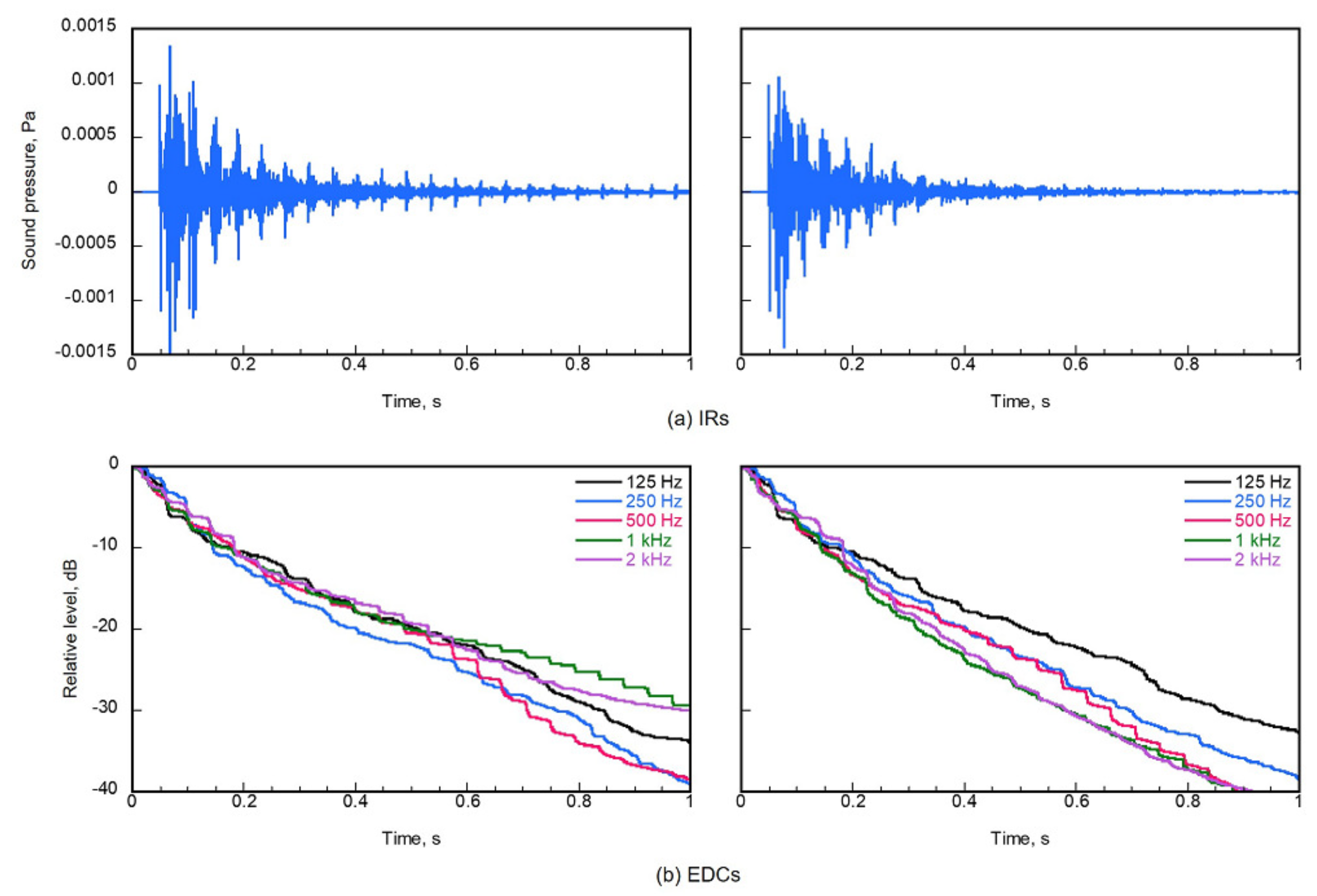
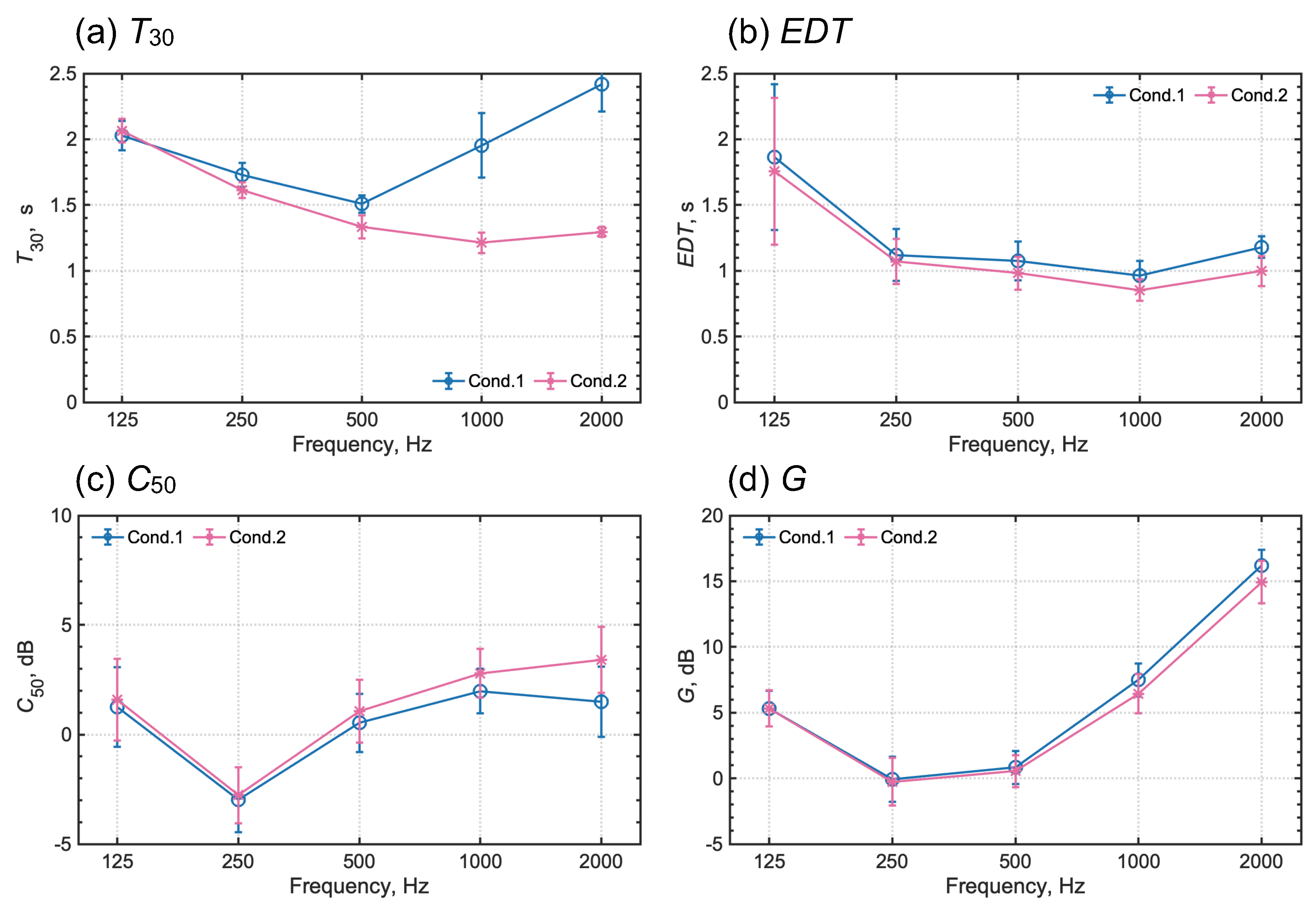
1.1. Background
Wave-based acoustics simulation methods can model acoustics in architectural spaces [
1] such as concert halls and classrooms accurately based on the wave equation or the Helmholtz equation using numerical techniques such as the finite element method (FEM) [
2], finite difference method [
3,
4], and boundary element method [
5]. A benefit of wave-based simulations is that they can accurately assess effects of two key technologies of sound absorption and sound scattering for room acoustics control [
6]. With sound absorbers and acoustic diffusers, one can design a comfortable indoor sound environment by controlling noise levels and reverberation times according to room use. Consequently, wave-based simulations are reliable prediction tools for room acoustics design. Additionally, such simulations can further accommodate virtual reality (VR) technology. The use of such simulations in VR for engineering [
7,
8] and entertainment [
9,
10] is becoming an attractive application in recent years. An attractive feature of VR with wave-based simulations is that spatial sound field reproduction by ambisonics [
11,
12] with binaural rendering are conducted easily. That is true because expansion coefficients for spherical harmonics are accessed by placement of virtual microphone array [
13] or numerical differentiation [
14]. Subsequently, decoding and binaural auralization with headphones are accomplished using virtual studio technology plugins such as Resonance Audio [
15] and SPARTA [
16].
However, the main difficulty in applying wave-based simulations to architectural acoustic simulations is the necessary imposition of expensive computational loads, i.e., colossal memory consumption and long computational times, because architectural spaces have large dimensions compared to the acoustic wavelength at audible frequencies. Wave-based simulations require discretization of spaces with smaller-sized elements than the acoustic wavelength of interest to keep the discretization error, designated as the dispersion error, within an acceptable level. Although continuous progress in computing technology widens the applicable range of wave-based simulations, more efficient wave-based simulation methods able to reduce the dispersion error with smaller computational efforts than existing methods are necessary for application to architectural acoustic design. To this end, many researchers have examined the development of efficient wave-based simulation methods to date. For example, one can find reports of studies using higher-order finite-difference time-domain (FDTD) methods [
17,
18,
19] and higher-order frequency-domain and time-domain FEMs [
20,
21,
22,
23,
24,
25,
26]. Among other methods, this study addresses a time-domain FEM having explicit time-marching scheme, with the proposal of efficient acoustic simulation methods for large-scale room acoustics simulations.
Some efficient wave-based room acoustics simulation methods with dispersion-reduced FEMs using low-order finite elements (FEs) in both the frequency domain and time domain have been developed [
27,
28,
29,
30,
31,
32,
33,
34]. They have been applied respectively to acoustics simulation in a simple-shaped concert hall [
31], simulations of reverberation absorption coefficient measurements of sound absorbers with woven and non-woven fabrics [
32], and acoustics improvement of an existing meeting room with microperforated panel absorbers [
33]. The salient feature of the dispersion-reduced FEMs is that they can maintain dispersion error at a low level with low-order FEs without increasing additional computational costs. The methods are able to do so because of the use of modified integration rule (MIR) [
35,
36], which uses numerical integration points able to reduce dispersion error for element matrix construction. Consequently, the methods can decrease the total number of degrees of freedom (DOFs) without increasing the matrix’s bandwidth more than higher-order FEM. The computational costs required per element are lower than those of higher-order methods. For development, first, dispersion-reduced implicit time-domain FEM (TD-FEM) [
27] and frequency-domain FEM (FD-FEM) [
29] have been developed for room acoustics simulation. A dispersion-reduced high-order FD-FEM and TD-FEM using spline FEs have also been proposed in an earlier report of the relevant literature [
26]. Subsequently, a dispersion-reduced explicit TD-FEM with fourth-order accuracy in terms of dispersion error was proposed to accelerate a computational speed for acoustic simulations further in architectural spaces discretized only with rectangular FEs [
28,
30]. Later, by developing a time integration method called the modified Adams method for time discretization [
34], the limitation of using rectangular FEs was removed without accuracy reduction caused by dispersion error. However, the explicit TD-FEM with the modified Adams method still has the important shortcoming that includes numerical dissipation error. With the error, sound energy decreases over time despite the use of a lossless wave equation. Although the attenuation level in sound energy can be reduced using a smaller time interval value, the strategy entails increased computational costs.
More recently, a dissipation-free fourth-order accurate explicit TD-FEM for room acoustics simulation [
37] has been proposed, which overcomes shortcomings in TD-FEM with the modified Adams method. It achieves a dissipation-free scheme using a newly developed three-step time-integration method based on the general form of linear multi-step time integration method [
38]. Furthermore, the dissipation-free explicit TD-FEM can enhance the capability of sound field approximation at higher frequencies using an optimization method with no additional computational costs. In the optimized method, the dispersion errors in axial and diagonal directions are minimized at a specific mesh or element resolution with optimized MIR and weight coefficients in time integration. The basic performance of the dissipation-free and dispersion-optimized explicit TD-FEMs has been examined for simply shaped room acoustics problems with rigid boundaries at wideband frequencies. Those examinations showed outstanding performance against a standard second-order accurate implicit TD-FEM. Nevertheless, the method still lacks implementation of absorbing boundary conditions (BCs) to reflect the effects of sound absorbers such as porous materials. Therefore, its performance for practical room acoustic modeling remains unclear.
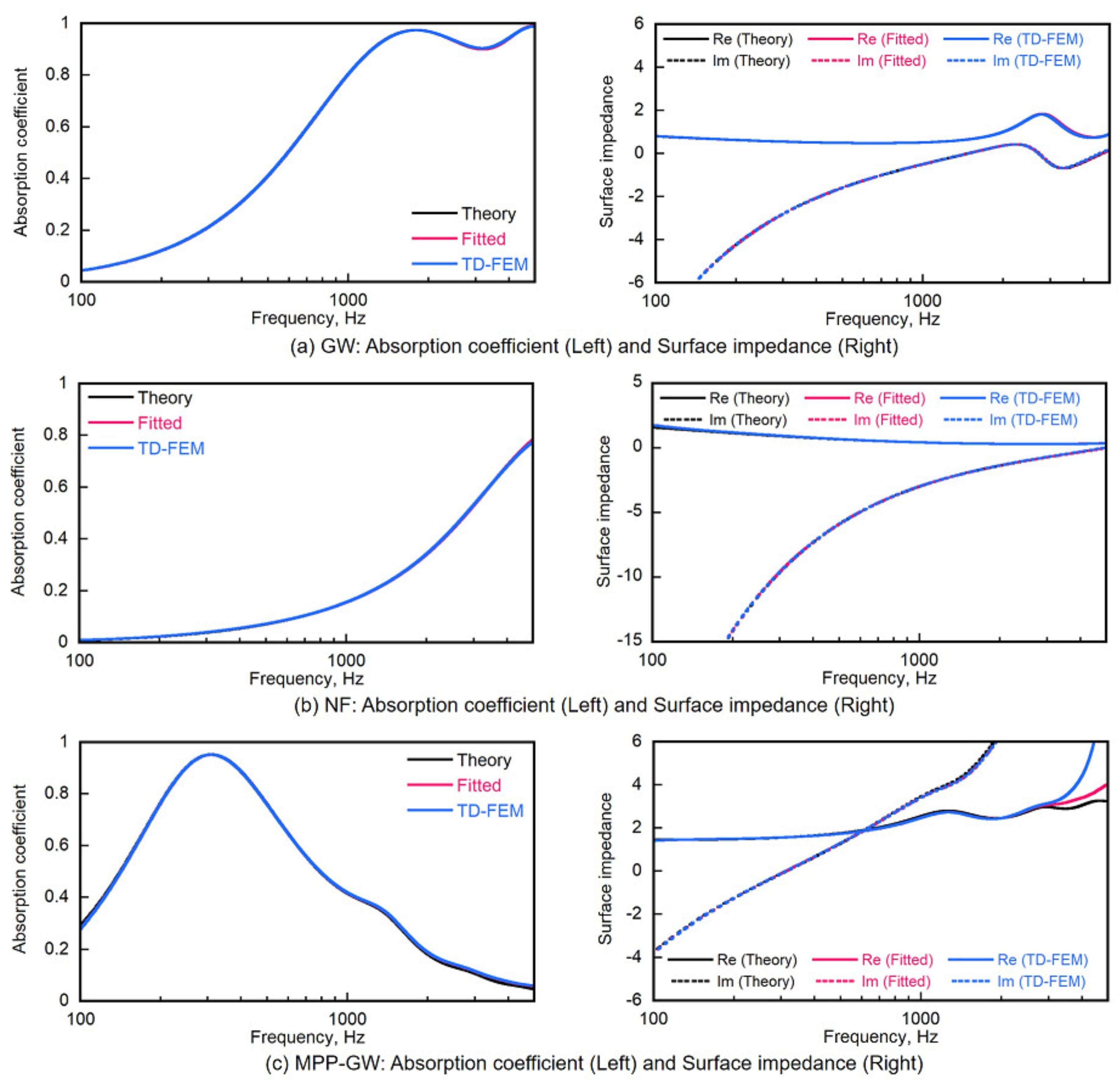
The quality of sound absorption modeling is well known to have a strong effect on the resulting accuracy in sound field predictions. Ideally, using an extended-reaction BC ability is desirable to address both frequency dependence and incident-angle dependence in sound absorption characteristics of sound absorbers. Note that uncertainty in input data concerning sound absorption modeling also has a considerable effect on calculation results [
39,
40]. A local-reaction BC that simplifies the incident-angle dependence is another selection because the computation becomes easier with the surface impedance of sound absorbers than the extended-reaction BCs that require discretization of materials according to corresponding partial differential equations. Although the implementation of frequency-dependence into time-domain methods is difficult because of the inclusion of convolution operation, very recently developed time-domain methods [
23,
41,
42,
43,
44,
45] can specifically address the frequency-dependence in the local-reaction BC and extended-reaction BC efficiently. This report also addresses the implementation of frequency-dependent local-reaction impedance BCs into the dissipation-free and dispersion-optimized explicit TD-FEM using auxiliary differential equations method [
46].
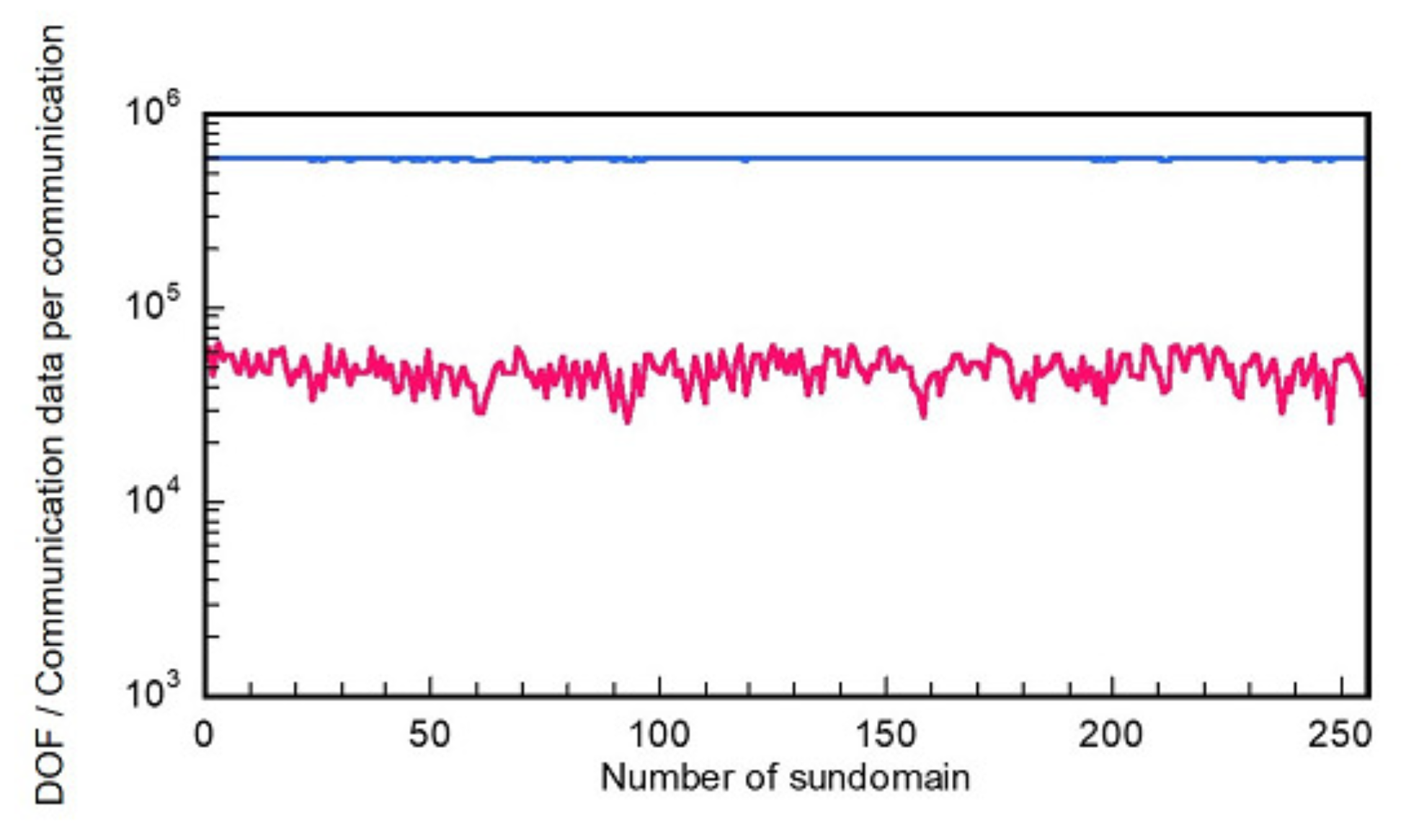
Furthermore, the use of parallel computing technology for wave-based room acoustics simulation is a simple choice for extending its applicable range to large architectural spaces at high frequencies. Because cloud-computing environments such as Amazon Web Service [
47], Microsoft Azure [
48], and Google Cloud [
49] are becoming increasingly familiar in recent years, the development of massively parallel solvers is an exciting subject. Some earlier studies have presented excellent parallel performance of parallel wave-based acoustics simulation with a high performance computing (HPC) system having many CPU cores or GPUs [
50,
51,
52,
53,
54,
55]. A marked speeding up of acoustics simulation with a parallel implicit TD-FEM using spline FEs have also been demonstrated for a simply shaped hall with 13,000
[
50] when using an HPC system with 256 cores about ten years ago. Because of this marked performance gain with large-scale parallel computing can also anticipate for a dissipation-free and dispersion-optimized explicit TD-FEM, as a practical demonstration, we will examine the parallel performance for calculating an impulse response in an auditorium model, including frequency-dependent impedance BCs of two porous-type sound absorbers and a Helmholtz-type sound absorber.
1.2. Purpose of This Study
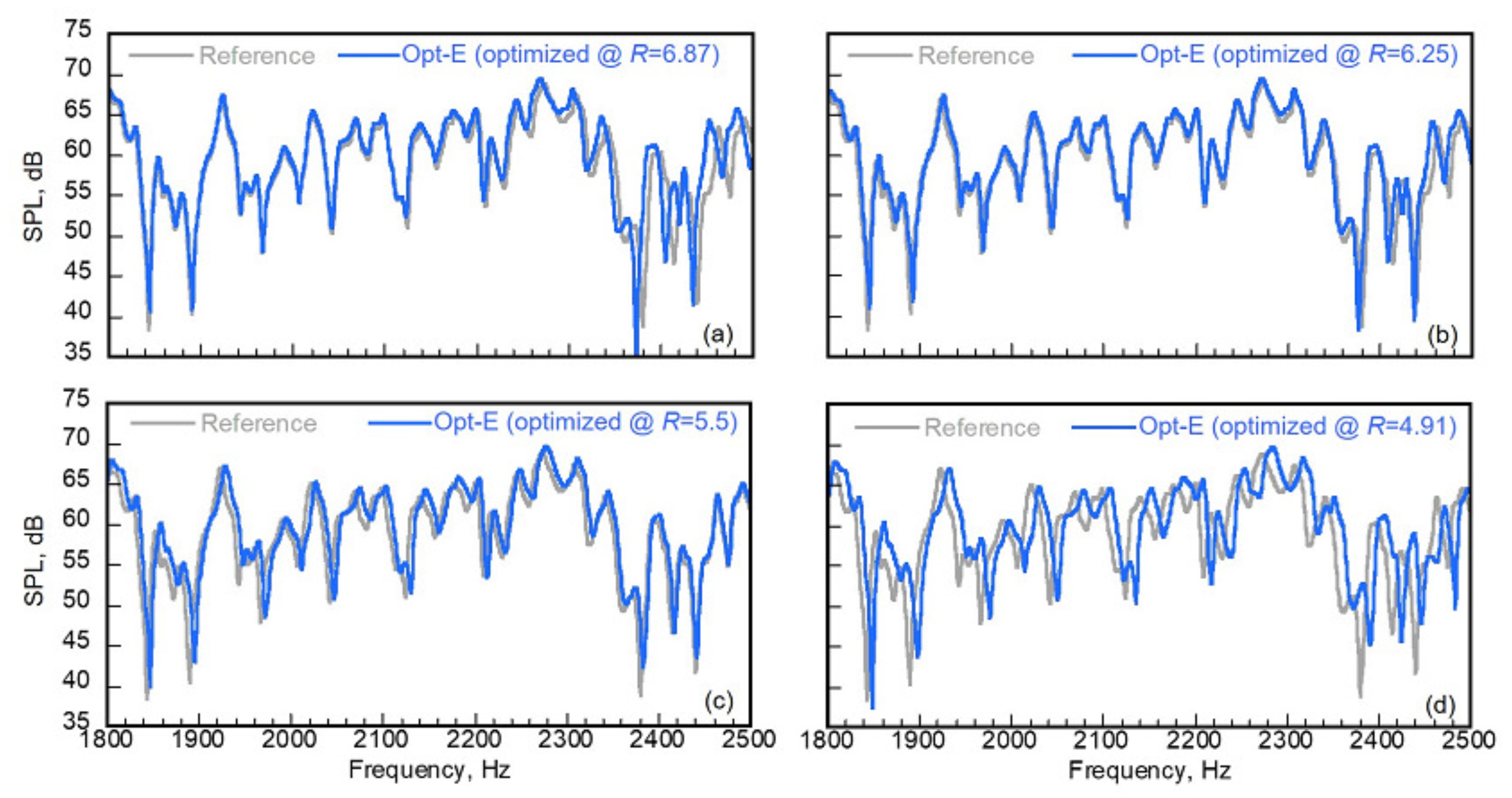
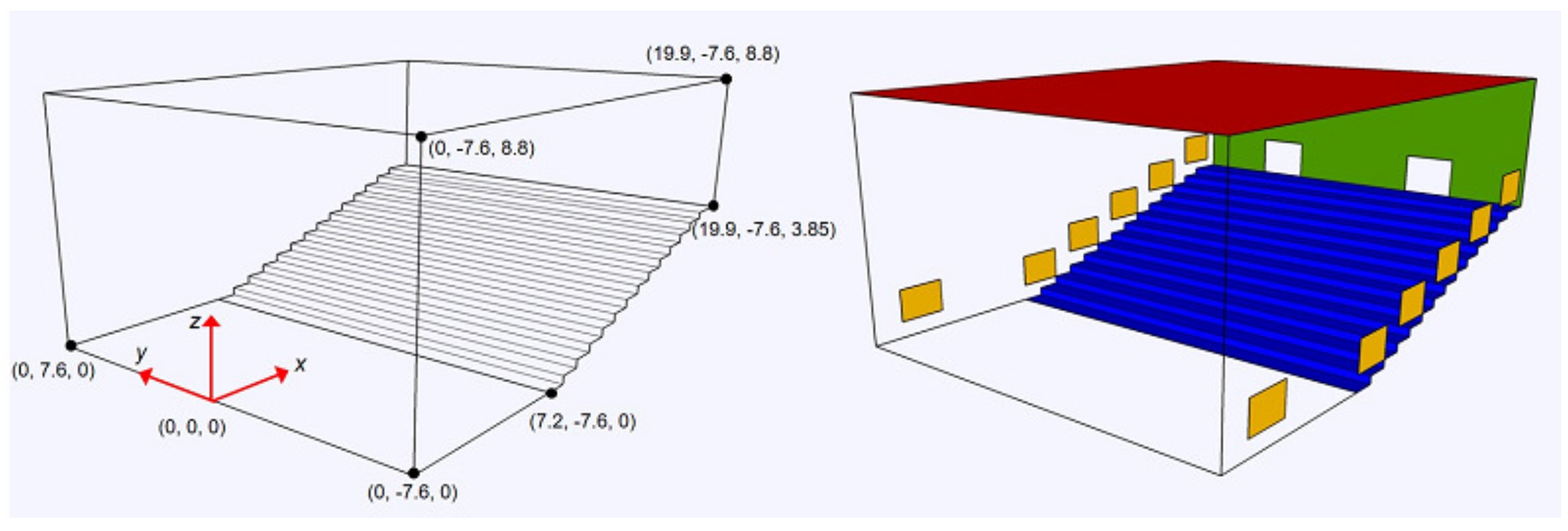
The present study proposes a parallel wave-based room-acoustics simulation method with a dissipation-free and dispersion-optimized explicit TD-FEM, with eventual demonstration of its practicality for acoustics simulation at kilohertz frequency range in a large room. As the salient point of novelty of the present work, we present the completely new simulation method for large-scale room acoustics simulation composed of a time-marching scheme to deal with frequency-dependent impedance BC and a DDM-based parallel computation algorithm. It can predict an impulse response up to three seconds in an auditorium of 2271
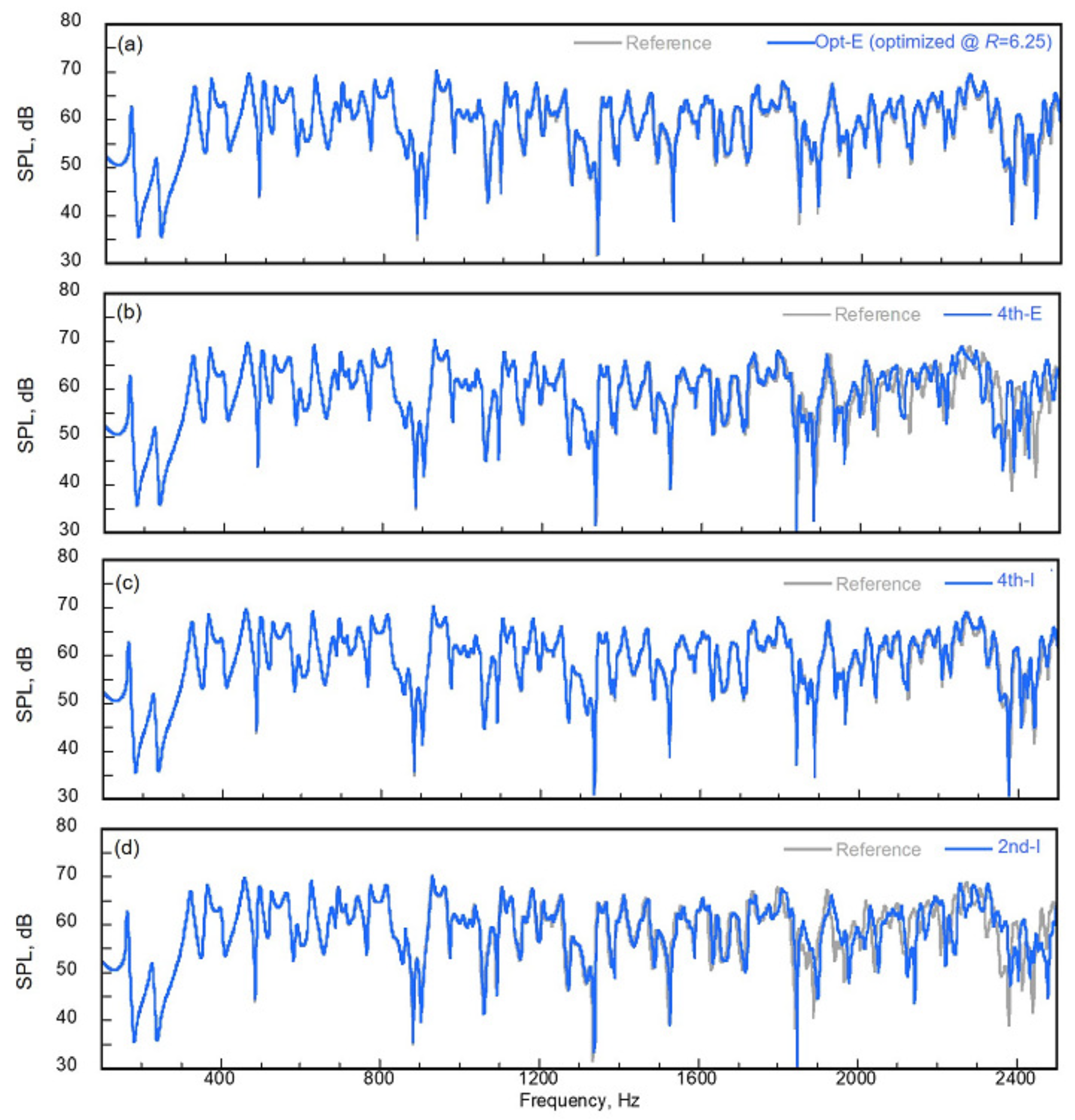
having multiple frequency-dependent impedance BCs within 9000 s using 512 cores. Our study also includes two validation studies that use impedance tube problems and a small cubic room problem with frequency-dependent impedance BCs. For the latter problem, we show the performance of the proposed method over existing TD-FEMs and the efficient numerical setup for the proposed method. Hereinafter, the proposed dissipation-free and dispersion-optimized explicit TD-FEM and the non-optimized fourth-order explicit TD-FEM, i.e., the dissipation-free method only, are abbreviated respectively to the Opt-E TD-FEM and the 4th-E TD-FEM. This paper is organized as follows.
Section 2 describes the theory of proposed time-marching scheme with Opt-E and 4th-E TD-FEMs including frequency-dependent impedance BCs. This section also includes, for readers’ convenience, details of theories of other FEM-based room acoustic solvers used herein.
Section 3 presents tests of the validity of the proposed methods with the impedance tube problem and cubic room problems.
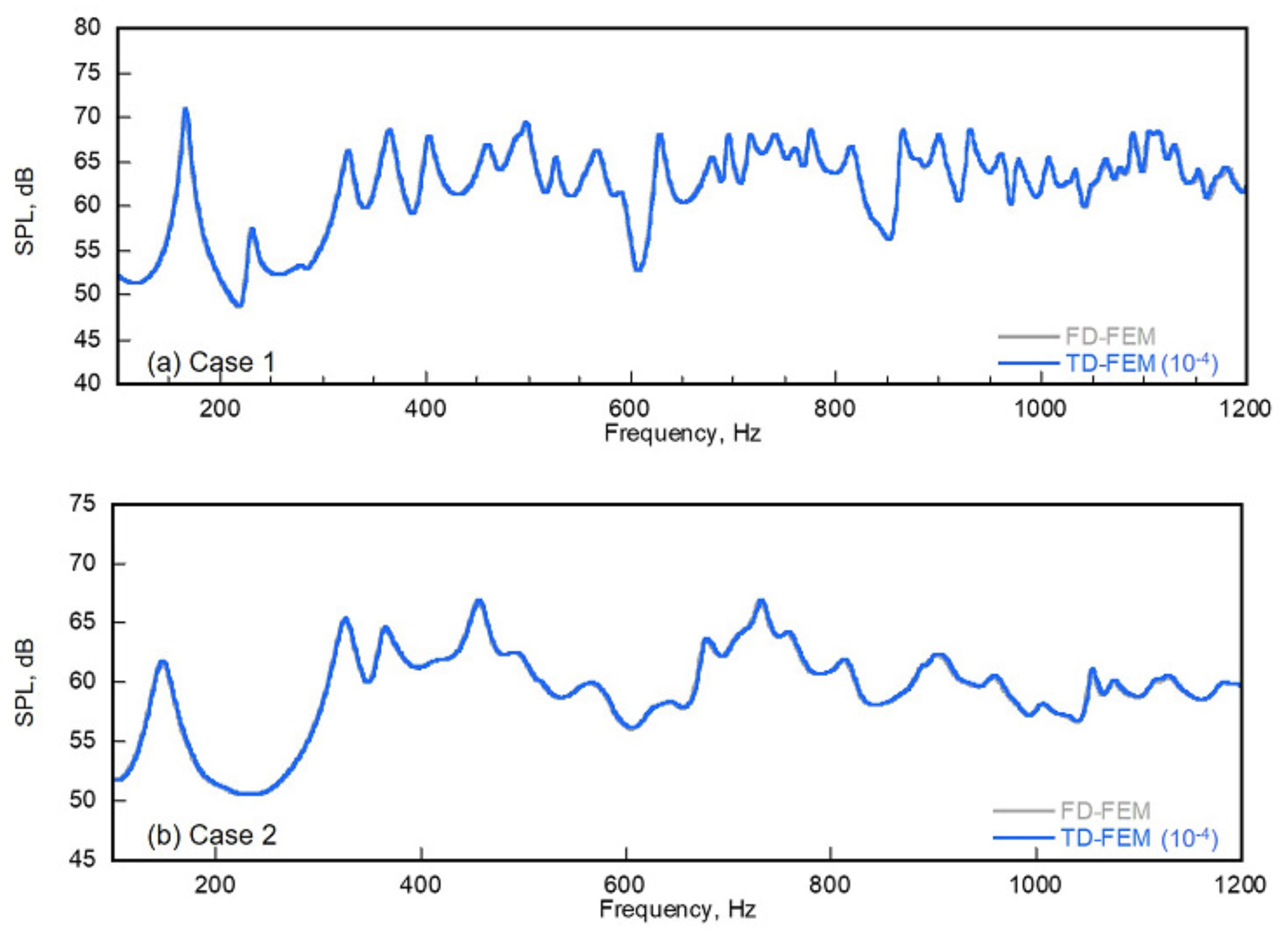
Section 4 examines the efficiency of the proposed method over two existing implicit TD-FEM, including a proposal of the efficient optimization setup for the proposed methods.
Section 5 demonstrates the practicality of parallel Opt-E TD-FEM using a hybrid framework with Message Passing Interface (MPI) and OpenMP to large-scale room acoustics simulation with an auditorium model with the volume of 2271
.
Section 6 concludes the paper. All computational codes used in the present study are in-house software written with Fortran 90.