Modeling and Optimizing the Effect of 3D Printed Origami Bubble Aggregate on the Mechanical and Deformation Properties of Rubberized ECC
Abstract
:1. Introduction
2. Materials and Methods
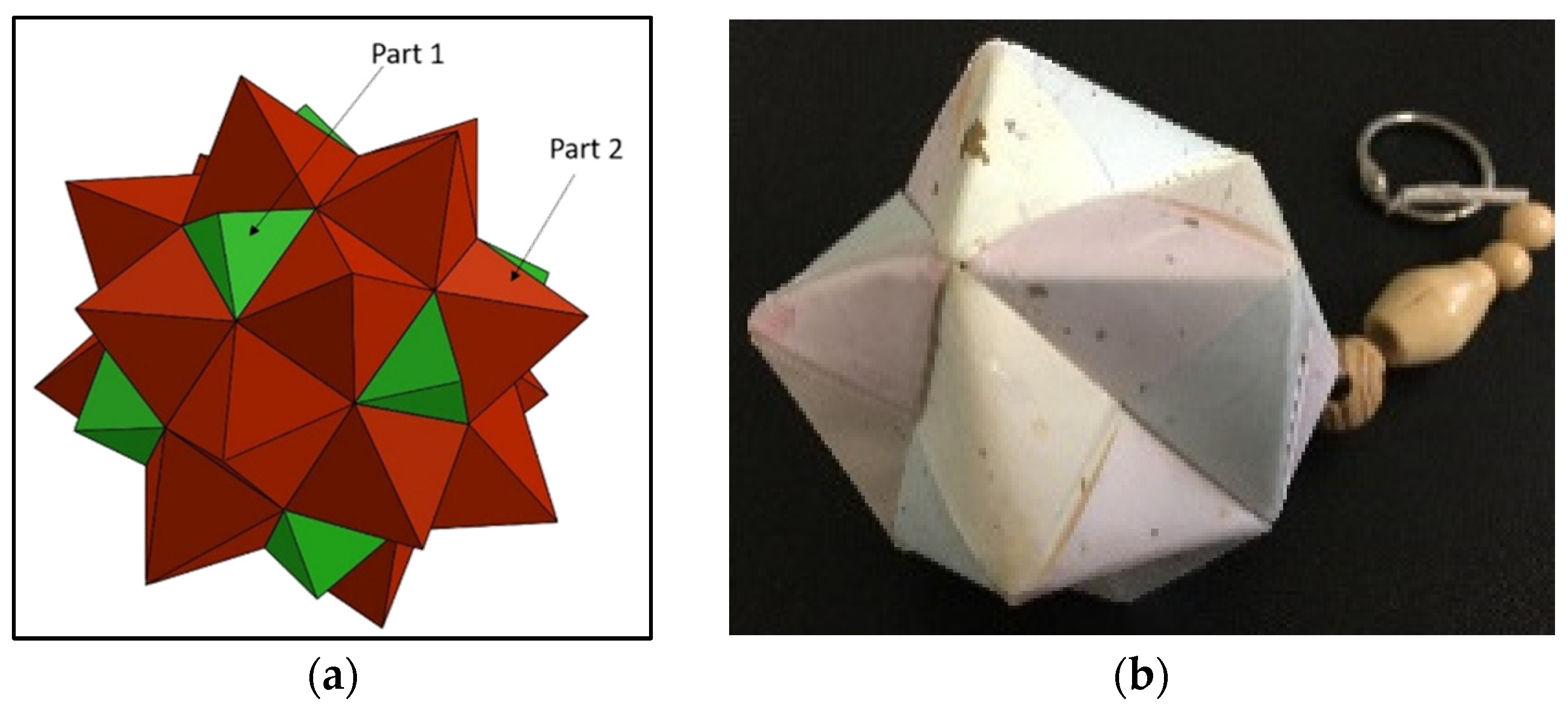
2.1. Materials
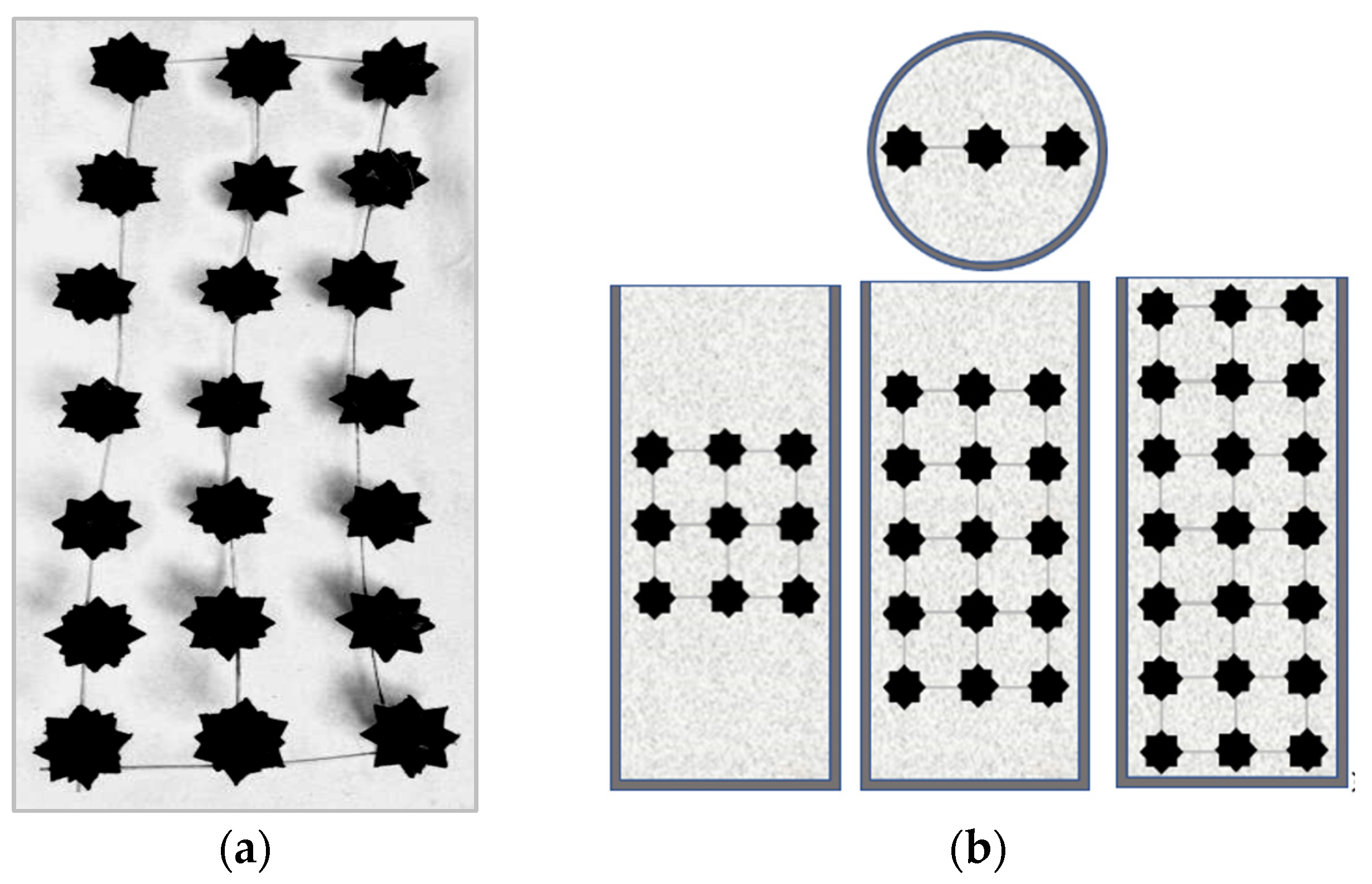
2.2. RSM Mix Proportion, Sample Preparation, and Testing
3. Results and Discussion
3.1. Density of OBA-RECC
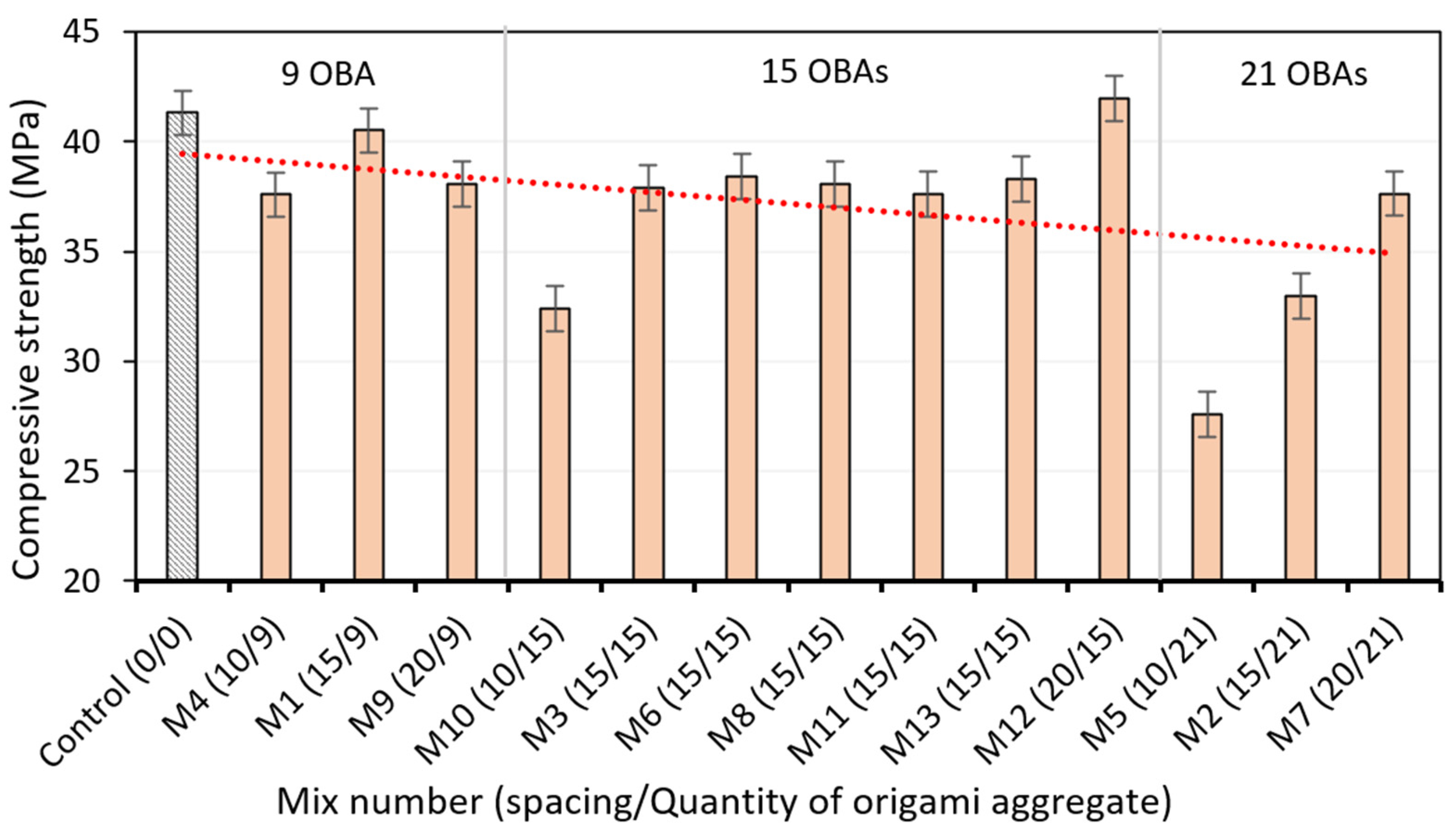
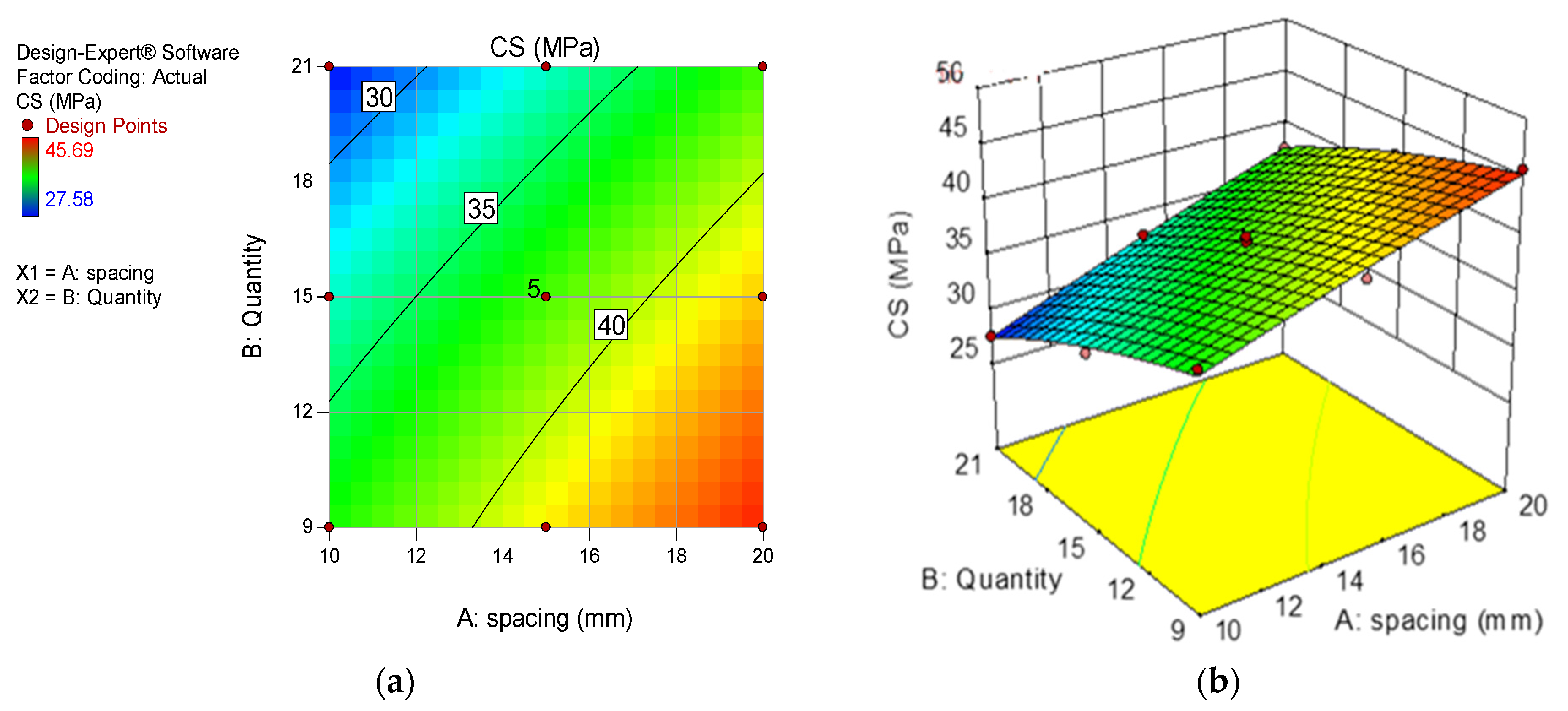
3.2. Compressive Strength of OBA-RECC
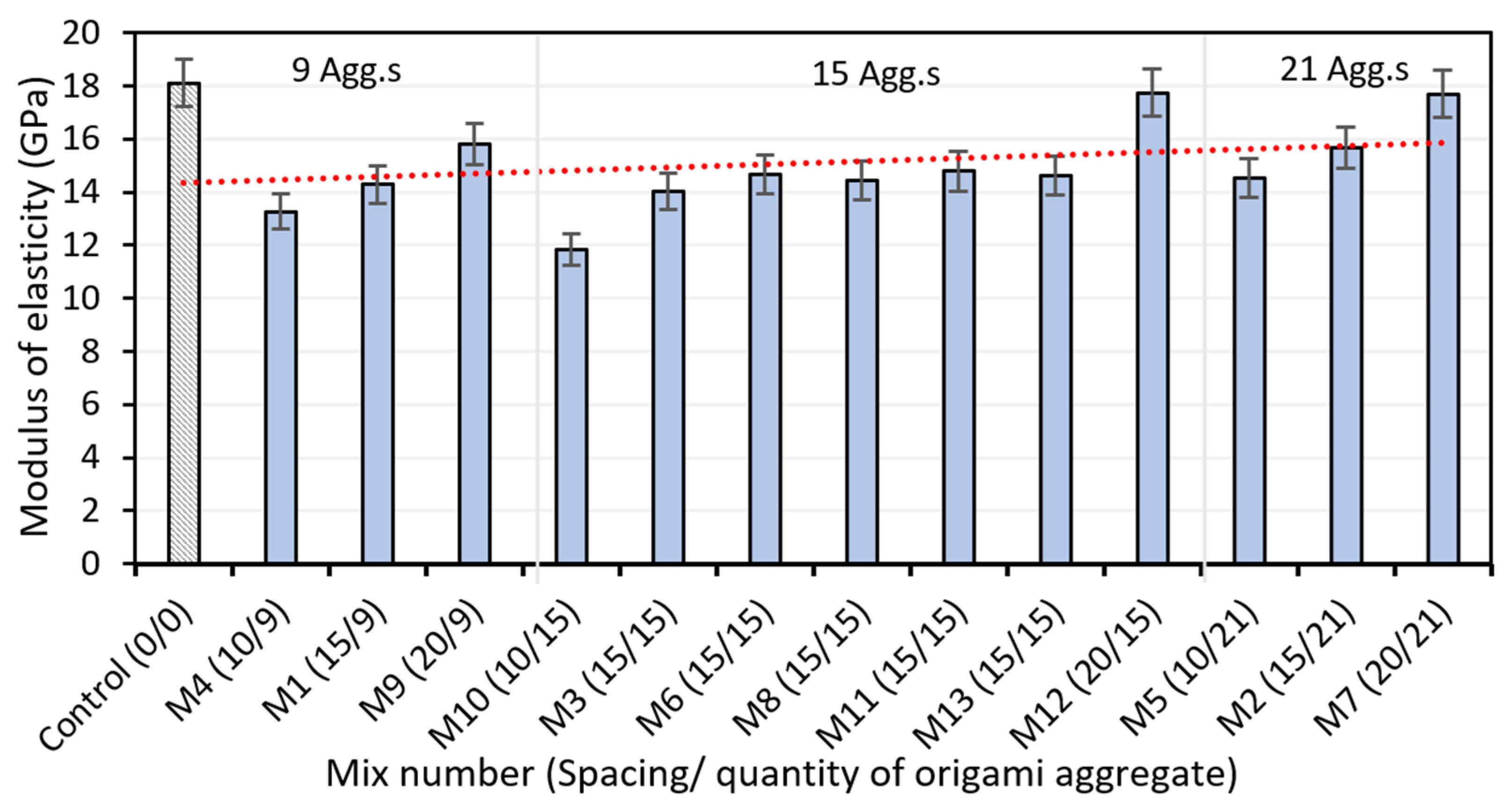
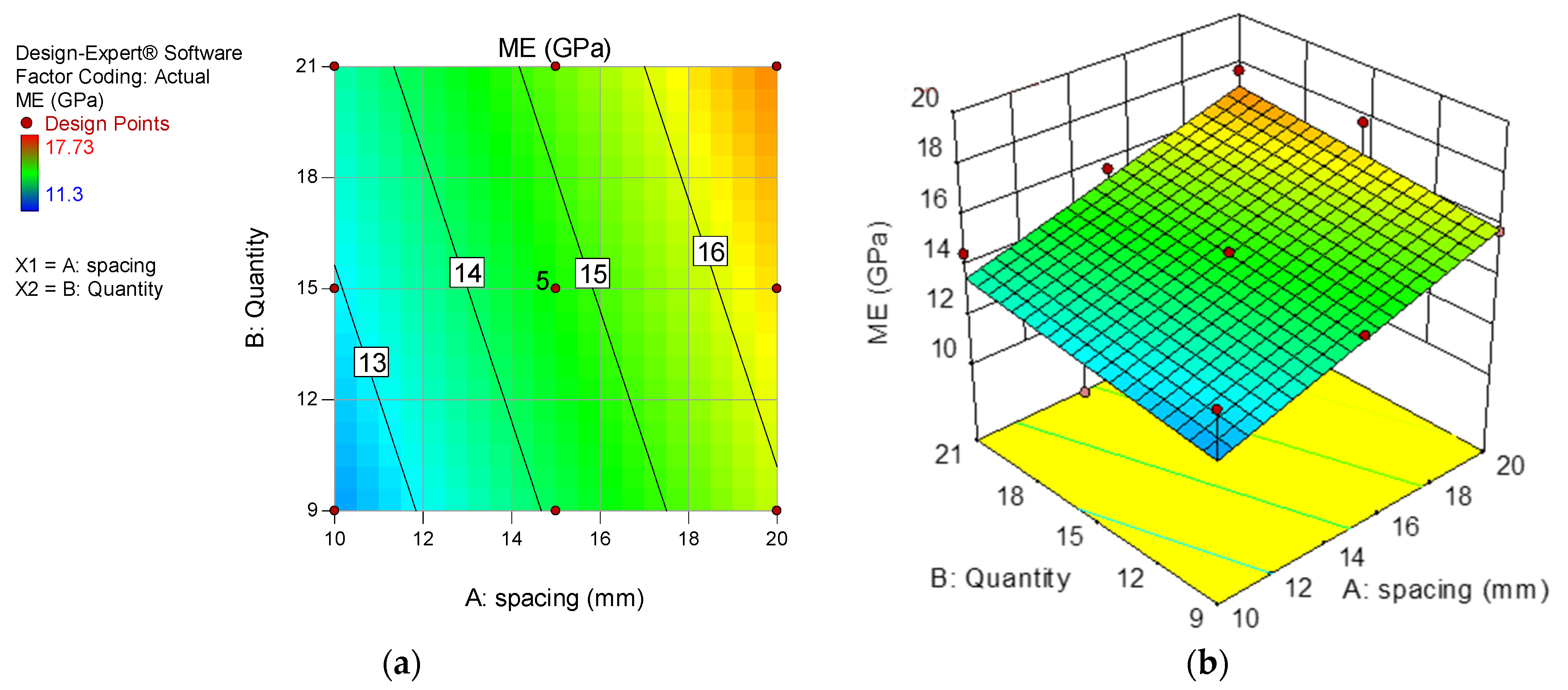
3.3. Modulus of Elasticity and Poisson’s Ratio of OBA-RECC
4. RSM Analysis
4.1. Model Development and ANOVA
4.2. Model Graphs and Diagnostic Plots
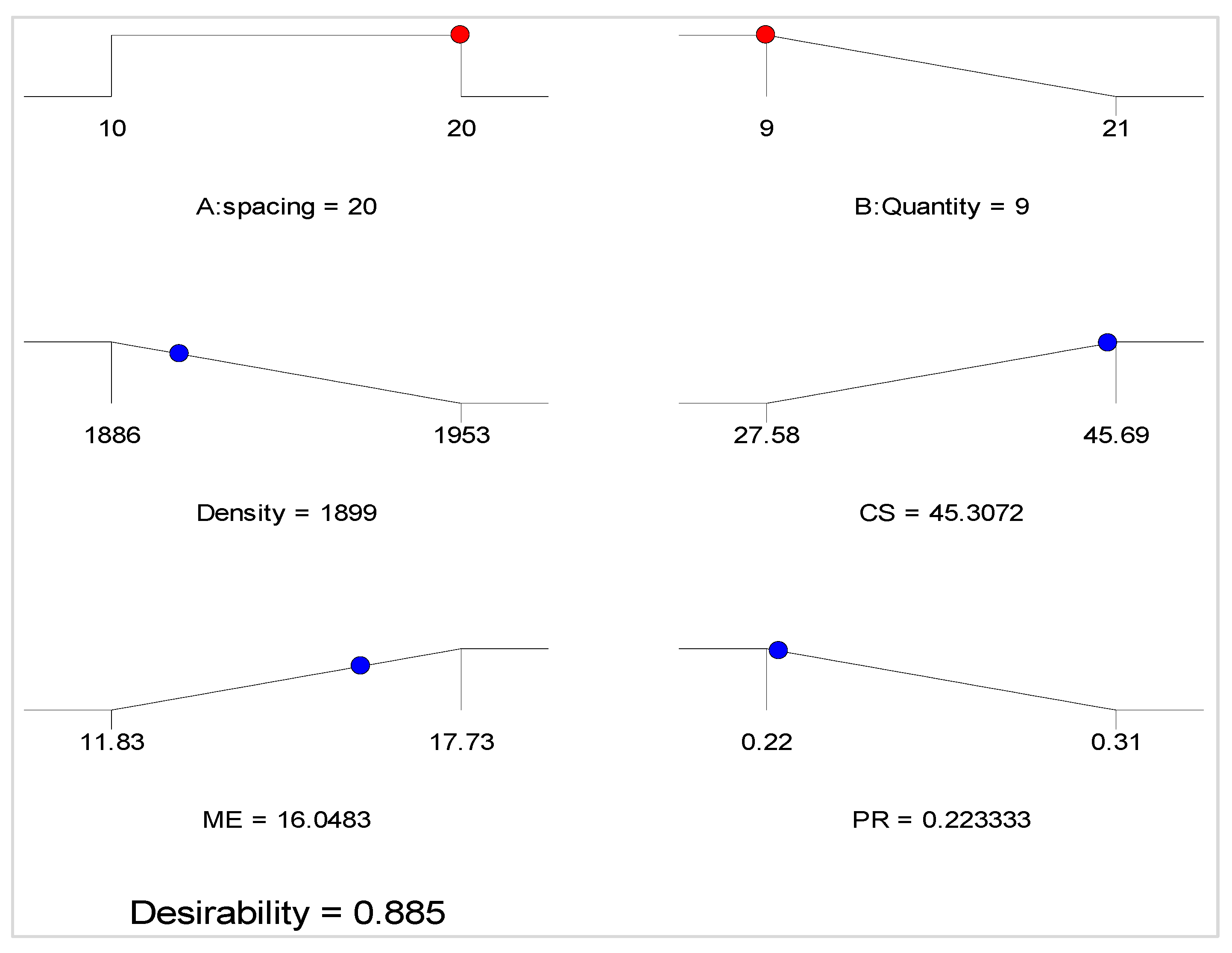
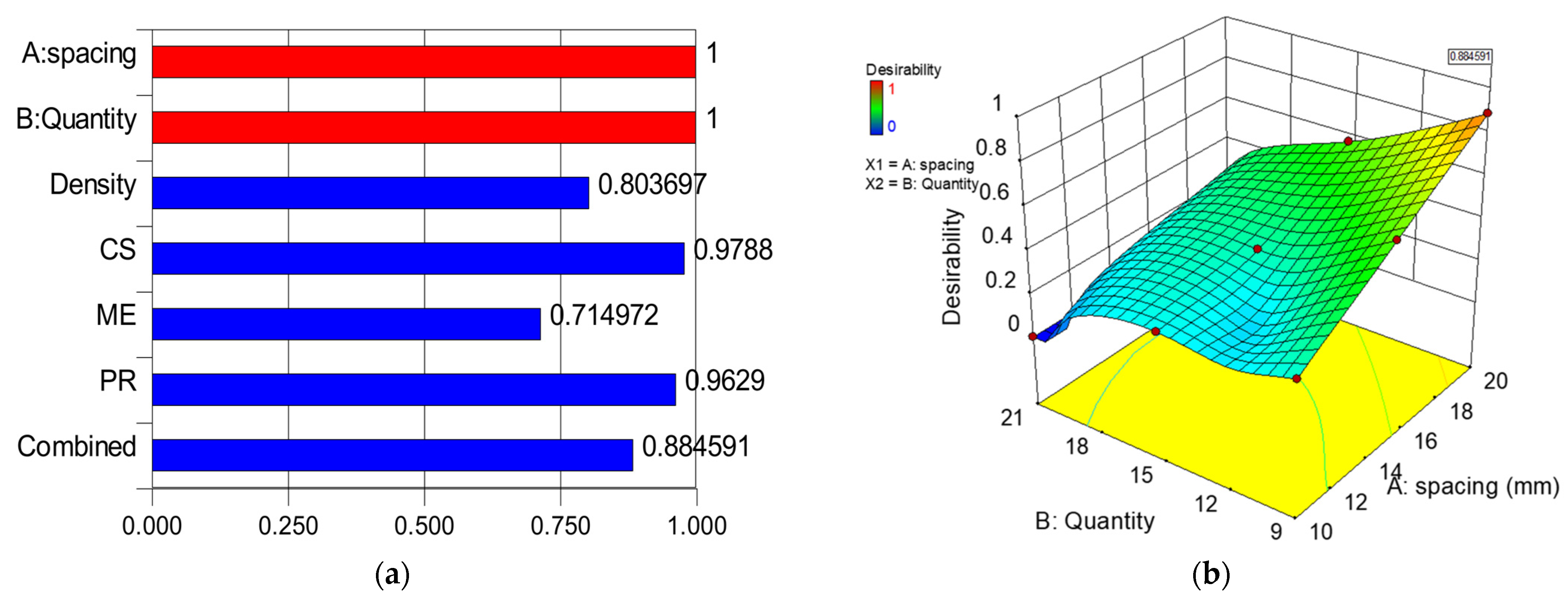
4.3. Multi-Objective Optimization
4.4. Experimental Validation
5. Conclusions
- Using origami bubble aggregate (OBA) to produce a lightweight ECC is a novel approach, and an RECC with a density of 1781 kg/m3 can be produced, with a 20% lower density than the control RECC.
- Compared to other hollow bodies employed in earlier studies, RECC with significant compressive strength can be produced using 15 OBAs at spacings between 15 and 20 mm.
- At all OBA quantities, the modulus of elasticity was higher at higher OBA spacings, which were close to the values of the control RECC mix. On the other hand, lower Poisson’s ratios than control RECC were obtained at a quantity of 9 OBA at all the spacings under consideration. Nevertheless, the trend changed with higher OBA quantities, with the highest ME values obtained at lower spacings.
- Predictive response models were developed and validated using ANOVA with high R2 ranging between 51 and 99%. In order to obtain the levels of the input factors that will yield the best performance, multi-objective optimization was performed, which produced optimal input factors of 20 mm and 9 OBAs that will give the optimum density, compressive strength, modulus of elasticity, and Poisson’s ratio of 1899 kg/m3, 45.3 MPa, 16.1 GPa, and 0.22, respectively, at a very high desirability value of 88.5%. Experimental validation showed very good agreement between the experimental and predicted response values at an acceptable error of less than 10% for all the models.
- This research focused on the density reduction effect of OBAs on ECC and the consequent effect on the compressive strength, modulus of elasticity, and Poisson’s ratio of the composite. Other properties of the OBA-RECC not covered here are presently being investigated.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; Li, J.; Yang, E.-H. Development of Ultra-Lightweight and High Strength Engineered Cementitious Composites. J. Compos. Sci. 2021, 5, 113. [Google Scholar] [CrossRef]
- Somasundaram, S.; Ramasamy, K.A.; Mallika, G.S. Development of light weight engineered cementitious composites. In Proceedings of the 3rd National Conference on Current and Emerging Process Technologies CONFEST 2020, Erode, India, 25 January 2020. [Google Scholar] [CrossRef]
- Yan, X.; Chen, P.S.; Al-Fakih, A.; Liu, B.; Mohammed, B.S.; Jin, J. Experiments and Mechanical Simulation on Bubble Concrete: Studies on the Effects of Shape and Position of Hollow Bodies Mixed in Concrete. Crystals 2021, 11, 858. [Google Scholar] [CrossRef]
- Yan XChen, P.S.; Liu, B.; Mohammed, B.S.; Jin, J. Effect of Hollow Body Material on Mechanical Properties of Bubble Concrete. Crystals 2022, 12, 708. [Google Scholar] [CrossRef]
- Chen, P.S.; Tsukinaga, Y. Basic research on the development of light weight concrete mixed with hollow spheres. J. Soc. Mater. Sci. Jpn. 2015, 64, 711–717. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.S. Bubble Concrete; Japan Patent Office: Tokyo, Japan, 2008. [Google Scholar]
- Chen, P.S. A study report on light weight concrete mixed with high strength hollow bubbles. In Proceeding of the AIJ Tohoku Chapter Architectural Research Meeting (Kouzoukei); Architectural Institute of Japan: Tokyo, Japan, 2008. [Google Scholar] [CrossRef]
- Yan, X.; Chen, P.S.; Liu, B.; Mohammed, B.S.; Jin, J. Effect of Hollow Bodies on the Strength and Density of Bubble Concrete. In Proceedings of the AWAM International Conference in Civil Engineering (AICCE’22), Penang, Malaysia, 21–22 August 2022. [Google Scholar]
- Mohammed, B.S.; Achara, B.E.; Nuruddin, M.F.; Yaw, M.; Zulkefli, M.Z. Properties of nano-silica-modified self-compacting engineered cementitious composites. J. Clean. Prod. 2017, 162, 1225–1238. [Google Scholar] [CrossRef]
- Li, V.C. Engineered Cementitious Composites (ECC)—Material, Structural, and Durability Performance. In Concrete Construction Engineering Handbook, Nawy, E., Ed.; CRC Press: Boca Raton, FL, USA, 2008; Available online: https://tinyurl.com/ycxdsnby (accessed on 23 October 2022).
- Li, V.C. Damage Tolerant ECC for Integrity of Structures Under Extreme Loads. In Structures Congress 2009; ASCE: Ausin, TX, USA, 2009. [Google Scholar] [CrossRef] [Green Version]
- Lepech, M.D.; Li, V.C.; Robertson, R.E.; Keoleian, G.A. Design of Green Engineered Cementitious Composites for Improved Sustainability. ACI Mater. J. 2008, 105, 567. [Google Scholar]
- Lye, H.L.; Mohammed, B.S.; Liew, M.S.; Wahab, M.M.A.; Al-fakih, A. Bond behaviour of CFRP-strengthened ECC using Response Surface Methodology (RSM). Case Stud. Constr. Mater. 2020, 12, e00327. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q. Matrix tailoring of Engineered Cementitious Composites (ECC) with non-oil-coated, low tensile strength PVA fiber. Constr. Build. Mater. 2018, 161, 420–431. [Google Scholar] [CrossRef]
- Abdulkadir, I.; Mohammed, B.S.; Liew, M.S.; Wahab, M.M.A.; Zawawi, N.A.W.A.; As’ad, S. A review of the effect of waste tire rubber on the properties of ECC. Intern. J. Adv. Appl. Sci. 2020, 7, 105–116. [Google Scholar]
- Abdulkadir, I.; Mohammed, B.S.; Liew, M.S.; Wahab, M.M.A. Modelling and multi-objective optimization of the fresh and mechanical properties of self-compacting high volume fly ash ECC (HVFA-ECC) using response surface methodology (RSM). Case Stud. Constr. Mater. 2021, 14, e00525. [Google Scholar] [CrossRef]
- Zhang, Z.; Yuvaraj ADi, J.; Qian, S. Matrix design of light weight, high strength, high ductility ECC. Constr. Build. Mater. 2019, 210, 188–197. [Google Scholar] [CrossRef]
- Wang, S.; Li, V. Lightweight engineered cementitious composites (ECC). In Proceedings of the 4th International RILEM Workshop on High Performance Fiber Reinforced Cement Composites (HPFRCC 4), Ann Arbor, MI, USA, 16–18 June 2003; RILEM Publications: Paris, France, 2003. [Google Scholar]
- Huang, X.; Ranade, R.; Zhang, Q.; Ni, W.; Li, V.C. Mechanical and thermal properties of green lightweight engineered cementitious composites. Constr. Build. Mater. 2013, 48, 954–960. [Google Scholar] [CrossRef]
- Singh, S.B.; Munjal, P. Engineered cementitious composite and its applications. Mater. Today Proc. 2020, 32, 797–802. [Google Scholar] [CrossRef]
- Li, V.C. On engineered cementitious composites (ECC) a review of the material and its applications. J. Adv. Concr. Technol. 2003, 1, 215–230. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, B.S.; Nuruddin, M.F.; Aswin, M.; Mahamood, N.; Al-Mattarneh, H. Structural Behavior of Reinforced Self-Compacted Engineered Cementitious Composite Beams. Adv. Mater. Sci. Eng. 2016, 2016, 5615124. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, B.S.; Yen, L.Y.; Haruna, S.; Seng Huat, M.L.; Abdulkadir, I.; Al-Fakih, A.; Liew, M.S.; Zawawi, N.A.W.A. Effect of Elevated Temperature on the Compressive Strength and Durability Properties of Crumb Rubber Engineered Cementitious Composite. Materials 2020, 13, 3516. [Google Scholar] [CrossRef] [PubMed]
- Abdulkadir, I.; Mohammed, B.S.; Ali, M.O.A.; Liew, M.S. Effects of Graphene Oxide and Crumb Rubber on the Fresh Properties of Self-Compacting Engineered Cementitious Composite Using Response Surface Methodology. Materials 2022, 15, 2519. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, B.S.; Achara, B.E.; Liew, M.S.; Alaloul, W.S.; Khed, V.C. Effects of elevated temperature on the tensile properties of NS-modified self-consolidating engineered cementitious composites and property optimization using response surface methodology (RSM). Constr. Build. Mater. 2019, 206, 449–469. [Google Scholar] [CrossRef]
- BS EN 12390-7:2000; Testing Hardened Concrete. British Standards: London, UK, 2000.
- ASTM C 39/C 39M-01; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM: West Conshohocken, PA, USA, 2001.
- Mohammed, B.S.; Xian, L.W.; Haruna, S.; Liew, M.S.; Abdulkadir, I.; Zawawi, N.A.W.A. Deformation Properties of Rubberized Engineered Cementitious Composites Using Response Surface Methodology. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 45, 729–740. [Google Scholar] [CrossRef]
- Khed, V.C.; Mohammed, B.S.; Zawawi, N.A.W.A. Development of response surface models for self-compacting hybrid fibre reinforced rubberized cementitious composite. Constr. Build. Mater. 2020, 232, 117191. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization. In Search Methodologies: Introductory Tutorials in Optimization and Decision Support Techniques, Burke, E.K., Kendall, G., Eds.; Springer: New York, NY, USA; Heidelberg, Germany; Dordrecht, The Netherlands; London, UK, 2014. [Google Scholar]











| Composition | CaO | SiO2 | Fe2O3 | Al2O3 | K2O | SO3 | MgO | LOI |
|---|---|---|---|---|---|---|---|---|
| OPC (%) | 81.2 | 8.59 | 3.18 | 2.00 | 0.72 | 2.78 | 0.62 | 2.2 |
| FA (%) | 6.57 | 62.4 | 9.17 | 15.3 | 1.49 | 0.65 | 0.77 | 1.25 |
| Run | Input Variables | Quantities in Kg/m3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| A: Spacing of OBA (mm) | B: Quantity of OBA | SP | CR | PVA | FA | OPC | Sand | Water | |
| Control | 0 | 0 | 5.78 | 13 | 26 | 705.65 | 577.35 | 454 | 320 |
| 1 | 15 | 9 | 5.78 | 13 | 26 | 705.65 | 577.35 | 454 | 320 |
| 2 | 15 | 21 | 5.78 | 13 | 26 | 705.65 | 577.35 | 454 | 320 |
| 3 | 15 | 15 | 5.78 | 13 | 26 | 705.65 | 577.35 | 454 | 320 |
| 4 | 10 | 9 | 5.78 | 13 | 26 | 705.65 | 577.35 | 454 | 320 |
| 5 | 10 | 21 | 5.78 | 13 | 26 | 705.65 | 577.35 | 454 | 320 |
| 6 | 15 | 15 | 5.78 | 13 | 26 | 705.65 | 577.35 | 454 | 320 |
| 7 | 20 | 21 | 5.78 | 13 | 26 | 705.65 | 577.35 | 454 | 320 |
| 8 | 15 | 15 | 5.78 | 13 | 26 | 705.65 | 577.35 | 454 | 320 |
| 9 | 20 | 9 | 5.78 | 13 | 26 | 705.65 | 577.35 | 454 | 320 |
| 10 | 10 | 15 | 5.78 | 13 | 26 | 705.65 | 577.35 | 454 | 320 |
| 11 | 15 | 15 | 5.78 | 13 | 26 | 705.65 | 577.35 | 454 | 320 |
| 12 | 20 | 15 | 5.78 | 13 | 26 | 705.65 | 577.35 | 454 | 320 |
| 13 | 15 | 15 | 5.78 | 13 | 26 | 705.65 | 577.35 | 454 | 320 |
| Response | Source | Sum of Squares | Df | Mean Square | F-Value | p-Value > F | Significance |
|---|---|---|---|---|---|---|---|
| Density (kg/m3) | Model | 5355.5 | 5 | 1071.1 | 23.16 | 0.0003 | YES |
| A-Spacing | 204.17 | 1 | 204.17 | 4.41 | 0.0737 | NO | |
| B-Quantity | 682.67 | 1 | 682.67 | 14.76 | 0.0064 | YES | |
| AB | 1190.25 | 1 | 1190.25 | 25.74 | 0.0014 | YES | |
| A2 | 352.24 | 1 | 352.24 | 7.62 | 0.0281 | YES | |
| B2 | 1837.45 | 1 | 1837.45 | 39.73 | 0.0004 | YES | |
| Residual | 323.73 | 7 | 46.25 | ||||
| Lack of fit | 262.93 | 3 | 87.64 | 5.77 | 0.0618 | NO | |
| Pure error | 60.8 | 4 | 15.2 | ||||
| Cor Total | 5679.23 | 12 | |||||
| Compressive strength (MPa) | Model | 240.57 | 5 | 48.11 | 147.38 | <0.0001 | YES |
| A-Spacing | 128.07 | 1 | 128.07 | 392.29 | <0.0001 | YES | |
| B-Quantity | 109.23 | 1 | 109.23 | 334.58 | <0.0001 | YES | |
| AB | 0.94 | 1 | 0.94 | 2.88 | 0.1334 | NO | |
| A2 | 0.19 | 1 | 0.19 | 0.59 | 0.4686 | NO | |
| B2 | 1.41 | 1 | 1.41 | 4.31 | 0.0766 | NO | |
| Residual | 2.29 | 7 | 0.33 | ||||
| Lack of fit | 1.88 | 3 | 0.63 | 6.26 | 0.0543 | NO | |
| Pure error | 0.4 | 4 | 0.1 | ||||
| Cor Total | 242.85 | 12 | |||||
| Modulus of elasticity (GPa) | Model | 20.8 | 2 | 10.4 | 5.17 | 0.0287 | YES |
| A-Spacing | 18.73 | 1 | 18.73 | 9.31 | 0.0122 | YES | |
| B-Quantity | 2.08 | 1 | 2.08 | 1.03 | 0.3336 | NO | |
| Residual | 20.12 | 10 | 2.01 | ||||
| Lack of fit | 11.51 | 6 | 1.92 | 0.89 | 0.5726 | NO | |
| Pure error | 8.61 | 4 | 2.15 | ||||
| Cor Total | 40.93 | 12 | |||||
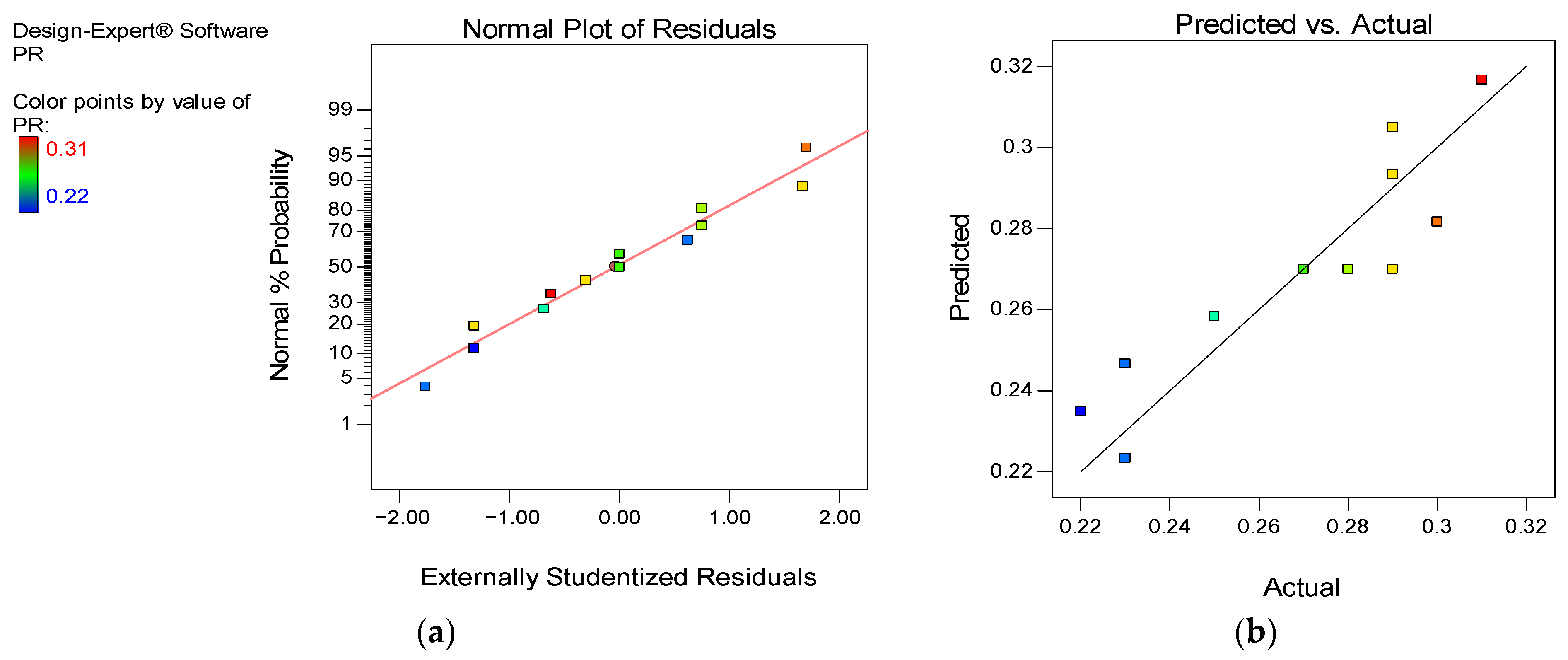
| Poisson’s ratio | Model | 8.17 × 10−3 | 2 | 4.08 × 10−3 | 22.27 | 0.0002 | YES |
| A-Spacing | 8.17 × 10−4 | 1 | 8.17× 10−4 | 4.45 | 0.061 | YES | |
| B-Quantity | 7.35 × 10−3 | 1 | 7.35 × 10−3 | 40.09 | <0.0001 | YES | |
| Residual | 1.83 × 10−3 | 10 | 1.83 × 10−4 | ||||
| Lack of fit | 1.55 × 10−3 | 6 | 2.59 × 10−4 | 3.7 | 0.1131 | NO | |
| Pure error | 2.80 × 10−4 | 4 | 7.00 × 10−5 | ||||
| Cor Total | 1.00 × 10−2 | 12 |
| Parameter | D | CS | ME | PR |
|---|---|---|---|---|
| Std. Dev. | 6.80 | 0.57 | 1.42 | 0.01 |
| Mean | 1931.54 | 37.43 | 14.70 | 0.27 |
| CV % | 0.35 | 1.53 | 9.65 | 5.01 |
| PRESS | 2763.22 | 16.18 | 33.97 | 0.00 |
| −2 Log Likelihood | 78.69 | 14.29 | 42.57 | −78.37 |
| R2 | 0.94 | 0.99 | 0.51 | 0.82 |
| Adj R2 | 0.90 | 0.98 | 0.41 | 0.78 |
| Pred R2 | 0.51 | 0.93 | 0.17 | 0.67 |
| Adeq Precision | 12.81 | 45.79 | 6.91 | 14.35 |
| BIC | 94.08 | 29.68 | 50.27 | −70.68 |
| AICc | 104.69 | 40.29 | 51.24 | −69.71 |
| Factors | Unit | Goal | Lower Limit | Upper Limit | |
|---|---|---|---|---|---|
| Input variables | A: Spacing | mm | In range | 10 | 20 |
| B: Quantity | - | Minimize | 9 | 21 | |
| Responses | D | Kg/m3 | Minimize | 1886 | 1953 |
| CS | MPa | Maximize | 27.58 | 45.69 | |
| ME | GPa | Maximize | 11.83 | 17.73 | |
| PR | - | Minimize | 0.22 | 0.31 | |
| Response | Experimental Result | Predicted Result | Percentage Error (%) |
|---|---|---|---|
| D (kg/m3) | 1781 | 1899 | 6.2 |
| CS (MPa) | 49.8 | 45.3 | 9.9 |
| ME (GPa) | 18.2 | 16.1 | 8.7 |
| PR | 0.21 | 0.22 | 4.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choo, J.; Mohammed, B.S.; Chen, P.-S.; Abdulkadir, I.; Yan, X. Modeling and Optimizing the Effect of 3D Printed Origami Bubble Aggregate on the Mechanical and Deformation Properties of Rubberized ECC. Buildings 2022, 12, 2201. https://doi.org/10.3390/buildings12122201
Choo J, Mohammed BS, Chen P-S, Abdulkadir I, Yan X. Modeling and Optimizing the Effect of 3D Printed Origami Bubble Aggregate on the Mechanical and Deformation Properties of Rubberized ECC. Buildings. 2022; 12(12):2201. https://doi.org/10.3390/buildings12122201
Chicago/Turabian StyleChoo, Joshua, Bashar S. Mohammed, Pei-Shan Chen, Isyaka Abdulkadir, and Xiangdong Yan. 2022. "Modeling and Optimizing the Effect of 3D Printed Origami Bubble Aggregate on the Mechanical and Deformation Properties of Rubberized ECC" Buildings 12, no. 12: 2201. https://doi.org/10.3390/buildings12122201
APA StyleChoo, J., Mohammed, B. S., Chen, P.-S., Abdulkadir, I., & Yan, X. (2022). Modeling and Optimizing the Effect of 3D Printed Origami Bubble Aggregate on the Mechanical and Deformation Properties of Rubberized ECC. Buildings, 12(12), 2201. https://doi.org/10.3390/buildings12122201






