Research on the Shear Behaviour of Composite Shear Connectors
Abstract
:1. Introduction
2. Experimental Program
2.1. Design of Specimens
2.2. Specimen Fabrication
2.3. Loading Scheme and Measurements
3. Test Results and Analysis
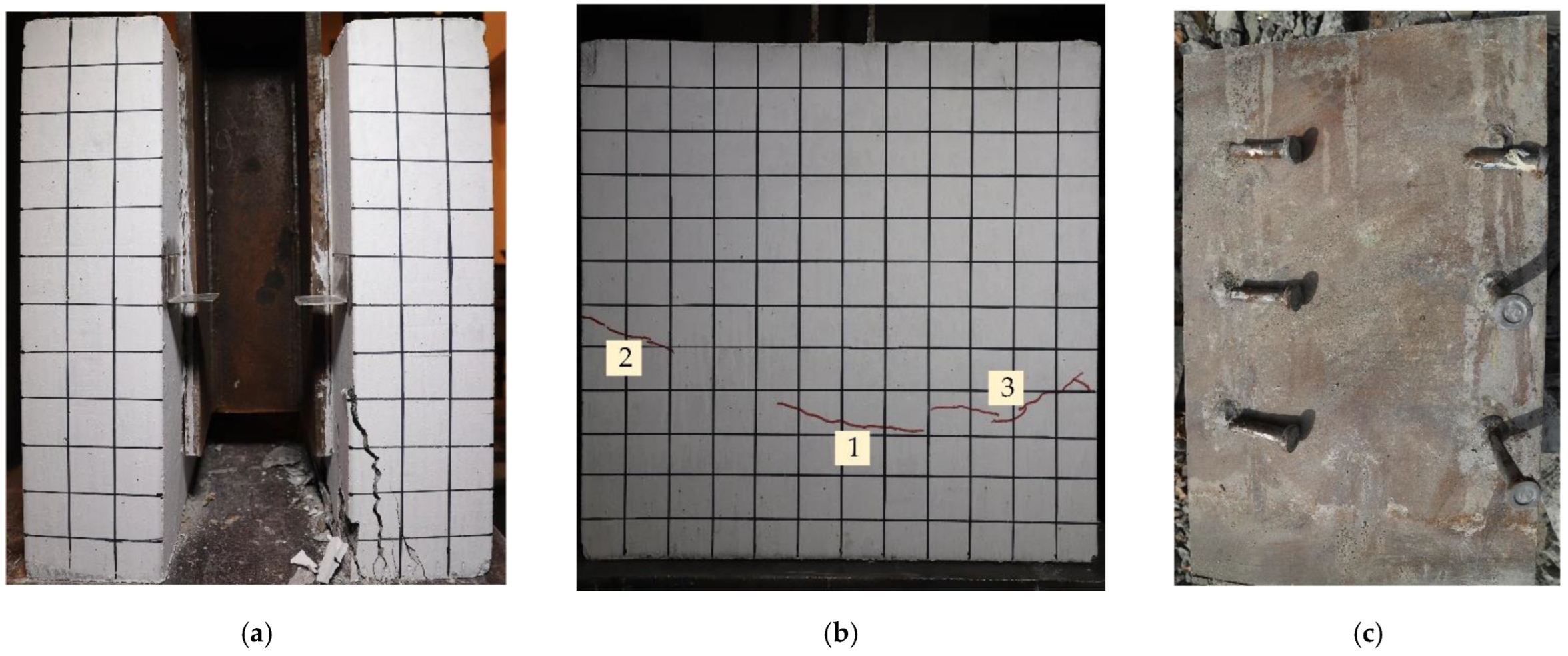
3.1. Failure Modes
3.1.1. Welded Stud Shear Connector
3.1.2. PBL Shear Connector
3.1.3. Composite Shear Connector with End-Bearing Concrete
3.1.4. Composite Shear Connector without End-Bearing Concrete
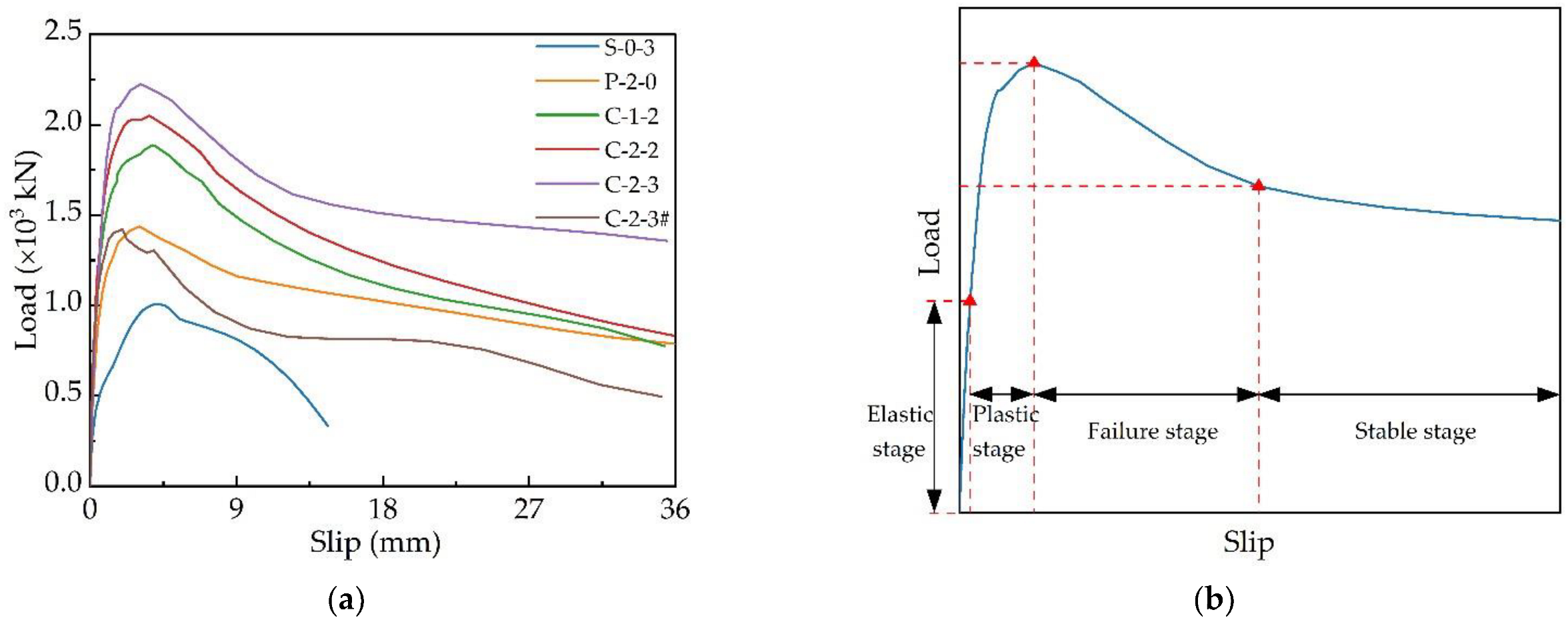
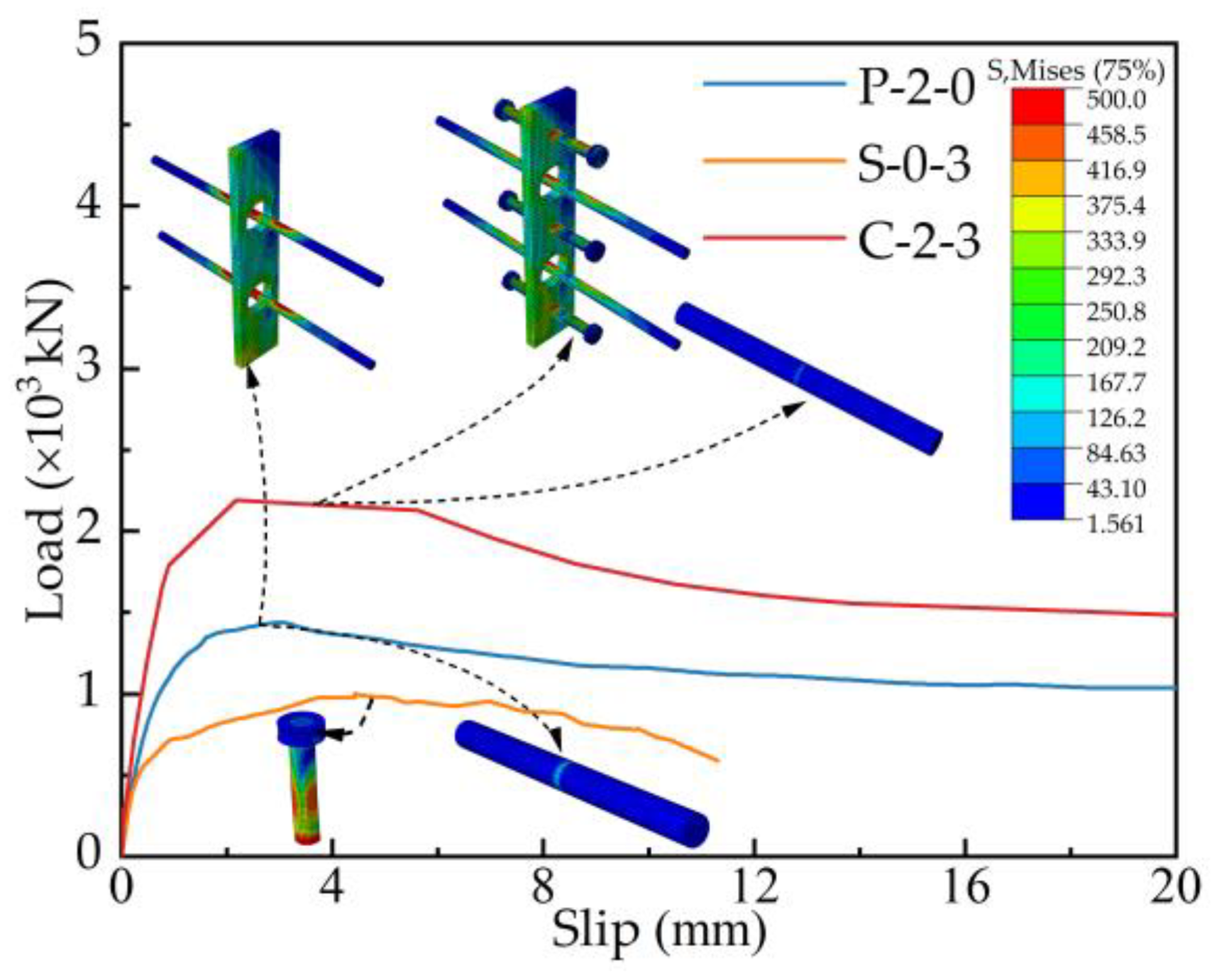
3.2. Load–Slip Curves
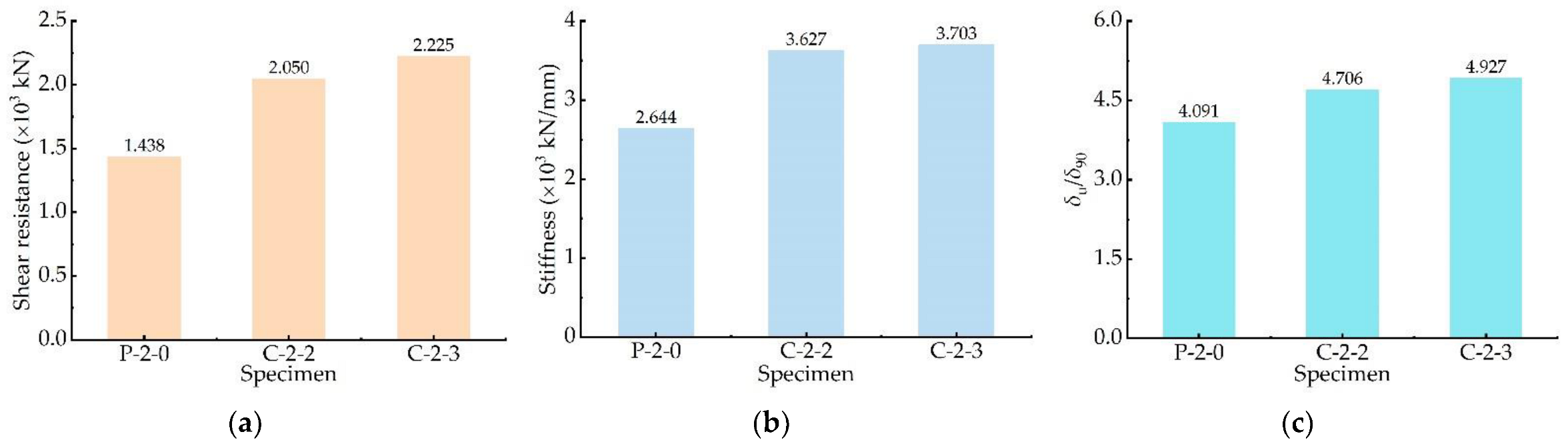
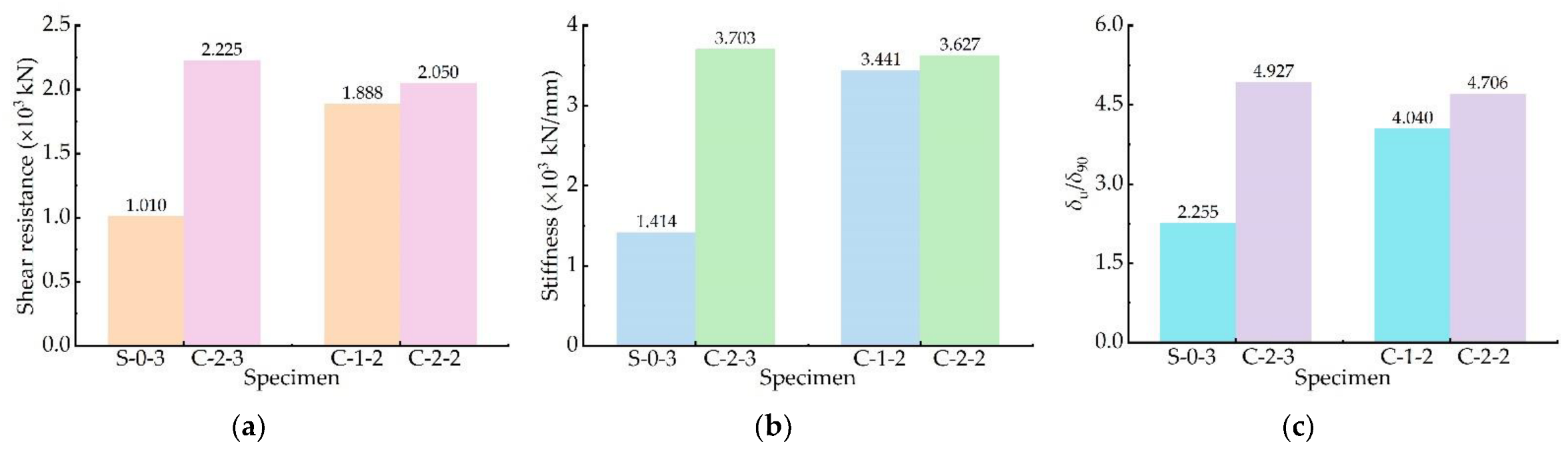
3.3. Result Analysis
3.3.1. Influence of Welded Stud Number
3.3.2. Influence of Perforated Hole Number
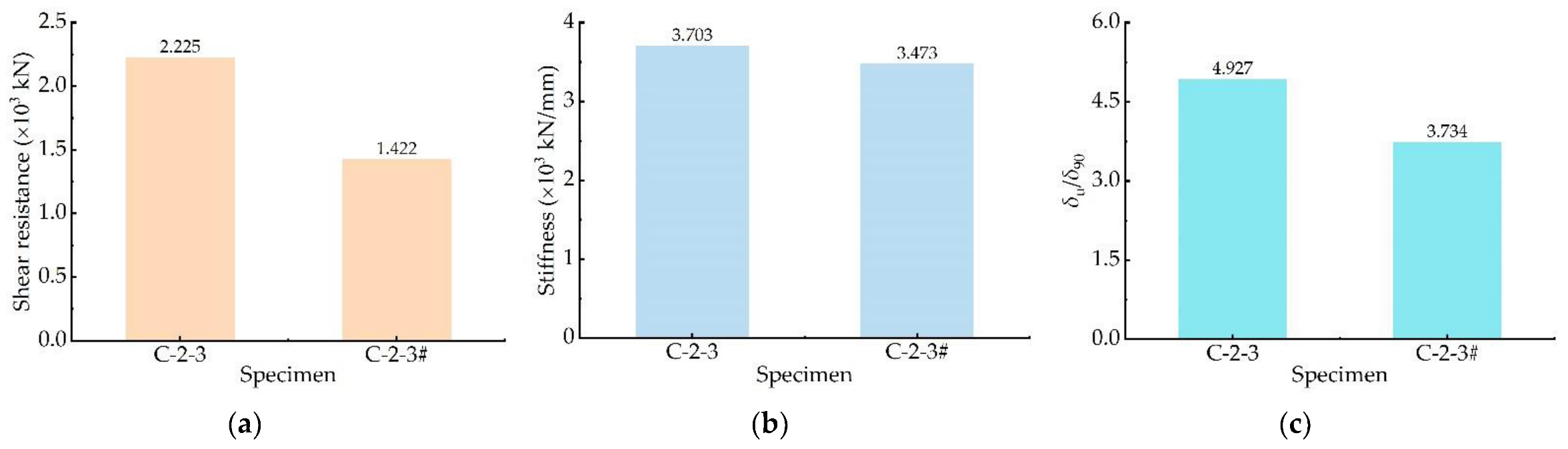
3.3.3. Influence of End-Bearing Mode
4. Numerical Analysis
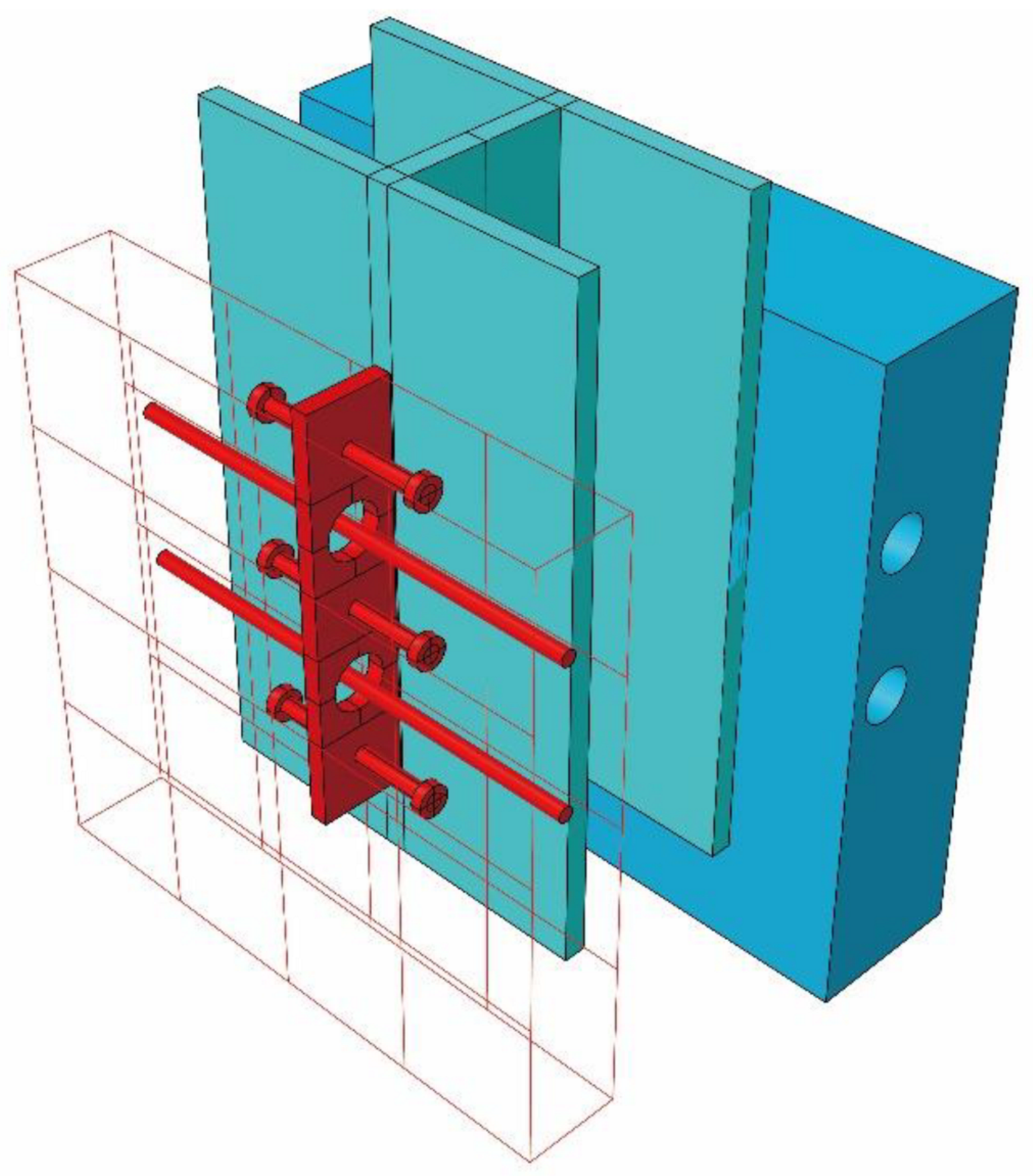
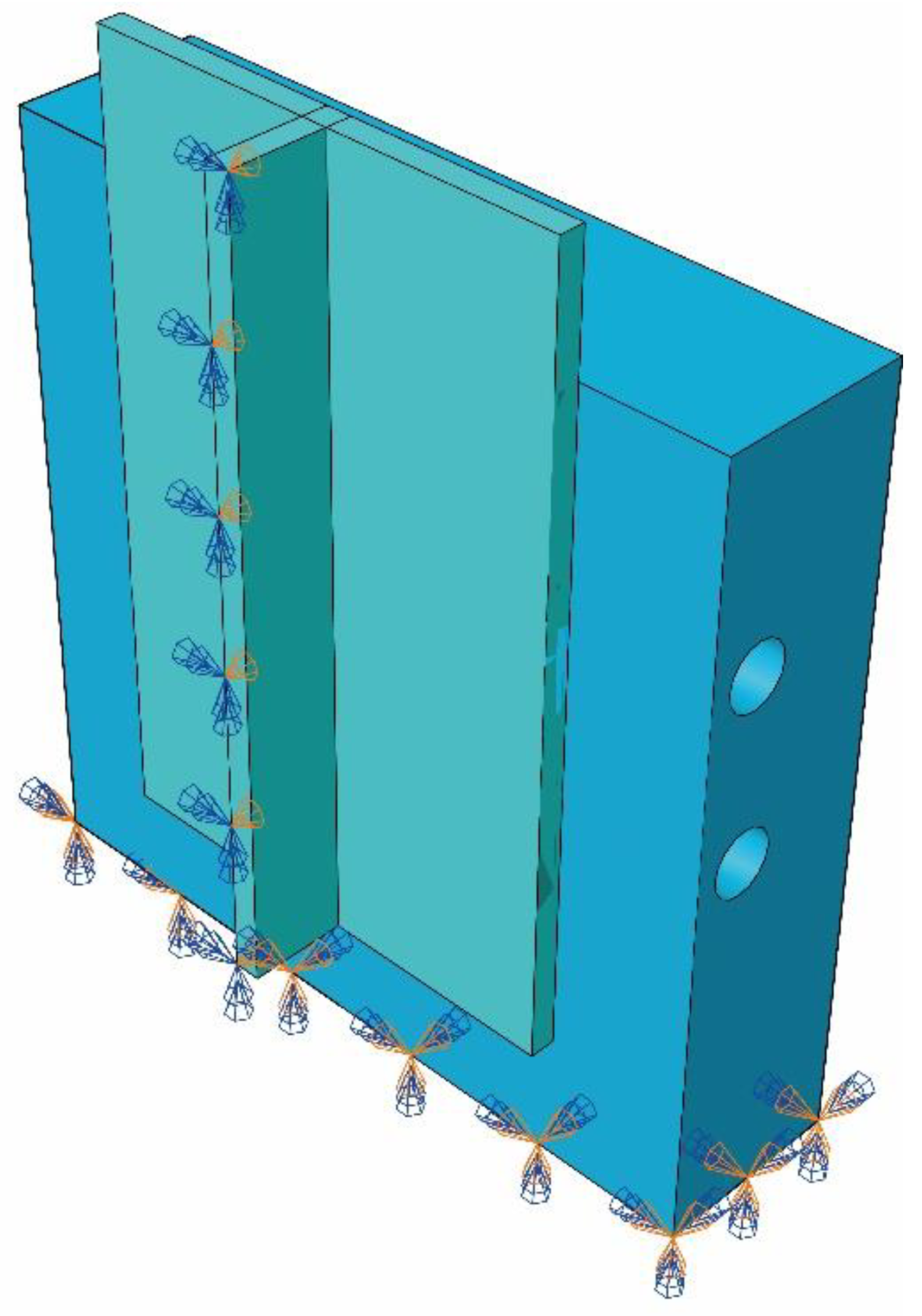
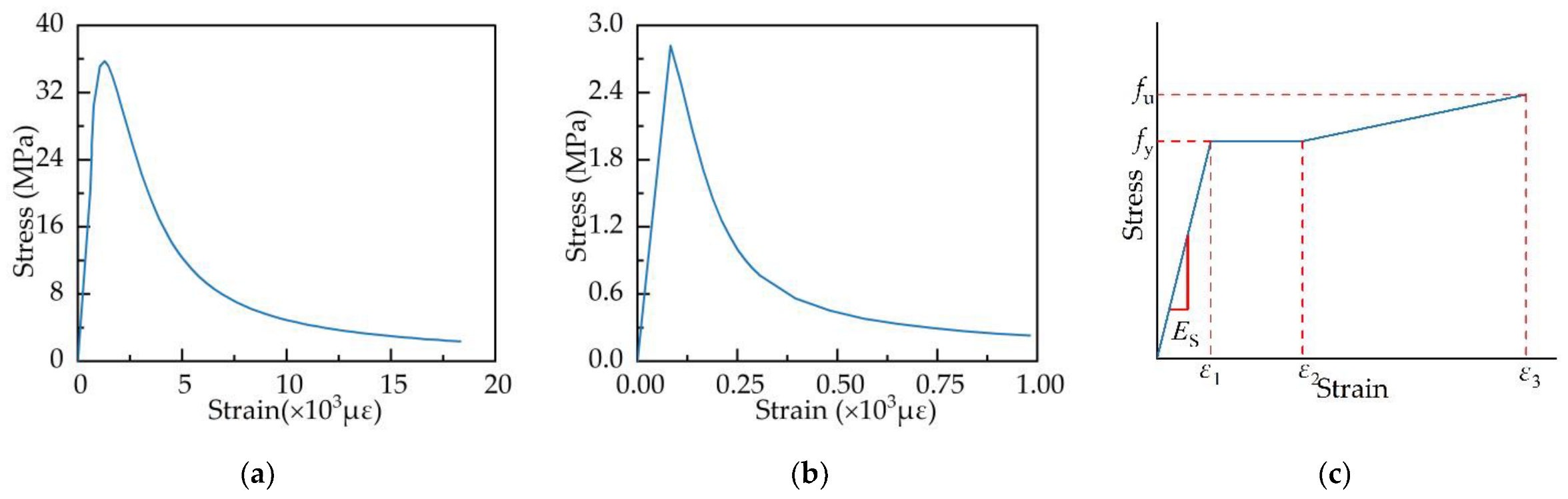
4.1. Finite Element Models
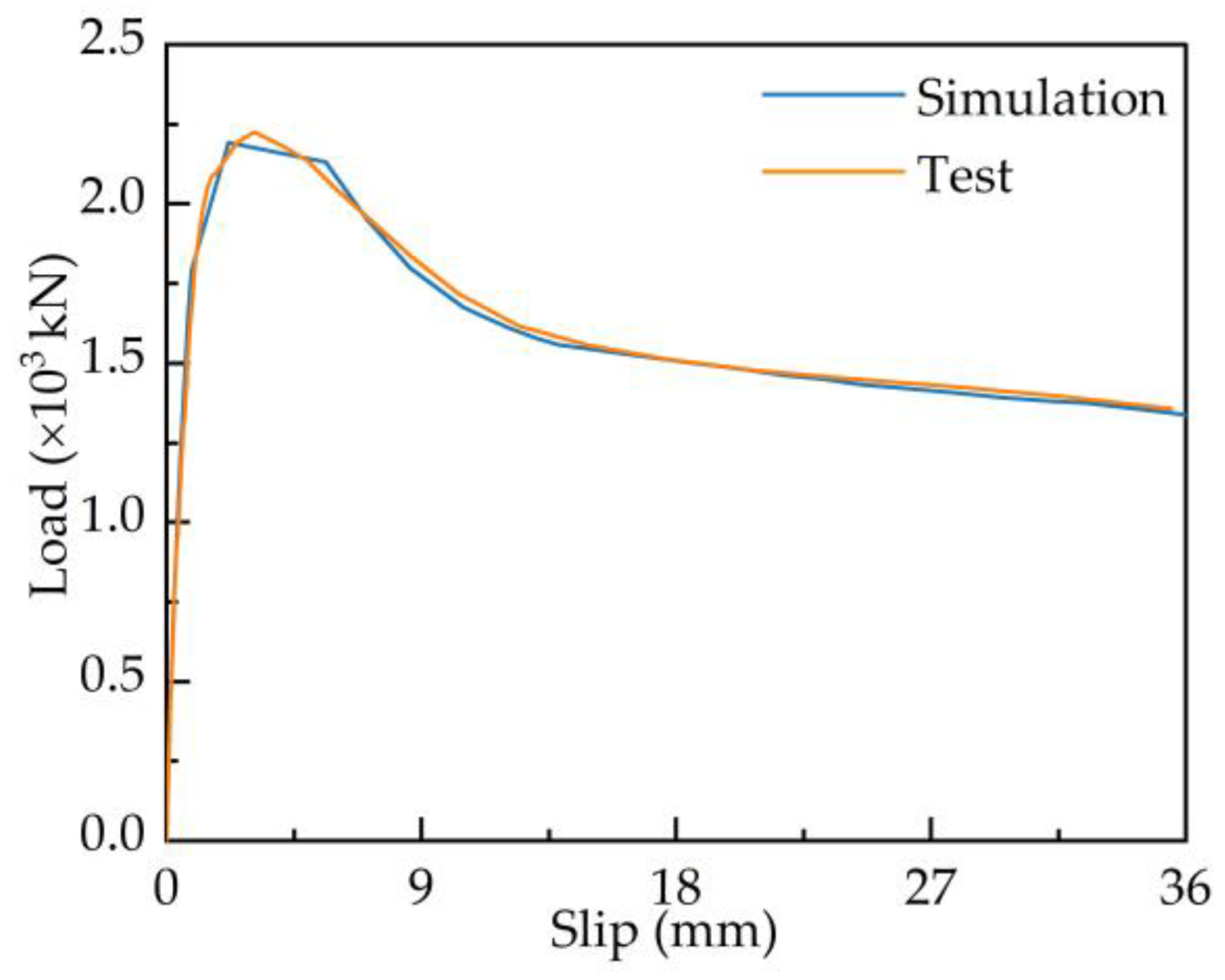
4.2. Model Validation
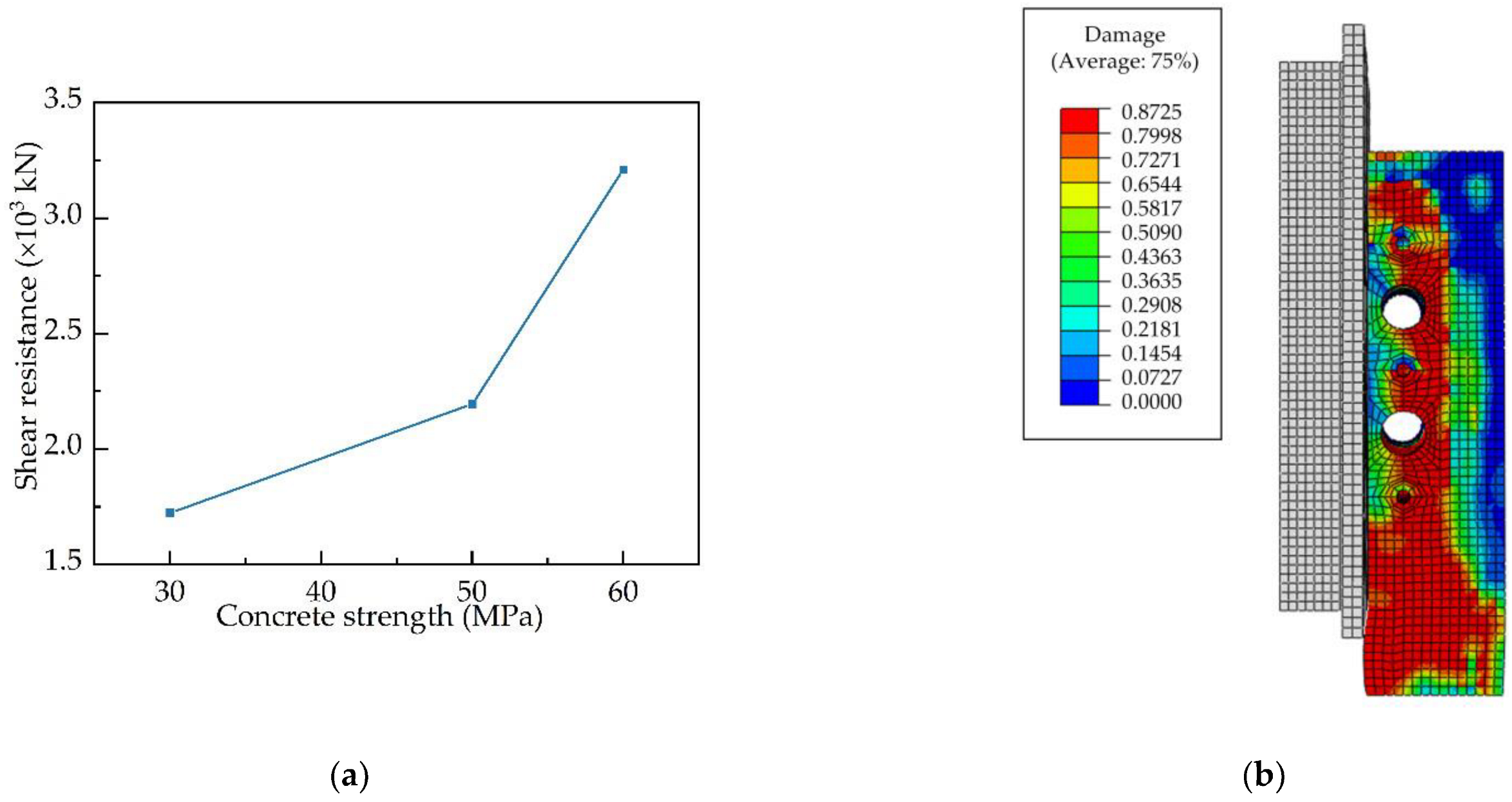
4.3. Parametric Analysis
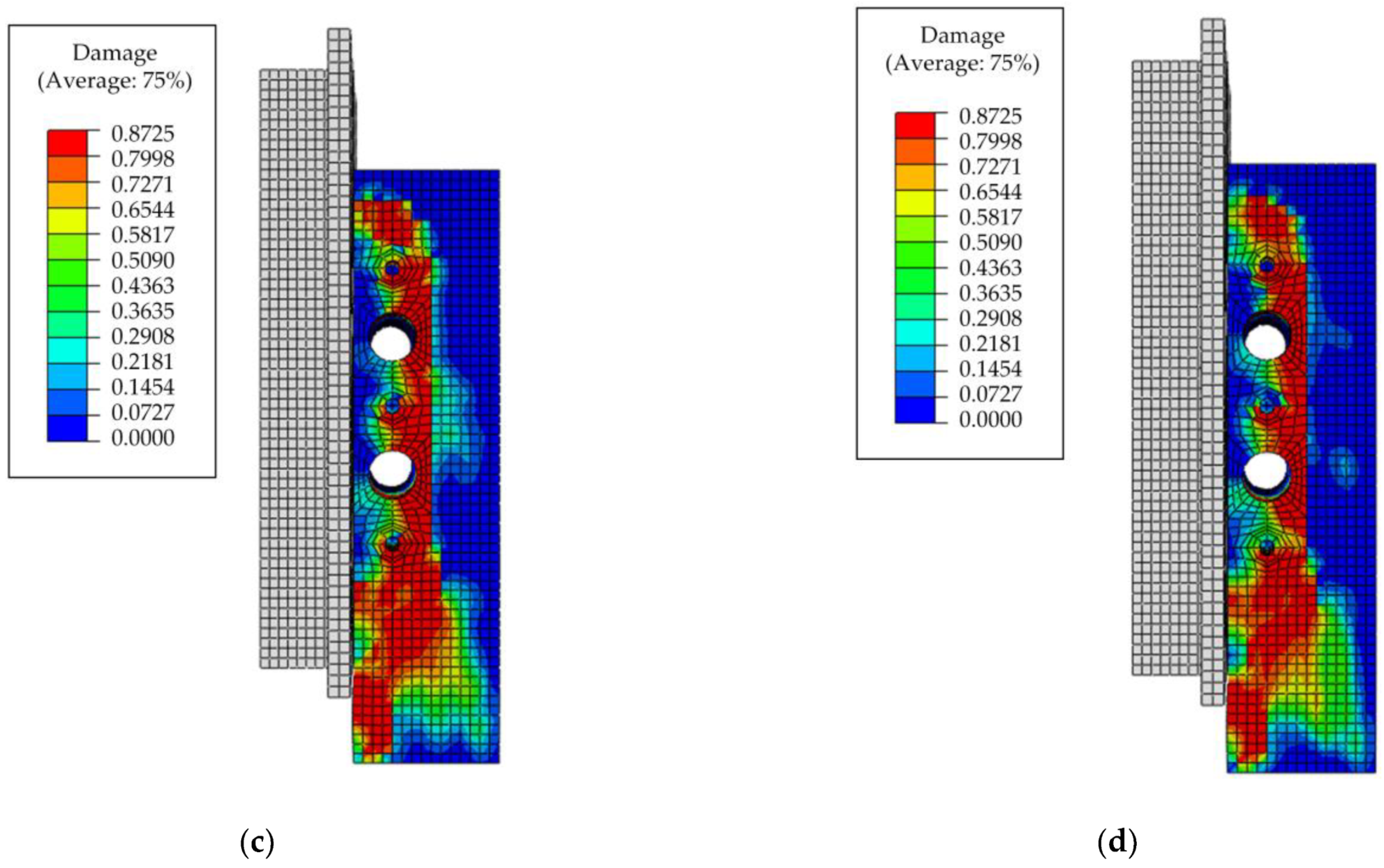
4.3.1. Concrete Strength
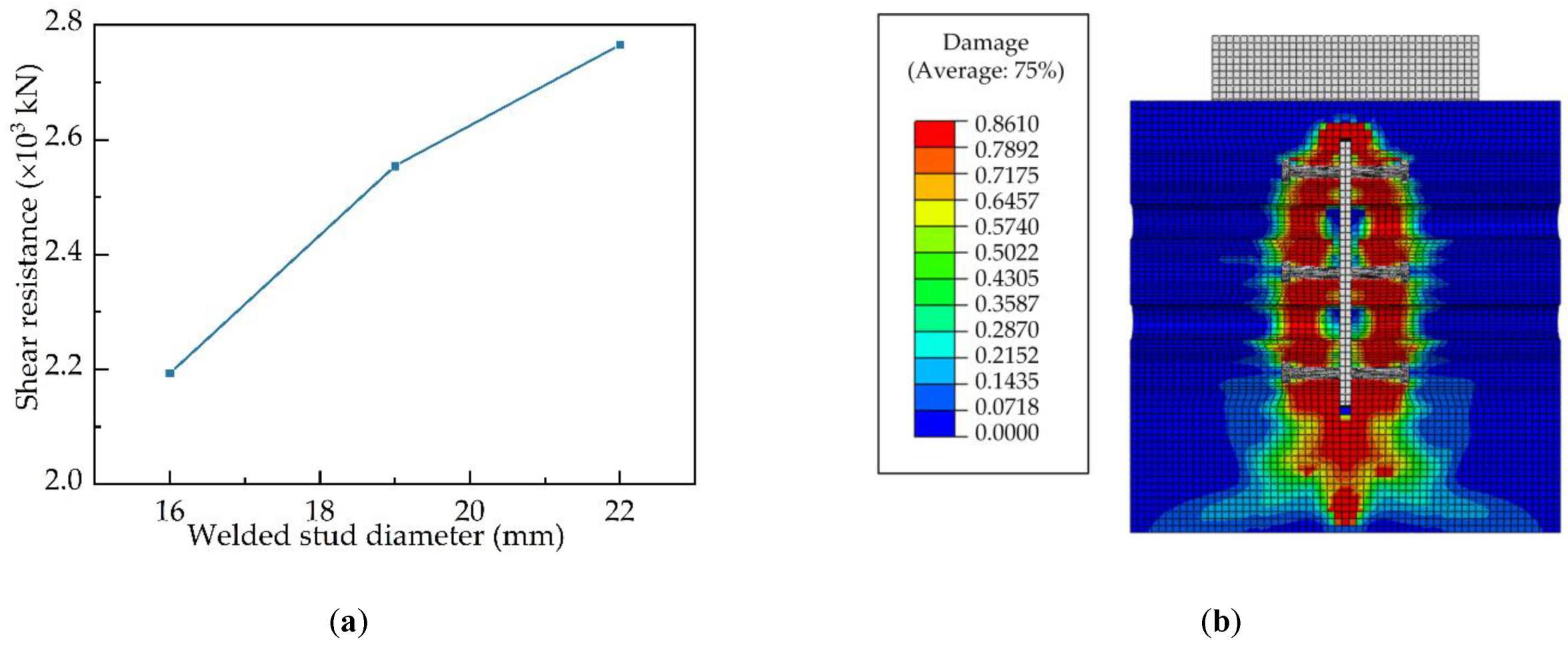
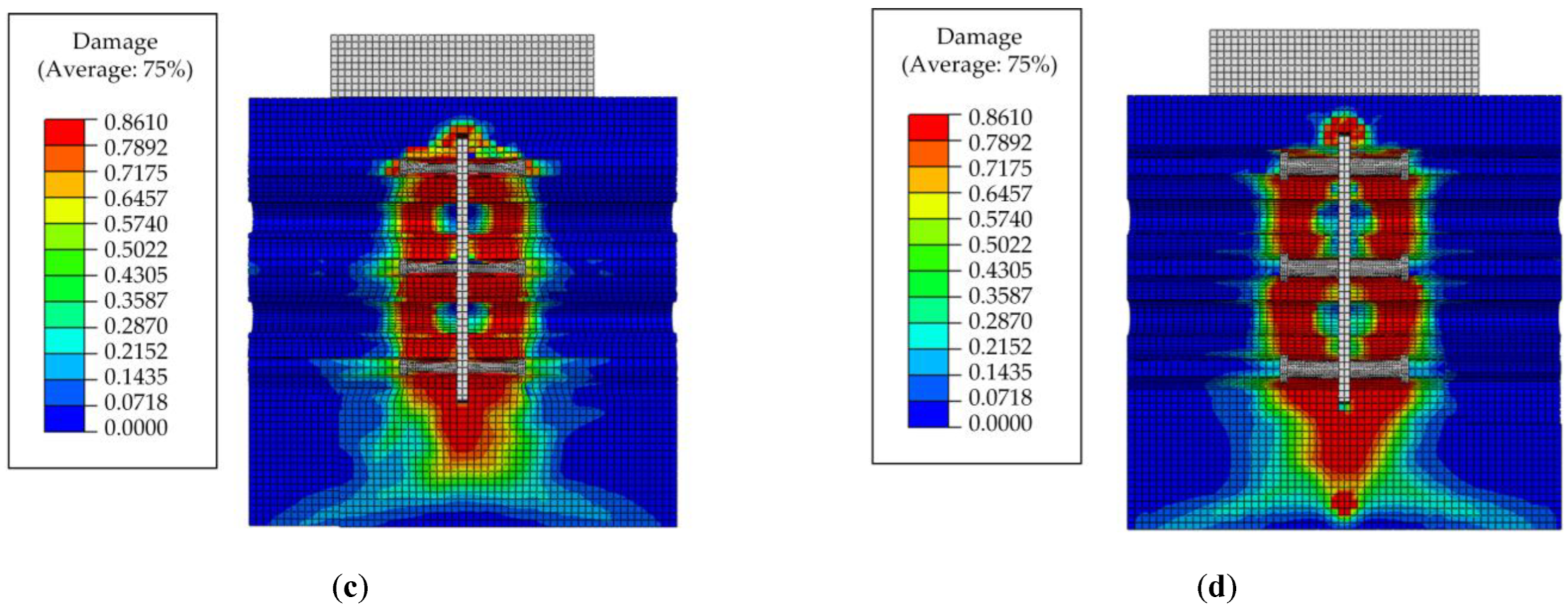
4.3.2. Welded Stud Diameter
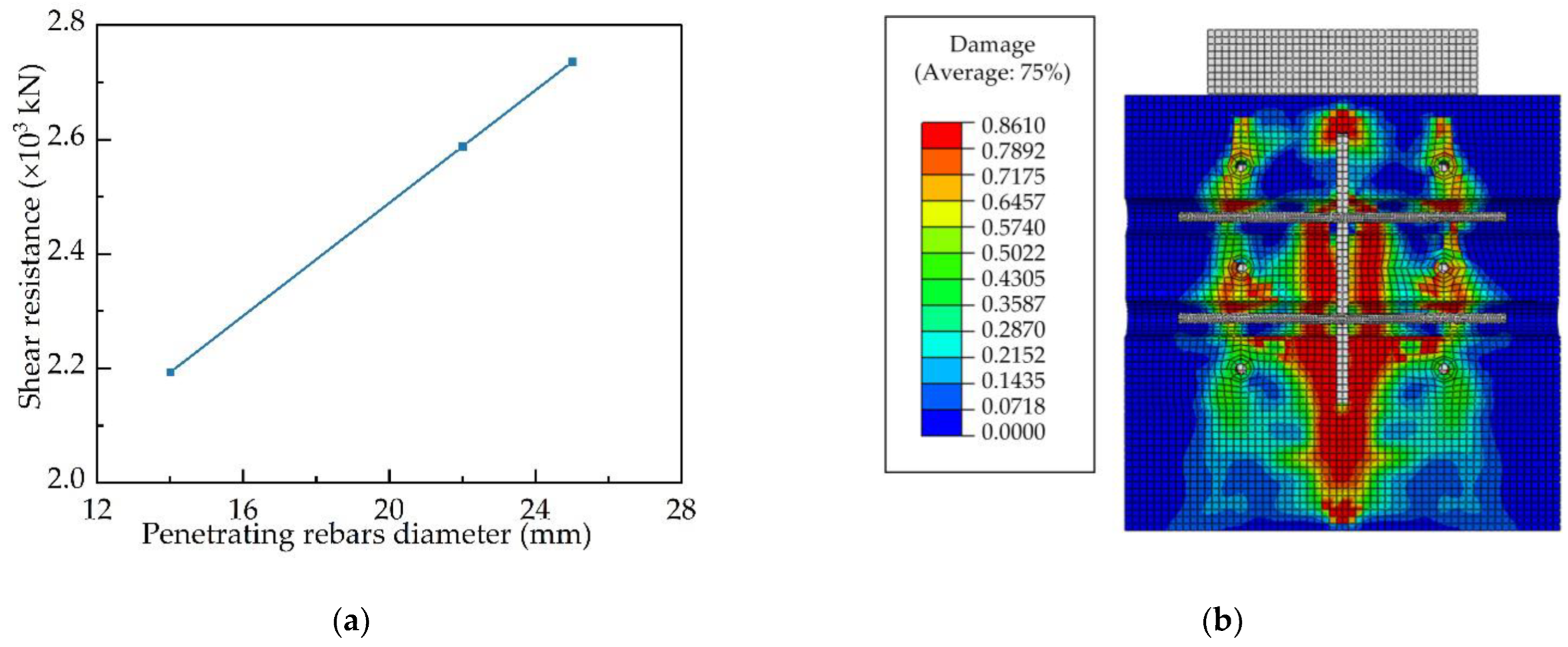
4.3.3. Penetrating Rebars Diameter
5. Conclusions
- (1)
- There are apparent differences in the failure modes of the three types of connectors. When the welded stud connector was damaged, the studs were cut off. Splitting failure occurred in the side of the concrete slab of the PBL connector, and the H-beam detached from the concrete. The concrete slab of the composite connectors with end-bearing concrete had splitting cracks, diagonal shear symmetric cracks, and bending deformation of the welded studs and penetrating rebars. For the composite connector without end-bearing concrete, brittle failure occurred in the concrete in the slotted area.
- (2)
- The composite connectors’ shear resistance, stiffness, and ductility meet the code requirements and are significantly better than those of welded stud connectors and PBL connectors. Increasing the number of welded studs and perforated holes and setting end-bearing concrete significantly improve the shear behaviours. The concrete in the slotted area is prone to brittle failure for the specimen without end-bearing concrete, reducing the overall performance.
- (3)
- Numerical investigations were carried out to parametrically analyse the composite connectors’ penetrating rebar diameter, welded stud diameter and concrete strength. The results indicate that the shear resistance increases as the penetrating rebar diameter, welded stud diameter, and concrete strength increase. In addition, as the strength of the concrete increases, the compressive damage area and overall damage level of the concrete can be effectively reduced.
- (4)
- Generally, the new composite shear connectors have a more excellent performance than conventional connectors. It has a promising application in bridge engineering. In addition, the noncontinuous arrangement of composite shear connectors is recommended in large-span composite bridges for ease of transport and to reduce welding deformation, which also can fully utilise the end-bearing concrete.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Q.; Jia, D.; Bao, Y.; Cheng, Z.; Xiao, L.; Bu, Y. Internal Force Transfer Effect-Based Fatigue Damage Evaluation for PBL Shear Connector Groups. J. Constr. Steel Res. 2018, 148, 469–478. [Google Scholar] [CrossRef]
- Classen, M. Limitations on the Use of Partial Shear Connection in Composite Beams with Steel T-sections and Uniformly Spaced Rib Shear Connectors. J. Constr. Steel Res. 2018, 142, 99–112. [Google Scholar] [CrossRef]
- Kim, S.; Kim, K.; Park, S.; Jung, C.; Choi, J. Comparison of Hysteretic Performance of Stubby Y-type Perfobond Rib and Stud Shear Connectors. Eng. Struct. 2017, 147, 144. [Google Scholar] [CrossRef]
- Zhang, S.; Jia, Y.; Ding, Y. Study on the Flexural Behavior of Steel-Concrete Composite Beams Based on the Shear Performance of Headed Stud Connectors. Buildings 2022, 12, 961. [Google Scholar] [CrossRef]
- Vasdravellis, G.; Valente, M.; Castiglioni, C.A. Dynamic Response of Composite Frames with Different Shear Connection Degree. J. Constr. Steel Res. 2009, 65, 2050–2061. [Google Scholar] [CrossRef]
- Xu, X.; Zeng, S.; He, W.; Hou, Z.; He, D.; Yang, T. Numerical Study on the Tensile Performance of Headed Stud Shear Connectors with Head-Sectional Damage. Materials 2022, 15, 2802. [Google Scholar] [CrossRef]
- He, S.; Fang, Z.; Fang, Y.; Liu, M.; Liu, L.; Mosallam, A.S. Experimental Study on Perfobond Strip Connector in Steel–Concrete Joints of Hybrid Bridges. J. Constr. Steel Res. 2016, 118, 169–179. [Google Scholar] [CrossRef]
- Wu, F.; Tang, W.; Xue, C.; Sun, G.; Feng, Y.; Zhang, H. Experimental Investigation on the Static Performance of Stud Connectors in Steel-HSFRC Composite Beams. Materials 2021, 14, 2744. [Google Scholar] [CrossRef]
- Peng, K.; Liu, L.; Wu, F.; Wang, R.; Lei, S.; Zhang, X. Experimental and Numerical Analyses of Stud Shear Connectors in Steel–SFRCC Composite Beams. Materials 2022, 15, 4665. [Google Scholar] [CrossRef]
- Zhang, H.; Ling, Z. Finite Element Modeling on Shear Performance of Grouted Stud Connectors for Steel–Timber Composite Beams. Materials 2022, 15, 1196. [Google Scholar] [CrossRef]
- Wu, F.; Feng, Y.; Dai, J.; Wang, G.; Zhang, J. Study on Mechanical Properties of Stud Shear Connectors in Steel-UHPC Composite Structures. Eng. Mech. 2022, 39, 222–234, 243. [Google Scholar]
- Viest, I.M. Investigation of Stud Shear Connectors for Composite Concrete and Steel T-Beams. ACI J. Proc. 1956, 52, 875–892. [Google Scholar] [CrossRef]
- Ollgaard, J.G.; Slutter, R.G.; Fisher, J.W. Shear Strength of Stud Connectors in Lightweight and Normal Weight Concrete. Eng. J. Am. Inst. Steel Constr. 1971, 8, 55–64. [Google Scholar]
- Nguyen, H.T.; Kim, S.E. Finite Element Modeling of Push-Out Tests for Large Stud Shear Connectors. J. Constr. Steel Res. 2009, 65, 1909–1920. [Google Scholar] [CrossRef]
- EN 1994-2; Eurocode-4: Design of Composite Steel and Concrete Structures, Part 2: Composite Bridges. CEN-European Committee for Standardization: Brussels, Belgium, 1997.
- AASHTO LRFD. Bridge Design Specifications, 3rd ed; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2004. [Google Scholar]
- Xu, C.; Sugiura, K. Parametric Push-Out Analysis on Group Studs Shear Connector Under Effect of Bending-Induced Concrete Cracks. J. Constr. Steel Res. 2013, 89, 86–97. [Google Scholar] [CrossRef]
- Dönmez, A.A. Size Effect on the Shear Capacity of Headed Studs. Adv. Struct. Eng. 2021, 24, 815–826. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Vitek, J.L. Compound Size Effect in Composite Beams with Softening Connectors. I: Energy Approach. J. Eng. Mech. 1999, 125, 1308–1314. [Google Scholar]
- Gattesco, N.; Giuriani, E.; Gubana, A. Low-Cycle Fatigue Test on Stud Shear Connectors. J. Struct. Eng. 1997, 123, 145–150. [Google Scholar] [CrossRef]
- Xu, C.; Su, Q.; Masuya, H. Static and Fatigue Behavior of the Stud Shear Connector in Lightweight Concrete. Int. J. Steel Struct. 2018, 18, 569–581. [Google Scholar] [CrossRef]
- Gu, J.; Liu, D.; Deng, W.; Zhang, J. Experimental Study on the Shear Resistance of a Comb-Type Perfobond Rib Shear Connector. J. Constr. Steel Res. 2019, 158, 279–289. [Google Scholar] [CrossRef]
- Leonhardt, F.; Andra, W.; Andra, H.; Harre, W. New Improved Bonding Means for Composite Loadbearing Structures with High Fatigue Strength. Beton-Und Stahlbetonbau 1987, 82, 325–331. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, B.; Cui, S.; Lui, E.M. Experimental Research on PBL Connectors Considering the Effects of Concrete Stress State and Other Connection Parameters. J. Bridge Eng. 2018, 23, 04017125. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Y. Experimental Study on Mechanical Behavior of PBL Shear Connectors. J. Bridge Eng. 2018, 23, 04018062. [Google Scholar] [CrossRef]
- Deng, W.; Xiong, Y.; Liu, D.; Zhang, J. Static and Fatigue Behavior of Shear Connectors for a Steel-Concrete Composite Girder. J. Constr. Steel Res. 2019, 159, 134–146. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, C.; Deng, K.; Wang, W. Load Sharing and Slip Distribution in Multiple Holes of a Perfobond Rib Shear Connector. J. Struct. Eng. 2018, 144, 04018147. [Google Scholar] [CrossRef]
- Kim, H.; Jeong, Y. Experimental Investigation on Behaviour of Steel–Concrete Composite Bridge Decks with Perfobond Ribs. J. Constr. Steel Res. 2006, 62, 463–471. [Google Scholar] [CrossRef]
- Wu, F.; Liu, S.; Xue, C.; Yang, K.; Feng, Y.; Zhang, H. Experimental Study on the Mechanical Properties of Perfobond Rib Shear Connectors with Steel Fiber High Strength Concrete. Materials 2021, 14, 3345. [Google Scholar] [CrossRef]
- Su, Q.; Wang, W.; Luan, H.; Yang, G. Experimental Research on Bearing Mechanism of Perfobond Rib Shear Connectors. J. Constr. Steel Res. 2014, 95, 22–31. [Google Scholar] [CrossRef]
- Zhang, Q.; Pei, S.; Cheng, Z.; Bao, Y.; Li, Q. Theoretical and Experimental Studies of the Internal Force Transfer Mechanism of Perfobond Rib Shear Connector Group. J. Bridge Eng. 2017, 22, 04016112. [Google Scholar] [CrossRef]
- Liu, Y.; Xin, H.; Liu, Y. Load Transfer Mechanism and Fatigue Performance Evaluation of Suspender-Girder Composite Anchorage Joints at Serviceability Stage. J. Constr. Steel Res. 2018, 145, 82–96. [Google Scholar] [CrossRef]
- Kim, S.; Choi, K.; Park, S.; Park, S.; Jung, C. Experimental Shear Resistance Evaluation of Y-type Perfobond Rib Shear Connector. J. Constr. Steel Res. 2013, 82, 1–18. [Google Scholar] [CrossRef]
- Su, Q.; Li, C.; Wang, W. Experiment on Shear Transferring Mechanics of Perfobond Rib Connector. J. Tongji Univ. (Nat. Sci.) 2013, 41, 1623–1629. [Google Scholar]
- Wang, B.; Huang, Q.; Liu, X. Comparison of Static and Fatigue Behaviors between Stud and Perfobond Shear Connectors. KSCE J. Civ. Eng. 2019, 23, 217–227. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, S.; Rong, B. Investigation on Shear Behavior of Studs and PBL Shear Connectors in Steel-Concrete Hybrid Bridge Girder. Structures 2022, 43, 1422–1435. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Y. Experimental Study on the Shear Capacity of PBL Shear Connectors. Eng. Mech. 2018, 35, 89–96. [Google Scholar]
- Kim, S.; Choi, J.; Park, S.; Ahn, J.; Jung, C. Behavior of Composite Girder with Y-type Perfobond Rib Shear Connectors. J. Constr. Steel Res. 2014, 103, 275–289. [Google Scholar] [CrossRef]
- Kim, S.; Heo, W.; Woo, K.; Jung, C.; Park, S. End-Bearing Resistance of Y-type Perfobond Rib According to Rib Width–Height Ratio. J. Constr. Steel Res. 2014, 103, 101–116. [Google Scholar] [CrossRef]
- Kim, S.; Park, S.; Heo, W.; Jung, C. Shear Resistance Characteristic and Ductility of Y-type Perfobond Rib Shear Connector. Steel Compos. Struct. 2015, 18, 497–517. [Google Scholar] [CrossRef]
- Kim, S.; Park, S.; Kim, K.; Jung, C. Generalized Formulation for Shear Resistance on Y-type Perfobond Rib Shear Connectors. J. Constr. Steel Res. 2017, 128, 245–260. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2011.

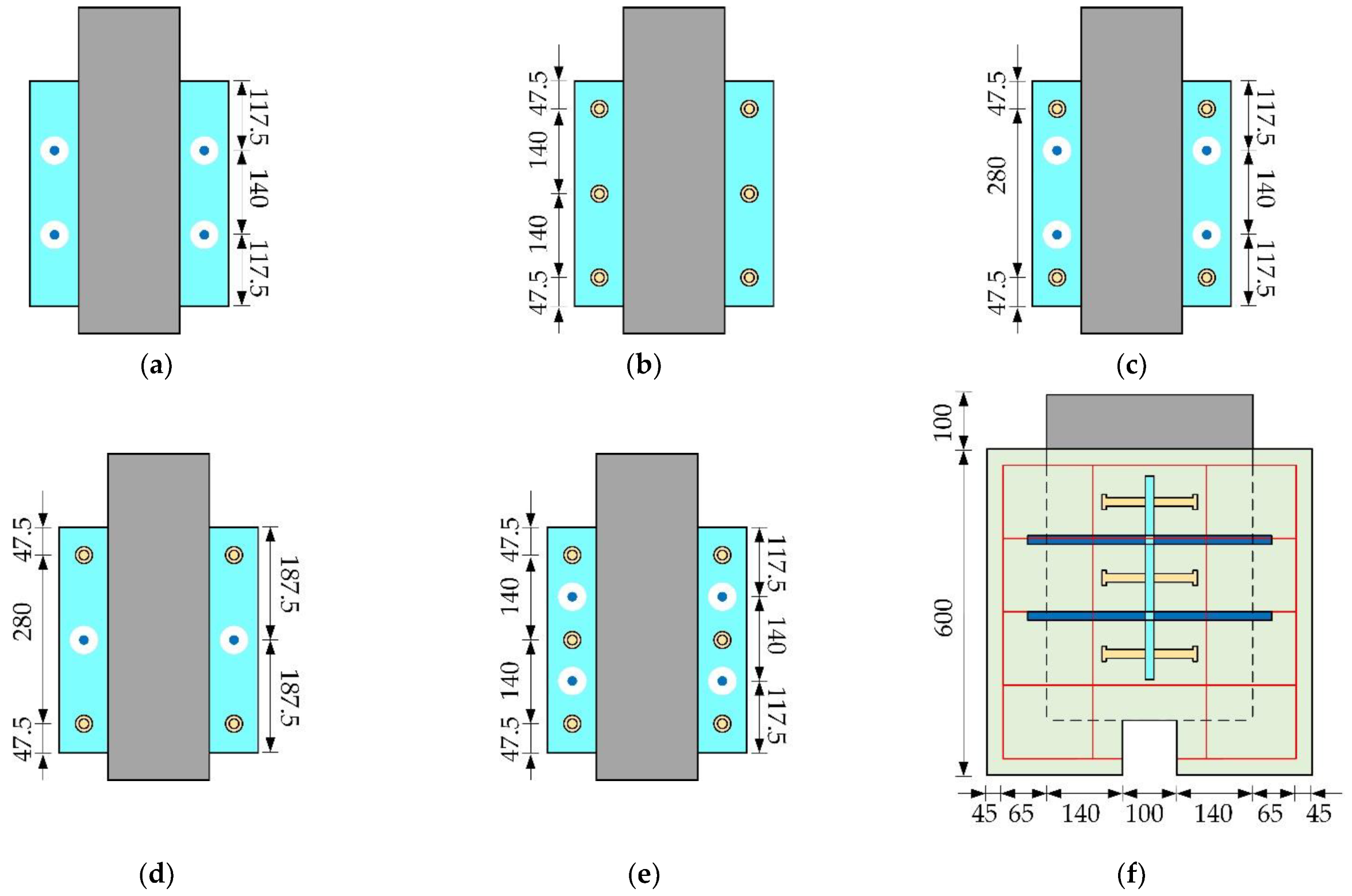








| Specimens | Perforated Steel Plate | Hole | Penetrating Rebar | Welded Stud | |||||
|---|---|---|---|---|---|---|---|---|---|
| Height (mm) | Thickness (mm) | Diameter (mm) | Number | Diameter (mm) | Number | Length (mm) | Diameter (mm) | Number | |
| S-0-3 | / | / | / | / | / | / | 80 | 16 | 2 × 3 |
| P-2-0 | 80 | 16 | 50 | 2 | 14 | 2 | / | / | / |
| C-1-2 | 80 | 16 | 50 | 1 | 14 | 1 | 80 | 16 | 2 × 2 |
| C-2-2 | 80 | 16 | 50 | 2 | 14 | 2 | 80 | 16 | 2 × 2 |
| C-2-3 | 80 | 16 | 50 | 2 | 14 | 2 | 80 | 16 | 2 × 3 |
| C-2-3# | 80 | 16 | 50 | 2 | 14 | 2 | 80 | 16 | 2 × 3 |
| Material | Yield Strength fy (MPa) | Ultimate Strength fu (MPa) | Elastic Modulus Es (GPa) |
|---|---|---|---|
| Structural rebar | 554 | 700 | 206 |
| Penetrating rebar | 483 | 677 | 212 |
| Welded stud | 367 | 420 | 207 |
| H-beam | 383 | 501 | 209 |
| Perforated steel plate | 419 | 561 | 208 |
| Specimen | Pmax (kN) | Prk (kN) | δ90 (mm) | δu (mm) | K (kN/mm) | δu/δ90 |
|---|---|---|---|---|---|---|
| S-0-3 | 1010.13 | 909.12 | 2.68 | 6.04 | 1413.86 | 2.25 |
| P-2-0 | 1438.38 | 1294.54 | 1.50 | 6.15 | 2644.46 | 4.09 |
| C-1-2 | 1887.87 | 1699.08 | 1.64 | 6.62 | 3440.67 | 4.04 |
| C-2-2 | 2049.69 | 1844.72 | 1.38 | 6.51 | 3626.65 | 4.71 |
| C-2-3 | 2225.26 | 2002.74 | 1.33 | 6.55 | 3702.63 | 4.93 |
| C-2-3# | 1422.03 | 1279.83 | 1.11 | 4.15 | 3473.36 | 3.73 |
| Number | Contact Type | Normal Behavior | Tangential Behavior |
|---|---|---|---|
| Contact 1 | General Contact | Hard contact | 0.1 (Penalty function) |
| Contact 2 | General Contact | Hard contact | 0.904 (Penalty function) |
| Material | fy (MPa) | fu (MPa) | ε1 | ε2 | ε3 |
|---|---|---|---|---|---|
| Structural rebar | 554 | 700 | 0.002689 | 0.010609 | 0.024509 |
| Penetrating rebar | 483 | 677 | 0.002278 | 0.011525 | 0.025745 |
| Welded stud | 367 | 420 | 0.001773 | 0.009773 | 0.013582 |
| H-beam | 383 | 501 | 0.001833 | 0.017342 | 0.047949 |
| Perforated steel plate | 419 | 561 | 0.002014 | 0.019272 | 0.050558 |
| Specimen | Test Result Ft (kN) | Simulation Fs (kN) | Accuracy (Fs/Ft) |
|---|---|---|---|
| S-0-3 | 1010.13 | 1000.08 | 99.01% |
| P-2-0 | 1438.38 | 1400.23 | 97.35% |
| C-1-2 | 1887.87 | 1817.63 | 96.28% |
| C-2-2 | 2049.69 | 1983.49 | 96.77% |
| C-2-3 | 2225.26 | 2193.18 | 98.56% |
| C-2-3# | 1422.03 | 1356.04 | 95.36% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, C.; Fan, Z.; Wu, F.; Liu, L.; He, L.; Cui, X. Research on the Shear Behaviour of Composite Shear Connectors. Buildings 2022, 12, 1726. https://doi.org/10.3390/buildings12101726
Xue C, Fan Z, Wu F, Liu L, He L, Cui X. Research on the Shear Behaviour of Composite Shear Connectors. Buildings. 2022; 12(10):1726. https://doi.org/10.3390/buildings12101726
Chicago/Turabian StyleXue, Chengfeng, Zhou Fan, Fangwen Wu, Laijun Liu, Lanqing He, and Xuan Cui. 2022. "Research on the Shear Behaviour of Composite Shear Connectors" Buildings 12, no. 10: 1726. https://doi.org/10.3390/buildings12101726
APA StyleXue, C., Fan, Z., Wu, F., Liu, L., He, L., & Cui, X. (2022). Research on the Shear Behaviour of Composite Shear Connectors. Buildings, 12(10), 1726. https://doi.org/10.3390/buildings12101726






