Architectural Characteristics of Different Configurations Based on New Geometric Determinations for the Conoid
Abstract
1. Introduction
Outline of the Problem
2. Methods and Materials
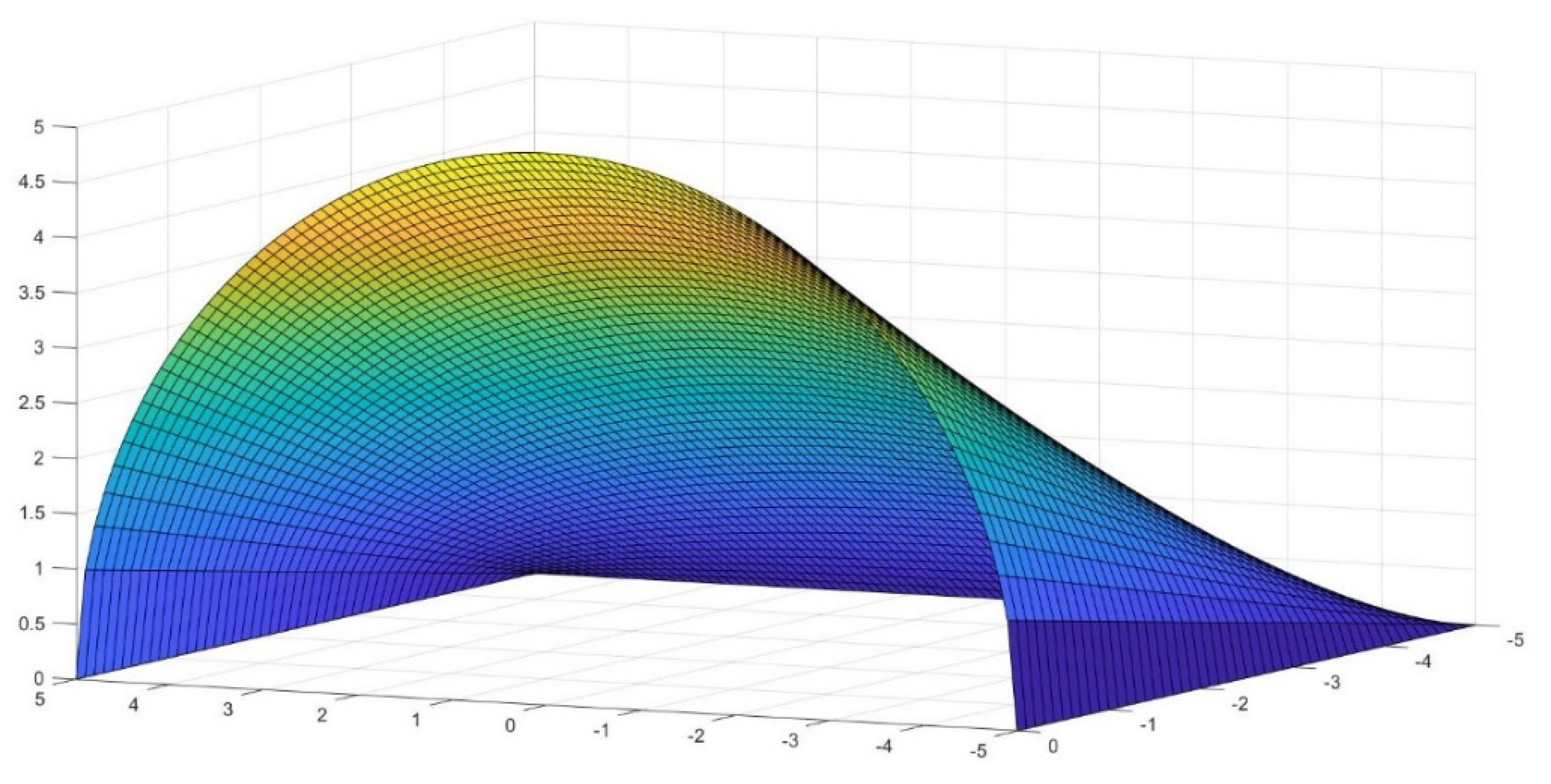
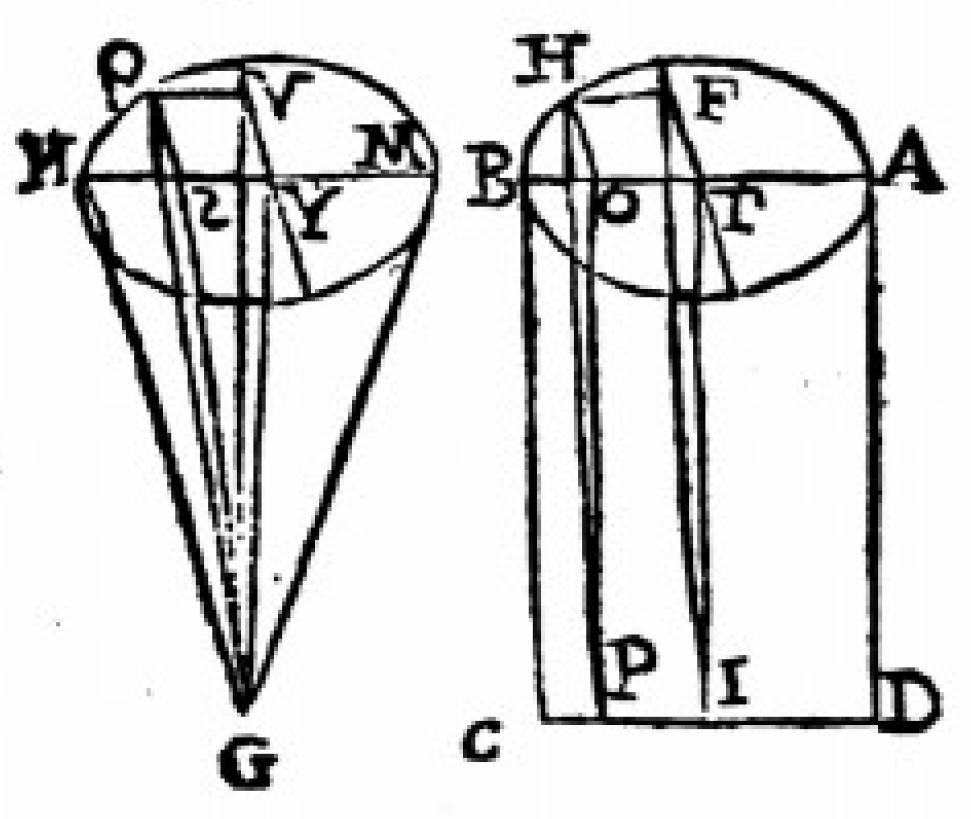
2.1. Resolution of the Proposed Approximation
2.2. Discussion of the Findings
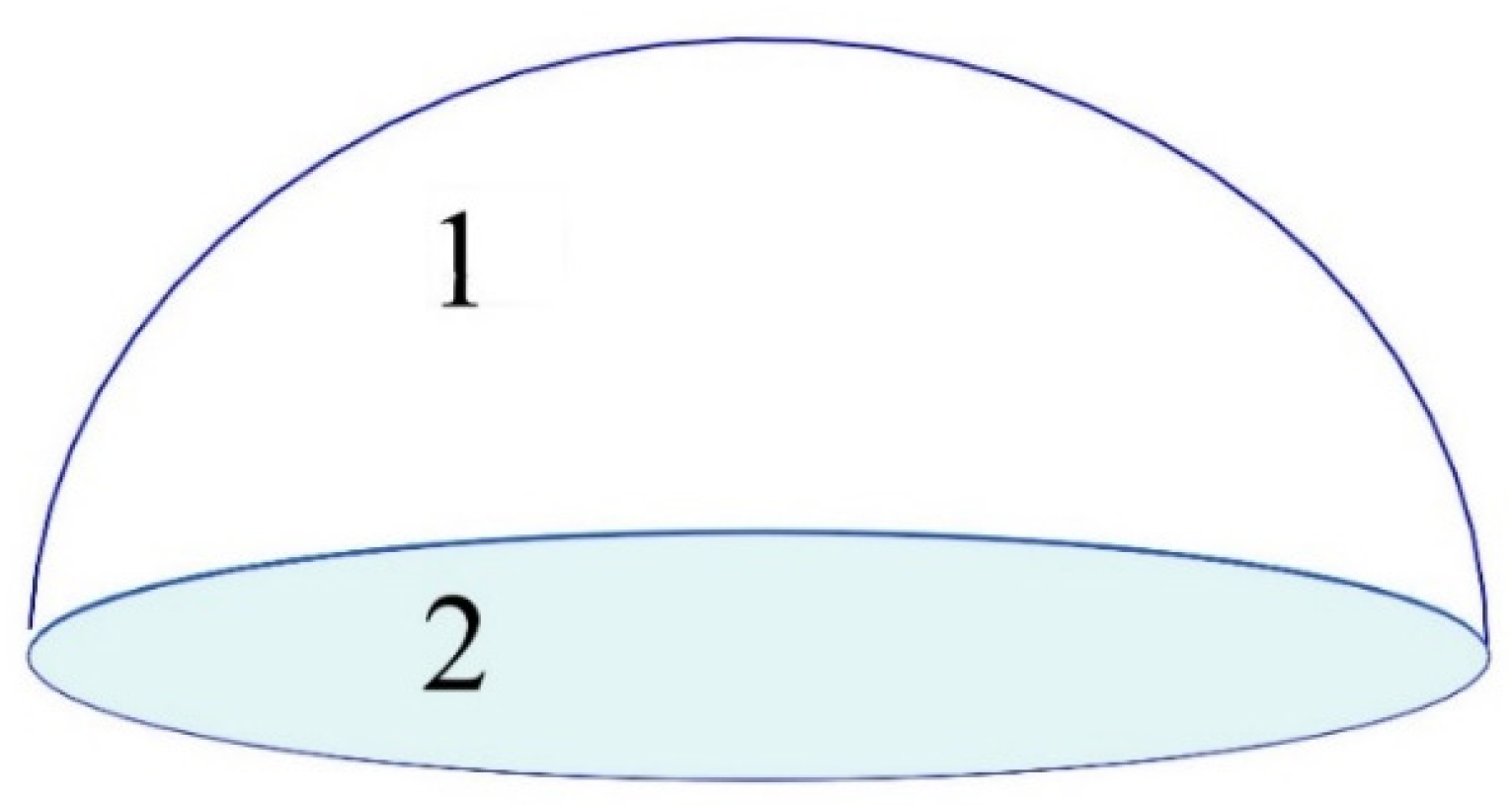
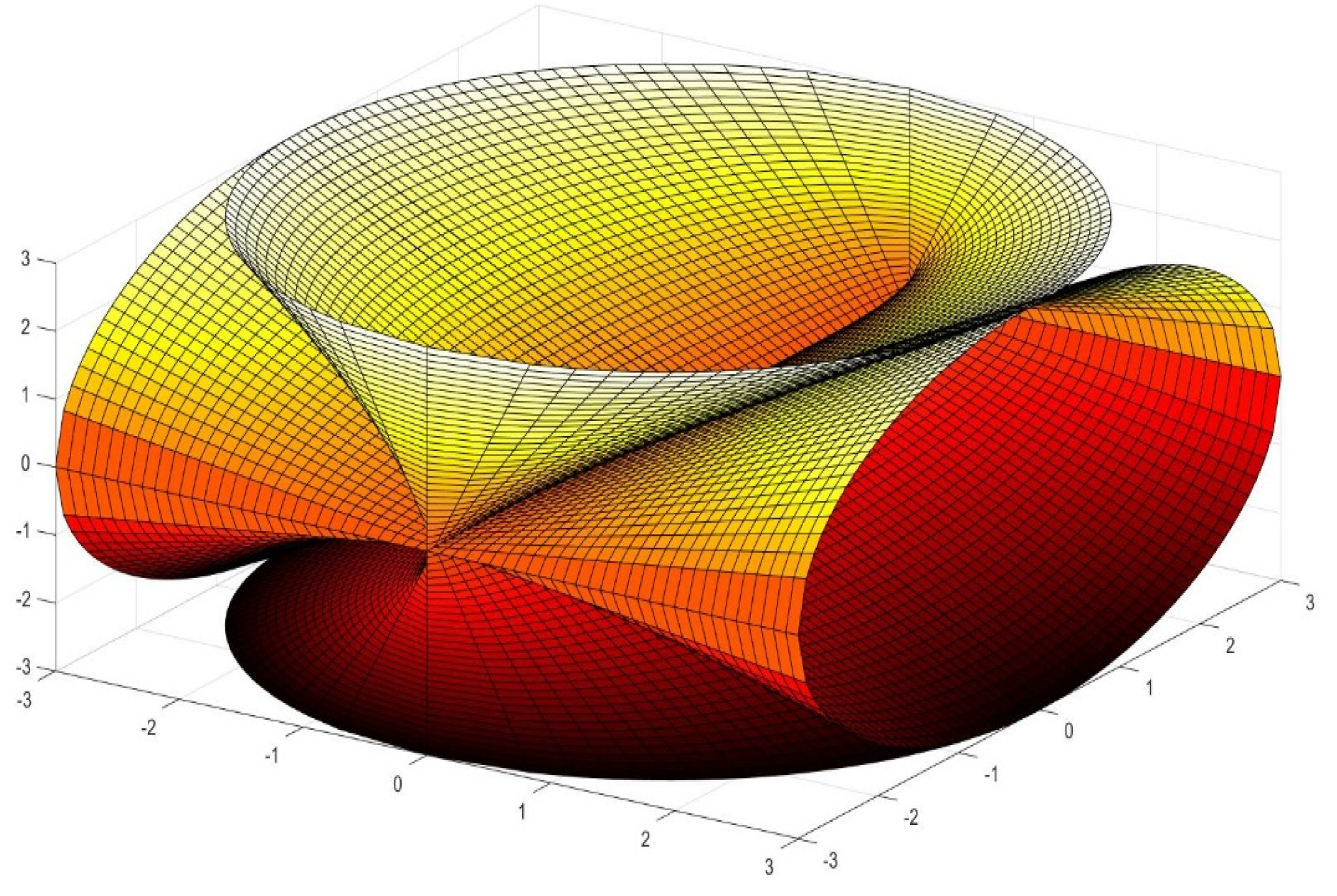
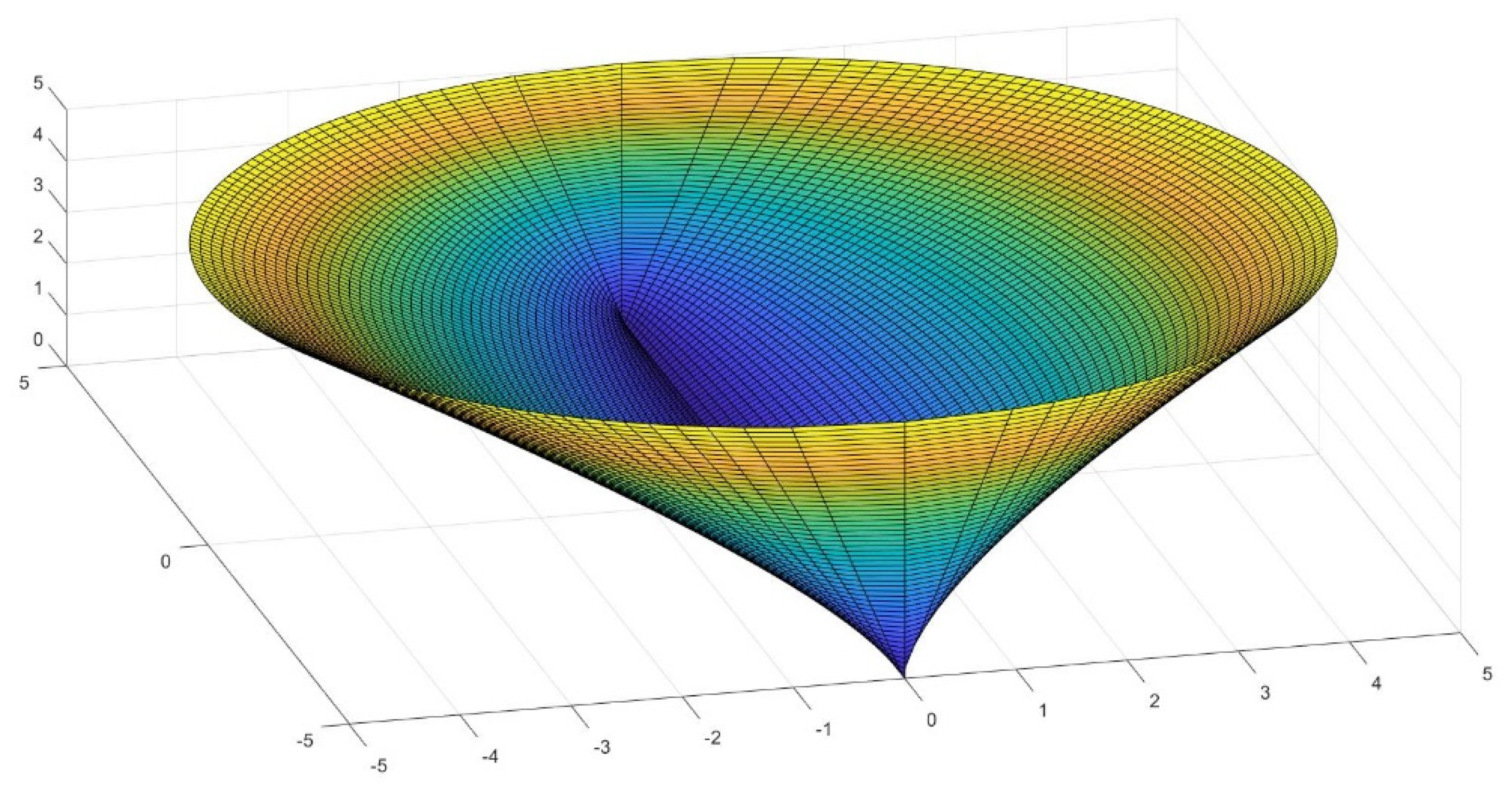
2.3. Definition of the Antisphera
2.4. Comparison with Other Approximate Computing Methods
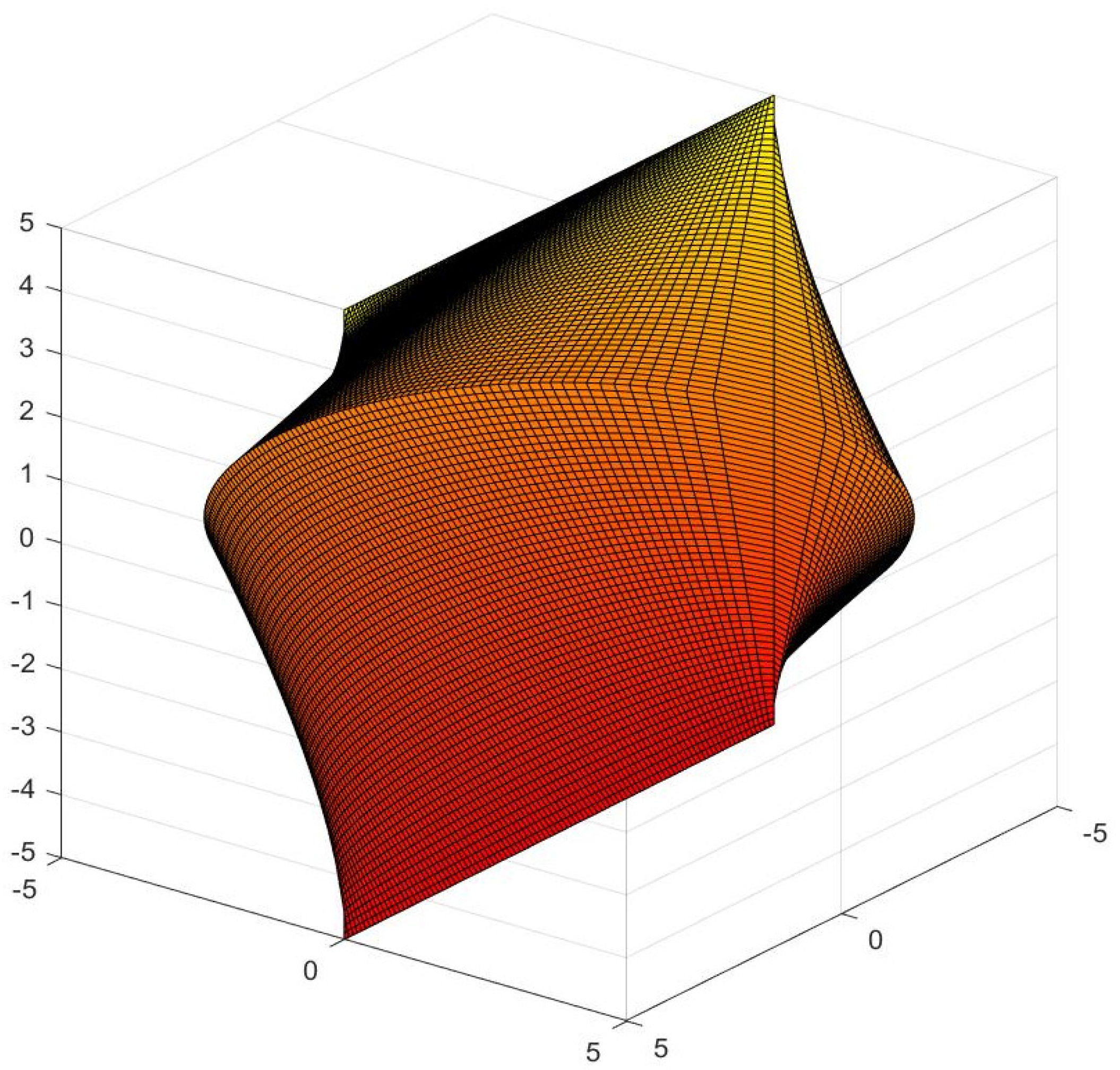
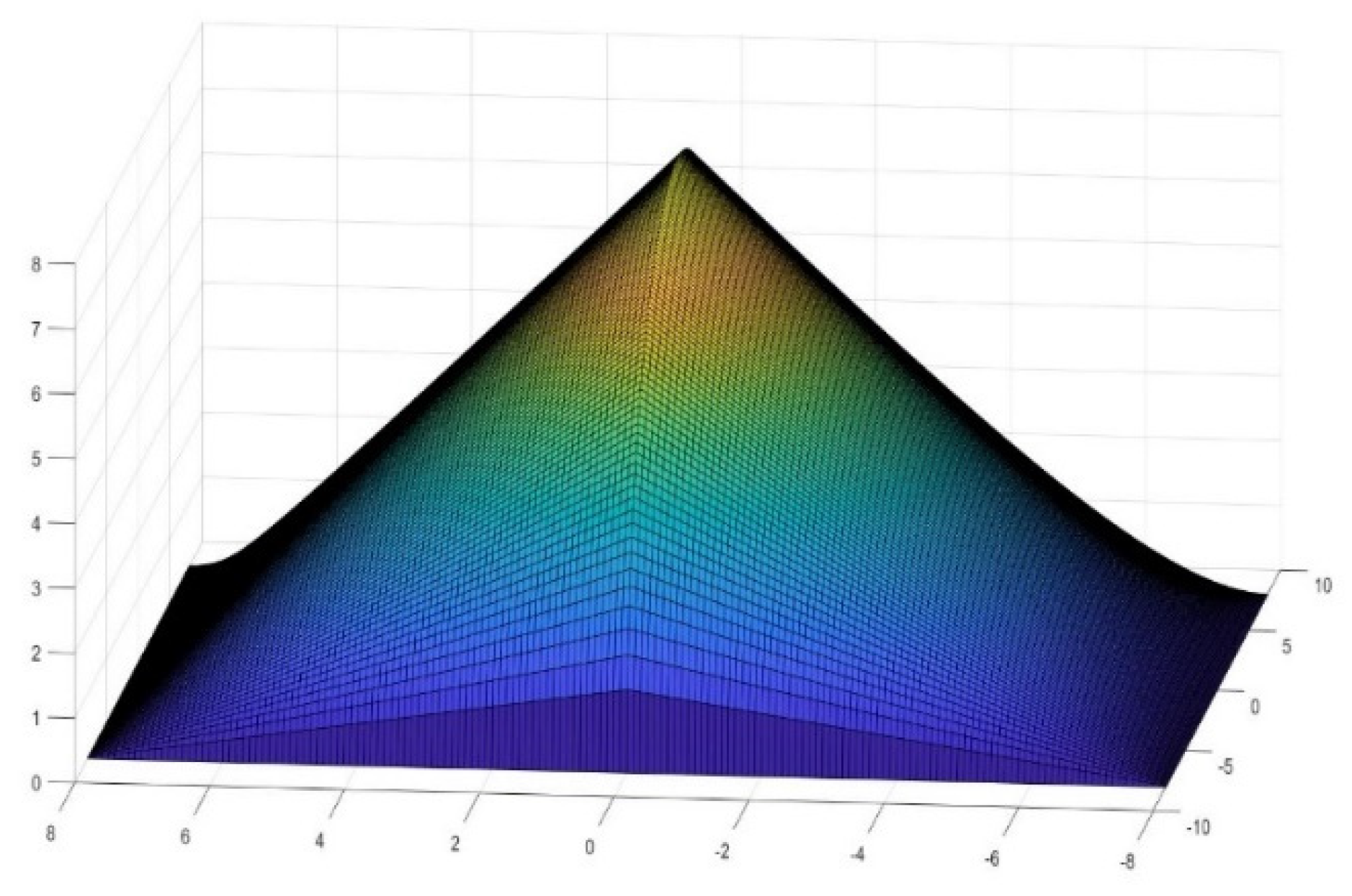
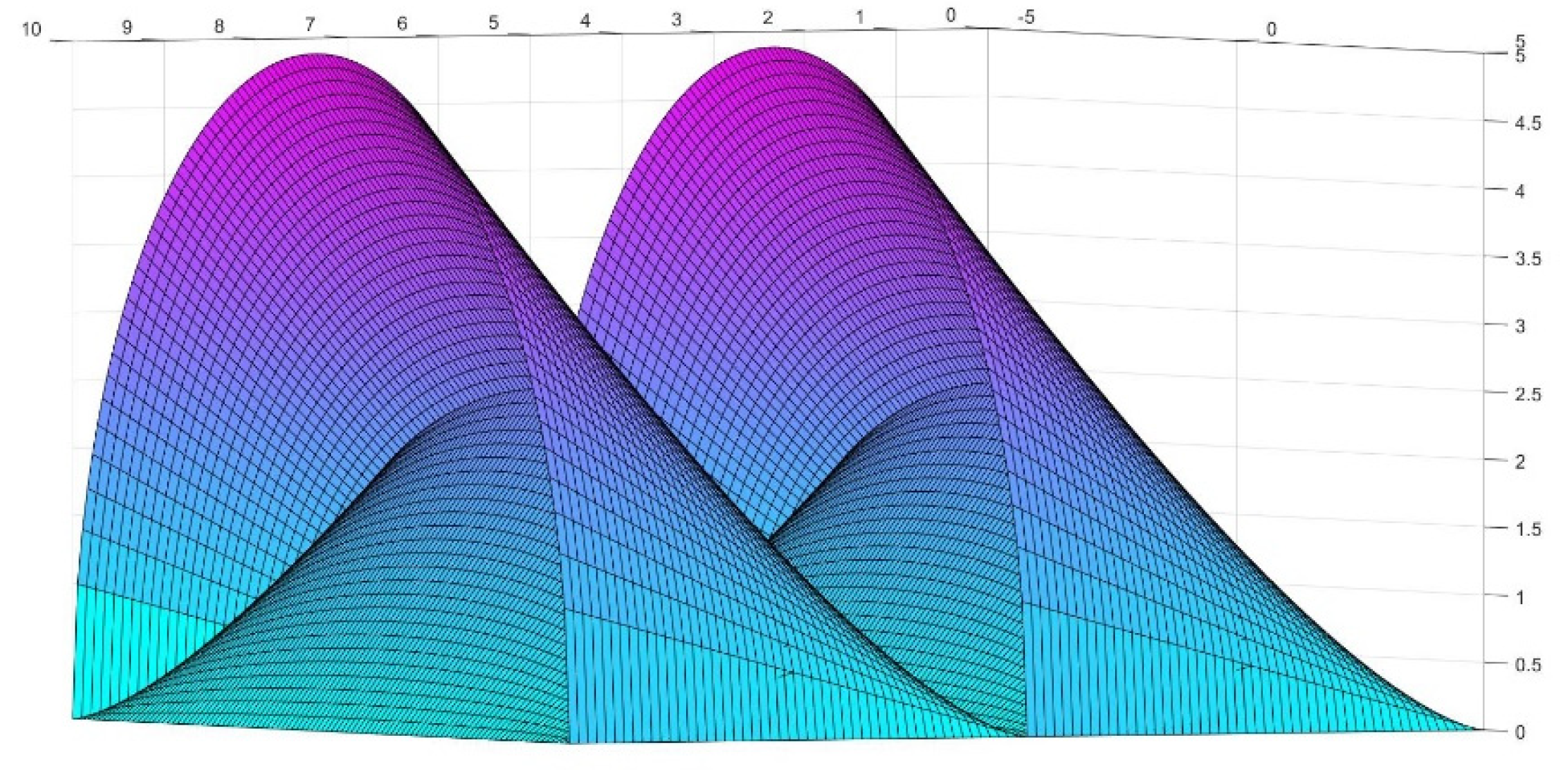
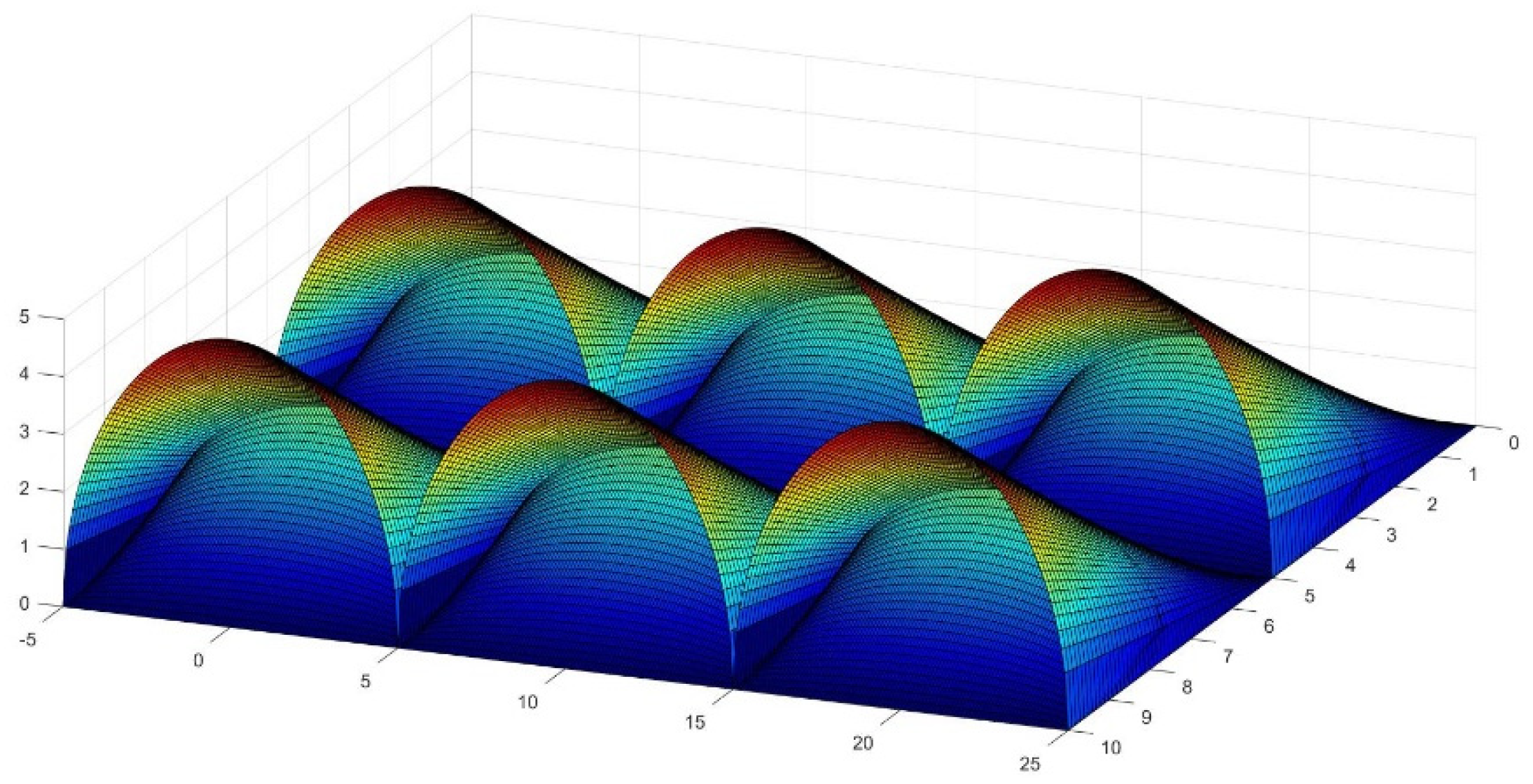
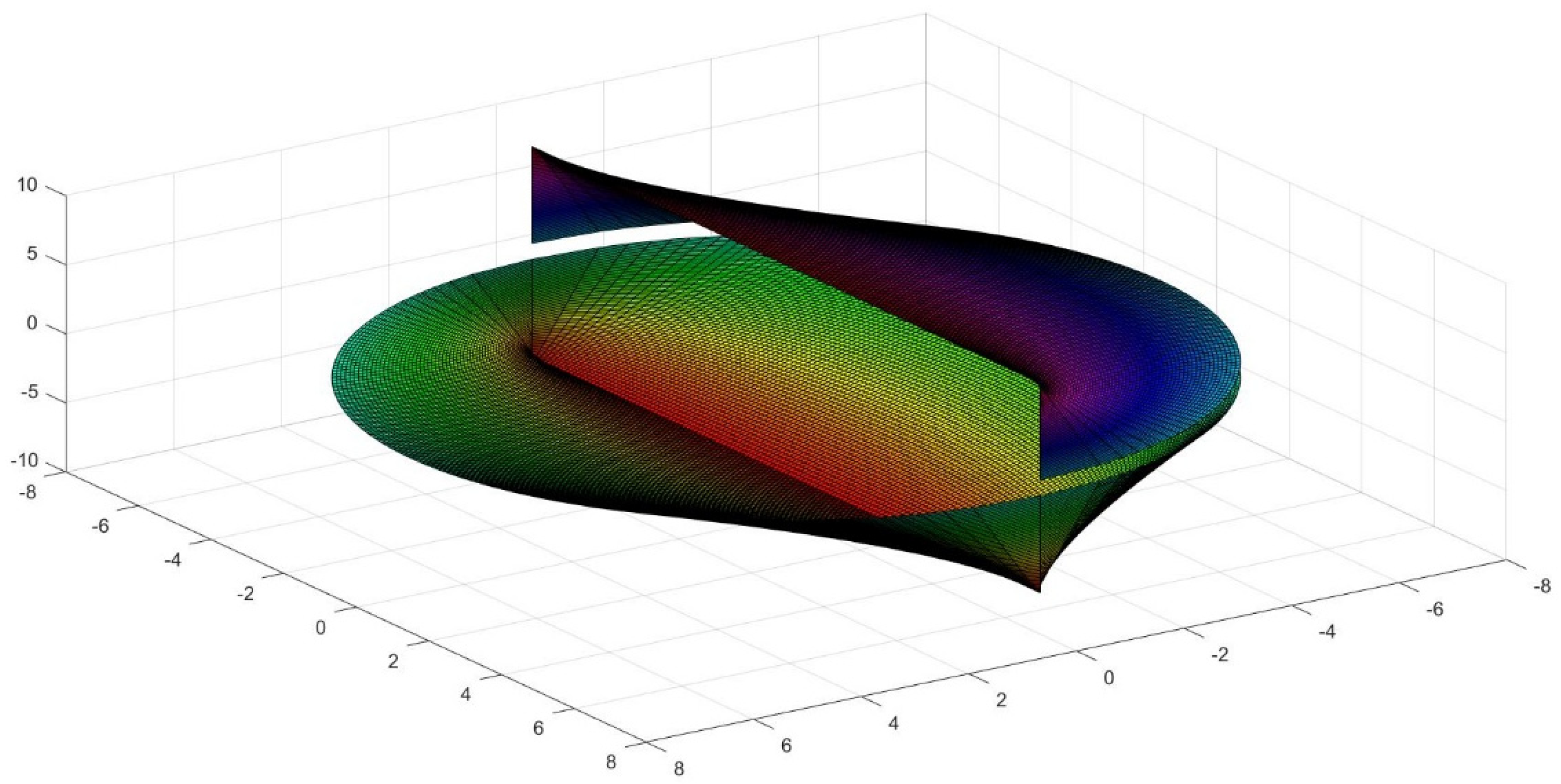
2.5. Discussion for Higher Values of the Conoid Angle
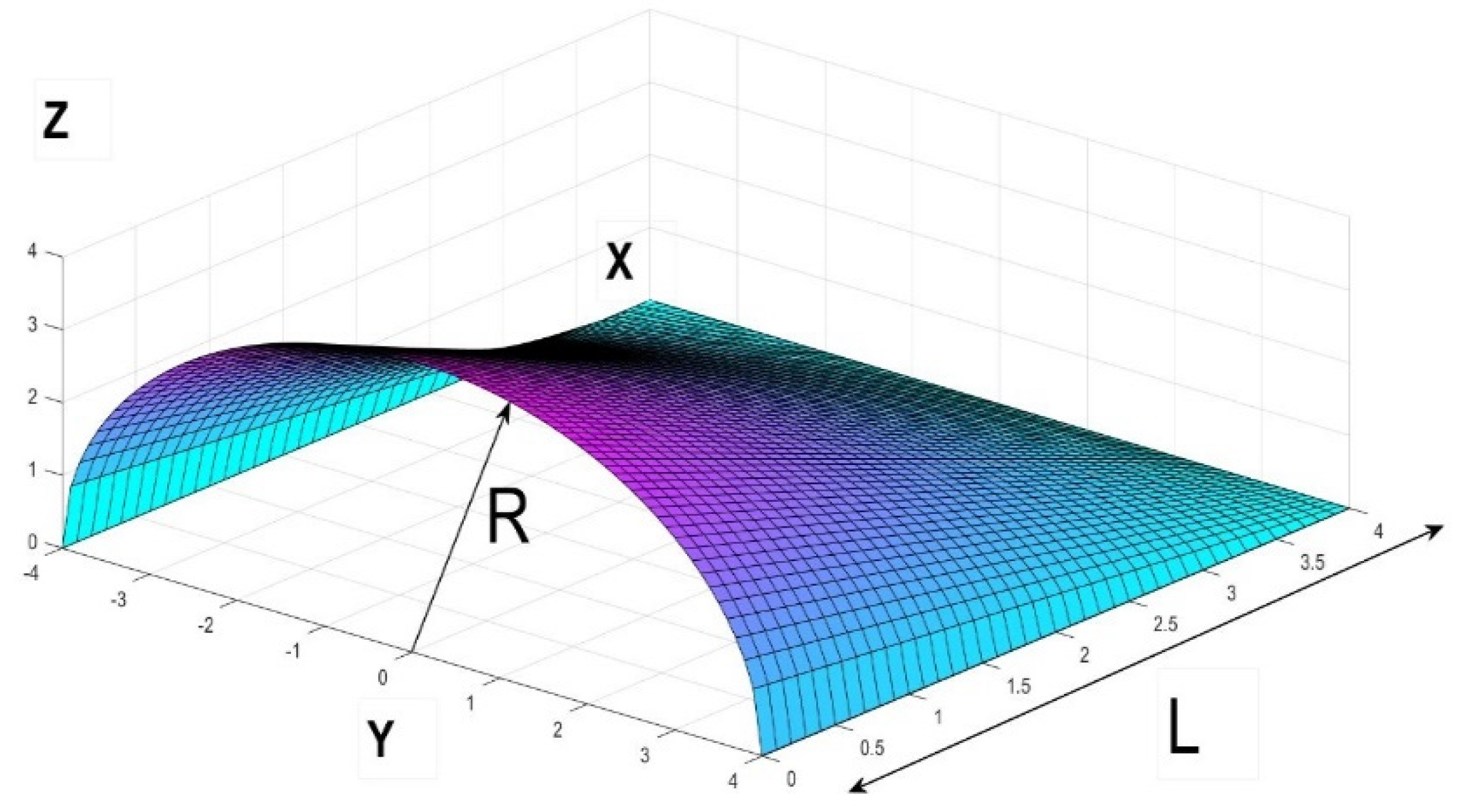
2.6. Calculations of the Area for an Elliptic Conoid
2.7. Calculations of the Volume of the Conoid
3. Repercussions for Radiative Heat Transfer
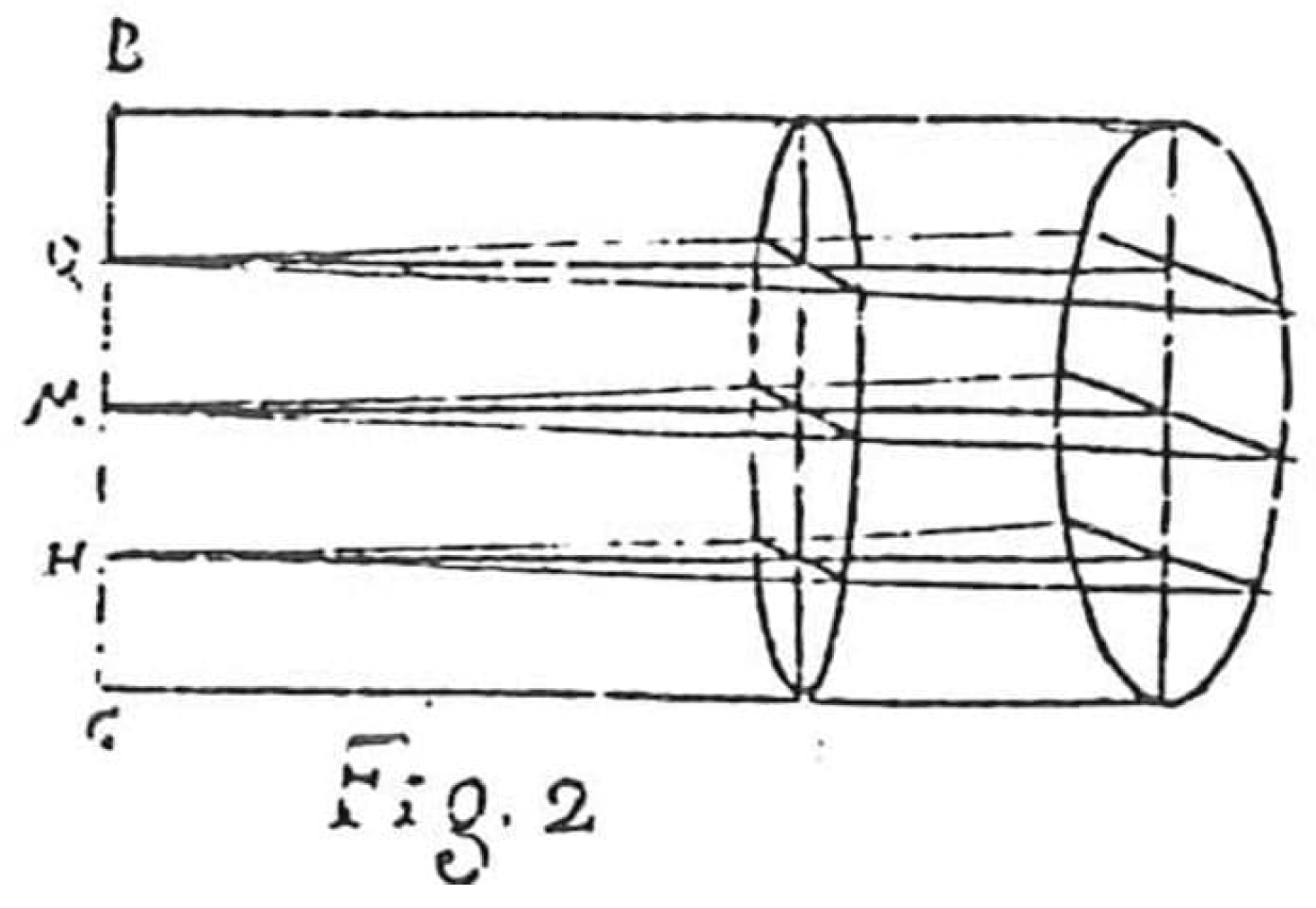
3.1. Introduction to the Problem of Surface Factors
3.2. Example 1
3.3. Example 2
3.4. Example 3
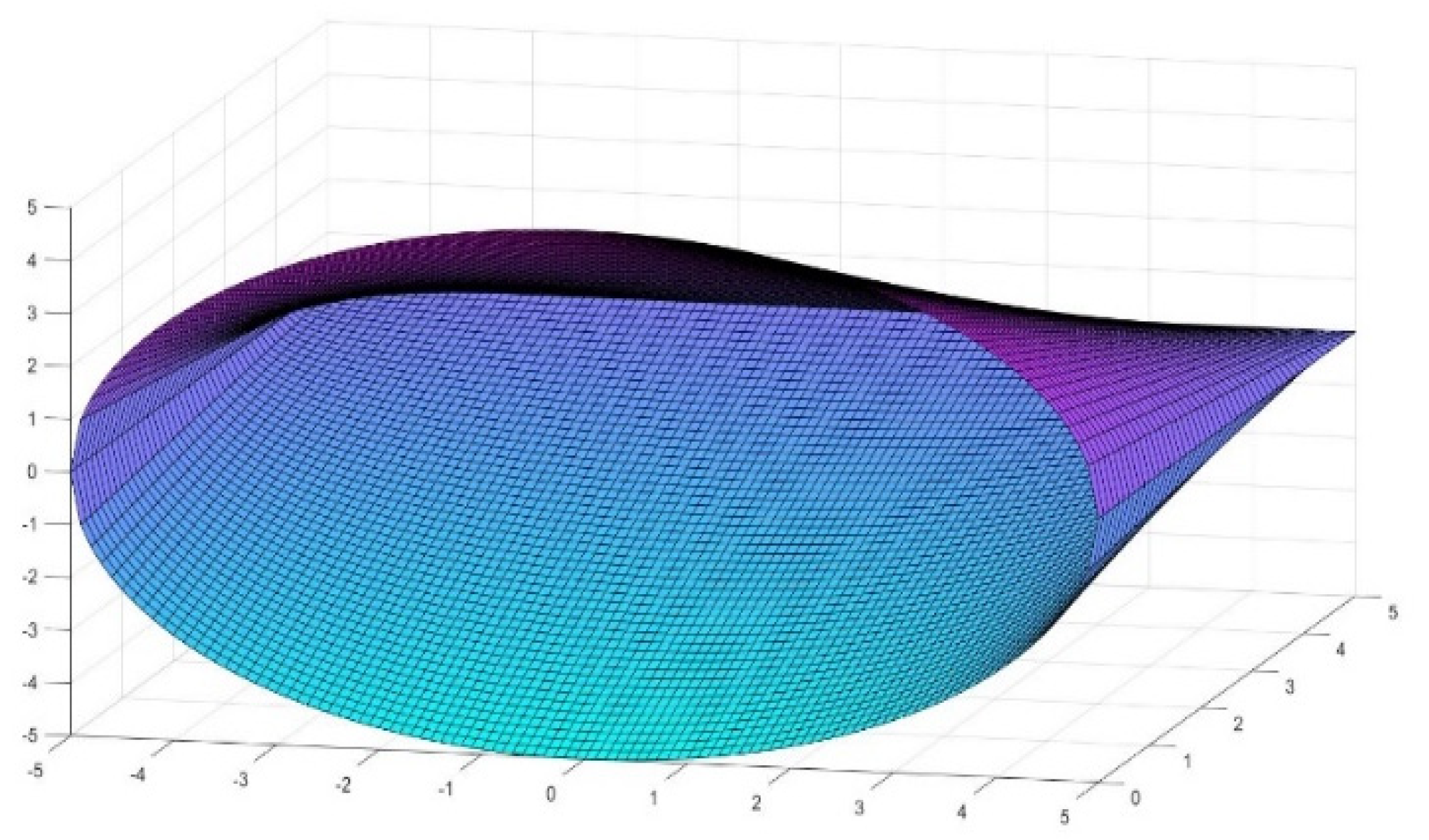
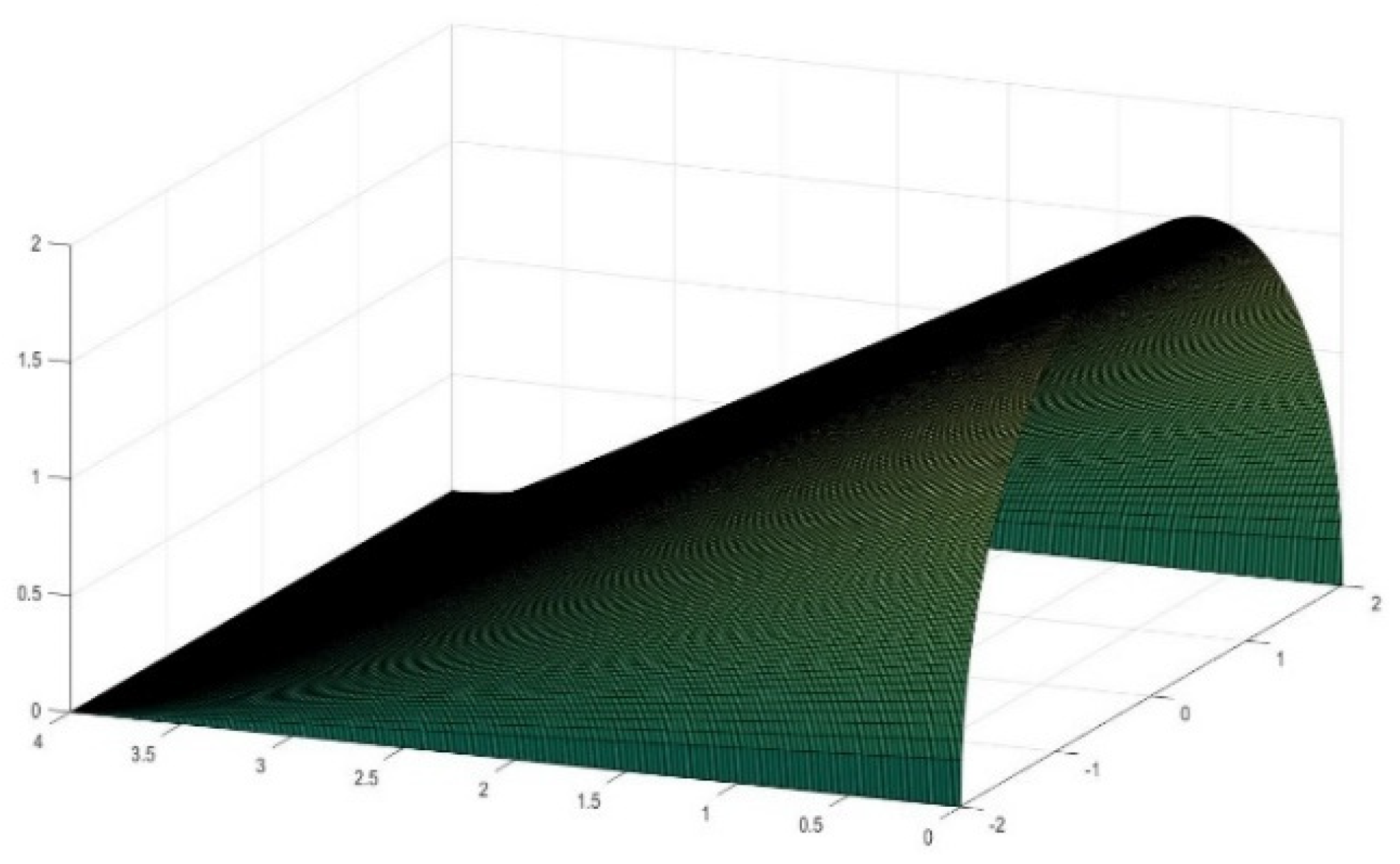
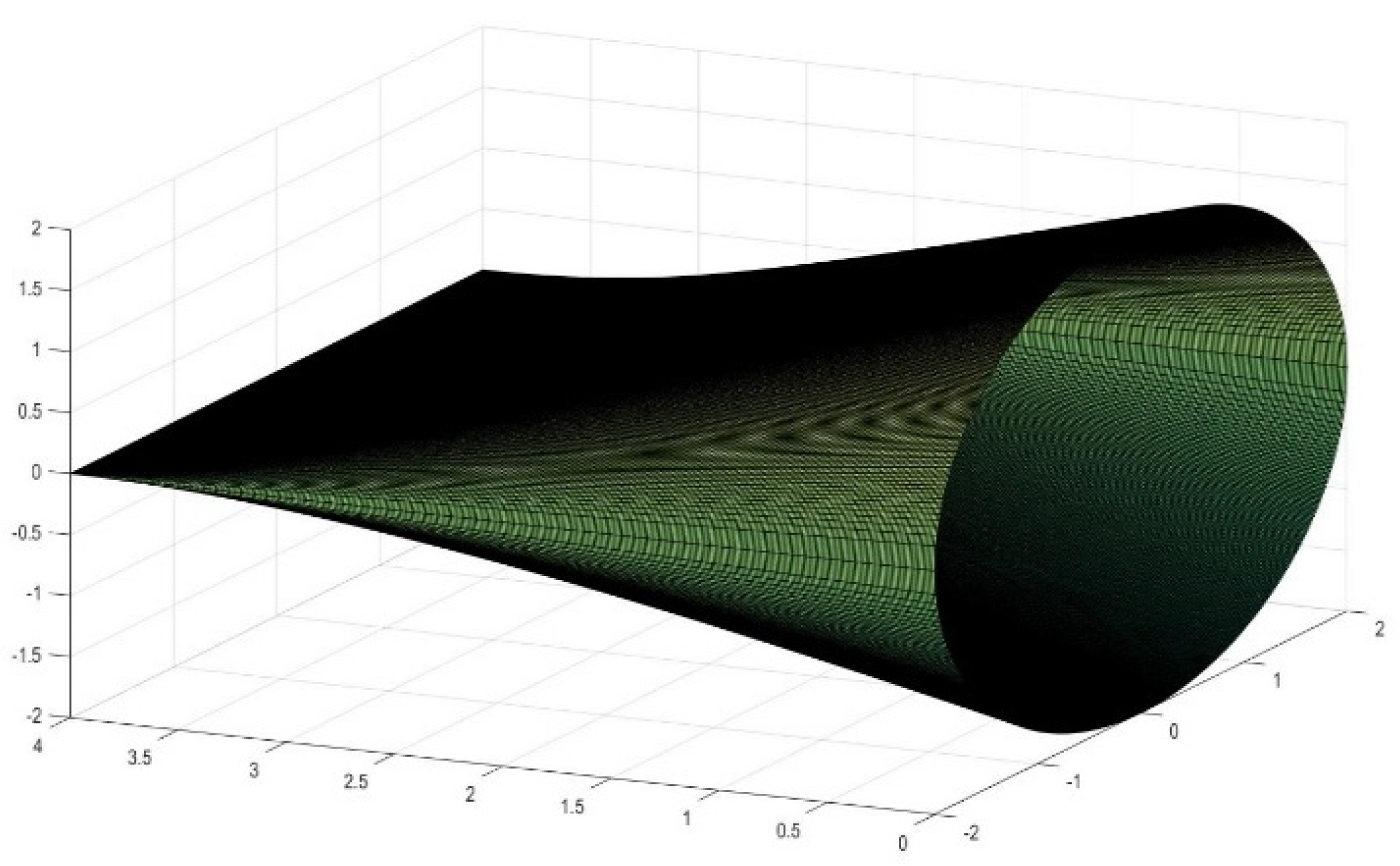
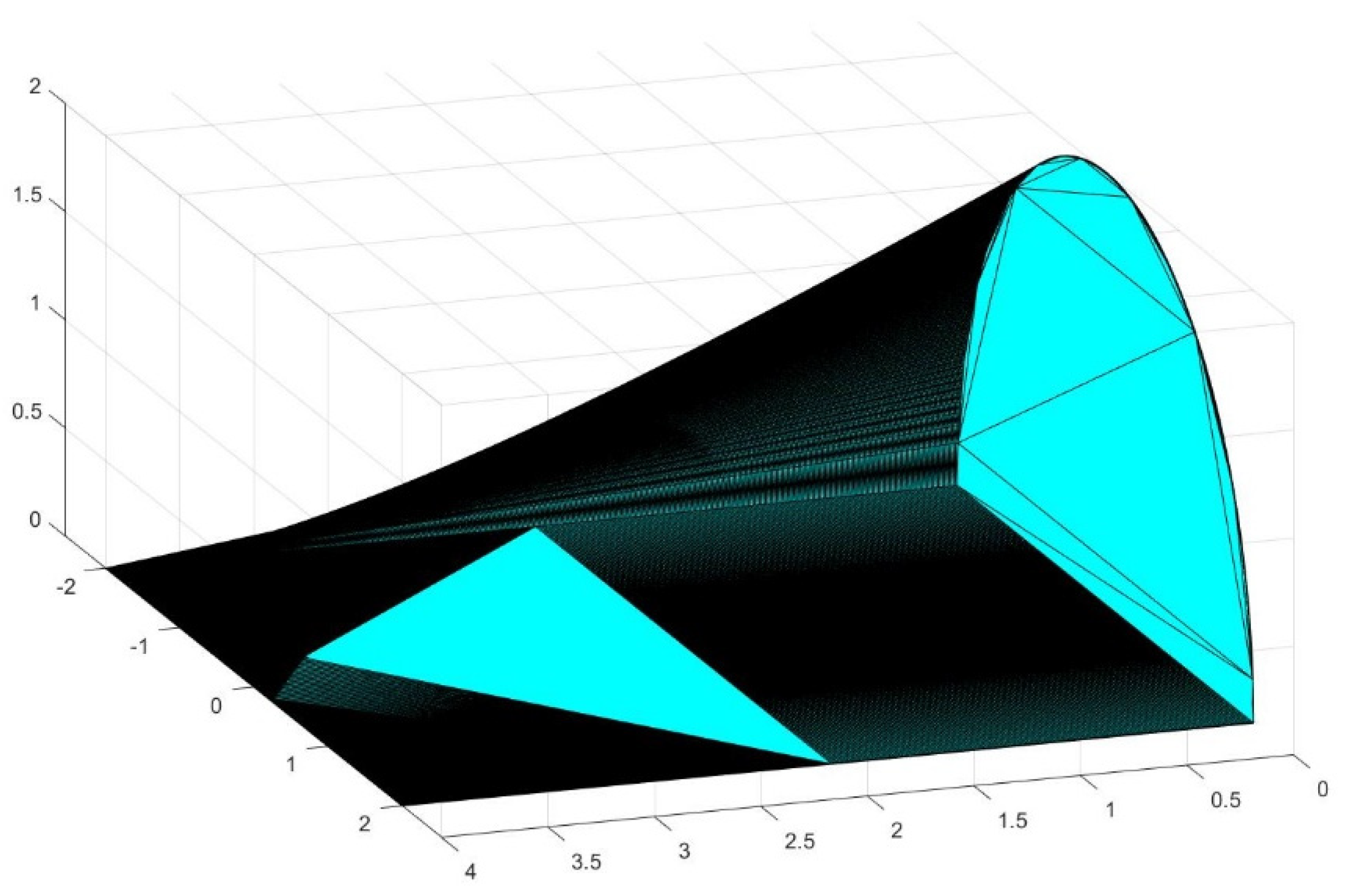
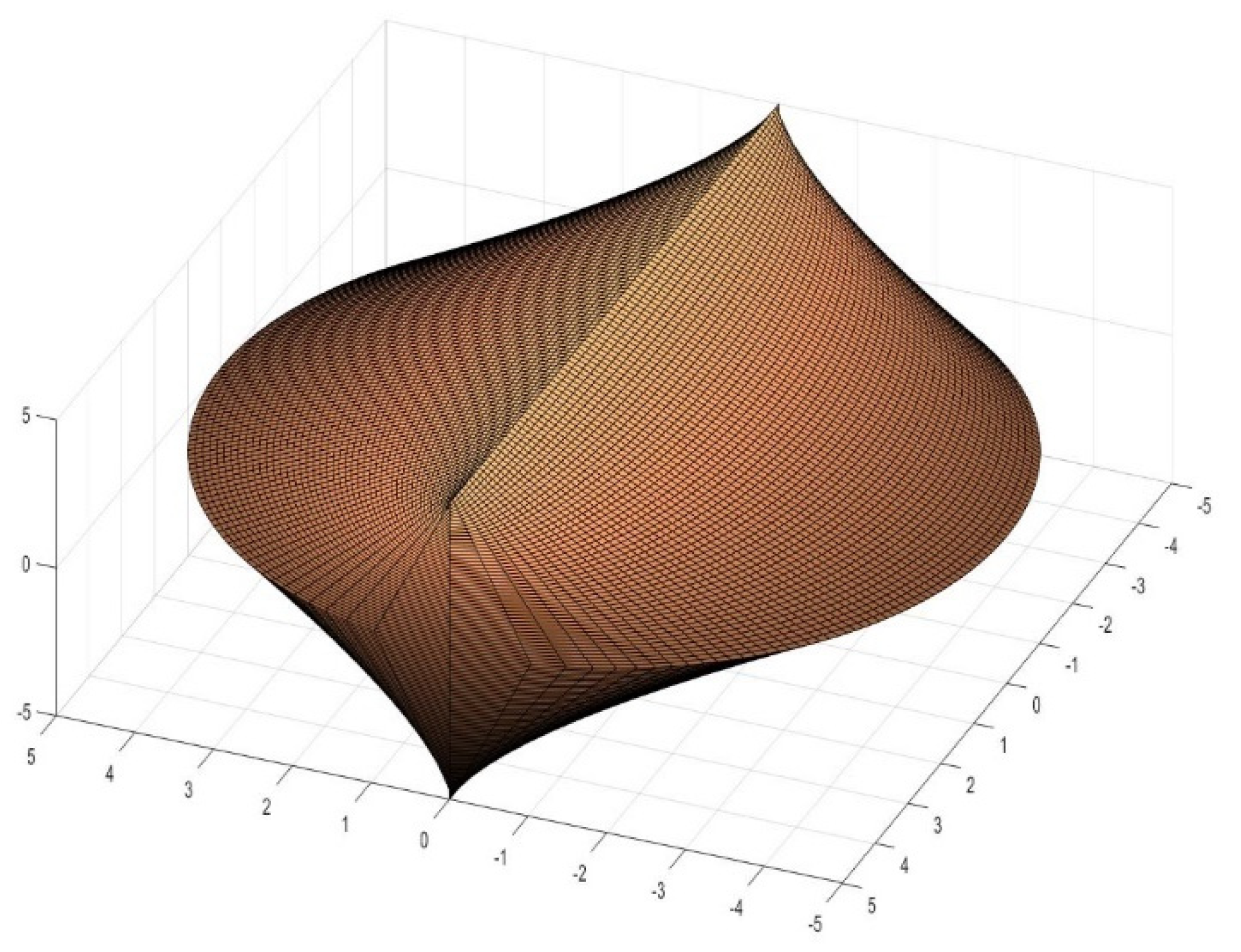
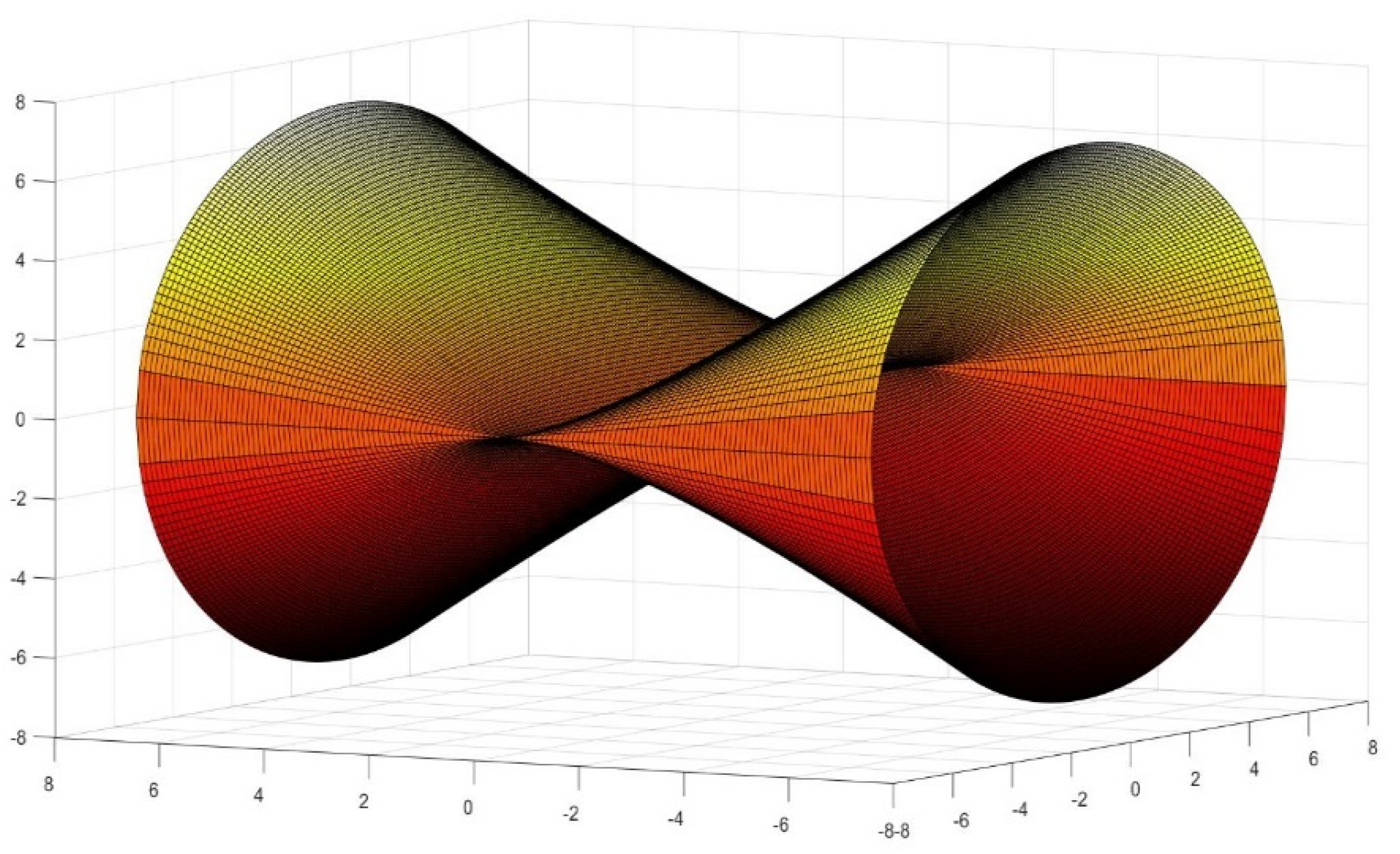
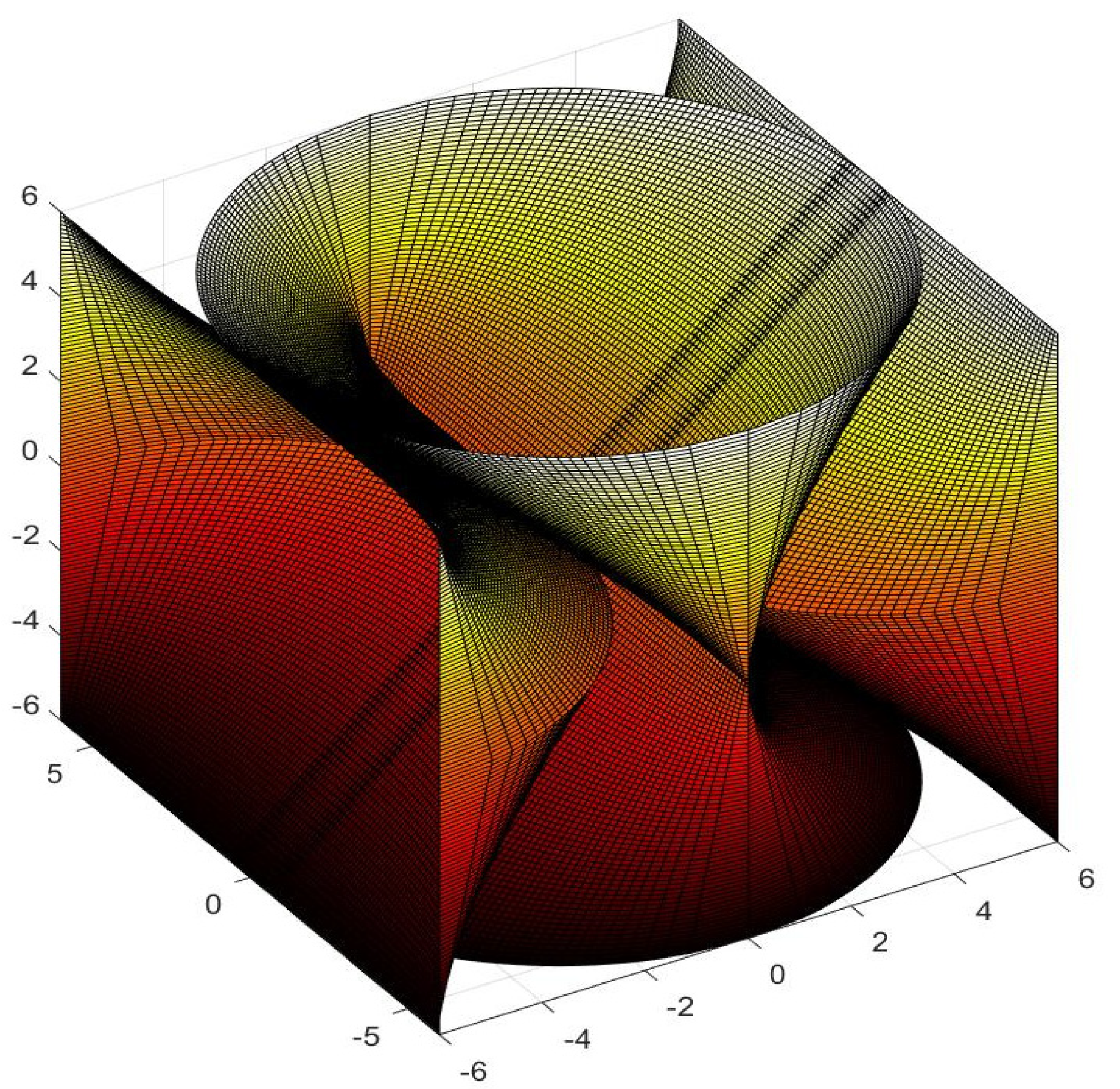
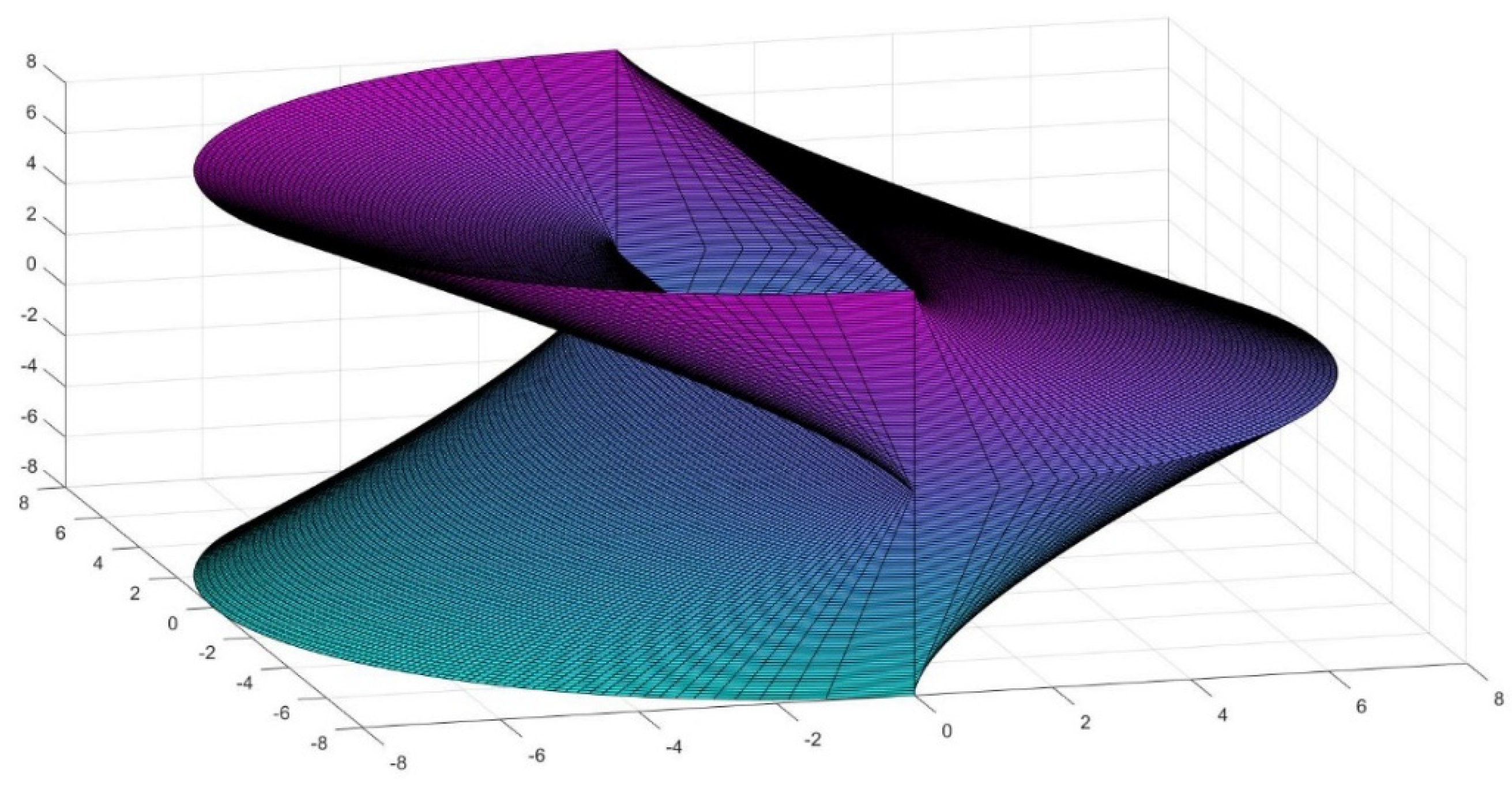
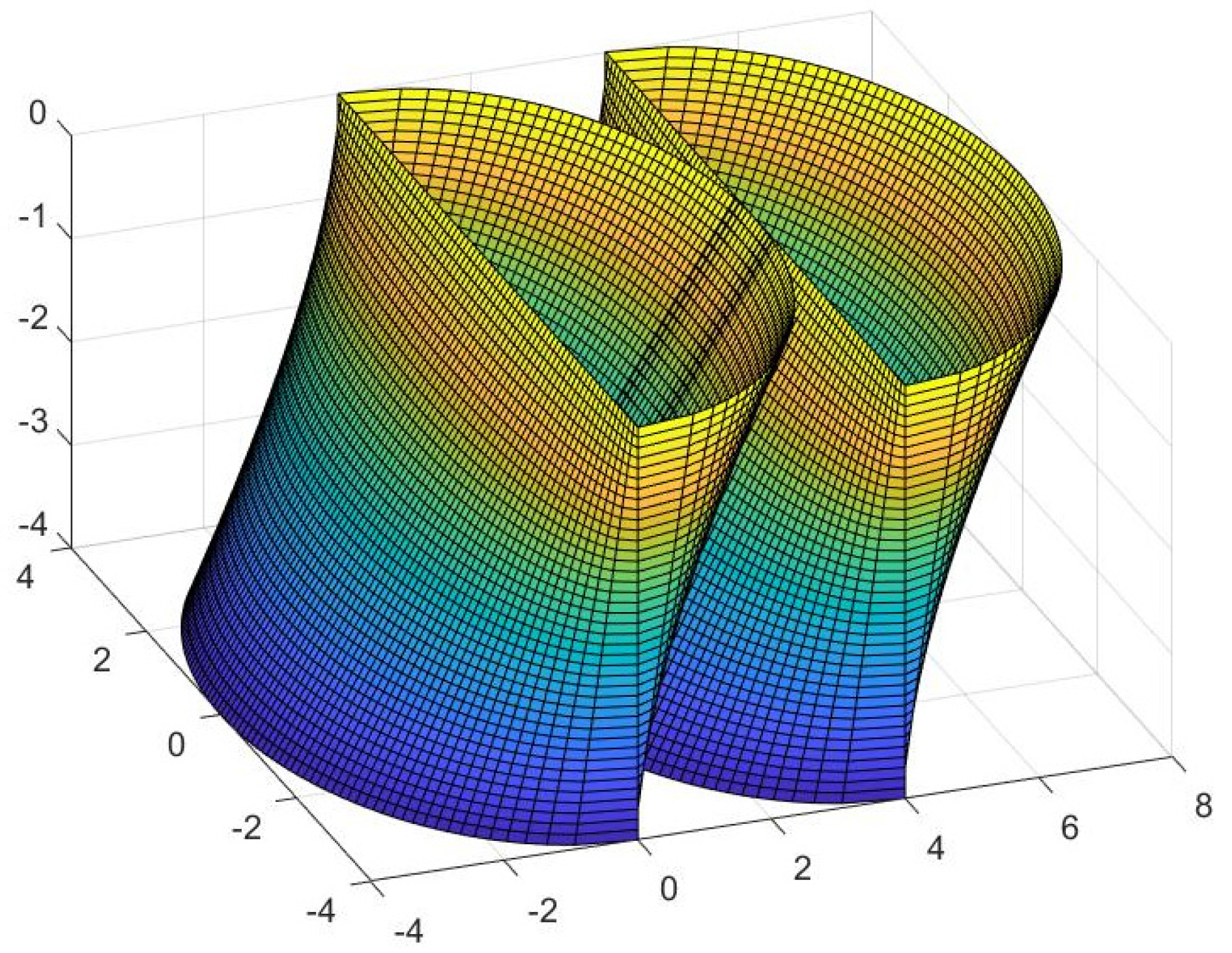
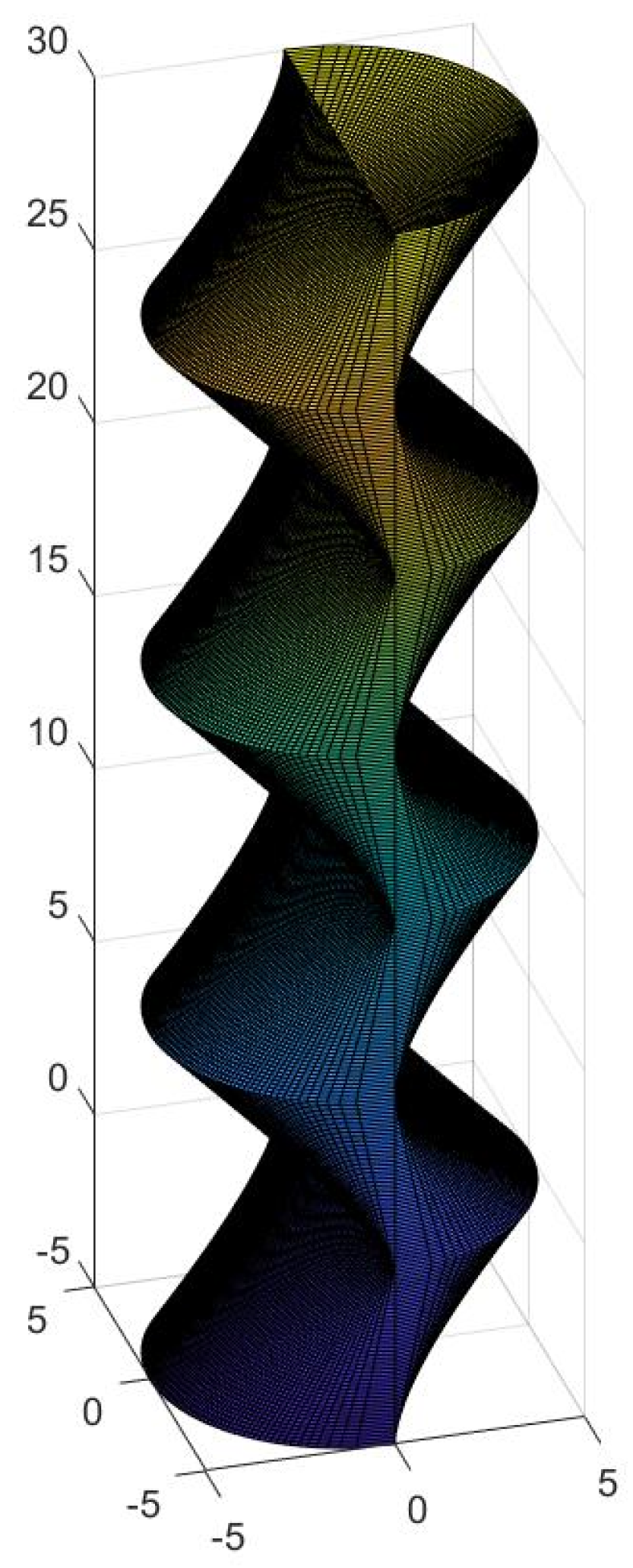
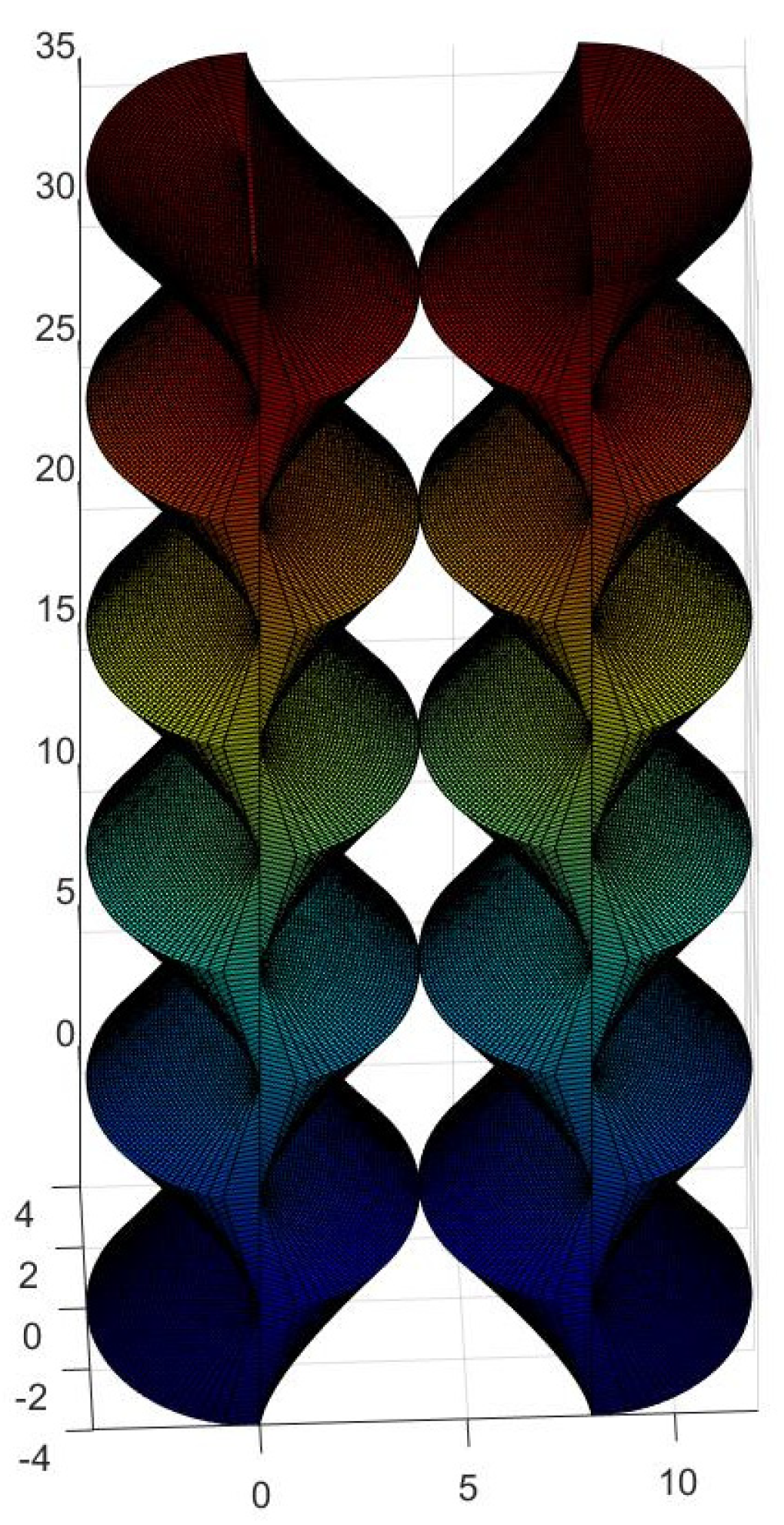
4. Generation of New Figures Based on the Previous Findings
5. Architectural and Engineering Significance of the Geometric Findings
5.1. Historical Evolution
5.2. Recent Projects of Conoids Realized by J. M. Cabeza-Lainez
5.3. Future Proposals
6. Repercussions for Technology
7. Conclusions and Future Aims
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- The Bible. 1 Kings 7:23. “And He Made the Sea of Cast Bronze, Ten Cubits from One Brim to the Other; It Was Completely Round. Its Height Was Five Cubits, and a Line of Thirty Cubits Measured Its Circumference”. Available online: https://biblehub.com/1_kings/7-23.htm (accessed on 29 August 2021).
- Ramanujan, S. Ramanujan’s Collected Works; Chelsea Publishing Company: New York, NY, USA, 1962. [Google Scholar]
- Jeffrey, A.; Dai, H. Handbook of Mathematical Formulas and Integrals; Elsevier Academic Press: Burlington, MA, USA, 2008. [Google Scholar]
- Weisstein, E.W. (Ed.) Trascendent Numbers; MathWorld; Wolfram Research: Champaign, IL, USA, 2014. [Google Scholar]
- Guarini, C.G. Euclides Adauctus et Methodicus Mathematicaque Universalis; Baptistae Zappatae Bibliopolae S.R.C.: Turin, Italy, 1671; Available online: https://books.google.com.au/books?id=K13t3cDYJAkC&printsec=frontcover#v=onepage&q&f=false (accessed on 7 September 2021).
- Cabeza-Lainez, J.M. Fundamentos de Transferencia Radiante Luminosa o la Verdadera Naturaleza del Factor de Forma y sus Modelos de Cálculo; Netbiblio: Seville, Spain, 2010. [Google Scholar]
- Salguero-Andújar, F.; Cabeza-Lainez, J.-M. New Computational Geometry Methods Applied to Solve Complex Problems of Radiative Transfer. Mathematics 2020, 8, 2176. [Google Scholar] [CrossRef]
- Cabeza-Lainez, J.M.; Pulido-Arcas, J.A. New configuration factors for curved surfaces. J. Quant. Spectrosc. Radiat. Transf. 2012, 117, 71–80. [Google Scholar] [CrossRef]
- Cabeza-Lainez, J.M.; Pulido-Arcas, J.A.; Sanchez-Montañés, B.; Rubio-Bellido, C. New Configuration Factor between a Circle and a Point-Plane at Random Positions. Int. J. Heat Mass Transf. 2014, 69, 147–150. [Google Scholar] [CrossRef]
- Andujar, F.S.; Rodriguez-Cunill, I.; Cabeza-Lainez, J.M. The Problem of Lighting in Underground Domes, Vaults, and Tunnel-Like Structures of Antiquity; An Application to the Sustainability of Prominent Asian Heritage (India, Korea, China). Sustainability 2019, 11, 5865. [Google Scholar] [CrossRef]
- Doganoff, I. Berechnung von Kugelschalen über Rechteckigem Grundriß. Mit Berechnungsdiagrammen; Mitteilungen aus dem Institut für Massivbau Hannover: Düsseldorf, Germany, 1962. [Google Scholar]
- Almodovar-Melendo, J.-M.; Cabeza-Lainez, J.-M.; Rodriguez-Cunill, I. Lighting Features in Historical Buildings: Scientific Analysis of the Church of Saint Louis of the Frenchmen in Sevilla. Sustainability 2018, 10, 3352. [Google Scholar] [CrossRef]
- Ramswamy, S.G. Design and Construction of Concrete Shell Roofs; CBS Publishers & Distributors Private Limited: Delhi, India, 2004. [Google Scholar]
- Doganoff, I.; Hoffmann, C.; Rühle, H. Shell and Fold Structure Roofs Out of Precast, Pre-Stressed Reinforced Concrete Elements; Institute Eduardo Torroja: Madrid, Spain, 1964. [Google Scholar]
- Sahoo, S. Dynamic Characters of Stiffened Composite Conoidal Shell Roofs with Cutouts: Design Aids and Selection Guidelines. J. Eng. 2013, 2013, 230120. [Google Scholar] [CrossRef]
- Das, H.S.; Chakravorty, D. Design aids and selection guidelines for composite conoidal shell roofs. A finite element application. J. Reinf. Plast. Compos. 2007, 26, 1793–1819. [Google Scholar] [CrossRef]
- Cabeza-Lainez, J.; López-de-Asiain-y-Martín, J.; Moreno-Jiménez, V. Rehabilitación del pabellón Plaza de América de la Exposición Universal de 1992. Rev. Edificación Ecoconstrucción 1997, 27. Available online: https://hdl.handle.net/10171/16978 (accessed on 1 May 2021).
- Chaubey, A.; Kumar, A.; Fic, S.; Barnat-Hunek, D.; Sadowska-Buraczewska, B. Hygrothermal Analysis of Laminated Composite Skew Conoids. Materials 2019, 12, 225. [Google Scholar] [CrossRef] [PubMed]
- Dzwierzynska, J.; Prokopska, A. Pre-Rationalized Parametric Designing of Roof Shells Formed by Repetitive Modules of Catalan Surfaces. Symmetry 2018, 10, 105. [Google Scholar] [CrossRef]
- Cross, H. The Column Analogy; University of Illinois: Urbana, IL, USA, 1930; Volume 28, Available online: https://www.ideals.illinois.edu/bitstream/handle/2142/4229/engineeringexperv00000i00215.pdf?sequence=3 (accessed on 20 September 2021).
- Cabeza-Lainez, J.M.; Verdejo, J.R.J.; Macias, B.S.-M.; Calero, J.I.P. The Key-role of Eladio Dieste, Spain and the Americas in the Evolution from Brickwork to Architectural Form. J. Asian Archit. Build. Eng. 2009, 8, 355–362. [Google Scholar] [CrossRef][Green Version]
- Cabeza-Lainez, J.; Almodovar-Melendo, J.-M.; Dominguez, I. Daylight and Architectural Simulation of the Egebjerg School (Denmark): Sustainable Features of a New Type of Skylight. Sustainability 2019, 11, 5878. [Google Scholar] [CrossRef]



















| Radius = L Unit | Alpha- Shape | Cabeza Approx. | Grass- Hopper | Delta Δ Alphas | Delta Δ Grassh |
|---|---|---|---|---|---|
| 0.25 | 0.1958 | 0.1862 | 0.1842 | 0.0096 | −0.002 |
| 0.50 | 0.7712 | 0.7446 | 0.7369 | 0.0266 | −0.0077 |
| 1 | 3.0726 | 2.9784 | 2.9476 | 0.942 | −0.308 |
| 2 | 12.155 | 11.913 | 11.790 | 0.242 | −0.123 |
| 3 | 27.734 | 26.805 | 26.528 | 0.929 | −0.277 |
| 4 | 48.886 | 47.654 | 47.161 | 1.232 | −0.493 |
| 5 | 76.019 | 74.460 | 73.690 | 1.559 | −0.77 |
| 6 | 109.27 | 107.22 | 106.11 | 2.05 | −1.11 |
| 7 | 148.83 | 145.94 | 144.43 | 2.89 | −1.51 |
| 8 | 194.54 | 190.61 | 188.64 | 3.93 | −1.97 |
| 9 | 246.41 | 241.25 | 238.75 | 5.16 | −2.5 |
| 10 | 304.254 | 297.841 | 294.76 | 6.413 | −3.081 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabeza-Lainez, J. Architectural Characteristics of Different Configurations Based on New Geometric Determinations for the Conoid. Buildings 2022, 12, 10. https://doi.org/10.3390/buildings12010010
Cabeza-Lainez J. Architectural Characteristics of Different Configurations Based on New Geometric Determinations for the Conoid. Buildings. 2022; 12(1):10. https://doi.org/10.3390/buildings12010010
Chicago/Turabian StyleCabeza-Lainez, Joseph. 2022. "Architectural Characteristics of Different Configurations Based on New Geometric Determinations for the Conoid" Buildings 12, no. 1: 10. https://doi.org/10.3390/buildings12010010
APA StyleCabeza-Lainez, J. (2022). Architectural Characteristics of Different Configurations Based on New Geometric Determinations for the Conoid. Buildings, 12(1), 10. https://doi.org/10.3390/buildings12010010






