Intervention Strategies for the Seismic Improvement of Masonry Buildings Based on FME Validation: The Case of a Terraced Building Struck by the 2016 Central Italy Earthquake
Abstract
:1. Introduction
1.1. Seismic Risk of Residential Buildings
1.2. Strenghening of Masonry Buildings
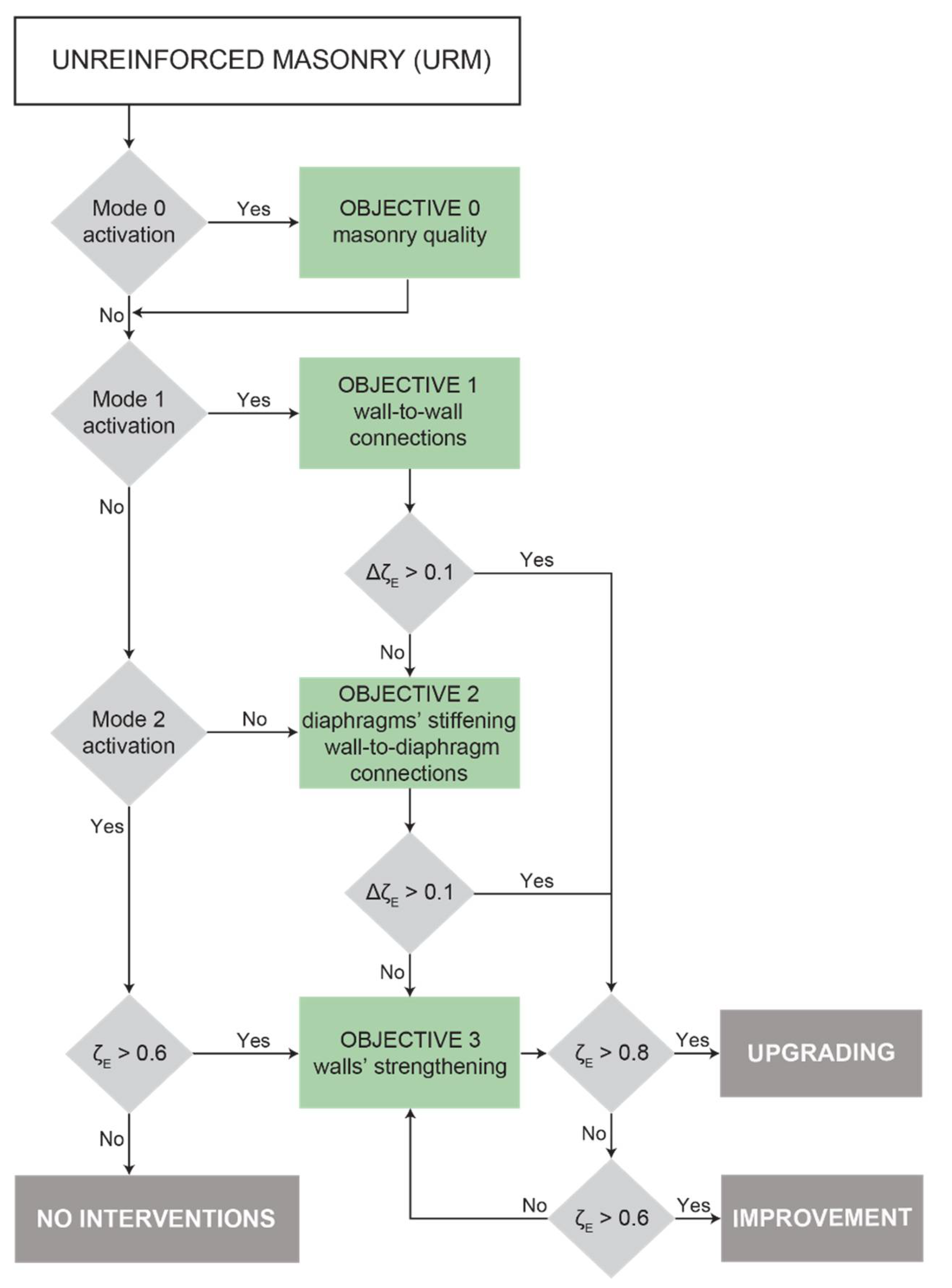
- (a)
- Repair interventions aim to prevent local collapse mechanisms, restore and/or improve the capacity of damaged or undamaged portions, leaving ζE unchanged. These actions, although circumscribed to single macroblocks (e.g., walls or portions of them delimited by discontinuities), are a staple in URM buildings, which especially suffer from brittle OOP failure and, secondarily, from weak IP response [26].
- (b)
- Improvement interventions aim to increase the safety level of an existing structure, without reaching those levels required for new constructions: ζE must be increased by 0.1 for ordinary buildings, but it should reach at least 0.6 in buildings for public use (e.g., schools) or which serve strategic functions (e.g., town halls).
- (c)
- Upgrading refers to those interventions which are able to make the structure achieve the safety level of a new one (ζE = 1) (e.g., extensions or substantial structural changes); however, a target of ζE = 0.8 is allowed in the cases of functional and usage changes.
2. Materials and Methods
2.1. Urban and Seismic Context
2.2. Case Study Description
2.3. Structural Characterization
2.4. Seismic Behaviour
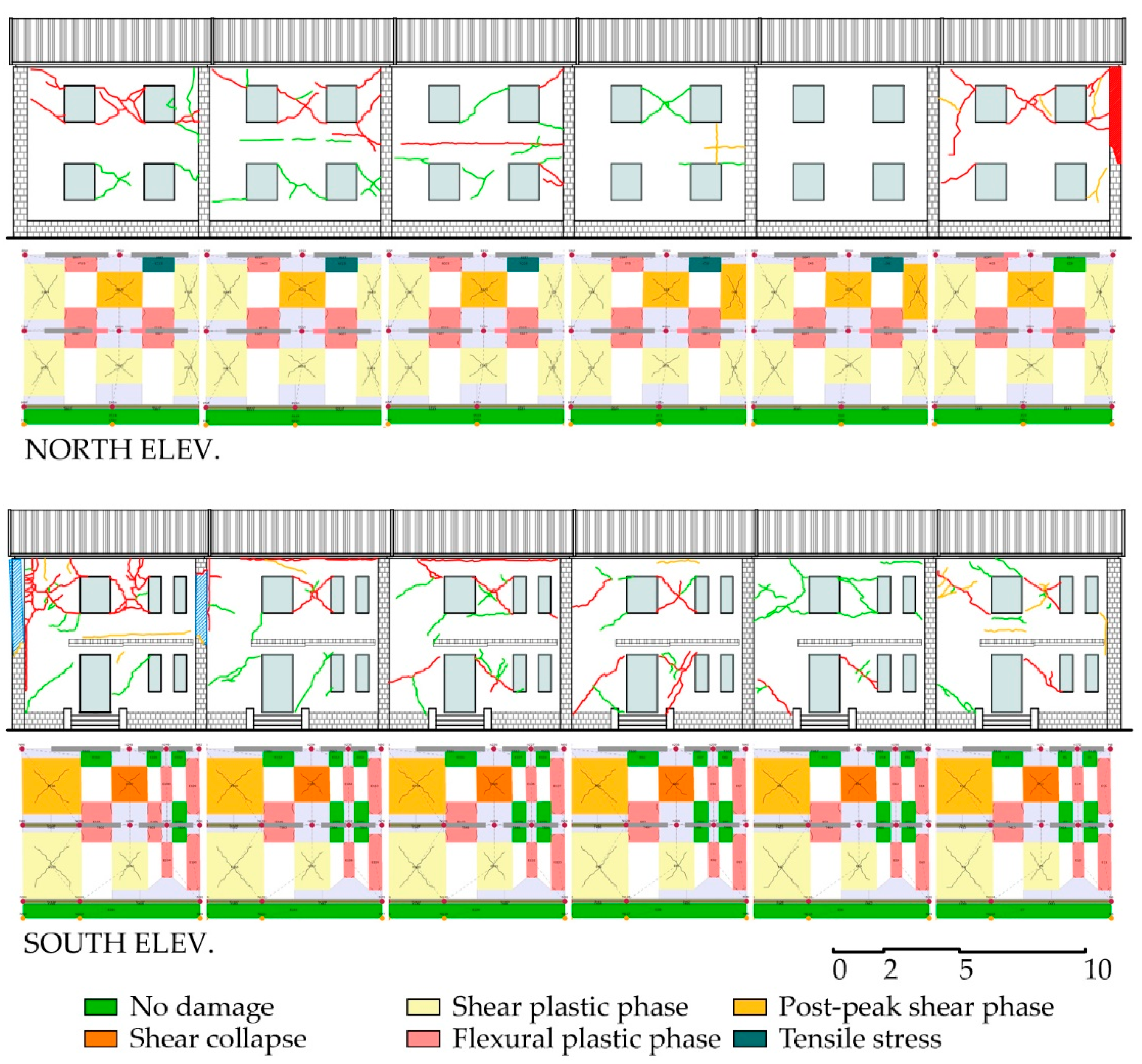
- Diagonal shear damage in piers of the north, south, and east facades, heavier in the extreme units (no. 1 and 6) and in the upper storeys (Figure 8a–c);
- Light flexural and/or crushing cracks in spandrels;
- Local crumbling and OOP collapses of panels in the west and east facades of unit no. 6 (Figure 8d–e);
- Activation of the overturning in the first storey of unit no. 6 in M3 masonry walls (Figure 8b) and shear cracks at the ground floor;
- Shear failure of non-structural partitions and slight to moderate IP damage of internal loadbearing walls (although this datum is limited to a few units);
- Sliding cracks at floor levels, mainly in internal units (Figure 8f).
2.5. FME Modeling
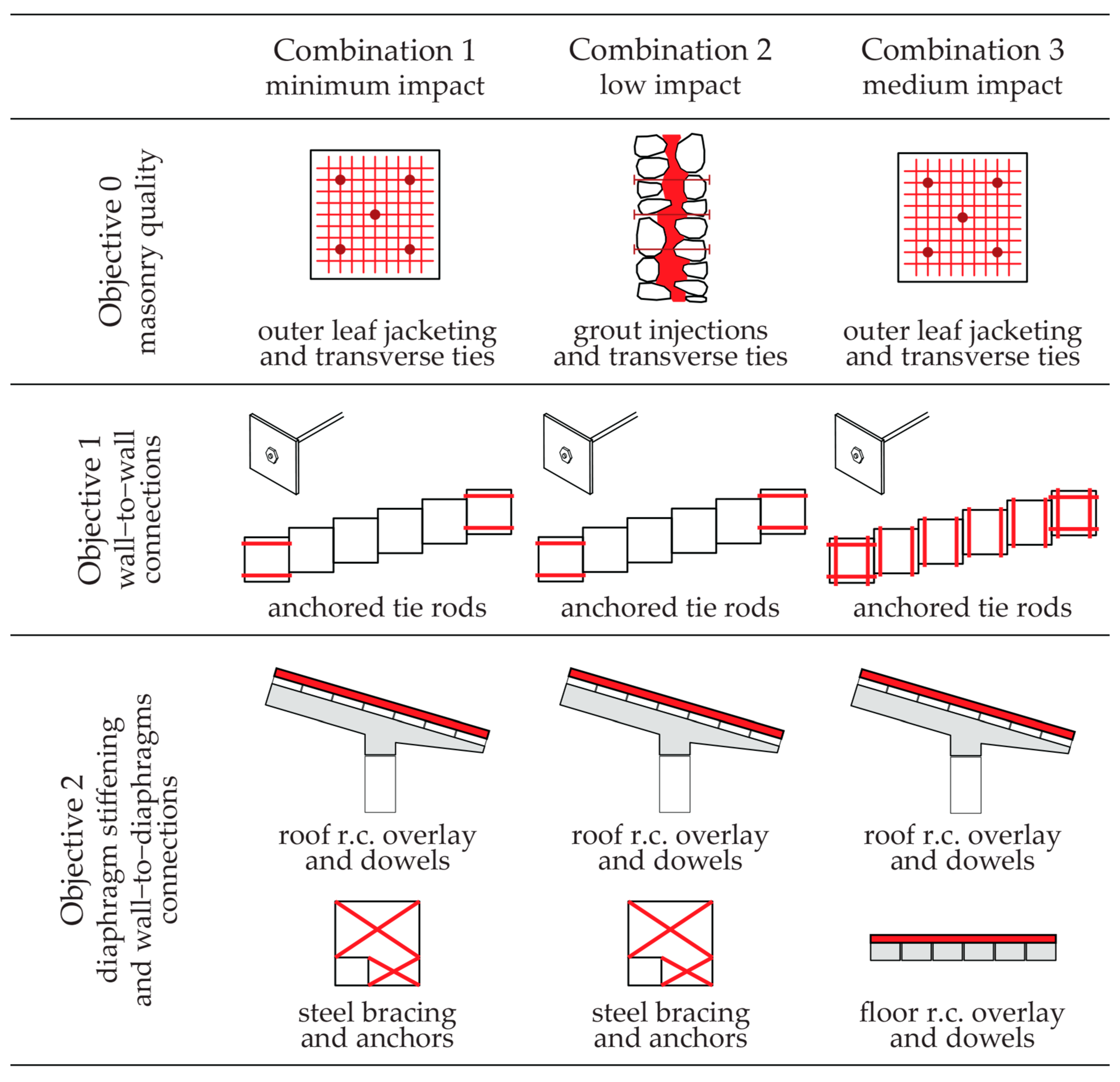
2.6. Strenghtening Strategies
- Combination 1 (minimum impact) refers to light interventions on both horizontal (bracing of floors at intrados) and vertical (innovative jacketing on masonry outer leaf only) components, and tying on extreme units only;
- Combination 2 (low impact) adds the action on the building’s fabric by increasing the masonry compactness with grout injections;
- Combination 3 (medium impact) acts in a similar way on diaphragms and differs from combination 1 in the r.c. overlay on the three floor slabs and the tying of all units.
3. Results and Discussion
3.1. Assessment of as-Built Conditions
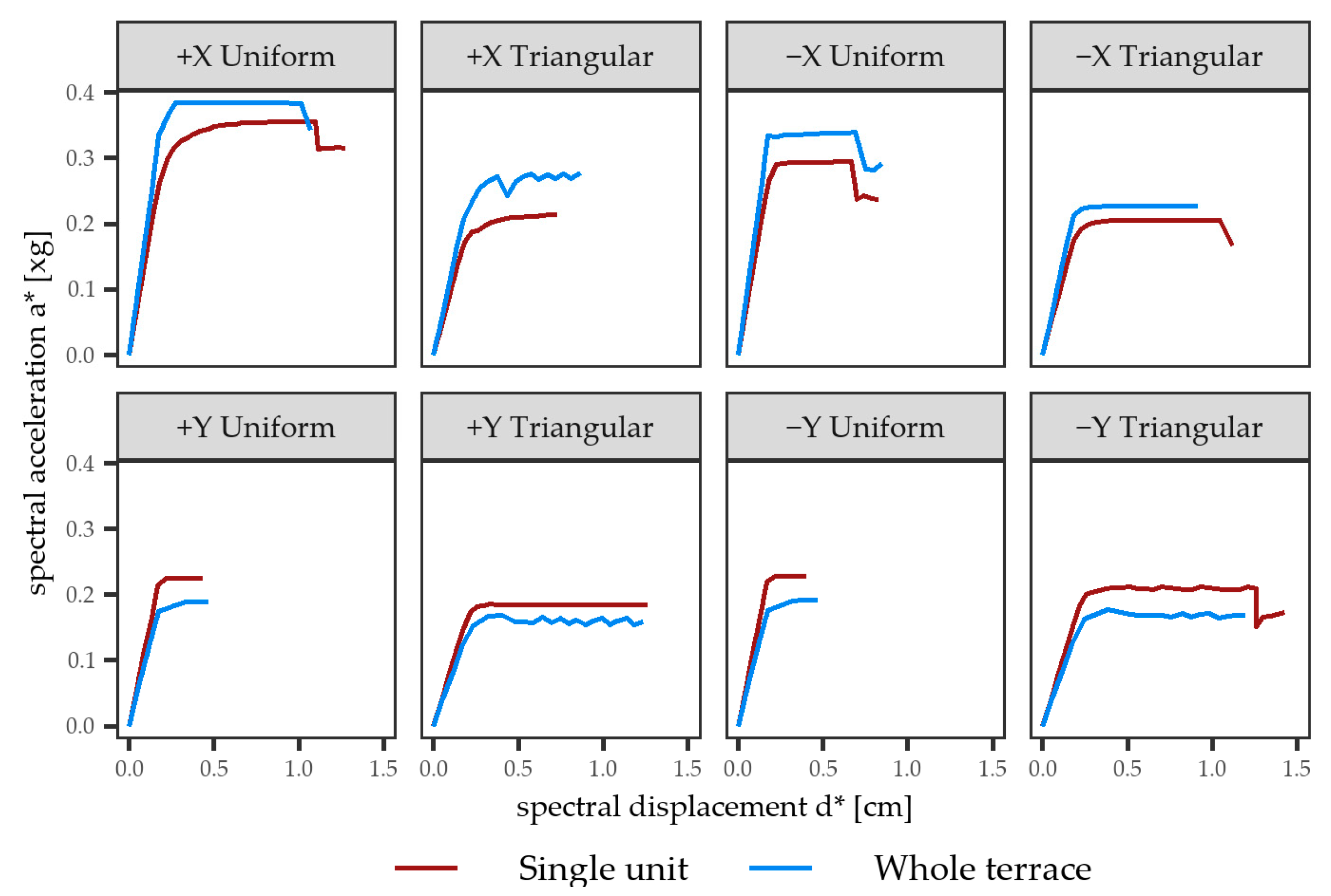
3.1.1. Overall Behaviour
3.1.2. Local Behaviour
3.2. Assessment of Strengthened Conditions
4. Conclusions
- (a)
- The requirements of recently passed seismic codes in Italy, in terms of both intervention techniques and quantification of the improvement, were organized in an incremental procedure, which combined structural behaviour (modes 0, 1, 2) with the respective targets to be achieved through interventions (objectives) and the corresponding performance ratios (ζE).
- (b)
- The comparison between the numerical results obtained for the single unit and the whole terrace for the as-built conditions highlighted the effect of irregularity of the overall building (ζE at the SD limit state reduced by about 25% for the whole terrace), particularly in the transverse (Y) direction.
- (c)
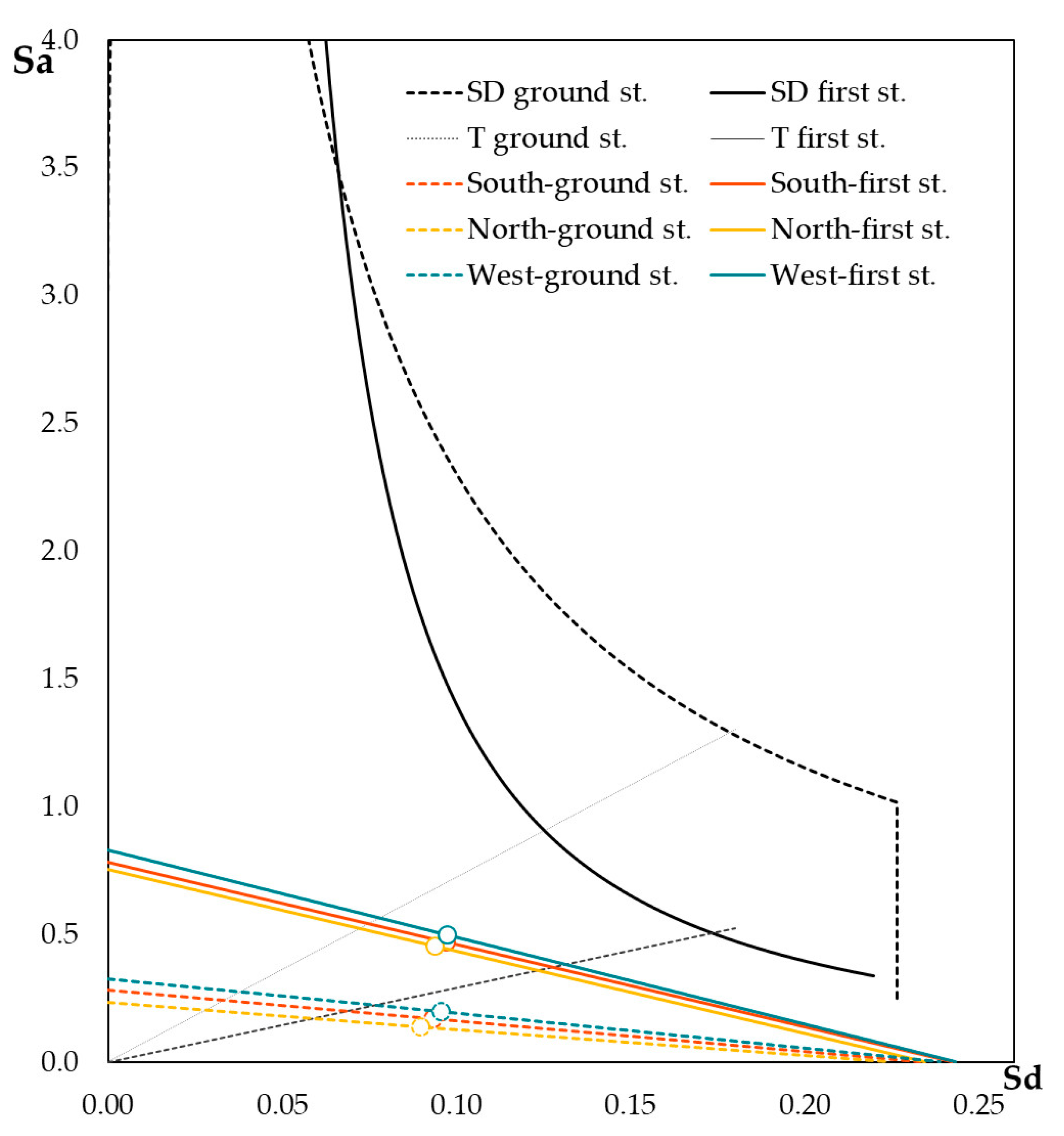
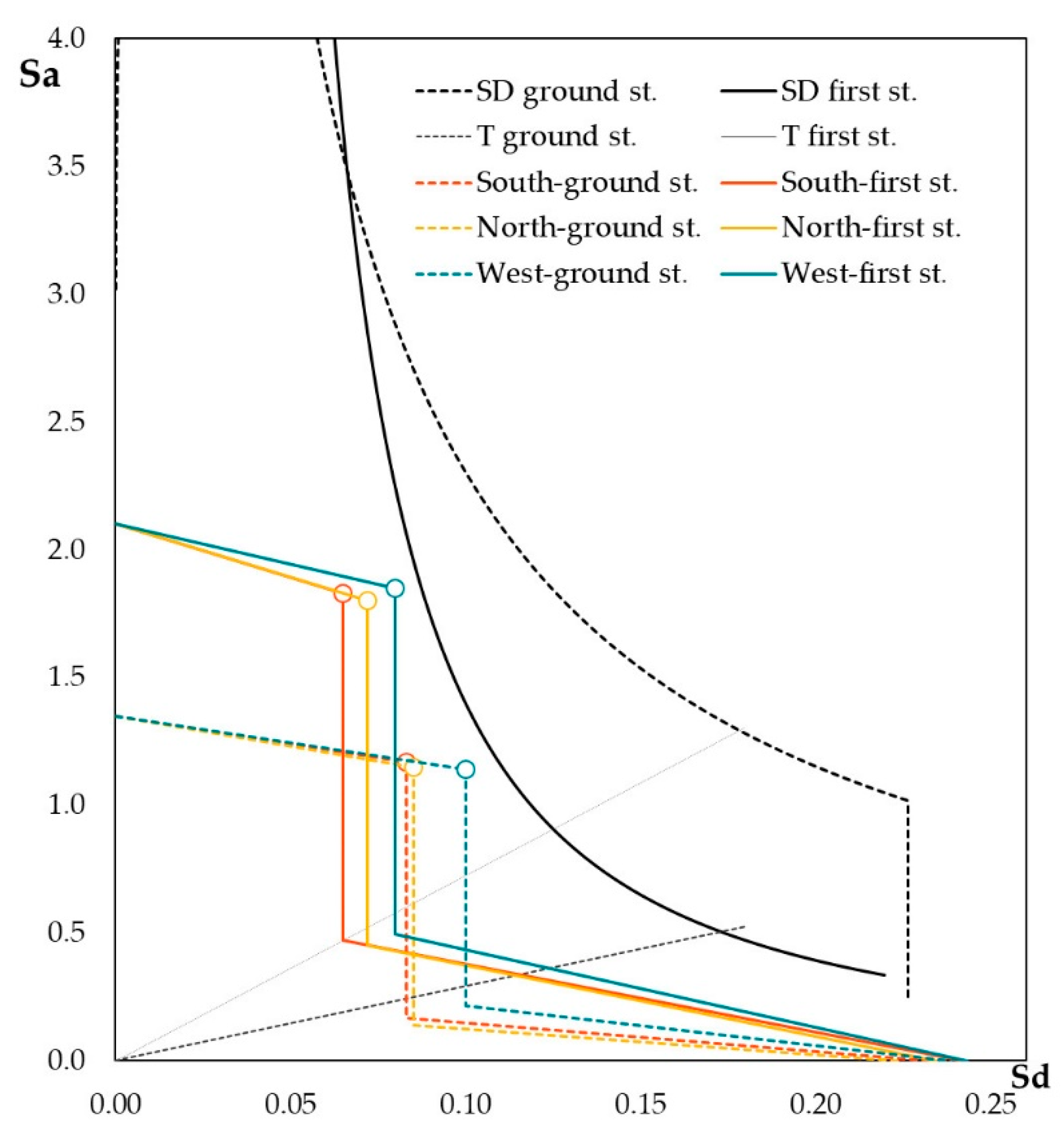
- The local kinematic analysis was performed on the two levels (ground and first floors) of three facades of an extreme unit. The results, on average, did not vary according to the three walls and the two hinges’ positions and were rather conservative (i.e., the activation coefficient c ranged between a fifth and a half of the expected PGA); however, the capacity curves at SD limit state in the Sa–Sd plane indicated a displacement demand of the ground spectrum greater than that obtained from its floor formulation by 50%.
- (d)
- By excluding intrusive interventions (e.g., those with a high impact on usage continuity and demanding construction works, partial substitutions), three strengthening strategies with increasing impact (minimum, low, medium) were proposed. These included intervention techniques aimed at counteracting, progressively, a building’s seismic vulnerability towards an overall favourable behaviour.
- (e)
- For the case study, except for the unavoidable r.c. overlay of the roof, strengthening techniques referred to one-side installation (e.g., FRCM jacketing or grout injections for walls, steel bracing at intrados of floors or r.c. overlay, the latter limited to the highest impact combination) and the improvement of connections, either at overall (tie rods among opposite walls) or local (transverse ties in multi-leaf cross-sections of walls, dowels between diaphragms and walls) scale.
- (f)
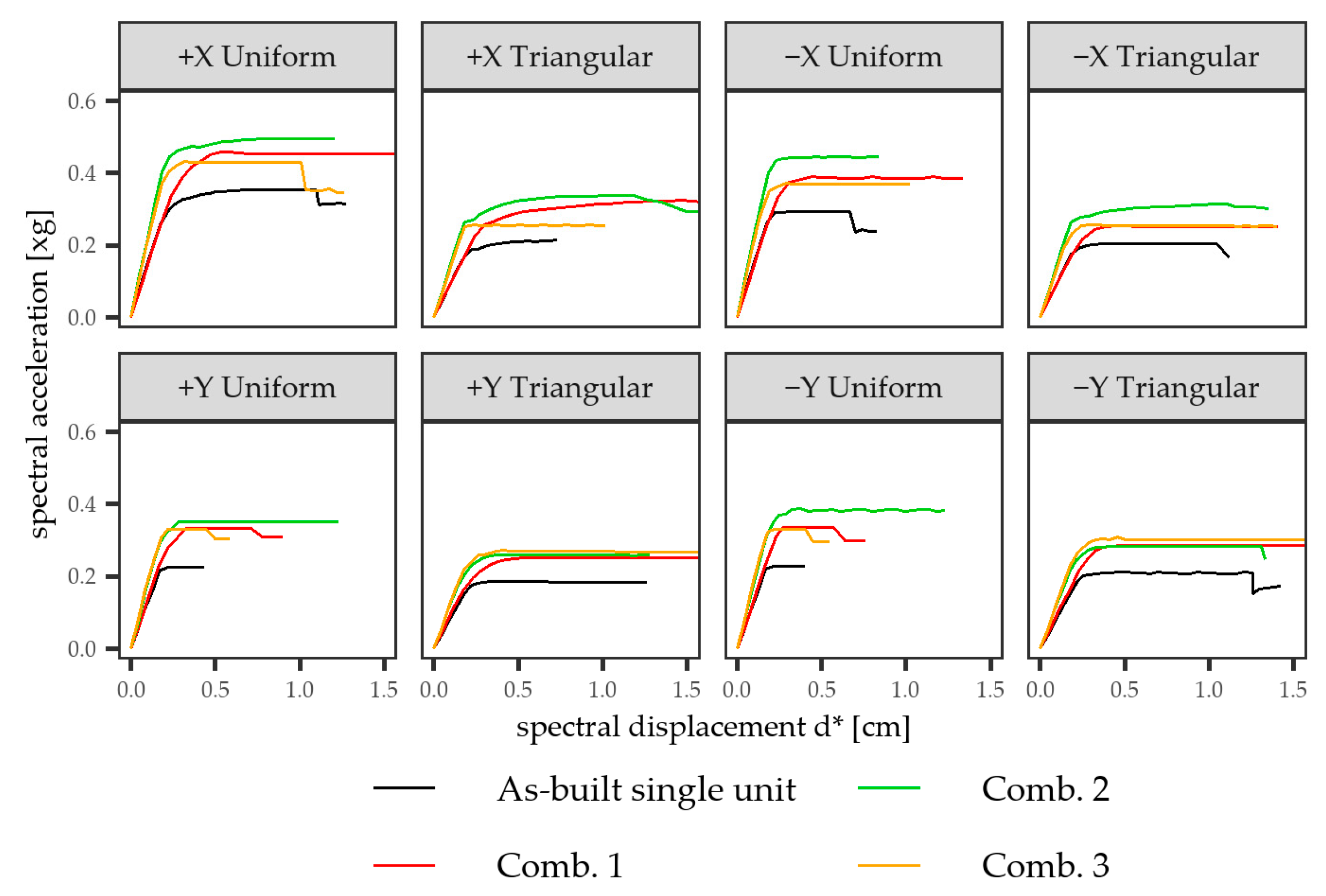
- The effect of the individual intervention techniques on the performance of the single-unit model was particularly evident for grout injections: ζE at the SD limit state increased by 107% in comparison with the as-built conditions, and it was more than twice than that of the FRCM jacketing. Transverse ties applied to improve connections among masonry leaves had a minimum effect, and alone they were not sufficient to reach the target improvement defined by the code. Neither did stiffening interventions on diaphragms affect the performance of the single unit, and did not attain, if not in combination with the wall’s enhancement, the minimum requirement for improvement.
- (g)
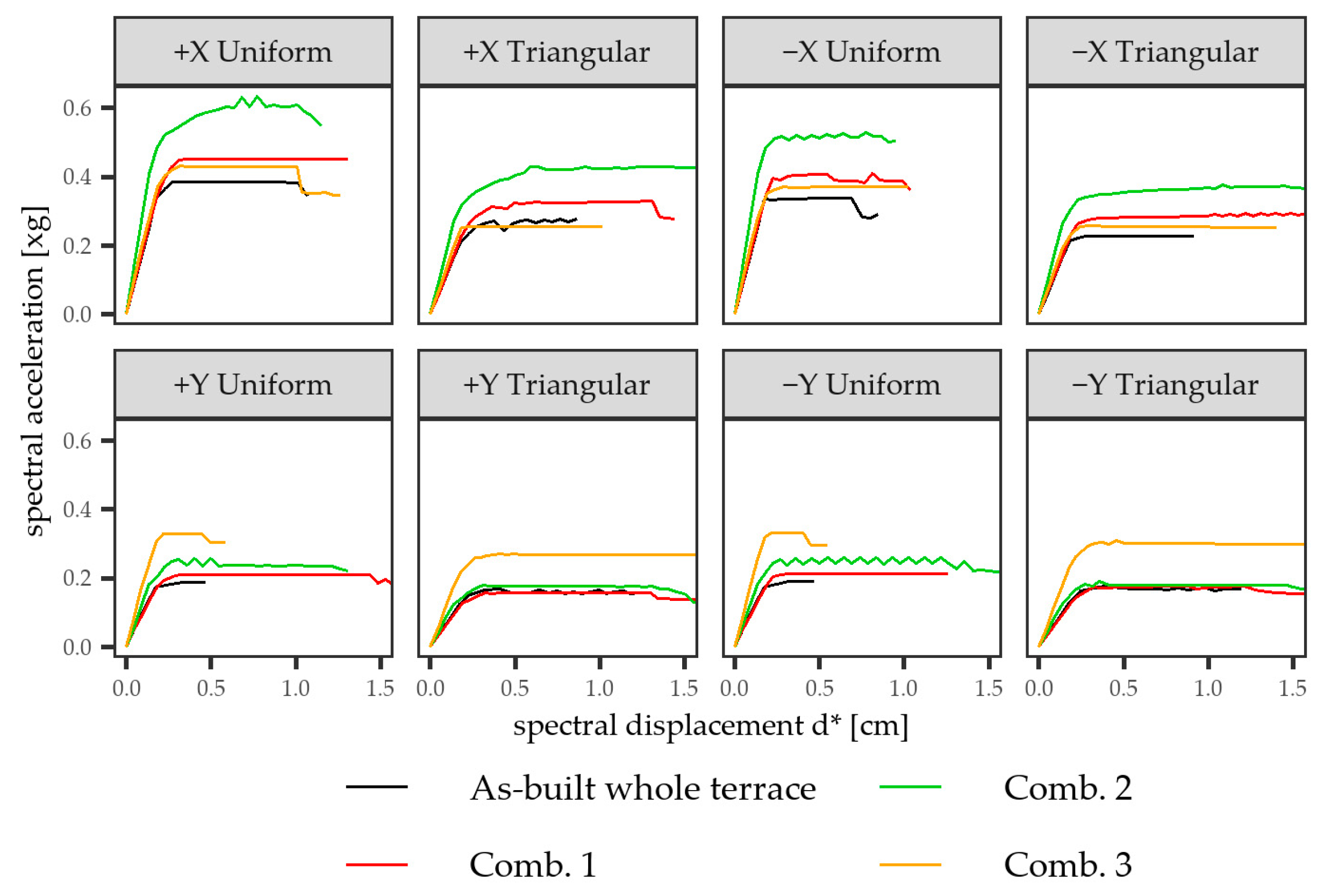
- All combination cases, indeed, for either the single unit or the whole terrace, presented a good increase in ζE (over 0.6 for almost all the cases); this confirmed the reliability of the incremental procedure and, at the same time, offered an opportunity to quantify the actual improvement as a guide for the choice of a building’s strengthening techniques.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Economidou, M.; Atanasiu, B.; Despret, C.; Maio, J.; Nolte, I.; Rapf, O. Europe’s Buildings under the Microscope. A Country-by-Country Review of the Energy Performance of Buildings; Buildings Performance Institute Europe (BPIE): Brussels, Belgium, 2011. [Google Scholar]
- Tsionis, G.; Apostolska, R.; Taucer, F. Seismic Strengthening of RC Buildings; EUR 26945; Publications Office of the European Union: Luxembourg, 2014; p. JRC91949. [Google Scholar] [CrossRef]
- Da Porto, F.; Donà, M.; Rosti, A.; Rota, M.; Lagomarsino, S.; Cattari, S.; Borzi, B.; Onida, M.; De Gregorio, D.; Perelli, F.L.; et al. Comparative analysis of the fragility curves for Italian residential masonry and RC buildings. Bull. Earthq. Eng. 2021, 19, 3209–3252. [Google Scholar] [CrossRef]
- ISTAT Italian National Institute of Statistics. 2011. Available online: https://www.istat.it/it/archivio/104317 (accessed on 1 June 2021).
- Giardini, D.; Wössner, J.; Danciu, L. Mapping Europe’s Seismic Hazard. EOS 2014, 95, 261–262. [Google Scholar] [CrossRef] [Green Version]
- President of the Council of Ministers. Primi Elementi in Materia di Criteri Generali per la Classificazione Sismica del Territorio Nazionale e di Normative Tecniche per le Costruzioni in Zona Sismica; Ordinance: Rome, Italy, 2003. (In Italian) [Google Scholar]
- Stucchi, M.; Meletti, C.; Montaldo, V.; Crowley, H.; Calvi, G.M.; Boschi, E. Seismic Hazard Assessment (2003–2009) for the Italian Building Code. Bull. Seism. Soc. Am. 2011, 101, 1885–1911. [Google Scholar] [CrossRef]
- Valluzzi, M.R.; Sbrogiò, L.; Saretta, Y.; Wenliuhan, H. Seismic Response of Masonry Buildings in Historical Centres Struck by the 2016 Central Italy Earthquake. Impact of Building Features on Damage Evaluation. Int. J. Arch. Herit. 2021, 1–26. [Google Scholar] [CrossRef]
- Kallioras, S.; Graziotti, F.; Penna, A. Numerical assessment of the dynamic response of a URM terraced house exposed to induced seismicity. Bull. Earthq. Eng. 2019, 17, 1521–1552. [Google Scholar] [CrossRef]
- Valluzzi, M.R.; Cardani, G.; Saisi, A.; Binda, L.; Modena, C. Study of the seismic vulnerability of complex masonry buildings. In Proceedings of the 9th International Conference on Structural Studies, Repairs and Maintenance of Heritage Architecture, Msida, Malta, 22–24 June 2005; pp. 301–310. [Google Scholar] [CrossRef]
- Binda, L.; Anzani, A.; Cardani, G. Methodologies for the evaluation of seismic vulnerability of complex masonry buildings: Case histories in the historic centre of Sulmona. In Heritage Masonry–Materials and Structures; Syngellakis, S., Ed.; WIT Press: Southampton, UK, 2014. [Google Scholar]
- Maio, R.; Vicente, R.; Formisano, A.; Varum, H. Seismic vulnerability of building aggregates through hybrid and indirect assessment techniques. Bull. Earthq. Eng. 2015, 13, 2995–3014. [Google Scholar] [CrossRef] [Green Version]
- Grillanda, N.; Valente, M.; Milani, G.; Chiozzi, A.; Tralli, A. Advanced numerical strategies for seismic assessment of historical masonry aggregates. Eng. Struct. 2020, 212, 110441. [Google Scholar] [CrossRef]
- Valente, M.; Milani, G.; Grande, E.; Formisano, A. Historical masonry building aggregates: Advanced numerical insight for an effective seismic assessment on two row housing compounds. Eng. Struct. 2019, 190, 360–379. [Google Scholar] [CrossRef]
- Tomaževič, M.; Bosiljkov, V.; Weiss, P. Structural behavior factor for masonry structures. In Proceedings of the 13th World Con-ference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; p. 2642. [Google Scholar]
- Lagomarsino, S.; Penna, A.; Galasco, A.; Cattari, S. TREMURI program: An equivalent frame model for the nonlinear seismic analysis of masonry buildings. Eng. Struct. 2013, 56, 1787–1799. [Google Scholar] [CrossRef]
- Saretta, Y.; Sbrogiò, L.; Valluzzi, M.R. Seismic response of masonry buildings in historical centres struck by the 2016 Central Italy earthquake. Calibration of a vulnerability model for strengthened conditions. Constr. Build. Mater. 2021, 299, 123911. [Google Scholar] [CrossRef]
- Sbrogiò, L.; Saretta, Y.; Valluzzi, M.R. Empirical performance levels of strengthened masonry buildings struck by 2016 Central Italy earthquake: Proposal of a new taxonomy. Int. J. Archit. Herit. submitted.
- Sisti, R.; Di Ludovico, M.; Borri, A.; Prota, A. Damage assessment and the effectiveness of prevention: The response of ordinary unreinforced masonry buildings in Norcia during the Central Italy 2016–2017 seismic sequence. Bull. Earthq. Eng. 2019, 17, 5609–5629. [Google Scholar] [CrossRef]
- Sorrentino, L.; Cattari, S.; Da Porto, F.; Magenes, G.; Penna, A. Seismic behaviour of ordinary masonry buildings during the 2016 central Italy earthquakes. Bull. Earthq. Eng. 2019, 17, 5583–5607. [Google Scholar] [CrossRef] [Green Version]
- Ministry of Infrastructures and Transportations. Ministerial Decree 17/01/2018. Aggiornamento delle ‘Norme Tecniche per le Costruzioni’. 2018. Available online: https://www.gazzettaufficiale.it/eli/id/2018/2/20/18A00716/sg (accessed on 30 June 2021). (In Italian)
- Ministry of Infrastructures and Transportations. Regulation n. 7/2019. Istruzioni per L’applicazione dell’Aggiornamento delle “Norme Tecniche per le Costruzioni” di cui al Decreto Ministeriale 17 Gennaio. 2018. Available online: https://www.gazzettaufficiale.it/eli/id/2019/02/11/19A00855/sg (accessed on 30 June 2021). (In Italian)
- European Committee for Standardization. Eurocode 8: Design of Structures for Earthquake Resistance–Part 3: Assessment and Retrofitting of Buildings; CEN: Brussels, Belgium, 2005. [Google Scholar]
- Ministry of Infrastructures and Transportations. Ministerial Decree 07/03/2017, Linee Guida per la Classificazione del Rischio Sismico delle Costruzioni; Ministry of Infrastructures and Transportations: Rome, Italy, 2017. (In Italian)
- Cosenza, E.; Del Vecchio, C.; Di Ludovico, M.; Dolce, M.; Moroni, C.; Prota, A.; Renzi, E. The Italian guidelines for seismic risk classification of constructions: Technical principles and validation. Bull. Earthq. Eng. 2018, 16, 5905–5935. [Google Scholar] [CrossRef]
- Abrams, D.P.; AlShawa, O.; Lourenço, P.B.; Sorrentino, L. Out-of-plane seismic response of unreinforced masonry walls: Conceptual discussion, research needs, and modeling issues. Int. J. Archit. Herit. 2017, 11, 22–30. [Google Scholar] [CrossRef]
- ICOMOS. Charter of Cracow. Principles for Conservation and Restoration of Built Heritage; ICOMOS: Paris, France, 2000. [Google Scholar]
- ICOMOS. ICOMOS Charter—Principles for the Analysis, Conservation and Structural Restoration of Architectural Heritage; ICOMOS: Paris, France, 2003. [Google Scholar]
- Tomaževič, M. Earthquake-Resistant Design of Masonry Buildings. Innovation in Structures and Construction; Imperial College Press: London, UK, 1999. [Google Scholar]
- Baggio, C.; Bernardini, A.; Colozza, R.; Corazza, L.; Dalla Bella, M.; Pasquale, G.D.; Dolce, M.; Goretti, A.; Martinelli, A.; Orsini, G.; et al. Field Manual for Post-Earthquake Damage and Safety Assessment and Short-Term Counter-Measures (AeDES); Pinto, A.V., Taucer, F., Eds.; EU JRC: Luxembourg, 2007. [Google Scholar]
- Valluzzi, M.R.; Sbrogiò, L. Vulnerability of architectural heritage in seismic area: Constructive aspects and effect of interventions. In Cultural Landscape in Practice. Conservation vs. Emergencies; Amoruso, G., Salerno, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 203–218. [Google Scholar] [CrossRef]
- Corradini, S. La Pieve ed i Castelli. Appunti per la Storia del Territorio; Micheloni: Recanati, Italy, 1979; pp. 86–182. (In Italian) [Google Scholar]
- Grünthal, G. European Macroseismic Scale 1998. Cahiers du Centre Européen de Géodynamique et de Séismologie, 15; European Center for Geodynamics and Seismology: Luxembourg, 1998. [Google Scholar]
- Locati, M.; Camassi, R.; Rovida, A.; Ercolani, E.; Bernardini, F.; Castelli, V.; Caracciolo, C.H.; Tertulliani, A.; Rossi, A.; Azzaro, R.; et al. Italian Macroseismic Database (DBMI15), Version 3.0 2021, 3228 Earthquakes, 123956 Macroseismic Data Points; INGV: Rome, Italy, 2019. [Google Scholar]
- Lenzi, U.; Lenzi, A.; Pinti, S. Microzonazione Sismica, Relazione Illustrativa; Regione Marche, Comune di Pieve Torina; Municipality of Pieve Torina: Regione Marche, Italy, 2018. (In Italian) [Google Scholar]
- Sextos, A.; De Risi, R.; Pagliaroli, A.; Foti, S.; Passeri, F.; Ausilio, E.; Cairo, R.; Capatti, M.C.; Chiabrando, F.; Chiaradonna, A.; et al. Local Site Effects and Incremental Damage of Buildings during the 2016 Central Italy Earthquake Sequence. Earthq. Spectra 2018, 34, 1639–1669. [Google Scholar] [CrossRef] [Green Version]
- Stucchi, M.; Meletti, C.; Montaldo, V.; Akinci, A.; Faccioli, E.; Gasperini, P.; Malagnini, L.; Valensise, G. Pericolosità Sismica di Riferimento per il Territorio Nazionale MPS04; INGV: Rome, Italy, 2004. [Google Scholar]
- Ministry of Public Works. Ministerial Decree 10/02/1983, Aggiornamento delle Zone Sismiche della Regione Marche; Ministry of Public Works: Rome, Italy, 1983. (In Italian)
- Borri, A.; Corradi, M.; De Maria, A. The Failure of Masonry Walls by Disaggregation and the Masonry Quality Index. Heritage 2020, 3, 1162–1198. [Google Scholar] [CrossRef]
- AA.VV. Manualetto RDB; RDB: Piacenza, Italy, 1982. (In Italian) [Google Scholar]
- Italian Royal Decree No. 2229, 03/04/1930, Norme per L’esecuzione delle Opere in Conglomerato Cementizio Semplice od Armato. 1939. (In Italian)
- Guerrini, G.; Salvatori, C.; Senaldi, I.; Penna, A. Experimental and Numerical Assessment of Seismic Retrofit Solutions for Stone Masonry Buildings. Geosciences 2021, 11, 230. [Google Scholar] [CrossRef]
- Cattari, S.; Lagomarsino, S. Seismic assessment of mixed masonry-reinforced concrete buildings by non-linear static analyses. Earthq. Struct. 2013, 4, 241–264. [Google Scholar] [CrossRef] [Green Version]
- European Committee for Standardization. Eurocode 2: Design of Concrete Structures-Part 1-1: General Rules and Rules for Buildings; CEN: Brussels, Belgium, 2004. [Google Scholar]
- Messali, F.; Metelli, G.; Plizzari, G. Experimental results on the retrofitting of hollow brick masonry walls with reinforced high performance mortar coatings. Constr. Build. Mater. 2017, 141, 619–630. [Google Scholar] [CrossRef]
- Turnšek, V.; Čačovič, F. Some experimental results on the strength of brick masonry walls. In Proceedings of the 2nd Int Brick Masonry Conference, Stoke-on-Trent, UK, 12–15 April 1970; pp. 149–156. [Google Scholar]
- Ricci, P.; Verderame, G.M.; Manfredi, G. Analisi statistica delle proprietà meccaniche degli acciai da cemento armato utilizzati tra il 1950 e il 1980. In Proceedings of the L’ingegneria sismica in Italia, XIV Convegno ANIDIS, Bari, Italy, 18–22 September 2011. (In Italian). [Google Scholar]
- Corradi, M.; Tedeschi, C.; Binda, L.; Borri, A. Experimental evaluation of shear and compression strength of masonry wall before and after reinforcement: Deep repointing. Constr. Build. Mater. 2008, 22, 463–472. [Google Scholar] [CrossRef] [Green Version]
- Valluzzi, M.R.; Binda, L.; Modena, C. Experimental and analytical studies for the choice of repair techniques applied to historic buildings. Mater. Struct. 2002, 35, 285–292. [Google Scholar] [CrossRef]
- ACI 549.6R-20. Guide to Design and Construction of Externally Bonded Fabric-Reinforced Cementitious Matrix (FRCM) and Steel-Reinforced Grout (SRG) Systems for Repair and Strengthening Masonry Structures; ACI: Farmington Hills, MI, USA, 2020. [Google Scholar]
- CNR-DT 215/2018. Advisory Committee on Technical Recommendations for Construction. Guide for the Design and Construction of Externally Bonded Fibre Reinforced Inorganic Matrix Systems for Strengthening Existing Structures; CNR: Rome, Italy, 2020. [Google Scholar]
- Ferretti, F.; Incerti, A.; Ferracuti, B.; Mazzotti, C. FRCM Strengthened Masonry Panels: The Role of Mechanical Anchorages and Symmetric Layouts. Key Eng. Mater. 2017, 747, 334–341. [Google Scholar] [CrossRef]
- Del Zoppo, M.; Di Ludovico, M.; Prota, A. Analysis of FRCM and CRM parameters for the in-plane shear strengthening of different URM types. Compos. Part B Eng. 2019, 171, 20–33. [Google Scholar] [CrossRef]
- Valluzzi, M.R.; Cescatti, E.; Cardani, G.; Cantini, L.; Zanzi, L.; Colla, C.; Casarin, F. Calibration of sonic pulse velocity tests for detection of variable conditions in masonry walls. Constr. Build. Mater. 2018, 192, 272–286. [Google Scholar] [CrossRef]
- CNR-DT 200 R1/2013. Advisory Committee on Technical Recommendations for Construction. Guide for the Design and Construction of Externally Systems for Strengthening Existing Structures; CNR: Rome, Italy, 2014. [Google Scholar]
- Pisani, M.A. Theoretical approach to the evaluation of the load-carrying capacity of the tie rod anchor system in a masonry wall. Eng. Struct. 2016, 124, 85–95. [Google Scholar] [CrossRef]
- Podestà, S.; Scandolo, L. Earthquakes and Tie-Rods: Assessment, Design, and Ductility Issues. Int. J. Arch. Herit. 2019, 13, 329–339. [Google Scholar] [CrossRef]



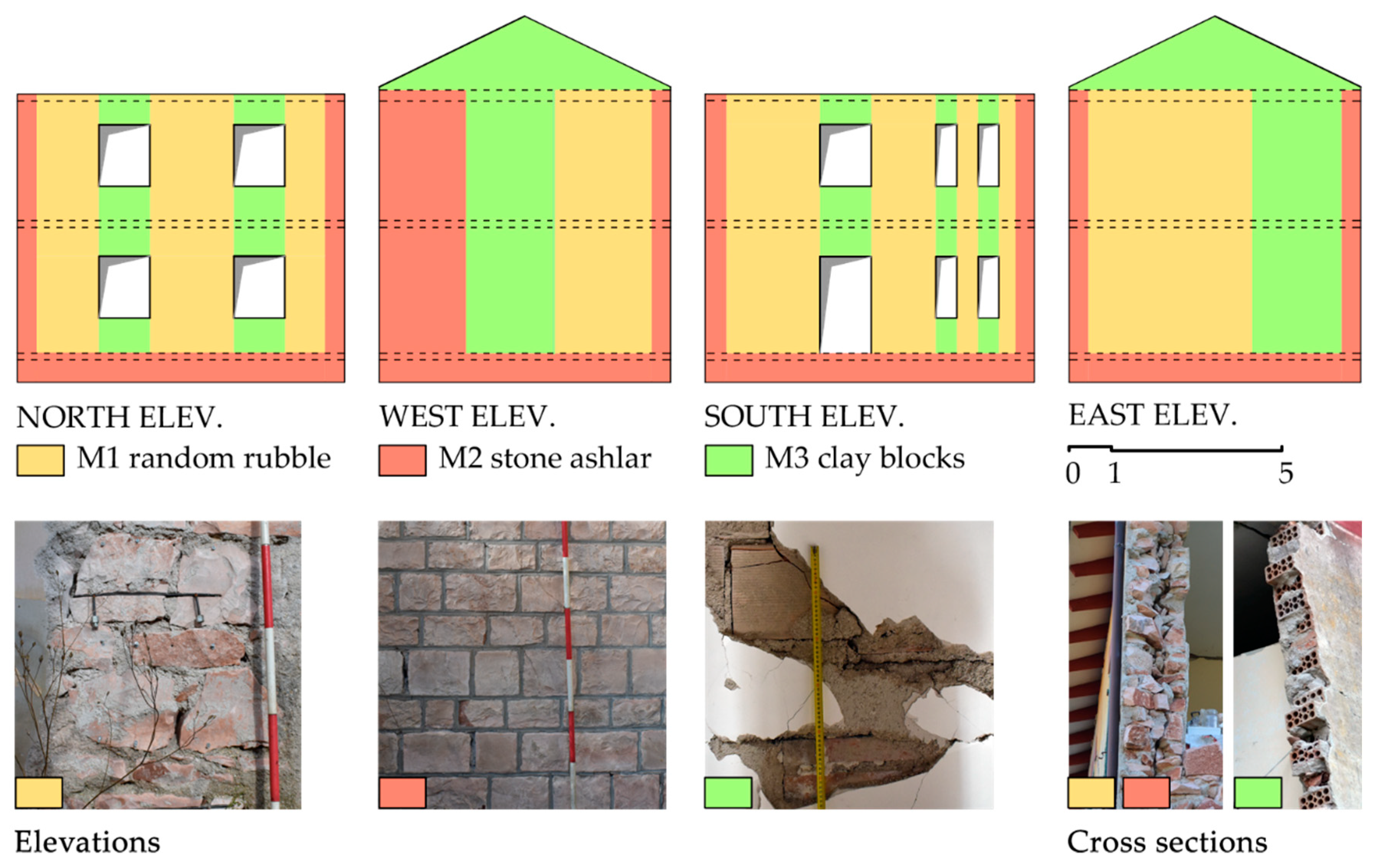




| Material | Compressive Strength fm (MPa) | Shear Strength τ0 (MPa) | Young’s Modulus E (MPa) | Shear Modulus G (MPa) | Specific Weight w (kN/m3) |
|---|---|---|---|---|---|
| M1 | 1.00 | 0.018 | 870 | 290 | 19 |
| M3 | 1.56 | 0.090 | 4370 | 1748 | 10 |
| Storey | Thickness (cm) | gk1 (kg/m2) | gk2 (kg/m2) | qk (kg/m2) | Ψ2j |
|---|---|---|---|---|---|
| Ground | 16 | 130 | 50 | 200 | 0.3 |
| First | 16 | 130 | 90 | 200 | 0.3 |
| Ceiling | 12 | 110 | 0 | 50 | 0 |
| Roof | 12 | 110 | 60 | 50 | 0 |
| Material | No. of Layers | Equivalent Textile Thickness | Young’s Modulus of Grid | Maximum Strain | Debonding Strength |
|---|---|---|---|---|---|
| tf (mm) | Ef (MPa) | εfd (%) | ffd (MPa) | ||
| Limestone | 1 | 0.031 | 73600 | 0.18 | 106.75 |
| Clay blocks | 1 | 0.031 | 73600 | 0.28 | 166.43 |
| Wall | Hinge Position | ζE | |
|---|---|---|---|
| DL | SD | ||
| South facade | Ground floor | 0.211 | 0.291 |
| First storey | 0.383 | 0.375 | |
| West facade | Ground floor | 0.247 | 0.298 |
| First storey | 0.405 | 0.386 | |
| North facade | Ground floor | 0.175 | 0.280 |
| First storey | 0.369 | 0.362 | |
| Intervention | ζE | ΔζE | ΔζE (%) |
|---|---|---|---|
| As-built | 0.379 | ||
| One-side FRCM jacketing | 0.562 | 0.183 | 48 |
| Grout injections | 0.786 | 0.407 | 107 |
| Transverse ties | 0.466 | 0.087 | 23 |
| One-side FRCM jacketing and transverse ties | 0.658 | 0.279 | 74 |
| Grout injections and transverse ties | 0.836 | 0.457 | 121 |
| Tie rods along X direction | 0.379 | 0 | 0 |
| Tie rods along X and Y directions | 0.379 | 0 | 0 |
| R.c. overlay on roof | 0.393 | 0.014 | 4 |
| Steel bracings | 0.379 | 0 | 0 |
| R.c. overlay on floors | 0.388 | 0.009 | 2 |
| R.c. overlay on both roof and floors | 0.393 | 0.014 | 4 |
| Model | Intervention | ζE | ΔζE | ΔζE (%) |
|---|---|---|---|---|
| Single unit (no. 6) | As-built | 0.379 | ||
| Combination 1 | 0.658 | 0.279 | 74 | |
| Combination 2 | 0.799 | 0.420 | 111 | |
| Combination 3 | 0.658 | 0.279 | 74 | |
| Whole terrace | As-built | 0.283 | ||
| Combination 1 | 0.512 | 0.229 | 81 | |
| Combination 2 | 0.626 | 0.343 | 121 | |
| Combination 3 | 0.617 | 0.334 | 118 |
| Wall | Hinge Position | ζE | ΔζE | ||
|---|---|---|---|---|---|
| DL | SD | DL | SD | ||
| South facade | Ground floor | 1.000 | 0.939 | 0.789 | 0.648 |
| First storey | 1.000 | 0.960 | 0.617 | 0.585 | |
| West facade | Ground floor | 1.000 | 0.998 | 0.753 | 0.700 |
| First storey | 1.000 | 1.060 | 0.595 | 0.674 | |
| North facade | Ground floor | 1.000 | 0.947 | 0.825 | 0.667 |
| First storey | 1.000 | 0.983 | 0.631 | 0.621 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valluzzi, M.R.; Sbrogiò, L.; Saretta, Y. Intervention Strategies for the Seismic Improvement of Masonry Buildings Based on FME Validation: The Case of a Terraced Building Struck by the 2016 Central Italy Earthquake. Buildings 2021, 11, 404. https://doi.org/10.3390/buildings11090404
Valluzzi MR, Sbrogiò L, Saretta Y. Intervention Strategies for the Seismic Improvement of Masonry Buildings Based on FME Validation: The Case of a Terraced Building Struck by the 2016 Central Italy Earthquake. Buildings. 2021; 11(9):404. https://doi.org/10.3390/buildings11090404
Chicago/Turabian StyleValluzzi, Maria Rosa, Luca Sbrogiò, and Ylenia Saretta. 2021. "Intervention Strategies for the Seismic Improvement of Masonry Buildings Based on FME Validation: The Case of a Terraced Building Struck by the 2016 Central Italy Earthquake" Buildings 11, no. 9: 404. https://doi.org/10.3390/buildings11090404
APA StyleValluzzi, M. R., Sbrogiò, L., & Saretta, Y. (2021). Intervention Strategies for the Seismic Improvement of Masonry Buildings Based on FME Validation: The Case of a Terraced Building Struck by the 2016 Central Italy Earthquake. Buildings, 11(9), 404. https://doi.org/10.3390/buildings11090404







