Abstract
In this paper, we present a simulation-based approach for effectively estimating delay risks in project schedules and predicting the possibilities of in-time project completion for various deadlines. The main contribution of this study is the development of a novel approach for duration risk quantification, which uses a newly introduced equation for total risk estimation regarding activities’ durations, and quantifying the manager’s experience as expressed through a questionnaire. In addition, the proposed approach integrates these preferences into a simulation-based framework used for estimating the activities’ durations variation and predicting the actual project duration with more accuracy. Furthermore, using different distributions according to each activity characteristic supports decision making from a wide range of experts, from risk-averse to risk-seeking managers. The proposed method was applied to estimate the total project completion time of a complicated hotel renovation project and the possibility for the project to be delivered within an imposed deadline. The promising results in comparison to the classic PERT method proved that this process can better express the uncertainty and provide project risk managers with better predictions when estimating budget and time-critical overruns under lack of knowledge and historical data.
1. Introduction
The total project duration is one of the most important indices illustrating the efficient management of resources to complete the deliverables within the proper quality standards. In practice, the project baseline schedule includes vulnerability due to the existing uncertainty regarding the actual activities’ durations and costs. Thus, duration prediction is an important issue in baseline scheduling and while constructing the updated interim baseline schedules during the execution of the project. Generally, treating risks associated with project schedule and costs is quite an important process for efficient project management and completion of a project in time and within budget. As risk management contains risk identification, risk analysis, risk mitigation actions, and monitoring of risks that could arise during project execution. Regarding the quantitative risk analysis, classic methods proposed in the past are the Program Evaluation and Review Technique (PERT) [1], the Graphical Evaluation and Review Technique (GERT) [2] introduced for treating uncertainty in schedules. PERT was the first approach that extended the Critical Path Method [3] to probabilistic durations environment, as it considers beta distribution for modeling the activities’ durations, with proven value in managing complex projects. On the other hand, GERT provides the framework for both probabilistic branching of activities and duration estimation, but it is rarely used because of its complexity of modeling. In addition, Monte Carlo simulation has been introduced to project scheduling under uncertainty, and used in combination with PERT, providing a generalized approach of the latter.
Project risk analysis is recognized as one of the most critical aspects of project scheduling and management. Numerous studies have been developed to predict tasks’ execution durations by analyzing risks with the Monte Carlo simulation process. Various studies proposed probabilistic approaches for estimating cost and duration risks in construction projects. Barraza and Bueno [4] developed a probabilistic approach and a graphical representation for both actual cost and elapsed time to support forecasting of final cost and project duration, while Barraza [5] used an approach based on Monte Carlo simulation for stochastic allocation of project allowances, and estimated the project time contingency of the project activities. In their study, Alarcón et al. [6] provided a model for the duration and cost contingency assessments with application to the Panama Canal expansion program, and Nguyen et al. [7], constructed a model for time prediction, applied to a high-rise building project. Elshaer [8] used simulation for activities’ duration prediction in an earned schedule management framework, while [9] developed an innovative model to capture uncertainty in cost and duration of complex transportation projects. Recently, Farshchian and Heravi [10] proposed an approach using an agent-based simulation model to consider uncertainty in project durations and costs, and Bianco et al. [11] considered a stochastic formulation of the problem and developed an approach assuming Beta probability density function for the activities’ duration variables.
There are numerous studies that proposed a wide variety of methods for risk estimation in projects, that either incorporate simulation or not. More specifically, Sarigiannidis and Chatzoglou [12] investigated whether project risks are interconnected with people quality and process quality, in software development projects, and Thompson et al. [13] introduced the use of Tracy–Widom distribution to represent the duration of project tasks with quite good results. Elbarkouky et al. [14] proposed an approach based on fuzzy logic and expert judgments to determine construction project contingency, while Hajifathalian et al. [15] used a novel approach and simulations to provide evidence about the value of planning under different construction circumstances. In addition, Qazi et al. [16] used simulation to document the functionality of their approach using Expected Utility Theory and Bayesian Belief Networks to formulate a decision problem that captures the interdependency between complexity drivers, risks, and objectives. Zhang et al. [17] developed an integrated dynamic default tree (DFT) and discrete-time Bayesian network (DTBN) simulation approach to make predictions about tunnel boring machine performance, and Tao et al. [18] introduced a graphical evaluation and review technique model and used simulation to determine the key factors that affect the schedule of a new product development project. Recently, Paz et al. [19] proposed a new mathematical formulation for the simulation model in which the “potential impact” of a risk factor was used. Then, the simulation process used to validate the functionality of the model via an already constructed construction university project was proposed.
Furthermore, plenty of studies have applied Monte Carlo Simulation approaches for risk estimation. Kirytopoulos et al. [20] studied the importance of using historical information, and the right distribution selection in activity duration estimation for Monte Carlo simulation process, while Vanhoucke [21] developed a bottom-up and a top-down project tracking method and applied them on projects with uncertain durations, subjected to Monte Carlo simulations. In their study, Jun and El-Rayes [22] presented a probabilistic model that focuses on the most significant paths in the project network so as to reduce the computational time that Monte Carlo simulation needed. Vanhoucke [23] proposed project control efficiency measurements using a Monte Carlo simulation and empirical project data from schedule risk analysis and earned value management processes, and Choudhry et al. [24] used Monte Carlo simulation and a questionnaire to analyze risks in bridge construction. Tran, and Molenaar [25] used a stochastic agent-based simulation to consider probabilities about several project uncertainties. Additionally, Wang et al. [26] proposed a robust formulation to minimize the operational costs in a building energy system along with a column and constraint generation algorithm. Then, they used a Monte Carlo simulation to test the performance of the proposed approach, and Firouzi et al. [27] proposed a copula-based Monte Carlo simulation method for predicting projects’ total costs with dependent cost items.
In their study, Kerkhove and Vanhoucke [28] proposed a model for enhancing durations uncertainty with the influence of weather conditions and used Monte Carlo simulation and a heuristic approach to estimate the net present value of an offshore construction project. Chang and Ko, [29] proposed a new approach to estimate standard deviations of lognormal cost variables in the Monte Carlo analysis of construction risks. In their study, Erol et al. [30] used Monte Carlo simulation to demonstrate the advantages of lean construction in residential building projects, while Francis [31] used Monte Carlo simulation to consider the impact of construction operations, execution processes, and work with doubtful results, and impose scheduling constraints.
Recently, Chang et al. [32] proposed an approach for activity risk estimation based on seven risk-levels and used the Monte Carlo simulation (MCS) method to apply sensitivity analysis of activities’ durations, and Lorenzo et al. [33] developed a strategy to find a best-fit distribution developed, since as they stated, normal distribution cannot illustrate the uncertainty in complex projects with many activities and paths, while the Extreme Value distribution which was suggested in the literature as an alternative, was found to be of limited practical utility.
In their study, Aderbag et al. [34] analyzed cost and schedule risks of a housing construction project using a Monte Carlo simulation-based approach, while Walȩdzik and Mańdziuk [35] proposed an algorithmic approach based in Monte Carlo Tree Search to solve the Risk-Aware Project Scheduling Problem, which is a stochastic extension of the classic Resource Constrained Project Scheduling Project (RCPSP). Also, Ntzeremes and Kirytopoulos [36] proposed a new stochastic method for quantitative fire risk assessment in underground road tunnels.
Furthermore, Rausch et al. [37] applied Monte Carlo simulation for tolerance analysis in the production of assemblies that need fewer or no reworks during assembly fit-up during offsite construction. In addition, the study of Tokdemir et al. [38] introduced a delay risk assessment method for projects scheduled by line-of-balance (LOB) method and used a Monte Carlo simulation for risk quantification. A great recent survey about managing uncertainty in projects is presented in the study of Aven [39].
The objective of this research is to fill the existing research gap for an approach that estimates the probability of project completion within a specific deadline, based on a case-sensitive project questionnaire that reflects the expertise and preferences of the project risk manager and then, using Monte Carlo simulation, to analyze them, extract probabilities of in time execution, and perform an extensive sensitivity analysis which better illustrates the amount of risk that the project is exposed to. The remainder of the paper is organized by the following sections: (2) the proposed approach, (3) the description of the application in a construction project, and (4) the conclusions section.
2. The Proposed Approach
The proposed approach can be implemented while starting the project to predict the finish time more accurately, and also, throughout the implementation of the project to update the initial prediction according to the real data of the project execution. The flowchart of the proposed methodology is shown in Figure 1. Initially, the activities of the project are categorized according to their nature. In this study, we considered five different categories (preparation–earthworks, building works, electrical and mechanical installations, installation of equipment, completion and testing). It is worth mentioning that this step is very important since statistical distributions will be assigned to activities’ categories rather than singular activities, which is something that affects the total results. Furthermore, this categorization will cause an effect to the total amount of resources used since it is considered that the tasks belonging to the same category will employ similar groups of work resources. Next, the risk identification questionnaire is answered by the expert risk manager, and the answers are analyzed. In the quantification of preferences step, the expert’s answers are, first, reviewed to determine if there are some missing. Moreover, according to the answers, statistical distributions are assigned to each activity or groups of similar activities as well as a range to express uncertainty, if the distribution needs to. The total risk is calculated according to a simple proposed equation that is described in more detail in Section 2.4. These values are the input of the Monte Carlo simulation process, which is applied in the next step. Conclusions derived from the results are reviewed, and the project risk manager considers whether the total delay risk is tolerable. In case that the amount of risk is not acceptable, they are reduced by employing proper policies, and the process loops back to the second step, and the manager fills in the questionnaire again. This loop is executed until the total risk is tolerable.
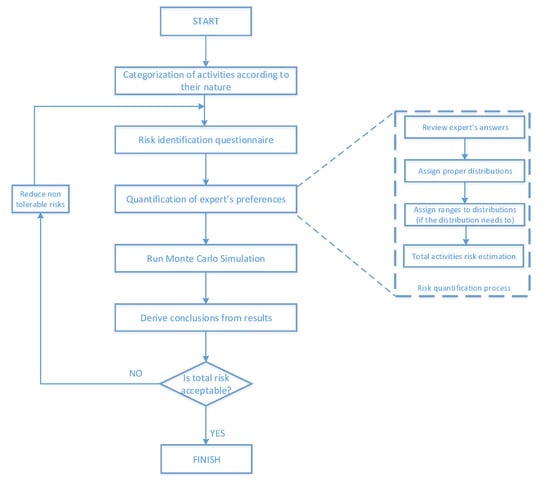
Figure 1.
The flowchart of the proposed approach for risk analysis.
2.1. The Risk Identification Questionnaire
As mentioned in Kirytopoulos [20], the availability of historical data for actual construction project activities’ durations is not guaranteed for each activity of every project. However, given that these data are considered as extremely important for total project duration estimation, we introduce a new questionnaire to get the preferences and generally illustrate the expertise of the construction project manager regarding the risk factors that could impact each activity and how much. The questionnaire consists of three parts, separated according to the nature of information targeted. The first part contains information about the experience of the corresponding project manager. The second part consisted of general risk factors identification questions, inspired by El-Sayegh et al. [40]. These questions focus on expressing the risk manager’s judgments about the probability of risk appearance and the corresponding time impact, in terms of duration delay. Two of the questions are related to the probability and impact of each risk factor, expressed using a Likert type five-point scale (Very Low, Low, Moderate, High, Very High). The numerical equal to the above ranges from [0,1] with a 0.25 step.
The questions investigate the existence of various types of risks according to its source, including risks from the construction company (e.g., inefficient planning, health and safety issues, low construction quality), from the project owner (e.g., delays in payments, changes to feasibility during construction), from governmental factors (e.g., delays in licensing, changes in rules and regulations, political instability), from socioeconomic factors (e.g., criminal acts, staff cultural differences), and environmental factors (e.g., project environmental negative impact, weather volatility and/or natural disasters). The third part allows the risk manager to insert an optimistic and a pessimistic estimation of the duration deviation time from the one which was initially planned. These estimations are inserted in subsets of the project tasks organized in four categories according to the nature of the work processed.
2.2. Distributions Assignment
In this study, given that there were no historical data available regarding the activities’ durations, we used a pragmatic approach to select the distribution assigned to each category of activities. Our main goal was to match the tasks’ nature as it appeared in real-life with the distributions’ characteristics, and employ easy to parameterize distributions that do not require expert statistical knowledge from the project risk manager.
The risk manager should treat some issues to consider the activity nature and behavior, and determine the lower and upper bounds, in case they exist. Furthermore, the manager has to estimate the most likely value of a given distribution, if needed. In the present study, we included some simple, practical, and easy to use distributions, such as the uniform continuous, the PERT, and the triangular distribution.
The uniform continuous distribution refers to instances that all results within a range have an equal probability of happening, while the upper and lower bounds depicted by the minimum and maximum possible values. The primary use of the uniform distribution is to illustrate the uncertainty where there are no specific data available, or there is no information or any kind of knowledge about outputs’ possibilities except awareness about the set of upper and lower bounds. The uniform distribution is considered as a basic distribution in risk analysis and simulation processes since samples created with it are used as input to the inversion process used to create samples of other distributions’ values [41].
The triangular distribution is a reasonable choice when the goal is to express continuous uncertainty in a practical way, since it needs a most likely value estimation, frequently corresponding to the base case scenario, and a minimum and maximum value as lower and upper bounds, respectively. The distribution is employed to explain general uncertainty concepts for which not much historical information is available, but the experience exists to estimate the most possible value.
The PERT distribution is defined as a special case of the beta distribution using three estimators: the minimum, most likely, and maximum values, similar to the triangular distribution. It is primarily used as a realistic alternative to the triangular and beta distributions and, generally, produces a more precise representation of procedures, tending to have a lower percentage of values in its tails for non-symmetric parameters [41]. The limitation of the PERT distribution is that it is bounded on both sides, which could be considered as a drawback when approximating the duration of an activity that is usually unbounded. However, this is often not applicable, or in many instances, the approximation of an unbounded process with a bounded distribution can be considered adequate [41].
2.3. Range Consideration
In the third section of the questionnaire, the expert answered questions that are specified to the present project. Given that the activities were grouped into four groups according to the nature of the task, the manager estimated if the tasks of a group could terminate earlier (optimistic) than the most likely duration, which is considered in the deterministic case, and if it is possible to delay the activities. The estimation is expressed as a percentage of early completion or lag. The manager could choose the preferred level of early completion or delay from a range of −40% to + 40% in a 10% step (Table 3).
In the present project case, five tasks’ categories were defined. (a) preparation–earthworks, (b) building works, (c) electrical and mechanical installations, (d) installation of equipment, and (e) completion and testing.
2.4. Extract Total Risk Estimation for the Activities
Calculating the total risk associated with each group of tasks consisted of a simple equation and the answers of the manager to the questions of the three questionnaire sections. The total risk was expressed as a range in which lower bound is the optimistic scenario (completion earlier than most likely expected), and the upper bound is the pessimistic scenario (completion with a delay over the most likely expected duration). These values, and the deterministic duration for each task, were input for the simulation process. The lower (optimistic) and the upper (pessimistic) bounds were calculated using Equations (1) and (2), respectively:
where:
is the calculated deviation of early completion of an activity group j;
is the calculated deviation of late completion of an activity group j;
the sum of the multiplication of Probability (P) and Impact (I) for every question answered;
is the total number of the questions answered;
is the manager’s experience index;
is the estimated earlier duration deviation for each group of tasks (j), as considered by the manager in Section 3 of the questionnaire;
is the estimated deviation for each group of tasks (j), as considered by the manager in Section 3 of the questionnaire;
is the number of activities’ groups.
It worth mentioning that the answers of the risk manager in Sections 1 and 2 of the questionnaire work as correction indices for the range estimation made in Section 3. Essentially, the range was reduced or extended according to the specific manager’s years of risk management experience, and the business environment that the project was realized. The experience of the manager was classified into five different classes, namely, 0–5 years, 6–10 years, 11–15 years, 16–25, and more than 25 years of similar work experience. The takes values between the range [0, 0.2] with a step of 0.05.
2.5. Monte Carlo Simulation
Monte Carlo simulation is a popular technique for risk analysis in which every risk factor is modeled by a statistical distribution, and several scenario iterations are realized, each one using different random values that belong to the predefined distributions. A critical part of this process is the selection of the proper distribution to represent the uncertainty of each risk factor, and this can be derived using historical data or the judgments of the risk manager. Usually, given the unique characteristics of the projects as organizations, very often, there are no historical statistical data to extract distributions from, and the subjective choices of the manager, based on prior knowledge and experiences, is the only way to proceed with the analysis.
3. Application in a Construction Project in GREECE
In the present study, we applied the proposed approach to analyze activity delay risks in a 5-star hotel renovation project and specifically, in the construction of a swimming pool complex accompanied by supporting constructions (e.g., engine room, rainwater drainage networks), and a large surrounding plant area. The simulation experiments performed using the programming language Visual Basic for Applications, which is embedded in Microsoft Excel 2016 software package, and the makespan calculations realized with Microsoft Project 2016. The project was about to update the facilities of a currently operating top-rated hotel, so the owner company imposed on the construction company a “hard” constraint of finalizing by the next season’s starting date (1 June 2019), namely terminating by 31 May 2019. The project initialized on 25 October 2018 and the Critical Path Method resulted in a schedule with a duration of 152 days, specifically ending on 24 May 2019. The actual project duration was found to be 159 days. Note that five working dates were considered without any holidays. Considering this project end date, without performing any risk analysis method, the project risk manager would, theoretically, believe that the project will be completed about a calendar week earlier than the deadline. Table 1 includes the key data of the project program.

Table 1.
The data of the case study example.
Following the method illustrated in Figure 1, we categorized the activities according to the nature of the task performed. The five categories were: preparation–earthworks, building works, installation of equipment, electrical and mechanical installations, and completion and testing. Table 2 illustrates the tasks’ IDs organized in the above groups.

Table 2.
Categorization of tasks.
Next, the proposed questionnaire was completed by the project risk manager, who plays the role of the expert-decision maker. It should be noted that the method and the questionnaire can support multiple decision-makers with appropriate modifications to the calculations. Table 3 contains the questionnaire and the answers of the expert to each section and question. Note that, for expressing the meaning of the linguistic variable regarding the probability of occurring a risk and its impact on the schedule, we use the scale proposed in Project Management Body Of Knowledge (PMBOK) [42], illustrated in Table 4.

Table 3.
The questionnaire with the answers of the expert.

Table 4.
The probability and impact scale used in the questionnaire [42].
The columns “Probability (P)” and “Impact (I)” of Table 5 have the information about the numerical value assigned with the linguistic variable of the expert’s answers in the fifteen questions of Section 2. The last column contains the multiplication of probability and impact values, and the last value of this column illustrates the average value for all answers of the decision-maker.

Table 5.
The expert’s answers to questions of Section 2.
The expert’s answers to Section 3, illustrated in Table 6, where the first column describes the names of the tasks’ groups, the next two columns include the optimistic and pessimistic estimation of the decision-maker regarding the duration of the activities of this group. Columns 4 and 5 contain the “Corrected” optimistic and pessimistic values that are the estimated values after integrating the answers of Section 2, derived by applying Equations (1) and (2). This range was used for modifying the duration of each task, with respect to the group to which it belongs. Table 7 includes the activities’ data that served as input to the following Monte Carlo simulation process.

Table 6.
The expert’s answers to questions of Section 3.

Table 7.
The simulation input data for the project’s activities.
The first three columns (and columns 8–10) of the table describe each task’s ID, category, and deterministic duration considered for the CPM calculations. Columns 4 to 7 (and 11–14) contain the integrated value of range (optimistic, pessimistic) over the deterministic value that works as lower and upper bound for the activity duration during the simulation process. For example, the values for the first activity (with ID = 3, and PE group) were calculated as follows: the duration of the activity was multiplied with the corrected optimistic deviation percentage (from Table 6 for each task group), and then the difference was calculated, namely, . In the same way, the . Note that the values of Table 5 were extracted using Equations (1) and (2). In addition, the distribution used for each task group was selected by the decision-maker, as described in Section 3 of this paper.
The results’ summary statistics for 1000 iterations of Monte Carlo simulation runs are illustrated in Table 8. The information contained in this table, along with results illustrated in the following tables and figures, were used for performing the “Derive conclusions from results” step of our approach (Figure 1). These conclusions are necessary for the risk manager to determine whether the total risk is acceptable, and whether to continue project activities as initially programmed, or, in the case that the risk is not considered as tolerable, to have a clear view on which part of the project to perform risk mitigation actions. In Table 8, column 2, the results of the proposed approach are described, namely using a different distribution for each task category and ranges determined by the expert and analytical method using the proposed equation. The following four columns include results for running simulations with the activities using PERT, triangular, and uniform distributions, under the same expert’s estimations derived by the questionnaire. In addition, the mean and standard deviation used in the classic PERT method are shown in the last column. Note that, in the present study, the classic PERT method was used as a benchmark for comparison reasons.

Table 8.
Summary statistics for the results of the analysis.
Regarding mean durations and deviations, using PERT distribution (which is a generalization of beta distribution used in PERT method) resulted in a very similar duration to the PERT method and a similar standard deviation, as well, that was 155.89 and 155.98 days, respectively, meaning that the project ended on 30 May 2019, only one working day (and two calendar days) before the deadline. Using triangular distribution to all the activities led to a clearly larger mean duration with the finish date 5 June 2019. Additionally, considering uniform distribution to all activities’ duration results in a mean of nearly 164 days, namely project termination on 11 June 2019. The proposed approach led to a mean duration of almost 158 working days and finishing on 3 June 2019.
In any case, performing risk analysis clearly illustrates that the project would not end at the deterministic duration. Moreover, applying only the classic PERT method, the project manager concluded that, marginally, the project would finish before the deadline. Simulation processes under any other of the distributions of this analysis, integrated with the expert’s estimations, showed that the project was at high risk of not completing on time. This could have vital consequences to the construction company since 31 May 2019 was a “hard” constraint and could not be violated in any sense.
Table 9 illustrates percentiles for project duration during each method used. This table, in cooperation with the findings of the previous one, could provide very interesting insights into the risk manager. Generally, the deterministic duration of 152 days had less than 5% confirmation probability, which was independent of the method. The scarcity of this duration confirmation was also substantiated by the fact that only in our approach and in PERT distribution, the minimum found duration was below the deterministic 152 days, namely 151 and 151.71 days.

Table 9.
Results’ percentiles for each method of the present analysis.
Furthermore, it is observed that the duration of 155.98 days, which was the mean duration of the benchmark PERT method with a 50% possibility of appearance, gathered possibilities less than 5% in triangular and uniform distribution usage scenarios, and less than 25% in our approach. In the PERT distribution usage scenario, it was a less than 55% possibility to appear.
In addition, the real deadline of the project on 31 May 2019 (157 workdays) was possible by less than 40% in our approach and less than 75% in the PERT distribution, less than 10% in triangular, less than 5% in uniform, and less than 75% in the PERT method. The present finding illustrates that the manager had a wide range of different tools to correctly describe the uncertainty. Triangular and uniform distribution provided much more pessimistic results than the PERT distribution and classic method. It worth mentioning that our approach works as an intermediate option that collaborates with characteristics from each distribution used, according to the nature of the activities realized, since we try to balance the “optimism” of PERT distribution with the “Pessimism” of the triangular and uniform distributions. Moreover, the different strategies provided to the risk manager are shown in Figure 2, which describes the duration curves of each distribution for the different percentiles of this analysis, proving that triangular and uniform distributions provided, by far, a much more pessimistic output than the PERT method and distribution. Our approach works as an intermediate strategy that alerts the manager to rising delay risks but not leading to overly pessimistic estimations that may lead to implementing ineffective mitigation measures with implications for the budget.
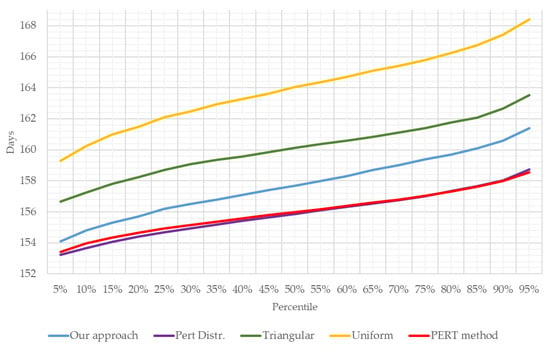
Figure 2.
Resulting curves for our approach and the compared methods.
After determining the possibilities of completing the project 0n time, we performed an extended analysis of how the specific activities affect the total project duration. Figure 3 illustrates a tornado graph in which the activities are ranked according to the range of minimum-maximum project duration caused by the specific activity’s duration range. This information can support the risk manager in making decisions about which task or group of tasks to target during the implementation of mitigation measures. Note that the baseline duration was 157.72 days. An interesting conclusion derived from this figure is that the duration of the first six more important tasks was expressed by uniform distribution, while the other three belong to the “building works” category, and their duration was expressed by PERT distribution. The last activity on this list was an “electrical and mechanical installations” task, expressed by uniform distribution.
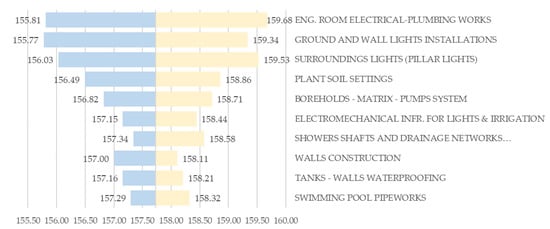
Figure 3.
Tornado graph for the ten most important activities for the total project duration.
4. Conclusions
In this article, we presented a simulation-based strategy for efficiently estimating delay risks in project schedules. Initially, we conducted tests to explore the effect of using various statistical distributions to express uncertain durations of particular tasks. We also suggest a questionnaire-based strategy to assign proper distributions to project activities’ durations according to their nature and the expert’s preferences, to manage the lack of knowledge and/or historical data. The proposed strategy was applied to estimate the total completion time of a complex project with very rigorous deadlines and financial penalties for delay. The effectivity of the suggested technique was screened against the classic PERT technique, with the findings being very promising since the present process can better predict the duration uncertainty and provide a helpful tool for planning budget and time overruns treatment measures to project risk managers. The main contribution of this paper is that it introduces an approach for estimating project duration risks, which incorporates the project risk manager’s experience with statistical distributions and its ranges, via a simple equation. The proposed approach works within a simulation-based framework and enables making more accurate predictions about the actual project duration.
This approach can ultimately provide the project risk manager with a powerful tool for considering the possibilities of timely project completion. Furthermore, applying very popular and widely used distributions for expressing durations give the manager the opportunity to select a strategy in scheduling according to his risk acceptance profile. In other words, a risk seeker manager could select the PERT distribution or even the PERT method since they result in smaller schedule extensions in contrast to triangular and uniform distributions, which result in larger project delays and could be selected by more risk-averse managers. Given the fact that considering too much uncertainty in durations can increase the costs of risk mitigation actions, without any real benefit in practice, we adopted an approach that gives the option to the project manager to select different distributions for each activity category and integrate the random values with the experience and preferences via a questionnaire and a simple equation for merging estimations.
Although the results of the proposed approach are promising, this study could be extended and improved by applying further research on the risk factors included in the questionnaire, with a higher level of customization to the specific project under study, and by investigating the usage of other statistical distributions for expressing the duration of activities. In addition, monitoring and analysis of risk factors that could have an impact on costs, resources used for executing the project and time arrivals of material resources, could be the main topic of a future study that will extend the present model. Finally, an extension to group decision making and validating the results through testing on a larger number of real project cases are among the future research plans of the authors.
Author Contributions
Conceptualization, G.K.K., D.E.K.; data curation, G.K.K., A.S.X., T.T.T.; formal analysis, G.K.K., T.T.T., D.E.K.; investigation, G.K.K., T.T.T.; methodology, G.K.K., A.S.X., D.E.K.; writing—original draft, G.K.K.; writing—review and editing, G.K.K., A.S.X., D.E.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
We declare no conflict of interest.
References
- Malcolm, D.G.; Roseboom, J.H.; Clark, C.E.; Fazar, W. Application of a Technique for Research and Development Program Evaluation. Oper. Res. 1959, 7, 646–669. [Google Scholar] [CrossRef]
- Taylor, B.W. Project management using GERT analysis. Proj. Manag. Q. 1978, 9, 15–20. [Google Scholar]
- Kelley, J.E. Critical-Path Planning and Scheduling: Mathematical Basis. Oper. Res. 1961, 9, 296–320. [Google Scholar] [CrossRef]
- Barraza, G.A.; Bueno, R.A. Probabilistic Control of Project Performance Using Control Limit Curves. J. Constr. Eng. Manag. 2007, 133, 957–965. [Google Scholar] [CrossRef]
- Barraza, G.A. Probabilistic estimation and allocation of project time contingency. J. Constr. Eng. Manag. 2011, 137, 259–265. [Google Scholar] [CrossRef]
- Alarcón, L.F.; Ashley, D.B.; de Hanily, A.S.; Molenaar, K.R.; Ungo, R. Risk Planning and Management for the Panama Canal Expansion Program. J. Constr. Eng. Manag. 2011, 137, 762–771. [Google Scholar] [CrossRef]
- Nguyen, L.D.; Phan, D.H.; Tang, L.C.M. Simulating construction duration for multistory buildings with controlling activities. J. Constr. Eng. Manag. 2013, 139, 951–959. [Google Scholar] [CrossRef]
- Elshaer, R. Impact of sensitivity information on the prediction of project’s duration using earned schedule method. Int. J. Proj. Manag. 2013, 31, 579–588. [Google Scholar] [CrossRef]
- Moret, Y.; Einstein, H.H. Construction Cost and Duration Uncertainty Model: Application to High-Speed Rail Line Project. J. Constr. Eng. Manag. 2016, 142. [Google Scholar] [CrossRef]
- Farshchian, M.M.; Heravi, G. Probabilistic Assessment of Cost, Time, and Revenue in a Portfolio of Projects Using Stochastic Agent-Based Simulation. J. Constr. Eng. Manag. 2018, 144. [Google Scholar] [CrossRef]
- Bianco, L.; Caramia, M.; Giordani, S. A chance constrained optimization approach for resource unconstrained project scheduling with uncertainty in activity execution intensity. Comput. Ind. Eng. 2019, 128, 831–836. [Google Scholar] [CrossRef]
- Sarigiannidis, L.; Chatzoglou, P.D. Quality vs risk: An investigation of their relationship in software development projects. Int. J. Proj. Manag. 2014, 32, 1073–1082. [Google Scholar] [CrossRef]
- Thompson, R.; Lucko, G.; Su, Y. Reconsidering an Appropriate Probability Distribution Function for Construction Simulations. Constr. Res. Congr. 2016, 2522–2531. [Google Scholar] [CrossRef]
- Elbarkouky, M.M.G.; Fayek, A.R.; Siraj, N.B.; Sadeghi, N. Fuzzy arithmetic risk analysis approach to determine construction project contingency. J. Constr. Eng. Manag. 2016, 142. [Google Scholar] [CrossRef]
- Hajifathalian, K.; Howell, G.; Wambeke, B.W.; Hsiang, S.M.; Liu, M. Oops Simulation: Cost-Benefits Trade-Off Analysis of Reliable Planning for Construction Activities. J. Constr. Eng. Manag. 2016, 142. [Google Scholar] [CrossRef]
- Qazi, A.; Quigley, J.; Dickson, A.; Kirytopoulos, K. Project Complexity and Risk Management (ProCRiM): Towards modelling project complexity driven risk paths in construction projects. Int. J. Proj. Manag. 2016, 34, 1183–1198. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.; Skibniewski, M.J. Simulation-based analysis of tunnel boring machine performance in tunneling excavation. J. Comput. Civ. Eng. 2016, 30. [Google Scholar] [CrossRef]
- Tao, L.; Wu, D.; Liu, S.; Lambert, J.H. Schedule risk analysis for new-product development: The GERT method extended by a characteristic function. Reliab. Eng. Syst. Saf. 2017, 167, 464–473. [Google Scholar] [CrossRef]
- Paz, J.C.; Rozenboim, D.; Cuadros, Á.; Cano, S.; Escobar, J.W. A simulation-based scheduling methodology for construction projects considering the potential impacts of delay risks. Constr. Econ. Build. 2018, 18, 41–69. [Google Scholar] [CrossRef]
- Kirytopoulos, K.A.; Leopoulos, V.N.; Diamantas, V.K. PERT vs. Monte Carlo Simulation along with the suitable distribution effect. Int. J. Proj. Organ. Manag. 2008, 1, 24–46. [Google Scholar] [CrossRef]
- Vanhoucke, M. On the dynamic use of project performance and schedule risk information during project tracking. Omega 2011, 39, 416–426. [Google Scholar] [CrossRef]
- Jun, D.H.; El-Rayes, K. Fast and accurate risk evaluation for scheduling large-scale construction projects. J. Comput. Civ. Eng. 2011, 25, 407–417. [Google Scholar] [CrossRef]
- Vanhoucke, M. Measuring the efficiency of project control using fictitious and empirical project data. Int. J. Proj. Manag. 2012, 30, 252–263. [Google Scholar] [CrossRef]
- Choudhry, R.M.; Aslam, M.A.; Arain, F.M. Cost and schedule risk analysis of bridge construction in Pakistan: Establishing risk guidelines. J. Constr. Eng. Manag. 2014, 140. [Google Scholar] [CrossRef]
- Tran, D.Q.; Molenaar, K.R. Risk-Based Project Delivery Selection Model for Highway Design and Construction. J. Constr. Eng. Manag. 2015, 141. [Google Scholar] [CrossRef]
- Wang, C.; Jiao, B.; Guo, L.; Tian, Z.; Niu, J.; Li, S. Robust scheduling of building energy system under uncertainty. Appl. Energy 2016, 167, 366–376. [Google Scholar] [CrossRef]
- Firouzi, A.; Yang, W.; Li, C.-Q. Prediction of total cost of construction project with dependent cost items. J. Constr. Eng. Manag. 2016, 142. [Google Scholar] [CrossRef]
- Kerkhove, L.-P.; Vanhoucke, M. Optimised scheduling for weather sensitive offshore construction projects. Omega (United Kingdom) 2017, 66, 58–78. [Google Scholar] [CrossRef]
- Chang, C.-Y.; Ko, J.-W. New Approach to Estimating the Standard Deviations of Lognormal Cost Variables in the Monte Carlo Analysis of Construction Risks. J. Constr. Eng. Manag. 2017, 143. [Google Scholar] [CrossRef]
- Erol, H.; Dikmen, I.; Birgonul, M.T. Measuring the impact of lean construction practices on project duration and variability: A simulation-based study on residential buildings. J. Civ. Eng. Manag. 2017, 23, 241–251. [Google Scholar] [CrossRef]
- Francis, A. Simulating Uncertainties in Construction Projects with Chronographical Scheduling Logic. J. Constr. Eng. Manag. 2017, 143. [Google Scholar] [CrossRef]
- Chang, H.-K.; Yu, W.-D.; Cheng, S.-T. A new project scheduling method based on activity risk duration and systems simulation. J. Technol. 2018, 33, 1–16. [Google Scholar]
- Lorenzo, S.-M.; Antonio, A.-A.; Laura, G.-H.; Palomo-Romero, J.M.; Ayuso-Muñoz, J.L. New Approach to the Distribution of Project Completion Time in PERT Networks. J. Constr. Eng. Manag. 2018, 144, 4018094. [Google Scholar]
- Aderbag, M.A.; Elmabrouk, S.K.; Sherif, M.A. Risk analysis related to costing and scheduling of construction projects. In Proceedings of the International Conference on Industrial Engineering and Operations Management, IEOM Society International, Bandung, Indonesia, 6–8 March 2018. [Google Scholar]
- Walȩdzik, K.; Mańdziuk, J. Applying hybrid Monte Carlo Tree Search methods to Risk-Aware Project Scheduling Problem. Inf. Sci. 2018, 460, 450–468. [Google Scholar] [CrossRef]
- Ntzeremes, P.; Kirytopoulos, K. Applying a stochastic-based approach for developing a quantitative risk assessment method on the fire safety of underground road tunnels. Tunn. Undergr. Space Technol. 2018, 81, 619–631. [Google Scholar] [CrossRef]
- Rausch, C.; Nahangi, M.; Haas, C.; Liang, W. Monte Carlo simulation for tolerance analysis in prefabrication and offsite construction. Autom. Constr. 2019, 103, 300–314. [Google Scholar] [CrossRef]
- Tokdemir, O.B.; Erol, H.; Dikmen, I. Delay Risk Assessment of Repetitive Construction Projects Using Line-of-Balance Scheduling and Monte Carlo Simulation. J. Constr. Eng. Manag. 2019, 145. [Google Scholar] [CrossRef]
- Aven, T. Risk assessment and risk management: Review of recent advances on their foundation. Eur. J. Oper. Res. 2016, 253, 1–13. [Google Scholar] [CrossRef]
- El-Sayegh Sameh, M.; Mansour Mahmoud, H. Risk Assessment and Allocation in Highway Construction Projects in the UAE. J. Manag. Eng. 2015, 31, 4015004. [Google Scholar] [CrossRef]
- Rees, M. Business Risk ans Simulation Modelling in Practice Using Excel, VBA and @RISK; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2015. [Google Scholar]
- PMI. PMBOK Guide, 6th ed.; Project Management Institute: Newtown Square, PA, USA, 2017. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).