Improving the Accuracy of a Hygrothermal Model for Wood-Frame Walls: A Cold-Climate Study
Abstract
1. Introduction
2. Measurements
2.1. Overview of Field Measurements
2.2. Material Property Measurements
3. Hygrothermal Model: Initial Design Values
3.1. Database Material Properties
3.2. Boundary Conditions
3.3. Numerical Parameters
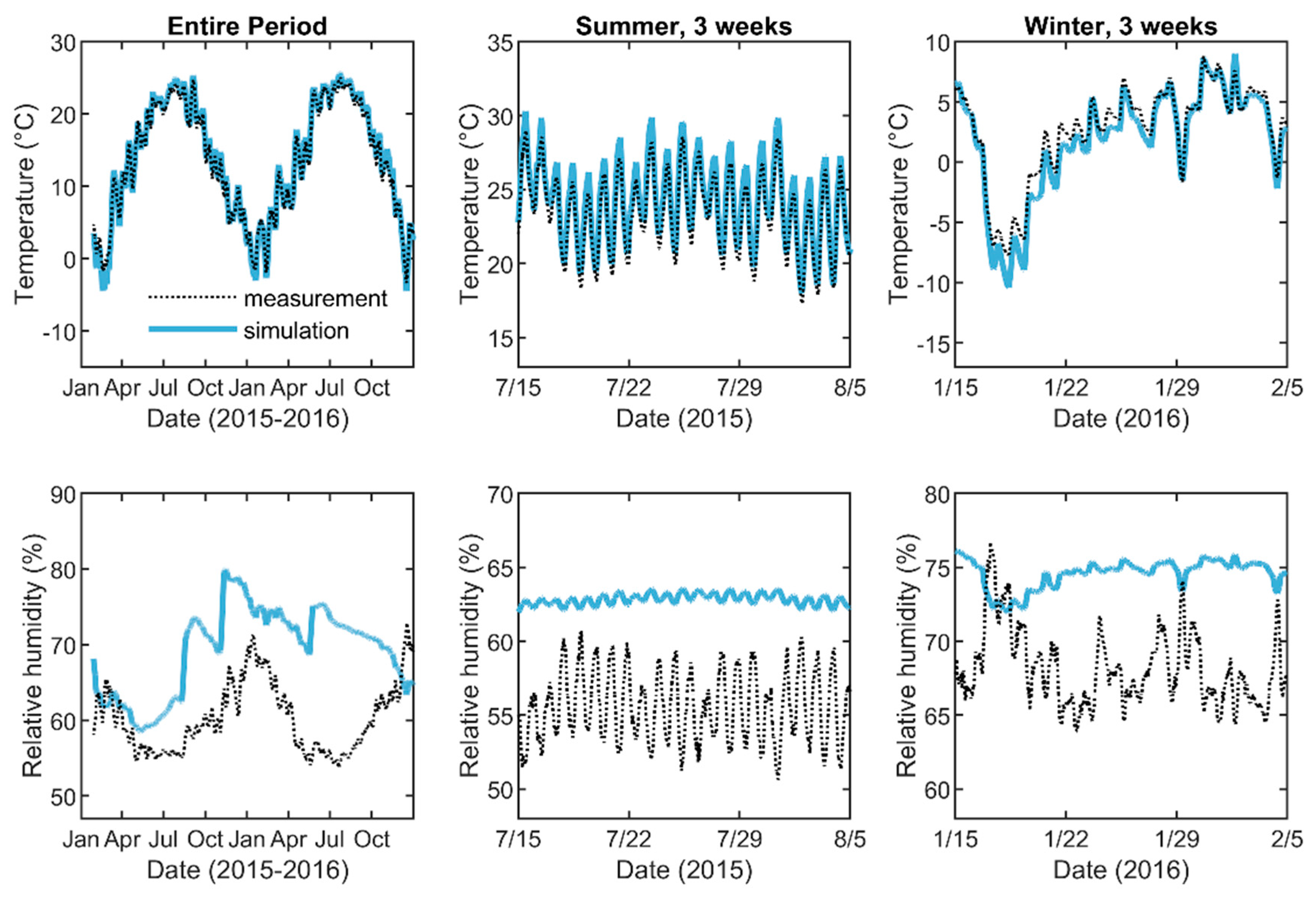
3.4. Results
4. Overview of Improvements to the Model
4.1. Customized Material Properties
4.1.1. Vinyl Siding
4.1.2. Extruded Polystyrene
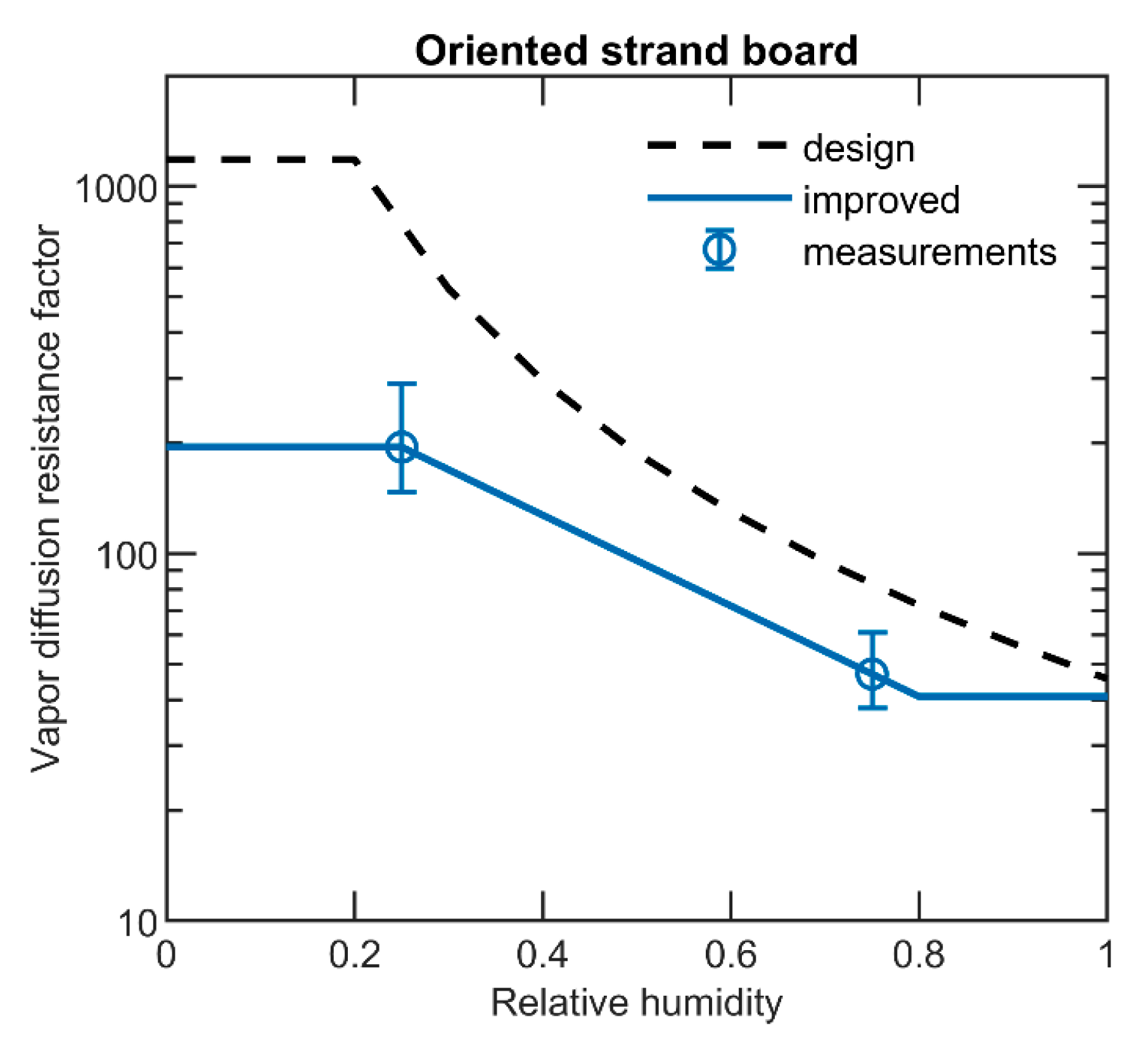
4.1.3. Oriented Strand Board
4.1.4. Fiberglass
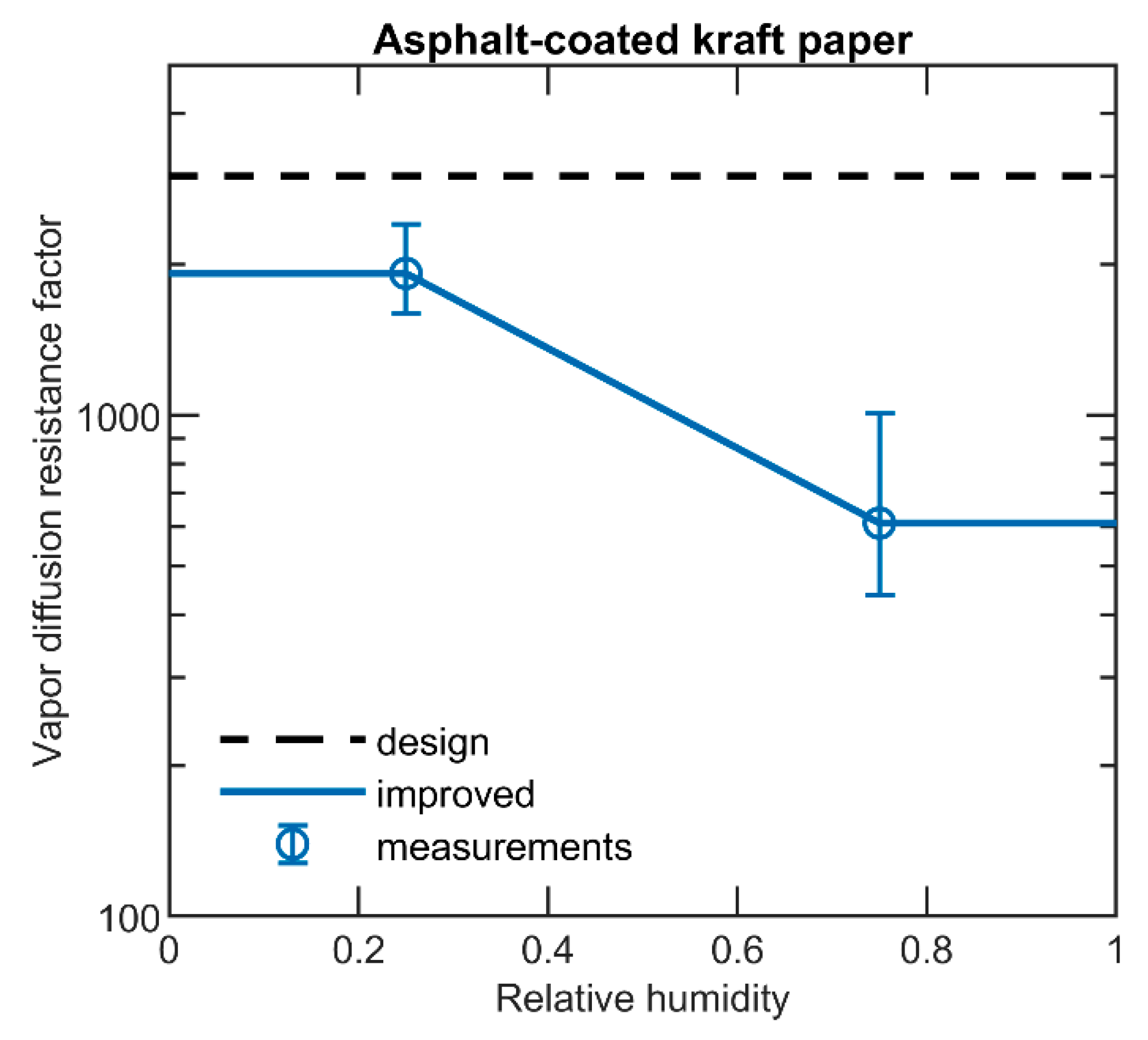
4.1.5. Asphalt-Coated Kraft Paper
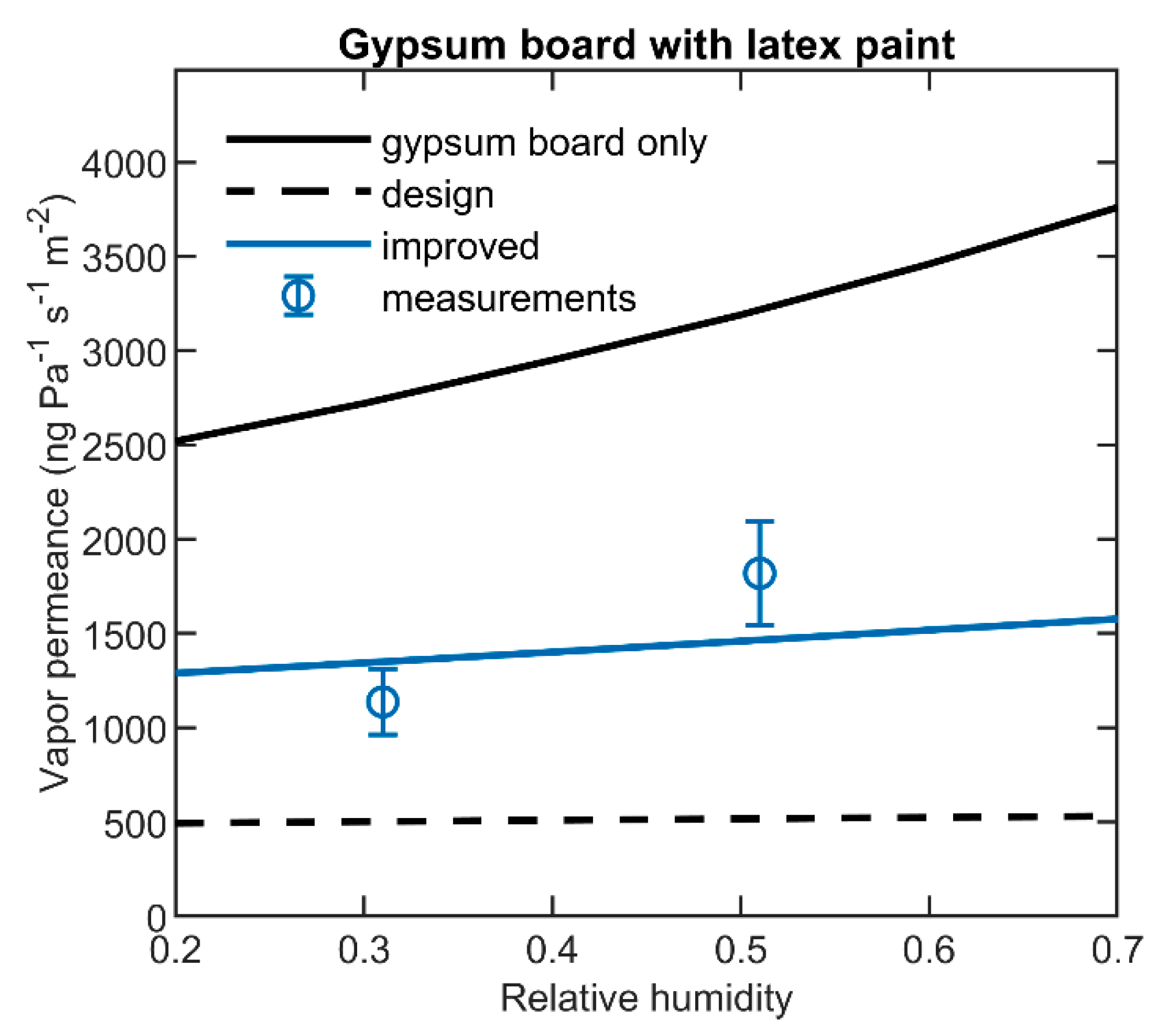
4.1.6. Latex Paint on Gypsum Board
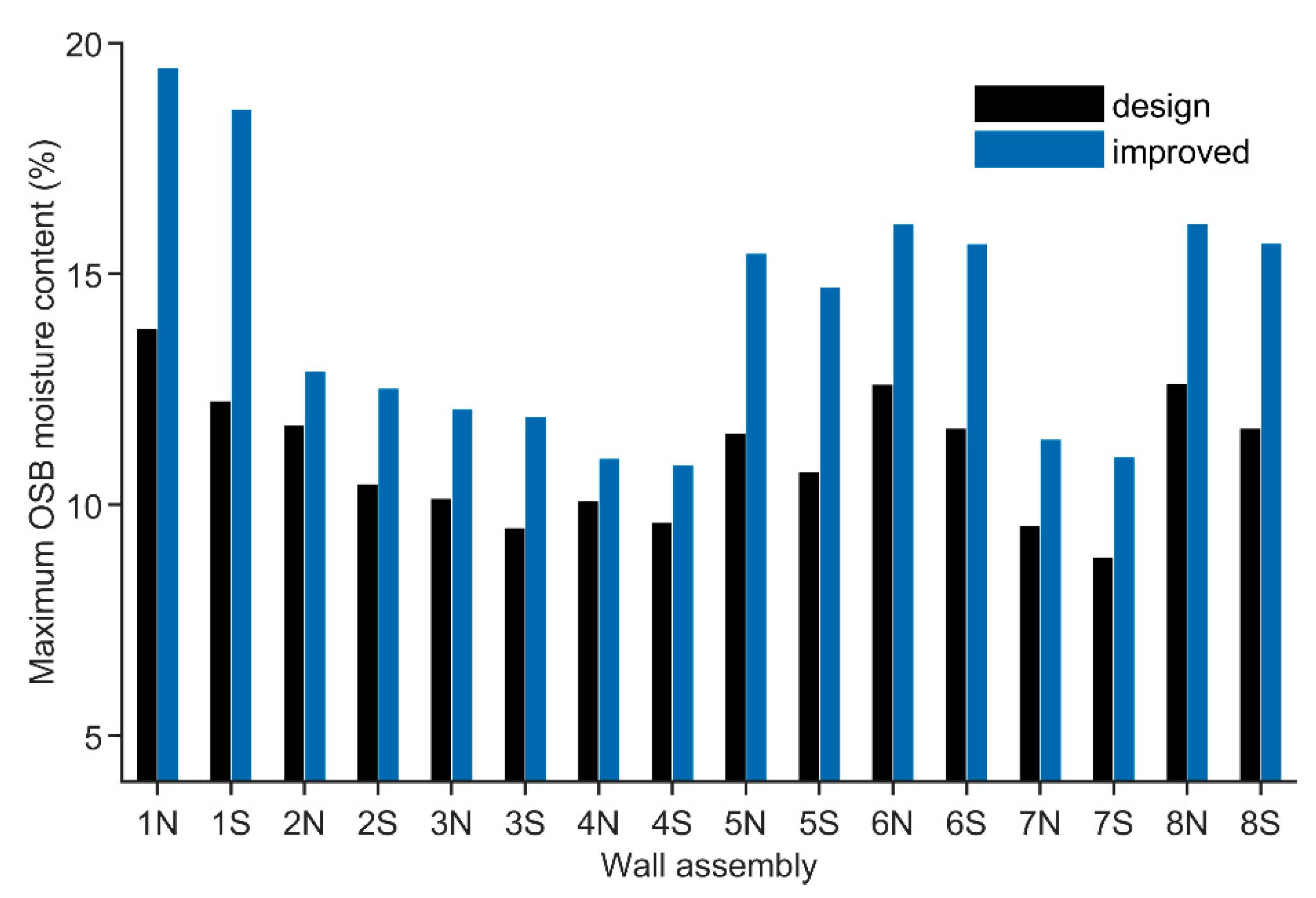
4.2. Changes in Simulation Results from Improvements
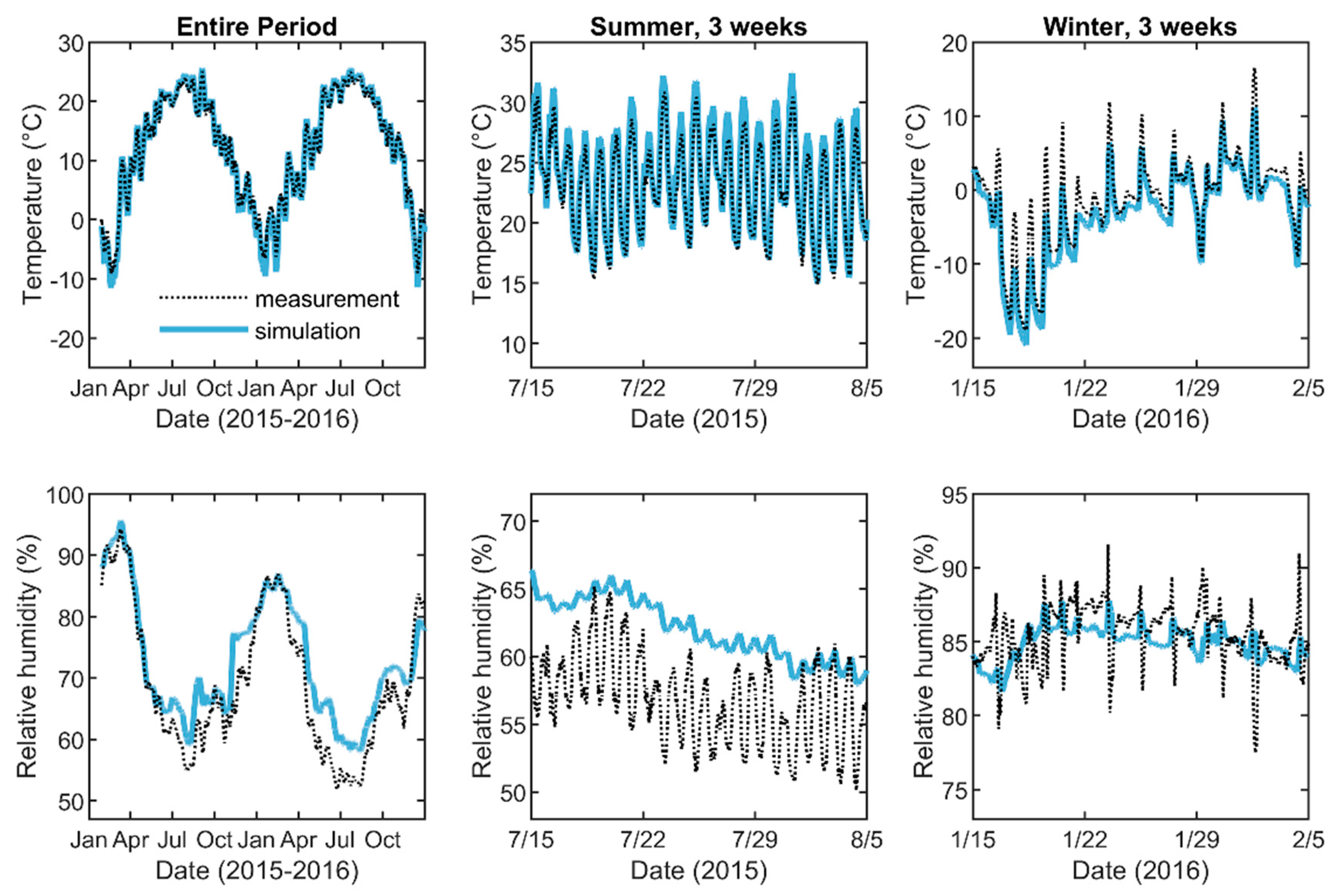
5. Comparison of Improved Simulations with Measurements
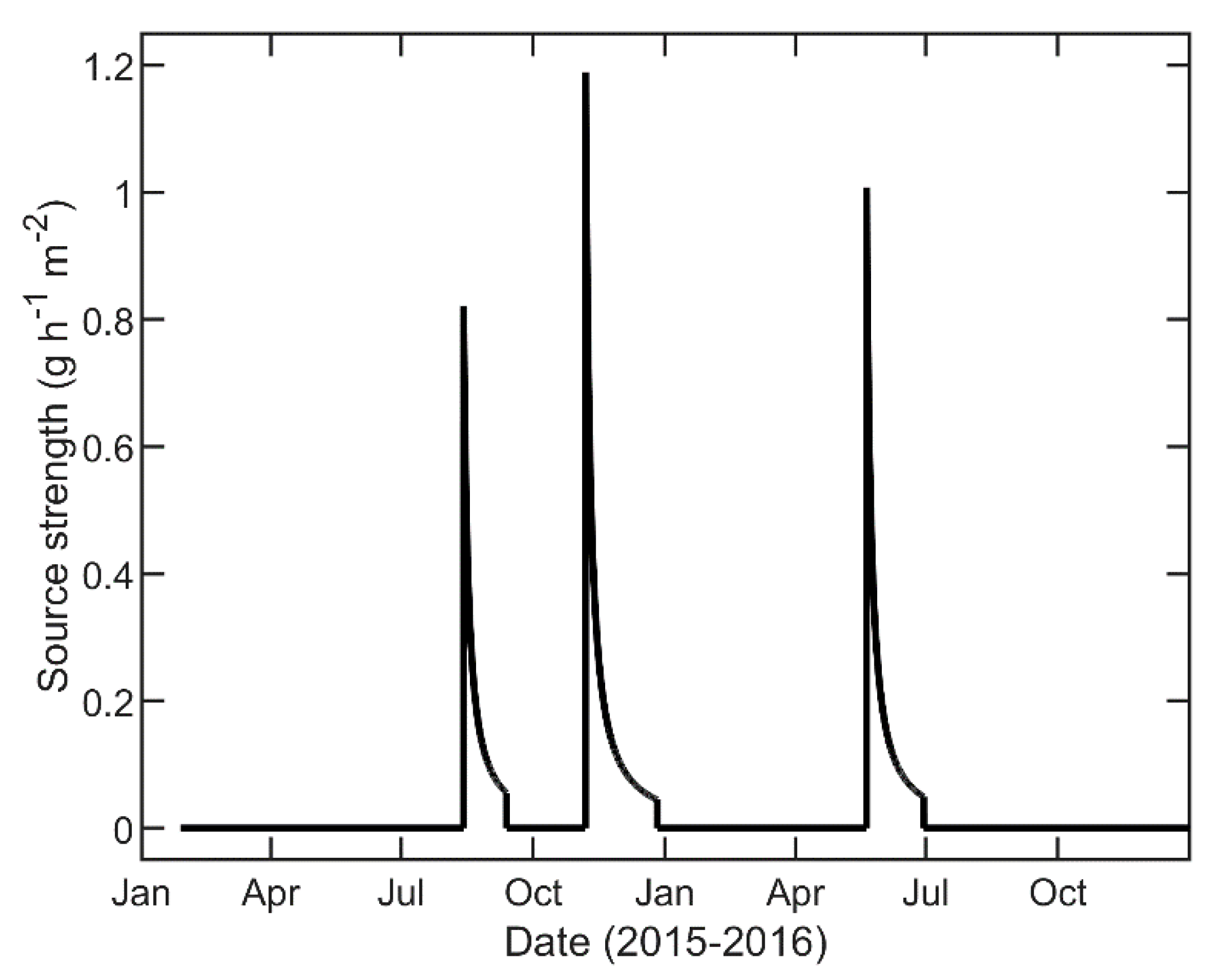
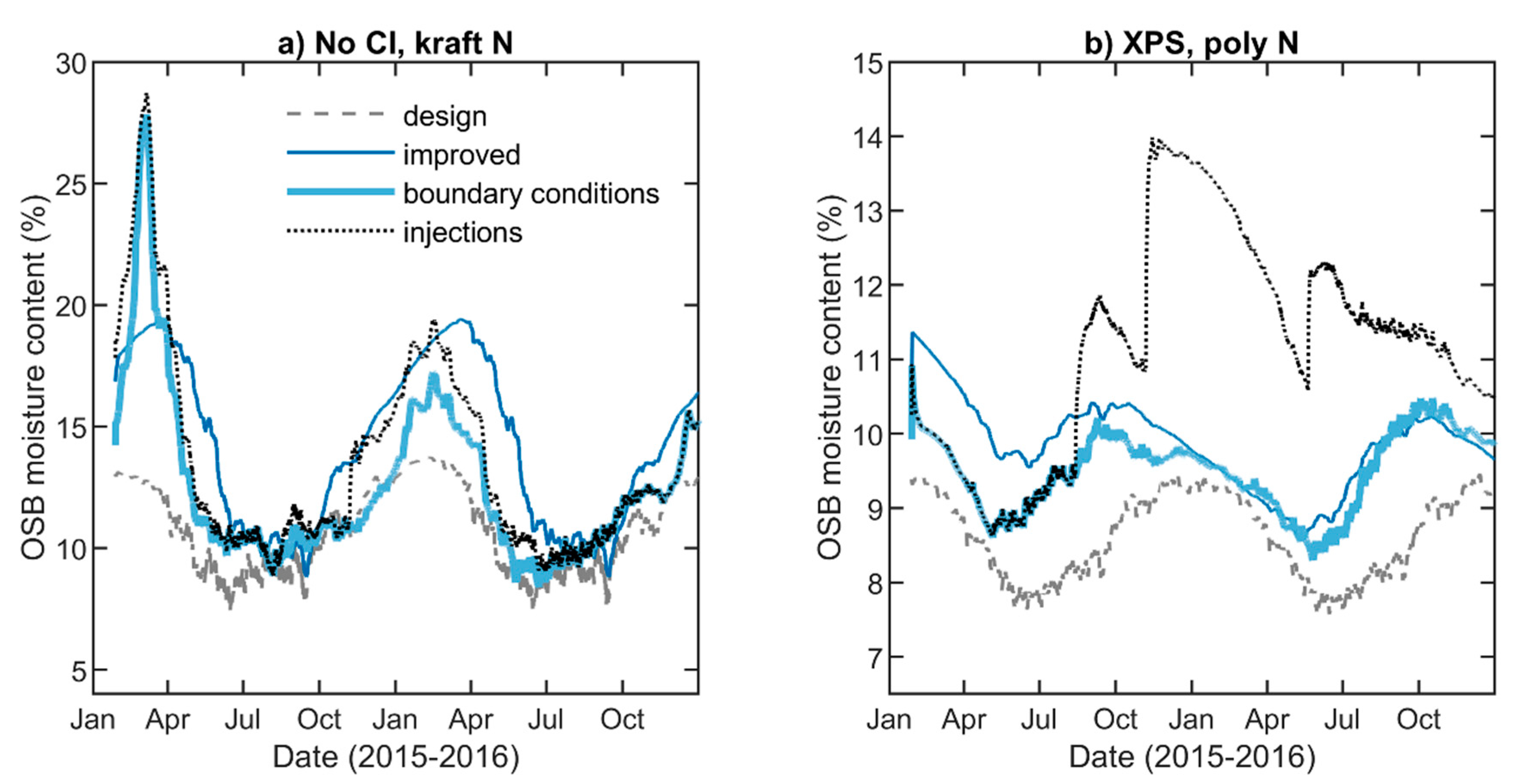
5.1. Model Adjustments to Facilitate Comparison
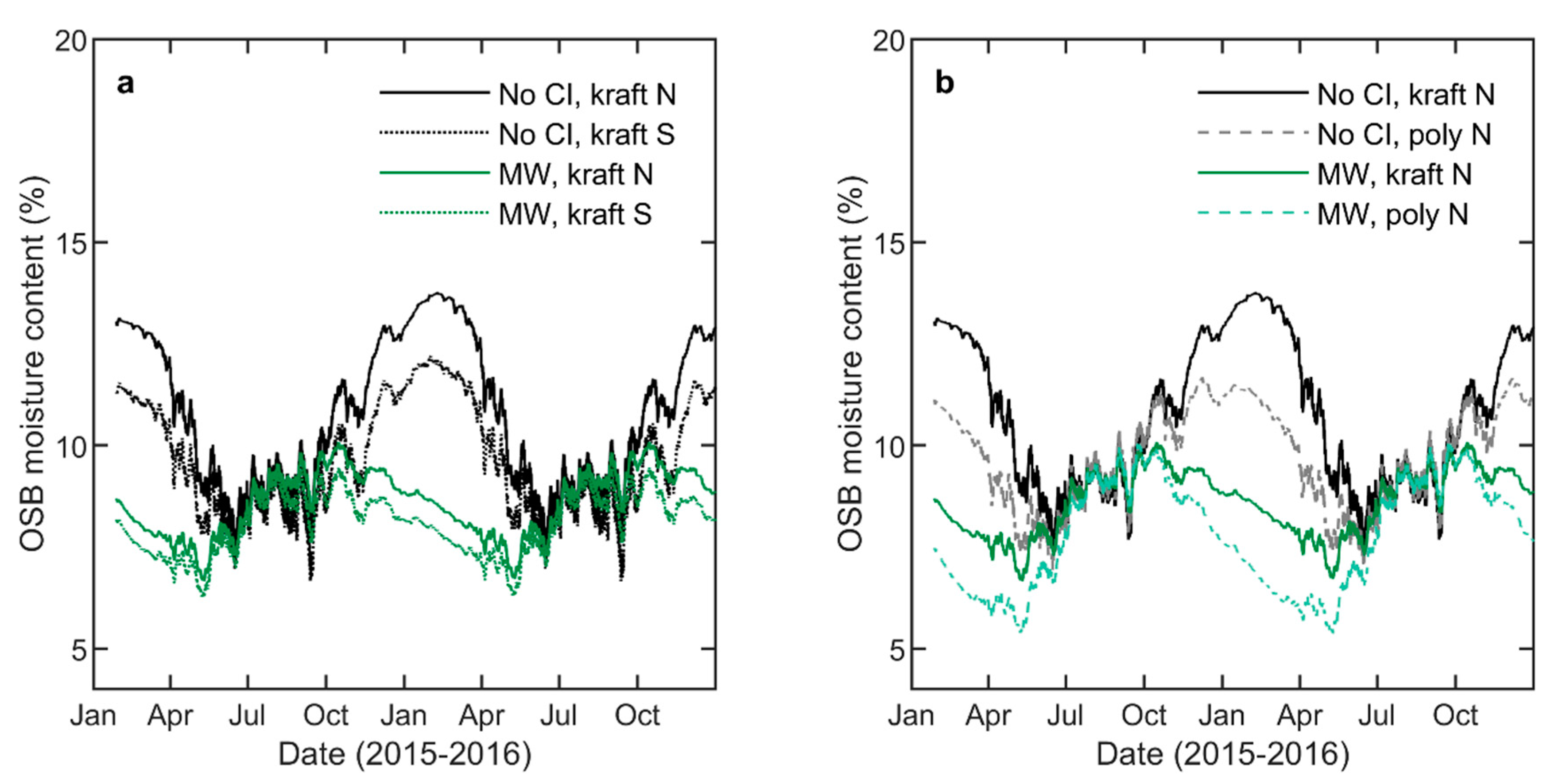
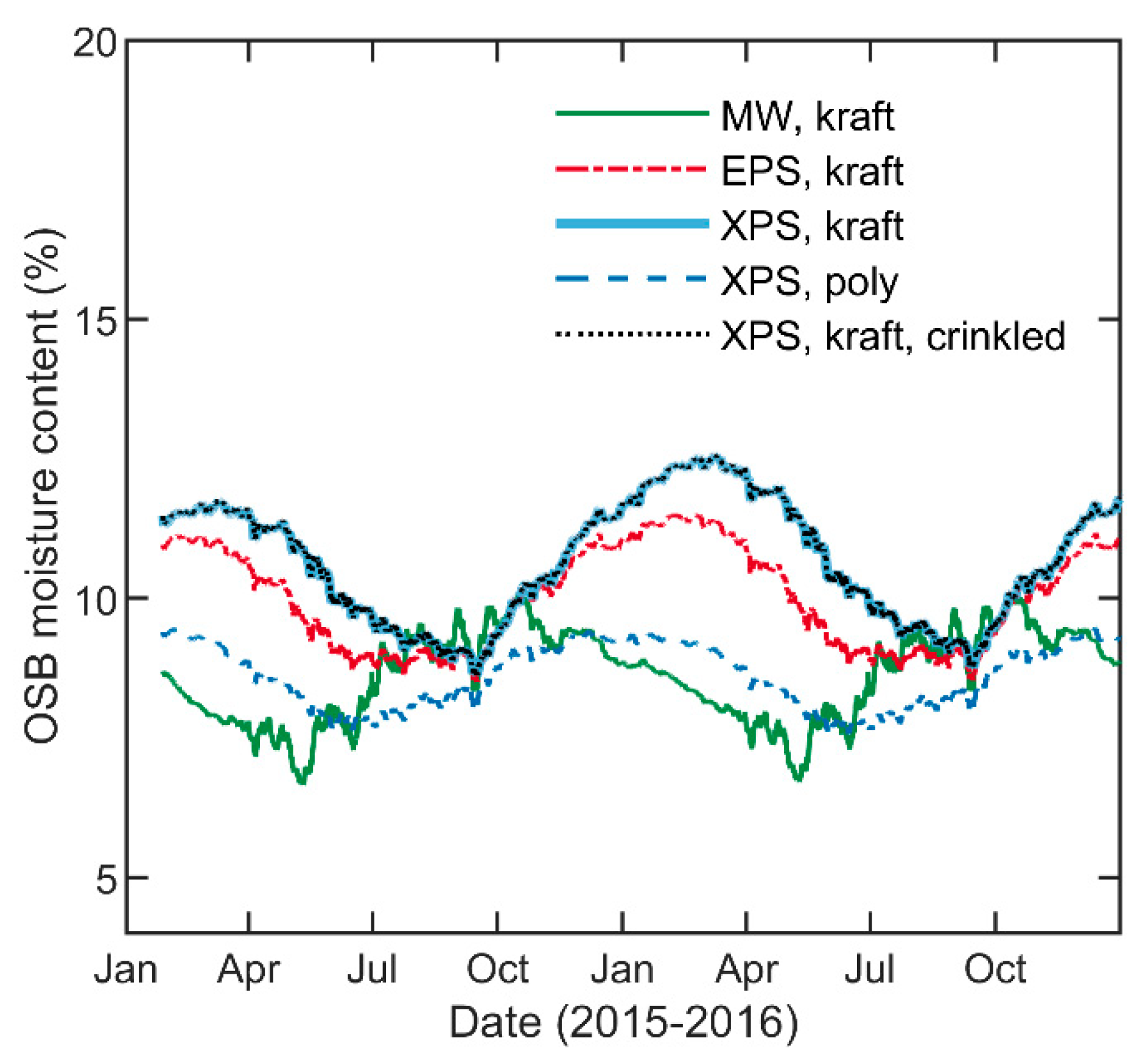
5.2. OSB Moisture Content
5.3. Temperature and Relative Humidity
5.4. Quantitative Comparison of Simulations with Measurements
6. Sensitivity Analysis
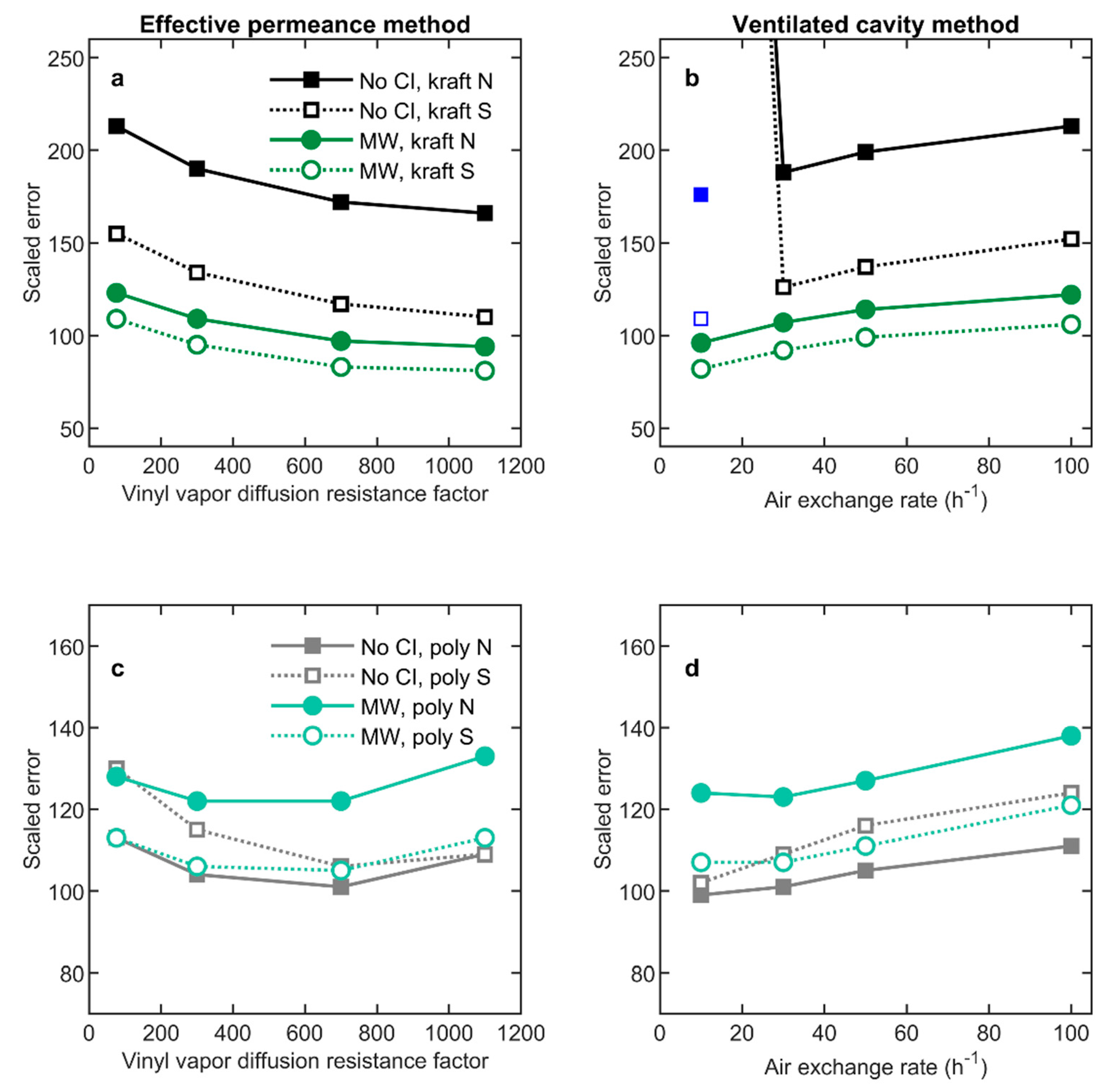
6.1. Vinyl Siding
6.1.1. Effective Vapor Permeance
6.1.2. Ventilated Air Cavity
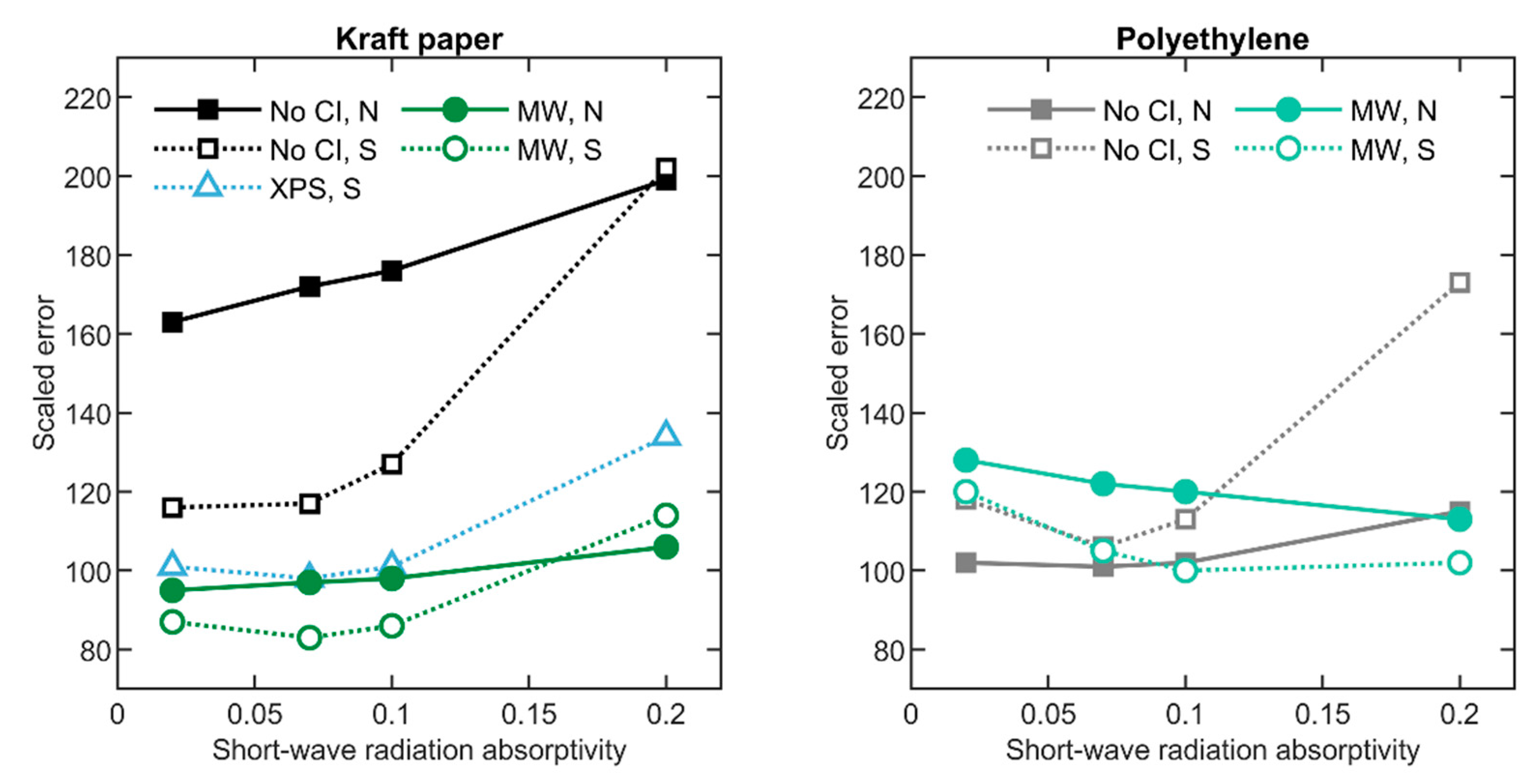
6.2. Short-Wave Radiation Absorptivity
6.3. Exterior Surface Heat Transfer Coefficient
6.4. Fiberglass
6.5. Asphalt-Coated Kraft Paper
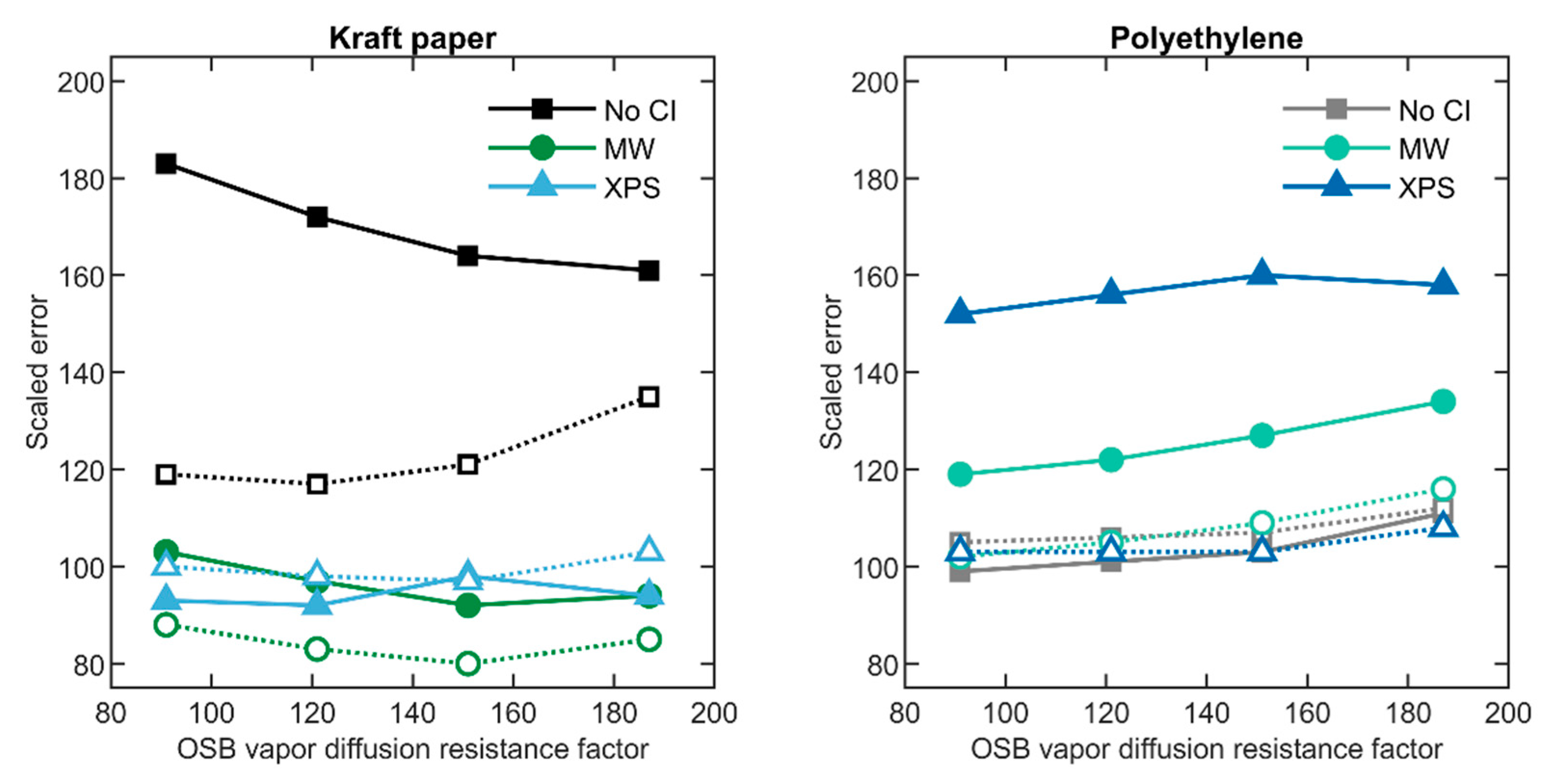
6.6. Oriented Strand Board
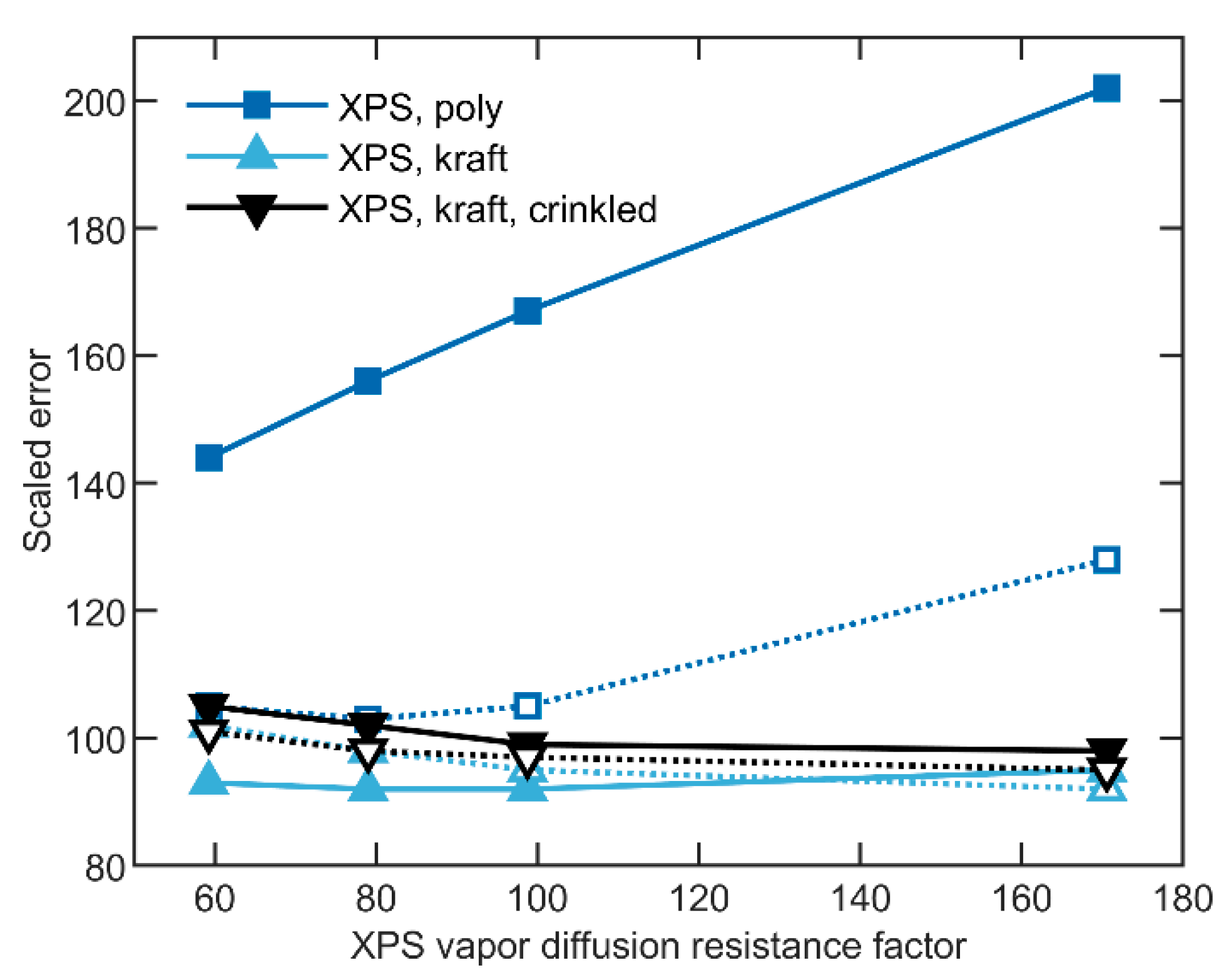
6.7. Extruded Polystyrene
6.8. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Property Data Used in Hygrothermal Simulations
Appendix A.1. Vinyl Siding—Installed Directly on Sheathing or Insulation—Effective Permeance
| Property | Value | Design |
|---|---|---|
| Thickness, mm | 1.11 | |
| Bulk density, kg/m3 | 829 | |
| Porosity, m3/m3 | 1 | 0.001 |
| Specific heat capacity (dry), J/(kg·K) | 2299 | |
| Thermal conductivity, W/(m·K) | 0.17 | |
| Thermal conductivity temperature coefficient, W/(m·K2) | 0.0002 | |
| Water vapor diffusion resistance factor | 700 | 76 |
| RH | Water Content, kg/m3 | RH | Water Content, kg/m3 |
|---|---|---|---|
| 0 | 0 | 0.93 | 5.72 |
| 0.5 | 0.485 | 0.94 | 6.6 |
| 0.6 | 0.724 | 0.95 | 7.77 |
| 0.7 | 1.12 | 0.96 | 9.41 |
| 0.8 | 1.88 | 0.97 | 11.9 |
| 0.85 | 2.62 | 0.98 | 15.9 |
| 0.9 | 4.03 | 0.99 | 23.9 |
| 0.91 | 4.48 | 0.995 | 31.8 |
| 0.92 | 5.03 | 1 | 47.1 |
Appendix A.2. Extruded Polystyrene (XPS) Insulation
| Property | Value | Design |
|---|---|---|
| Thickness, mm | 25.4 | |
| Bulk density, kg/m3 | 28.6 | |
| Porosity, m3/m3 | 0.99 | |
| Specific heat capacity (dry), J/(kg·K) | 1470 | |
| Thermal conductivity, W/(m·K) | 0.025 | |
| Thermal conductivity temperature coefficient, W/(m·K2) | 0.0002 | |
| Water vapor diffusion resistance factor | 79 | 170.56 |
| RH | Water Content, kg/m3 |
|---|---|
| 0 | 0 |
| 0.1 | 0.009 |
| 0.5 | 0.08 |
| 0.8 | 0.31 |
| 0.9 | 0.66 |
| 0.97 | 1.95 |
| 0.99 | 3.94 |
| 0.999 | 7.09 |
| 1 | 7.77 |
Appendix A.3. Expanded Polystyrene (EPS) Insulation
| Property | Value |
|---|---|
| Thickness, mm | 38.1 |
| Bulk density, kg/m3 | 14.8 |
| Porosity, m3/m3 | 0.99 |
| Specific heat capacity (dry), J/(kg·K) | 1470 |
| Thermal conductivity, W/(m·K) | 0.036 |
| Thermal conductivity temperature coefficient, W/(m·K2) | 0.0002 |
| Water vapor diffusion resistance factor | 73.01 |
| RH | Water Content, kg/m3 |
|---|---|
| 0 | 0 |
| 0.1 | 0.004 |
| 0.5 | 0.031 |
| 0.8 | 0.12 |
| 0.9 | 0.26 |
| 0.97 | 0.77 |
| 0.99 | 1.55 |
| 0.999 | 2.78 |
| 1 | 3.05 |
| RH | µ-Value |
|---|---|
| 0 | 73.01 |
| 0.1 | 73 |
| 0.2 | 67.34 |
| 0.3 | 61.93 |
| 0.4 | 57.17 |
| 0.5 | 52.55 |
| 0.6 | 48.39 |
| 0.7 | 44.65 |
| 0.8 | 41.04 |
| 0.9 | 37.83 |
| 1 | 34.8 |
Appendix A.4. Mineral Wool (MW) Insulation
| Property | Value |
|---|---|
| Thickness, mm | 38.1 |
| Bulk density, kg/m3 | 128 |
| Porosity, m3/m3 | 0.954 |
| Specific heat capacity (dry), J/(kg·K) | 850 |
| Thermal conductivity, W/(m·K) | 0.0322 |
| Thermal conductivity temperature coefficient, W/(m·K2) | 0.0002 |
| Water vapor diffusion resistance factor | 1.3 |
| RH | Water Content, kg/m3 | RH | Water Content, kg/m3 |
|---|---|---|---|
| 0 | 0 | 0.99 | 33.43 |
| 0.65 | 0.4 | 0.995 | 87.9 |
| 0.8 | 0.7 | 0.999 | 269.26 |
| 0.93 | 2.2 | 0.9995 | 298.73 |
| 0.97 | 5.9 | 0.9999 | 312.96 |
| 0.98 | 12 | 1 | 314 |
| Water Content, kg/m3 | Thermal Conductivity, W/(m·K) |
|---|---|
| 0 | 0.0322 |
| 10 | 0.033 |
| 20 | 0.034 |
| 50 | 0.038 |
| 100 | 0.043 |
| 200 | 0.062 |
| 300 | 0.09 |
| 400 | 0.13 |
| 500 | 0.18 |
| 600 | 0.24 |
| 700 | 0.32 |
| 800 | 0.42 |
| 900 | 0.54 |
| 954 | 0.6 |
Appendix A.5. Spun Bonded Polyolefin Membrane (SBP)
| Property | Value |
|---|---|
| Thickness, mm | 1 |
| Bulk density, kg/m3 | 65 |
| Porosity, m3/m3 | 0.001 |
| Specific heat capacity (dry), J/(kg·K) | 1500 |
| Thermal conductivity, W/(m·K) | 2.3 |
| Thermal conductivity temperature coefficient, W/(m·K2) | 0.0002 |
| Water vapor diffusion resistance factor | 49.3 |
Appendix A.6. Spun Bonded Polyolefin Membrane with Crinkled Surface (SBPC)
| Property | Value |
|---|---|
| Thickness, mm | 1 |
| Bulk density, kg/m3 | 67 |
| Porosity, m3/m3 | 0.001 |
| Specific heat capacity (dry), J/(kg·K) | 1500 |
| Thermal conductivity, W/(m·K) | 2.3 |
| Thermal conductivity temperature coefficient, W/(m·K2) | 0.0002 |
| Water vapor diffusion resistance factor | 65.6 |
Appendix A.7. Oriented Strand Board (OSB)
Appendix A.7.1. Improved Model
| Property | Value | Design |
|---|---|---|
| Thickness, mm | 11.1 | |
| Bulk density, kg/m3 | 534 | 575 |
| Porosity, m3/m3 | 0.64 | 0.8625 |
| Specific heat capacity (dry), J/(kg·K) | 1280 | 1880 |
| Thermal conductivity, W/(m·K) | 0.0806 | 0.084 |
| Thermal conductivity temperature coefficient, W/(m·K2) | 0.0002 | |
| Water vapor diffusion resistance factor | 195 | 1182 |
| RH | Water Content, kg/m3 | RH | Water Content, kg/m3 |
|---|---|---|---|
| 0 | 0 | 0.7 | 57.1 |
| 0.1 | 12.7 | 0.8 | 71.9 |
| 0.2 | 20.1 | 0.9 | 95.1 |
| 0.3 | 26.1 | 0.95 | 112.7 |
| 0.4 | 32 | 0.98 | 126.6 |
| 0.5 | 38.6 | 1 | 333 |
| 0.6 | 46.6 | - | - |
| RH | µ-Value |
|---|---|
| 0 | 195 |
| 0.25 | 195 |
| 0.75 | 47 |
| 0.8 | 40.8 |
| 1 | 40.8 |
| Water Content, kg/m3 | D (Suction), m2/s | D (Redistribution), m2/s |
|---|---|---|
| 0 | 0 | 0 |
| 71.9 | 7.37 × 10−13 | 7.37 × 10−13 |
| 333 | 1.66 × 10−10 | 1.66 × 10−11 |
Appendix A.7.2. WUFI Database Low Density (575 kg/m3) OSB Entries
| RH | Water Content, kg/m3 |
|---|---|
| 0 | 0 |
| 0.49 | 29.6 |
| 0.695 | 55.2 |
| 0.905 | 87.4 |
| 1 | 333.5 |
| RH | µ-Value |
|---|---|
| 0 | 1182 |
| 0.1 | 1182 |
| 0.2 | 1182 |
| 0.3 | 525.5 |
| 0.4 | 295.5 |
| 0.5 | 187.5 |
| 0.6 | 130 |
| 0.7 | 95 |
| 0.8 | 72.3 |
| 0.9 | 56.9 |
| 1 | 45.6 |
| Water Content, kg/m3 | D (Suction), m2/s | D (Redistribution), m2/s |
|---|---|---|
| 0 | 0 | 0 |
| 71.3 | 7.24 × 10−13 | 7.24 × 10−13 |
| 333.5 | 1.65 × 10−10 | 1.65 × 10−11 |
Appendix A.8. Fiberglass Batt Cavity Insulation (Used with Additional 5 mm Air Gap)
| Property | Value | Design |
|---|---|---|
| Thickness, mm | 135 | 140 |
| Bulk density, kg/m3 | 30 | |
| Porosity, m3/m3 | 0.008 | 0.99 |
| Specific heat capacity (dry), J/(kg·K) | 840 | |
| Thermal conductivity, W/(m·K) | 0.0398 | 0.035 |
| Thermal conductivity temperature coefficient, W/(m·K2) | 0.0002 | |
| Water vapor diffusion resistance factor | 1.3 |
| Water Content, kg/m3 | Thermal Conductivity, W/(m·K) | Design |
|---|---|---|
| 0 | 0.0398 | 0.035 |
| 50 | 0.05 | 0.043 |
| 100 | 0.05 | 0.049 |
Appendix A.9. Kraft Paper Facing
| Property | Value | Design |
|---|---|---|
| Thickness, mm | 1 | |
| Bulk density, kg/m3 | 120 | |
| Porosity, m3/m3 | 0.6 | |
| Specific heat capacity (dry), J/(kg·K) | 1500 | |
| Thermal conductivity, W/(m·K) | 0.42 | |
| Thermal conductivity temperature coefficient, W/(m·K2) | 0.0002 | |
| Water vapor diffusion resistance factor | 1919 | 3000 |
| RH | Water Content, kg/m3 |
|---|---|
| 0 | 0 |
| 0.5 | 0.6 |
| 0.8 | 1.8 |
| 0.9 | 2.6 |
| 0.97 | 3.5 |
| 1 | 11.2 |
| RH | µ-Value |
|---|---|
| 0 | 1919 |
| 0.25 | 1919 |
| 0.75 | 609 |
| 1 | 609 |
Appendix A.10. Polyethylene Membrane (PE)
| Property | Value |
|---|---|
| Thickness, mm | 1 |
| Bulk density, kg/m3 | 130 |
| Porosity, m3/m3 | 0.001 |
| Specific heat capacity (dry), J/(kg·K) | 2300 |
| Thermal conductivity, W/(m·K) | 2.3 |
| Thermal conductivity temperature coefficient, W/(m·K2) | 0.0002 |
| Water vapor diffusion resistance factor | 50,000 |
Appendix A.11. Interior Gypsum Board
| Property | Value |
|---|---|
| Thickness, mm | 12.5 |
| Bulk density, kg/m3 | 625 |
| Porosity, m3/m3 | 0.706 |
| Specific heat capacity (dry), J/(kg·K) | 870 |
| Thermal conductivity, W/(m·K) | 0.16 |
| Thermal conductivity temperature coefficient, W/(m·K2) | 0.0002 |
| Water vapor diffusion resistance factor | 7.03 |
| RH | Water Content, kg/m3 |
|---|---|
| 0 | 0 |
| 0.505 | 4.34275 |
| 0.71 | 6.15625 |
| 0.896 | 11.3125 |
| 0.99 | 93 |
| 1 | 430.625 |
| RH | µ-Value |
|---|---|
| 0 | 7.03 |
| 0.1 | 7.03 |
| 0.2 | 6.48 |
| 0.3 | 5.98 |
| 0.4 | 5.5 |
| 0.5 | 5.05 |
| 0.6 | 4.63 |
| 0.7 | 4.24 |
| 0.8 | 3.87 |
| 0.9 | 3.52 |
| 1 | 3.19 |
References
- Britt, M. New DOE analysis supports use of 2018 IECC. Building Safety Journal. 3 June 2019. Available online: https://www.iccsafe.org/building-safety-journal/bsj-technical/new-doe-analysis-supports-use-of-2018-iecc/ (accessed on 10 November 2020).
- Mendon, V.V.; Lucas, R.G.; Goel, S. Cost-Effectiveness Analysis of the 2009 and 2012 IECC Residential Provisions—Technical Support Document; Pacific Northwest National Lab: Richland, WA, USA, 2012.
- Spinu, M. Design without Compromise: Balancing Durable and Energy-Efficient Buildings. The Construction Specifier. 1 November 2012. Available online: https://www.constructionspecifier.com/design-without-compromise-balancing-durable-and-energy-efficient-buildings/ (accessed on 10 November 2020).
- Glass, S.V.; Boardman, C.R.; Yeh, B.; Chow, K. Moisture monitoring of wood-frame walls with and without exterior insulation in the Midwestern U.S. In Proceedings of the Healthy, Intelligent, and Resilient Buildings and Urban Environments, International Association of Building Physics, Syracuse, NY, USA, 23–26 September 2018; pp. 163–168. [Google Scholar] [CrossRef]
- Boardman, C.R.; Glass, S.V.; Munson, R.; Yeh, B.; Chow, K. Field Moisture Performance of Wood-Framed Walls with Exterior Insulation in a Cold Climate; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2019; pp. 1–42.
- Fraunhofer IBP WUFI Home Page. Fraunhofer Institute for Building Physics. 2020. Available online: https://wufi.de/en/ (accessed on 10 December 2020).
- Trechsel, H.R. (Ed.) Moisture Analysis and Condensation Control in Building Envelopes; ASTM Manual Series, MNL 40; ASTM: West Conshohocken, PA, USA, 2001; ISBN 978-0-8031-2089-1. [Google Scholar]
- Trechsel, H.R. Overview of ASTM MNL 40, moisture analysis and condensation control in building envelopes. Perform. Exter. Build. Walls 2003. [Google Scholar] [CrossRef]
- Karagiozis, A.; Kunzel, H.; Holm, A. WUFI-ORNL/IBP—A North American hygrothermal model. In Proceedings of the Performance of Exterior Envelopes of Whole Buildings VIII International Conference, ASHRAE, Clearwater Beach, FL, USA, 2–7 December 2001. [Google Scholar]
- Finch, G.; Straube, J. Ventilated wall claddings: Review, field performance, and hygrothermal modeling. In Proceedings of the Thermal Performance of the Exterior Envelopes of Whole Buildings X International Conference, Clearwater Beach, FL, USA, 2–7 December 2007. [Google Scholar]
- Straube, J.; Smegal, J. Building America Special Research Project—High-R Walls Case Study Analysis; Building Science Corporation: Somerville, MA, USA, 2014. [Google Scholar]
- Glass, S.V.; Kochkin, V.; Drumheller, S.C.; Barta, L. Moisture performance of energy-efficient and conventional wood-frame wall assemblies in a mixed-humid climate. Buildings 2015, 5, 759–782. [Google Scholar] [CrossRef]
- Fraunhofer IBP Validation. Available online: https://wufi.de/en/software/validation/ (accessed on 22 July 2020).
- Mundt Petersen, S.; Arfvidsson, J. Comparison of field measurements and calculation of relative humidity and temperature in wood framed walls. In Proceedings of the Thermophysics 2010, Valtice, Czech Republic, 2–5 November 2010; Zmeskal, O., Ed.; Faculty of Chemistry, Brno University of Technology: Valtice, Czech Republic, 2010; pp. 93–101. [Google Scholar]
- Mundt Petersen, S.O.; Harderup, L.-E. Validation of a one-dimensional transient heat and moisture calculation tool under real conditions. In Proceedings of the Thermal Performance of the Exterior Envelopes of Whole Buildings XII International Conference, Clearwater Beach, FL, USA, 1–5 December 2013. [Google Scholar]
- Lstiburek, J.; Ueno, K.; Musunuru, S. Modeling Enclosure Design in Above-Grade Walls: Final Measure Guideline; Building Technologies Office, U.S. Department of Energy: Oak Ridge, TN, USA, 2015. Available online: https://www.buildingscience.com/documents/building-america-reports/ba-1509-modeling-enclosure-design-above-grade-walls-measure/ (accessed on 10 December 2020).
- Lstiburek, J.; Ueno, K.; Musunuru, S. Modeling Enclosure Design in Above-Grade Walls; U.S. Department of Energy: Oak Ridge, TN, USA, 2016. Available online: https://www.nrel.gov/docs/fy16osti/65480.pdf (accessed on 10 December 2020).
- Fox, M.J. Hygrothermal Performance of Highly Insulated Wood Frame Walls with Air Leakage: Field Measurements and Simulations; Ryerson University: Toronto, ON, Canada, 2014. [Google Scholar]
- Trainor, T.M.; Smegal, J.; Straube, J.; Parekh, A. Measured and predicted moisture performance of high-R wall assemblies in cold climates. In Proceedings of the Thermal Performance of the Exterior of Envelopes of Whole Buildings XIII International Conference, Clearwater Beach, FL, USA, 4–8 December 2016. [Google Scholar]
- Fischer, S. What I learned with WUFI modeling software. Green Building Advisor. 4 October 2018. Available online: https://www.greenbuildingadvisor.com/article/learned-wufi-modeling-software (accessed on 10 December 2020).
- Standard methods for water vapor transmission of materials. In ASTM E96/E96M-16; ASTM International: West Conshohocken, PA, USA, 2016.
- Kumaran, M.K. Hygrothermal properties of building materials. In Moisture Analysis and Condensation Control in Building Envelopes; Trechsel, H.R., Ed.; ASTM International: West Conshohocken, PA, USA, 2001; pp. 29–65. ISBN 978-0-8031-2089-1. [Google Scholar]
- Kumaran, M.K.; Lackey, J.C.; Normandin, N.; Tariku, F.; van Reenen, D. A Thermal and Moisture Transport Property Database for Common Building and Insulating Materials: Final Report from ASHRAE Research Project 1018-RP; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2002. [Google Scholar]
- Ojanen, T.; Ahonen, J.; Simonson, C.J. Moisture performance characteristics of OSB and spruce plywood exterior sheathing products. In Research in Building Physics and Building Engineering, Proceedings of the Third International Building Physics Conference, Montreal, QC, Canada, 28–31 August 2006; Fazio, P., Ge, H., Rao, J., Desmarais, G., Eds.; Taylor & Francis: London, UK, 2006; pp. 97–105. ISBN 978-0-415-41675-7. [Google Scholar]
- Timusk, P.C.; Pressnail, K.D.; Cooper, P.A. The effects of board density, resin content and component layers on the permeability properties of mill-fabricated oriented strandboard. In Proceedings of the 12th Canadian Conference of Building Science and Technology, Quebec Building Envelope Council, Montreal, QC, Canada, 6–8 May 2009; pp. 325–334. [Google Scholar]
- Burch, D.M.; Thomas, W.C.; Fanney, A.H. Water vapor permeability measurements of common building materials. ASHRAE Trans. 1992, 98, 486–494. [Google Scholar]
- Gatland, S. Comparison of water vapor permeance data of common interior building materials in North American wall systems. In Proceedings of the 10th Canadian Conference on Building Science and Technology, Ottawa, ON, Canada, 12–13 May 2005; pp. 182–194. [Google Scholar]
- NAHB Research Center. Moisture Performance of Wood-Based Sheathing on Exterior Walls Clad with Absorptive Materials; NAHB Research Center: Upper Marlboro, MD, USA, 2010. [Google Scholar]
- American Society of Heating, Refrigerating and Air-Conditioning Engineers. 2017 ASHRAE Handbook of Fundamentals; Owen, M.S., Ed.; ASHRAE: Atlanta, GA, USA, 2017; ISBN 978-1-939200-57-0. [Google Scholar]
- Martin, P.C.; Verschoor, J.D. Investigation of Water Vapor Migration and Moisture Storage in an Insulated Wall Structure: Final Report from ASHRAE Research Project 496-RP; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 1994. [Google Scholar]
- Glass, S.V. Hygrothermal Analysis of Wood-Frame Assemblies in a Mixed-Humid Climate; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2013; pp. 1–25.
- Criteria for moisture-control design analysis in buildings. In ANSI/ASHRAE Standard 160-2016; ASHRAE: Atlanta, GA, USA, 2016.
- Carll, C.G.; Highley, T.L. Decay of wood and wood-based products above ground in buildings. J. Test. Eval. 1999, 27, 150–158. [Google Scholar] [CrossRef]
- Building Science Corporation Info-312: Vapor Permeance of Some Building Materials. Available online: https://www.buildingscience.com/documents/information-sheets/info-312-vapor-permeance-some-materials (accessed on 24 March 2020).
- Boardman, C.R.; Glass, S.V.; Lebow, P.K. Simple and accurate temperature correction for moisture pin calibrations in oriented strand board. Build. Environ. 2017, 112, 250–260. [Google Scholar] [CrossRef]
- Boardman, C.R.; Glass, S.V.; Chow, K.; Yeh, B. Hygrothermal modeling of wall drying after water injection. In Proceedings of the Thermal Performance of the Exterior Envelopes of Whole Buildings XIV International Conference, Clearwater Beach, FL, USA, 9–12 December 2019. [Google Scholar]
- Igaz, R.; Kristak, L.; Gatjanska, M.; Kucerka, M. Thermophysical Properties of OSB boards versus equilibrium moisture content. BioResources 2017, 12, 8106–8118. [Google Scholar]
- Kumaran, M.K. Materials Properties; Final Report, Vol. 3, Task 3, International Energy Agency Annex 24-Heat, Air and Moisture Transfer Through New and Retrofitted Insulated Envelope Parts (HAMTIE); Laboratorium Bouwfysica, Katholieke University-Leuven: Leuven, Belgium, 1996; Available online: http://www.ecbcs.org/Data/publications/EBC_Annex_24_Report_3.pdf (accessed on 8 December 2020).
- Kumaran, M.K. A thermal and moisture property database for common building and insulation materials. ASHRAE Trans. 2006, 112, 485–497. [Google Scholar]
- Straube, J.F.; van Straaten, R.; Burnett, E.F.P. Field studies of ventilation drying. In Proceedings of the Thermal Performance of the Exterior Envelopes of Whole Buildings IX International Conference, Clearwater Beach, FL, USA, 5–10 December 2004. [Google Scholar]
- Tsongas, G.A. Damage in multifamily housing walls with vinyl siding. ASHRAE J. 2017, 59, 44–52. [Google Scholar]
- Boardman, C.R.; Glass, S.V.; Zelinka, S.L. Moisture redistribution in full-scale wood-frame wall assemblies: Measurements and engineering approximation. Buildings 2020, 10, 141. [Google Scholar] [CrossRef]
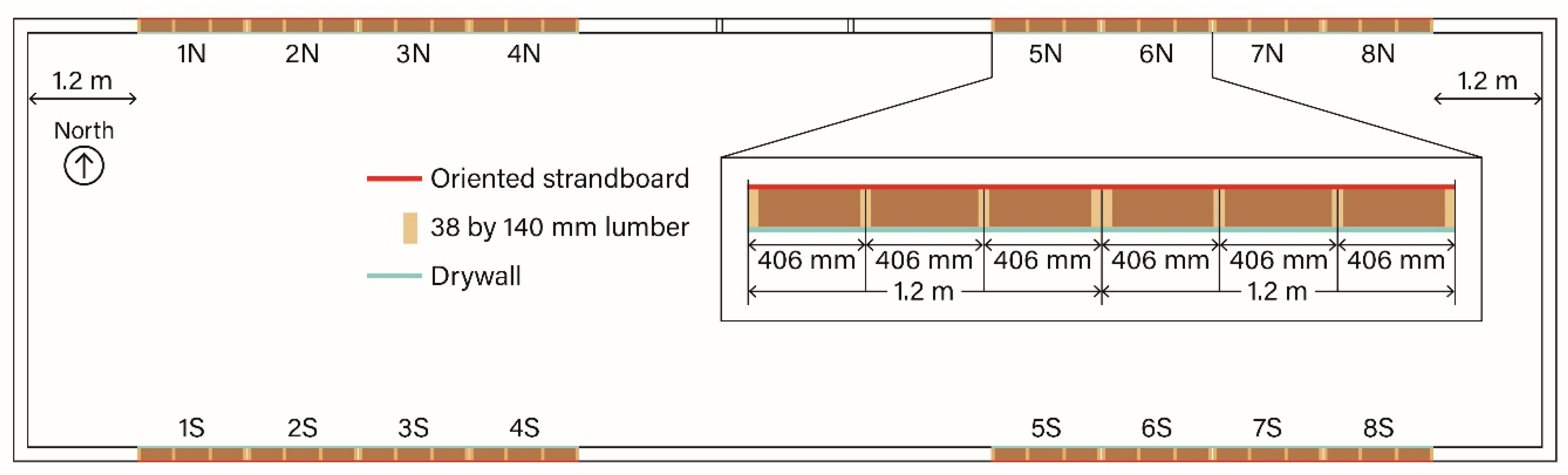
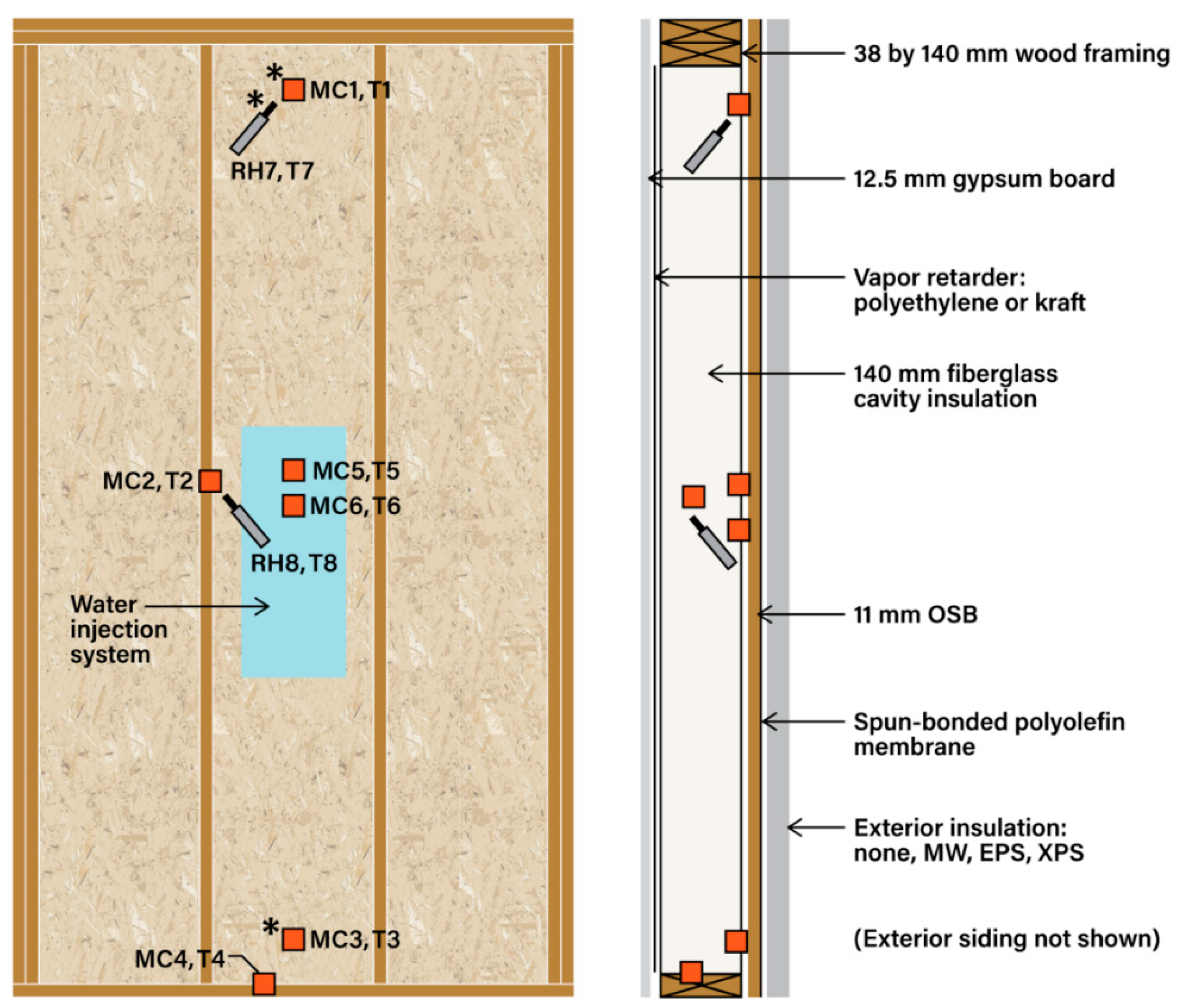
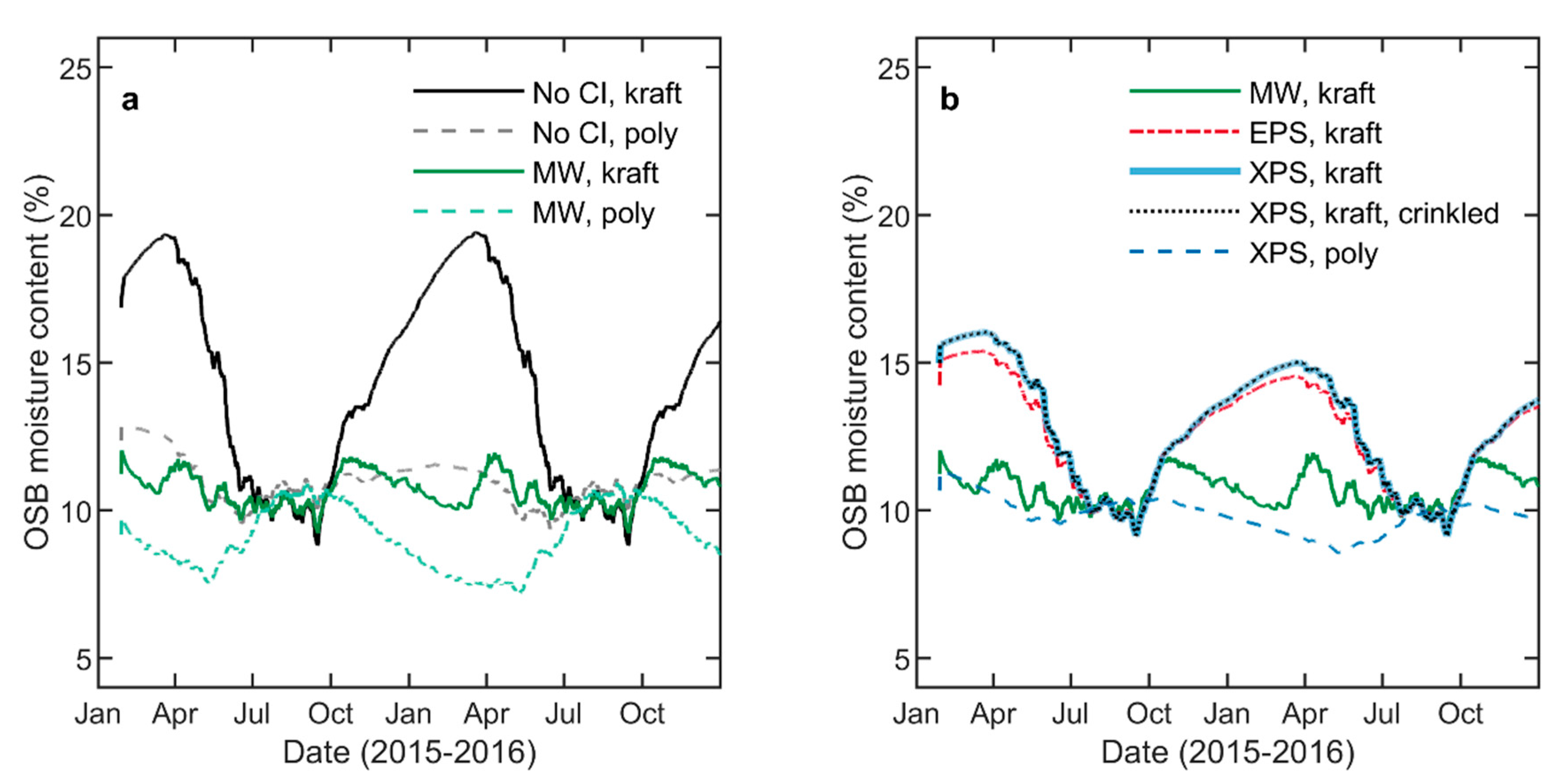
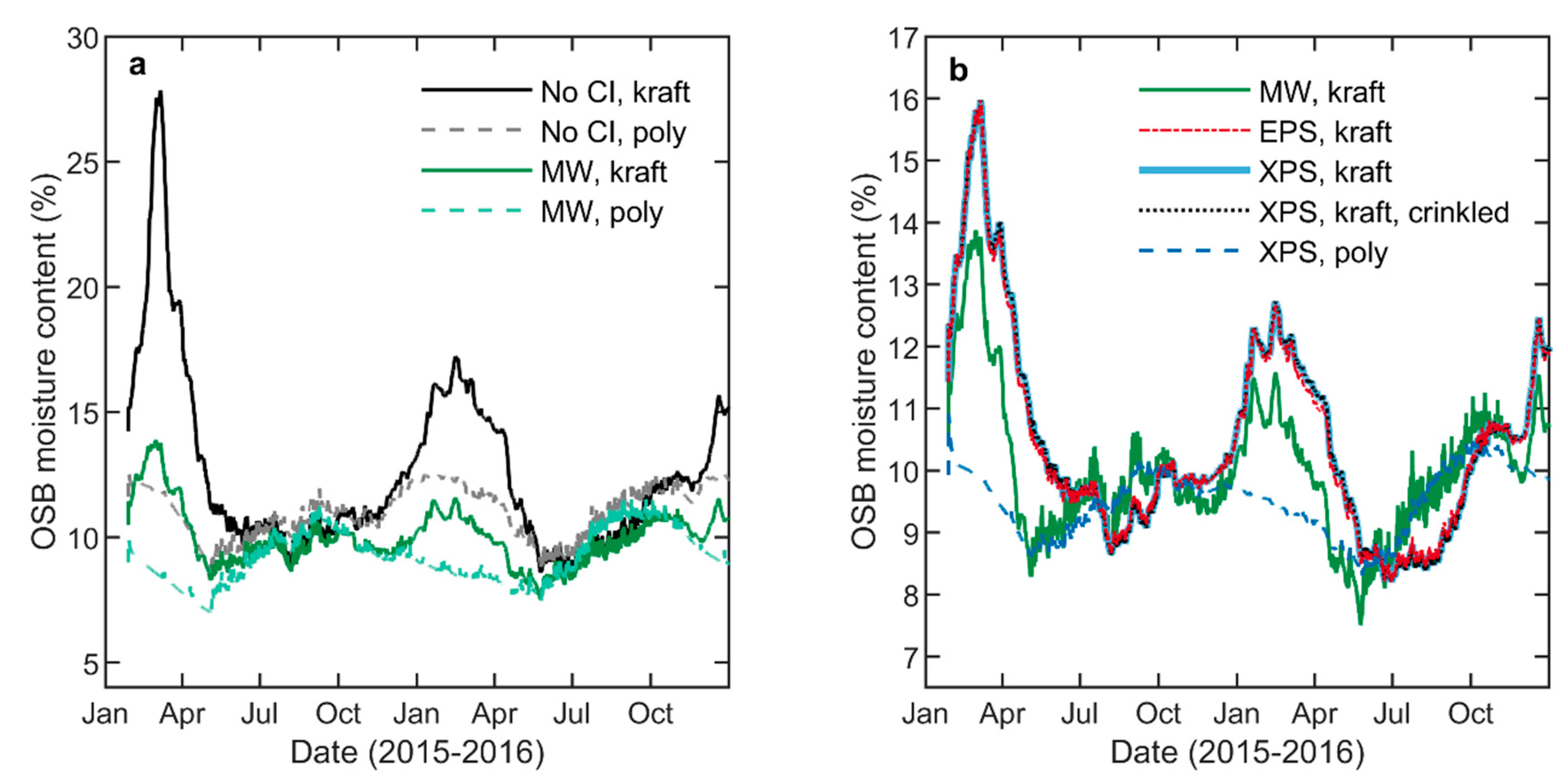

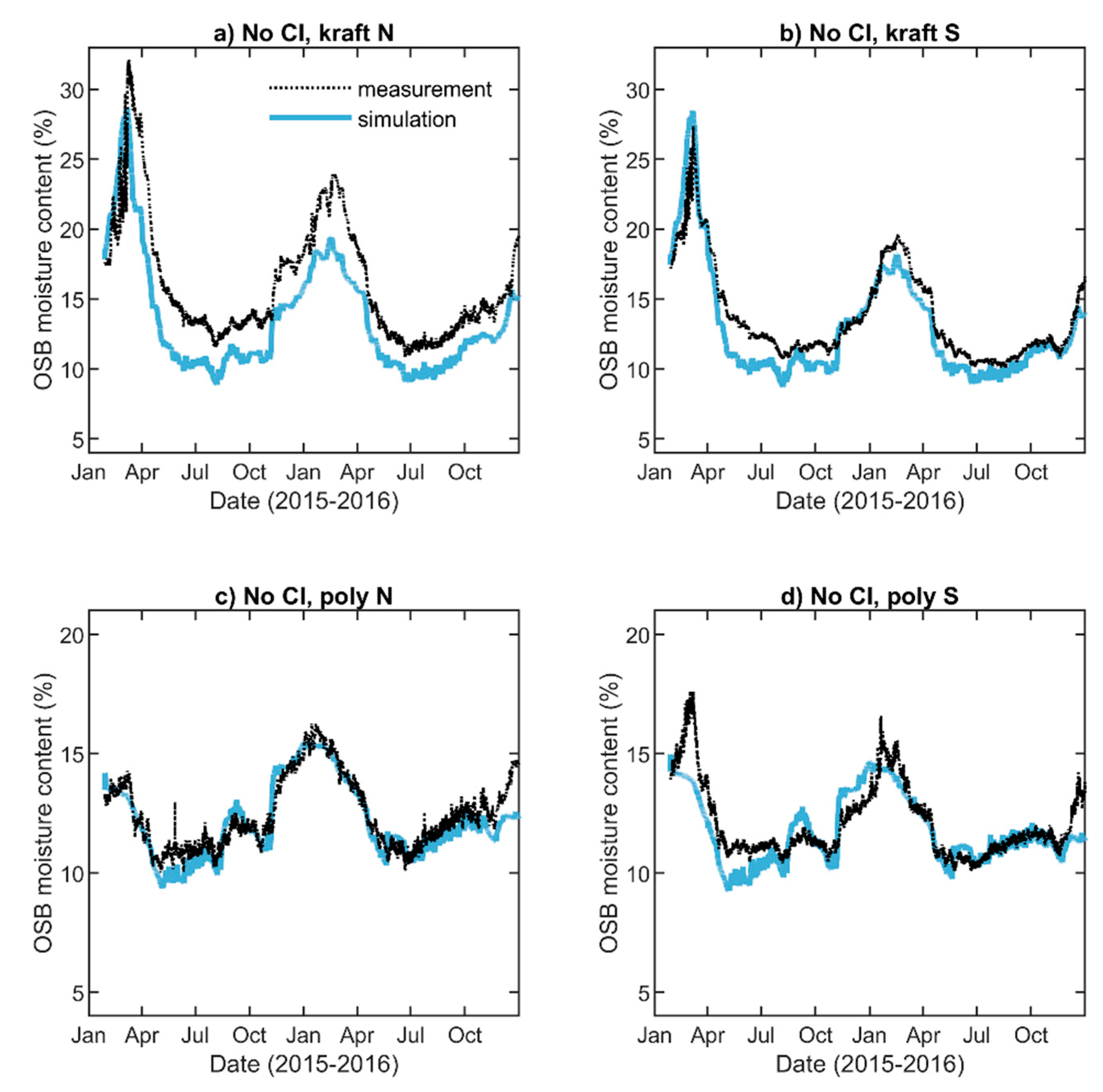
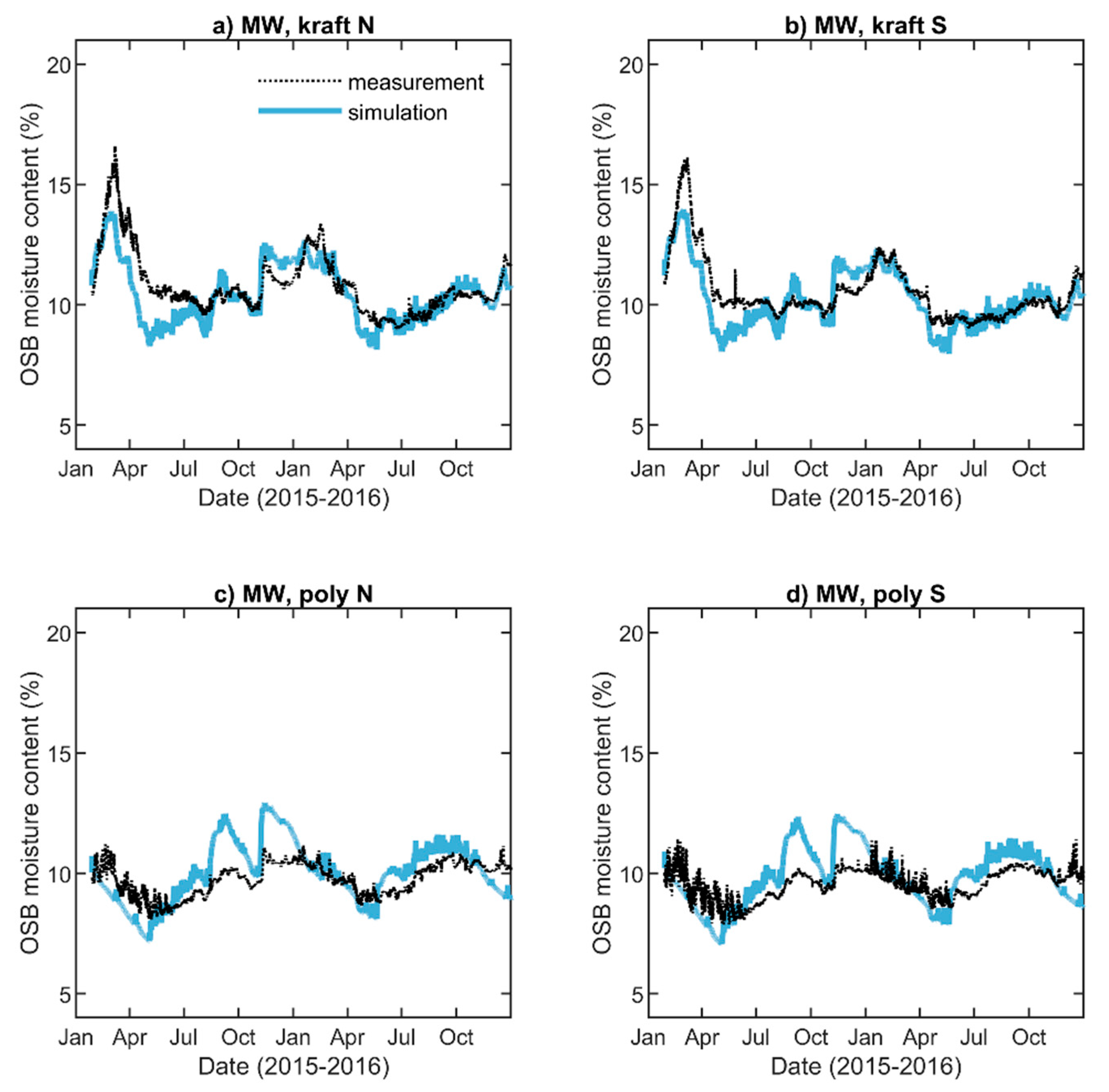
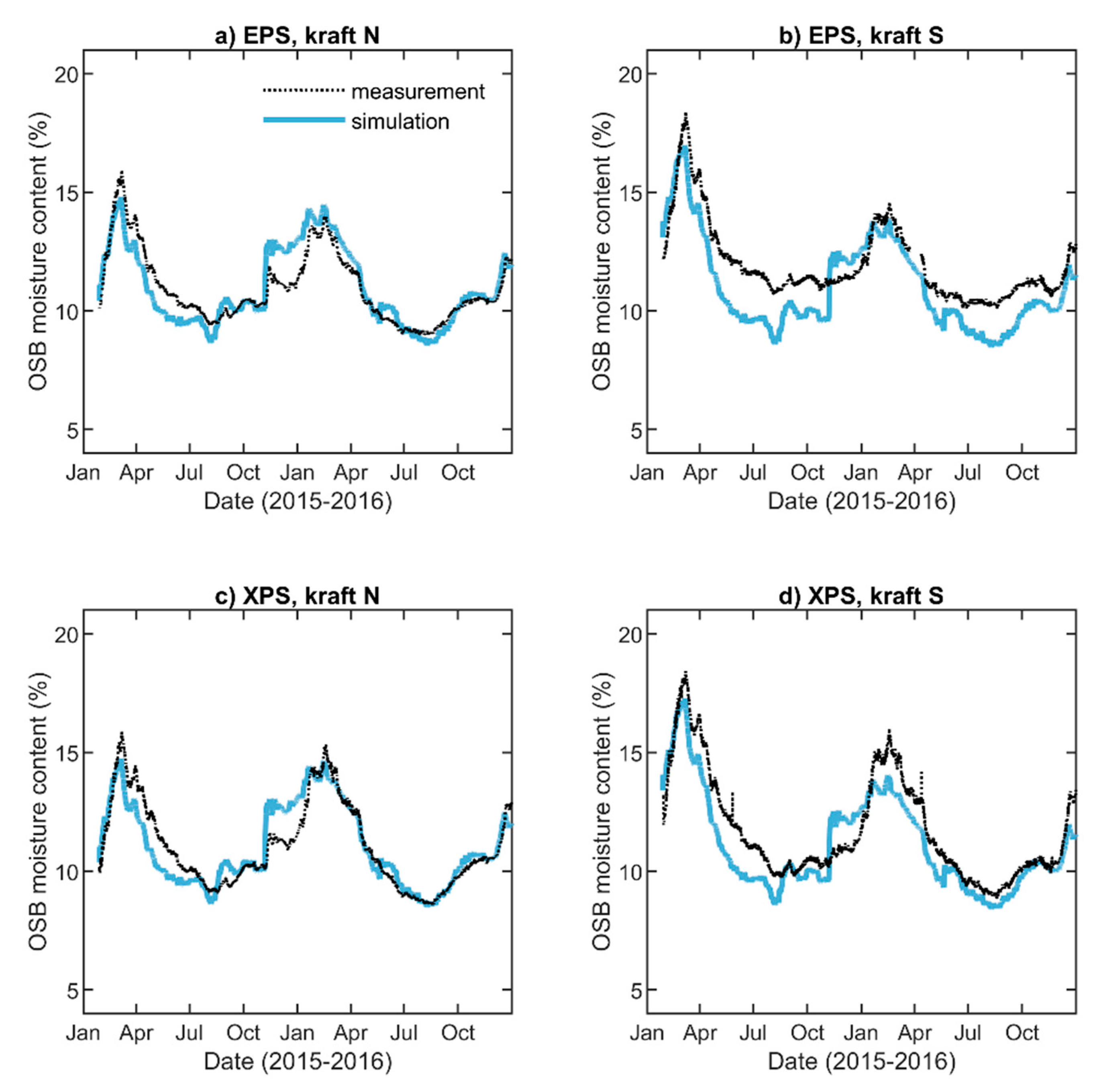
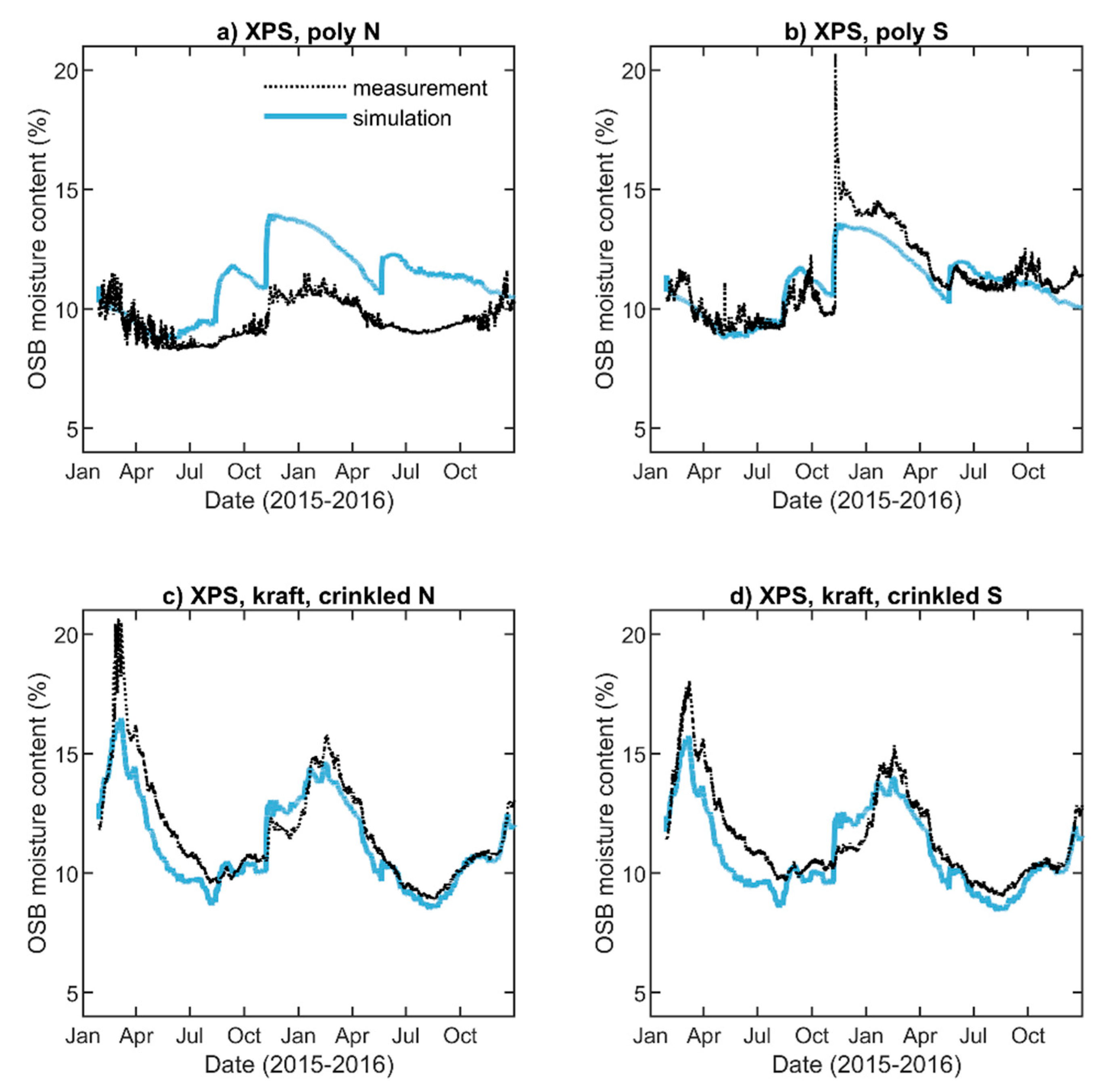
| Wall | Interior Vapor Retarder | House Wrap | Exterior Insulation | Label |
|---|---|---|---|---|
| 1 | Kraft paper | Flat polyolefin | None | No CI, kraft |
| 2 | Polyethylene | Flat polyolefin | None | No CI, poly |
| 3 | Kraft paper | Flat polyolefin | 38 mm Mineral Wool | MW, kraft |
| 4 | Polyethylene | Flat polyolefin | 38 mm Mineral Wool | MW, poly |
| 5 | Kraft paper | Flat polyolefin | 38 mm Expanded Polystyrene | EPS, kraft |
| 6 | Kraft paper | Flat polyolefin | 25.4 mm Extruded Polystyrene | XPS, kraft |
| 7 | Polyethylene | Flat polyolefin | 25.4 mm Extruded Polystyrene | XPS, poly |
| 8 | Kraft paper | Crinkled polyolefin | 25.4 mm Extruded Polystyrene | XPS, kraft, crinkled |
| Material | Relative Humidity (%) | Water Vapor Permeance | Literature a | ||
|---|---|---|---|---|---|
| Boundary Conditions | Mean | (ng Pa−1 s−1 m−2) | (US perm) | (ng Pa−1 s−1 m−2) | |
| Oriented strand board | 0–50 | 25 | 92 ± 30 | 1.6 ± 0.5 | 13–190 |
| 50–100 | 75 | 380 ± 89 | 6.6 ± 1.6 | 160–520 | |
| Asphalt-coated kraft paper | 0–50 | 25 | 103 ± 21 | 1.8 ± 0.4 | 9–195 |
| 50–100 | 75 | 325 ± 128 | 5.6 ± 2.2 | 9–240 | |
| Gypsum board with latex paint | 0–62 | 31 | 1140 ± 170 | 19.8 ± 3.0 | 208–2300 |
| 27–75 | 51 | 1820 ± 280 | 31.7 ± 4.8 | 404–2300 | |
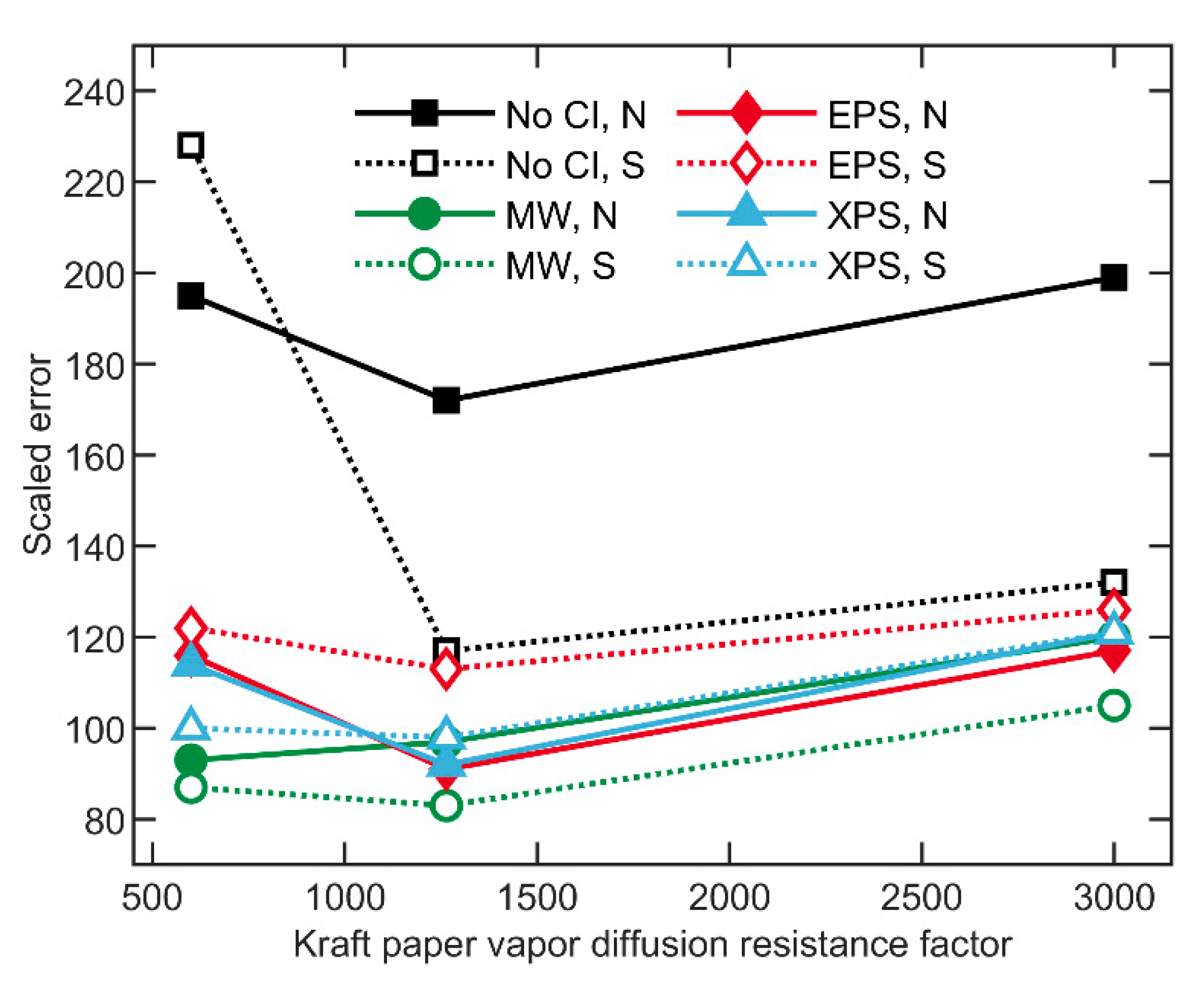
| Wall | Label | S | N | Average |
| 1 | No CI, kraft | 117 | 172 | 145 |
| 2 | No CI, poly | 106 | 101 | 103 |
| 3 | MW, kraft | 83 | 97 | 90 |
| 4 | MW, poly | 105 | 122 | 114 |
| 5 | EPS, kraft | 113 | 91 | 102 |
| 6 | XPS, kraft | 98 | 92 | 95 |
| 7 | XPS, poly | 103 | 156 | 129 |
| 8 | XPS, kraft, crinkled | 98 | 102 | 100 |
| - | Average | 103 | 116 | - |
| RMSE | 1S | 2S | 3S | 4S | 5S | 6S | 7S | 8S |
| OSB MC | 1.50 | 0.93 | 0.78 | 0.99 | 1.49 | 1.03 | 0.83 | 0.99 |
| T | 1.52 | 1.53 | 1.01 | 1.26 | 1.10 | 1.05 | 1.34 | 1.04 |
| RH | 5.53 | 7.63 | 6.39 | 8.16 | 6.50 | 7.38 | 8.68 | 7.71 |
| Scaled Error | 117 | 106 | 83 | 105 | 113 | 98 | 103 | 98 |
| Bias T | −0.18 | −0.15 | 0.36 | −0.23 | −0.25 | 0.11 | −0.09 | 0.31 |
| Bias RH | 3.40 | 0.83 | 3.17 | 6.95 | 4.10 | 3.97 | 7.41 | 4.53 |
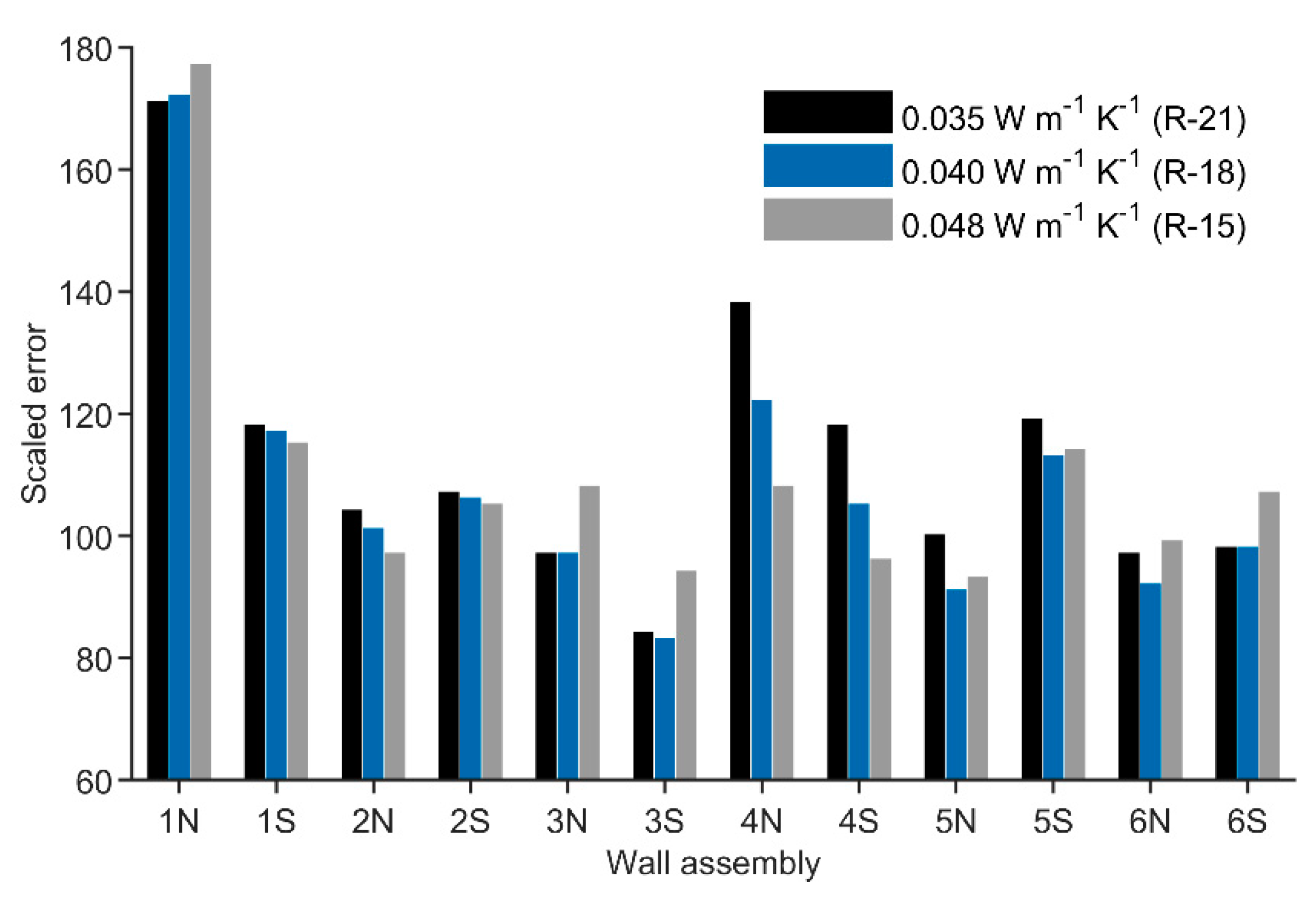
| Wall | Label | Base | Wind | Diff |
| 1N | No CI, kraft N | 172 | 175 | 1.7% |
| 1S | No CI, kraft S | 117 | 119 | 1.7% |
| 2N | No CI, poly N | 101 | 101 | 0.0% |
| 2S | No CI, poly S | 106 | 106 | 0.0% |
| 3N | MW, kraft N | 97 | 97 | 0.0% |
| 3S | MW, kraft S | 83 | 83 | 0.0% |
| 4N | MW, poly N | 122 | 119 | −2.5% |
| 4S | MW, poly S | 105 | 101 | −3.8% |
| 6N | XPS, kraft N | 92 | 92 | 0.0% |
| 6S | XPS, kraft S | 98 | 99 | 1.0% |
| 7N | XPS, poly N | 156 | 152 | −2.6% |
| 7S | XPS, poly S | 103 | 102 | −1.0% |
| - | Average | - | - | −0.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boardman, C.R.; Glass, S.V. Improving the Accuracy of a Hygrothermal Model for Wood-Frame Walls: A Cold-Climate Study. Buildings 2020, 10, 236. https://doi.org/10.3390/buildings10120236
Boardman CR, Glass SV. Improving the Accuracy of a Hygrothermal Model for Wood-Frame Walls: A Cold-Climate Study. Buildings. 2020; 10(12):236. https://doi.org/10.3390/buildings10120236
Chicago/Turabian StyleBoardman, Charles R., and Samuel V. Glass. 2020. "Improving the Accuracy of a Hygrothermal Model for Wood-Frame Walls: A Cold-Climate Study" Buildings 10, no. 12: 236. https://doi.org/10.3390/buildings10120236
APA StyleBoardman, C. R., & Glass, S. V. (2020). Improving the Accuracy of a Hygrothermal Model for Wood-Frame Walls: A Cold-Climate Study. Buildings, 10(12), 236. https://doi.org/10.3390/buildings10120236






