The Role of Microstructure on the Tensile Plastic Behaviour of Ductile Iron GJS 400 Produced through Different Cooling Rates—Part II: Tensile Modelling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material
2.2. Tensile Tests and Microstructure Plasticity Model
3. Results
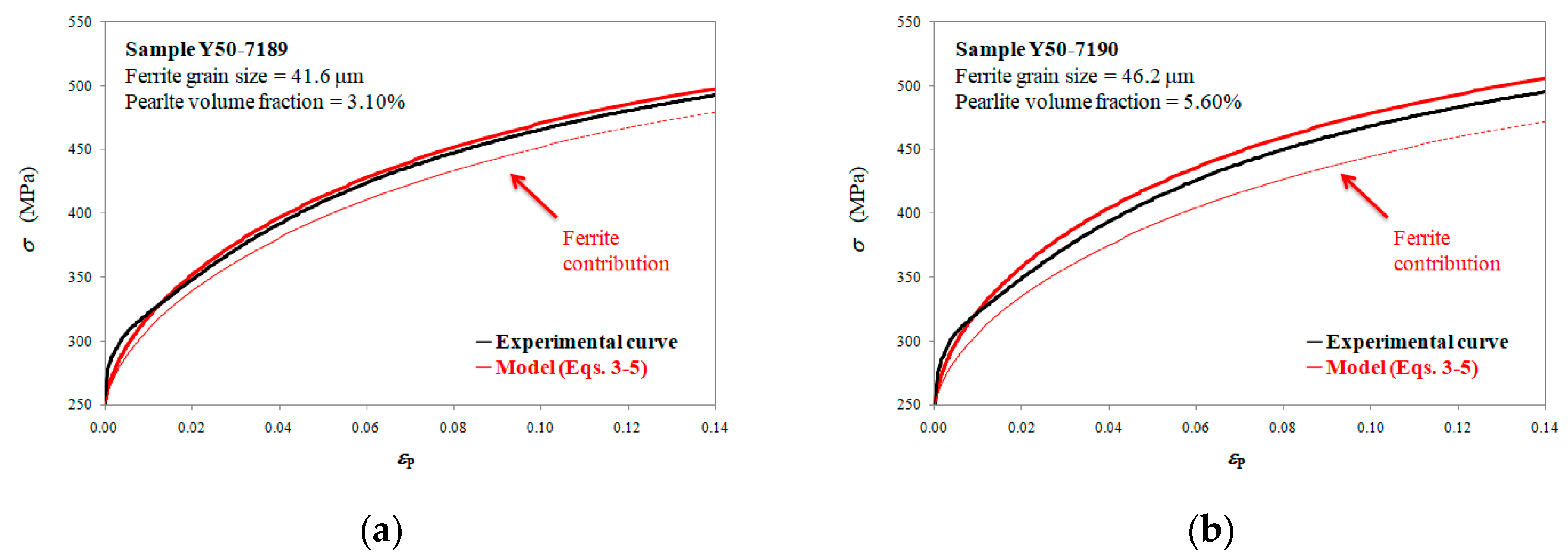
3.1. Model Calibration
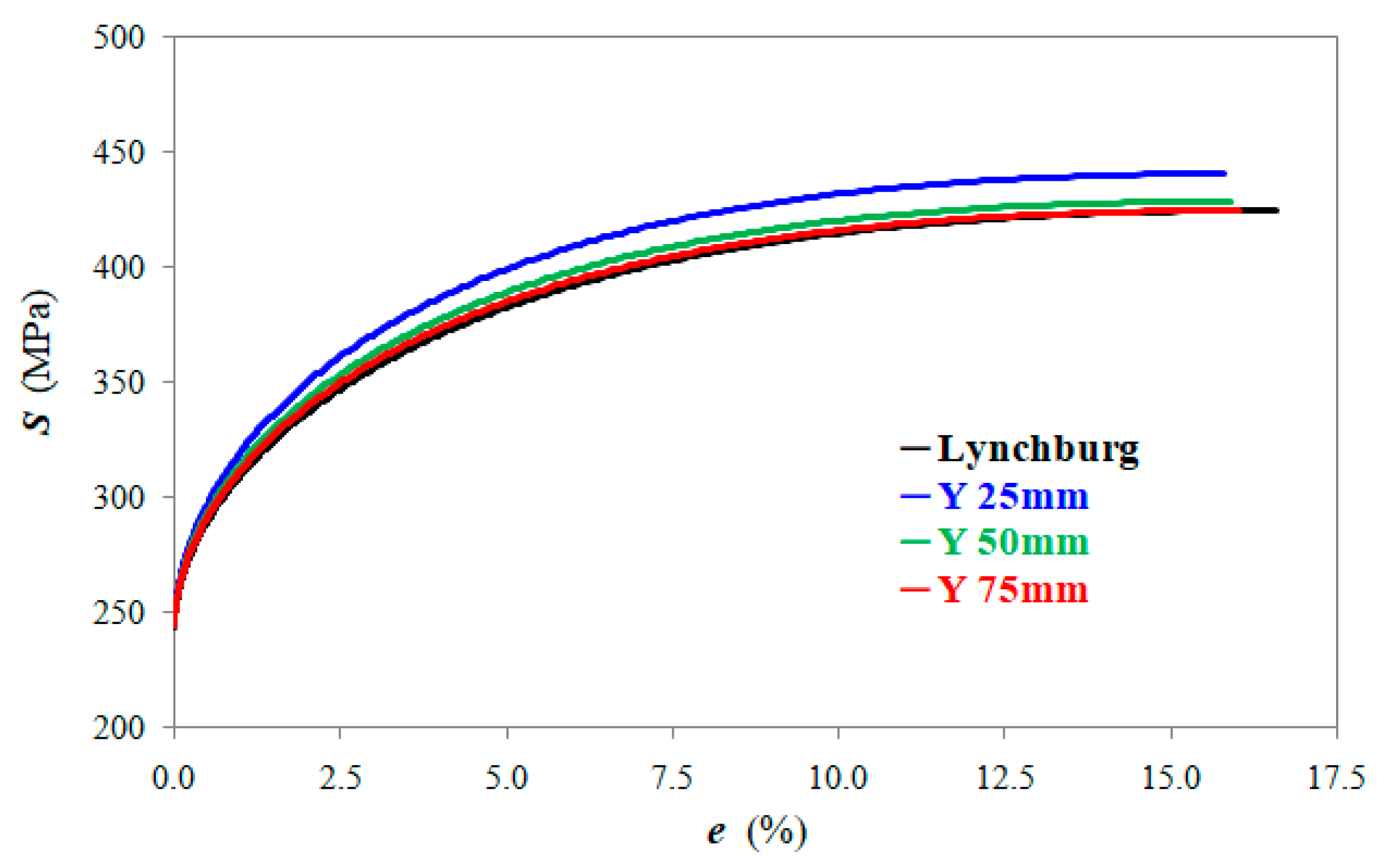
3.2. Model Prediction
4. Discussion
4.1. Considerations of the Minimum Requirements of Data Statistics Complying with the Standards ASTM E2567-16a and ASTM E112-13
4.2. Microstructure Parameters Relevant to Describing the Plastic Behaviour of GJS 400
4.3. Considerations of Other Microstructural Parameters
5. Conclusions
- This model described very well the experimental flow curves at high strains, while at low strains, minor mismatching was present. This mismatching was ascribed to the graphite-matrix decohesion;
- The plastic behaviour of the GJS 400 with different microstructures depended mainly on the ferritic grain size and pearlitic volume fraction, while the other microstructure parameters were not needed to rationalize the GJS 400’s plastic behaviour;
- The correlation between the mechanical constituents (ferrite and pearlite), physical parameters, and microstructure was validated, so the use of dislocation-related-dislocation density constitutive equations (like the Voce and Estrin equations) for different DI grades reported in previous investigations was also validated;
- The results proved that the data gathered while complying with the minimum requirements of the standards’ statistics were not enough to produce accurate microstructural data.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Mechanistic Equation of Strain Hardening and Physical Parameters
- Λ = dislocation mean free path related to the dislocation cells in ferrite;
- D = ferritic grain size or pearlitic island size;
- λ = interlamellar spacing in pearlite.
References
- Gonzaga, R.A.; Carrasquilla, J.F. Influence of an appropriate balance of the alloying elements on microstructure and on mechanical properties of nodular cast iron. J. Mater. Process. Tech. 2005, 162, 293–297. [Google Scholar] [CrossRef]
- Gonzaga, R.A. Influence of ferrite and pearlite content on mechanical properties of ductile cast irons. Mater. Sci. Eng. A 2013, 567, 1–8. [Google Scholar] [CrossRef]
- Alhussein, A.; Risbet, M.; Bastien, A.; Chobaut, J.P.; Balloy, D.; Favergeon, J. Influence of silicon and addition elements on the mechanical behaviour of ferritic ductile cast iron. Mater. Sci. Eng. A 2014, 605, 222–228. [Google Scholar] [CrossRef]
- Bradley, W.L.; Srinivasan, M.N. Fracture and fracture toughness of cast irons. Int. Mater. Rev. 1990, 35, 129–161. [Google Scholar] [CrossRef]
- Iacoviello, F.; Di Bartolomeo, O.; Di Cocco, V.; Piacente, V. Damaging micro-mechanisms in ferritic-pearlitic ductile cast irons. Mater. Sci. Eng. A 2008, 478, 181–186. [Google Scholar] [CrossRef]
- Di Cocco, V.; Iacoviello, F.; Rossi, A.; Iacoviello, D. Macro and microscopical approach to the damaging mechanisms analysis in a ferritic ductile cast iron. Theor. Appl. Fract. Mech. 2014, 69, 26–33. [Google Scholar] [CrossRef]
- Guo, X.; Stefanescu, D.M.; Chuzhoy, L.; Pershing, M.A.; Biltgen, G.L. A Mechanical Properties Model for Ductile Iron. AFS Trans. 1997, 105, 47–54. [Google Scholar]
- Donelan, P. Modelling microstructural and mechanical properties of ferritic ductile cast iron. Mater. Sci. Tech. Ser. 2000, 16, 261–269. [Google Scholar] [CrossRef]
- Kasvayee, K.A.; Ghassemali, E.; Svensson, I.L.; Olofsson, J.; Jarfors, A.E.W. Characterization and modeling of the mechanical behavior of high silicon ductile iron. Mater. Sci. Eng. A 2017, 708, 159–170. [Google Scholar] [CrossRef]
- Svensson, I.L.; Sjögren, T. On modeling and simulation of mechanical properties of cast irons with different morphologies of graphite. Int. J. Met. 2009, 3, 67–77. [Google Scholar] [CrossRef]
- Olofsson, J.; Salomonsson, K.; Svensson, I.L. Modelling and simulations of ductile iron solidification induced variations in mechanical behaviour on component and microstructural level. IOP Conf. Ser. Mater. Sci. Eng. 2015, 84, 012026. [Google Scholar] [CrossRef]
- Hütter, G.; Zybell, L.; Kuna, M. Micromechanisms of fracture in nodular cast iron: From experimental findings towards modeling strategies—A review. Eng. Fract. Mech. 2015, 144, 118–141. [Google Scholar] [CrossRef]
- Goodrich, G.M. Cast iron microstructure anomalies and their causes. AFS Trans. 1997, 105, 669–683. [Google Scholar]
- Iwabuchi, Y.; Narita, H.; Tsumura, O. Toughness and Ductility of heavy-walled ferritic spheroidal-graphite iron castings. Res. Rep. Kushiro Natl. Coll. 2003, 37, 1–9. [Google Scholar]
- Nilsson, K.F.; Blagoeva, D.; Moretto, P. An experimental and numerical analysis to correlate variation in ductility to defects and microstructure in ductile cast iron components. Eng. Fract. Mech. 2006, 73, 1133–1157. [Google Scholar] [CrossRef]
- Nilsson, K.F.; Vokal, V. Analysis of ductile cast iron tensile tests to relate ductility variation to casting defects and material microstructure. Mater. Sci. Eng. A 2009, 502, 54–63. [Google Scholar] [CrossRef]
- Angella, G.; Ripamonti, D.; Górny, M.; Masaggia, S.; Zanardi, F. The role of microstructure on tensile plastic behaviour of ductile iron GJS 400 produced through different cooling rates—Part I: Microstructure. Metals 2019, in press. [Google Scholar]
- Rivera, G.; Boeri, R.; Sikora, J. Revealing the solidification structure of nodular iron. Int. J. Cast Metal. Res. 1995, 8, 1–5. [Google Scholar] [CrossRef]
- Rivera, G.; Boeri, R.; Sikora, J. Revealing and characterizing solidification structure of ductile cast iron. Mater. Sci. Technol. 2002, 18, 691–698. [Google Scholar] [CrossRef]
- Follansbee, P.S.; Kocks, U.F. A Constitutive Description of the Deformation of Copper Based on the Use of the Mechanical Threshold Stress as an Internal State Variable. Acta Metall. Mater. 1988, 36, 81–93. [Google Scholar] [CrossRef]
- Follansbee, P.S. Structure Evolution in Austenitic Stainless Steels -A State Variable Model Assessment. Mater. Sci. Appl. 2015, 6, 457–463. [Google Scholar] [CrossRef]
- Kocks, U.F.; Mecking, H. Physics and phenomenology of strain hardening: The FCC case. Prog. Mater. Sci. 2003, 48, 171–273. [Google Scholar] [CrossRef]
- Estrin, Y.; Mecking, H. A unified phenomenological description of work hardening and creep based on one- parameter models. Acta Metall. Mater. 1984, 32, 57–70. [Google Scholar] [CrossRef]
- Estrin, Y. Dislocation theory based constitutive modelling: Foundations and applications. J. Mater. Process. Tech. 1998, 80, 33–39. [Google Scholar] [CrossRef]
- Angella, G. Strain hardening analysis of an austenitic stainless steel at high temperatures based on the one-parameter model. Mater. Sci. Eng. A 2012, 532, 381–391. [Google Scholar] [CrossRef]
- Angella, G.; Donnini, R.; Maldini, M.; Ripamonti, D. Combination between Voce formalism and improved Kocks-Mecking approach to model small strains of flow curves at high temperatures. Mater. Sci. Eng. A 2014, 594, 381–388. [Google Scholar] [CrossRef]
- Angella, G.; Zanardi, F.; Donnini, R. On the significance to use dislocation-density-related constitutive equations to correlate strain hardening with microstructure of metallic alloys: The case of conventional and austempered ductile irons. J. Alloy. Compd. 2016, 669, 262–271. [Google Scholar] [CrossRef]
- Donnini, R.; Fabrizi, A.; Bonollo, F.; Zanardi, F.; Angella, G. Assessment of the Microstructure Evolution of an Austempered Ductile Iron During Austempering Process Through Strain Hardening Analysis. Met. Mater. Int. 2017, 23, 855–864. [Google Scholar] [CrossRef]
- Caballero, F.G.; Garcìa de Andrés, C.; Capdevila, C. Characterization and morphological analysis of pearlite in a eutectoid steel. Mater. Charact. 2000, 45, 111–116. [Google Scholar] [CrossRef] [Green Version]
- Dieter, G.E. Mechanical Metallurgy; McGraw-Hill Book Company: New York, NY, USA, 1988; pp. 208–212. [Google Scholar]
- Byun, T.S.; Kim, I.S. Tensile properties and inhomogeneous deformation of ferrite-martensite dual phase steels. J. Mater. Sci. 1998, 9, 85–92. [Google Scholar] [CrossRef]
- Park, K.; Nishiyama, M.; Nakada, N.; Tsuchiyama, T.; Takaki, S. Effect of the martensite distribution on the strain hardening and ductile fracture behaviours of dual phase steel. Mater. Sci. Eng. A 2014, 604, 135–141. [Google Scholar] [CrossRef]
- Alibeyki, M.; Mirzadeh, H.; Najafi, M.; Kalhor, A. Modification of rule of mixtures for estimation of the mechanical properties of dual phase steels. J. Mater. Eng. Perform. 2017, 26, 2683–2688. [Google Scholar] [CrossRef]
- Modi, O.P.; Deshmukh, N.; Mondal, D.P.; Jha, A.K.; Yegneswaran, A.H.; Khair, H.K. Effect of interlamellar spacing on the mechanical properties of 0.65% C steel. Mater. Charact. 2001, 46, 347–352. [Google Scholar] [CrossRef]
- Benavides-Treviño, J.R.; Perez-Gonzalez, F.A.; Hernandez, M.A.L.; Garcia, E.; Juarez-Hernandez, A. Influence of the cooling rate on the amount of graphite nodules and interlamellar space in pearlite phase in a ductile iron. Indian J. Eng. Mater. Sci. 2018, 25, 330–334. [Google Scholar]
- Dong, M.J.; Prioul, C.; Francois, D. Damage effect on the fracture toughness of nodular cast iron: Part I. damage characterization and plastic flow stress modelling. Metall. Mater. Trans. A 1997, 28, 2245–2254. [Google Scholar] [CrossRef]
- Guillemer-Neel, C.; Feaugas, X.; Clavel, M. Mechanical behavior and damage kinetics in nodular cast iron: Part I. Damage mechanisms. Metall. Mater. Trans. A 2000, 31, 3063–3074. [Google Scholar] [CrossRef]
- Guillemer-Neel, C.; Feaugas, X.; Clavel, M. Mechanical behavior and damage kinetics in nodular cast iron: Part II. Hardening and damage. Metall. Mater. Trans. A 2000, 31, 3075–3086. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Andriollo, T.; Fæster, S.; Liu, W.; Hattel, J.; Barabash, R.I. Three-dimensional local residual stress and orientation gradients near graphite nodules in ductile cast iron. Acta Metall. Mater. 2016, 121, 173–180. [Google Scholar] [CrossRef] [Green Version]
- Andriollo, T.; Zhang, Y.; Fæster, S.; Thorborg, J.; Hattel, J. Impact of micro-scale residual stress on in-situ tensile testing of ductile cast iron: Digital volume correlation vs. model with fully resolved microstructure vs. periodic unit cell. J. Mech. Phys. Solids 2019, 125, 714–735. [Google Scholar] [CrossRef]





| C | Si | Mg | Mn | Cu | Ni | Cr | P | S | Fe |
|---|---|---|---|---|---|---|---|---|---|
| 3.63 | 2.45 | 0.046 | 0.129 | 0.133 | 0.0168 | 0.023 | 0.038 | 0.0043 | Bal. |
| Mould | Nodule Count (mm−2) | Nodule Size (μm) | Nodularity (%) | Pearlite Volume Fraction (%) | Ferrite Grain Size (μm) |
|---|---|---|---|---|---|
| Lynchburg 25 mm | 261 ± 15 | 24.3 ± 0.6 | 89.8 ± 3.0 | - | 37.3 ± 3.2 |
| Y 25 mm | 242 ± 11 | 24.9 ± 0.5 | 91.2 ± 1.6 | 3.8 ± 0.4 | 39.2 ± 2.3 |
| Y 50 mm | 116 ± 14 | 31.5 ± 1.0 | 87.1 ± 1.4 | 4.0 ± 1.6 | 48.6 ± 4.7 |
| Y 75 mm | 105 ± 9 | 34.5 ± 0.5 | 83.2 ± 4.6 | 3.0 ± 0.5 | 47.5 ± 7.2 |
| Mould | Rm (MPa) | Rmexp (MPa) | en (%) | enexp (%) | YS (MPa) | YSexp (MPa) |
|---|---|---|---|---|---|---|
| Lynchburg 25 mm | 424.4 | 424.3 | 16.6 | 16.7 | 277.2 | 288.3 |
| Y 25 mm | 440.5 | 440.7 | 15.8 | 16.0 | 277.9 | 294.2 |
| Y 50 mm | 428.4 | 429.8 | 15.9 | 16.2 | 278.7 | 288.8 |
| Y 75 mm | 424.5 | 426.5 | 16.0 | 16.0 | 277. | 287.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angella, G.; Donnini, R.; Ripamonti, D.; Górny, M.; Zanardi, F. The Role of Microstructure on the Tensile Plastic Behaviour of Ductile Iron GJS 400 Produced through Different Cooling Rates—Part II: Tensile Modelling. Metals 2019, 9, 1019. https://doi.org/10.3390/met9091019
Angella G, Donnini R, Ripamonti D, Górny M, Zanardi F. The Role of Microstructure on the Tensile Plastic Behaviour of Ductile Iron GJS 400 Produced through Different Cooling Rates—Part II: Tensile Modelling. Metals. 2019; 9(9):1019. https://doi.org/10.3390/met9091019
Chicago/Turabian StyleAngella, Giuliano, Riccardo Donnini, Dario Ripamonti, Marcin Górny, and Franco Zanardi. 2019. "The Role of Microstructure on the Tensile Plastic Behaviour of Ductile Iron GJS 400 Produced through Different Cooling Rates—Part II: Tensile Modelling" Metals 9, no. 9: 1019. https://doi.org/10.3390/met9091019
APA StyleAngella, G., Donnini, R., Ripamonti, D., Górny, M., & Zanardi, F. (2019). The Role of Microstructure on the Tensile Plastic Behaviour of Ductile Iron GJS 400 Produced through Different Cooling Rates—Part II: Tensile Modelling. Metals, 9(9), 1019. https://doi.org/10.3390/met9091019








