Spectral Characterization of Copper and Iron Sulfide Combustion: A Multivariate Data Analysis Approach for Mineral Identification on the Blend

Abstract

The pyrometallurgical processes for primary copper production have only off-line and time-demanding analytical techniques to characterize the in and out streams of the smelting and converting steps. Since these processes are highly exothermic, relevant process information could potentially be obtained from the visible and near-infrared radiation emitted to the environment. In this work, we apply spectral sensing and multivariate data analysis methodologies to identify and classify copper and iron sulfide minerals present in the blend from spectra measured during their combustion in a laboratory drop-tube setup, in which chemical reactions that take place in flash smelting furnaces can be reproduced. Controlled combustion experiments were conducted with two industrial concentrates and with high-grade mineral species as well, with a focus on pyrite and chalcopyrite. Exploratory analysis by means of Principal Component Analysis (PCA) applied on the spectral data depicted high correlation features among species with similar elemental compositions. Classification algorithms were tested on the spectral data, and a classification accuracy of 95.3% with a support vector machine (SVM) algorithm with a Gaussian kernel was achieved. The results obtained by the described procedures are shown to be very promising as a first step in the development of a predictive and analytical tool in search of fitting the current need for real-time control of pyrometallurgical processes.

1. Introduction

The flash smelting process was developed in Finland in the late 1940s, and it has become one of the main copper production technologies in the world, given its high production and fast implementation capabilities at industrial and commercial scales. This process has attracted the interest of researchers for more than five decades, from the first works that allowed understanding the mineralogy and combustion kinetics of specific mineral particles, to modern works focused on the development and application of computer fluid dynamics (CFD) models [1,2,3].

Mineral oxidation at high temperatures is the core in such processes, since it involves complex energy and mass transfer mechanisms, as well as gaseous and intermediate species production. The research related to this combustion process has tried to uncover the chemical and physical behaviors of those mineral particles present in copper concentrates in flash smelting conditions [4,5,6]. The species involved during the combustion absorb and emit energy with specific characteristics, which can be used to retrieve information about the process condition [7]. In particular, optical information at specific wavelengths has been used to describe the oxidation of the main sulfide minerals such as chalcopyrite (CuFeS₂) and pyrite (FeS₂) [4,6], to estimate ignition temperatures [8,9,10], single particle temperature [4,6], and to model particle size distributions [11].

In the combustion research field, visible and near-infrared (VIS-NIR) spectroscopic techniques are applied to characterize and retrieve relevant process information, e.g., Keyvan et al. [12,13] estimated natural gas flame temperature by means of the two-color pyrometry method; Romero et al. [14] developed a real-time temperature and composition monitoring system for natural gas flames in a glass production process; and Cai et al. [15] used least squares regression methods to fit coal flame spectral emission by means of using gray body models based on Planck’s radiation law, with temperature and emissivity as regression parameters.

Recently, researchers have reported on spectral measurements from laboratory-scale experiments of copper concentrate combustion [16], and exploratory results depicted some spectral features related to the combustion process, such as Cu_xO spectral emissions at 606 nm and 616 nm, as well as a direct correlation among sulfur content in samples and broad band spectral intensity amplitudes. Furthermore, chemometrics techniques, i.e., analytical tools applied for the chemical characterization of samples, appear as a great tool to gain new insights from great volumes of data such as spectral data. One of these applications was shown in the work of Stumpe et. Al. [17]. The researchers achieved classifying different slag species coming from the steel industry by means of PCA and SIMCA (Soft Independent Modelling of Class Analogy) models applied to the mid-infrared spectra. Finally, industrial equipment applying radiometric techniques to control copper pyrometallurgical processes has been developed, the Optical Process Controller (OPC) monitoring system manufactured by Scandinavian Emissions Technology (Semtech) company. They discovered that lead species such as PbS and PbO can be used as tracers to follow the conversion process state [18,19].

In this work, classification and exploratory analysis algorithms are applied to characterize high-grade sulfide minerals by means of their VIS-NIR spectral radiation emitted from controlled combustion experiments. Spectral information is measured in absolute radiometric amplitudes with a previously-calibrated spectrometer and algorithms such as PCA, SIMCA, PLS-DA (Partial Least Squares-Discriminant Analysis), k-Nearest Neighbors (k-NN), and SVM are applied to visualize the spectral information behavior and to develop predictive classification models, so a short overview about these methods is introduced in the next section. Classification model performance and comparisons are evaluated during the training and validation process with cross-validation techniques, accuracy, and error metrics.

The work is organized as follows: in Section 2, a description of the combustion setup and an overview about the sensing techniques, preprocessing, and classification algorithms are given; in Section 3, the results are discussed, and in Section 4, some conclusions and future work are outlined.

2. Materials and Methods

In Figure 1, the experimental setup is depicted. This experimental setup was installed in the Metallurgical Engineering Department at the Universidad of Concepción, Concepción, Chile. The system mainly consisted of: (i) gas and solid feeding systems; (ii) a reaction zone heated by an electrical furnace; and (iii) an optical sensing system.

The solid feeding system consisted of a LAMBDA DOSER^® (Lambda CZ s.r.o., Brno, Czech Republic) of 0.2 L, with a feeding rate controller. Solids were fed by means of a water-cooled lance manufactured of stainless-steel; this system also refrigerates the optical fiber installed through the center to measure the radiation emitted in the zenithal position of the incandescent cloud of particles during combustion. The reaction zone was made with a stainless-steel tube of a 0.12-m inner diameter with a thickness of 3 mm, vertically positioned and heated on the surface by a controlled electrical furnace able to reach 1473 K. The furnace temperature was monitored by means of a K-type thermocouple. The process gas entering the reaction zone was a mixture of oxygen and nitrogen, and flows were controlled with mass flow controllers.

In Figure 2, the general data acquisition and preprocessing pipeline is depicted. Particles during combustion emitted radiation from the reaction zone, and the radiation was guided to a spectrometer by a cooled optical fiber probe (Avantes Inc., Louisville, CO, USA) specially designed for high-temperature environments. In this work, the VIS-NIR spectrometer USB4000 (Ocean Optis Inc., Dunedin, FL, USA) was used to acquire the spectral data in the range from 400–900 nm with an average spectral resolution of ~0.22 nm; also, the spectrometer was calibrated to measure the emitted radiation in absolute irradiance units (µW/(cm²∙nm)). The monitoring, acquisition, and spectrometer configuration stages were controlled with software developed in LabView™ (National Instruments Corporation, Austin, TX, USA ). Moreover, from a spectral point of view, it was assumed that the main spectral features were emitted by particles in ignition and that hot gasses inside the reaction zone, e.g., SO₂, N₂, and O₂, were optically transparent in the analyzed spectral range.

In order to manipulate the spectral data, the applied algorithms assumed the data as a matrix X_MxN with columns representing the variables or sampling wavelengths, λ_i, I = 1, …, N, with each row representing a spectrum, I_j, j = 1, …, M, measured at some instant, as depicted in Figure 2. In this work, the number of acquired spectra for each experiment was related to material availability, and a total of N = 2576 discrete wavelengths in the 400–900 nm range were analyzed.

After the data were acquired, further preprocessing could be necessary to compensate for external perturbations such as particles size distribution and unstable feeding rates. Such methodologies are described next.

Signal processing and algorithm implementations were conducted in MATLAB^® (The MathWorks, Inc., Natick, MA, USA) [20], with the PLS Toolbox 5.2 (Eigenvector Research, Inc., Manson, WA, USA) [21] and the Classification Learner App from the Machine Learning Toolbox^TM (MATLAB^®).

2.1. VIS-NIR Spectral Signal Preprocessing

Spectral radiation emitted by objects at a high temperature are described by a continuous radiation spectral feature, I_bb(λ,T), that follows a black body emission as a function of wavelength and object temperature. This radiation can be modeled by Planck’s radiation law [16]. Since real bodies are not ideal emitters, an emissivity function, ε, that measures thermal energy emission efficiency was added to the model; thus, I_c(λ,T) = ε·I_bb(λ,T). This emissivity function can be wavelength independent (gray bodies) or wavelength dependent (real bodies). Moreover, in combustion processes, line, I_d, and molecular, I_m, emissions can be produced; thus, a measured spectrum can be modeled as I(λ,T) = ε·I_bb(λ,T) + I_d(λ) + I_m(λ) + n, with n being a normally-distributed noise component.

As mentioned earlier, the acquired spectra require some preprocessing due to experimental issues, which produce high variance among spectral intensities at different acquisition times. In spectroscopy, some of the techniques suitable for external perturbation corrections are mainly divided into two groups: (i) transformation methods over spectral samples like MSC (Multiplicative Scatter Correction) and SNV (Standard Normal Variate) normalization methods, an; (ii) signal smoothing coupled with derivative procedures such as the Savitzky–Golay (SG) algorithm. An exhaustive description of the aforementioned methods can be found in [22]. It has been shown in works by some authors that applying preprocessing algorithms improves the performance in regression or classification models developed from the data [23].

2.2. Principal Component Analysis

After the preprocessing stage, an exploratory analysis was performed. For this purpose, PCA [24] was implemented with MATLAB^® and the PLS Toolbox. The goal of this method was to approximate the data matrix X_MxN by the product of two matrices:

X = T·L^T

(1)

where T is the score matrix with M rows and d columns equal to the number of Principal Components (PCs), and the L matrix is the loading matrix with d columns and N rows. This analysis allows reducing the dimensionality of the original data to visualize their behavior easily in a reduced space; it also allows assessing the most important variables that contribute to the variance in the original dataset. This exploratory method is also the base for classification algorithms such as the SIMCA and PLS-DA methods.

2.3. Classification Methods

In this work, the k-NN, SIMCA, PLSDA, and SVM classification methods were implemented. To implement such methods, a spectral training set was needed, with each spectrum representing a known class or category, e.g., 0 and 1 for chalcopyrite and pyrite, respectively, then, by having this set or by developing the classification model, predictions on new spectral samples can be performed. Figure 3 summarizes a general implementation of the classification algorithms to conduct predictions for new data.

The k-NN method classifies an unknown spectrum by taking a distance measure (Euclidean or Mahalanobis distance) to its nearest neighbors, of known categories. Therefore, an unknown sample is classified according to the classes of its closest neighbors [25]. The SIMCA method [26] calculates a PCA model on each spectral training dataset belonging to a known class. Then, it defines boundaries around the reduced sample space for each class with a given probability, commonly of 95%, which allows classes to overlap and, thus, a sample to belong to one or more categories with a defined probability.

The PLS-DA method is an adaptation of the Partial Least Squares regression method (PLS). In this method, the target class or dependent variables are required; thus, a matrix Y is generated containing the encoded classes as 0 and 1. PLS-DA reduces the dimensionality of measured variables, but in this case, through partial least squares. Once the new Latent Variables (LVs) are calculated, the discriminant analysis is carried out, and the boundaries between the classes are established. The classification of new samples in the discriminant analysis is based on their probability to belong to one or another class: the class with higher probability is assigned to the sample [27]. Finally, the SVM method constructs linear decision surfaces over the original input vectors (samples) or mapped vectors into a high-dimension feature space through the implementation of kernel functions; in this work, two different types of kernel functions were investigated: linear and Gaussian (RBF) [28].

For the accuracy of the trained model, confusion matrices (also known as misclassification matrices) are presented [24]. These tables summarize the classification performance by depicting the number of: False Positive estimations (FP); False Negative estimations (FN); True Positive estimations (TP) and True Negative estimations (TN). This allows a more detailed analysis than the mere proportion of correct classifications (accuracy). Then, Matthews’s correlation coefficient (MCC) is also estimated; this metric can be estimated from the confusion matrix as:

$$\mathrm{MCC} =\frac{\mathrm{TP} \times \mathrm{TN} - \mathrm{FP}\times \mathrm{FN}}{\sqrt{\left(\mathrm{TP} + \mathrm{FP}\right)\left( \mathrm{TP} + \mathrm{FN} \right)\left( \mathrm{TN} + \mathrm{FP} \right)( \mathrm{TN} + \mathrm{FN} )}}$$

(2)

For the defined metric, Equation (2), MCC takes values between –1 and +1: MCC = +1 represents a perfect prediction; MCC = −1 indicates a total disagreement between the predicted and observed classes, and value of MCC = 0 represents a prediction no better than a random prediction. Note that this metric can be only used in binary classification problems, in our case, we were only predicting the presence of chalcopyrite or pyrite, since they are the main mineralogical species present in the copper concentrates analyzed in this work.

2.4. Raw Materials and Experimental Design

Raw materials used in this work consisted of high-grade sulfide minerals mainly present in copper concentrates.

Table 1. List of sample minerals.

Minerals	Abbreviations	Formula	p80
Chalcopyrite	Cpy	CuFeS2	37 µm
Pyrite	Py	FeS2	35 µm
Bornite	Bn	Cu5FeS4	32 µm
Covelline	Cv	CuS	32 µm
Chalcocite	Cs	Cu2S	37 µm
Pyrrhotite	Po	FeS	35 µm
Enargite	Enr	Cu3AsS4	42 µm

depicts these species together with their p80 size parameter, chemical formula, and abbreviations. Some of them were acquired from Ward’s Natural Science and Northern Geological Suppliers, others by means of local suppliers.

Minerals were prepared with standard laboratory procedures to achieve dry and similar size distributions. The mineralogy and size distribution of the samples were determined by means of X-Ray Diffraction (XRD) and laser diffraction, respectively.

Table 2. Qualitative results by X-ray diffraction.

Sample	Mineralogical Composition
	Cpy	Py	Bn	Cs	Cv	Po	Enr
Chalcopyrite	***	Tr	-	*	-	-	-
Pyrite	-	***	-	-	-	-	-
Bornite	*	-	***	-	-	-	-
Chalcocite	*	-	-	***	-	-	-
Covelline	Tr	-	-	*	***	-	-
Pyrrhotite	-	*	-	-	-	***	-
Enargite	Tr?	Tr	-	-	-	-	***

*** = most abundant phase, ** = abundant phase, * = minority phase, - = no presence, Tr = trace phase, ? = uncertainty phase.

shows the qualitative analysis produced by the XRD method.

Two different copper concentrates were also used as raw material, and their mineralogical composition is shown in

Table 3. Mineralogical composition of copper concentrate measured with a QEMSCAN^®.

Mineral (%)	Concentrate A	Concentrate B
Chalcopyrite	32.7	66.7
Pyrite	45.5	16.5
Bornite	3.2	2.1
Covelline	0.8	0.1
Quartz	0.9	1.7
Muscovite	1.3	2.0
Others	15.6	10.9

.

The experimental design considered the combustion of mineral samples under fixed operating conditions for all experiments, and such conditions were assessed as optimal from exploratory experiments to ensure high signal to noise ratios, while the values were: a furnace operating temperature of 1273 K and an 80%v O₂, 20%v N₂ process gas. Nitrogen and oxygen flows were adjusted accordingly to ensure laminar flow conditions inside the drop-tube. For each experiment, 0.03 kg of sample were fed to the drop-tube.

Finally, combustion products were collected by means of a receptacle located at the bottom of the drop-tube; the receptacle was water cooled to stop as fast as possible the chemical transformations in order to have representative samples from the high-temperature oxidation process., and the products were treated to conduct further analysis by QEMSCAN^® (Quantitative Evaluation of Minerals by SCANning electron microscopy, FEI Company, Hillsboro - Oregon, USA) technology.

3. Results and Discussion

In Figure 4, average measurements of calibrated spectra from each species are depicted, and differences among spectral intensities along the sensed spectral range are observed, with pyrite emission producing the highest intensity pattern. Moreover, the pyrite spectrum shows a pronounced peak at 588 nm and a doublet at 765.8–769.3 nm, and the same peaks appear in the pyrrhotite, but with less intensity. These signals were associated with sodium and potassium emissions, respectively, in previous works [16]. On the other hand, the chalcopyrite spectrum shows slightly perceptible peaks, while the other mineral species show only continuum spectral patterns.

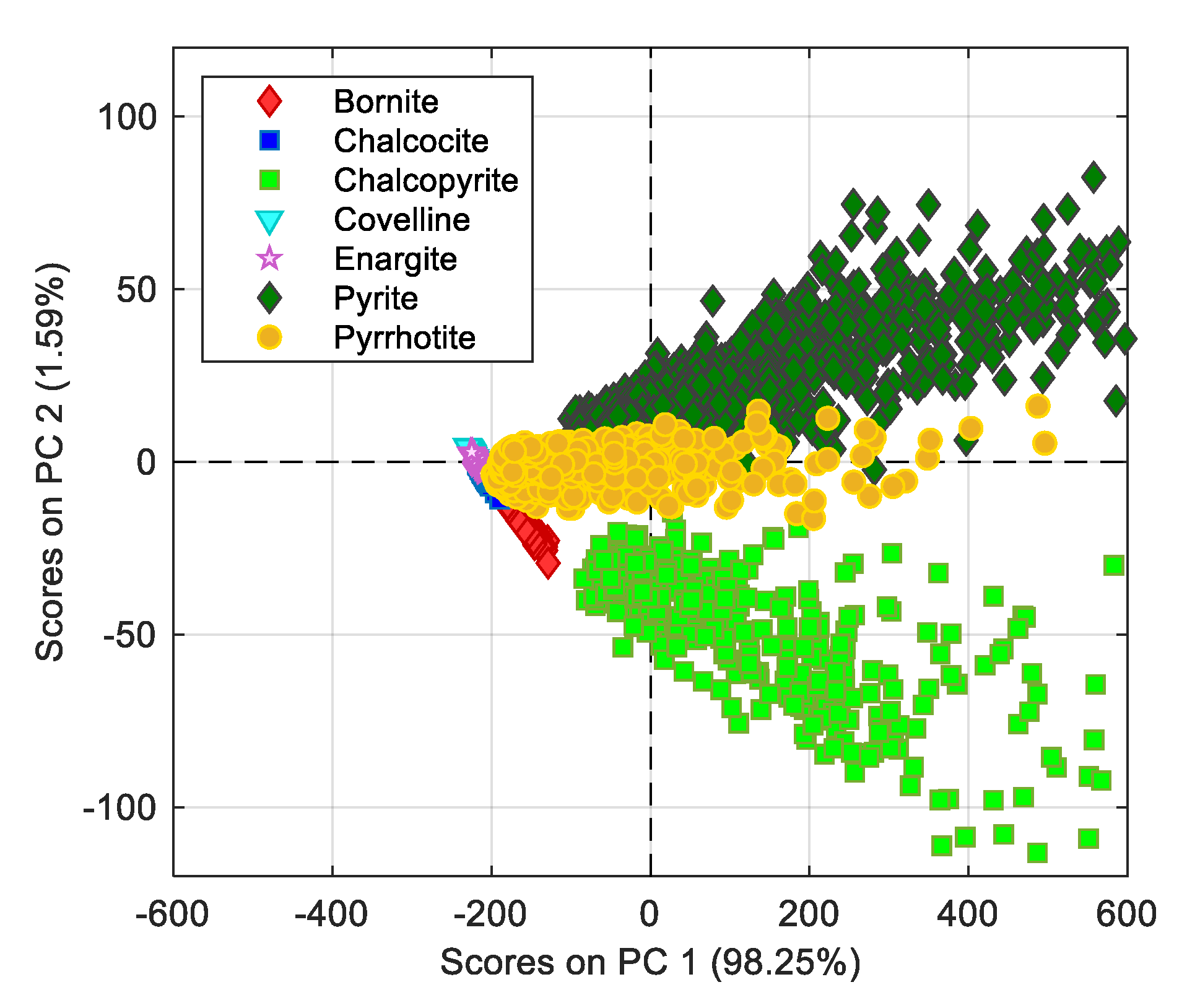
In order to compare the emission spectra from the different mineral species, a single measurement matrix was constructed containing all the data, following the structure described in Figure 2. Because the size of the measurement matrix was very large, the application of principal component analysis (PCA) was chosen as an alternative to visualize the patterns of possible mineral species. Results from PCA application are depicted in the scatterplot of Figure 5. The score analysis shows four very marked groups, two related to chalcopyrite and pyrite emissions, one produced by pyrrhotite scores, slightly overlapping on the pyrite spectra, and one group with the other species, which indicates a high correlation among their spectral emission patterns.

The pyrrhotite scores’ behavior can be explained by the fact that at temperatures above 873 K, the oxidation of chalcopyrite and pyrite occurs mainly through the decomposition of sulfur to produce FeS according to the reactions:

$${\mathrm{CuFeS}}_{2\left(\mathrm{s}\right)}+1/2{\mathrm{O}}_{2\left(\mathrm{g}\right)}\to 1/2{\mathrm{Cu}}_2{\mathrm{S}}_{\left(\mathrm{s}\right)}+{\mathrm{FeS}}_{\left(\mathrm{s}\right)}+1/2{\mathrm{SO}}_{2\left(\mathrm{g}\right)}$$

(3)

$${\mathrm{FeS}}_{2\left(\mathrm{s}\right)}+{\mathrm{O}}_{2\left(\mathrm{g}\right)}\to {\mathrm{FeS}}_{\left(\mathrm{s}\right)}+{\mathrm{SO}}_{2\left(\mathrm{g}\right)}$$

(4)

The spectra from the combustion of the sulfides presented in the previous equations can be confused with the spectra of the sulfide mineral species. As mentioned earlier, the overlapping among the score groups produced by bornite, chalcocite, covelline, and enargite [29,30,31] emissions can be justified by the fact that the product of their thermal decomposition is Cu₂S (reactions thermodynamically favorable under the temperature attained by the combustion flames in each experiment), as shown in the following reactions:

$${\mathrm{Cu}}_5{\mathrm{FeS}}_4\to 5/2{\mathrm{Cu}}_2\mathrm{S}+\mathrm{FeS}+1/4{\mathrm{S}}_{2\left(\mathrm{g}\right)},$$

(5)

$${\mathrm{Cu}}_3{\mathrm{AsS}}_4\to 3/2{\mathrm{Cu}}_2\mathrm{S}+1/2{\mathrm{As}}_2{\mathrm{S}}_3+1/2{\mathrm{S}}_{2\left(\mathrm{g}\right)},$$

(6)

$$\mathrm{CuS}\to 1/2{\mathrm{Cu}}_2\mathrm{S}+1/4{\mathrm{S}}_{2\left(\mathrm{g}\right)},$$

(7)

Moreover, the results of PCA applied on copper sulfide spectra had a very marked separation with the chalcopyrite scores; in this case, this separation was given by the PC1, with most of chalcopyrite scores located on the negative side of PC2.

In

Table 4. Mineralogical composition of sulfide combustion products determined by QEMSCAN^®.

Products (%)	Py	Po	Cpy	Enr	Bn	Cv	Cs
Delafossite	0.04	0.02	33.70	0.70	0.62	0.24	0.36
FeOx	82.25	94.33	22.90	1.24	3.34	0.51	0.55
Chalcocite	0.00	0.00	2.52	52.01	19.38	77.38	83.27
Cuprite	0.00	0.00	1.43	28.92	18.44	16.63	15.68
Bornite	0.03	0.00	7.80	0.18	44.53	0.33	0.02
Enargite	0.00	0.00	0.00	15.41	0.25	0.00	0.00
Covellite	0.00	0.00	0.01	0.10	8.84	3.13	0.05
Other	17.68	5.65	31.64	1.44	4.60	1.78	0.07

, the mineralogical composition of the combustion products is summarized. It can be seen that products from enargite and covelline combustion have a high content of the Cu₂S phase (chalcocite). On the other hand, bornite and chalcocite partially reacted, and they also depicted low intensity profiles, so their radiation was prone to be overshadowed by the radiation emitted by the furnace walls.

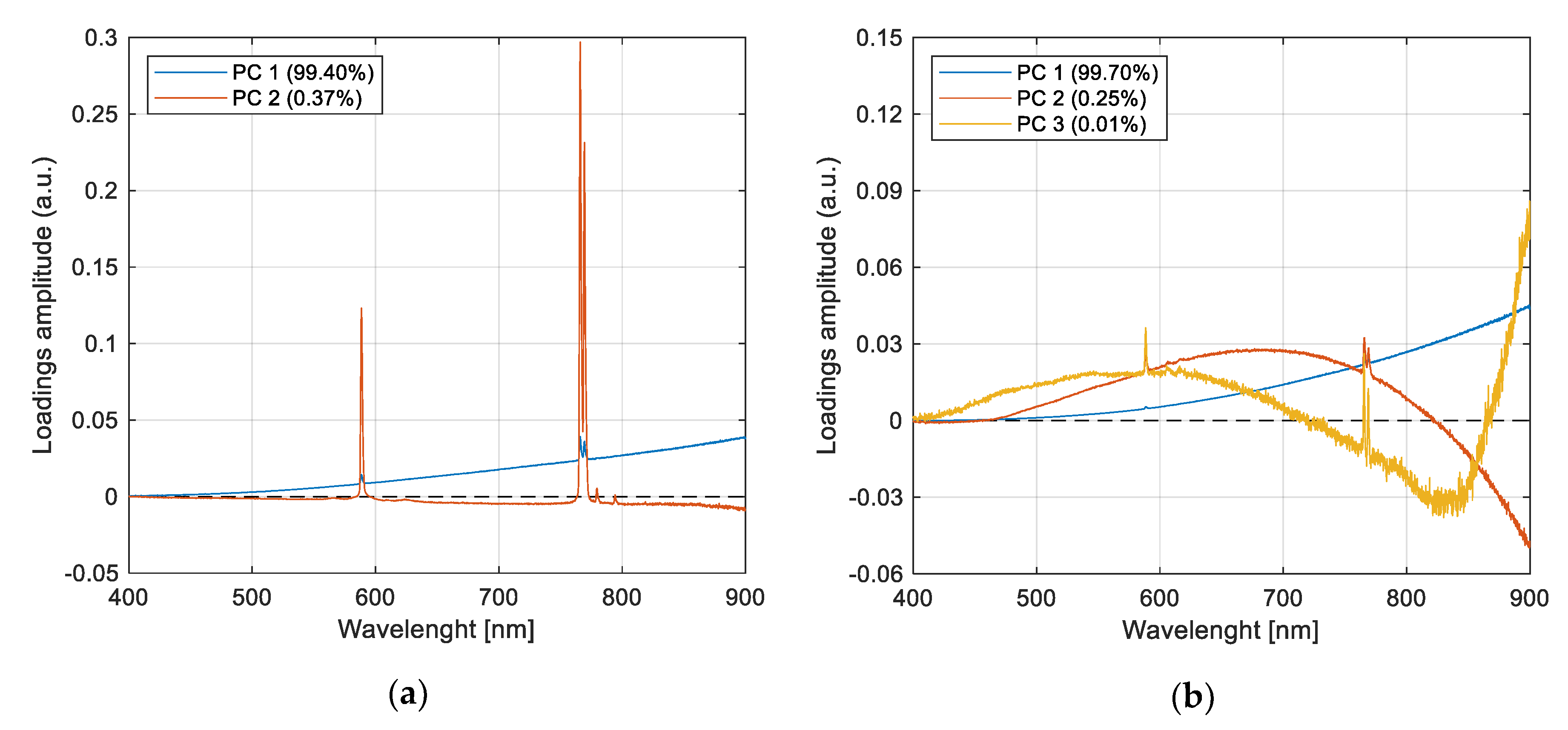
In Figure 6a, the plot of PCs loadings depicts the variables’ (wavelengths) behavior for pyrite and chalcopyrite combustion spectra. The peaks mentioned above and less intense peaks at 779.1 and 793.9 nm are observed. These peaks have been previously reported and may be associated with iron species [16]. These peaks are also observed in the loadings obtained with PCA using only pyrite spectra. For chalcopyrite spectra, loadings depict peaks at 606 and 616 nm (Figure 6b), and they are associated with the presence of copper oxides [32]. Note that loading vectors only give an idea of the wavelengths’ contribution to spectral data variance and that in any case, their amplitude can be interpreted as a relative concentration in the original spectra; however, they can be seen as a first approach to elucidate the structure of spectral patterns hidden in the data because of their weak emissions. Loading analysis for other species presented no relevant spectral patterns, so they are not shown in this work.

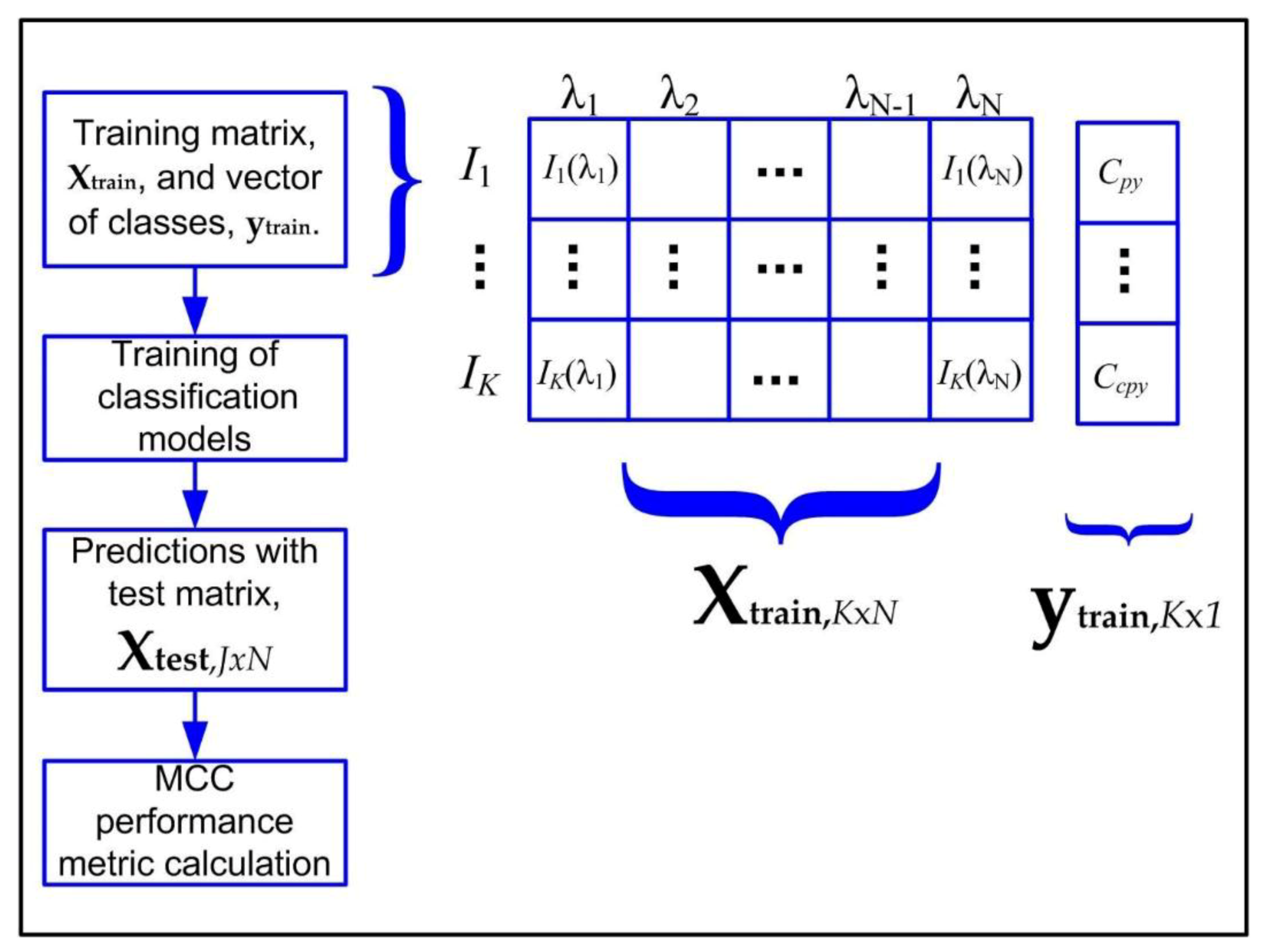
Due to the promising results obtained with PCA, supervised classification methods such as k-NN, PLS-DA, SIMCA, and SVM were applied. In this section, only chalcopyrite and pyrite emissions are considered for analysis. To accomplish this, a training matrix was constructed from the emission spectra that presented the best differentiation between mineral species, as depicted in Figure 3. Under this assumption, 750 chalcopyrite and 750 pyrite spectra were chosen randomly. Finally, trained classification models were evaluated on 500 spectra from chalcopyrite and pyrite combustion, spectra from Copper Concentrate A and Copper Concentrate B combustion, and finally, spectra from mixtures of pyrite/chalcopyrite in proportions of 30% Cpy-70% Py and 70% Cpy-30% Py combustion.

From the set of applied preprocessing methods, the mean centering approach was chosen since it presented a good justification of the accumulated variance from exploratory PCA analysis with a good segregation of sample scores and low values of the root mean squared error of cross-validation for the different methods’ implementation. In this work, a 10-fold cross-validation method was implemented to estimate the optimum parameters of the trained models.

Table 5. Calibration of the models depicting optimum parameters and performances evaluated with a 10-fold cross-validation procedure.

Model	Optimum Parameters	MCC
k-NN	2 neighbors	1
SIMCA	2 PCs for each species	0.983
PLS-DA	7 LVs	1
SVM	Fine Gaussian kernel	1

summarizes the optimum assessed parameters for each implemented method.

Table 6. Prediction of chalcopyrite, pyrite, concentrates, and sulfide mixture by the trained models.

Model		Model Prediction
		Cpy	Py	ConA	ConB	Py 70%-Cpy 30%	Py 30%-Cpy 70%
k-NN	MCC	0.886		-		-
	Cpy	227	6	250	250	250	240
	Py	23	244	0	0	0	10
SIMCA	MCC	0.721		-		-
	Cpy	240	64	0	241	207	84
	Py	40	186	250	9	43	166
PLS-DA	MCC	0.900		-		-
	Cpy	236	11	2	244	235	160
	Py	14	239	248	6	15	90
SVM	MCC	0.953		-		-
	Cpy	250	12	6	250	249	235
	Py	0	238	244	0	1	15

summarizes the results of predictions over the test matrices by using the optimal models, the values of the MCC metric, and confusion matrices. It can be seen that during the predictions, the k-NN model was not considered appropriate for the detection of pyrite combustion spectra, because it had a low specificity (a large number of false positive samples); the same issue is observed with SIMCA, with higher rates of false positives for both species; the PLS-DA and SVM methods show the best classification results for the sulfide mineral species’ predictions. In the case of predicting the class of copper concentrates, Concentrate A was mainly classified with a higher presence of pyrite, and the opposite can be observed for Concentrate B, which was accurate by considering their mineralogical composition; see Table 3. The same results can be observed from the binary mixture combustion, and the algorithms predicted the high presence of pyrite or chalcopyrite species, accordingly.

4. Conclusions

From the results, it can be concluded that depending on the degree of reaction of sulfide species, the spectra emitted can show patterns that allowed them to be differentiated, such as the pyrite and pyrrhotite spectra in which emission peaks can be observed at 588, 765.8, and 769.3 nm, while species like chalcopyrite required a multivariate analysis to uncover these peaks. In this case, by applying PCA to the spectral datasets, peaks related to copper phases (606 and 616 nm) and others related to the oxidation of iron sulfides (779.1 and 793.9 nm) were found. These results allowed evaluating the efficiency of the classification models by means of methods such as k-NN, SIMCA, PLS-DA, and SVM. With all these methods, a good degree of prediction was observed against pyrite and chalcopyrite spectra, while applying these methods to the spectra of copper concentrates’ combustion or binary mixtures, the results were accurate in the sense that a higher presence of the two analyzed species was predicted. Finally, the classification results with an SVM approach and with a Gaussian mapping function of the original spectra generated the best classification results with 95.3% accuracy. In future work, we will extend this analysis to perform regression predictions so that an estimation of the proportion of sulfide mineral species during combustion in real scenarios can be performed.