Spin Crossover in Three Mononuclear Iron (III) Schiff Base Complexes
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis
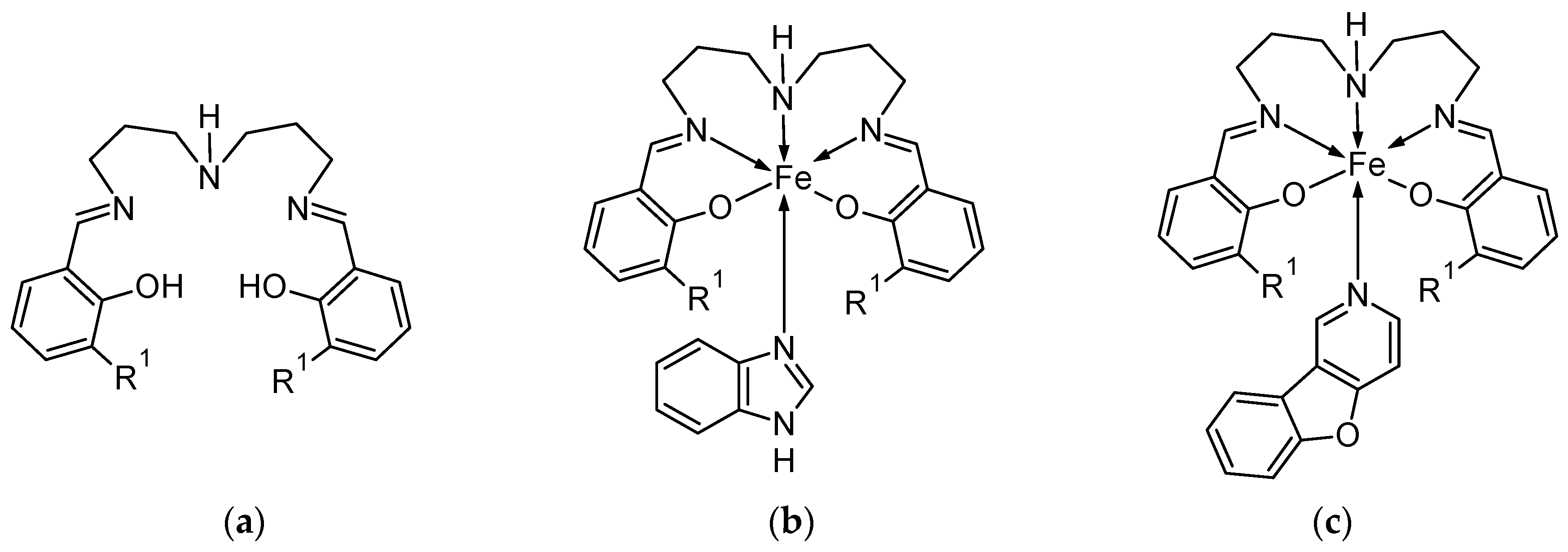
2.1.1. Ligands
2.1.2. Mononuclear Precursors
2.1.3. Mononuclear Complexes 1a, 2a, and 2b
2.1.4. Elemental Analysis
2.2. Theoretical Calculations
3. Results and Discussion
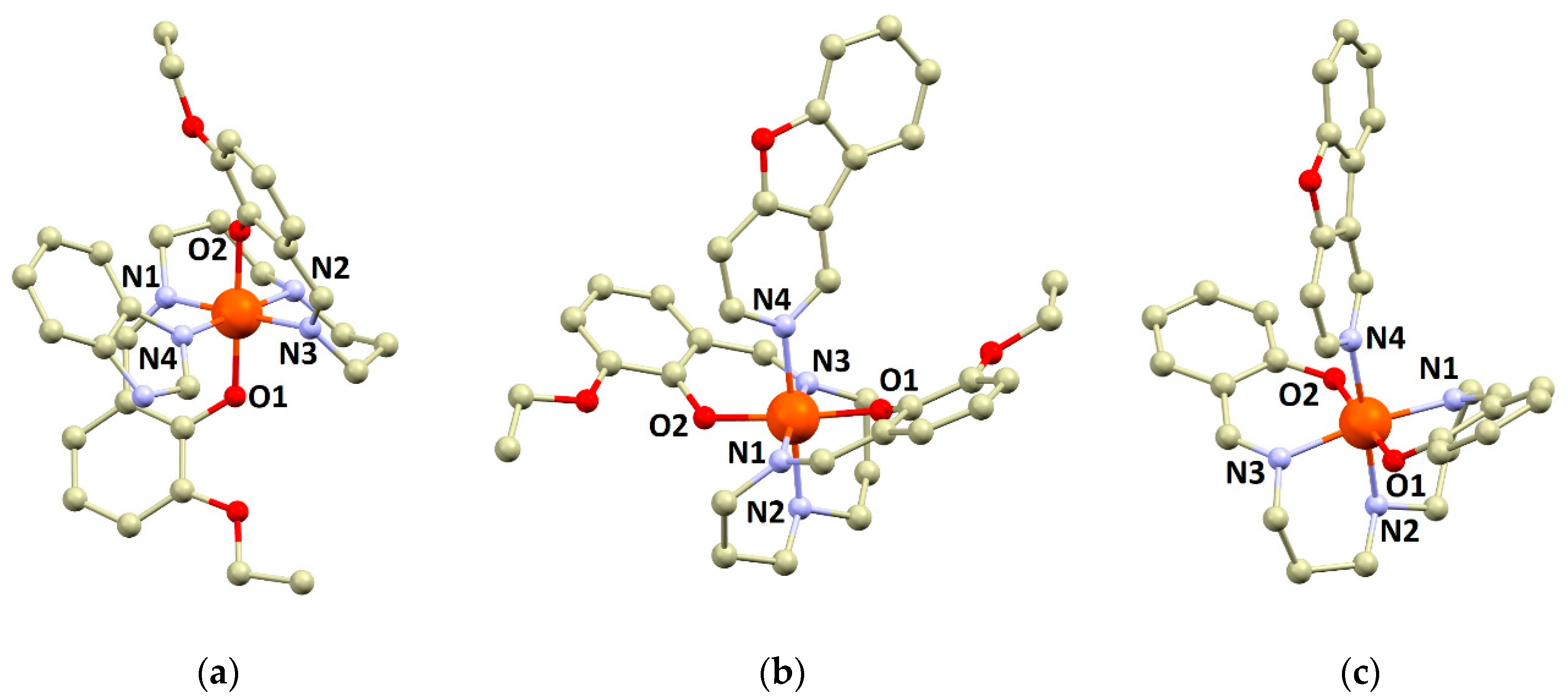
3.1. Crystal Structures
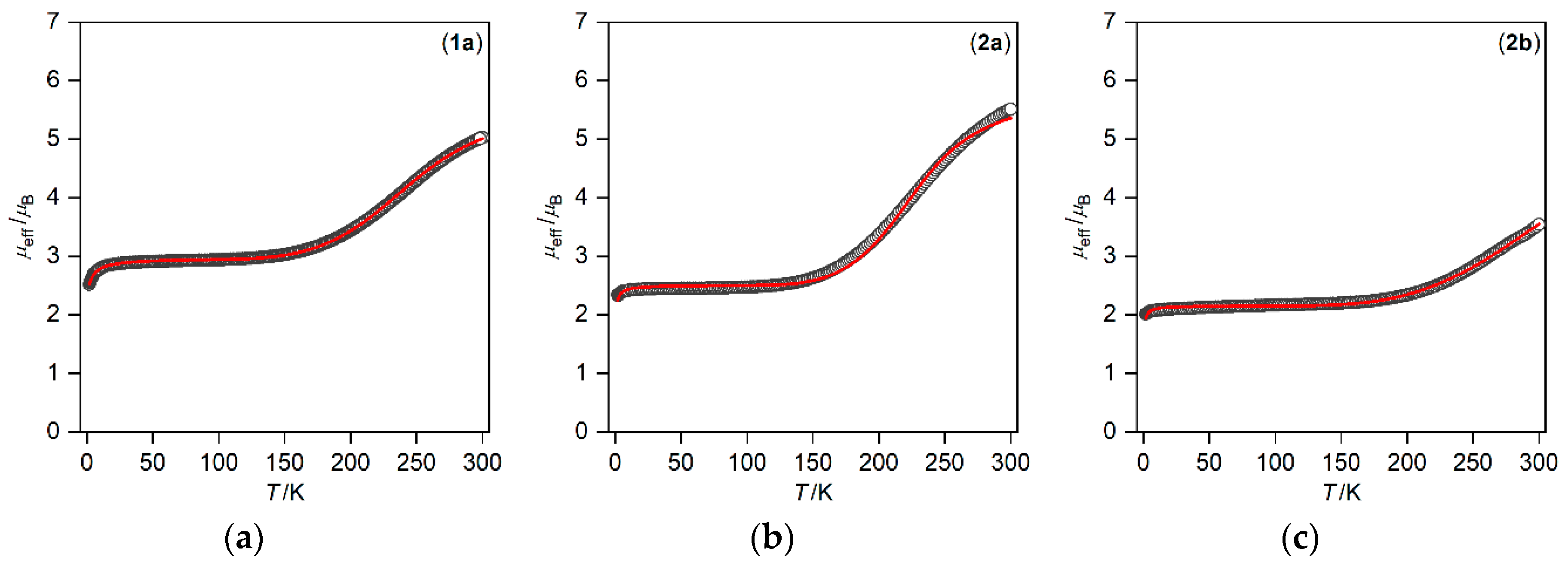
3.2. Magnetic Properties
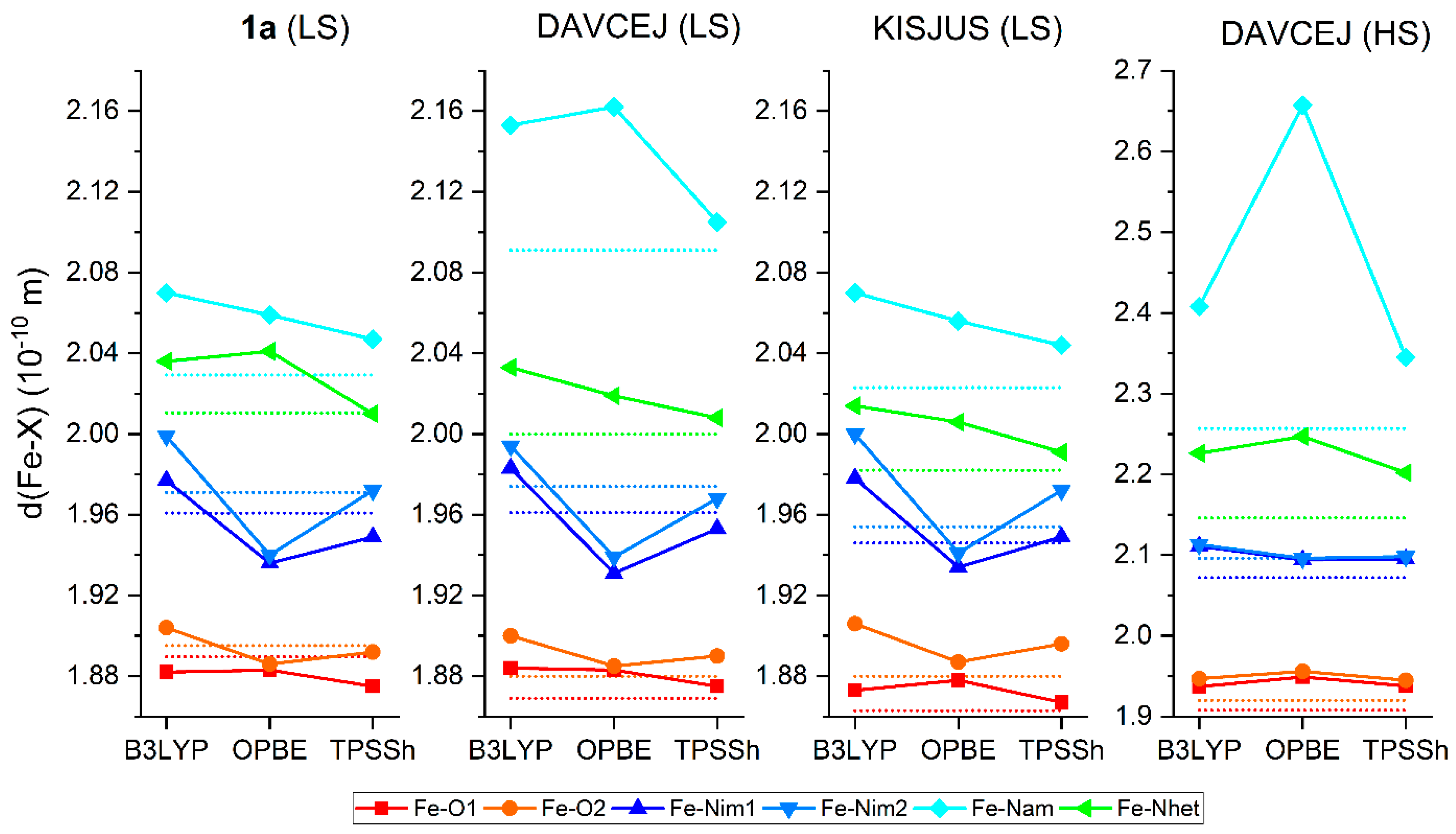
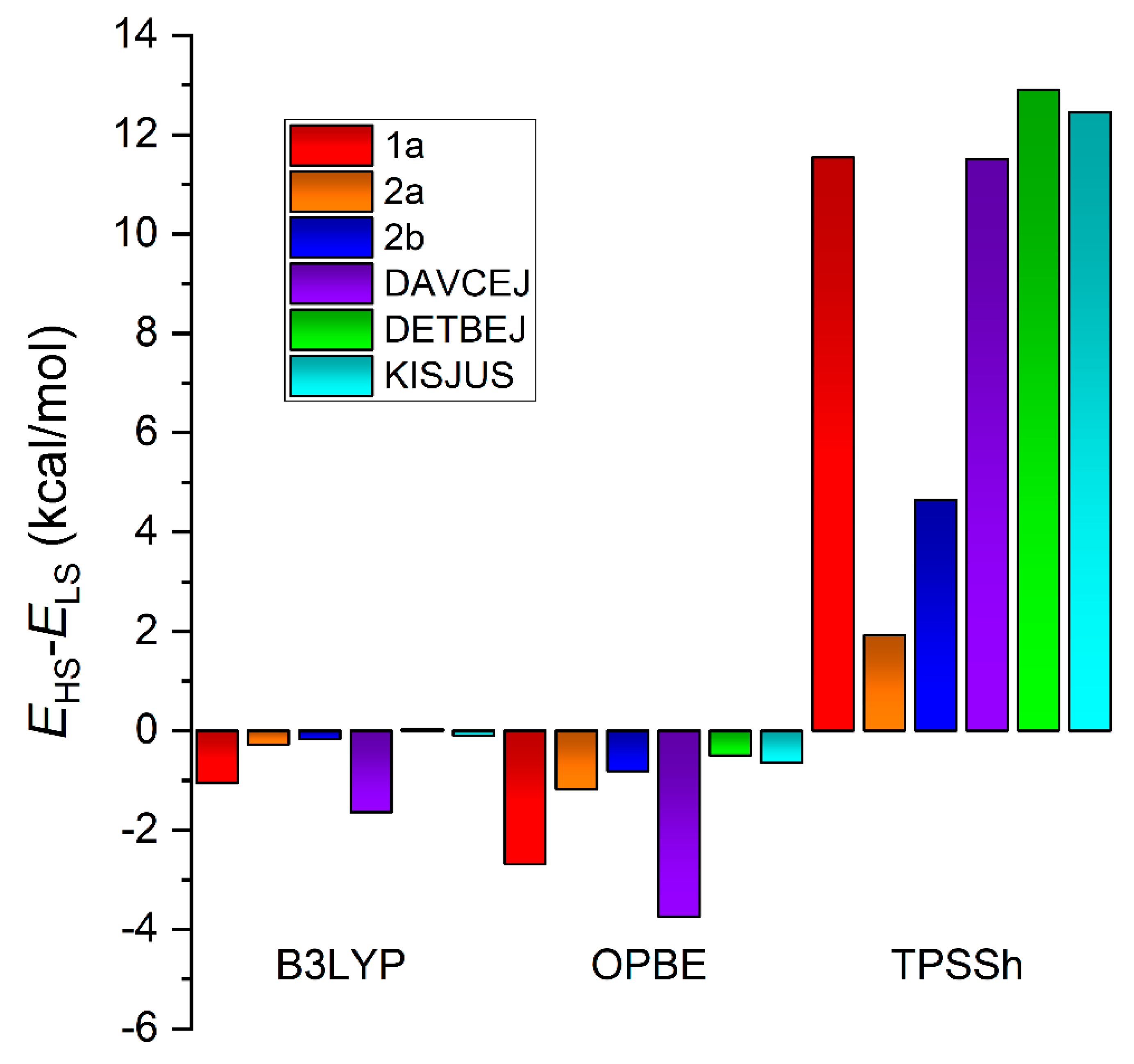
3.3. Theoretical Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Van Koningsbruggen, P.J.; Maeda, Y.; Oshio, H. Iron(III) spin crossover compounds. In Spin Crossover in Transition Metal Compounds I; Gütlich, P., Goodwin, H.A., Eds.; Springer: Berlin, Germany, 2004; pp. 259–324. [Google Scholar]
- Harding, D.J.; Harding, P.; Phonsri, W. Spin crossover in iron(III) complexes. Coord. Chem. Rev. 2016, 313, 38–61. [Google Scholar] [CrossRef]
- Nemec, I.; Boča, R.; Herchel, R.; Trávníček, Z.; Gembický, M.; Linert, W. Dinuclear Fe(III) complexes with spin crossover. Monatshefte Chem. Chem. Mon. 2009, 140, 815–828. [Google Scholar] [CrossRef]
- Herchel, R.; Boča, R.; Gembický, M.; Kožísek, J.; Renz, F. Spin Crossover in a Tetranuclear Cr(III)−Fe(III)3 Complex. Inorg. Chem. 2004, 43, 4103–4105. [Google Scholar] [CrossRef] [PubMed]
- Nemec, I.; Herchel, R.; Boča, R.; Trávníček, Z.; Svoboda, I.; Fuess, H.; Linert, W. Tuning of spin crossover behaviour in iron(III) complexes involving pentadentate Schiff bases and pseudohalides. Dalton Trans. 2011, 40, 10090–10099. [Google Scholar] [CrossRef] [PubMed]
- Nemec, I.; Herchel, R.; Trávníček, Z. The relationship between the strength of hydrogen bonding and spin crossover behaviour in a series of iron(iii) Schiff base complexes. Dalton Trans. 2015, 44, 4474–4484. [Google Scholar] [CrossRef] [PubMed]
- Pogány, L.; Brachňaková, B.; Moncol, J.; Pavlik, J.; Nemec, I.; Trávníček, Z.; Mazúr, M.; Bučinský, L.; Suchánek, L.; Šalitroš, I. Impact of substituent variation on the presence of thermal spin crossover in a series of mononuclear iron(III) schiff base complexes with terminal pseudohalido co-ligands. Chem. A Eur. J. 2018, 24, 5191–5203. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, N.; Ohta, S.; Yoshimura, C.; Ohyoshi, A.; Kohata, S.; Okawa, H.; Maeda, Y. Studies on spin-equilibrium iron(III) complexes. Part 1. Syntheses and magnetic properties of a new family of spin cross-over iron(III) complexes with a unidentate ligand over a wide range of the spectrochemical series and a quinquedentate ligand derived. J. Chem. Soc. Dalt. Trans. 1985, 12, 2575. [Google Scholar] [CrossRef]
- Boča, R.; Fukuda, Y.; Gembický, M.; Herchel, R.; Jaroščiak, R.; Linert, W.; Renz, F.; Yuzurihara, J. Spin crossover in mononuclear and binuclear iron(III) complexes with pentadentate Schiff-base ligands. Chem. Phys. Lett. 2000, 325, 411–419. [Google Scholar] [CrossRef]
- Tanimura, K.; Kitashima, R.; Bréfuel, N.; Nakamura, M.; Matsumoto, N.; Shova, S.; Tuchagues, J.-P. Infinite chain structure and steep spin crossover of a Fe III Complex with a N3O2 pentadentate schiff-base ligand and 4-aminopyridine. Bull. Chem. Soc. Jpn. 2005, 78, 1279–1282. [Google Scholar] [CrossRef]
- Faulmann, C.; Dorbes, S.; De Bonneval, B.G.; Molnár, G.; Bousseksou, A.; Gomez-Garcia, C.J.; Coronado, E.; Valade, L. Towards molecular conductors with a spin-crossover phenomenon: Crystal structures, magnetic properties and Mössbauer spectra of [Fe(salten)mepepy][M(dmit)2] complexes. Eur. J. Inorg. Chem. 2005, 3261–3270. [Google Scholar] [CrossRef]
- Bannwarth, A.; Schmidt, S.O.; Peters, G.; Sönnichsen, F.D.; Thimm, W.; Herges, R.; Tuczek, F. feiii spin-crossover complexes with photoisomerizable ligands: Experimental and theoretical studies on the ligand-driven light-induced spin change effect. Eur. J. Inorg. Chem. 2012, 2012, 2776–2783. [Google Scholar] [CrossRef]
- Bobošík, V.; Krutošíková, A.; Jordis, U. Synthesis and reactions of 2,3-dimethylfuro[3,2-c]pyridines. Monatshefte für Chemie Chem. Mon 1995, 126, 747–752. [Google Scholar] [CrossRef]
- Bencková, M.; Krutošíková, A. Synthesis of pyrrolo[2′,3′:4,5]furo[3,2-c]pyridines. Monatshefte Chem. Chem. Mon. 1995, 126, 753–758. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Handy, N.C.; Cohen, A.J. Left-right correlation energy. Mol. Phys. 2001, 99, 403–412. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Kurth, S.; Zupan, A.; Blaha, P. Accurate density functional with correct formal properties: A step beyond the generalized gradient approximation. Phys. Rev. Lett. 1999, 82, 2544–2547. [Google Scholar] [CrossRef]
- Perdew, J.P.; Tao, J.; Staroverov, V.N.; Scuseria, G.E. Meta-generalized gradient approximation: Explanation of a realistic nonempirical density functional. J. Chem. Phys. 2004, 120, 6898–6911. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
- Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, approximate and parallel Hartree-Fock and hybrid DFT calculations. A “chain-of-spheres” algorithm for the Hartree-Fock exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
- Izsák, R.; Neese, F. An overlap fitted chain of spheres exchange method. J. Chem. Phys. 2011, 135, 144105. [Google Scholar] [CrossRef] [PubMed]
- Seeger, R.; Pople, J.A. Self-consistent Molecular Orbital Methods. XVIII. Constraints and Stability in Hartree–Fock Theory. J. Chem. Phys. 1977, 66, 3045–3050. [Google Scholar] [CrossRef]
- Bauernschmitt, R.; Ahlrichs, R. Stability Analysis for Solutions of the Closed Shell Kohn–Sham Equation. J. Chem. Phys. 1996, 104, 9047–9052. [Google Scholar] [CrossRef]
- Spek, A.L. Platon Squeeze: A tool for the calculation of the disordered solvent contribution to the calculated structure factors. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 9–18. [Google Scholar] [CrossRef] [PubMed]
- Nemec, I.; Boča, R.; Gembický, M.; Dlháň, L.; Herchel, R.; Renz, F. High-spin Schiff-base dinuclear iron(III) complexes bridged by N-oxide ligands. Inorg. Chim. Acta 2009, 362, 4754–4759. [Google Scholar] [CrossRef]
- Guionneau, P.; Marchivie, M.; Bravic, G.; Letard, J.F.; Chasseau, D. Structural aspects of spin crossover. Example of the [(FeLn)-L-II(NCS)(2)] complexes. Top. Curr. Chem. 2004, 234, 97. [Google Scholar]
- Bari, R.A.; Sivardière, J. Low-spin-high-spin transitions in transition-metal-ion compounds. Phys. Rev. B 1972, 5, 4466–4471. [Google Scholar] [CrossRef]
- Wajnflasz, J. Etude de la transition “Low Spin”-„High Spin” dans les complexes octaédriques d’ion de transition. Phys. Status Solidi 1970, 40, 537–545. [Google Scholar] [CrossRef]
- Boča, R.; Linert, W. Is There a Need for New Models of the Spin Crossover? Monatshefte Chem. Chem. Mon. 2003, 134, 199–216. [Google Scholar] [CrossRef]
- Siig, O.S.; Kepp, K.P. Iron(II) and Iron(III) spin crossover: Toward an optimal density functional. J. Phys. Chem. A 2018, 122, 4208–4217. [Google Scholar] [CrossRef] [PubMed]
- Cirera, J.; Via-Nadal, M.; Ruiz, E. Benchmarking density functional methods for calculation of state energies of first row spin-crossover molecules. Inorg. Chem. 2018, 57, 14097–14105. [Google Scholar] [CrossRef] [PubMed]
- Swart, M.; Groenhof, A.R.; Ehlers, A.W.; Lammertsma, K. Validation of exchange−correlation functionals for spin states of iron complexes. J. Phys. Chem. A 2004, 108, 5479–5483. [Google Scholar] [CrossRef]
| Compound | 1a | 2a | 2b |
|---|---|---|---|
| Formula | C55H57BFeN5O4 | C59H58BFeN4O5 | C55H50BFeN4O3 |
| Formula weight | 918.71 | 969.75 | 881.65 |
| Crystal system | Triclinic | Triclinic | Monoclinic |
| Space group | P-1 | P-1 | P21/c |
| Cell parameters | |||
| a/Å | 10.1648(7) | 13.2869(4) | 19.1978(10) |
| b/Å | 15.2130(10) | 13.6926(5) | 11.7562(13) |
| c/Å | 16.2320(10) | 16.4083(6) | 21.381(2) |
| α/° | 81.990(6) | 70.732(3) | 90 |
| β/° | 72.359(6) | 78.232(3) | 110.458(8) |
| γ/° | 86.049(6) | 67.395(3) | 90 |
| V/Å3 | 2367.7(3) | 2591.29(17) | 4521.2(8) |
| Z | 2 | 2 | 4 |
| T/K | 100(2) | 190(2) | 293(2) |
| Density, Dc/g cm−3 | 1.289 | 1.243 | 1.295 |
| Abs. coefficient/mm−1 | 0.371 | 0.344 | 0.384 |
| Data/restraints/param | 8326/0/601 | 6630/3/644 | 7931/0/577 |
| R1a, wR2b (all data) | 0.0660, 0.1073 | 0.0545, 0.0867 | 0.0618, 0.0810 |
| R1a, wR2b [I > 2σ(I)] | 0.0379, 0.0978 | 0.0355, 0.0829 | 0.0340, 0.0763 |
| Goodness of fit | 1.049 | 1.028 | 0.954 |
| CSD number | 1939657 | 1939658 | 1939656 |
| Compound | gLS | ΘLS | xrHS | Δ (K) | γ (K) | reff | ΔH (J mol−1) | ΔS (J K−1 mol−1) | T1/2 (K) |
|---|---|---|---|---|---|---|---|---|---|
| 1a | 2.34 | −4.3 | 0.15 | 930 | 116 | 35.0 | 7730 | 29.6 | 262 |
| 2a | 2.01 | −1.5 | 0.10 | 1200 | 95 | 150 | 9975 | 41.7 | 239 |
| 2b | 2.01 | −0.8 | 0.05 | 1033 | 127 | 17 | 8592 | 23.6 | 365 |
| Method | Compound | Fe–O | Fe–Nim | Fe–Nam | Fe–Nhetero |
|---|---|---|---|---|---|
| X-ray analysis | 1a (LS) | 1.8896/1.8951 | 1.9608/1.971 | 2.0293 | 2.0105 |
| DAVCEJ (LS) | 1.869/1.880 | 1.961/1.974 | 2.091 | 2.000 | |
| DAVCEJ01 (HS) | 1.908/1.920 | 2.072/2.096 | 2.257 | 2.146 | |
| KISJUS (LS, 100 K) | 1.863/1.880 | 1.946/1.954 | 2.023 | 1.982 | |
| TPSSh (LS) | 1a | 1.875/1.892 | 1.949/1.972 | 2.047 | 2.010 |
| 2a | 1.872/1.880 | 1.979/1.984 | 2.054 | 2.050 | |
| 2b | 1.888/1.889 | 2.000/2.010 | 2.084 | 2.099 | |
| DAVCEJ | 1.875/1.890 | 1.953/1.968 | 2.105 | 2.008 | |
| DETBEJ | 1.872/1.899 | 1.953/1.978 | 2.044 | 2.016 | |
| KISJUS | 1.867/1.896 | 1.949/1.972 | 2.044 | 1.991 | |
| TPSSh (HS) | 1a (HS) | 1.931/1.950 | 2.104/2.113 | 2.282 | 2.201 |
| 2a (HS) | 1.934/1.936 | 2.105/2.109 | 2.281 | 2.229 | |
| 2b (HS) | 1.939/1.942 | 2.104/2.107 | 2.276 | 2.225 | |
| DAVCEJ (HS) | 1.938/1.945 | 2.095/2.098 | 2.345 | 2.202 | |
| DETBEJ (HS) | 1.938/1.939 | 2.105/2.109 | 2.276 | 2.228 | |
| KISJUS (HS) | 1.935/1.945 | 2.107/2.109 | 2.286 | 2.174 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nemec, I.; Svoboda, I.; Herchel, R. Spin Crossover in Three Mononuclear Iron (III) Schiff Base Complexes. Metals 2019, 9, 849. https://doi.org/10.3390/met9080849
Nemec I, Svoboda I, Herchel R. Spin Crossover in Three Mononuclear Iron (III) Schiff Base Complexes. Metals. 2019; 9(8):849. https://doi.org/10.3390/met9080849
Chicago/Turabian StyleNemec, Ivan, Ingrid Svoboda, and Radovan Herchel. 2019. "Spin Crossover in Three Mononuclear Iron (III) Schiff Base Complexes" Metals 9, no. 8: 849. https://doi.org/10.3390/met9080849
APA StyleNemec, I., Svoboda, I., & Herchel, R. (2019). Spin Crossover in Three Mononuclear Iron (III) Schiff Base Complexes. Metals, 9(8), 849. https://doi.org/10.3390/met9080849






