From Statistical Correlations to Stochasticity and Size Effects in Sub-Micron Crystal Plasticity
Abstract
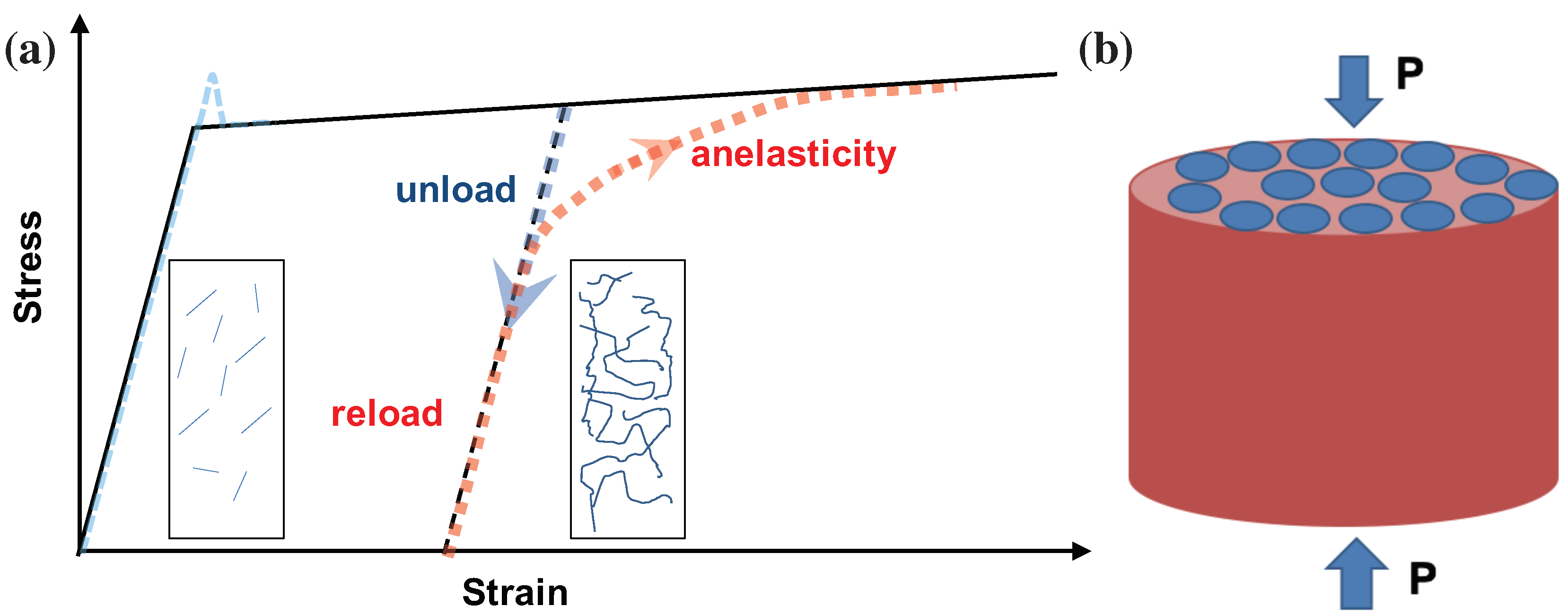
1. Introduction
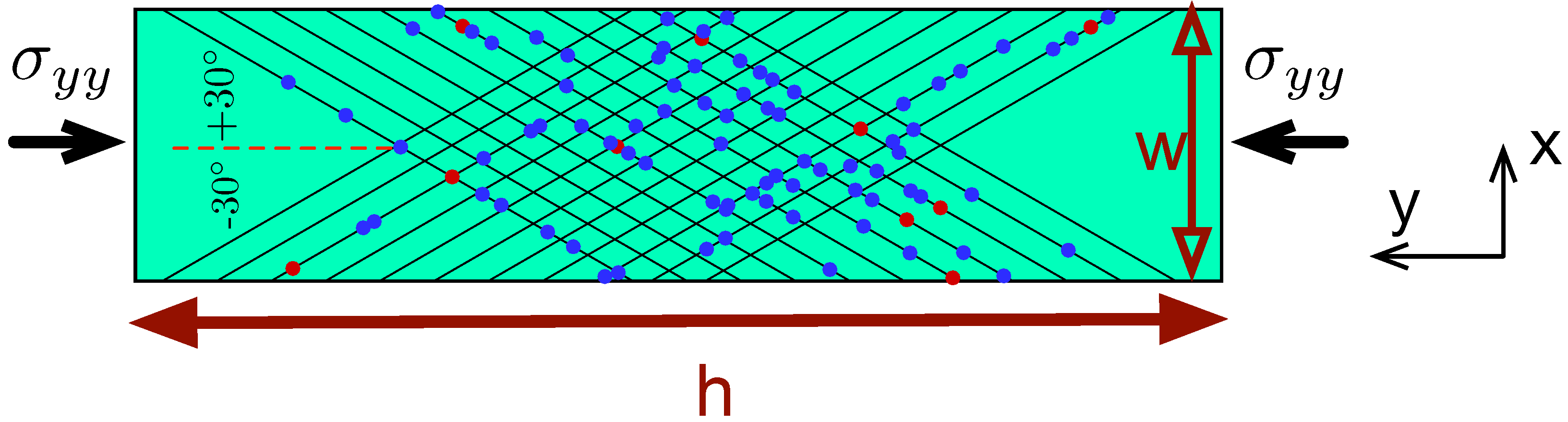
2. Model Description
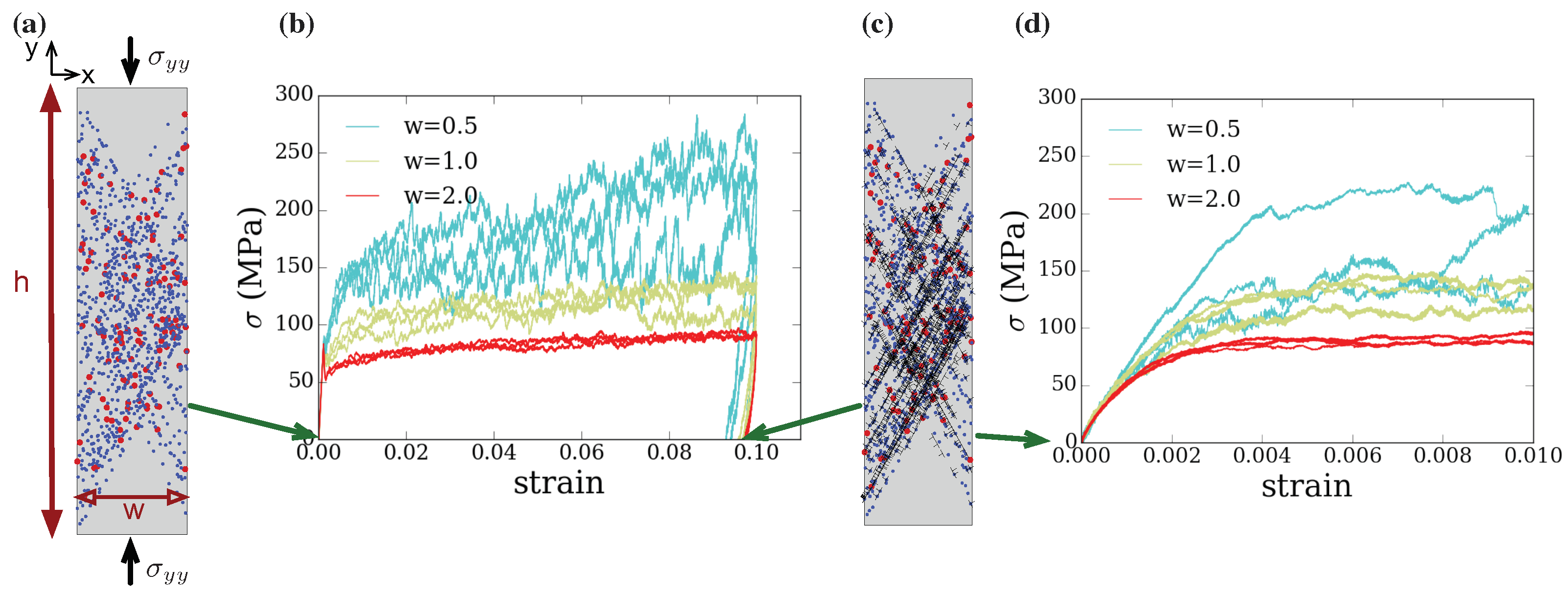
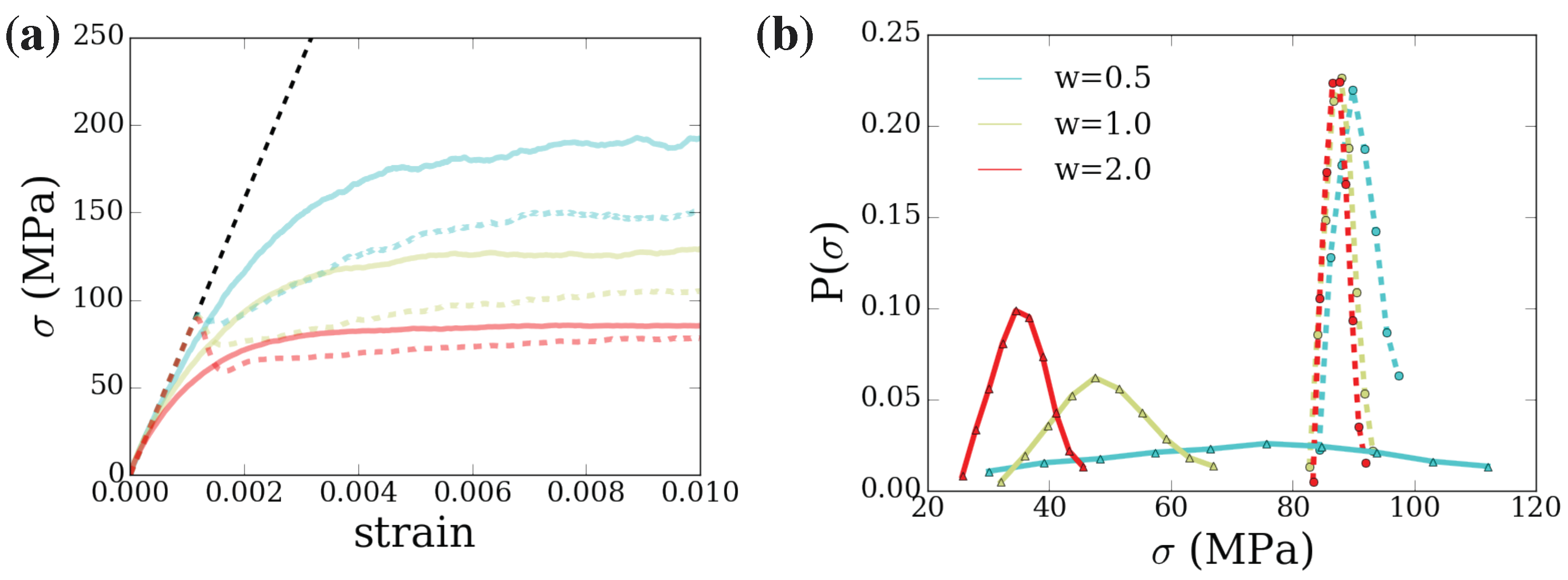
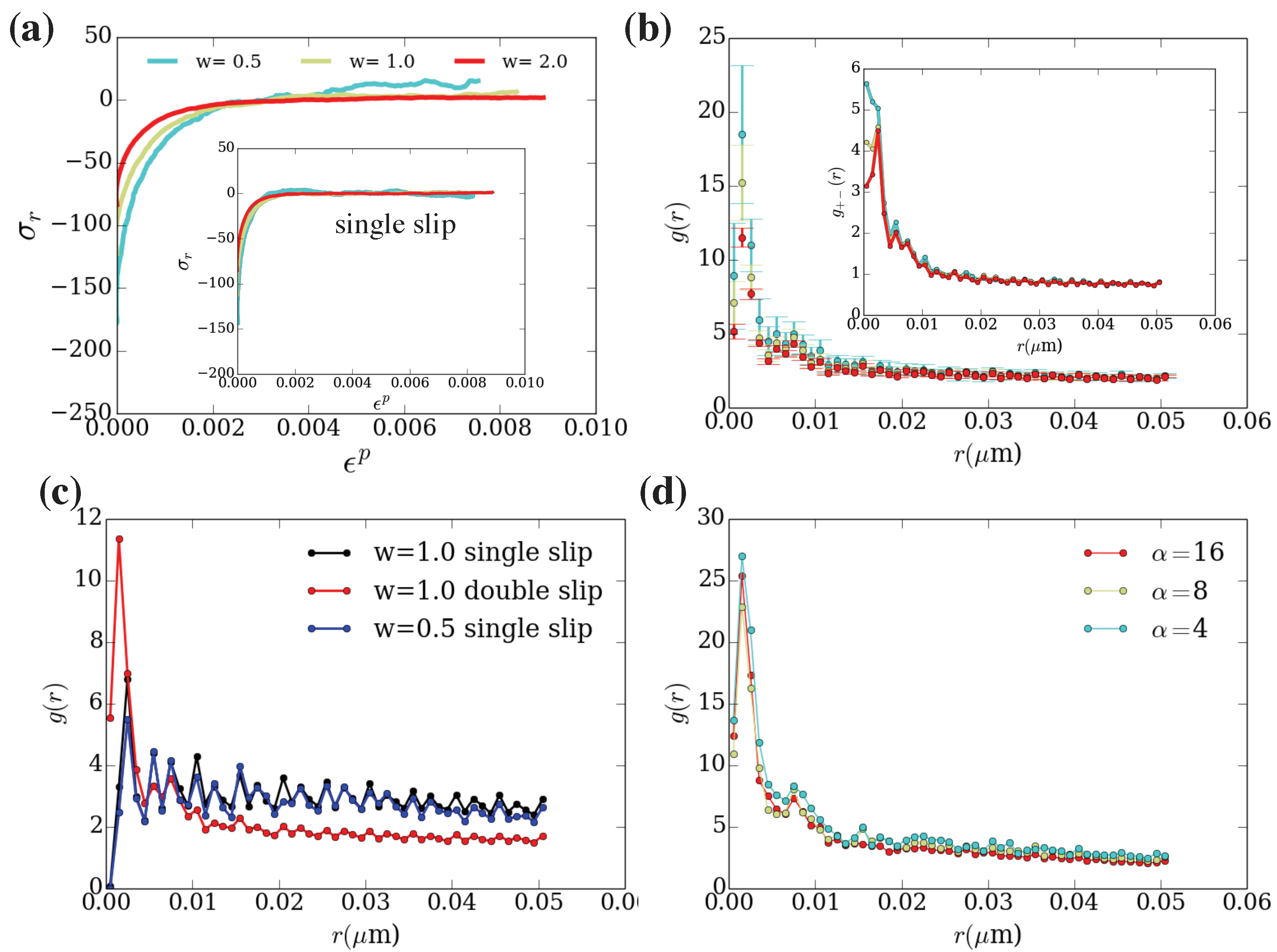
3. The Mechanical Response of Finite Small Volumes in Multi-Slip Conditions
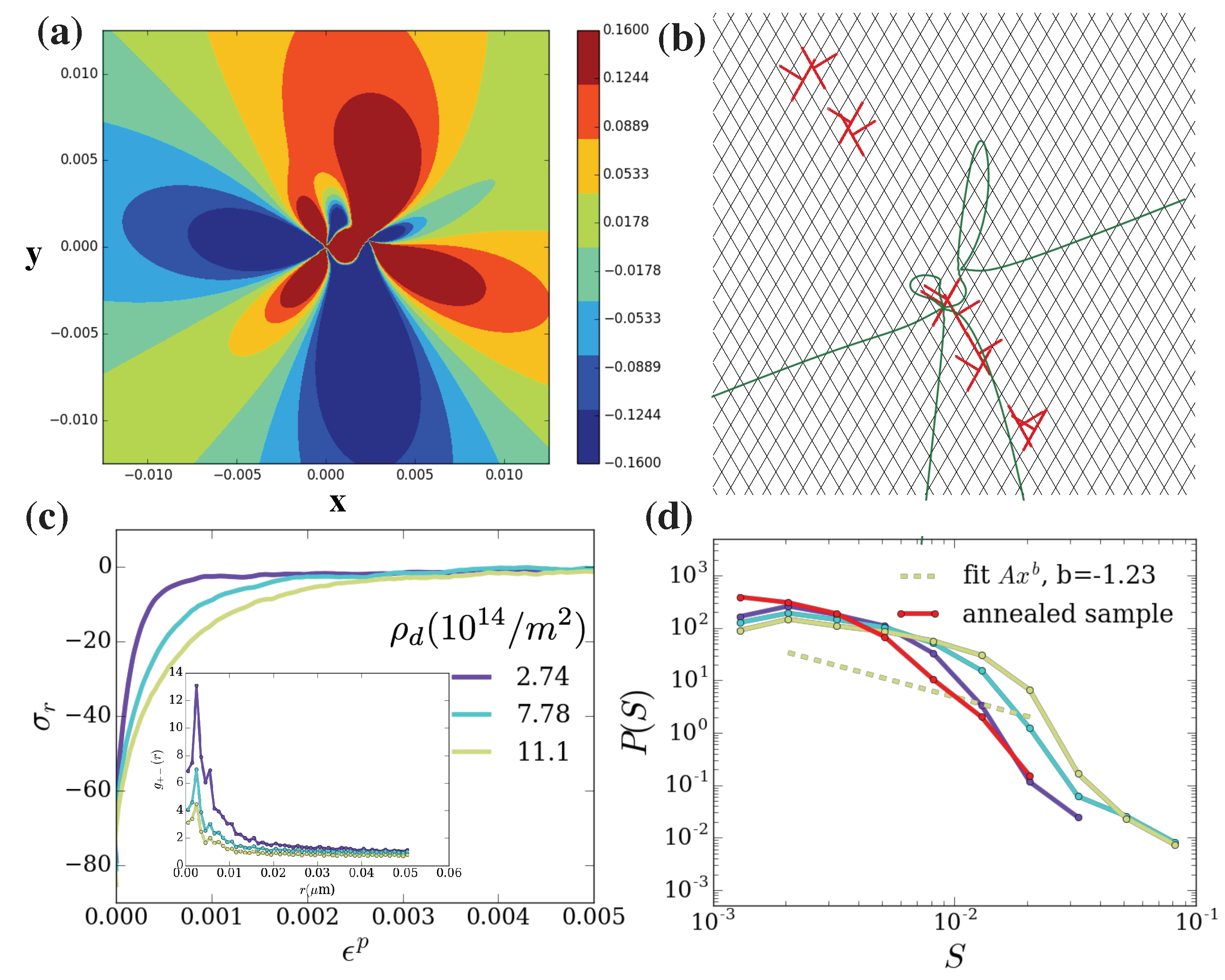
4. Dislocation Pair Correlations and Single-Slip vs. Multi-Slip Loading Conditions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Needleman, A. Postbifurcation behavior and imperfection sensitivity of elastic-plastic circular plates. Int. J. Mech. Sci. 1975, 17, 1–13. [Google Scholar] [CrossRef]
- Asaro, R.; Lubarda, V. Mechanics of Solids and Materials; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Uchic, M.D.; Shade, P.A.; Dimiduk, D.M. Plasticity of micrometer-scale single crystals in compression. Annu. Rev. Mater. Res. 2009, 39, 361–386. [Google Scholar] [CrossRef]
- Dimiduk, D.M.; Uchic, M.D.; Rao, S.; Woodward, C.; Parthasarathy, T. Overview of experiments on microcrystal plasticity in FCC-derivative materials: Selected challenges for modelling and simulation of plasticity. Model. Simul. Mater. Sci. Eng. 2007, 15, 135. [Google Scholar] [CrossRef]
- Uchic, M.D.; Dimiduk, D.M.; Florando, J.; Nix, W. Exploring specimen size effects in plastic deformation of Ni3 (Al, Ta). MRS Proc. 2002, 753. [Google Scholar] [CrossRef]
- Greer, J.R.; De Hosson, J.T.M. Plasticity in small-sized metallic systems: Intrinsic versus extrinsic size effect. Prog. Mater. Sci. 2011, 56, 654–724. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Cui, Y.; Ghoniem, N. Avalanches and plastic flow in crystal plasticity: An overview. Model. Simul. Mater. Sci. Eng. 2017, 26, 013001. [Google Scholar] [CrossRef]
- Cui, Y.; Lin, P.; Liu, Z.; Zhuang, Z. Theoretical and numerical investigations of single arm dislocation source controlled plastic flow in FCC micropillars. Int. J. Plast. 2014, 55, 279–292. [Google Scholar] [CrossRef]
- Jennings, A.T.; Li, J.; Greer, J.R. Emergence of strain-rate sensitivity in Cu nanopillars: Transition from dislocation multiplication to dislocation nucleation. Acta Mater. 2011, 59, 5627–5637. [Google Scholar] [CrossRef]
- Agnihotri, P.K.; Van der Giessen, E. On the rate sensitivity in discrete dislocation plasticity. Mech. Mater. 2015, 90, 37–46. [Google Scholar] [CrossRef]
- Xiang, Y.; Vlassak, J. Bauschinger and size effects in thin-film plasticity. Acta Mater. 2006, 54, 5449–5460. [Google Scholar] [CrossRef]
- Nicola, L.; Xiang, Y.; Vlassak, J.; Van der Giessen, E.; Needleman, A. Plastic deformation of freestanding thin films: Experiments and modeling. J. Mech. Phys. Solids 2006, 54, 2089–2110. [Google Scholar] [CrossRef]
- Shishvan, S.S.; Van der Giessen, E. Distribution of dislocation source length and the size dependent yield strength in freestanding thin films. J. Mech. Phys. Solids 2010, 58, 678–695. [Google Scholar] [CrossRef]
- Chan, P.Y.; Tsekenis, G.; Dantzig, J.; Dahmen, K.A.; Goldenfeld, N. Plasticity and dislocation dynamics in a phase field crystal model. Phys. Rev. Lett. 2010, 105, 015502. [Google Scholar] [CrossRef]
- Zhang, P.; Salman, O.U.; Zhang, J.Y.; Liu, G.; Weiss, J.; Truskinovsky, L.; Sun, J. Taming intermittent plasticity at small scales. Acta Mater. 2017, 128, 351–364. [Google Scholar] [CrossRef]
- Ni, X.; Zhang, H.; Liarte, D.B.; McFaul, L.W.; Dahmen, K.A.; Sethna, J.P.; Greer, J.R. Yield precursor dislocation avalanches in small crystals: The irreversibility transition. arXiv 2018, arXiv:1802.04040. [Google Scholar] [CrossRef]
- Ni, X.; Papanikolaou, S.; Vajente, G.; Adhikari, R.X.; Greer, J.R. Probing microplasticity in small-scale fcc crystals via dynamic mechanical analysis. Phys. Rev. Lett. 2017, 118, 155501. [Google Scholar] [CrossRef] [PubMed]
- Zener, C. Elasticity and Anelasticity of Metals; University of Chicago Press: Chicago, IL, USA, 1948. [Google Scholar]
- Cleveland, R.; Ghosh, A. Inelastic effects on springback in metals. Int. J. Plast. 2002, 18, 769–785. [Google Scholar] [CrossRef]
- Kim, H.; Kim, C.; Barlat, F.; Pavlina, E.; Lee, M.G. Nonlinear elastic behaviors of low and high strength steels in unloading and reloading. Mater. Sci. Eng. A 2013, 562, 161–171. [Google Scholar] [CrossRef]
- Ghosh, A. A physically-based constitutive model for metal deformation. Acta Metall. 1980, 28, 1443–1465. [Google Scholar] [CrossRef]
- Perez, R.; Benito, J.; Prado, J. Study of the inelastic response of TRIP steels after plastic deformation. ISIJ Int. 2005, 45, 1925–1933. [Google Scholar] [CrossRef]
- van Liempt, P.; Sietsma, J. A physically based yield criterion I. Determination of the yield stress based on analysis of pre-yield dislocation behaviour. Mater. Sci. Eng. A 2016, 662, 80–87. [Google Scholar] [CrossRef]
- Arechabaleta, Z.; van Liempt, P.; Sietsma, J. Quantification of dislocation structures from anelastic deformation behaviour. Acta Mater. 2016, 115, 314–323. [Google Scholar] [CrossRef]
- Greer, J.R.; Oliver, W.C.; Nix, W.D. Size dependence of mechanical properties of gold at the micron scale in the absence of strain gradients. Acta Mater. 2005, 53, 1821–1830. [Google Scholar] [CrossRef]
- Greer, J.R.; Nix, W.D. Nanoscale gold pillars strengthened through dislocation starvation. Phys. Rev. B 2006, 73, 245410. [Google Scholar] [CrossRef]
- Shan, Z.; Mishra, R.K.; Asif, S.S.; Warren, O.L.; Minor, A.M. Mechanical annealing and source-limited deformation in submicrometre-diameter Ni crystals. Nat. Mater. 2008, 7, 115–119. [Google Scholar] [CrossRef] [PubMed]
- Sethna, J.P.; Bierbaum, M.K.; Dahmen, K.A.; Goodrich, C.P.; Greer, J.R.; Hayden, L.X.; Kent-Dobias, J.P.; Lee, E.D.; Liarte, D.B.; Ni, X.; et al. Deformation of crystals: Connections with statistical physics. Annu. Rev. Mater. Res. 2017, 47, 217–246. [Google Scholar] [CrossRef]
- Anderson, P.M.; Hirth, J.P.; Lothe, J. Theory of Dislocations; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Kleemola, H.; Nieminen, M. On the strain-hardening parameters of metals. Metall. Trans. 1974, 5, 1863–1866. [Google Scholar] [CrossRef]
- Ghosh, A. The influence of strain hardening and strain-rate sensitivity on sheet metal forming. J. Eng. Mater. Technol. 1977, 99, 264–274. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. Material rate dependence and localized deformation in crystalline solids. Acta Metall. 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Ghosh, A. Tensile instability and necking in materials with strain hardening and strain-rate hardening. Acta Metall. 1977, 25, 1413–1424. [Google Scholar] [CrossRef]
- Fan, Z.; Mingzhi, H.; Deke, S. The relationship between the strain-hardening exponent n and the microstructure of metals. Mater. Sci. Eng. A 1989, 122, 211–213. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Song, H.; Van der Giessen, E. Obstacles and sources in dislocation dynamics: Strengthening and statistics of abrupt plastic events in nanopillar compression. J. Mech. Phys. Solids 2017, 102, 17–29. [Google Scholar] [CrossRef]
- Van der Giessen, E.; Needleman, A. Discrete dislocation plasticity: A simple planar model. Model. Simul. Mater. Sci. Eng. 1995, 3, 689. [Google Scholar] [CrossRef]
- Papanikolaou, S. Learning local, quenched disorder in plasticity and other crackling noise phenomena. arXiv 2018, arXiv:1803.03603. [Google Scholar] [CrossRef]
- Chaikin, P.M.; Lubensky, T.C.; Witten, T.A. Principles of Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ispánovity, P.D.; Laurson, L.; Zaiser, M.; Groma, I.; Zapperi, S.; Alava, M.J. Avalanches in 2D dislocation systems: Plastic yielding is not depinning. Phys. Rev. Lett. 2014, 112, 235501. [Google Scholar] [CrossRef] [PubMed]
- Zaiser, M. Scale invariance in plastic flow of crystalline solids. Adv. Phys. 2006, 55, 185–245. [Google Scholar] [CrossRef]
- Tsekenis, G.; Goldenfeld, N.; Dahmen, K.A. Dislocations jam at any density. Phys. Rev. Lett. 2011, 106, 105501. [Google Scholar] [CrossRef] [PubMed]
- Zaiser, M.; Aifantis, E.C. Randomness and slip avalanches in gradient plasticity. Int. J. Plast. 2006, 22, 1432–1455. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Bohn, F.; Sommer, R.; Durin, G.; Zapperi, S.; Sethna, J. Universality beyond power laws and the average avalanche shape. Nat. Phys. 2011, 7, 316–320. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Dimiduk, D.; Choi, W.; Sethna, J.; Uchic, M.; Woodward, C.; Zapperi, S. Quasi-periodic events in crystal plasticity and the self-organized avalanche oscillator. Nature 2012, 490, 517–521. [Google Scholar] [CrossRef]
- Miguel, M.C.; Vespignani, A.; Zapperi, S.; Weiss, J.; Grasso, J.R. Intermittent dislocation flow in viscoplastic deformation. Nature 2001, 410, 667–671. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H.; Papanikolaou, S. From Statistical Correlations to Stochasticity and Size Effects in Sub-Micron Crystal Plasticity. Metals 2019, 9, 835. https://doi.org/10.3390/met9080835
Song H, Papanikolaou S. From Statistical Correlations to Stochasticity and Size Effects in Sub-Micron Crystal Plasticity. Metals. 2019; 9(8):835. https://doi.org/10.3390/met9080835
Chicago/Turabian StyleSong, Hengxu, and Stefanos Papanikolaou. 2019. "From Statistical Correlations to Stochasticity and Size Effects in Sub-Micron Crystal Plasticity" Metals 9, no. 8: 835. https://doi.org/10.3390/met9080835
APA StyleSong, H., & Papanikolaou, S. (2019). From Statistical Correlations to Stochasticity and Size Effects in Sub-Micron Crystal Plasticity. Metals, 9(8), 835. https://doi.org/10.3390/met9080835





