Quantitative Analysis of Inclusion Engineering on the Fatigue Property Improvement of Bearing Steel
Abstract
1. Introduction
2. Materials and Experimental Procedures
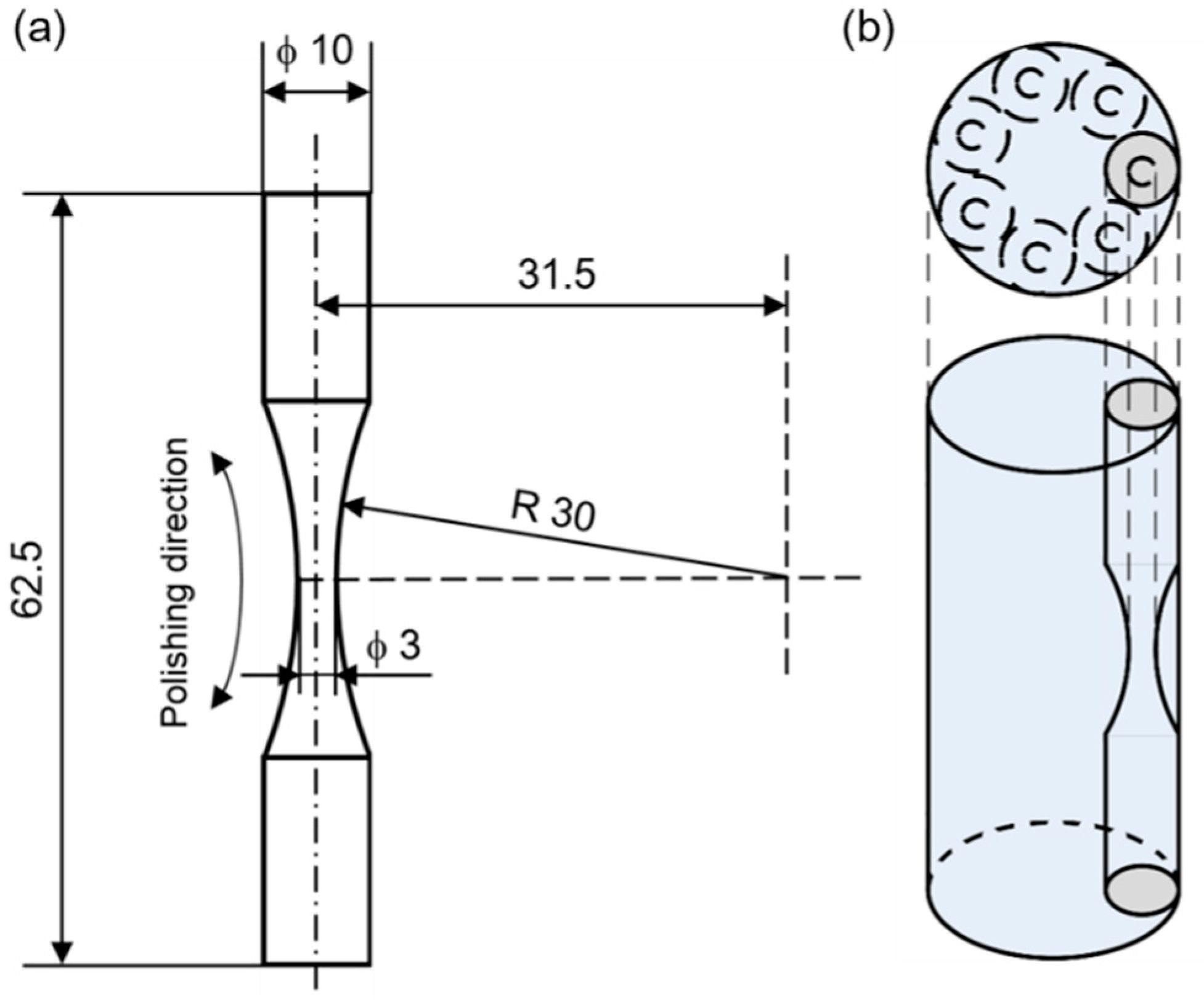
2.1. Material Preparation
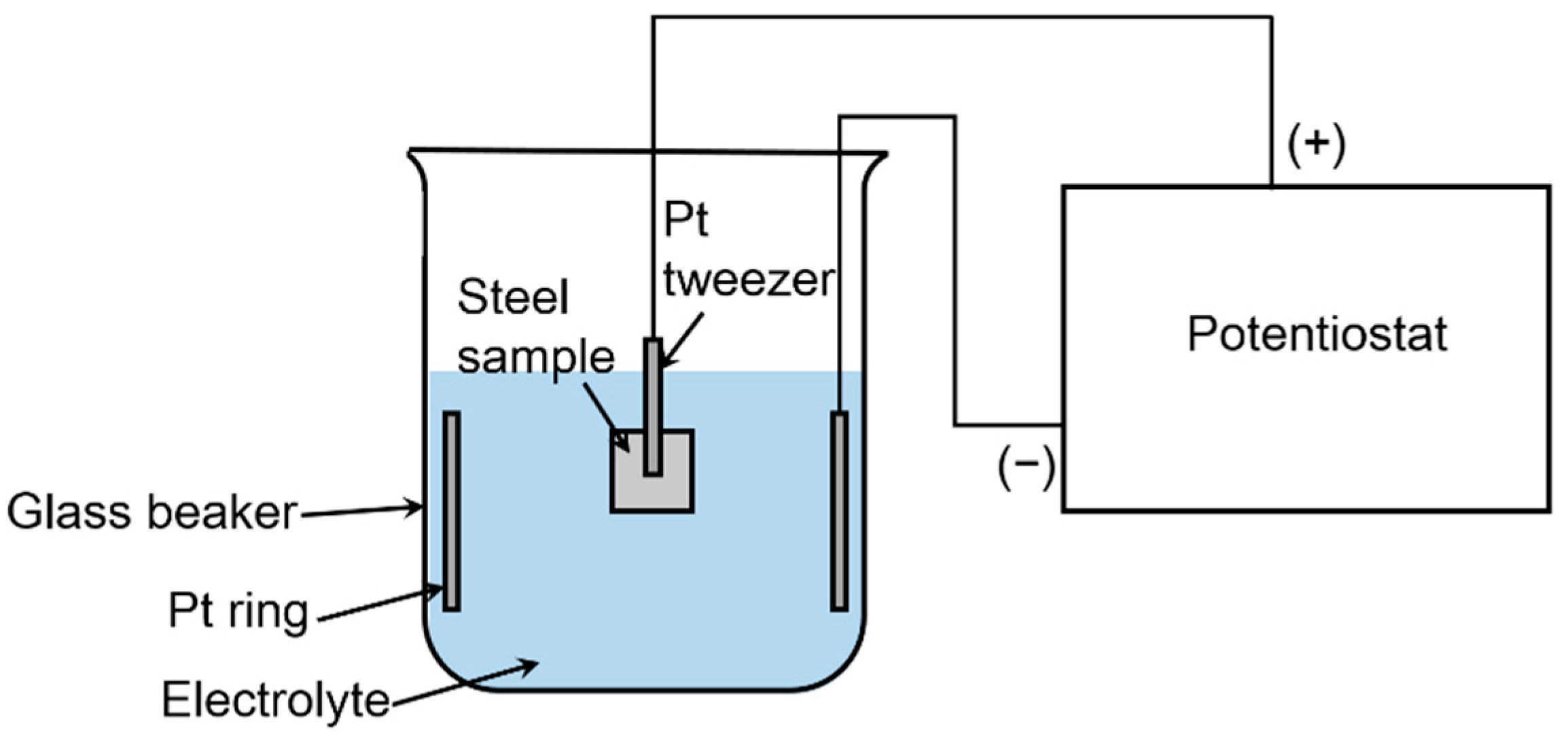
2.2. Fatigue Tests
2.3. Inclusion Analysis Methods
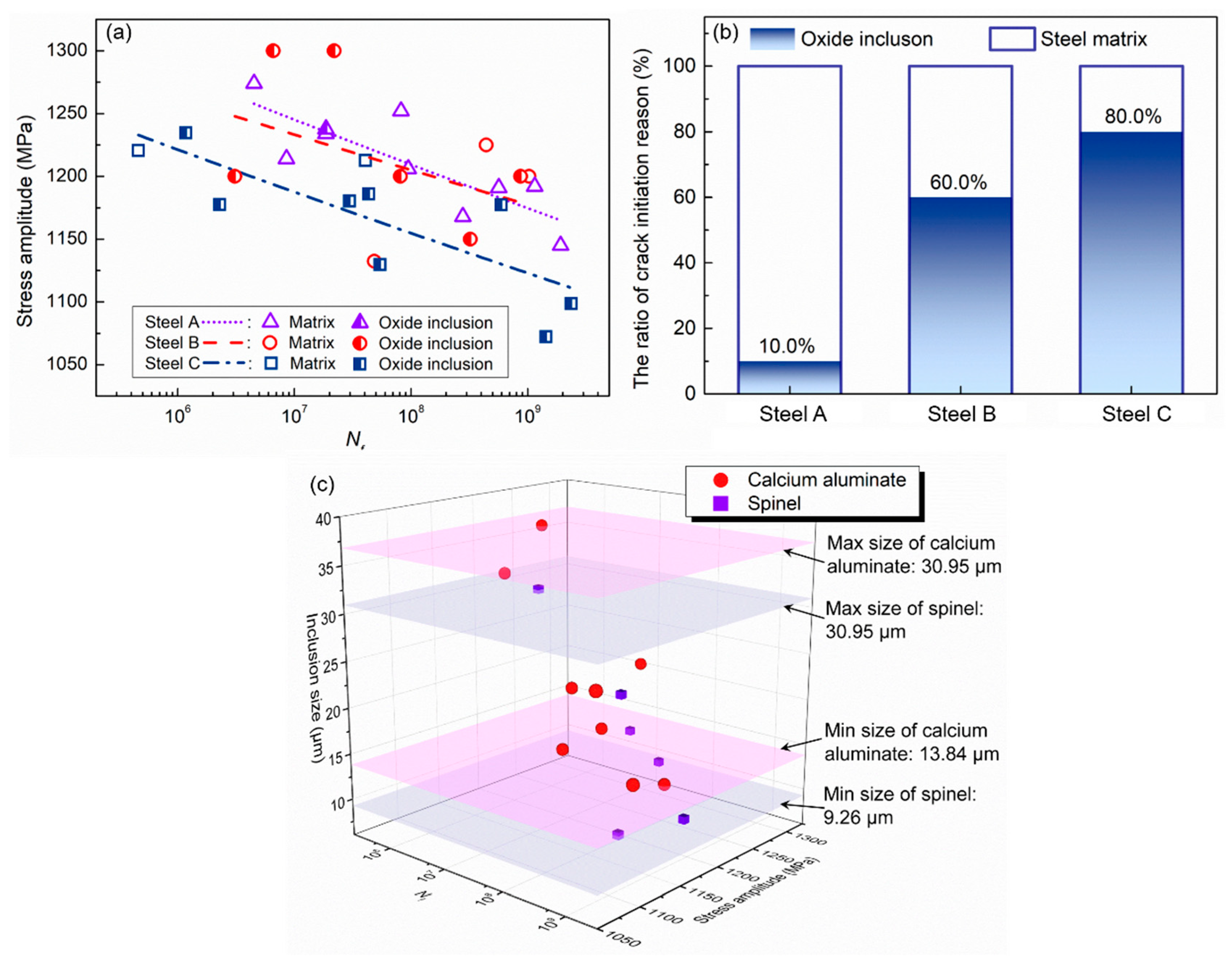
3. Results
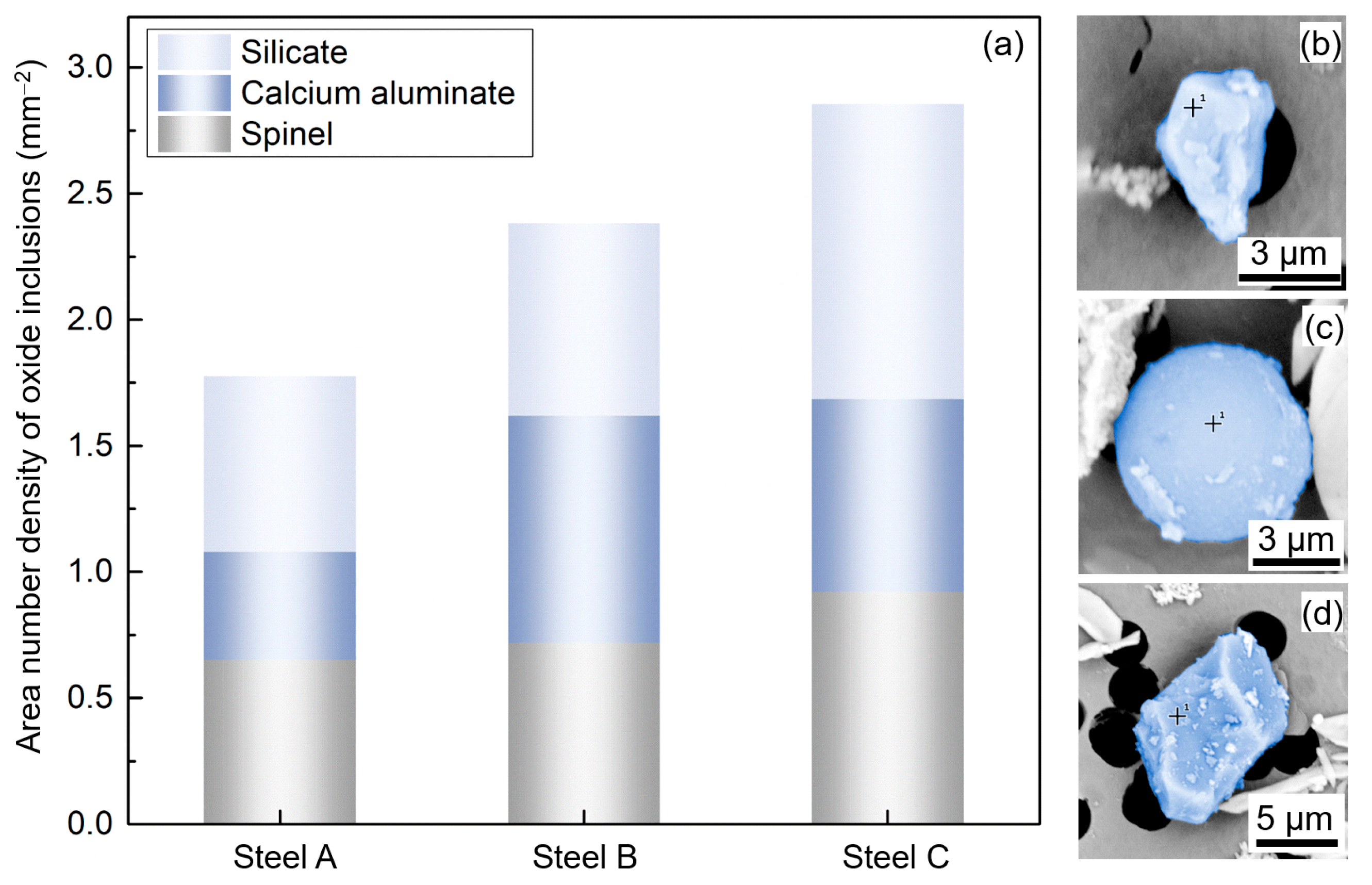
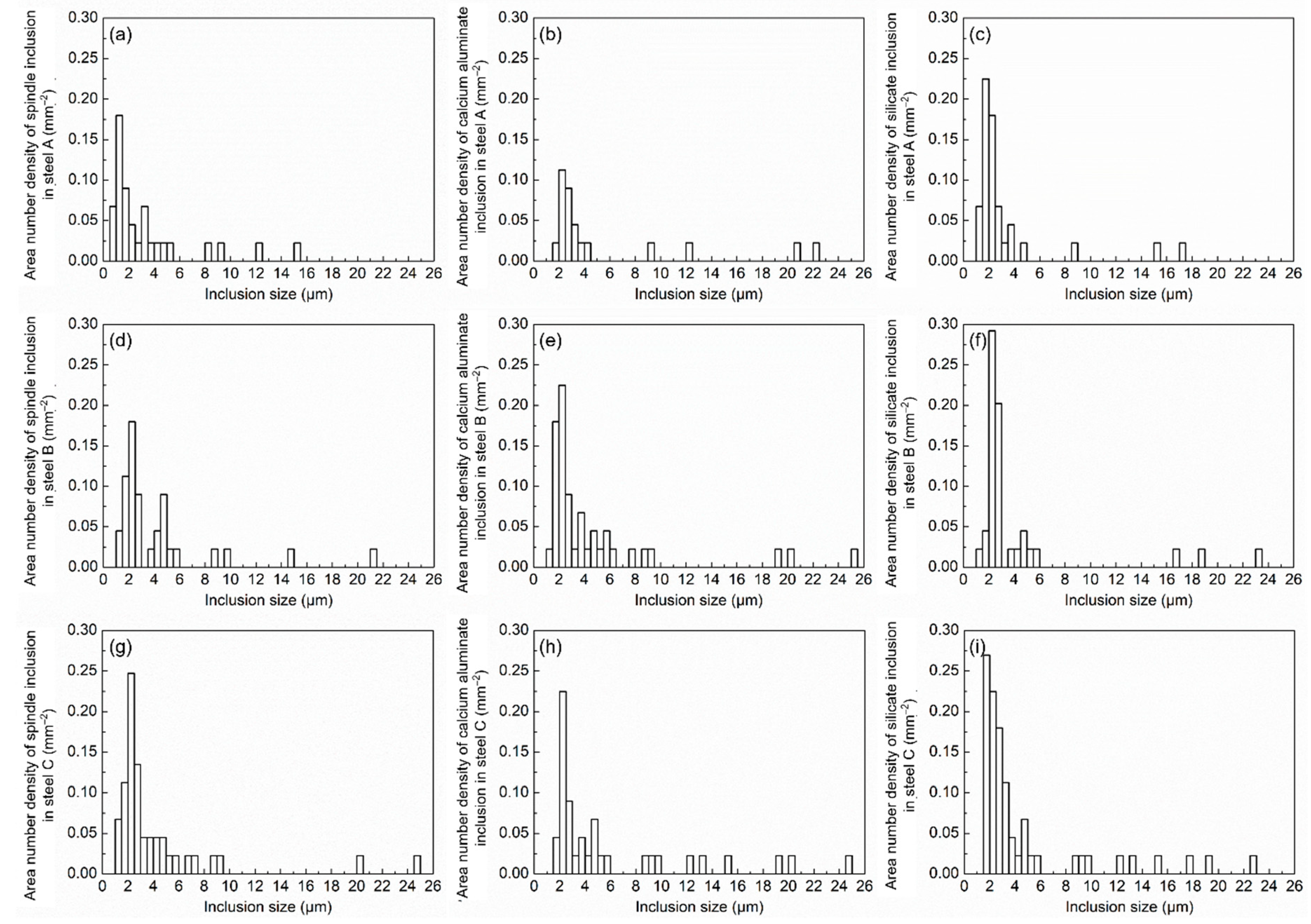
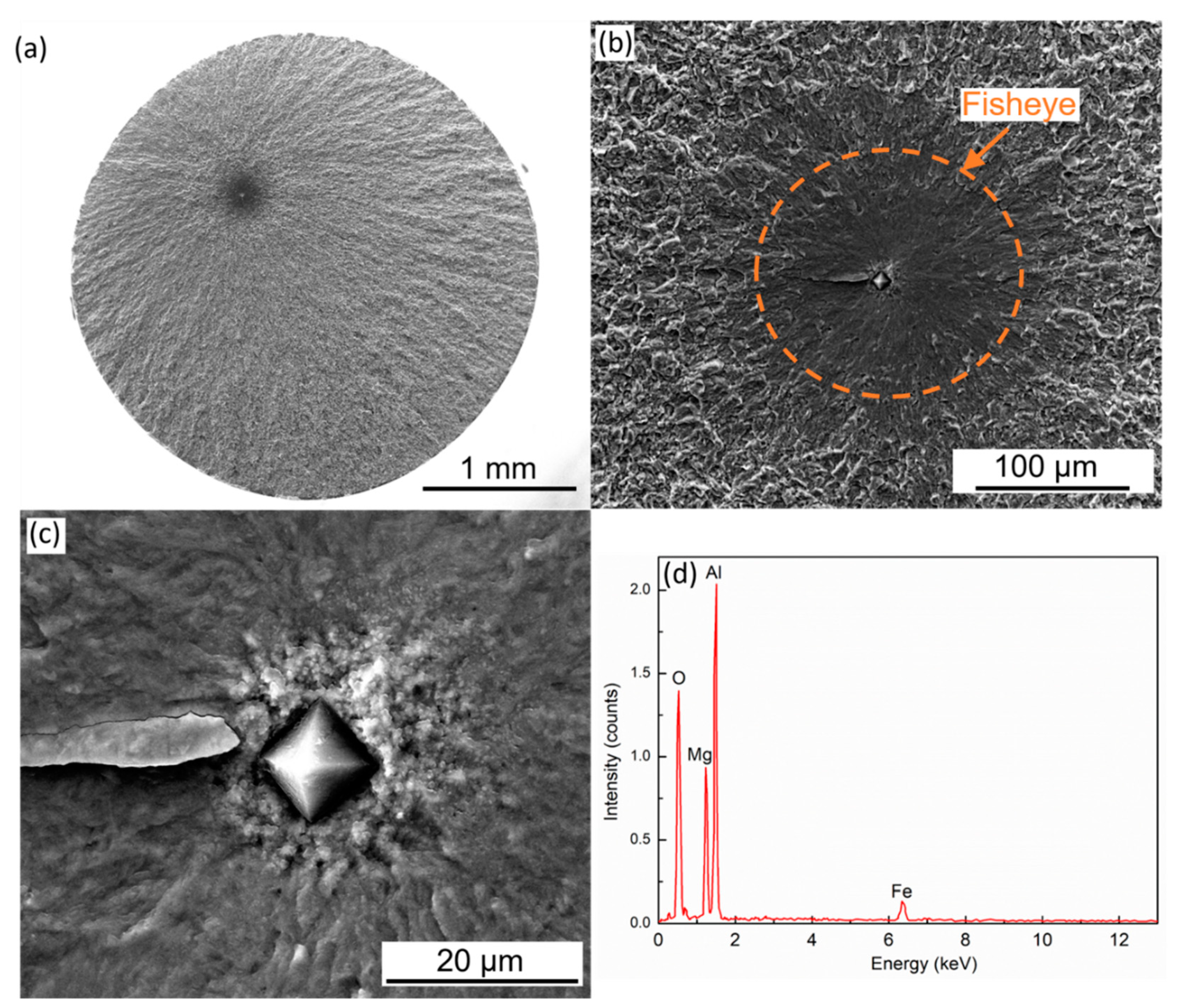
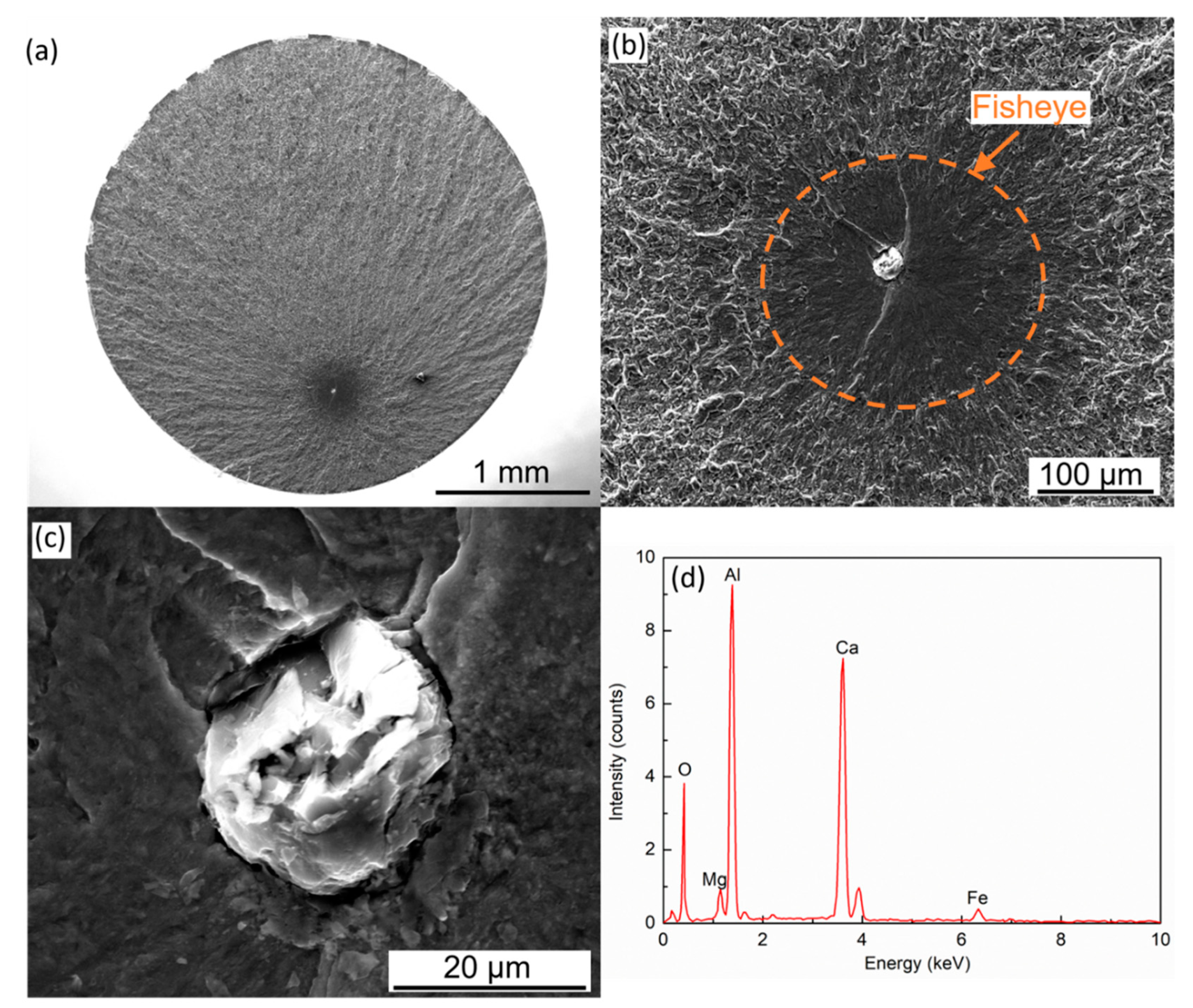
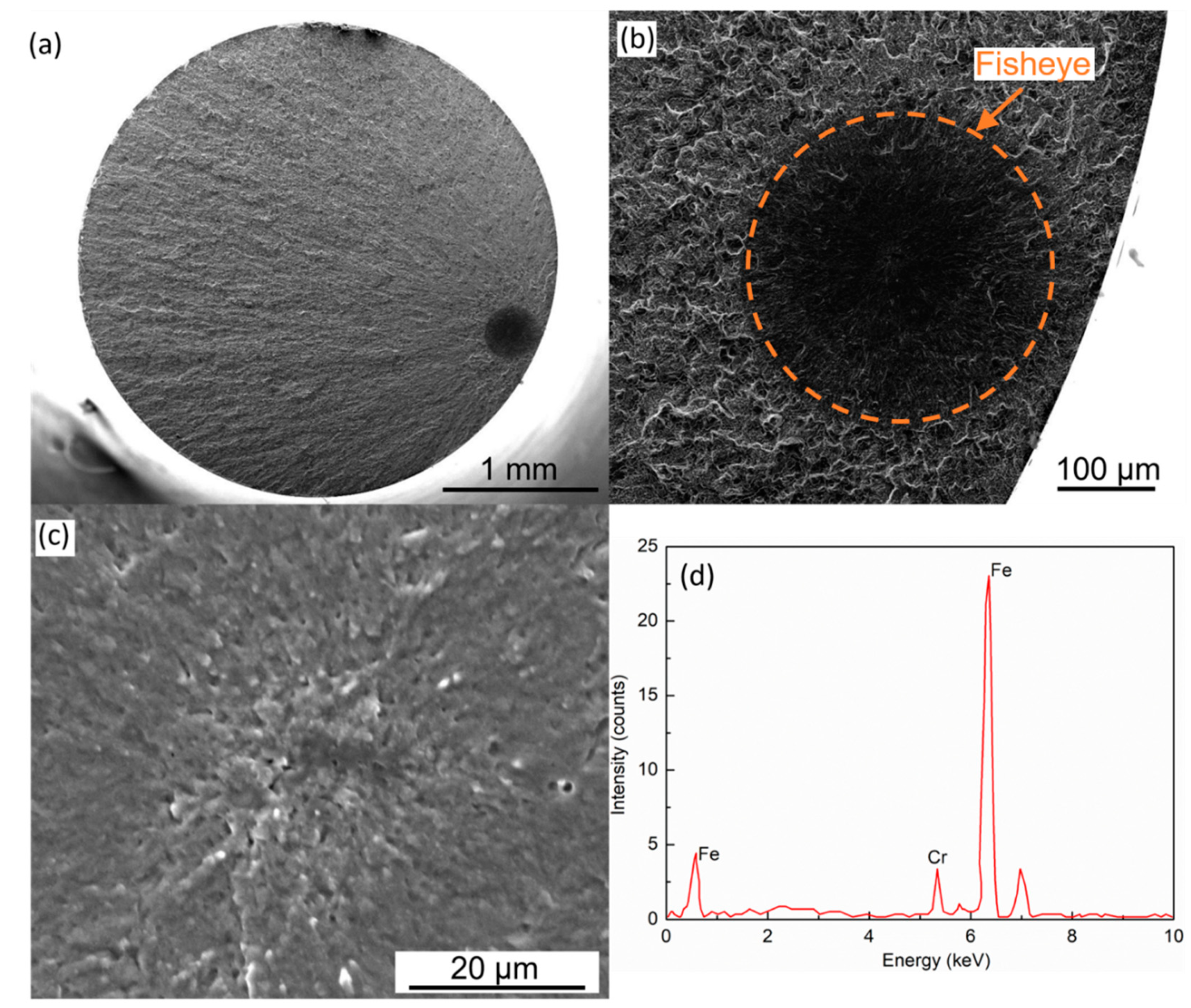
3.1. Characterization of Oxide Inclusions
3.2. Characterization of Fatigue Properties
4. Discussion
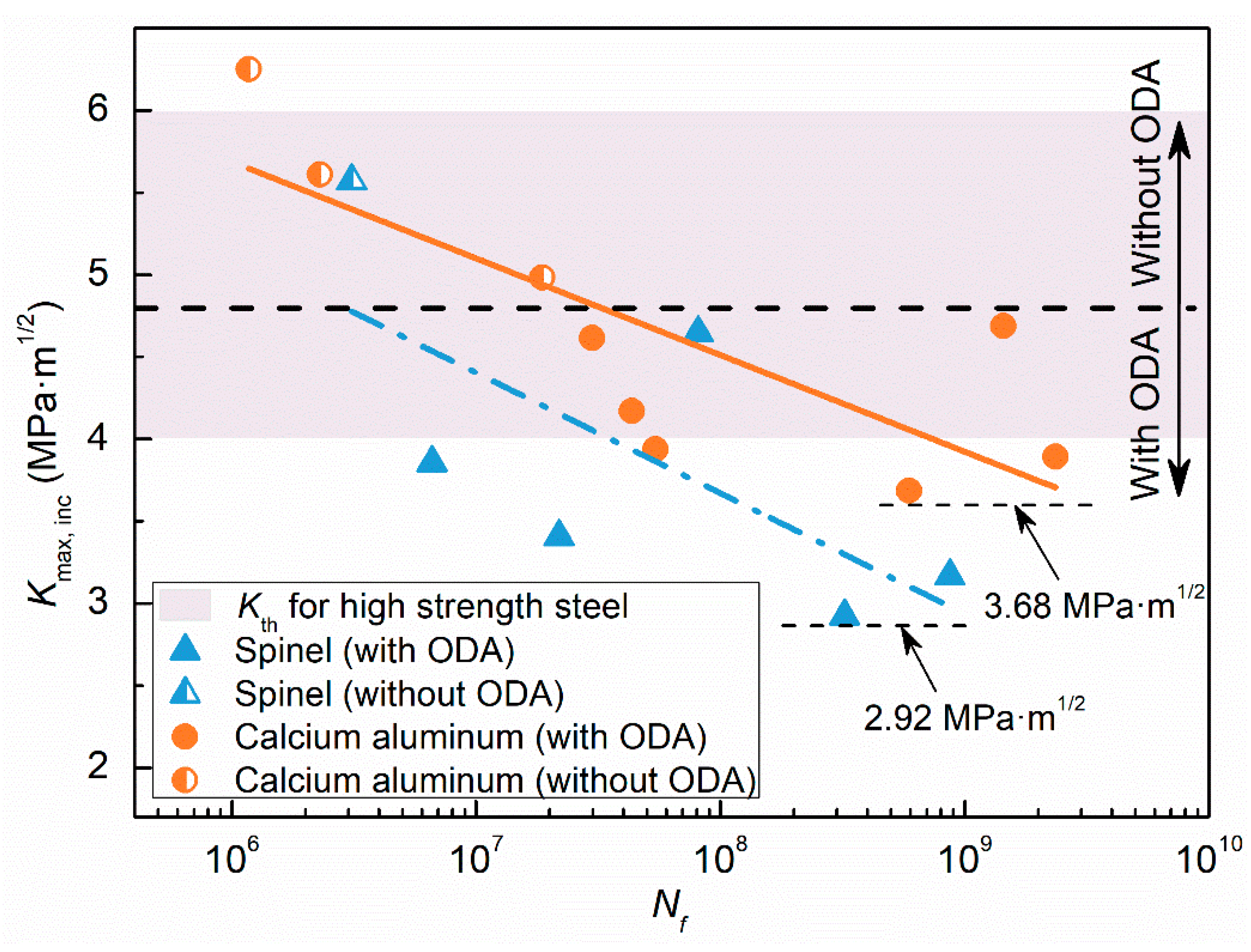
4.1. The Effect of Oxide Inclusions on Fatigue Properties
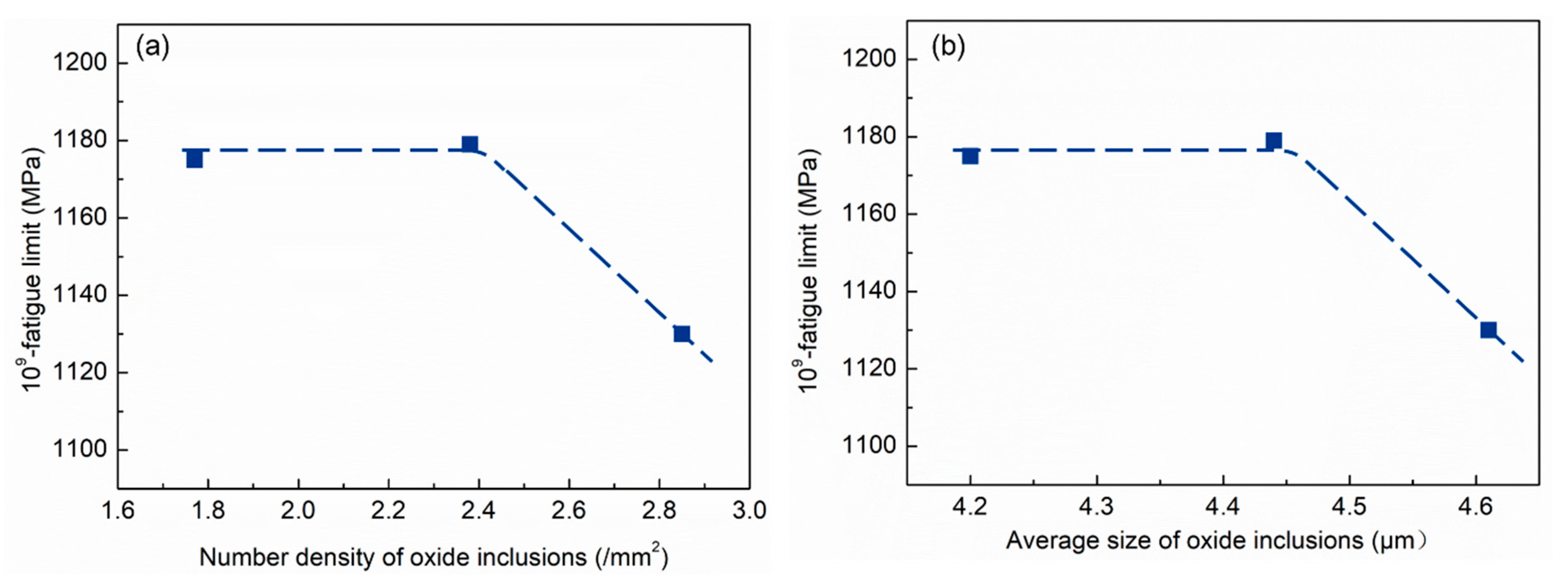
4.1.1. The Correlation between 109-Fatigue Limit and the Inclusion Characteristics
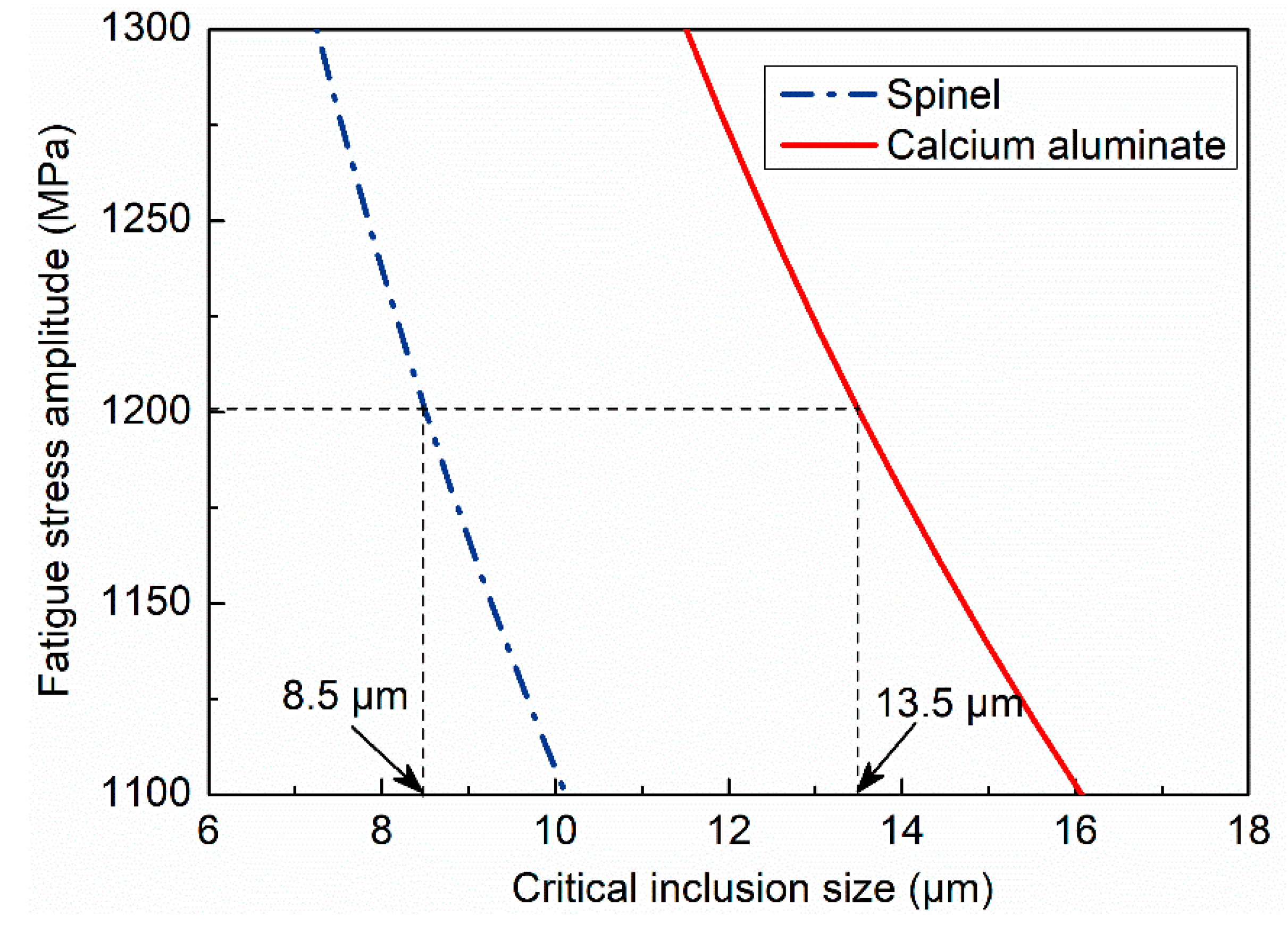
4.1.2. The Critical Size of Different Types of Inclusions
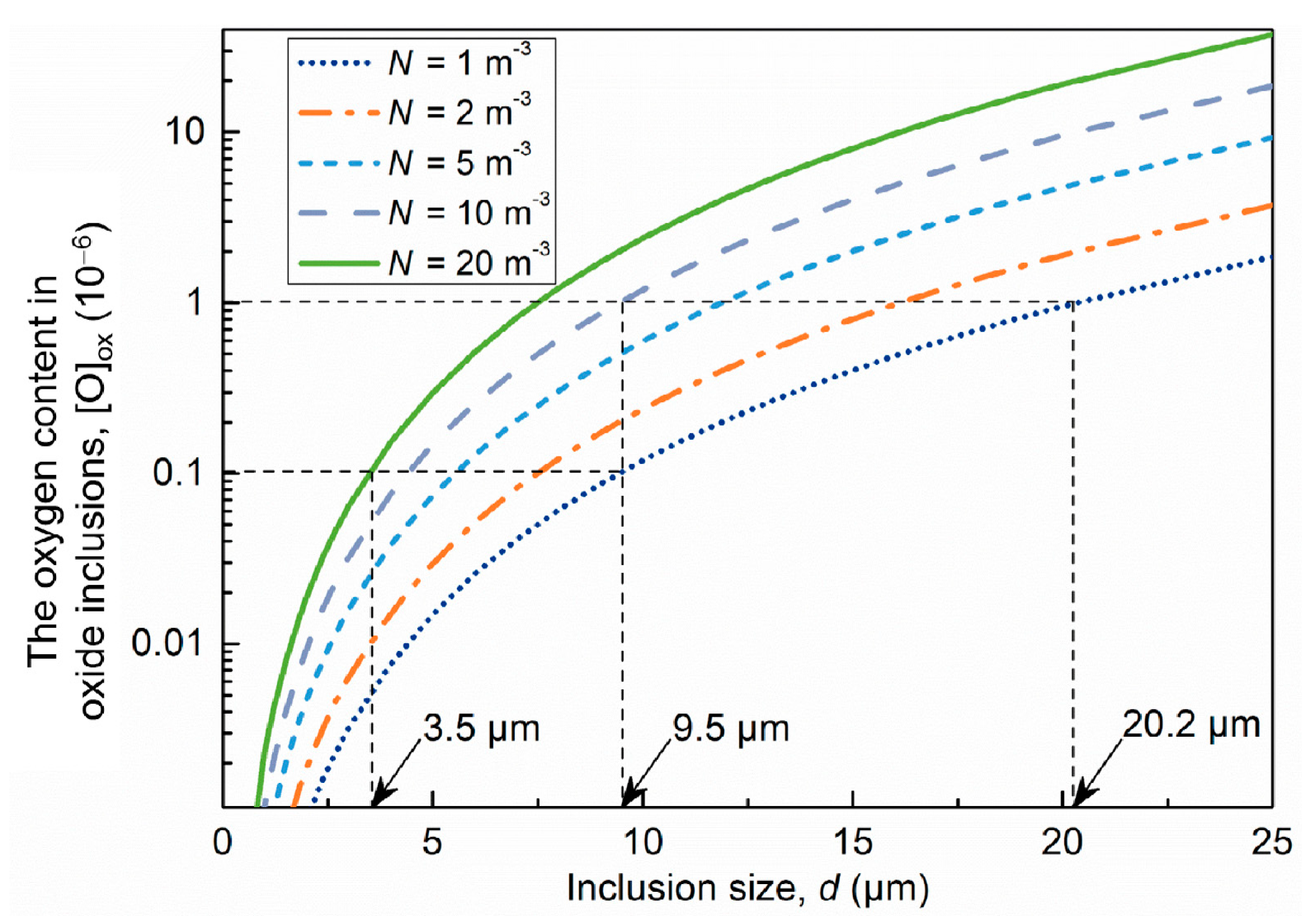
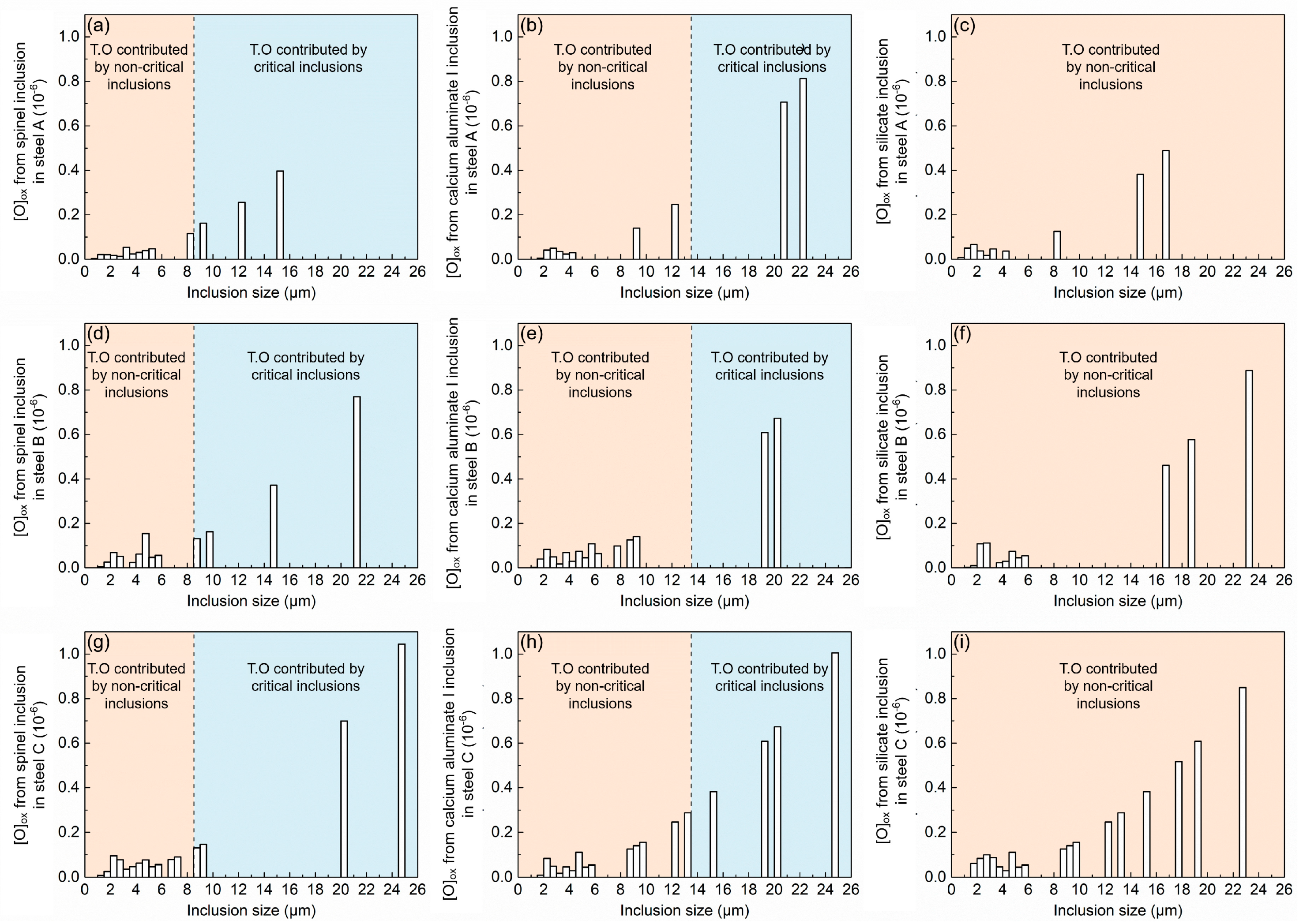
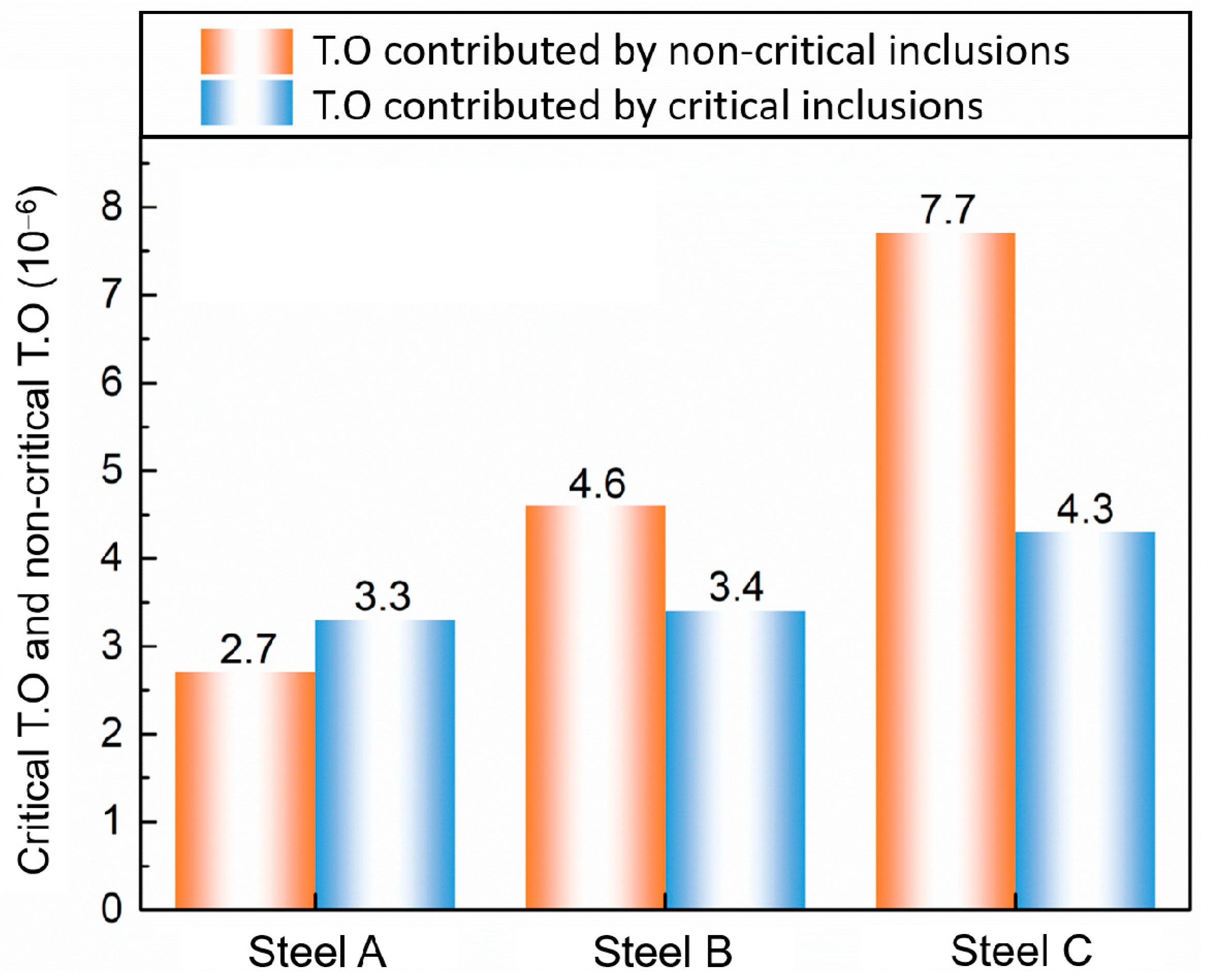
4.2. The Relation between Oxide Inclusions and the Cleanliness Indicator T.O
5. Conclusions and Summary
Author Contributions
Funding
Conflicts of Interest
References
- Kang, J.H.; Hosseinkhani, B.; Rivera-Díaz-del-Castillo, P.E.J. Rolling contact fatigue in bearings: Multiscale overview. Mater. Sci. Tech. 2012, 28, 44–49. [Google Scholar] [CrossRef]
- Sakai, T.; Sato, Y.; Oguma, N. Characteristic S-N properties of high-carbon-chromium-bearing steel under axial loading in long-life fatigue. Fatigue Fract. Eng. Mater. 2002, 25, 765–773. [Google Scholar] [CrossRef]
- Shiozawa, K.; Lu, L.; Ishihara, S. S-N curve characteristics and subsurface crack initiation behaviour in ultra-long life fatigue of a high carbon-chromium bearing steel. Fatigue Fract. Eng. Mater. 2001, 24, 781–790. [Google Scholar] [CrossRef]
- Akiniwa, Y.; Miyamoto, N.; Tsuru, H.; Tanaka, K. Notch effect on fatigue strength reduction of bearing steel in the very high cycle regime. Int. J. Fatigue 2006, 28, 1555–1565. [Google Scholar] [CrossRef]
- Li, W.; Sakai, T.; Li, Q.; Lu, L.T.; Wang, P. Reliability evaluation on very high cycle fatigue property of GCr15 bearing steel. Int. J. Fatigue 2010, 32, 1096–1107. [Google Scholar] [CrossRef]
- Chen, S.H.; Jiang, M.; He, X.F.; Wang, X.H. Top slag refining for inclusion composition transform control in tire cord steel. Int. J. Min. Met. Mater. 2012, 19, 490–498. [Google Scholar] [CrossRef]
- Cai, X.; Bao, Y.; Lin, L.; Gu, C. Effect of Al content on the evolution of non-metallic Inclusions in Si-Mn deoxidized steel. Steel Res. Int. 2016, 87, 1168–1178. [Google Scholar] [CrossRef]
- Park, J.S.; Park, J.H. Effect of slag composition on the concentration of Al2O3 in the inclusions in Si-Mn-killed steel. Metall. Mater. Trans. B 2014, 45, 953–960. [Google Scholar] [CrossRef]
- Ma, W.; Bao, Y.; Wang, M.; Zhao, L. Influence of slag composition on bearing steel cleanness. Ironmak. Steelmak. 2014, 41, 26–30. [Google Scholar] [CrossRef]
- Hou, Z.; Jiang, M.; Yang, E.; Gao, S.; Wang, X. Inclusion characterization in aluminum-deoxidized special steel with certain sulfur content under combined influences of slag refining, calcium treatment, and reoxidation. Metall. Mater. Trans. B 2018, 49, 3056–3066. [Google Scholar] [CrossRef]
- Tabatabaei, Y.; Coley, K.S.; Irons, G.A.; Sun, S. Model of inclusion evolution during calcium treatment in the ladle furnace. Metall. Mater. Trans. B 2018, 49, 2022–2037. [Google Scholar] [CrossRef]
- Ma, W.; Bao, Y.; Wang, M.; Zhao, L. Effect of Mg and Ca treatment on behavior and particle size of inclusions in bearing steels. ISIJ Int. 2014, 54, 536–542. [Google Scholar] [CrossRef]
- Bessho, N.; Yamasaki, H.; Fujii, T.; Nozaki, T.; Hiwasa, S. Removal of Inclusion from Molten Steel in Continuous Casting Tundish. ISIJ Int. 1992, 32, 157–163. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, L.; Ling, H.; Wang, Y.; Pan, D.; Ren, Q.; Wang, X. A reaction model for prediction of inclusion evolution during reoxidation of Ca-treated Al-killed steels in tundish. Metall. Mater. Trans. B 2017, 48, 1433–1438. [Google Scholar] [CrossRef]
- Ni, P.; Jonsson, L.T.I.; Ersson, M.; Jönsson, P.G. Non-metallic inclusion behaviors in a new tundishand SEN design using a swirling flow during continuous casting of steel. Steel Res. Int. 2017, 83, 1600155. [Google Scholar] [CrossRef]
- Murakami, Y.; Endo, M. Effects of defects, inclusions and inhomogeneities on fatigue strength. Int. J. Fatigue 1994, 16, 163–182. [Google Scholar] [CrossRef]
- Murakami, Y.; Yokoyama, N.; Nagata, J. Mechanism of fatigue failure in ultralong life regime. Fatigue Fract. Eng. Mater. 2002, 25, 735–746. [Google Scholar] [CrossRef]
- Spriestersbach, D.; Grad, P.; Kerscher, E. Influence of different non-metallic inclusion types on the crack initiation in high-strength steels in the VHCF regime. Int. J. Fatigue 2014, 64, 114–120. [Google Scholar] [CrossRef]
- Gu, C.; Lian, J.; Bao, Y.; Münstermann, S. Microstructure-based fatigue modelling with residual stresses: Prediction of the microcrack initiation around inclusions. Mat. Sci. Eng. A 2019, 751, 133–141. [Google Scholar] [CrossRef]
- Gu, C.; Lian, J.; Bao, Y.; Xiao, W.; Münstermann, S. Numerical study of the effect of inclusions on the residual stress distribution in high-strength martensitic steels during cooling. Appl. Sci. 2019, 9, 455. [Google Scholar] [CrossRef]
- Gu, C.; Lian, J.; Bao, Y.; Xie, Q.; Münstermann, S. Microstructure based fatigue modelling with residual stresses: Prediction of the fatigue life for various inclusion sizes. Int. J. Fatigue 2014. under review. [Google Scholar]
- Lian, J.; Sharaf, M.; Archie, F.; Münstermann, S. A hybrid approach for modelling of plasticity and failure behaviour of advanced high-strength steel sheets. Int. J. Damage Mech. 2012, 22, 188–218. [Google Scholar] [CrossRef]
- Murakami, Y.; Nomoto, T.; Ueda, T. Factors influencing the mechanism of superlong fatigue failure in steels. Fatigue Fract. Eng. Mater. 1999, 22, 581–590. [Google Scholar] [CrossRef]
- Murakami, Y.; Nomoto, T.; Ueda, T.; Murakami, Y. On the mechanism of fatigue failure in the superlong life regime (N > 107 cycles). Part II: A fractographic investigation. Fatigue Fract. Eng. Mater. 2000, 23, 903–910. [Google Scholar] [CrossRef]
- Murakami, Y.; Nomoto, T.; Ueda, T.; Murakami, Y. On the mechanism of fatigue failure in the superlong life regime (N > 107 cycles). Part I: Influence of hydrogen trapped by inclusions. Fatigue Fract. Eng. Mater. 2000, 23, 893–902. [Google Scholar] [CrossRef]
- Gu, C.; Bao, Y.P.; Gan, P.; Lian, J.H.; Münstermann, S. An experimental study on the impact of deoxidation methods on the fatigue properties of bearing steels. Steel Res. Int. 2018, 89, 1800129. [Google Scholar] [CrossRef]
- Bertrand, J.; Molinero, J.; Landa, S.; Elvira, R.; Wild, M.; Barthold, G.; Valentin, P.; Schifferl, H. Metallurgy of plastic inclusions to improve fatigue life of engineering steels. Ironmak. Steelmak. 2003, 30, 165–169. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z.; Li, S.; Liu, Y.; Chen, S.; Hui, W.; Weng, Y. Effect of Hydrogen on Fatigue Strength of High-Strength Steels in the VHCF Regime. Adv. Eng. Mater. 2009, 11, 561–567. [Google Scholar] [CrossRef]
- Alexander Stopher, M.; Rivera-Diaz-del-Castillo, P.E.J. Hydrogen embrittlement in bearing steels. Mater. Sci. Tech. 2016, 32, 1184–1193. [Google Scholar] [CrossRef]
- Louthan, M.R. Hydrogen Embrittlement of Metals: A Primer for the Failure Analyst. J. Fail. Anal. Prev. 2008, 8, 289–307. [Google Scholar] [CrossRef]
- Murakami, Y.; Usuki, H. Quantitative evaluation of effects of non-metallic inclusions on fatigue strength of high strength steels. II: Fatigue limit evaluation based on statistics for extreme values of inclusion size. Int. J. Fatigue 1989, 11, 299–307. [Google Scholar] [CrossRef]
- Gu, C.; Bao, Y.P.; Gan, P.; Wang, M.; He, J.S. Effect of main inclusions on crack initiation in bearing steel in the very high cycle fatigue regime. Int. J. Miner. Metal. Mater. 2018, 25, 623–629. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 83rd ed.; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- DeHoff, R.T. Quantitative Microscopy, 1st ed.; McGraw-Hill Book Company: New York, NY, USA, 1968. [Google Scholar]
| Steel No. | C/mass% | Si/mass% | Mn/mass% | P/mass% | S/mass% | Cr/mass% | Al/mass% | T.O/mass% |
|---|---|---|---|---|---|---|---|---|
| Steel A | 1.004 | 0.241 | 0.348 | 0.0168 | 0.0048 | 1.31 | 0.0195 | 0.0006 |
| Steel B | 1.001 | 0.247 | 0.349 | 0.0119 | 0.0035 | 1.34 | 0.0122 | 0.0008 |
| Steel C | 1.005 | 0.208 | 0.317 | 0.0137 | 0.0041 | 1.32 | 0.0078 | 0.0012 |
| Steel No. | C | α |
|---|---|---|
| Steel A | 1527.0 | −0.013 |
| Steel B | 1450.0 | −0.010 |
| Steel C | 1444.8 | −0.012 |
| Al2O3 | MgO | SiO2 | CaO |
|---|---|---|---|
| 3970 | 3600 | 2500 | 3350 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, C.; Wang, M.; Bao, Y.; Wang, F.; Lian, J. Quantitative Analysis of Inclusion Engineering on the Fatigue Property Improvement of Bearing Steel. Metals 2019, 9, 476. https://doi.org/10.3390/met9040476
Gu C, Wang M, Bao Y, Wang F, Lian J. Quantitative Analysis of Inclusion Engineering on the Fatigue Property Improvement of Bearing Steel. Metals. 2019; 9(4):476. https://doi.org/10.3390/met9040476
Chicago/Turabian StyleGu, Chao, Min Wang, Yanping Bao, Fuming Wang, and Junhe Lian. 2019. "Quantitative Analysis of Inclusion Engineering on the Fatigue Property Improvement of Bearing Steel" Metals 9, no. 4: 476. https://doi.org/10.3390/met9040476
APA StyleGu, C., Wang, M., Bao, Y., Wang, F., & Lian, J. (2019). Quantitative Analysis of Inclusion Engineering on the Fatigue Property Improvement of Bearing Steel. Metals, 9(4), 476. https://doi.org/10.3390/met9040476






