Material Flow in Ultrasonic Orbital Microforming
Abstract
1. Introduction
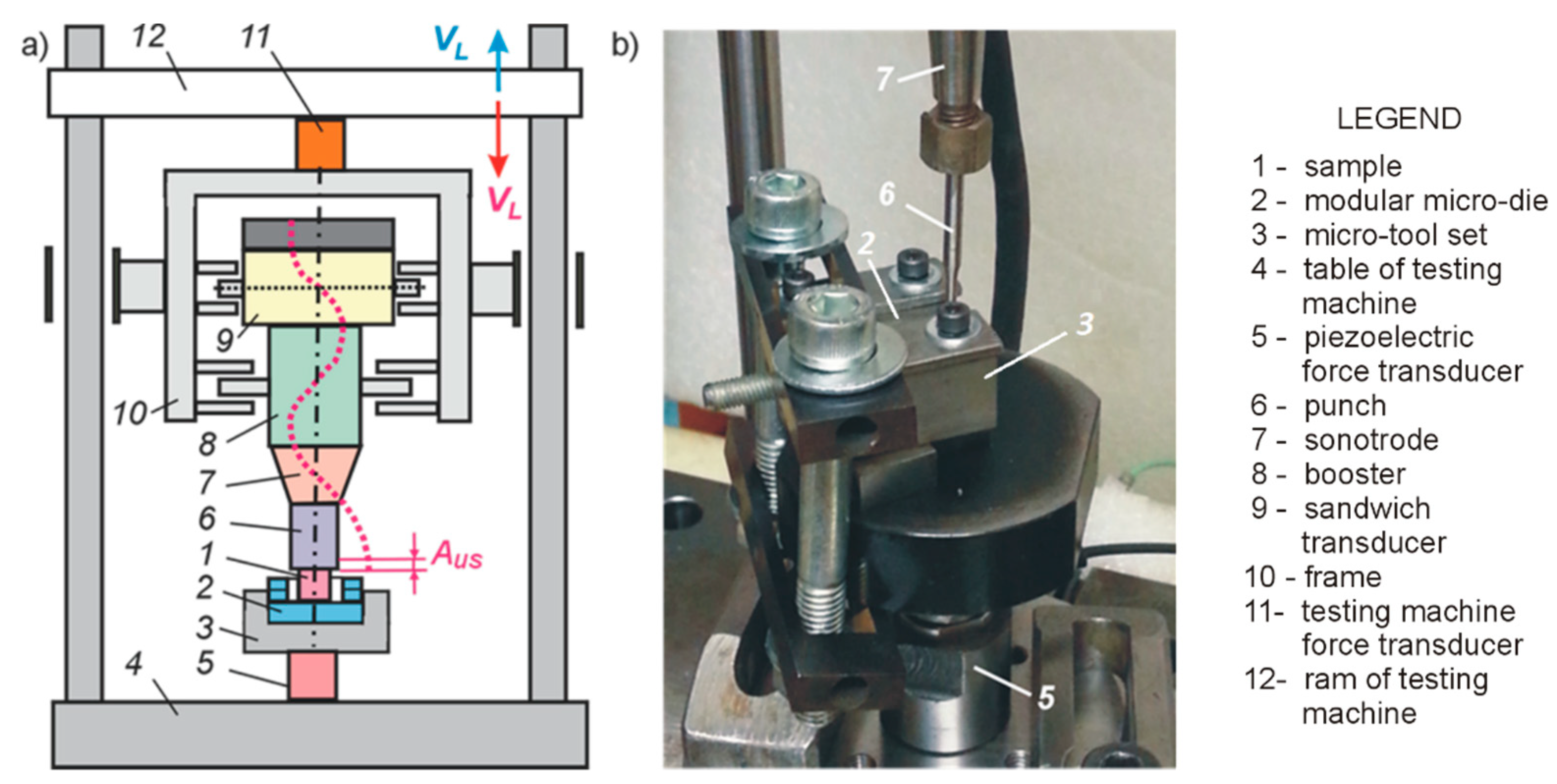
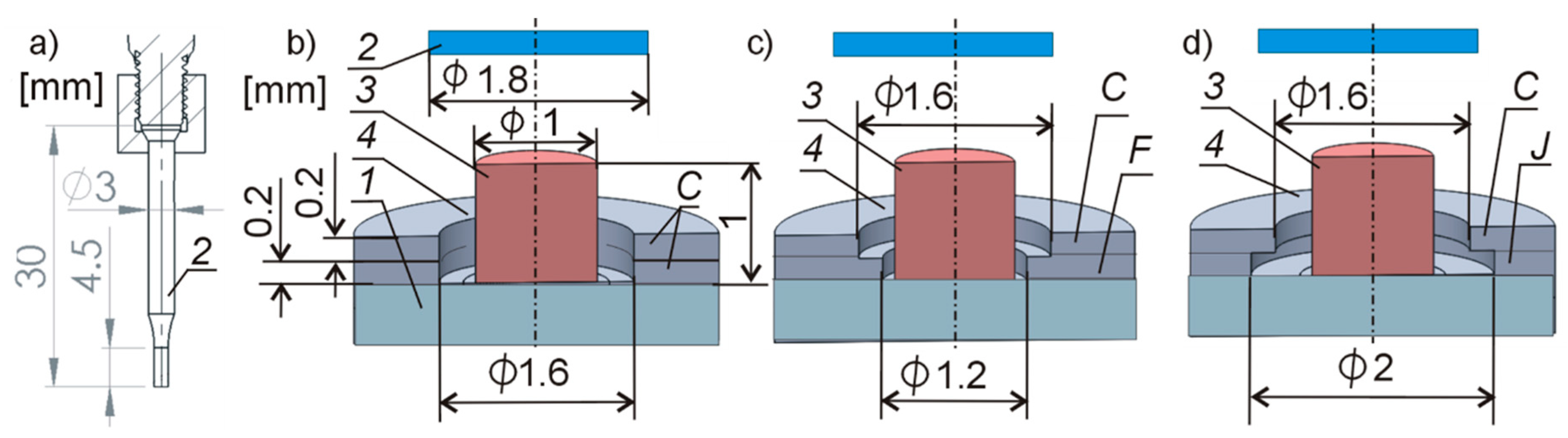
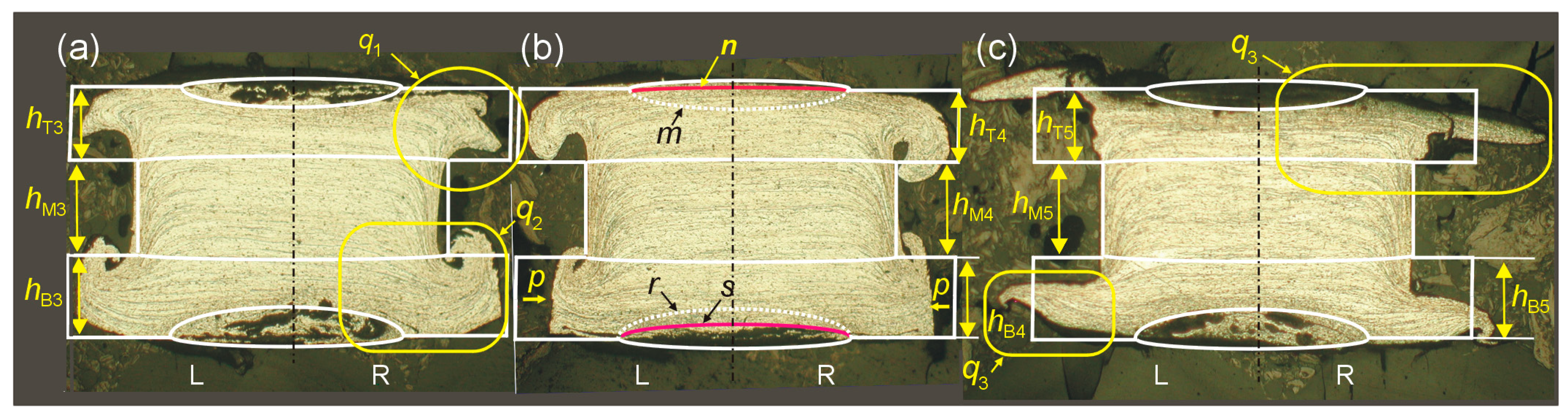
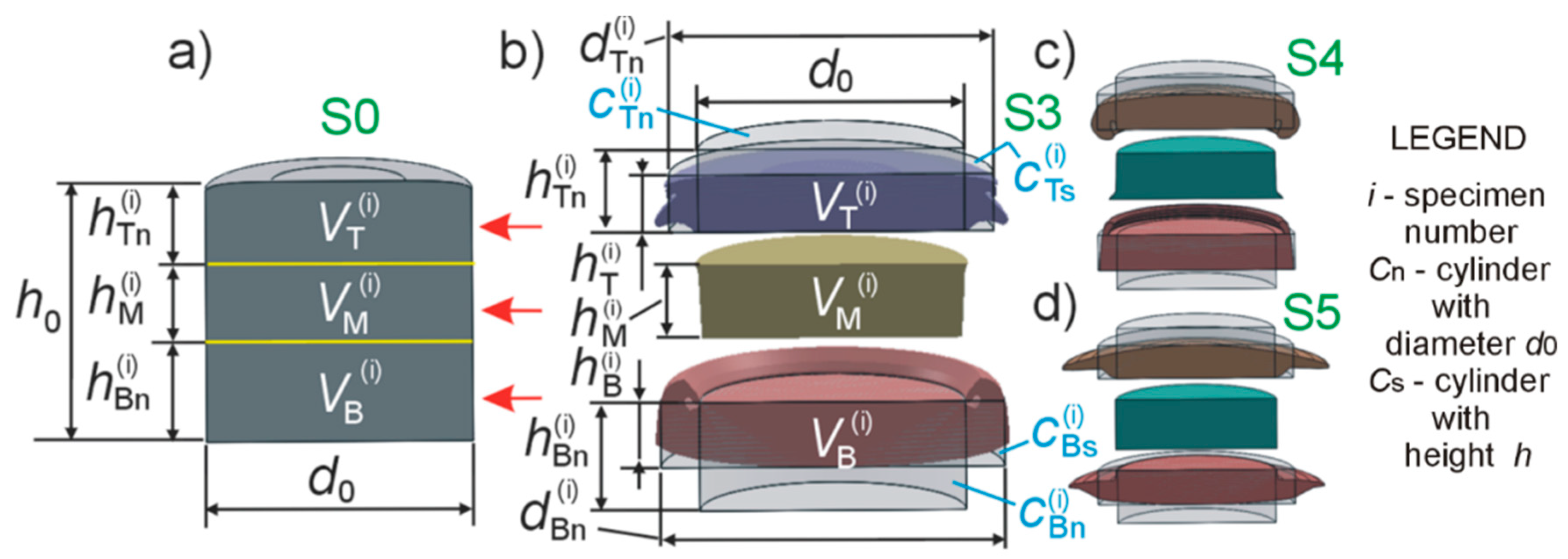
2. Materials and Methods
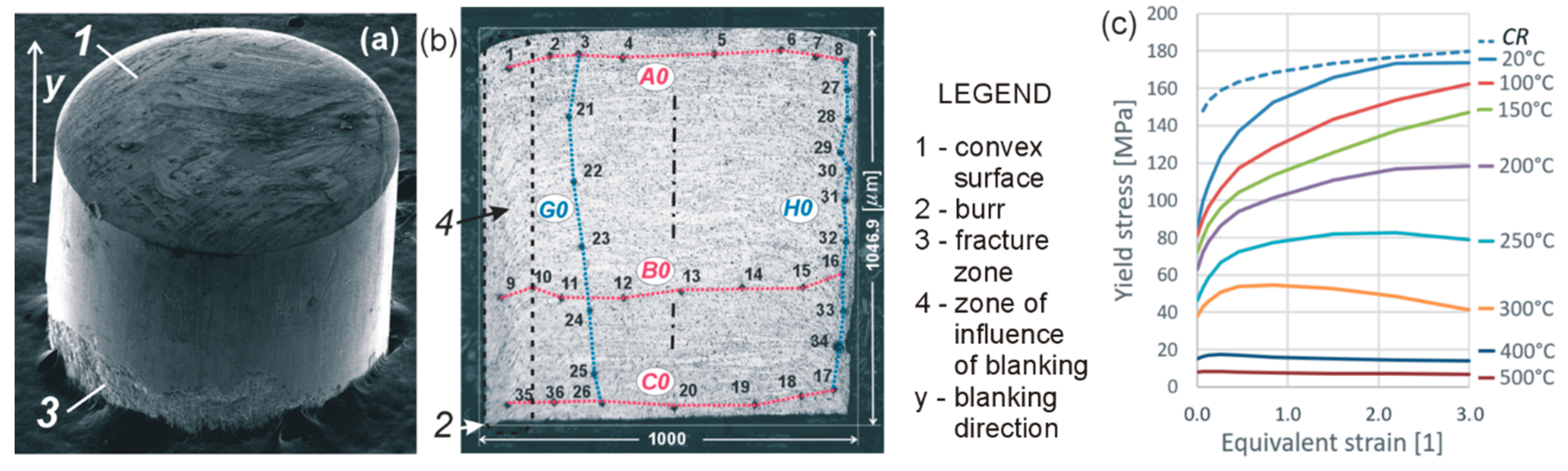
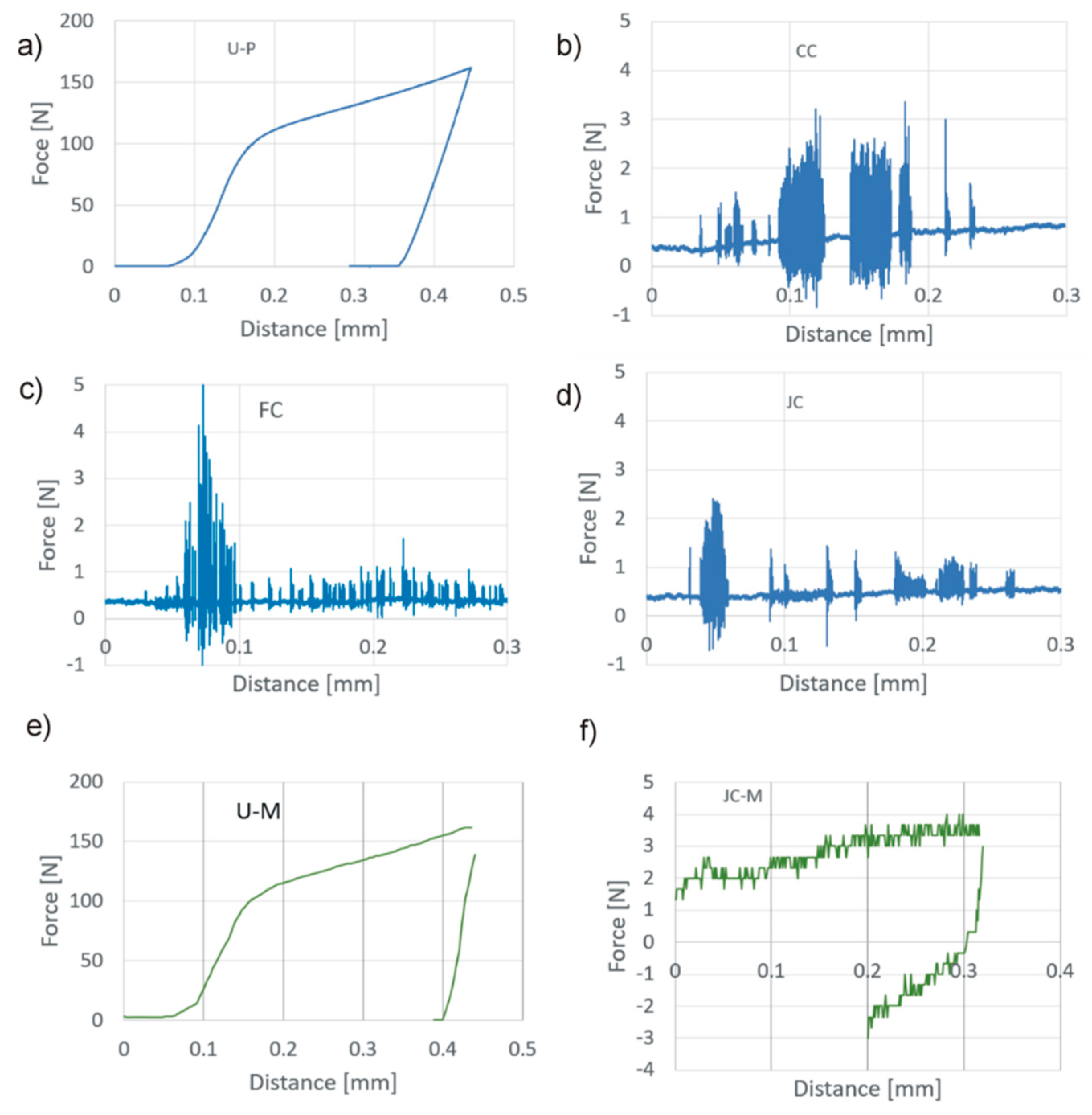
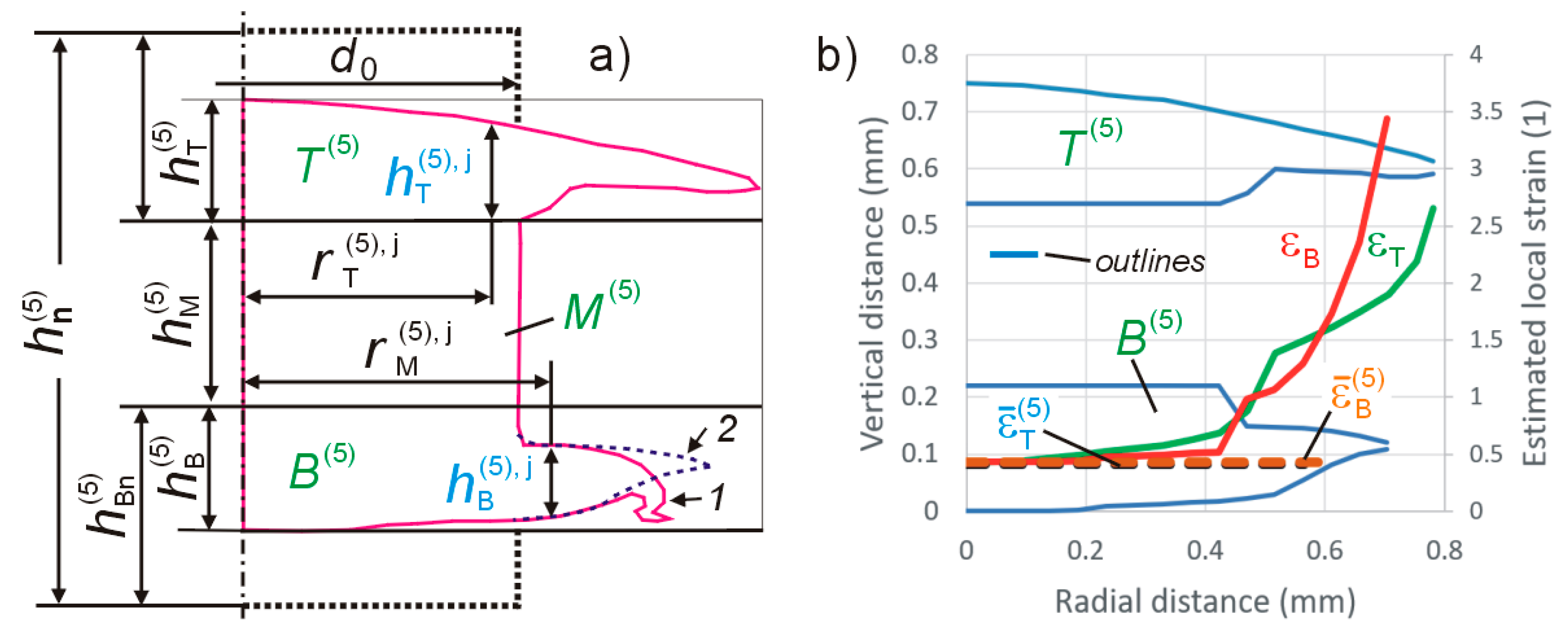
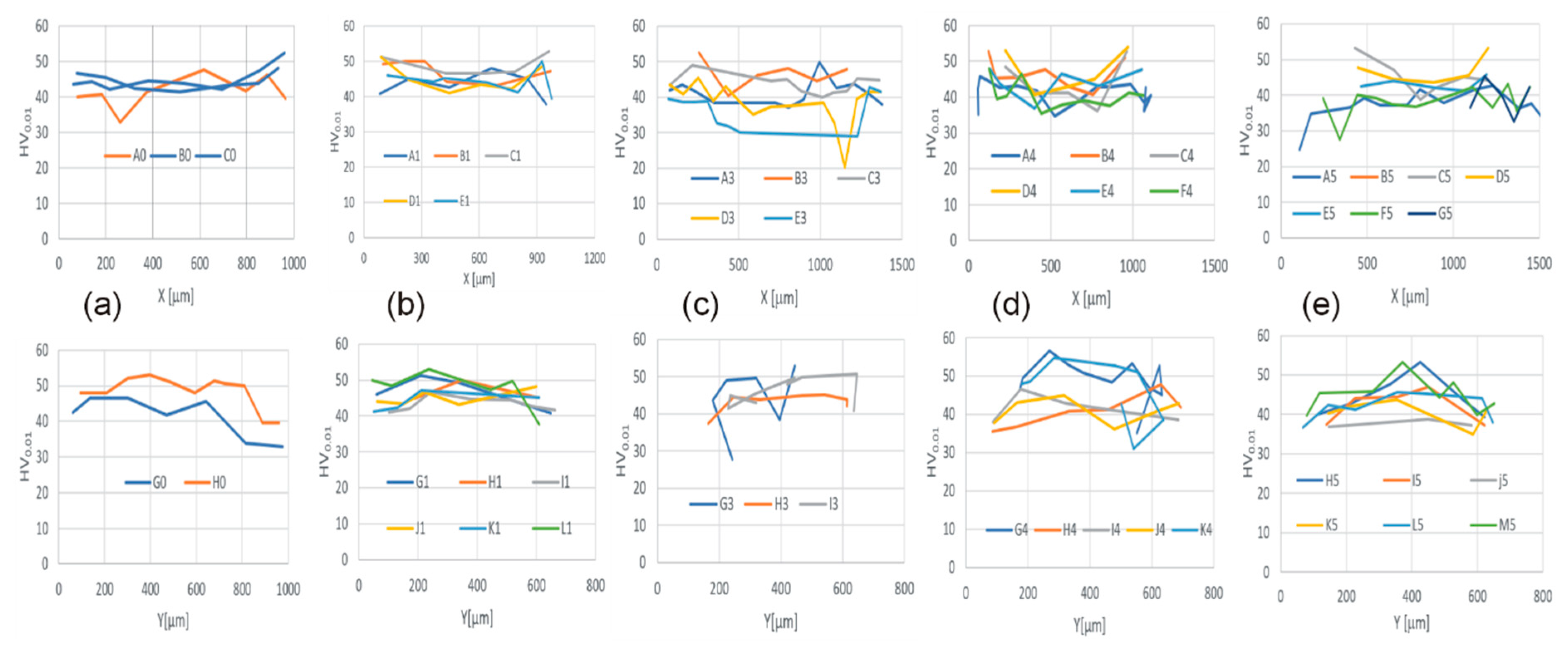
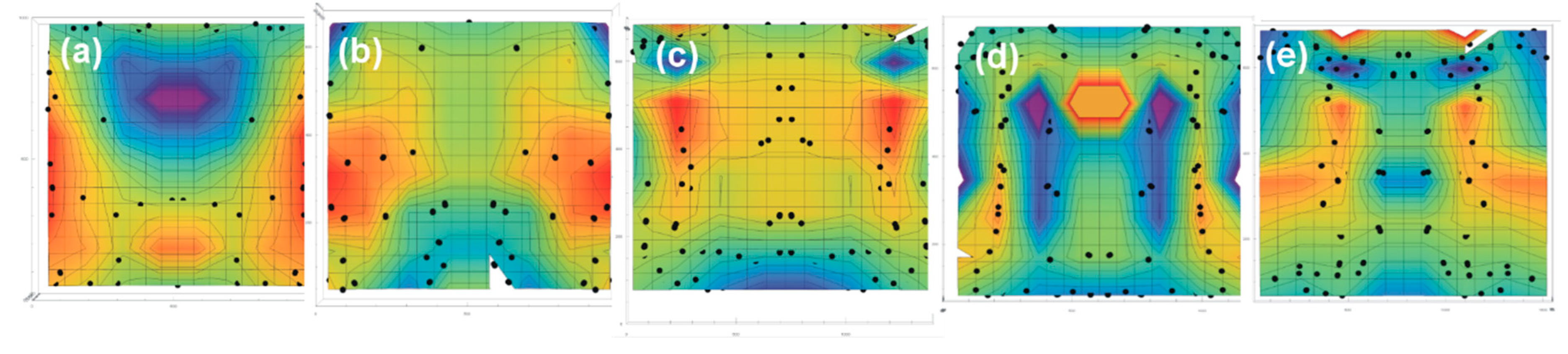
3. Results
4. Discussions
5. Conclusions and Future Work Suggestions
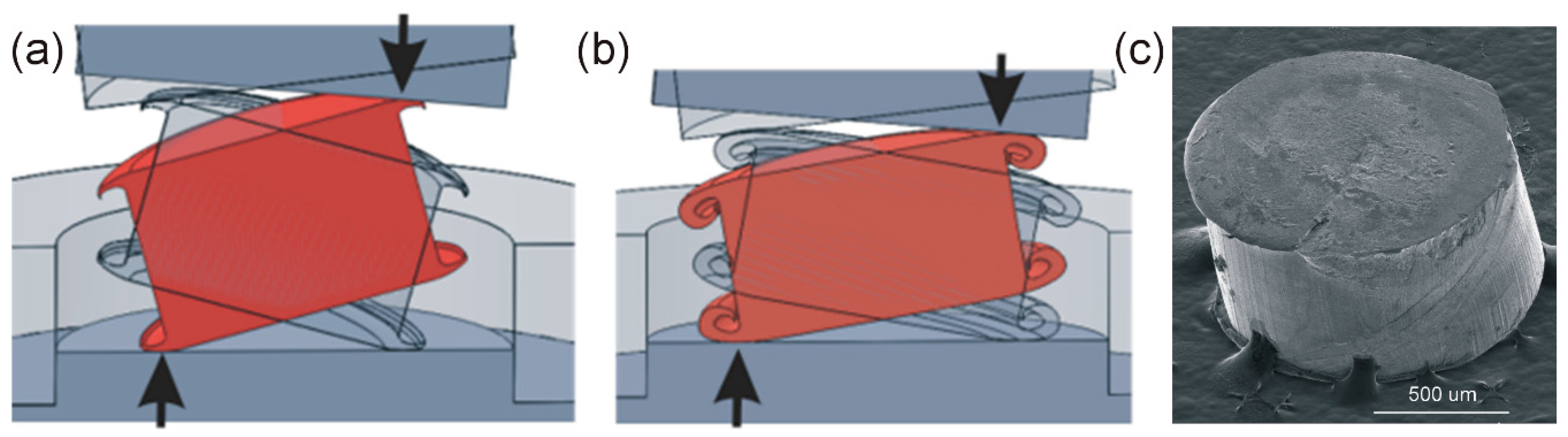
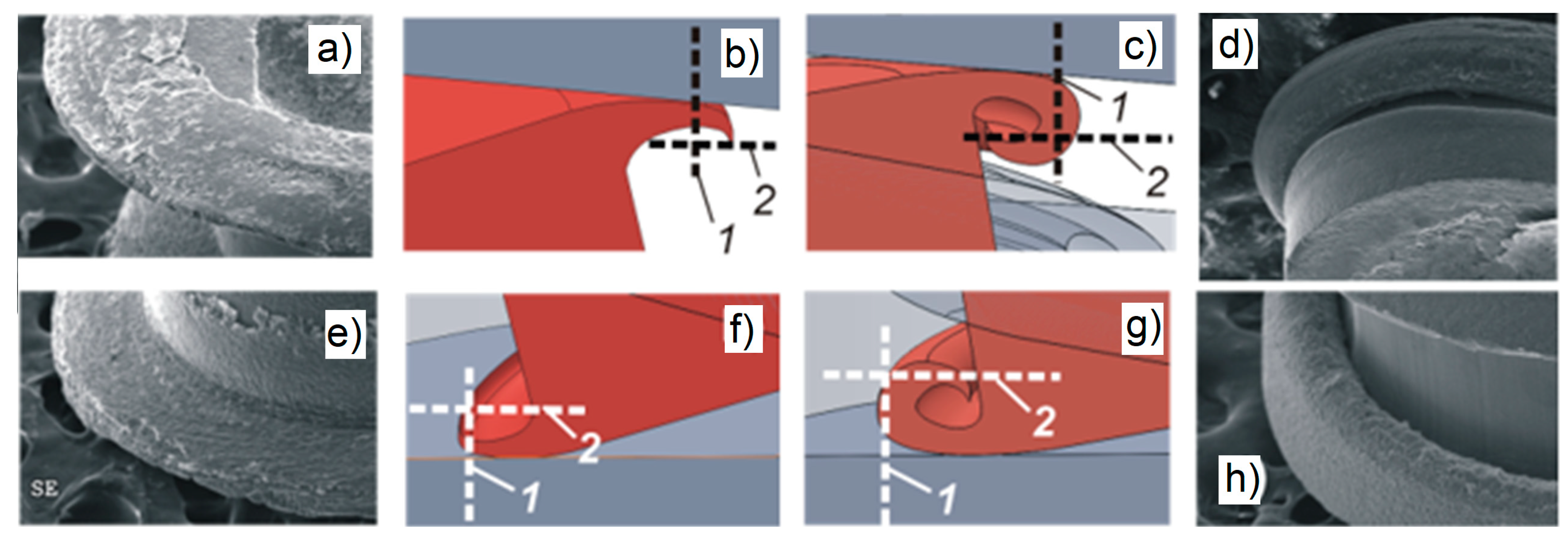
- The OMF process causes the initial deformation of the edge material of the rotating workpiece. In further phases of the process, the deformation expands on both sides towards the center of the object.
- In the UOM process under investigation, only the upper and lower part of the workpiece is deformed, occupying approximately 70% of the volume. The middle part of the sample remains undeformed.
- During the UOM process, the material flows in layers of different flow velocity, which is most probably caused by the generation of heat at the interface of the workpiece-tool due to intense plastic deformation and friction resulting from the sliding edge of the rotating sample on the tool surface during the initial centrifugation phase.
- It was observed that the deformation takes place in phases between which breaks occur, during which the deformation does not take place.
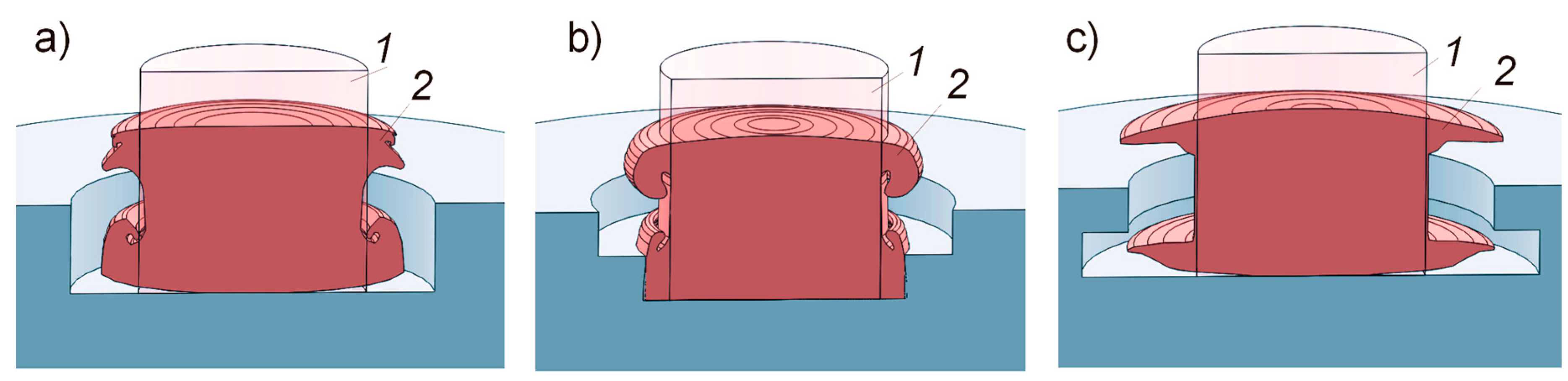
- The progressive deformation can be modified by the internal shape of the micro-die in which the UOM process takes place.
- The internal shape of the die in which the UOM process takes place affects the final shape of the microproduct.
- The shape of the microproduct obtained during UOM process does not accurately reflect the shape of the matrix in which this process takes place.
Funding
Conflicts of Interest
References
- Ma, J.; Gong, F.; Yang, Z.; Zeng, W. Microdeep drawing of C1100 microsquare cups using microforming technology. Int. J. Adv. Manuf. Tech. 2016, 82, 1363–1369. [Google Scholar] [CrossRef]
- Olejnik, L.; Presz, W.; Rosochowski, A. Backward extrusion using micro-blanked aluminium sheet. Int. J. Mater. Form. 2009, 2, 617–620. [Google Scholar] [CrossRef]
- Geiger, M.; Kleiner, M.; Eckstein, R.; Tiesler, N.; Engel, U. Microforming. CIRP Ann. 2001, 50, 445–462. [Google Scholar] [CrossRef]
- Kocańda, A.; Presz, W.; Adamczyk, G.; Czyżewski, P.; Mazurek, W. Contact pressure distribution in upsetting of compound metals. J. Mater. Process. Tech. 1996, 60, 343–348. [Google Scholar] [CrossRef]
- Presz, W. Contact phenomena in microblanking. Int. J. Mater. Form. 2008, 1, 471–474. [Google Scholar] [CrossRef]
- Sałaciński, T.; Winiarski, M.; Chmielewski, T.; Świercz, R. Surface finishing using ceramic fiber brush tools. In Proceedings of the 26th Anniversary International Conference on Metallurgy and Materials (METAL), Brno, Czech Republic, 24–26 May 2017; pp. 1222–1226. [Google Scholar]
- Tiesler, N. Microforming—Size effects in friction and their influence on extrusion process. Wire 2002, 52, 34–38. [Google Scholar]
- Engel, U. Tribology in microforming. Wear 2006, 260, 265–273. [Google Scholar] [CrossRef]
- Cheng, C.; Wan, M.; Meng, B. Size effect on the forming limit of sheet metal in micro-scaled plastic deformation considering free surface roughening. Proc. Eng. 2017, 207, 1010–1015. [Google Scholar] [CrossRef]
- Wang, C.; Guo, B.; Shan, D.; Zhang, M.; Bai, X. Tribological behaviors in microforming considering microscopically trapped lubricant at contact interface. Int. J. Adv. Manuf. Tech. 2014, 71, 2083–2090. [Google Scholar] [CrossRef]
- Presz, W. The method of determining the tendency to galling in vibration assisted microforming. In Proceedings of the 27th International Conference on Metallurgy and Materials, Brno, Czech Republic, 23–25 May 2018; pp. 450–456. [Google Scholar]
- Muster, A.; Presz, W. Influence of initial surface roughness on galling behaviour of steel-steel couple. Scand. J. Metall. 1999, 28, 5–8. [Google Scholar]
- Skowrońska, B.; Szulc, J.; Chmielewski, T.; Sałaciński, T.; Świercz, R. Properties and microstructure of hybride PLASMA+MAG welded joints of thermomechanically treated S700MC. In Proceedings of the 27th International Conference on Metallurgy and Materials, Brno, Czech Republic, 23–25 May 2018; pp. 849–854. [Google Scholar]
- Ghassemali, E.; Tan, M.J.; Wah, C.B.; Jarfors, A.E.; Lim, S.C.V. Grain size and workpiece dimension effects on material flow in an open-die micro-forging/extrusion process. Mater. Sci. Eng. 2013, 582, 379–388. [Google Scholar] [CrossRef]
- Presz, W.; Cacko, R. Analysis of the influence of of a rivet yield stress distribution on the micro-SPR joint—Initial approach. Arch. Civ. Mech. Eng. 2010, 10, 69–75. [Google Scholar] [CrossRef]
- Pintu, K.; Sudhansu, S.P. A review on properties and microstructure of micro-extruded product using SPD and as-cast material. Sadhana 2018, 43, 77. [Google Scholar]
- Ran, J.Q.; Fu, M.W.; Chan, W.L. The influence of size effect on the ductile fracture in micro-scaled plastic deformation. Int. J. Plast. 2013, 41, 65–81. [Google Scholar] [CrossRef]
- Wang, J.L.; Fu, M.W.; Shi, S.Q. Influences of size effect and stress condition on ductile fracture behavior in micro-scaled plastic deformation. Mater. Des. 2017, 131, 69–80. [Google Scholar] [CrossRef]
- Presz, W.; Andersen, B.; Wanheim, T. Piezoelectric driven micro-press for microforming. J. Achiev. Mater. Manuf. Eng. 2006, 18, 411–414. [Google Scholar]
- Cannella, E.; Nielsen, E.; Stolfi, A. Designing a tool system for lowering friction during the ejection of in-die sintered micro gears. Micromachines 2017, 8, 214. [Google Scholar] [CrossRef]
- Paldan, N.A.; Arentoft, M.; Eriksen, R.S.; Mangeot, C. Piezo driven prestressing of die-system for microforming of metal components. Int. J. Mater Form. Suppl. 2008, 1, 467–470. [Google Scholar] [CrossRef]
- Presz, W. Scale effect in design of the pre-stressed micro-dies for microforming. Comput. Methods Mater. Sci. 2016, 16, 196–203. [Google Scholar]
- Presz, W.; Rosochowski, M. Application of semi-physical modeling of interface surface roughness in design of pre-stressed microforming dies. Int. Conf. on the Technology of Plasticity, Cambridge, U.K. Procedia Eng. 2017, 207, 1004–1009. [Google Scholar] [CrossRef]
- Presz, W.; Cacko, R. Application of complex micro-die for extrusion of micro-rivets for micro-joining. In Proceedings of the 26th International Conference on Metallurgy and Materials (METAL), Brno, Czech Republic, 24–26 May 2017; pp. 514–520. [Google Scholar]
- Presz, W.; Cacko, R. Bimetallic micro-punches for micro-blanking processes. Archiv. Metall. Mater. 2018, 1, 29–34. [Google Scholar]
- Piwnik, J.; Mogielnicki, K.; Gabrylewski, M.; Baranowski, P. The experimental tool for micro-extrusion of metals. Archiv. Foundry Eng. 2011, 2, 195–198. [Google Scholar]
- Ghassemali, E.; Jarfors, A.E.W.; Tan, M.J.; Lim, S.C.V. On the microstructure of micro-pins manufactured by a novel progressive microforming process. Int. J. Mater. Form. 2013, 6, 65–74. [Google Scholar] [CrossRef]
- Stellin, T.; van Tijum, R.; Engel, U. Modelling and experimental study of a microforging process from metal strip for the reduction of defects in mass production. Prod. Eng. Re. Dev. 2016, 10, 103–112. [Google Scholar] [CrossRef]
- Gong, F.; Guo, B. Size effects on mechanical properties of copper thin sheet in uniaxial tensile tests. Medziagotyra 2014, 20, 509–512. [Google Scholar] [CrossRef]
- Presz, W. The method of micro-upsetting in uneven temperature Distribution. In Proceedings of the 27th International Conference on Metallurgy and Materials, Brno, Czech Republic, 23–25 May 2018. s2.0-85056217326. [Google Scholar]
- Liu, Y.; Wang, C.; Han, H.; Shan, D.; Guo, B. Investigation on effect of ultrasonic vibration on micro-blanking process of copper foil. Int. J. Adv. Manuf. Tech. 2017, 93, 2243–2249. [Google Scholar] [CrossRef]
- Huang, G.; Gary, J.-C. Laser-induced high-strain-rate superplastic 3-D microforming of metallic thin films. J. Microelectromech. Syst. 2010, 19, 273–281. [Google Scholar]
- Djavanroodi, F.; Ahmadian, H.; Koohkan, K.; Naseri, R. Ultrasonic assisted-ECAP. Ultrasonics 2013, 53, 1089–1096. [Google Scholar] [CrossRef]
- Christina, B.; Gracious, N. Influence of ultrasonic vibration on micro-extrusion. Ultrasonics 2011, 51, 606–616. [Google Scholar]
- Hung, J.-C.; Hung, C. The influence of ultrasonic-vibration on hot upsetting. Ultrasonics 2005, 43, 692–698. [Google Scholar] [CrossRef] [PubMed]
- Presz, W.; Kulik, T. Ultrasonic vibrations as an impulse for glass transition in microforming of bulk metallic glass. Archiv. Civ. Mech. Eng. 2018, 19, 100–113. [Google Scholar] [CrossRef]
- Abdul, A.S.; Lucas, M. The effect of ultrasonic excitation in metal forming tests. Appl. Mech. Mater. 2010, 24, 311–316. [Google Scholar] [CrossRef]
- Presz, W.; Cacko, R. Ultrasonic assisted microforming. In Proceedings of the 26th International Conference on Metallurgy and Materials (METAL), Brno, Czech Republic, 24–26 May 2017; pp. 521–526. [Google Scholar]
- Shimizu, T.; Kakegawa, T.; Yang, M. Micro-texturing of DLC thin film coatings and its tribological performance under dry sliding friction for microforming operation. Procedia Eng. 2014, 81, 1884–1889. [Google Scholar] [CrossRef]
- Daud, Y.; Lucas, M.; Huang, Z. Superimposed ultrasonic oscillations in compression tests of aluminium. Ultrasonics 2006, 44, 511–515. [Google Scholar] [CrossRef]
- Zhou, H.; Cui, H.; Qin, Q.H.; Wang, H.; Shen, Y. A comparative study of mechanical and microstructural characteristics of aluminium and titanium undergoing ultrasonic assisted compression testing. Mater. Sci. Eng. 2017, 682, 376–388. [Google Scholar] [CrossRef]
- Hu, J.; Shimizu, T.; Yang, M. Investigation on ultrasonic volume effects: Stress superposition, acoustic softening and dynamic impact. Ultrason. Sonochem. 2018, 48, 240–248. [Google Scholar] [CrossRef]
- Hung, C.; Tsai, Y.-C. Investigation of the effects of ultrasonic vibration-assistedmicro-upsetting on brass. J. Mater. Sci. Eng. 2013, 580, 125–132. [Google Scholar] [CrossRef]
- Raja, R.; Lakshminarasimhan, S.; Murugesan, P. Investigation of barreling radius and top surface area for cold upsetting of aluminum specimens. Int. J. Mod. Eng. Res. 2013, 3, 3852–3862. [Google Scholar]
- Zhou, H.; Cui, H.; Qin, Q.H. Influence of ultrasonic vibration on the plasticity of metals during compression process. J. Mater. Process. Tech. 2018, 251, 146–159. [Google Scholar] [CrossRef]
- Yao, Z.; Kim, G.Y.; Faidley, L.; Zou, Q.; Mei, D.; Chen, Z. Effects of superimposed high-frequency vibration on deformation of aluminium in micro/meso-scale upsetting. J. Mater. Process. Tech. 2012, 212, 640–646. [Google Scholar] [CrossRef]
- Liu, Y.; Suslov, S.; Han, Q.; Hua, L.; Xu, C. Comparison between ultrasonic vibration-assisted upsetting and conven-tional upsetting. Metall. Mater. Trans. 2013, 44, 3232–3244. [Google Scholar] [CrossRef]
- Presz, W. Dynamic effect in ultrasonic assisted micro-upsetting. In Proceedings of the 21st International ESAFORM Conference on Material Forming, Palermo, Italy, 23–25 April 2018; p. 100012. [Google Scholar]
- Hu, J.; Shimizu, T.; Yoshino, T.; Shiratori, T.; Yang, M. Ultrasonic dynamic impact effect on deformation of aluminum during micro-compression tests. J. Mater. Process. Tech. 2018, 258, 144–154. [Google Scholar] [CrossRef]
- Presz, W. Ultrasonic orbital microforming—A new possibility in the forming of microparts. Metals 2018, 8, 889. [Google Scholar] [CrossRef]



| Amplitude | Ram Velocity | |||
|---|---|---|---|---|
| At Surface of Booster | At Surface of Punch Nose | Amplification of Sonotrode | Loading | Unloading |
| (µm) | (µm) | (1) | (mm/min); (m/s) | (mm/min); (m/s) |
| 2.5 | 16.0 | 6.3 | 0.2; 3.3 × 10−6 | 0.02; 3.3 × 10−7 |
| E (GPa) | Re (MPa) | ν (1) | C (MPa) | N (1) |
|---|---|---|---|---|
| 70 | 135 | 0.32 | 170 | 0.05 |
| Specimen | V (mm3) | h (mm) | ||||||
|---|---|---|---|---|---|---|---|---|
| All | T | M | B | All | T | M | B | |
| S3 | 0.783 | 0.25 | 0.206 | 0.327 | 0.752 | 0.22 | 0.283 | 0.25 |
| S4 | 0.773 | 0.262 | 0.238 | 0.273 | 0.747 | 0.223 | 0.297 | 0.227 |
| S5 | 0.781 | 0.253 | 0.262 | 0.266 | 0.752 | 0.212 | 0.32 | 0.22 |
| Specimen | hn (mm) | ds. (mm) | ε (1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| T | M | B | T | M | B | T | M | B | |
| S3 | 0.318 | 0.263 | 0.417 | 1.202 | 0.964 | 1.291 | 0.368 | 0 | 0.511 |
| S4 | 0.334 | 0.304 | 0.347 | 1.223 | 1.011 | 1.236 | 0.402 | 0 | 0.424 |
| S5 | 0.322 | 0.334 | 0.339 | 1.232 | 1.022 | 1.241 | 0.417 | 0 | 0.432 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Presz, W. Material Flow in Ultrasonic Orbital Microforming. Metals 2019, 9, 475. https://doi.org/10.3390/met9040475
Presz W. Material Flow in Ultrasonic Orbital Microforming. Metals. 2019; 9(4):475. https://doi.org/10.3390/met9040475
Chicago/Turabian StylePresz, Wojciech. 2019. "Material Flow in Ultrasonic Orbital Microforming" Metals 9, no. 4: 475. https://doi.org/10.3390/met9040475
APA StylePresz, W. (2019). Material Flow in Ultrasonic Orbital Microforming. Metals, 9(4), 475. https://doi.org/10.3390/met9040475





