Electromagnetic Forces in Continuous Casting of Steel Slabs
Abstract
1. Introduction
2. Tools to Quantify Electromagnetic Effects
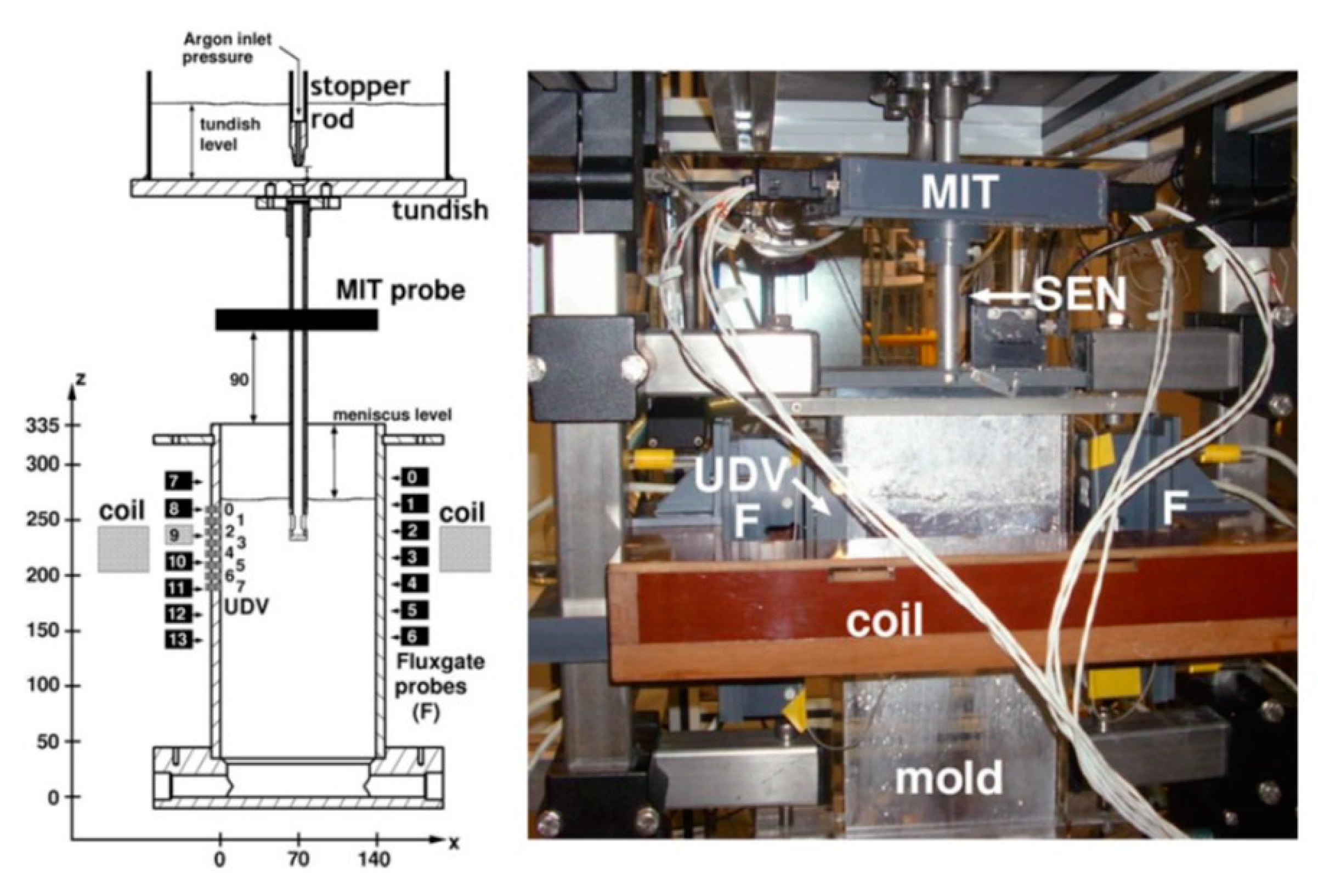
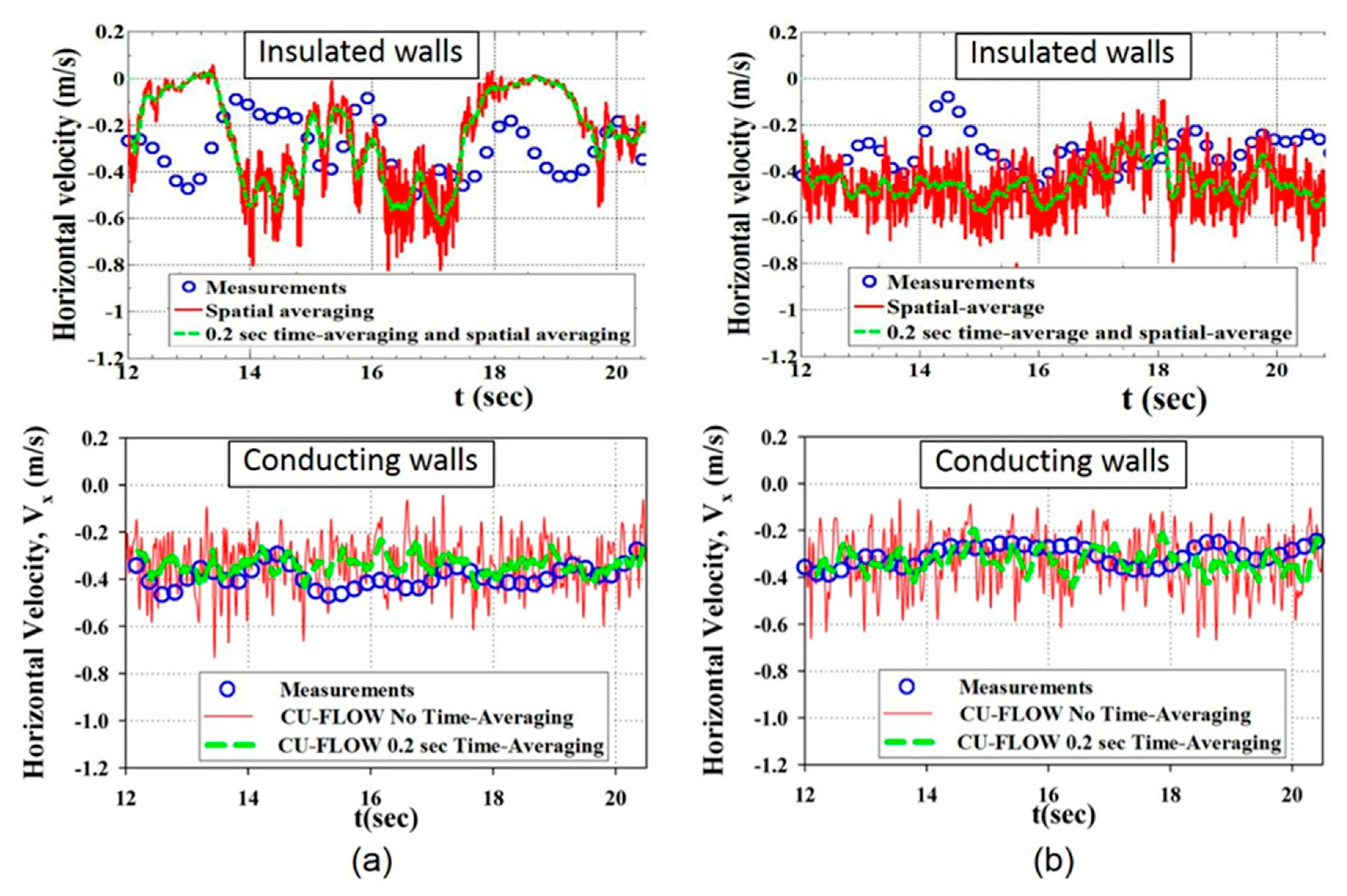
2.1. Plant Measurements of Fluid Flow Velocity
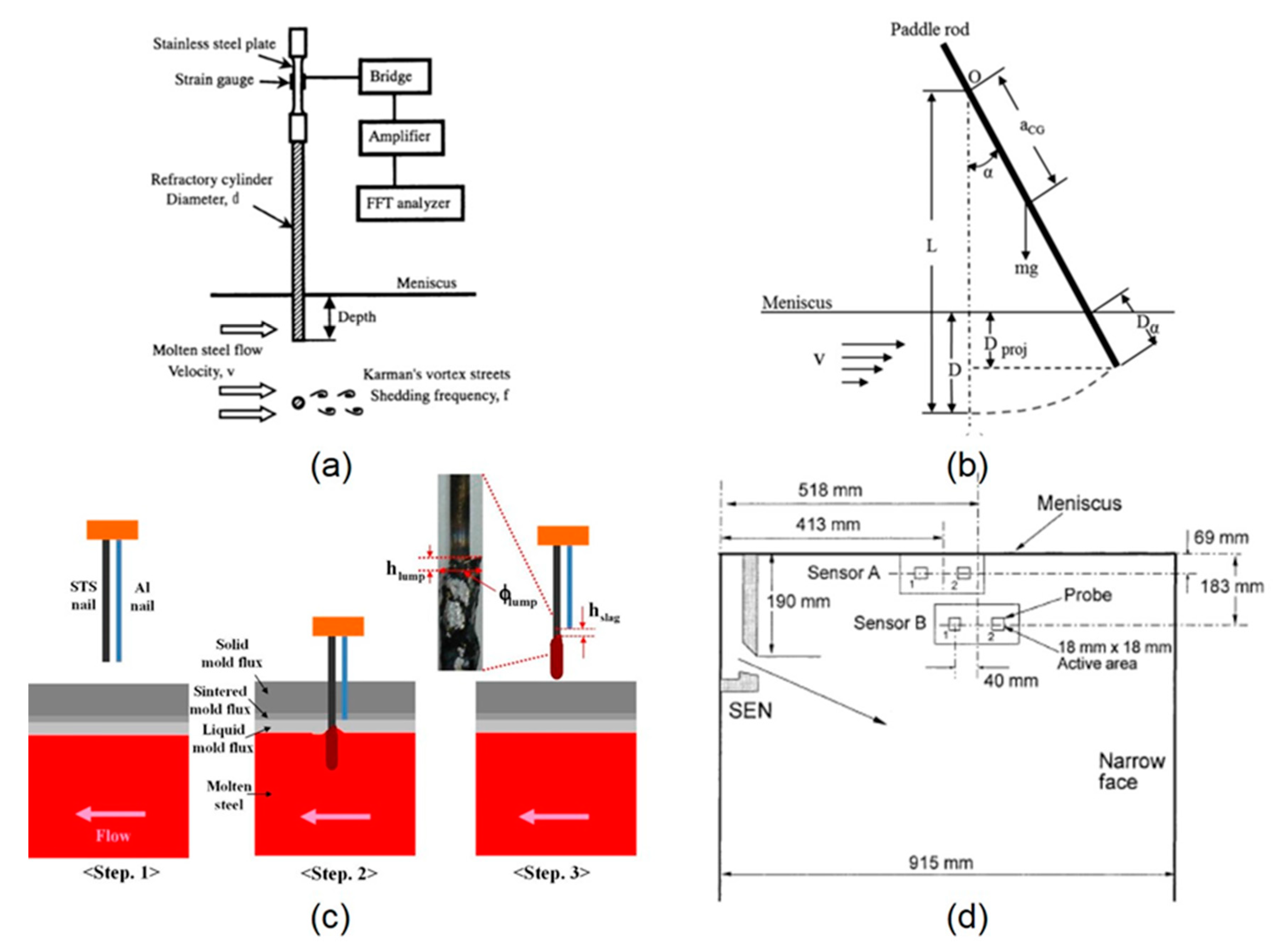
2.1.1. Strain Gauge Rod Tests
2.1.2. Paddle Rod Tests
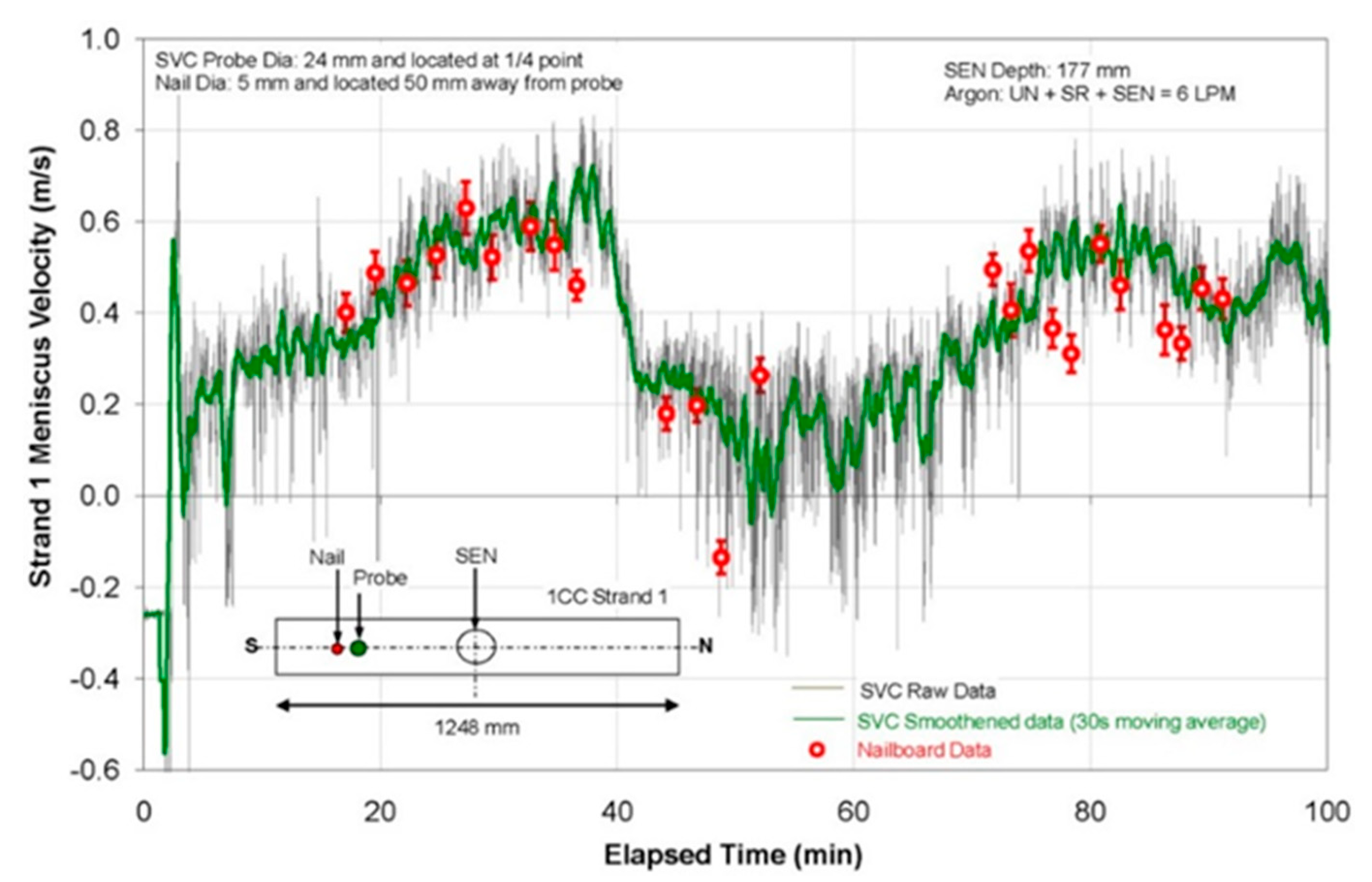
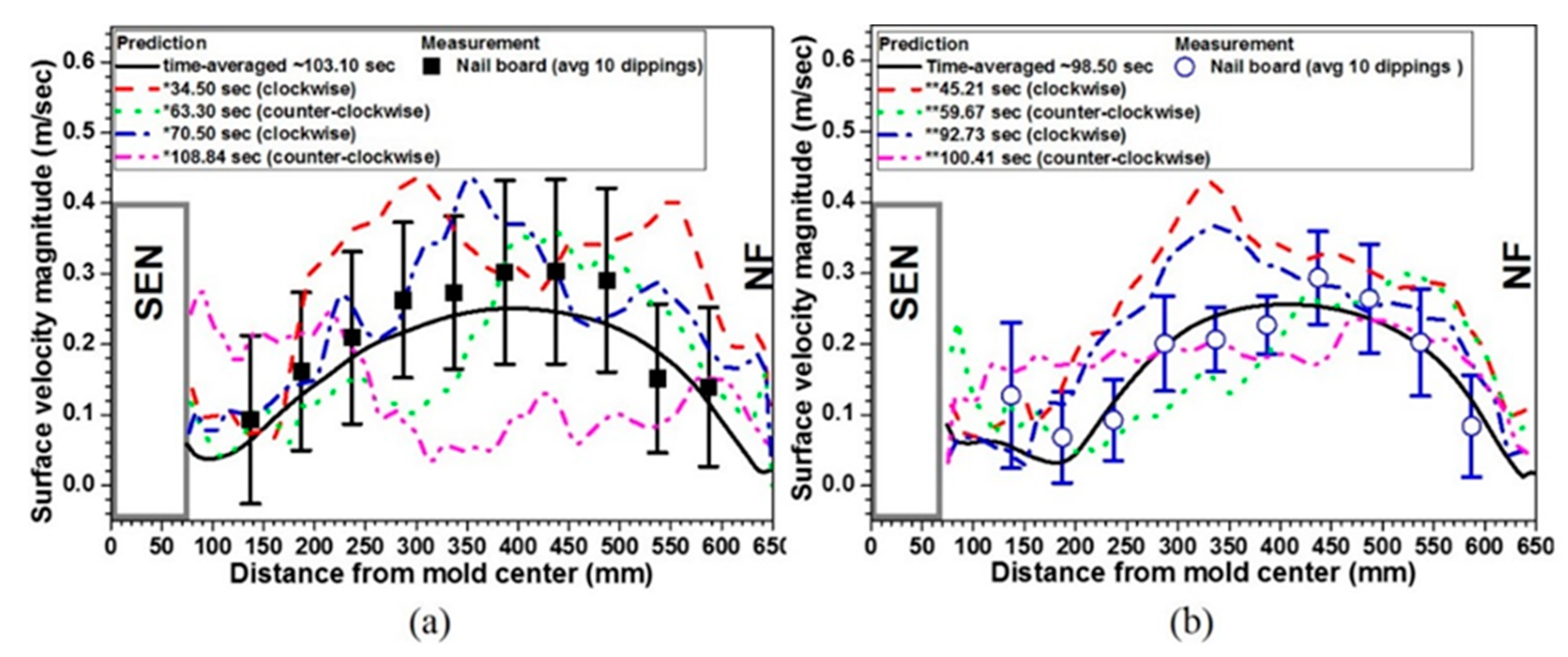
2.1.3. Nail Dipping Tests
2.1.4. Electromagnetic Mold Flow Control (MFC) Sensor Measurements
2.1.5. Columnar Dendrite Angle Measurements
2.1.6. Other Methods
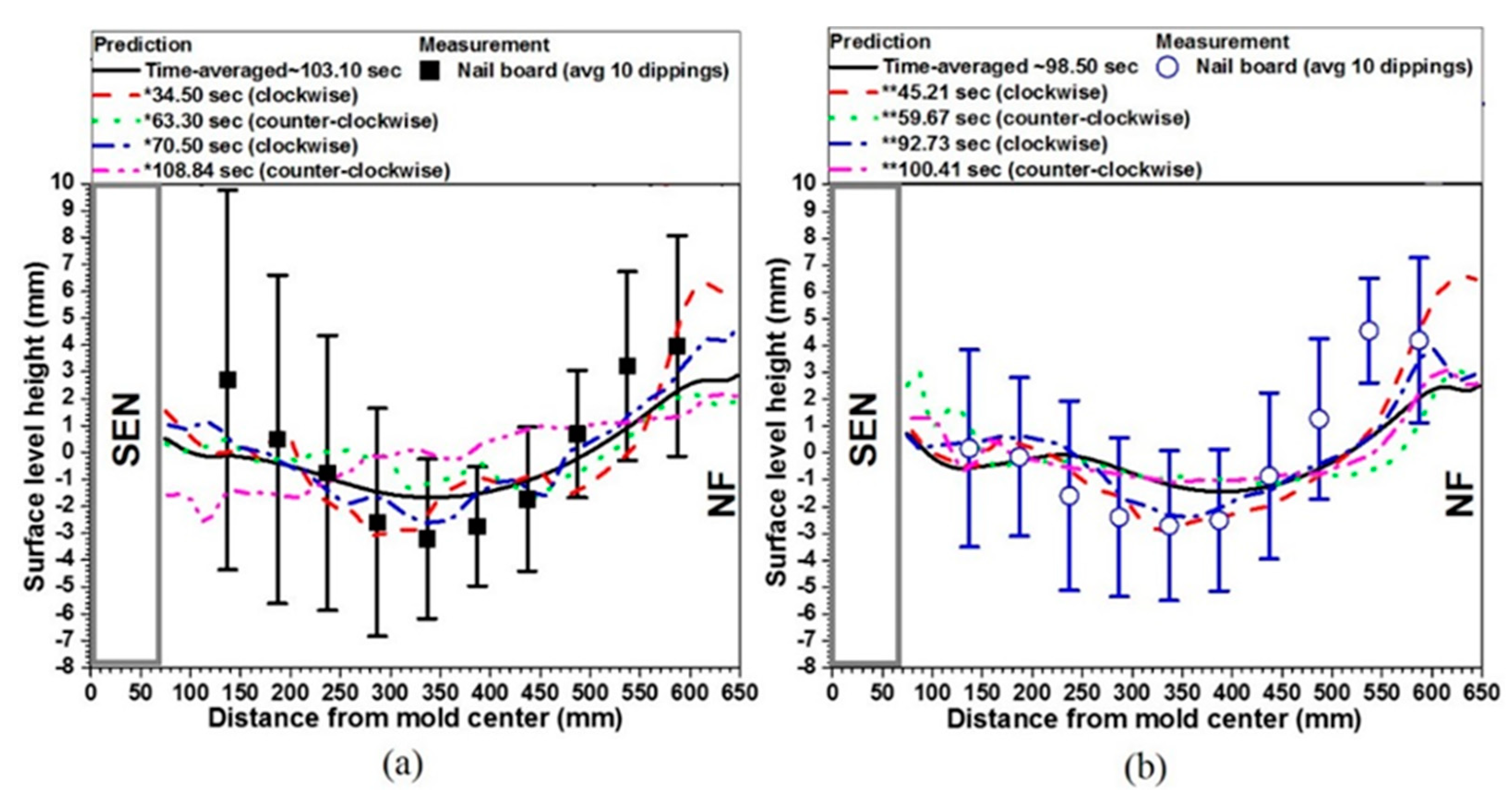
2.2. Plant Measurements of Surface Level Profile and Fluctuations
2.2.1. Eddy Current Sensor Measurements
2.2.2. Nail Board Tests
2.2.3. Sheet Dipping Tests
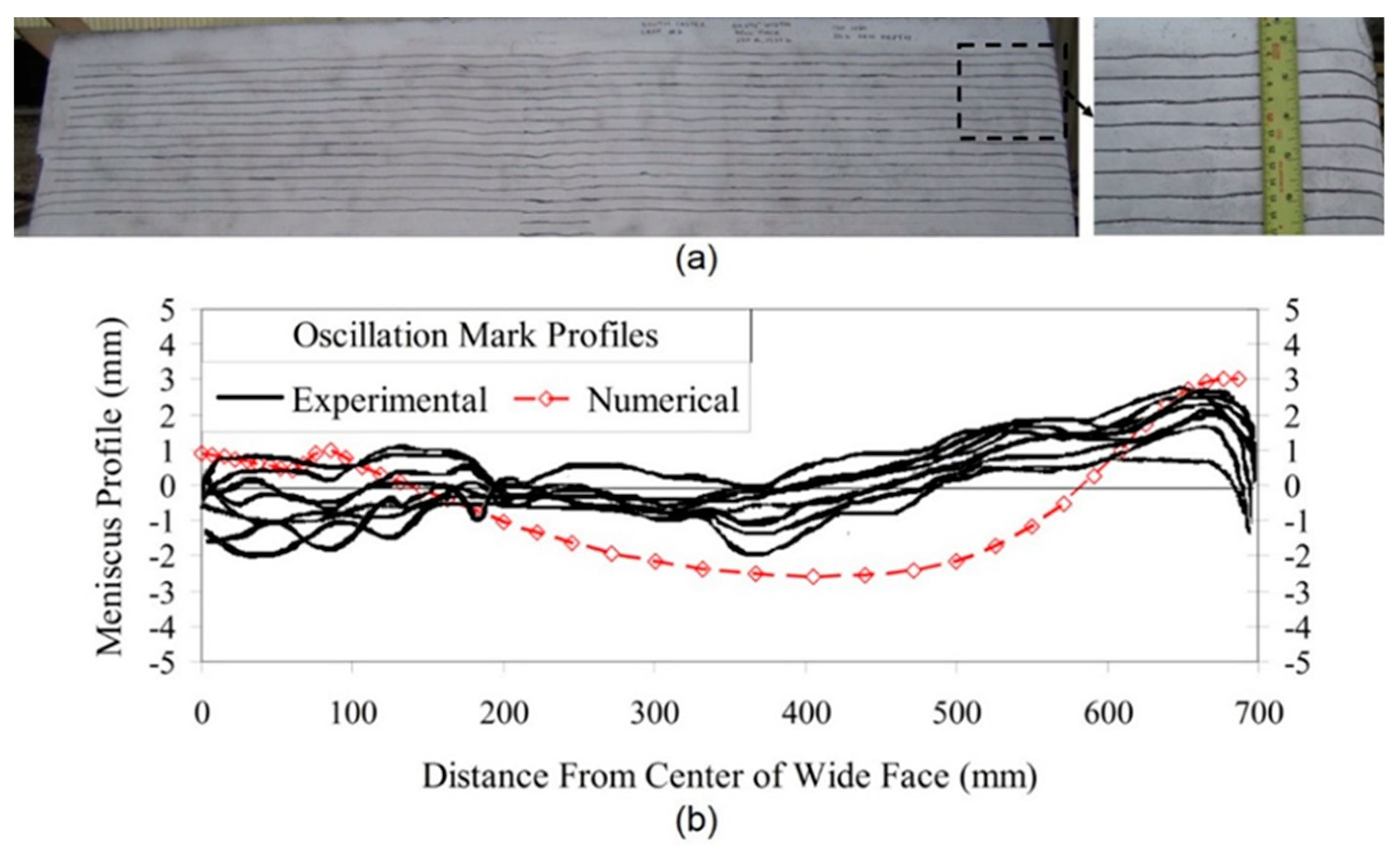
2.2.4. Oscillation Mark Measurements
2.3. Plant Measurements of Particle Capture
2.3.1. Ultrasonic Testing (UT) Measurements
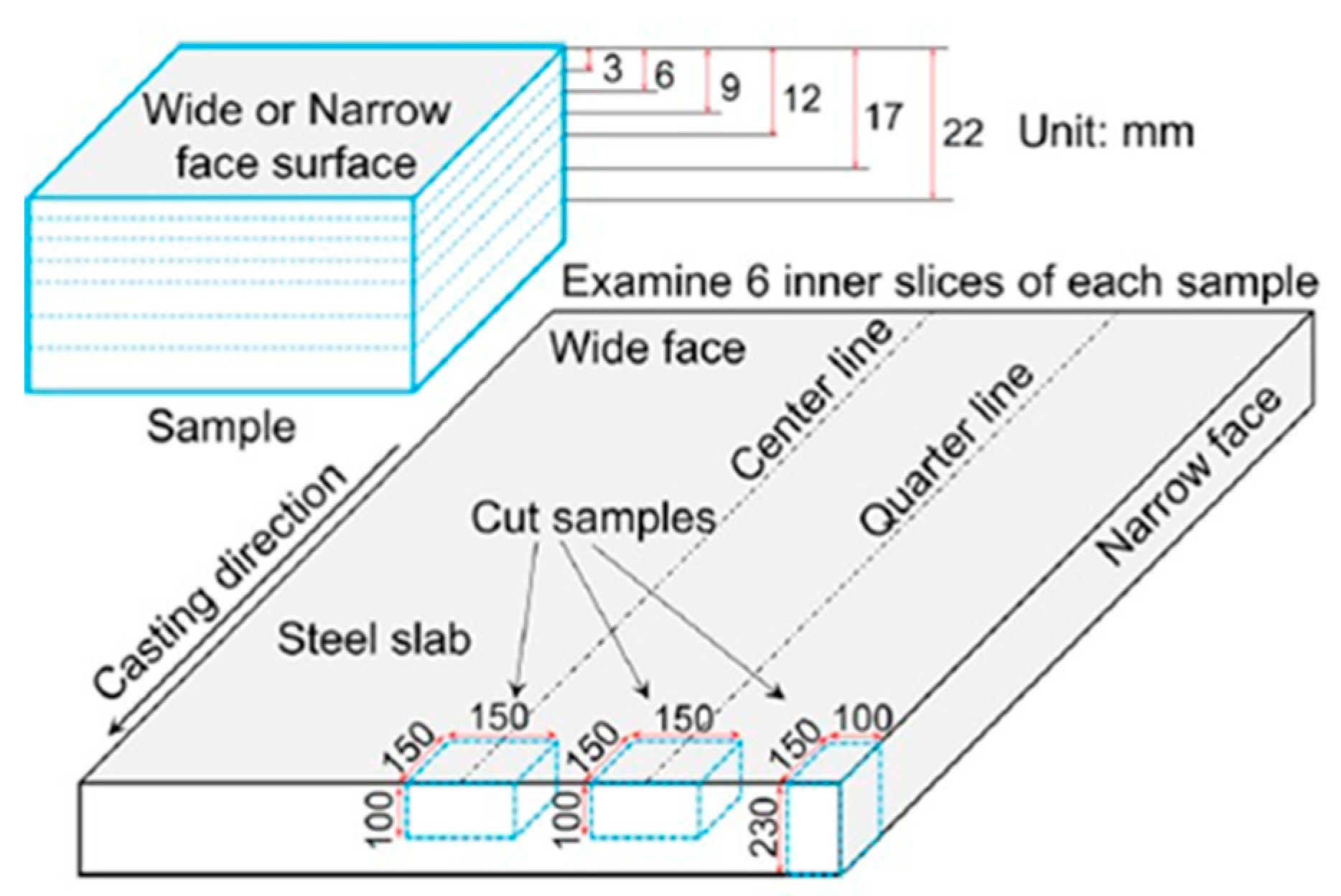
2.3.2. Step Milling Measurements
2.3.3. Other Methods to Measure Particle Capture
2.4. Lab Scale Modeling
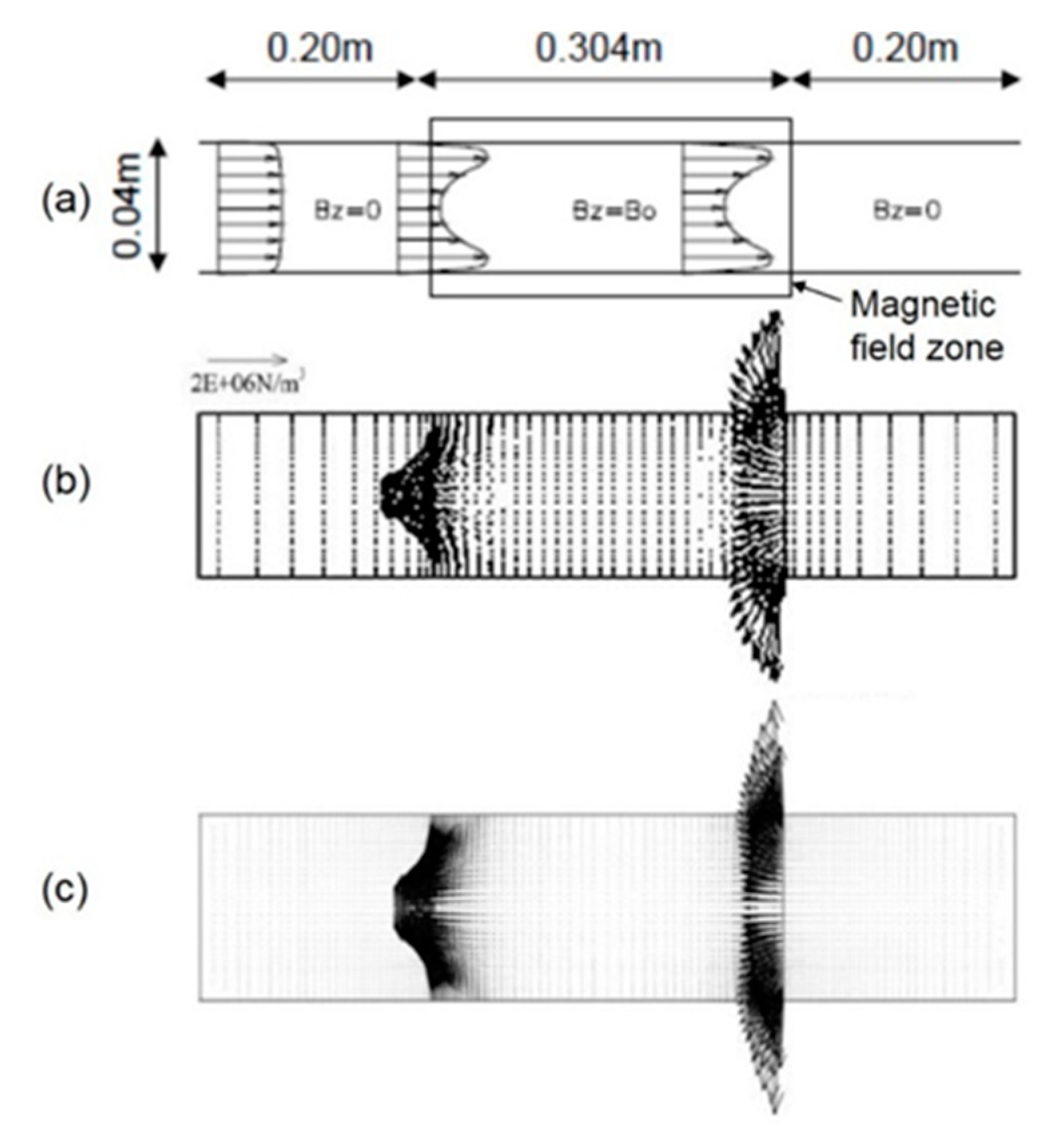
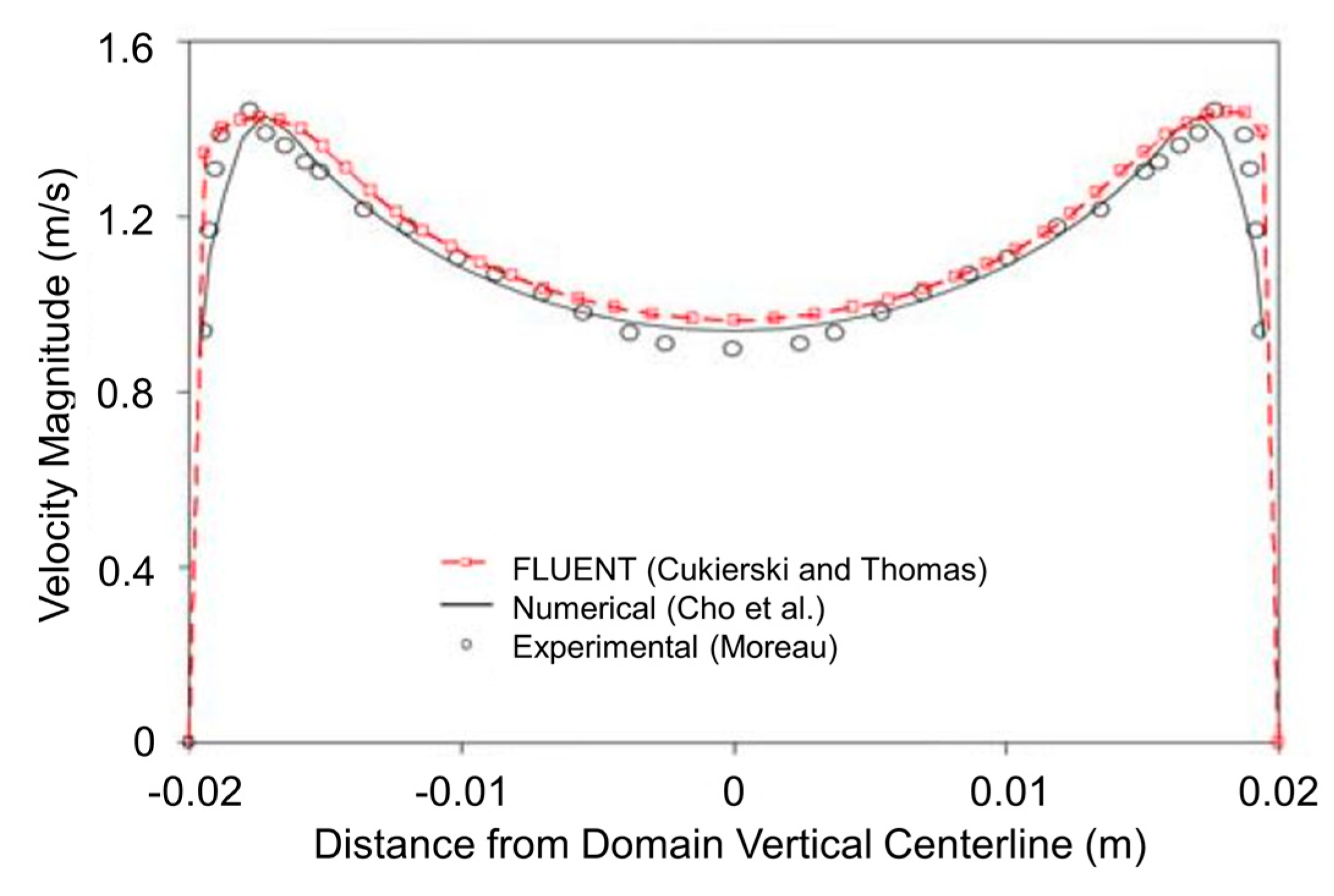
2.5. Computational Modeling: Magnetohydrodynamics (MHD) Models
3. Electromagnetic Effects on Fluid Flow Pattern
3.1. Local EMBr
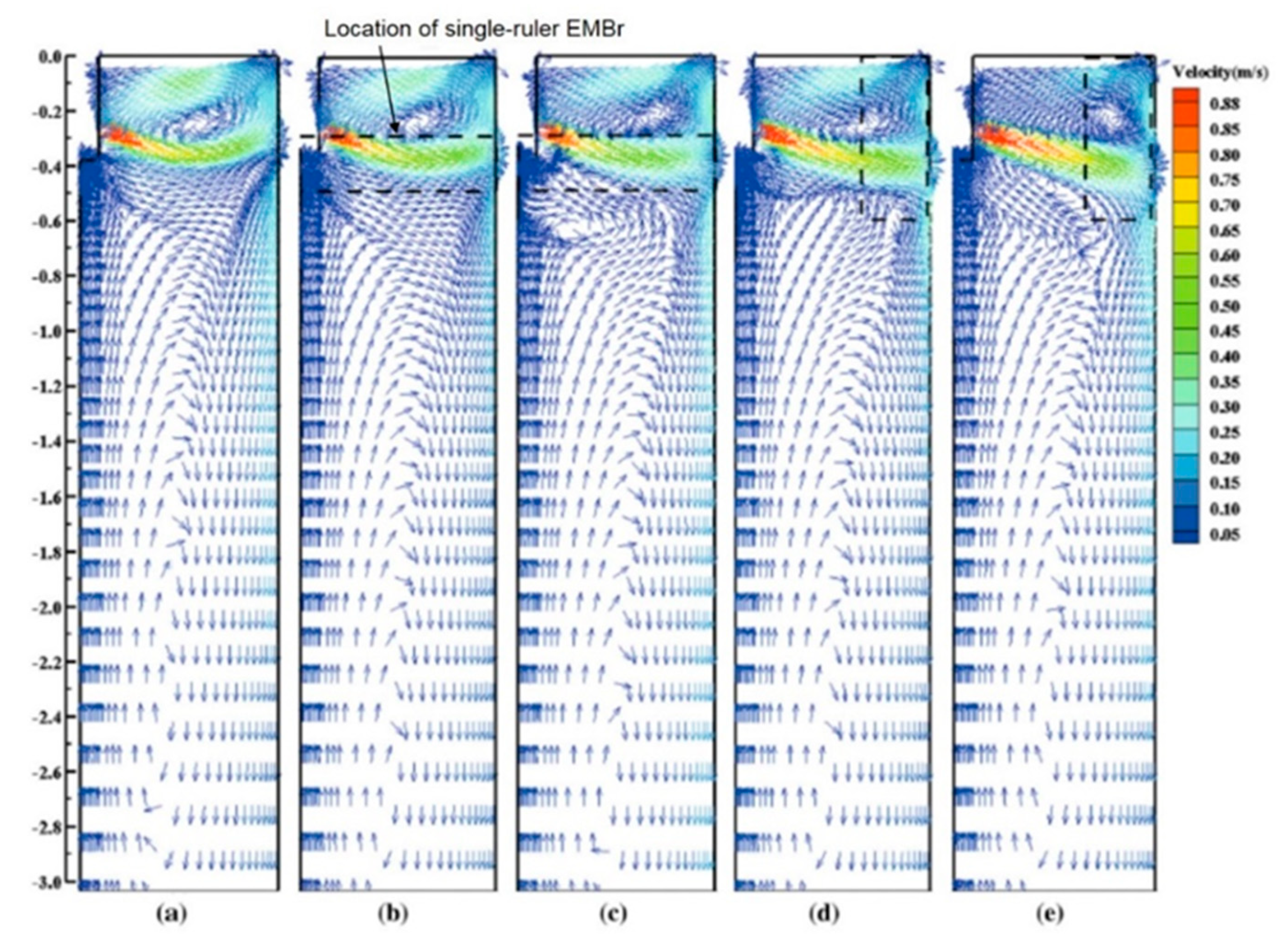
3.2. Single-Ruler EMBr
3.3. Double-Ruler EMBr
3.4. MM-EMB
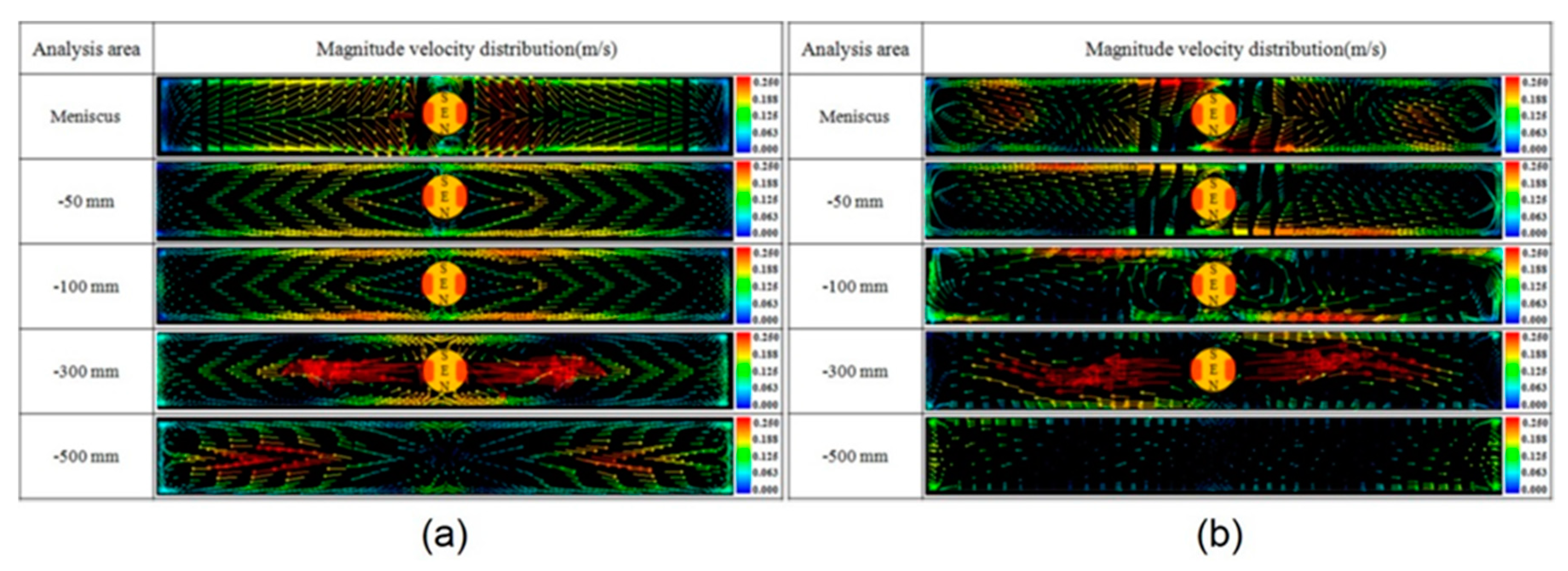
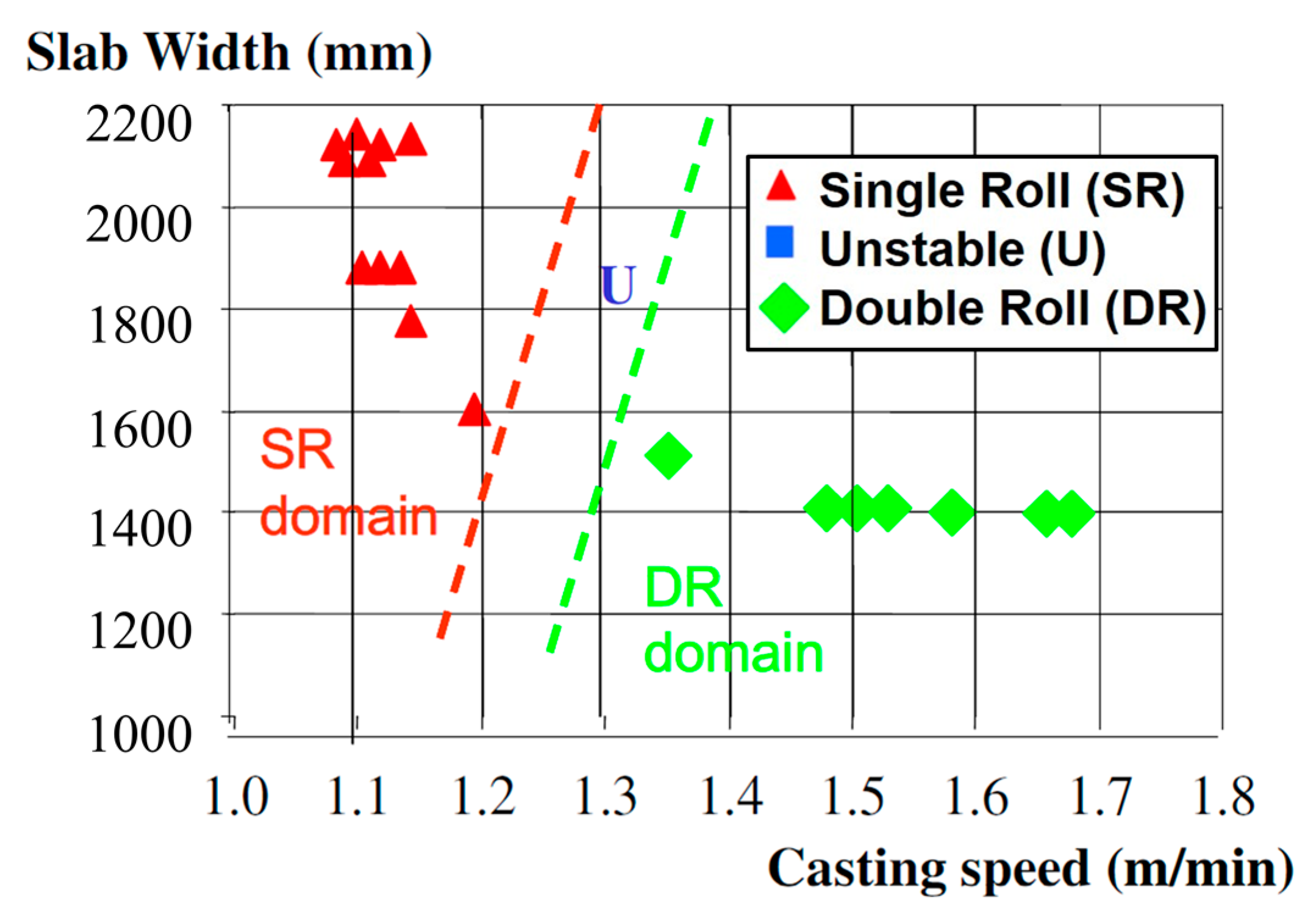
3.5. Moving Fields: EMLS, EMLA, EMRS, M-EMS, EMC, and SEMS
3.6. Combined Traveling and Static Fields
4. Electromagnetic Flow Control and Surface Instability Effects
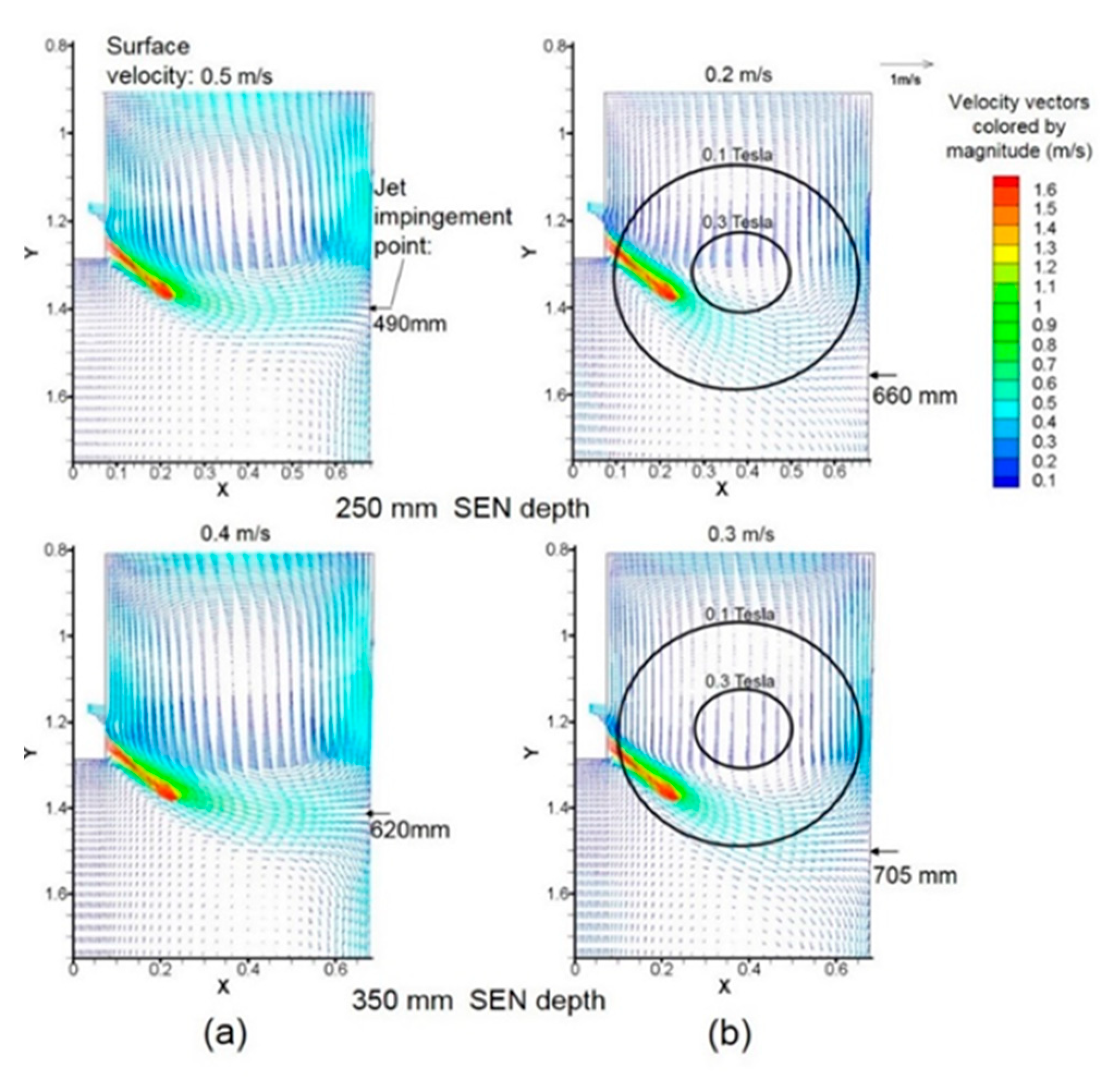
4.1. Local and Single-Ruler EMBr
4.2. Double-Ruler EMBr
4.3. Moving Fields: EMLS, EMLA, and EMRS
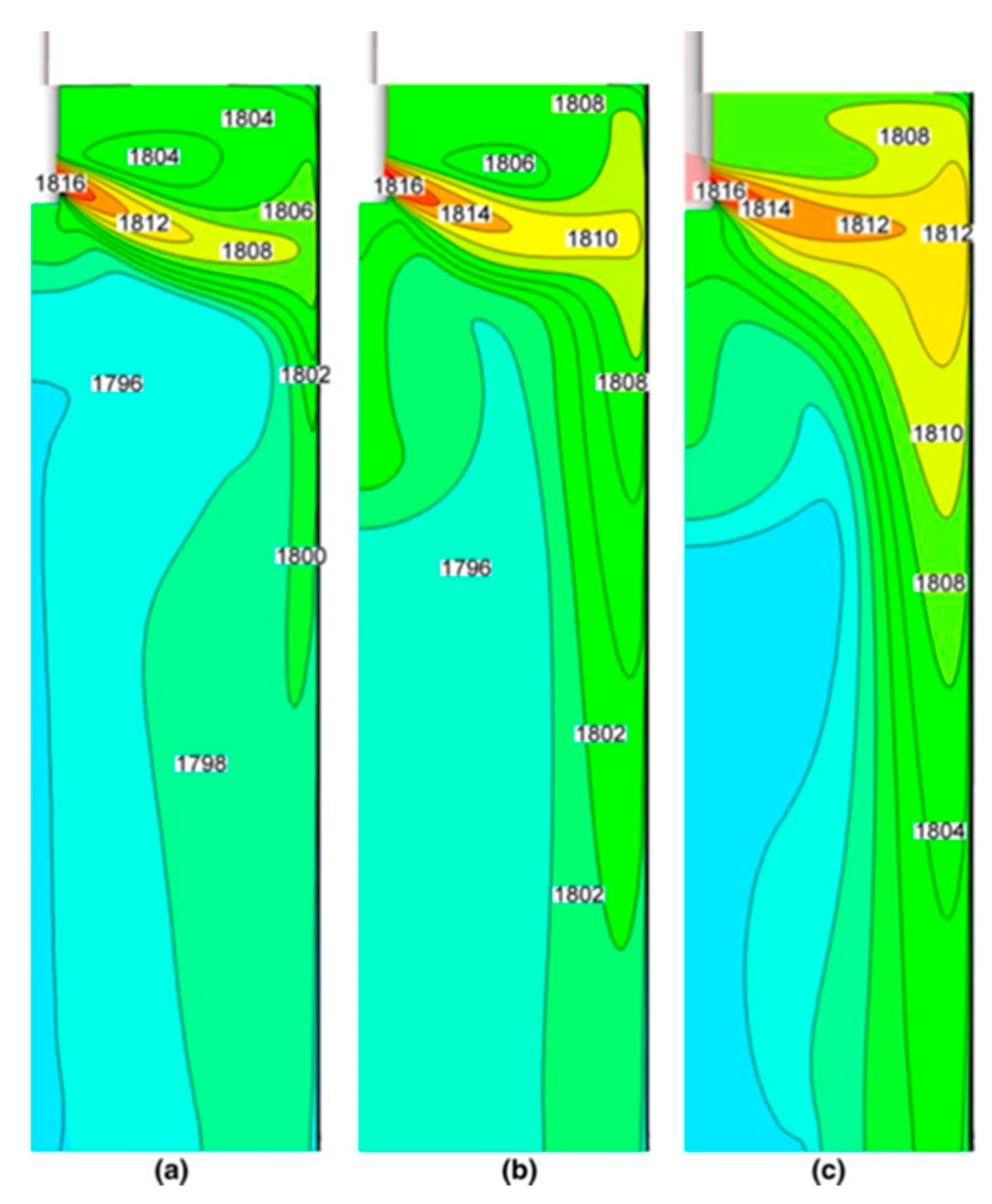
5. Electromagnetic Effects on Superheat Transport and Initial Solidification
5.1. Static Magnetic Fields
5.2. Horizontally-moving Magnetic Fields: EMRS, M-EMS, and EMLA
5.3. Vertically Rotating Field near Meniscus: EMC
6. Electromagnetic Effects on Particle Transport and Capture
6.1. Local and Single-Ruler EMBr
6.2. Double-Ruler EMBr
6.3. Moving Magnetic Fields
7. Electromagnetic Effects on Grain Structure and Internal Quality
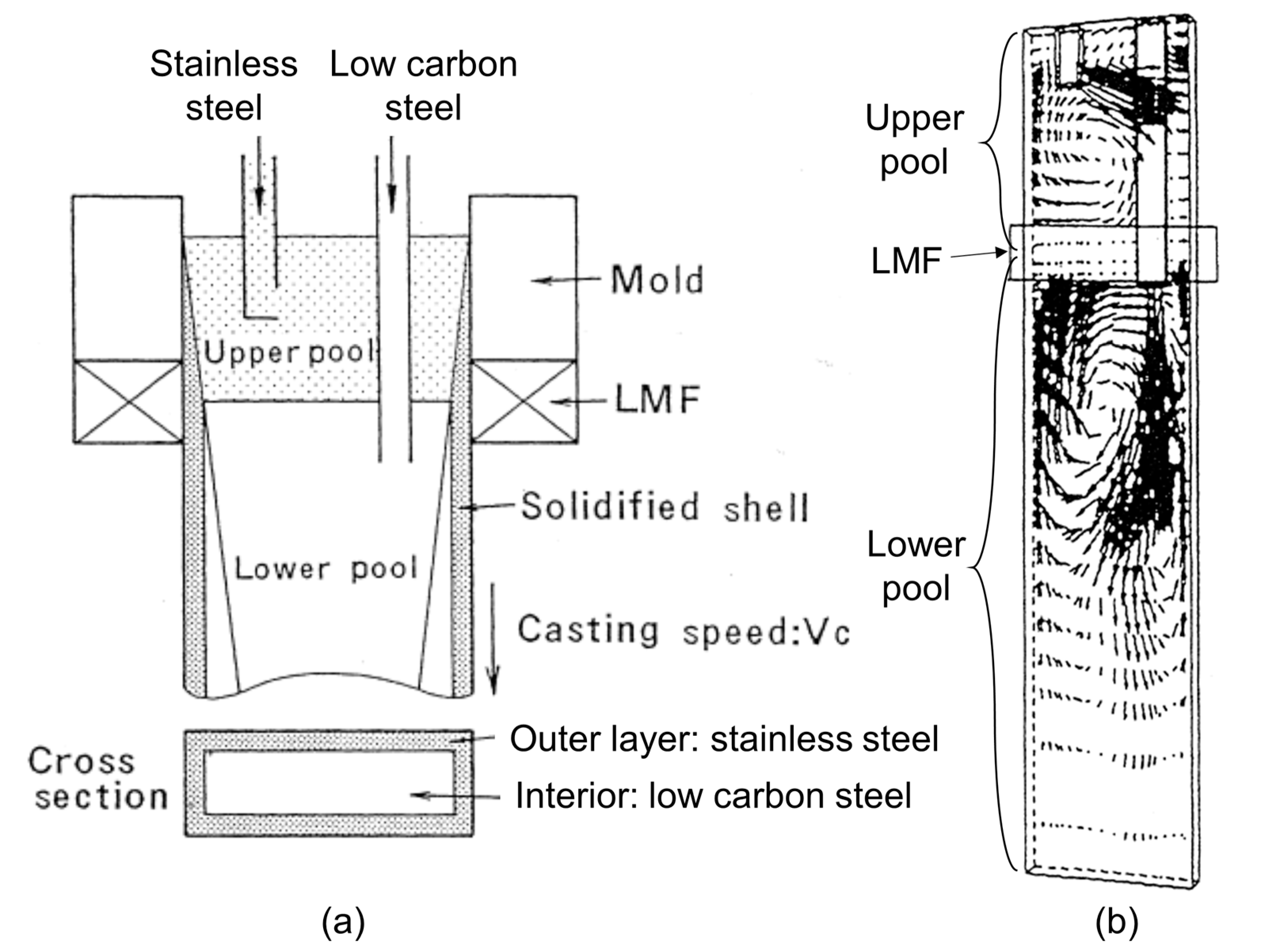
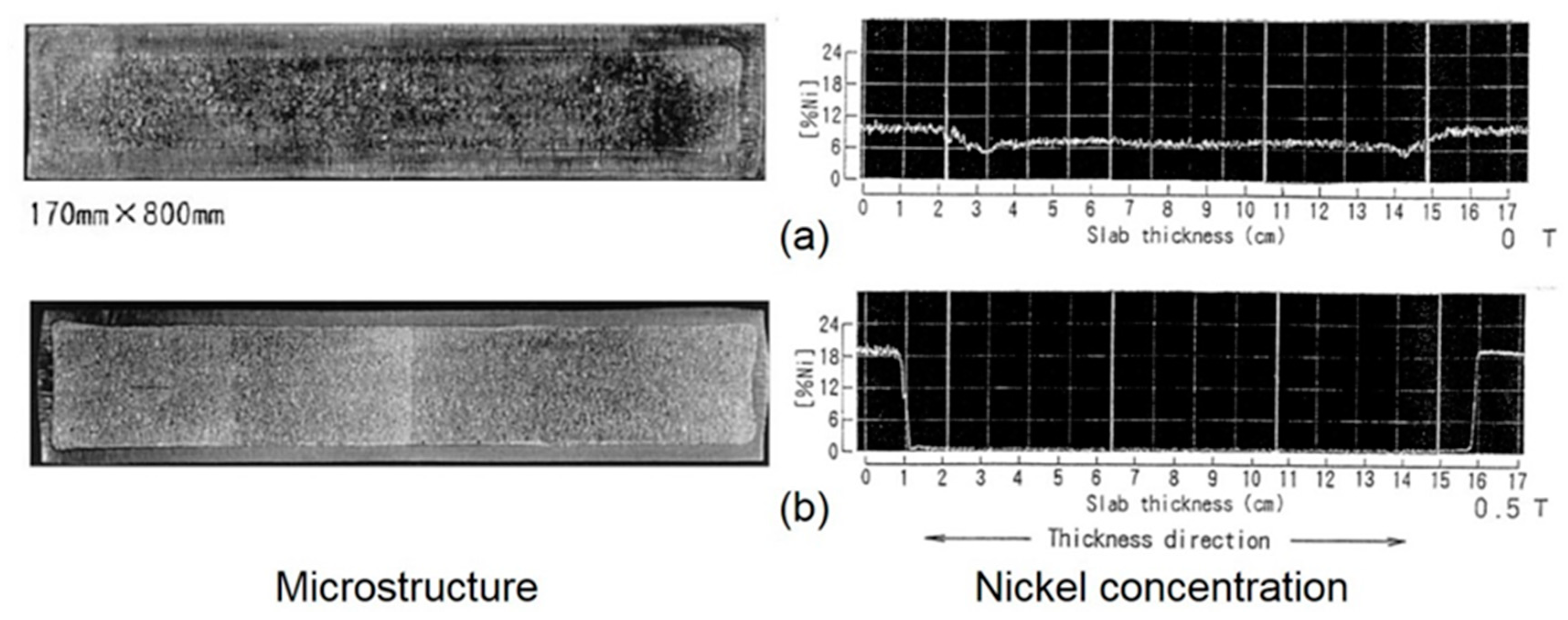
8. Electromagnetic Control of Steel Composition Distribution: Clad Steel Casting
9. Summary and Conclusions
- Combining several plant measurement methods is recommended to quantify the flow fluid and effects on quality, owing to the complexity of the continuous casting process with electromagnetics and the difficulty of making direct measurements.
- Computational modeling validated with plant measurements and lab experiments is the best way to quantify and understand the effects of electromagnetic forces on fluid flow, superheat transfer, solidification, particle transport and capture, grain structure, steel composition, and other phenomena and defects.
- Static magnetic fields (local, single-ruler, and double-ruler EMBr and EMB), moving magnetic fields (EMLS, EMLA, EMRS/M-EMS, EMC, and SEMS), and combined systems have been developed to affect the flow pattern and flow stability, aiming to control the intensity of surface flows in the mold to reduce various defects including surface defects, slag entrainment, inclusion entrapment, and deep oscillation marks, and/or to control internal cleanliness, grain structure, segregation, and porosity.
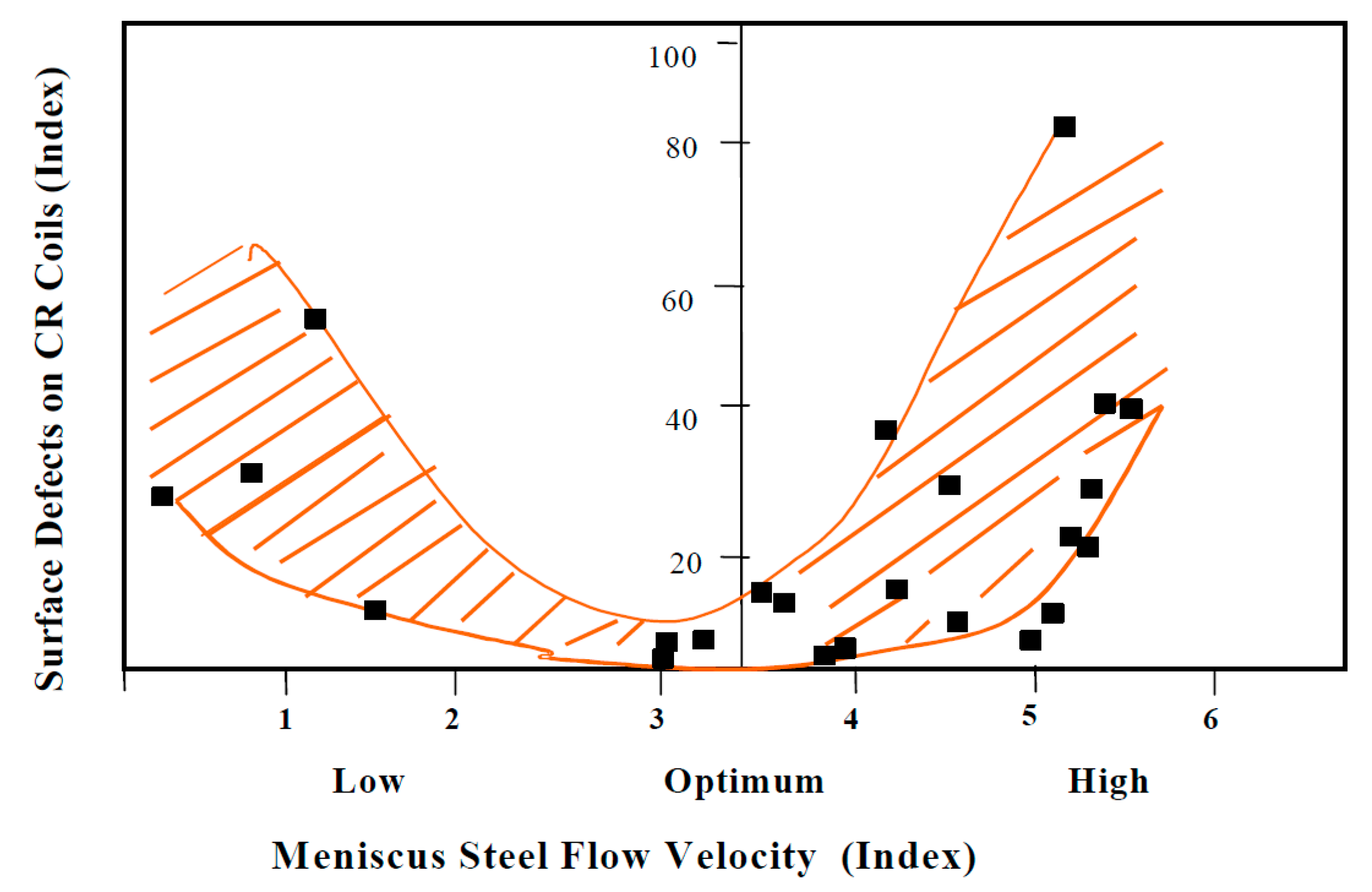
- EMBr, EMB, EMLS, and EMLA are designed to maintain a stable double-roll flow pattern which keeps surface velocity, profile, and level fluctuations within a safe operating window, which is most useful for higher casting speed operations, especially thin-slab casting.
- Placing static EMBr fields at a proper location relative to the flowing jets is critical to achieving the flow objectives. A strong magnetic field above the jet core tends to deflect the jets downward, and to slow surface velocity, which decreases variations in surface level and profile. In this case, care is needed to avoid over cooling the surface if the field is too strong.
- On the other hand, a strong magnetic field below the jet core tends to deflect the jets upwards, increasing surface velocities when casting at low speed and lessening deep penetration of inclusions. In this case, care is needed to avoid upward excessive surface flows, if the field is too strong.
- Locating the core of an EMBr magnetic field directly across the jets exiting the nozzle ports should be avoided to prevent unstable jet flow and associated defects.
- A static ruler EMBr field across the nozzle above the ports helps to stabilize flow inside the nozzle, with consequent improvement of flow stability in the mold.
- Maintaining proper ruler-EMBr field strength across the mold towards the narrow faces is important to reduce surface level fluctuations near the meniscus and jet penetration deep into the mold cavity.
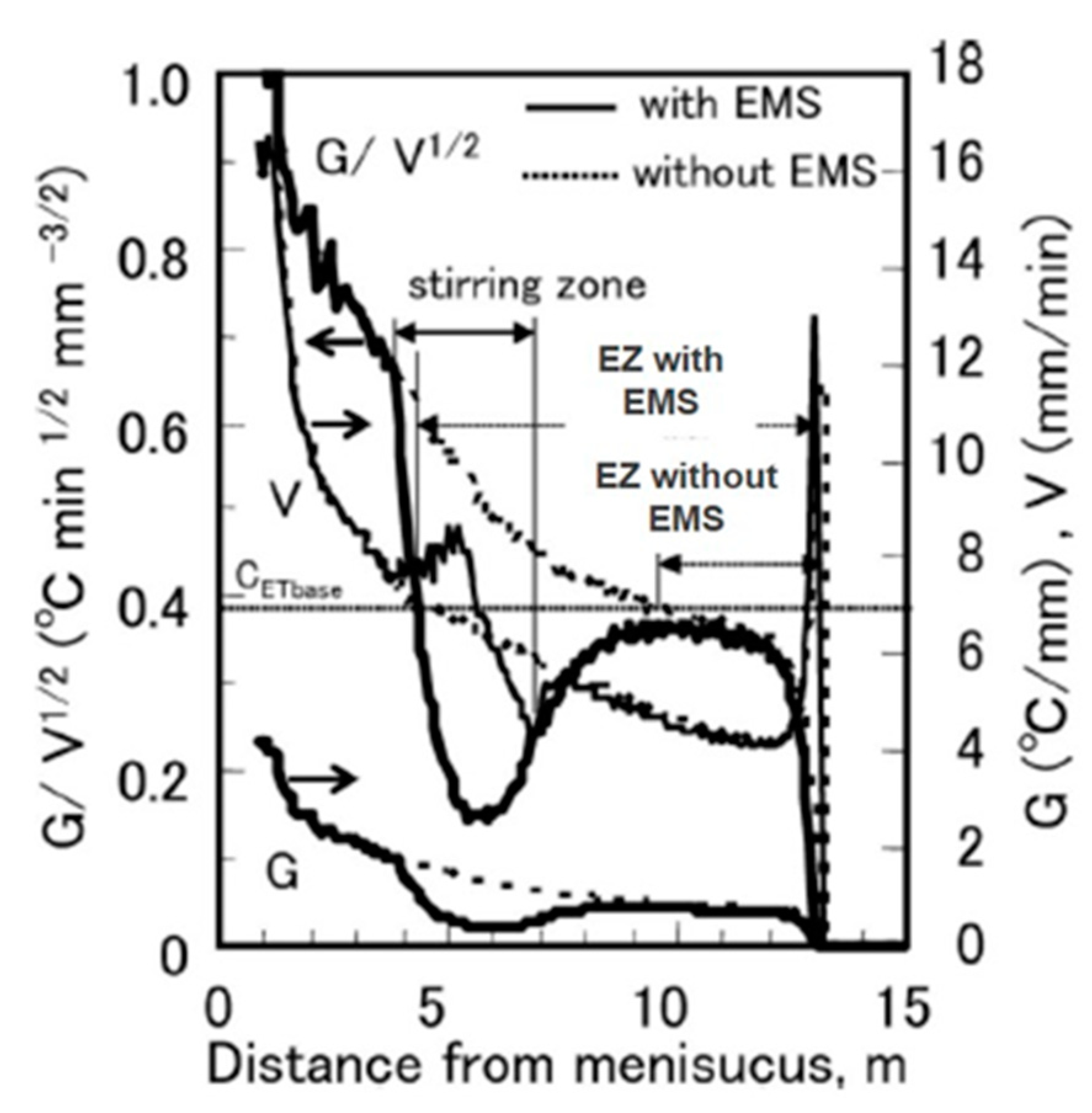
- Moving magnetic fields in the mold (EMLS, EMLA, EMRS, and M-EMS) actively drive the flow, providing an alternative method to achieve flow objectives. These include: EMLS moving fields towards the SEN, aiming to lower surface velocity and turbulence; EMLA moving fields towards the narrow faces, aiming to increase surface velocity and turbulence; and EMRS (M-EMS) fields rotating around the perimeter of the mold surface, aiming (in part) to wash particles away from the solidifying steel shell to lessen particle capture.
- Superheat transport and initial solidification depend greatly on the mold flow pattern. Thus, adjusting the magnetic fields to deflect (static fields) or accelerate (EMLA) the jet upwards towards the top surface in the mold can reduce meniscus freezing, hook formation, and oscillation mark depth. Furthermore, rotating magnetic fields generated by EMRS (M-EMS), or EMC can make superheat and temperature near the meniscus more uniform.
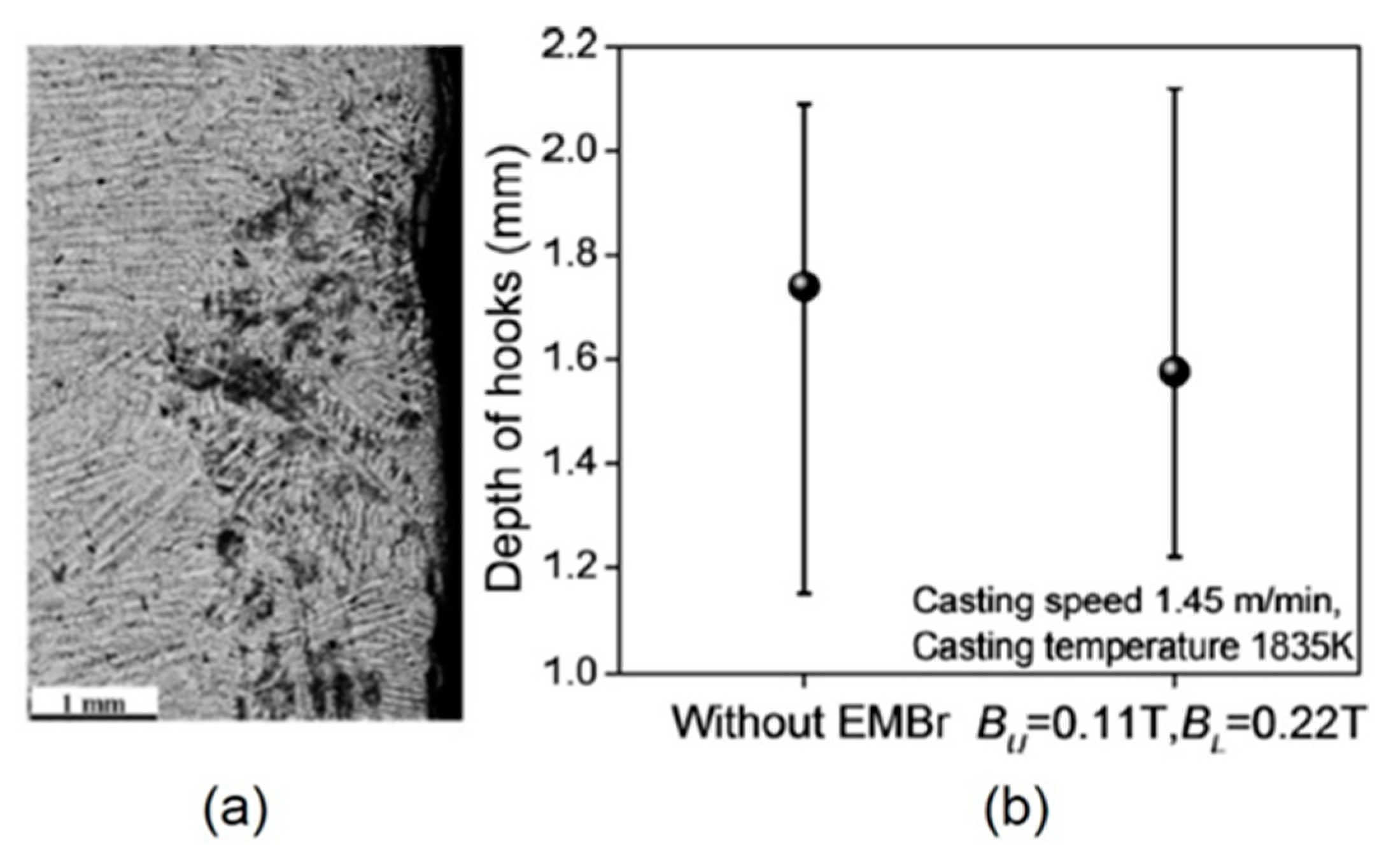
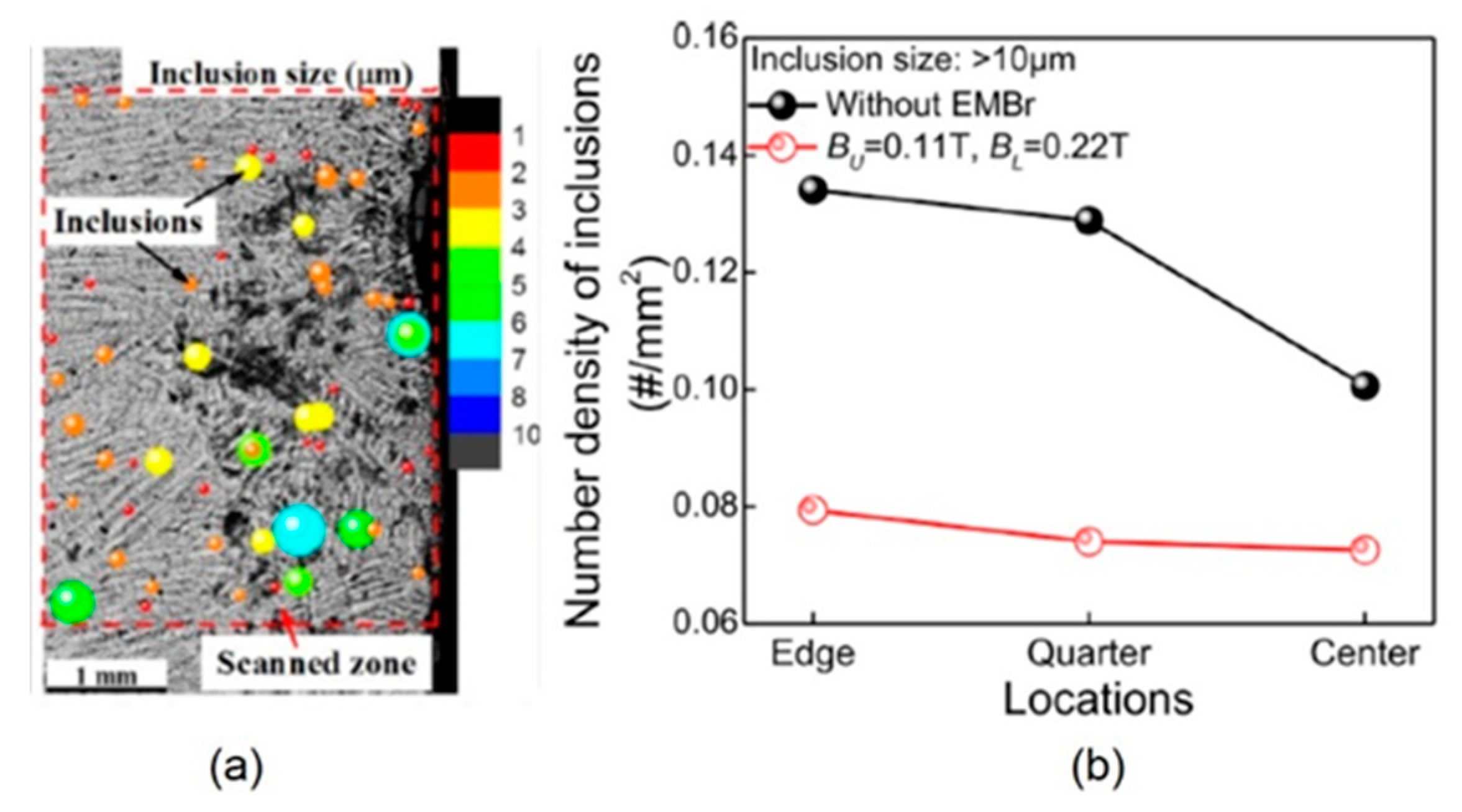
- Lessening the jet impingement depth, with a uniform ruler EMBr field across the mold below the jet, can reduce particle capture deep into the solidifying steel shell. In addition, the washing effect generated by a rotating flow pattern with EMRS or M-EMS can reduce surface defects including particle capture during initial solidification at the meniscus including subsurface hooks.
- Below the mold, horizontally-moving fields towards one narrow face (SEMS) produces vertically rotating flows in the strand region, which mixes superheat, resulting in increased equiaxed grains, and less center segregation and porosity defects.
- Strong static magnetic fields can enable clad steel casting, by helping to separate two steel alloys without mixing, by generating two separate flow recirculation zones above and below the magnetic field.
- The application of combined fields, employing a traveling field either horizontally (via EMRS or M-EMS) or vertically (EMC) in the upper part of the mold and a static field (single-ruler EMBr) in the lower part of a mold, has great potential to reduce both surface and internal defects: The horizontally-moving field around the perimeter of the mold surface can wash away particles at the solidifying steel shell front and prevent their capture. At the same time, the static field prevents the jet flow go deep into the mold cavity, thereby reducing particle penetration, capture, and internal defects.
- The vertically moving EMC field near the meniscus can greatly reduce oscillation mark and hook depth.
- One of the greatest benefits of electromagnetics over conventional flow control devices, (such as port geometry) is the potential to adjust the field strength during operation according to the current flow conditions. Even better is the potential to adjust the magnetic field according to real-time feedback from in-mold sensors, such as multiple sensors of surface level, in order to maintain the intensity of surface flows in window of safe operation real time. More work is needed to implement this into practice.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Steel Association. Table 4. Production of Continuously Cast Steel. In Steel Statistical Yearbook 2018; World Steel Association: Brussels, Belgium, 2018; pp. 9–12. [Google Scholar]
- Thomas, B.G. Chapter 14. Fluid Flow in the Mold. In Making, Shaping and Treating of Steel, 11th ed.; Cramb, A., Ed.; Casting Volume; AISE Steel Foundation: Pittsburgh, PA, USA, 2003; Volume 5, pp. 14.1–14.41. [Google Scholar]
- Thomas, B.G. Chapter 15. Continuous Casting of Steel. In Modeling for Casting and Solidification Processing; Yu, O., Ed.; Marcel Dekker: New York, NY, USA, 2001; pp. 499–540. [Google Scholar]
- Thomas, B.G. Modeling of Continuous Casting Defects Related to Mold Fluid Flow. Iron Steel Technol. 2006, 3, 128–143. [Google Scholar]
- Najjar, F.M.; Thomas, B.G.; Hershey, D.E. Numerical Study of Steady Turbulent Flow through Bifurcated Nozzles in Continuous Casting. Metall. Mater. Trans. B 1995, 26B, 749–765. [Google Scholar] [CrossRef]
- Calderon-Ramos, I.; Morales, R.D.; Salazar-Campoy, M. Modeling Flow Turbulence in a Continuous Casting Slab Mold Comparing the use of Two Bifurcated Nozzles with Square and Circular Ports. Steel Res. Int. 2015, 86, 1610–1621. [Google Scholar] [CrossRef]
- Salazar-Campoy, M.M.; Morales, R.D.; Najera-Bastida, A.; Calderon-Ramos, I.; Cedillo-Hernandez, V.; Delgado-Pureco, J.C. A Physical Model to Study the Effects of Nozzle Design on Dispersed Two-Phase Flows in a Slab Mold Casting Ultra-Low-Carbon Steels. Metall. Mater. Trans. B 2018, 49B, 812–830. [Google Scholar] [CrossRef]
- Cho, S.-M.; Thomas, B.G.; Kim, S.-H. Effect of Nozzle Port Angle on Transient Flow and Surface Slag Behavior during Continuous Steel slab casting. Metall. Mater. Trans. B 2018, 50B, 52–76. [Google Scholar] [CrossRef]
- Thomas, B.G.; Mika, L.J.; Najjar, F.M. Simulation of Fluid Flow inside a Continuous Slab-Casting Machine. Metall. Mater. Trans. B 1990, 21B, 387–400. [Google Scholar] [CrossRef]
- Cho, S.-M.; Thomas, B.G.; Lee, H.-J.; Kim, S.-H. Effect of Nozzle Port Angle on Mold Surface Flow in Steel Slab Casting. Iron Steel Technol. 2017, 14, 76–84. [Google Scholar]
- Chaudhary, R.; Lee, G.-G.; Thomas, B.G.; Kim, S.-H. Transient Mold Fluid Flow with Well- and Mountain-Bottom Nozzles in Continuous Casting of Steel. Metall. Mater. Trans. B 2008, 39B, 870–884. [Google Scholar] [CrossRef]
- Gursoy, K.A.; Yavuz, M.M. Effect of Flow Rate Controllers and their Opening Levels on Liquid Steel Flow in Continuous Casting Mold. ISIJ Int. 2016, 56, 554–563. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L. Transient Fluid Flow Phenomena during Continuous Casting: Part II—Cast Speed Change, Temperature Fluctuation, and Steel Grade Mixing. ISIJ Int. 2010, 50, 1783–1791. [Google Scholar] [CrossRef]
- Bai, H.; Thomas, B.G. Turbulent Flow of Liquid Steel and Argon Bubbles in Slide gate Tundish Nozzles: Part II. Effect of Operation Conditions and Nozzle Design. Metall. Mater. Trans. B 2001, 32B, 269–284. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Qi, F.S.; Li, B.K.; Cheung, S.C.P. Modeling of bubble behaviors and size distribution in a slab continuous casting mold. Int. J. Multiphase Flow 2016, 79, 190–201. [Google Scholar] [CrossRef]
- Dauby, P.H. Continuous casting: Make better steel and more of it! Revue de Métallurgie 2012, 109, 113–136. [Google Scholar] [CrossRef]
- Jin, K.; Vanka, S.P.; Thomas, B.G. Large Eddy Simulations of the Effects of EMBr and SEN Submergence Depth on Turbulent Flow in the Mold Region of a Steel Caster. Metall. Mater. Trans. B 2017, 48B, 162–178. [Google Scholar] [CrossRef]
- Jacobi, H.F. Investigation of Centreline Segregation and Centreline Porosity in CC-Slabs. Steel Res. Int. 2003, 74, 667–678. [Google Scholar] [CrossRef]
- El-Bealy, M.O. Macrosegregation Quality Criteria and Mechanical Soft Reduction for Central Quality Problems in Continuous Casting of Steel. Mater. Sci. Appl. 2014, 5, 724–744. [Google Scholar] [CrossRef][Green Version]
- Thomas, B.G. Review on Modeling and Simulation of Continuous Casting. Steel Res. Int. 2018, 89, 1700312. [Google Scholar] [CrossRef]
- Thomas, B.G. Chapter 5. Modeling of Continuous Casting. In Making, Shaping and Treating of Steel, 11th ed.; Cramb, A., Ed.; Casting Volume; AISE Steel Foundation: Pittsburgh, PA, USA, 2003; Volume 5, pp. 5.1–5.24. [Google Scholar]
- Thomas, B.G.; Zhang, L. Mathematical Modeling of Fluid Flow in Continuous Casting. ISIJ Int. 2001, 41, 1181–1193. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhao, B.; Vanka, S.P.; Thomas, B.G. Study of Computational Issues in Simulation of Transient Flow in Continuous Casting. Steel Res. Int. 2005, 76, 33–43. [Google Scholar] [CrossRef]
- Kollberg, S.; Lofgren, P.M.; Hanley, P. Improving Quality and Productivity in Thick Slab Casting by Direct Control of ElectroMagnetic Brake (EMBR). In Proceedings of the AISTech 2004, Nashville, TN, USA, 15–17 September 2004; pp. 977–984. [Google Scholar]
- Zeze, M.; Harada, H.; Takeuchi, E.; Ishii, T. Application of DC Magnetic Field for the Control of Flow in the Continuous Casting Strand. In Proceedings of the 76th Steelmaking Conference, Dallas, TX, USA, 28–31 March 1993; pp. 267–272. [Google Scholar]
- Qian, Z.-D.; Wu, Y.-L. Large Eddy Simulation of Turbulent Flow with the Effects of DC Magnetic Field and Vortex Brake Application in Continuous Casting. ISIJ Int. 2004, 44, 100–107. [Google Scholar] [CrossRef]
- Singh, R.; Thomas, B.G.; Vanka, S.P. Effects of a Magnetic Field on Turbulent Flow in the Mold Region of a Steel Caster. Metall. Mater. Trans. B 2013, 44B, 1201–1221. [Google Scholar] [CrossRef]
- Thomas, B.G.; Singh, R.; Vanka, S.P.; Timmel, K.; Eckert, S.; Gerbeth, G. Effect of Single-Ruler Electromagnetic Braking (EMBr) Location on Transient Flow in Continuous Casting. J. Manuf. Sci. Prod. 2015, 15, 93–104. [Google Scholar] [CrossRef]
- Chaudhary, R.; Thomas, B.; Vanka, S. Effect of Electromagnetic Ruler Braking (EMBr) on Transient Turbulent Flow in Continuous Slab Casting using Large Eddy Simulations. Metall. Mater. Trans. B 2012, 43, 532–553. [Google Scholar] [CrossRef]
- Harada, H.; Takeuchi, E.; Zeze, M.; Tanaka, H. MHD analysis in hydromagnetic casting process of clad steel slabs. Appl. Math. Modell. 1998, 22, 873–882. [Google Scholar] [CrossRef]
- Kunstreich, S. Recent developments of electromagnetic actuators for continuous casting of long and flat products. MILLENNIUM STEEL 2014, 57–63. [Google Scholar]
- Kunstreich, S.; Dauby, P.H. Effect of liquid steel flow pattern on slab quality and the need for dynamic electromagnetic control in the mold. Ironmak. Steelmak. 2005, 32, 80–86. [Google Scholar] [CrossRef]
- Kunstreich, S. Electromagnetic stirring for continuous casting-Part 2. Rev. Met. Paris. 2003, 100, 1043–1061. [Google Scholar] [CrossRef]
- Nakashima, J.; Fukuda, J.; Kiyose, A.; Kawase, T.; Ohtani, Y.; Doki, M. Improvement of Slab Surface Quality with In-mold Electromagnetic Stirring; Nippon Steel and Sumitomo Metal Corporation: Tokyo, Japan, 2002; pp. 61–67. [Google Scholar]
- Fujisaki, K. In-Mold Electromagnetic Stirring in Continuous Casting. IEEE TRANSACTIONS ON INDUSTRY APPLICATIONS 2001, 37, 1098–1104. [Google Scholar] [CrossRef]
- Tani, M.; Zeze, M.; Toh, T.; Tsunenari, K.; Umetsu, K.; Hayashi, K.; Tanaka, K.; Fukunaga, S. Electromagnetic Casting Technique for Slab Casting. Nippon Steel Technical Report 2013, 104, 62–68. [Google Scholar] [CrossRef]
- Cha, P.-R.; Hwang, Y.-S.; Nam, H.-S.; Chung, S.-H.; Yoo, J.-K. 3D Numerical Analysis on Electromagnetic and Fluid Dynamic Phenomena in a Soft Contact Electromagnetic Slab Caster. ISIJ Int. 1998, 38, 403–410. [Google Scholar] [CrossRef]
- Toh, T.; Takeuchi, E.; Hojo, M.; Kawai, H.; Matsumura, S. Electromagnetic Control of Initial Solidification in Continuous Casting of Steel by Low Frequency Alternating Magnetic Field. ISIJ Int. 1997, 37, 1112–1119. [Google Scholar] [CrossRef]
- Kubota, J.; Kubo, N.; Ishii, T.; Suzuki, M.; Aramaki, N.; Nishimachi, R. Steel Flow Control in Continuous Slab Caster Mold by Traveling Magnetic Field. NKK TECHNICAL REVIEW 2001, 85, 1–9. [Google Scholar]
- Kunstreich, S. Electromagnetic stirring for continuous casting-Part 1. Rev. Met. Paris. 2003, 100, 395–408. [Google Scholar] [CrossRef]
- Dubke, M.; Tacke, K.-H.; Spitzer, K.-H.; Schwerdtfeger, K. Flow fields in electromagnetic stirring of rectangular strands with linear inductors: Part I. theory and experiments with cold models. Metall. Trans. B. 1988, 19B, 581–593. [Google Scholar] [CrossRef]
- Gong, J.; Liu, H.-p.; Wang, X.-h.; Bao, Y.-p. Numerical Simulation of Electromagnetic Field and Flow Pattern in a Continuous Slab Caster with in roll-type Strand Electromagnetic Stirring. J. Iron Steel Res. Int. 2015, 22, 414–422. [Google Scholar] [CrossRef]
- Kim, G.H.; Kwon, S.H.; Won, Y.M.; Lee, C.H. Enhancement of slab internal quality by electromagnetic stirring of molten steel. In Proceedings of the 8th International Conference on Electromagnetic Processing of Materials (EPM 2015), Cannes, France, 12–16 October 2015. [Google Scholar]
- Kunstreich, S. Strand electromagnetic stirring (S-EMS) for thick slab casters: Box-type or In-roll stirrers? Millennium Steel 2008, 122–124. [Google Scholar]
- El-Kaddah, N.; Natarajan, T.T. Electromagnetic Stirring of Steel: Effect of Stirring Design on Mixing in Horizontal Electromagnetic Stirring of Steel Slabs. In Proceedings of the Second International Conference on CFD in the Mineral and Process Industries, Melbourne, Australia, 6–8 December 1999; pp. 339–344. [Google Scholar]
- Dubke, M.; Tacke, K.-H.; Spitzer, K.-H.; Schwerdtfeger, K. Flow fields in electromagnetic stirring of rectangular strands with linear inductors: Part II. Computation of flow fields in billets, blooms, and slabs of steel. Metall. Trans. B. 1988, 19B, 595–602. [Google Scholar] [CrossRef]
- Lambert, V.; Galpin, J.-M.; Hackl, H.R.; Jacobson, N.P. New Strong Strand Stirrer Boosting Quality for Ferritic Stainless Steel. Iron Steel Technol. 2008, 5, 71–79. [Google Scholar]
- Sedén, M.; Jacobson, N.; Lehman, A.; Eriksson, J.-E. Control of Flow Behavior by FC Mold G3 in Slab Casting Process. In Proceedings of the 8th European Continuous Casting Conference, Graz, Austria, 23–26 June 2014. [Google Scholar]
- Qian, Z.-D.; Wu, Y.-L.; Li, B.-W.; He, J.-C. Numerical Analysis of the Influences of Operational Parameters on the Fluid Flow in Mold with Hybrid Magnetic Fields. ISIJ Int. 2002, 42, 1259–1265. [Google Scholar] [CrossRef]
- Yavuz, M.M. The Effects of Electromagnetic Brake on Liquid Steel Flow in Thin Slab Caster. Steel Res. Int. 2011, 82, 809–818. [Google Scholar] [CrossRef]
- Domgin, J.-F.; Anderhuber, M.; Doncker, M.D.; Paepe, A.D. Optimization of an Electromagnetic Technology in ArcelorMittal Gent for Improving Products Quality in Steel Industry. J. Manuf. Sci. Prod. 2015, 15, 105–117. [Google Scholar] [CrossRef]
- Mizukami, H.; Hanao, M.; Hiraki, S.; Kawamoto, M.; Watanabe, T.; Hayashi, A.; Iguchi, M. Measurement of Meniscus Flow Velocity in High Speed Continuous Casting Mold. Tetsu-to-Hagane 2000, 86, 265–270. [Google Scholar] [CrossRef][Green Version]
- Iguchi, M.; Terauchi, Y. Karman Vortex Probe for the Detection of Molten Metal Surface Flow in Low Velocity Range. ISIJ Int. 2002, 42, 939–943. [Google Scholar] [CrossRef]
- Iguchi, M.; Kawabata, H.; Ogura, T.; Hayashi, A.; Terauchi, Y. A New Probe for Directly Measuring Flow Velocity in a Continuous Casting Mold. ISIJ Int. 1996, 36, S190–S193. [Google Scholar] [CrossRef]
- Han, S.-W.; Cho, H.-J.; Jin, S.-Y.; Sedén, M.; Lee, I.-B.; Sohn, I. Effects of Simultaneous Static and Traveling Magnetic Fields on the Molten Steel Flow in a Continuous Casting Mold. Metall. Mater. Trans. B 2018, 49B, 2757–2769. [Google Scholar] [CrossRef]
- Kubota, J.; Kubo, N.; Suzuki, M.; Ishii, T.; Nishimachi, R.; Aramaki, N. Steel Flow Control with Travelling Magnetic Field for Slab Continuous Caster Mold. Tetsu-to-Hagane 2000, 86, 69–75. [Google Scholar] [CrossRef]
- Jin, K.; Vanka, S.P.; Thomas, B.G.; Ruan, X. Large Eddy Simulations of the Effects of Double-Ruler Electromagnetic Braking and Nozzle Submergence Depth on Molten Steel Flow in A Commercial Continuous Casting Mold. In Proceedings of the TMS Annual Meeting, CFD Modeling and Simulation in Materials Processing Symposium 2016, Nashville, TN, USA, 14–18 March 2016; pp. 159–166. [Google Scholar]
- Dauby, P.H.; Emling, W.H.; Sobolewski, R. Lubrication in the Mold: A Multiple Variable System. Ironmaker Steelmaker 1986, 13, 28–36. [Google Scholar]
- Mcdavid, R.M.; Thomas, B.G. Flow and Thermal Behavior of the Top Surface Flux/Powder Layers in Continuous Casting Molds. Metall. Mater. Trans. B 1996, 27B, 672–685. [Google Scholar] [CrossRef]
- Cho, S.-M.; Lee, H.-J.; Kim, S.-H.; Chaudhary, R.; Thomas, B.G.; Lee, D.-H.; Kim, Y.-J.; Choi, W.-R.; Kim, S.-K.; Kim, H.-S. Measurement of Transient Meniscus Flow in Steel Continuous Casters and Effect of Electromagnetic Braking. In Proceedings of the TMS Annual Meeting Symposium 2011, San Diego, CA, USA, 27 February–3 March 2011. [Google Scholar]
- Cukierski, K.; Thomas, B.G. Flow Control with Local Electromagnetic Braking in Continuous Casting of Steel Slabs. Metall. Mater. Trans. B 2008, 38B, 94–107. [Google Scholar] [CrossRef]
- Liu, R.; Thomas, B.G.; Sengupta, J.; Chung, S.D.; Trinh, M. Measurements of Molten Steel Surface Velocity and Effect of Stopper-rod Movement on Transient Multiphase Fluid Flow in Continuous Casting. ISIJ Int. 2014, 54, 2314–2323. [Google Scholar] [CrossRef]
- Rietow, B.; Thomas, B.G. Using Nail Board Experiments to Quantify Surface Velocity in the CC Mold. In Proceedings of the AISTech 2008, Pittsburgh, PA, USA, 5–8 May 2018; pp. 1–11. [Google Scholar]
- Cho, S.-M.; Kim, S.-H.; Thomas, B.G. Transient Fluid Flow during Steady Continuous Casting of Steel Slabs: Part I. Measurements and Modeling of Two-phase Flow. ISIJ Int. 2014, 54, 845–854. [Google Scholar] [CrossRef]
- Köhler, K.U.; Andrzejewski, P.; Julius, E.; Haubrich, H. Steel Flow Velocity Measurement and Flow Pattern Monitoring in the Mould. In Proceedings of the 78th Steelmaking Conference, Nashville, TN, USA, 2–5 April 1995; pp. 445–449. [Google Scholar]
- Thomas, B.G.; Yuan, Q.; Sivaraj Sivaramakrishnan, S.; Shi, T.; Vanka, S.P.; Assar, M.B. Comparison of Four Methods to Evaluate Fluid Velocities in a Continuous Slab Casting Mold. ISIJ Int. 2001, 41, 1262–1271. [Google Scholar] [CrossRef]
- Assar, M.; Dauby, P.H.; Lawson, G.D. Opening the Black Box: PIV and MFC Measurements in a Continuous Caster Mold. In Proceedings of the 83rd Steelmaking Conference, Pittsburgh, PA, USA, 26–29 March 2000. [Google Scholar]
- Okano, S.; Nishimura, T.; Ooi, H.; Chino, T. Relation between Large Inclusions and Growth Directions of Columnar Dendrites in Continuously Cast Slabs. Tetsu-to-Hagane 1975, 61, 2982–2990. [Google Scholar] [CrossRef][Green Version]
- Esaka, H.; Toh, T.; Harada, H.; Takeuchi, E.; Fujisaki, K. Deflection of Steel Dendrite Growing in the Fluid Flow Driven by Electromagnetic Stirrer. Tetsu-to-Hagane 2000, 86, 247–251. [Google Scholar] [CrossRef][Green Version]
- Wang, X.; Wang, S.; Zhang, L.; Sridhar, S.; Conejo, A.; Liu, X. Analysis on the Deflection Angle of Columnar Dendrites of Continuous Casting Steel Billets Under the Influence of Mold Electromagnetic Stirring. Metall. Mater. Trans. A 2016, 47A, 5496–5509. [Google Scholar] [CrossRef]
- Melissari, B.; Argyropoulos, S.A. Measurement of Magnitude and Direction of Velocity in High-Temperature Liquid Metals. Part I: Mathematical Modeling. Metall. Mater. Trans. B 2005, 36B, 691–700. [Google Scholar] [CrossRef]
- Melissari, B.; Argyropoulos, S.A. Measurement of Magnitude and Direction of Velocity in High-Temperature Liquid Metals. Part II: Experimental Measurements. Metall. Mater. Trans. B 2005, 36B, 639–649. [Google Scholar] [CrossRef]
- Argyropoulos, S.A. Measuring velocity in high-temperature liquid metals: A review. Scand. J. Metall. 2000, 30, 273–285. [Google Scholar] [CrossRef]
- Hibbeler, L.C.; Thomas, B.G. Mold Slag Entrainment Mechanisms in Continuous Casting Molds. Iron Steel Technol. 2013, 10, 121–134. [Google Scholar]
- Kubota, J.; Okitoto, K.; Shirayata, A.; Murakati, H. Meniscus Flow Control in the Mold by Traveling Magnetic Field for High Speed Slab Caster. In Proceedings of the 74th Steelmaking Conference, Washington, DC, USA, 14–17 April 1991; pp. 233–241. [Google Scholar]
- Akhtar, A.; Thomas, B.G.; Sengupta, J. Analysis of Nail Board Measurements of Liquid Slag Layer Depth. In Proceedings of the AISTech 2016, Pittsburgh, PA, USA, 16–19 May 2016; pp. 1427–1438. [Google Scholar]
- Yuan, Q.; Thomas, B.G.; Vanka, S.P. Study of Transient Flow and Particle Transport in Continuous Steel Caster Molds: Part I. Fluid Flow. Metall. Mater. Trans. B 2004, 35B, 685–702. [Google Scholar] [CrossRef]
- Zhang, L.; Thomas, B.G. State of the Art in Evaluation and Control of Steel Cleanliness. ISIJ Int. 2003, 43, 271–291. [Google Scholar] [CrossRef]
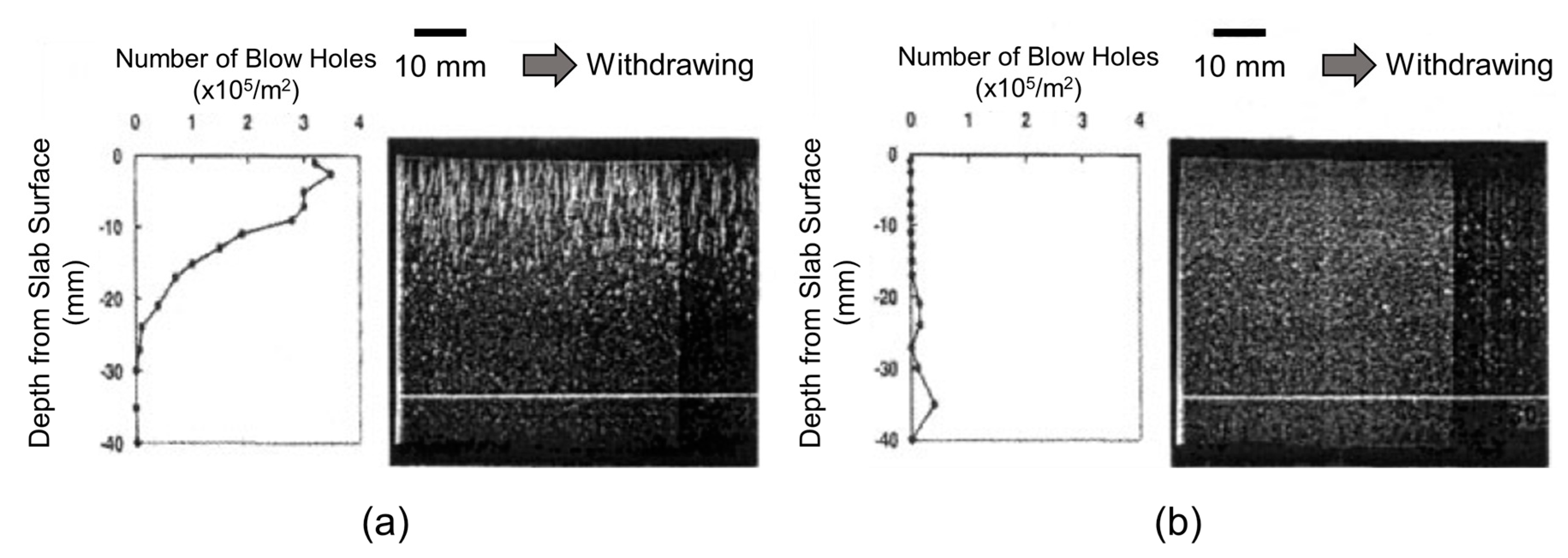
- Furumai, K.; Matsui, Y.; Murai, T.; Miki, Y. Evaluation of Defect Distribution in Continuously-Cast Slabs by Using Ultrasonic Defect Detection System and Effect of Electromagnetic Brake on Decreasing Unbalanced Flow in Mold. ISIJ Int. 2015, 55, 2135–2141. [Google Scholar] [CrossRef]
- Lee, G.-G.; Shin, H.-J.; Thomas, B.G.; Kim, S.-H. Asymmetric Multi-phase Fluid Flow and Particle Entrapment in a Continuous Casting Mold. In Proceedings of the AISTech 2008, Pittsburgh, PA, USA, 5–8 May 2008. [Google Scholar]
- Ren, Y.; Wang, Y.; Li, S.; Zhang, L.; Zuo, X.; Lekakh, S.N.; Peaslee, K. Detection of Non-metallic Inclusions in Steel Continuous Casting Billets. Metall. Mater. Trans. B 2014, 45B, 1291–1303. [Google Scholar] [CrossRef]
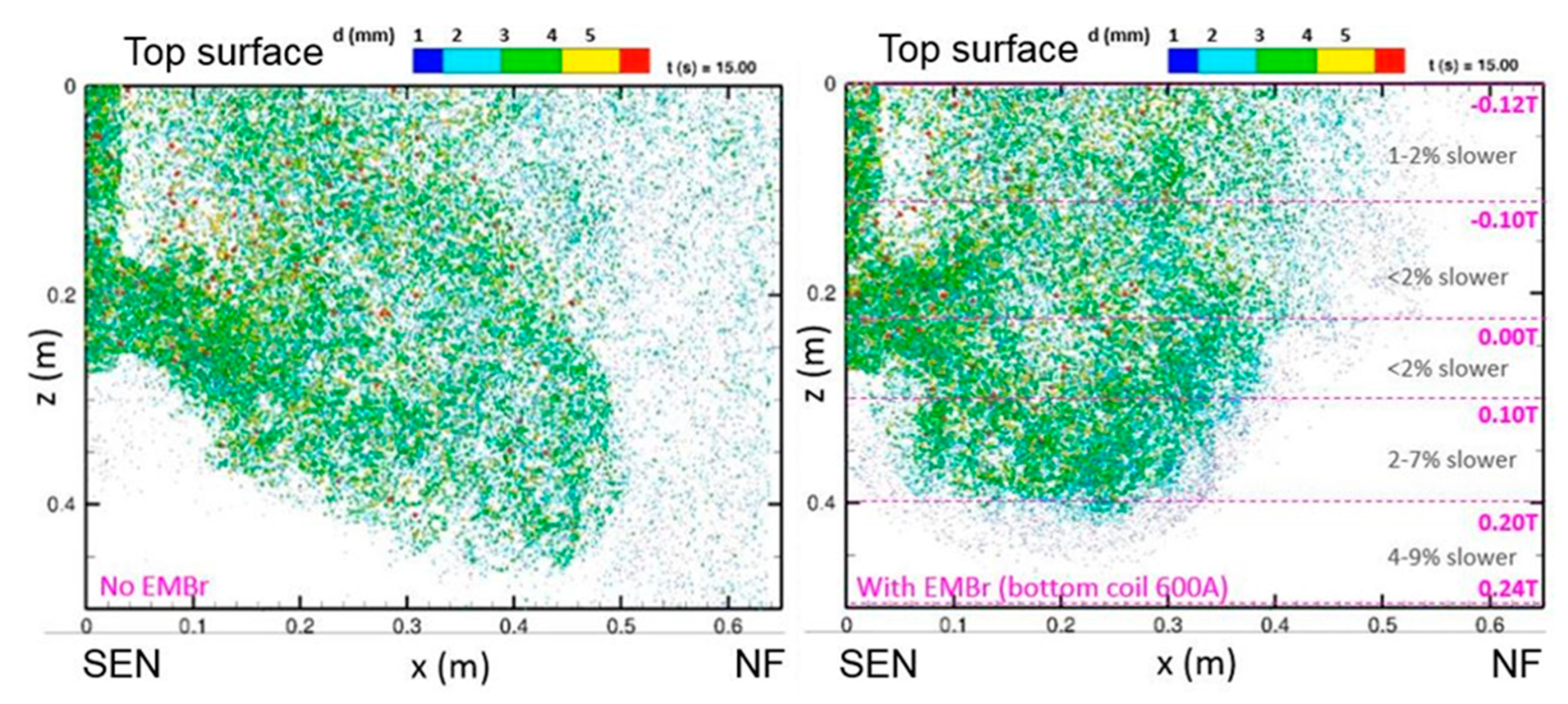
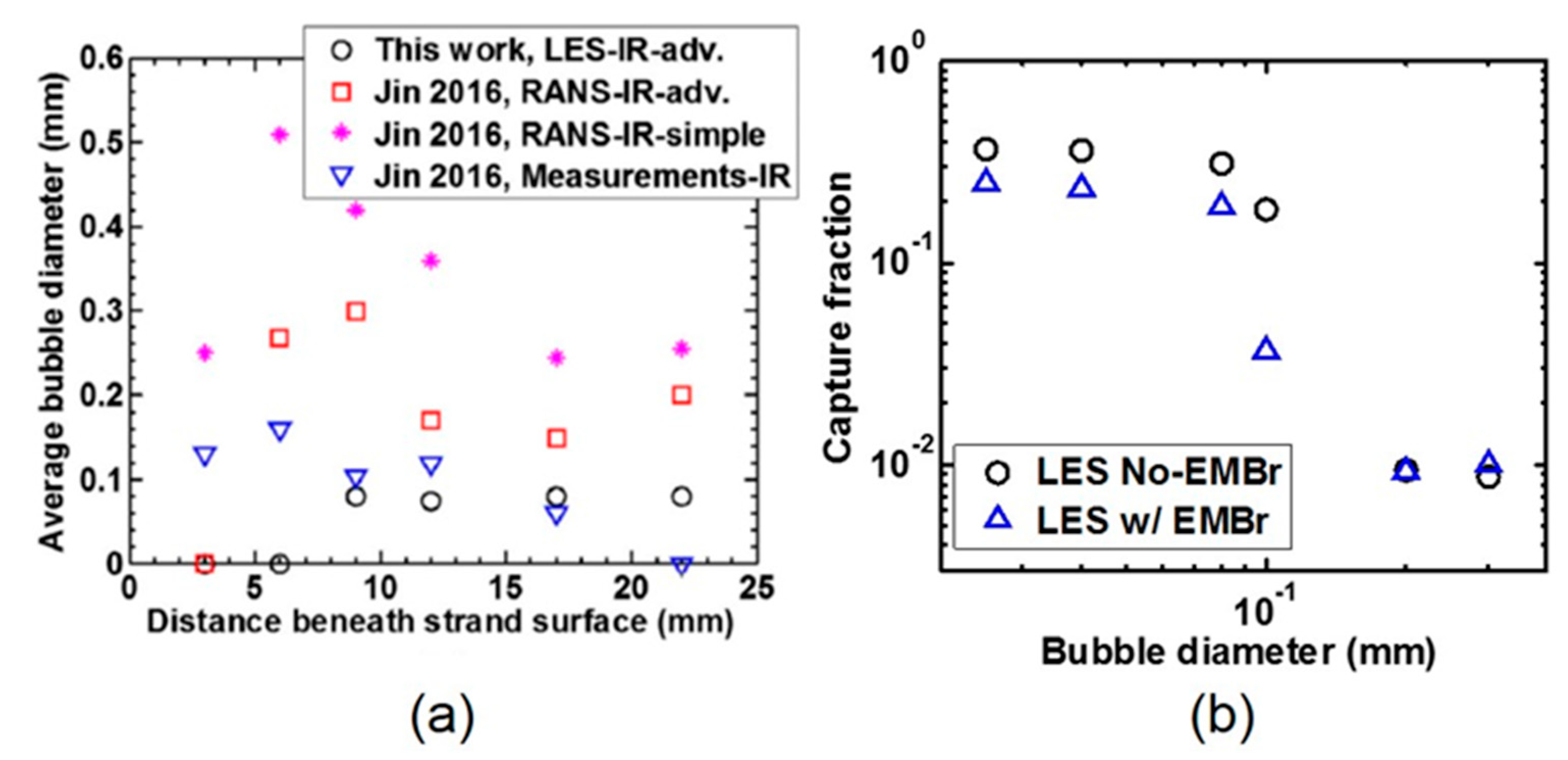
- Jin, K.; Thomas, B.G.; Ruan, X. Modeling and Measurements of Multiphase Flow and Bubble Entrapment in Steel Continuous Casting. Metall. Mater. Trans. B 2016, 47B, 548–565. [Google Scholar] [CrossRef]
- Demmon, F.; Gass, R.; Yin, H. Step Milling as a Tool for Characterizing Defects in Slabs at ArcelorMittal. Iron Steel Technol. 2015, 12, 82–91. [Google Scholar]
- Yang, H.; Tehranchi, F.; Eriksson, J.-E.; Song, J. Water Modeling of Stirring and Braking Processes in a Slab Caster Mold. In Proceedings of the AISTech 2010, Pittsburgh, PA, USA, 3–6 May 2010; pp. 135–146. [Google Scholar]
- Yang, H.; Sedén, M.; Jacobson, N.; Eriksson, J.-E.; Hackl, H. Development of the Third-Generation FC Mold by Numerical and Water Model Simulations. In Proceedings of the AISTech 2012, Atlanta, GA, USA, 7–9 May 2012. [Google Scholar]
- Timmel, K.; Kratzsch, C.; Asad, A.; Schurmann, D.; Schwarze, R.; Eckert, S. Experimental and Numerical Modeling of Fluid Flow Processes in Continuous Casting: Results from the LIMMCAST-Project. In Proceedings of the Final LIMTECH Colloquium and International Symposium on Liquid Metal Technologies, Dresden, Germany, 19–20 September 2017; IOP Conf. Series: Materials Science and Engineering. p. 012019. [Google Scholar]
- Wondrak, T.; Eckert, S.; Gerbeth, G.; Klotsche, K.; Stefani, F.; Timmel, K.; Peyton, A.J.; Terzija, N.; Yin, W. Combined Electromagnetic Tomography for Determining Two-phase Flow Characteristics in the Submerged Entry Nozzle and in the Mold of a Continuous Casting Model. Metall. Mater. Trans. B 2011, 42B, 1201–1210. [Google Scholar] [CrossRef]
- Timmel, K.; Eckert, S.; Gerbeth, G. Experimental Investigation of the Flow in a Continuous-Casting Mold under the Influence of a Transverse, Direct Current Magnetic Field. Metall. Mater. Trans. B 2011, 42B, 68–80. [Google Scholar] [CrossRef]
- Chaudhary, R.; Rietow, B.T.; Thomas, B.G. Difference between Physical Water Models and Steel Continuous Caster: A Theoretical Evaluation. In Proceedings of the Materials Science and Technology 2009, Pittsburgh, PA, USA, 25–29 October 2009; pp. 1090–1101. [Google Scholar]
- Harada, H.; Toh, T.; Ishii, T.; Kaneko, K.; Takeuchi, E. Effect of Magnetic Field Conditions on the Electromagnetic Braking Efficiency. ISIJ Int. 2001, 41, 1236–1244. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Thomas, B.G.; Yuan, Q.; Mahmood, S.; Liu, R.; Chaudhary, R. Transport and Entrapment of Particles in Steel Continuous Casting. Metall. Mater. Trans. B 2014, 45B, 22–35. [Google Scholar] [CrossRef]
- ANSYS FLUENT 14.5-Theory Guide; ANSYS. Inc.: Canonsburg, PA, USA, 2012.
- Kumar, P.; Vanka, S.P. Effects of confinement on bubble dynamics in a square duct. Int. J. Multiphase Flow 2015, 77, 32–47. [Google Scholar] [CrossRef]
- Moreau, R. Magnetohydrodynamics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990; pp. 110–164. [Google Scholar]
- Davidson, P.A. Introduction to Magnetohydrodynamics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017; pp. 27–184. [Google Scholar]
- Cho, M.J.; Kim, I.C.; Kim, S.J.; Kim, J.K. 3-D Turbulent Heat & Fluid Flow Analysis with Solidification under Electro-Magnetic Field. Trans. KSME 1999, 23B, 1491–1502. [Google Scholar]
- Sengupta, J.; Shin, H.-J.; Thomas, B.G.; Kim, S.-H. Micrograph Evidence of Meniscus Solidification and Sub-Surface Microstructure Evolution in Continuous-Cast Ultra-Low Carbon Steels. Acta Mater. 2006, 54, 1165–1173. [Google Scholar] [CrossRef]
- Sengupta, J.; Thomas, B.G.; Shin, H.-J.; Lee, G.-G.; Kim, S.-H. A New Mechanism of Hook Formation during Continuous Casting of Ultra-Low-Carbon Steel Slabs. Metall. Mater. Trans. A. 2006, 37A, 1597–1611. [Google Scholar] [CrossRef]
- Takatani, K.; Nakai, K.; Kasai, N.; Watanabe, T.; Nakajima, H. Analysis of Heat Transfer and Fluid Flow in the Continuous Casting Mold with Electromagnetic Brake. ISIJ Int. 1989, 29, 1063–1068. [Google Scholar] [CrossRef]
- Kim, D.-S.; Kim, W.-S.; Cho, K.-H. Numerical Simulation of the Coupled Turbulent Flow and Macroscopic Solidification in Continuous Casting with Electromagnetic Brake. ISIJ Int. 2000, 40, 670–676. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L. Fluid Flow-Related Transport Phenomena in Steel Slab Continuous Casting Strands under Electromagnetic Brake. Metall. Mater. Trans. B 2011, 42B, 1319–1351. [Google Scholar] [CrossRef]
- Teshima, T.; Osame, M.; Okimoto, K.; Nimura, Y. Improvement of Surface Property of Steel at High Casting Speed. In Proceedings of the 71th Steelmaking Conference, Toronto, Canada, 17–20 April 1988; pp. 111–118. [Google Scholar]
- Hwang, Y.-S.; Cha, P.-R.; Nam, H.-S.; Moon, K.-H.; Yoon, J.-K. Numerical Analysis of the Influences of Operational Parameters on the Fluid Flow and Meniscus Shape in Slab Caster with EMBR. ISIJ Int. 1997, 37. [Google Scholar] [CrossRef]
- Tian, X.-Y.; Li, B.-W.; He, J.-C. Electromagnetic Brake Effects on the Funnel Shape Mold of a Thin Slab Caster Based on a New Type Magnet. Metall. Mater. Trans. B 2009, 40B, 596–604. [Google Scholar] [CrossRef]
- Zhang, L.-S.; Zhang, X.-F.; Wang, B.; Liu, Q.; Hu, Z.-G. Numerical Analysis of the Influences of Operational Parameters on the Braking Effect of EMBr in a CSP Funnel- Type Mold. Metall. Mater. Trans. B 2014, 45B, 295–306. [Google Scholar] [CrossRef]
- Xu, L.; Wang, E.; Karcher, C.; Deng, A.; Xu, X. Numerical Simulation of the Effects of Horizontal and Vertical EMBr on Jet Flow and Mold Level Fluctuation in Continuous Casting. Metall. Mater. Trans. B 2018, 49B, 2779–2793. [Google Scholar] [CrossRef]
- Li, F.; Wang, E.; Feng, M.; Li, Z. Simulation Research of Flow Field in Continuous Casting Mold with Vertical Electromagnetic Brake. ISIJ Int. 2015, 55, 814–820. [Google Scholar] [CrossRef][Green Version]
- Li, Z.; Wang, E.; Zhang, L.; Xu, Y.; Deng, A. Influence of Vertical Electromagnetic Brake on the Steel/Slag Interface Behavior in a Slab Mold. Metall. Mater. Trans. B 2017, 48B, 2389–2402. [Google Scholar] [CrossRef]
- Cho, S.-M.; Thomas, B.G.; Kim, S.-H. Transient Fluid Flow during Steady Continuous Casting of Steel Slabs: Part II. Effect of Double-Ruler Electro-Magnetic Braking. ISIJ Int. 2014, 54, 855–864. [Google Scholar] [CrossRef]
- Cho, S.-M.; Thomas, B.G.; Kim, S.-H. Transient Two-Phase Flow in Slide-Gate Nozzle and Mold of Continuous Steel Slab Casting with and without Double-Ruler Electro-Magnetic Braking. Metall. Mater. Trans. B 2016, 47B, 3080–3098. [Google Scholar] [CrossRef]
- Singh, R.; Thomas, B.G.; Vanka, S.P. Large Eddy Simulations of Double-Ruler Electromagnetic Field Effect on Transient Flow During Continuous Casting. Metall. Mater. Trans. B 2014, 45B, 1098–1115. [Google Scholar] [CrossRef]
- Yu, H.; ZHU, M. Numerical Simulation of the Effects of Electromagnetic Brake and Argon Gas Injection on the Three-dimensional Multiphase Flow and Heat Transfer in Slab Continuous Casting Mold. ISIJ Int. 2008, 48, 584–591. [Google Scholar] [CrossRef]
- Sarkar, S.; Singh, V.; Ajmani, S.K.; Singh, R.K.; Chanko, E.Z. Effect of Argon Injection in Meniscus Flow and Turbulence Intensity Distribution in Continuous Slab Casting Mold Under the Influence of Double Ruler Magnetic Field. ISIJ Int. 2018, 58, 68–77. [Google Scholar] [CrossRef]
- Sarkar, S.; Singh, V.; Ajmani, S.K.; Ranjan, R.; Rajasekar, K. Effect of Double Ruler Magnetic Field in Controlling Meniscus Flow and Turbulence Intensity Distribution in Continuous Slab Casting Mold. ISIJ Int. 2016, 56, 2181–2190. [Google Scholar] [CrossRef]
- Li, B.; Okane, T.; Umeda, T. Modeling of Molten Metal Flow in a Continuous Casting Process Considering the Effects of Argon Gas Injection and Static Magnetic-Field Application. Metall. Mater. Trans. B 2000, 31B, 1491–1503. [Google Scholar] [CrossRef]
- Idogawa, A.; Sugizawa, M.; Takeuchi, S.; Sorimachi, K.; Fujii, T. Control of Molten Steel Flow in Continuous Casting Mold by Two Static Magnetic Fields Imposed on Whole Width. Mater. Sci. Eng. A 1993, A173, 293–297. [Google Scholar] [CrossRef]
- Kunstreich, S.; Gautreau, T.; Ren, J.Y.; Codutti, A.; Guastini, F.; Petronio, M. Development and Validation of Multi-Mode® EMB, a New Electromagnetic Brake for Thin Slab Casters. In Proceedings of the 8th European Continuous Casting Conference, Graz, Austria, 23–26 June 2016. [Google Scholar]
- Kubo, N.; Kubota, J.; Suzuki, M.; Ishii, T. Molten Steel Flow Control under Electromagnetic Level Accelerator in Continuous Casting Mold. ISIJ Int. 2007, 47, 988–995. [Google Scholar] [CrossRef]
- Kubo, N.; Ishii, T.; Kubota, J.; Ikagawa, T. Numerical Simulation of Molten Steel Flow under a Magnetic Field with Argon Gas Bubbling in a Continuous Casting Mold. ISIJ Int. 2004, 44, 556–564. [Google Scholar] [CrossRef][Green Version]
- Okazawa, K.; Toh, T.; Fukuda, J.; Kawase, T.; Toki, M. Fluid Flow in a Continuous Casting Mold Driven by Linear Induction Motors. ISIJ Int. 2001, 41, 851–858. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, J.; Lei, S.; Dong, Q. Numerical Study on the Capture of Large Inclusion in Slab Continuous Casting with the Effect of In-mold Electromagnetic Stirring. ISIJ Int. 2017, 57, 2165–2174. [Google Scholar] [CrossRef]
- Li, B.; Okane, T.; Umeda, T. Modeling of Biased Flow Phenomena Associated with the Effects of Static Magnetic-Field Application and Argon Gas Injection in Slab Continuous Casting of Steel. Metall. Mater. Trans. B 2001, 32B, 1053–1066. [Google Scholar] [CrossRef]
- Moon, K.H.; Shin, H.K.; Kim, B.J.; Chung, J.Y.; Hwang, Y.S.; Yoon, J.K. Flow Control of Molten Steel by Electromagnetic Brake in the Continuous Casting Mold. ISIJ Int. 1996, 36, S201–S203. [Google Scholar] [CrossRef]
- Liu, Z.; Vakhrushev, A.; Wu, M.; Karimi-Sibaki, E.; Kharicha, A.; Ludwig, A.; Li, B. Effect of an Electrically-Conducting Wall on Transient Magnetohydrodynamic Flow in a Continuous-Casting Mold with an Electromagnetic Brake. Metals 2018, 8, 609. [Google Scholar] [CrossRef]
- Miao, X.; Timmel, K.; Lucas, D.; Ren, Z.; Eckert, S.; Gerbeth, G. Effect of an Electromagnetic Brake on the Turbulent Melt Flow in a Continuous-Casting Mold. Metall. Mater. Trans. B 2012, 43B, 954–972. [Google Scholar] [CrossRef]
- Tian, X.-Y.; Zou, F.; Li, B.-W.; He, J.-C. Numerical Analysis of Coupled Fluid Flow, Heat Transfer and Macroscopic Solidification in the Thin Slab Funnel Shape Mold with a New Type EMBr. Metall. Mater. Trans. B 2010, 41B, 112–120. [Google Scholar] [CrossRef]
- Hwang, J.Y.; Cho, M.J.; Thomas, B.G.; Cho, S.M. Numerical Simulation of Turbulent Steel CEM® Mold under High Mass Flow Condition. In Proceedings of the 9th International Symposium on Electromagnetic Processing of Materials (EPM2018), Hyogo, Japan, 14–18 October 2018; p. 012033. [Google Scholar]
- Satou, Y.; Baba, N.; Kasai, N.; Mutou, A.; Hanao, M. Increase of Casting Speed of Hypo-peritectic Steel at Kashima No.3 Caster. In Proceedings of the AISTech 2009, St. Louis, MO, USA, 4–7 May 2009; pp. 663–671. [Google Scholar]
- Wang, S.; Zhang, X.; Zhang, L.; Wang, Q. Influence of Electromagnetic Brake on Hook Growth and Inclusion Entrapment beneath the Surface of Low-Carbon Continuous Casting Slabs. Steel Res. Int. 2018, 89, 1800263. [Google Scholar] [CrossRef]
- Zhang, L.; Aoki, J.; Thomas, B.G. Inclusion Removal by Bubble Flotation in a Continuous Casting Mold. Metall. Mater. Trans. B 2006, 37B, 361–379. [Google Scholar] [CrossRef]
- Gass, R.; Knoepke, H.; Moscoe, J.; Shah, R.; Beck, J.; Dzierzawski, J.; Ponikvar, P.E. Conversion of Ispat Inland’s No. 1 Slab Caster to Vertical Bending. In Proceedings of the ISSTech 2003 Conference, Indianapolis, Indiana, 27–30 April 2003; pp. 3–18. [Google Scholar]
- Jin, K.; Kumar, P.; Vanka, S.P.; Thomas, B.G. Rise of an argon bubble in liquid steel in the presence of a transverse magnetic field. Phys. Fluids 2016, 28, 093301. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, A.; Zhang, L. Effect of Slide Gate and EMBr on the Transport of Inclusions and Bubbles in Slab Continuous Casting Strands. Steel Res. Int. 2011, 82, 428–439. [Google Scholar] [CrossRef]
- Yuan, Q.; Thomas, B.G.; Vanka, S.P. Study of Transient Flow and Particle Transport in Continuous Steel Caster Molds: Part II. Particle Transport. Metall. Mater. Trans. B 2004, 35B, 703–714. [Google Scholar] [CrossRef]
- Jin, K.; Vanka, S.P.; Thomas, B.G. Large Eddy Simulations of Electromagnetic Braking Effects on Argon Bubble Transport and Capture in a Steel Continuous Casting Mold. Metall. Mater. Trans. B 2018, 49B, 1360–1377. [Google Scholar] [CrossRef]
- Shibata, H.; Yin, H.; Yoshinaga, S.; Emi, T.; Suzuki, M. ln-situ Observation of Inclusions in Steel Melt Engulfment and Pushing by Advancing Melt/Solid of Nonmetallic Interface. ISIJ Int. 1998, 38, 149–156. [Google Scholar] [CrossRef]
- Lee, S.-M.; Kim, S.-J.; Kang, Y.-B.; Lee, H.-G. Numerical Analysis of Surface Tension Gradient Effect on the Behavior of Gas Bubbles at the Solid/Liquid Interface of Steel. ISIJ Int. 2012, 52, 1730–1739. [Google Scholar] [CrossRef]
- Pesteanu, O. The Washing Effect in Electromagnetic Rotational Stirrers for Continuous Casting. ISIJ Int. 2005, 45, 1073–1075. [Google Scholar] [CrossRef]
- Pesteanu, O. Short Contribution to the Study of the Washing Effect in Electromagnetic Stirrers for Continuous Casting. ISIJ Int. 2003, 43, 1861–1862. [Google Scholar] [CrossRef]
- Toh, T.; Hasegawa, H.; Harada, H. Evaluation of Multiphase Phenomena in Mold Pool under In-mold Electromagnetic Stirring in Steel Continuous Casting. ISIJ Int. 2001, 41, 1245–1251. [Google Scholar] [CrossRef]
- Kittaka, S.; Fukuokaya, T.; Maruki, Y.; Kanki, T. Nippon Steel Strand Electro-Magnetic Stirrer “S-EMS” for Slab Caster; Nippon Steel: Tokyo, Japan, 2003; pp. 70–74. [Google Scholar]
- Xu, Y.; Xu, X.-J.; Li, Z.; Wang, T.; Deng, A.-Y.; Wang, E.-G. Dendrite Growth Characteristics and Segregation Control of Bearing Steel Billet with Rotational Electromagnetic Stirring. High Temp. Mater. Proc. 2017, 36, 339–346. [Google Scholar] [CrossRef]
- Shibata, H.; Itoyama, S.; Kishimoto, Y.; Takeuchi, S.; Sekiguchi, H. Prediction of Equiaxed Crystal Ratio in Continuously Cast Steel Slab by Simplified Columnar-to-Equiaxed Transition Model. ISIJ Int. 2006, 46, 921–930. [Google Scholar] [CrossRef][Green Version]
- Bridge, M.R.; Rogers, G.D. Structural Effects and Band Segregate Formation during the Electromagnetic Stirring of Strand-Cast Steel. Metall. Trans. B. 1984, 15B, 581–589. [Google Scholar] [CrossRef]





| Fluid | Melting Temperature (°C) | Density (kg/m3) | Dynamic Viscosity (kg/m·s) | Electrical Conductivity (/Ω·m) | Thermal Conductivity (W/m·K) |
|---|---|---|---|---|---|
| Steel | 1480–1510 | 7000 | 0.0067 | 714,000 | 35.0 |
| Water | 0 | 998.2 | 0.001 | 0.05 | 0.60 |
| Mercury | −38.8 | 13,534 | 0.001555 | 1,020,000 | 8.3 |
| Sn60Bi40 | 138–170 | 8250 | 0.0016 | 1,050,000 | 35 |
| Ga68In20Sn12 | 10.5 | 6360 | 0.0021 | 3,290,000 | 39 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, S.-M.; Thomas, B.G. Electromagnetic Forces in Continuous Casting of Steel Slabs. Metals 2019, 9, 471. https://doi.org/10.3390/met9040471
Cho S-M, Thomas BG. Electromagnetic Forces in Continuous Casting of Steel Slabs. Metals. 2019; 9(4):471. https://doi.org/10.3390/met9040471
Chicago/Turabian StyleCho, Seong-Mook, and Brian G. Thomas. 2019. "Electromagnetic Forces in Continuous Casting of Steel Slabs" Metals 9, no. 4: 471. https://doi.org/10.3390/met9040471
APA StyleCho, S.-M., & Thomas, B. G. (2019). Electromagnetic Forces in Continuous Casting of Steel Slabs. Metals, 9(4), 471. https://doi.org/10.3390/met9040471






