1. Introduction
The use of stainless steels is spreading in all those sectors where the working conditions of various mechanical components are quite critical and could trigger structural problems of the component.
Following their good strength/ductility combination coupled with their excellent corrosion resistance [
1], stainless steels are adopted in many applications including automotive [
2], construction and building [
3], oil and gas [
4], aeronautical [
5], medical [
6,
7], and food [
8].
In the abovementioned sectors, the mechanical components have to work in environments that can be saturated with aggressive substances, risking undermining the mechanical properties of the material and thus inducing possible problems of strength [
9]. It is, therefore, evident that, in this context, the use of stainless materials becomes essential and, therefore, is increasingly widespread.
Stainless steel owes its resistance to corrosion to a simple chemical reaction: the combination of chrome in steel and the oxygen in the air or water on the surface form a very thin passivation film. This film protects the component against all aggressive substances. If this film is damaged, however, it spontaneously reforms from the steel matrix [
10,
11,
12,
13]. For this reason, stainless steels are generally called self-passivation steel. The main actor in the self-passivation phenomenon is chrome. When the oxygen content is above a certain level, chrome reacts with this, forming a layer of chromium oxide or hydroxide. This thin film (with a thickness of the order of a few atoms, 3 ÷ 5
mm) protects the underlying metal from the action of external agents. The corrosion resistance also depends on the surface morphology: the more the surface is smooth and homogeneous, the greater its resistance to corrosion will be.
On the basis of this, many researchers of different scientific backgrounds are actively working, studying the properties of stainless steels both from a chemical [
11,
12,
13,
14,
15,
16] and from a structural point of view [
17,
18,
19,
20,
21,
22]. The first category is a majority focus on studying how the properties of these materials vary according to their chemical composition and electrochemical behaviour, while the second category is mainly focus on the consequences generated by a possible mechanical degradation of the component surface.
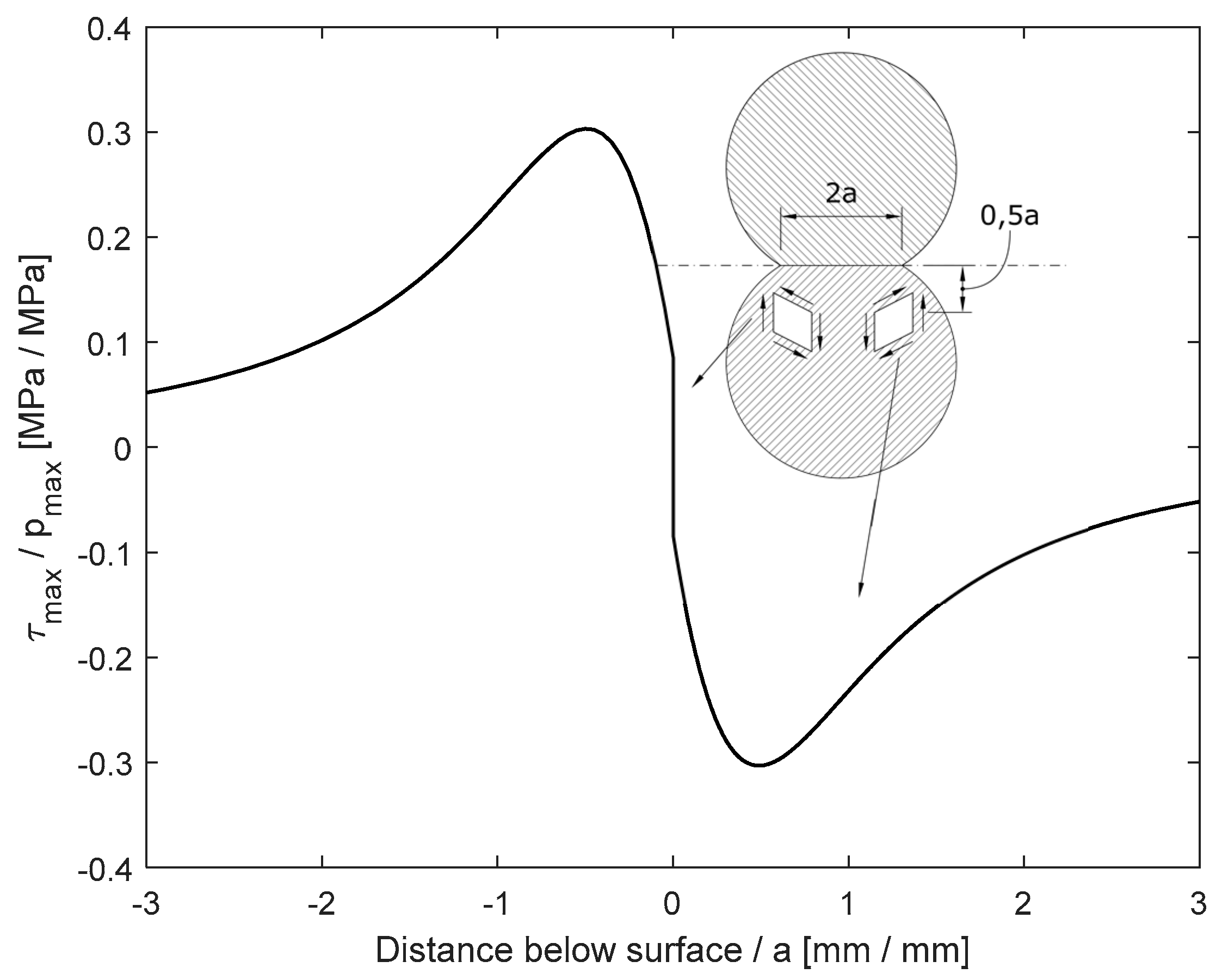
It is known how mechanical components working in contact are subjected to degradation issues. The two most common phenomena that induced the degradation of a mechanical component are pitting and spalling [
23]. According to the American Society for Metals (ASM) handbook, “Usually, pitting is the result of surface cracks caused by metal-to-metal contact of asperities or defects due to low lubricant film thickness” [
24]. Even if the starting point of pitting phenomena is still under investigation by the scientific community, the link between bodies working in contact and pitting issues is real and approved without doubts [
25].
Given the reduction of the antioxidant properties that occur in the case of a degradation of the surface layer of components, an efficient tool for predicting and evaluating contact fatigue may help the design engineer when they have to face this kind of problem.
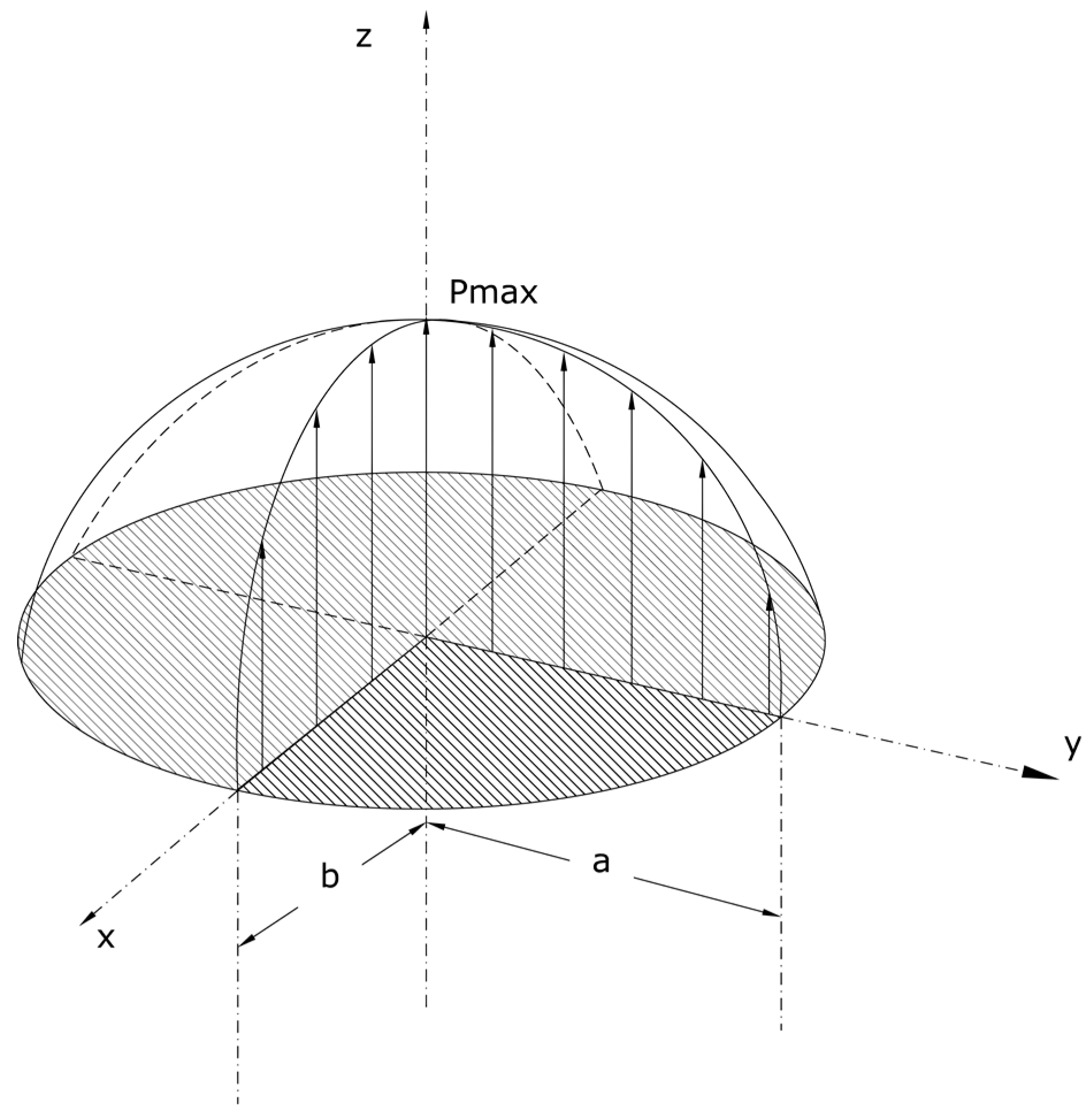
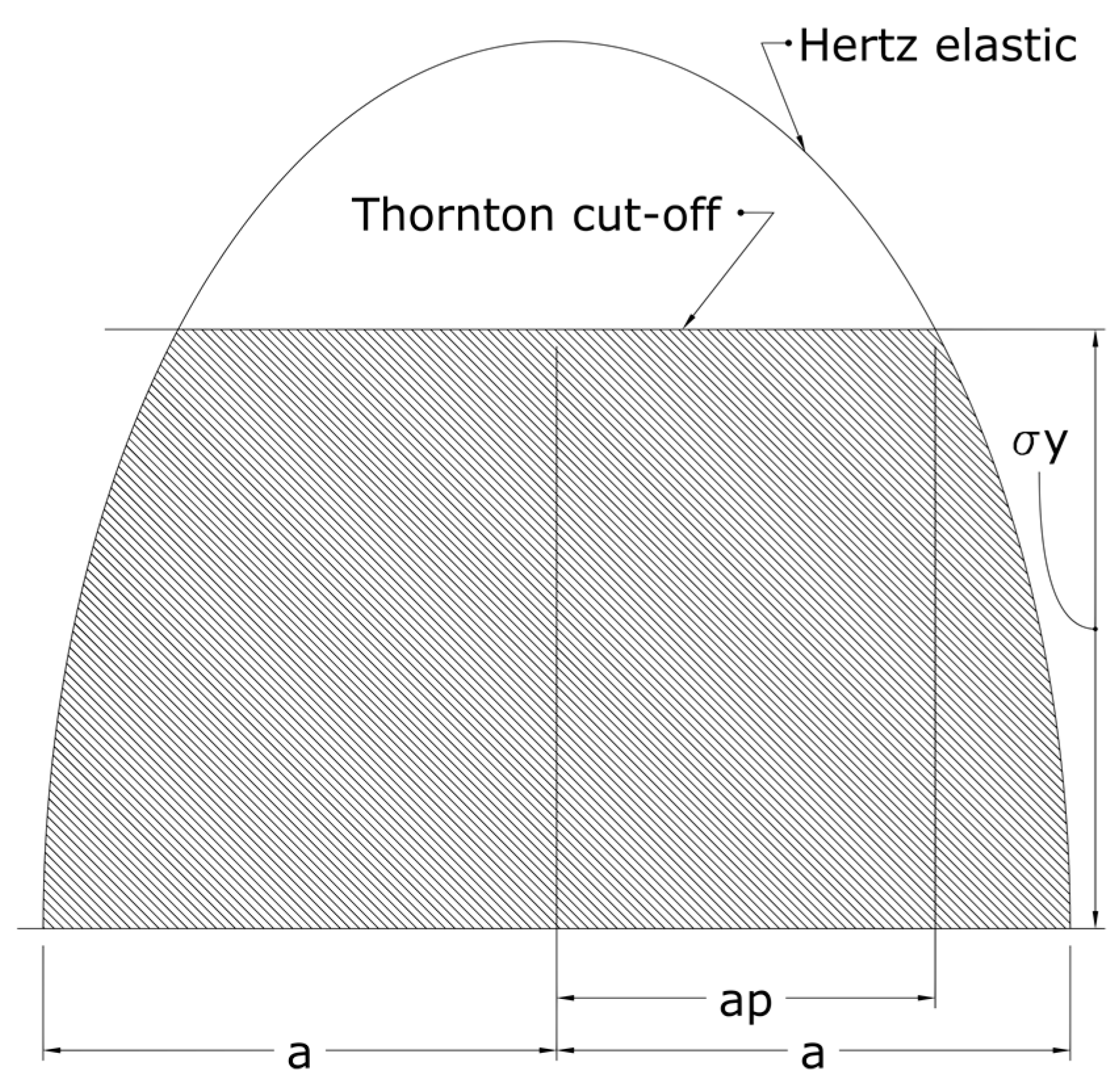
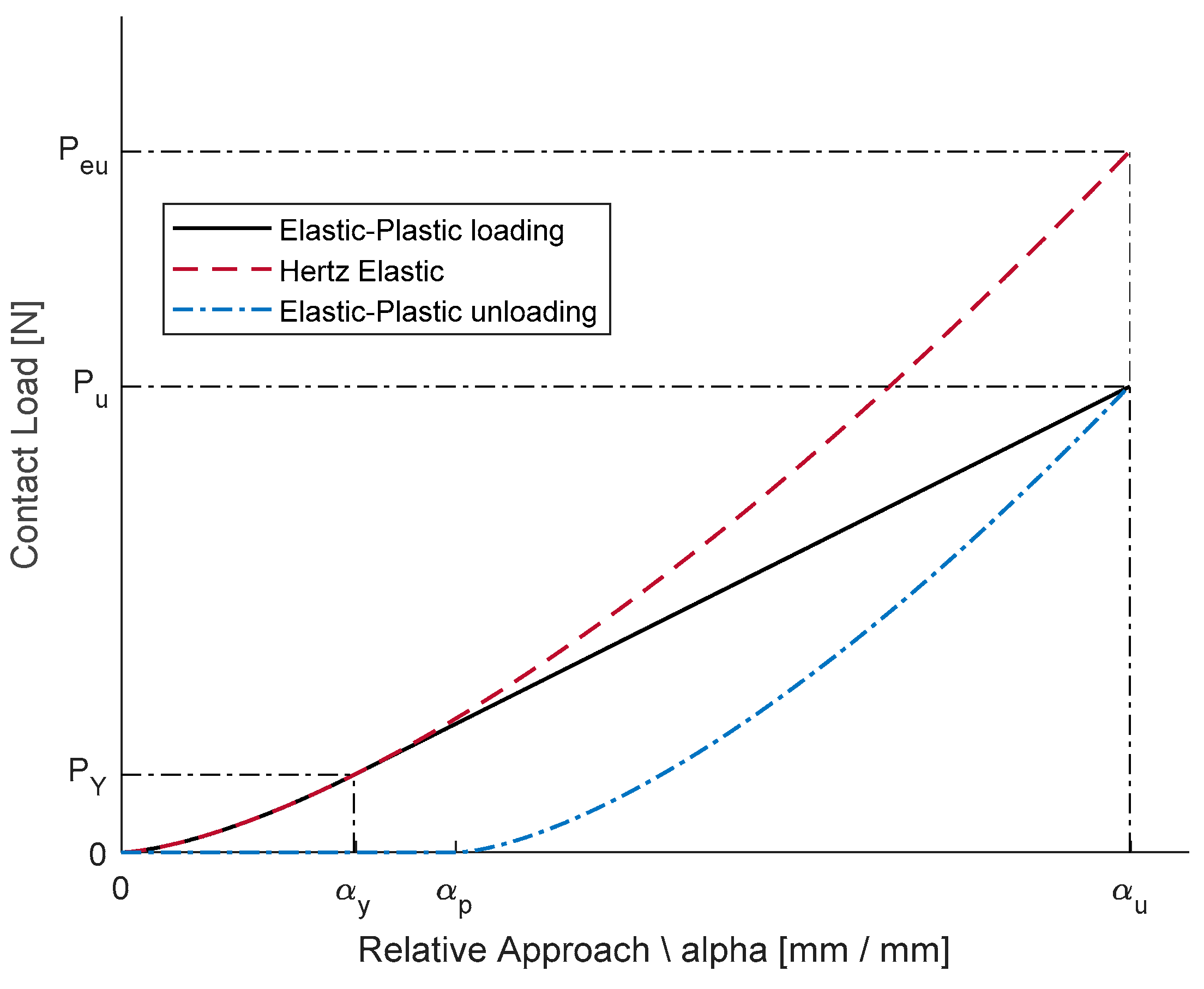
To solve mechanical contact issues, engineers must generally choice between a kinematic-theoretical approach and a numerical approach. The first exploits the kinematic laws to determine impact forces and then applies the Hertz theory [
26,
27] to calculate stresses. This approach requires, however, an assessment of the initial condition of contact dynamics. This aspect it is often so complex to make that this method is not applicable in a real complex model. The second approach is based on the explicit finite element method (FEM), that allows a more accurate assessment of both the impact forces and surface pressures. The major drawback of this type of approach is the computational time: To obtain reliable results in terms of stresses, very complex models and, so, impracticable times of the simulations are generally required [
28].
The present work seeks to propose a simple procedure for the evaluation of pressures and contact stresses in mechanical components that may result in surface resistance (pitting) issues. The aim of the work is that of evaluating, by calculation, the possible occurrence of pitting phenomena, trying to avoid such phenomenon at the beginning of the design stage [
29,
30,
31].
The attempt of the authors is to find a trade-off between the efficiency requirement on one side and the effectiveness of the other one, typical in the design scenario and in contrast with the time and economic constraints of industries.
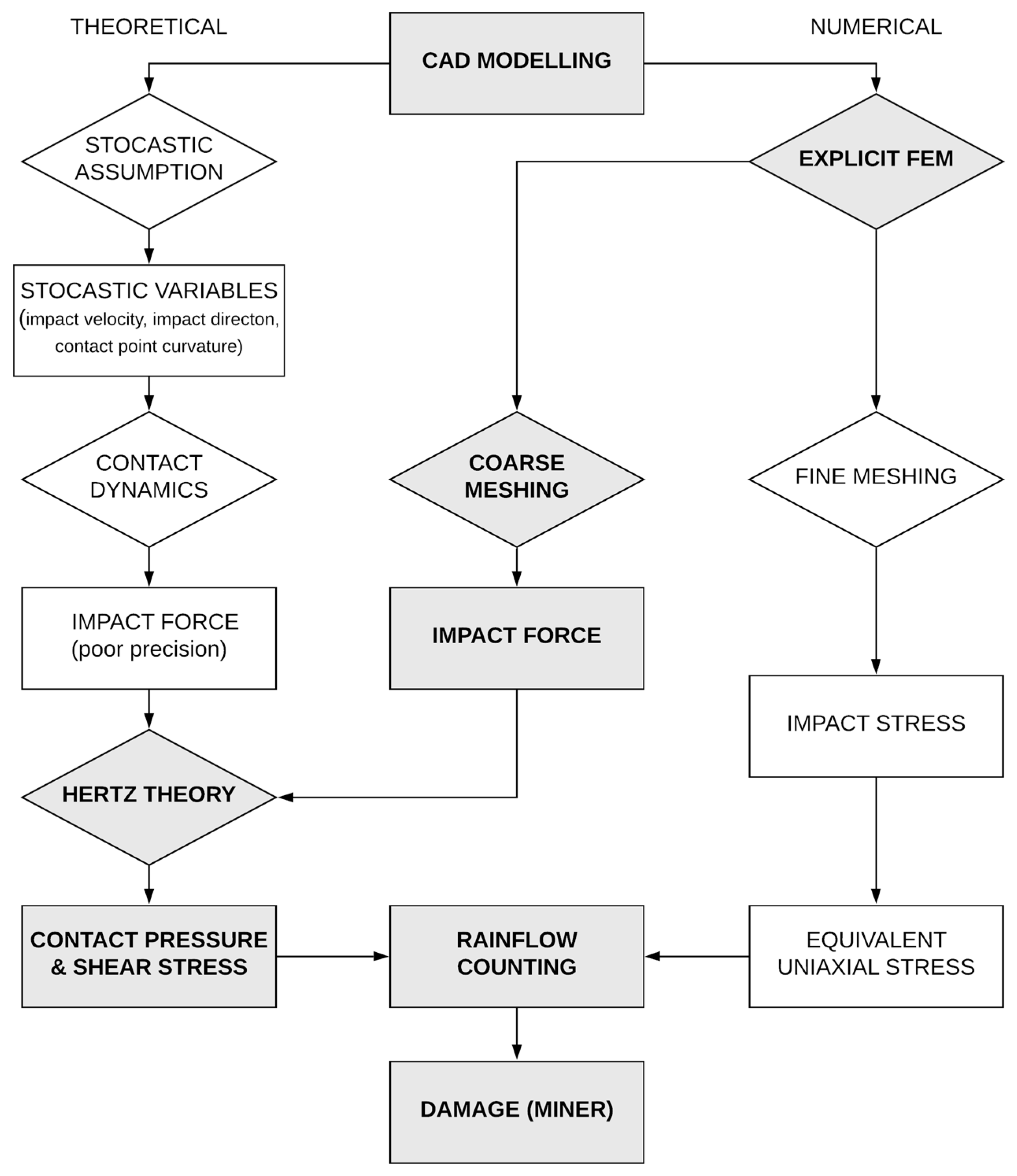
For this reason, the authors developed a hybrid approach, theoretical-numerical, which allows the calculation effort to speed up obtaining, at the same time, reliable results. Developing a finite element model not voted to contact stress calculation but only to contact forces evaluation involves a drastic reduction in computational efforts. Once contact forces are known, the classical Hertz theory [
27] is used to estimate the stresses on the component surface.
The fully theoretical and numerical procedures and the hybrid one proposed in this activity are devoted to evaluating contact stress due to bodies in contact. The evaluation of fatigue life is a shared step of all three methodologies, and it is always based on the assessment of the fatigue curve and on the damage computational model. In this case, the linear accumulation law of Palmgren-Miner [
32] is used. The proposed hybrid method was validated on a simple case of sphere-plane contact. At the end, a more complex case study was used to validate the effectiveness of the proposed approach. The mechanical component used as benchmark is a stainless-steel recirculation mechanism of a ball screw developed for aeronautical applications by a leader company in this sector.
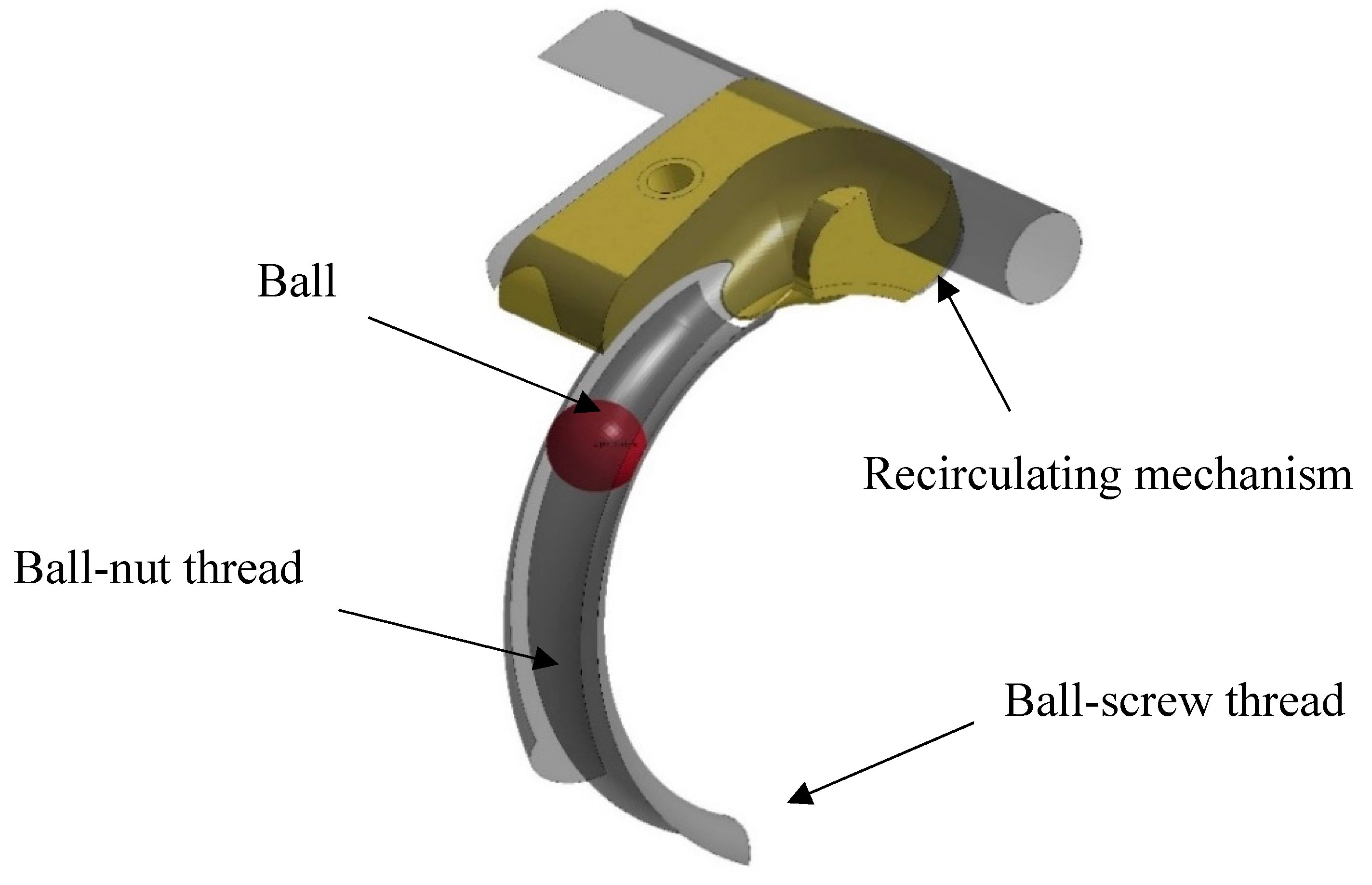
As a matter of fact, ball screws are used successfully in all those applications, both industrial and aeronautical, in which high-speed and high-accuracy movements of components are required. Ball screws in aeronautical field are generally used for moving mobile surfaces (flaps and slats) and the stabilizer. For this reason, they are exposed to atmospheric conditions that are sufficiently critical to require the use of stainless steels.
Due to the high speed with which these systems have to work, one of the most frequently encountered problem by ball-screw manufacturers is the premature failure of the evolving components in contact [
26]. The areas most affected by surface fatigue problems in a ball screw are essentially two: the contact zone between the screw tracks and the balls themselves during normal operation and the impact zone in the recirculation mechanism where the balls are forced to abruptly change direction [
33,
34]. The high number of impacts to which a recirculation system is generally subject tend to generate a plastic deformation of the recirculation system itself. This modifies the geometry of the system, causing a rapid increase in the maximum contact pressure on the surface. This aspect is often shown in a wear on the surface of the recirculation mechanism (pitting) which leads to a reduction of the antioxidant properties of the stainless steel used and consequently to a drastic reduction of the fatigue strength of the component.
Since this phenomenon is often rediscovered, numerous studies have been carried out trying to better understand the phenomenon of the ball’s impact during the recirculation phase and to propose different approaches for the estimation of the life of ball screws. Jiang et al. [
35] studied the dynamics and impact forces of spheres in a recirculation mechanism, using a multi-body code and trying to optimize the geometry of the recirculation mechanism itself. Braccesi et al. [
36] presented a relationship between the Hertz equivalent elastic stress limit with typical design parameters such as the allowable material stress, the geometric characteristics in contact areas, the impact angles, and the rotational speed for different types of materials, using an elastic-plastic model for a curved body in contact. Zhang et al. [
37] studied the influence of various factors on the impact forces generated between the spheres and recirculation mechanism for different types of materials and for different recirculation geometries.
Although the available methods for the calculation of surface fatigue strength are multiple, the one proposed in the present activity is aimed at being user-friendly for all those realities that have not enough resources to devote to the development of complex models that are multi-body model or finite elements model. What is immediately highlighted by the proposed approach is that, remaining linked to the theory and exploiting the numerical simulation, it is possible to obtain a more accurate estimation of the fatigue life than would be obtained using a completely kinematic-theoretic approach. At the same time, the solution is very close to that obtainable from a completely numerical approach but, obviously, with a drastic reduction of the computational effort.
3. Theoretical vs. Numerical: The Birth of a Hybrid Method
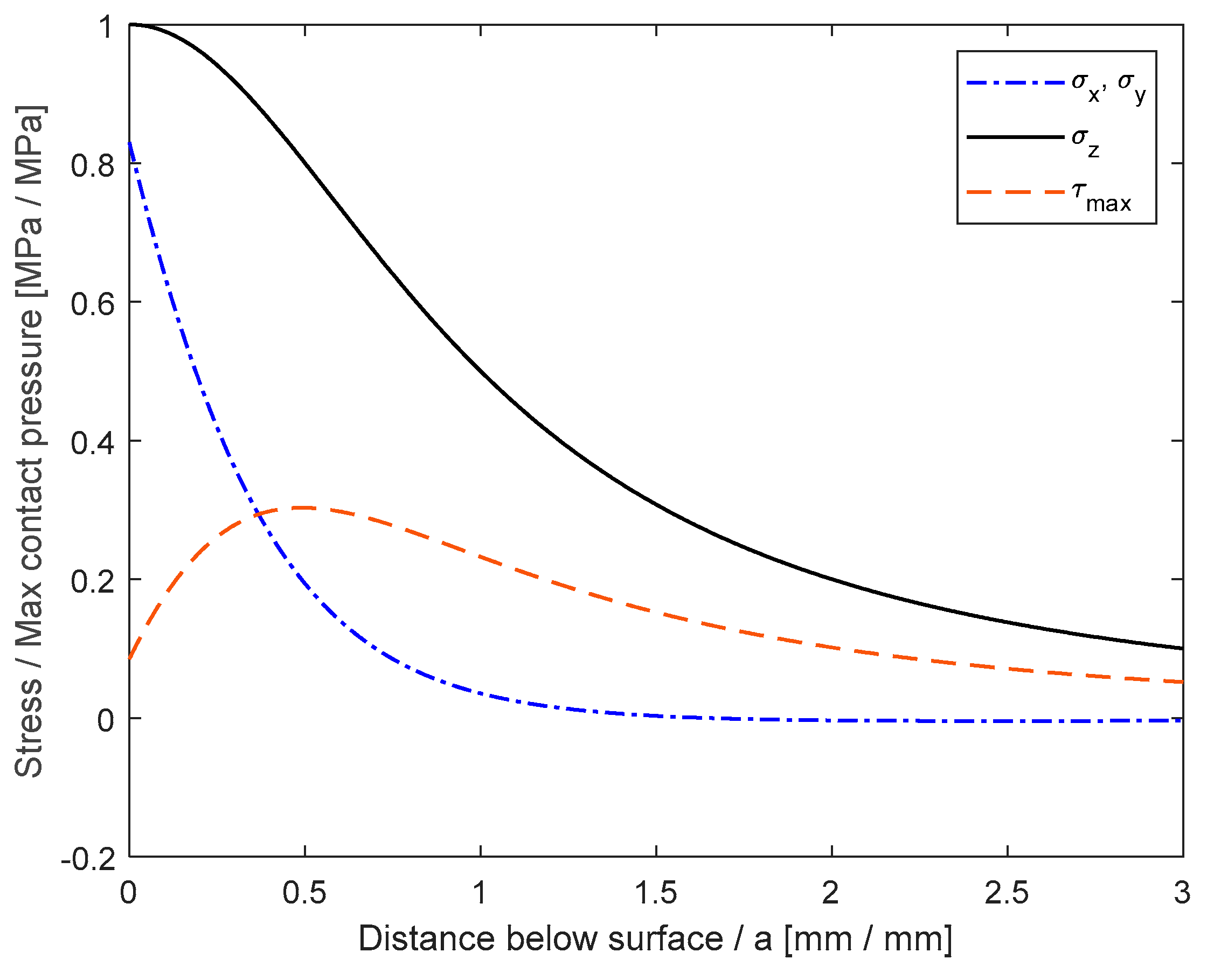
In the previous paragraph, the theoretical approach for contact stress evaluation and contact fatigue prediction was briefly explained. The theoretical method exploits the kinematical laws [
43] and the Hertz theory [
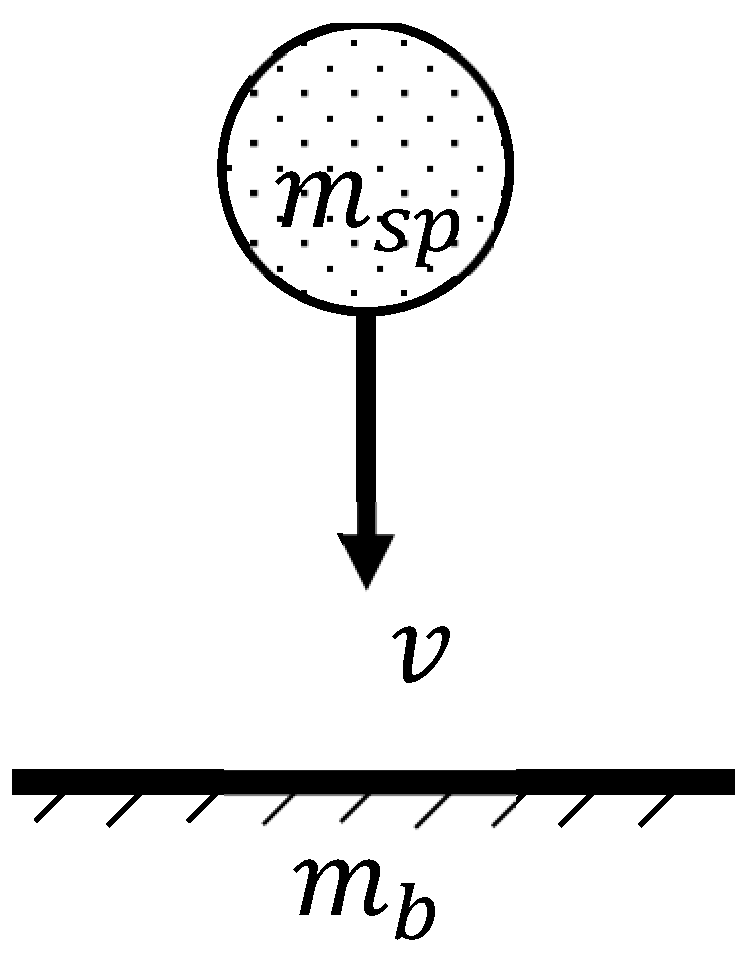
27], determining the surface fatigue life of the component. A second option that can be followed by the mechanical designer is a completely numerical approach that, exploiting the potentialities of explicit dynamic analysis codes, allows the very accurate determination of both the forces and the contact pressures. To demonstrate the potentials and limitations of both approaches, a simple test case has been analyzed, i.e., a sphere that falls from a 26-mm height on a plane, determining both impact forces and contact pressures. To this aim, the inputs shown in
Table 1 were considered.
It has been imposed that the sphere falls perpendicular to the plane and, therefore, with an angle of
. From the inputs of
Table 1 the estimated impact velocity is
. Taking advantage of the equations described in
Section 2.1, a contact force of
and a maximum contact pressure of
was determined.
The same case study was reproduced in an explicit finite element environment (LS-DYNA FEM code) in which the same parameters previously obtained were evaluated.
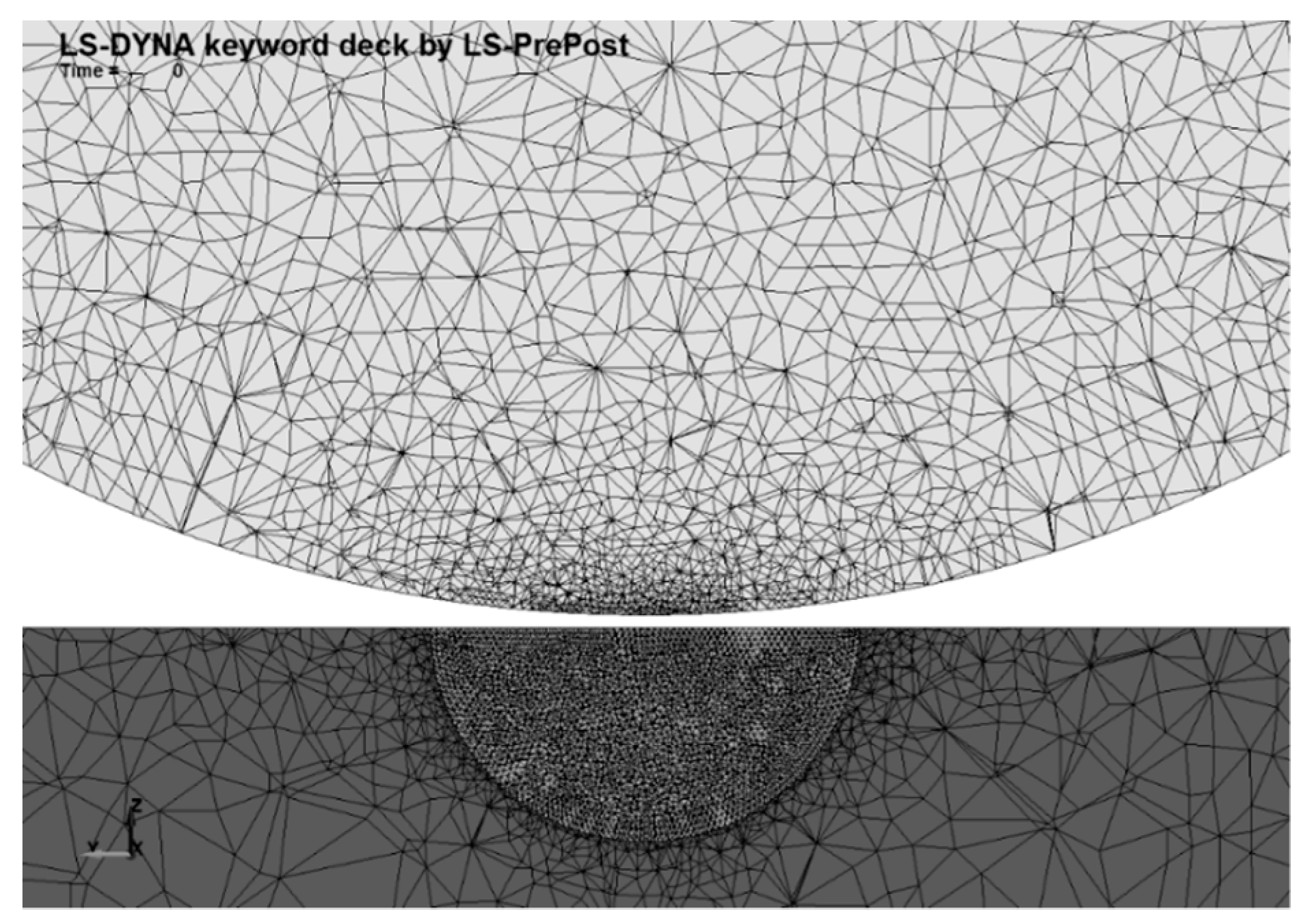
Figure 7 shows the initial instant of the simulation and the used mesh. 4-node tetrahedral elements were used both for the sphere and for the impact plane. The simulation foresees 1,199,262 elements and 4,797,048 nodes. To model the contact between two bodies, the contact type “automatic surface to surface” available in LS-DYNA was used.
To reduce the calculation effort, the sphere was placed near the contact plane and the analytically calculated initial velocity was set. This allowed for a drastic reduction in the calculation effort.
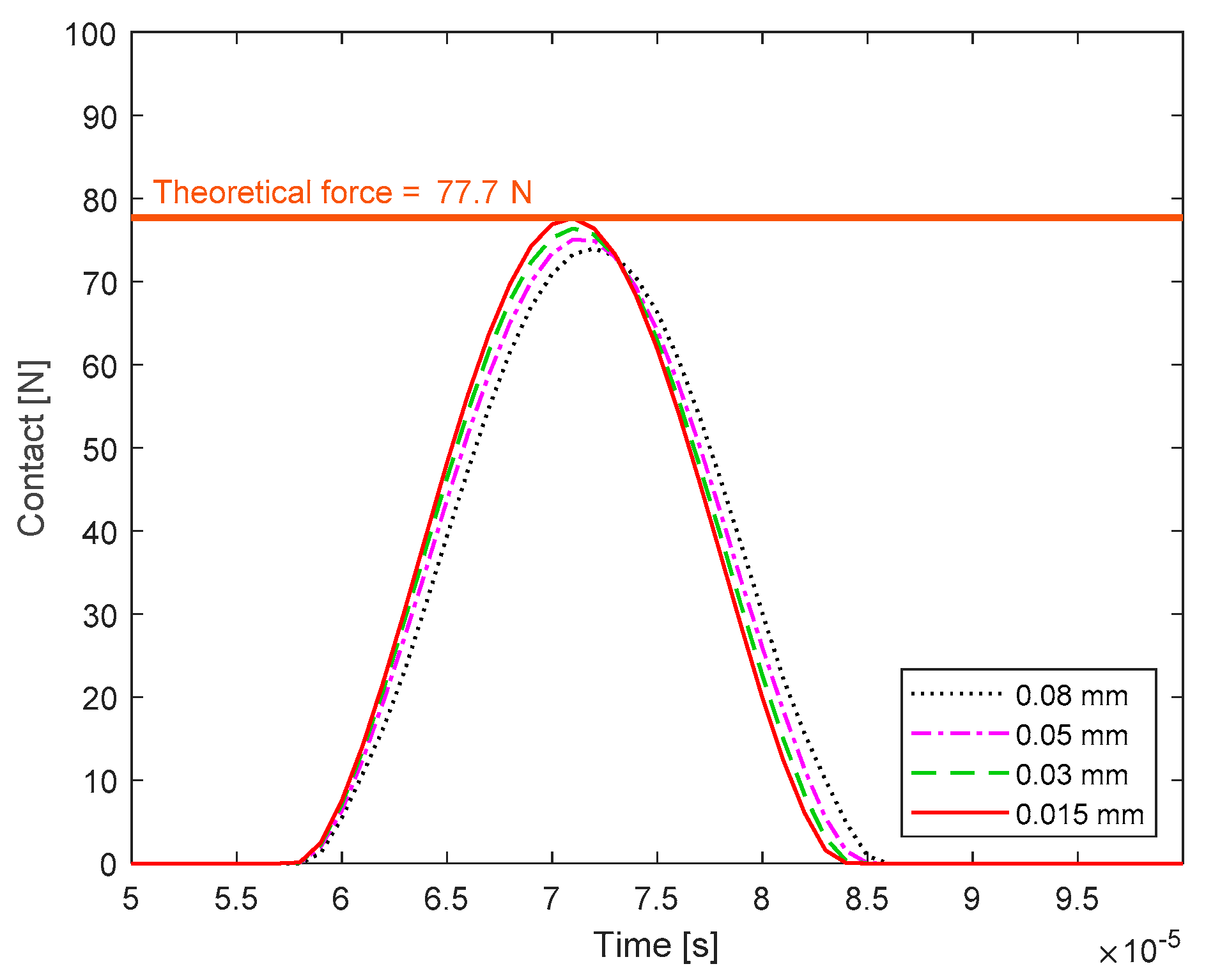
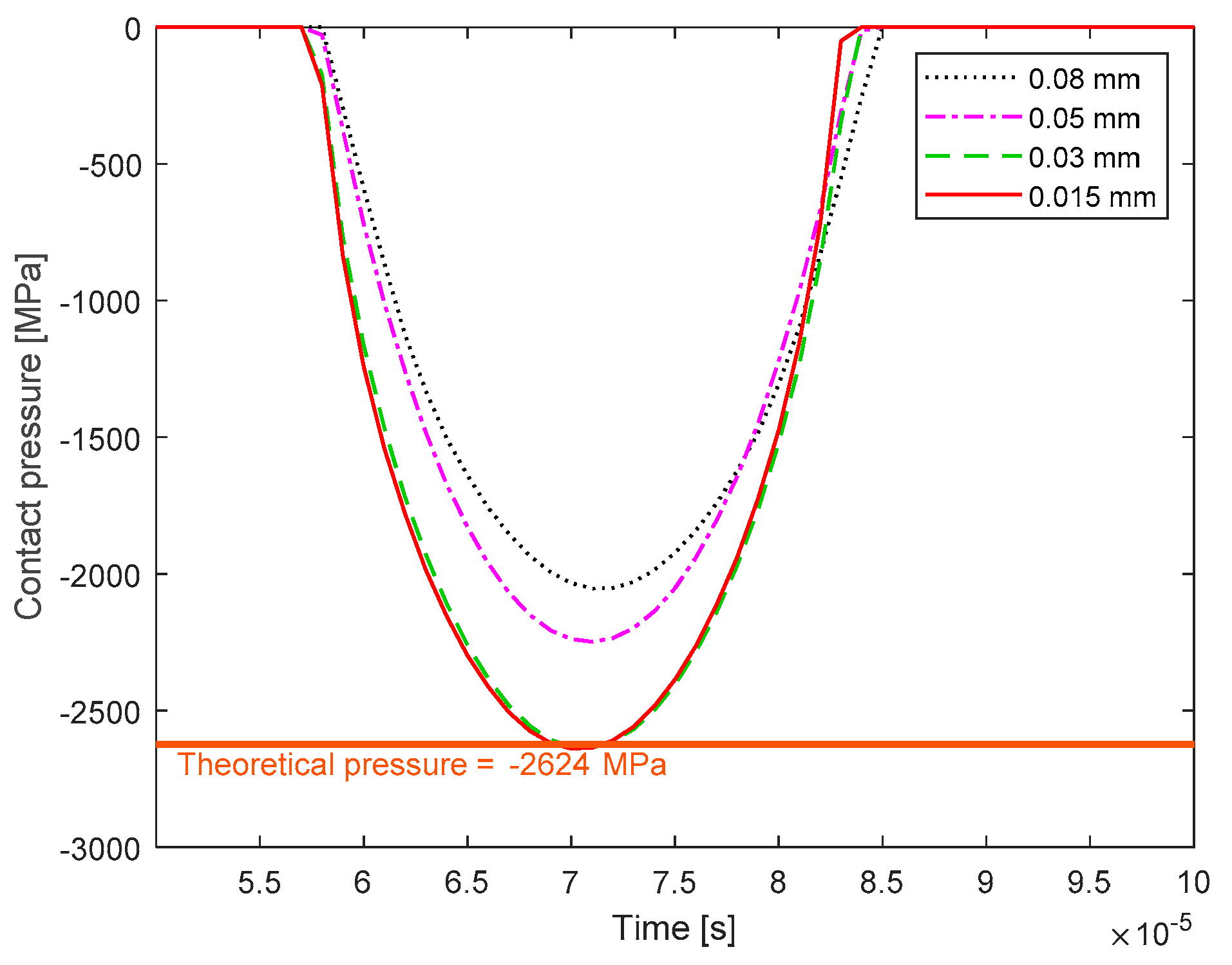
Figure 8 shows the trends of the contact force obtained from the numerical analysis as the mesh size changes. The obtained results show that the mesh has a negligible influence on the calculation of the contact force. The obtained force values are identical to those theoretically obtained.
Figure 9 instead shows the contact pressure trends obtained from the numerical analysis when the mesh dimensions vary.
It is clear that when the mesh varies, the results are significantly different. To get results close to the theoretical ones, it is necessary to use a very fine mesh. This fact is directly related to the calculation time necessary for the simulation, which is as much larger as the mesh is finer.
From the results thus obtained, one might think that a completely theoretical approach may be sufficient to determine both impact forces and contact pressures without the aid of explicit FEM codes. It is important to highlight, however, that, to accurately determine both impact forces and contact pressures exploiting theoretical laws, it is necessary to assess a set of variables such as the trajectory of the bodies, the speed of impact, the radii of curvatures, the stiffness of the bodies, etc. In complex real models these variables are not a priori known since they are random variable. For this reason, a suitable way would be a stochastic approach.
In this context, the hybrid method proposed in this activity represents a way out to bypass the weakness of previously described approaches. Exploiting the potentialities of the finite element analysis software (where initial variables are automatically known), it is possible to obtain contact forces in a relatively short time, since forces are sufficiently independent from the mesh size. Once contact forces are known, contact stresses can be accurately computed using the Hertz theory [
27] (See
Section 2.2) and the fatigue life can be easily addressed. In such a way, it is possible to not deal with such complex models to often not be feasible. In
Figure 10, a summarizing flow chart is proposed.
4. Test Case
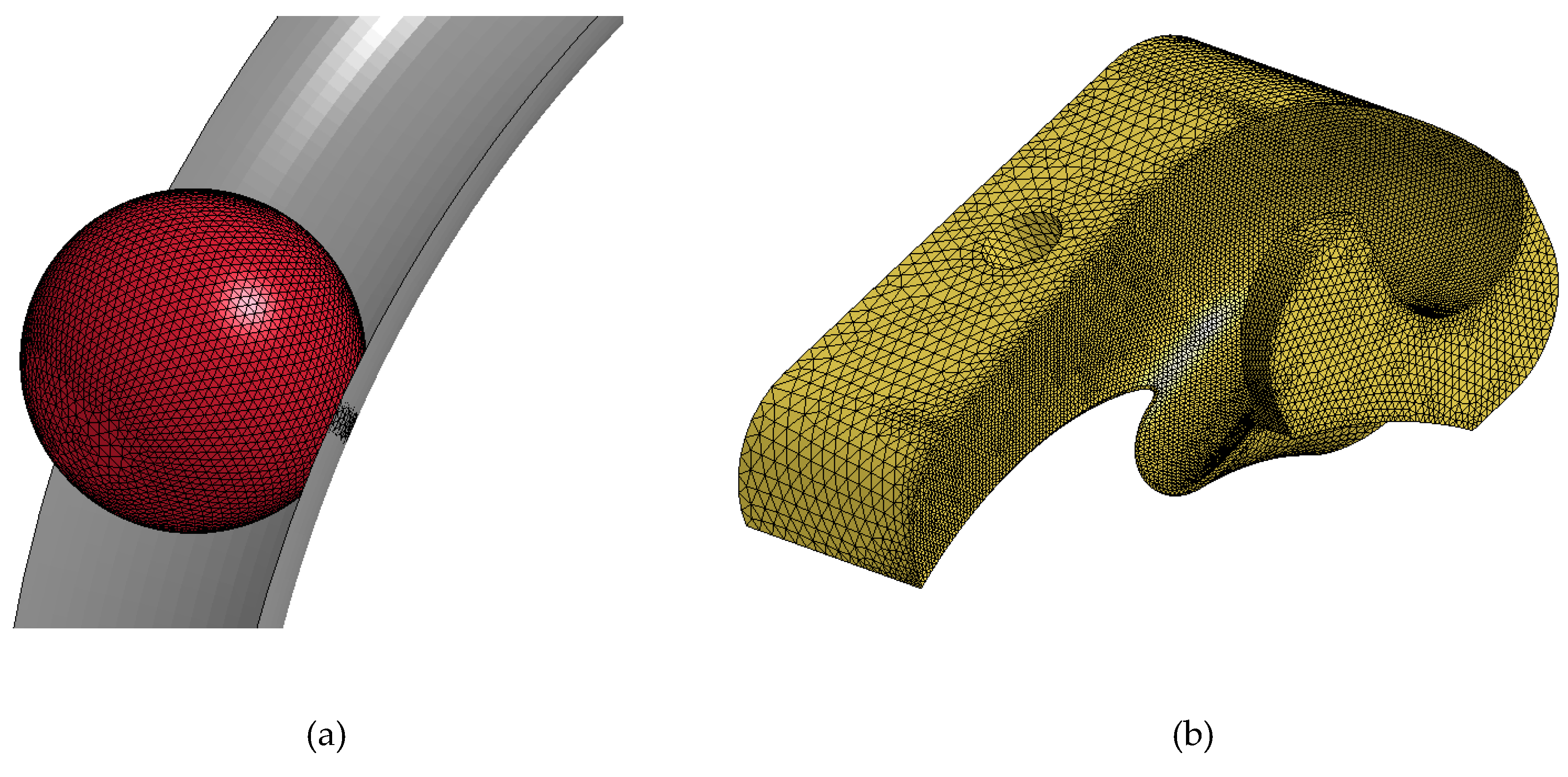
To evaluate the goodness of the proposed hybrid method for calculating the surface fatigue life of stainless-steel components, an explicit finite elements analysis was performed on the recirculating system of a ball screw using LS-DYNA FEM code. It often happens that these components, due to their function, are subjected to a series of impulses that may cause surface fatigue problems. The recirculating ball screw used in this activity is an existing ball screw used in different applications. This has a center sphere diameter of , a screw pitch equal to , a sphere diameter of , and a radial insert. Since attention was paid to the recirculation system and, therefore, only to an evaluation of the fatigue life of the recirculating mechanism only to reduce the simulation effort, it was decided to model only the ball screw and ball-nut surfaces that act as a guide for the sphere through shell elements. A total of 57,918 elements and 231,672 were used to mesh the ball screw and ball-nut surfaces. The sphere and the insert have been modelled with solid 4-node tetrahedral elements. A total of 246,533 element and 986,132 nodes were used for the sphere and the recirculating mechanism. This allowed for a good approximation in the curvature, both of the sphere and of the recirculation mechanism, thus obtaining a good approximation with regard to the physics of the impact that has been simulated. In this activity, the roughness of cooperating surfaces was set equal to zero due to the accuracy of the manufacturing process.
The following figure shows the model used for this analysis.
The recirculating mechanism of
Figure 11 is made of 17–4 PH steel: 17–4 PH stainless steel is, in fact, one of the steels obtained by precipitation and hardening most used in aeronautics. In fact, this material, besides being stainless, offers excellent mechanical characteristics.
Table 2 summarizes some features of the material.
Figure 12 shows the mesh obtained with the parameters previously illustrated.
About the boundary conditions, the recirculating system has been fixed in correspondence with the hole. This hole is, in fact, used to fasten the recirculation mechanism on the seat obtained in the ball nut. Furthermore, five degrees of freedom of the ball nut were constrained (three rotations and two displacement), as this system is a rotating ball screw. The principal inertia tensor and the mass of the total ball screw were assigned to the ball-screw surface with the aim of reproducing the real movement of the ball screw itself. This means that the ball screw only rotates while the ball nut performs a linear motion. A rotation speed of the screw was set equal to . The contact type “automatic surface to surface” allowable in LS-DYNA was used to model the contact between the sphere and the recirculating mechanism.
To model the system as more realistic as possible, it is necessary to consider also a viscosity dissipation inherent the material. For this purpose, a percentage damping was imposed in a frequency range between and . This frequency range was taken into consideration following a modal analysis of the recirculation system only, imposing the same conditions of constraint of the dynamic analysis. What emerged from the modal analysis is that the vibrating modes that mostly participate in the total vibration are the first and are all in the range between and .
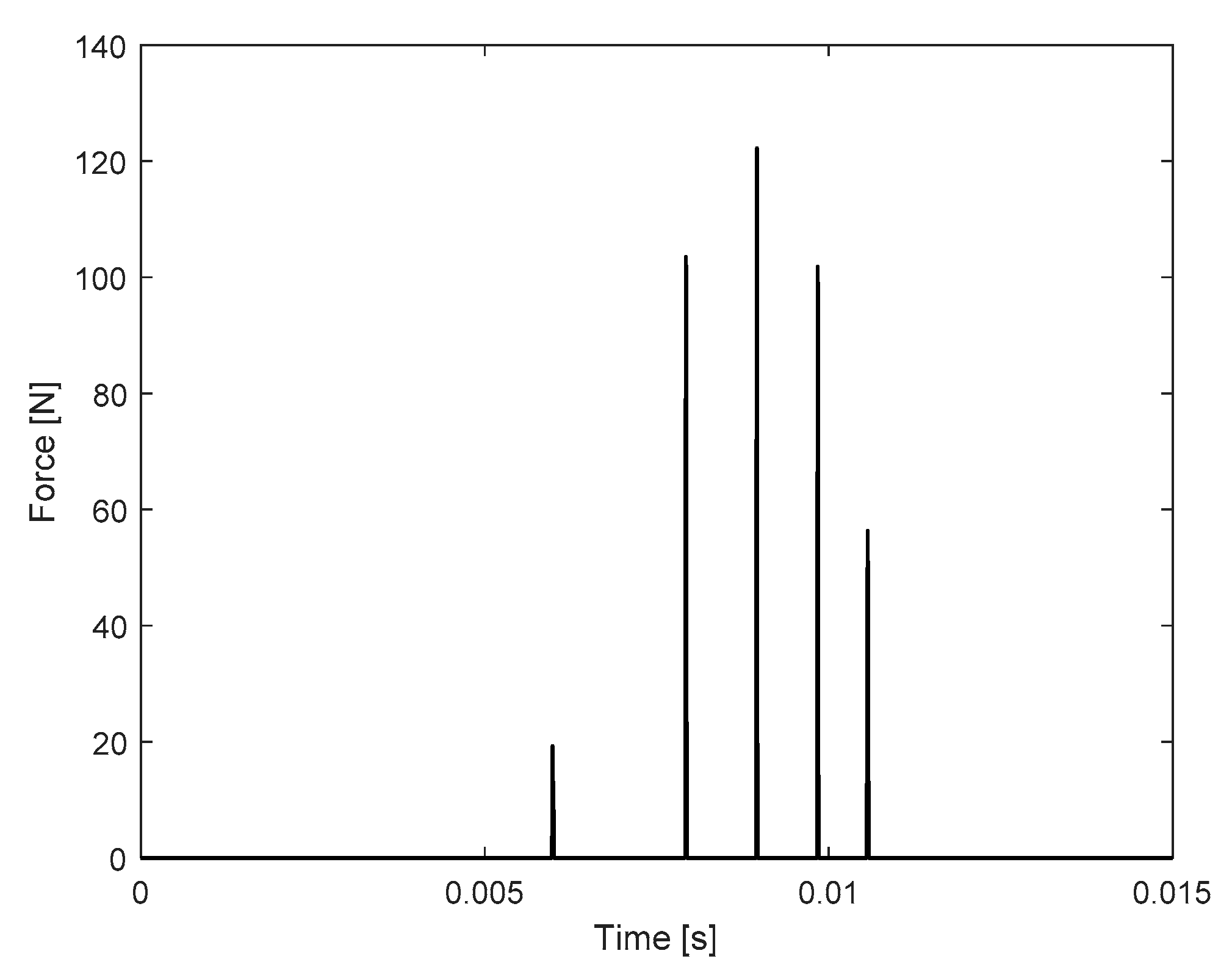
The impact forces used to evaluate the surface fatigue life were extrapolated from the performed simulation.
Figure 13 shows the trend of the impact force as a function of time. As visible, the maximum value is equal to about
To evaluate the fatigue life of the component, first the fatigue strength curves expressed in terms of alternating surface stress and alternating pressure were first obtained for three different level of reliability, equal to
,
, and
, adopting Equation (21) shown in
Section 2.3 and using the characteristics of the material shown in
Table 2. Starting from the hardness of the material, corresponding to
, the surface ultimate stress
of the material was obtained according the Equation (26).
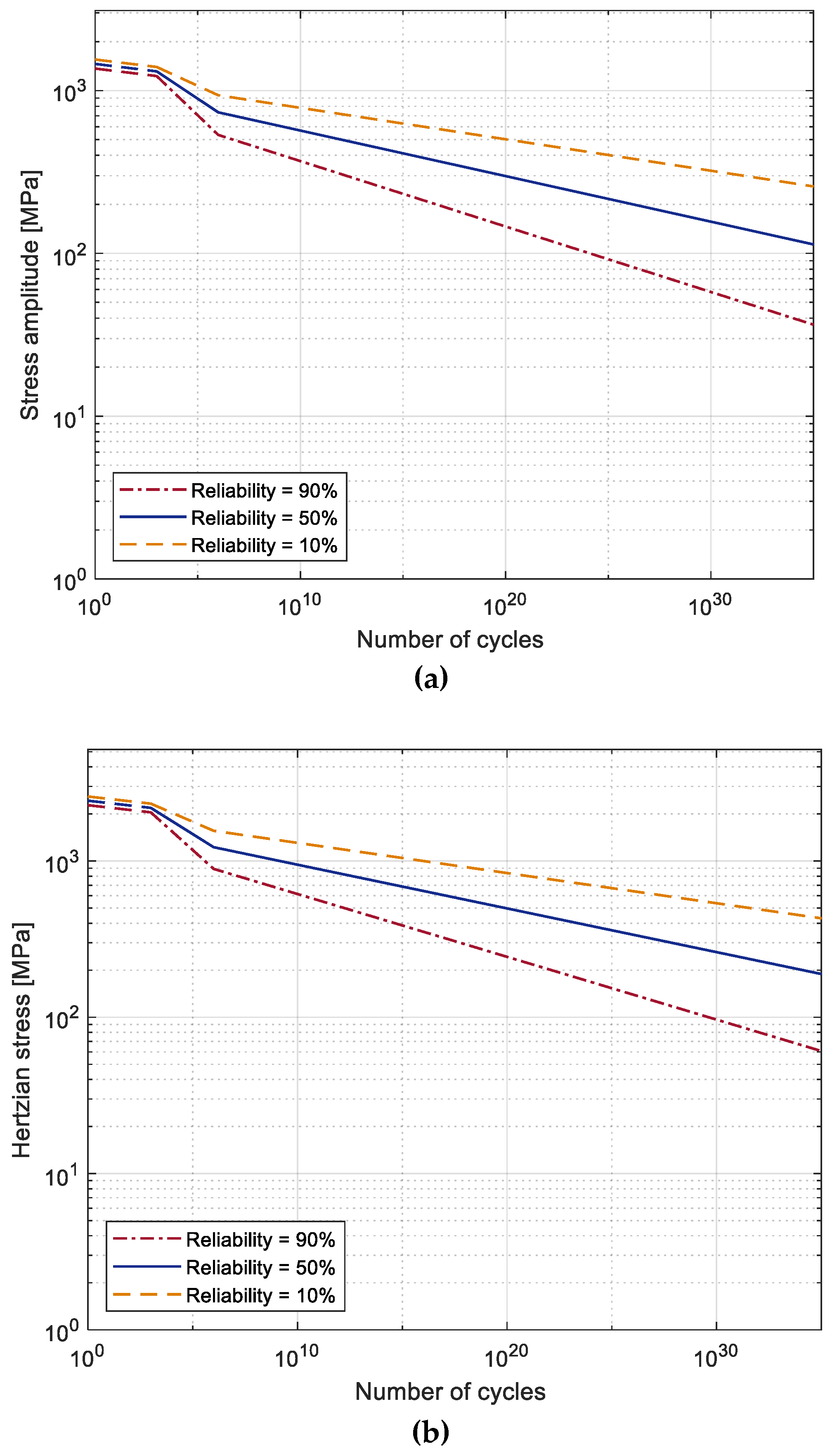
The fatigue strength curves, both in terms of the alternating stress and contact pressure are shown in
Figure 14. As shown in
Figure 14 for the slope of the fatigue curve after
cycles, the hypothesis of Hybach [
31,
41] was taken into account. The Hybach hypothesis states that the slope of the fatigue curve after
cycles is one third of the slope of the previous stretch.
The ball screw in question has been used for a total duration of
. Considering a screw pitch equal to
and a number of spheres per turn equal to
, the total duration in number of cycles corresponds to
cycles. The alternating surface stress and contact pressure values obtainable from the curves of
Figure 14 are shown in
Table 3 for the different considered reliability values.
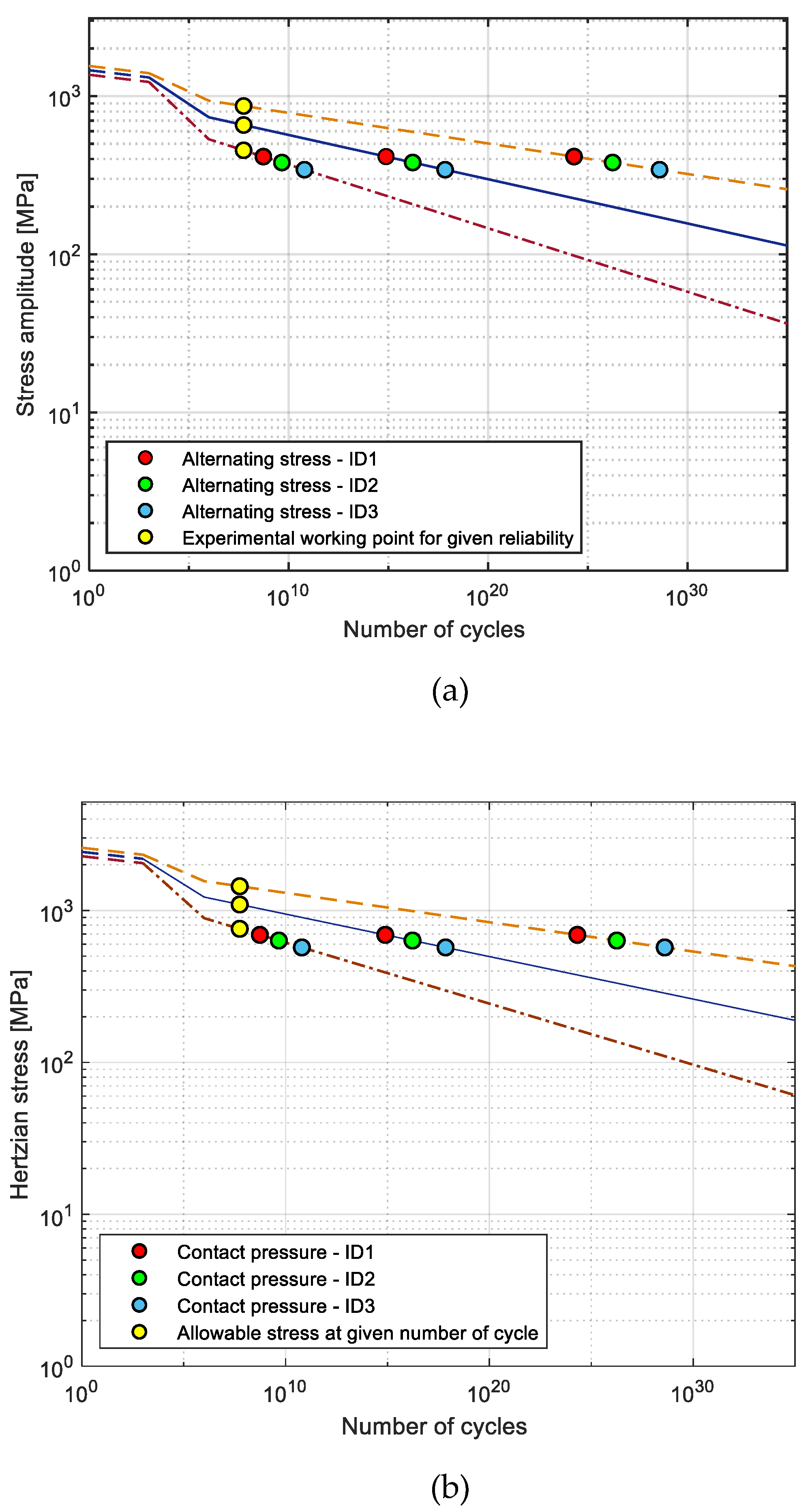
The values shown in
Table 3 are also graphically shown in
Figure 15 by the yellow dots. In order to estimate the surface fatigue life, it is still necessary to calculate the semiaxes of the contact ellipse using the Hertz theory (
Section 2.1). From the 3D model, three different combinations of the curvature radii at the contact point have been calculated as shown in
Table 4. Applying the maximum force obtained by the simulation, equal to 120 N, and considering the obtained curvature radii, it was possible to estimate the maximum alternating stress and the maximum pressure. These values are shown in
Table 4.
By tracing these values in the fatigue strength curves, it is possible to determine from the intersection with the curves the number of cycles to which the component can withstand for the three reliability values considered in terms of both the maximum alternating stress and the maximum pressure as shown in
Figure 15. The obtained cycles at each surface stress values or contact pressure are shown in
Table 5 for all the reliability values considered.
As shown in
Figure 15 and in
Table 5, these values attest that no surface fatigue problems are expected for this component. This fact was also found on the real recirculating mechanism, where no surface fatigue problem was detected by a visual inspection.
5. Conclusions
Stainless steels are necessarily used in all sectors, from aerospace to medical, where mechanical components find themselves working in environmental conditions full of aggressive substances that can affect the mechanical properties of the component itself. The antioxidant properties of such steels are due to the surface film that is created thanks to a chemical reaction between chromium and oxygen. Although stainless steels are, by nature, self-passivating, i.e., the protective film spontaneously recreates thanks to a chemical reaction between oxygen and chrome, problems related to a degradation of the surface can lead to a slowing down the self-passivation process or, in the worst cases, to a total loss of antioxidant properties. One of the main causes of surface deterioration is related to surface fatigue issues. When two or more evolving bodies are working against each other, a stress state is generated on the surface, which can cause opening cracks. The two most common phenomena are pitting and spalling. To minimize the probability of occurrences of this phenomenon, it is necessary that, at least during the design stage, the surface resistance of the component is verified.
The evaluation of surface fatigue strength can be addressed with two different approaches. The first one is a completely theoretical approach which, merging the impact dynamic laws and the Hertz theory, allows an estimation of the contact stresses and, therefore, an evaluation of the fatigue life of the component. However, this approach requires an assessment of a set of variables, such as bodies trajectory, velocity, stiffness, and curvature radii, in order to obtained accurate results. If these quantities are known, the theoretical approach allows for an accurate estimate of both the impact forces and the contact stresses. The determination of these quantities tends to be, however, particularly complex in real models in which all the abovementioned quantities are random variables.
In this context, the second possible approach for the estimation of surface fatigue strength is a completely numerical approach. This, exploiting the potentialities of the finite element codes, allows the drawbacks of the theoretical approach to be overcome regardless of the complexity of the model. The major drawback of this approach is the need to use meshes so fine that makes the simulation not always feasible.
To merge the benefits of both approaches, in this activity, a hybrid theoretical-numerical calculation method has been proposed, which allows a drastic reduction in the calculation effort obtaining, at the same time, accurate results. This method exploits the potentialities of finite element software to determine the impact forces, bypassing the inconvenience of assessing dynamic variables hardly a priori known. Once the impact forces are assessed, classical formulas of Hertz theory and fatigue are used to evaluate the fatigue life of the component. This possibility raised a comparison of the results obtained by an explicit finite element analysis and the theoretical results for a simple case study, a sphere-plane impact, for different mesh sizes. From the comparison carried out, it was highlighted that the force values obtained are independent from the mesh size and very close to, almost identical, those obtained by using the shock theory. It is not valid instead in the case of contact pressures where results are strongly influenced by mesh size. This means that to obtain the pressure and/or contact stress directly from a numerical simulation, a fine mesh is necessary.
The main advantage of the proposed method is to drastically reduce the calculation effort while obtaining results consistent with reality as well. Given these aspects, the proposed calculation method is aimed to all those realities in which it is necessary to reduce the computational effort as much as possible without precluding the goodness of the results.
The proposed hybrid method was then validated on an aeronautical component, a recirculation system of a ball screw. This component, in fact, is subjected to many shocks due to the balls that it is often subjected to surface fatigue problems. The obtained results show how it is possible to obtain realistic results in terms of fatigue life with relatively short calculation times.