Close Range Explosive Loading on Steel Column in the Framework of Anisotropic Viscoplasticity
Abstract
1. Introduction
2. Constitutive Assumptions
2.1. Introductory Remarks
2.2. Description of the Surrounding Air and the Condensed Charge
2.3. Behavior of the Steel Column
- (i)
- Existence of the free energy function . Formally, we apply the following form (cf. [53] for extensive discussion on such an assumption):where denotes a set of internal state variables which describe the dissipation effects and is temperature.
- (ii)
- The axiom of objectivity (spatial covariance). The material model should be invariant with respect to any superposed motion (diffeomorphism).
- (iii)
- The axiom of the entropy production. For every regular process the constitutive functions should satisfy the second law of thermodynamics.
- (iv)
- The evolution equation for the internal state variable vector should be of the form:where evolution function has to be determined based on the experimental observations.
- (i)
- the field equations:
- (ii)
- the boundary conditions:
- (a)
- displacement is prescribed on a part of and tractions are prescribed on a part of , where and ,
- (b)
- heat flux is prescribed on , and
- (iii)
- the initial conditions are given for each particle at ,
- The elastic range is isotropic and independent of microdamage state, thus (for more general setup cf. [24]):where are Lam constants.
- The thermal expansion is isotropic, thus:where is the thermal expansion coefficient.
- The rate dependence of fracture porosity has the form [24]:where can be thought of as a quasi-static fracture porosity and denotes equivalent critical velocity of microdamage.
- The normalised directions of viscoplastic flow, under the above assumptions, are defined as:where represents the stress deviator, , are the first and the second invariants of Kirchhoff stress tensor and deviatoric part of the Kirchhoff stress tensor, respectively, .
- The microdamage mechanism assumes the growth term only ( while nucleation is replaced by the initial microdamage distribution assumption), therefore taking the additional assumptions [16,62]: (i) Velocity of the microdamage growth is coaxial with the principal directions of the stress state, and (ii) only positive (tension) principal stresses induces the growth of the microdamage, one has:where are the material parameters, and is the third invariant of deviatoric part of the Kirchhoff stress tensor.
- The tensor is a symmetric part of the fourth order unity tensor [16]:hence:and:where are the principal values of the Kirchhoff stress tensor.
- Lastly, for temperature evolution, the following relation is considered:
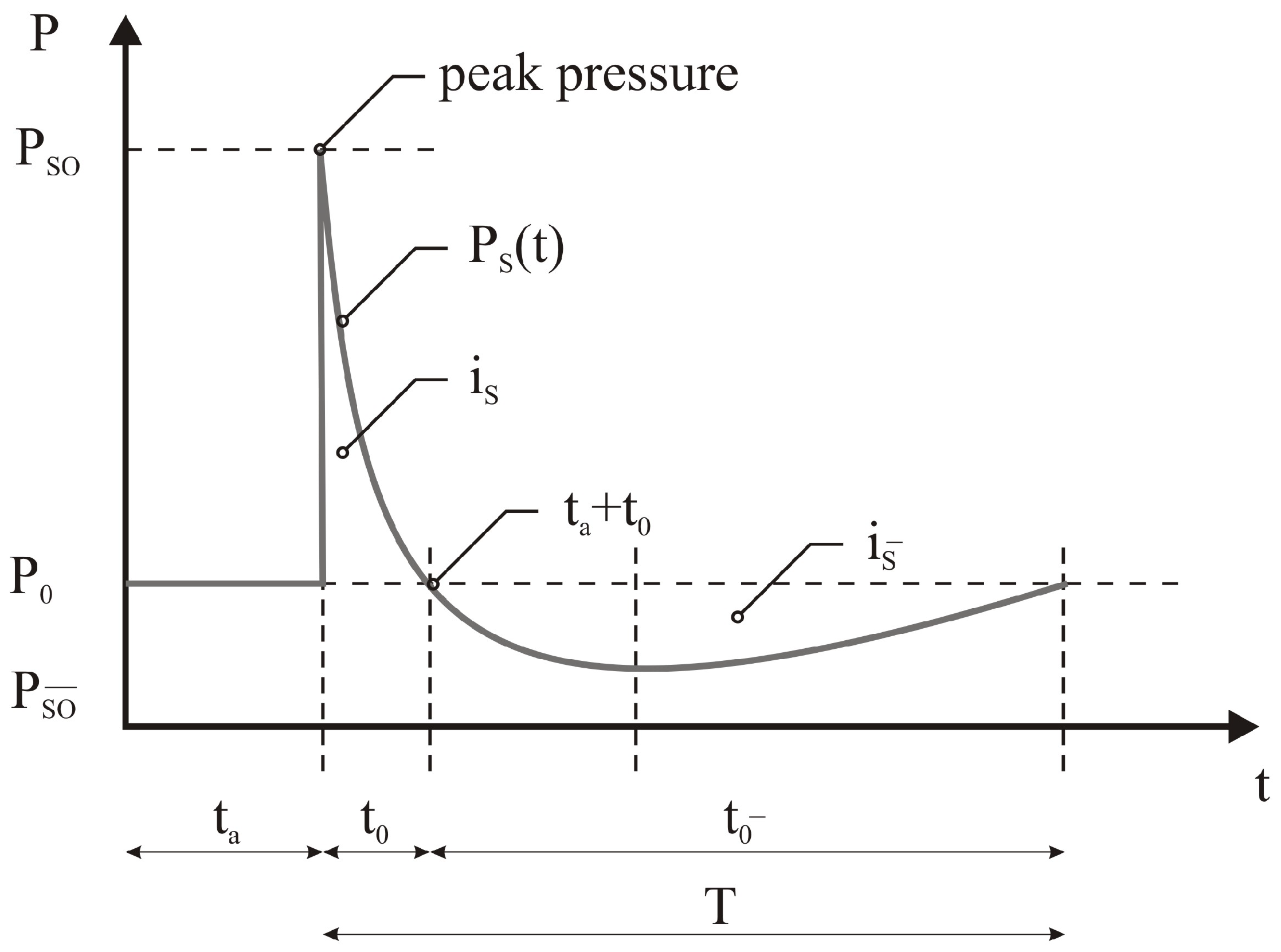
3. Numerical Prediction of Blast Effect on Steel Column
3.1. Introductory Remarks
- After the ignition moment in the centre of the explosive, the combustion wave goes through the charge domain, and then releases a high amount of kinetic and thermal energies;
- the transition phase generates a high pressure wave on the charge and ambient boundaries; and
- finally, the pressure reaches the obstacle boundaries and induces the thermomechanical process within its bounds, which is of strong wave character.
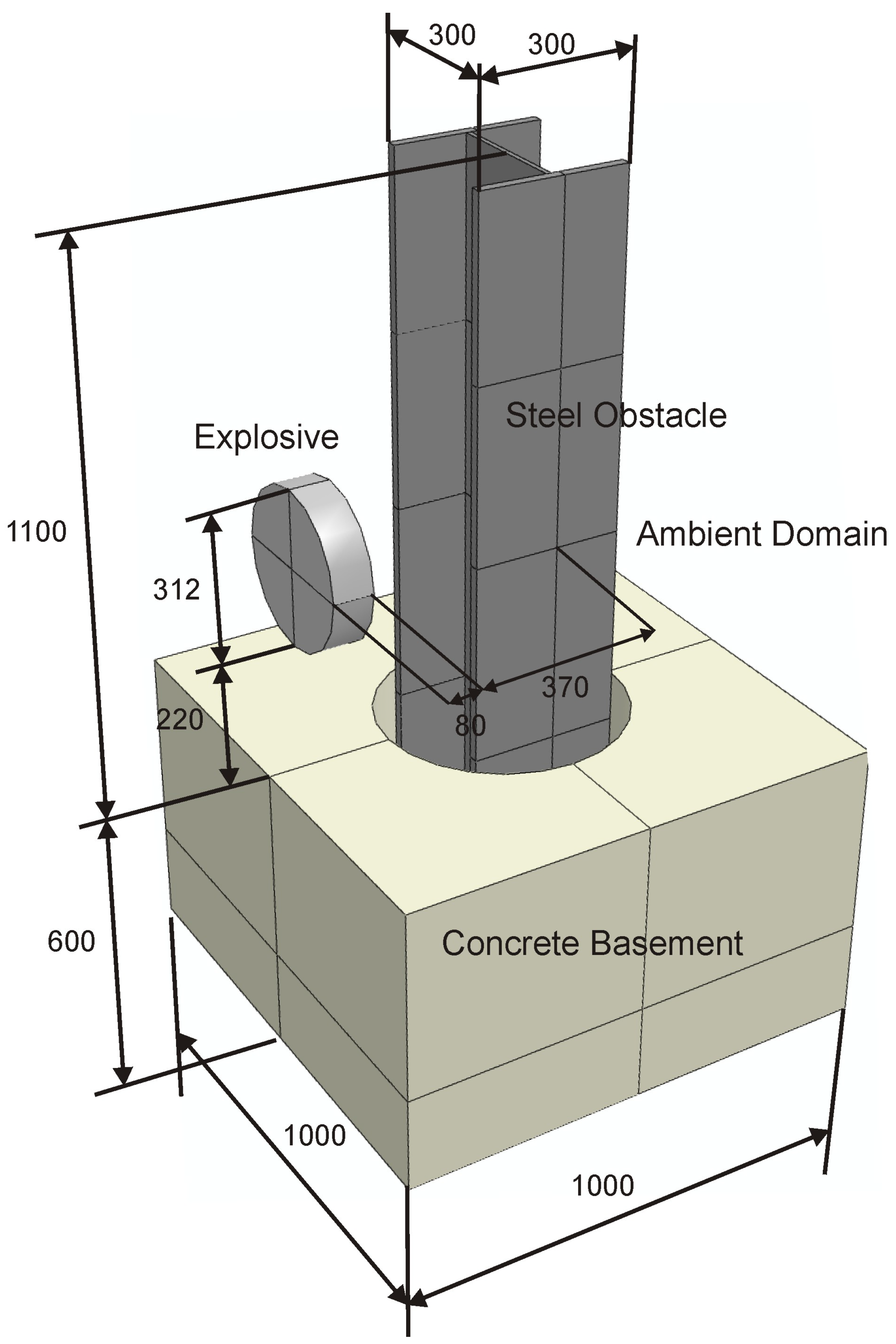
3.2. Steel Column Modeling Assumptions
3.3. Results
- High quality of the numerical results symmetry is observed,
- equivalent plastic strains are locally as high as ca. in the strain localization zones,
- the temperature in the strain localization zones is as high as ca. 800 C,
- the evolution of the porosity is restricted to the zones of high plastic strains,
- thermal stresses can be locally as high as 2000 MPa or more,
- the displacement field is localised in the zone of the evolving flying fragment, whereas in the remaining part for ms reaches ca. m,
- the strain hardening causes the Huber–Mises–Hencky stresses to be as high as ca. 900 MPa, and
- air pressure is highly scattered in the fluid domain and reaches locally 150 MPa (161 MPa according to the standards cf. [20]).
4. Experimental Validation
- High-speed camera Phantom v711 with mobile stand,
- Bosch GLM 80 Professional Laser Rangefinder, and
- ICP Free-field Blast Pressure “Pencil” Probe.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Grimsmo, E.; Clausen, A.; Aalberg, A.; Langseth, M. A numerical study of beam-to-column joints subjected to impact. Eng. Struct. 2016, 120, 103–115. [Google Scholar] [CrossRef]
- Aune, V.; Valsamos, G.; Casadei, F.; Langseth, M.; Børvik, T. On the dynamic response of blast-loaded steel plates with and without pre-formed holes. Int. J. Impact Eng. 2017, 108, 27–46. [Google Scholar]
- Nassr, A.; Razaqpur, A.; Tait, M.; Campidelli, M.; Foo, S. Strength and stability of steel beam columns under blast load. Int. J. Impact Eng. 2013, 55, 34–48. [Google Scholar]
- Formica, G.; Sansalone, V.; Casciaro, R. A mixed solution strategy for the nonlinear analysis of brick masonry walls. Comput. Methods Appl. Mech. Eng. 2002, 191, 5847–5876. [Google Scholar] [CrossRef]
- Sabuwala, T.; Linzell, D.; Krauthammer, T. Finite element analysis of steel beam to column connections subjected to blast loads. Int. J. Impact Eng. 2005, 31, 861–876. [Google Scholar] [CrossRef]
- Rigby, S.; Tyas, A.; Bennett, T. Elastic-plastic response of plates subjected to cleared blast loads. Int. J. Impact Eng. 2014, 66, 37–47. [Google Scholar] [CrossRef]
- Neuberger, A.; Peles, S.; Rittel, D. Springback of circular clamped armor steel plates subjected to spherical air-blast loading. Int. J. Impact Eng. 2009, 36, 53–60. [Google Scholar] [CrossRef]
- Makarem, F.; Abed, F. Nonlinear finite element modeling of dynamic localizations in high strength steel columns under impact. Int. J. Impact Eng. 2013, 52, 47–61. [Google Scholar] [CrossRef]
- Denny, J.; Clubley, S. Long-duration blast loading & response of steel column sections at different angles of incidence. Eng. Struct. 2019, 178, 331–342. [Google Scholar]
- Fu, S.; Gao, X.; Chen, X. The similarity law and its verification of cylindrical lattice shell model under internal explosion. Int. J. Impact Eng. 2018, 122, 38–49. [Google Scholar] [CrossRef]
- Hadianfard, M.; Malekpour, S.; Momeni, M. Reliability analysis of H-section steel columns under blast loading. Struct. Saf. 2018, 75, 45–56. [Google Scholar] [CrossRef]
- Malachowski, J.; Klasztorny, M.; Mazurkiewicz, L.; Kołodziejczyk, D.; Niezgoda, T. Numerical assessment of the selected supporting element carrying capacity of critical infrastructure facility. J. Konbin 2013, 26, 29–42. [Google Scholar] [CrossRef]
- Sumelka, W. Role of Covariance in Continuum Damage Mechanics. ASCE J. Eng. Mech. 2013, 139, 1610–1620. [Google Scholar] [CrossRef]
- Sumelka, W.; Łodygowski, T. The influence of the initial microdamage anisotropy on macrodamage mode during extremely fast thermomechanical processes. Arch. Appl. Mech. 2011, 81, 1973–1992. [Google Scholar] [CrossRef]
- Perzyna, P. The Thermodynamical Theory of Elasto-Viscoplasticity. Eng. Trans. 2005, 53, 235–316. [Google Scholar]
- Glema, A.; Łodygowski, T.; Sumelka, W.; Perzyna, P. The Numerical Analysis of the Intrinsic Anisotropic Microdamage Evolution in Elasto-Viscoplastic Solids. Int. J. Damage Mech. 2009, 18, 205–231. [Google Scholar] [CrossRef]
- Lodygowski, T.; Rusinek, A.; Jankowiak, T.; Sumelka, W. Selected topics of high speed machining analysis. Eng. Trans. 2012, 60, 69–96. [Google Scholar]
- Litoński, J. Plastic flow of a Tube under Adiabatic Torsion. Bull. Acad. Pol. Sci. Ser. Sci. Tech. 1977, XXV, 7–14. [Google Scholar]
- Rusinek, A.; Klepaczko, J. Shear testing of a sheet steel at wide range of strain rates and a constitutive relation with strain-rate and temperature dependence of the flow stress. Int. J. Plast. 2001, 17, 87–115. [Google Scholar] [CrossRef]
- Sielicki, P.; Stachowski, M. Implementation of sapper-blast-module, a rapid prediction software for blast wave properties. Cent. Eur. J. Energ. Mater. 2015, 12, 473–486. [Google Scholar]
- US Army Manual, Department of The Army, The Navy, and The Air Force. Structures to Resist the Effects of Accidental Explosions; UFC 3-340-02; Department of The Army, The Navy, and The Air Force: Washington, DC, USA, 2008.
- Rankine, W. On the thermodynamic theory of waves of finite longitudinal disturbance. Philos. Transl. 1870, 160, 277–288. [Google Scholar]
- Sielicki, P. Masonry Failure under Unusual Impulse Loading; Publishing House of Poznan University of Technology: Poznan, Poland, 2013; ISBN 978-83-7775-274-6. [Google Scholar]
- Sumelka, W. The Constitutive Model of the Anisotropy Evolution for Metals with Microstructural Defects; Publishing House of Poznan University of Technology: Poznań, Poland, 2009. [Google Scholar]
- Brode, H. Numerical solutions of spherical blast waves. J. Appl. Phys. 1955, 26, 766. [Google Scholar] [CrossRef]
- Kingery, C.; Bulmash, G. Airblast Parameters From TNT Spherical Air Burst And Hemispherical Surface Burst; Ballistic Research Laboratory: Aberdeen Proving Ground, MD, USA, 1984. [Google Scholar]
- Abaqus 6.13. Documentation Collection. Available online: https://www.3ds.com/products-services/simulia/support/documentation/ (accessed on 11 March 2019).
- Wodarczyk, E. Wstp do Mechaniki Wybuchu; Wydawnictwo Naukowe PWN: Warszawa, Poland, 1994. (In Polish) [Google Scholar]
- Hallquist, J. LS-Dyna, Theoretical Manual; California Livermore Software Technology Corporation: Livermore, CA, USA, 2008. [Google Scholar]
- Jach, K. Komputerowe Modelowanie Dynamicznych Oddziaywa Cia Metod Punktw Swobodnych; PWN: Warsaw, Poland, 2000. (In Polish) [Google Scholar]
- Stenberg, D. Spherical Explosions and the Equation of State of Water; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1978.
- Gathers, G. Shock Wave Physics and Equation of State Modelling; World Scientific Publishing Co., Pte. Ltd.: Singapore, 1994. [Google Scholar]
- Dobratz, B. Explosive Handbook; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1981.
- Larcher, M.; Casadei, F. Explosions in Complex Geometries—A Comparison of Several Approaches. Int. J. Prot. Struct. 2010, 1, 169–195. [Google Scholar] [CrossRef]
- Rigby, S.; Sielicki, P. An investigation of TNT equivalence of hemispherical PE4 charges. Eng. Trans. 2014, 62, 423–435. [Google Scholar]
- Rigby, S.E.; Tyas, A.; Curry, R.J.; Langdon, G.S. Experimental Measurement of Specific Impulse Distribution and Transient Deformation of Plates Subjected to Near-Field Explosive Blasts. Exp. Mech. 2019, 59, 163–178. [Google Scholar] [CrossRef]
- Sumelka, W.; Łodygowski, T. Thermal stresses in metallic materials due to extreme loading conditions. ASME J. Eng. Mater. Technol. 2013, 135, 021009. [Google Scholar] [CrossRef]
- Łodygowski, T.; Sumelka, W. Damage Induced by Viscoplasitc Waves Interaction. Vib. Phys. Syst. 2012, 25, 23–32. [Google Scholar]
- Eftis, J.; Carrasco, C.; Osegueda, R. A constitutive-microdamage model to simulate hypervelocity projectile-target impact, material damage and fracture. Int. J. Plast. 2003, 19, 1321–1354. [Google Scholar] [CrossRef]
- Sumelka, W.; Łodygowski, T. Reduction of the number of material parameters by ANN approximation. Comput. Mech. 2013, 52, 287–300. [Google Scholar] [CrossRef][Green Version]
- Nemat-Nasser, S.; Guo, W.G. Thermomechanical response of DH-36 steel plates over a wide range of strain rates and temperatures. Mech. Mater. 2003, 35, 1023–1047. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Guo, W.G. Thermomechanical response of HSLA-65 steel plates: Experiments and modeling. Mech. Mater. 2005, 37, 379–405. [Google Scholar] [CrossRef]
- Moćko, W.; Kowalewski, Z. Application of FEM in the assessment of phenomena associated with dynamic investigations on a miniaturised ICT testing stand. Kovove Mater.-Metal. Mater. 2013, 51, 71–82. [Google Scholar]
- Perzyna, P. The Thermodynamical Theory of Elasto-viscoplasticity Accounting for Microshear Banding and Induced Anisotropy Effects. Mechanics 2008, 27, 25–42. [Google Scholar]
- Glema, A.; Łodygowski, T.; Sumelka, W. Nowacki’s Double Shear Test in the Framework of the Anisotropic Thermo-Elasto-Vicsoplastic Material Model. J. Theor. Appl. Mech. 2010, 48, 973–1001. [Google Scholar]
- Truesdell, C.; Noll, W. The non-linear field theories of mechanics. In Handbuch der Physik; Flügge, S., Ed.; Springer: Berlin, Germany, 1965; Volume III/3. [Google Scholar]
- Marsden, J.; Hughes, T. Mathematical Foundations of Elasticity; Prentice-Hall: Upper Saddle River, NJ, USA, 1983. [Google Scholar]
- Haupt, P. Continuum Mechanics and Theory of Materials, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Lee, E. Elastic-plastic deformation at finite strain. ASME J. Appl. Mech. 1969, 36, 1–6. [Google Scholar] [CrossRef]
- Perzyna, P. Interactions of elastic-viscoplastic waves and localization phenomena in solids. In Proceedings of the IUTAM Symposium on Nonlinear Waves in Solids, Victoria, BC, Canada, 15–20 August 1995; pp. 114–121. [Google Scholar]
- Lu, J.; Papadopoulos, P. A covariant constitutive description of anisotropic non-linear elasticity. J. Appl. Math. Phys. (ZAMP) 2000, 51, 204–217. [Google Scholar] [CrossRef]
- Lu, J.; Papadopoulos, P. A covariant formulation of anisotropic finite plasticity: Theoretical developments. Comput. Methods Appl. Mech. Eng. 2004, 193, 5339–5358. [Google Scholar] [CrossRef]
- Duszek–Perzyna, M.; Perzyna, P. Analysis of anisotropy and plastic spin effects on localization phenomena. Arch. Appl. Mech. 1998, 68, 352–374. [Google Scholar] [CrossRef]
- Dornowski, W.; Perzyna, P. Analysis of the influence of various effects on cycle fatigue damage in dynamic process. Arch. Appl. Mech. 2002, 72, 418–438. [Google Scholar] [CrossRef]
- Dornowski, W.; Perzyna, P. Localized fracture phenomena in thermo-viscoplastic flow process under cyclic dynamic loadings. Acta Mech. 2002, 155, 233–255. [Google Scholar] [CrossRef]
- Glema, A.; Łodygowski, T.; Perzyna, P. Numerical investigation of dynamic shear bands in inelastic solids as a problem of mesomechanics. Comput. Mech. 2008, 41, 219–229. [Google Scholar] [CrossRef]
- Perzyna, P. Instability phenomena and adiabatic shear band localization in thermoplastic flow process. Acta Mech. 1994, 106, 173–205. [Google Scholar] [CrossRef]
- Łodygowski, T. Theoretical and Numerical Aspects of Plastic Strain Localization; Publishing House of Poznan University of Technology: Poznań, Poland, 1996; Volume 312. [Google Scholar]
- Shima, S.; Oyane, M. Plasticity for porous solids. Int. J. Mech. Sci. 1976, 18, 285–291. [Google Scholar] [CrossRef]
- Perzyna, P. Internal state variable description of dynamic fracture of ductile solids. Int. J. Solids Struct. 1986, 22, 797–818. [Google Scholar] [CrossRef]
- Perzyna, P. Constitutive modeling for brittle dynamic fracture in dissipative solids. Arch. Mech. 1986, 38, 725–738. [Google Scholar]
- Dornowski, W. Influence of Finite Deformations on the Growth Mechanism of Microvoids Contained in Structural Metals. Arch. Mech. 1999, 51, 71–86. [Google Scholar]
- Łodygowski, T.; Perzyna, P.; Lengnick, M.; Stein, E. Viscoplastic numerical analysis of dynamic plastic shear localization for a ductile material. Arch. Mech. 1994, 46, 541–557. [Google Scholar]
- Łodygowski, T. On avoiding of spurious mesh sensitivity in numerical analysis of plastic strain localization. Comput. Assist. Mech. Eng. Sci. 1995, 2, 231–248. [Google Scholar]
- Glema, A. Analysis of Wave Nature in Plastic Strain Localization in Solids; Rozprawy; Publishing House of Poznan University of Technology: Poznań, Poland, 2004; Volume 379. (In Polish) [Google Scholar]
- Benson, D.J. Computational methods in Lagrangian and Eulerian hydrocodes. Comput. Methods Appl. Mech. Eng. 1992, 99, 235–394. [Google Scholar] [CrossRef]
- Benson, D.J.; Okazawa, S. Contact in a multi-material Eulerian finite element formulation. Comput. Methods Appl. Mech. Eng. 2004, 193, 4277–4298. [Google Scholar] [CrossRef]


| Jones–Wilkins–Lee (JWL) Properties for TNT Explosive | ||
|---|---|---|
| A | Pa | |
| B | Pa | |
| - | ||
| - | ||
| - | ||
| 6930 | ||
| 1630 | ||
| 0 | Pa·s | |
| Ideal gas (IG) properties for Ambient Air | ||
| R | 287 | |
| 101,325 | ||
| 0 | ||
| Pa·s | ||
| Material Parameters for S355 Steel | |||
|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sielicki, P.W.; Sumelka, W.; Łodygowski, T. Close Range Explosive Loading on Steel Column in the Framework of Anisotropic Viscoplasticity. Metals 2019, 9, 454. https://doi.org/10.3390/met9040454
Sielicki PW, Sumelka W, Łodygowski T. Close Range Explosive Loading on Steel Column in the Framework of Anisotropic Viscoplasticity. Metals. 2019; 9(4):454. https://doi.org/10.3390/met9040454
Chicago/Turabian StyleSielicki, Piotr Witold, Wojciech Sumelka, and Tomasz Łodygowski. 2019. "Close Range Explosive Loading on Steel Column in the Framework of Anisotropic Viscoplasticity" Metals 9, no. 4: 454. https://doi.org/10.3390/met9040454
APA StyleSielicki, P. W., Sumelka, W., & Łodygowski, T. (2019). Close Range Explosive Loading on Steel Column in the Framework of Anisotropic Viscoplasticity. Metals, 9(4), 454. https://doi.org/10.3390/met9040454






