A Hierarchical Multiscale Modeling Investigation on the Behavior of Microtextured Regions in Ti-6242 α/β Processing
Abstract
1. Introduction
2. Crystal Plasticity Model and Simulation Setup
2.1. Titanium Crystal Plasticity Model Calibration
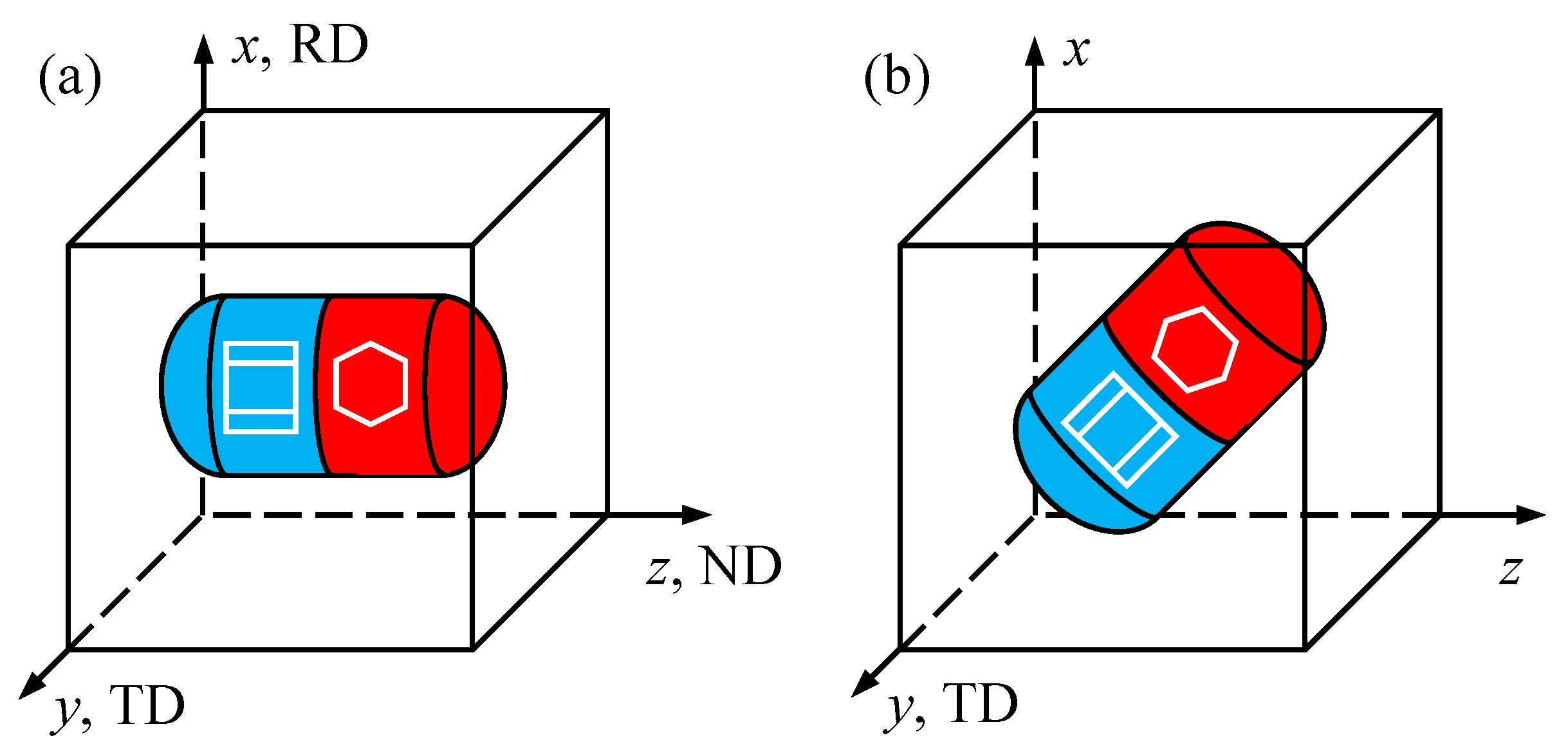
2.2. Statistically Equivalent Microstructure
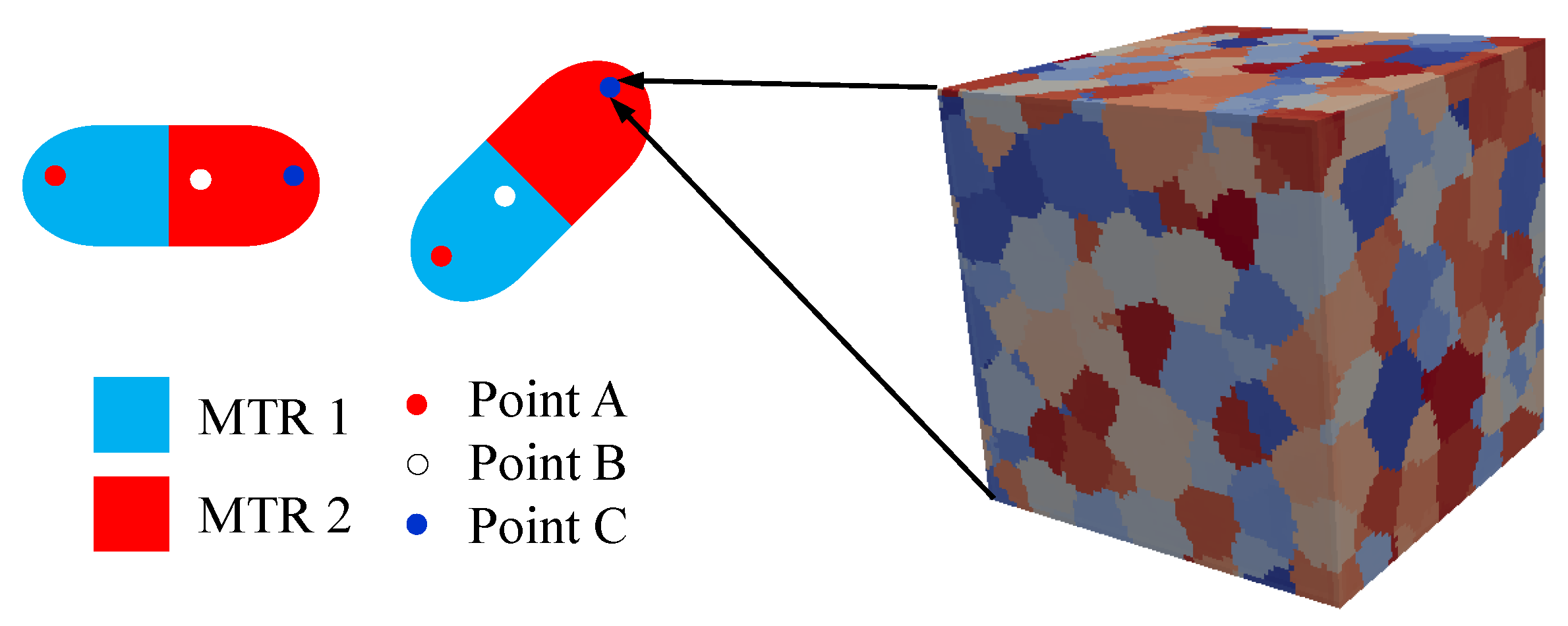
2.3. Hierarchical Multiscale Modeling Framework
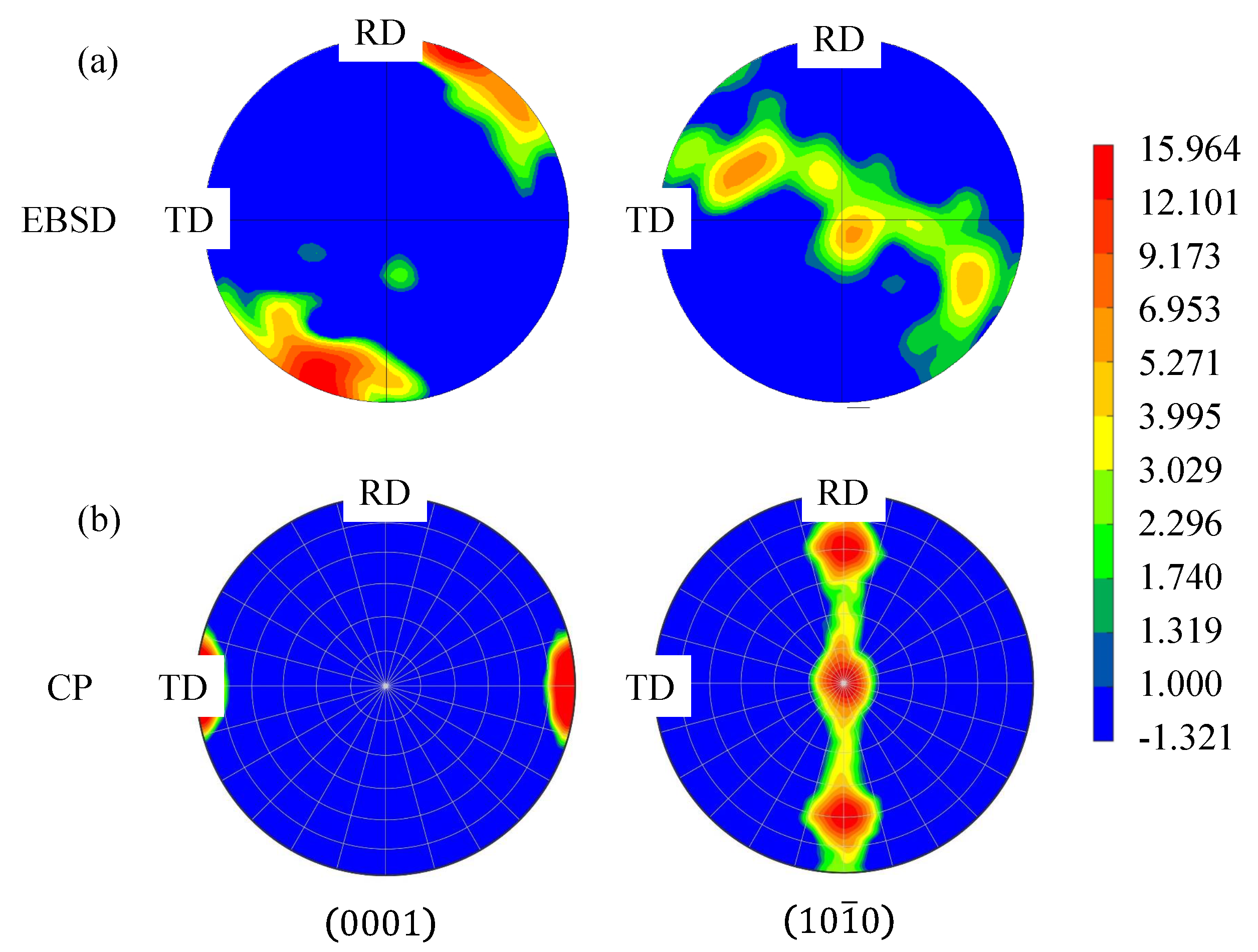
2.4. High-Temperature Compression Experiment
3. Results and Discussion
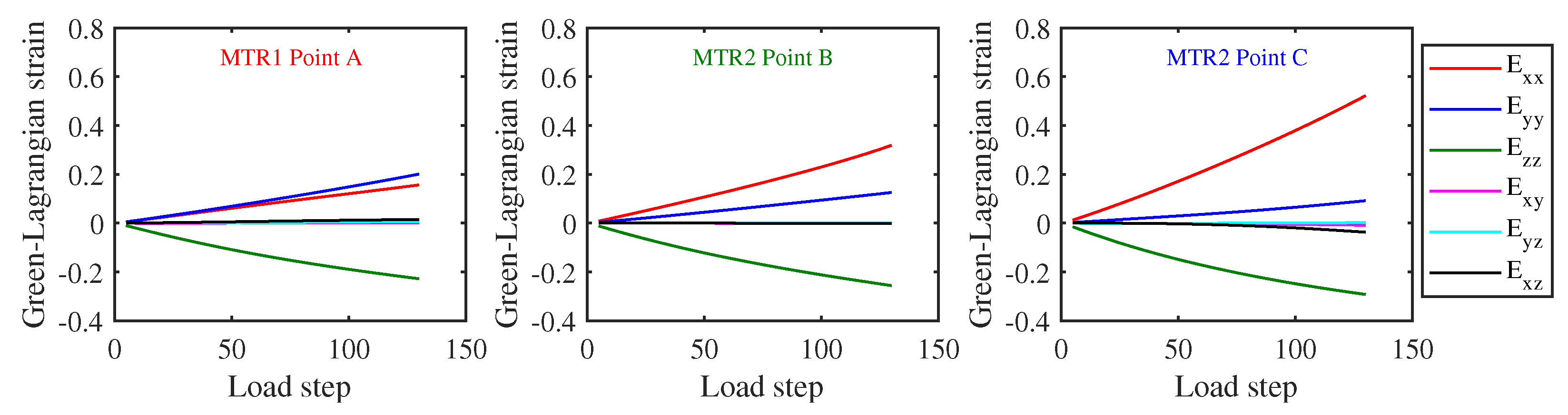
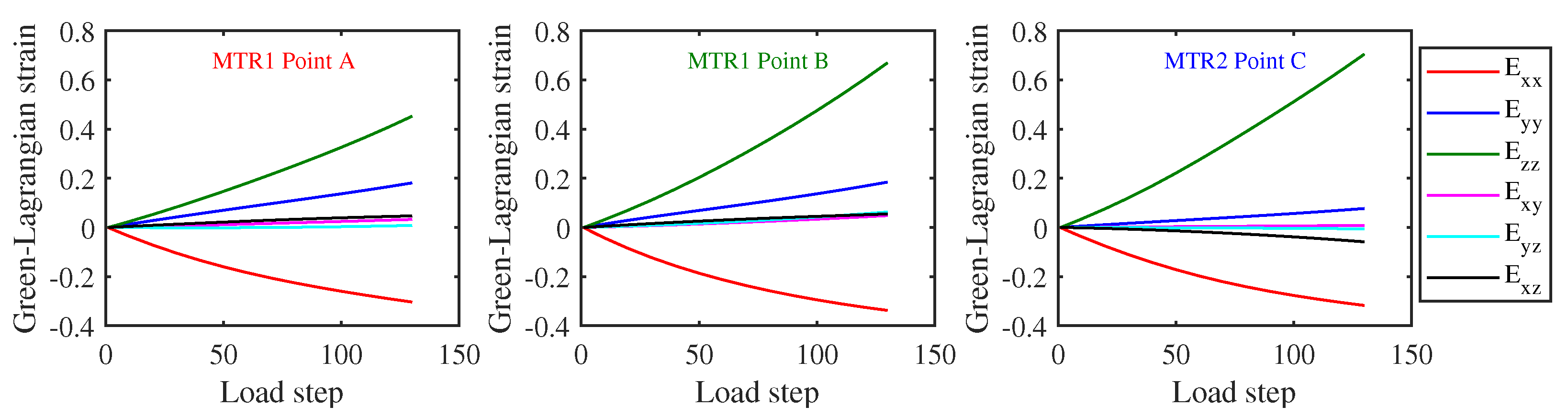
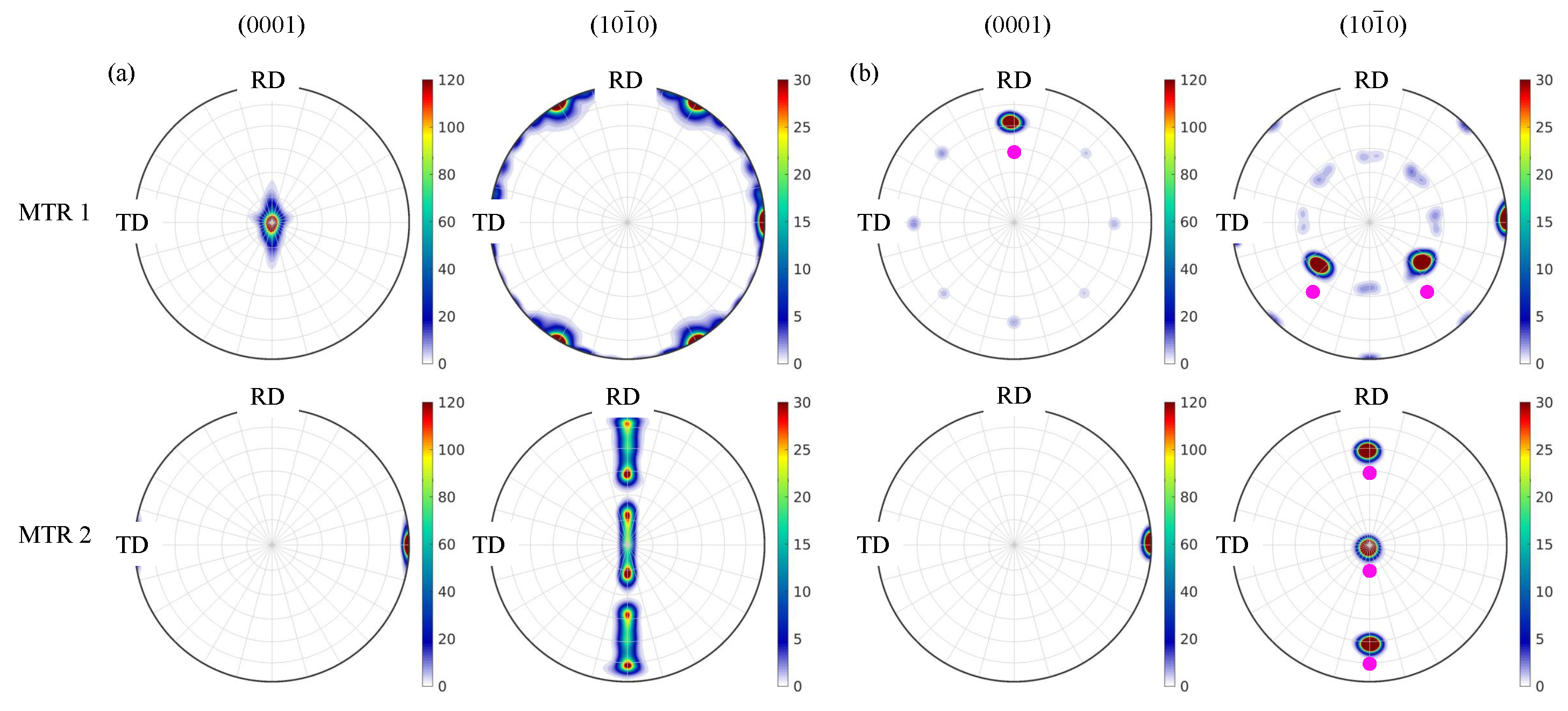
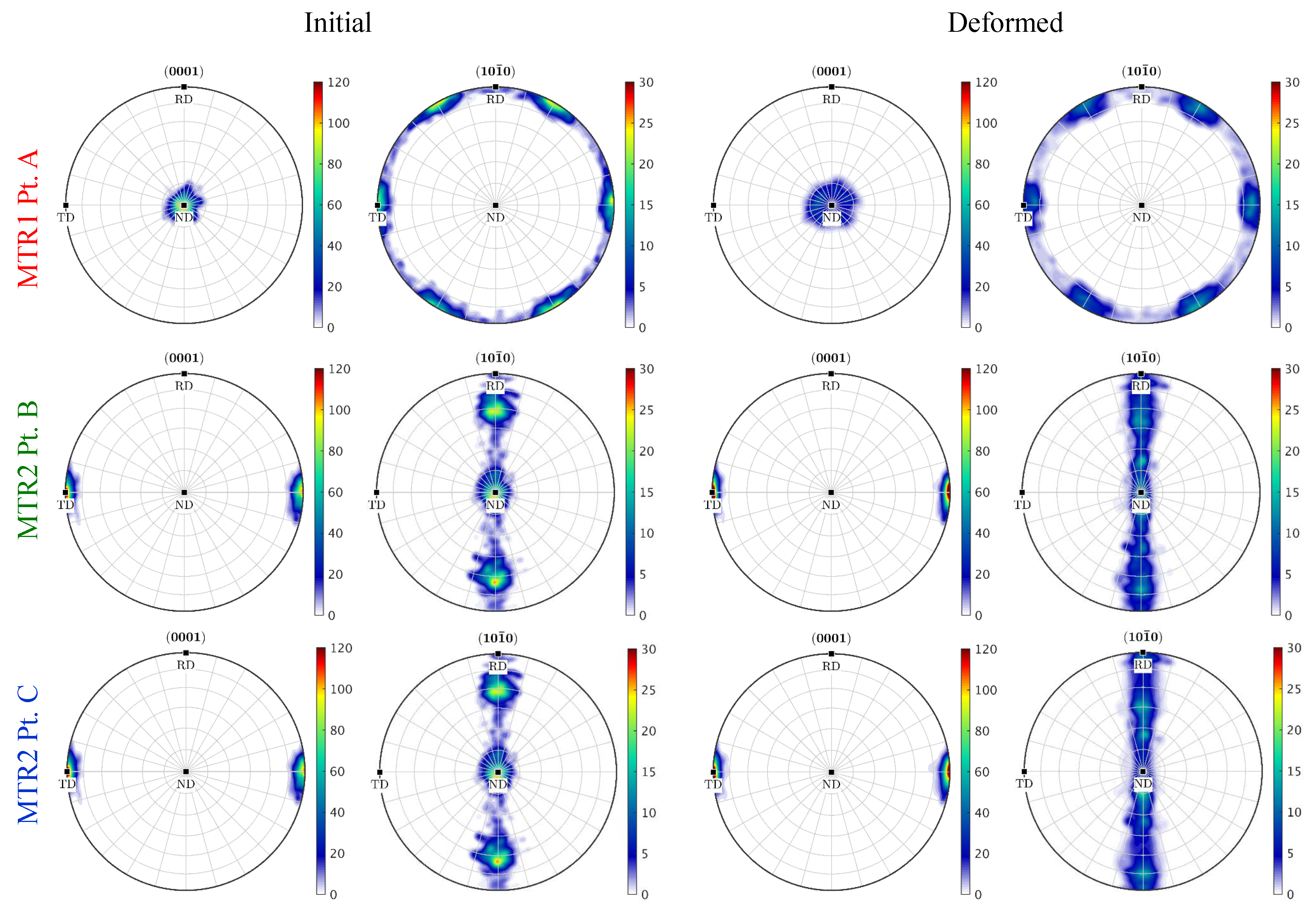
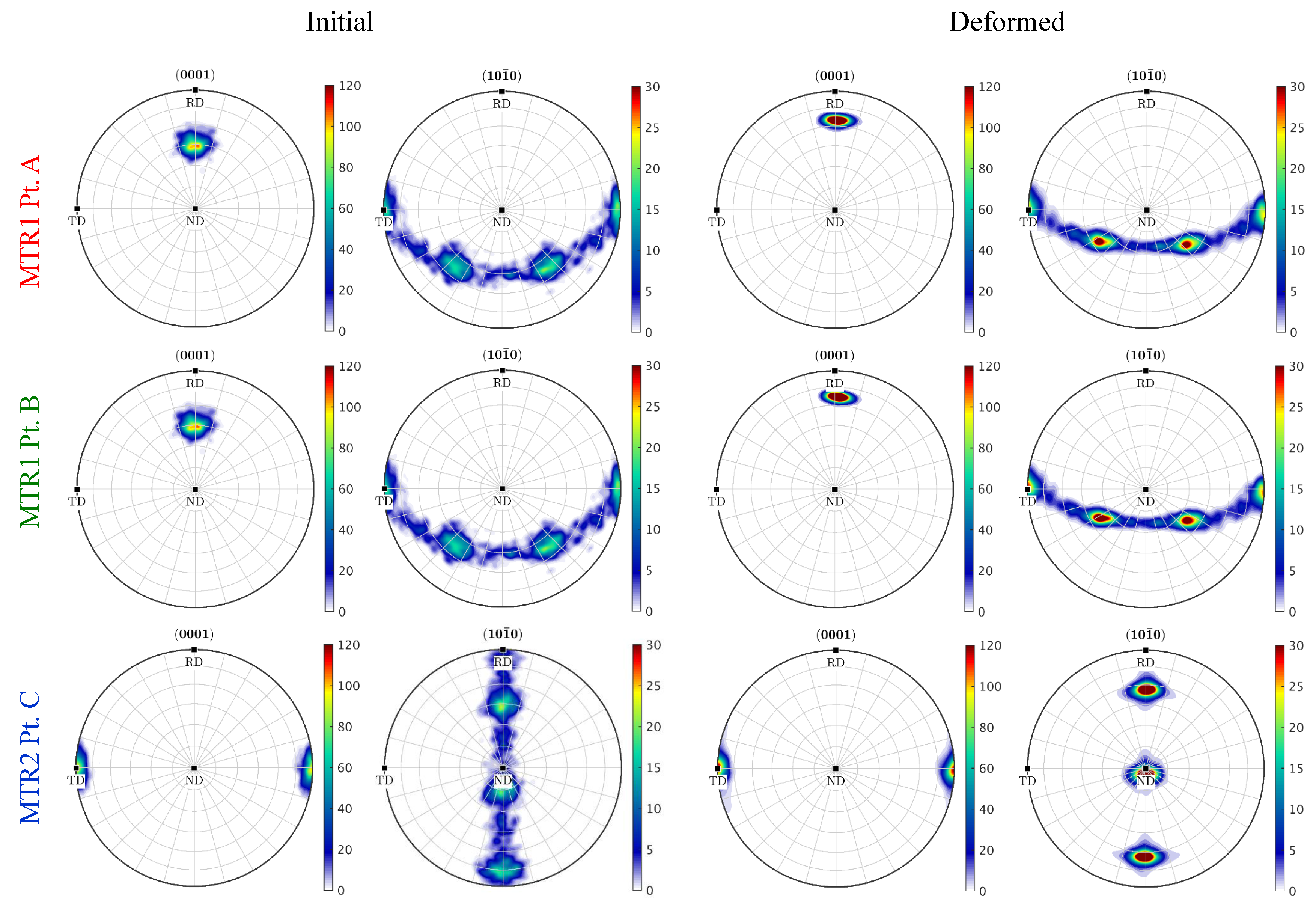
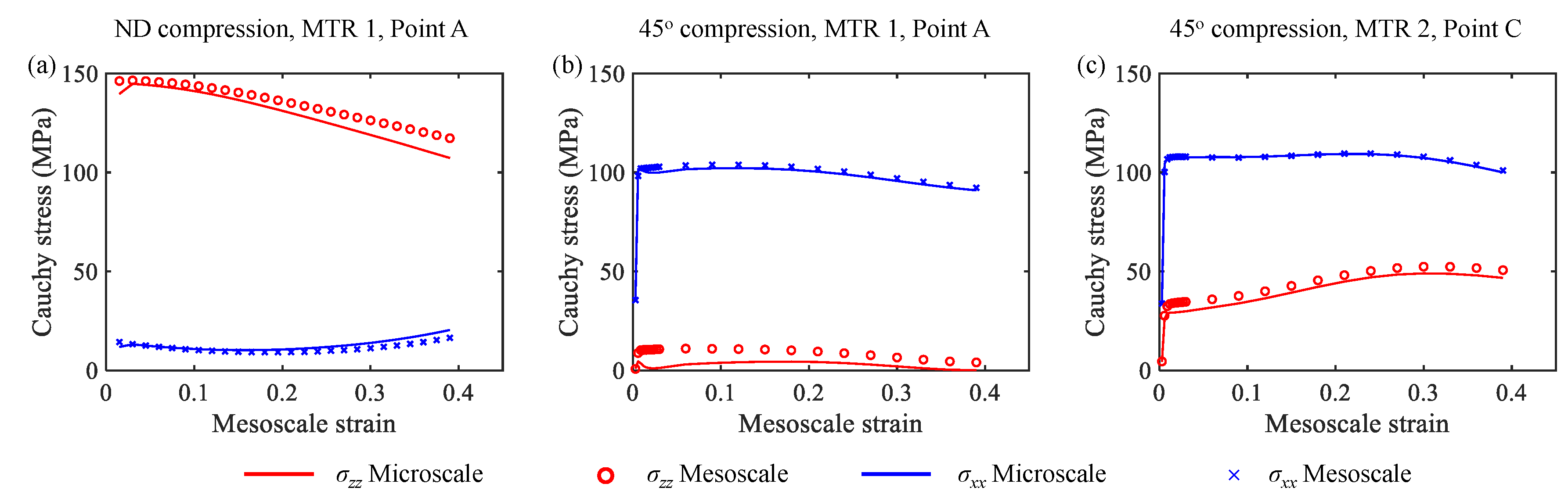
3.1. Comparison between Idealized MTR and Statistically Equivalent MTR
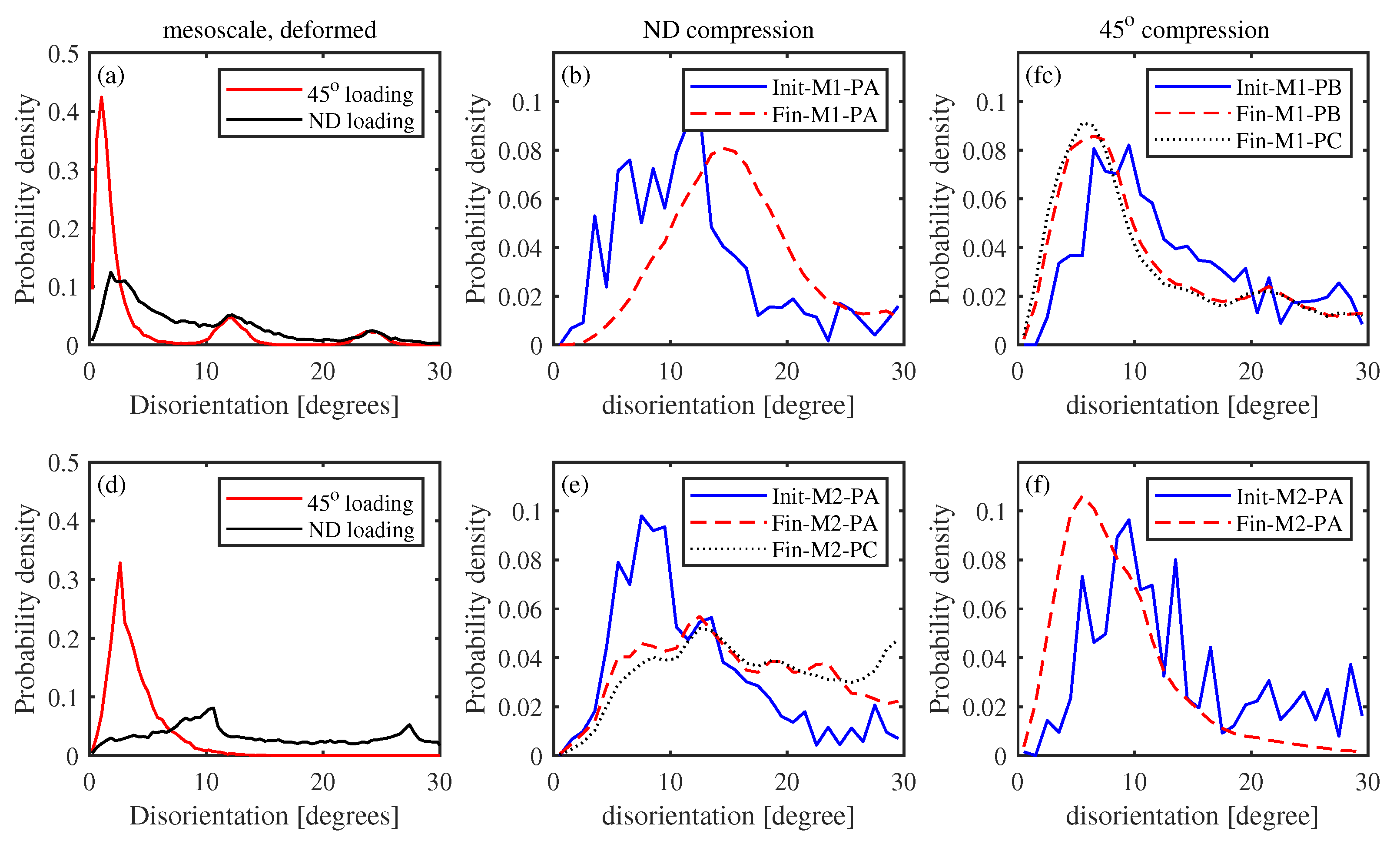
3.2. Disorientation Evolution of Statistically Equivalent MTR
4. Conclusions
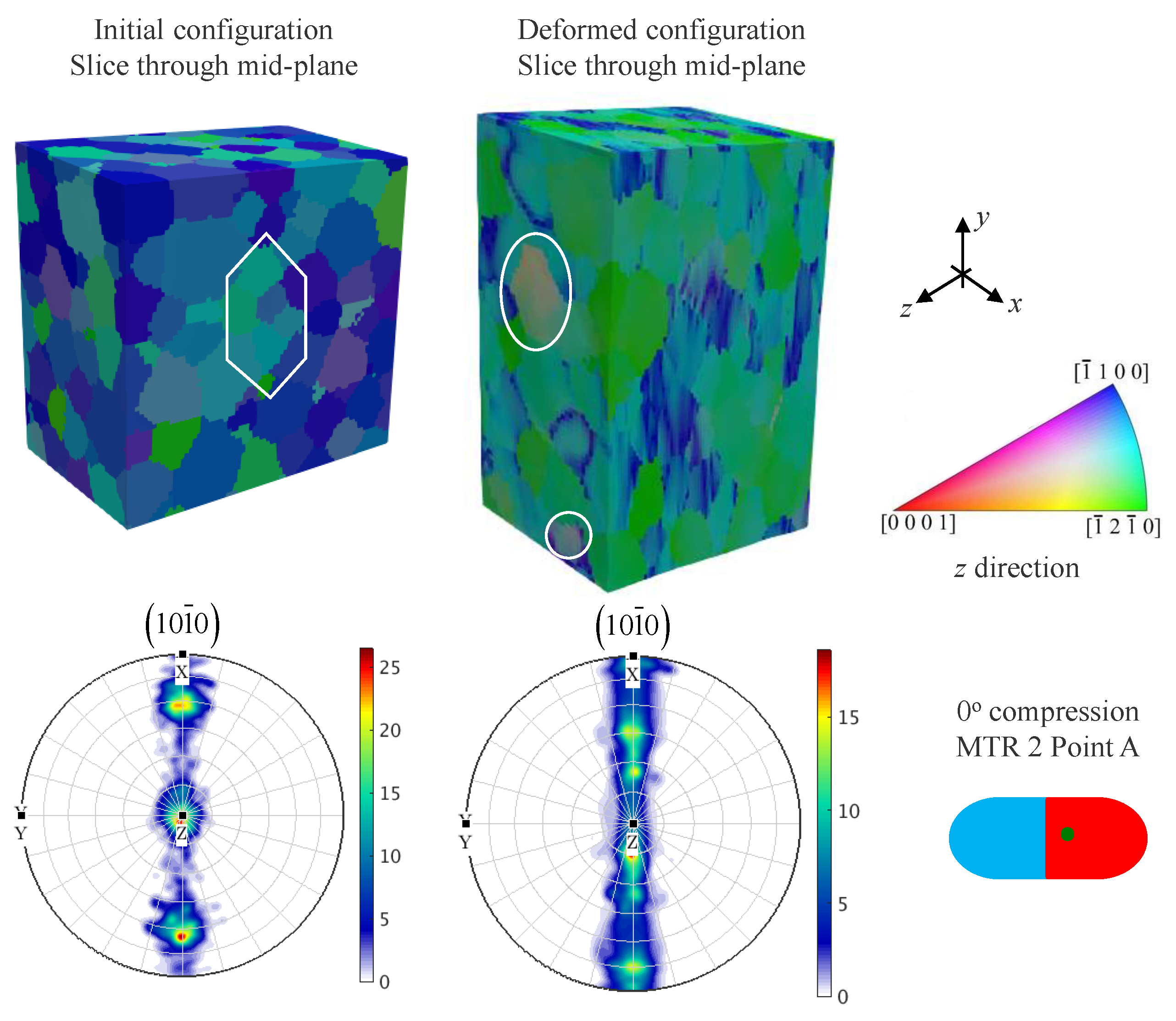
- While the c-axis parallel loading of the MTR produced the largest breakdown, the efficiency was limited by its resistance to plastic deformation. When the compression direction was parallel to the basal plane, orientation scattering around the c-axis was obvious, but the c-axis remained similarly oriented.
- The stability of MTRs under different loading directions can be captured by the microscale simulation with distributed initial orientation. More specifically, the scattering of the c-axis was observed in the ND compression case, and the lattice rotation and sharpening was observed in the compression case.
- The initial position of the microscale simulation within the mesoscale model had minor influence on the microstructure evolution in both the ND compression case and the compression case. Therefore, the variations in stress and strain states near the MTR–MTR and MTR–matrix interfaces compared to the MTR interior had little influence on the relative breakdown efficiency at 1172 K.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MTR | microtextured region |
| CP | crystal plasticity |
| FEM | finite element method |
References
- Bache, M.; Cope, M.; Davies, H.; Evans, W.; Harrison, G. Dwell sensitive fatigue in a near alpha titanium alloy at ambient temperature. Int. J. Fatigue 1997, 19, 83–88. [Google Scholar] [CrossRef]
- Heckel, T.; Tovar, A.G.; Christ, H.J. Fatigue of the near-alpha Ti-alloy Ti6242. Exp. Mech. 2010, 50, 483–489. [Google Scholar] [CrossRef]
- Weiss, I.; Froes, F.; Eylon, D.; Welsch, G. Modification of alpha morphology in Ti-6Al-4V by thermomechanical processing. Metall. Mater. Trans. A 1986, 17, 1935–1947. [Google Scholar] [CrossRef]
- Pilchak, A.L. Fatigue crack growth rates in alpha titanium: Faceted vs. striation growth. Scr. Mater. 2013, 68, 277–280. [Google Scholar] [CrossRef]
- Zheng, Z.; Balint, D.S.; Dunne, F.P. Dwell fatigue in two Ti alloys: An integrated crystal plasticity and discrete dislocation study. J. Mech. Phys. Solids 2016, 96, 411–427. [Google Scholar] [CrossRef]
- Germain, L.; Gey, N.; Humbert, M.; Vo, P.; Jahazi, M.; Bocher, P. Texture heterogeneities induced by subtransus processing of near α titanium alloys. Acta Mater. 2008, 56, 4298–4308. [Google Scholar] [CrossRef]
- Leo Prakash, D.G.; Honniball, P.; Rugg, D.; Withers, P.J.; Quinta da Fonseca, J.; Preuss, M. The effect of β phase on microstructure and texture evolution during thermomechanical processing of α + β Ti alloy. Acta Mater. 2013, 61, 3200–3213. [Google Scholar] [CrossRef]
- Bieler, T.R.; Semiatin, S.L. The origins of heterogeneous deformation during primary hot working of Ti–6Al–4V. Int. J. Plast. 2002, 18, 1165–1189. [Google Scholar] [CrossRef]
- Gey, N.; Bocher, P.; Uta, E.; Germain, L.; Humbert, M. Texture and microtexture variations in a near-α titanium forged disk of bimodal microstructure. Acta Mater. 2012, 60, 2647–2655. [Google Scholar] [CrossRef]
- Miller, V.; Semiatin, S.; Szczepanski, C.; Pilchak, A. Optimization of VPSC model parameters for two-phase titanium alloys: Flow stress vs orientation distribution function metrics. Metall. Mater. Trans. A 2018, 49, 3624–3636. [Google Scholar] [CrossRef]
- Miller, V.; Echlin, M.; Beyerlein, I.; Pollock, T. Polycrystal plasticity simulation of microtextured titanium. In Proceedings of the 13th World Conference on Titanium, San Diego, CA, USA, 16–20 August 2015; pp. 209–214. [Google Scholar]
- Ma, R.; Pilchak, A.L.; Semiatin, S.L.; Truster, T.J. Modeling the evolution of microtextured regions during α/β processing using the crystal plasticity finite element method. Int. J. Plast. 2018, 107, 189–206. [Google Scholar] [CrossRef]
- Pilchak, A.L.; Shank, J.; Tucker, J.C.; Srivatsa, S.; Fagin, P.N.; Semiatin, S.L. A dataset for the development, verification, and validation of microstructure-sensitive process models for near-α titanium alloys. Integrating Mater. Manuf. Innov. 2016, 5, 14. [Google Scholar] [CrossRef]
- Dodds, R. WARP3D: 3-D nonlinear Finite Element Analysis of Solids for Fracture and Fatigue Processes. 2019. Available online: http://www.warp3d.net (accessed on 15 February 2019).
- Pilchak, A.; Szczepanski, C.; Shaffer, J.; Salem, A.; Semiatin, S. Characterization of microstructure, texture, and microtexture in near-alpha titanium mill products. Metall. Mater. Trans. A 2013, 44, 4881–4890. [Google Scholar] [CrossRef]
- Deka, D.; Joseph, D.S.; Ghosh, S.; Mills, M.J. Crystal plasticity modeling of deformation and creep in polycrystalline Ti-6242. Metall. Mater. Trans. A 2006, 37, 1371–1388. [Google Scholar] [CrossRef]
- Bantounas, I.; Lindley, T.C.; Rugg, D.; Dye, D. Effect of microtexture on fatigue cracking in Ti–6Al–4V. Acta Mater. 2007, 55, 5655–5665. [Google Scholar] [CrossRef]
- Echlin, M.P.; Stinville, J.C.; Miller, V.M.; Lenthe, W.C.; Pollock, T.M. Incipient slip and long range plastic strain localization in microtextured Ti-6Al-4V titanium. Acta Mater. 2016, 114, 164–175. [Google Scholar] [CrossRef]
- Mainprice, D.; Hielscher, R.; Schaeben, H. Calculating anisotropic physical properties from texture data using the MTEX open-source package. Geol. Soc. Lond. Spec. Publ. 2011, 360, 175–192. [Google Scholar] [CrossRef]
- Bantounas, I.; Dye, D.; Lindley, T.C. The role of microtexture on the faceted fracture morphology in Ti–6Al–4V subjected to high-cycle fatigue. Acta Mater. 2010, 58, 3908–3918. [Google Scholar] [CrossRef]
- Pilchak, A.L. The Effect of Friction Stir Processing on the Microstructure, Mechanical Properties and Fracture Behavior of Investment Cast Ti-6Al-4V. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2009. [Google Scholar]
- Zhang, X.; Oskay, C. Eigenstrain based reduced order homogenization for polycrystalline materials. Comput. Meth. Appl. Mech. Eng. 2015, 297, 408–436. [Google Scholar] [CrossRef]
- Zhang, X.; Oskay, C. Sparse and scalable eigenstrain-based reduced order homogenization models for polycrystal plasticity. Comput. Meth. Appl. Mech. Eng. 2017, 326, 241–269. [Google Scholar] [CrossRef]
| (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) |
|---|---|---|---|---|---|
| 132.8 | 159.4 | 76.56 | 67.19 | 39.84 | 28.12 |
| Basal | Prismatic | Pyramidal | |
|---|---|---|---|
| 0.12 | 0.12 | 0.12 | |
| 69.38 | 46.25 | 208.13 | |
| 4.69 | 9.72 | 28.22 | |
| 68.08 | 54.46 | 163.4 | |
| n | 0.14 | 0.15 | 0.15 |
| r | 0.30 | 0.29 | 0.29 |
| m | 0.20 | 0.20 | 0.20 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, R.; Truster, T.J. A Hierarchical Multiscale Modeling Investigation on the Behavior of Microtextured Regions in Ti-6242 α/β Processing. Metals 2019, 9, 233. https://doi.org/10.3390/met9020233
Ma R, Truster TJ. A Hierarchical Multiscale Modeling Investigation on the Behavior of Microtextured Regions in Ti-6242 α/β Processing. Metals. 2019; 9(2):233. https://doi.org/10.3390/met9020233
Chicago/Turabian StyleMa, Ran, and Timothy J. Truster. 2019. "A Hierarchical Multiscale Modeling Investigation on the Behavior of Microtextured Regions in Ti-6242 α/β Processing" Metals 9, no. 2: 233. https://doi.org/10.3390/met9020233
APA StyleMa, R., & Truster, T. J. (2019). A Hierarchical Multiscale Modeling Investigation on the Behavior of Microtextured Regions in Ti-6242 α/β Processing. Metals, 9(2), 233. https://doi.org/10.3390/met9020233






