Quantifying the Contribution of Crystallographic Texture and Grain Morphology on the Elastic and Plastic Anisotropy of bcc Steel
Abstract
1. Introduction
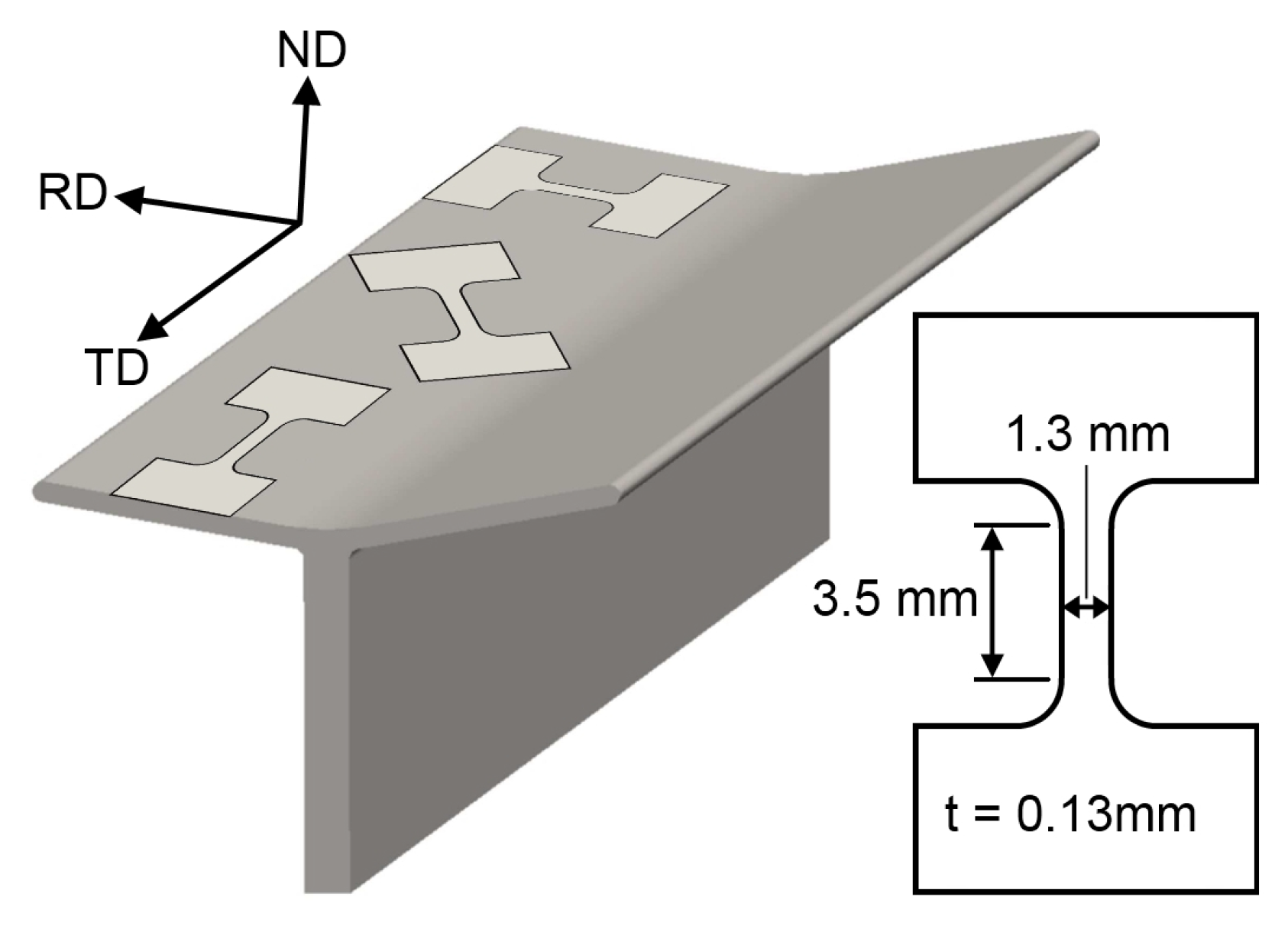
2. Material: Composition, Processing and Characterization
3. Simulation Setup
3.1. Microstructure Representation
- I a
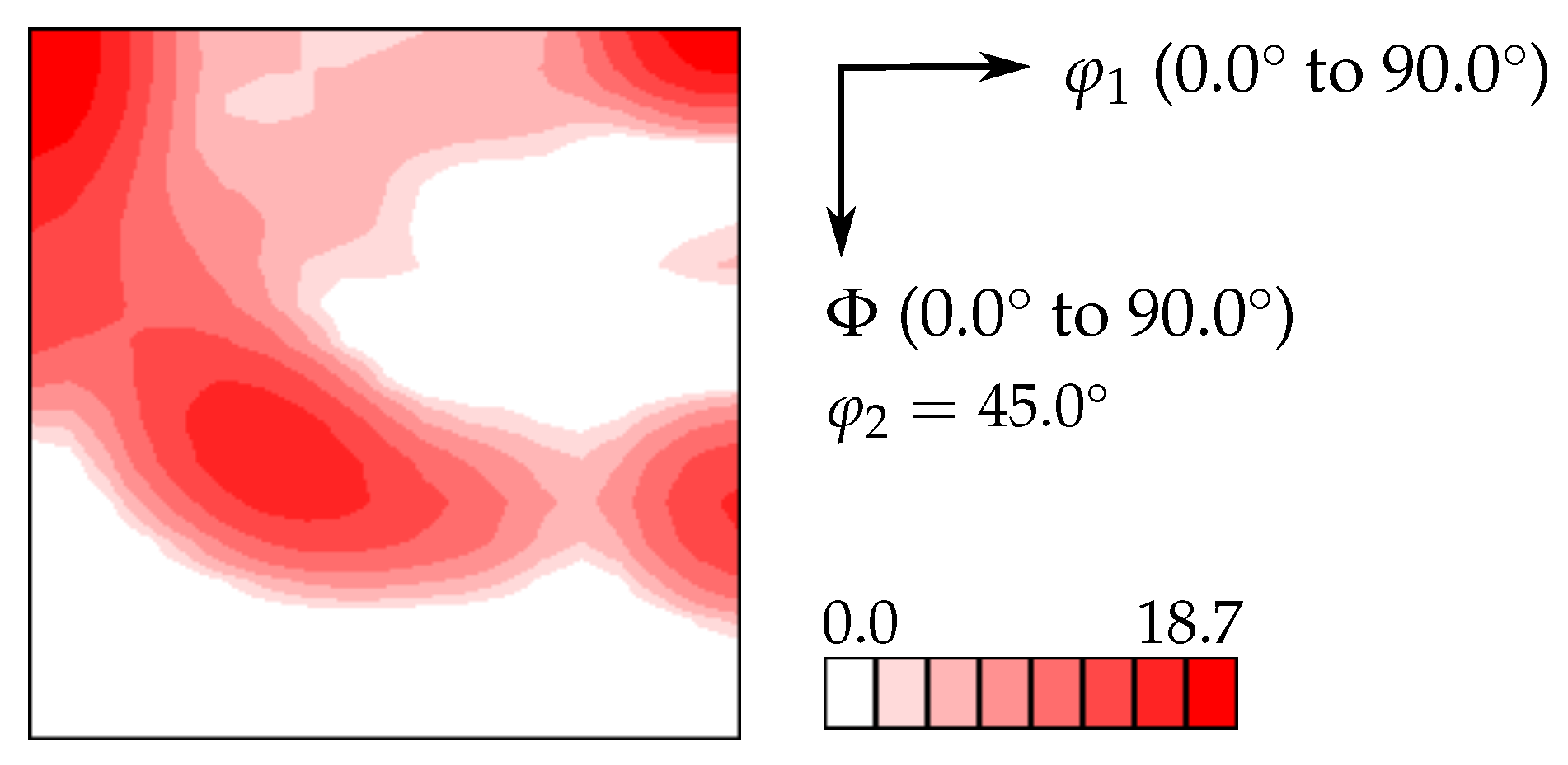
- Direct takeover 2D: These 2D full-field models are based on a direct takeover of the measured crystallographic orientation on each of the = 2,561,600 points (see Figure 2).
- I b
- Random orientation assignment 2D: By randomly shuffling the measured crystallographic orientations among the points, a second set of resolved 2D microstructures has been created.
- I c
- Random orientation assignment 3D: The random distribution of almost all (Less than 2% of the discrete crystallographic orientations had to be discarded when distributing them on an equi-gridded cube ().) measured orientations on a 3D grid with = 2,515,456 points gives a third set of microstructure variants.
- I d
- 2DVoronoitessellation: A regular grid of = 4,096,576 pixel is divided into 1000 grains with a periodic Voronoi tessellation. Each grain gets a homogeneous initial orientation assigned.
- I e
- 3DVoronoitessellation: Similarly, a 160 = 4,096,000 voxel grid is divided into 1000 equiaxed grains with a periodic Voronoi tessellation. The resulting microstructure for the RD-section is shown in Figure 4b.
- II a
- 3D microstructure without grain information: This TCCP-FEM model is conceptually a combination of variant I c (Random orientation assignment 3D) and I e (3D Voronoi tessellation): 1000 orientations are assigned to the points of a grid.
- II b
- 3D microstructure with globular grains: The same geometric representation as for variant I e (3D Voronoi tessellation) is used but the 1000 orientations represent the texture of all three measurements. To investigate the influence of the grain shape separately from the influence of the strong crystallographic texture present in the probed material, a variant of this microstructure is created in which 1000 randomly sampled orientations are assigned to the grains.
- II c
- 3D microstructure with elongated grains: To generate elongated grains, a standard Voronoi tesselation of 1000 seed points is performed on a grid from which only every eights plane along the last direction is used. The resulting grain structure with a grain aspect ratio of 8:8:1 (RD:TD:ND) and initial homogeneous orientation per grain is shown in Figure 4c. To investigate the influence of the grain shape separately from the influence of the strong crystallographic texture present in the probed material, a variant of this microstructure is created in which 1000 randomly sampled orientations are assigned to the grains.
3.2. Constitutive Model for Crystal Plasticity
3.3. Numerical Solver and Boundary Conditions
4. Results
4.1. Average Behaviour
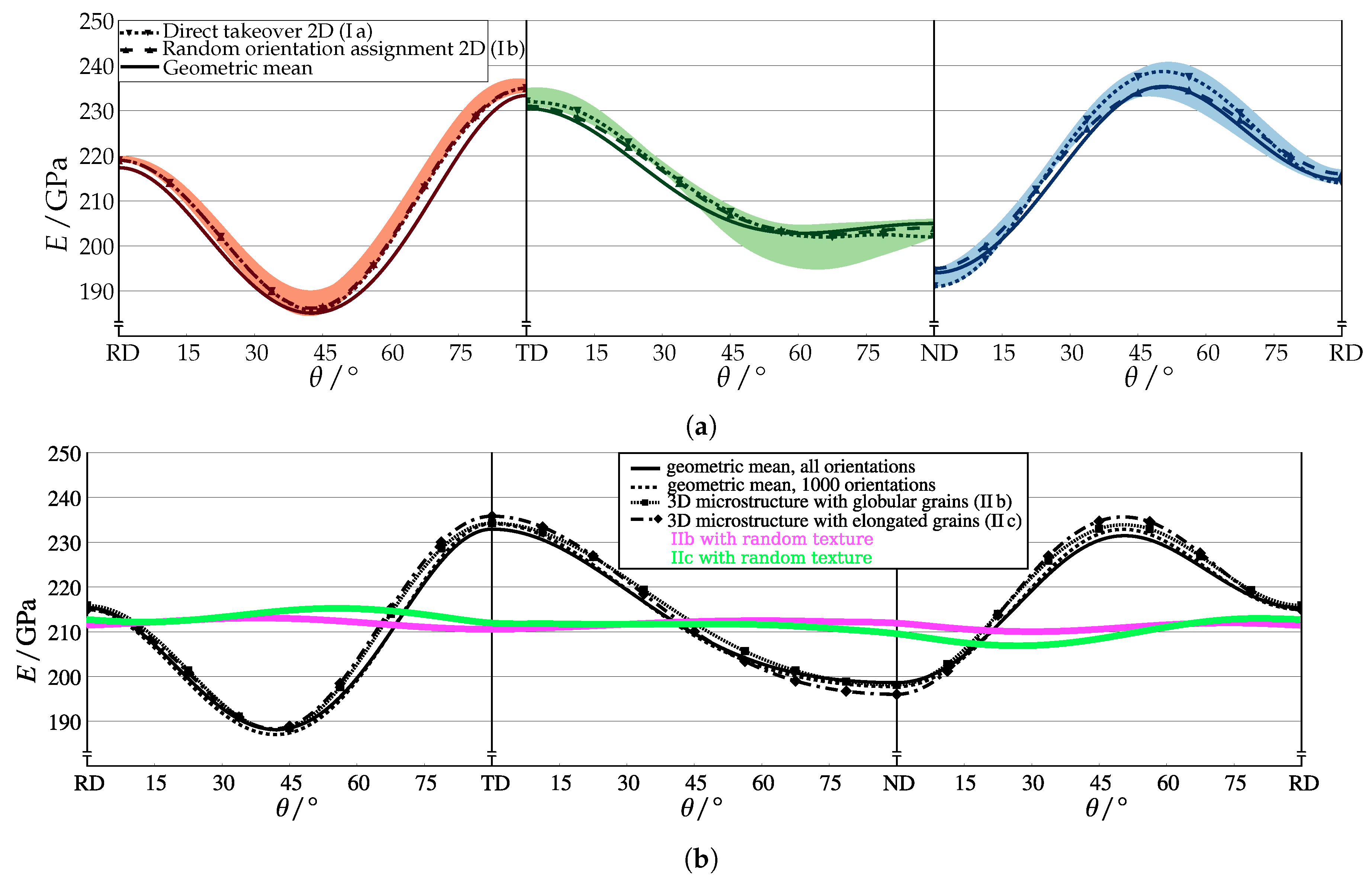
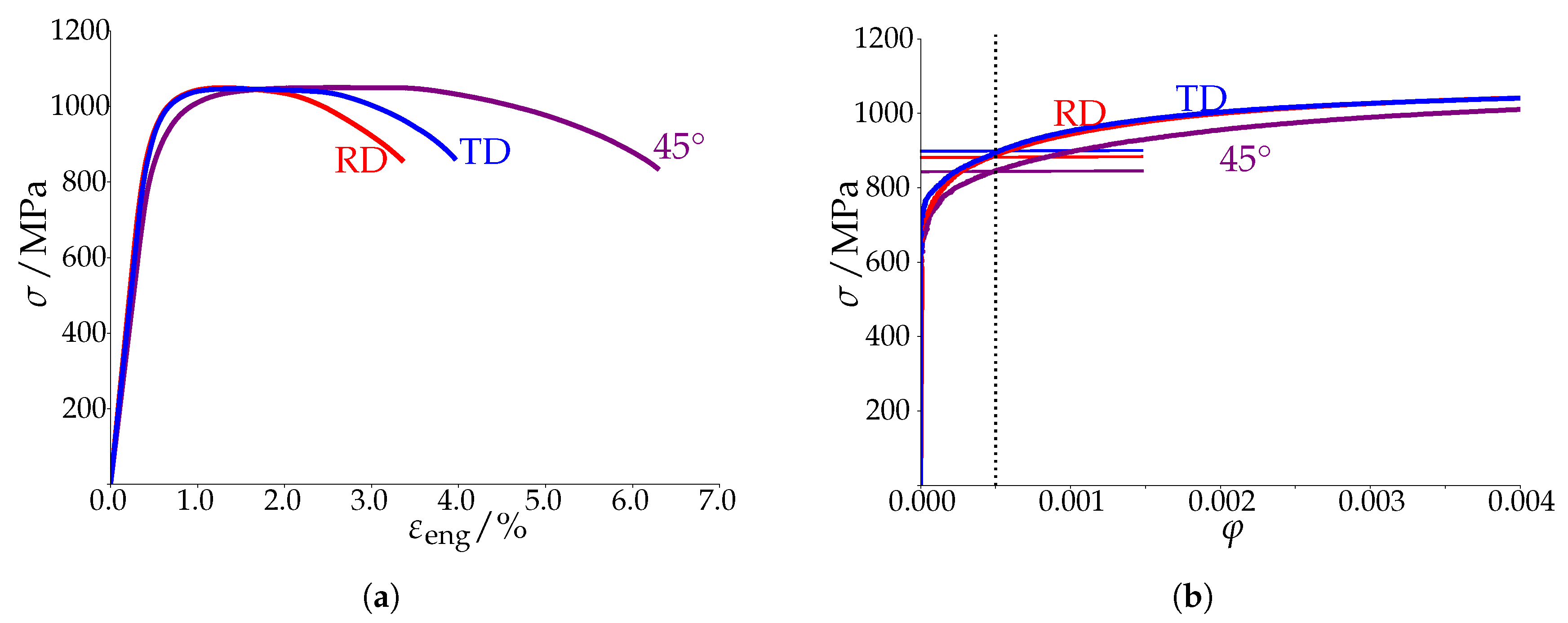
- The yield stress calculated for the individual sections with the analytic approach depends slightly on the data set, it differs by 30 (i.e., 3.4%) for the yield stress in TD direction , see Table 3a.
- The various microstructure models used for the individual data (I a to I e) predict differences of up to 38 ( calculated from ND-section data), see Table 3a.
- The yield stress in RD, , predicted by all simulations is lower than the value obtained from the analytic expression.
- Sampling 1000 orientations from the combined texture results in an increase of the predicted yield stress by 4 –12 when employing the analytic approach, see Table 3b.
- Employing the simpler models (II a: 3D microstructure without grain information and II b: 3D microstructure with globular grains) lowers and and increases in comparison to model II c (3D microstructure with elongated grains) which has the most realistic grain geometry, see Table 3b.
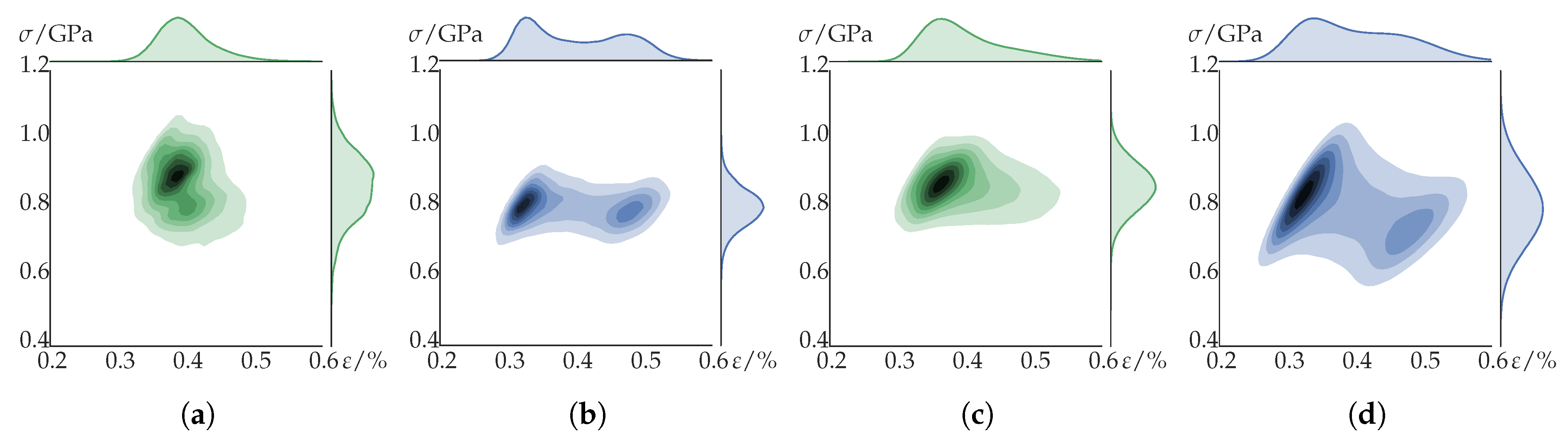
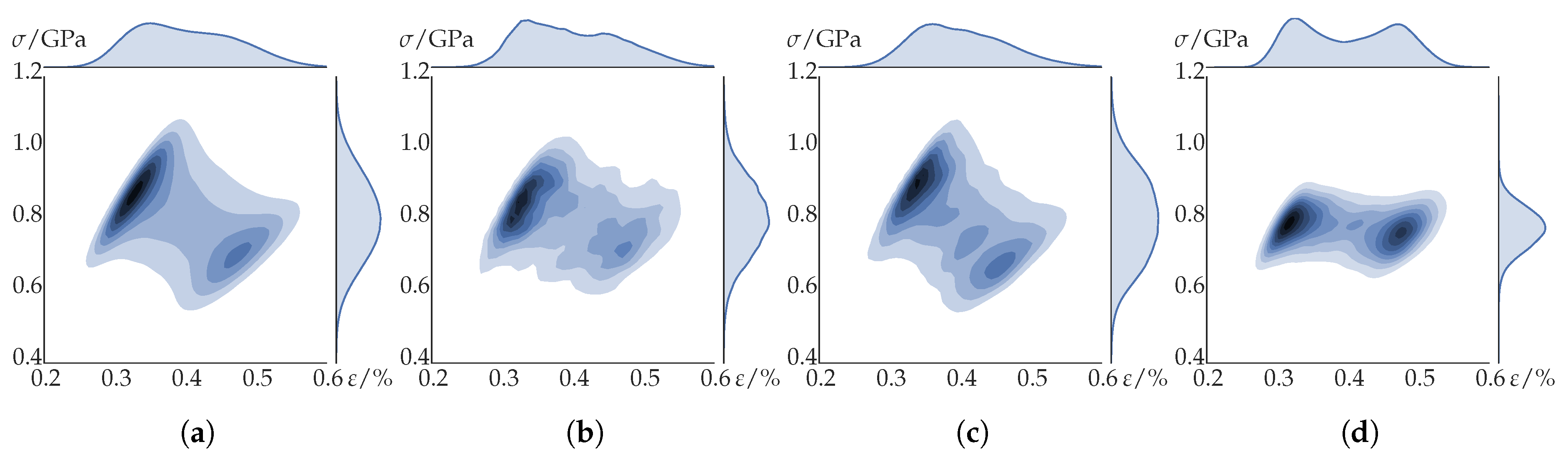
4.2. Micro-Mechanical Behaviour
5. Discussion
6. Conclusions
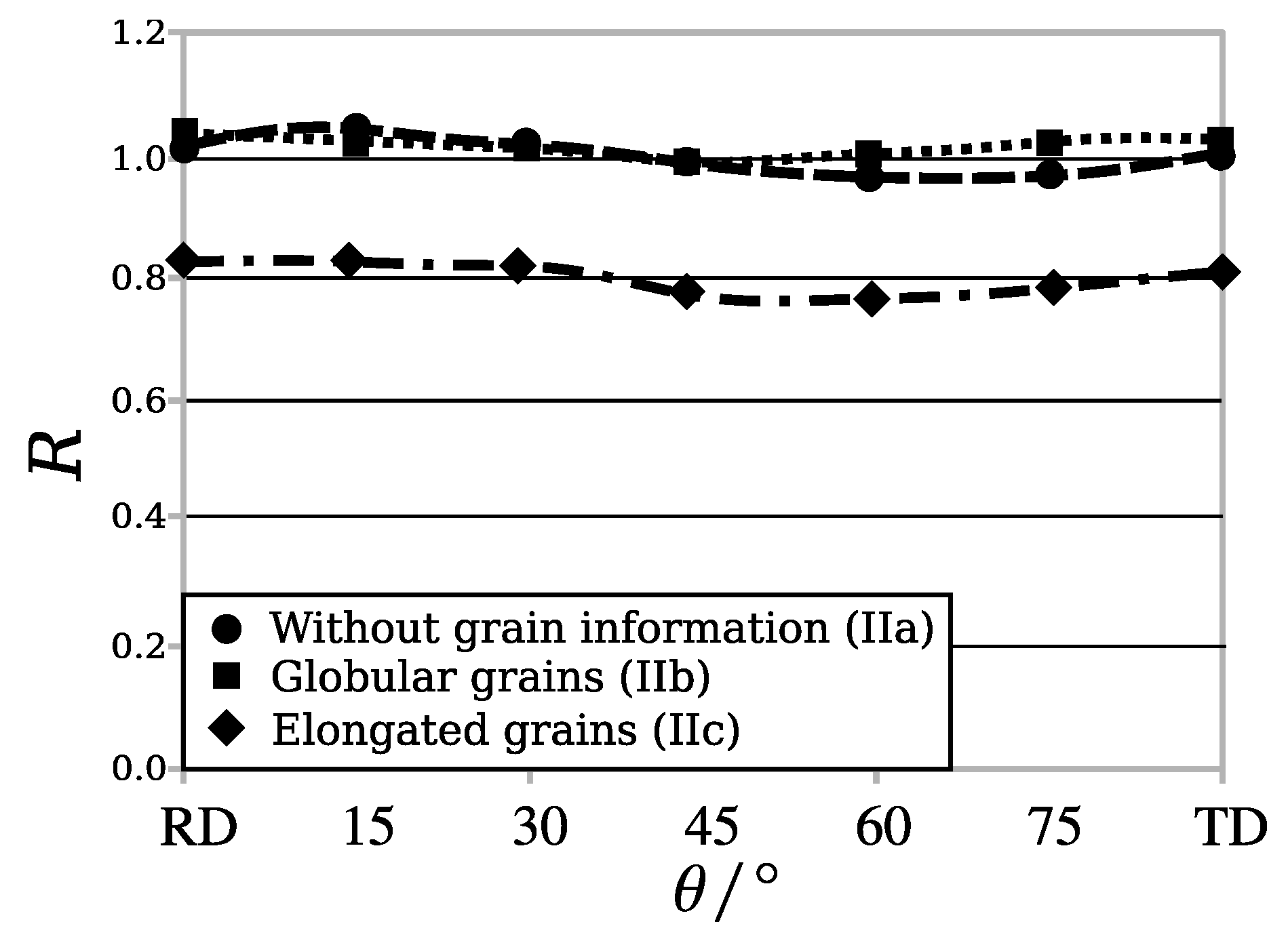
- The grain morphology only has a minor impact on anisotropic elastic and plastic properties, with differences of less than 3% between microstructure based and solely texture based numerical models.
- Statistically sufficient orientation measurements are more important than grain morphology. Even measuring 2000 grains does not ensure obtaining a representative orientation data.
- The HybridIa method enables a significant reduction of the orientation data that is required to accurately represent the texture.
- The simple analytic approach based on the geometric mean is suitable for estimating anisotropic elastic properties, since it yields very similar results as more complex numerical simulations.
- The underlying isostrain assumption of the Taylor model renders it an unsuitable choice for materials consisting of non-equiaxed grains with very strong anistropic behaviour.
7. Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Raabe, D.; Klose, P.; Engl, B.; Imlau, K.P.; Friedel, F.; Roters, F. Concepts for integrating plastic anisotropy into metal forming simulations. Adv. Eng. Mater. 2002, 4, 169–180. [Google Scholar] [CrossRef]
- Fritzen, F.; Böhlke, T. Three-dimensional finite element implementation of the nonuniform transformation field analysis. Int. J. Numer. Methods Eng. 2010, 84, 803–829. [Google Scholar] [CrossRef]
- Michel, J.C.; Suquet, P. A model-reduction approach to the micromechanical analysis of polycrystalline materials. Comput. Mech. 2016, 57, 483–508. [Google Scholar] [CrossRef]
- Brands, D.; Balzani, D.; Scheunemann, L.; Schröder, J.; Richter, H.; Raabe, D. Computational modeling of dual-phase steels based on representative three-dimensional microstructures obtained from EBSD data. Arch. Appl. Mech. 2016, 86, 575–598. [Google Scholar] [CrossRef]
- Tjahjanto, D.D.; Eisenlohr, P.; Roters, F. Multiscale deep drawing analysis of dual-phase steels using grain cluster-based RGC scheme. Model. Simul. Mater. Sci. Eng. 2015, 23, 045005. [Google Scholar] [CrossRef]
- Banabic, D. Sheet Metal Forming Processes; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Kraska, M.; Doig, M.; Tikhomirov, D.; Raabe, D.; Roters, F. Virtual material testing for stamping simulations based on polycrystal plasticity. Comput. Mater. Sci. 2009, 46, 383–392. [Google Scholar] [CrossRef]
- Zhang, H.; Diehl, M.; Roters, F.; Raabe, D. A virtual laboratory for initial yield surface determination using high resolution crystal plasticity simulations. Int. J. Plast. 2016, 80, 111–138. [Google Scholar] [CrossRef]
- Gawad, J.; Van Bael, A.; Eyckens, P.; Samaey, G.; Van Houtte, P.; Roose, D. Hierarchical multi-scale modeling of texture induced plastic anisotropy in sheet forming. Comput. Mater. Sci. 2013, 66, 65–83. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization, and multiscale methods in crystal plasticity finite element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Marin, E.B.; Dawson, P.R. Elastoplastic finite element analyses of metal deformations using polycrystal constitutive models. Comput. Methods Appl. Mech. Eng. 1998, 165, 23–41. [Google Scholar] [CrossRef]
- Beaudoin, A.J.; Dawson, P.R.; Mathur, K.K.; Kocks, U.F.; Korzekwa, D.A. Application of polycrystal plasticity to sheet forming. Comput. Methods Appl. Mech. Eng. 1994, 117, 49–70. [Google Scholar] [CrossRef]
- Mathur, K.K.; Dawson, P.R. On modeling the development of crystallographic texture in bulk forming processes. Int. J. Plast. 1989, 5, 67–94. [Google Scholar] [CrossRef]
- Barbe, F.; Decker, L.; Jeulin, D.; Cailletaud, G. Intergranular and intragranular behaviour of polycrystalline aggregates. Part 1: F.E. model. Int. J. Plast. 2001, 17, 513–536. [Google Scholar] [CrossRef]
- Groche, P.; Vucic, D.; Jöckel, M. Basics of linear flow splitting. J. Mater. Process. Technol. 2007, 183, 249–255. [Google Scholar] [CrossRef]
- Groche, P.; Bruder, E.; Gramlich, S. (Eds.) Manufacturing Integrated Design; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Bruder, E.; Ahmels, L.; Niehuesbernd, J.; Müller, C. Manufacturing-induced material properties of linear flow split and linear bend split profiles. Mater. Werkst. 2017, 48, 41–52. [Google Scholar] [CrossRef]
- Hölscher, M.; Raabe, D.; Lücke, K. Rolling and recrystallization textures of bcc steels. Steel Res. Int. 1991, 62, 567–575. [Google Scholar] [CrossRef]
- Niehuesbernd, J.; Müller, C.; Pantleon, W.; Bruder, E. Quantification of local and global elastic anisotropy in ultrafine grained gradient microstructures, produced by linear flow splitting. Mater. Sci. Eng. A 2013, 560, 273–277. [Google Scholar] [CrossRef]
- Voigt, W. Über die Beziehung zwischen den beiden Elastizitätskonstanten isotroper Körper. Ann. Phys. 1889, 38, 573–587. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Jöchen, K.; Böhlke, T.; Fritzen, F. Influence of the Crystallographic and the Morphological Texture on the Elastic Properties of Fcc Crystal Aggregates. Solid State Phenom. 2010, 160, 83–86. [Google Scholar] [CrossRef]
- Kiewel, H.; Fritsche, L. Calculation of effective elastic moduli of polycrystalline materials including nontextured samples and fiber textures. Phys. Rev. B 1994, 50, 5–16. [Google Scholar] [CrossRef] [PubMed]
- Taylor, G.I. Plastic strain in metals. J. Inst. Met. 1938, 62, 307–324. [Google Scholar]
- Roters, F.; Zhao, Z. Application of the Texture Component Crystal Plasticity Finite Element Method for Deep Drawing Simulations—A Comparison with Hill’s Yield Criterion. Adv. Eng. Mater. 2002, 4, 221–223. [Google Scholar] [CrossRef]
- Böhlke, T.; Risy, G.; Bertram, A. A texture component model for anisotropic polycrystal plasticity. Comput. Mater. Sci. 2005, 32, 284–293. [Google Scholar] [CrossRef]
- Eisenlohr, P.; Roters, F. Selecting sets of discrete orientations for accurate texture reconstruction. Comput. Mater. Sci. 2008, 42, 670–678. [Google Scholar] [CrossRef]
- Jöchen, K.; Böhlke, T. Representative reduction of crystallographic orientation data. J. Appl. Crystallogr. 2013, 46, 960–971. [Google Scholar] [CrossRef]
- Bachmann, F.; Hielscher, R.; Schaeben, H. Texture Analysis with MTEX—Free and Open Source Software Toolbox. Solid State Phenom. 2010, 160, 63–68. [Google Scholar] [CrossRef]
- Diehl, M. High-Resolution Crystal Plasticity Simulations; Apprimus Wissenschaftsverlag: Aachen, Germany, 2016. [Google Scholar]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. A 1976, 348, 101–127. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. An analysis of nonuniform and localized deformation in ductile single crystals. Acta Metall. 1982, 30, 1087–1119. [Google Scholar] [CrossRef]
- Rayne, J.A.; Chandrasekhar, B.S. Elastic Constants of Iron from 4.2 to 300 °K. Phys. Rev. 1961, 122, 1714–1716. [Google Scholar] [CrossRef]
- Adams, J.J.; Agosta, D.S.; Leisure, R.G.; Ledbetter, H. Elastic constants of monocrystal iron from 3 to 500 K. J. Appl. Phys. 2006, 100, 113530. [Google Scholar] [CrossRef]
- Tasan, C.C.; Hoefnagels, J.P.M.; Diehl, M.; Yan, D.; Roters, F.; Raabe, D. Strain localization and damage in dual phase steels investigated by coupled in-situ deformation experiments-crystal plasticity simulations. Int. J. Plast. 2014, 63, 198–210. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Kords, C.; Tjahjanto, D.D.; Diehl, M.; Raabe, D. DAMASK: The Düsseldorf Advanced Material Simulation Kit for studying crystal plasticity using an FE based or a spectral numerical solver. In Procedia IUTAM: IUTAM Symposium on Linking Scales in Computation: From Microstructure to Macroscale Properties; Cazacu, O., Ed.; Elsevier: Amsterdam, The Netherlands, 2012; Volume 3, pp. 3–10. [Google Scholar] [CrossRef]
- Roters, F.; Diehl, M.; Shanthraj, P.; Eisenlohr, P.; Reuber, C.; Wong, S.L.; Maiti, T.; Ebrahimi, A.; Hochrainer, T.; Fabritius, H.O.; et al. DAMASK—The Düsseldorf Advanced Material Simulation Kit for Modelling Multi-Physics Crystal Plasticity, Damage, and Thermal Phenomena from the Single Crystal up to the Component Scale. Comput. Mater. Sci. 2019, 158, 420–478. [Google Scholar] [CrossRef]
- Lahellec, N.; Michel, J.C.; Moulinec, H.; Suquet, P. Analysis of Inhomogeneous Materials at Large Strains Using Fast Fourier Transforms. In IUTAM Symposium on Computational Mechanics of Solid Materials at Large Strains; Solid Mechanics and Its Applications; Miehe, C., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001; Volume 108, pp. 247–258. [Google Scholar] [CrossRef]
- Moulinec, H.; Suquet, P. A numerical method for computing the overall response of nonlinear composites with complex microstructure. Comput. Methods Appl. Mech. Eng. 1998, 157, 69–94. [Google Scholar] [CrossRef]
- Lebensohn, R.A. N-site modeling of a 3D viscoplastic polycrystal using fast Fourier transform. Acta Mater. 2001, 49, 2723–2737. [Google Scholar] [CrossRef]
- Eisenlohr, P.; Diehl, M.; Lebensohn, R.A.; Roters, F. A spectral method solution to crystal elasto-viscoplasticity at finite strains. Int. J. Plast. 2013, 46, 37–53. [Google Scholar] [CrossRef]
- Shanthraj, P.; Eisenlohr, P.; Diehl, M.; Roters, F. Numerically robust spectral methods for crystal plasticity simulations of heterogeneous materials. Int. J. Plast. 2015, 66, 31–45. [Google Scholar] [CrossRef]
- Christensen, R.M. Observations on the definition of yield stress. Acta Mech. 2008, 196, 239–244. [Google Scholar] [CrossRef]
- Sachs, G. Mitteilungen der Deutschen Materialprüfungsanstalten; Chapter Zur Ableitung einer Fließbedingung; Springer: Berlin/Heidelberg, Germany, 1929; pp. 94–97. [Google Scholar] [CrossRef]
- Leffers, T.; Van Houtte, P. Calculated and experimental orientation distributions of twin lamellae in rolled brass. Acta Metall. 1989, 37, 1191–1198. [Google Scholar] [CrossRef]
- Ahzi, S.; Asaro, R.J.; Parks, D.M. Application of crystal plasticity theory for mechanically processed BSCCO superconductors. Mech. Mater. 1993, 15, 201–222. [Google Scholar] [CrossRef]
- Molinari, A.; Canova, G.R.; Ahzi, S. A self-consistent approach of the large deformation polycrystal viscoplasticity. Acta Metall. 1987, 35, 2983–2994. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Tomé, C.N. A self-consistent anisotropic approach for the simulation of plastic deformation and texture development of polycrystals: Application to zirconium alloys. Acta Metall. Mater. 1993, 41, 2611–2624. [Google Scholar] [CrossRef]
- Field, D.P.; Trivedi, P.B.; Wright, S.I.; Kumar, M. Analysis of local orientation gradients in deformed single crystals. Ultramicroscopy 2005, 103, 33–39. [Google Scholar] [CrossRef]
- Kiewel, H.; Bunge, H.J.; Fritsche, L. Effect of the Grain Shape on the Elastic Constants of Polycrystalline Materials. Textures Microstruct. 1996, 28, 17–33. [Google Scholar] [CrossRef]
- Jöchen, K. Homogenization of the Linear and Non-linear Mechanical behaviour of Polycrystals; KIT Scientific Publishing: Karlsruhe, Germany, 2013. [Google Scholar] [CrossRef]
- Crumbach, M.; Pomana, G.; Wagner, P.; Gottstein, G. A Taylor Type Deformation Texture Model Considering Grain Interaction and Material Properties. Part I—Fundamentals. In Recrystallisation and Grain Growth, Proceedings of the First Joint Conference; Gottstein, G., Molodov, D.A., Eds.; Springer: Berlin, Germany, 2001; pp. 1053–1060. [Google Scholar]
- Van Houtte, P. Deformation texture prediction: From the Taylor model to the advanced Lamel model. Int. J. Plast. 2005, 21, 589–624. [Google Scholar] [CrossRef]
- Eisenlohr, P.; Tjahjanto, D.D.; Hochrainer, T.; Roters, F.; Raabe, D. Texture Prediction from a Novel Grain Cluster-Based Homogenization Scheme. Int. J. Mater. Form. 2009, 2, 523–526. [Google Scholar] [CrossRef]
- Tjahjanto, D.D.; Eisenlohr, P.; Roters, F. Relaxed Grain Cluster (RGC) Homogenization Scheme. Int. J. Mater. Form. 2009, 2, 939–942. [Google Scholar] [CrossRef]
- Tasan, C.C.; Diehl, M.; Yan, D.; Bechtold, M.; Roters, F.; Schemmann, L.; Zheng, C.; Peranio, N.; Ponge, D.; Koyama, M.; et al. An overview of dual-phase steels: Advances in microstructure-oriented processing and micromechanically guided design. Annu. Rev. Mater. Res. 2015, 45, 391–431. [Google Scholar] [CrossRef]
- Appel, F.; Wagner, R. Microstructure and deformation of two-phase γ-titanium aluminides. Mater. Sci. Eng. R Rep. 1998, 22, 187–268. [Google Scholar] [CrossRef]
- Zeghadi, A.; N’guyen, F.; Forest, S.; Gourgues, A.F.; Bouaziz, O. Ensemble averaging stress–strain fields in polycrystalline aggregates with a constrained surface microstructure—Part 1: Anisotropic elastic behaviour. Philos. Mag. 2007, 87, 1401–1424. [Google Scholar] [CrossRef]
- Zeghadi, A.; Forest, S.; Gourgues, A.F.; Bouaziz, O. Ensemble averaging stress–strain fields in polycrystalline aggregates with a constrained surface microstructure—Part 2: Crystal plasticity. Philos. Mag. 2007, 87, 1425–1446. [Google Scholar] [CrossRef]
- Zaefferer, S.; Wright, S.I.; Raabe, D. Three-Dimensional Orientation Microscopy in a Focused Ion Beam–Scanning Electron Microscope: A New Dimension of Microstructure Characterization. Metall. Mater. Trans. A 2008, 39, 374–389. [Google Scholar] [CrossRef]
- Wang, L.; Li, M.; Almer, J.; Bieler, T.; Barabash, R. Microstructural characterization of polycrystalline materials by synchrotron X-rays. Front. Mater. Sci. 2013, 7, 156–169. [Google Scholar] [CrossRef]
- Pospiech, J.; Sztwiertnia, K.; Haessner, F. The Misorientation Distribution Function. Textures Microstruct. 1986, 6, 201–215. [Google Scholar] [CrossRef]
- Miodownik, M.; Godfrey, A.W.; Holm, E.A.; Hughes, D.A. On boundary misorientation distribution functions and how to incorporate them into three-dimensional models of microstructural evolution. Acta Mater. 1999, 47, 2661–2668. [Google Scholar] [CrossRef]
- Groeber, M.; Ghosh, S.; Uchic, M.D.; Dimiduk, D.M. A framework for automated analysis and simulation of 3D polycrystalline microstructures. Part 1: Statistical characterization. Acta Mater. 2008, 56, 1257–1273. [Google Scholar] [CrossRef]
- Groeber, M.; Ghosh, S.; Uchic, M.D.; Dimiduk, D.M. A framework for automated analysis and simulation of 3D polycrystalline microstructures. Part 2: Synthetic structure generation. Acta Mater. 2008, 56, 1274–1287. [Google Scholar] [CrossRef]
- Groeber, M.A.; Jackson, M.A. DREAM.3D: A Digital Representation Environment for the Analysis of Microstructure in 3D. Integr. Mater. Manuf. Innov. 2014, 3, 5. [Google Scholar] [CrossRef]
- Diehl, M.; Groeber, M.; Haase, C.; Molodov, D.A.; Roters, F.; Raabe, D. Identifying Structure–Property Relationships Through DREAM.3D Representative Volume Elements and DAMASK Crystal Plasticity Simulations: An Integrated Computational Materials Engineering Approach. JOM 2017, 69, 848–855. [Google Scholar] [CrossRef]
- Ma, A.; Roters, F.; Raabe, D. A dislocation density based consitutive law for BCC materials in crystal plasticity FEM. Comput. Mater. Sci. 2007, 39, 91–95. [Google Scholar] [CrossRef]
- Wong, S.L.; Madivala, M.; Prahl, U.; Roters, F.; Raabe, D. A crystal plasticity model for twinning- and transformation-induced plasticity. Acta Mater. 2016, 118, 140–151. [Google Scholar] [CrossRef]
- Cereceda, D.; Diehl, M.; Roters, F.; Raabe, D.; Perlado, J.M.; Marian, J. Unraveling the temperature dependence of the yield strength in single-crystal tungsten using atomistically-informed crystal plasticity calculations. Int. J. Plast. 2016, 78, 242–265. [Google Scholar] [CrossRef]
- Reuber, C.; Eisenlohr, P.; Roters, F.; Raabe, D. Dislocation density distribution around an indent in single-crystalline nickel: Comparing nonlocal crystal plasticity finite element predictions with experiments. Acta Mater. 2014, 71, 333–348. [Google Scholar] [CrossRef]
- Shanthraj, P.; Sharma, L.; Svendsen, B.; Roters, F.; Raabe, D. A phase field model for damage in elasto-viscoplastic materials. Comput. Methods Appl. Mech. Eng. 2016, 312, 167–185. [Google Scholar] [CrossRef]
- Shanthraj, P.; Svendsen, B.; Sharma, L.; Roters, F.; Raabe, D. Elasto-viscoplastic phase field modelling of anisotropic cleavage fracture. J. Mech. Phys. Solids 2017, 99, 19–34. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Thibault, J.; Woodward, C.; Shanthraj, P.; Roters, F. Brittle to Quasi-Brittle Transition and Crack Initiation Precursors in Disordered Crystals. arXiv 2017, arXiv:1707.04332v1. [Google Scholar]



| (a) | ||
|---|---|---|
| Property | Value | Unit |
| 230 | ||
| 134 | ||
| 116 | ||
| (b) | ||
|---|---|---|
| Property | Value | Unit |
| 1.0 | / | |
| 354 | ||
| 837 | ||
| 361 | ||
| 1538 | ||
| 1.0 | ||
| Coplanar | 1.0 | |
| Non-coplanar | 1.4 | |
| n | 20.0 | |
| a | 2.0 | |
| (a) | |||
|---|---|---|---|
| ND-Section | RD-Section | TD-Section | |
| - | |||
| - | |||
| - | |||
| (b) | |||||
|---|---|---|---|---|---|
| Geometric Mean | Simulation | ||||
| All Orientations | 1000 Orientations | II a | II b | II c | |
| 198 | 198 | 199 | 198 | 196 | |
| 215 | 215 | 216 | 216 | 215 | |
| 233 | 234 | 235 | 234 | 236 | |
| (a) | |||
|---|---|---|---|
| ND-Section | RD-Section | TD-Section | |
| - | |||
| - | |||
| - | |||
| (b) | |||||
|---|---|---|---|---|---|
| Geometric Mean | Simulation | ||||
| All Orientations | 1000 Orientations | II a | II b | II c | |
| 778 | 782 | 857 | 853 | 877 | |
| 874 | 883 | 842 | 837 | 825 | |
| 890 | 902 | 888 | 885 | 890 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diehl, M.; Niehuesbernd, J.; Bruder, E. Quantifying the Contribution of Crystallographic Texture and Grain Morphology on the Elastic and Plastic Anisotropy of bcc Steel. Metals 2019, 9, 1252. https://doi.org/10.3390/met9121252
Diehl M, Niehuesbernd J, Bruder E. Quantifying the Contribution of Crystallographic Texture and Grain Morphology on the Elastic and Plastic Anisotropy of bcc Steel. Metals. 2019; 9(12):1252. https://doi.org/10.3390/met9121252
Chicago/Turabian StyleDiehl, Martin, Jörn Niehuesbernd, and Enrico Bruder. 2019. "Quantifying the Contribution of Crystallographic Texture and Grain Morphology on the Elastic and Plastic Anisotropy of bcc Steel" Metals 9, no. 12: 1252. https://doi.org/10.3390/met9121252
APA StyleDiehl, M., Niehuesbernd, J., & Bruder, E. (2019). Quantifying the Contribution of Crystallographic Texture and Grain Morphology on the Elastic and Plastic Anisotropy of bcc Steel. Metals, 9(12), 1252. https://doi.org/10.3390/met9121252






