Microstructures and Hardness Prediction of an Ultrafine-Grained Al-2024 Alloy
Abstract
1. Introduction
2. Materials and Methods
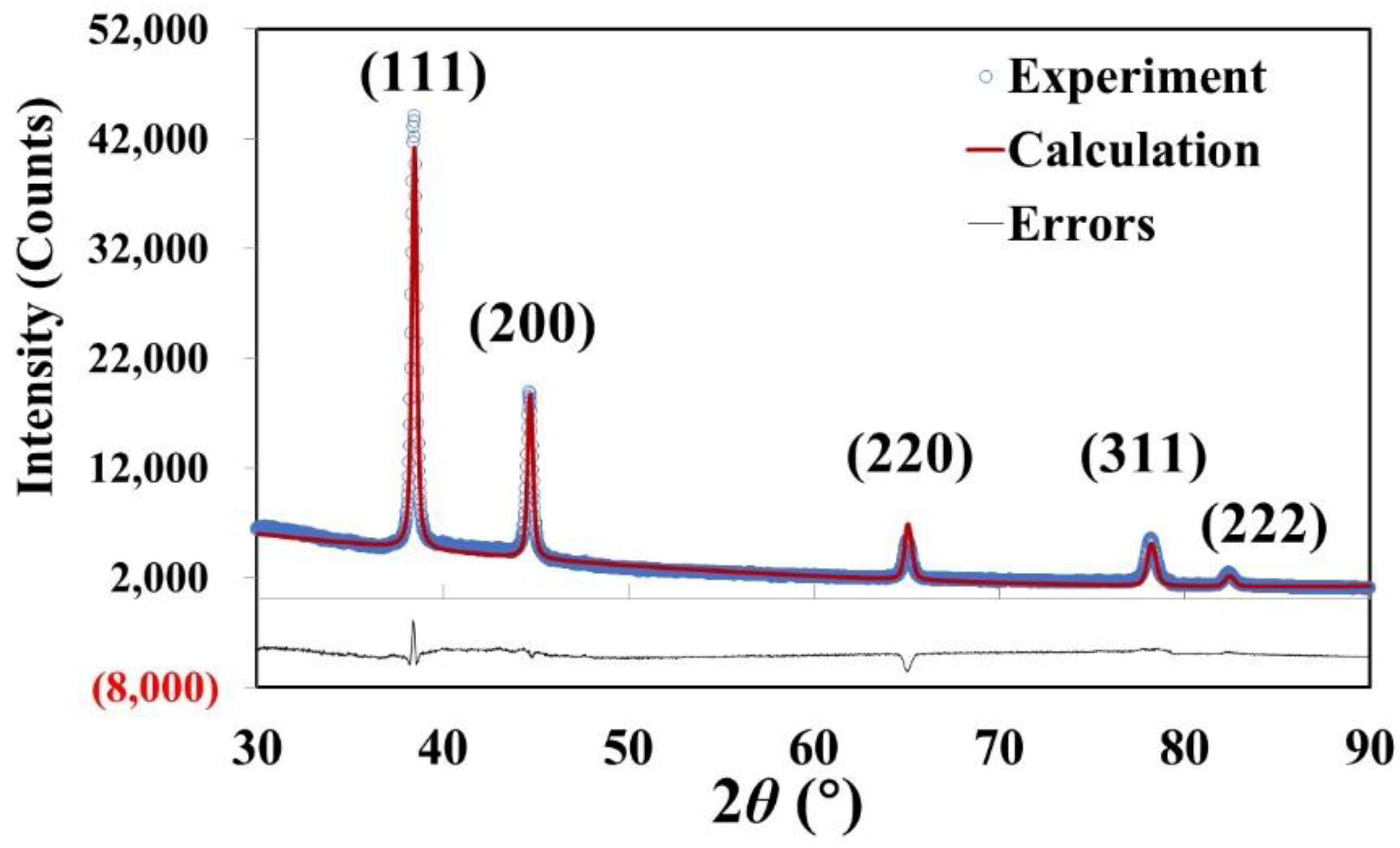
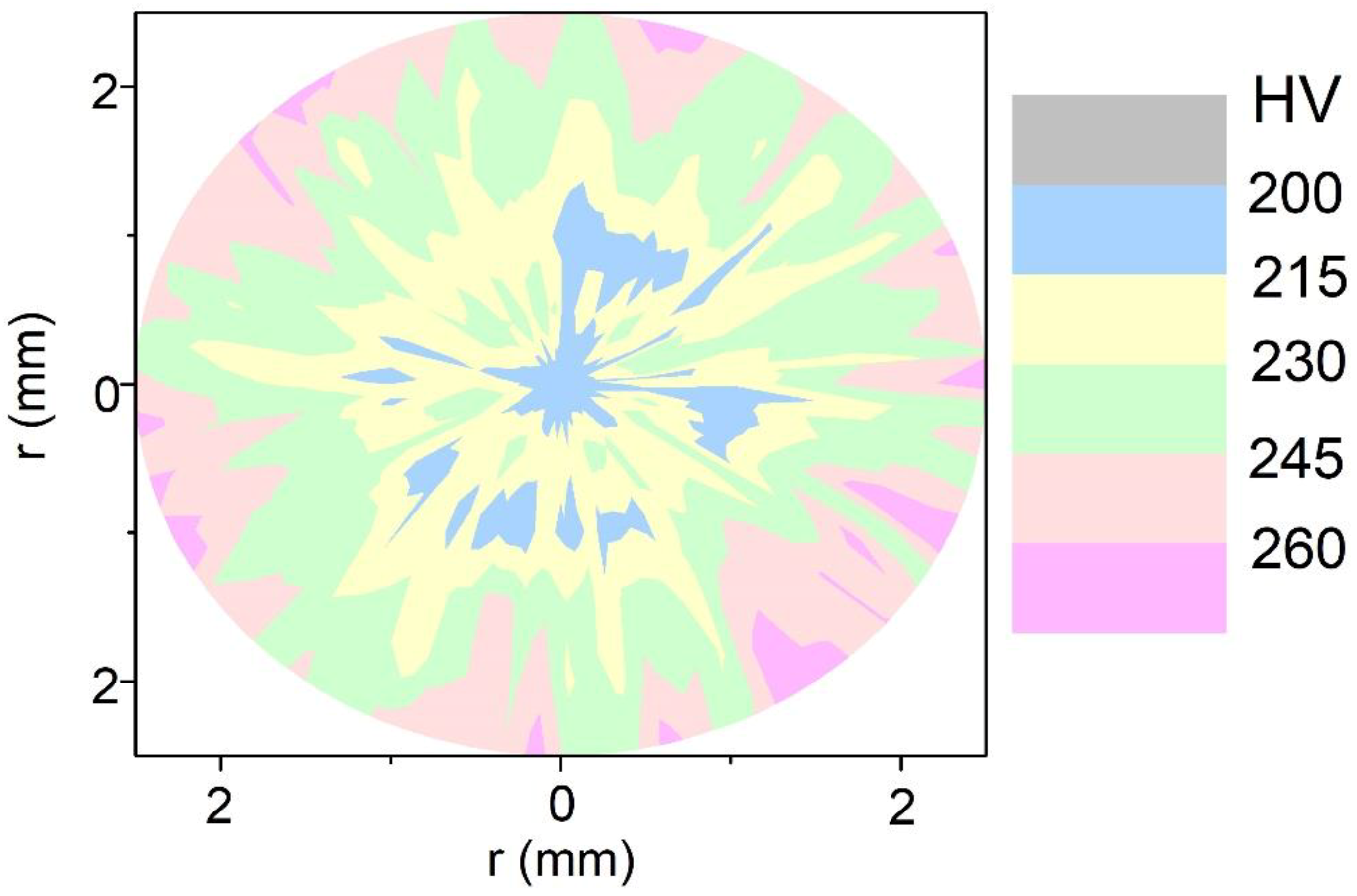
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhilyaev, A.P.; Langdon, T.G. Using high-pressure torsion for metal processing: Fundamentals and applications. Prog. Mater. Sci. 2008, 53, 893–979. [Google Scholar] [CrossRef]
- Vinogradov, A.; Estrin, Y. Analytical and numerical approaches to modelling severe plastic deformation. Prog. Mater. Sci. 2018, 95, 172–242. [Google Scholar] [CrossRef]
- Edalati, K.; Horita, Z. A review on high-pressure torsion (HPT) from 1935 to 1988. Mater. Sci. Eng. A 2016, 652, 325–352. [Google Scholar] [CrossRef]
- Starink, M.J.; Gao, N.; Kamp, N.; Wang, S.C.; Pitcher, P.D.; Sinclair, I. Relations between microstructure, precipitation, age-formability and damage tolerance of Al–Cu–Mg–Li (Mn, Zr, Sc) alloys for age forming. Mater. Sci. Eng. A 2006, 418, 241–249. [Google Scholar] [CrossRef]
- Wang, S.C.; Lefebvre, F.; Yan, J.L.; Sinclair, I.; Starink, M.J. VPPA welds of Al-2024 alloys: Analysis and modelling of local microstructure and strength. Mater. Sci. Eng. A 2006, 431, 123–136. [Google Scholar] [CrossRef]
- Vafaei, R.; Toroghinejad, M.R.; Pippan, R. Evaluation of mechanical behavior of nano-grained 2024 Al alloy during high pressure torsion (HPT) process at various temperatures. Mater. Sci. Eng. A 2012, 536, 73–81. [Google Scholar] [CrossRef]
- Alhamidi, A.; Horita, Z. Grain refinement and high strain rate superplasticity in alumunium 2024 alloy processed by high-pressure torsion. Mater. Sci. Eng. A 2015, 622, 139–145. [Google Scholar] [CrossRef]
- Wang, S.C.; Starink, M.J. The assessment of GPB2/S structures in Al-Cu-Mg alloys. Mater. Sci. Eng. A 2004, 386, 156–163. [Google Scholar] [CrossRef]
- Wang, S.C.; Starink, M.J. Precipitates and intermetallic phases in precipitation hardening Al–Cu–Mg–(Li) based alloys. Int. Mater. Rev. 2005, 50, 193–215. [Google Scholar] [CrossRef]
- Parel, T.S.; Wang, S.C.; Starink, M.J. Hardening of an Al–Cu–Mg alloy containing Types I and II S phase precipitates. Mater. Des. 2010, 31, S2–S5. [Google Scholar] [CrossRef]
- Sha, G.; Marceau, R.K.W.; Gao, X.; Muddle, B.C.; Ringer, S.P. Nanostructure of aluminium alloy 2024: Segregation, clustering and precipitation processes. Acta Mater. 2011, 59, 1659–1670. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, N.; Sha, G.; Ringer, S.P.; Starink, M.J. Strengthening of an Al–Cu–Mg alloy processed by high-pressure torsion due to clusters, defects and defect–cluster complexes. Mater. Sci. Eng. A 2015, 627, 10–20. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, N.; Sha, G.; Ringer, S.P.; Starink, M.J. Microstructural evolution, strengthening and thermal stability of an ultrafine-grained Al–Cu–Mg alloy. Acta Mater. 2016, 109, 202–212. [Google Scholar] [CrossRef]
- Starink, M.J.; Qiao, X.G.; Zhang, J.; Gao, N. Predicting grain refinement by cold severe plastic deformation in alloys using volume averaged dislocation generation. Acta Mater. 2009, 57, 5796–5811. [Google Scholar] [CrossRef]
- Ma, K.; Hu, T.; Yang, H.; Topping, T.; Yousefiani, A.; Lavernia, E.J.; Schoenung, J.M. Coupling of dislocations and precipitates: Impact on the mechanical behavior of ultrafine grained Al–Zn–Mg alloys. Acta Mater. 2016, 103, 153–164. [Google Scholar] [CrossRef]
- Thorvaldsen, A. The intercept method—1. Evaluation of grain shape. Acta Mater. 1997, 45, 587–594. [Google Scholar] [CrossRef]
- Wang, S.C.; Li, C.Z.; Yan, M.G. Determination of structure of Al20Cu2Mn3 phase in Al-Cu-Mn alloys. Mater. Res. Bull. 1989, 24, 1267–1270. [Google Scholar]
- Chen, Y.Q.; Pan, S.P.; Liu, W.H.; Liu, X.; Tang, C.P. Morphologies, orientation relationships, and evolution of the T-phase in an Al-Cu-Mg-Mn alloy during homogenisation. J. Alloys Compd. 2017, 709, 213–226. [Google Scholar] [CrossRef]
- Sauvage, X.; Enikeev, N.; Valiev, R.; Nasedkina, Y.; Murashkin, M. Atomic-scale analysis of the segregation and precipitation mechanisms in a severely deformed Al–Mg alloy. Acta Mater. 2014, 72, 125–136. [Google Scholar] [CrossRef]
- Sauvage, X.; Ganeev, A.; Ivanisenko, Y.; Enikeev, N.; Murashkin, M.; Valiev, R. Grain Boundary Segregation in UFG Alloys Processed by Severe Plastic Deformation. Adv. Eng. Mater. 2012, 14, 968–974. [Google Scholar] [CrossRef]
- Sauvage, X.; Wilde, G.; Divinski, S.V.; Horita, Z.; Valiev, R.Z. Grain boundaries in ultrafine grained materials processed by severe plastic deformation and related phenomena. Mater. Sci. Eng. A 2012, 540, 1–12. [Google Scholar] [CrossRef]
- Williamson, G.K.; Smallman, R.E., III. Dislocation densities in some annealed and cold-worked metals from measurements on the X-ray debye-scherrer spectrum. Philos. Mag. 1956, 1, 34–46. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Liao, X.Z.; Jin, Z.; Valiev, R.Z.; Zhu, Y.T. Microstructures and mechanical properties of ultrafine grained 7075 Al alloy processed by ECAP and their evolutions dring annealing. Acta Mater. 2004, 52, 4589–4599. [Google Scholar] [CrossRef]
- Ferrari, M.; Lutterotti, L. Method for the simultaneous determination of anisotropic residual stresses and texture by X-ray diffraction. J. Appl. Phys. 1994, 76, 7246–7255. [Google Scholar] [CrossRef]
- Lutterotti, L.; Gialanella, S. X-ray diffraction characterization of heavily deformed metallic specimens. Acta Mater. 1998, 46, 101–110. [Google Scholar] [CrossRef]
- Beygelzimer, Y.; Kulagin, R.; Toth, L.S.; Ivanisenko, Y. The Self-similarity theory of high pressure torsion. Beilstein. J. Nanotechnol. 2016, 7, 1267–1277. [Google Scholar] [CrossRef]
- Kulagin, R.; Beygelzimer, Y.; Ivanisenko, Y.; Mazilkin, A.; Hahn, H. Modelling of high pressure torsion using FEM. Procedia Eng. 2017, 207, 1445–1450. [Google Scholar] [CrossRef]
- Kratochvíl, J.; Kružík, M.; Sedláček, R. A model of ultrafine microstructure evolution in materials deformed by high-pressure torsion. Acta Mater. 2009, 57, 739–748. [Google Scholar] [CrossRef]
- Chookajorn, T.; Murdoch, H.A.; Schuh, C.A. Design of Stable Nanocrystalline Alloys. Science 2012, 337, 951–954. [Google Scholar] [CrossRef]
- Ringer, S.P.; Sakurai, T.; Polmear, I.J. Origins of hardening in aged Al-Cu-Mg-(Ag) alloys. Acta Mater. 1997, 45, 3731–3744. [Google Scholar] [CrossRef]
- Starink, M.J.; Wang, S.C. The thermodynamics of and strengthening due to co-clusters: General theory and application to the case of Al-Cu-Mg alloys. Acta Mater. 2009, 57, 2376–2389. [Google Scholar] [CrossRef]
- Meyers, M.A.; Mishra, A.; Benson, D.J. Mechanical properties of nanocrystalline materials. Prog. Mater. Sci. 2006, 51, 427–556. [Google Scholar] [CrossRef]
- Starink, M.J.; Wang, S.C. A model for the yield strength of overaged Al–Zn–Mg–Cu alloys. Acta Mater. 2003, 51, 5131–5150. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, N.; Starink, M.J. Microstructure development and hardening during high pressure torsion of commercially pure aluminium: Strain reversal experiments and a dislocation based model. Mater. Sci. Eng. A 2011, 528, 2581–2591. [Google Scholar] [CrossRef]
- Hansen, N. Hall–Petch relation and boundary strengthening. Scr. Mater. 2004, 51, 801–806. [Google Scholar] [CrossRef]
- Shanmugasundaram, T.; Heilmaier, M.; Murty, B.S.; Sarma, V.S. On the Hall–Petch relationship in a nanostructured Al–Cu alloy. Mater. Sci. Eng. A 2010, 527, 7821–7825. [Google Scholar] [CrossRef]
- Starink, M.J.; Cheng, X.; Yang, S. Hardening of pure metals by high-pressure torsion: A physically based model employing volume-averaged defect evolutions. Acta Mater. 2013, 61, 183–192. [Google Scholar] [CrossRef]
- Shewmon, P.G. Diffusion in Solids; McGraw-Hill: New York, NY, USA, 1963; p. 200. [Google Scholar]
- Wang, S.C.; Zhu, Z.; Starink, M.J. Estimation of dislocation densities in cold rolled Al-Mg-Cu-Mn alloys by combination of yield strength data, EBSD and strength models. J. Microsc. 2005, 217, 174–178. [Google Scholar] [CrossRef]
- Starink, M.J.; Gao, N.; Davin, L.; Yan, J.; Cerezo, A. Room temperature precipitation in quenched Al–Cu–Mg alloys: A model for the reaction kinetics and yield strength development. Philos. Mag. 2005, 85, 1395–1417. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Tang, Y.; Zhang, H.; Hu, N.; Gao, N.; Starink, M.J. Microstructures and Hardness Prediction of an Ultrafine-Grained Al-2024 Alloy. Metals 2019, 9, 1182. https://doi.org/10.3390/met9111182
Chen Y, Tang Y, Zhang H, Hu N, Gao N, Starink MJ. Microstructures and Hardness Prediction of an Ultrafine-Grained Al-2024 Alloy. Metals. 2019; 9(11):1182. https://doi.org/10.3390/met9111182
Chicago/Turabian StyleChen, Ying, Yuanchen Tang, Houan Zhang, Nan Hu, Nong Gao, and Marco J. Starink. 2019. "Microstructures and Hardness Prediction of an Ultrafine-Grained Al-2024 Alloy" Metals 9, no. 11: 1182. https://doi.org/10.3390/met9111182
APA StyleChen, Y., Tang, Y., Zhang, H., Hu, N., Gao, N., & Starink, M. J. (2019). Microstructures and Hardness Prediction of an Ultrafine-Grained Al-2024 Alloy. Metals, 9(11), 1182. https://doi.org/10.3390/met9111182





