Measurement of Metal Velocity in Sand Casting during Mold Filling
Abstract
1. Introduction
1.1. Water Modeling Experiments
1.2. X-Ray Radiography
1.3. Capacitive Sensors
1.4. 3D-Printed Smart Molds
1.5. Contactless Techniques—Magnetohydrodynamics and Ultrasound Doppler Velocimetry
1.6. Contact Techniques
1.7. Research Objectives
2. Materials and Methods
2.1. Experimental Methodology
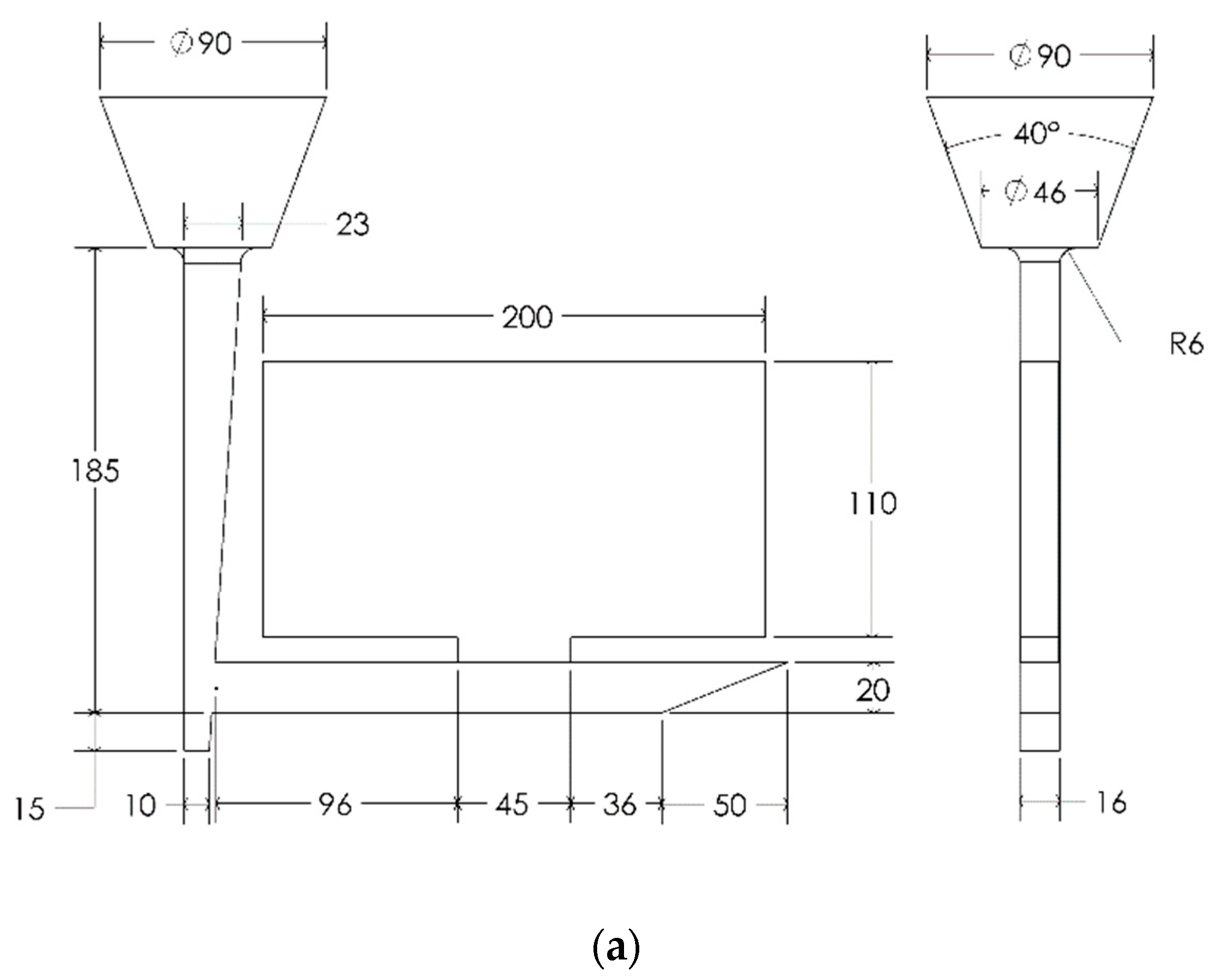
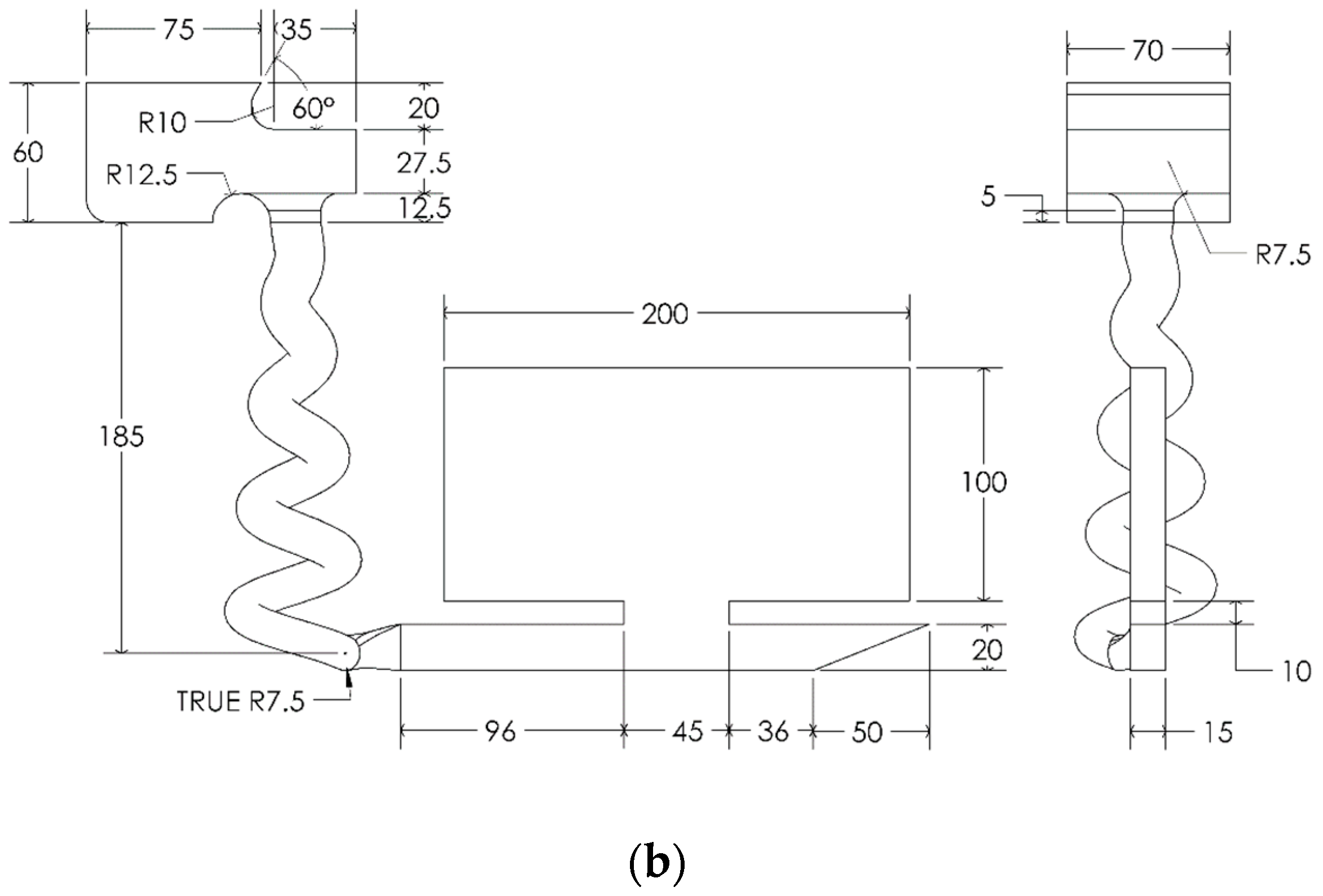
2.2. Straight and Conical-Helix Sprued 3D-Printed Molds
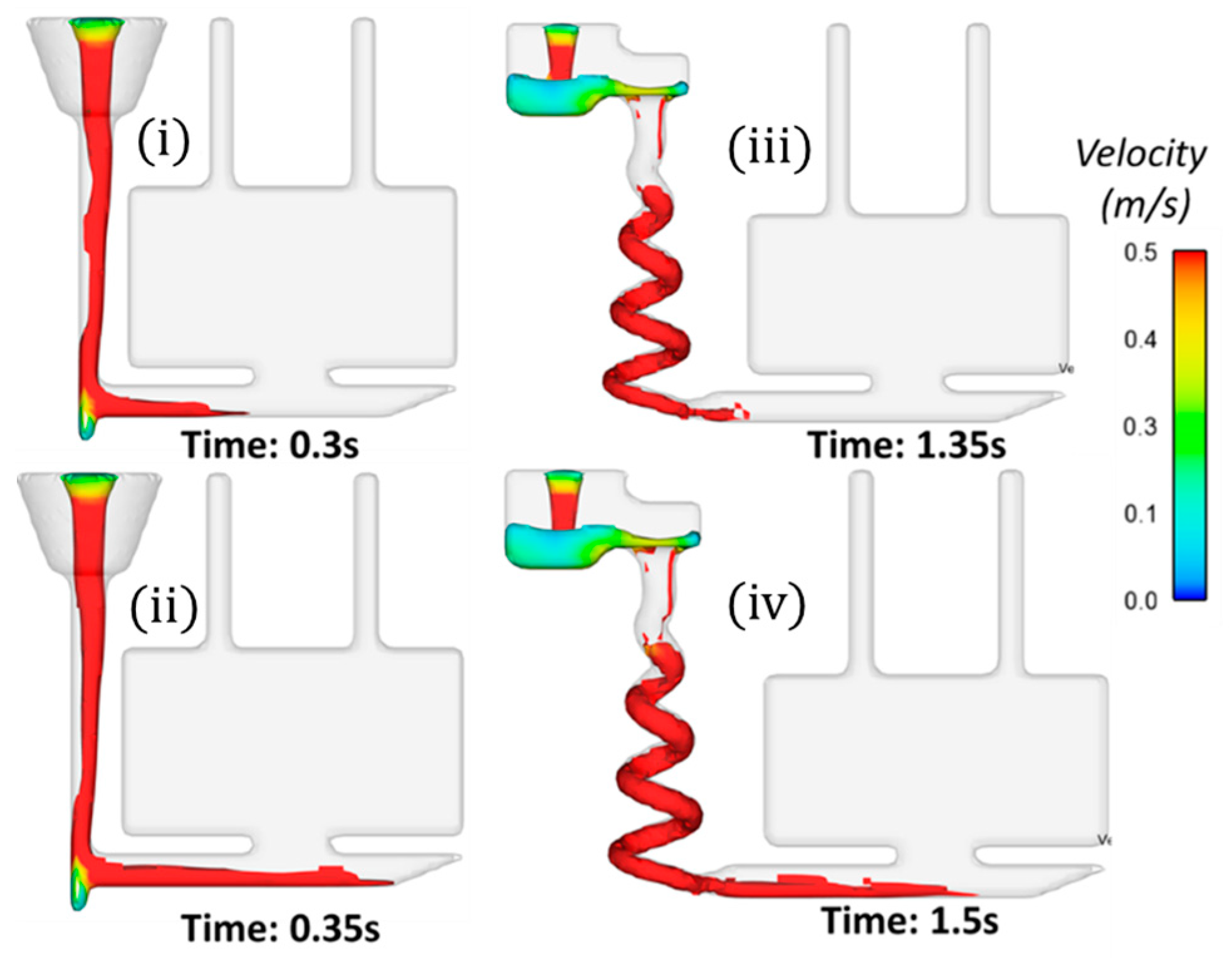
2.3. Computational Simulations
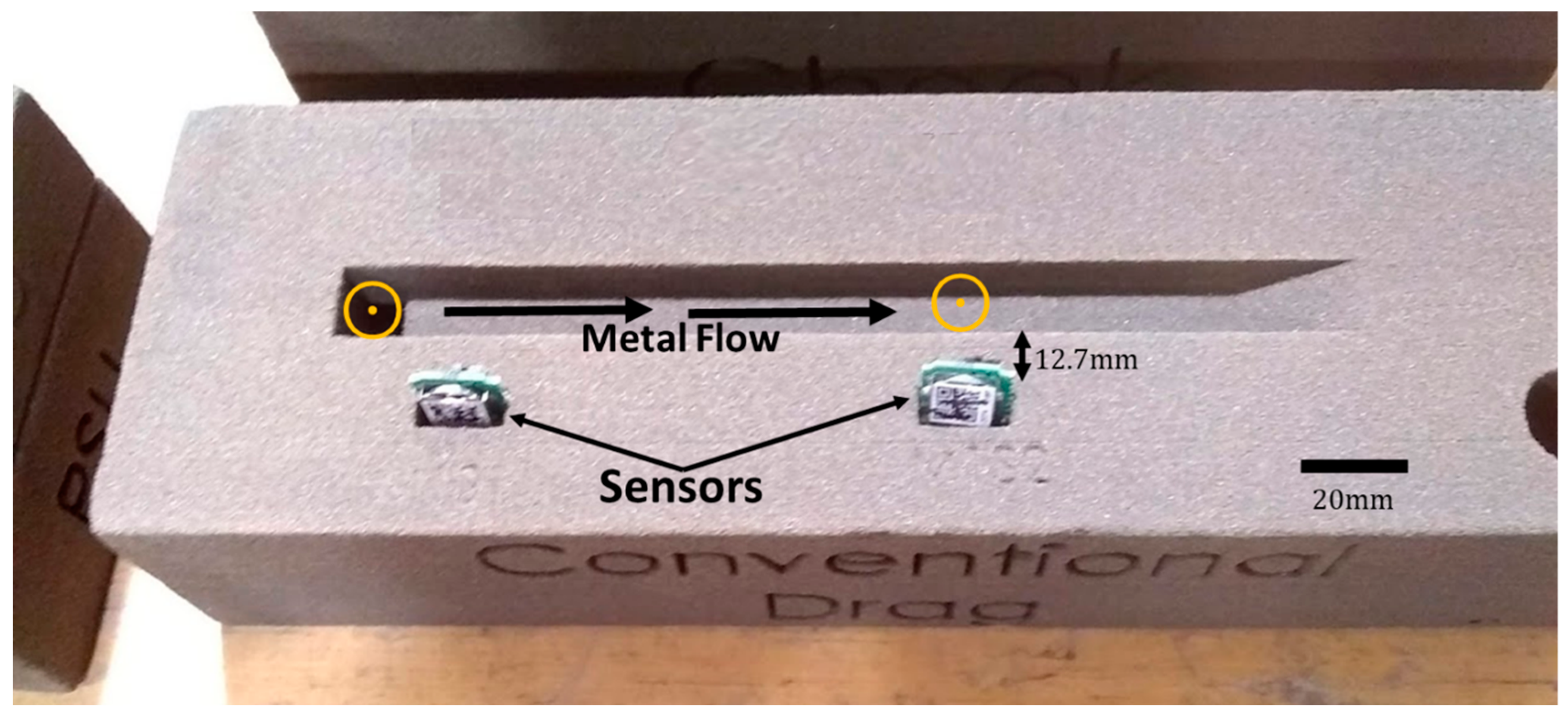
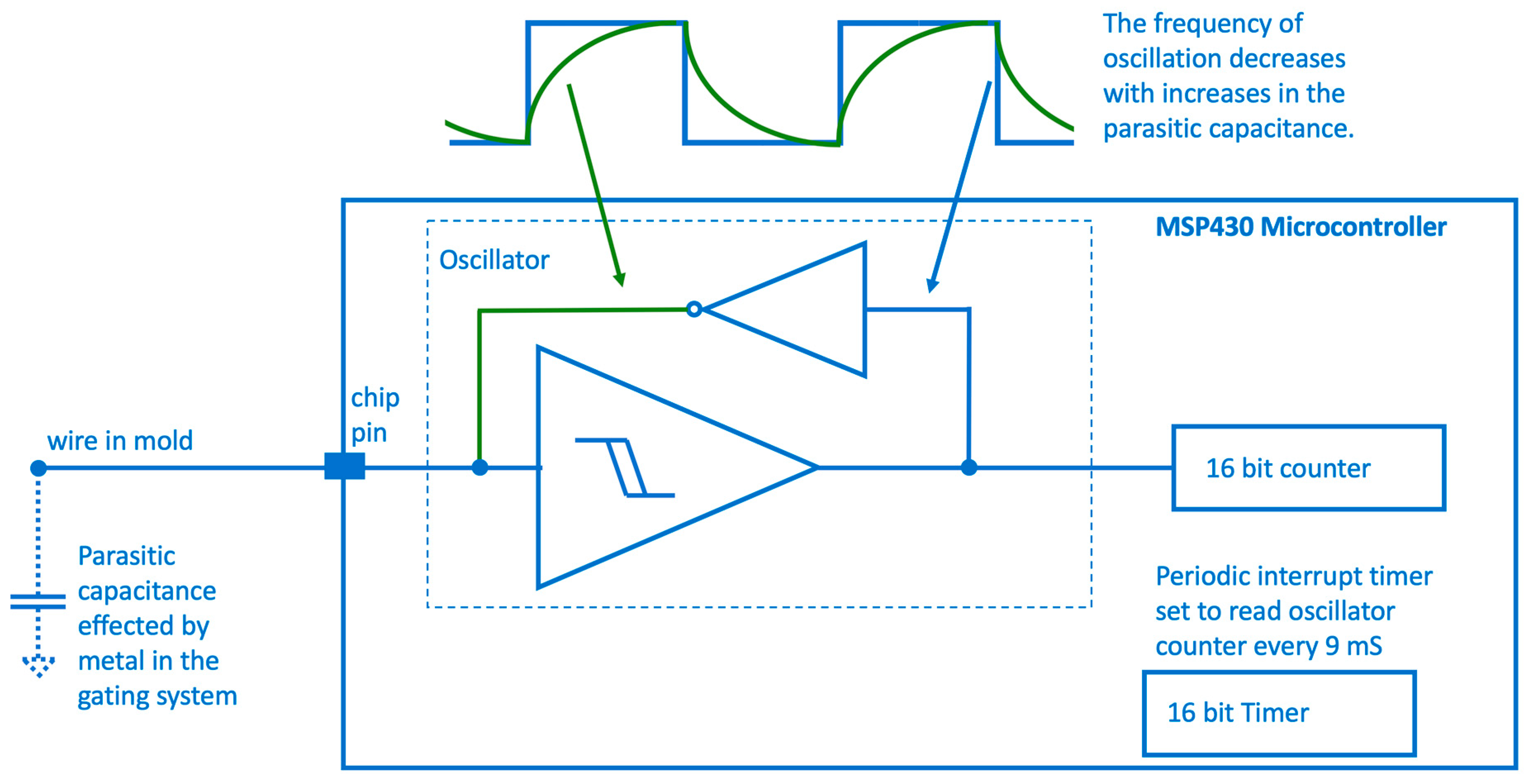
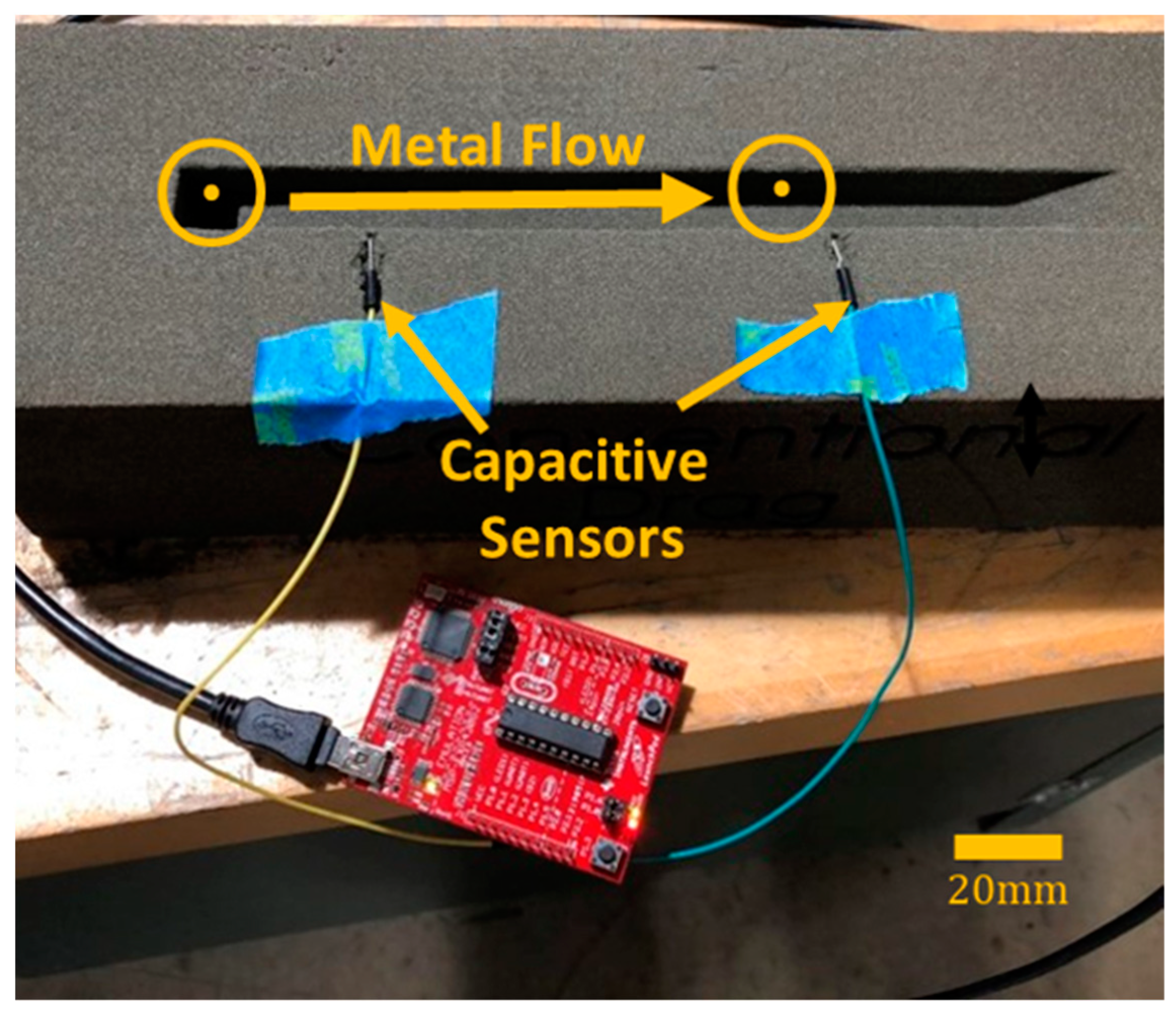
2.4. Capacitive Sensors
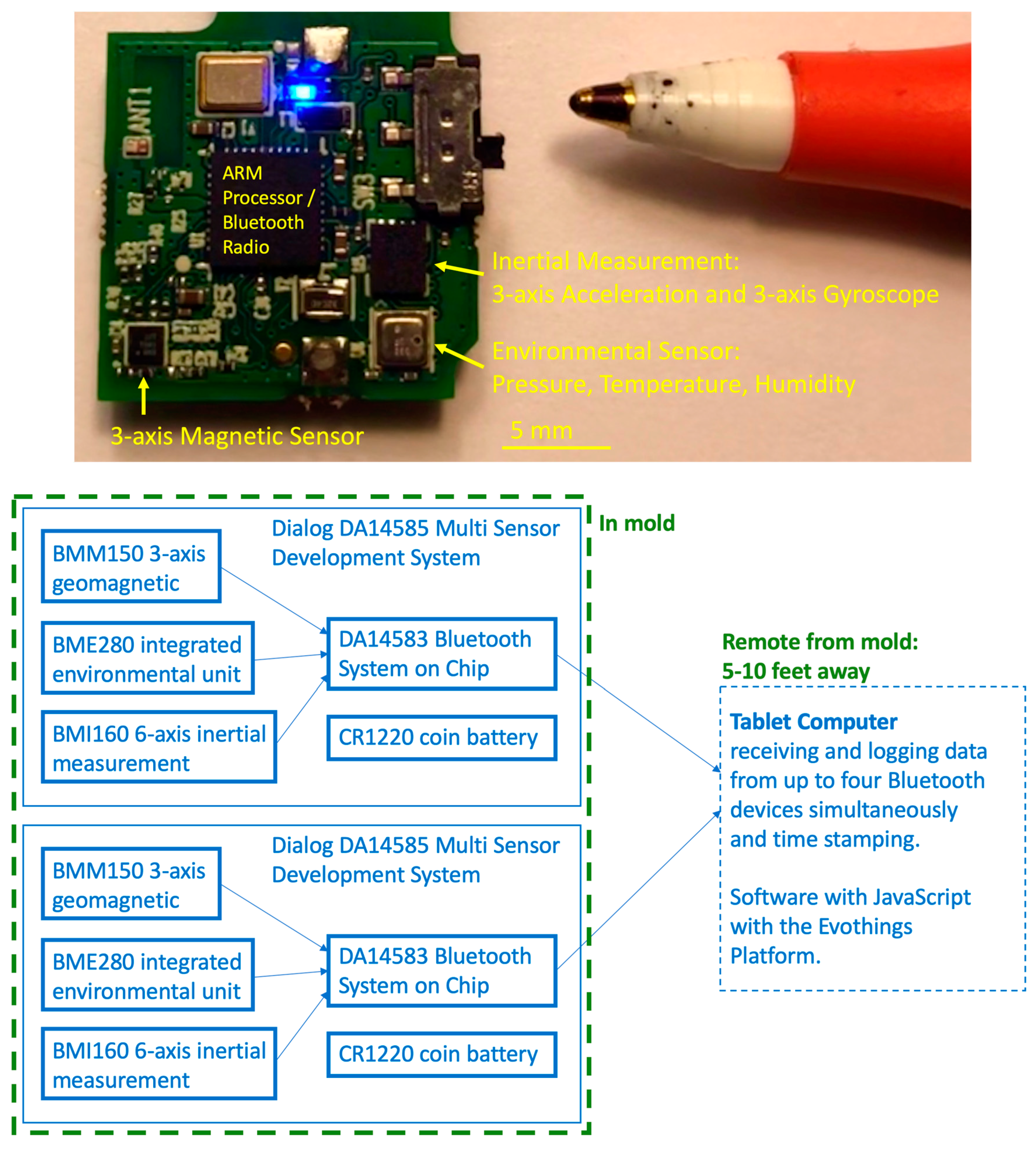
2.5. Magnetic Flux Sensors
3. Results
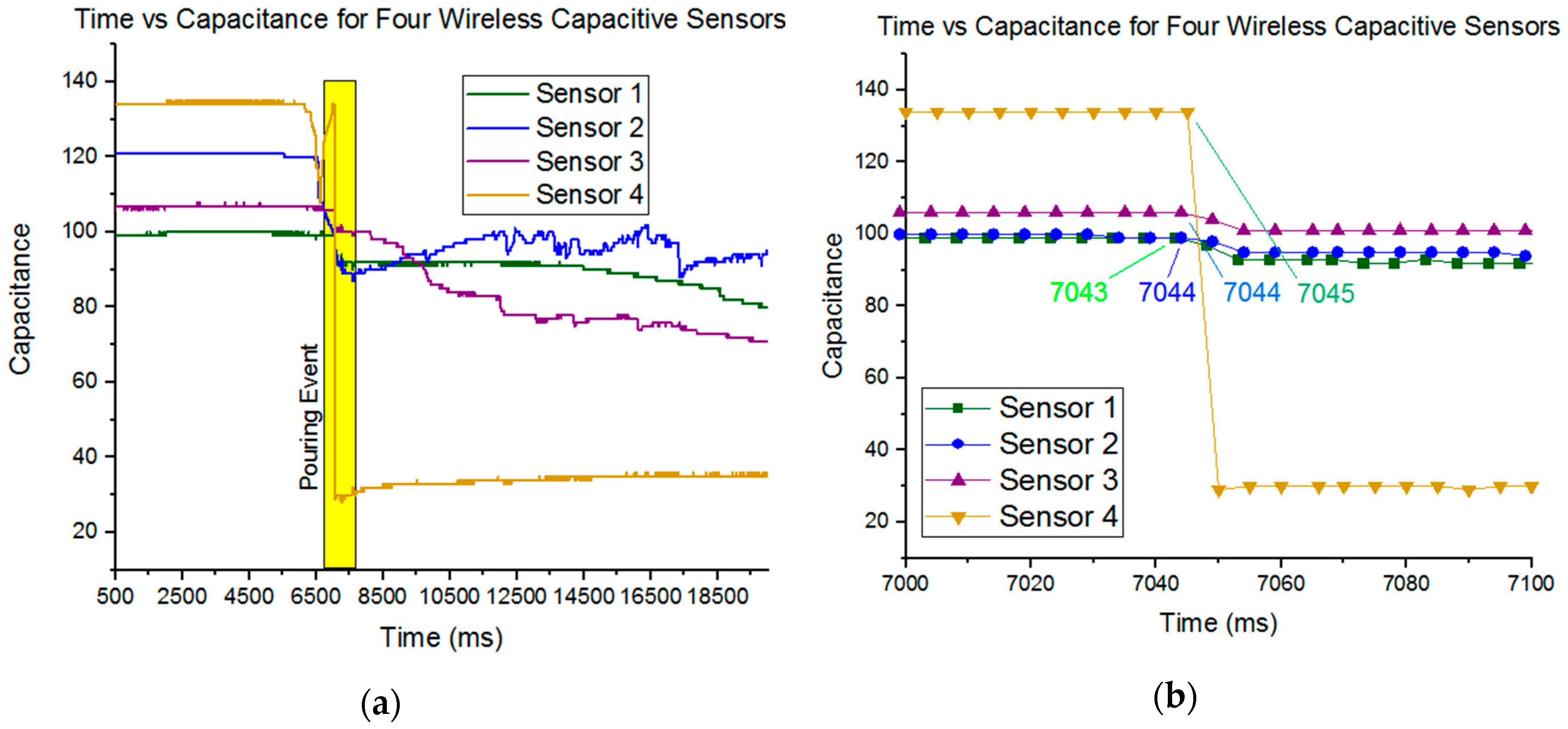
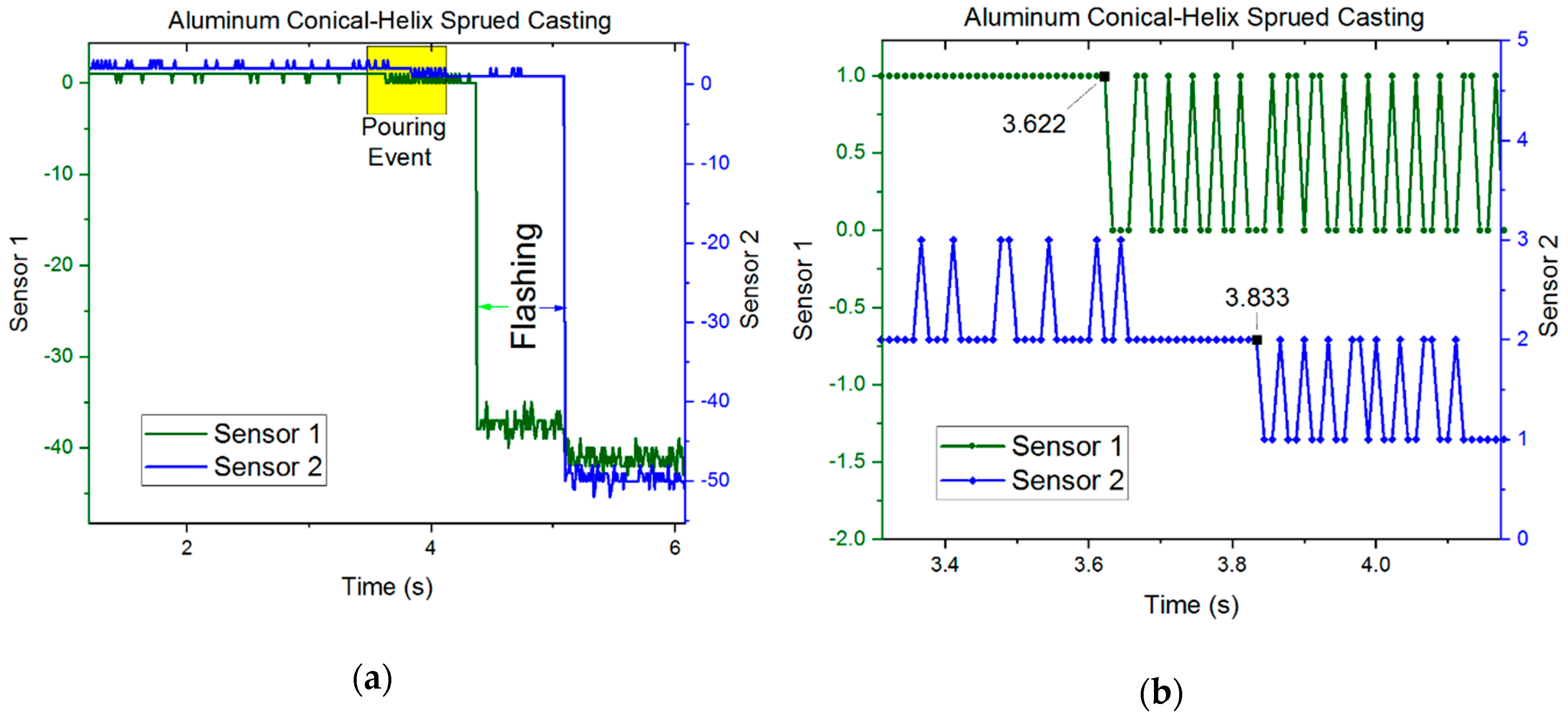
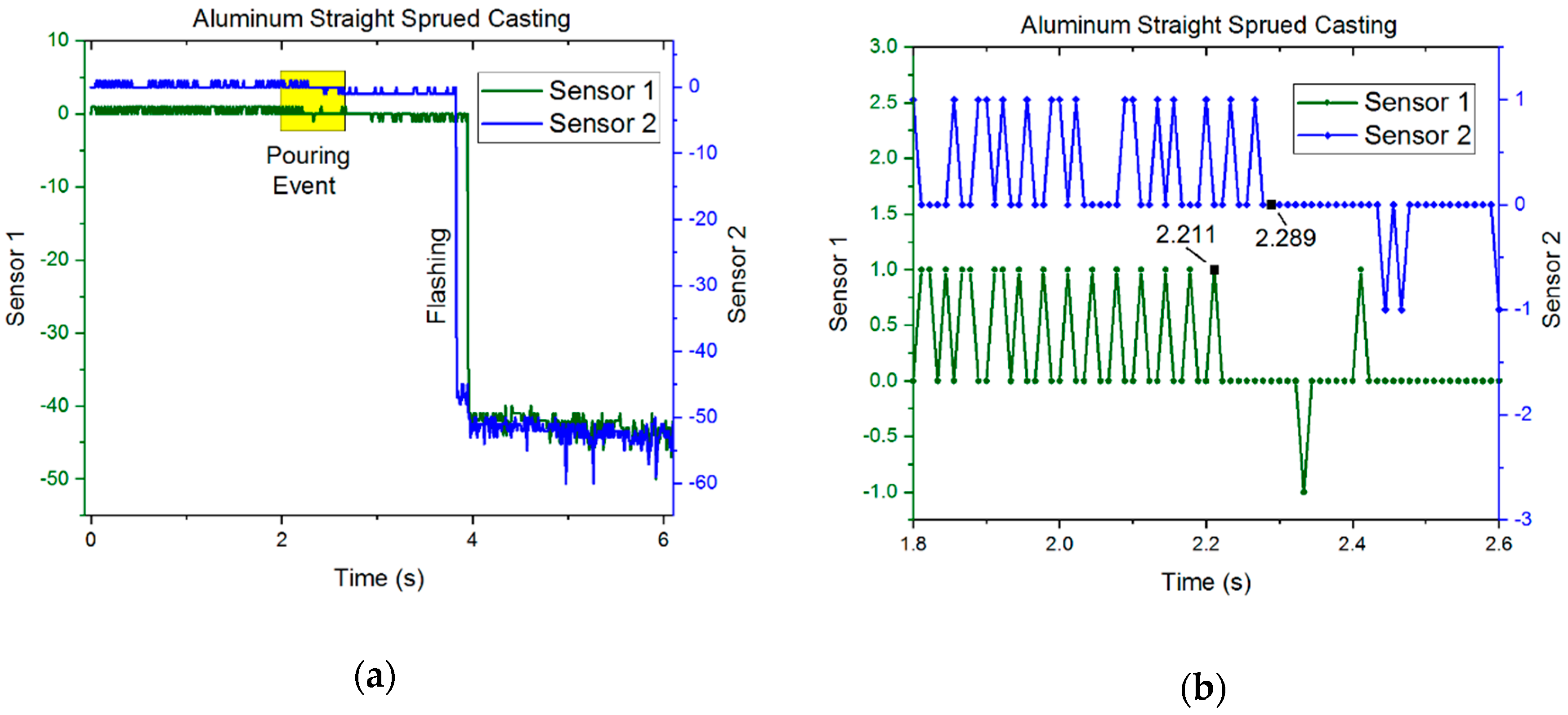
3.1. Results—Capacitive Sensors
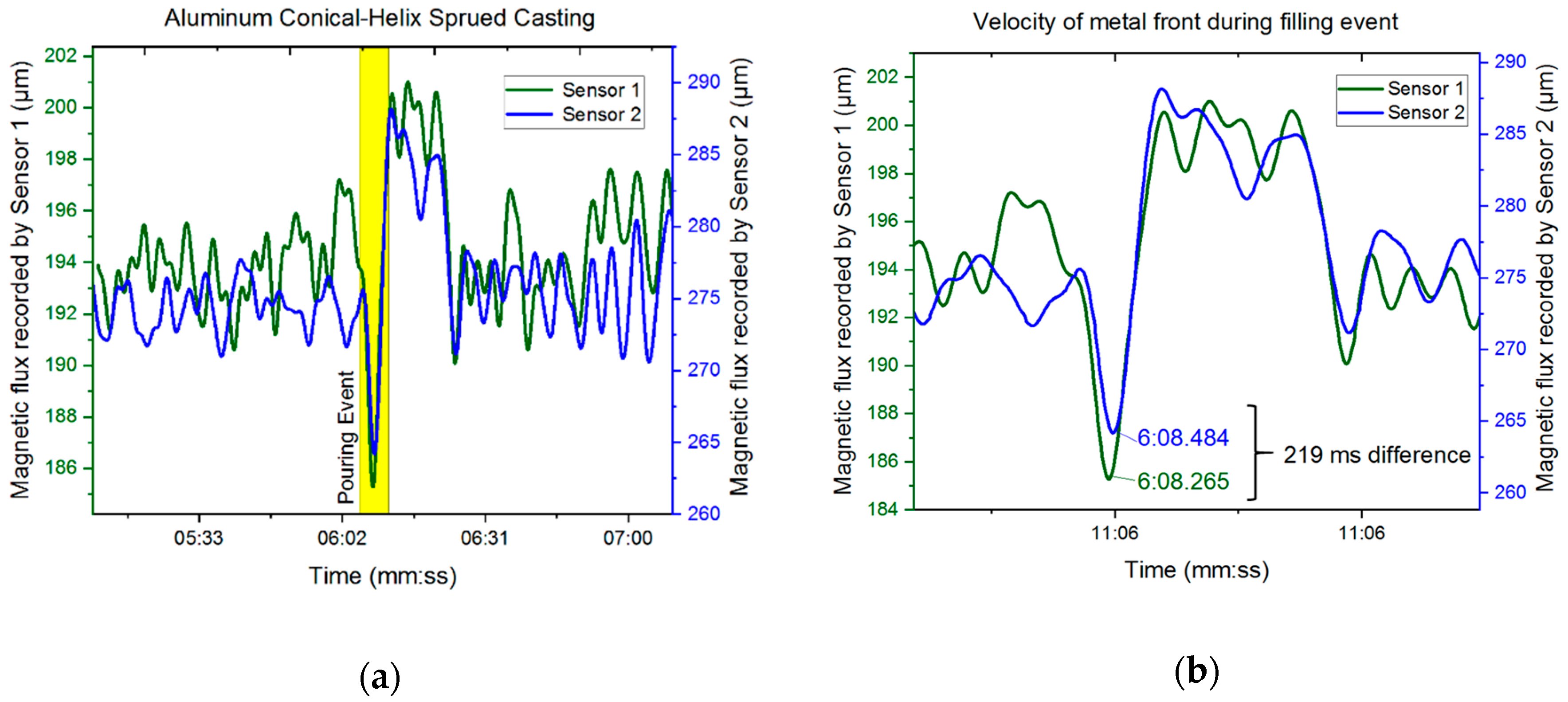
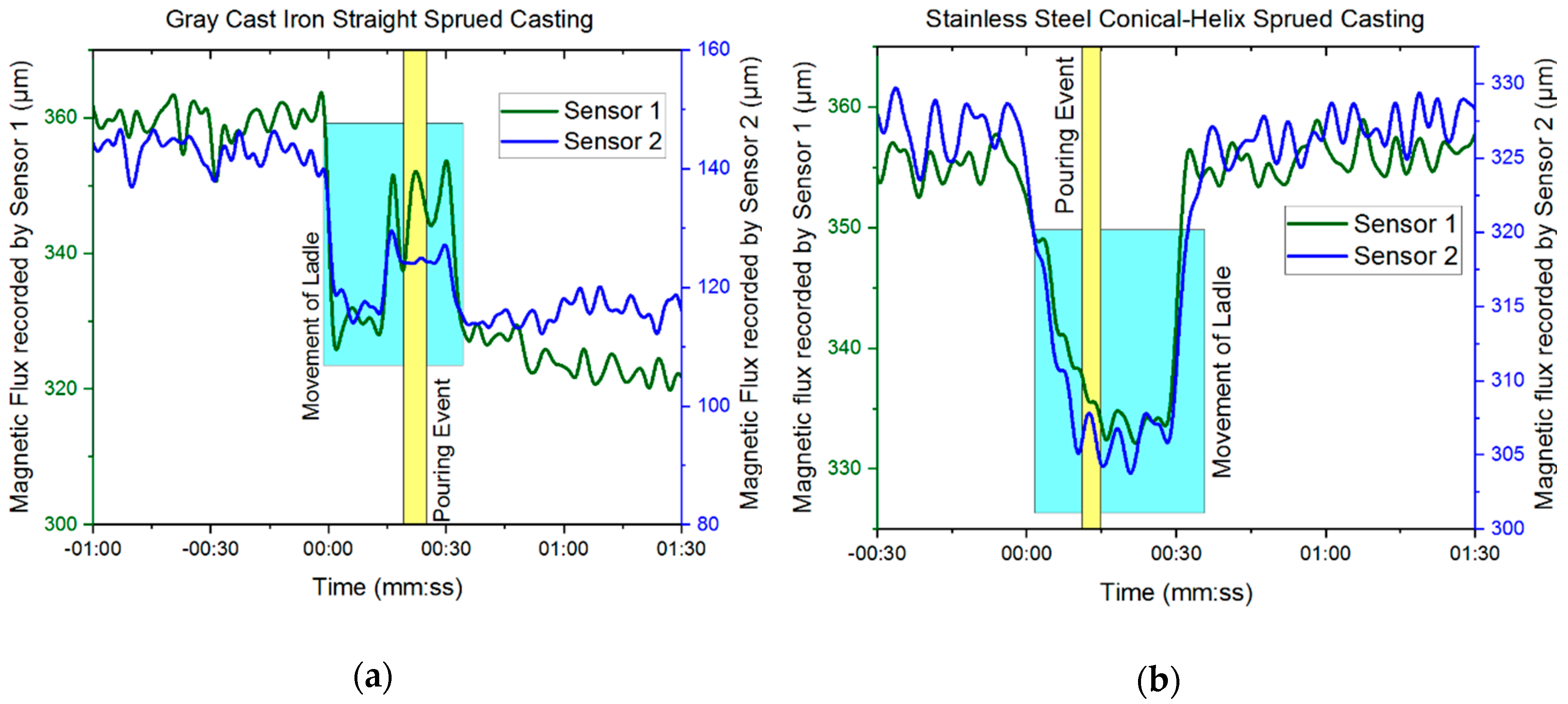
3.2. Results—Magnetic Flux Sensors
4. Discussions
5. Conclusions
- To the best of the authors’ knowledge, this is the first reported study on employing either capacitive or magnetic sensors to measure melt flow velocity in castings.
- The novel idea of employing capacitive sensing to detect conductive property of liquid metal flows to measure melt velocities results in close agreement to computational simulation (2–5%).
- Miniature IoT sensors can be easily embedded into sand molds for non-intrusive measurement of electromagnetic flux generated by liquid metal flows. By placing two such sensors separated by a known distance and detecting the time difference between the liquid metal travel from the first to the second sensor, the average velocity can be calculated.
- Dialog IoT sensors can operate for weeks on a small coin battery and could be inserted into the interior of 3D-printed sand molds and survive sufficiently long to collect data during the subsequent casting. Although changes in magnetic flux of the pouring event are captured by the magnetometer sensor, the current sampling rate limits its applications in metal flow monitoring.
- Results show that sensors are suitable for rapid experimental validation of various iterations for design optimization of gating systems.
- 3D sand-printing facilitates the rapid fabrication of complex molds and cores. Designers can take advantage of this design freedom to optimize gating systems, thereby decreasing turbulence of the liquid metal.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- ASTM52900-15 Standard Terminology for Additive Manufacturing—General Principles—Terminology. ASTM Int. 2015. [CrossRef]
- ExOne S-Max® Industrial Production Printers (2018). Available online: https://www.exone.com/Systems/Production-Printers/S-Max (accessed on 24 June 2019).
- Almaghariz, E.S.; Conner, B.P.; Lenner, L.; Gullapalli, R.; Manogharan, G.P.; Lamoncha, B.; Fang, M. Quantifying the role of part design complexity in using 3d sand printing for molds and cores. Int. J. Met. 2016, 10, 240–252. [Google Scholar] [CrossRef]
- Walker, J.; Harris, E.; Lynagh, C.; Beck, A.; Lonardo, R.; Vuksanovich, B.; Thiel, J.; Rogers, K.; Conner, B.; MacDonald, E. 3D Printed Smart Molds for Sand Casting. Int. J. Met. 2018, 12, 785–796. [Google Scholar] [CrossRef]
- Hodder, K.J.; Chalaturnyk, R.J. Bridging additive manufacturing and sand casting: Utilizing foundry sand. Addit. Manuf. 2019, 28, 649–660. [Google Scholar] [CrossRef]
- Wang, J.; Sama, S.R.; Manogharan, G. Re-Thinking Design Methodology for Castings: 3D Sand-Printing and Topology Optimization. Int. J. Met. 2019, 13, 2–17. [Google Scholar] [CrossRef]
- Sama, S.R.; Wang, J.; Manogharan, G. Non-conventional mold design for metal casting using 3D sand-printing. J. Manuf. Process. 2018, 34, 765–775. [Google Scholar] [CrossRef]
- Sama, S.R.; Badamo, T.; Lynch, P.; Manogharan, G. Novel sprue designs in metal casting via 3D sand-printing. Addit. Manuf. 2019, 25, 563–578. [Google Scholar] [CrossRef]
- Sama, S.R.; Badamo, T.; Manogharan, G. Case Studies on Integrating 3D Sand-Printing Technology into the Production Portfolio of a Sand-Casting Foundry. Int. J. Met. 2019, 1–13. [Google Scholar] [CrossRef]
- Campbell, J. Complete Casting Handbook: Metal Casting Processes, Metallurgy, Techniques and Design; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Dalquist, S.; Dalquist, S.; Gutowski, T. Life cycle analysis of conventional manufacturing techniques: Sand casting. In Proceedings of the ASME 2004 IMECE, Anaheim, CA, USA, 13–19 November 2004; pp. 631–641. [Google Scholar]
- Monroe, R. Porosity in Castings. ChemInform 2006, 37, 1–28. [Google Scholar] [CrossRef]
- Divandari, M.; Campbell, J. The Mechanism of Bubble Damage in Castings. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2017; pp. 49–64. [Google Scholar]
- Sun, Z.; Hu, H.; Chen, X. Numerical optimization of gating system parameters for a magnesium alloy casting with multiple performance characteristics. J. Mater. Process. Technol. 2008, 199, 256–264. [Google Scholar] [CrossRef]
- Modaresi, A.; Safikhani, A.; Noohi, A.M.S.; Hamidnezhad, N.; Maki, S.M. Gating system design and simulation of gray iron casting to eliminate oxide layers caused by turbulence. Int. J. Met. 2017, 11, 328–339. [Google Scholar] [CrossRef]
- Kor, J.; Chen, X.; Hu, H. Multi-objective optimal gating and riser design for metal-casting. In Proceedings of the 2009 IEEE Control Applications, (CCA) & Intelligent Control (ISIC), St. Petersburg, Russia, 8–10 July 2009; Volume 1, pp. 428–433. [Google Scholar]
- Esparza, C.E.; Guerrero-Mata, M.P.; Ríos-Mercado, R.Z. Optimal design of gating systems by gradient search methods. Comput. Mater. Sci. 2006, 36, 457–467. [Google Scholar] [CrossRef]
- Rabinovich, E. Mécanique Des Fluides. In Comptes Rendus (Doklady) de L’Académie Des Sciences de L’URSS; Académie des sciences de l’URSS: Moscow, Russia, 1946; Volume 54, p. 391. [Google Scholar]
- Swift, R.E.; Jackson, J.H.; Eastwood, L.W. A study of principles of gating. AFS Trans. 1949, 57, 76–88. [Google Scholar]
- Beckermann, C. Water Modeling of Steel Flow, Air Entrainment and Filtration. In Proceedings of the 46th SFSA Technical and Operating Conference, Chicago, IL, USA, 4–7 November 1992; pp. 1–18. [Google Scholar]
- Ruddle, R.W. The Running and Gating of Sand Casting; Institute of Metals: London, UK, 1956; pp. 19–29. [Google Scholar]
- Srinivasan, M.N.; Kondic, V. Progress in the hydraulics of gating. Br. Foundrym. 1963, 426–432. [Google Scholar]
- Jaiganesh, V.; Prakasan, K. Hydraulics, dimensional analysis and visualization of flow through unpressurized gating systems using water models. Eng. J. 2016, 20, 165–185. [Google Scholar] [CrossRef]
- Cuesta, J.A.; Morinigo, D.; de Castro, I.; Mozo, D. Water analogue experiments as an accurate simulation method of the filling of gravity castings. Trans. Am. Foundry Soc. 2006, 114, 137–150. [Google Scholar]
- Jain, S.C.; Beckermann, C. Analysis of Water Modeling of Air Entrainment. In Proceedings of the 48th SFSA Technical and Operating Conference, Chicago, IL, USA, 9–12 November 1994; pp. 1–18. [Google Scholar]
- Bate, C. Fundamental Study On 3D Sand Printed Molds: Metal Flow and Thermal Properties. Master’s Thesis, Pennsylvania State University, State College, PA, USA, 2019. [Google Scholar]
- Diószegi, A.; Björklind, T.; Diószegi, Z. Surface turbulence at flow of gray cast iron. Key Eng. Mater. 2011, 457, 422–427. [Google Scholar] [CrossRef]
- Bilal Naim Shaikh, M.; Ahmad, S.; Khan, A.; Ali, M. Optimization of Multi-Gate Systems in Casting Process: Experimental and Simulation Studies. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 404. [Google Scholar]
- Renukananda, K.H.; Ravi, B. Multi-Gate Systems in Casting Process: Comparative Study of Liquid Metal and Water Flow. Mater. Manuf. Process. 2016, 31, 1091–1101. [Google Scholar] [CrossRef]
- Ravi, B. Rapid Casting Development. In Proceedings of the Rapid Manufacturing Seminar, TEAMTECH 2006, Bangalore, India, 28 February–2 March 2006; pp. 1–11. [Google Scholar]
- Cleary, P.; Ha, J.; Alguine, V.; Nguyen, T. Flow Modelling in Casting Processes. Appl. Math. Model. 2002, 26, 171–190. [Google Scholar] [CrossRef]
- Orlenius, J.; Diószegi, A.; Diószegi, Z. Gas absorption in grey cast iron during mould filling. Int. J. Cast Met. Res. 2008, 21, 427–434. [Google Scholar] [CrossRef]
- Marashdeh, Q.; Fan, L.S.; Du, B.; Warsito, W. Electrical capacitance tomography—A perspective. Ind. Eng. Chem. Res. 2008, 47, 3708–3719. [Google Scholar] [CrossRef]
- Barve, Y.D.; Abdelrahman, M.A.; Deabes, W.A. Integrated technique for data transmission reliability in metal fill monitoring using wireless sensor network. In Proceedings of the ITNG2010—International Conference on Information Technology: New Generations, Las Vegas, NV, USA, 12–14 April 2010; pp. 903–907. [Google Scholar]
- Abdelrahman, M.; Arulanantham, J.P.; Dinwiddie, R.; Walford, G.; Vondra, F. Monitoring metal-fill in a lost foam casting process. ISA Trans. 2006, 45, 459–475. [Google Scholar] [CrossRef]
- Junga, P.K.R.; Abdelrahman, M.; Thurmer, C.; Deabes, W.A. Reliable metal-fill monitoring system using wireless sensor networks. In Proceedings of the International Conference on Information Technology: New Generation (ITNG 2008), Las Vegas, NV, USA, 7–9 April 2008; pp. 1284–1285. [Google Scholar]
- Dialog Semiconductor. SmartBond™ DA14583 IoT Sensor Development Kit. Available online: https://www.digikey.com/en/pdf/d/dialog-semiconductor/smartbond-da14583-iot (accessed on 24 June 2019).
- Walker, J.M.; Prokop, A.; Lynagh, C.; Vuksanovich, B.; Conner, B.; Rogers, K.; Thiel, J.; MacDonald, E. Real-time process monitoring of core shifts during metal casting with wireless sensing and 3D sand printing. Addit. Manuf. 2019, 27, 54–60. [Google Scholar] [CrossRef]
- Ricou, R.; Vives, C. Local velocity and mass transfer measurements in molten metals using an incorporated magnet probe. Int. J. Heat Mass Transf. 1982, 25, 1579–1588. [Google Scholar] [CrossRef]
- Vives, C.; Ricou, R.; Chambarel, A. Procedes et Dispositifs Pour Mesurer Localement des Vitesses Instantanees dun Fluid Electroconducteur, Notamxnent dun Metal Fondu. French Patent ANVAR 79/19818, 1979. [Google Scholar]
- Hayashi, H.; Becker, A.; Evans, J.W. Toward a probe for velocity measurement in molten metals at high temperatures. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 1999, 30, 623–630. [Google Scholar] [CrossRef]
- Suh, J.W.; Lee, Z.H. Melt velocity measurement by a noncontacting electromagnetic probe. Rev. Sci. Instrum. 2000, 71, 2241–2245. [Google Scholar] [CrossRef]
- Meyer, J.L.; Szekely, J.; Vives, C.; Ricou, R. A comprehensive study of the induced current, the electromagnetic force field, and the velocity field in a complex electromagnetically driven flow system. Metall. Trans. B 1987, 18, 529–538. [Google Scholar] [CrossRef]
- Mikrovas, A.C. Measurement of Magnitude of Velocity in High-Temperature Liquid Metals. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 1992. [Google Scholar]
- Molokov, S.; Moreau, R.; Moffat, K. (Eds.) Velocity measurement techniques for liquid metal flows. In Magnetohydrodynamics; Springer Science & Business Media: Berlin, Germany, 2007; pp. 275–294. [Google Scholar]
- Stefani, F.; Gerbeth, G. A contactless method for velocity reconstruction in electrically conducting fluids. Meas. Sci. Technol. 2000, 11, 758–765. [Google Scholar] [CrossRef]
- Takeda, Y. Development of an ultrasound velocity profile monitor. Nucl. Eng. Des. 1991, 126, 277–284. [Google Scholar] [CrossRef]
- Moreau, R. Local and instantaneous measurements in liquid metal MHD. In Proceedings of the Dynamic Flow Conference 1978 on Dynamic Measurements in Unsteady Flows 1978; Springer: Dordrecht, The Netherlands, 1978; pp. 65–79. [Google Scholar]
- Argyropoulos, S.A. Measuring velocity in high-temperature liquid metals: A review. Scand. J. Metall. 2001, 30, 273–285. [Google Scholar] [CrossRef]
- Platienks, I.A. Comparison of the Hot-Wire Anemometer and Conduction Methods for Mercury Measurements. Magnit. Gidrod. 1971, 7, 197. [Google Scholar]
- Lee, H.C.; Evans, J.W.; Vivès, C. Velocity measurement in Wood’s metal using an incorporated magnet probe. Metall. Trans. B 1984, 15, 734–736. [Google Scholar] [CrossRef]
- Eckert, S.; Witke, W.; Gerbeth, G. A new mechano-optical technique to measure local velocities in opaque fluids. Flow Meas. Instrum. 2000, 11, 71–78. [Google Scholar] [CrossRef]
- Iguchi, M.; Takeuchi, M.; Kawabata, H.; Ebina, K.; Morita, Z.I. Development of a Kármán vortex probe for measuring the velocity of molten metal flow. Mater. Trans. JIM 1994, 35, 716–721. [Google Scholar] [CrossRef][Green Version]
- Wukovich, N.; Metevelis, G. Gating: The Foundryman’s Dilemma or Fifty Years of Data and Still Asking How? In Proceedings of the 93 rd AFS Casting Congress, San Antonio, TX, USA, 7–11 May 1989. [Google Scholar]
- Muenprasertdee, P. Solidification Modeling of Iron Castings Using SOLIDCast. Master’s Thesis, West Virginia University, Morgantown, WV, USA, 2007. [Google Scholar]
- Albus, Z. Enabling Single Touch Capacitive Sensing with MSP430. In Proceedings of the MSP430 Advanced Technical Conference, Dallas, TX, USA, 7–9 November 2006; p. 47. [Google Scholar]
- Sensortec, B. Data Sheet BMM150 Geomagnetic Sensor. 2013. Available online: https://ae-bst.resource.bosch.com/media/_tech/media/datasheets/BST-BMM150-DS001.pdf (accessed on 24 June 2019).


| Si | Cu | Mg | Fe | Mn | Zn |
|---|---|---|---|---|---|
| 5.5–6.5 | 3–4 | <0.1 | <0.8 | <0.5 | <1 |
| Velocity | SSC | CHSC |
|---|---|---|
| At Sprue Exit | 1.45 | 0.64 |
| Near Ingate | 1.23 | 0.34 |
| Average | 1.34 | 0.49 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sama, S.R.; MacDonald, E.; Voigt, R.; Manogharan, G. Measurement of Metal Velocity in Sand Casting during Mold Filling. Metals 2019, 9, 1079. https://doi.org/10.3390/met9101079
Sama SR, MacDonald E, Voigt R, Manogharan G. Measurement of Metal Velocity in Sand Casting during Mold Filling. Metals. 2019; 9(10):1079. https://doi.org/10.3390/met9101079
Chicago/Turabian StyleSama, Santosh Reddy, Eric MacDonald, Robert Voigt, and Guha Manogharan. 2019. "Measurement of Metal Velocity in Sand Casting during Mold Filling" Metals 9, no. 10: 1079. https://doi.org/10.3390/met9101079
APA StyleSama, S. R., MacDonald, E., Voigt, R., & Manogharan, G. (2019). Measurement of Metal Velocity in Sand Casting during Mold Filling. Metals, 9(10), 1079. https://doi.org/10.3390/met9101079






