Abstract
Estimating the effect of graphene oxide (GO) reinforcement on overall properties of aluminum (Al) matrix composites experimentally is time-consuming and involves high manufacturing costs and sophisticated characterizations. An attempt was made in this paper to predict the mechanical properties of GO/Al composites by using a micromechanical finite element approach. The materials used for prediction included monolayer and multilayer GO layers distributed uniformly on the spherical Al matrix particles. The estimation was done by assuming that a representative volumetric element (RVE) represents the composite structure, and reinforcement and matrix were modeled as continuum. The load transfer between the GO reinforcement and Al was modeled using joint elements that connect the two materials. The numerical results from the finite element model were compared with Voigt model and experimental results from the GO/Al composites produced at optimized process parameters. A good agreement of numerical results with the theoretical models was noted. The load-bearing capacity of the Al matrix increased with the addition of GO layers, however, Young’s modulus of the GO/Al composites decreased with an increase in the number of layers from monolayer to 5 layers. The numerical results presented in this paper have demonstrated the applicability of the current approach for predicting the overall properties of composites.
1. Introduction
Graphene, a 2D wonder material, has drawn attention of many researchers globally due to its exceptional properties. The extraordinary properties of graphene include Young’s modulus of 1 Tpa, intrinsic strength of 130 GPa [1,2] which makes it an ideal candidate in structural applications. The unique combination of high strength and low weight [3] and an additional feature of providing strong adhesion between filler and matrix [4] makes graphene a promising material in hybrid composite systems. Graphene and its derivatives were reported to be successful reinforcement materials in literature [5] and had been applied to both metal and polymer matrices [6]. The high strength and stiffness of graphene have led to the development of new categories of advanced functional materials that can be used in energy storage and sensor applications. To use full potential of graphene as reinforcement in composite materials, it is necessary to obtain good dispersion and at the same time graphene should be of monolayer.
Numerous experimental efforts have been put forward to investigate the effect of graphene reinforcement onto the metallic matrices and thus producing a composite with better mechanical performance than the base materials. Liu et al. [7] have managed to embed graphene nanosheets (GNS) into Al matrix through powder metallurgy. This resulted in an increase of 43% in hardness compared to base Al for 0.15 wt.% of GNS reinforcement on Al matrix. Li et al. [8] have reported formation of aluminium carbide (Al4C3) in GNS/Al composites fabricated through high energy ball milling process. This has resulted in reduction in overall mechanical properties of the composites and dislocations at interface regions were also reported. To enhance the mechanical performance of the composites it is necessary to provide an efficient load transfer between matrix and reinforcement. Rashad et al. [9] have reported Orowan looping in 0.3 wt.% graphene nanoplatelet (GNP)/Al composite that resulted in 11.8% increase in hardness. Guybuz et al. [10] have produced GNP/Al composites at various wt.% of GNP reinforcement. It was reported that higher wt.% of GNP reinforcement on Al led to the reduction in mechanical properties of the composite. This was due to the weak contact area between the GNP and Al particles, which increased the porosity in the composites. The ultimate tensile strength (UTS) of Al was increased by 62% when reinforced with 0.3 wt.% of reduced graphene oxide (rGO) but this increase is only 20% of the full potential of graphene. This was due to the weak interfacial bonding between rGO and Al and incomplete reduction of GO [11]. To investigate the effect of GO on Al without reduction of GO, Bhagya et al. [12] have tried to fabricate GO/Al composites through powder metallurgy and have reported an increase of 28% in Vickers hardness compared to Al when reinforced with 0.2 wt.% of GO.
Trying not only to produce composites with better mechanical performance but also to predict the mechanical behavior of composites at various process parameters have become one of the key research areas recently. The design and embedding of graphene sheets into the metallic matrices have resulted in several practical applications and have called for the need to develop theoretical methods to accurately predict mechanical performance. Atomic modeling using molecular dynamics was used by Pendele et al. [13] to predict the mechanical behavior of graphene composites. They reported an increase of 23% in Young’s moduli with 7.67% of graphene reinforcement. Multiscale modeling approach was used by Montazeri et al. [14] to predict the effect of inclusions of graphene sheets in polymer matrix composites (PMC) on mechanical performance of graphene nanocomposites. Chandra et al. [15] have reported a similar approach to predict the tensile properties of graphene nanocomposites. Their model has displayed the ability to predict nonlinear behavior and failure mechanisms in PMCs. Spanos et al. [16] have proposed a multiscale finite element model to predict the mechanical properties of graphene nanocomposites. In this model, matrix was modeled as continuum and reinforcement were modeled based on atomic structure of graphene, and the effect of size of graphene sheets on elastic mechanical properties of graphene-based composites was successfully investigated. The delamination and debonding phenomenon in graphene nanocomposites were investigated by Vissarion et al. [17]. It was reported that the stronger bonds led to the increase in mechanical strength of the composites owing to the cohesive bond between the matrix and reinforcement. The reduction in stiffness of the nanocomposite was reported which caused due to the wrinkles on graphene sheets which can be altered by the waviness amplitude of the graphene sheets.
In the present paper, a computational finite element model based on micromechanical theory was used to evaluate the effect of graphene reinforcement on mechanical performance of GO/Al nanocomposite. High dependence of graphene on its volume percentage and number of graphene layers were considered as process parameters in modeling of the composite. The three-dimensional modeling of composite involved considering continuum approach for both matrix (Al) and reinforcement (GO), and joint elements were used to create bonding between Al and GO. The macroscopic representation of Al and GO in the composite were considered to reduce the computational cost and to increase computational efficiency. The previous studies in the literature reported the use of similar technique as reported in this paper for carbon nanotubes (CNTs) and pristine graphene [18]. According to the knowledge of the authors, this is the first time that this modeling was used for predicting the mechanical performance of GO-reinforced Al matrix composites. The predicted results were compared with the experimental and analytical modeling from literature, and the ability of GO as reinforcement was also evaluated.
2. Materials and Methods
In this section, the finite element (FE) modeling of GO/Al composite is described, and the representative volumetric element (RVE) based on micromechanical approach modeling is used. The matrix and reinforcement materials were modeled using the mechanical properties at the macroscopic scale.
2.1. Finite Element Modeling of GO/Al Composite
FE modeling and analysis of GO/Al composite was performed to investigate the effect of GO existence in Al matrix, number of GO layers, and % of Al particles coated with GO on performance of GO/Al composites. Structural analysis was performed on the composites to predict the stress distribution. The number of GO layers obtained from micro Raman investigation are used to develop FE model in-line with experimental investigations [12]. The volume fraction of the GO reinforcement was calculated according to the percentage of GO coated onto the Al particles. Due to the complexity of the model, GO reinforced Al particles and joint elements were modeled in Hyper MeshTM followed by importing model to ANSYS 16.2 for further investigations. Al particles of 35 µm and GO layers of 0.134 nm [19] were modeled in a cube of 140 µm × 140 µm × 140µm. The contacts/connections between Al particles and GO sheets were modeled using joint elements; all degrees of freedom were constrained at 0 and a compressive static load of 2.5 N is applied in Y-direction. The properties of the materials used in current study are given in Table 1. The Young’s modulus values considered in the modeling were much similar to the values reported in the literature; however, the Poisson’s ratio of the graphene sheets varied in between 0.06 and 0.45 [20,21,22] and there was no proper experimental result backup to claim the value of Poisson’s ratio [23]. The value considered in current studies was adopted from the data sheet (MSDS) of GO received from Graphenea, Spain.

Table 1.
Properties of materials used in graphene oxide (GO)/Al composite modeling.
2.1.1. Assumptions
While modeling the GO/Al composites in ANSYS, the following assumptions were applied:
- The Al particles were considered spherical and equisized
- GO reinforcement is uniformly distributed on to the Al particles
- No interfacial compounds formed in between GO and Al particles
- The matrix and reinforcement are isotropic materials
- Effect of porosity is neglected
2.1.2. Boundary Conditions
While modeling the GO/Al composites in ANSYS, the following boundary conditions were applied:
- The displacement degrees of freedom are constrained at 0.Ux = 0 at X = 0, Uy = 0 at Y = 0, and Uz = 0 at Z = 0
- The rotational degrees of freedom are constrained at 0.ωx = 0 at X = 0, ωy = 0 at Y = 0, and ωz = 0 at Z = 0
- A compressive load of 2.5 N is applied in Y-direction at Y = 140 µm
- Fixed joints within built constrained equations is used as a contact in between the particles
The FE model of GO/Al composite with applied boundary conditions is shown in Figure 1.
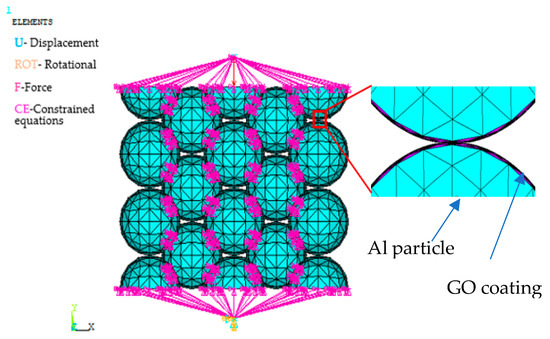
Figure 1.
Schematic representation of finite element (FE) model of GO/Al composite.
2.1.3. Mesh Convergence of GO/Al Composite
FE model of GO/Al composites developed in current research work is investigated for grid independence by varying the element size. The complexity of the current model, i.e., element size, is recorded against the response, i.e., stress and the convergence tests are performed on both pure Al particles and GO reinforced Al. As shown in Figure 2a, it can be noted that the FE model without GO layers is converged at 0.2 µm of element size. FE model of GO/Al composite is converged at element size of 0.2 µm for Al particles and element size of 0.05 nm for GO coating (shown in Figure 2b). The difference in stress value obtained from the model for element size 0.2 and 0.1 for Al particles is around 1%. The difference in stress value obtained for GO coating in GO/Al model for element size 0.01 nm and 0.005 nm is around 2.5%. The difference in stress values in both cases is under 5%. Hence, the convergence results are in acceptability range and the model can be extended for further analysis.
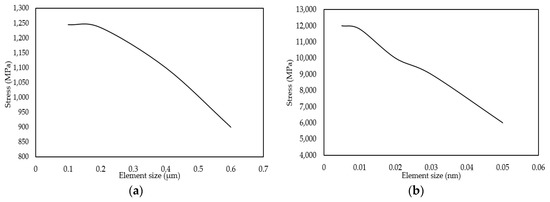
Figure 2.
Convergence plots of FE model: (a) No GO layers on Al particles; (b) Al particles covered with GO layer.
2.2. Analytical Modeling of GO/Al Composite
The effective properties of the composites can be estimated by the rule of mixtures (ROM), which is one of the intuitive and simple methods to find composite properties using its constituents. The Voigt model was applied to calculate the stress response for comparison with the FE and experimental results. Figure 3 shows the schematic representation of GO/Al composites. Based on the volume percentage of the GO reinforcement, the coating thickness varies in terms of number of layers, for instance, for 0.1% of GO, the Al particles will be covered with 3 layers of GO (in accordance with the experimental observation [12]). The analytical modeling of the composites was performed at various volume fraction of the reinforcement of 0.05, 0.15, 0.2, and 0.5. Young’s moduli of the materials used are given in Table 1. The effective Young’s modulus of the GO/Al composites at various process parameters can be calculated using the Equations (1)–(3) [24].
where, is the effective stress of composite; , are the volume fractions of reinforcement and matrix; , are the flow stresses of reinforcement and matrix; , , are the Young’s moduli of composite, reinforcement, and matrix, respectively. is the volume fraction of GO and is calculated by Equation (4).
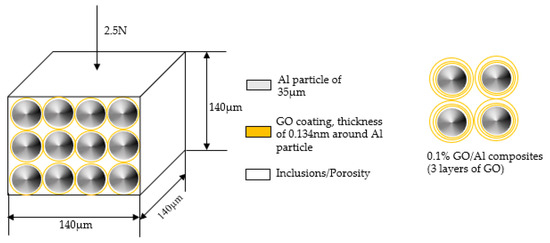
Figure 3.
Representation of GO/Al composite with monolayer of GO reinforcement (40% porosity) and 3 layers of GO reinforcement (32% porosity) on Al particles.
While working with the composites it is important to consider various strengthening mechanisms to obtain maximum strength of the composite. The strengthening efficiency of the composite is determined by the load-bearing capacity of the reinforcement and interruption of plastic deformation of matrix by the addition of reinforcement [25]. The strengthening of the metal matrix composites (MMC) can be influenced by microstructural changes, dislocation mechanisms, and variation in thermal expansion coefficient, etc. In the current article, Taylor strengthening caused by mismatch in modulus between matrix, reinforcement, and strengthening due to load-bearing of nano-reinforcement are considered in the analytical model. For the comparison purposes, the yield strength of the composites at various volume fraction of GO reinforcement was estimated by considering the strengthening mechanism. The Equations (5)–(7) noted below used in the analytical model to calculate the strength of GO/Al composite were taken from previous work [26,27]. In the current analytical modeling, Hall–Petch effect and Forest strengthening were neglected as there are not sufficient results from experiments for correlation; these mechanisms will be considered in the extension of current work. For comparison, the yield strength of the FE model was estimated using the stress–strain graphs at each volume fraction of the reinforcement.
where, is the strengthening contribution due to load-bearing, is the volume percentage of GO reinforcement, is the 0.2% yield strength of the composite, is the strengthening due to elastic modulus mismatch (Taylor strengthening), is the proportionality constant, is the shear modulus of pure Al, b is the Burges vector, and is the volume fraction of GO.
3. Results
3.1. Effect of GO Addition on Stress Distribution and Young’s Modulus of GO/Al Composites
The stress distribution in the GO/Al composites without and with GO layer reinforcement on Al particles is shown in Figure 4a,b, respectively. It can be noted from the stress profiles that the stress is distributed along the particles without any obstruction. This is due to the existence of joints between the particles that provided a perfect bond. It can also be noted that the maximum stress experienced by the Al particles without GO reinforcement, i.e., 1281 MPa, is lower than that of the maximum stress experienced by Al particles reinforced with GO layers, i.e., 12,042.4 MPa. This is due to the high load-bearing capacity of GO layers compared to Al particles that protect Al particles by consuming the maximum load in the applied load. This observation is in-line with the ROM which states that the strength of the material increases with the addition of reinforcement.

Figure 4.
Representation of GO/Al composite with monolayer of GO reinforcement on Al particles: (a) Stress contour of Al particles without GO reinforcement; (b) Stress contour of GO/Al composite with Al particles coated with monolayer GO.
In Figure 5, the comparison of proposed model with the existing theory, ROM, and experimental studies [8,11,12,25,28,29] is presented for the reasons of validation and verification. It can be noted from the graph that Young’s modulus obtained from simulations is ~3 times higher than the experimental values. It can also be noted that the developed composite model follows similar trend as the analytical model, however, when compared with the experimental values, an opposite trend can be observed. To gain more confidence on the developed model, the measured yield stress of the composites using experimental data [12] was compared against yield stress obtained from both analytical modeling and FE modeling. The yield stress in the analytical model is calculated using Equations (5)–(7) and the yield stress in the FE model was calculated from the compressive stress–strain graphs. It can be noted that there is a variation in stress values in experimental and analytical model as the experiments carried out involve many aspects such as contamination, humid conditions, etc. However, the yield stress follows a similar trend in both analytical and FE model which can imply that the FE model can be further used and refined to meet the practical conditions. It is evident from Figure 5 that it is highly difficult to achieve consistent results during experimental studies at high volume fraction of graphene reinforcement as it involves factors such as mixing parameters of matrix and reinforcement, purity of raw materials, and production techniques used to produce composites. The mixing parameters are considered to be crucial which vary depending on the method of mixing and volume fraction of the reinforcement. The variation of the experimental process parameters was not taken into account in the model reported in the present paper, which is expected to have led to the variation between the experimental and simulation results. For instance, the experimental studies have shown that at higher volume fractions, the graphene tends to agglomerate, leading to a reduction in strength which was not accommodated in model and hence an increasing trend was reported from the simulation. It can be seen that the model reports an ideal case for the GO/Al composites which has followed a similar trend with the analytical theory. This means that the boundary conditions and the mesh employed are acceptable and the ideal case values can be used as benchmarking while working with the GO/Al composites, irrespective of the processing methods.
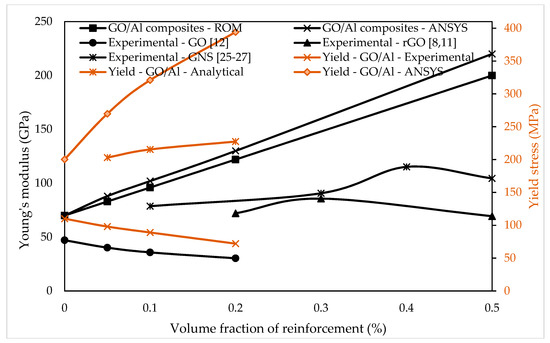
Figure 5.
Comparison of Young’s modulus of GO/Al composite developed in ANSYS with ROM and experimental studies at different volume fractions and comparison of Yield stress of GO/Al composite estimated in analytical modeling with experimental studies.
Many models such as Clyne model, Zhang and Chen model, modified Clyne model, and summation models are available to find the cumulative effect of strengthening mechanisms on the yield strength of the composites. In the current study, pure Al was reinforced with GO at various vol% of GO, and the contribution of Hall–Petch and Forest strengthening were not considered due to lack of available experimental data, these mechanisms will be considered in future studies. The individual contribution of strengthening mechanisms and summation was consolidated in Table 2 and compared against the yield strength obtained from experimental and FE model. Among the mechanisms, Taylor strengthening has shown a noticeable effect compared to load-bearing as the volume percentage of GO reinforcement is low. The effect of load-bearing strengthening is negligible. However, from the summation of the strengthening mechanism, it can be noted that the yield strength of the GO/Al composites has increased, and the strength is expected to vary with the consideration of Forest strengthening and Hall–Petch. The reason behind this expectation is that mismatch of coefficient of thermal expansion resulted due to the processing of the composites will result in dislocations and contribute to the increase in dislocation density and, hence, increase in strength of the composite.

Table 2.
Comparison of yield stress obtained from experimental, analytical, and FE model.
3.2. Effect of GO Layers on Stress Distribution of GO/Al Composites
The effect of addition of GO layers in terms of number of GO layers coated on Al particles was indirectly examined through micro Raman analysis. This was used as one of the processing parameters in the simulation studies. Figure 6a shows the stress contour profiles of GO/Al composites reinforced with 5 layers of GO on Al particles. Figure 6b shows the stress profile in corresponding Al particles. It can be noted from the profiles that the addition of GO to the Al particles have enhanced the strength of GO/Al composite compared to the pristine Al.
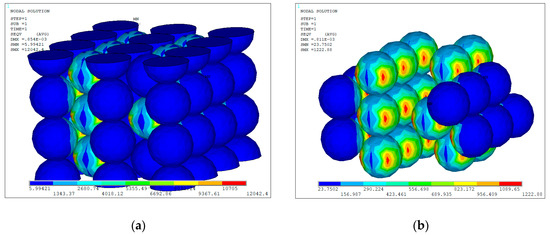
Figure 6.
Stress contours of 5 layer GO reinforced Al composite: (a) 5 layered GO/Al; (b) Corresponding Al particles.
The stress distribution pattern was not affected by the variation of number of GO layers but the maximum stress experienced by the composite varied with variation in number of GO layers. Figure 7 shows the maximum stress values obtained in GO/Al composites at various processing conditions. It can be noted from the figure that the stress experienced by Al particles reduced whereas the stress experienced by coating, i.e., GO coated Al particles, increased with addition of monolayer GO. However, further increase in number of GO layers to 2 and 5 has resulted in reduction in maximum stress.
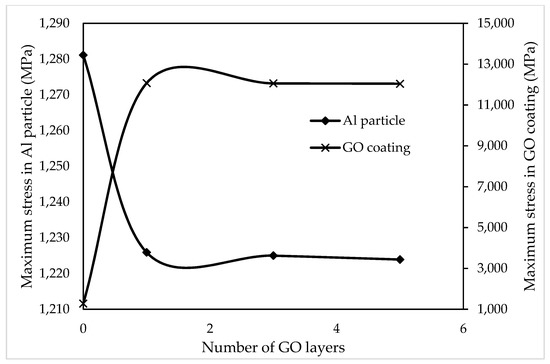
Figure 7.
Comparison of maximum stress in GO/Al composites at different number of GO layers.
3.3. Effect of GO Layers on Young’s Modulus of GO/Al Composites
The GO/Al composite model developed in the current work is designed in such a way that it assumes a stable Young’s modulus for the matrix material. Monolayer, 2 layers, and 5 layers of GO sheets with same dimensions were used as reinforcement in nanocomposite. For a range of volume percentage of GO reinforcement, the results are consolidated in Figure 8. The increase in Young’s modulus is higher when monolayer GO is used as reinforcement, it can also be observed that the increase is with increase in volume fraction of GO.
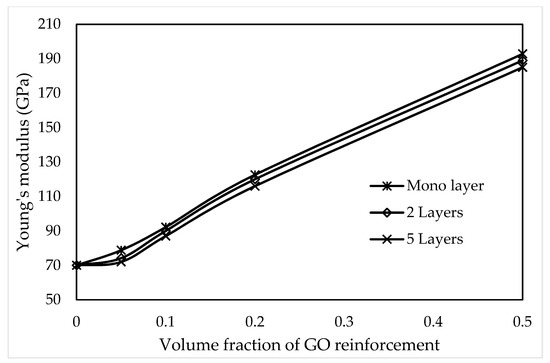
Figure 8.
Young’s modulus of GO/Al composites at different numbers of GO layers.
4. Discussion
The results obtained in the current study show a good convergence with the analytical models. The comparison of proposed model with ROM presented in the current research has shown an increase in Young’s modulus as the concentration of GO increases. There is a linear increase in all cases reported in current study except the experimental observations [12], where the agglomeration of GO in Al matrix has prompted the reduction in properties. The agglomeration phenomena in graphene reinforced Al composites at high volume fraction of graphene was reported by many researchers that led to the reduction in overall performance of the composites [10,30,31]. While modeling the GO/Al composites, the authors have considered the experimental observations reported by previous work and recorded from the production of GO/Al composites using liquid infiltration technique followed by powder metallurgical route [12]. Average particle size of 35 µm was recorded in SEM micrographs, this was considered in current modeling. From recorded SEM micrographs and elemental analysis using EDX at multiple locations of the GO/Al composites, authors have noted that GO was present in the Al matrix [12]. The Young’s modulus of GO/Al composite modeled in current work at perfect bonding, with GO reinforcement has exceeded the ROM, this phenomenon was recorded in similar work reported in the literature [15,32]. This has happened since the ROM is a simplified model for property estimation of composites which does not account for the bonding between matrix and reinforcement and size of the particles. The overestimate of the properties in current research represents the upper bound value of the composite at that concerning processing condition which can be used for comparison purposes.
The GO/Al composite reported in this paper was modeled by considering an assumption that there is strong bonding between GO and Al particles which has a strength equal to the strength of GO. However, the size of the GO sheet reinforcement on Al particles will also affect the mechanical properties of the composite [16,18]; in present scenario, the stiffness of the interface and size of the GO sheet were kept constant and volume fraction is varied. A soft interface leads to a weak composite and the hard interface leads to a stiff composite whereas the mediate interface is desirable to obtain optimum stiffness of the overall composite [16]. In the present scenario, the bonding between the GO and Al was kept at a mediate value, i.e., to the strength of GO which has resulted in better Young’s modulus than the value obtained with ROM.
The size of the RVE is another factor that was kept constant in present case. It was recorded from the previous studies that the variation in RVE size which was caused by the variation in dimensions of matrix and reinforcement affects the performance of the composite [33]. The optimum stiffness of the GO/Al composites in present modeling work is a result of wrinkle-free GO sheets. It was reported in the literature that the wrinkles on the graphene sheets will result in a decrease in stiffness of the composite due to the variation in amplitude of the sheets [17]. The orientation of graphene sheets is one of the factors that affect the overall performance of the composites, and the spatial orientation of GO flakes was studied by using orientation distribution function (ODF) [34] and polarized Raman spectroscopy [35]. However, the modeling results reported in the literature were not directly related to the quantitative analysis of orientation of graphene sheets and, hence, the cumulative effect of spatial orientation of sheets on mechanical properties of the composite was not derived.
The stiffness of the GO/Al composite model developed in current research work increases with decrease in number of layers of GO sheet reinforcement on Al particles. The slight variation in values was recorded due to the delamination between the GO sheets upon the application of load. The effect of orientation of GO sheets and variation of bond strength on mechanical properties of Al matrix composite is the future prospect of this work.
5. Conclusions
To develop an efficient computational model to predict the elastic properties of the GO/Al composite is a fundamental issue and motivation behind the current research work. In this study, the 3D micromechanical FE model was developed to predict the properties of GO/Al composite at various processing conditions. Macroscopic properties were used to describe matrix and reinforcement and joint elements to describe bonding. The effect of GO reinforcement on mechanical performance of Al particles is revealed and the dependence of existence of number of layers is considered. The model developed is attractive due to the avoidance of complex steps involved in detailed representation of nanostructure of matrix and reinforcement and significant reduction of experimental efforts, computational cost, and computational time. The results revealed the dependence of existence of GO reinforcement, volume fraction of GO, and number of layers of GO on elastic properties of GO/Al composite. The model developed can be generalized for the use of various matrix and reinforcement materials at various processing conditions.
Author Contributions
The methodology, validation, writing, and data analysis were conducted by B.L.D. Project administration, review, editing, and supervision were provided by S.N. and D.B.
Funding
The work reported in this paper is funded by City, University of London and ERASMUS+ traineeship 2016-1-UK01-KA103-023552. This research is partially supported by a research grant from Science Foundation Ireland (SFI) under Grant Number 16/RC/3872 and is cofunded under the European Regional Development Fund.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, C.G.; Park, S.; Ruoff, R.S.; Dodabalapur, A. Integration of reduced graphene oxide into organic field-effect transistors as conducting electrodes and as a metal modification layer. Appl. Phys. Lett. 2009, 95, 3–5. [Google Scholar] [CrossRef]
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282–286. [Google Scholar] [CrossRef]
- Xia, F.; Mueller, T.; Lin, Y.; Valdes-garcia, A. Ultrafast graphene photodetector. Nat. Nanotechnol. 2009, 4, 839–843. [Google Scholar] [CrossRef] [PubMed]
- Dasari, B.L.; Nouri, J.M.; Brabazon, D.; Naher, S. Graphene and derivatives – Synthesis techniques, properties and their energy applications. Energy 2017, 140, 766–778. [Google Scholar] [CrossRef]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.Z.; Koratkar, N. Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef] [PubMed]
- Sreenivasulu, B.; Ramji, B.R.; Nagaral, M. A Review on Graphene Reinforced Polymer Matrix Composites. Mater. Today Proc. 2018, 5, 2419–2428. [Google Scholar] [CrossRef]
- Liu, J.; Khan, U.; Coleman, J.; Fernandez, B.; Rodriguez, P.; Naher, S.; Brabazon, D. Graphene oxide and graphene nanosheet reinforced aluminium matrix composites: Powder synthesis and prepared composite characteristics. Mater. Des. 2016, 94, 87–94. [Google Scholar] [CrossRef]
- Li, G.; Xiong, B. Effects of graphene content on microstructures and tensile property of graphene-nanosheets/aluminum composites. J. Alloys Compd. 2017, 697, 31–36. [Google Scholar] [CrossRef]
- Rashad, M.; Pan, F.; Tang, A.; Asif, M. Effect of Graphene Nanoplatelets addition on mechanical properties of pure aluminum using a semi-powder method. Prog. Nat. Sci. Mater. Int. 2014, 24, 101–108. [Google Scholar] [CrossRef]
- Gürbüz, M.; Can Şenel, M.; Koç, E. The effect of sintering time, temperature, and graphene addition on the hardness and microstructure of aluminum composites. J. Compos. Mater. 2017, 52, 553–563. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z.; Fan, G.; Pan, H.; Chen, Z.; Zhang, D. Reinforcement with graphene nanosheets in aluminum matrix composites. Scr. Mater. 2012, 66, 594–597. [Google Scholar] [CrossRef]
- Dasari, B.L.; Morshed, M.; Nouri, J.M.; Brabazon, D.; Naher, S. Mechanical properties of graphene oxide reinforced aluminium matrix composites. Compos. Part B Eng. 2018, 145, 136–144. [Google Scholar] [CrossRef]
- Andreea, M.; Ţă, M.I.; Iovu, H. Molecular modeling of mechanical properties of the chitosan based graphene composites. UPB Sci. Bull. Ser. B Chem. Mater. Sci. 2014, 76, 3–8. [Google Scholar]
- Montazeri, a.; Rafii-Tabar, H. Multiscale modeling of graphene- and nanotube-based reinforced polymer nanocomposites. Phys. Lett. A 2011, 375, 4034–4040. [Google Scholar] [CrossRef]
- Chandra, Y.; Scarpa, F.; Chowdhury, R.; Adhikari, S.; Sienz, J. Multiscale hybrid atomistic-FE approach for the nonlinear tensile behaviour of graphene nanocomposites. Compos. Part A Appl. Sci. Manuf. 2013, 46, 147–153. [Google Scholar] [CrossRef]
- Spanos, K.N.; Georgantzinos, S.K.; Anifantis, N.K. Mechanical properties of graphene nanocomposites: A multiscale finite element prediction. Compos. Struct. 2015, 132, 536–544. [Google Scholar] [CrossRef]
- Papadopoulos, V.; Seventekidis, P.; Sotiropoulos, G. Stochastic multiscale modeling of graphene reinforced composites. Eng. Struct. 2017, 145, 176–189. [Google Scholar] [CrossRef]
- Giannopoulos, G.I. Elastic buckling and flexural rigidity of graphene nanoribbons by using a unique translational spring element per interatomic interaction. Comput. Mater. Sci. 2012, 53, 388–395. [Google Scholar] [CrossRef]
- Arroyo, M.; Belytschko, T. Finite crystal elasticity of carbon nanotubes based on the exponential Cauchy-Born rule. Phys. Rev. B 2004, 69, 1–11. [Google Scholar] [CrossRef]
- Li, C.; Chou, T. A structural mechanics approach for the analysis of carbon nanotubes. Int. J. Solids Struct. 2003, 40, 2487–2499. [Google Scholar] [CrossRef]
- Cao, G. Atomistic Studies of Mechanical Properties of Graphene. Polymers (Basel) 2014, 6, 2404–2432. [Google Scholar] [CrossRef]
- Goyenola, C.; Denis, P.A.; Mombrú, Á.W. Mechanical and Electronic Properties of Graphene Nanostructures. Phys. Appl. Graphene Theory 2011, 349–366. [Google Scholar]
- Baykasoglu, C.; Mugan, A. Dynamic analysis of single-layer graphene sheets. Comput. Mater. Sci. 2012, 55, 228–236. [Google Scholar] [CrossRef]
- Kim, H.S.; Hong, S.I.; Kim, S.J. On the rule of mixtures for predicting the mechanical properties of composites with homogeneously distributed soft and hard particles. J. Mater. Process. Technol. 2001, 112, 109–113. [Google Scholar] [CrossRef]
- Shin, S.E.; Choi, H.J.; Shin, J.H.; Bae, D.H. Strengthening behavior of few-layered graphene/aluminum composites. Carbon N. Y. 2015, 82, 143–151. [Google Scholar] [CrossRef]
- Dunand, D.C.; Mortensen, A. Reinforced silver chloride as a model material for the study of dislocations in metal matrix composites. Mater. Sci. Eng. A 1991, 144, 179–188. [Google Scholar] [CrossRef]
- Chawla, N.; Chawla, K.K. Microstructure-based modeling of the deformation behavior of particle reinforced metal matrix composites. J. Mater. Sci. 2006, 41, 913–925. [Google Scholar] [CrossRef]
- Li, Z.; Fan, G.; Tan, Z.; Guo, Q.; Xiong, D.; Su, Y.; Li, Z.; Zhang, D. Uniform dispersion of graphene oxide in aluminum powder by direct electrostatic adsorption for fabrication of graphene/aluminum composites. Nanotechnology 2014, 25, 325601. [Google Scholar] [CrossRef]
- Bartolucci, S.F.; Paras, J.; Rafiee, M.A.; Rafiee, J.; Lee, S.; Kapoor, D.; Koratkar, N. Graphene-aluminum nanocomposites. Mater. Sci. Eng. A 2011, 528, 7933–7937. [Google Scholar] [CrossRef]
- Tabandeh-Khorshid, M.; Omrani, E.; Menezes, P.L.; Rohatgi, P.K. Tribological performance of self-lubricating aluminum matrix nanocomposites: Role of graphene nanoplatelets. Eng. Sci. Technol. an Int. J. 2016, 19, 463–469. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.; Geng, L. Improving graphene distribution and mechanical properties of GNP/Al composites by cold drawing. Mater. Des. 2018, 144, 159–168. [Google Scholar] [CrossRef]
- Cho, J.; Luo, J.J.; Daniel, I.M. Mechanical characterization of graphite / epoxy nanocomposites by multi-scale analysis. Science 2007, 67, 2399–2407. [Google Scholar] [CrossRef]
- Giannopoulos, G.I.; Kallivokas, I.G. Mechanical properties of graphene based nanocomposites incorporating a hybrid interphase. Finite Elem. Anal. Des. 2014, 90, 31–40. [Google Scholar] [CrossRef]
- Li, Z.; Young, R.J.; Wilson, N.R.; Kinloch, I.A.; Vallés, C.; Li, Z. Effect of the orientation of graphene-based nanoplatelets upon the Young’s modulus of nanocomposites. Compos. Sci. Technol. 2016, 123, 125–133. [Google Scholar] [CrossRef]
- Liang, Q.; Yao, X.; Wang, W.; Liu, Y.; Wong, C.P. A Three-Dimensional Vertically Aligned Functionalized Multilayer Graphene Architecture-An Approach for Graphene-based Thermal Interfacial Materials. ACS Nano 2011, 5, 2392–2401. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).